A parameter-free variational coupling approach for trimmed isogeometric thin shells

Abstract

The non-symmetric variant of Nitsche’s method was recently applied successfully for variationally enforcing boundary and interface conditions in non-boundary-fitted discretizations. In contrast to its symmetric variant, it does not require stabilization terms and therefore does not depend on the appropriate estimation of stabilization parameters. In this paper, we further consolidate the non-symmetric Nitsche approach by establishing its application in isogeometric thin shell analysis, where variational coupling techniques are of particular interest for enforcing interface conditions along trimming curves. To this end, we extend its variational formulation within Kirchhoff–Love shell theory, combine it with the finite cell method, and apply the resulting framework to a range of representative shell problems based on trimmed NURBS surfaces. We demonstrate that the non-symmetric variant applied in this context is stable and can lead to the same accuracy in terms of displacements and stresses as its symmetric counterpart. Based on our numerical evidence, the non-symmetric Nitsche method is a viable parameter-free alternative to the symmetric variant in elastostatic shell analysis.

1 Introduction

The boundary representation paradigm (B-rep) [1, 2] constitutes the backbone of current computer-aided geometric design (CAD) tools. In B-rep, geometric shapes are described by boundary information and topological relations. Boundaries are represented in terms of two-parameter polynomial functions, such as non-uniform rational B-splines (NURBS) [3, 4]. The success of the B-rep concept in CAD is closely connected to the trimming paradigm, which significantly increases the flexibility of the method to represent complex arbitrary shapes in 3D [2]. A trimmed NURBS surface is defined by a set of trimming curves described in the parameter space of the NURBS surface. The trimming curves form outer and inner loops that define the topology of the trimmed surface based on their orientation. The parts of the surface that are “trimmed away” are not visualized by the CAD tool. The trimming concept is illustrated in Fig. 1 for a simple perforated surface.

More complex B-rep objects can be easily constructed by joining several trimmed NURBS surfaces along common trimming curves. It is important to note that trimming curves typically are only approximations of exact intersection curves, depending on a given tolerance. This leads to small gaps and overlaps between the space curves of two neighboring trimmed surfaces, so that NURBS-based B-Rep models are classified as not water-tight. For more details, we refer to the excellent summary and further references given in [5].

Fig. 1

The concept of a trimmed NURBS surface. a NURBS surface $\mathbf{r }(\xi _1,\xi _2)$ with trimming curve $C(\theta )$. b Surface and trimming curve in the parameter space $(\xi _1,\xi _2)$

Integrated design-through-analysis workflows for thin shell structures described by trimmed NURBS surfaces can be based on the combination of concepts from isogeometric analysis and embedded domain methods. In this context, we identify four key components [5,6,7,8,9]:

• 1. ability to query geometric information related to trimmed surfaces from CAD data structures,

• 2. efficient and accurate isogeometric shell technology,

• 3. quadrature methods for the integration of stiffness and residual forms in trimmed elements,

• 4. methods to enforce boundary and coupling conditions at non-matching trimming curves.

We note that there also exist methods for the isogeometric analysis of volumetric geometries defined by B-rep surfaces, e.g., based on embedded domain methods [10, 11] or boundary element methods [12, 13]. From a technology viewpoint, the latter three components of the above list profit from significant progress in both isogeometric analysis and embedded domain methods in recent years. On the isogeometric side, a variety of advanced formulations for isogeometric shell analysis on spline surfaces have been developed, e.g., based on solid shell theories [14, 15], Kirchhoff–Love [16] and Reissner–Mindlin theories [17,18,19], and hierarchic combinations thereof [20]. Isogeometric shells have been successfully applied for large-deformation analysis [21], in conjunction with various nonlinear material models [22, 23], and in contact and fluid-structure interaction problems [24,25,26,27]. On the embedded domain side, the importance of geometrically faithful quadrature of trimmed elements and corresponding techniques have been discussed in a series of recent papers [27,28,29,30,31,32,33,34,35]. For the weak enforcement of boundary and interface conditions at trimming curves and surfaces, variational methods such as Lagrange multiplier [36,37,38] or Nitsche techniques [39,40,41,42,43,44] have been successfully developed.

Focusing on the latter component, this paper explores the use of the non-symmetric Nitsche method for the parameter-free weak enforcement of boundary and interface conditions in the context of isogeometric shell analysis of trimmed NURBS surfaces. Symmetric variants of Nitsche methods are accurate and robust, but their performance crucially depends on appropriate estimates of the stabilization parameters involved [40, 44, 45]. If estimates are too large, the method degrades to a penalty method, which adversely influences consistency, accuracy and robustness. If they are too small, stability is lost. Moreover, accurate estimation techniques are often delicate from an algorithmic viewpoint [43, 44, 46]. Therefore, there has been an increasing interest in methods that can enforce boundary and interface conditions without mesh dependent stabilization parameters [38, 47,48,49].

Originally introduced in the context of discontinuous Galerkin methods by Baumann, Oden and coworkers [50,51,52,53], the non-symmetric form of Nitsche’s method is based on variationally consistent numerical flux conditions that are introduced in such a way that the criterion for stability is (weakly) satisfied. Therefore, it does not require the introduction of additional stabilization terms with associated parameters and, in contrast to the symmetric form of Nitsche’s method, its performance does not depend on the accuracy of the variational estimate or the reliability and robustness of associated numerical algorithms. On the other hand, the non-symmetric Nitsche method leads to unsymmetric system matrices and its numerical analysis framework does not cover optimal convergence rates of the $L^2$ error [54,55,56,57,58].

This paper extends recent work [59,60,61] that demonstrated the potential of the non-symmetric Nitsche method for parameter-free analysis in the context of non-matching and non-boundary-fitted discretizations. We provide numerical evidence that the non-symmetric Nitsche method is a viable alternative to symmetric variants of Nitsche’s method for elastostatic shell analysis, where the accuracy of derivative quantities such as bending moment resultants are of primary importance. The non-symmetric Nitsche method thus enables isogeometric shell analysis of trimmed NURBS surfaces without the burden of estimating appropriate element-wise stabilization parameters.

Our paper is structured as follows: Sect. 2 reviews the basic formulation of the symmetric and non-symmetric Nitsche methods for a Laplace model problem, including the element-wise estimation of stabilization parameters for the former. Section 3 provides a concise summary of the isogeometric Kirchhoff–Love shell formulation. In Sect. 4, we formulate the non-symmetric Nitsche method for weakly enforcing boundary and coupling conditions in thin Kirchhoff–Love shells. We also briefly review the finite cell method [62] as a tool for integrating trimmed shell elements. Section 5 presents a series of numerical experiments that corroborate the competitive performance of the parameter-free non-symmetric Nitsche method in comparison to the stabilized symmetric variant. We illustrate the effect of the missing symmetry on the (now complex) eigenvalue spectrum and the potential of increasing robustness by re-introducing moderate stabilization. Section 5 puts the numerical results into perspective and motivates future work.

2 The non-symmetric variant of Nitsche’s method for unfitted discretizations

To introduce the non-symmetric Nitsche method, we review its derivation for a Laplace problem in the context of unfitted meshes based on the presentation in [61], adopting the terminology of its original Discontinuous Galerkin formulation [50, 51]. We also compare the resulting parameter-free formulation with a symmetric form that is based on stabilization parameters [40, 44].

2.1 A Laplace model problem

We consider the following Laplace model problem

$$\begin{aligned} - \varDelta u = 0 \;\;\;\;\;\;&{\text {on}} \; \varOmega \end{aligned}$$

(1)

$$\begin{aligned} u = g \;\;\;\;\;\;&{\text {on}} \; \varGamma _D \end{aligned}$$

(2)

In addition to the Dirichlet boundary $\varGamma _D$, we assume an interface $\varGamma ^{\star }$ that divides the domain $\varOmega$ into two subdomains ${\mathcal {K}}_i$, $i=\{1,2\}$ (see Fig. 2 for an illustration). We assume that the boundary $\partial {\mathcal {K}}_i$ of each subdomain can be partitioned into sections with sufficient regularity. We define $u^+$ and $\varvec{n}^+$ as the value of the primary variable and the outward unit normal on $\partial {\mathcal {K}}_i$, and $u^-$ and $\varvec{n}^-$ as the value of the primary variable and the outward unit normal of the neighboring subdomain, if the boundary point belongs to $\varGamma ^{\star }$. We can then formulate for each subdomain ${\mathcal {K}}_i$ the following boundary and interface conditions

$$\begin{aligned} u^+ - g&= 0 \;\;\;\;\;\; {\text {on}} \; \partial {\mathcal {K}}_i \subset \varGamma _D \end{aligned}$$

(3)

$$\begin{aligned} u^+ - u^-&= 0 \;\;\;\;\;\; {\text {on}} \; \partial {\mathcal {K}}_i \subset \varGamma ^{\star } \end{aligned}$$

(4)

$$\begin{aligned} \nabla u^+ \cdot \varvec{n}^+ + \nabla u^- \cdot \varvec{n}^-&= 0 \;\;\;\;\;\; {\text {on}} \; \partial {\mathcal {K}}_i \subset \varGamma ^{\star } \end{aligned}$$

(5)

Focusing an a specific example, we consider a square domain $\varOmega \in \left[ 0 , 1 \right] ^2$, where we impose nonzero boundary conditions $u(x,0)=\sin (\pi x)$ and $u=0$ on all other boundaries. We obtain the analytical solution [40]

$$\begin{aligned} u_{ex}(x,y) =\left[ \cosh (\pi y) - \coth (\pi ) \sinh (\pi y) \right] \sin (\pi x) \end{aligned}$$

(6)

Fig. 2

Domain $\varOmega$ divided into two subdomains and discretized by unfitted meshes. The plus/minus signs on the normals refer to the left subdomain in green. (Color figure online)

2.2 Variational formulation

Following the unified framework in [55], we start the derivation of the variational form of Nitsche-type methods by rewriting the problem (1) as a first-order system

$$\begin{aligned} \sigma =\nabla u, \;\;\;\;\;\; - \nabla \cdot \sigma =0 \end{aligned}$$

(7)

Multiplying the first and second equations by suitable test functions $\tau$ and v, respectively, and performing integration by parts on each subdomain ${\mathcal {K}}$, we find

$$\begin{aligned} \int _{{\mathcal {K}}_i} \sigma \cdot \tau \; {\text {d}}\varOmega =&- \int _{{\mathcal {K}}_i} u \, \nabla \cdot \tau \; {\text {d}}\varOmega + \int _{\partial {\mathcal {K}}_i} u \, \varvec{n}^+ \cdot \tau \; {\text {d}}\varGamma \end{aligned}$$

(8)

$$\begin{aligned} \int _{{\mathcal {K}}_i} \sigma \cdot \nabla v \; {\text {d}}\varOmega =&\int _{\partial {\mathcal {K}}_i} \sigma \cdot \varvec{n}^+ \, v \; {\text {d}}\varGamma \end{aligned}$$

(9)

The solution space for u and $\sigma$ associated with each subdomain ${\mathcal {K}}_i$ is ${\mathcal {S}}=L^2({\mathcal {K}}_i)$, where $L^2$ is the space of square integrable functions. The test function space for v and $\tau$ associated with each subdomain ${\mathcal {K}}_i$ is ${\mathcal {V}}=H^1({\mathcal {K}}_i)$, where $H^1$ is the space of square integrable functions with square integrable first derivatives.

We then discretize (8) and (9) such that $u_h\in {\mathcal {S}}_h\subset {\mathcal {S}}$ and $\sigma _h\in {\mathcal {S}}_h\subset {\mathcal {S}}$, arriving at the flux formulation [55, 63]: Find $u_h$ and $\sigma _h$ such that for all ${\mathcal {K}}$ we have

$$\begin{aligned} \int _{{\mathcal {K}}_i} \sigma _h\cdot \tau \; {\text {d}}\varOmega&= - \int _{{\mathcal {K}}_i} u_h \,\nabla \cdot \tau \; {\text {d}}\varOmega + \int _{\partial {\mathcal {K}}_i}\widehat{u} \, \varvec{n}^+ \cdot \tau \; {\text {d}}\varGamma \end{aligned}$$

(10)

$$\begin{aligned} \int _{{\mathcal {K}}_i} \sigma _h \cdot \nabla v \; {\text {d}}\varOmega&= \int _{\partial {\mathcal {K}}_i} \widehat{\sigma }\cdot \varvec{n}^+ \, v \; {\text {d}}\varGamma \end{aligned}$$

(11)

where the numerical fluxes $\widehat{\sigma }$ and $\widehat{u}$ are approximations to $\sigma =\nabla u$ and to u, respectively, on the boundary $\partial {\mathcal {K}}_i$. Focusing on coupling conditions, we assume that definitions (10) and (11) are applied on meshes with finite elements that are conforming to the Dirichlet boundary $\varGamma _D$, but can be arbitrarily intersected by the embedded interface $\varGamma ^{\star }$.

In the next step, we design expressions in terms of $\sigma _h$ and $u_h$ for the numerical fluxes. To arrive at the non-symmetric Nitsche method, we choose

$$\begin{aligned} \widehat{u}&= \frac{3}{2} u_h^+ - \frac{1}{2} u_h^- \end{aligned}$$

(12)

$$\begin{aligned} \widehat{\sigma }&= \frac{1}{2} \left( \nabla u_h^+ + \nabla u_h^-\right) \end{aligned}$$

(13)

for boundaries $\partial {\mathcal {K}}_i\subset \varGamma ^{\star }$ on the interior interface.

The final form of the non-symmetric Nitsche method is the primal formulation of (10) and (11), which can be obtained by relating $\sigma _h$ and $\tau$ to $u_h$ and v. To this end, we first consider integration by parts

$$\begin{aligned}&- \int _{{\mathcal {K}}_i} u_h \, \nabla \cdot \tau \; {\text {d}}\varOmega \nonumber \\&\quad =\int _{{\mathcal {K}}_i} \nabla u_h \, = \cdot \tau \; {\text {d}}\varOmega - \int _{\partial {\mathcal {K}}_i} u_h \, \varvec{n}^+ \cdot \tau \; {\text {d}}\varGamma \end{aligned}$$

(14)

where we restrict $u_h\in {\mathcal {V}}_h\subset H^1({\mathcal {K}}_i)$. Inserting (14) and the flux approximation (12) into (10), and identifying $\tau = \nabla v$ yields the following expression

$$\begin{aligned}&\int _{{\mathcal {K}}_i} \sigma _h \cdot \nabla v \; {\text {d}}\varOmega = \int _{{\mathcal {K}}_i} \nabla u_h \, \cdot \nabla v \; {\text {d}}\varOmega \; \nonumber \\&\qquad +\int _{\partial {\mathcal {K}}_i \, \subset \, \varGamma ^{\star }} \frac{1}{2} \left( u_h^+ - u_h^-\right) \varvec{n}^+ \cdot \nabla v \; {\text {d}}\varGamma \end{aligned}$$

(15)

Inserting the flux approximation (13) into (11), relating the result to the left-hand side of (15) and summing over the two subdomains ${\mathcal {K}}_i$ yields the following primal formulation: Find $u_h$ such that $B(u_h,v) = l(v)$, with

$$\begin{aligned} B(u_h,v) =&\sum _i \int _{{\mathcal {K}}_i} \nabla u_h \, \cdot \nabla v \; {\text {d}}\varOmega \; \nonumber \\&+\int _{\varGamma ^{\star }} \llbracket u_h \rrbracket \{\nabla v\} {\text {d}}\varGamma \, - \, \int _{\varGamma ^{\star }} \{\nabla u_h\} \llbracket v \rrbracket \, {\text {d}}\varGamma \end{aligned}$$

(16)

where $l(v)=0$ in our example. For a compact notation, we use the jump operator for scalar quantities as

$$\begin{aligned} \llbracket u_h \rrbracket = u_h^+ \varvec{n}^+ + u_h^- \varvec{n}^- \end{aligned}$$

(17)

and the average operator for vector quantities as

$$\begin{aligned} \{\nabla u_h\} = \frac{1}{2} (\nabla u_h^+ + \nabla u_h^-) \end{aligned}$$

(18)

Fig. 3

Laplace model problem: unfitted meshes with embedded interface (red line) and solution field for $p=2$. (Color figure online)

We discretize the domain $\varOmega$ with two overlapping Cartesian meshes of different size. We use a straight line rotated by $\pi /8$ about the center point to trim away overlapping portions of the two meshes, creating an embedded interface. Figure 3 illustrates the trimmed mesh and the trimming curve. We use the recursive quadrature approach applied in the finite cell method [62] to evaluate the integrals in (16) over intersected elements. To ensure accuracy, we employ eight levels of quadrature sub-cells. More details on the finite cell method will be given in the context of trimmed shell elements in Sect. 4. To integrate over the immersed boundary, we divide the straight line into 1D sub-elements irrespective of the underlying Cartesian mesh. The corresponding solution field obtained with the non-symmetric Nitsche method (16) and quadratic B-splines is plotted in Fig. 3.

2.3 Comparison with the symmetric Nitsche method

We compare the non-symmetric Nitsche method given in (16) with a symmetric variant of Nitsche’s method recently introduced by Annavarapu et al. [42, 44, 46], designed for superior performance in interface problems. The method is based on a weighting of the consistency terms at embedded interfaces, which has been shown to improve the accuracy and robustness with respect to the classical Nitsche approach in the presence of cut elements. Its variational form reads as follows: Find $u_h$ such that $B(u_h,v)=l(v)$, with

$$\begin{aligned} B(u_h,v) =&{\sum _i\int _{{\mathcal {K}}_i}} \nabla u_h \, \cdot \nabla v \;{\text {d}}\varOmega \nonumber \\&-\int _{\varGamma ^{\star }} \llbracket u_h \rrbracket \cdot \left\langle \nabla v \right\rangle _\gamma \;{\text {d}}\varGamma \, - \int _{\varGamma ^{\star }} \left\langle \nabla u_h\right\rangle _\gamma \cdot \llbracket v \rrbracket \, {\text {d}}\varGamma \nonumber \\&+ \alpha \int _{\varGamma ^{\star }} \llbracket u_h \rrbracket \cdot \llbracket v \rrbracket \; {\text {d}}\varGamma \end{aligned}$$

(19)

and $l(v)=0$ for our example. The weighting operator across the interface is defined as

$$\begin{aligned} \left\langle \nabla u\right\rangle _\gamma = \gamma \nabla u^+ + (1-\gamma ) \nabla u^- \end{aligned}$$

(20)

We observe that in constrast to the non-symmetric form (16), the symmetric variant of Nitsche’s method includes an additional parameter $\alpha$, which ensure that (19) is coercive, that is, stable. For optimal performance of the method, $\alpha$ needs to be chosen as small as possible. Element-wise configuration dependent stabilization parameters can be estimated based on a local eigenvalue problem [7, 40, 43, 44]. The particular method (19) makes use of one-sided inequalities to establish estimates of local stabilization parameters. They can be computed from separate eigenvalue problems on each side of the interface that have the following form

$$\begin{aligned} \varvec{A} \varvec{x} = \lambda \varvec{B} \varvec{x}. \end{aligned}$$

(21)

An eigenvalue problem (21) is defined in each element with support at the interface. For the Laplace problem, the matrices in (21) are defined as

$$\begin{aligned} \left[ \varvec{A}\right] _{ij}&= \int _{\varGamma ^e} \left( \nabla N_i \cdot \varvec{n}^+ \right) \left( \nabla N_j \cdot \varvec{n}^+ \right) \, {\text {d}}\varGamma \end{aligned}$$

(22)

$$\begin{aligned} \left[ \varvec{B}\right] _{ij}&= \int _{\varOmega ^e} \nabla N_i \cdot \nabla N_j \; {\text {d}}\varOmega \end{aligned}$$

(23)

The contribution of the individual embedded mesh of each subdomain ${\mathcal {K}}_i$ to the discrete system can be computed and assembled separately.

Fig. 4

Element-wise maximum eigenvalues, computed separately on each side of the immersed interface from the local eigenvalue problem (21)

Following [44], we compute the stabilization parameter $\alpha$ and the weighting factor $\gamma ^+$ at each location of the interface as

$$\begin{aligned} \alpha =&\frac{1}{1/C^+ + 1/C^-} \end{aligned}$$

(24)

$$\begin{aligned} \gamma =&\frac{1/C^+}{1/C^+ + 1/C^-} \end{aligned}$$

(25)

where $C^+$ and $C^-$ are the element-wise maximum eigenvalues computed on the current and opposite side of the interface, respectively. Figure 4 shows the results of the eigenvalue computations on each side of the interface, illustrating that the size of the eigenvalues depends strongly on the size of the cut element. The weighted definition (24) of $\alpha$ prevents that a large eigenvalue on one side dominates the stabilization.

Fig. 5

Laplace model problem: distribution of the absolute error (amplified in all plots for better visibility). a Non-symmetric Nitsche. b Symmetric Nitsche with local stabilization

Fig. 6

Laplace model problem: convergence of the $L^2$ and $H^1$ errors with quadratic B-splines. a $L^2$ norm. b $H^1$ semi-norm

We compare the performance of the non-symmetric Nitsche method with the weighted variant of Nitsche’s method (19). Figure 5 plots the absolute error distribution on two trimmed Cartesian meshes of quadratic B-splines with $12\times 12$ and $23\times 23$ elements. The error of the solution field itself is larger for the non-symmetric Nitsche method than for the two symmetric variants of Nitsche’s method. This is due to the reduced level of accuracy of the non-symmetric Nitsche method in the $L^2$ norm. Figure 6a, b show the convergence of the $L^2$ and $H^1$ errors as the Cartesian mesh is uniformly refined. We observe that for the relative error in the $L^2$ norm, the error of the non-symmetric Nitsche method converges at the same optimal rate, but exhibits a larger error constant than the symmetric method. For the relative error in the $H^1$ semi-norm, however, the non-symmetric Nitsche method achieves to the same optimal accuracy as its symmetric counterpart.

This observation is the starting point for the present work. In shell analysis, the accuracy of the derivatives of the primal variable, i.e. the stress, is much more important than the accuracy of the primal variable itself, i.e. the displacement vector. Therefore, the optimal convergence in $H^1$ delivered by the non-symmetric Nitsche method is of primary importance, while its reduced $L^2$ accuracy is acceptable. We note that in the remainder of this work, we employ the relative error in strain energy to measure accuracy, whose convergence behavior is similar to the $H^1$ error. Computing the $H^1$ for complex shell structures is difficult, as exact solution fields are mostly unknown, while strain energy can be easily computed, and high-fidelity reference values for the strain energy are available in the literature for many benchmark examples.

Fig. 7

Shell geometry description in undeformed and deformed configurations

3 Isogeometric Kirchhoff–Love shells

In this section, we review a compact rotation-free Kirchhoff–Love shell formulation, based on the work of Kiendl et al. [16], whose discretization requires $C^1$ continuous basis functions. We note that this requirement is naturally satisfied in isogeometric analysis, where we use the same higher-order continuous spline basis functions to describe the geometry of CAD surfaces and the displacements of the shell formulation.

We use an upper case notation for quantities, which refer to the undeformed reference configuration, and a lower case notation for quantities, which refer to the current deformed configuration. Greek indices take values $\{1,2\}$ and Latin indices take values $\{1,2,3\}$.

3.1 Kirchhoff–Love shells

In the current configuration, the position ${\mathbf {x}}$ of a material point within the shell body is described by

$$\begin{aligned} {\mathbf {x}}(\xi _{1},\xi _{2},\xi _{3})= & {} {\mathbf {r}}(\xi _{1},\xi _{2}) +\xi _{3}t{\mathbf {a}}_{3}(\xi _{1},\xi _{2}). \end{aligned}$$

(26)

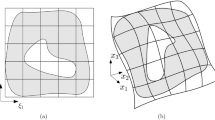
In this equation, ${\mathbf {r}}$ is the location vector of the shell mid-surface, $\xi _{i}$ are the curvilinear coordinates, where $\xi _{3}\in [-0.5,0.5]$, t is the shell thickness, and ${\mathbf {a}}_{3}$ is the normal director of the mid-surface (see Fig. 7 for details).

Based on the Kirchhoff–Love assumptions [64, 65], the 3D strain tensor ${\mathbf {E}}$ reduces to the in-plane strain components

$$\begin{aligned} {\mathbf {E}} = {\mathrm {E}}_{\alpha \beta } \,{\mathbf {G}}^{\alpha }\otimes {\mathbf {G}}^{\beta }. \end{aligned}$$

(27)

The covariant components ${\mathrm {E}}_{\alpha \beta }$ are represented as

$$\begin{aligned} {\mathrm {E}}_{\alpha \beta }= & {} \frac{1}{2}\,(g_{\alpha \beta }-G_{\alpha \beta }). \end{aligned}$$

(28)

Detailed descriptions of the covariant and contravariant basis can be found in [66]. The strain tensor (27) is further split into in-plane and out-of-plane contributions

$$\begin{aligned} {\mathrm {E}}_{\alpha \beta }= & {} \varepsilon _{\alpha \beta } + \xi _{3}\, t\,\kappa _{\alpha \beta }, \end{aligned}$$

(29)

with $\varepsilon _{\alpha \beta }$ and $(\xi _{3}\, t\, \kappa _{\alpha \beta })$ independently representing membrane and bending effects. Membrane and bending strains are defined as

$$\begin{aligned} \varepsilon _{\alpha \beta }= & {} \frac{1}{2}({\mathrm {a}}_{\alpha \beta }-{\mathrm {A}}_{\alpha \beta }), \end{aligned}$$

(30)

$$\begin{aligned} {\mathrm {a}}_{\alpha \beta }= & {} {\mathbf {a}}_{\alpha } \cdot {\mathbf {a}}_{\beta }, \end{aligned}$$

(31)

$$\begin{aligned} {\mathrm {A}}_{\alpha \beta }= & {} {\mathbf {A}}_{\alpha } \cdot {\mathbf {A}}_{\beta }, \end{aligned}$$

(32)

and

$$\begin{aligned} \kappa _{\alpha \beta }= & {} {\mathrm {B}}_{\alpha \beta }-{\mathrm {b}}_{\alpha \beta }, \end{aligned}$$

(33)

$$\begin{aligned} {\mathrm {b}}_{\alpha \beta }= & {} {\mathbf {a}}_{\alpha ,\beta } \cdot {\mathbf {a}}_{3}, \end{aligned}$$

(34)

$$\begin{aligned} {\mathrm {B}}_{\alpha \beta }= & {} {\mathbf {A}}_{\alpha ,\beta } \cdot {\mathbf {A}}_{3}, \end{aligned}$$

(35)

where $\kappa _{\alpha \beta }$ represents the curvature of the shell mid-surface, ${\mathbf {a}}_{\alpha }={\mathbf {r}}_{,\alpha }$, and ${\mathbf {a}}_{\alpha ,\beta } = {\mathbf {r}}_{,\alpha \beta }$.

The strain relations ${\mathrm {E}}_{\alpha \beta }$ are defined in the contravariant basis and a transformation to the local Cartesian coordinate system ${\mathbf {e}}_{\gamma }$ follows as

$$\begin{aligned} \bar{{\mathrm {E}}}_{\gamma \delta }= & {} {\mathrm {E}}_{\alpha \beta }({\mathbf {e}}_{\gamma }\cdot {\mathbf {G}}^{\alpha })({\mathbf {G}}^{\beta }\cdot {\mathbf {e}}_{\delta }), \end{aligned}$$

(36)

containing only in-plane strain components.

The relation between stresses and strains is established with the constitutive equations in Voigt notation

$$\begin{aligned} \begin{bmatrix} \bar{{\mathrm {S}}}^{11} \\ \bar{{\mathrm {S}}}^{22} \\ \bar{{\mathrm {S}}}^{12} \\ \end{bmatrix}= & {} \hat{{\mathbf {C}}}\; \begin{bmatrix} \bar{{\mathrm {E}}}_{11} \\ \bar{{\mathrm {E}}}_{22} \\ 2\,\bar{{\mathrm {E}}}_{12} \end{bmatrix}, \end{aligned}$$

(37)

where $\bar{S^{\alpha \beta }}$ denotes the stress tensor coefficients and $\hat{{\mathbf {C}}}$ is the reduced material matrix for plane stress problems [65]. Integration of the stress components over the shell thickness provides the force and moment stress resultants $\bar{{\mathbf {n}}}$ and $\bar{{\mathbf {m}}}$, written in Voigt notation as

$$\begin{aligned} \begin{bmatrix} \bar{n}^{11} \\ \bar{n}^{22} \\ \bar{n}^{12} \end{bmatrix}= & {} t\cdot \hat{{\mathbf {C}}}\; \begin{bmatrix} \bar{\varepsilon }_{11} \\ \bar{\varepsilon }_{22} \\ 2\,\bar{\varepsilon }_{12} \end{bmatrix}, \end{aligned}$$

(38)

and

$$\begin{aligned} \begin{bmatrix} \bar{m}^{11} \\ \bar{m}^{22} \\ \bar{m}^{12} \end{bmatrix}= & {} \frac{t^{3}}{12}\cdot \hat{{\mathbf {C}}}\; \begin{bmatrix} \bar{\kappa }_{11} \\ \bar{\kappa }_{22} \\ 2\,\bar{\kappa }_{12} \end{bmatrix}. \end{aligned}$$

(39)

3.2 Governing equations and discretization

Using the principle of virtual work, we obtain a variational form of equilibrium as

$$\begin{aligned} {\mathcal {W}}({\mathbf {u}},\delta {\mathbf {u}}) = {\mathcal {W}}_I({\mathbf {u}},\delta {\mathbf {u}})+{\mathcal {W}}_E({\mathbf {u}},\delta {\mathbf {u}}) = {\mathbf {0}}. \end{aligned}$$

(40)

The internal and external work integrals are defined as

$$\begin{aligned} {\mathcal {W}}_{I}({\mathbf {u}},\delta {\mathbf {u}})= & {} -\int _{\varOmega } ({\mathbf {n}}: \delta \varvec{\varepsilon } + {\mathbf {m}} : \delta \varvec{\kappa }) \ dA, \end{aligned}$$

(41)

$$\begin{aligned} {\mathcal {W}}_E({\mathbf {u}},\delta {\mathbf {u}})= & {} \int _{\varOmega } {\mathbf {p}} \cdot \delta {\mathbf {u}} \,dA + \int _{\varGamma _{t}}{\mathbf {t}}_{0} \cdot \delta {\mathbf {u}} \, dS, \end{aligned}$$

(42)

where dA and dS are differential elements of the mid-surface area and the boundary of the shell domain, respectively. The quantities $\delta {\mathbf {u}}$, $\delta \varvec{\varepsilon }$ and $\delta \varvec{\kappa }$ are the variations of displacements and strains. The vectors ${\mathbf {t}}_{0}$ and ${\mathbf {p}}$ denote the traction per unit length along the Neumann boundary $\varGamma _{t}$ and the domain load per unit area on the mid-surface, respectively.

The displacements of the mid-surface are discretized using spline basis functions $R_{i}$ as

$$\begin{aligned} {\mathbf {u}}= & {} \sum _{i}R_{i} \ {\mathbf {U}}_{i}, \end{aligned}$$

(43)

where ${\mathbf {U}}_{i}$ corresponding unknowns that can be interpreted as mid-surface control point displacements.

The first and second derivatives of the virtual work integrals with respect to the introduced unknown displacement components of (43) provide the residual forces and the shell stiffness, respectively. For linear elasticity, the stiffness matrix reads

$$\begin{aligned} {\mathbf {K}}= & {} \int _{\varOmega } \left( \frac{\partial {\mathbf {n}}}{\partial {\mathbf {U}}_{s}}: \frac{\partial \varvec{\varepsilon }}{\partial {\mathbf {U}}_{r}} + \frac{\partial {\mathbf {m}}}{\partial {\mathbf {U}}_{s}}: \frac{\partial \varvec{\kappa }}{\partial {\mathbf {U}}_{r}} \right) \, dA, \end{aligned}$$

(44)

For further details on how to compute geometric quantities such as differential elements and partial derivatives, we refer to [8, 67].

4 A non-symmetric Nitsche formulation for trimmed Kirchhoff–Love shells

In the following, we extend the non-symmetric variant of Nitsche’s method to weakly enforce constraints in the context of the variational rotation-free Kirchhoff–Love shell formulation. We first derive non-symmetric Nitsche formulations for displacement boundary conditions and coupling conditions and discuss aspects of their isogeometric discretization. We then illustrate a paradigm for parameter-free isogeometric analysis of trimmed CAD surfaces, based on weakly enforced coupling conditions via the non-symmetric Nitsche method and the finite cell method.

4.1 Weakly enforced boundary conditions

Dirichlet boundary conditions of the isogeometric Kirchhoff–Love shell comprise prescribed mid-surface displacements ${\mathbf {u}}_0$ and rotations ${\varvec{\Phi }}_0$ along corresponding Dirichlet boundaries $\varGamma _u$ and $\varGamma _{\theta }$. Following the notation introduced in Sect. 2.1 for the Laplace problem, they are expressed as

$$\begin{aligned}&{\mathbf {u}}^{+}-{\mathbf {u}}_{0} = {\mathbf {0}} \quad \, {\mathbf {x}} \in \varGamma _{u}, \end{aligned}$$

(45)

$$\begin{aligned}&{\varvec{\Phi }}^{+} - {\varvec{\Phi }}_{0} = {\mathbf {0}}\quad \, {\mathbf {x}}\in \varGamma _{\theta }, \end{aligned}$$

(46)

where ${\varvec{\Phi }}^{+}={\mathbf {a}}_{3}^{+}-{\mathbf {A}}_{3}^{+}$ denotes the angle between the deformed and the undeformed shell configuration. We note that the following holds: $\varGamma =\varGamma _u\cup \varGamma _{\theta }\cup \varGamma _t$ and $(\varGamma _u\cup \varGamma _{\theta })\cap \varGamma _t=\emptyset$, where $\varGamma$ is the complete domain boundary and $\varGamma _t$ is the Neumann boundary.

We now add a non-symmetric Nitsche extension to the variational formulation, such that

$$\begin{aligned} {\mathcal {W}}_E({\mathbf {u}},\delta {\mathbf {u}})+{\mathcal {W}}_I({\mathbf {u}},\delta {\mathbf {u}})-{\mathcal {W}}^{NIT}({\mathbf {u}},\delta {\mathbf {u}})= & {} {\mathbf {0}}. \end{aligned}$$

(47)

The term ${\mathcal {W}}^{NIT}({\mathbf {u}},\delta {\mathbf {u}})$ represents the work of the Nitsche extension. We can split this term into internal and external work components. For the internal component, we find

$$\begin{aligned} {\mathcal {W}}_{I}^{NIT}= & {} + \int _{\varGamma _{u}} \delta \left( N^{\alpha } + b^{\alpha }_{\gamma }M^{\gamma }\right) \cdot u_{(\alpha )}\,dS \nonumber \\&- \int _{\varGamma _{u}} \left( N^{\alpha } + b^{\alpha }_{\gamma }M^{\gamma }\right) \cdot \delta u_{(\alpha )} \,dS \nonumber \\&-\int _{\varGamma _{u}} \delta \left( Q + M_{(d),s}\right) \cdot u_{(3)} \,dS \nonumber \\&+\int _{\varGamma _{u}} \left( Q + M_{(d),s}\right) \cdot \delta u_{(3)} \,dS \nonumber \\&+\int _{\varGamma _{\theta }} \delta M_{(t)} \cdot \varPhi _{(d)} \,dS\nonumber \\&-\int _{\varGamma _{\theta }} M_{(t)} \cdot \delta \varPhi _{(d)}\,dS, \end{aligned}$$

(48)

and for the external component, we find

$$\begin{aligned} {\mathcal {W}}_{E}^{NIT}= & {} \int _{\varGamma _{u}} \delta \left( N^{\alpha } + b^{\alpha }_{\gamma }M^{\gamma }\right) \cdot u_{0(\alpha )} \,dS\nonumber \\&- \int _{\varGamma _{u}} \delta \left( Q + M_{(d),s}\right) \cdot u_{0(3)} \,dS\nonumber \\&+\int _{\varGamma _{\theta }} \delta M_{(t)} \cdot \varPhi _{0(d)} \,dS. \end{aligned}$$

(49)

Here, ${\mathbf {u}}_0=\{u_{0(\alpha )},u_{0(3)}\}$ and $\varPhi _{0(d)}$ represent the prescribed displacements and rotations along the Dirichlet boundary. The term $(\varPhi _{(d)} = \varvec{\varPhi }\cdot {\mathbf {d}})$ denotes the rotation along the normal direction of the boundary. The term $(N^{\alpha }+b^{\alpha }_{\gamma }M^{\gamma })$ is the effective membrane force, $(Q+M_{(d),s})$ the effective shear force, and $(M_{(t)})$ the bending moment in direction of the boundary normal ${\mathbf {d}}$. For details on their definition in the context of co- and contravariant bases, we refer for example to [8, 67].

4.2 Weakly enforced coupling constraints

Following the notation of Sect. 2.1 for the Laplace problem, the displacement continuity and force compatibility conditions for the shell formulation at the coupling interface $\varGamma ^{\star }$ are

$$\begin{aligned} {\mathbf {u}}^{+} - {\mathbf {u}}^{-}= & {} {\mathbf {0}}\quad {\text { on }} \varGamma ^{\star } \end{aligned}$$

(50)

$$\begin{aligned} \varvec{\sigma }^{+}\,{\mathbf {d}}^{+}+\varvec{\sigma }^{-}\,{\mathbf {d}}^{-}= & {} {\mathbf {0}} \quad {\text { on }} \varGamma ^{\star } \end{aligned}$$

(51)

where $(\varvec{\sigma }\,{\mathbf {d}})$ is the traction at the coupling interface.

The governing equations of the principal of virtual work (40) can be extended in the sense of (47) and the non-symmetric Nitsche coupling for the Kirchhoff–Love shell formulation follows as

$$\begin{aligned} {\mathcal {W}}^{NIT}= & {} + \int _{\varGamma ^{\star }} \delta \{N^{\alpha } + b^{\alpha }_{\gamma }M^{\gamma }\}\cdot \{u_{(\alpha )}\}\,dS \nonumber \\&- \int _{\varGamma ^{\star }} \{N^{\alpha } + b^{\alpha }_{\gamma }M^{\gamma }\}\cdot \delta \{u_{(\alpha )}\}\,dS \nonumber \\&-\int _{\varGamma ^{\star }} \delta \{Q + M_{(d),s}\}\cdot \{u_{(3)}\}\,dS \nonumber \\&+ \int _{\varGamma ^{\star }} \{Q + M_{(d),s}\}\cdot \delta \{u_{(3)}\}\,dS \nonumber \\&+\int _{\varGamma ^{\star }} \delta \{M_{(t)}\}\cdot \{\varPhi _{(d)}\}\,dS \nonumber \\&- \int _{\varGamma ^{\star }} \{M_{(t)}\}\cdot \delta \{\varPhi _{(d)}\}\,dS. \end{aligned}$$

(52)

The terms in brackets are defined as follows:

$$\begin{aligned} \{N^{\alpha }+b^{\alpha }_{\gamma }M^{\gamma }\}:= & {} \beta \, \left( N^{\alpha }+b^{\alpha }_{\gamma }M^{\gamma }\right) ^{+}\nonumber \\&+\, (1-\beta )\,\left( N^{\alpha }+b^{\alpha }_{\gamma }M^{\gamma }\right) ^{-} \end{aligned}$$

(53)

$$\begin{aligned} \{Q + M_{(d),s}\}:= & {} \beta \, \left( Q + M_{(d),s}\right) ^{+} \nonumber \\&+\, (1-\beta )\, \left( Q + M_{(d),s}\right) ^{-} \end{aligned}$$

(54)

$$\begin{aligned} \{M_{(t)}\}:= & {} \beta \, M_{(t)}^{+} + (1-\beta )\, M_{(t)}^{-} \end{aligned}$$

(55)

$$\begin{aligned} \{{\mathbf {u}}\}:= & {} {\mathbf {u}}^{+}-{\mathbf {u}}^{-} \end{aligned}$$

(56)

$$\begin{aligned} \{{\varvec{\Phi }}\}:= & {} \left( {\mathbf {a}}^{+}_{3} - {\mathbf {a}}^{-}_{3}\right) - \left( {\mathbf {A}}_{3}^{+}-{\mathbf {A}}_{3}^{-}\right) . \end{aligned}$$

(57)

In contrast to the weak formulation of boundary conditions above, the external work contribution is zero. In (53) to (55), $\beta$ controls the contribution of each of the two coupled domains, $\varOmega ^{(1)}$ and $\varOmega ^{(2)}$, to enforce the traction compatibility condition. In the extreme cases $\beta =\{0,1\}$, the condition is fully shifted to one of the domains, leaving the kinematic conditions (56) and (57) untouched. In this paper we choose $\beta =0.5$.

Looking at (48), (49) and (52), we observe that the pairs of the non-symmetric Nitsche terms of the Kirchhoff–Love shell have the same structure as the pair of terms in (16) for the Laplace model problem. In particular, each pair has terms with opposite signs. This leads to the property of weak stability [61], which enables the non-symmetric Nitsche method to be stable without the addition of extra stabilization terms.

4.3 Discretization aspects

When the complete variational formulation (47) is discretized (see Sect. 3.2), the internal work integrals (48) and (52) and the external work integral (49) lead to an algebraic system of the form

$$\begin{aligned} \left( K^{INT}_{rs} + K^{NIT}_{rs} - K^{NIT}_{sr}\right) \,u_r = f^{EXT}_{r} + f^{NIT}_{r}. \end{aligned}$$

(58)

The terms $(K^{INT}_{rs}\,u_r)$ and $f^{EXT}_{r}$ denote the internal elastic and external forces of the standard shell problem. The matrix $K^{NIT}_{rs}$, its transpose $K^{NIT}_{sr}$ and the vector $f^{NIT}_{r}$ refer to corresponding contributions of the non-symmetric Nitsche method, which maintain the total number of equations of the shell discretization, but perturb the symmetry properties of the stiffness matrix.

The matrix and vector coefficients of the discrete equations follow from the partial derivatives of Eqs. (48) and (49) with respect to the displacement degrees of freedom in analogy to (44). In particular, the discretized form $K^{NIT}_{rs}$ is computed as

$$\begin{aligned} K^{NIT}_{rs}= & {} \int _{\varGamma _{u}}\frac{\partial \left( N^{\alpha } + b^{\alpha }_{\gamma }M^{\gamma }\right) }{\partial {\mathbf {U}}_{r}}\cdot \frac{\partial u_{(\alpha )}}{\partial {\mathbf {U}}_{s}}\,dS \nonumber \\&- \int _{\varGamma _{u}} \frac{\partial \left( Q + M_{(d),s}\right) }{\partial {\mathbf {U}}_{r}}\cdot \frac{\partial u_{(3)}}{\partial {\mathbf {U}}_{s}}\,dS \nonumber \\&+ \int _{\varGamma _{\theta }} \frac{\partial M_{(t)}}{\partial {\mathbf {U}}_{r}}\cdot \frac{\partial \varPhi _{(d)}}{\partial {\mathbf {U}}_{s}}\,dS. \end{aligned}$$

(59)

The force vector contribution $f^{NIT}_{r}$ is computed as

$$\begin{aligned} f^{NIT}_{r}= & {} \int _{\varGamma _{u}} \frac{\partial \left( N^{\alpha }+ b^{\alpha }_{\gamma }M^{\gamma }\right) }{\partial {\mathbf {U}}_{r}}\cdot u_{0(\alpha )} \,dS \nonumber \\&-\int _{\varGamma _{u}} \frac{\partial \left( Q + M_{(d),s}\right) }{\partial {\mathbf {U}}_{r}}\cdot u_{0(3)} \,dS \nonumber \\&+\int _{\varGamma _{\theta }} \frac{\partial M_{(t)}}{\partial {\mathbf {U}}_{r}}\cdot \varPhi _{0(d)} \,dS, \end{aligned}$$

(60)

where the partial derivatives with respect to ${\mathbf {U}}_r$ follow from linearization at ${\mathbf {u}} = {\mathbf {0}}$:

$$\begin{aligned} \frac{\partial \left( N^{\alpha } + b^{\alpha }_{\gamma }M^{\gamma }\right) }{\partial {\mathbf {U}}_{r}}\bigg |_{{\mathbf {u}}=0}= & {} \left( n^{\beta \alpha }_{,r} + 2 b^{\alpha }_{\gamma } m^{\beta \gamma }_{,r} \right) d_{\beta } \end{aligned}$$

(61)

$$\begin{aligned} \frac{\partial M_{(d),s}}{\partial {\mathbf {U}}_{r}}\bigg |_{{\mathbf {u}}=0}= & {} \Big (\left( m^{\alpha \beta }\vert _{\gamma }\right) _{,r}\, d_{\alpha }\, t_{\beta } \nonumber \\&+\,m^{\alpha \beta }_{,r}\, d_{\alpha \vert \gamma }\, t_{\beta } \nonumber \\&+\,m^{\alpha \beta }_{,r}\, d_{\alpha }\, t_{\beta \vert \gamma }\Big )\,t^{\gamma } \end{aligned}$$

(62)

$$\begin{aligned} \frac{\partial Q}{\partial {\mathbf {U}}_{r}}\bigg |_{{\mathbf {u}}=0}= & {} \Big ((m^{\alpha \beta }_{,\alpha })_{,r} + \varGamma ^{\alpha }_{\lambda \alpha }m^{\lambda \beta }_{,r}\nonumber \\&+\,\varGamma ^{\beta }_{\lambda \alpha }m^{\alpha \lambda }_{,r} \Big ) d_{\beta } \end{aligned}$$

(63)

$$\begin{aligned} \frac{\partial M_{(t)}}{\partial {\mathbf {U}}_{r}}\bigg |_{{\mathbf {u}}=0}= & {} m^{\alpha \beta }_{,r} d_{\alpha } d_{\beta } \end{aligned}$$

(64)

The second term $K^{NIT}_{sr}$ is simply the transpose of (59). For details on taking derivatives and covariant derivatives of stress resultants $n^{\alpha \beta }$ and bending moments $m^{\alpha \beta }$, we refer, e.g., to [8, 67].

4.4 Derivatives of normals and tangents along trimming curves

In general, the trimming curves ${\mathcal {C}}(\theta )$ and the trimmed surface ${\mathbf {x}}(\xi _{1},\xi _{2})$ have independent parameterizations $(\theta )$ and $(\xi _{1},\xi _{2})$ for which, in general, no simple analytical relation can be found. As a consequence, special attention must be given to the derivatives of the normal $d_{\alpha }$ and tangent $t_{\alpha }$ along an interface or domain boundary.

The covariant derivatives of $d_{\alpha \vert \gamma }$ and $t_{\beta \vert \gamma }$ used in (62) can be expressed as

$$\begin{aligned} d_{\alpha \vert \gamma }= & {} d_{\alpha ,\gamma } - \varGamma _{\alpha \gamma }^{\lambda }d_{\lambda }, \end{aligned}$$

(65)

$$\begin{aligned} t_{\beta \vert \gamma }= & {} t_{\beta ,\gamma } - \varGamma _{\beta \gamma }^{\lambda }t_{\lambda }, \end{aligned}$$

(66)

where $d_{\lambda }$ and $t_{\lambda }$ can be computed based on the trimming curve ${\mathcal {C}}(\theta )$ and the base vectors of the underlying shell surface ${\mathbf {x}}(\xi ,\eta )$. The derivatives $d_{\alpha ,\gamma }$ and $t_{\beta ,\gamma }$ are

$$\begin{aligned} d_{\alpha ,\gamma }= & {} ({\mathbf {d}}\cdot {\mathbf {A}}_{\alpha })_{,\gamma } = {\mathbf {d}}_{,\gamma }\cdot {\mathbf {A}}_{\alpha } + {\mathbf {d}}\cdot {\mathbf {A}}_{\alpha ,\gamma },\end{aligned}$$

(67)

$$\begin{aligned} t_{\beta ,\gamma }= & {} ({\mathbf {t}}\cdot {\mathbf {A}}_{\beta })_{,\gamma } = {\mathbf {t}}_{,\gamma }\cdot {\mathbf {A}}_{\beta } + {\mathbf {t}}\cdot {\mathbf {A}}_{\beta ,\gamma }, \end{aligned}$$

(68)

with

$$\begin{aligned} \hat{{\mathbf {t}}}= & {} \left( \frac{\partial {\mathcal {C}}}{\partial \theta }\right) \end{aligned}$$

(69)

$$\begin{aligned} \hat{{\mathbf {t}}}_{,\gamma }= & {} \left( \frac{\partial {\mathcal {C}}}{\partial \theta }\right) _{,\gamma } = \frac{\partial ^{2} {\mathcal {C}}}{\partial \theta ^{2}} \, \frac{\partial \theta }{\partial \gamma } \end{aligned}$$

(70)

and

$$\begin{aligned} \frac{\partial \theta }{\partial \gamma }= & {} \frac{1}{\hat{{\mathbf {t}}}\cdot {\mathbf {A}}^{\gamma }}. \end{aligned}$$

(71)

The hat symbol indicates that the tangent and normal vectors used in (69)–(73) are no longer of unit length and require normalization to be used in (67) and (68). The normal vector along the trimmed boundary can be constructed as

$$\begin{aligned} \hat{{\mathbf {d}}}= & {} \hat{{\mathbf {t}}}\times {\mathbf {A}}_{3} = {\mathbf {A}}_{1}(\hat{{\mathbf {t}}}\cdot {\mathbf {A}}_{2})-{\mathbf {A}}_{2}(\hat{{\mathbf {t}}}\cdot {\mathbf {A}}_{1}), \end{aligned}$$

(72)

with the derivative

$$\begin{aligned} \hat{{\mathbf {d}}}_{,\gamma }= & {} {\mathbf {A}}_{1,\gamma }\left( \hat{{\mathbf {t}}}\cdot {\mathbf {A}}_{2}\right) -{\mathbf {A}}_{2,\gamma }\left( \hat{{\mathbf {t}}}\cdot {\mathbf {A}}_{1}\right) \nonumber \\&+ {\mathbf {A}}_{1}\left( \hat{{\mathbf {t}}}_{,\gamma }\cdot {\mathbf {A}}_{2}+\hat{{\mathbf {t}}}\cdot {\mathbf {A}}_{2,\gamma }\right) \nonumber \\&- {\mathbf {A}}_{2}\left( \hat{{\mathbf {t}}}_{,\gamma }\cdot {\mathbf {A}}_{1}+\hat{{\mathbf {t}}}\cdot {\mathbf {A}}_{1,\gamma }\right) . \end{aligned}$$

(73)

4.5 Integration in trimmed shell elements

The integrals of the Kirchhoff–Love shell formulation (41) and (42) as well as the integrals of the non-symmetric Nitsche extension (48), (49) and (52) are defined over the physical shell domain and corresponding boundaries and interfaces, which are parametrized in terms of trimmed surfaces and trimming curves (see Fig. 1). The evaluation of these integrals therefore requires numerical quadrature over trimmed shell elements and along trimming curves, for which we employ the finite cell method [62].

In the finite cell approach, the part of the geometric parametrization, which is trimmed away, is interpreted as a fictitious domain. In the fictitious domain, stresses and forces are penalized such that their contribution to the total strain energy becomes insignificant. This enables a smooth extension of the solution into the fictitious domain, so that the approximation of the solution in the physical domain is higher-order accurate and its gradients remain unaffected up to the geometric boundary [68]. The penalization approach is based on an indicator function $\alpha ({\mathbf {x}})=\{0,1\}$, which is one in the physical domain and zero in the fictitious domain. We note that maintaining a small factor $\alpha \ll 1$ in the fictitious domain can improve the conditioning of the discrete system, while not affecting the error at practical engineering accuracy levels.

The integral of an arbitrary function $f({\mathbf {x}})$ over a trimmed element domain can then be evaluated as

$$\begin{aligned} \int _{\varOmega _{cell}} f({\mathbf {x}})\,d\varOmega= & {} \int _{\varOmega _{fict}} \epsilon f({\mathbf {x}})\,d\varOmega \nonumber \\&+\sum _{sc}\Big (\int _{\varOmega _{phys_{sc}}}(\alpha -\epsilon )f({\mathbf {x}})\,d\varOmega \Big ) \end{aligned}$$

(74)

where $\epsilon$ denotes the value of $\alpha \ll 1$ in the fictitious domain for improving conditioning. To resolve the discontinuity in the indicator function along the trimming curve, the finite cell method employs a quad-tree based sub-cell integration scheme, which aggregates quadrature points around the trimming curve. Sub-cells and quadrature points for a trimmed shell element in the parameter space are illustrated in Fig. 8. Details on algorithms and data structures can be found for instance in [41].

Fig. 8

The finite cell method for a trimmed shell element: sub-cells aggregate quadrature points along the trimming curve in the parameter space

5 Numerical examples

In the following, we demonstrate the performance of the non-symmetric Nitsche approach with a number of examples, highlighting both advantages and aspects that we think need further attention. We also compare the results of the non-symmetric Nitsche method to those obtained with the symmetric Nitsche variant.

Fig. 9

Simply supported plate model

Fig. 10

Simply supported plate: convergence of conforming and non-conforming patch coupling. a Symmetric Nitsche method. b Non-symmetric Nitsche method

5.1 Simply supported plate

The first benchmark is a simply supported thin plate, which we use to assess the quality of the bending solution for a coupled non-matching discretization and its corresponding error distribution. The geometry of the plate, the material properties and the boundary conditions are shown in Fig. 9. We analyze an untrimmed matching configuration that consists of two conforming patches of $8\times 8$ elements, and an untrimmed non-matching configuration that consists of two patches of $8\times 8$ and $16\times 16$ elements. In both configurations, we apply the non-symmetric Nitsche method to impose boundary conditions at the outer boundaries and coupling conditions along a straight interface in the center of the plate (see Fig. 9). To asses the accuracy of the non-symmetric Nitsche method, we compare numerical solutions for a uniform pressure load $\bar{p}$ with the analytical solution given in [69].

Figure 10a, b shows the convergence of the strain energy error obtained with cubic, quartic and quintic polynomial basis B-spline functions and uniform refinement of both patches, when we use the symmetric and non-symmetric Nitsche method, respectively. We observe that the non-symmetric Nitsche method achieves rates that are close to optimal for $p=3$ and optimal for $p=4$ and 5, and error levels that are comparable with a single patch reference solution. In comparison to the symmetric Nitsche method and element-wise stabilization parameters, the non-symmetric Nitsche method generally achieves equivalent levels of accuracy, although some plotted points indicate a slightly reduced accuracy, in particular for $p=3.$ Figure 11 plots the bending moment of the non-conforming coupled model computed with the coarsest discretization and the corresponding error distribution over the plate domain. The solution plot confirms the high-fidelity accuracy level achieved at the coupling interface, being free of any jumps or oscillations in the solution. The error plot indicates that the error from the corner singularities of the plate problem are much more pronounced than the errors at the interface. A ‘hinge’-effect in terms of a kink as commonly observed for strong coupling schemes is completely absent. This indicates that the bending and in-plane shear-based flux are accurately transferred across the coupling interface.

We conclude that for pure bending problems and untrimmed configurations, the non-symmetric Nitsche method leads to accurate results that essentially are comparable to single patch solutions. We emphasize that the non-symmetric Nitsche method does not involve any stabilization terms and hence does not require any additional stabilization parameter.

Fig. 11

Simply supported plate: moment stress resultants $m_{11}$ over the deformed geometry and corresponding error plot

Fig. 12

Scordelis–Lo problem

Fig. 13

Scordelis–Lo problem: geometry, trimming data and mesh of two test configurations

Fig. 14

Scordelis–Lo shell: convergence of the vertical displacement at point A

Fig. 15

Scordelis–Lo shell: moment and force stress resultant $m_{11}$, $m_{12}$ and $q_{11}$, $q_{12}$, respectively

5.2 Scordelis–Lo shell

The barrel vault shown in Fig. 12 represents a thin shell with rigid end diaphragms under self-weight loading, which has become a widely used benchmark for thin shell formulations as part of the shell obstacle course [70]. Material properties and boundary conditions are also given in Fig. 12.

We discretize the shell by multiple trimmed NURBS patches with polynomial degree $p=4$ that need to be coupled along trimming curves. The three patches, their coarsest discretization, and corresponding trimming curves are shown in Fig. 13. We observe that the trimming curves lead to arbitrary cuts in the outer patches. To weakly enforce boundary and coupling conditions, we employ the symmetric and non-symmetric variants of Nitsche’s method. For the symmetric Nitsche method in the current problem, we derive element-wise stabilization parameters from a local eigenvalue problem of the form of (21) [7].

Figure 14 plots the convergence of the vertical displacement under uniform mesh refinement at mid-point A of one of the shell rims (the location is shown in Fig. 12). We observe that the results of the non-symmetric variant are slightly more accurate than the results of the symmetric method.

Figure 15 shows the moment and force stress resultants on the deformed configuration, obtained with the non-symmetric Nitsche method. We observe that the derivative based solution fields for $q_{ik}, i,k\in \{1,2\}$ are smooth and continuous across the coupling interfaces at the trimming curves. Comparison with single-patch solutions with comparable degrees of freedom indicate that the quality of the trimmed solution is equivalent.

Figure 16 plots the convergence in energy norm for both symmetric and non-symmetric Nitsche variants. We computed a reference strain energy¹ by extrapolating results of a uniform p-refinement [72]. It is well known that the convergence behavior of the symmetric Nitsche approach for this example is extremely sensitive to the stabilization parameter and requires local estimates close to the lower bound for optimal performance [8]. We observe that both methods achieve optimal rates of convergence. The parameter-free non-symmetric variant achieves a level of accuracy comparable to the symmetric method, however, without the need for fine-tuning stabilization parameters.

5.3 Hemispherical shell with a stiffener

The hemispherical thin shell with a volumetric stiffener [71], originally introduced in [73] and also known as the Girkmann problem, is a classical benchmark for the ability to couple thin shells and solid elements. Geometric details and material properties of the structure are given in Fig. 17. The shell is subject to gravity loading and a constant pressure acting on the shell and the stiffener. Due to the rotational symmetry, we consider only a quarter of the structure and apply symmetry boundary conditions. Furthermore, vertical displacements at the bottom face of the stiffener are constrained.

Fig. 16

Scordelis–Lo shell: convergence in energy norm for the non-symmetric and symmetric Nitsche methods

Fig. 17

Hemispherical shell with stiffener [71]

Fig. 18

Hemispherical shell: patch structure and discretization

Fig. 19

Hemispherical shell: total displacement on deformed structure ($\times 500$)

Fig. 20

Hemispherical shell: von Mises stress distribution (finer mesh, $p=4$)

Fig. 21

Hemispherical shell: convergence of the total displacements at point A and B (reference from [71])

We model the geometry of the stiffener and the lower part of the shell with two trivariate NURBS patches that transfer into isogeometric solid elements. The central and upper parts of the hemispherical shell are modeled with a bivariate NURBS surface that transfers into isogeometric thin shell elements. Figure 18 illustrates the patch structure of both volumetric and surface parts. All three patches are connected in a weak sense with the non-symmetric Nitsche method. For coupling solid and thin shell elements, we consider all shear components of the three-dimensional stress state to ensure consistency in the coupling formulation. For further details, we refer to [8].

We consider the original NURBS model with $8\times 8$ thin shell elements and a finer model with 8 elements along the $\xi _1$ and 16 along $\xi _2$ directions (see Fig. 18). We perform stress analysis for both models, successively increasing the polynomial degree from $p=3$ to $p=6$. Figure 19 plots the total displacement field $|{\mathbf {u}}|$, plotted on the deformed configuration of the structure for the finer discretization at polynomial degree $p=4$. It shows a smooth transition from the solid to the thin shell model without jumps or oscillations. Figure 20 plots the corresponding von Mises stress distribution in the volumetric part of the structure that is discretized with solid elements.

At the re-entrant corner, where the stress singularity is located, we observe a small jump in the stress between the beam-like stiffener and the lower hemispherical shell part. The high fidelity of the solution fields at a very coarse mesh size is further confirmed in Fig. 21, which plots the convergence of the total displacements at locations A and B. We observe rapid convergence towards the reference values given in [71].

Fig. 22

Model description of the intersecting tubular shell structure. a Geometry, b patch-interface structure, c connector detail

5.4 Intersecting tubes

To illustrate the robustness of the non-symmetric Nitsche method for the analysis of complex trimmed structures, we consider two intersecting tubes, which represent a generic connector configuration, e.g., in pipe networks or large steel trusses. Figure 22 illustrates the CAD geometry designed in the freeform modeler Rhino 3D [74], the corresponding NURBS patch structure, and trimming procedure. Due to the symmetry of the structure, only one half of the structure is modeled. The connection of the two perpendicular tubes is designed with a NURBS curve swept along the interfaces. Patch 1 is discretized with $62\times 40$ elements, patch 2 with $38\times 28$ elements and patch 3 with $24\times 16$ elements, all with a polynomial degree $p=4$.

We perform stress analysis for an inner pressure loading of 1.0MPa, where we use isogeometric thin shell elements, the finite cell method for mitigating trimmed regions, and the non-symmetric Nitsche method for enforcing symmetry boundary conditions and interface coupling constraints. We emphasize again that the non-symmetric Nitsche method is completely parameter-free. Details on material parameters and boundary conditions are also given in Fig. 22. The total displacements plotted on the deformed structure and the von Mises stresses plotted around the connector and the connecting interfaces are shown in Figs. 23 and 24, respectively. We note that we replaced the stress components missing in the thin shell formulation with corresponding force stress resultants. Both plots illustrate that the non-symmetric Nitsche method leads to smooth solution fields without jumps or oscillations. This indicates the high fidelity of the stress solution near the trimmed region and directly at the trimming interface. We observe an equivalent accuracy level for the moment stress resultants, presented in Fig. 25.

We compare the performance of the non-symmetric Nitsche method to the standard symmetric Nitsche approach that requires stabilization and the estimation of element-wise parameters. To this end, Figure 26a, b plot the normal force flux and moment flux directly at the interface that connects patches 1 and 2. We observe that both methods lead to nearly identical results. This confirms the excellent performance of the parameter-free non-symmetric method for coupling complex trimmed shell structures, despite the absence of stabilization.

5.5 Spectrum analysis and complex eigenmodes

In the next step, we study the influence of the non-symmetric Nitsche method on the eigenmode spectrum of a shell configuration with trimming and weakly enforced interface constraints. To this end, we consider the stiffened cylindrical panel shown in Fig. 27.

Fig. 23

Intersectiong tubes: total displacements plotted on the deformed structure

Fig. 24

Intersectiong tubes: von Mises stress distribution close to the coupling interfaces

The face sheet and each of the two beam-like stiffeners are modeled with single NURBS patches that are coupled in a weak sense with the non-symmetric Nitsche method. The panel also features a trimmed cut-out, which is mitigated by the finite cell method as described in Sect. 4.5. Figure 27 shows all geometric parameters, the patch structure and material properties. The face sheet of the panel is discretized with $22\times 33$ thin shell elements of polynomial degree $p=4$. The stiffeners are discretized with solid elements, which are constructed in a tensor-product sense by $16\times 2$ in-plane elements of degree $p=4$ and a single element of cubic degree through the thickness.

The spectrum of the panel is computed as the solution of a generalized algebraic eigenvalue problem [75] of the form

$$\begin{aligned} {\mathbf {K}}\,\phi _i= & {} \omega _{i}^2\,{\mathbf {M}}\,\phi _i \quad i=1,\ldots ,N \end{aligned}$$

(75)

where ${\mathbf {K}}$ is the stiffness matrix (58) and ${\mathbf {M}}$ is the consistent mass matrix [75]. N is the total number of degrees of freedom, which limits the mode index i. Equation (75) can be interpreted as a free vibration problem, where $\omega _i [s^{-1}]$ represents the ith eigenfrequency and $\phi _i$ the corresponding eigenmode. The matrix ${\mathbf {M}}$ is in general real, symmetric and semi-definite. The symmetric Nitsche method with stabilization preserves these properties [55]. For the non-symmetric method, the stiffness matrix ${\mathbf {K}}$ is real, but non-symmetric, and therefore complex eigenvalues must be expected [76].

Fig. 25

Intersectiong tubes: moment stress resultants in the interface region

We compute the discrete spectrum of the panel, using the non-symmetric Nitsche method. The resulting spectrum reproduces exactly six zero eigenvalues, which indicates that the non-symmetric Nitsche method leads to rank sufficient stiffness matrices. We compare the discrete spectra computed with the symmetric and non-symmetric variants of Nitsche’s method, with specific attention to the pattern of complex eigenvalues in the latter. To this end, we first sort both spectra in ascending order and discard the imaginary part of all eigenvalues computed with the non-symmetric method. We then compute the absolute difference between each eigenvalue pair and normalize the result with the corresponding eigenvalue of the symmetric method. Figure 28a, b plot the normalized difference for each eigenvalue pair over the complete spectrum and for the first 10% of the eigenmodes, respectively. In addition, eigenvalues computed with the non-symmetric Nitsche method that had an imaginary part are highlighted by blue dots. Figure 29 illustrates the size of their imaginary part by plotting the ratio with respect to the real part for each complex eigenvalue.

Fig. 26

Intersecting tubes: comparison between non-symmetric and symmetric results for flux quantities plotted directly at the coupling interface. a Normal force flux, b normal moment flux

We observe that the first 10% of the spectrum yields relative differences below 10% of the eigenvalue size and is free of complex eigenvalues. The accuracy of a discretized elastostatic boundary value problem predominantly depends on the accuracy of the lowest eigenvalues, which can be shown by a spectral representation of the solution coefficients [77]. Therefore, this observation supports the high fidelity results and excellent numerical properties of the non-symmetric Nitsche method that we have seen in the previous elastostatic benchmarks. This is further confirmed by comparing corresponding eigenmodes computed with the symmetric and the non-symmetric variant of Nitsche’s method, some of which are plotted in Fig. 30. Complex eigenvalues exhibit imaginary parts whose absolute values are several orders of magnitude smaller than the real part, except for a few eigenvalues whose imaginary part is of the same order than the real part. They do not appear in the first 15% of the eigenvalues, but frequently occur in the remainder of the spectrum.

Fig. 27

Stiffened cylinder panel: geometry, patches and discretization

Fig. 28

Stiffened cylinder panel: relative difference between frequency pairs computed with the non-symmetric and symmetric Nitsche methods. Blue dots represent complex eigenvalues of the non-symmetric method. a Complete spectrum b Lowest eigenvalues (10 % of the spectrum). (Color figure online)

5.6 Robustness and additional stabilization

In the context of the non-symmetric interior penalty discontinous Galerkin method [55, 57], penalty-free non-symmetric Nitsche formulations have been reported to lead to oscillations near interfaces [78]. One way to effectively reduce these oscillations is to introduce a stabilization term, that has the same form as in the symmetric Nitsche method. For the Kirchhoff–Love shell formulation, this leads to two stabilization terms that are formulated in terms of displacements of the mid surface ${\mathbf {u}}$ and the interface normal vector ${\mathbf {d}}$

Fig. 29

Stiffened cylindrical panel: size of imaginary parts versus size of real part for each complex eigenvalue

$$\begin{aligned} {\mathcal {W}}^{NIT,st}= & {} \int _{\varGamma _{\star }} \tau _S\, t\;\delta \{{\mathbf {u}}\}\cdot \{{\mathbf {u}}\}\,dS \nonumber \\&+ \int _{\varGamma _{\star }} \tau _S \,\frac{t^{3}}{12}\; \delta \{{\varvec{\Phi }}\}\cdot \{{\varvec{\Phi }}\}\,dS \nonumber \\&+ \int _{\varGamma _{\star }} \tau _N\,t\,\big ({\mathbf {d}}\cdot \delta \{{\mathbf {u}}\}\big ) \big (\{{\mathbf {u}}\}\cdot {\mathbf {d}}\big )\,dS \nonumber \\&+ \int _{\varGamma _{\star }} \tau _N\, \frac{t^{3}}{12}\,\big ({\mathbf {d}}\cdot \delta \{{\varvec{\Phi }}\}\big )\big (\{{\varvec{\Phi }}\}\cdot {\mathbf {d}}\big )\,dS. \end{aligned}$$

(76)

All quantities are defined as in Sects. 2, 3 and 4. In particular, the average operator for vector quantities is defined in (18), t denotes the shell thickness, and the terms in brackets correspond to definitions (53) to (57). We note that the stabilization terms of equation (76) refer to the global Cartesian basis.

Fig. 30

Stiffened cylindrical panel: eigenmodes at different frequencies. The left and right part of the (anti-)symmetric modes represents the symmetric and non-symmetric result, respectively

For optimal convergence, the size of the stabilization parameters $\tau _S$ and $\tau _N$ is proportional to the material properties, here the Lamé constants $\lambda$ and $\nu$, inversely proportional to the characteristic element width h, and dependent on constants $C_S$ and $C_N$, influenced by the polynomial degree p [79, 80]:

$$\begin{aligned} \tau _{S}= & {} C_S(p)\,\frac{\nu }{h}, \end{aligned}$$

(77)

$$\begin{aligned} \tau _{N}= & {} C_N(p)\,\frac{\lambda }{h}. \end{aligned}$$

(78)

Values of $C_S$ and $C_N$ can be estimated from the largest eigenvalue of an eigenvalue problem of the form (21).

We construct a simple example to examine the possible impact of missing stabilization on the solution accuracy close to the interface. To this end, we consider the cantilevered plate shown in Fig. 31, with a line load at the cantilever tip. The plate is discretized by two B-spline patches, which consists of $8\times 8$ and $16\times 16$ elements. The two patches are coupled weakly with the non-symmetric Nitsche method, where we add the stabilization terms (76).

Figure 32 plots the bending moment computed with the non-symmetric Nitsche method at different values $C=C_S=C_N$, which determines the level of stabilization via relations (77). We observe that the parameter-free variant leads to local oscillations at the coupling interface, which can be mitigated by increasing the level of stabilization. At a moderate parameter of $C=100.0$, the moment solution is completely free of oscillations.

We emphasize that for any of the more complex examples we computed, we have not encountered a degradation in local accuracy (e.g., in the form of oscillations) when applying the non-symmetric Nitsche method without stabilization. Figure 33 plots moment resultants for different stabilization levels along the dashed blue line shown in Fig. 31. We observe that oscillations in the parameter-free moment solution are small (within 10% of the absolute value at the interface) and limited to the immediate near-interface region.

Fig. 31

Cantilevered plate: geometry, material properties, boundary conditions

Fig. 32

Cantilevered plate: bending moment computed with the non-symmetric Nitsche method and different levels of stabilization, applied in the sense of the non-symmetric interior penalty discontinuous Galerkin method [55]

6 Summary, conclusions and outlook

In this paper, we explored the use of the non-symmetric Nitsche method for weakly imposing boundary and interface conditions in isogeometric shell analysis of trimmed NURBS surfaces. In this context, the non-symmetric Nitsche method is attractive, because it is parameter-free and does not require the estimation of appropriate stabilization parameters.

We first introduced the non-symmetric Nitsche method on unfitted meshes for a simple Laplace model problem and reviewed the isogeometric Kirchhoff–Love formulation for thin rotation-free shells. We then extended the non-symmetric Nitsche formulation to the Kirchhoff–Love shell setting and integrated the results into a framework for the analysis of trimmed surfaces based on the finite cell method.

Fig. 33

Cantilevered plate: bending moment plotted along dashed blue line shown in Fig. 31. (Color figure online)

We demonstrated the excellent performance of this framework for a series of numerical experiments. The examples include the classical Scordelis–Lo shell, the hemispherical shell with a stiffener and a generic connector based on intersecting tubes. Our results confirm that the non-symmetric Nitsche method is stable, achieves good accuracy and convergence in the strain energy error, and does not show any spurious stress oscillations for any of the complex examples examined. This is in agreement with a series of recent studies that employed the non-symmetric Nitsche method in different analysis scenarios [59,60,61, 81,82,83]. For example, Burman noted in [59] that he has “not managed to construct an example exhibiting the suboptimal convergence order” when enforcing boundary conditions on fitted meshes with the non-symmetric Nitsche method. For elastostatic shell analysis, where the accuracy of the derivatives of the primal variable, i.e. the stress, is much more important than the accuracy of the primal variable itself, i.e. the displacement vector, its reduced displacement accuracy is acceptable from an engineering point of view.

On the other hand, we also illustrated the distribution of complex eigenvalues in the spectrum. They occur due to the missing symmetry of the stiffness matrix, which is perturbed due to contributions of the non-symmetric Nitsche method. Complex eigenvalues occur only in the higher modes, and therefore do not have an impact on the accuracy and numerical properties of elastostatic shell analysis. However, their impact on explicit dynamics shell calculations, important for crash dynamics and metal forming, is unclear at this point and remains to be explored in the future.

In addition, we were able to find one example, a simple cantilever plate with a manufactured interface in the center, where the absence of stabilization parameters in the non-symmetric Nitsche method had an effect on the solution accuracy in the direct vicinity of the interface. In line with [78], we could remove all oscillations by re-introducing moderate stabilization. Although we did not see similar oscillations in any other example we computed, the potential of increasing robustness by moderate stabilization should be further examined in the future. In this context, it is of particular interest whether associated optimal stabilization parameters are smaller than the ones required by the symmetric Nitsche method. This could be important for unfitted discretizations, where stabilization parameters are very sensitive to cut elements, with significant impact on local accuracy and stability. This sensitivity is alleviated by smaller stabilization parameters, leading to better accuracy at the interface.

In summary, we think that the parameter-free non-symmetric Nitsche method constitutes a viable alternative to symmetric variants of Nitsche’s method, enabling isogeometric shell analysis of trimmed NURBS surfaces without the burden of estimating appropriate element-wise stabilization parameters. The complex eigenspectrum and the potential loss of stress accuracy close to the trimming interface are aspects that warrant further study.