2D numerical model for studying frictional sliding

Abstract

The onset of frictional motion couples complex spatiotemporal dynamics of discrete contacts with different orders of magnitude at time and length scales. In order to reveal how these individual scales affect the frictional sliding, we establish a 2D multiscale spring-block model for the frictional sliding at an elastic slider-rigid interface. In this model, the rupture of frictional interface is described by three different types of locally microscopic motion: pinned, sliding and dislocated states. By using realistic boundary conditions, our numerical results can precisely reproduce the loading curves found in previous experiments. The precursor events, corresponding to a discrete sequence of rapid crack-like fronts propagating partially in the contact zone, can also be shown in our simulation. From the analysis of the microscopic motion, we characterize the evolution of the real contact area and the corresponding interface motion at the mesoscale level, and show that the evolution corresponds to four distinct and inter-related phases: detachment, fast and slow slip motion, as well as the rest of slip. These mesoscale behaviors are completely consistent with the existing experimental results and their physical mechanisms can be explained by the detailed information of the numerical simulation. The study is established on a bottom-up multiscale model which provides a comprehensive picture about the complex spatiotemporal dynamics of frictional sliding.

1 Introduction

Since the seminal work of Bowden and Tabor [1], it has been recognized that the relative motion of two contacting bodies under applied shear forces is controlled by the discrete contacts that make up their interface. Based on this knowledge, many studies have been performed for bridging the gap between the microscopic interactions that define local frictional resistance and the macroscopic motions that appear in large blocks [2, 3]. Among them, the onset of frictional sliding is central to understanding the physical mechanisms involved in tribology [4,5,6,7,8,9], mechanics of fracture [10, 11], and earthquake dynamics [12,13,14].

The onset of sliding is related to the failure of the ensemble of discrete contacts at the interface. Detailed measurements in recent experiments have revealed that the rupture process is mediated by the propagation of crack-like microscopic fronts (rupture fronts) [2, 7, 15]. These rupture fronts arrest before the overall sliding of the interface is initialized [16, 17], and the length and number of these precursors significantly depend on the spatial stress distribution at the interface [7]. Whereas the average motion of large, slowly sliding bodies is well-described by empirical friction law, interface overall strength is a dynamic entity that should be determined by both the real contact area and the contacts’ shear strength. Recent experiments have examined how the real contact areas evolve with the corresponding interface motion, and found that the local motion experiences fast slip as well as slow slip over different characteristic timescales [15].

Theoretically, these experimental observations can be studied using various combined models with elastodynamic descriptions (bulk models) for contacting bodies and friction laws characterizing the local shear strength at the interface. The bulk models play a role of relating the macroscopic loading conditions to the stress field along the contact interface at a mesoscopic scale level. This scale level requires discretization of the macroscopic interface treated with a 1D [18, 19] or 2D model [20,21,22,23,24]. The simplest bulk model is probably the 1D spring-block model, which has been popular in the friction [18] and earthquake [25]. In this model, the total mass of the slider is distributed among a linear chain of blocks that interact with their neighbors. The main limitation of 1D models is that it is unable to accurately reproduce realistic stress distribution at the interface. In order to reproduce the heterogeneous stress distribution at the interface easily, the 2D spring-block model is often used to discretize the linear elastic contact body [20].

Due to the complexity of the microscopic mechanisms in the contact shear strength, some simple friction laws, such as Amonton$-$Coulomb (A–C) description with slip-weakening or velocity-weakening [26, 27], rate-and-state friction laws [22, 28,29,30], are often used to describe the friction strength at the level of a mesoscopic region or an individual micro-contact. While each of these friction laws could reproduce some aspects of the experimental phenomenon exhibited in the onset of friction sliding, they, by their nature, cannot explain how the individual contacts evolve and interact to produce the overall friction behavior.

Recently, Trømborg et al. [20] developed a novel model for studying the spatiotemporal features of the rupture dynamics observed in the experiments [16]. In this model, the elastic slider is represented by a 2D spring-block model consisting of lattice and springs connecting them. The multi-contact nature of the interface is modeled through an array of tangential springs attached in parallel to each interface block. The individual spring behavior is characterized as two motion states, pinned state and sliding state. A pinned spring stretches linearly elastically as the block moves, while a sliding spring takes a tangential force proportional to the normal force on the corresponding block. In addition, the sliding spring is modeled with a characteristic timescale controlling the relaxation of sliding micro-junctions. Namely, after a random time interval, the sliding spring is replaced immediately by a pinned, unloaded spring representing a new junction formed elsewhere and a new cycle starts. The simulation based on the model can successfully reproduce the short-time slip dynamics, and can spontaneously produce both slow and fast rupture fronts and the transitions between them.

Despite the remarkable success of the model in reproducing many features of friction dynamics, there are still ambiguities in the interpretation of some experimental phenomena. From Trømborg’s model, it can be seen that the slow slip is due to the micro-contacts being in pinned state, while the fast slip is due to the micro-contacts being in sliding state. Correspondingly, the local contact area in the slow slip phase would be different from that in the fast slip phase. Nevertheless, the experimental measurements shew that the local contact area remains almost constant during the fast and slow slip phases [15, 16]. Trømborg’s model assumes that the number of micro-contacts per block remains unchanged, while its stiffness varies with pressure. This assumption seems to be consistent with the case where the interface is in an elastic regime. In addition, Trømborg’s model only introduces a single time scale controlling the fast dynamics. Experimentally, there are two characteristic time scales [15]: one is the short scale of the fast slip phase controlled by the fast dynamics, and the other is the relative large time scale of the slow slip phase that controls the slow sliding motion of the block. Researchers from Fineberg’s group explained that the local motion of the slow slip may be analogous to large-scale frictional motion governed by the contact dynamics of “rigid” micro-contacts [15, 31]. Also, the slow slip events widely studied in earthquake community corresponds to a phenomenon that a relative large displacement exists on the interface [32, 33]. We therefore surmise that the slow slip motion may be related to the dislocation of interlocking micro-contacts.

In order to better understand the existing experimental phenomena, we develop a novel asperity model that describes the individual spring behavior as three distinct motion states: pinned, sliding and dislocated. Compared to the Trømborg’s micro-contact model, a dislocated state is added, and two time scales are introduced: one for the sliding state, and the other for the dislocated state. Furthermore, we specify that the number of the tangential springs per block is not a constant, but depends on the block pressure. The model is applied to numerically study the experiments of Maegawa et al. [7], and found that the model could reproduce the experimental loading curve fairly well. We also use this multi-scale model to investigate how the non-uniform normal loading affects the propagation of precursor events. In addition, how the real contact area and the corresponding interface motion evolve from extremely short to large time scales will be discussed in detail.

The paper is organized as follows. The numerical model is introduced in Sect. 2, where the description for the friction law of an individual asperity and the law for the deformation of the bulk material is given in detail. In Sect. 3, we perform numerical investigation for the experiments done by Maegawa et al. [7]. Comparison between the numerical and experimental results for the loading curves are given. How the properties of the precursor events are affected by the non-uniform normal loading will be discussed in this section. In Sect. 4, a detailed analysis is performed for the evolution of local real contact area and the corresponding interface motion. The physical mechanisms in connection with the fast and slow slip motion are exposed based on the numerical simulation. A conclusion is drawn in Sect. 5.

2 Model description

In this section, we first present an elastodynamic description for the contacting bodies, then propose an asperity model to characterize the microscale junction dynamics. In order to describe the heterogeneous stress field induced by the macroscopic loading conditions, a 2D spring-block model is established to discretize the elastic contact body [34]. The normal interaction of the micro-contacts at the interface is modeled using the method proposed by Bowden and Tabor [1]. The tangential interaction of the micro-contacts is based on a novel asperity model in which the micro-contact experiences three distinct states: pinned, sliding and dislocated states.

2.1 Elastodynamic descriptions of contacting body

We study the onset of frictional sliding that appears in a system shown in Fig. 1, where the frictional interface is formed between two polymethyl methacrylate (PMMA) blocks. This system is consistent with the experiment done by Maegawa et al. [7]. The base block is fixed and can be modelled as a rigid surface. The slider is made of linearly elastic material with elastic modulus E and poison ratio $\nu$, and it has mass M and sizes L and H in the horizontal (x) and vertical (z) directions, respectively. We use B to represent the width of the slider along y direction. The normal load is applied on the top surface of the slider through two load cells. The normal forces in the left and right load cells are denoted as $F_{\mathrm{{ZA}}}$ and $F_{\mathrm{{ZB}}}$, respectively. If $F_{\mathrm{{ZA}}}$ and $F_{\mathrm{{ZB}}}$ are equal, it is considered as uniform loading. Otherwise it is called non-uniform loading. A tangential load which is applied at the trailing edge of the slider increases from zero.

Fig. 1

Schematic diagram of friction experiments under non-uniform normal loading. The load is supported by the asperities having heights greater than the separation between the reference planes (bottom)

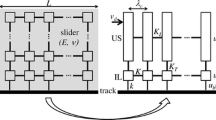
The slider is modeled as a square lattice of $N=N_{x}N_{z}$ point masses (of mass $m=M/N$) connected by internal springs, thus rotational degree of freedom within the bulk is not included. As shown in Fig. 2, each internal block is coupled to its four nearest neighbors by four straight springs of equilibrium length $l_{\mathrm{{s}}}=L/(N_{x}-1) = H/(N_{z} -1)$. The block is also coupled to other next-nearest blocks through four diagonal springs with equilibrium length $\sqrt{2}l_{\mathrm{{s}}}$. Giving an isotropic elastic model with Poisson’s ratio $\nu = 1/3$, the straight and diagonal springs take stiffness $K=3BE/4$ and K/2, respectively [34,35,36].

The spring force $F_{ij}$ exerted on block i by block j is thus expressed as

$$\begin{aligned} \varvec{F}_{ij} = \left\{ \begin{aligned}&k_{ij}(r_{ij} - l_{ij})\frac{\Delta \varvec{x}_{ij}}{r_{ij}},\\&0, \;\; \text {if }i \text { and } j \text { blocks are not connected}. \end{aligned} \right. \end{aligned}$$

(1)

where $\varvec{F}_{ij} = (F^{x}_{ij}, F^{z}_{ij})$, $\varvec{x} = (x, z)$, $\Delta \varvec{x}_{ij} =\varvec{x}_j - \varvec{x}_i$, $r_{ij} = |\varvec{x}_{ij}|$, and $k_{ij}$ and $l_{ij}$ are the stiffness and equilibrium length of the spring connecting blocks i and j. In order to avoid the artificial oscillations of the blocks, we introduce viscous force between blocks,

$$\begin{aligned} \varvec{C}_{ij} = \eta (\dot{\varvec{x}}_j - \dot{\varvec{x}}_i), \end{aligned}$$

(2)

where the damping coefficient is set as $\eta = \sqrt{0.5Km}$ [20].

Fig. 2

Elastodynamics of the elastic slider is described by a spring-block network, and the frictional interface is modeled using surface springs. The enlargement of the ellipse is given in Fig. 3a

The top blocks of the slider are subjected to time-independent vertical forces as

$$\begin{aligned} W_i = \left\{ \begin{aligned}&\frac{F_{\mathrm{{N}}}}{N_{x}}\left( 1+\frac{2i-N_{x}}{N_{x}}\theta \right) , \;\;i=1, 2, \cdots , N_{x},\\&0, \;\; \text {otherwise}, \end{aligned} \right. \end{aligned}$$

(3)

where $F_{\mathrm{{N}}} = F_{\mathrm{{ZA}}} + F_{\mathrm{{ZB}}}$ is the total normal load, and $\theta \in [-1,1]$ is a parameter describing the non-uniformity degree of the normal loading.

Both vertical boundaries of the slider are free, except for a time-dependent horizontal driving force $F_{\mathrm{{S}}}$. The force is applied to the slider trailing edge ($x=0$) through a load spring with stiffness $K_{\mathrm{{S}}}$. One end of this spring is attached to the trailing edge at height h, whilst the other end of the spring moves at a constant speed V. The time-varying horizontal force $F_{\mathrm{{S}}}$ changes as

$$\begin{aligned} F_{\mathrm{{S}}} = K_{\mathrm{{S}}} (Vt - x_{\mathrm{{h}}}(t)), \end{aligned}$$

(4)

where $x_{\mathrm{{h}}}(t)$ represents the horizontal displacement of the attached point at the trailing edge.

Due to the interaction with the elastic substrate the bottom blocks are subjected to both normal and tangential (friction) forces, denoted as $P_i(t)$ and $f_i(t)$, respectively. By assuming that both the slider and the substrate are of the same material, the normal contact stiffness of these blocks with the elastic base is equal to $K_{\mathrm{{b}}}= K/2$. The normal force $P_{\mathrm{{b}}}(t)$ experienced by each bottom block can be computed by

$$\begin{aligned} P_{\mathrm{{b}}}(t) = \left\{ \begin{aligned}&-K_{\mathrm{{b}}}z_i, \;\; \text {if}\; z_i(t)\le 0, \\&0, \;\;\text {if}\; z_i(t)>0, \end{aligned} \right. \end{aligned}$$

(5)

where $z_i(t)$ is the vertical displacement of the $i\mathrm{{th}}$ bottom block at the interface. It is worth noting that $z_i(t)>0$ means that the block detaches from the interface, thus the corresponding tangential force, $f_i$ should be equal to zero. For the case $z_i(t)<0$, the tangential force $f_i$ should depend on the friction state at the interface. This will be discussed in the subsequent subsection.

Let us denote $\varvec{F}_{j}^{(\cdot )}$ and $\varvec{C}_{j}^{(\cdot )}$ as the resultant forces originated from the internal springs and dashpots connected with $j\mathrm{{th}}$ block. Considering the boundary conditions of each block and neglecting the effect of gravity on the frictional motion, the mesoscale model of the elastic slider is governed by the following equations:

$$\begin{aligned} \left\{ \begin{aligned} m \ddot{\varvec{x}}^{\mathrm{{u}}}(j,t)&= \varvec{F}_{j}^{\mathrm{{u}}} + \varvec{C}_{j}^{\mathrm{{u}}} + \varvec{W}_{\mathrm{{u}}},\;\; \text {up blocks},\\ m \ddot{\varvec{x}}^{\mathrm{{d}}}(j,t)&= \varvec{F}_{j}^{\mathrm{{d}}} + \varvec{C}_{j}^{\mathrm{{d}}} + \varvec{F}_{\mathrm{{d}}},\;\; \text {driving block},\\ m \ddot{\varvec{x}}^{\mathrm{{b}}}(j,t)&= \varvec{F}_{j}^{\mathrm{{b}}} + \varvec{C}_{j}^{\mathrm{{b}}} + \varvec{P}_{\mathrm{{b}}},\;\; \text {bottom blocks},\\ m \ddot{\varvec{x}}^{\mathrm{{o}}}(j,t)&= \varvec{F}_{j}^{\mathrm{{o}}} + \varvec{C}_{j}^{\mathrm{{o}}},\;\; \qquad \text {other blocks},\\ \end{aligned} \right. \end{aligned}$$

(6)

where $\varvec{W}_{\mathrm{{u}}} {=} (0, -W_i)$, $\varvec{F}_{\mathrm{{d}}}= (F_{\mathrm{{S}}}, 0)$, $\varvec{P}_{\mathrm{{b}}} {=} (-f_i(t), P_{\mathrm{{b}}}(t))$. $\varvec{x}^{\mathrm{{u}}}(j,t)$, $\varvec{x}^{\mathrm{{d}}}(j,t)$, $\varvec{x}^{\mathrm{{b}}}(j,t)$, and $\varvec{x}^{\mathrm{{o}}}(j,t)$ represent the displacement vectors of blocks under different boundary conditions.

2.2 Description of the interface roughness

Essentially, the frictional interface is made up of myriad randomly distributed micro-contacts, whose real contact area is smaller than the nominal contact area by orders of magnitude [1, 37]. For understanding the mechanism underlying the onset of frictional sliding, a description for the interface asperities should be provided at first.

Bowden and Tabor [1] assumed that touching asperities on the interface are fully plastic, from which they obtained a linear relation between normal load and real contact area. This relationship is extended by Greenwood and Williamson [38] into the case where the interface is in elastic regime. Here, we assume that the interface is in a fully plastic regime. In this case, the average normal stress $\sigma _{\mathrm{{p}}}$ at the contact tip is approximately equal to the material hardness H. The hardness is related to the material yield stress as $H \approx 3\sigma _{y}$. Suppose that ${\bar{r}}$ represents the average contact radius of these touching asperities. The normal load applied on each asperity can be computed as $p = \uppi {\bar{r}}^2 H$. Then the total number of touching asperities under normal load $F_{\mathrm{{N}}}$ can be roughly estimated as

$$\begin{aligned} N = \frac{F_{\mathrm{{N}}}}{p}. \end{aligned}$$

(7)

The number of the asperities on $i{\mathrm{{th}}}$ bottom block is given by

$$\begin{aligned} N^{\mathrm{{b}}}(i,t) = \frac{P_{\mathrm{{b}}}(t)}{p}. \end{aligned}$$

(8)

It is worth noting that $F_{\mathrm{{N}}}$ is constant, while $P_{\mathrm{{b}}}(t)$ changes dynamically by Eq. (5). This means that N should be constant, while $N^{\mathrm{{b}}}(i,t)$ is time-dependent. The relation between N and $N^{\mathrm{{b}}}(i,t)$ is as follows: $\sum _{i=1}^{N_{x}} N^{\mathrm{{b}}}(i, t) = N$. Generally, we can use $N^{\mathrm{{b}}}(i,t)$ to represent the local real contact area of $i\mathrm {th}$ bottom block [37].

2.3 Modeling the friction of a touching asperity

For each micro-contact, it is subjected to both normal and tangential forces. Here a nonlinear spring is used, as shown in Fig. 3a, to represent the tangential force applied in each micro-contact. On the basis of previous models [18, 20] and existing experimental observation [15], we consider that the following physical aspects are essential to model the individual spring behavior of the touching asperity.

Fig. 3

a Tangential springs attached on the bottom block. b Three micro-scale interacting states between a pair of asperities on the contact surface (top) and the corresponding force curves (bottom). c The probability density function $P(t_{\mathrm{{s}}})$ and $P(t_{\mathrm{{d}}})$ of the micro-contacts in the sliding state and the dislocated state, respectively

• A pinned state In this state the micro-contact behaves elastically and deforms with the motion of the slider. It bears a shear force f(t) that is smaller than a certain threshold $f_{\mathrm{{thr}}}$.

• A time-controlled shear-relaxation process When $f_{\mathrm{{thr}}}$ is reached, a microscopic fracture-like event occurs, and activates a thermal process, leading to time-controlled shear-relaxations [31]. This process experiences a time interval with a typical value, which correlates the fast slip dynamics of the frictional interface [15].

• A time-controlled dislocated state The touched asperities, after the time-controlled shear-relaxation, are immediately dislocated from each other, resulting in new micro-contacts with time-controlled slip motion [31].

• Stick rejuvenation The cessation of the time-controlled dislocated state marks the initiation of the stick rejuvenation and strengthening that are generally associated with a pinned state.

Figure 3b describes the physical aspects of a micro-contact that consists of two contacting sphere-like asperities. Due to the initial compression, the two touching asperities are flattened with the same plane (pinned state). Separation commences on the compressed plane when the micro-contact enters into a time-controlled shear-relaxation process (sliding state). After that, a new micro-contact is formed and it immediately enters into a time-controlled dislocated state (dislocated state), and then the following stick rejuvenation makes the micro-contact enter into a pinned state (pinned state). Unless otherwise stated, we specify that the velocity to the right is positive.

Each micro-contact is subjected to the same constant normal load p and its tangential interaction is represented by a tangential spring attached in parallel to the relevant interfacial block. The static friction threshold $f_{\mathrm{{thr}}}$ is assumed to be time independent, and its value is given by $f_{\mathrm{{thr}}} = \mu _{\mathrm{{s}}} p$, where $\mu _{\mathrm{{s}}}$ is the static coefficient of micro-contact friction. As the micro-contact is in a sliding state, the sliding friction force of the micro-contact is determined by a time-independent sliding coefficient $\mu _{\mathrm{{d}}}$. Thus, the friction force of a sliding spring j on block i is given by

$$\begin{aligned} f_{ij}^{\mathrm{{s}}} = \mu _{\mathrm{{d}}} p. \end{aligned}$$

(9)

According to the two characteristic coefficients of micro-contact friction, the friction relations of micro-contact in different motion states can be obtained. For the pinned spring j of block i, the tangential force on the block is computed as

$$\begin{aligned} f_{ij}^{\mathrm{{p}}}(x_{ij},t) = f_{ij}^0 + k_{\mathrm{{s}}}(x_i(t)-x_{ij}), \end{aligned}$$

(10)

where $x_{ij}$ is the displacement of block i at the instant when spring j enters into a pinned state and $x_i(t)$ is the temporal position of the block, $k_{\mathrm{{s}}}$ is the tangential stiffness, which can be determined by Mindlin theory [39]. $f_{ij}^0$ is the initial tangential force of pinned spring j. It is worth noting that the value of $f_{ij}^0$ is tightly linked with the history of the normal and tangential loading of the system. If the pinned state is initialized through a dislocated state, the initial friction force is related to a sliding friction (see Fig. 3b), thus we should have $f_{ij}^0=\mu _{\mathrm{{d}}}p$.

For the micro-contact in a dislocated state, the contact geometry of the two touching asperities should be considered in modeling. The touching asperities are assumed to take the same sphere-like shape, and the contact angle between them is $\varphi$. Let us denote by $f_{\mathrm{{n}}}$ and $f_{\mathrm{{t}}}$ as the normal and tangential components along the contact surface, respectively, and they satisfy $f_{\mathrm{{t}}}= \mu _{\mathrm{{d}}} f_{\mathrm{{n}}}$, corresponding to the friction relation of the micro-contact in the sliding state. Noting that the vertical force of each micro-contact is equal to p, we therefore should have $f_{\mathrm{{n}}}(\cos \varphi -\mu _{\mathrm{{d}}}\sin \varphi )=p$, and the horizontal force $f_{ij}^{\mathrm{{d}}}(\varphi ,t)$ of spring j on block i can be written as

$$\begin{aligned} f_{ij}^{\mathrm{{d}}}(\varphi ,t)=\frac{\mu _{\mathrm{{d}}}}{1-\mu _{\mathrm{{d}}}\tan \varphi }p+\frac{\tan \varphi }{1-\mu _{\mathrm{{d}}}\tan \varphi }p \equiv f_{ij}^{\mathrm{{t}}} + f_{ij}^{\mathrm{{n}}}, \end{aligned}$$

(11)

where $f_{ij}^{\mathrm{{t}}}$ and $f_{ij}^{\mathrm{{n}}}$ are the horizontal components induced by the tangential and normal forces, respectively. It is clear that $f_{ij}^{\mathrm{{d}}}(\varphi ,t)$ decreases as $\varphi$ gets smaller and it becomes as large as the sliding force $f_{ij}^{\mathrm{{s}}}$ when $\varphi$ equals zero.

We use $t_{\mathrm{{s}}}$ and $t_{\mathrm{{d}}}$ to characterize the time scales of the slip and dislocated states, respectively. Due to the random distribution of micro-contacts, the two time scales essentially should satisfy certain probability. Here both $t_{\mathrm{{s}}}$ and $t_{\mathrm{{d}}}$ are supposed to follow Gaussian distribution (see Fig. 3c). Noting that the negative time should be excluded, we modify the probability density function of $t_{\mathrm{{s}}}$ and $t_{\mathrm{{d}}}$ as

$$\begin{aligned} \left\{ \begin{aligned} P(t_{\mathrm{{s}}})&=\frac{1}{\sqrt{2\uppi }\sigma _{\mathrm{{s}}}}\mathrm{{e}}^{\dfrac{-(t_{\mathrm{{s}}}-{\overline{t}}_{\mathrm{{s}}})^2}{2{\sigma _{\mathrm{{s}}}}^2}},\;\;t_{\mathrm{{s}}}>0,\\ P(t_{\mathrm{{d}}})&=\frac{1}{\sqrt{2\uppi }\sigma _{\mathrm{{d}}}}\mathrm{{e}}^{\dfrac{-(t_{\mathrm{{d}}}-{\overline{t}}_{\mathrm{{d}}})^2}{2{\sigma _{\mathrm{{d}}}}^2}},\;\;t_{\mathrm{{d}}}>0, \end{aligned} \right. \end{aligned}$$

(12)

where ${\overline{t}}_{\mathrm{{s}}}$ and ${\overline{t}}_{\mathrm{{d}}}$ are average time, $\sigma _{\mathrm{{s}}}$ and $\sigma _{\mathrm{{d}}}$ are mean square deviation of $P(t_{\mathrm{{s}}})$ and $P(t_{\mathrm{{d}}})$, respectively. We assume that all the micro-contacts in a dislocated state take the same initial contact angel $\varphi _0$, and the angle decreases linearly with time, namely

$$\begin{aligned} \tan \varphi (t)=\frac{t_{\mathrm{{d}}}-t}{t_{\mathrm{{d}}}}\tan {\varphi _0}. \end{aligned}$$

(13)

As $\tan \varphi (t)$ becomes zero, the asperities get pinned, then next cycle starts. The pinned-sliding-dislocated cycle would repeat again and again in the motion of micro contacts.

Note that block i may reverse its motion due to the block oscillation, namely, the velocity of the block changes its direction. At the instant of the reverse motion occurring, spring j attached at the block i may be in a sliding or dislocated state. In this case, we should consider the effect of the deformation relaxation on the friction forces of the these springs. The tangential force of a slipping spring j on the reversed block i is modified as

$$\begin{aligned} f_{ij}^{\mathrm{{s}}} = \mu _{\mathrm{{d}}} p + k_{\mathrm{{s}}}(x_i(t)-x_{ij}), \end{aligned}$$

(14)

where $x_{ij}$ is the displacement of block i at the instant when it just reverses its velocity direction. The above equation exists while $|f_{ij}^{\mathrm{{s}}}| \le \mu _{\mathrm{{d}}} p$.

For a dislocated spring attached at a block with a reversed motion, we assume that the contact angle $\varphi$ is fixed and the part $f_{ij}^{\mathrm{{n}}}$ in Eq. (11) remains unchanged. Nevertheless, we consider the effect of the deformation relaxation on the part $f_{ij}^{\mathrm{{t}}}$

$$\begin{aligned} f_{ij}^{\mathrm{{t}}} = f_{ij}^{\mathrm{{t}},0}+ k_{\mathrm{{s}}}(x_i(t)-x_{ij}), \end{aligned}$$

(15)

where $x_{ij}$ is the displacement of block i at the instant when it just reverses its velocity direction, and $f_{ij}^{\mathrm{{t}},0}$ is the initial value of $f_{ij}^{\mathrm{{t}}}$ at that instant. It is worth noting that the above equality exists while $f_{ij}^{\mathrm{{t}}} \le f_{ij}^{\mathrm{{t}},0}$. When $f_{ij}^{\mathrm{{t}}}$ decreases to zero, separation occurs at the current micro-contact. In this case, we consider that a new micro-contact is formed immediately, and its behavior starts from a unloaded pinned state ($f_{ij}^0$ in Eq. (10) is equal to zero).

Fig. 4

Flow chart of the motion state of a micro-contact during one cycle. $\mathrm {C}1-\mathrm {C}6$ represent transfer conditions between different motion states

To summarize how the friction force of each micro-contact is determined with respect to different motion state, we plot a flow chart in Fig. 4. In the beginning of the cycle, the micro-contact is in pinned state, and the friction force offered by this micro-contact could be calculated by Eq. (10). The micro-contact changes from the pinned state to the sliding state once the local threshold is reached, namely $|f_{ij}^{\mathrm{{p}}}|>f_{\mathrm{{thr}}}$. At the start of the sliding state, we first use Eq. (9) to compute the friction force, then check the velocity direction of the block. If the direction remains unchanged, the friction state is in a regular case where Eq. (9) is still used to determine the friction force. If the block reverses its motion, the friction state enters into a relaxation case where the friction force is computed as Eq. (14). It is worth noting that the friction state of the junction may switch between the two cases within a random time interval $t_{\mathrm{{s}}}$, a characteristic time scale responsible for the sliding phase. Similar to the sliding phase, we should consider the relaxation effect induced by the reverse motion of the block in the dislocated phase. If no reverse motion appears in the dislocated phase, the friction state is in a regular case where the friction force can be calculated by Eq. (11). As the friction state is in a relaxation case, the friction force should be determined by Eq. (15). The friction state may switch between the two cases within a random time interval $t_{\mathrm{{d}}}$, another characteristic time scale responsible for the dislocated phase. After $t_{\mathrm{{d}}}$, the dislocated phase will be transferred into a pinned phase.

In terms of the motion state of each micro-contact behavior, the frictional force exerted on block i can then be computed as

$$\begin{aligned} f_{i}(t) = \sum _{j=1}^{N_{\mathrm{{s}}}}f_{ij}^{\mathrm{{s}}} + \sum _{j=1}^{N_{\mathrm{{p}}}} f_{ij}^{\mathrm{{p}}} +\sum _{j=1}^{N_{\mathrm{{d}}}} f_{ij}^{\mathrm{{d}}}, \end{aligned}$$

(16)

where $N_{\mathrm{{s}}}$, $N_{\mathrm{{p}}}$ and $N_{\mathrm{{d}}}$ are the spring numbers of block i in the sliding, pinned and dislocated states, respectively.

3 Numerical results and precursor events

In this section, the multiscale model is used to investigate the onset dynamics of friction for various loading conditions reported in Refs. [7, 15, 16]. Table 1 presents the loading condition and material constants in accordance with Maegawa’s experiment [7]. The slider is described by a spring-block model with parameters shown in Table 2. The physical parameters modeling the micro-contact interactions are listed in Table 3.

It has been found from existing experiments that the loading condition significantly influences the onset dynamics of friction [7]. In this section, we will first give detailed information on how the system is initialized and the boundary conditions are applied. Then the simulation results are compared with the existing experiments. Finally, how the properties of precursor events are affected by different loading conditions will be discussed in detail.

Table 1 Material constants of the slider and the loading condition

Table 2 Parameters for the spring-block model

Table 3 Model parameters of micro-contact interaction

3.1 Initialization of the system and the loading curve

For simulating the onset dynamics of frictional sliding, the system is initialized in terms of the following process. At the beginning of the simulation, only the full normal load with no tangential load is applied on the top of the slider. We then solve Eq. (6) using fourth order Runge−Kutta method, through which the state of the system is updated step by step until the system reaches a steady state. This steady state corresponds to a scenario where the velocity and the acceleration of each block is close to zero.

Fig. 5

Distribution of the normal forces (red dashed line) and the tangential forces (blue dash-dotted line) when the slider is just subjected to a normal load $F_N= 400$ N with a uniform distribution

The time step size is set as $2\times 10^{-7}$ s to perform the simulation. It was found that the steady state can be achieved after 50,000 steps. Fig. 5 shows the distributions of the normal and tangential forces when a normal load $F_{\mathrm{{N}}}=400$ N is uniformly distributed on the top blocks of the system. Due to the frictional effect of the bottom interface and the Poisson expansion of the block elasticity, the normal force profile of the bottom interface is symmetric and weakly non-uniform, while the tangential force profile is anti-symmetric. These stresses are in excellent agreement with those expected from contact mechanics and those measured in previous experiments [40].

After the system reaches a steady state, a tangential load $F_{\mathrm{{S}}}$ is applied to the system for investigating the typical frictional experiment done by Maegawa et al. [7], where $F_{\mathrm{{S}}}$ increases linearly for a constant loading rate ($K_{\mathrm{{S}}} V =80$ N/s). Figure 6 shows the loading curves obtained from our numerical simulation and the experimental observation in Ref. [7]. It can be seen that the time for the occurrence of the macroscopic sliding and the period of the stick-slip cycle achieve good consistency between our simulation and the experiments. Our simulation also reveals that there are a series of rapid crack-like precursors that propagate partially through the interface. These precursors occur at imposed shear force that are well below the maximum static frictional force, and the propagation length of each precursor event is shown in the bottom panel of Fig. 6. Clearly, the length of the first several precursor events is far away from the leading edge of the slider, and the length of each precursor event increases successively until the entire interface begins to slide.

Fig. 6

Typical loading curves obtained from the experiment by Maegawa et al. [7] (blue) and the simulation (red) under the loading condition $F_N=400$ N, $h=5$ mm. The bottom figure shows the normalized length of precursors obtained from the simulation

Note that our model includes some artificial parameters whose values, at present, cannot be directly determined from experiments or theoretical analysis. The uncertainty of these model parameters inevitably leads to errors in numerical predictions. From Fig. 6 it is clear that there are visible differences for the maximum frictional force between our numerical results and the experimental findings (the coefficients characterizing the micro-contact friction are different from the global quantities of the system [41].). In addition, the number of the precursor events from our simulation is smaller than the one found from Maegawa’s experiment. Nevertheless, in most cases one may expect to obtain qualitative understanding about the characteristics of the frictional motion, instead of very accurate results. In the following, we will qualitatively investigate how the precursor events vary with the system configuration and the loading conditions when the model parameters given in Tables 2 and  3 remain unchanged.

3.2 Precursors under different loading configurations

In order to understand the dynamics of precursors within the onset of frictional sliding, Rubinstein et al. [16] experimentally investigated how the lengths l of precursors vary with different normal load $F_{\mathrm{{N}}}$ and different heights h of tangential load ($F_{\mathrm{{S}}}$) position. The experiments demonstrated that l grows approximately linearly with $F_{\mathrm{{S}}}$ until rapid growth occurs at l—L/2. The 23 different experiments they performed also shew that $F_{\mathrm{{S}}}$ – $(l/L)F_{\mathrm{{N}}}$ can collapse into a single curve. This simple scaling can be ascribed as a local generalization of the Amontons−Coulomb law: $\tau _{\mathrm{{S}}} = \mu _{\mathrm{{S}}} \sigma _{\mathrm{{N}}}$, $\tau _{\mathrm{{S}}}$ and $\sigma _{\mathrm{{N}}}$ are the local shear and normal stresses, respectively, and $\mu _{\mathrm{{S}}}$ is the local static coefficient of friction. This simple scaling can be explained as follows [16]: local slip redistributes the stress along the precursor length, yielding a mean stress of $\tau _{\mathrm{{S}}}$ – $F_{\mathrm{{S}}}/l$. Meanwhile, along the whole length of the interface there is a mean normal stress of $\sigma _{\mathrm{{N}}}$ – $F_{\mathrm{{N}}}/L$. If the generalized Amontons−Coulomb law comes to be true, the scaling $F_{\mathrm{{S}}}$ – $(l/L)F_{\mathrm{{N}}}$ should collapse into a single curve.

Fig. 7

Lengths l of precursor events under different normal loads $F_{\mathrm{{N}}}$ applied at the same position $h=5$ mm, and a case of $F_{\mathrm{{N}}}=0.4$ kN at a different position $h=2.5$ mm. al vs. $F_{\mathrm{{S}}}$ in four different loading configuration. b (l/L) vs. $F_{\mathrm{{S}}}/F_{\mathrm{{N}}}$ in four different loading configuration

We expect that the same scaling for $F_{\mathrm{{S}}}$ – $(l/L)F_{\mathrm{{N}}}$ could be observed from our numerical results. Here, numerical investigations are performed by remaining the model parameters shown in Tables 1, 2 and 3 unchanged, but vary the normal load at the range $0.4~\mathrm {kN} \le F_{\mathrm{{N}}} \le 2$ kN. Figure 7 shows that the results for all conditions indeed can be collapsed on a single curve by plotting l/L as a function of $F_{\mathrm{{S}}}/F_{\mathrm{{N}}}$. In particular, we excellently reproduce the transition from a roughly linear increase up to $l/L \approx 0.5$ to a more rapid growth for longer precursors.

It can be found from Fig. 7 that the results for the case of $F_{\mathrm{{N}}}=0.4$ kN at a height $h=2.5$ mm also follow the same scaling law. This means that the loading position h seems to have little effect on the scaling. Position h, by its nature, is associated with the degree of nonuniformity of the normal distribution induced by the torque $(F_{\mathrm{{S}}} \times h)$. When great nonuniformity of the normal distribution appears in the interface, the profile of the scaling law would change definitely. Maegawa et al. [7] performed experimental observations for the frictional dynamics of a slider subjected to a linear time-independent distribution of vertical forces. The degree of nonuniformity of the distribution is described by $\theta$ (Eq. (3)): $\theta =0$ denotes uniform loading; $\theta <0$ and $\theta >0$ correspond to the nonuniform loading conditions $F_{\mathrm{{ZA}}} > F_{\mathrm{{ZB}}}$ and $F_{\mathrm{{ZA}}} < F_{\mathrm{{ZB}}}$, respectively. The experiments demonstrated that both the number of precursor events and the increasing rate of the propagation length are influenced by the value of $\theta$. Fig. 8 shows our numerical results about how the value of $\theta$ affects the number of the precursor events and the profiles of the curves of (l/L) vs $F_{\mathrm{{S}}}/F_{\mathrm{{N}}}$. The number of precursor events increases when $\theta$ changes from $-0.833$ to 0.833. Meanwhile, the lower the normal load on the trailing edge, the lower the tangential force required to nucleate precursors. Nevertheless, the system under different loading conditions requires the same threshold force to initialize its global sliding ($l/L=1$). Namely, the static friction coefficient of the global sliding seems to be independent of the loading conditions. These simulated phenomena are the same as the experimental observation in Ref. [7].

Fig. 8

Effect of the normal force nonuniformity on a the curve of (l/L) vs $F_{\mathrm{{S}}}/F_{\mathrm{{N}}}$, and b the number of the precursor events. The meaning of the symbols are the same as Fig. 7

3.3 Local dynamics at the frictional interface

As a precursor passes through the interface, contacts re-form and strengthen, leading to the variation of the interface strength. In order to better understand the rupture process on the interface, Ben-David et al. [15] examined how the local real contact area A(x, t) and concurrent slip displacement u(x, t) are related throughout the microscopic motion of asperities. They identified four distinct and inter-related phases of contact area evolution that exist in a single rupture event. The first phase (phase I) is termed as detachment, in which the contact fracture takes place. Then fast slip (phase II) immediately commences, followed by a slow slip phase (phase III). Phase IV is related to contact rejuvenation during which slip ceases.

In essence, the four phases of the evolution that are observed from experiments can be understood as the collective behaviors of the asperities, which can be simulated through our simulation. In the following, we focus on the first precursor event shown in Fig. 6 to understand the relationship between the mesoscale behaviors of the bottom blocks and the microscale behaviors of the asperities on the rough interface.

Let us first remind how the real contact area was measured in experiments [7, 15, 16, 40]. The interface between two blocks of PMMA is illuminated with a laser sheet at a shallow angle. This results in total internal reflection in the areas that are out of contact, and transmission only at the points of real contact. Contact breaking and renewal is seen as changes in the intensity level of image pixels captured by a fast camera.

Fig. 9

Mesoscopic behavior of bottom blocks before, during and after the onset of the first rupture event. a Evolution of local contact area (top) and local displacement (bottom) of a specific block ($i=6$). Four phases are marked: detachment (I), fast slip (II), slow slip (III) and rejuvenation (IV). We stretch the time axis for clarifying the four phases. b Evolution of the percentages of the micro-contacts in three different contact states. c Normalized slip curves of ten bottom blocks (from $i=1$ to 10). The inset shows the section of the curve associated with the transition between phase II and phase III. d Free-body force diagram of 6th block (top), and the time histories of the left force $LF_i$, right force $RF_i$ and the friction force $f_i$ (bottom)

Obviously, the measurement principle allows that the evolution of the pinned micro-contacts would be well reflected by the intensity changes of image pixels. Noting that each tangential spring in our numerical model can enter a different state of pinned, slipping and dislocation, the instantaneous number of pinned micro-contacts is chosen to represent the evolution of the local contact area of each block. Let $N_{\mathrm{{p}}}(i,0)$ be the number of the pinned micro-contacts of bottom block i before the rupture front arrives, and $N_{\mathrm{{p}}}(i,t)$ be the instantaneous number of pinned micro-contacts during the rupture wave. Normalized number of the pinned micro-contacts ${\widetilde{N}}_{\mathrm{{p}}}(i,t)$ is then expressed as

$$\begin{aligned} {\widetilde{N}}_{\mathrm{{p}}}(i,t) = \frac{N_{\mathrm{{p}}}(i,t)}{N_{\mathrm{{p}}}(i,0)}, \end{aligned}$$

(17)

which can be considered as an index characterizing the evolution of the local real contact area. The concurrent slip displacement u(i, t) of $i\mathrm {th}$ bottom block can be calculated by $u(i,t) = x^{\mathrm{{b}}}(i,t) -(i-1)l_{\mathrm{{s}}}$, where $x^{\mathrm{{b}}}(i,t)$ is the position of the block at time t.

Figure 9a shows the evolution of ${\widetilde{N}}_{\mathrm{{p}}}(6,t)$ and u(6, t) of $6\mathrm{{th}}$ block before, during and after the first rupture event in Fig. 6a. In Fig. 9b, we plot the evolution of the contact states of all micro-contacts in $6\mathrm{{th}}$ block. Clearly, the local dynamics of the block experiences four distinct phases that exactly coincide with the experimental observations: detachment (phase I), rapid slip (phase II), slow slip (phase III) and rejuvenation (phase IV). Phase I features that all the micro-contacts are in pinned state, and the local displacement of the block increases gradually. As the elastic displacement is larger than the threshold of static friction, a rupture event occurs, resulting in ${\widetilde{N}}_{\mathrm{{p}}}(i,t) \approx 0$. Namely, almost all of the micro-contacts immediately enter into a sliding state after the rupture event. The subsequent fast slip phase is characterized by a high slip velocity. Then some sliding springs enter into either pinned or dislocated state, resulting in a slow slip phase (phase III), in which the number of dislocated springs increases gradually. Phase III is characterized by a velocity much slower than that in phase II, and it ends at the instant when the number of dislocated micro-contacts arrives at its maximum. We consider that phase IV starts when the number of pinned springs increases gradually.

It was found from the experiments [15] that the features of the local motion are independent of the magnitude of total slip displacement (${\varDelta }_{\mathrm{{tot}}}$), the measurement location, details of loading and the geometry of the blocks. This property is verified by examining the normalized displacements of 10 bottom blocks when the rupture front passes. The normalized displacement of $i^{\mathrm{{th}}}$ block is defined as ${\varDelta }/{\varDelta }_{\mathrm{{tot}}}$, where ${\varDelta }=u(i,t)-u(i,0)$ is the displacement difference of $i^{\mathrm{{th}}}$ block motion within the time interval from current time t to the instant when fast slip starts. ${\varDelta }_{\mathrm{{tot}}}$ is the total displacement of the block from the beginning of its fast slip motion to the end of its slow slip motion. These normalized displacements of 10 different blocks are plotted in Fig. 9c, yielding an approximate collapse of the slip history, which was completely consistent with the experimental observation [15].

Both our numerical results and the experiments in Ref. [15] show that there is a sharp transition between phases II and III. In particular, the transition features a characteristic that the normalized displacement decreases first and then increases with time. In order to understand the physical mechanism underlying the transition behavior between the fast and slow slip phases, we plot in Fig. 9d the time histories of the forces exerted on $6\mathrm{{th}}$ bottom block, where $LF_{i}$ and $RF_{i}$ represent the forces applied to the left and right sides of the block, respectively, and $f_i$ represents the friction force. We should have $LF_{i}=RF_{i}+f_i$ before the arrival of the rupture front. The rupture event destroys the equilibrium due to the sudden decrease of $f_i$, causing the block to enter into a fast slip phase. At the end of the fast slip phase, the local slip displacement reaches maximum, then the block begins a reverse motion (the block changes the direction of its velocity). The reverse motion leads to a decrease in friction and triggers a relatively slow slip fluctuation. With the increase of the dislocated micro-contacts, the friction of the block increases slightly at first, and then decreases gradually, thus the block is in a slow slip motion. After the rupture wave passes through the block, its motion enters into phase IV, in which the interface friction is dominated by the pinned micro-contacts, and the local interface becomes strengthened gradually.

The local dynamics of the interface is summarized as follows. The fast slip phase results from the sudden reduction of the friction force, $f_i$, which is caused from the rupture of the micro-contacts; The slow slip phase is caused by the dislocation motion of micro-contacts; The transition between fast slip phase and slow slip phase is related to a slip fluctuation, triggered by the inertial motion of the block. The intensity of the inertial motion, in general, increases with the difference between the static and dynamic friction coefficient $\mu _{\mathrm{{s}}}-\mu _{\mathrm{{d}}}$. The transition between the slow slip phase and the rejuvenation phase is closely related to the timescale ${t}_{\mathrm{{d}}}$. The essence of ${t}_{\mathrm{{d}}}$ is associated with the geometric size of the asperities on the contact interface.

4 Conclusions

In order to understand the onset of frictional sliding between two elastic bodies, we have established a multiscale model that combines a multi-junction friction law with a 2D spring-block model. The spring-block model is used to transfer the external shear and normal loads to the interface deformation, and the frictional interaction is modelled as a set of junctions attached to each interface unit in the bulk discretization. Compared to the model proposed by Trømborg et al. [20], the principal differences are that a dislocated state is assigned to the junction behavior, and two characteristic timescales observed from experiments are also introduced into the junction friction law. Physically, the two timescales are associated with the thermally activated relaxations of the slipping micro-junction and the removal of a dislocated junction, respectively [31].

By numerically investigating the loading configurations of experiments done by Maegawa et al. [7], we show that the model can precisely reproduce the distribution of normal and tangential forces and the profiles of loading curves. In addition, the qualitative properties of the precursor events that have been observed from different experiments can be captured by the numerical model. How the non-uniform normal loading affects the precursor dynamics is also examined numerically.

Finally, we expose the evolution of local real contact area and concurrent local slip displacement through scrutinizing the details of a precursor event. It can be seen that the evolution corresponds to four distinct and inter-related phases : detachment, fast and slow slip motion, as well as the rest of slip. This is completely consistent with the existing experimental results [15]. In addition, we can clarify the physical mechanisms underlying the transitions among these phases through the analysis for the dynamics of an interface unit in the bulk discretization. We believe that the present study has made a direct bridge between the interface microscopic interactions and the macroscopic motions of frictional systems.