Diffusiophoresis of a charged particle in a charged cavity with arbitrary electric double layer thickness

Abstract

An analysis is presented for the diffusiophoretic motion of a charged colloidal sphere located at the center of a charged spherical cavity filled with an electrolyte solution at the quasisteady state for the case of arbitrary electric double layers. The electrokinetic equations governing the ionic concentration, electric potential, and velocity distributions in the fluid are linearized with assumption that the system is slightly distorted from equilibrium. These linearized differential equations are solved using a perturbation method with the zeta potentials of the particle and cavity as the small perturbation parameters. An explicit formula for the diffusiophoretic velocity of the particle as a combination of the electrophoretic and chemiphoretic contributions valid for arbitrary values of $\kappa a$ and $a/b$ is obtained by balancing the electrostatic and hydrodynamic forces exerted on it, where $\kappa$ is the Debye screening parameter, $a$ is the radius of the particle, and $b$ is the radius of the cavity. The effect of the charged cavity wall on the diffusiophoresis of the particle is interesting and can be significant. The contributions from the diffusioosmotic (electroosmotic and chemiosmotic) flow taking place along the cavity wall and from the wall-corrected diffusiophoretic force to the particle velocity are comparably important, and this diffusioosmotic flow can reverse the direction of diffusiophoresis. The particle velocity in general increases with an increase in $\kappa a$ and decreases with an increase in $a/b$, but exceptions exist.

1 Introduction

Diffusiophoresis refers to the migration of colloidal particles in response to an imposed solute concentration gradient (Prieve et al. 1984; Khair 2013; Keh 2016) and furnishes a mechanism for various applications such as particle analysis and manipulation in microfluidic or lab-on-a-chip devices (Anderson 1989; Abecassis et al. 2009; Cevheri and Yoda 2014), latex film coating (Smith and Prieve 1982), DNA translocation and sequencing (Wanunu et al. 2010; Hatlo et al. 2011), autonomous motion of micromotors (Sen et al. 2009; Brown and Poon 2014; Oshanin et al. 2017), and many others (Velegol et al. 2016; Rangharajan et al. 2016). For the diffusiophoresis of a charged particle in an electrolyte solution, the particle-solute interactions are in the electrostatic range of the order Debye screening length ${\kappa ^{ - 1}}$. Most analytical studies for the diffusiophoresis of charged particles are restricted to the case of thin electric double layer (Pawar et al. 1993; Tu and Keh 2000). With the assumption of a weak applied electrolyte concentration gradient that the transport system is only slightly perturbed from the equilibrium state, diffusiophoresis has also been analyzed for charged hard and soft spheres with arbitrary values of $\kappa a$, where $a$ is the radius of the particle (Prieve and Roman 1987; Keh and Wei 2000; Huang and Keh 2012; Li and Keh 2016).

For diffusiophoresis in microfluidic and other practical applications, particles are not isolated and it is of interest to determine if the presence of confining walls significantly affects the migration of a particle (Lee et al. 2010; Joo et al. 2010; Wang and Keh 2015). For the case of infinitesimally thin electric double layer ($\kappa a \to \infty$), the normalized fluid velocity distribution around a particle undergoing diffusiophoresis is the same as that for electrophoresis of the particle (Anderson 1989) and the wall effects on electrophoresis in this limit, which have been extensively examined (Lee and Keh 2014, and citations therein), can be employed to construe those on diffusiophoresis. With knowledge that the wall effects on diffusiophoresis are different from those on electrophoresis when the polarization effect of the finite double layer is incorporated, the diffusiophoretic motions of a colloidal sphere with a thin polarized double layer parallel (Chen and Keh 2005) and perpendicular (Keh and Jan 1996; Chang and Keh 2008) to one or two plates as well as along the axis of a microtube (Chiu and Keh 2017b) were investigated through the use of a boundary collocation method. However, the boundary effects on the diffusiophoresis of a charged particle with an arbitrary value of $\kappa a$ have not been analytically studied.

The system of a spherical particle migrating in a spherical cavity can be an idealized model for the diffusiophoresis in microchannels or matrices consisting of connecting pores or in dead-end pores involved in systems of self-regulated drug delivery (Kar et al. 2015; Shin et al. 2016). In addition, the motion of each of an array of charged Janus balls (about 100 μm in diameter) in its own elastomer-made and solvent-filled charged cavity (which is only 10–40% larger than the ball) between two thin transparent plastic sheets controlled by imposing a voltage or electrolyte gradient across the sheets was applied to a technology of electric paper displays (Crawford 2000). Although the geometry of the spherical cavity is an idealized abstraction of some other practical systems such as a cylindrical pore, the result of boundary effects on electrophoretic mobility of a charged sphere obtained in this geometry (Zydney 1995) agrees well with that for a circular cylindrical pore (Keh and Chiou 1996). Actually, the diffusiophoretic motion of a spherical particle with a thin but polarized double layer in a concentric charged spherical cavity has been analytically examined (Chiu and Keh 2017a) and that of a soft sphere with a thin or thick double layer at an arbitrary position in an uncharged spherical cavity was numerically investigated (Zhang et al. 2009).

In this paper, the diffusiophoretic motion of a dielectric sphere with an arbitrary double layer at the center of a charged spherical cavity is analyzed as the system is slightly distorted from equilibrium. The electrostatic potential, ionic concentration (electrochemical potential energy), and fluid velocity profiles are determined as power series expansions in the small dimensionless zeta potentials associated with the particle and cavity by solving the linearized electrokinetic equations. An explicit analytical solution of the migration velocity of the confined particle is obtained and shows that the effects of the cavity wall and its surface potential or charge on the diffusiophoresis of the particle are interesting and can be significant in general situations.

2 Electrokinetic equations

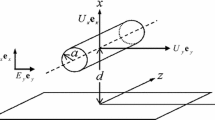
We consider the quasisteady diffusiophoresis of a charged colloidal sphere of radius $a$ at the center of a charged spherical cavity of radius $b$ filled with a fluid solution of a symmetric electrolyte with a uniformly imposed concentration gradient $\nabla {n^\infty }$ (i.e., a linearly prescribed concentration distribution $n_{{}}^{\infty }$) in the $z$ direction, as shown in Fig. 1. The origin of the spherical coordinates $(r,\theta ,\phi )$ is placed at the center of the cavity. Evidently, this transport system is axially symmetric about the $z$ axis and independent of the coordinate $\phi$.

Fig. 1

Geometric sketch for the diffusiophoresis of a charged spherical particle at the center of a charged spherical cavity

2.1 Governing equations

Conservation of both ionic species of the symmetric electrolyte of valence $Z$ requires that

$$\nabla \cdot \left[{n_ \pm }{\mathbf{u}} - {D_ \pm }\left(\nabla {n_ \pm } \pm \frac{{Ze{n_ \pm }}}{{kT}}\nabla \psi \right)\right]=0,$$

(1)

where $\psi (r,\theta )$ is the electric potential distribution, ${\mathbf{u}}(r,\theta )$ is the fluid velocity field, ${n_ \pm }(r,\theta )$ and ${D_ \pm }$ are the concentration fields and diffusion coefficients, respectively, of the ionic species (the subscripts $+$ and $-$ refer to cation and anion, respectively), $e$ is the elementary electric charge, $k$ is Boltzmann’s constant, and $T$ is the absolute temperature.

The Poisson equation gives a relation between the electric potential and the space charge density,

$${\nabla ^2}\psi = - \frac{{Ze}}{\varepsilon }({n_+} - {n_ - }),$$

(2)

where $\varepsilon$ is the dielectric permittivity of the electrolyte solution.

The fluid motion is governed by the Stokes equations with the electric effect,

$$\eta {\nabla ^2}{\mathbf{u}}=\nabla p+Ze({n_+} - {n_ - })\nabla \psi ,$$

(3)

$$\nabla \cdot {\mathbf{u}}=0,$$

(4)

where $p(r,\theta )$ is the dynamic pressure distribution and $\eta$ is the viscosity of the fluid. In Eqs. (1)–(3), ${D_ \pm }$, $\varepsilon$, and $\eta$ are taken to be constant.

2.2 Boundary conditions

The boundary conditions at the particle surface with a uniform zeta potential $\zeta$ are

$$r=a\!:\,{{\mathbf{e}}_r} \cdot \left(\nabla {n_ \pm } \pm \frac{{Ze{n_ \pm }}}{{kT}}\nabla \psi \right)=0,$$

(5a)

$$\psi =\zeta +\delta \psi ,$$

(5b)

$${\mathbf{u}}=U{{\mathbf{e}}_z},$$

(5c)

where ${{\mathbf{e}}_r}$ and ${{\mathbf{e}}_z}$ are the unit vectors in the $r$ and $z$ directions, respectively, $\delta \psi (r,\theta )$ is the electric potential perturbation to the equilibrium state defined by Eq. (7b), and $U$ is the migration velocity of the dielectric particle undergoing diffusiophoresis within the cavity to be determined. Eq. (5a) means that neither ions can penetrate into the particle.

The boundary conditions at the cavity wall with a uniform zeta potential ${\zeta _b}$ are

$$r=b\!:\,{n_ \pm }=n_{0}^{\infty }+\left| {\nabla {n^\infty }} \right|{\text{ }}r\cos \theta ,$$

(6a)

$$\psi ={\zeta _b} - \frac{{\beta \alpha kT}}{{Zea}}r\cos \theta ,$$

(6b)

$${\mathbf{u}}={\mathbf{0}},$$

(6c)

where $n_{0}^{\infty }$ is the prescribed electrolyte concentration $n_{{}}^{\infty }$ at $z=0$ or the particle center, $\alpha =a\left| {\nabla {n^\infty }} \right|/n_{0}^{\infty }$, and $\beta =({D_+} - {D_ - })/({D_+}+{D_ - })$. The electric potential distribution in Eq. (6b) gives the induced electric field $(\beta \alpha kT/Zea){{\mathbf{e}}_z}$ derived from the requirement that the cationic and anionic fluxes in the solution are equal in the absence of the particle.

2.3 Linearized electrokinetic equations

We assume that the relative electrolyte concentration gradient $\alpha$ is small and the system is only slightly distorted from equilibrium, thus

$${n_ \pm }=n_{ \pm }^{{({\text{eq}})}}+\delta {n_ \pm },$$

(7a)

$$\psi ={\psi ^{({\text{eq}})}}+\delta \psi ,$$

(7b)

$$p={p^{({\text{eq}})}}+\delta p,$$

(7c)

where $n_{ \pm }^{{({\text{eq}})}}(r)$, ${\psi ^{({\text{eq}})}}(r)$, and ${p^{({\text{eq}})}}(r)$ are the equilibrium distributions of the concentrations of the ionic species, electric potential, and dynamic pressure, respectively, and $\delta {n_ \pm }(r,\theta )$, $\delta \psi (r,\theta )$, and $\delta p(r,\theta )$ are the corresponding small perturbations to equilibrium.

Substituting Eqs. (7a), (7b) and (7c) into Eqs. (1)–(3), using the relation between $n_{ \pm }^{{({\text{eq}})}}$ and ${\psi ^{({\text{eq}})}}$ in the Boltzmann distribution, and neglecting the products of the small perturbations $\delta {n_ \pm }$, $\delta \psi$, and ${\mathbf{u}}$, one obtains

$${\nabla ^2}\delta {\mu _ \pm }= \pm \frac{{Ze}}{{kT}}\nabla {\psi ^{({\text{eq}})}} \cdot \left( {\nabla \delta {\mu _ \pm } - \frac{{kT}}{{{D_ \pm }}}{\mathbf{u}}} \right),$$

(8)

$${\nabla ^2}\delta \psi =\frac{{Zen_{0}^{\infty }}}{{\varepsilon kT}}\left\{ {(\delta {\mu _ - }+Ze\delta \psi )\exp \left[ {\frac{{Ze}}{{kT}}{\psi ^{({\text{eq}})}}} \right] - (\delta {\mu _+} - Ze\delta \psi )\exp \left[ { - \frac{{Ze}}{{kT}}{\psi ^{({\text{eq}})}}} \right]} \right\},$$

(9)

$$\eta {\nabla ^2}{\mathbf{u}}=\nabla \delta p - \varepsilon [{\nabla ^2}{\psi ^{({\text{eq}})}}\nabla \delta \psi +{\nabla ^2}\delta \psi \nabla {\psi ^{({\text{eq}})}}],$$

(10)

where the ionic electrochemical potential energy perturbations

$$\delta {\mu _ \pm }(r,\theta )=\frac{{kT}}{{n_{ \pm }^{{({\text{eq}})}}}}\delta {n_ \pm } \pm Ze\delta \psi .$$

(11)

The boundary conditions for $\delta {\mu _ \pm }$ and $\delta \psi$ resulting from Eqs. (5a), (5b), (6a) and (6b) are

$$r=a\!:\,\frac{{\partial \delta {\mu _ \pm }}}{{\partial r}}=0,$$

(12a)

$$\frac{{\partial \delta \psi }}{{\partial r}}=0,$$

(12b)

$$r=b\!:\,\delta {\mu _ \pm }=kT(1 \mp \beta )\frac{\alpha }{a}r\cos \theta ,$$

(13a)

$$\delta \psi = - \frac{{kT}}{{Ze}}\beta \frac{\alpha }{a}r\cos \theta .$$

(13b)

The boundary conditions for the fluid velocity ${\mathbf{u}}$ have been given by Eqs. (5c) and (6c).

3 Solution of the electrokinetic equations

3.1 Equilibrium electric potential

The equilibrium electric potential ${\psi ^{({\text{eq}})}}$ satisfying the Poisson–Boltzmann equation and relevant boundary conditions derived from Eqs. (2), (5b) and (6b) with $\nabla \mathbf{n}^{\infty }=0$ are

$${\psi ^{({\text{eq}})}}={\psi _{{\text{eq0}}1}}(r)\overline {\zeta } +{\psi _{{\text{eq}}10}}(r){\overline {\zeta } _b}+{\text{O}}({\overline {\zeta } ^3},{\text{ }}{\overline {\zeta } ^2}{\overline {\zeta } _b},{\text{ }}\overline {\zeta } \overline {\zeta } _{b}^{2},{\text{ }}\overline {\zeta } _{b}^{3}),$$

(14)

where

$${\psi _{{\text{eq}}01}}=\frac{{kTa}}{{Zer}}\frac{{{{\text{e}}^{2\kappa b}} - {{\text{e}}^{2\kappa r}}}}{{{{\text{e}}^{2\kappa b}} - {{\text{e}}^{2\kappa a}}}}{{\text{e}}^{ - \kappa (r - a)}},$$

(15a)

$${\psi _{{\text{eq}}10}}=\frac{{kTb}}{{Zer}}\frac{{{{\text{e}}^{2\kappa r}} - {{\text{e}}^{2\kappa a}}}}{{{{\text{e}}^{2\kappa b}} - {{\text{e}}^{2\kappa a}}}}{{\text{e}}^{\kappa (b - r)}},$$

(15b)

$\overline {\zeta } =Ze\zeta /kT$, ${\overline {\zeta } _b}=Ze{\zeta _b}/kT$, and $\kappa ={(2{Z^2}{{\text{e}}^2}n_{0}^{\infty }/\varepsilon kT)^{1/2}}$ is the reciprocal Debye length. Expression (14) for ${\psi ^{({\text{eq}})}}$ as a power series in the small dimensionless particle and cavity zeta potentials up to the first orders ${\text{O}}(\overline {\zeta } ,{\text{ }}{\overline {\zeta } _b})$ is the solution to the linearized Poisson–Boltzmann equation. The contribution from the effects of the second orders ${\text{O}}({\overline {\zeta } ^2},{\text{ }}\overline {\zeta } \overline {\zeta } _{b}^{{}},{\text{ }}\overline {\zeta } _{b}^{2})$ to ${\psi ^{({\text{eq}})}}$ in Eq. (14) vanishes only for the case of symmetric electrolyte solutions.

Using Eqs. (14), (15a) and (15b) together with the Gauss conditions at $r=a$ and $r=b$, we obtain the following relations between the surface charge densities and the zeta potentials of a dielectric sphere within a concentric spherical cavity:

$$\zeta =\frac{1}{\varepsilon }\frac{{a[{{\text{e}}^{2\kappa b}}(\kappa b - 1)+{{\text{e}}^{2\kappa a}}(\kappa b+1)]\sigma +2\kappa {b^2}{{\text{e}}^{\kappa (a+b)}}{\sigma _b}}}{{{{\text{e}}^{2\kappa b}}(\kappa a+1)(\kappa b - 1) - {{\text{e}}^{2\kappa a}}(\kappa a - 1)(\kappa b+1)}},$$

(16a)

$${\zeta _b}=\frac{1}{\varepsilon }\frac{{2\kappa {a^2}{{\text{e}}^{\kappa (a+b)}}\sigma +b[{{\text{e}}^{2\kappa a}}(\kappa a - 1)+{{\text{e}}^{2\kappa b}}(\kappa a+1)]{\sigma _b}}}{{{{\text{e}}^{2\kappa b}}(\kappa a+1)(\kappa b - 1) - {{\text{e}}^{2\kappa a}}(\kappa a - 1)(\kappa b+1)}},$$

(16b)

where $\sigma$ and ${\sigma _b}$ are the surface charge densities of the particle and cavity, respectively. Namely the solution of ${\psi ^{({\text{eq}})}}$ given by Eq. (14) after the substitution of Eqs. (16a) and (16b) also applies to the case of constant surface charge densities.

3.2 Perturbed quantities

To solve the small perturbations $\delta {\mu _ \pm }$, $\delta \psi$, ${\mathbf{u}}$, and $\delta p$ in terms of the particle velocity $U$ when the dimensionless zeta potentials $\bar {\zeta }$ and ${\bar {\zeta }_b}$ are small, these variables can be written as perturbation expansions in powers of $\bar {\zeta }$ and ${\bar {\zeta }_b}$, such as

$$U={U_{01}}\overline {\zeta } +{U_{10}}{\overline {\zeta } _b}+{U_{02}}{\overline {\zeta } ^2}+{U_{11}}\overline {\zeta } {\overline {\zeta } _b}+{U_{20}}{\overline {\zeta } _b}^{2}+ \cdot \cdot \cdot ,$$

(17)

where the coefficients ${U_{ij}}$ to be determined are independent of $\bar {\zeta }$ and ${\bar {\zeta }_b}$. Note that, there are no zeroth-order terms of $\bar {\zeta }$ and ${\bar {\zeta }_b}$ in ${\mathbf{u}}$, $\delta p$, and $U$. Substituting these perturbation expansions and ${\psi ^{({\text{eq}})}}$ given by Eq. (14) into the governing Eqs. (4) and (8)–(10) and boundary conditions (5c), (6c), (12a), (12b), (13a) and (13b), we obtain the following results for $\delta {\mu _ \pm }$, $\delta \psi$ (to the first orders $\bar {\zeta }$ and ${\bar {\zeta }_b}$), the $r$ and $\theta$ components of ${\mathbf{u}}$, and $\delta p$ (to the second orders ${\overline {\zeta } ^2}$, $\overline {\zeta } {\overline {\zeta } _b}$, and $\overline {\zeta } _{b}^{2}$):

$$\delta {\mu _ \pm }=kT(1 \mp \beta )\alpha ({F_{\mu 00}} \mp {F_{\mu 01}}\overline {\zeta } \mp {F_{\mu 10}}{\overline {\zeta } _b})\cos \theta ,$$

(18)

$$\delta \psi =\frac{{kT}}{{Ze}}\alpha ( - \beta {F_{\psi 00}}+{F_{\psi 01}}\overline {\zeta } +{F_{\psi 10}}{\overline {\zeta } _b})\cos \theta ,$$

(19)

$$\begin{aligned} {u_r} & =\left[\left({U_{01}}{F_{00r}} - \frac{{kT}}{{\eta {a^2}}}\beta \alpha {F_{01r}}\right)\overline {\zeta } +\left({U_{10}}{F_{00r}} - \frac{{kT}}{{\eta {a^2}}}\beta \alpha {F_{10r}}\right){\overline {\zeta } _b}+\left({U_{02}}{F_{00r}}+\frac{{kT}}{{\eta {a^2}}}\alpha {F_{02r}}\right){\overline {\zeta } ^2} \right.\\ & \quad \left. +\left({U_{11}}{F_{00r}}+\frac{{kT}}{{\eta {a^2}}}\alpha {F_{11r}}\right)\overline {\zeta } {\overline {\zeta } _b}+\left({U_{20}}{F_{00r}}+\frac{{kT}}{{\eta {a^2}}}\alpha {F_{20r}}\right){\overline {\zeta } _b}^{2}\right]\cos \theta , \\ \end{aligned}$$

(20a)

$$\begin{aligned} {u_\theta } & = \left[\left({U_{01}}{F_{00\theta }} - \frac{{kT}}{{\eta {a^2}}}\beta \alpha {F_{01\theta }}\right)\overline {\zeta } +\left({U_{10}}{F_{00\theta }} - \frac{{kT}}{{\eta {a^2}}}\beta \alpha {F_{10\theta }}\right){\overline {\zeta } _b}+\left({U_{02}}{F_{00\theta }}+\frac{{kT}}{{\eta {a^2}}}\alpha {F_{02\theta }}\right){\overline {\zeta } ^2} \right. \\ & \quad \left. +\left({U_{11}}{F_{00\theta }}+\frac{{kT}}{{\eta {a^2}}}\alpha {F_{11\theta }}\right)\overline {\zeta } {\overline {\zeta } _b}+\left({U_{20}}{F_{00\theta }}+\frac{{kT}}{{\eta {a^2}}}\alpha {F_{20\theta }}\right){\overline {\zeta } _b}^{2}\right]\sin \theta , \\ \end{aligned}$$

(20b)

$$\begin{aligned} \delta p & =\frac{\eta }{a} \left \{ \left({U_{01}}{F_{p00}} - \frac{{kT}}{{\eta {a^2}}}\beta \alpha {F_{p01}} - \frac{{\varepsilon kT}}{{\eta Ze}}{\kappa ^2}a\beta \alpha {\psi _{{\text{eq}}01}}{F_{\psi 00}}\right)\overline {\zeta } \right. \\ & \quad +\left({U_{10}}{F_{p00}} - \frac{{kT}}{{\eta {a^2}}}\beta \alpha {F_{p10}} - \frac{{\varepsilon kT}}{{\eta Ze}}{\kappa ^2}a\beta \alpha {\psi _{{\text{eq}}10}}{F_{\psi 00}}\right){\overline {\zeta } _b} \\ & \quad + \left({U_{02}}{F_{p00}}+\frac{{kT}}{{\eta {a^2}}}\alpha {F_{p02}}+\frac{{\varepsilon kT}}{{\eta Ze}}{\kappa ^2}a\alpha {\psi _{{\text{eq}}01}}{F_{\psi 01}}\right){\overline {\zeta } ^2} \\ & \quad +\left[{U_{11}}{F_{p00}}+\frac{{kT}}{{\eta {a^2}}}\alpha {F_{p11}}+\frac{{\varepsilon kT}}{{\eta Ze}}{\kappa ^2}a\alpha ({\psi _{{\text{eq}}01}}{F_{\psi 10}}+{\psi _{{\text{eq}}10}}{F_{\psi 01}})\right]\overline {\zeta } {\overline {\zeta } _b} \\ & \quad \left. +\left({U_{20}}{F_{p00}}+\frac{{kT}}{{\eta {a^2}}}\alpha {F_{p20}}+\frac{{\varepsilon kT}}{{\eta Ze}}{\kappa ^2}a\alpha {\psi _{{\text{eq}}10}}{F_{\psi 10}}\right){\overline {\zeta } _b}^{2} \right\} \cos \theta , \\ \end{aligned}$$

(20c)

where ${F_{\mu ij}}$, ${F_{\psi ij}}$, ${F_{ijr}}$, ${F_{ij\theta }}$, and ${F_{pij}}$ with $i$ and $j$ equal to 0, 1, and 2 are dimensionless functions of $r$ defined by Eqs. (35)–(37), (43a), (43b), (43c), (44a), (44b) and (44c) in the “Appendix”. Note that, the solutions of $\delta {\mu _ \pm }$ and $\delta \psi$ to the orders $\bar {\zeta }$ and ${\bar {\zeta }_b}$, which are sufficient for the calculation of the particle velocity to the orders ${\overline {\zeta } ^2}$, $\overline {\zeta } {\overline {\zeta } _b}$, and $\overline {\zeta } _{b}^{2}$, do not contain the influence of the fluid motion on the electric double layers.

4 Diffusiophoretic velocity

4.1 Forces exerted on the particle

The total force acting on the charged spherical particle in the electrolyte solution inside a concentric charged cavity can be expressed as the sum of the electric force and hydrodynamic force exerted on the particle. The electric force is given by

$${\mathbf{F}_e}=2\pi {a^2}\varepsilon \int_{0}^{\pi } {{{[\nabla \delta \psi \nabla {\psi ^{({\text{eq}})}}]}_{r=a}}{\text{ }} \cdot {\mathbf{e}_r}\sin \theta {\text{d}}\theta } .$$

(21)

Substitution of Eqs. (14) and (19) into Eq. (21) results in (to the second orders)

$$\begin{aligned} {\mathbf{F}_e} & =\frac{{8\pi kT}}{{3Ze}}\varepsilon a\alpha \left[ { - \beta \left( {{F_{\psi 00}}\frac{{{\text{d}}{\psi _{{\text{eq}}01}}}}{{{\text{d}}r}}\overline {\zeta } +{F_{\psi 00}}\frac{{{\text{d}}{\psi _{{\text{eq}}10}}}}{{{\text{d}}r}}{{\overline {\zeta } }_b}} \right)} \right. \\ & \quad {\left. {+\,{F_{\psi 01}}\frac{{{\text{d}}{\psi _{{\text{eq}}01}}}}{{{\text{d}}r}}{{\overline {\zeta } }^2}+\left( {{F_{\psi 10}}\frac{{{\text{d}}{\psi _{{\text{eq}}01}}}}{{{\text{d}}r}}+{F_{\psi 01}}\frac{{{\text{d}}{\psi _{{\text{eq}}10}}}}{{{\text{d}}r}}} \right)\overline {\zeta } {{\overline {\zeta } }_b}+{F_{\psi 10}}\frac{{{\text{d}}{\psi _{{\text{eq}}10}}}}{{{\text{d}}r}}{{\overline {\zeta } }_b}^{2}} \right]_{r=a}}{\mathbf{e}_z}. \\ \end{aligned}$$

(22)

The hydrodynamic drag force is given by the integral of the fluid pressure and viscous stress over the particle surface,

$${\mathbf{F}_h}=2\pi {a^2}\int_{0}^{\pi } {{{\{ - \delta p\mathbf{I}+\eta [\nabla \mathbf{u}+{{(\nabla \mathbf{u})}^{\text{T}}}]\} }_{r=a}} \cdot {\mathbf{e}_r}\sin \theta {\text{d}}\theta } ,$$

(23)

where ${\mathbf{I}}$ is the unit dyadic. Substitution of Eqs. (20a), (20b) and (20c) into the above equation leads to

$$\begin{aligned} {\mathbf{F}_h} & = - 4\pi \left\{ {\left[ {\eta a{U_{01}}{C_{002}} - \frac{{kT}}{a}\beta \alpha {C_{012}} - \frac{{\varepsilon kT}}{{3Ze}}{{(\kappa a)}^2}\beta \alpha {\psi _{{\text{eq}}01}}{F_{\psi 00}}} \right]\overline {\zeta } } \right. \\ & \quad +\left[ {\eta a{U_{10}}{C_{002}} - \frac{{kT}}{a}\beta \alpha {C_{102}}} \right]{\overline {\zeta } _b} \\ & \quad +\left[ {\eta a{U_{02}}{C_{002}}+\frac{{kT}}{a}\alpha {C_{022}}+\frac{{\varepsilon kT}}{{3Ze}}{{(\kappa a)}^2}\alpha {\psi _{{\text{eq}}01}}{F_{\psi 01}}} \right]{\overline {\zeta } ^2} \\ & \quad +\left[ {\eta a{U_{11}}{C_{002}}+\frac{{kT}}{a}\alpha {C_{112}}+\frac{{\varepsilon kT}}{{3Ze}}{{(\kappa a)}^2}\alpha {\psi _{{\text{eq}}01}}{F_{\psi 10}}} \right]\overline {\zeta } {\overline {\zeta } _b} \\ & \quad {\left. {+\left[ {\eta a{U_{20}}{C_{002}}+\frac{{kT}}{a}\alpha {C_{202}}} \right]{{\overline {\zeta } }_b}^{2}} \right\}_{r=a}}{\mathbf{e}_z} , \\ \end{aligned}$$

(24)

where the dimensionless coefficients ${C_{002}}$, ${C_{012}}$, ${C_{102}}$, ${C_{022}}$, ${C_{112}}$ and ${C_{202}}$ are given by Eqs. (45a), (45b), (45c), (45d), (46a), (46b), (46c) and (46d).

4.2 Velocity of the particle

At the quasisteady state, the total force acting on the particle is zero. Using this constraint after the addition of Eqs. (22) and (24), we obtain

$${U_{01}}=\frac{{Ze\beta {U^*}}}{{3\varepsilon akT{C_{002}}}}{\left[ {3Ze{C_{012}}+\varepsilon {a^2}{F_{\psi 00}}\left( {{\kappa ^2}a{\psi _{{\text{eq}}01}} - 2\frac{{{\text{d}}{\psi _{{\text{eq}}01}}}}{{{\text{d}}r}}} \right)} \right]_{r=a}},$$

(25a)

$${U_{10}}=\frac{{Ze\beta {U^*}}}{{3\varepsilon akT{C_{002}}}}{\left[ {3Ze{C_{102}} - 2\varepsilon {a^2}{F_{\psi 00}}\frac{{{\text{d}}{\psi _{{\text{eq}}10}}}}{{{\text{d}}r}}} \right]_{r=a}},$$

(25b)

$${U_{02}}=\frac{{ - Ze{U^*}}}{{3\varepsilon akT{C_{002}}}}{\left[ {3Ze{C_{022}}+\varepsilon {a^2}{F_{\psi 01}}\left( {{\kappa ^2}a{\psi _{{\text{eq}}01}} - 2\frac{{{\text{d}}{\psi _{{\text{eq}}01}}}}{{{\text{d}}r}}} \right)} \right]_{r=a}},$$

(26a)

$${U_{11}}=\frac{{ - Ze{U^*}}}{{3\varepsilon akT{C_{002}}}}{\left\{ {3Ze{C_{112}}+\varepsilon {a^2}\left[ {{F_{\psi 10}}\left( {{\kappa ^2}a{\psi _{{\text{eq}}01}} - 2\frac{{{\text{d}}{\psi _{{\text{eq}}01}}}}{{{\text{d}}r}}} \right) - 2{F_{\psi 01}}\frac{{{\text{d}}{\psi _{{\text{eq}}10}}}}{{{\text{d}}r}}} \right]} \right\}_{r=a}},$$

(26b)

$${U_{20}}=\frac{{ - Ze{U^*}}}{{3\varepsilon akT{C_{002}}}}{\left[ {3Ze{C_{202}} - 2\varepsilon {a^2}{F_{\psi 10}}\frac{{{\text{d}}{\psi _{{\text{eq}}10}}}}{{{\text{d}}r}}} \right]_{r=a}},$$

(26c)

where the characteristic particle velocity

$${U^*}=\frac{{\varepsilon \alpha }}{{\eta a}}{\left( {\frac{{kT}}{{Ze}}} \right)^2}.$$

(27)

The diffusiophoretic velocity $U$ of the charged particle inside the charged cavity is expressed in the expansion form of Eq. (17) with the leading coefficients, which are functions of the electrokinetic radius $\kappa a$ and the particle-to-cavity radius ratio $a/b$, given by Eqs. (25a), (25b), (26a), (26b) and (26c). This expansion with the substitution of Eqs. (16a) and (16b) is also valid for the case of constant surface charge densities of the particle and cavity. Since the solutions of $\delta {\mu _ \pm }$ and $\delta \psi$ given by Eqs. (18) and (19) are not affected by the fluid flow, the effect of the relaxation of the mobile ions in the electric double layers adjacent to the solid surfaces is not embodied in Eq. (17) up to the orders ${\overline {\zeta } ^2}$, $\overline {\zeta } {\overline {\zeta } _b}$, and $\overline {\zeta } _{b}^{2}$. Recently, the diffusiophoretic motion of a spherical particle with the polarization effect of its thin double layer in a charged cavity has been analyzed to some extent (Chiu and Keh 2017a).

In Eq. (17) for the migration velocity of the confined particle undergoing diffusiophoresis, the ${\text{O}}(\overline {\zeta } ,{\text{ }}{\overline {\zeta } _b})$ (first-order) and ${\text{O}}({\overline {\zeta } ^2},{\text{ }}\overline {\zeta } \overline {\zeta } _{b}^{{}},{\text{ }}\overline {\zeta } _{b}^{2})$ (second-order) terms represent contributions from the electrophoresis [due to the induced electric field given by Eq. (6b)] and chemiphoresis (due to the nonuniform adsorption of counterions over the particle surface), respectively. The charge on the cavity wall (effect of ${\text{ }}{\overline {\zeta } _b}$) modifies the motion of the particle via the wall-corrected electric potential distribution over the particle surface as well as the diffusioosmotic (electroosmotic and chemiosmotic) circulation flow caused by the interaction of the applied electrolyte concentration gradient with the double layer adjoining the wall (significant at large $\kappa b$). Note that ${U_{01}}\overline {\zeta } +{U_{02}}{\overline {\zeta } ^2}$ and ${U_{10}}{\overline {\zeta } _b}+{U_{20}}{\overline {\zeta } _b}^{2}$ can be taken as the diffusiophoretic (electrophoretic and chemiphoretic) velocity of a charged particle in an uncharged cavity (${\zeta _b}=0$) and the migration velocity of an uncharged particle ($\zeta =0$) in a charged cavity induced by diffusioosmosis (electroosmosis and chemiosmosis), respectively. In addition, Eqs. (25a) and (25b) agrees with the previous results obtained for the electrophoresis of a more general charged sphere within a concentric charged cavity (Keh and Hsieh 2008; Chen and Keh 2013).

5 Results and discussion

5.1 The velocity coefficients ${U_{01}}$ and ${U_{10}}$ for electrophoresis

The dimensionless velocities ${U_{01}}/\beta {U^*}$ and ${U_{10}}/\beta {U^*}$ for the electrophoresis of a charged spherical particle in a concentric charged spherical cavity calculated from Eqs. (25a) and (25b) are functions of the electrokinetic particle radius $\kappa a$ and the particle-to-cavity radius ratio $a/b$ only. For very thin electric double layers adjacent to the solid surfaces ($\kappa a \to \infty$), Eqs. (25a) and (25b) leads to

$$\frac{{{U_{01}}}}{{\beta {U^*}}}={(1 - \xi )^2}\frac{{2+4\xi +6{\xi ^2}+3{\xi ^3}}}{{(2+{\xi ^3})(1 - {\xi ^5})}},$$

(28a)

$$\frac{{{U_{10}}}}{{\beta {U^*}}}={(1 - \xi )^2}\frac{{6+12\xi +8{\xi ^2}+7{\xi ^3}+6{\xi ^4}+4{\xi ^5}+2{\xi ^6}}}{{3(2+{\xi ^3})(1 - {\xi ^5})}},$$

(28b)

where $\xi =a/b$. For very thick double layers ($\kappa b=0$), Eqs. (25a) and (25b) leads to

$$\frac{{{U_{01}}}}{{\beta {U^*}}}= - \frac{{{U_{10}}}}{{\beta {U^*}}}=\frac{{{{(1 - \xi )}^2}(4+7\xi +4{\xi ^2})}}{{3(2+{\xi ^3})(1+\xi +{\xi ^2}+{\xi ^3}+{\xi ^4})}}.$$

(29)

Note that the sign of ${U_{10}}/\beta {U^*}$ is positive and negative in the limits $\kappa a \to \infty$ and $\kappa a=0$, respectively, but the sign of ${U_{01}}/\beta {U^*}$ is positive for both limits.

As $a/b=0$ (the cavity wall is very far from the particle), Eqs. (25a) and (25b) becomes

$$\frac{{{U_{01}}}}{{\beta {U^*}}}=1 - {{\text{e}}^{\kappa a}}[5{E_7}(\kappa a) - 2{E_5}(\kappa a)],$$

(30a)

$$\frac{{{U_{10}}}}{{\beta {U^*}}}=1,$$

(30b)

where

$${E_n}(\kappa a)={(\kappa a)^{n - 1}}\int_{{\kappa a}}^{{{\text{ }}\infty }} {{t^{ - n}}{{\text{e}}^{ - t}}{\text{d}}t} .$$

(31)

Note that ${U_{10}}/\beta {U^*}$ is singular (equal to values from $- 2/3$ to 1) for the limiting case of $\kappa a=0$ and $a/b=0$. As $a/b=1$ (the particle fills the cavity up entirely), Eqs. (25a) and (25b) yields ${U_{01}}={U_{10}}=0$ as expected.

The dimensionless velocities ${U_{01}}/\beta {U^*}$ and ${U_{10}}/\beta {U^*}$ as calculated from Eqs. (25a) and (25b) are plotted versus the parameters $\kappa a$ and $a/b$ in Figs. 2 and 3, respectively. Certainly, ${U_{01}}/\beta {U^*}$ is always positive and the sign of the product $\beta \zeta$ determines the direction of electrophoresis. For a specified value of $a/b$, the value of ${U_{01}}/\beta {U^*}$ increases with an increase in $\kappa a$ (a decrease in the overlap of electric double layers). For a fixed value of $\kappa a$, the value of ${U_{01}}/\beta {U^*}$ decreases with an increase in $a/b$ from a value between 2/3 (as $\kappa a=0$) and unity (as $\kappa a \to \infty$) at $a/b=0$ (as predicted by Eq. (30a) for an unconfined spherical particle) to zero at $a/b=1$.

Fig. 2

The dimensionless velocity ${U_{01}}/\beta {U^*}$ for the electrophoresis of a charged spherical particle in a spherical cavity as calculated from Eq. (25a) versus the parameters $\kappa a$ and $a/b$

Fig. 3

The dimensionless velocity ${U_{10}}/\beta {U^*}$ for a spherical particle in a charged spherical cavity with electroosmosis as calculated from Eq. (25b) versus the parameters $\kappa a$ and $a/b$

On the other hand, ${U_{10}}/\beta {U^*}$, which has the same order of magnitude as ${U_{01}}/\beta {U^*}$, can be either positive or negative, depending on the parameters $\kappa a$ and $a/b$. For a specified value of $a/b$, the value of ${U_{10}}/\beta {U^*}$ also increases with an increase in $\kappa a$, but from a negative constant as $\kappa a=0$ to a positive constant as $\kappa a \to \infty$, which is understood that the electroosmotic circulation flow developing from the interaction of the induced electric field with the electric double layer adjacent to the cavity wall drives an uncharged particle to move in opposite directions when the double layer varies from thin to thick. For a finite value of $\kappa a$, the dimensionless velocity ${U_{10}}/\beta {U^*}$ may not be a monotonic function of $a/b$ (have a minimum which is negative at a moderate value of $a/b$) but still equals unity at $a/b=0$ and vanishes at $a/b=1$. When $\kappa a \to \infty$/$\kappa a=0$, as predicted by Eqs. (28b)/(29), ${U_{10}}/\beta {U^*}$ decreases/increases monotonically with an increase in $a/b$ from unity/$- 2/3$ at $a/b=0$ to zero at $a/b=1$.

To determine the first-order migration velocity ${U_1}={U_{01}}\overline {\zeta } +{U_{10}}{\overline {\zeta } _b}$ of a charged particle undergoing electrophoresis in a charged cavity with zeta potentials of same or opposite signs, not only the parameters $\kappa a$ and $a/b$ but also the zeta potentials $\overline {\zeta }$ and ${\overline {\zeta } _b}$ have to be specified. Since Figs. 2 and 3 indicate that the values of ${U_{01}}$ and ${U_{10}}$ are in the same order of magnitude, the effect of the cavity wall can conspicuously enhance or reduce the velocity of the particle. In Fig. 4, the normalized particle velocity ${U_1}/\overline {\zeta } \beta {U^*}$ is plotted versus the cavity-to-particle zeta potential ratio ${\overline {\zeta } _b}/\overline {\zeta }$ (as a linear function) for various values of $\kappa a$ and $a/b$ (in straight lines with the slope ${U_{10}}/\beta {U^*}$, which can be either positive or negative). As expected, the cavity wall effect on the migration of the particle can be significant as the magnitude of ${\overline {\zeta } _b}/\overline {\zeta }$ is large. When the magnitude of ${\overline {\zeta } _b}/\overline {\zeta }$ is greater than about unity, the confined particle may reverse the direction of its velocity from that of electrophoresis in an unbounded fluid. Again, the magnitude of ${U_1}/\overline {\zeta } \beta {U^*}$ in general increases with an increase in $\kappa a$ and decreases with an increase in $a/b$.

Fig. 4

The normalized velocity ${U_1}/\overline {\zeta } \beta {U^*}$ for the electrophoresis of a charged spherical particle in a charged spherical cavity versus the zeta potential ratio ${\overline {\zeta } _b}/\overline {\zeta }$: a $\kappa a=1$; b $a/b=0.5$

5.2 The velocity coefficients ${U_{02}}$, ${U_{11}}$, and ${U_{20}}$ for chemiphoresis

The dimensionless velocities ${U_{02}}/{U^*}$, ${U_{11}}/{U^*}$, and ${U_{20}}/{U^*}$ for the chemiphoresis of a charged particle in a charged cavity calculated from Eqs. (26a), (26b) and (26c) are also functions of the electrokinetic radius $\kappa a$ and radius ratio $a/b$ only. In the limit $\kappa a \to \infty$, Eqs. (26a), (26b) and (26c) leads to

$$\frac{{{U_{02}}}}{{{U^*}}}=\frac{{{U_{01}}}}{{8\beta {U^*}}},$$

(32a)

$$\frac{{{U_{11}}}}{{{U^*}}}=0,$$

(32b)

$$\frac{{{U_{20}}}}{{{U^*}}}=\frac{{{U_{10}}}}{{8\beta {U^*}}},$$

(32c)

where ${U_{01}}$ and ${U_{10}}$ are given by Eqs. (28a) and (28b). Eqs. (32a), (32b) and (32c) together with Eqs. (28a) and (28b) agrees with the analytical formula obtained by Chiu and Keh (2017a) for the diffusiophoretic mobility of a charged sphere in a concentric charged cavity with thin but polarized double layers. In the limit $\kappa a=0$, Eqs. (26a), (26b) and (26c) leads to

$$\frac{{{U_{02}}}}{{{U^*}}}=\frac{{{U_{11}}}}{{{U^*}}}=\frac{{{U_{20}}}}{{{U^*}}}=0.$$

(33)

As $a/b=0$, Eqs. (26a), (26b) and (26c) becomes

$$\begin{aligned} \frac{{{U_{02}}}}{{{U^*}}} & =\frac{1}{8}\left\{ {1+\frac{1}{3}{{\text{e}}^{2\kappa a}}[10{E_6}(2\kappa a)+7{E_8}(2\kappa a)] - 40{{\text{e}}^{2\kappa a}}{E_7}(\kappa a)[{E_3}(\kappa a) - {E_5}(\kappa a)]} \right. \\ & \quad \left. {+{\text{ }}\frac{4}{3}{{\text{e}}^{\kappa a}}[3{E_3}(\kappa a)+9{E_4}(\kappa a) - 7{E_5}(\kappa a) - 15{E_6}(\kappa a)]} \right\} , \\ \end{aligned}$$

(34a)

$$\frac{{{U_{11}}}}{{{U^*}}}={\text{ 0,}}$$

(34b)

$${\text{ }}\frac{{{U_{20}}}}{{{U^*}}}=\frac{1}{8},$$

(34c)

where ${E_n}(\kappa a)$ was defined by Eq. (31). As $a/b=1$, Eqs. (26a), (26b) and (26c) gives ${U_{02}}={U_{11}}={U_{20}}=0$ as expected.

The dimensionless velocities ${U_{02}}/{U^*}$, ${U_{11}}/{U^*}$, and ${U_{20}}/{U^*}$ as calculated from Eqs. (26a), (26b) and (26c) are plotted versus the parameters $\kappa a$ and $a/b$ in Figs. 5, 6 and 7, respectively. The values of ${U_{02}}/{U^*}$ and ${U_{20}}/{U^*}$ can be either positive or negative, but ${U_{11}}/{U^*}$ for the coupling effect of $\overline {\zeta }$ and ${\text{ }}{\overline {\zeta } _b}$ is always positive. Interestingly, none of these second-order velocities is a monotonic function of either $\kappa a$ or $a/b$, and local minima (which are negative for ${U_{02}}/{U^*}$ and ${U_{20}}/{U^*}$) and maxima (which are positive) may exist at moderate values of $\kappa a$ and $a/b$. As a general trend, the values of ${U_{02}}/{U^*}$ and ${U_{20}}/{U^*}$ tend to decrease with an increase in $a/b$ and increase with an increase in $\kappa a$. In the limit $\kappa a \to \infty$, as predicted by Eqs. (32a) and (32c), both ${U_{02}}/{U^*}$ and ${U_{20}}/{U^*}$ decrease monotonically with an increase in $a/b$ from 1/8 at $a/b=0$ to zero at $a/b=1$. In the limit $\kappa a=0$, as predicted by Eq. (33), all the three dimensionless velocities vanish. In the limit $a/b=0$, as predicted by Eq. (34a), ${U_{02}}/{U^*}$ increases monotonically with an increase in $\kappa a$ from zero as $\kappa a=0$ to 1/8 as $\kappa a \to \infty$.

Fig. 5

The dimensionless velocity ${U_{02}}/{U^*}$ for the chemiphoresis of a charged spherical particle in a spherical cavity as calculated from Eq. (26a) versus the parameters $\kappa a$ and $a/b$

Fig. 6

The dimensionless velocity ${U_{11}}/{U^*}$ for a charged spherical particle in a charged spherical cavity as calculated from Eq. (26b) versus the parameters $\kappa a$ and $a/b$

Fig. 7

The dimensionless velocity ${U_{20}}/{U^*}$ for a spherical particle in a charged spherical cavity with chemiosmosis as calculated from Eq. (26c) versus the parameters $\kappa a$ and $a/b$

The second-order migration velocity ${U_2}={U_{02}}{\overline {\zeta } ^2}+{U_{11}}\overline {\zeta } {\overline {\zeta } _b}+{U_{20}}{\overline {\zeta } _b}^{2}$ of a charged particle undergoing chemiphoresis in a charged cavity depends on the parameters $\kappa a$ and $a/b$ as well as the zeta potentials $\overline {\zeta }$ and ${\overline {\zeta } _b}$. In Fig. 8, the normalized particle velocity ${U_2}/{\overline {\zeta } ^2}{U^*}$ is plotted versus the ratio ${\overline {\zeta } _b}/\overline {\zeta }$ for various values of $\kappa a$ and $a/b$ in parabolic curves which can concave upward (with positive ${U_{20}}/{U^*}$) or downward (with negative ${U_{20}}/{U^*}$). Therefore, when the value of ${\overline {\zeta } _b}/\overline {\zeta }$ varies, the particle may reverse the direction of this velocity twice for fixed values of $\kappa a$ and $a/b$. Again, the cavity wall effect on the motion of the particle can be significant if the magnitude of ${\overline {\zeta } _b}/\overline {\zeta }$ is greater than the order unity, and the magnitude of ${U_2}/{\overline {\zeta } ^2}{U^*}$ in general increases with an increase in $\kappa a$ from zero at $\kappa a=0$ and decreases with an increase in $a/b$ to zero at $a/b=1$.

Fig. 8

The normalized velocity ${U_2}/{\overline {\zeta } ^2}{U^*}$ for the chemiphoresis of a charged spherical particle in a charged spherical cavity versus the zeta potential ratio ${\overline {\zeta } _b}/\overline {\zeta }$: a $\kappa a=1$; b $a/b=0.5$

5.3 Diffusiophoretic velocity

For the case of a charged spherical particle undergoing diffusiophoresis within a concentric charged cavity filled with a symmetric electrolyte solution having equal cation and anion diffusion coefficients ($\beta =0$, associated with the aqueous KCl solution), Fig. 8 already gives the result of its normalized migration velocity $U/{U^*}$ calculated from Eq. (17) [equal to ${U_2}/{U^*}$ with only chemiphoretic and chemiosmotic contributions] as a function of the parameters $\kappa a$ and $a/b$ as well as the zeta potentials $\overline {\zeta }$ and ${\overline {\zeta } _b}$. In Fig. 9, $U/{U^*}$ is plotted versus ${\overline {\zeta } _b}$ with $\overline {\zeta } =1$ and various values of $\kappa a$ and $a/b$ for a typical case that the cation and anion are unequal in diffusivity ($\beta = -\,0.2$, associated with the aqueous NaCl solution), and both electrophoresis and chemiphoresis exist (as a combination of Figs. 4, 8). Since our analysis is based on the assumption of small zeta potentials, the magnitudes of $\overline {\zeta }$ and ${\overline {\zeta } _b}$ considered are less than 2. Because the wall effect on the chemiphoresis of the particle may be in competition with that on the induced electrophoresis, for specified values of $\kappa a$ and $a/b$, the particle may reverse the direction of its velocity more than once when the zeta potential ratio ${\overline {\zeta } _b}/\overline {\zeta }$ varies monotonically, and the cavity wall effect can be significant as the magnitude of ${\overline {\zeta } _b}/\overline {\zeta }$ is greater than the order unity. The magnitude of $U/{U^*}$ does not vary monotonically with the relative separation distance for some situations but in general decreases with an increase in $a/b$ to zero at $a/b=1$.

Fig. 9

The normalized velocity $U/{U^*}$ for the diffusiophoresis of a charged spherical particle in a charged spherical cavity with $\beta = - 0.2$ and $\overline {\zeta } =1$ versus the zeta potential ${\overline {\zeta } _b}$: a $\kappa a=1$; b $a/b=0.5$

6 Conclusions

In this work, the quasisteady diffusiophoresis of a charged spherical particle situated at the center of a charged spherical cavity caused by a prescribed concentration gradient of a symmetric electrolyte is analyzed for the general case of arbitrary values of the particle-to-cavity radius ratio $a/b$ and electrokinetic particle radius $\kappa a$. Solving the linearized electrokinetic equations applicable to the transport system, which is assumed slightly distorted from equilibrium, by a perturbation method, we obtain the electric potential profile, ionic electrochemical potential energy distributions, and velocity field in the electrolyte solution as power expansions in the small zeta potentials associated with the particle and cavity. The requirement that the sum of the electrostatic and hydrodynamic forces acting on the particle vanishes results in an explicit expression, Eqs. (17) and (25a)–(27), for the diffusiophoretic velocity of the particle as a function of the parameters $a/b$ and $\kappa a$ to the second orders of the zeta potentials. The contributions from the diffusioosmotic flow taking place along the cavity wall and from the wall-corrected diffusiophoretic force to the particle velocity are equivalently important, and this diffusioosmotic flow can reverse the direction of the particle velocity.

Appendix: functions in Eqs. (18)–(20c)

In Eqs. (18) and (19),

$${F_{\mu 00}}(r)={F_{\psi 00}}(r)=\frac{1}{{{\chi _{}}}}\left( {\frac{r}{a}+\frac{{{a^2}}}{{2{r^2}}}} \right),$$

(35)

$$\begin{aligned} F_{{\mu ij}} (r) & = \frac{{Zer}}{{3kTa\chi _{{}} }}\Bigg\{ {\frac{{a^{3} A_{{\mu ij}} (a,b) + 2(1 - \chi )B_{{\mu ij}} (a,b)}}{{2\chi r^{3} }} + \frac{{1 - \chi }}{\chi }\left[ {A_{{\mu ij}} (a,b) + \frac{2}{{a^{3} }}B_{{\mu ij}} (a,b)} \right]} \\ & {\quad + \frac{1}{{r^{3} }}B_{{\mu ij}} (a,r) + A_{{\mu ij}} (r,b)} \Bigg\}, \\ \end{aligned}$$

(36)

$$\begin{aligned} {F_{\psi ij}}(r) & =\frac{1}{{{\kappa ^3}{r^2}}}\Bigg\{ {\frac{{[{g_{1+}}(\kappa a) - {{\text{e}}^{2\kappa a}}{g_{1 - }}(\kappa a)]{A_{\psi ij}}(a,b)+2{g_{1+}}(\kappa a){B_{\psi ij}}(a,b)}}{{{{\text{e}}^{2\kappa a}}{g_{2+}}(\kappa b){g_{1 - }}(\kappa a) - {{\text{e}}^{2\kappa b}}{g_{2 - }}(\kappa b){g_{1+}}(\kappa a)}}} \\ & \quad \times \left[ {{g_{2+}}(\kappa b)\gamma (\kappa r)+\frac{1}{2}\{ {g_{2+}}(\kappa b) - {{\text{e}}^{2\kappa b}}{g_{2 - }}(\kappa b)\} (\kappa r+1){{\text{e}}^{ - \kappa r}}} \right] \\ & \quad +\gamma (\kappa r){A_{\psi ij}}(r,b) - (\kappa r+1){{\text{e}}^{ - \kappa r}}{B_{\psi ij}}(r,b) \Bigg\} , \\ \end{aligned}$$

(37)

where ($i$,$j$) equal to (0,1) or (1,0), $\chi =1+{a^3}/2{b^3}$,

$${A_{\mu ij}}(x,y)=\int_{x}^{y} {\left( {1 - \frac{{{a^3}}}{{{r^3}}}} \right)\frac{{{\text{d}}{\psi _{{\text{eq}}ij}}}}{{{\text{d}}r}}} {\text{d}}r,$$

(38a)

$${B_{\mu ij}}(x,y)=\int_{x}^{y} {({r^3} - {a^3})\frac{{{\text{d}}{\psi _{{\text{eq}}ij}}}}{{{\text{d}}r}}} {\text{d}}r,$$

(38b)

$${A_{\psi ij}}(x,y)={\kappa ^2}\int_{x}^{y} {{{\text{e}}^{ - \kappa r}}(\kappa r+1){W_{ij}}(r){\text{d}}r} ,$$

(39a)

$${B_{\psi ij}}(x,y)={\kappa ^2}\int_{x}^{y} {\gamma (\kappa r){W_{ij}}(r){\text{d}}r} ,$$

(39b)

$${g_{1 \pm }}(x)=2 \pm 2x+{x^2},$$

(40a)

$${g_{2 \pm }}(x)=1 \pm x,$$

(40b)

$$\gamma (x)=\sinh x - x\cosh x,$$

(41)

$${W_{ij}}(r)=\left[ {{F_{\mu ij}}(r)+\frac{{Ze}}{{kT}}{\psi _{{\text{eq}}ij}}(r){F_{\mu 00}}(r)} \right].$$

(42)

In Eqs. (20a), (20b) and (20c),

$${F_{00r}}(r)={C_{001}}+{C_{002}}\frac{a}{r}+{C_{003}}{\left( {\frac{a}{r}} \right)^3}+{C_{004}}{\left( {\frac{r}{a}} \right)^2},$$

(43a)

$${F_{00\theta }}(r)= - {C_{001}} - \frac{{{C_{002}}}}{2}\frac{a}{r}+\frac{{{C_{003}}}}{2}{\left( {\frac{a}{r}} \right)^3} - 2{C_{004}}{\left( {\frac{r}{a}} \right)^2},$$

(43b)

$${F_{p00}}(r)={C_{002}}{\left( {\frac{a}{r}} \right)^2}+10{C_{004}}\frac{r}{a},$$

(43c)

$$\begin{aligned} {F_{ijr}}(r) & ={C_{ij1}}+{C_{ij2}}\frac{a}{r}+{C_{ij3}}{\left( {\frac{a}{r}} \right)^3}+{C_{ij4}}{\left( {\frac{r}{a}} \right)^2}+\frac{1}{5}{\left( {\frac{a}{r}} \right)^3}J_{{ij}}^{{(5)}}(r) \\ & \quad - \frac{a}{r}J_{{ij}}^{{(3)}}(r)+J_{{ij}}^{{(2)}}(r) - \frac{1}{5}{\left( {\frac{r}{a}} \right)^2}J_{{ij}}^{{(0)}}(r), \\ \end{aligned}$$

(44a)

$$\begin{aligned} {F_{ij\theta }}(r) & = - {C_{ij1}} - \frac{{{C_{ij2}}}}{2}\frac{a}{r}+\frac{{{C_{ij3}}}}{2}{\left( {\frac{a}{r}} \right)^3} - 2{C_{ij4}}{\left( {\frac{r}{a}} \right)^2}+\frac{1}{{10}}{\left( {\frac{a}{r}} \right)^3}J_{{ij}}^{{(5)}}(r) \\ & \quad +\frac{a}{{2r}}J_{{ij}}^{{(3)}}(r) - J_{{ij}}^{{(2)}}(r)+\frac{2}{5}{\left( {\frac{r}{a}} \right)^2}J_{{ij}}^{{(0)}}(r), \\ \end{aligned}$$

(44b)

$${F_{pij}}(r)={C_{ij2}}{\left( {\frac{a}{r}} \right)^2}+10{C_{ij4}}\frac{r}{a} - 2\frac{r}{a}J_{{ij}}^{{(0)}}(r) - {\left( {\frac{a}{r}} \right)^2}J_{{ij}}^{{(3)}}(r),$$

(44c)

where ($i$,$j$) equals (0,1), (1,0), (0,2), (1,1), and (2,0),

$${C_{001}}=\frac{1}{\omega }a(4{a^4}+4{a^3}b+4{a^2}{b^2}+9a{b^3}+9{b^4}),$$

(45a)

$${C_{002}}= - \frac{6}{\omega }b({a^4}+{a^3}b+{a^2}{b^2}+a{b^3}+{b^4}),$$

(45b)

$${C_{003}}=\frac{2}{\omega }{b^3}({a^2}+ab+{b^2}),$$

(45c)

$${C_{004}}= - \frac{3}{\omega }{a^3}b(a+b),$$

(45d)

$$\begin{aligned} {C_{ij1}} & ={\left( {\frac{b}{a}} \right)^2}{C_{004}}J_{{ij}}^{{(0)}}(b)+\frac{1}{\omega }b{\text{(}}9{a^4}+9{a^3}b+4{a^2}{b^2}+4a{b^3}+4{b^4}{\text{)}}J_{{ij}}^{{(2)}}(b) \\ & \quad +\frac{a}{b}{C_{002}}J_{{ij}}^{{(3)}}(b)+{\left( {\frac{a}{b}} \right)^3}{C_{003}}J_{{ij}}^{{(5)}}(b), \\ \end{aligned}$$

(46a)

$${C_{ij2}}={C_{003}}J_{{ij}}^{{(0)}}(b)+{C_{002}}J_{{ij}}^{{(2)}}(b)+{C_{001}}J_{{ij}}^{{(3)}}(b)+{C_{004}}J_{{ij}}^{{(5)}}(b),$$

(46b)

$$\begin{aligned} {C_{ij3}} & = - \frac{6}{{5\omega }}{b^5}J_{{ij}}^{{(0)}}(b)+{C_{003}}J_{{ij}}^{{(2)}}(b)+{\left( {\frac{b}{a}} \right)^2}{C_{004}}J_{{ij}}^{{(3)}}(b) \\ & \quad - \frac{1}{{5\omega }}{a^3}(4{a^2} - 5ab - 5{b^2})J_{{ij}}^{{(5)}}(b), \\ \end{aligned}$$

(46c)

$$\begin{aligned} {C_{ij4}} & =\frac{1}{{5\omega }}{b^3}(5{a^2}+5ab - 4{b^2})J_{{ij}}^{{(0)}}(b)+{C_{004}}J_{{ij}}^{{(2)}}(b) \\ & \quad +{\left( {\frac{a}{b}} \right)^3}{C_{003}}J_{{ij}}^{{(3)}}(b) - \frac{6}{{5\omega }}{a^5}J_{{ij}}^{{(5)}}(b) , \\ \end{aligned}$$

(46d)

$$\omega ={{\text{(}}a - b{\text{)}}^3}{\text{(}}4{a^2}+7ab+4{b^2}{\text{),}}$$

(47)

$$J_{{ij}}^{{(n)}}(r)=\int_{a}^{r} {{{\left( {\frac{r}{a}} \right)}^n}{G_{ij}}(r){\text{d}}r} ,$$

(48)

$${G_{01}}(r)=\frac{{\varepsilon {\kappa ^2}{a^4}}}{{3Zer}}{F_{\mu 00}}(r)\frac{{{\text{d}}{\psi _{{\text{eq}}01}}}}{{{\text{d}}r}},$$

(49a)

$${G_{10}}(r)=\frac{{\varepsilon {\kappa ^2}{a^4}}}{{3Zer}}{F_{\mu 00}}(r)\frac{{{\text{d}}{\psi _{{\text{eq}}10}}}}{{{\text{d}}r}},$$

(49b)

$${G_{02}}(r)= - \frac{{\varepsilon {\kappa ^2}{a^4}}}{{3Zer}}{W_{01}}(r)\frac{{{\text{d}}{\psi _{{\text{eq}}01}}}}{{{\text{d}}r}},$$

(50a)

$${G_{11}}(r)= - \frac{{\varepsilon {\kappa ^2}{a^4}}}{{3Zer}}\left[ {{W_{01}}(r)\frac{{{\text{d}}{\psi _{{\text{eq}}10}}}}{{{\text{d}}r}}+{W_{10}}(r)\frac{{{\text{d}}{\psi _{{\text{eq}}01}}}}{{{\text{d}}r}}} \right],$$

(50b)

$${G_{20}}(r)= - \frac{{\varepsilon {\kappa ^2}{a^4}}}{{3Zer}}{W_{10}}(r)\frac{{{\text{d}}{\psi _{{\text{eq}}10}}}}{{{\text{d}}r}}.$$

(50c)