1 Introduction

A charged solid surface in contact with an electrolyte solution is surrounded by a diffuse cloud of ions carrying a total charge equal and opposite in sign to that of the solid surface. This distribution of fixed charge and adjacent diffuse ions is known as an electric double layer. When a charged colloidal particle is subjected to an external electric field, a force is exerted on both parts of the double layer. The suspended particle is attracted toward the electrode of its opposite sign, while the ions in the diffuse layer migrate in the other direction. This particle motion is termed electrophoresis and has long been applied to the particle analysis and separation in a variety of physicochemical and biomedical systems (Hunter 1981; Masliyah and Bhattacharjee 2006).

The electrophoretic velocity U 0 of a dielectric particle of arbitrary shape and thin double layer (relative to the local radii of curvature of the particle) in an unbounded ionic solution is related to the uniformly imposed electric field E ∞ by the well-known Smoluchowski equation (Morrison 1970; Anderson 1989),

$${\mathbf{U}}_{0} = \frac{{\varepsilon \zeta_{\text{p}} }}{\eta }{\mathbf{E}}_{\infty } ,$$
(1)

where η and ε are the viscosity and permittivity, respectively, of the fluid, and \(\zeta_{\text{p}}\) is the zeta potential associated with the particle surface. Since the thickness of the double layer usually ranges from several to tens of nanometers, which is much smaller than the typical particle size, Eq. 1 has been used widely in practice.

On the other hand, the interaction between the ions in the mobile portion of the double layer adjoining a charged solid surface with the zeta potential \(\zeta_{\text{w}}\) and an external electric field generates a tangential velocity for the fluid within the diffuse layer. This electroosmotic velocity at each point on the outer edge of the thin diffuse layer, which appears as a slip velocity relative to the frame of the solid surface, is given by the classic Helmholtz equation,

$${\mathbf{v}}_{\text{s}} = - \frac{{\varepsilon \zeta_{\text{w}} }}{\eta }{\mathbf{E}}_{\text{s}} ,$$
(2)

where E s is the component of the local electric field tangential to the dielectric solid surface.

In real situations of electrophoresis in microfluidic and other practical applications, colloidal particles are not isolated and will move near solid boundaries (Smith et al. 2000; Kang and Li 2009). Electrophoresis in porous media is often applied because the unwanted mix-up caused by free convection due to Joule heating can be avoided. Microporous gels or membranes can be used to achieve high electric fields and permit separations based on both the size and the charge of the particles (such as DNA fragments, proteins, and other macromolecules) (Jorgenson 1986). In capillary electrophoresis, gels in the column can minimize the particle diffusion, prevent the particle adsorption to the walls, and eliminate electroosmosis, while serving as the anti-convective media (Ewing et al. 1989). Therefore, it is of great interest to determine how the presence of various neighboring boundaries affects the electrophoretic motion of particles.

Using a method of reflections, Keh and Anderson (1985) analyzed the electrophoretic motions of a charged sphere with a thin double layer normal to a conducting plane, parallel to an insulating plane, along the axis of a circular tube, and on the mid-plane between two parallel plates. On the other hand, through the use of spherical bipolar coordinates or a lubrication theory, semi-analytical solutions for the electrophoretic velocity of a dielectric sphere in the vicinity of a plane wall have been obtained in two principal cases: the migration perpendicular to a conducting plane (Morrison and Stukel 1970; Loewenberg and Davis 1995) and the movement parallel to a dielectric plane (Keh and Chen 1988; Yariv and Brenner 2003). The boundary effects on electrophoresis were also studied analytically or semi-analytically for a spherical particle located at the center of a spherical cavity (Zydney 1995; Keh and Hsieh 2007), at an axial (Keh and Chiou 1996) or eccentric (Yariv and Brenner 2002) position in a circular tube, and at an arbitrary position between two parallel plane walls (Unni et al. 2007; Chang and Keh 2008). An important result of these investigations is that the boundary effects on electrophoresis are weaker than on sedimentation, because the fluid velocity field dragged by an electrophoretic particle with a thin double layer decays faster than that caused by a stokeslet.

The system of a spherical particle moving inside a spherical cavity can be an idealized model for the electrophoresis in media or microchannels composed of connecting spherical pores and the location of the particle within the cavity can play an important role (Chen 2011). The purpose of this article is to obtain a semi-analytical solution for the axisymmetric electrophoresis of a dielectric sphere in a nonconcentric spherical cavity with thin double layers. The electrostatic and hydrodynamic equations governing the system are solved by using the boundary collocation method, and the wall-corrected electrophoretic mobility of the particle is obtained with good convergence for various cases. Some interesting features of the boundary effect on the electrokinetic migration of the particle are revealed from the results.

2 Analysis

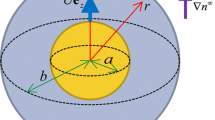
We consider the axisymmetric electrophoretic motion of a dielectric spherical particle of radius a and zeta potential \(\zeta_{\text{p}}\) in an electrolyte solution within a spherical cavity (pore) of radius b and zeta potential \(\zeta_{\text{w}}\), as shown in Fig. 1, at the quasi-steady state. Here, (ρ, ϕ, z) and (r 2, θ 2, ϕ) represent the circular cylindrical and spherical coordinate systems, respectively, with the origin at the center of the cavity. The center of the particle is located on the z axis away from the cavity center at a distance d. A uniform electric field E ∞ e z is imposed to the fluid, where e z is the unit vector in the z direction. The thickness of the electric double layers adjoining the particle and cavity surfaces is assumed to be much smaller than the particle radius and the spacing between the solid surfaces. Our objective is to obtain the correction to Eq. 1 for the particle velocity due to the presence of the cavity wall.

Fig. 1
figure 1

Geometrical sketch for the axisymmetric electrokinetic migration of a spherical particle in a spherical cavity

Full size image

Before determining the electrokinetic migration velocity of the confined particle, it is necessary to ascertain the electric potential and velocity distributions in the fluid phase.

2.1 Electric potential distribution

The fluid outside the thin double layers is of uniform composition, electric neutrality, and constant conductivity; hence, the electric potential distribution ψ (r, θ) is governed by the Laplace equation from charge conservation,

$$\nabla^{2} \psi = 0.$$
(3)

Since the particle is non-conducting, the boundary condition for \(\psi\) at its surface (or more precisely, the outer edge of the double layer) is

$$r_{1} = a:\quad \frac{\partial \psi }{{\partial r_{1} }} = 0,$$
(4)

where (r 1, θ 1, ϕ) are the spherical coordinates based on the center of the particle.

Given the uniformly applied electric field, the legitimate boundary condition for the electric potential at the cavity wall is

$$r_{2} = b:\quad \psi = - E_{\infty } r_{2} \cos \theta_{2}$$
(5)

in the Dirichlet approach (Keh and Hsieh 2007) or

$$r_{2} = b:\quad \frac{\partial \psi }{{\partial r_{2} }} = - E_{\infty } \cos \theta_{2}$$
(6)

in the Neumann approach (Zydney 1995). Both approaches lead to the electric field E ∞ez in the whole fluid phase when the particle does not exist. Note that the angular component of the electric potential gradient at the cavity wall is not specified in the Neumann approach.

The general solution of the electric potential distribution can be expressed as

$$\psi = E_{\infty } \sum\limits_{m = 0}^{\infty } {[S_{1m} r_{1}^{ - m - 1} } P_{m} (\cos \theta_{1} ) + S_{2m} r_{2}^{m} P_{m} (\cos \theta_{2} )],$$
(7)

where P m is the Legendre polynomial of order m, and the unknown constants S 1m and S 2m need to be determined using the boundary conditions at the particle surface and cavity wall. In the construction of the solution in Eq. 7, the superposition of the general solutions to Eq. 3 in spherical coordinates as written from two different origins can be employed due to the linearity of the governing equation (Keh and Lee 2010). In order to use Eq. 7, r i and cosθ i should be expressed in terms of the cylindrical coordinates ρ and z, as shown in Eqs. 32 and 33 in the “Appendix”.

Applying the boundary conditions given by Eqs. 4–7, we obtain

$$\sum\limits_{m = 0}^{\infty } {\{ (m + 1)S_{1m} a^{ - m - 2} } P_{m} (\cos \theta_{1} ) - S_{2m} [\delta_{m}^{(1)} (\rho ,z)]_{{r_{1} = a}} \} = 0,$$
(8)
$$\sum\limits_{m = 0}^{\infty } {\{ S_{1m} [r_{1}^{ - m - 1} } P_{m} (\cos \theta_{1} )]_{{r_{2} = b}} + S_{2m} b^{m} P_{m} (\cos \theta_{2} )\} = - b\cos \theta_{2} ,$$
(9)
$$\sum\limits_{m = 0}^{\infty } {\{ S_{1m} [\delta_{m}^{(2)} (\rho ,z)]_{{r_{2} = b}} } + mS_{2m} b^{m - 1} P_{m} (\cos \theta_{2} )\} = - \cos \theta_{2} ,$$
(10)

where the definitions of the functions \(\delta_{m}^{(1)}\) and \(\delta_{m}^{(2)}\) are given by Eqs. 26 and 27.

A collocation technique (Keh and Jan 1996) to truncate the infinite series in Eq. 7 after M terms and enforce the boundary conditions in Eqs. 8 and 9 or 10 at M discrete points on each longitudinal arc of the particle and cavity surfaces (with values of θ i between 0 and π) leads to a system of 2M simultaneous linear algebraic equations. This matrix equation can be numerically solved to yield the 2M unknown constants S 1m and S 2m required in the truncated form of Eq. 7 for the electric potential distribution. In principle, the accuracy of the boundary collocation technique can be improved to any degree by taking a sufficiently large value of M.

2.2 Fluid velocity distribution

With knowledge of the solution for the electric potential field, we can now proceed to find the fluid velocity distribution. Owing to the low Reynolds number, the fluid motion outside the thin double layers is governed by the Stokes equations,

$$\eta \nabla^{2} {\mathbf{v}} - \nabla p = {\mathbf{0}},$$
(11)
$$\nabla \cdot {\mathbf{v}} = 0,$$
(12)

where v is the fluid velocity field and p is the dynamic pressure distribution.

Since the local electric field acting on the diffuse ions within the thin double layer at each solid surface produces a relative tangential fluid velocity at the outer edge of the double layer as given by the Helmholtz expression in Eq. 2 for the electroosmotic flow, the boundary conditions for the fluid velocity require that

$$r_{1} = a:\quad {\mathbf{v}} = U{\mathbf{e}}_{z} + \frac{{\varepsilon \zeta_{\text{p}} }}{\eta }\frac{\partial \psi }{{r_{1} \partial \theta_{1} }}{\mathbf{e}}_{\theta 1} ,$$
(13)
$$r_{2} = b:\quad {\mathbf{v}} = \frac{{\varepsilon \zeta_{\text{w}} }}{\eta }\frac{\partial \psi }{{r_{2} \partial \theta_{2} }}{\mathbf{e}}_{\theta 2} .$$
(14)

Here, U is the migration velocity of the particle to be determined, e θ1 and e θ2 are the unit vectors along the θ 1 and θ 2 coordinates, respectively, and the expression for \(\psi\) has already been given by Eq. 7 with constants determined from Eqs. 8 and 9 or 10. There is no rotation of the particle due to the axial symmetry of the system.

The cylindrical-coordinate components of the fluid velocity can be expressed as

$$v_{\rho } = \sum\limits_{n = 2}^{\infty } {[B_{n} B^{\prime}_{n} (r_{1} ,\theta_{1} ) + D_{n} D^{\prime}_{n} (r_{1} ,\theta_{1} ) + A_{n} A^{\prime}_{n} (r_{2} ,\theta_{2} ) + C_{n} C^{\prime}_{n} (r_{2} ,\theta_{2} )]} ,$$
(15)
$$v_{z} = \sum\limits_{n = 2}^{\infty } {[B_{n} B^{\prime\prime}_{n} (r_{1} ,\theta_{1} ) + D_{n}, D^{\prime\prime}_{n} (r_{1} ,\theta_{1} ) + A_{n} A^{\prime\prime}_{n} (r_{2} ,\theta_{2} ) + C_{n} C^{\prime\prime}_{n} (r_{2} ,\theta_{2} )]} ,$$
(16)

where the functions \(B^{\prime}_{n}\), \(D^{\prime}_{n},\), \(B^{\prime\prime}_{n}\), \(D^{\prime\prime}_{n}\) \(A^{\prime}_{n}\), \(C^{\prime}_{n}\), \(A^{\prime\prime}_{n}\), and \(C^{\prime\prime}_{n}\) are given by Eqs. 26–33 in Keh and Lee (2010) for the creeping motion of a confined particle with the same geometry but driven by gravity, and B n , D n , A n , and C n are the unknown constants to be determined.

Applying the boundary conditions in Eqs. 13 and 14 along the particle surface and cavity wall together with Eqs. 7–15 and 16, we obtain

$$\begin{gathered} \sum\limits_{n = 2}^{\infty } {\{ B_{n} B^{\prime}_{n} (a,\theta_{1} ) + D_{n} D^{\prime}_{n} (a,\theta_{1} ) + [A_{n} A^{\prime}_{n} (r_{2} ,\theta_{2} ) + C_{n} C^{\prime}_{n} (r_{2} ,\theta_{2} )]_{{r_{1} = a}} } \} \hfill \\ = U_{0} \sum\limits_{m = 0}^{\infty } {\{ S_{1m} \delta_{m}^{(3)} (a,\theta_{1} ) + S_{2m} [\delta_{m}^{(4)} (\rho ,z)]_{{r_{1} = a}} } \} \cos \theta_{1} , \hfill \\ \end{gathered}$$
(17)
$$\begin{gathered} \sum\limits_{n = 2}^{\infty } {\{ B_{n} B^{\prime\prime}_{n} (a,\theta_{1} ) + D_{n} D^{\prime\prime}_{n} (a,\theta_{1} ) + [A_{n} A^{\prime\prime}_{n} (r_{2} ,\theta_{2} ) + C_{n} C^{\prime\prime}_{n} (r_{2} ,\theta_{2} )]_{{r_{1} = a}} } \} \hfill \\ = U - U_{0} \sum\limits_{m = 0}^{\infty } {\{ S_{1m} \delta_{m}^{(3)} (a,\theta_{1} ) + S_{2m} [\delta_{m}^{(4)} (\rho ,z)]_{{r_{1} = a}} } \} \sin \theta_{1} ; \hfill \\ \end{gathered}$$
(18)
$$\begin{gathered} \sum\limits_{n = 2}^{\infty } {\{ [B_{n} B^{\prime}_{n} (r_{1} ,\theta_{1} ) + D_{n} D^{\prime}_{n} (r_{1} ,\theta_{1} )]_{{r_{2} = b}} + A_{n} A^{\prime}_{n} (b,\theta_{2} ) + C_{n} C^{\prime}_{n} (b,\theta_{2} )\} } \hfill \\ = U_{0} \frac{{\zeta_{\text{w}} }}{{\zeta_{\text{p}} }}\sum\limits_{m = 0}^{\infty } {\{ S_{1m} [\delta_{m}^{(5)} (\rho ,z)]_{{r_{2} = b}} + S_{2m} \delta_{m}^{(6)} (b,\theta_{2} )} \} \cos \theta_{2} , \hfill \\ \end{gathered}$$
(19)
$$\begin{gathered} \sum\limits_{n = 2}^{\infty } {\{ [B_{n} B^{\prime\prime}_{n} (r_{1} ,\theta_{1} ) + D_{n} D^{\prime\prime}_{n} (r_{1} ,\theta_{1} )]_{{r_{2} = b}} + A_{n} A^{\prime\prime}_{n} (b,\theta_{2} ) + C_{n} C^{\prime\prime}_{n} (b,\theta_{2} )\} } \hfill \\ = - U_{0} \frac{{\zeta_{\text{w}} }}{{\zeta_{\text{p}} }}\sum\limits_{m = 0}^{\infty } {\{ S_{1m} [\delta_{m}^{(5)} (\rho ,z)]_{{r_{2} = b}} + S_{2m} \delta_{m}^{(6)} (b,\theta_{2} )} \} \sin \theta_{2} . \hfill \\ \end{gathered}$$
(20)

Here, \(U_{0} = \varepsilon \zeta_{p} E_{\infty } /\eta\) is the electrophoretic velocity of the particle in an infinite volume of the same fluid given by Eq. 1, the functions \(\delta_{m}^{(3)}\), \(\delta_{m}^{(4)}\), \(\delta_{m}^{(5)}\), and \(\delta_{m}^{(6)}\) are defined by Eqs. 28–31, and the first M constants S 1m and S 2m have been determined through the procedure given in the previous subsection.

Equations 17–20 can be satisfied by utilizing the boundary collocation method presented for the solution of the electric potential field. Along the longitudinal arcs at the particle and cavity surfaces, these equations are applied, respectively, at N discrete points, and the infinite series in Eqs. 15 and 16 are truncated after N terms. This generates a set of 4N linear algebraic equations for the 4N unknown constants A n , B n , C n , and D n . The fluid velocity field is obtained once these constants are solved for a sufficiently large number of N.

2.3 Particle velocity

The drag force acting on the particle by the fluid can be determined from

$$F = 4\pi \eta D_{2} .$$
(21)

Since the particle is freely suspended in the surrounding fluid, the net force on the particle must vanish. Applying this constraint to Eq. 21, one has

$$D_{2} = 0.$$
(22)

To determine the electrokinetic migration velocity U of the confined particle, Eq. 22 and the 4N algebraic equations resulting from Eqs. 17–20 need to be solved simultaneously.

Owing to the linearity of the problem, the obtained particle velocity can be expressed as a superimposed form

$$U = U_{0} \left( {M_{\text{p}} + \frac{{\zeta_{\text{w}} }}{{\zeta_{\text{p}} }}M_{\text{w}} } \right),$$
(23)

where the dimensionless coefficients M p and M w are functions of the normalized particle size a/b and deviation distance of the particle center from the cavity center d/(b − a). The coefficient M p represents the normalized electrophoretic mobility of the charged particle inside a cavity with uncharged wall \(\left( {\zeta_{\text{w}} = 0} \right)\) relative to its Smoluchowski result given by Eq. 1, whereas M w denotes the normalized mobility of an uncharged sphere \(\left( {\zeta_{\text{p}} = 0} \right)\) in the charged cavity caused by the electroosmotic flow recirculation that develops from the interaction of the applied electric field with the thin double layer adjacent to the cavity wall. The cavity-to-particle zeta potential ratio \(\zeta_{\text{w}} /\zeta_{\text{p}}\) corresponds to the strength and direction of the cavity-induced electroosmotic flow relative to the electrophoretic driving force exerted on the particle.

3 Results and discussion

The numerical results for the electrokinetic migration of a spherical particle within a spherical cavity caused by an imposed electric field along the line through the particle and cavity centers can be obtained by using the boundary collocation method described in the previous section. The system of linear algebraic equations to be solved for the constants S 1m and S 2m is constructed from Eqs. 8 and 9 or 10 and that for A n , B n , C n , and D n is composed of Eqs. 17–20. The details of the collocation scheme used for this work were given by Keh and Lee (2010), in which very good accuracy and convergence behavior have been achieved.

The collocation solutions for the dimensionless electrokinetic mobilities M p and M w of a spherical particle inside a spherical cavity defined by Eq. 23 are presented in Table 1 and Figs. 2 and 3 for various values of the particle-to-cavity radius ratio a/b and normalized distance between the particle and cavity centers d/(b − a). All of the numerical results converge to at least the significant digits as shown in the table. Both M p and M w are positive; thus, the contribution to the particle velocity from the cavity-induced electroosmotic flow is in the same/opposite direction with respect to that from the electrophoretic driving force if the zeta potential ratio \(\zeta_{\text{w}} /\zeta_{\text{p}}\) is positive/negative. For given values of a/b and d/(b − a), the values of M p and M w predicted from using the Neumann boundary condition at the cavity wall in Eq. 6 are always greater than their corresponding results obtained from using the Dirichlet boundary condition in Eq. 5, since the local electric field in the fluid between the particle surface and cavity wall resulting from the Neumann condition is higher than that from the Dirichlet condition [e.g., with a factor (1 + λ 3/2)/(1 − λ 3), where λ = a/b, for the concentric case d/(b − a) = 0].

Table 1 The normalized electrokinetic mobilities M p and M w of a spherical particle within a spherical cavity for various values of a/b and d/(b − a)
Full size table
Fig. 2
figure 2

Plots of the normalized electrophoretic mobility M p of a charged sphere in an uncharged spherical cavity for various values of a/b and d/(b − a). The solid and dashed curves represent the cases using the Dirichlet condition in Eq. 5 and Neumann condition in Eq. 6, respectively, at the cavity wall

Full size image
Fig. 3
figure 3

Plots of the normalized electrokinetic mobility M w of an uncharged sphere in a charged spherical cavity for various values of a/b and d/(b − a). The solid and dashed curves represent the cases using the Dirichlet condition in Eq. 5 and Neumann condition in Eq. 6, respectively, at the cavity wall

Full size image

For the particular case of a spherical particle positioned at the center of a spherical cavity, the exact solution of the normalized electrokinetic mobilities has been obtained as (Keh and Hsieh 2007)

$$M_{\text{p}} = \frac{{2 - 5\lambda^{3} + 3\lambda^{5} }}{{2\nu (1 - \lambda^{5} )}},$$
(24)
$$M_{\text{w}} = \frac{{6 - 10\lambda^{2} + 3\lambda^{3} - \lambda^{5} + 2\lambda^{8} }}{{6\nu (1 - \lambda^{5} )}},$$
(25)

where v = 1+λ 3/2 if the Dirichlet condition in Eq. 5 is employed, whereas v = 1−λ 3 if the Neumann condition in Eq. 6 is used. In the limit a/b = 0 (the cavity wall is at an infinite distance from the particle), the conditions in Eqs. 5 and 6 become identical (with v = 1) and Eqs. 24 and 25 reduce to M p = M w = 1. Our collocation results of M p and M w for the concentric case d/(b − a) = 0 shown in Figs. 2 and 3 are in excellent agreement with this analytical solution.

The results in Table 1 and Fig. 2 illustrate that the normalized electrophoretic mobility M p of the charged particle decreases monotonically with increases in the particle-to-cavity radius ratio a/b and in the normalized distance between the particle and cavity centers d/(b − a), keeping the other parameter unchanged, and M p equals zero (for the Dirichlet condition at the cavity wall) or 1/2 (for the Neumann condition) in the touching limit of the two surfaces at a/b = 1 or d/(b − a) = 1. Thus, the net effect of the approach of the cavity wall to the particle, dominated by the contribution from viscous retardation, is to reduce the electrophoretic driving force. For a specified value of a/b, the viscous interaction between the particle and the cavity wall intensifies on the part of the particle surface close to the cavity wall and weakens on that far from the wall with an enhanced retardation in the net effect as the value of d/(b − a) increases. This boundary effect on the electrophoresis is significant. Evidently, M p = 1 as a/(b − d) = 0 (which also implies that a/b = 0 and the wall is infinitely far from the particle).

The results in Table 1 and Fig. 3 indicate that the dimensionless electrokinetic mobility M w of the particle also decreases monotonically with an increase in the normalized center-to-center distance d/(b − a) and equals zero (for the Dirichlet condition at the cavity wall) or 1/2 (for the Neumann condition) at d/(b − a) = 1 for any fixed value of the particle-to-cavity radius ratio a/b. Thus, the net effect of the approach of the cavity wall to the particle is also to reduce the cavity-induced electroosmotic sweeping force on the particle. On the other hand, M w decreases monotonically with an increase in a/b to zero or 1/2 at a/b = 1 when the value of d/(b − a) is small, but first increases with an increase in a/b from a/b = 0 and attains a maximum before it starts decreasing to zero or 1/2 at a/b = 1 when the value of d/(b − a) becomes relatively large. Interestingly, M w is not equal to unity as a/(b − d) = 0 except for the concentric case d/(b − a) = 0. Note that, for any given values of a/b and d/(b − a), M p is greater than M w (in spite of their comparable magnitudes), no matter whether Eq. 5 or 6 is used for the boundary condition of the electric potential at the cavity wall.

The results for the electrokinetic migration velocity of a charged spherical particle in a charged spherical cavity normalized by its electrophoretic velocity in an unbounded fluid, U/U 0, versus the radius ratio a/b for various values of the zeta potential ratio \(\zeta_{\text{w}} /\zeta_{\text{p}}\) and normalized center-to-center distance d/(b − a) are presented in Fig. 4. For constant values of a/b and d/(b − a), as expected, the value of U/U 0 increases monotonically with an increase in \(\zeta_{\text{w}} /\zeta_{\text{p}}\). When the value of \(\zeta_{\text{w}} /\zeta_{\text{p}}\) is positive, the presence of the cavity can greatly enhance the electrophoretic migration of the particle, and this great enhancement is attributed to the electroosmotic flow recirculation arising from the interaction between the applied electric field and the charged cavity wall. As long as the value of \(\zeta_{\text{w}} /\zeta_{\text{p}}\) is greater than −1, the value of U/U 0 is positive. When the value of \(\zeta_{\text{w}} /\zeta_{\text{p}}\) is smaller than about −1, however, the value of U/U 0 may become negative, meaning that the velocity of the particle reverses its direction due to the relatively strong effect of the cavity-induced electroosmotic flow in the opposite direction. For a specified value of \(\zeta_{\text{w}} /\zeta_{\text{p}}\), the magnitude of \(\zeta_{\text{w}} /\zeta_{\text{p}}\) in general decreases with an increase in a/b or d/(b − a). Note that, although the normalized electrokinetic mobilities M p and M w are both monotonic decreasing functions of a/b for small values of d/(b − a), the magnitude of U/U 0 calculated using Eq. 23 for fixed values of d/(b − a) and \(\zeta_{\text{w}} /\zeta_{\text{p}}\) may increase with increasing a/b (at small a/b) before going through a maximum under some conditions. For given values of \(\zeta_{\text{w}} /\zeta_{\text{p}}\), a/b, and d/(b − a), the magnitude of U/U 0 predicted from using the Neumann condition at the cavity wall in general is greater than that predicted from using the Dirichlet condition.

Fig. 4
figure 4

Plots of the normalized electrokinetic migration velocity U/U 0 of a charged sphere in a charged spherical cavity versus the radius ratio a/b with the zeta potential ratio \(\zeta_{\text{w}} /\zeta_{\text{p}}\) as a parameter: a using the Dirichlet condition in Eq. 5; b using the Neumann condition in Eq. 6. The solid and dashed curves denote the cases of d/(b − a) = 0 and d/(b − a) = 0.5, respectively

Full size image

For the creeping motion of a spherical particle in a spherical cavity along the line of their centers driven by a gravitational field, the semi-analytical solution of the particle mobility has been obtained by using the boundary collocation method (Keh and Lee 2010). A comparison of this solution with the present result shows that the wall effect on electrophoresis is weaker than that on sedimentation.

We note that the Dirichlet and Neumann boundary conditions for the electric potential at the cavity wall given by Eqs. 5 and 6, respectively, lead to somewhat different results of the migration velocity of the confined particle. These boundary conditions have also been widely used at the virtual surface of a spherical cell in the unit cell model to obtain the mean electrophoretic mobility of a suspension of identical charged spheres [e.g., Zharkikh and Shilov (1982) and Ohshima (1997) used Dirichlet condition, whereas Levine and Neale (1974) and Kozak and Davis (1989) used Neumann condition]. It has been shown that the electrophoretic mobility predicted from Eq. 5 rather than from Eq. 6 in the cell model agrees well with that calculated from the statistical-mechanics model for dilute suspensions of spherical particles (Keh and Wei 2000). Our results also indicate that the tendency of the dependence of the particle mobility on the parameters a/b and d/(b − a) resulting from Eq. 5 is more reasonable than that from Eq. 6, where the normalized mobility of the particle in the touching limit vanishes for the former case and is finite (=1/2) for the latter one. The boundary condition in Eq. 6 is not as accurate as that in Eq. 5, probably due to the fact that the angular component of the electric potential gradient at the cavity wall is not specified in Eq. 6.

4 Conclusions

A semi-analytical investigation of the electrophoretic motion of a charged spherical particle arbitrarily positioned within a charged spherical cavity along the line of their centers using a boundary collocation method is presented in the limit of thin electric double layers. The Laplace and Stokes equations are solved for the electric potential and velocity fields, respectively, in the fluid phase, and numerical results for the electrokinetic migration velocity of the particle are obtained for various values of the relative particle radius, distance between the particle and cavity centers, and zeta potential of the cavity wall. For the particular case of a particle in a concentric cavity, these results are in excellent agreement with the explicit formulas given by Eqs. 24 and 25. The electroosmotic flow induced by the interaction between the applied electric field and the thin double layer adjoining the cavity wall can lead to a significant enhancement/reduction in the electrophoretic migration of the particle if the ratio of their zeta potentials is positive/negative. When the particle is situated closer to the cavity wall or becomes larger, the wall effect of hydrodynamic retardation increases and the electrophoresis of the particle slows down. The boundary effects on the electrophoresis can be significant in appropriate situations.