1 Introduction

Two-phase flows in microfluidic devices gained considerably in importance during the last two decades (Stone et al. 2004; Günther and Jensen 2006). The key for success of these microfluidic tools is the fluid compartmentalization, allowing the miniaturization and manipulation of small liquid portions at high throughput rates with a limited number of necessary controls. Reduced liquid quantities are commonly used as individual reactors in several biological and chemical applications (Köhler and Cahill 2014), as well as in industrial processes (Abadie et al. 2012) and in micro-scale heat and mass transfer equipments (Leung et al. 2011; Warnier et al. 2010; Mikaelian et al. 2015). Bubbles and droplets often flow in microchannels with a round or rectangular/square cross section (Kreutzer et al. 2005; Khodaparast et al. 2015; Mikaelian et al. 2015).

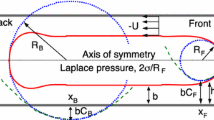
The dynamics of a bubble in a microchannel has been the subjects of several studies, since the seminal works of Fairbrother and Stubbs (1935), Taylor (1961) and Bretherton (1961). These long bubbles, also referred to as Taylor bubbles, flowing in a tube of radius R, have been characterized by the thickness \(H_{\infty }\) of the uniform film separating them from the tube walls, the minimum thickness \(H_{\textsf {min}}\) of the film, the plane curvature of the front and rear caps in the (z, r) or (x, y) plane, \(\kappa _f\) and \(\kappa _r\), as well as by their velocity \(U_d\). Bretherton (1961) used a lubrication approach to derive the asymptotic scalings in the limit of small capillary numbers, \(Ca = \mu _o U_d/\gamma\), where \(\mu _o\) is the dynamic viscosity of the outer fluid and \(\gamma\) the surface tension. In particular, Bretherton (1961) showed that in the limit of \(Ca \rightarrow 0\), the film thickness scales as \(H_{\infty }/R \sim 0.643 (3 Ca)^{2/3}\) and that the plane curvature of the front and rear caps scales as \(\kappa _{f,r} R \sim 1+\beta _{f,r}(3 Ca)^{2/3}\), with \(\beta _{f,r}\) a different coefficient for front and rear caps. The uniform thin-film region is connected to the static cap of constant curvature at the extremities of the bubble through a dynamic meniscus (Cantat 2013) (see Fig. 1).

Fig. 1
figure 1

Sketch of the front meniscus of the bubble advancing at velocity \(U_d\) in a capillary of radius R with indication of the uniform thin-film region of thickness \(H_{\infty }\), the dynamic meniscus region and the static meniscus region. The plane curvature \(\kappa _f\) of the front static cap in the (z, r) or (x, y) plane is also highlighted

Full size image

The counterpart theory for a bubble in a square duct was derived by Wong et al. (1995a, b). However, these scalings agree with Taylor’s experimental results (Taylor 1961) only in the small Ca limit, namely when \(Ca \lessapprox 10^{-3}\). To understand the dynamics of confined bubbles in a broader parameter range, researchers have performed experiments (Chen 1986; Aussillous and Quéré 2000; Fuerstman et al. 2007; Han and Shikazono 2009; Boden et al. 2014) as well as numerical simulations (Shen and Udell 1985; Reinelt and Saffman 1985; Ratulowski and Chang 1989; Giavedoni and Saita 1997, 1999; Heil 2001; Kreutzer et al. 2005; Lac and Sherwood 2009; Gupta et al. 2013; Anjos et al. 2014a, b; Langewisch and Buongiorno 2015). As an outcome, several correlations have been proposed for the evolutions of the relevant quantities as a function of the different parameters [see, for example, Han and Shikazono (2009) and Langewisch and Buongiorno (2015)]. Among them, Aussillous and Quéré (2000) proposed an ad hoc rational function with a fitting parameter for the film thickness which is in good agreement with the experimental results of Taylor (1961) for capillary numbers up to 1. The two recent works of Klaseboer et al. (2014) and Cherukumudi et al. (2015) tried to put a theoretical basis to this extended Bretherton’s theory for larger Ca.

In contrast to bubbles, which have experienced a vast interest of the scientific community, little amount of effort has been made for droplets whose viscosities are comparable to or much larger than that of the outer fluid. Yet, droplets of arbitrary viscosities are crucial for Lab-on-a-Chip applications (Anna 2016). A first theoretical investigation of the effect of the inner phase viscosity was conducted by Schwartz et al. (1986), motivated by the discrepancy in the predicted and the measured film thicknesses of long bubbles in capillaries. They demonstrated that the non-vanishing inner-to-outer viscosity ratio could thicken the film.  Hodges et al. (2004) further extended the theory and showed that the film becomes even thicker at intermediate viscosity ratios. Numerical simulations have been performed to investigate the droplets in capillaries (Martinez and Udell 1990; Tsai and Miksis 1994; Lac and Sherwood 2009).

Models predicting the characteristic quantities such as the uniform film thickness and the meniscus curvatures of droplets in capillaries over a wide range of capillary numbers are still missing. For example, the velocity of a droplet of finite viscosity flowing in a channel still remains a simple question yet an open challenge. Such a prediction is, however, of paramount importance for the correct design of droplet microfluidic devices. As an example, Jakiela et al. (2011) performed extensive experiments for droplets in square ducts, showing complex dependencies of the droplet velocity on the capillary number, viscosity ratio and droplet length. Also, what is the pressure drop induced by the presence of a drop in a channel? This question is crucial and has been the subjects of recent works, for example, Warnier et al. (2010) and Ładosz et al. (2016). Other quantities, such as the minimum film thickness \(H_{\textsf {min}}\), have to be accurately predicted as well. \(H_{\textsf {min}}\) becomes essential for heat transfer or cleaning of microchannels applications (Magnini et al. 2017; Khodaparast et al. 2017). Furthermore, being able to predict the flow field inside and outside of the droplet is crucial if one is interested in the mixing capabilities of the system.

Here, we aim at bridging this gap by combining asymptotic derivations with accurate numerical simulations to propose physically inspired empirical models, for the characteristic quantities of a droplet of arbitrary viscosity ratio flowing in an axisymmetric or planar capillary with a constant velocity. The model coefficients are specified by fitting laws. The present work provides the reader with a rigorous theoretical basis, which can be exploited to understand the dynamics of viscous droplets. The considered capillary numbers vary from \(10^{-4}\) to 1 and the inner-to-outer viscosity ratio from 0 to \(10^5\). Following the work of Schwartz et al. (1986), we extend the low-capillary-number asymptotical results obtained with the lubrication approach of Bretherton (1961) for bubbles to viscous droplets. Numerical simulations based on finite element method (FEM) employing the arbitrary Lagrangian–Eulerian (ALE) formulation are performed to validate the theoretical models and then extend them to the large-capillary-number range, \(Ca\sim O(1)\), where the lubrication analysis fails.

The paper is structured in a way to build, step by step, the models for the uniform film thickness, the front and rear droplet’s interface plane curvatures as well as those for the front and rear pressure drops required to compute the total pressure drop along a droplet in a channel. We present the problem setup, governing equations, numerical methods and the validations in Sect. 2. The flow fields inside and outside of the droplets as a function of the capillary numbers and viscosity ratios are shown in Sect. 3. In particular, the flow profiles in the uniform-film region are derived in Sect. 3.1 and the flow patterns are presented in Sect. 3.2. The theoretical part starts with the asymptotic derivation of the model for the uniform film thickness in Sect. 4. The derivation of the lubrication equation is detailed in Sect. 4.1, followed by the film thickness model in Sect. 4.2 and its extension to larger capillary numbers in Sect. 4.3. With the knowledge of the film thickness, the droplet velocity can be computed analytically (see Sect. 5). The minimum film thickness separating the droplet form the channel walls is discussed in Sect. 6. To build a total pressure drop model, one still needs the knowledge of the front and rear cap mean curvatures (see Sect. 7.1), the front and rear pressure jumps (see Sects. 7.2 and 7.4) and the front and rear normal viscous stress jumps (see Sect. 7.3). The stress evolutions at the channel centerline and at the wall are presented in Sects. 8.1 and 8.2, respectively. Eventually, one can sum up all these contributions to build the total pressure drop, which is described in Sect. 8.3. We summarize our results in Sect. 9.

2 Governing equations and numerical methods

2.1 Problem setup

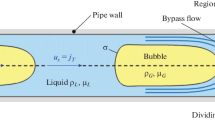
We consider an immiscible droplet of volume \(\Omega\) and dynamic viscosity \(\mu _i\) translating at a steady velocity \(U_d\) in a planar channel/axisymmetric tube of width/diameter 2R filled with an outer fluid of dynamic viscosity \(\mu _o\). The volume flux of the outer fluid is \(q_o\), resulting in an average velocity \(U_{\infty }=q_o/(2R)\) and \(U_{\infty }=q_o/(\pi R^2)\) for the planar and axisymmetric configuration, respectively (see Fig. 2). Given the small droplet velocity and size, the Reynolds number Re is small and inertial effects can be neglected. Buoyancy is also neglected. The relevant dimensionless numbers include the droplet capillary number \(Ca = \mu _o U_d/\gamma\) with \(\gamma\) being the surface tension of the droplet interface and the dynamic viscosity ratio \(\lambda = \mu _i/\mu _o\) between the droplet and the outer fluid. The capillary number based on the mean flow velocity is \(Ca_{\infty }=\mu _o U_{\infty }/\gamma\).

Fig. 2
figure 2

Sketch of the axisymmetric (z, r) and planar (x, y) configurations in the frame of reference moving with the droplet. The flow profiles in the uniform film region are shown in Fig. 7

Full size image

For the numerical simulations, the droplet capillary number has been varied within \(10^{-4}\lessapprox Ca \lessapprox 1\) to guarantee that the lubrication film is only influenced by the hydrodynamic forces and the dynamics is steady. For smaller capillary numbers, non-hydrodynamic forces such as disjoining pressures due to intermolecular forces might come into play as reported by the recent experiments of Huerre et al. (2015); while for larger capillary numbers, instability and unsteadiness might arise, where the droplet might form a re-entrant cavity at its rear (Tsai and Miksis 1994), which eventually breaks up into satellite droplets. The viscosity ratios investigated numerically are from the well-known bubble limit of \(\lambda =0\) of Bretherton (1961) to highly viscous droplets of \(\lambda =100\) that have been scarcely investigated.

We consider both a three-dimensional axisymmetric tube and a two-dimensional planar channel featured by the span-wise invariance. Note that the latter configuration does not correspond to the Hele–Shaw-cell-like microfluidic chips, where Darcy or Brinkman equations are more appropriate to describe the flow (Boos and Thess 1997; Nagel and Gallaire 2015).

It is worth noting that the confined droplet has to be long enough to develop a region of uniformly thick film at its center (Cantat 2013) (see Fig. 2). However, a long axisymmetric droplet is likely to become unstable to the Rayleigh–Plateau instability. The uniform film region would resemble to a coaxial jet, which is known to be unstable to perturbations with a wavelength longer than \(2\pi (R-H_{\infty })\) (Eggers and Villermaux 2008). Within this range of droplet lengths, we found that the effect of droplet volume \(\Omega\) is insignificant and hence it is fixed to \(\Omega /R^3=12.9\) for the axisymmetric geometry and \(\Omega /R^2=9.3\) for the planar case.

2.2 Governing equations

The governing equations are the incompressible Stokes equations for the velocity \(\mathbf {u}=(u,v)\) and pressure p:

$$\begin{aligned} \nabla \cdot \mathbf {u} = 0 \end{aligned}$$
(1)
$$\begin{aligned} \nabla \cdot \varvec{\sigma }= \mathbf {0}, \end{aligned}$$
(2)

where \(\varvec{\sigma } = - p {\mathbf {I}} + \mu \left[ \left( \nabla \mathbf {u} \right) + \left( \nabla \mathbf {u} \right) ^T \right]\) denotes the total stress tensor and \(\mu\) the dynamic viscosity as \(\mu _i\) (resp. \(\mu _o\)) inside (resp. outside) the droplet.

The imposed dynamic boundary conditions at the interface are the continuity of tangential stresses

$$\begin{aligned} \Delta \left[ ({\mathbf {I}}-\mathbf {n}\mathbf {n}) \left( {\varvec{\sigma }} \mathbf {n} \right) \right] = \mathbf {0} , \end{aligned}$$
(3)

and the discontinuity of normal stresses due to the Laplace pressure jump

$$\begin{aligned} \Delta \left( {\varvec{\sigma }} \mathbf {n} \right) = - \gamma \mathscr {C} \mathbf {n}. \end{aligned}$$
(4)

\(\Delta\) denotes the difference between the inner and outer quantities, \(\mathbf {n}\) the unit normal vector on the interface towards the outer fluid, and \(\mathscr {C} = \nabla _S \cdot \mathbf {n}\) the interfacial mean curvature (\(\nabla _S\) is the surface gradient). The plane curvature of the interface in the (z, r) or (x, y) plane is denoted as \(\kappa\) and its value at the front and rear droplet extremities is given by \(\kappa _f\) and \(\kappa _r\), respectively. The mean curvature at the front and rear droplet extremities, which lie on the symmetry axis, is, therefore, given by \(\mathscr {C}_{f,r} = \chi \kappa _{f,r}\), where \(\chi = 1\) or 2 for a planar or an axisymmetric configuration, respectively. At any other point on the droplet interface, the mean curvature is given by the sum of the two principal curvatures.

2.3 Numerical methods and implementations

Equations (1)–(2) with boundary conditions (3)–(4) are solved by the commercial FEM package COMSOL Multiphysics and the interface is well represented by the arbitrary Lagrangian–Eulerian (ALE) technique. Compared to the commonly known diffuse interface methods such as volume-of-fluid, phase-field, level-set and front-tracking all relying on a fixed Eulerian grid, the ALE approach captures the interface more accurately. Since the interface is always explicitly represented by the discretization points (see Fig. 3), the fluid quantities (viscosity, density, etc.), pressure and normal viscous stresses are discontinuous across the interface. This technique has been used to simulate three-dimensional bubbles in complex microchannels (Anjos et al. 2014b), liquid films coating the interior of cylinders (Hazel et al. 2012), two-phase flows with surfactants (Ganesan et al. 2017; Ganesan and Tobiska 2012) and head-on binary droplet collisions (Li 2016), to name a few. The Moving Mesh module of COMSOL Multiphysics has been recently employed by Rivero-Rodriguez and Scheid (2018) and Hadikhani et al. (2018) to investigate the inertial and capillary migration of bubbles in round and rectangular microchannels.

Despite the high fidelity in interface capturing, it is commonly more challenging to develop in-house ALE implementations compared to the diffuse interface counterparts. Additional difficulty arises in the case of large interfacial deformations, when the computational mesh might become highly nonuniform and skewed. It is, therefore, necessary to remesh the computational domain and to obtain all the quantities on the new mesh via interpolation. Hence, special expertise in scientific computing and tremendous amount of development efforts are required to implement an in-house ALE-based multi-phase flow solvers, which have prevented large portion of the research community from enjoying the high fidelity and elegance of the ALE methods.

Hereby, large mesh deformations can be avoided not only thanks to the convenient moving mesh module of COMSOL, but also by solving the problem in the moving frame of the droplet. To achieve so, we impose a laminar Poiseuille inflow of mean velocity \(U_{\infty }-U_d\) at the inlet of the channel and the velocity \(-U_d\) at the walls, where the unknown droplet velocity \(U_d\) is obtained as part of the solution together with that of the flow field, at each time step, by applying an extra constraint of zero volume-integrated velocity inside the droplet. Such constraints with additional unknowns are imposed in COMSOL Multiphysics by utilizing its so-called ’Global Equations’. This strategy ensures that the deforming droplet barely translates in the streamwise direction, staying approximately at its initial position (say in the center of the domain). Hence, the mesh quality and the robustness of the ALE formulation are appropriately guaranteed.

In this work, we are only concerned with the steady dynamics of the droplet reaching its equilibrium shape. We do not solve the steady Stokes Eq. (2) strictly but maintain a negligible time-derivative term \(Re \frac{\partial \mathbf {u}}{\partial t}\) for time marching. This procedure can be seen as an iterative scheme to find steady solutions of the Stokes equations. Since, indeed, the time-derivative term vanishes when the equilibrium state is reached, the solutions to the steady Stokes equations are eventually obtained.

It has to be stressed that the computed transient dynamics is not physical and only the final steady solution should be considered. Theoretically, the stability of the latter might be affected by the time-derivative term. However, in practice, no unstable phenomena or multiple-branch solutions were observed in our study. We monitored, during each simulation, the temporal evolution of the velocity, the mean and minimum film thickness as well as the front and rear plane curvatures of the droplet, which exhibited precise time invariance without exception when the equilibrium state was reached. Our method, therefore, converges to valid stationary solutions, which will be seen in Sect. 2.4 to compare well with asymptotic estimates and numerical solutions from the literature.

To reduce the computational cost, half of the channel is considered and axisymmetric or symmetric boundary conditions are imposed at the channel centerline for the axisymmetric and planar configurations, respectively. The setup in COMSOL Multiphysics is intrinsically parallel and the computing time required for an individual case needs no more than 1 h based on a standard desktop computer.

A typical mesh is shown in Fig. 3. Triangular/quadrilateral elements are used to discretize the domain inside/outside the droplet. Furthermore, a mesh refinement is performed to best resolve the thin lubrication film (see inset of Fig. 3). It is worth noting that quadrilateral elements have to be used to discretize the thin film because this region might undergo large radial deformation resulting in highly distorted and skewed triangular elements if used.

Fig. 3
figure 3

Computational mesh. Inset: mesh refinement in the thin-film region. The triangular inner phase (blue) and quadrilateral outer phase meshes (red) are separated by the explicitly discretized interface (dashed green). (Color figure online)

Full size image

2.4 Validation

Our numerical results are first validated for a bubble (\(\lambda =0\)) comparing the film thickness with the classical asymptotic theory \(H_{\infty }/R \sim 0.643 (3 Ca)^{2/3}\) of Bretherton (1961) in the low-Ca limit (see Fig. 4). Excellent agreement is revealed even when the capillary number is \(10^{-4}\); the discrepancy at larger Ca is mostly because of the asymptotic nature of the model that becomes less accurate for increasing Ca. At larger capillary numbers, we compare the uniform film thickness with the FEM-based numerical results of Giavedoni and Saita (1997) for a bubble, showing perfect agreement in Fig. 5; agreements for the front and rear plane curvatures are also observed and are not reported here.

For viscosity ratios \(\lambda>0\), we have validated our setup against the results from an axisymmetric boundary integral method (BIM) solver (Lac and Sherwood 2009) for a droplet with \(Ca_{\infty }=0.05\) of viscosity ratios \(\lambda =0.1\) and 10, again exhibiting perfect agreement as displayed in Fig. 6.

Based on the carefully performed validations against the theory, numerical results from FEM and BIM solvers, we are confident that the developed COMSOL implementation can be used to carry out high-fidelity two-phase simulations efficiently, at least for the 2D- and 3D-axisymmetric configurations.

Fig. 4
figure 4

Comparison between the uniform film thickness of the classical Bretherton  bubble obtained by the FEM-ALE simulations (symbols) and by the asymptotic prediction of Bretherton (1961) (solid line) for the planar channel

Full size image
Fig. 5
figure 5

Comparison between the uniform film thickness between the wall and a bubble obtained by the FEM-ALE simulations (full black circles) and that of Giavedoni and Saita (1997) (empty red squares) for the planar channel. (Color figure online)

Full size image
Fig. 6
figure 6

Comparison between the droplet profiles obtained by the FEM-ALE computations (blue dashed) and the BIM (red solid) computations of Lac and Sherwood (2009) for an axisymmetric droplet in a tube with \(Ca_{\infty }=0.05\) of viscosity ratios \(\lambda =0.1\) (upper half domain) and \(\lambda =10\) (lower half domain). (Color figure online)

Full size image

3 Flow field

3.1 Velocity profiles in the thin-film region

For a sufficiently long droplet/bubble, a certain portion of the lubrication film is of uniform thickness \(H_{\infty }\) (Bretherton 1961) (see Figs. 2 and 8). Within this portion, the velocity field both inside and outside the droplet is invariant in the streamwise direction and resembles the well-known bi-Poiseuille profile that typically arises in several interfacial flows, for example, a coaxial jet (Herrada et al. 2008) (see Fig. 7). For \(\lambda \ll 1\), the velocity profile in the film is almost linear, whereas for \(\lambda \gg 1\), the velocity inside of the droplet is almost constant (plug-like profile). Nevertheless, the parabolic component of these profiles is crucial for the accurate prediction of the droplet velocity (see Sect. 5).

Fig. 7
figure 7

Inner and outer phase velocity profiles in the uniform film region of an axisymmetric droplet with \(Ca_{\infty } = 0.1\) and viscosity ratios \(\lambda = 0.01\), 1 and 100, represented in the laboratory frame. (Color figure online)

Full size image

Assuming the bi-Poiseuille velocity profile, we describe the streamwise velocity \(u_i(r)\) inside and \(u_o(r)\) outside the droplet as a function of the off-centerline distance r as:

$$\begin{aligned} u_i(r) = \frac{1}{4 \mu _i} \frac{\mathrm{{d}} p_i}{\mathrm{{d}}z} r^2 + A_i \ln \;r + B_i,\end{aligned}$$
(5)
$$\begin{aligned} u_o(r) = \frac{1}{4 \mu _o} \frac{\mathrm{{d}} p_o}{\mathrm{{d}}z} r^2 + A_o\ln \;r + B_o, \end{aligned}$$
(6)

where \(p_i\) and \(p_o\) are the inner and outer pressures, respectively, and \(A_i\), \(B_i\), \(A_o\) and \(B_o\) are undetermined constants. Given the finiteness of \(u_i(r)\) at \(r=0\), we have \(A_i=0\). By satisfying the no-slip boundary condition on the channel walls \(u_o(R) = -U_d\), the continuity of velocities and tangential stresses on the interface \(r=\tilde{r}=R-H\), namely \(u_i(\tilde{r}) = u_o(\tilde{r})\) and

$$\begin{aligned} \mu _i \frac{\mathrm{{d}} u_i}{\mathrm{{d}}z}\bigg \vert _{r=\tilde{r}} = \mu _o \frac{\mathrm{{d}} u_o}{\mathrm{{d}}z}\bigg \vert _{r=\tilde{r}}, \end{aligned}$$
(7)

we obtain the remaining constants

$$\begin{aligned} A_o&= {} \frac{1}{2 \mu _o} \left( \frac{\mathrm{{d}} p_i}{\mathrm{{d}}z}-\frac{\mathrm{{d}} p_o}{\mathrm{{d}}z}\right) \tilde{r}^2,\end{aligned}$$
(8)
$$\begin{aligned} B_i&= -\,\frac{1}{4 \mu _i \mu _o} \left[ \frac{\mathrm{{d}} p_o}{\mathrm{{d}}z} (R^2 - \tilde{r}^2) \mu _i + \frac{\mathrm{{d}} p_i}{\mathrm{{d}}z} \tilde{r}^2 \mu _o \right. \nonumber \\&\quad+ \left. 2 \left( \frac{\mathrm{{d}} p_i}{\mathrm{{d}}z} - \frac{\mathrm{{d}} p_o}{\mathrm{{d}}z}\right) \tilde{r}^2 \mu _i \ln \left( \frac{R}{\tilde{r}}\right) \right] -U_d,\end{aligned}$$
(9)
$$\begin{aligned} B_o&= {} -\frac{1}{4 \mu _o}\left[ \frac{\mathrm{{d}} p_o}{\mathrm{{d}}z} R^2 +2\left( \frac{\mathrm{{d}} p_i}{\mathrm{{d}}z}- \frac{\mathrm{{d}} p_o}{\mathrm{{d}}z}\right) \tilde{r}^2 \ln R \right] -U_d. \end{aligned}$$
(10)

Under the assumption of a slowly evolving film thickness, this velocity profile also holds in the nearby regions, where the thickness is H rather than \(H_{\infty }\). The derivation for the planar geometry is given in Appendix 1.

3.2 Recirculating flow patterns

The axisymmetric velocity profile in the channel away from the droplet, in its moving reference frame, is given by

$$\begin{aligned} u_{\infty }(r) = 2 U_{\infty }\left[ 1-\left( \frac{r}{R}\right) ^2\right] -U_d. \end{aligned}$$
(11)

As will become clear in Sect. 5, the droplet velocity can be obtained by imposing mass conservation. For the particular case of a bubble with \(\lambda = 0\), mass conservation reads \((U_{\infty }-U_d)\pi R^2 = - \pi [R^2-(R-H_{\infty })^2] U_d\) (Stone 2010), yielding \(U_{\infty }/U_d = (1-H_{\infty }/R)^2\). The velocity profile (11) can, therefore, be expressed as a function of \(H_{\infty }/R\). As pointed out by Giavedoni and Saita (1997), when \(\lambda =0\), the velocity at the centerline \(u_{\infty }(r=0)\) in the bubble frame changes sign when \(H_{\infty }=H_{\infty }^{\star }=(1-1/\sqrt{2})R\). As a consequence, when the uniform film thicknesses is below \(H_{\infty }^{\star }\), \(u_{\infty }(0)>0\), an external recirculating flow pattern forms ahead of and behind the bubble. For the planar configuration, the critical film thickness for the appearance of the flow recirculation is \(H_{\infty }^{\star }= R/3\).

Based on the flow profiles derived in Sect. 3 and mass conservation (see Sect. 5), we can generalize the critical thickness \(H_{\infty }^{\star }\) to non-vanishing viscosity ratios (\(\lambda>0\)) as (see Appendix 4 for the derivations):

$$\begin{aligned} \frac{H_{\infty }^{\star }}{R} = 1-\sqrt{\frac{(\lambda -1)(2 \lambda -1)}{2}}\frac{1}{\lambda -1} \end{aligned}$$
(12)

for the axisymmetric case and

$$\begin{aligned} \frac{H_{\infty }^{\star }}{R} = \frac{1}{3}\frac{1}{1-\lambda } \end{aligned}$$
(13)

for the planar case. \(H_{\infty }^{\star }/R\) reaches the value of 1 when \(\lambda = 1/2\) or \(\lambda = 2/3\), for the axisymmetric and planar configuration, respectively. Nevertheless, the uniform film thickness is always much smaller than the channel half-width, \(H_{\infty }\ll R\). For a fixed volume of fluid, large film thicknesses would correspond to long droplets, which might be unstable to the Rayleigh–Plateau instability as discussed in Sect. 2.1.

For viscosity ratios \(\lambda \ge 1/2\) (\(\lambda \ge 2/3\)) for the axisymmetric (planar) configuration, there is no critical film thickness above which the recirculation zones disappear, meaning that a recirculation region always exists for any capillary number.

At low capillary numbers, when the film thickness is below \(H_{\infty }^{\star }\), the external recirculating flows are strong enough to induce the recirculation inside the droplet as well. Consequently, besides the two droplet vertices as permanent stagnation points (blue circles in Fig. 8), two stagnation rings emerge on the front and rear part of the axisymmetric interface (red stars in Fig. 8); likewise, four stagnation points arise in the planar case. The stagnation rings/points on the dynamic meniscus (red stars in Fig. 8) move outwards to the droplet vertices when Ca increases. When \(H_{\infty }>H_{\infty }^{\star }\), these stagnation rings/points disappear, taking away with the recirculation regions accordingly (see Fig. 8b). Only the stagnation points at the droplet vertices remain.

However, since the stagnation rings/points at the droplet interface move outwards to the front and rear extremities when the film thickness increases with the capillary number, the recirculation regions might eventually detach from the interface before the critical film thickness \({H_{\infty }^{\star }}\) is reached. Nevertheless, since recirculation regions exist far away from the droplet as long as \(H_{\infty }<H_{\infty }^{\star }\), another flow pattern must exist close to the droplet interface. The detached stagnation points are located on the centerline outside the droplet, and no recirculating flow is present in the region between the detached stagnation point and the one at the droplet vertex (see rear of droplet in Fig. 8d). Contrasting with the case of Fig. 8c, where the stagnation points on the dynamic meniscus induce recirculating flow inside the droplet at both front and rear parts, the inner rear recirculation zone disappears when the capillary number increases, as shown in Fig. 8d. This indicates that the detachment of the recirculation region is not fore-aft symmetric. There is a large range of parameters for which a rear stagnation point is not at the droplet interface anymore and thus there is no recirculation inside the rear part of the droplet. We have found that the critical film thickness for which the stagnation ring/point at the rear detaches from the droplet interface corresponds to when the rear plane curvature of the droplet changes the sign (see also Sect. 7.1). For both the flow patterns as well as for the plane curvatures, the fore-aft asymmetry increases with the capillary number.

Fig. 8
figure 8

Streamlines and recirculation patterns for an axisymmetric droplet with different capillary numbers \(Ca_{\infty }\) and viscosity ratios \(\lambda\) in a frame of reference moving with the droplet. The results are obtained from FEM-ALE numerical simulations. The permanent stagnation points at the droplet vertices are highlighted by blue circles, whereas the (Ca, \(\lambda\))-dependent stagnation rings/points are highlighted by red stars. Insets: detailed flow pattern at the droplet front and rear for \(\lambda = 0.3\) and \(Ca_{\infty }=0.6\). (Color figure online)

Full size image

The phase diagram with the main different types of flow patterns as a function of the viscosity ratio \(\lambda\) and film thickness \(H_{\infty }/R\) is shown in Fig. 9. Note that for viscosity ratios \(\lambda \ge 1/2\) (\(\lambda \ge 2/3\)), the recirculation regions will be attached or detached from or to the droplet interface depending on the the uniform film thickness. Other very peculiar flow fields, as a detached finite recirculation region at the rear or a detached recirculation region at the front as observed by Giavedoni and Saita (1997, 1999), can be obtained for some parameter combinations. However, since the flow field structures are not the main aim of this work, an extended parametric study to detect all possible patterns has not been performed. Nevertheless, our current results do not validate all the flow patterns predicted in Hodges et al. (2004) based on asymptotic arguments, which indeed have not been verified neither experimentally nor numerically.

Fig. 9
figure 9

Diagram of the main possible flow patterns for the axisymmetric configuration. The streamlines corresponding to the points a–d are shown in Fig. 8. (Color figure online)

Full size image

The flow fields for the planar configuration are not presented here as they are similar to those for the axisymmetric configuration.

4 Film thickness

4.1 Asymptotic results in the low-Ca limit

By following the work of Schwartz et al. (1986), we derive an implicit expression predicting the thickness \(H_{\infty }\) of the uniformly thick lubrication film in the low-Ca limit when \(H/R \ll 1\) satisfies. The derivation of the axisymmetric case is presented below, see Appendix 2 for the planar case.

The flow rates at any axial location where the external film thickness is H are:

$$\begin{aligned} q_i&= {} 2 \pi \int _0^{R-H} u_i(r) r \mathrm{{d}}r \nonumber \\&= {} -\pi ( R-H)^2 \left\{ U_d + \frac{1}{8 \mu _i \mu _o} \left[ 2 \frac{\mathrm{{d}} p_o}{\mathrm{{d}}z} H (2 R - H) \mu _i \right. \right. \nonumber \\& \quad + \frac{\mathrm{{d}} p_i}{\mathrm{{d}}z}(R-H)^2\mu _o \nonumber \\& \quad + \left. \left. 4 \left( \frac{\mathrm{{d}} p_i}{\mathrm{{d}}z}-\frac{\mathrm{{d}} p_o}{\mathrm{{d}}z}\right) (R-H)^2 \mu _i \ln \left( \frac{R}{R-H}\right) \right] \right\} , \end{aligned}$$
(14)
$$\begin{aligned} q_o&= {} 2 \pi \int _{R-H}^{R} u_o(r) r \mathrm{{d}}r \nonumber \\&= {} - \frac{\pi }{8 \mu _o}\left\{ H(2R-H) \left[ H^2\left( 2\frac{\mathrm{{d}} p_i}{\mathrm{{d}}z} -3\frac{\mathrm{{d}} p_o}{\mathrm{{d}}z}\right) \right. \right. \nonumber \\& \quad + \left. 2\left( \frac{\mathrm{{d}} p_i}{\mathrm{{d}}z}-\frac{\mathrm{{d}} p_o}{\mathrm{{d}}z}\right) R^2 -H\left( 4\frac{\mathrm{{d}} p_i}{\mathrm{{d}}z} - 6\frac{\mathrm{{d}} p_o}{\mathrm{{d}}z}\right) R\right] \nonumber \\& \quad + \left. 4 \left( \frac{\mathrm{{d}} p_i}{\mathrm{{d}}z}-\frac{\mathrm{{d}} p_o}{\mathrm{{d}}z}\right) (R-H)^4 \ln \left( \frac{R}{R-H}\right) \right\} \nonumber \\& \quad - \pi H(2R-H) U_d. \end{aligned}$$
(15)

Assuming that \(H/R \ll 1\), the volumetric fluxes up to the second order are

$$\begin{aligned} q_i \approx - \pi R^2 \left( U_d + \frac{1}{8 \mu _i}\frac{\mathrm{{d}} p_i}{\mathrm{{d}}z} R^2 + \frac{1}{2 \mu _o}\frac{\mathrm{{d}} p_i}{\mathrm{{d}}z} R H + \frac{1}{2 \mu _o}\frac{\mathrm{{d}} p_o}{\mathrm{{d}}z} H^2 \right) , \end{aligned}$$
(16)
$$\begin{aligned} q_o \approx - 2 \pi R H \left( U_d + \frac{1}{4 \mu _o}\frac{\mathrm{{d}} p_i}{dz}H R + \frac{1}{3 \mu _o}\frac{\mathrm{{d}} p_o}{\mathrm{{d}}z} H^2 \right). \end{aligned}$$
(17)

In the droplet frame, the inner flow rate is \(q_i =0\). Furthermore, in the region with a uniformly thick film, \(H=H_{\infty }\); the inner and outer pressure gradients balance, \(\frac{\mathrm{{d}} p_i}{\mathrm{{d}} z}=\frac{\mathrm{{d}} p_o}{dz}\). Using these two conditions, one can obtain the pressure gradient in the uniform film region

$$\begin{aligned} \frac{\mathrm{{d}} p}{\mathrm{{d}}z} \bigg \vert _{r=R-H_{\infty }} \approx -\frac{8 \mu _i U_d}{R^2+4 \lambda H_{\infty } R + 4 \lambda H_{\infty }^2} \end{aligned}$$
(18)

and the outer flow rate in the \(H_{\infty }/R \ll 1\) limit is

$$\begin{aligned} q_o\approx & {} -2 \pi R H_{\infty } \left[ \frac{3 R^2 + 6 \lambda H_{\infty } R +4 \lambda H_{\infty }^2 }{ 3 (R^2 + 4 \lambda H_{\infty } R+4 \lambda H_{\infty }^2)}\right] U_d \nonumber \\\approx & {} - 2 \pi R H_{\infty } \left( \frac{ R + 2 \lambda H_{\infty } }{ R + 4 \lambda H_{\infty } }\right) U_d. \end{aligned}$$
(19)

In the dynamic meniscus regions, the inner and outer pressure gradients are not equal and their difference is proportional to the mean curvature of the interface at \(r=R-H\), through Laplace’s law. By assuming a quasi-parallel flow whose radial velocity is weaker than the axial velocity by one order of magnitude and a small capillary number, the normal stress condition at the interface is not affected by viscous stresses. Hence, the axial gradient of the normal stress condition reads

$$\begin{aligned} \frac{\mathrm{{d}} p_i}{\mathrm{{d}}z} - \frac{\mathrm{{d}} p_o}{\mathrm{{d}}z} = \gamma \frac{\mathrm{{d}}^3 H}{\mathrm{{d}} z^3}, \end{aligned}$$
(20)

where the axial gradient of the curvature in the azimuthal direction is neglected as it is an order smaller. The pressure gradients \(\mathrm{{d}}p_i/\mathrm{{d}}z\) and \(\mathrm{{d}}p_o/\mathrm{{d}}z\) as functions of H can be obtained from Eqs. (16) and (17) imposing mass conservation, i.e. imposing \(q_i=0\) and \(q_o\) given by Eq. (19):

$$\begin{aligned} \frac{\mathrm{{d}} p_i}{\mathrm{{d}}z} \approx \frac{4 \lambda (-6 H_{\infty }^2 \lambda + 4 H_{\infty } H \lambda - 3 H_{\infty } R + H R) \mu _o U_d }{H R (4 H_{\infty } \lambda + R) (H \lambda + R) }, \end{aligned}$$
(21)
$$\begin{aligned} \frac{\mathrm{{d}} p_o}{\mathrm{{d}}z} \approx \frac{3 (H_{\infty } - H) [8 H_{\infty } H \lambda ^2 + 2 (H_{\infty } + H) \lambda R + R^2] \mu _o U_d}{H^3 (4 H_{\infty } \lambda + R) (H \lambda + R)}. \end{aligned}$$
(22)

By plugging Eqs. (21) and (22) into Eq. (20) and adopting the change of variables \(H = H_{\infty } \eta\) and \(z = H_{\infty } (3 Ca)^{-1/3} \xi\) in the spirit of Bretherton (1961), we obtain an universal governing equation for the scaled film thickness \(\eta\) when taking the limit \(H_{\infty }/R\rightarrow 0\):

$$\begin{aligned} \frac{\mathrm{{d}}^3 \eta }{\mathrm{{d}}\xi ^3} = \frac{\eta -1}{\eta ^3}\left[ \frac{1+2 m (1+ \eta + 4 m \eta )}{(1+4m)(1+m\eta )}\right] , \end{aligned}$$
(23)

where

$$\begin{aligned} m = \lambda \frac{H_{\infty }}{R} \end{aligned}$$

denotes the rescaled viscosity ratio. The corresponding planar counterpart reads (see derivation in Appendix 2)

$$\begin{aligned} \frac{\mathrm{{d}}^3 \eta }{\mathrm{{d}}\xi ^3} =2\frac{\eta -1}{\eta ^3}\left[ \frac{2+3 m (1+ \eta + 3 m \eta )}{(1+3m)(4+3m\eta )}\right]. \end{aligned}$$
(24)

If the limit of vanishing uniform film thickness is not considered, the resulting equations for \(\eta\) would depend on \(H_{\infty }/R\) (de Ryck 2002). In the limit of \(m\rightarrow 0\), the classical Landau–Levich–Derjaguin–Bretherton equation (Landau and Levich 1942; Derjaguin 1943; Bretherton 1961) is retrieved for both configurations. Following Bretherton (1961), Eqs. (23) and (24) can be integrated to find the uniform film thickness \(H_{\infty }/R\) (see also Cantat (2013) for more details).

First, the equations can be linearized in the uniform film region around \(\eta \approx 1\), giving

$$\begin{aligned} \frac{\mathrm{{d}}^3 \eta }{\mathrm{{d}}\xi ^3} = K (\eta - 1) , \end{aligned}$$
(25)

where K is a constant depending on the geometrical configurations and the viscosity ratio m. Equation (25) has a monotonically increasing solution with respect to \(\xi\) for the front dynamic meniscus, \(\xi \rightarrow \infty\), and an oscillatorily increasing solution for the rear, \(\xi \rightarrow -\infty\), as derived in Sect. 6. The solution of the front meniscus is \(\eta (\xi ) = 1 + \alpha \exp (K^{1/3} \xi )\), where \(\alpha\) is a small parameter, typically \(10^{-6}\). Second, the nonlinear Eqs. (23) and (24) can be integrated numerically as an initial value problem with a fourth-order Runge–Kutta scheme, starting from the linear solution until the plane curvature of the interface profile becomes constant. A region of constant plane curvature, called static meniscus region (see Fig. 1) exists as \(\mathrm{d}^3\eta /\mathrm{d} \xi ^3 \approx 0\) for \(\eta \gg 1\) (see red line on Fig. 11). In the static meniscus region, the interface profile is a parabola: \(\eta = P\xi ^2/2 + C \xi + D\), or, in terms of film thickness, \(H=P(3 Ca)^{2/3} z^2 /(2H_{\infty })+ C(3Ca)^{1/3}z + D H_{\infty }\), where P, C and D are real-valued constants. Thus, P is set by the constant plane curvature obtained by the integration of the nonlinear equation.

The procedure can be repeated for any rescaled viscosity ratio m and the obtained results for the coefficient P can well described by the fitting law (Schwartz et al. 1986):

$$\begin{aligned} P(m) = \frac{0.643}{2}\left\{ 1 + 2^{2/3} +(2^{2/3}-1)\tanh \left[ 1.2 \log _{10} m + c_1\right] \right\} , \end{aligned}$$
(26)

where the constant \(c_1=0.1657\) for the axisymmetric configuration and \(c_1= 0.0159\) for the planar configuration (see Fig. 10). The well-known limits for a bubble \(P(0) = 0.643\) (Bretherton 1961) and a very viscous droplet \(P(m\rightarrow \infty ) = 2^{2/3} P(0)\) (Cantat 2013) are recovered.

Fig. 10
figure 10

Film-thickness coefficient P obtained for discrete m values (symbols) and fitting law (26) (solid lines) as a function of the rescaled viscosity ratio m. (Color figure online)

Full size image

To obtain the uniform film thickness, the matching principle proposed by Bretherton (1961) is employed. The plane curvature \(\kappa = \mathrm{{d}}^2H/\mathrm{{d}}z^2 = P(3 Ca)^{2/3} /H_{\infty }\) in the static region has to match that of the front hemispherical cap of radius R, which exists for small capillary numbers (see red dashed line in Fig. 11). A rigorous asymptotic matching can be found in Park and Homsy (1984) for a bubble with \(m=0\). When \(m\ne 0\), the coefficient P(m) depends implicitly on \(H_{\infty }\), and thus on Ca, through m, leading to an implicit asymptotic relation for \(H_{\infty }/R\) as:

$$\begin{aligned} \frac{H_{\infty }}{R}=P(m) (3 Ca)^{2/3}. \end{aligned}$$
(27)

Strictly speaking, the uniform film thickness of viscous droplets (\(\lambda \ne 0\)) in the low Ca limit does not scale with \(Ca^{2/3}\) as for a bubble (\(\lambda =0\)).

Fig. 11
figure 11

Plane curvature of the droplet interface for exponentially increasing capillary numbers in the range \(10^{-4}< Ca < 1\), obtained from FEM-ALE numerical simulations, where \(\lambda = 1\). The dashed red line is for the smallest Ca. The z axis is rescaled by the droplet length to facilitate the comparison. Insets: zoom-in on the front and rear menisci. Similar profiles are obtained for other viscosity ratios. (Color figure online)

Full size image

4.2 Empirical model in the low-Ca limit

Equation (27) holds for capillary numbers as low as below \(10^{-3}\) (Bretherton 1961). We solve Eq. (27) numerically and present the coefficient P and the uniform film thickness \(H_{\infty }/R\) versus Ca in Fig. 12 for the axisymmetric case. To derive an explicit formulation to predict the film thickness in this Ca regime, we define \(\bar{P}\) as a Ca-averaged value of P and define the empirical model

$$\begin{aligned} \frac{H_{\infty }}{R} =\bar{P}(\lambda ) (3 Ca)^{2/3}, \end{aligned}$$
(28)

where \(\bar{P}(\lambda )\) is independent of Ca (see dashed lines in Fig. 12a) and can be approximated by the fitting law (see Fig. 13):

$$\begin{aligned} \bar{P} (\lambda )&= {} \frac{0.643}{2}\left\{ 1 + 2^{2/3}\right. \nonumber \\& \quad \left. +\,(2^{2/3}-1)\tanh \left[ 1.28 \log _{10} \lambda + c_2\right] \right\} , \end{aligned}$$
(29)

where the constant \(c_2= -2.36\) for the axisymmetric case and \(c_2= -2.52\) for the planar case are obtained by fitting. For \(\lambda = 0\), \(\bar{P}=0.643\) is recovered and \(H_{\infty }/R\) indeed scales with \(Ca^{2/3}\), at least when \(Ca<10^{-3}\). Figure 12b also shows that the empirically obtained film thickness (dashed lines) Eq. (28) agrees reasonably well with the FEM-ALE simulation results (symbols), whereas the implicit law (solid lines) Eq. (27) slightly underestimates them at very low Ca. To cure this mismatch, Hodges et al. (2004) proposed a modified interface condition, which, however, is found to overestimate the thickness more than that underestimated by the original implicit law.

Fig. 12
figure 12

a Coefficient P (solid lines) obtained by solving Eq. (27) and the mean coefficient \(\bar{P}\) (dashed lines) for the axisymmetric configuration. The viscosity ratios are \(\lambda = 0\), 50 and 100. b The uniform film thickness \(H_{\infty }/R\) from Eq. (27) (solid lines) and Eq. (28) (dashed lines), compared to the FEM-ALE simulation results (symbols). (Color figure online)

Full size image
Fig. 13
figure 13

Mean coefficient \(\bar{P}\) (symbols) obtained by Ca-averaging the results of the implicit relation Eq. (27) and fitting law (solid lines) Eq. (29) versus the viscosity ratio \(\lambda\). (Color figure online)

Full size image

4.3 Model for \(10^{-3}\lessapprox Ca \lessapprox 1\)

Despite the explicit law for the uniform-film thickness prediction with \(\bar{P}\) proved to be satisfactory, its validity range is restricted to low capillary numbers. As known since the experiments of Taylor (1961), the film thickness of a bubble saturates for increasing Ca. Aussillous and Quéré (2000) proposed a model for \(\lambda =0\), which agrees well with the experimental data of Taylor (1961), further inspiring the two very recent works of Klaseboer et al. (2014), Cherukumudi et al. (2015). In the same vain, we propose an empirical model for the film thickness \(H_{\infty }\) as a function of both Ca and \(\lambda\)

$$\begin{aligned} \frac{H_{\infty }}{R}=\frac{\bar{P}(\lambda )(3Ca)^{2/3}}{1+\bar{P} (\lambda )Q(\lambda )(3Ca)^{2/3}}, \end{aligned}$$
(30)

where the coefficient Q is obtained by fitting Eq. (30) to the database constructed from our extensive FEM-ALE simulations over a broad range of Ca for different \(\lambda\). The proposed function of \(Q(\lambda )\) is given in Appendix 5 and plotted in Fig. 14. For an axisymmetric bubble, we find \(Q=2.48\), in accordance with the estimation \(Q=2.5\) of Aussillous and Quéré (2000). We now present in Fig. 15 the numerical film thickness (symbols) and the empirical model (lines) for \(\lambda =1\). For the sake of clarity, the results for \(\lambda = 0\) and 100 are shown in Appendix 1 in Fig. 25. For \(\lambda = 1\), the thickness of the two configurations coincides. However, when \(Ca \sim O(1)\), the film is thicker in the planar configuration than in the axisymmetric one for a bubble (\(\lambda =0\)); the trend reverses for a highly viscous droplet (\(\lambda =100\)). This \(\lambda\)-dependence of the film thickness is indeed implied by the crossover of the two fitting functions \(Q(\lambda )\) at \(\lambda = 1\) shown in Fig. 14.

Fig. 14
figure 14

Coefficient Q obtained for the simulated viscosity ratios (symbols) and proposed fitting law (see Appendix 5) as a function of the viscosity ratio \(\lambda\). (Color figure online)

Full size image
Fig. 15
figure 15

Uniform film thickness given by Eq. (30) (lines) and FEM-ALE numerical results (symbols) as a function of the droplet capillary number for \(\lambda = 1\) and both axisymmetric (blue solid line, full symbols) and planar (dashed red line, empty symbols) geometries. Cross and circle correspond to a droplet with 37 and \(82\%\), respectively, larger volume than the standard one used for the axisymmetric geometry. (Color figure online)

Full size image

It has to be noted that when the capillary number is increased, the regions of constant plane curvature in the static front and rear caps reduce in size and eventually disappear (see Fig. 11), and this for all viscosity ratios. The matching to a region of constant plane curvature for large capillary numbers as proposed by Klaseboer et al. (2014) and Cherukumudi et al. (2015) might be questionable for this Ca-range.

The uniform film thickness of droplets with 37 and \(82\%\) larger volume, resulting in longer droplets, are compared in Fig. 15, showing that as long as such a uniform region exists, the results are independent of the droplet length.

5 Droplet velocity

Equipped with the model of the uniform-film thickness \(H_{\infty }\), we derive the droplet velocity based on the velocity profiles in the uniform-film region given in Sect. 3.1. At the location \(H=H_{\infty }\) where the interface is flat, the pressure gradients are equal, \(\mathrm{{d}}p_i/\mathrm{{d}}z=\mathrm{{d}}p_o/\mathrm{{d}}z=\mathrm{{d}}p/\mathrm{{d}}z\). We further use \(q_o= \pi R^2 (U_{\infty }-U_d)\) imposed by mass conservation and \(q_i=0\) (in the moving frame of the droplet) to obtain the analytical expressions for the pressure gradient

$$\begin{aligned} \frac{\mathrm{{d}} p}{\mathrm{{d}}z} \bigg \vert _{r=R-H_{\infty }} = \frac{-8 R^2 U_{\infty } \mu _i}{(R-H_{\infty })^4+H_{\infty }(2R-H_{\infty })(2R^2-2H_{\infty }R +H_{\infty }^2)\lambda }, \end{aligned}$$
(31)

and for the droplet velocity

$$\begin{aligned} U_d= \frac{R^2[(R-H_{\infty })^2+2 H_{\infty }(2R-H_{\infty })\lambda ]}{(R-H_{\infty })^4+H_{\infty }(2R-H_{\infty })(2R^2-2H_{\infty }R+H_{\infty }^2)\lambda }U_{\infty }. \end{aligned}$$
(32)

The relative velocity of the axisymmetric droplet with respect to the underlying velocity reads

$$\begin{aligned} \frac{U_d-U_{\infty }}{U_d} = \frac{\left( 2-\frac{H_{\infty }}{R}\right) \frac{H_{\infty }}{R} \left[ 1+ \left( 2-\frac{H_{\infty }}{R}\right) \frac{H_{\infty }}{R}(\lambda -1) \right] }{1+\left( 2-\frac{H_{\infty }}{R}\right) \frac{H_{\infty }}{R}(2\lambda -1)}. \end{aligned}$$
(33)

An analogous derivation for the planar configuration yields (see Appendix 3):

$$\begin{aligned} \frac{U_d-U_{\infty }}{U_d} = \frac{\frac{H_{\infty }}{R} \left\{ 2-\frac{H_{\infty }}{R} \left[ 4+2 \frac{H_{\infty }}{R}(\lambda -1) -3 \lambda \right] \right\} }{2+\left( 2-\frac{H_{\infty }}{R}\right) \frac{H_{\infty }}{R}(3\lambda -2)}. \end{aligned}$$
(34)

Equations (30) and (32) form a system of the two unknowns, namely the droplet capillary number Ca and the uniform film thickness \(H_{\infty }/R\). It is important to remind that the former is related to the droplet velocity via \(Ca = Ca_{\infty }U_d/U_{\infty }\). For a given combination of inflow capillary number \(Ca_{\infty }\) and viscosity ratio \(\lambda\) as the input, the system can be solved numerically (see Matlab file filmThicknessAndVelocity.m in the Supplementary Material) outputting Ca and \(H_{\infty }/R\). The predicted relative velocity \(({U_d-U_{\infty }})/{U_d}\) (lines) agrees well the FEM-ALE simulation results (symbols) as shown in Fig. 16.

Fig. 16
figure 16

Relative droplet velocity (lines) predicted by Eqs. (33) and (34) together with the proposed empirical model for the uniform film thickness (30) and the results of the FEM-ALE numerical simulations (symbols) as a function of capillary number \(Ca_{\infty }\) for \(\lambda = 0\) (a), 1 (b) and 100 (c) and both axisymmetric (blue solid line, full symbols) and planar (dashed red line, empty symbols) geometries. Long dashed gray lines correspond to the asymptotic estimates of Eqs. (35) and (36). (Color figure online)

Full size image

In the limit of \({H_{\infty }}/{R}\rightarrow 0\), the relative velocity can be approximated asymptotically as

$$\begin{aligned} \frac{U_d-U_{\infty }}{U_d} = 2 \left( \frac{H_{\infty }}{R}\right) - (1+4 \lambda ) \left( \frac{H_{\infty }}{R}\right) ^2 + O\left( \frac{H_{\infty }}{R}\right) ^3 \end{aligned}$$
(35)

for the axisymmetric case, and

$$\begin{aligned} \frac{U_d-U_{\infty }}{U_d} = \left( \frac{H_{\infty }}{R}\right) -\frac{3\lambda }{2} \left( \frac{H_{\infty }}{R}\right) ^2 + O\left( \frac{H_{\infty }}{R}\right) ^3 \end{aligned}$$
(36)

for the planar geometry. For very low capillary numbers, the asymptotic estimates predict that the relative droplet velocity scales with \(H_{\infty }/R\), and hence with \(Ca^{2/3}\) (Stone 2010). The viscosity ratio \(\lambda\) only enters at second order of \(H_{\infty }/R\), which, however, influences the validity range of the asymptotic estimates (35) and (36) considerably. The asymptotic estimates are exact for \(\lambda = 0\). In this case, Eqs. (35) and (36) reduce to the well-known predictions for bubbles \((2-H_{\infty }/R)H_{\infty }/R\) and \(H_{\infty }/R\) (Bretherton 1961; Stone 2010; Langewisch and Buongiorno 2015), respectively (see Fig. 16a). For non-vanishing \(\lambda\), the complete expressions (33) and (34) should be employed (see Fig. 16b). For example, the asymptotic estimate for \(\lambda = 100\) is only valid when \(Ca_{\infty } < 10^{-4}\) (see Fig. 16c).

6 Minimum film thickness

At low capillary numbers Ca, the droplet interface exhibits an oscillatory profile between the uniform thin film and the rear static cap (see Fig. 11). The minimum film thickness in the low Ca limit can be computed by integrating the lubrication Eqs. (23) or (24) for \(\xi =0\) to \(\xi \rightarrow -\infty\). The initial condition for this initial value problem is given by the solution of the linear equation (25) for negative \(\xi\): \(\eta = 1+\alpha \exp (-K^{1/3} \xi /2) \cos (\sqrt{3} K^{1/3} \xi /2+\phi )\), where \(\alpha\) is a small parameter of order \(10^{-6}\) and \(\phi\) is a parameter taken such that the constant plane curvature of the nonlinear integrated solution at \(\xi \rightarrow -\infty\) is equal to the one of the front static cap (Bretherton 1961; Cantat 2013) as discussed in Sect. 4.1. Note that the linear solution for the rear dynamic meniscus presents oscillations. The minimum film thickness of the obtained profile is found to follow the empirical model (Bretherton 1961):

$$\begin{aligned} \frac{H_{\text {min}}}{R} = F(m) P(m) (3Ca)^{2/3} \quad \text {with} \quad m=\lambda \frac{H_{\infty }}{R} , \end{aligned}$$
(37)

where F(m) is a coefficient obtained through fitting Eq. (37) to our numerical database (see Fig. 17a). Similar to the mean coefficient \(\bar{P}\) adopted in Sect. 4, a Ca-averaged F(m) can be introduced as \(\bar{F}\), which is further assumed as 0.716 in view of its very weak dependence on \(\lambda\) shown in Fig. 17b.

Fig. 17
figure 17

a Minimum film-thickness coefficient F as a function of the rescaled viscosity ratio m. b Mean coefficient \(\bar{F}\) (symbols) and fitting law (solid line) as a function of the viscosity ratio \(\lambda\). (Color figure online)

Full size image

The minimum film thickness is bounded by the thickness of the uniform film and hence will saturate at large capillary numbers. Thus, for sufficiently large Ca values, the oscillations at the rear interface would disappear and \(H_{\text {min}}=H_{\infty }\). It is, therefore, natural to propose a rational function model of \(H_{\text {min}}\) for a broader Ca-range as the one for \(H_{\infty }\):

$$\begin{aligned} \frac{H_{\text {min}}}{R}=\frac{\bar{P}(\lambda )\bar{F}(3Ca)^{2/3}}{1+\bar{P}(\lambda )\bar{F}G(\lambda )(3Ca)^{2/3}}. \end{aligned}$$
(38)

The above minimum film thickness model (38) together with the coefficient G is in good agreement with the results of the numerical simulations (see Figs. 18 and 26).

Fig. 18
figure 18

Minimum film thickness given by Eq. (38) (lines) and FEM-ALE numerical results (symbols) as a function of the droplet capillary number for \(\lambda = 1\) and both axisymmetric (blue solid line, full symbols) and planar (dashed red line, empty symbols) geometries. (Color figure online)

Full size image

The proposed fitting of the coefficient G as a function of the viscosity ratio (see Fig. 19) is given in Appendix 5.

Fig. 19
figure 19

Coefficient G obtained for the simulated viscosity ratios (symbols) and proposed fitting law (71) (solid lines) as a function of the viscosity ratio \(\lambda\). (Color figure online)

Full size image

7 Front and rear total stress jumps

The dynamics of a translating bubble in a capillary tube has been characterized since the seminal work of Bretherton (1961) not only by the mean and minimum film thickness, the relative velocity compared to the mean velocity, but also by the mean curvature of the front and rear static menisci. In fact, for \(Ca\rightarrow 0\), the pressure drop across the interface is directly related to the expression of its mean curvature via the Laplace's law. Having generalized the film thickness and droplet velocity models for non-vanishing viscosity ratios, we are hereby focusing on the evolution of the plane curvature of the front and rear static caps versus the capillary number and viscosity ratio. The mean curvature at the droplet extremities is equivalent to the corresponding plane curvature for the planar configuration or to its double for the axisymmetric configuration: \(\mathscr {C}_{f,r} = \chi \kappa _{f,r}\), with \(\chi =2\) (resp. \(\chi =1\)) for the axisymmetric (resp. planar) configuration (see Sect. 2.2). As will be shown, given the rather broad range of capillary numbers considered (approaching O(1)), it is insufficient to consider the interface mean curvature alone to provide an accurate prediction of the pressure drop, but the jump in the normal viscous stress has to be accounted for.

For the incompressible Newtonian fluids considered, the viscous stress tensor is \(\varvec{\tau } = \mu \left[ \left( \nabla \mathbf {u} \right) + \left( \nabla \mathbf {u} \right) ^T \right]\), and hence the z-direction normal total stress \(\sigma _{zz}\) is given by

$$\begin{aligned} \sigma _{zz} = - p + \tau _{zz} = -p + 2 \mu \frac{\partial u}{\partial z}. \end{aligned}$$
(39)

Applying the difference (between inner and outer phases) operator \(\Delta\) to Eq. (39) and based on the dynamic boundary condition in the normal direction (4) at the droplet front and rear extremities, we get

$$\begin{aligned} \Delta \sigma _{zz_{f,r}}= - \Delta p_{f,r} + \Delta \tau _{zz_{f,r}} = - \gamma \chi \kappa _{f,r}, \end{aligned}$$
(40)

which indicates that the total stress jump at the front/rear extremities scales with the local interface mean curvature and is the sum of the pressure jump and the normal viscous stress jump. These quantities will be modeled separately in the following sections.

7.1 Front and rear plane curvatures

In the spirit of the empirical film thickness model, the plane curvature \(\kappa _f\) of the front meniscus and that of the rear, \(\kappa _r\), are approximated by the rational function model

$$\begin{aligned} \kappa _{f,r}R = \frac{1+T_{f,r}(\lambda )(3 Ca)^{2/3}}{1+Z_{f,r}(\lambda ) (3 Ca)^{2/3}}, \end{aligned}$$
(41)

where \(T_{f,r}\) and \(Z_{f,r}\) as \(\lambda\)-dependent constants are obtained by fitting Eq. (41) to the FEM-ALE data (see Appendix 5). It is worth noting that the asymptotic series of the proposed expression,

$$\begin{aligned} \kappa _{f,r}R \sim 1+(T_{f,r}-Z_{f,r})(3Ca)^{2/3}+O(Ca^{4/3}), \end{aligned}$$
(42)

is in line with the law proposed by Bretherton (1961), namely \(1+\beta _{f,r}(3Ca)^{2/3}+O(Ca^{4/3})\). Thus, the empirical model (41), which is in excellent agreement with the numerical results (see Figs. 20 and  21 as well as Figs. 27 and  28), can be regarded as an empirical extension of Bretherton’s law to a broader capillary numbers range up to 1. The mean curvature at the droplet extremities is given by \(\mathscr {C}_{f,r} = \chi \kappa _{f,r}\).

Fig. 20
figure 20

Curvature \(\kappa _f\) of the front meniscus predicted by the model Eq. (41) (lines) and FEM-ALE data (symbols) versus Ca for both axisymmetric (blue line, full symbols) and planar (red dashed line, empty symbols) geometries, where the viscosity ratio is \(\lambda = 1\). (Color figure online)

Full size image
Fig. 21
figure 21

The rear counterpart \(\kappa _r\) of Fig. 20. (Color figure online)

Full size image

7.2 Front and rear pressure jumps: classical model

Following the literature (Bretherton 1961; Cherukumudi et al. 2015), the dimensionless pressure jump \({\Delta p_{f,r} R}/{\gamma }=(p_{{f,r}}^i - p_{{f,r}}^o)R/\gamma\) at the front and rear of the droplet is described by the empirical model

$$\begin{aligned} \frac{\Delta p_{f,r} R}{\gamma } = \chi \left[ 1+S_{f,r}(\lambda ) (3 Ca)^{2/3}\right] , \end{aligned}$$
(43)

where \(\chi =2\) (resp. \(\chi =1\)) for the axisymmetric (resp. planar), and \(S_{f,r}\) is a \(\lambda\)-dependent coefficient. Equation (43) is in fact inspired by the curvature model proposed by Bretherton (1961) exploiting the Laplace's law (Cherukumudi et al. 2015), reason why we call it classical model. The coefficient \(S_{f,r}\) could be derived from the integration of the lubrication equation (23) or (24), which is valid in the low-Ca limit when the viscous stresses and their jumps are negligible. To broaden the Ca range of the model, we obtain \(S_{f,r}\) through fitting to the FEM-ALE data. Nevertheless, as visible in Figs. 22 and 23, the model fails to precisely describe the numerical data, particularly for the rear pressure jump at high Ca values (see Fig. 23).

After explaining our model for the normal viscous stress jump in Sect. 7.3, we will show in Sect. 7.4 that the pressure jump can be better approximated by summing up the two contributions from the interface mean curvature and the normal viscous stress jump, which are modeled separately. The importance of the normal viscous stress jump for the pressure jump is already noticeable when comparing the evolutions of the plane curvature \(\kappa _{f,r}\) and the ones of the pressure jump \(\Delta p_{f,r} / \gamma\) in Figs. 20 and 22 or in Figs. 21 and 23.

Fig. 22
figure 22

Front pressure jump \(\Delta p_f\) given by Eq. (43) (solid lines) and front normal viscous stress jump \(\Delta \tau _{{zz}_{f}}\) by Eq. (44) (inset, solid lines) and FEM-ALE data (symbols) versus Ca for both axisymmetric (blue line, full symbols) and planar (red line, empty symbols) geometries, where the viscosity ratio is \(\lambda = 0\). The dashed lines correspond to the improved pressure jump model Eq. (46). Note the different scale in the insets. (Color figure online)

Full size image
Fig. 23
figure 23

The rear counterpart, pressure jump \(\Delta p_r\) and normal viscous stress jump \(\Delta \tau _{{zz}_{r}}\), of Fig. 22. (Color figure online)

Full size image

7.3 Front and rear normal viscous stress jumps

The dimensionless normal viscous stress jump \(\Delta \tau _{zz} R /\gamma = (\tau _{{zz}_{f,r}}^i - \tau _{{zz}_{f,r}}^o )R/\gamma\) at the front and at the rear of the droplet is approximated by the following model:

$$\begin{aligned} \frac{\Delta \tau _{zz_{f,r}} R}{\gamma } = \frac{M_{f,r}(\lambda ) (3Ca)+N_{f,r}(\lambda ) (3Ca)^{4/3}}{1+O_{f,r}(\lambda )(3Ca)}, \end{aligned}$$
(44)

where \(M_{f,r}\), \(N_{f,r}\) and \(O_{f,r}\) are viscosity-ratio-dependent coefficients found by fitting Eq. (44) to the FEM-ALE data. The normal viscous stress jumps indeed scale with Ca for small capillary numbers, as found by Bretherton (1961). The comparison between the model and the numerical results is shown in the insets of Figs. 22 and 23, where the results for \(\lambda = 0\) are shown. The results for \(\lambda = 1\) and 100 can be found in Figs. 29 and 30. The stress jump \(\Delta \tau _{zz}\) is found to be small in the case of \(\lambda =1\) and it varies with Ca non-monotonically for the other viscosity ratios.

7.4 Front and rear pressure jumps: improved model

Using the dynamic boundary condition in the normal direction evaluated at the front and rear caps of the droplet, Eq. (40), the pressure jump at the front and rear caps can also be computed as

$$\begin{aligned} \Delta p_{f,r} = \gamma \chi \kappa _{f,r} + \Delta \tau _{zz_{f,r}}. \end{aligned}$$
(45)

Thus, with the proposed models (41) and (44) for the interface curvatures and normal viscous stress jumps at hand, the pressure jump model reads

$$\begin{aligned} \frac{\Delta p_{f,r} R}{\gamma }&= {} \frac{M_{f,r}(\lambda ) (3Ca)+N_{f,r}(\lambda ) (3Ca)^{4/3}}{1+O_{f,r}(\lambda )(3Ca)} \nonumber \\& \quad + \chi \frac{1+T_{f,r}(\lambda )(3 Ca)^{2/3}}{1+Z_{f,r}(\lambda ) (3 Ca)^{2/3}}, \end{aligned}$$
(46)

which agrees with the FEM-ALE data better than Eq. (43) does (see dashed lines on Figs. 22 and 23 or Figs. 29 and 30). Therefore, the jump in normal viscous stresses has to be taken into account for \(Ca>10^{-3}\).

8 Stress distribution and total pressure drop

8.1 Stress distribution along the channel centerline

The flow field can be classified into parallel and non-parallel regions (see Fig. 8). The parallel regions are composed of the region sufficiently far away from the droplet and that encompassing the uniform lubrication film of constant thickness, where the flow is streamwise invariant. The profile of the streamwise velocity u(r) is parabolic and the radial velocity \(v \approx 0\). On the contrary, the flow is not parallel near the droplet extremities (see Fig. 8) where the flow stagnates. Therefore, the nearby streamwise velocity vary significantly, leading to a non-zero radial velocity v owing to the divergence-free condition.

We show in Fig. 24 the distribution of the total stress component \(\sigma _{zz}=-p + \tau _{zz}\), of the pressure p and of the viscous stress component \(\tau _{zz}=2 \mu \partial u/\partial z\) along the centerline of the channel. \(\tau _{zz}\) vanishes where the flow is approximately parallel. As seen in Sect. 7.3, \(\tau _{zz}\) is negligible at small Ca, typically below \(10^{-3}\).

Fig. 24
figure 24

Spatial evolution of the pressure p (red solid line), normal viscous stresses \(-\tau _{zz}\) (green dotted line) and total stresses \(-\sigma _{zz}\) (blue dashed line) along the centerline for \(Ca = 8.2\cdot 10^{-4}\) (a) and \(Ca = 8.8\cdot 10^{-3}\) (b), \(\lambda = 1\) and an axisymmetric configuration, obtained from the FEM-ALE numerical simulations. The linear pressure evolution without considering non-parallel flow effects is shown by the thin black lines. The total stresses jumps induced by the mean curvature at the interfaces are indicated by arrows. The droplet shape is indicated in blue. The pressure at the channel wall is indicated by the grey line. (Color figure online)

Full size image

Furthermore, for a larger but still moderate Ca number, it is observed in Fig. 24b that the pressure (red line) deviates from the linearly varying pressure, \(p_{\text {linear}}\) (black line), of the unperturbed flow (without droplet) featured with a constant pressure gradient. The deviation is attributed to the non-parallel flow structure near the front and rear caps of the droplet (see Fig. 8), hence the pressure based on \(p_{\text {linear}}\) needs to be corrected by \(\Delta p^{\text {NP}}=p-p_{\textsf {linear}}\). Typical values for the pressure corrections can be found in the Appendix 7. These corrections are particularly large at large viscosity ratios for the region inside of the droplet. We did not succeed in providing a model to quantify this pressure correction.

Finally, in agreement with the results of Sect. 7, the jump in total stress or pressure at the rear of the droplet is smaller than the one at the front.

8.2 Pressure distribution along the channel wall

The pressure distribution on the channel wall is presented in Fig. 24 as well (continuous grey line). The influence of the interface mean curvature is clearly visible. The non-monotonic pressure at the wall close the droplet rear results from the variation of the plane curvature in the dynamic meniscus region, where the interface oscillates (see also Fig. 11).

8.3 Droplet-induced total pressure drop along a channel

The prediction of the total pressure drop along a channel induced by the presence of a droplet flowing with a velocity \(U_d\) is of paramount importance for the design of two-phase flow pipe networks (Baroud et al. 2010; Ładosz et al. 2016). This allows for a coarse-grained quantification of the complicated local effects induced by the droplet. Droplets can thus be seen as punctual perturbations in the otherwise linear pressure evolution. In this section, we will show that it is possible to predict the total pressure drop induced by a droplet with the models proposed so far.

The total pressure drop can be defined as the difference between the pressure in the outer phase ahead and behind the droplet, namely \(\Delta p_{\textsf {tot}} = p_f^o-p_r^o\) (Kreutzer et al. 2005). It is given by

$$\begin{aligned} \Delta p_{\textsf {tot}}&= {} \Delta p_{o,r}^{\text {NP}} + \Delta p_r -\Delta p_{i,r}^{\text {NP}} \nonumber \\&+\frac{\mathrm{{d}}p_i}{\mathrm{{d}}z} L_d +\Delta p_{i,f}^{\text {NP}} - \Delta p_f - \Delta p_{o,f}^{\text {NP}} , \end{aligned}$$
(47)

where \(\Delta p_{f,r}\) are given by the model for the pressure jumps at interfaces, Eq. (46). The pressure gradient \(\mathrm{{d}}p_i/\mathrm{{d}}z\) in the parallel region inside the droplet is given by Eqs. (31) and (67) for the axisymmetric and planar geometries, respectively. Assuming the droplet of volume/area \(\Omega\) (axisymmetric/planar geometry) as a composition of two hemispherical caps of radius \(R-H_{\infty }\), with \(H_{\infty }\) given by Eq. (30), connected by a cylinder of the same radius, the droplet length \(L_d\) can be approximated at first order for low Ca, i.e. for \(H_{\infty }/R\ll 1\), as

$$\begin{aligned} L_d = \frac{(R+2 H_{\infty })}{\pi }\frac{\Omega }{R^3}+\frac{2}{3}(R-H_{\infty }) \end{aligned}$$
(48)

for the axisymmetric case and

$$\begin{aligned} L_d = \frac{(R+H_{\infty })}{2}\frac{\Omega }{R^2}+\frac{4-\pi }{2}(R-H_{\infty }) \end{aligned}$$
(49)

for the planar case.

Equivalently, the total pressure drop can also be calculated using the models for the normal viscous stress jump, Eq. (44), and the front and rear plane curvatures, Eq. (41), yielding

$$\begin{aligned} \Delta p_{\textsf {tot}}&= {} \Delta p_{o,r}^{\text {NP}} +\Delta \tau _{{zz}_r}+ \chi \gamma \kappa _r -\Delta p_{i,r}^{\text {NP}} \nonumber \\& \quad +\frac{\mathrm{{d}}p_i}{\mathrm{{d}}z} L_d +\Delta p_{i,f}^{\text {NP}} -\Delta \tau _{{zz}_f} - \chi \gamma \kappa _f - \Delta p_{o,f}^{\text {NP}} , \end{aligned}$$
(50)

where \(\chi =2\) for the axisymmetric configuration and \(\chi = 1\) for the planar one.

If we neglect the non-parallel flows effects on the pressure, \(\Delta p^{\text {NP}}\), the total pressure drop would then be

$$\begin{aligned} \Delta p_{\textsf {tot}} = \Delta p_r +\frac{\mathrm{{d}}p_i}{\mathrm{{d}}z} L_d - \Delta p_f. \end{aligned}$$
(51)

Neglecting the effects of the non-parallel flows would induce an error on the pressure drop, increasing with Ca. For a single droplet of volume \(\Omega = 12.9\), the error of Eq. (51) compared to the numerical results is less than \(3 \%\) for \(\lambda = 0\), but reaches \(15 \%\) for \(\lambda = 1\) and even \(48 \%\) for \(\lambda = 100\). It is thus important to include the corrections accounting for the non-parallel flow effects to predict the pressure drop accurately, especially when the viscosity ratio \(\lambda \gtrapprox 1\). Numerical simulations are, therefore, crucial to achieve so.

9 Conclusions

This paper generalizes the theory of a confined bubble flowing in an axisymmetric or planar channel to droplets of non-vanishing viscosity ratios. Empirical models for the relevant quantities such as the uniform and minimal film thicknesses separating the wall and the droplet, the front and rear droplet plane curvatures, the total pressure drop in the channel and the droplet velocity are derived for the range of capillary numbers from \(10^{-4}\) to 1, and viscosity ratios ranging from the value \(\lambda = 0\) for bubbles to highly viscous droplets. Following the work of Schwartz et al. (1986), we extend the low-capillary-number predictions obtained by the lubrication approach of Bretherton (1961) for bubbles to viscous droplets. Extensive finite-element simulations based on a moving-mesh arbitrary Lagrangian–Eulerian method (ALE) are performed for the viscosity-ratio range \(\lambda \in [0-100]\) to build a numerical database, based on which we propose empirical models for the relevant quantities. The models are inspired by the low-Ca theoretical asymptotes, but their validity range reaches large capillary numbers (\(Ca>10^{-3}\)), where the lubrication approach no longer holds.

We have found that the uniform film thickness for \(Ca<10^{-3}\) does not differ significantly with that of a bubble as long as \(\lambda <1\). For larger viscosity ratios, instead, the film thickness increases monotonically and saturates to a value \(2^{2/3}\) times the Bretherton’s scaling for bubbles when \(\lambda> 10^3\). The film thickness can be modeled by a rational function similar to that proposed by Aussillous and Quéré (2000) for bubbles, where the fitting coefficient Q depends on the viscosity ratio. Furthermore, the uniform film thickness saturates at large capillary numbers to a value depending on Q. The minimum film thickness can be predicted analogously. The velocity of a droplet can be unambiguously derived once the uniform film thickness is known. We have shown that considering the full expression of the droplet velocity is crucial as the asymptotic series for low Ca has a very restricted range of validity for non-vanishing viscosity ratios.

Furthermore, we have found that the evolution of the front and rear cap curvatures as a function of the capillary number differs from the one of the pressure jumps at the front and rear droplet interfaces. This is due to the normal viscous stress jumps. The contribution of the jumps has been overlooked in the literature, though it has to be considered for \(Ca>10^{-3}\). With all these models at hand, the pressure drop across a droplet can be computed, which will be valuable for engineering practices.

We have also shown that the flow patterns inside and outside of the droplet strongly depend on the capillary number and viscosity ratio. In particular, for \(\lambda < 1/2\) (\(\lambda < 2/3\)) for the axisymmetric (planar) configuration, when the film thickness is larger than a critical value \({H_{\infty }^{\star }}/{R}\), recirculating regions at the front and rear of the droplet disappear. Furthermore, the recirculation region in the outer phase detaches from the droplet’s rear interface for large film thickness yet smaller than \({H_{\infty }^{\star }}/{R}\), implying the disappearance of the inner recirculating region at the rear.

The considered problem in a planar configuration could be relevant for the study of a front propagation in a Hele–Shaw cell (Park and Homsy 1984; Reinelt and Saffman 1985), where the second-phase viscosity is non-vanishing. For instance, one could compute the amount of fluid left on the walls when a finger of immiscible fluid penetrates (Saffman and Taylor 1958). Furthermore, the problem in the planar configuration can be seen as a first step towards understanding the dynamics of pancake droplets in a Hele–Shaw cell (Huerre et al. 2015; Zhu and Gallaire 2016). Another possible outlook is the extension of the present theory to capillaries with polygonal cross sections, where the film between the droplet and the walls is not axisymmetric, but thick films known as gutters develop in the capillary corners. Three-dimensional numerical simulations are then necessary to resolve this asymmetry. A force balance will determine the droplet velocity and an equivalent pressure drop model could be proposed for these geometries.

Despite the fact that this work was motivated by the vast number of droplet-based microfluidic applications, the analytically derived Eq. (24) serves as a generalization of the well-known Landau–Levich–Derjaguin–Bretherton equation (Landau and Levich 1942; Derjaguin 1943; Bretherton 1961) when the second fluid has a non-negligible viscosity. This equation could, therefore, be adapted to predict the film thickness in coating problems with two immiscible liquids.