1 Introduction

The influence of surface active agents (surfactants) on the deformation of droplets and on the dynamics of the surrounding flow field is an active research area with numerous applications [12, 43]. In weak flows a nearly uniform concentration of the surfactants on the surface takes place and the behaviour of the flow is (after a suitable scaling) similar to flows without surfactants, but with reduced surface tension. Suppose that the flow field becomes stronger, thinning effects appear due to the stretching of the surface. This changes the surface tension locally. The convective transport induced by the flow field generates a local accumulation of surfactants and the resulting Marangoni forces may lead to a destabilization of the interface with essential consequences on the flow dynamics. This is a complex process, whose tailored use in applications requires a fundamental understanding of the mutual interplay.

We present advanced finite element methods that allow for a robust and accurate numerical solution of the underlying system of partial differential equations. A complete model of two-phase and free surface flows with surfactants is stated in Sect. 1.2. We consider adsorption and desorption of surfactants at the sharp interface between two fluids and their transport and diffusion in the fluid phases and along the interface. One way to solve two-phase problems is to use a diffusive interface and consider the limit when the thickness of the interface goes to zero. This type of approach will not be considered here. For a detailed discussion we refer to [1, 16, 17]. Alternatively, sharp interface models can be discretized by fitted or unfitted finite elements. An overview on the general framework of unfitted or so-called CutFEM has recently been given in [10]. Using the CutFEM approach is convenient since the same finite element spaces defined on a background mesh can be used for solving the partial differential equations in the bulk and on the surface. However, a drawback is that the finite element matrices become arbitrarily ill-conditioned depending on the position of the surface in the background mesh. Therefore, although the fact that moving meshes have to be handled, we prefer fitted finite element discretizations, in which the interface is aligned with the mesh [19, 21, 24, 25].

In Sect. 1.3 we summarize the principles of discretizing partial differential equations on surfaces. The numerical analysis for the solution of a scalar convection-diffusion equation on a surface is discussed. We also consider the Local Projection Stabilization (LPS) to suppress spurious oscillations in convection dominated cases. Finally, we summarize our studies on a system of convection-diffusion equations in bulk domains coupled with a convection-diffusion equation on an embedded fixed surface as a model for the surfactant transport.

In Sect. 1.4 we compare interface capturing and interface tracking methods that handle partial differential equations on moving domains. The Arbitrary Langrangian–Eulerian (ALE) method is described and some techniques to retain the mesh quality without remeshing are discussed. We use discretizations of second order in space and time and propose a semi-implicit splitting of the two-phase flow problem with surfactants into smaller problems, a Navier–Stokes type problem and a problem for the transport of surfactants.

Selected test examples demonstrate in Sect. 1.5 the challenges and the potential of numerical simulations for a better understanding of the mutual interplay of different phenomena at fluidic interfaces.

2 Two-Phase and Free Surface Flows

We state a system of partial differential equations modeling two-phase and free surface flows. The weak formulation of the problem is given for a fixed domain.

2.1 Mathematical Model

We consider an incompressible two-phase flow with surfactants in a fixed bounded domain \(\varOmega \subset \mathbb{R}^{d}\), d = 2, 3. Let the liquid filling the domain Ω 1(t) at time t ∈ [0, T] be completely surrounded by another liquid filling Ω 2(t) = Ω∖Ω 1(t). We assume that the two liquids are immiscible and separated by the sharp interface Γ(t) = ∂Ω 1(t). The model consists of the time-dependent incompressible Navier-Stokes equation in each phase

$$\displaystyle\begin{array}{rcl} \rho _{i}\left (\partial _{t}\mathbf{u} + \mathbf{u} \cdot \nabla \mathbf{u}\right ) -\nabla \cdot \mathbb{S}(\mathbf{u},p) =\rho _{i}g\mathbf{e},\qquad \nabla \cdot \mathbf{u} = 0\quad \text{ in }\varOmega _{i}(t) \times (0,T],\quad & &{}\end{array}$$
(1.1)

for i = 1, 2, the initial conditions

$$\displaystyle\begin{array}{rcl} \varOmega _{i}(0) =\varOmega _{i,0},\qquad \mathbf{u}(\cdot,0) = \mathbf{u}_{0},& &{}\end{array}$$
(1.2)

the kinematic and force balance conditions

$$\displaystyle\begin{array}{rcl} \mathbf{w} \cdot \mathbf{n} = \mathbf{u} \cdot \mathbf{n},\quad [\mathbf{u}] = \mathbf{0},\quad [\mathbb{S}(\mathbf{u},p)] \cdot \mathbf{n} =\sigma (c_{\varGamma })\mathscr{K}\mathbf{n} + \nabla _{\varGamma }\sigma (c_{\varGamma })\quad \text{on }\varGamma (t),\qquad & &{}\end{array}$$
(1.3)

and homogeneous Dirichlet-type boundary conditions on the fixed (in time) boundary ∂Ω. Here, u = (u 1, …, u d ) denotes the fluid velocity, p is the pressure, ρ i , i = 1, 2, are the densities of the corresponding fluid phases, g is the gravitational constant, and e is a unit vector in the direction of the gravitational force. Further, w on Γ(t) denotes the velocity of the interface, n is the outer unit normal vector (on Γ(t) directed outward of Ω 1(t)), \(\mathscr{K}\) is the sum of principal curvatures, [⋅ ] denotes the jump across the interface Γ(t), c Γ is the surfactant concentration on the interface, σ(c Γ ) is the surface tension coefficient depending on c Γ , and ∇ Γ is the surface gradient.

The stress tensor \(\mathbb{S}(\mathbf{u},p)\) for a Newtonian incompressible fluid and the velocity deformation tensor \(\mathbb{D}\) are given by

$$\displaystyle\begin{array}{rcl} \mathbb{S}_{i}(\mathbf{u},p) = 2\mu _{i}\mathbb{D}(\mathbf{u}) - p\mathbb{I},\qquad \mathbb{D}(\mathbf{u}) = \frac{1} {2}\left (\nabla \mathbf{u} + (\nabla \mathbf{u})^{T}\right ),\quad i = 1,2,& & {}\\ \end{array}$$

where μ i denotes the dynamic viscosity of the corresponding fluid phase, and \(\mathbb{I}\) is the identity tensor.

In case of a free surface flow, we assume that the effect of the flow field in the surrounding phase is negligible and thus, Ω(t): = Ω 1(t). The kinematic force balance condition (1.3) becomes

$$\displaystyle\begin{array}{rcl} \mathbf{w} \cdot \mathbf{n} = \mathbf{u} \cdot \mathbf{n},\quad \mathbb{S}(\mathbf{u},p) \cdot \mathbf{n} =\sigma (c_{\varGamma })\mathscr{K}\mathbf{n} + \nabla _{\varGamma }\sigma (c_{\varGamma })\quad \text{on }\varGamma (t).& &{}\end{array}$$
(1.4)

Note that in case of a two-phase flow (in contrast to a free surface flow) the pressure is determined only up to an additive constant. For a detailed discussion on the uniqueness of the pressure, we refer to [22].

The model has to be completed by a set of equations that describe the surfactant transport in the bulk phases and on the interface. Let us assume that the surfactant is soluble in both phases. Then, for the surfactant concentration c i , i = 1, 2, in the bulk phases we have

$$\displaystyle\begin{array}{rcl} \partial _{t}c_{i} + \mathbf{u} \cdot \nabla c_{i} = \nabla \cdot (D_{i}\nabla c_{i})\quad \text{in }\varOmega _{i}(t) \times (0,T],& &{}\end{array}$$
(1.5)

completed by the initial conditions

$$\displaystyle\begin{array}{rcl} c_{i}\big\vert _{t=0} = c_{i,0}\qquad \text{in }\varOmega _{i}(0),& &{}\end{array}$$
(1.6)

and the boundary conditions

$$\displaystyle\begin{array}{rcl} (-1)^{i}\mathbf{n} \cdot \left (D_{ i}\nabla c_{i}\right ) = S_{i}(c_{i},c_{\varGamma })\quad \text{on }\varGamma (t),\quad \mathbf{n} \cdot \left (D_{2}\nabla c_{2}\right ) = 0\quad \text{on }\partial \varOmega.& &{}\end{array}$$
(1.7)

Here, D i is the diffusion coefficient in phase i and S i is the source term. The surfactant concentration c Γ on the evolving surface satisfies the initial condition \(c_{\varGamma }\big\vert _{t=0} = c_{\varGamma,0}\) and the partial differential equation

$$\displaystyle\begin{array}{rcl} \dot{c}_{\varGamma } + (\nabla _{\varGamma }\cdot \mathbf{w})\,c_{\varGamma } + \nabla _{\varGamma }\cdot [c_{\varGamma }(\mathbf{u} -\mathbf{w})] = \nabla _{\varGamma }\cdot (D_{\varGamma }\nabla _{\varGamma }c_{\varGamma }) +\sum _{ i=1}^{2}S_{ i}(c_{i},c_{\varGamma })& &{}\end{array}$$
(1.8)

on Γ(t) × (0, T], where \(\dot{c}_{\varGamma }\) denotes the material derivative with respect to w and D Γ is the surface diffusion coefficient. It is assumed that the interface Γ is a closed surface, therefore no boundary condition is needed for (1.8).

Suppose the surfactant is soluble only in one phase or is even insoluble. Then, the corresponding equations in the other phase or in both phases are removed from the model (1.5)–(1.8).

Finally, the effect of the surfactant on the surface tension and the transport of surfactant between the interface and the bulk phase is modelled [15]. We consider the linear Henry equation of state

$$\displaystyle\begin{array}{rcl} S_{i}(c_{i},c_{\varGamma }) = k_{a,i}C_{\varGamma }^{\infty }c_{ i} - k_{d,i}c_{\varGamma }\quad \text{and}\quad \sigma (c_{\varGamma }) =\sigma _{0}\left (1 + E\left (1 - \frac{c_{\varGamma }} {C_{\varGamma }^{\infty }}\right )\right ),& &{}\end{array}$$
(1.9)

or the nonlinear Langmuir equation of state

$$\displaystyle\begin{array}{rcl} S_{i}(c_{i},c_{\varGamma }) = k_{a,i}(C_{\varGamma }^{\infty }- c_{\varGamma })c_{ i} - k_{d,i}c_{\varGamma }\ \text{and}\ \sigma (c_{\varGamma }) =\sigma _{0}\left (1 + E\ln \left (1 - \frac{c_{\varGamma }} {C_{\varGamma }^{\infty }}\right )\right ).& & \\ & &{}\end{array}$$
(1.10)

Here, k a, i and k d, i are the adsorption and desorption constants, respectively, σ 0 a reference surface tension, E the surface elasticity constant, and C Γ ∞ a reference surfactant concentration (linear case) or the maximum surface surfactant packing concentration (nonlinear case).

2.2 Dimensionless Weak Formulation in Fixed Domains

We introduce dimensionless variables by setting

$$\displaystyle\begin{array}{rcl} \tilde{\mathbf{x}} = \frac{\mathbf{x}} {L},\,\tilde{\mathbf{u}} = \frac{\mathbf{u}} {U_{\infty }},\,\tilde{\mathbf{w}} = \frac{\mathbf{w}} {U_{\infty }},\,\tilde{t} = \frac{U_{\infty }t} {L},\,\tilde{p} = \frac{p} {\rho _{1}U_{\infty }^{2}},\,\tilde{c}_{\varGamma } = \frac{c_{\varGamma }} {C_{\varGamma }^{\infty }},\,\tilde{c}_{i} = \frac{c_{i}} {C_{\infty }},& & {}\\ \end{array}$$

where L is a characteristic length, U ∞ is a characteristic velocity, and C ∞ is a characteristic surfactant concentration in the bulk regions. In order to simplify the notations we drop the tilde afterwards. Then, the model equations are parameterised by the following dimensionless numbers: the Reynolds number Re, the Weber number We, the Froude number Fr, the Peclet numbers for the bulk surfactant transport Pe i , the Peclet number for the surface surfactant transport Pe Γ , the Biot numbers Bi i , the Damköhler numbers Da i , the surface elasticity E, the surfactant scaling β, and the dimensionless scaling factors ρ 2∕ρ 1 and μ 2∕μ 1. In more detail, the dimensionless numbers are given by

$$\displaystyle\begin{array}{rcl} \text{Re} = \left \{\begin{array}{lr} Re_{1} & \mathbf{x} \in \varOmega _{1} \\ Re_{1}\mu _{1}/\mu _{2} & \mathbf{x} \in \varOmega _{2} \end{array} \right.,\quad \text{where }\text{Re}_{1} = \frac{\rho _{1}U_{\infty }L} {\mu _{1}},& & {}\\ \end{array}$$
$$\displaystyle\begin{array}{rcl} \text{We} = \frac{\rho _{1}U_{\infty }^{2}L} {\sigma _{0}},\quad \text{Fr} = \frac{U_{\infty }^{2}} {Lg},\quad \text{Pe}_{i} = \frac{U_{\infty }L} {D_{i}},\quad \text{Pe}_{\varGamma } = \frac{U_{\infty }L} {D_{\varGamma }},& & {}\\ \end{array}$$
$$\displaystyle\begin{array}{rcl} \text{Bi}_{i} = \frac{k_{d,i}L} {U_{\infty }},\quad \text{Da}_{i} = \frac{k_{a,i}C_{\varGamma }^{\infty }} {U_{\infty }},\quad \quad \beta = \frac{C_{\varGamma }^{\infty }} {LC_{\infty }},& & {}\\ \end{array}$$
$$\displaystyle\begin{array}{rcl} \text{with }i = 1,2,\text{ and }\rho = \left \{\begin{array}{lr} 1 &\mathbf{x} \in \varOmega _{1} \\ \rho _{2}/\rho _{1} & \mathbf{x} \in \varOmega _{2} \end{array} \right.\ .& & {}\\ \end{array}$$

The weak formulation of the problem is derived as usual. Multiplying with test functions v ∈ V (Ω): = H 0 1(Ω)d, q ∈ Q(Ω): = L 0 2(Ω), φ ∈ G(Ω): = H 1(Ω 1) × H 1(Ω 2), ψ ∈ M(Γ): = H 1(Γ), applying integration by parts to remove the highest order of differentiation, and incorporating the boundary conditions, we obtain the weak formulation of the two-phase problem:

Problem 1

Find (u, p, c, c Γ ) ∈ V × Q × G × M such that for all (v, q, φ, ψ) ∈ V × Q × G × M

$$\displaystyle\begin{array}{rcl} (\rho \partial _{t}\mathbf{u},\mathbf{v}) + a(\mathbf{u},\mathbf{u},\mathbf{v}) - b(\,p,\mathbf{v}) + b(q,\mathbf{u})& =& f(c_{\varGamma },\mathbf{v}), {}\\ (\partial _{t}c,\varphi ) + a_{c}(\mathbf{u},c,\varphi )& =& f_{c}(c,c_{\varGamma },\varphi ), {}\\ \frac{d} {dt}\int _{\varGamma }c_{\varGamma }\psi \,d\gamma + a_{\varGamma }(\mathbf{u} -\mathbf{w},c_{\varGamma },\psi )& =& f_{\varGamma }(c,c_{\varGamma },\psi ). {}\\ \end{array}$$

For the case of a free surface flow we set Ω(t) = Ω 1(t), Q(Ω): = L 2(Ω), and the equations on Ω 2(t) are omitted. The above forms are given by

$$\displaystyle\begin{array}{rcl} a(\mathbf{z},\mathbf{u},\mathbf{v})& =& \left ( \frac{2} {\text{Re}}\mathbb{D}(\mathbf{u}),\, \mathbb{D}(\mathbf{v})\right ) + \left (\rho (\mathbf{z} \cdot \nabla )\mathbf{u},\mathbf{v}\right ) {}\\ b(q,\mathbf{v})& =& (q,\nabla \cdot \mathbf{v}) {}\\ f(c_{\varGamma },\mathbf{v})& =& \frac{1} {\text{Fr}}(\,\rho \mathbf{e},\mathbf{v}) - \frac{1} {\text{We}}\left \langle \sigma (c_{\varGamma })(\mathbb{I} -\mathbf{n} \otimes \mathbf{n}),\nabla _{\varGamma }\mathbf{v}\right \rangle _{\varGamma } {}\\ a_{c}(\mathbf{z},c,\varphi )& =& \sum _{i=1}^{2}\left [ \frac{1} {\text{Pe}_{i}}(\nabla c_{i},\nabla \varphi _{i})_{\varOmega _{i}} + (\mathbf{z} \cdot \nabla c_{i},\varphi _{i})_{\varOmega _{i}}\right ] {}\\ & & {}\\ \end{array}$$
$$\displaystyle\begin{array}{rcl} f_{c}(c,c_{\varGamma },\varphi )& =& -\beta \sum _{i=1}^{2}\left \langle S_{ i}(c_{i},c_{\varGamma }),\varphi _{i}\right \rangle _{\varGamma } {}\\ a_{\varGamma }(\mathbf{z},c_{\varGamma },\psi )& =& \frac{1} {\text{Pe}_{\varGamma }}\left \langle \nabla _{\varGamma }c_{\varGamma },\nabla _{\varGamma }\psi \right \rangle _{\varGamma }-\left \langle c_{\varGamma }\mathbf{z},\nabla _{\varGamma }\psi \right \rangle _{\varGamma } {}\\ f_{\varGamma }(c,c_{\varGamma },\psi )& =& \sum _{i=1}^{2}\left \langle S_{ i}(c_{i},c_{\varGamma }),\psi \right \rangle _{\varGamma }. {}\\ \end{array}$$

Further, (⋅ , ⋅ ), \((\cdot,\cdot )_{\varOmega _{i}}\), and 〈⋅ , ⋅ 〉 Γ denote the inner product in L 2(Ω), L 2(Ω i ), and L 2(Γ), respectively, as well as its vector- and tensor-valued versions. The dimensionless surface tension law and the dimensionless source terms are given by

$$\displaystyle\begin{array}{rcl} \sigma (c_{\varGamma }) = 1 + E(1 - c_{\varGamma }),\qquad S(c_{i},c_{\varGamma }) = \frac{\text{Da}_{i}} {\beta } \,c_{i} -\text{Bi}_{i}\,c_{\varGamma }& & {}\\ \end{array}$$

in case of the Henry sorption isotherm and by

$$\displaystyle\begin{array}{rcl} \sigma (c_{\varGamma }) = 1 + E\ln (1 - c_{\varGamma }),\qquad S(c_{i},c_{\varGamma }) = \frac{\text{Da}_{i}} {\beta } \,c_{i}(1 - c_{\varGamma }) -\text{Bi}_{i}\,c_{\varGamma }& & {}\\ \end{array}$$

for the Langmuir sorption isotherm.

3 Finite Element Methods on Fixed Surfaces

The weak formulation of the two-phase or free surface flow contains an convection-diffusion type surface equation. Whereas finite element methods for bulk equations are well studied, the extension of these techniques to curved surfaces is an area of current research. The development of finite elements on surfaces started with the study of the Laplace-Beltrami equation on a fixed surface in [13]. An overview of the recent state of the art including different approaches and moving surfaces is given in [14].

In this section we present a finite element method for surface equations of convection-diffusion type. Additionally, we introduce a LPS technique for surface equations to reduce oscillations occurring at interior layers. The last part of this section handles a coupled convection-diffusion problem in the bulk phases and on the surface. Discretization techniques, solvability and error estimates are given.

3.1 Advection-Diffusion Problem

We study a steady state convection-diffusion equation on a given closed surface Γ instead of the surface equation (1.8) of the origin problem. By partial integration of the diffusion term we get the following problem

Problem 2

Find \(u \in H^{1}\left (\varGamma \right )\) such that for all \(v \in H^{1}\left (\varGamma \right )\)

$$\displaystyle{ \varepsilon \left \langle \nabla _{\varGamma }u,\nabla _{\varGamma }v\right \rangle _{\varGamma } + \left \langle \nabla _{\varGamma }u,\mathbf{w}v\right \rangle _{\varGamma } + \left \langle \sigma u,v\right \rangle _{\varGamma } = \left \langle \,f,v\right \rangle _{\varGamma }. }$$

Here, w and f are the given velocity field and right hand side, and ɛ the diffusion coefficient. We set σ = ∇ Γ ⋅ w + c with c being the reaction coefficient. Since Γ is not moving in time, we assume w ⋅ n = 0 on Γ. Further, we suppose \(0 <\sigma _{0} \leq \sigma -\frac{1} {2}\nabla _{\varGamma }\cdot \mathbf{w} \leq \sigma _{\infty }\) to get unique solvability of the problem.

3.2 Surface Approximation and Discrete Problem

In the discretization of the surface equation in Problem 2 using finite elements several additional particularities have to be taken into account.

The given surface Γ is discretized by Γ h , such that all nodes of Γ h are on Γ. The geometric error introduced by the different integration domains and surface operators is estimated in [14]. We consider isoparametric surface approximation of order k ≥ 1. In the simplest case, k = 1, the isoparametric surface Γ h is a linear interpolation of Γ by flat simplices. In the general case, Γ h is the union of curved simplices K, which are given as the image of a bijective mapping \(F_{K} \in \mathbb{P}_{k}(\widehat{K})^{d}\) of the reference simplex \(\widehat{K} \subset \mathbb{R}^{d-1}\). Thereby, \(\mathbb{P}_{k}(\widehat{K})\) is the space of polynomials of degree less than or equal to k. Hence, F K is a parametrisation of the element K over the reference triangle \(\widehat{K}\), which has to be taken into account. Additionally, we need to extend the quantities given on Γ to a neighbourhood U of Γ including Γ h . The extension operator. e is given as the constant extension along the surface normal.

Introducing a mapped Lagrangian surface finite element space of order k via

$$\displaystyle{ V _{h} =\{ v_{h} \in H^{1}\left (\varGamma _{ h}\right )\vert v_{h} \circ F_{K} \in \mathbb{P}_{k}(\widehat{K})\text{ for all elements }K\text{ in }\varGamma _{h}\} }$$
(1.11)

the discretized problem reads:

Problem 3

Find u h ∈ V h such that for all v h ∈ V h

$$\displaystyle{ a_{h}\left (u_{h},v_{h}\right ) = f_{h}\left (v_{h}\right ) }$$

with

$$\displaystyle\begin{array}{rcl} a_{h}\left (u_{h},v_{h}\right )& =& \varepsilon \left \langle \nabla _{\varGamma _{h}}u_{h},\nabla _{\varGamma _{h}}v_{h}\right \rangle _{\varGamma _{h}} + \left \langle \nabla _{\varGamma _{h}}u_{h},\mathbf{w}^{e}v_{ h}\right \rangle _{\varGamma _{h}} + \left \langle \sigma ^{e}u_{ h},v_{h}\right \rangle _{\varGamma _{h}} {}\\ f_{h}\left (v_{h}\right )& =& \left \langle \,f^{e},v_{ h}\right \rangle _{\varGamma _{h}}. {}\\ \end{array}$$

We want to point out that σ is discretized by \(\sigma ^{e} = \left (\nabla _{\varGamma }\cdot \mathbf{w}\right )^{e} + c^{e}\) instead of \(\nabla _{\varGamma _{h}} \cdot \mathbf{w}^{e} + c^{e}\). This transfers the assumptions from σ on Γ to σ e on Γ h . However, an estimate of the difference between the discrete divergence \(\nabla _{\varGamma _{h}} \cdot \mathbf{w}^{e}\) and the discretized divergence \(\left (\nabla _{\varGamma }\cdot \mathbf{w}\right )^{e}\) can be shown

$$\displaystyle{ \|\nabla _{\varGamma _{h}} \cdot \mathbf{w}^{e} -\left (\nabla _{\varGamma }\cdot \mathbf{w}\right )^{e}\|_{ \infty,\varGamma _{h}} \leq Ch^{k}\|\nabla _{\varGamma }\mathbf{w}\|_{ \infty,\varGamma }. }$$
(1.12)

3.3 Standard Galerkin FE Method

Using (1.12) the coercivity of the bilinear form a h in V h equipped with the standard H 1-norm is proven for h being small enough uniformly in ɛ and unique solvability follows. Considering convection dominated problems one is interested in error estimates uniformly in ɛ. We get coercivity of a h in V h equipped with the norm

$$\displaystyle{ \left \vert \left \vert \left \vert v\right \vert \right \vert \right \vert:= \left (\varepsilon \|\nabla _{\varGamma _{h}}v\|_{0,\varGamma _{h}}^{2} +\sigma _{ 0}\|v\|_{0,\varGamma _{h}}^{2}\right )^{1/2}. }$$

with a constant independent of ɛ.

The solution \(u:\varGamma \rightarrow \mathbb{R}\) of the continuous problem and the solution \(u_{h}:\varGamma _{h} \rightarrow \mathbb{R}\) are defined on different domains, thus cannot be compared directly. Therefore, the error between u h and the extension of u onto Γ h is evaluated. Using an isoparametric Galerkin approach of order k we obtain

$$\displaystyle\begin{array}{rcl} \left \vert \left \vert \left \vert u^{e} - u_{ h}\right \vert \right \vert \right \vert \leq & & C\left (h^{k+1}\left (\|u\|_{ k,\varGamma } +\|\, f\|_{0,\varGamma }\right ) + h^{k}\|u\|_{ k+1,\varGamma }\right ) {}\\ \end{array}$$

with a geometric error of order k + 1 and a finite element error of order k.

3.4 Local Projection Stabilization

For convection-diffusion equations in the bulk, it is well known that standard Galerkin finite element methods can lead to unphysical oscillations, if convection dominates diffusion and layers are unresolved by the mesh. Several stabilization techniques as Streamline Upwind Petrov Galerkin [29, 35], Continuous Interior Penalty [8, 9], and LPS [5, 33] have been developed for bulk equations. However, for surface equations only the Streamline Upwind Petrov Galerkin method on unfitted finite elements has been studied so far [38]. We present a LPS technique for fitted finite elements on surfaces.

LPS is based on an additional control over the gradient of the solution by adding a stabilization term to the discrete bilinear form a h . To define the stabilization term a discontinuous projection space D h is needed. The restriction of D h to one element K is denoted by D K . We introduce an elementwise L 2 projection \(\pi _{K}: L^{2}\left (K\right ) \rightarrow D_{K}\) into the projection space. We define the fluctuation operator \(\kappa _{K}: L^{2}\left (K\right ) \rightarrow L^{2}\left (K\right )\) as κ K = id −π K and set the stabilization term to

$$\displaystyle{ LPS\left (u_{h},v_{h}\right ) =\sum \limits _{K\in \varGamma _{h}}\gamma _{K}\left \langle \kappa _{K}\left (\nabla _{\varGamma _{h}}u_{h}\right ),\kappa _{K}\left (\nabla _{\varGamma _{h}}v_{h}\right )\right \rangle _{K}. }$$

Here γ K are the stabilization parameters. The error analysis of the method provides that γ K has to be chosen as γ K = γ 2 h K with a fixed γ to get the optimal convergence order. The best value of γ is problem dependent and has to be found empirically. The stabilized problem reads:

Problem 4

Find u h ∈ V h such that for all v h ∈ V h

$$\displaystyle{ a_{s}\left (u_{h},v_{h}\right ):= a_{h}\left (u_{h},v_{h}\right ) + LPS\left (u_{h},v_{h}\right ) = f_{h}\left (v_{h}\right ). }$$

According to the bilinear form a s we introduce the s-triple norm

$$\displaystyle{ \left \vert \left \vert \left \vert v\right \vert \right \vert \right \vert _{s} = \left (\varepsilon \|\nabla _{\varGamma _{h}}v\|_{0,\varGamma _{h}}^{2} +\sigma _{ 0}\|v\|_{0,\varGamma _{h}}^{2} +\sum \limits _{ K}\gamma _{K}\|\kappa _{K}\left (\nabla _{\varGamma _{h}}v\right )\|_{0,K}^{2}\right )^{1/2}. }$$

By construction we get the coercivity of a s in V h equipped with the s-triple norm under the same restriction for h as in the standard Galerkin case. Using the Lax-Milgram lemma the unique solvability of Problem 4 is shown.

We can improve the error estimate from Sect. 1.3.3 utilize the stronger s-triple norm following the idea from [33]. To this end, we assume the existence of a D h -orthogonal interpolator \(j_{h}: H^{2}\left (\varGamma _{h}\right ) \rightarrow V _{h}\) with interpolation order k. The existence of such an interpolator depends on the choice of V h and D h and is related to a local inf-sup condition. Common pairs on triangles are \(V _{h} = \mathbb{P}_{k}^{+}\), e.g. \(\mathbb{P}_{k}\) enriched by \(b \cdot \mathbb{P}_{k-1}\) where b | K ∈ H 0 1(K), \(\forall K \in \varGamma _{h}\), is a piecewise cubic function, and \(D_{h} = \mathbb{P}_{k-1}^{\text{disc}}\) [33].

For an isoparametric approach, e.g. \(V _{h} = \mathbb{P}_{k}^{+}\), \(D_{h} = \mathbb{P}_{k-1}^{\text{disc}}\) and surface approximation with polynomials of degree k, we get the following convergence estimate

$$\displaystyle{ \left \vert \left \vert \left \vert u^{e} - u_{ h}\right \vert \right \vert \right \vert _{s} \leq Ch^{k+1}\left (\|u\|_{ r,\varGamma } +\|\, f\|_{0,\varGamma }\right ) + Ch^{k}\left (\varepsilon ^{1/2} +\gamma h^{1/2}\right )\|u\|_{ k+1,\varGamma }. }$$

Thus, for LPS we have stability in the stronger s-triple norm and an improved k + 1∕2 order of convergence in the convection dominated case ɛ < h.

3.5 Coupled Bulk-Surface Transport Problem

The next step is to couple the investigated surface equation on Γ to steady-state convection-diffusion equations in the bulk domains Ω i . We study the problem

$$\displaystyle\begin{array}{rcl} -\varepsilon _{i}\varDelta u_{i} + \mathbf{w} \cdot \nabla u_{i} =& f_{i}& \text{in }\varOmega _{i},\,i = 1,2,{}\end{array}$$
(1.13)
$$\displaystyle\begin{array}{rcl} -\varepsilon _{\varGamma }\varDelta _{\varGamma }u_{\varGamma } + \mathbf{w} \cdot \nabla _{\varGamma }u_{\varGamma } =& L\sum _{i=1}^{2}S_{i}\left (u_{i},u_{\varGamma }\right ) + f_{\varGamma }& \text{on }\varGamma,{}\end{array}$$
(1.14)
$$\displaystyle\begin{array}{rcl} \left (-1\right )^{i}\varepsilon _{ i}\frac{\partial u_{i}} {\partial \mathbf{n}} =& S_{i}\left (u_{i},u_{\varGamma }\right )& \text{on }\varGamma,\,i = 1,2,{}\end{array}$$
(1.15)
$$\displaystyle\begin{array}{rcl} \varepsilon _{2}\frac{\partial u_{2}} {\partial \mathbf{n}} =& 0& \text{on }\partial \varOmega {}\end{array}$$
(1.16)

using the linear Henry source term, compare Sect. 1.2.1. We assume that the velocity field w satisfies ∇⋅ w = 0 in the bulk phases Ω i , i = 1, 2, ∇ Γ ⋅ w = 0 on the interface Γ, w ⋅ n = 0 on Γ ∪ ∂Ω and \(\mathbf{f} = \left (\,f_{1},f_{2},f_{\varGamma }\right )\) fulfilling the solvability condition

$$\displaystyle{ \int _{\varOmega _{1}}f_{1}\,dx +\int _{\varOmega _{2}}f_{2}\,dx + \frac{1} {L}\int _{\varGamma }f_{\varGamma }\,d\gamma = 0. }$$

The solution \(\mathbf{u} = \left (u_{1},u_{2},u_{\varGamma }\right )\) of this problem is only fixed up to an additive constant λ k, with k = (k 1, k 2, k Γ ) and \(S_{i}\left (k_{i},k_{\varGamma }\right ) = 0\), i = 1, 2. To get uniqueness the condition of a given mass M is added.

We build the weak formulation summing up scaled weak formulations of the single equations such that the terms coming from the source term become symmetric in u and v. We end up with the bilinear form

$$\displaystyle\begin{array}{rcl} a\left (\mathbf{u},\mathbf{v}\right )&:=& \sum \limits _{i=1}^{2}\alpha _{ i}\left [\varepsilon _{i}\left (\nabla u_{i},\nabla v_{i}\right )_{\varOmega _{i}} + \left (\mathbf{w} \cdot \nabla u_{i},v_{i}\right )_{\varOmega _{i}}\right ] {}\\ & & +\alpha _{\varGamma }\left [\varepsilon _{\varGamma }\left \langle \nabla _{\varGamma }u_{\varGamma },\nabla _{\varGamma }v_{\varGamma }\right \rangle _{\varGamma } + \left \langle \mathbf{w} \cdot \nabla _{\varGamma }u_{\varGamma },v_{\varGamma }\right \rangle _{\varGamma }\right ] {}\\ & & +k_{d,2}\left \langle S_{1}\left (u_{1},u_{\varGamma }\right ),S_{1}\left (v_{1},v_{\varGamma }\right )\right \rangle _{\varGamma } + k_{d,1}\left \langle S_{2}\left (u_{2},u_{\varGamma }\right ),S_{2}\left (v_{2},v_{\varGamma }\right )\right \rangle _{\varGamma }, {}\\ \end{array}$$

where we set α 1: = k a, 1 k d, 2, α 2: = k a, 2 k d, 1 and α Γ : = k d, 1 k d, 2∕L. One can easily check that under the additional mass condition the weak formulation is uniquely solvable.

For discretization we use an interface fitted triangulation of Ω. Let Γ h be the piecewise linear approximation of Γ as described in Sect. 1.3.2. The polygonal approximations Ω 1,h and Ω 2,h of Ω 1 and Ω 2 are aligned to Γ h , e.g. \(\overline{\varOmega }_{1,h} \cap \overline{\varOmega }_{2,h} =\varGamma _{h}\). The linear surface approximation leads to a geometric error of order two for the surface terms but for bulk terms we get only an order of 3∕2.

The approximation space V h is build by linear continuous finite elements in the bulk and on the surface. Then, introducing a discretized mass condition the discretized problem reads:

Problem 5

Find u h ∈ V h fulfilling the discretized mass condition such that

$$\displaystyle{ a_{h}\left (\mathbf{u}_{h},\mathbf{v}_{h}\right ) = f\left (\mathbf{v}_{h}\right ):=\sum \limits _{ i=1}^{2}\alpha _{ i}\left (\,f_{i},v_{h,i}\right )_{\varOmega _{i}} +\alpha _{\varGamma }\langle \,f_{\varGamma },v_{h,\varGamma }\rangle _{\varGamma }\quad \text{ for all }\mathbf{v}_{h} \in V _{h} }$$

with

$$\displaystyle\begin{array}{rcl} a_{h}\left (\mathbf{u}_{h},\mathbf{v}_{h}\right )&:=& \sum _{i=1}^{2}\alpha _{ i}\varepsilon _{i}\left (\nabla u_{h,i},\nabla v_{h,i}\right )_{\varOmega _{h,i}} +\alpha _{\varGamma }\varepsilon _{\varGamma }\left \langle \nabla _{\varGamma _{h}}u_{h,\varGamma },\nabla _{\varGamma _{h}}v_{h,\varGamma }\right \rangle _{\varGamma _{h}} {}\\ & +& \sum \limits _{i=1}^{2} \frac{\alpha _{i}} {2}\left [\left (\mathbf{w}^{e} \cdot \nabla u_{ h,i},v_{h,i}\right )_{\varOmega _{h,i}} -\left (\mathbf{w}^{e} \cdot \nabla v_{ h,i},u_{h,i}\right )_{\varOmega _{h,i}}\right ] {}\\ & +& \frac{\alpha _{\varGamma }} {2}\left [\left \langle \mathbf{w}^{e} \cdot \nabla _{\varGamma _{ h}}u_{h,\varGamma },v_{h,\varGamma }\right \rangle _{\varGamma _{h}} -\left \langle \mathbf{w}^{e} \cdot \nabla _{\varGamma _{ h}}v_{h,\varGamma },u_{h,\varGamma }\right \rangle _{\varGamma _{h}}\right ] {}\\ & +& k_{2,d}\left \langle S_{1}\left (u_{h,1},u_{h,\varGamma }\right ),S_{1}\left (v_{h,1},v_{h,\varGamma }\right )\right \rangle _{\varGamma _{h}} {}\\ & +& k_{1,d}\left \langle S_{2}\left (u_{h,2},u_{h,\varGamma }\right ),S_{2}\left (v_{h,2},v_{h,\varGamma }\right )\right \rangle _{\varGamma _{h}}. {}\\ \end{array}$$

In the space V h restricted to the functions fulfilling the discretized mass condition and equipped with the corresponding energy norm coercivity of a h is shown. Unique solvability follows directly.

Unfortunately, for this coupled bulk surface transport problem we do not have L 2-control uniformly in the diffusion parameters ɛ 1, ɛ 2, ɛ Γ as for the Problem 2. Nevertheless, numerical tests show that the LPS improves stability and for fixed ɛ first order convergence can be established.

In [28] a slightly different weak formulation of (1.13)–(1.16), leading to a non-coercive bilinear form, has been studied for an unfitted finite element method without stabilization. In addition to energy-type estimates an optimal L 2-estimate has been established.

4 Finite Element Methods in Moving Domains

We describe the numerical scheme developed for the two-phase model (1.1)–(1.10). One of the main characteristic is the application of the ALE method to handle unknown moving interfaces.

4.1 Interface Capturing and Tracking Methods

The interface position has to be determined by the solution of the model equations. Two main classes of methods have been developed in the past, the interface capturing methods and the interface tracking methods.

Both methods have their advantages and disadvantages. The interface capturing methods can handle topological changes, like break-up and coalescence of phases, well and automatically. On the other hand, the handling of the marker function and the reconstruction of the interface induces several difficulties, like the accurate incorporation of surface tension forces, due to the implicit nature of the method. On the contrary, handling topological changes is very difficult with the tracking methods, but incorporation of surface properties, like surface tension, is quite easy.

In the class of tracking methods, the distinction in unfitted and fitted schemes gives further choice with correlated advantages and disadvantages. The unfitted methods are easy to implement, since the marker grid is independent from the bulk grid, hence existing code can be extended easily. But, since unfitted methods cut cells, they introduce discontinuities in the interior of a mesh cell. Special methods, like XFEM, had to be developed to handle those discontinuities. The fitted schemes do not cut cells, hence discontinuities appear only across cell boundaries and are easy to handle. But, special treatment is need for the bulk mesh, otherwise the alignment is lost. The bulk grid can no longer be a fixed grid, therefore special methods, like the ALE method, had to be developed.

4.2 Arbitrary Lagrangian-Eulerian Method

The ALE method is an interface tracking method [36]. The tracking grid, i.e. the discrete interface, is part of the bulk grid itself, consisting of faces of it.

At each instance of time t, the evolving domain is described by a mapping \(\mathscr{A}_{t}:\hat{\varOmega }\rightarrow \varOmega (t)\) from a reference domain \(\hat{\varOmega }\) onto the domain Ω(t). A point x in the domain Ω(t) is given by \(\mathbf{x} =\mathscr{ A}_{t}(\hat{\mathbf{x}})\). Functions \(\hat{v}(t,\hat{\mathbf{x}})\) on the reference domain and functions v(t, x) on the evolving domain are related through \(\hat{v}(t,\hat{\mathbf{x}}) = v(t,\mathscr{A}_{t}(\hat{\mathbf{x}}))\).

Time derivatives can be expressed in a Lagrangian frame, respective the domain velocity w, such that a differential equation can be given regarding the evolving domain. In case of a convection-diffusion equation, the ALE form is given as

$$\displaystyle{ (\partial _{t}\hat{c}) \circ \mathscr{ A}_{t}^{-1} + D\varDelta c + (\mathbf{u} -\mathbf{w}) \cdot \nabla c = 0. }$$

Similarly, the Navier-Stokes equations are transformed as

$$\displaystyle{ (\partial _{t}\hat{\mathbf{u}}) \circ \mathscr{ A}_{t}^{-1} + (\mathbf{u} -\mathbf{w}) \cdot \nabla \mathbf{u} -\nabla \cdot \mathbb{S}(\mathbf{u},p) = g\mathbf{e} }$$

In both cases an additional convection term with the domain velocity w occurs. The time derivative is now a material derivative with respect to w. Note that the equations are evaluated on the evolving domain, also called Eulerian frame. The ALE form of the partial differential equations becomes the starting point for our finite element discretization.

The domain velocity is, to a certain degree, arbitrary, since the model prescribes only the normal component on the interface. The choice for the extension of w into the bulk domain is of importance for the stability of the scheme. Different choices and their advantages and disadvantages are discussed in the next subsection.

4.3 Computation of the Domain Velocity

During the evolution of the domain the grid quality may undergo a strong deterioration. Since the grid quality is important for the accuracy of the finite element solution, this has to be avoided. If the grid quality becomes poor, a remeshing has to be done, which is essentially a restart of the simulation. A new grid with good quality is generated from the old grid, the current solution is transferred to the new grid, and the simulation continues. This step is very costly and introduces additional errors. Thus, it is best to have as few remeshing steps as possible.

The freedom in the domain velocity, introduced by the ALE method, is used to decrease the number of remeshing steps, or to avoid them at all. Two choices are important, how to advance of the interface and how to extend the interface velocity to the bulk domain velocity.

A simple method to extend the domain velocity is to do a harmonic extension of the interface velocity. The harmonic extension is very fast, since it has a special block structure, which allows to solve for each component of w with one smaller system. Further, it can be shown that the harmonic extension is the method which shows minimal distortion in a L 2-sense [37].

A second method, that was used, is the linear elastic extension, where the grid is treated as a linear elastic body. The solution of the resulting system is more expensive, due to the coupling of the velocity components. But, under certain circumstances, the method shows better results in regions of large deformations [32].

In both cases, the additional problem of the domain velocity extension is solved by a first order finite element method. Since the velocity extension step has to be done in each nonlinear iteration step of the Navier-Stokes solver, the performance of the velocity extension step is crucial. We prefer the harmonic extension method, due to its features: being fast and overall good.

More important for the grid quality, than the velocity extension into the bulk, is the choice of the interface velocity. Since the interface velocity is coupled to the fluid motion, most of the domain deformation happens there. However, the freedom of choice for the tangential surface velocity can be used to optimize the point distribution and grid cell shape on the interface.

An obvious method to advance the interface is by moving the grid nodes in a classic way, as a function of the fluid velocity

$$\displaystyle{ \dot{\mathbf{x}} = \mathbf{w}\vert _{\varGamma } = \mathbf{F}(\mathbf{u})\quad \text{on}\ \varGamma. }$$
(1.17)

F can be chosen to be, either the full fluid velocity F(u) = u | Γ , or the normal component of the fluid velocity F(u) = (n ⋅ u | Γ )n. The classical discretization of this equation, e.g. with an Euler method, results in a stepping scheme for the n-th grid node x n i at time step i

$$\displaystyle{ \mathbf{x}_{n}^{i+1} = \mathbf{x}_{ n}^{i} +\varDelta t\mathbf{F}(\mathbf{u}_{ n}^{i+1}). }$$

In the continuous setting, both choices for F fulfill the kinematic interface condition of the model and result in identical interfaces, since they distinguish in the tangential component only. In the discrete setting, moving in normal direction only, can prevent local accumulation or coarsening of nodes. On the other hand, a local accumulation is often appreciated in order to resolve the local structure of the interface, hence full velocity has to be favored in those cases. The decision, which version is best, is not obvious and has to be taken from case to case. However, both versions suffer from the general problem that there is absolute no control of the node distribution and of the shape of surface cells.

In order to get more control over the node distribution, a new method has been developed by Barrett et al. [4]. A weak formulation of (1.17) with F(u) = (n ⋅ u | Γ )n was used and completed with an equation for the curvature using the weak form of Laplace-Beltrami identity \(\Delta _{\varGamma }\text{id} =\mathscr{ K}\mathbf{n}\).

Problem 6

For given \(\mathbf{x}^{n} \in \mathbb{P}_{k}(\varGamma _{h})^{d}\) find \((\mathbf{x}^{n+1},\mathscr{K}) \in \mathbb{P}_{k}(\varGamma _{h})^{d} \times \mathbb{P}_{k}(\varGamma _{h})\) such that for all \((\eta,\xi ) \in \mathbb{P}_{k}(\varGamma _{h})^{d} \times \mathbb{P}_{k}(\varGamma _{h})\)

$$\displaystyle\begin{array}{rcl} \left \langle \mathbf{x}^{n+1} -\mathbf{x}^{n},\xi \mathbf{n}\right \rangle _{\varGamma }^{h} -\varDelta t_{ n}\left \langle \mathbf{u},\xi \mathbf{n}\right \rangle _{\varGamma }& =& 0, {}\\ \left \langle \mathscr{K}\mathbf{n},\eta \right \rangle _{\varGamma }^{h} + \left \langle \nabla _{\varGamma }\mathbf{x}^{n+1},\nabla _{\varGamma }\eta \right \rangle _{\varGamma }& =& 0. {}\\ \end{array}$$

By using piecewise linear finite elements and a lumped version 〈⋅ , ⋅ 〉h of the bilinear form of certain terms it can be shown that the semi-discrete, time continuous problem has the property of equi distributed nodes in the 2d case. The fully discrete scheme reaches equi distribution of nodes after a few steps [3].

This approach has been extended to piecewise quadratic isoparametric finite elements. Unfortunately, it turned out that the good properties are not transferring. The equi distribution of nodes is lost or takes an unrealistic amount of iteration steps and therefore cannot keep up with the fluid motion. A solution to keep the very good properties of the scheme for piecewise linear elements for isoparametric elements too, is to apply the scheme on a refined piecewise linear grid defined by all nodes of the isoparametric grid and piecewise linear elements. Further, using the full bilinear forms instead of the lumped ones, the nodes distribute according to the curvature of the interface. In regions of high curvature a higher number of nodes accumulate than in regions of low curvature, which is a beneficial property, since it uses the existing nodes efficiently for problems with varying curvature.

By using a linear combination of the lumped and non-lumped scheme, the user gets a parameter to control the node distribution from equi distributed to curvature dependent.

4.4 Discretization in Time and Space

We consider the time discretization now. Let 0 = t 0 < t 1 < ⋯ < t N = T be a decomposition of a time interval [0, T] and Δt n = t n+1 − t n be the time step size from time t n to t n+1. Discrete functions and domains at time t n , n = 0, …, N get a superscript n, e.g. u n and Ω n. To emphasize the integration domain the forms get a superscript too. A generalized semi-discrete in time scheme of the two-phase flow problem with soluble surfactants reads:

Problem 7

For given Ω k n, k = 1, 2, u n, w n, p n, c n and c Γ n find \(\left (\mathbf{u}^{n+1},p^{n+1},\right.\left.c^{n+1},c_{\varGamma }^{n+1}\right ) \in V (\varOmega ^{n+1}) \times Q(\varOmega ^{n+1}) \times G(\varOmega ^{n+1}) \times M(\varGamma ^{n+1})\) such that for all \(\left (\mathbf{v},p,\varphi,\psi \right ) \in V (\varOmega ^{n+1}) \times Q(\varOmega ^{n+1}) \times G(\varOmega ^{n+1}) \times M(\varGamma ^{n+1})\)

$$\displaystyle\begin{array}{rcl} & \left (\rho \mathbf{u}^{n+1},\mathbf{v}\right )^{n+1} +\alpha \varDelta t_{n}\left [a^{n+1}\left (\mathbf{u}^{n+1} -\mathbf{w}^{n+1},\mathbf{u}^{n+1},\mathbf{v}\right )_{\varOmega ^{n+1}} - f^{n+1}(c_{\varGamma }^{n+1},\mathbf{v})\right ]& \\ & +\varDelta t_{n}\left [b^{n+1}(q,\mathbf{u}^{n+1}) - b^{n+1}(\,p^{n+1},\mathbf{v})\right ] & \\ =& \left (\rho \mathbf{u}^{n},\mathbf{v}\right )^{n} -\beta \varDelta t_{n}\left [a^{n}\left (\mathbf{u}^{n} -\mathbf{w}^{n},\mathbf{u}^{n},\mathbf{v}\right ) - f^{n}(c_{\varGamma }^{n},\mathbf{v})\right ] &{}\end{array}$$
(1.18)
$$\displaystyle\begin{array}{rcl} & & \left (c^{n+1},\varphi \right )^{n+1} +\alpha \varDelta t_{ n}\left [a_{c}^{n+1}\left (\mathbf{u}^{n+1} -\mathbf{w}^{n+1},c^{n+1},\varphi \right ) - f_{ c}^{n+1}(c^{n+1},c_{\varGamma }^{n+1},\varphi )\right ] \\ & =& \qquad \qquad \qquad \left (c^{n},\varphi \right )^{n} -\beta \varDelta t_{ n}\left [a_{c}^{n}\left (\mathbf{u}^{n} -\mathbf{w}^{n},c^{n},\varphi \right ) - f_{ c}^{n}(c^{n},c_{\varGamma }^{n},\varphi )\right ] {}\end{array}$$
(1.19)
$$\displaystyle\begin{array}{rcl} & & \left \langle c_{\varGamma }^{n+1},\psi \right \rangle ^{n+1} +\alpha \varDelta t_{ n}\left [a_{\varGamma }^{n+1}\left (\mathbf{u}^{n+1} -\mathbf{w}^{n+1},c_{\varGamma }^{n+1},\psi \right ) - f_{\varGamma }^{n+1}(c^{n+1},c_{\varGamma }^{n+1},\psi )\right ] \\ & =& \qquad \qquad \qquad \left \langle c_{\varGamma }^{n},\psi \right \rangle ^{n} -\beta \varDelta t_{ n}\left [a_{\varGamma }^{n}\left (\mathbf{u}^{n} -\mathbf{w}^{n},c_{\varGamma }^{n}\psi \right ) - f_{\varGamma }^{n}(c^{n},c_{\varGamma }^{n},\psi \right )] {}\end{array}$$
(1.20)

For different coefficients α and β, different time stepping methods are obtained. In particular, the backward Euler scheme, the forward Euler scheme and the Crank-Nicolson scheme, see Table 1.1.

Table 1.1 Coefficients for time stepping schemes
Full size table

By combining three time steps, of size θ, 1 − 2θ, and θ, to one step (t 3n , t 3(n+1)) and with \(\theta = 1 -\sqrt{2}/2\) and choosing the coefficient according to Table 1.1 the fractional-step-θ scheme is obtained [42]. The equation system given in Problem 7 is highly nonlinear. Decoupling strategies are developed in order to split the problem into several smaller and simpler problems. Considering c Γ explicit in the Navier-Stokes equations, they decouple from the surfactant transport equations. Further, the integration domains Ω and Γ are taken explicit in the Navier-Stokes step, but the domain velocity w is updated. The resulting problem is a standard Navier-Stokes problem with a modified convective velocity u n+1 − w n+1.

Problem 8

For given Ω k n, k = 1, 2, u n, w n, p n, and c Γ n find (u n+1, p n+1) ∈ V (Ω n) × Q(Ω n) such that for all (v, p) ∈ V (Ω n) × Q(Ω n)

$$\displaystyle\begin{array}{rcl} & & \left (\rho \mathbf{u}^{n+1},\mathbf{v}\right )^{n} +\alpha \varDelta t_{ n}\left [a^{n}\left (\mathbf{u}^{n+1} -\mathbf{w}^{n+1},\mathbf{u}^{n+1},\mathbf{v}\right ) - f^{n}(c_{\varGamma }^{n},\mathbf{v})\right ] \\ & & \qquad \qquad \qquad +\varDelta t_{n}\left [b^{n}(q,\mathbf{u}^{n+1}) - b^{n}(\,p^{n+1},\mathbf{v})\right ] \\ & =& \qquad \qquad \left (\rho \mathbf{u}^{n},\mathbf{v}\right )^{n} -\beta \varDelta t_{ n}\left [a^{n}\left (\mathbf{u}^{n} -\mathbf{w}^{n},\mathbf{u}^{n},\mathbf{v}\right ) - f^{n}(c_{\varGamma }^{n},\mathbf{v})\right ]. {}\end{array}$$
(1.21)

Having the solution of the Navier-Stokes step given in Problem 8, the grid can be updated to Ω i n+1, i = 1, 2, and Γ n+1. The functions u n+1, w n+1 and p n+1 are transferred implicit to the new grid.

After the Navier-Stokes step the surfactant transport is solved on the new grid Ω n+1 and Γ n+1, using the updated velocity fields u n+1 and w n+1. The surfactant transport equations for the bulk and the surface are decoupled likewise. For each equation the remaining information is taken explicit. Although, this would not be necessary for the linear Henry sorption law, in the case of the non-linear Langmuir sorption law a nonlinear iteration is required anyway.

Problem 9

For given Ω n+1, Γ n+1, u n+1, w n+1, c 0 n+1 = c n, c Γ, 0 n+1 = c Γ n find (c j n+1, c Γ, j n+1) ∈ G(Ω n+1) × M(Γ n+1), such that for all (φ, ψ) ∈ G(Ω n+1) × M(Γ n+1) and i = 1, 2, …, M

$$\displaystyle\begin{array}{rcl} & & \left (c_{j}^{n+1},\varphi \right )^{n+1} +\alpha \varDelta t_{ n}\left [a_{c}^{n+1}\left (\mathbf{u}^{n+1} -\mathbf{w}^{n+1},c_{ j}^{n+1},\varphi \right ) - f_{ c}^{n+1}(c_{ j}^{n+1},c_{\varGamma,j-1}^{n+1},\varphi )\right ] \\ & =& \qquad \qquad \qquad \left (c^{n},\varphi \right )^{n} -\beta \varDelta t_{ n}\left [a_{c}^{n}\left (\mathbf{u}^{n} -\mathbf{w}^{n},c^{n},\varphi \right ) - f_{ c}^{n}(c^{n},c_{\varGamma }^{n},\varphi )\right ] {}\end{array}$$
(1.22)
$$\displaystyle\begin{array}{rcl} & & \left \langle c_{\varGamma,j}^{n+1},\psi \right \rangle ^{n+1} +\alpha \varDelta t_{ n}\left [a_{\varGamma }^{n+1}(\mathbf{u}^{n+1} -\mathbf{w}^{n+1},c_{\varGamma,j}^{n+1},\psi ) - f_{\varGamma }^{n+1}(c_{ j}^{n+1},c_{\varGamma,j}^{n+1},\psi )\right ] \\ & =& \qquad \qquad \qquad \left \langle c_{\varGamma }^{n},\varphi \right \rangle ^{n} -\beta \varDelta t_{ n}\left [a_{\varGamma }^{n}(\mathbf{u}^{n} -\mathbf{w}^{n},c_{\varGamma }^{n},\psi ) - f_{\varGamma }^{n}(c^{n},c_{\varGamma }^{n},\psi )\right ]. {}\end{array}$$
(1.23)

Here, j is the nonlinear iteration step and M the number of nonlinear iterations, resulting from the stopping criterion.

Finally, we take a closer look to the spatial discretization. Pressure discontinuities across the interface are an inherent property of two-phase flows with surface stresses. A finite element space that resolves this discontinuities is essential to get an acceptable approximation order and to suppress spurious velocities and oscillations at the interface [23].

In the unfitted approach the finite element space is enriched by the XFEM finite element method [27] in order to resolve discontinuities in pressure and kinks in the velocity fields. If the grid is fitted to the interface velocity kinks are resolved automatically and pressure jumps are resolved by having either a classical element-wise discontinuous pressure space or by taking a continuous pressure but allow jumps across the interface. By the so called node doubling, where the degrees of freedom are not identified at the interface, the pressure can have different values for each phase at the interface.

For a polyhedral domain it can be shown that node doubling the pressure space at the interface results in an inf-sup stable pair of finite element spaces, as long the underlying finite element pair is inf-sup stable in each phase. For the standard Taylor-Hood finite element family this is the case, under the usual assumptions to the subdomains and their triangulations. For a smooth interface a corresponding result is still left open.

Apart from spurious velocities and a poor approximation, not allowing a discontinuous pressure also results in a poor mass conservation. In fact, the mass conservation can only be guaranteed having a phase-wise discontinuous pressure. If this is not the case, it can happen that one phase vanishes.

We use the standard isoparametric Taylor-Hood element \(\mathbb{P}_{2}/\mathbb{P}_{1}\) with node doubling in the pressure space, which can avoid the above-mentioned problems.

5 Numerical Results

The codes for numerical studies are all in-house developments. For the fully coupled time dependent Problem 1, a code based on MooNMD was developed. MooNMD is an in-house finite element code base written in C++. While the less demanding 2d and 3d axisymmetric computations are done with serial codes, the fully 3d computations are done with a parallelized version of the code base. The parallelization is done by domain decomposition and using the MPI standard. A numerical study of the fully coupled two-phase Problem 1 is given in [2] and will not repeated here. The fully coupled numerical studies presented in the following are free surface flows.

For the static shape computations in Sect. 1.5.2 a standalone code was developed in Matlab. This code is fully independent from the code developed for the fully coupled time dependent problems.

For the studies of surface equation in Sect. 1.5.1 a code in the language Julia [7], was developed. The code handles general differential equations on hypersurfaces in two or three dimensions. Stabilization by Local Projection is implemented.

5.1 Stabilized Advection-Diffusion Transport on a Surface

This example is inspired by Example 2 from [20], where a circular counter-clockwise flow in the domain [0, 1]2 is simulated. The problem is transferred to a curved surface, and Problem 2 is solved.

Given a cylinder of radius 0. 5 around the axis x = 0. 5 parallel to the y-axis with height one. We set Γ to the half of the cylinder, where z ≥ 0. The velocity field (−y, x) in the plane case [20] is transferred to the curved surface resulting in

$$\displaystyle{ \mathbf{w} = \left (-\pi yz, \frac{1} {\pi } \arccos (1 - 2x),-\frac{\pi } {2}(1 - 2x)\right )^{T}. }$$

The right hand side, diffusion and reaction coefficient are set to f = 0, ɛ = 10−8 and c = 0, respectively. Along the outflow boundary, \(\{\left (0,y,0\right )\vert y \in \left (0,1\right )\}\), we impose homogeneous Neumann conditions. On the remaining part of the boundary the following discontinuous Dirichlet-type boundary condition is prescribed

$$\displaystyle{ u_{D}(x,y,z):= \left \{\begin{array}{l} 1,\quad \text{if }y = 0\text{ and }x \in \left (\frac{1} {3}, \frac{2} {3}\right )\\ 0, \quad \text{else} \end{array} \right.. }$$

For the standard Galerkin approximation \(\mathbb{P}_{1}\) surface finite element space is used. This is compared to the LPS stabilized formulation using \(V _{h} = \mathbb{P}_{1}^{+}\) and \(D_{h} = \mathbb{P}_{0}^{\text{disc}}\) on the same mesh. The stabilization parameter is chosen as γ 2 = 1. 0 (high), γ 2 = 0. 1 (optimal), and γ 2 = 0. 01 (low).

The discontinuous Dirichlet-type boundary conditions lead to interior layers of the solution. As observed for bulk equations numerical oscillations around the layers occur for the unstabilized Galerkin method, compare Fig. 1.1 (left). LPS can reduce and localize these oscillations, see Fig. 1.1 (right). The influence of the stabilization parameter is visualized in Fig. 1.2. For small ɛ we expect the outflow profile to approximate a step function. We observe a tendency of smearing out for the (too) low stabilization parameter and increasing oscillations for the (too) high stabilization parameter [41].

Fig. 1.1
figure 1

\(\mathbb{P}_{1}\) part of the solutions of the transport problem on a surface for the standard \(\mathbb{P}_{1}\) (left) and the LPS-stabilized FEM with optimal stabilization parameter (right). View on x-y-plane

Full size image
Fig. 1.2
figure 2

\(\mathbb{P}_{1}\) part of the solutions of the transport problem on a surface at the outflow boundary for the LPS-stabilized FEM with low, optimal and high stabilization parameter

Full size image

5.2 Equilibrium Shape of a Pending Drop

In order to study the accuracy of the implemented algorithm we evaluate the shape of axisymmetric pendant droplets at a tip of a capillary. This is a typical situation in profile analysis tensiometry (PAT) for measuring the surface tension of liquids. In PAT a pendant drop is growing up to a certain volume at a capillary tip by a dosing system. The profile is then extracted from a picture of the drop by image processing and fitted to a solution of the Young-Laplace equation. It turns out that the shape of a dynamically generated drop differs considerably from the static shape, see e.g. [30]. We consider here the relaxation of clean and contaminated pendant drops at a tip of a capillary to the equilibrium state. For this two numerical schemes and are developed.

In [26] four different methods have been proposed to compute the static shape of axisymmetric drops at a tip of a capillary for a given drop volume and a given Bond number Bo = We∕Fr. The method used in this section is based on an equivalent formulation of the problem as a constrained minimization problem: Find the surface of minimal energy which encloses a given fixed drop volume Vol. Applying the method of Lagrange multiplier and using a discretization by continuous, piecewise linear finite elements, we have to solve a nonlinear algebraic system of equations. As the initial guess for the Newton method we chose a piecewise linear approximation of a spherical shape enclosing the given volume. More details on this method and alternatives can be found in [26].

A 3d axisymmetric version of the 3d code based on the techniques described in Sects. 1.2–1.4 has been developed. Instead of starting with the strong axisymmetric form of the partial differential equation and deriving a weak formulation in suitable weighted Sobolev spaces we follow the approach in [18] where the 3d axisymmetric forms are developed directly from the 3d Cartesian forms. One advantage of this technique is that the boundary conditions at the artificial boundary along the symmetry axis appear in a natural way.

The geometric configuration of our test problem is as follows. The dimensionless radius of the capillary tip is equal to one its height equals also one. The axisymmetric pendant drop is assumed to have a pinned contact line (circle of radius one). The volume of the drop below the capillary is chosen to be Vol = 60. We start our test series with a surfactant free drop in equilibrium for Bo = 0. 006708. As expected the drop stays in equilibrium and the bottom position remains unchanged, compare Table 1.2.

Table 1.2 Bottom positions in equilibrium for different Bond numbers
Full size table

Now we assume that the surface tension is suddenly reduced (uniformly over the surface Γ) leading to the Bond numbers Bo=0.013416 and Bo=0.03354, for two different values of surface tension. Since the drop is no longer in equilibrium, it starts to oscillate. In the dynamic computations with the 3d axisymmetric code, we chose Re = Fr = 1 such that We = Bo. We observe a perfect fit of the bottom position (Table 1.2 and Fig. 1.3) and the shape of the drop (Fig. 1.4 left) computed by the static code and the dynamic computations for t → ∞. Note that larger amplitudes appear for the larger Bond number (larger reduction of surface tension). For the largest Bond number of Bo=0.067080 there exist a static equilibrium, however, due to the large amplitudes the dynamic computations predict the detachment of the drop. Our interpretation is that the static equilibrium is not stable with respect to large perturbations.

Fig. 1.3
figure 3

Bottom position of a clean drop with suddenly reduced surface tension. Dynamic computations for Re = Fr = 1, We = Bo = 0. 013416 (left) and We = Bo = 0. 033540 (right)

Full size image
Fig. 1.4
figure 4

Left: Clean drop with suddenly reduced surface tension. Initial, equilibrium, and final shape after relaxation for Re = Fr = 1, We = Bo = 0. 033540. Right: Uniform surface surfactant concentration over time for a clean drop and two different initial bulk concentrations

Full size image

We close this test series with a surfactant free droplet in equilibrium for Bo = 0. 006708 and Vol = 60. Two uniform initial states for the bulk surfactant concentration are considered: \(\left (c_{0},c_{\varGamma,0}\right ) = \left (1,0\right )\) and \(\left (c_{0},c_{\varGamma,0}\right ) = \left (3,0\right )\). The dimensionless parameters are Re = Fr = 1, Pe = 1, Pe Γ = 10, Bi = 0, Da = 10, E = 0. 5, β = 100, and the Henry sorption law is used. Since Bi = 0 we have no desorption and only adsorption takes place. The increase of the surface surfactant concentration c Γ in the time interval [0, 5] can be seen in Fig. 1.4 right.

The surfactant at the surface leads to a reduction in the surface tension and the drop is no longer in equilibrium. As it can be seen from Figs. 1.4 and 1.5 the time scale for the adsorption is much shorter than the time scale to attain the equilibrium. We see from Fig. 1.5 and Table 1.3 that even for a very small change in the surface tension, due to surfactant, our numerical scheme accurately captures the dynamics and the equilibrium bottom position. We do not compare the shapes of the relaxed drop with the shape of the equilibrium in an extra figure since they are practically identical.

Fig. 1.5
figure 5

Relaxation of a drop with soluble surfactant with different initial bulk concentrations. c 0 = 1 (left) and c 0 = 3 (right)

Full size image
Table 1.3 Influence of adsorption of surfactants at the interface
Full size table

5.3 Freely Oscillating Droplet

A wide variety of analytical investigations of oscillating droplets make it an excellent choice for validation of numerical schemes and codes [31, 34, 40]. Here we will compare the theoretical models of oscillating droplets with soluble surfactant [40] and insoluble surfactant [34] to our fully three dimensional numerical scheme.

In the numerical computations gravity is neglected and the initial drop is in rest. The shape is given by a sphere of radius one perturbed with a spherical harmonic of second order and an amplitude of a 2 = 0. 1. The drop is not in equilibrium and starts to oscillate. The Weber number is fixed to We = 0. 0081 in all examples, which will induce roughly five oscillations in the time interval [0, 1]. The timestep size is Δt = 10−4, i.e. 10,000 steps per computation.

We consider two examples, an insoluble case with a Reynolds number of Re = 10. 684 and a soluble case with Re = 1. 0684. The Reynolds numbers are chosen such that the dimensionless viscosity \(\sqrt{ \text{We}}\text{Re}^{-1} <0.1\), a bound given in [6, 39] where nonlinear viscous effects become negligible and the analytic approximations are valid. In both examples, the bulk and surface Peclet, the Damköhler and Biot numbers are Pe = 1, Pe Γ = 1, Da = 1 and Bi = 1, respectively. The surface surfactant scaling factor β is set to one. The bulk surfactant concentration and the equilibrium surface surfactant concentration for the initial droplet is set to c eq = 0. 1111 and c Γ eq = 0. 1, respectively.

From the linearized theory for small-amplitude oscillations of a drop, we can predict the angular frequency and the damping rate of the oscillation [6, 11, 31, 39]. The results are given in Table 1.4, where ω 0,2 is the Lamb frequency, ω 2 the angular frequency, and δ 2 the damping rate of the second mode.

Table 1.4 Lamb frequency, angular frequency and damping rate for different Reynolds numbers
Full size table

Theoretical results for an oscillating droplet with insoluble surfactants are derived in [34]. A set of differential equations for the amplitude a l of the l-th mode of shape oscillation and amplitude g l of the l-th mode of the surface surfactant concentration are given. In order to compare the insoluble theory with the results here, the differential equations given in [34] are solved numerically with a Matlab code using the ode45 routine.

Results for higher viscosities and a soluble surfactant case are given in [40]. For the dimensionless complex frequency α an first order approximation \(\alpha = i(1 +\varepsilon +\mathscr{O}(\varepsilon ^{2}))\), is given, where ɛ is specified by an explicit correlation from the material properties. The damping rate is given by the real part, and the frequency by the imaginary part of ω 0,2 α

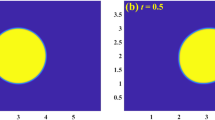
In Fig. 1.6 (left) a comparison of the normalized amplitudes of the shape oscillation in the soluble case is shown. Normalized means a 2(t) is scaled with a 2(0)−1 such that the graph starts at one. In the figure, the graph (sim) is the shape oscillation by our numerical computation and the graph (pred) is the shape oscillation obtain in [40]. We see a good agreement, although the prediction runs a little ahead.

Fig. 1.6
figure 6

Comparison of the course of the second mode of an freely oscillation drop with soluble surfactant (left) and insoluble surfactant (right), between the numerical simulation (sim) and the analytic prediction (pred), for (Re, E) = (1. 0684, 1. 0) and (Re, E) = (10. 684, 1. 0), respectively

Full size image

In Fig. 1.6 (right) a comparison of the normalized amplitudes of the shape oscillation in the insoluble case is shown. The graph (pred) is the prediction of the shape oscillation obtained by solving the equations in [34]. We see a good agreement, the prediction runs ahead again and shows less damping.

In Fig. 1.7 (left) the damping rates versus different surface elasticities for the numerical simulation (sim) and the prediction (pred) after [40] is shown. In Fig. 1.7 (right) the same is shown for the frequencies. We see a quite good agreement in the frequencies over the considered range of surface elasticities. The agreement gets better for low surface elasticities. Contrary, we see an increasing disagreement in the damping rates for lower surface elasticities and a better agreement for higher surface elasticities.

Fig. 1.7
figure 7

Damping rate versus surface elasticity (left) and angular frequency versus surface elasticity (right) for Re = 1. 0684 and soluble surfactant (left), for the numerical simulation (sim) and the analytic prediction (pred)

Full size image

In the case of insoluble surfactant, shown in Fig. 1.8, one gets a better agreement for the damping rates at lower surface elasticities. The angular frequencies are in good agreement for lower elasticities. Both, the mismatch in damping rate and the frequency increases with higher surface elasticities.

Fig. 1.8
figure 8

Damping rate versus surface elasticity (left) and angular frequency versus surface elasticity (right) for Re = 10. 684 and insoluble surfactant, for the numerical simulation (sim) and the analytic prediction (pred)

Full size image

This numerical example confirms, as expected, that the linear theory by Lamb [31] fails to predict damping rates and frequencies for the case of viscous fluids and fluids with surfactants present.

In both cases the numerical simulation overestimates the damping. The disagreement increases with the surface elasticity in the insoluble case, what one might expect, since the theory chosen from [34] is for small surface elasticities. Also, the backward Euler scheme used in the numerical simulation introduces numerical damping. Contrary, in the soluble case, the disagreement increases with lower surface elasticities, thus we expect a problem with the numerical damping, and a lower time step size or a time discretization which introduce less numerical damping could be necessary.

6 Summary

We summarize our main contributions within the SPP 1506:

  • Numerical analysis and implementation of a surface finite element method for convection-diffusion-reaction equations stabilized by local projection.

  • Extension of the local projection stabilization to a coupled bulk-surface transport problem. Error analysis and implementation.

  • Development and implementation of a higher order, fitted finite element method for two-phase and free surface flows with soluble and insoluble surfactants in 2d, 3d, and axisymmetric 3d cases.

  • Application and validation of the developed algorithms in drop profile analysis tensiometry.

  • Validation of different schemes within the SPP 1506 based on the Taylor flow problem. Comparison of numerical data and measurements of Taylor bubbles [2].