INTRODUCTION

Taylor flow is a special kind of slug flow in small channels, where the liquid slugs separating the elongated bullet-shaped bubbles (Taylor bubbles) are free from gas entrainment. This flow regime, which is also known as bubble train flow, segmented flow or capillary slug flow, occurs in microfluidic devices for applications in life sciences (lab-on-a-chip), material synthesis and chemical process engineering, e.g. in heat exchangers and catalytic multiphase capillary and monolithic reactors [1]. Among the various gas-liquid flow patterns in microchannels [2], Taylor flow is attractive because of its well-defined interfaces and flow conditions, which are easier to control than in macroscopic devices and because of its advantageous mass transfer properties. The latter stems from (i) the high interfacial area per unit volume, (ii) the thin liquid film that separates the gas bubble from the channel wall, and (iii) the recirculation in the liquid slug, which accounts for good mixing and a wall-normal convective transport in laminar flow [3]. For recent reviews on Taylor flow we refer to [4–7].

The shape of the Taylor bubble depends mainly on the (bubble) capillary number Cab = ubµL/σ and to a lesser extent on the Reynolds number Reb = ρLubD/µL. Here, ub denotes bubble velocity, ρL liquid density, µL liquid viscosity, σ surface tension and D the pipe diameter. At low Cab, both bubble ends form hemispherical caps connected by a uniform cylindrical section of radius Rb [8]. As Cab increases, the Taylor bubble gets more slender and the fore-aft symmetry is lost. In addition, there are capillary wave undulations where the uniform interface merges with the transition region in the rear [9]. The curvature of the bubble nose increases approaching a limiting value at Cab = O(1). The profile of the rear transition undertakes large deformations as its shape evolves from convex for small values of Cab to concave at large values of Cab [10]. For high bubble speeds, the trailing end develops re-entrant cavities of the continuous liquid phase [11] which cause bubble breakup at capillary numbers of order one and above [12, 13].

Of primary interest for many applications with Taylor flow is the thickness of the uniform liquid film δ = R − Rb. Several correlations have been suggested in the literature to relate δ with Cab, see below. For engineering practice, the direct benefit of these correlations is at first limited as the bubble velocity and thus Cab are not prior known in general. Often mass flow controllers serve to prescribe the gas and liquid flow rates QG and QL. For a straight channel with constant cross-section A, thus the superficial velocities jG = QG/A and jL = QL/A, the total superficial velocity (or total volumetric flux) jT = jG + jL and the volumetric flow rate ratio (dynamic holdup) β = QG/(QG + QL) = jG/jT are known. In contrast, the mean gas velocity uG and the void fraction α = jG/uG are unknown. In small channel Taylor flow, liquid slugs are usually free from gas entrainment to that ub = uG. Thus, Cab is unknown as well. Particularly useful for practical applications of Taylor flow would be a (preferentially) universal correlation that relates the bubble velocity, the liquid film thickness and other important hydrodynamic parameters of Taylor flow to the total superficial velocity jT. The purpose of the present paper is to develop such a correlation and to embed it in a unifying theoretical framework for characterization of Taylor flow hydrodynamics. Here we restrict our study to laminar gas-liquid Taylor flow through a straight circular pipe where the diameter is sufficiently low so that gravitational effects are negligible.

We formulate the desired correlation for the ratio between the (unknown) bubble velocity ub and the (known) mean velocity of the two-phase flow, i.e. the total superficial velocity jT. For two incompressible phases, the mean axial velocity in the liquid slug (us) equals jT [14]. Several researchers indicated the fundamental importance of this velocity ratio for Taylor flow [7, 14, 15]. Here, we denote η = ub/jT as the characteristic velocity ratio of Taylor flow. Since the proposed correlation for η is formulated in terms of prior known parameters only, it may also serve as closure relation for mechanistic models of Taylor flow in complement to closure relations for the Taylor bubble rise velocity proposed for larger channels [16].

The organization of the paper is as follows. We first give some fundamental relations in capillary Taylor flow. Thereafter, we summarize the state of the art in literature to elucidate the functional dependence of η on the (two-phase) capillary number Ca = jTµL/σ, which is based on jT as velocity scale. As main part, we present the development of the new model and its evaluation with respect to recent experimental and numerical data from literature. This is followed by a discussion of the accuracy, limitations and benefit of the model for predicting hydrodynamics of Taylor flow.

FUNDAMENTAL RELATIONS IN CAPILLARY TAYLOR FLOW

Conditions and Assumptions

We consider the laminar pressure-driven gas-liquid flow through a cylindrical horizontal capillary (radius R, diameter D = 2R, cross-sectional area A = πR2). Both phases are incompressible and immiscible Newtonian fluids. We assume that the gas density ρG, the liquid density ρL, the gas viscosity µG, the liquid viscosity µL and the coefficient of surface tension σ are all constant.

The importance of gravitational and buoyancy effects is usually quantified by the Eötvös number Eo = g(ρL − ρG)D2/σ or by the Bond number Bo = gρLD2/σ. Leung et al. [17] experimentally studied the effect of gravity in horizontal gas-liquid Taylor flow in three different millimeter-sized channels (D = 1.12, 1.69, 2.12 mm giving Eo = 0.287, 0.653 and 1.028). The authors observed gravity-induced drainage flow from the top to the bottom of the pipe within the liquid film resulting in bubble asymmetry. However, these effects diminish for small values of Eo and/or Ca. Magnini et al. [18] systematically investigated the effect of buoyancy on the Taylor bubble shape and velocity in vertical tubes by experiments and numerical simulations. The authors showed that buoyancy could have a notable effect even at Bond numbers below unity. Here we assume that the channel size is so small that gravity/buoyancy effects are negligible (Eo → 0), a criterion that should be fulfilled for submillimeter channels. Accordingly, the bubble profile and the flow field are assumed axisymmetric and steady in a frame of reference moving with the bubble.

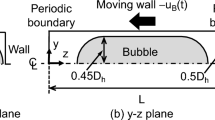
We further assume that the liquid slugs of Taylor flow are sufficiently long to form a fully developed parabolic velocity profile so that there is no interaction between neighboring bubbles. In addition, the bubble is assumed to be sufficiently long so that there is a region where the bubble has a cylindrical shape with the thickness of the liquid film being uniform and independent of bubble length as described in [19]. Such a situation occurs when the front and the back of the bubble are virtually independent. The inertia-free boundary integral computations of Lac and Sherwood [13] suggest that this is the case when the ratio between the radii of the undeformed bubble and the tube exceeds a value of 1.1. A further quantitative criterion for the minimum bubble length (relative to tube radius) in terms of Cab in absence of inertia and gravity is given in [20]. In the presence of inertia, the necessary bubble length to form a uniform film region steeply increases with Reb, in particular at high Cab [9]. Fig. 1 shows a sketch of the Taylor flow configuration under analysis with characteristic parameters. Real images of such Taylor bubbles can be found e.g. in reference [21].

Fig. 1.
figure 1

Sketch of axisymmetric Taylor flow in a circular pipe (radius R) with streamline patterns and important parameter.

Full size image

Mass Balance

A global mass balance for the two-phase flow yields [14, 22]

$$\underbrace {{{u}_{f}}{{A}_{f}}}_{ = {{Q}_{f}}} + \underbrace {{{u}_{b}}{{A}_{b}}}_{ = {{Q}_{b}}} = \underbrace {{{j}_{T}}A}_{ = {{Q}_{s}}}.$$
(1)

Here, uf is the mean axial velocity of the liquid in the uniform film region while \({{A}_{f}} = \pi (R_{{}}^{2} - R_{b}^{2})\) and \({{A}_{b}} = \pi R_{b}^{2}\) denote the cross-sectional area of the film and the bubble in this region, respectively.

For a compact notation, we introduce the wetting fraction

$$w = \frac{{{{A}_{f}}}}{A} = 1 - \frac{{R_{b}^{2}}}{{R_{{}}^{2}}} = 1 - {{\left( {1 - \frac{\delta }{R}} \right)}^{2}} = \frac{{2\delta }}{R}\left( {1 - \frac{\delta }{{2R}}} \right).$$
(2)

This quantity is of interest for the penetration of a gas phase into a capillary where it displaces a viscous liquid [23]. When gravitational forces are negligible, the thickness of the liquid film deposited at the wall becomes constant in a distance sufficiently far from the bubble tip [8, 24]. The relative cross-sectional area fraction w = Af/A then represents the fraction of liquid left behind the bubble. In terms of the wetting fraction, Eq. (1) can be expressed as

$$\frac{{{{u}_{b}}}}{{{{j}_{T}}}} = \frac{1}{{1 - w}}\frac{1}{{1 + {{Q}_{f}}/{{Q}_{b}}}},$$
(3)

a relation that will be useful later.

As further quantity of interest, we define the relative drift velocity

$$m = \frac{{{{u}_{b}} - {{j}_{T}}}}{{{{u}_{b}}}} = 1 - \frac{{{{j}_{T}}}}{{{{u}_{b}}}}.$$
(4)

From Eq. (3) it follows

$$m = 1 - (1 - w)\left( {1 + \frac{{{{Q}_{f}}}}{{{{Q}_{b}}}}} \right).$$
(5)

For a liquid film at rest it is Qf = uf = 0 and Eq. (5) yields

$$m = w = 1 - \frac{{R_{b}^{2}}}{{R_{{}}^{2}}} = \frac{{2\delta }}{R}\left( {1 - \frac{\delta }{{2R}}} \right).$$
(6)

Such a stagnant liquid film with zero velocity occurs in the constant film thickness region of inviscid bubbles that cannot exert tangential stresses [11]. In studies on the displacement of a viscous liquid in a capillary by the steady propagation of an inviscid semi-infinite finger [8, 25–27] or by a long inviscid bubble [28] m and w are often used synonymously.

Streamline Patterns in Liquid Slug

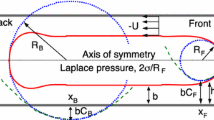
For gas-liquid mass transfer in Taylor flow, the streamline patterns in the liquid slug are of great importance [5]. These can be classified in recirculating flow (see sketch in Fig. 1) and complete bypass flow, resulting in different pathways for mass-transfer.

In a frame of reference moving with the Taylor bubble a recirculation pattern in the liquid slug occurs when the bubble velocity is lower than the liquid velocity on the channel axis, i.e. for ub < uL,max [23, 29]. For a liquid slug with a laminar fully developed parabolic velocity profile the maximum liquid velocity is given by uL,max = 2jT. Thus, for m < 0.5 streamline patterns show a recirculation region whereas for m > 0.5 complete bypass flow (CBF) occurs [11].

The cross-sectional regions with recirculation flow (in the channel center) and partial bypass flow (close to the walls) are separated by the dividing streamline [30], see Fig. 1. The position of the dividing streamline results from the condition that the axial flow rate in the recirculation area is zero in the moving frame of reference. The radial position of the dividing streamline (Rds) and the radial position where the velocity in the moving frame of reference is zero (R0) are given by [30]

$$\frac{{{{R}_{{{\text{ds}}}}}}}{R} = \frac{{\sqrt 2 {{R}_{{\text{0}}}}}}{R} = {{(2 - \eta )}^{{1/2}}}.$$
(7)

Thus, the relative cross-sectional area of the recirculation region is Ads/A = 2 − η.

The intensity of the recirculation can be quantified by the time needed for the liquid to move from one end of the liquid slug to the other end. A second characteristic time scale is the time needed by the liquid slug to travel a distance of its own length. Thulasidas et al. [30] used the ratio of both time scales to define a non-dimensional recirculation time. For a circular channel the non-dimensional recirculation time is [31]

$$\tau = {{\left( {\frac{1}{\eta } - \frac{1}{2}} \right)}^{{ - 1}}}.$$
(8)

LITERATURE RELATIONS FOR FILM THICKNESS AND BUBBLE VELOCITY

In this section, we summarize relations on the liquid film thickness and bubble velocity, which we will utilize in the subsequent section for the development of the new model.

Liquid Film Thickness

In his classical paper [24], Bretherton applied lubrication theory to the flow in the liquid film to derive the first theoretical expression for the film thickness. Using only local conditions at the bubble nose, the asymptotic film thickness is independent of bubble length and given by

$$\frac{{{{\delta }_{{{\text{Br}}}}}}}{R} = 0.643{{(3{\text{Ca}}_{b}^{{}})}^{{2/3}}} = \underbrace {1.3375}_{ = P}{\text{Ca}}_{b}^{{2/3}}.$$
(9)

Eq. (9) is only valid for very low capillary and Reynolds numbers and according to Bretherton’s own experiments accurate within 10% for Cab < 5 × 10−3.

By a scaling analysis, Aussilious and Quere (AQ) [32] derived the following equation for the liquid film thickness of a semi-infinite bubble in a circular tube

$$\frac{{{{\delta }_{{{\text{AQ}}}}}}}{R} = \frac{{P \cdot {\text{Ca}}_{b}^{{2/3}}}}{{1 + \underbrace {2.5}_{ = F} \times P \cdot {\text{Ca}}_{b}^{{2/3}}}} = \frac{{1.3375{\text{Ca}}_{b}^{{2/3}}}}{{1 + 3.344{\text{Ca}}_{b}^{{2/3}}}}.$$
(10)

The factor F = 2.5 is obtained empirically by fitting experimental data of Taylor [23]. This relation is valid in the range 10−3 ≤ Cab ≤ 1.4 and approximates Eq. (9) for small capillary numbers. Klaseboer et al. [33] presented an analytical extension of Bretherton’s work yielding an expression identical to Eq. (10), except F = FKGM = 2.79. Balestra, Zhu and Gallaire (BZG) [34] performed an extensive computational study on the hydrodynamics of Taylor bubbles and drops in capillaries under negligible gravity focusing on the effect of the viscosity ratio λ = µG/µL. Using COMSOL Multiphysics, they solved the Stokes equations by a moving mesh method for capillary numbers in the range 10–4 ≤ Ca ≤ 1. By fitting the numerical results for a bubble (λ = 0) , they found F = FBZG = 2.483 which is close to the value of AQ [32].

Eq. (10) neglects inertial effects, which can become important at higher velocities causing a non-monotonic dependence of the film thickness on the Reynolds number in a circular tube [8, 35] or a two-dimensional channel [36]. Han and Shikazono [37] proposed the correlation

$$\frac{{{{\delta }_{{{\text{HS}}}}}}}{R} = \frac{{0.643{{{(3{\text{C}}{{{\text{a}}}_{b}})}}^{{2/3}}}}}{{1\, + \,3.13{\text{Ca}}_{b}^{{2/3}}\, + \,0.504{\text{Ca}}_{b}^{{0.672}}{\text{Re}}_{b}^{{0.589}}\, - \,0.352{\text{We}}_{b}^{{0.629}}}} = 0.643{{f}_{{{\text{HS}}}}},$$
(11)

which accounts for inertial effects by Reb and the Weber number Web = CabReb. Eq. (11) was derived from film thicknesses measurements for water and ethanol with 0 < Cab < 0.4 and 0 < Reb < 2000. Howard and Walsh [7] found that this correlation predicts the film thickness best at higher capillary numbers amongst the existing correlations.

Langewisch and Buongiorno (LB) [38] studied capillary Taylor flow numerically with Ca and Re in the ranges 0.005−0.2 and 0−900, respectively. The density ratio was fixed to 0.001 and the viscosity ratio to λ = 0.01 while gravity is neglected. The authors proposed the following model for the film thickness

$$\frac{{{{\delta }_{{{\text{LB}}}}}}}{R} = \frac{{1.3375{\text{Ca}}_{{}}^{{2/3}}}}{{1 + 2.86\left[ {{\text{1}} + \Phi ({\text{Re}})} \right]{\text{Ca}}_{{}}^{{0.764}}}},$$
(12)

where

$$\Phi ({\text{Re}}) = \left\{ {\begin{array}{*{20}{c}} 0&{{\text{Re}} = 0} \\ {{{{\left( {\frac{{32.05}}{{{\text{Re}}_{{}}^{{0.593}}}}\, + \,4.564\, \times \,{{{10}}^{{ - 5}}}{\text{Re}}_{{}}^{{1.909}}} \right)}}^{{ - 1}}}}&{{\text{Re}} > 0} \end{array}} \right..$$
(13)

Here, Ca = Cab/η and Re = Reb/η represent the capillary and Reynolds number using jT as characteristic velocity scale, respectively. Kurimoto et al. [39] found that the film thickness model of LB [38] shows a better agreement with their numerical results as compared to the model of Han and Shikazono [37].

Bubble Velocity

Literature relations for the bubble velocity are usually formulated either in terms of m or η. By the definition of m in Eq. (4), it is η = 1 − m−1 so that both formulations are convertible.

Bretherton’s [24] analytical approach at low Cab resulted in the expression

$$m = 1.29{{(3{\text{Ca}}_{b}^{{}})}^{{2/3}}} = 2.683{\text{Ca}}_{b}^{{2/3}},$$
(14)

corresponding to

$$\eta = \frac{1}{{1 - m}} \approx 1 + m = 1 + 1.29{{(3{\text{Ca}}_{b}^{{}})}^{{2/3}}}.$$
(15)

Giavedoni and Saita [8] found that their numerical results for the film thickness match the theoretical correlation of Bretherton for Cab < 10−3. Fairbrother and Stubbs [40] suggested the empirical correlation

$$m = {\text{Ca}}_{b}^{{1/2}},$$
(16)

which is valid in the range 7.5 × 10−5 < Cab < 0.014. Experiments for very viscous fluids in 1.5−3 mm circular tubes by Taylor [23] indicate that the validity of Eq. (16) may be extended up to Cab = 0.09. Taylors experimental data up to Cab = 2 are well fitted by inserting the film thickness model of AQ [32] for a stagnant liquid film (m = w) into Eq. (2) giving

$$m = 1 - {{\left( {1 - \frac{{{{\delta }_{{{\text{AQ}}}}}}}{R}} \right)}^{2}} = 1 - {{\left( {1 - \frac{{P{\text{Ca}}_{b}^{{2/3}}}}{{1 + FP{\text{Ca}}_{b}^{{2/3}}}}} \right)}^{2}}.$$
(17)

For large capillary numbers, m adopts an asymptotic value, see discussion below.

Liu et al. [41] performed experiments in capillaries with circular and square cross-section with hydraulic diameters in the range of 0.9–3 mm using air and three different liquids in co-current upward flow. They fitted their experimental data for the ratio of bubble velocity to total superficial velocity by the correlation

$$\frac{{{{u}_{b}}}}{{{{j}_{T}}}} = \frac{1}{{1 - 0.61{\text{Ca}}_{{}}^{{0.33}}}},$$
(18)

which is valid in the range 2 × 10−4 ≤ Ca ≤ 0.39.

Abiev [22] developed a mathematical model for the bubble velocity and validated it by experimental data from literature [30, 42]. Based on calculations with this model, he proposed the following approximation for horizontal flow [43]

$$\frac{{{{u}_{b}}}}{{{{j}_{T}}}} = 1 + 1.716\left[ {1 - \exp \left( { - {{f}_{{{\text{Abiev}}}}}({\text{C}}{{{\text{a}}}_{b}})} \right)} \right],$$
(19)

where

$$\begin{gathered} {{f}_{{{\text{Abiev}}}}}({\text{C}}{{{\text{a}}}_{b}}) \\ = \exp \left[ { - 0.0204\, + \,0.4714{\kern 1pt} \ln {\text{C}}{{{\text{a}}}_{b}}\, - \,0.0211{{{(\ln {\text{C}}{{{\text{a}}}_{b}})}}^{2}}} \right]. \\ \end{gathered} $$
(20)

This relation is valid in the range 10−4 ≤ Cab ≤ 50.

The Taylor bubble velocity in slug flow is often modelled based on the drift flux approach [44, 45] which reads

$${{u}_{b}} = {{C}_{0}}{{j}_{T}} + {{u}_{d}}.$$
(21)

Here, C0 is the distribution parameter and ud is the drift velocity. The drift velocity is regarded zero in horizontal microchannels. With ub = jG/α and jT = jG/β Eq. (21) then yields the relation

$$\eta = \frac{{{{u}_{b}}}}{{{{j}_{T}}}} = \frac{\beta }{\alpha } = {{C}_{0}}.$$
(22)

In microchannels, the characteristic velocity ratio thus takes the role of the distribution parameter.

From a large number of experiments, Kurimoto et al. [21] proposed the following model for the distribution parameter

$${{C}_{0}} = 1 + \sqrt {{\text{W}}{{{\text{e}}}_{b}}\left[ {7.18 \times {{{10}}^{{ - 4}}} + 2.91 \times {\text{Re}}_{{}}^{{ - 0.875}}(1 - 0.845){\text{Re}}_{{}}^{{0.0259}}} \right]/f_{{{\text{HS}}}}^{{}}} ,$$
(23)

where fHS is defined in Eq. (11). This correlation has the disadvantage, that both, ub and jT must be known in order to evaluate Web and Re. Thus, an iterative procedure is required, which may hinder a broader practical application of this model.

A NEW CORRELATION FOR THE CHARACTERISTIC VELOCITY RATIO

The goal of this paper is to derive a simple yet accurate correlation for the characteristic velocity ratio η = ub/jT in terms of prior known non-dimensional parameters. Suo and Griffith [14] performed a dimensional analysis and obtained seven independent dimensionless groups. Here, the ratios of liquid-to-gas density and viscosity as well as the ratios of bubble and liquid slug length to tube diameter are all assumed large being without influence while gravity is negligible (cf. Section Conditions and Assumptions). The two remaining parameters from the dimensional analysis in [14] are the capillary number and the Ohnesorge number. As the latter can be expressed in terms of capillary number and Reynolds number, we base our correlation for η on Ca and Re.

Evaluation of Literature Data

To develop a new model we evaluate the information from literature collected in the previous section. For that purpose, we plot in Fig. 2 various relations for η as function of Ca. The correlation of Liu et al. [41] in Eq. (18) is an explicit relation of the form η = η (Ca) and can be plotted without further processing.

Fig. 2.
figure 2

Dependence of characteristic velocity ratio on capillary number and Reynolds number from various sources [32, 34, 38, 41, 43].

Full size image

The correlation of Abiev [22] in Eq. (19) is an implicit relation between η and Ca. Since we could not bring it in an explicit form, we evaluate it as follows. For a given set of values for Cab we compute by Eq. (19) the corresponding values of η and thereafter the corresponding values of Ca = Cab/η. This procedure yields the relation η = η(Ca) plotted in Fig. 2.

Next, we utilize correlations for the relative velocity m. By inserting relations for m into Eq. (4), one can evaluate the velocity ratio. In this way, we obtain by insertion of Eq. (17) the result

$$\begin{gathered} \eta = {{\left( {1 - \frac{{P{\text{Ca}}_{b}^{{2/3}}}}{{1 + FP{\text{Ca}}_{b}^{{2/3}}}}} \right)}^{{ - 2}}} \\ = {{\left( {1 - \frac{{P{{\eta }^{{2/3}}}{\text{Ca}}_{{}}^{{2/3}}}}{{1 + FP{{\eta }^{{2/3}}}{\text{Ca}}_{{}}^{{2/3}}}}} \right)}^{{ - 2}}}. \\ \end{gathered} $$
(24)

Eq. (24) represents again an implicit relation between η and Ca. Here we take F = FAQ = 2.5 and proceed as described above to plot it in Fig. 2. Similarly, we inserted and evaluated Eq. (14) of Bretherton [24] which is valid at low capillary numbers only. The corresponding graph overlaps with Eq. (24) and is not included in Fig. 2.

We now utilize correlations for the liquid film thickness to evaluate the characteristic velocity ratio. In gas-liquid Taylor flow, the viscosity ratio is typically very small resulting in negligible velocity in the liquid film. From Eq. (6) one obtains the relation

$$\eta = \frac{1}{{1 - w}} = \frac{{{{R}^{2}}}}{{R_{b}^{2}}} = {{\left( {1 - \frac{\delta }{R}} \right)}^{{ - 2}}}.$$
(25)

Thus, one can determine the velocity ratio from correlations for δ or Rb. Inserting the film thickness model of AQ [32] given in Eq. (10) into Eq. (25) yields Eq. (24). The film thickness models of LB [38] in Eq. (12) accounts for inertial effects by the Reynold number Re. Inserting Eq. (12) in Eq. (25) yields an explicit relation η = η(Ca, Re) which is plotted by the thin lines in Fig. 2 for various values of Re. This model has the disadvantage that the function Φ(Re = 0) in Eq. (13) is discontinuous at Re = 0. The film thickness model of Han and Shikazono [37] accounts for inertial effects by the Reynolds number Reb and the Weber number Web = CabReb. Inserting Eq. (11) in Eq. (25) yields together with Web = η2CaRe again an implicit relation of the form η = η(Ca, Re), which is however not evaluated here.

Included in Fig. 2 are numerical data from two recent numerical studies with state of the art CFD simulations (symbols). The results of BZG [34] for Re = 0 cover 20 distinct values of Ca in the range 0.0001−0.8 (taken from Fig. 16a in [34]). The numerical results of LB [38] cover 14 distinct values of Ca in the range 0.005 ≤ Ca ≤ 2 at various values of Re. In Fig. 2, only data for Re = 0, 2, 10, 20 and 100 are included while results for Re > 100 will be discussed in Fig. 3 below.

Fig. 3.
figure 3

Normalization of η data from numerical simulations [34, 38] by Eq. (36), representing the present model for vanishing Reynolds number.

Full size image

We now discuss Fig. 2 displaying the various data and relationships. All relations and data show a monotonic increase of η with Ca. With exception of the model of Liu et al. [41] in Eq. (18), all data virtually overlap for Ca < 0.02. In this range, η is close to unity indicating that the bubble moves only slightly faster than the total superficial velocity. The curve resulting from the film thickness model of AQ [32] in combination with the stagnant film assumption (SFA) is in the entire range of Ca in excellent agreement with the model of Abiev [43]. The same holds for the numerical data of LB [38] for Re = 0 and 2 in the range 0.005 ≤ Ca ≤ 1. Only the two data points at Ca = 1.5 and 2 show slightly lower values of η as compared to the model of Abiev [43]. For the larger values of Re, the numerical data of LB [38] show a continuous decrease of η with increase of Re. The viscosity ratio in the numerical simulations of LB [38] is λ = 0.01. The thin lines in Fig. 2 represent the film thickness model of LB [38] in combination with the stagnant film assumption for λ = 0. For Re ≤ 20, the lines agree very well with the numerical data, which indicates that the assumption of a stagnant liquid film is a reasonable approximation. For Re = 100, however, a slight deviation exists especially at large values of Ca.

Flows with Negligible Inertia

As a strategy for the development of our new model we first consider the limit Re = 0 and then introduce the effect of finite Re. The model development for vanishing Reynolds number relies on the principle of mass conservation, which we aim to combine with information from momentum equation.

Equation (3), which results from a global mass balance, shows that the characteristic velocity ratio ub/jT depends on the flow rate of the liquid film. Depending on the gas-to-liquid viscosity ratio λ = µG/µL, the liquid film may be stagnant (λ → 0) or be carried along by shear forces. Estimating the flow rate in the liquid film requires a momentum balance. To that end, one may approximate the uniform body of the bubble by a long concentric cylinder surrounded by an annular liquid film. Under the further assumption that the flow in both phases is fully developed and laminar, the radial profiles for the local velocity within the concentric gas core and the annular liquid film can be computed analytically [46, 47]. These velocity profiles are an important ingredient in the model of Abiev [22]. For the ratio of flow rates, it follows [14]

$$\frac{{{{Q}_{b}}}}{{{{Q}_{f}}}} = \frac{{1 - w}}{w}\left( {2 + \frac{1}{\lambda }\frac{{1 - w}}{w}} \right).$$
(26)

Inserting Eq. (26) in Eq. (3) yields after some algebraic manipulations

$$\eta = \frac{{1 - w(1 - 2\lambda )}}{{1 - (2w - {{w}^{2}})(1 - \lambda )}}.$$
(27)

In the literature, various forms of this relation exist. Eq. (27) is equivalent to Eq. (16) in [14], to Eq. (12) in [7] and to Eq. (32) in [34]. It is also equivalent to Eq. (5) in [48], with reference to earlier work in [11]. In the limit λ → 0, Eq. (27) reduces to Eq. (25).

With jT and λ given, Eq. (27) forms a system of two unknowns (ub and w) which one cannot solve analytically. By Eq. (2), w may be replaced by the bubble radius Rb or the liquid film thickness δ. Balestra et al. [34] combined Eq. (27) with a AQ-type film thickness model and solved the system for different values of the viscosity ratio λ numerically. More recently, Makuch et al. [48] performed a similar approach based on the Bretherton film thickness model in Eq. (9) extended for nonzero λ. The authors fitted the numerical results by a scaling function establishing an algebraic relationship valid for low values of Cab.

Here, we solve Eq. (27) in combination with the AQ [32] film thickness model in Eq. (10) numerically using the Matlab script provided by BZG [34] as supplemental material. Considering the viscosity ratio λ = 0 and different values of F proposed in literature, we obtained in this way graphs for the velocity ratio η = η (Ca) for the range 10−5 ≤ Ca ≤ 103. While values Ca ⪢ 1 may not represent physically stable Taylor flow as discussed below, the curves show some interesting features, which are useful for model development. With two distinct asymptotic limits Ca → 0 and Ca → ∞, the curves η (Ca) are of sigmoidal type and symmetric with respect to the inflection point. The lower asymptotic limit is η0 = η (Ca → 0) = 1 while the upper asymptotic limit η∞ = η (Ca→∞) depends on the value of F.

By virtue of Eq. (4), the existence of an upper asymptotic limit η∞ for large capillary numbers is consistent with the asymptotic value for the relative drift velocity m. The value m∞ = 0.56 reported by Taylor [23] for Cab = 2 corresponds to η∞ = 2.27. In experiments at a viscosity ratio λ = 2.5 × 10−5, Cox [49] considered capillary numbers up to Cab = 10 and reported a slightly higher asymptotic value m∞ = 0.60 corresponding to η∞ = 2.5. From boundary integral simulations for an inviscid bubble in creeping flow, Martinez and Udell [28] obtained the value m∞ = 0.59 for Cab = 10 corresponding to η∞ = 2.44. In a similar but more recent study, Lac and Sherwood [13] found an absolute maximal bubble velocity corresponding to η∞ = 2.5 when Ca becomes very large. The same value was reported by Dupont et al. [50] from volume of fluid computations.

Being valid under the assumptions of a stagnant liquid film and negligible inertia, Eq. (24) yields in the limit Ca → ∞ the relation

$$\begin{gathered} {{\eta }_{\infty }}({\text{Re}} \to 0) \\ = \mathop {\lim }\limits_{{\text{Ca}} \to \infty } {{\left( {\frac{{FP{{\eta }^{{2/3}}}{\text{Ca}}_{{}}^{{2/3}}}}{{(F - 1)P{{\eta }^{{2/3}}}{\text{Ca}}_{{}}^{{2/3}}}}} \right)}^{2}} = {{\left( {\frac{F}{{F - 1}}} \right)}^{2}}. \\ \end{gathered} $$
(28)

Values reported in literature for F range from 2.483 [34] to 2.79 [33] resulting in η∞ = 2.8 and 2.43 when inserted in Eq. (28), respectively. This and the values given above indicate a relatively large uncertainty for η∞ even when inertia is negligible.

The numerical data of LB [38] in Fig. 2 suggest that the upper asymptotic limit η∞ depends on Re. Furthermore, for any value of Re the relationship η = η (Ca) is not symmetric with respect to the inflection point. To fit an asymmetric sigmoidal curve, a five-parameter logistic (5PL) function is required [51]. Here we adopt the 5PL function provided by the data analysis software Origin (OriginLab Corporation)

$${{\eta }_{{{\text{5PL}}}}} = {{\eta }_{0}} + \frac{{{{\eta }_{\infty }} - {{\eta }_{0}}}}{{{{{\left[ {1 + {{{({\text{Ca}}/c)}}^{{ - h}}}} \right]}}^{s}}}}.$$
(29)

The reason is that fitting by Eq. (29) shows better convergence as compared to the 5PL function proposed by Gottschalk and Dunn [51] when the focus is on low values of Ca as it is the case here. Fixing the lower asymptote to η0 = η(Ca → 0) = 1, four free parameters remain where we restrict the domain to η∞ > 1, c > 0, h > 0 and s > 0.

To determine further of the four parameters, we consider the asymptotic limit of Bretherton in Eq. (15). For Cab → 0, the velocity ratio approach unity. Thus, for Cab → 0 it follows Ca → Cab so that the asymptotic limit in Eq. (15) can also be written as

$$\eta \approx 1 + 1.29{{(3{\text{Ca}})}^{{2/3}}}.$$
(30)

Our goal is to choose the parameters of the logistic function in such a way that the limit of Eq. (29) agrees with Bretherton’s limit in Eq. (30). In the limit Ca → 0 it is (Ca/c)−h ⪢ 1 so that Eq. (29) may be approximated as

$$\eta \approx 1 + ({{\eta }_{\infty }} - 1){{({\text{Ca}}/c)}^{{hs}}}.$$
(31)

Comparing Eq. (30) and Eq. (31) shows that both limits become identical when hs = 2/3 and (η∞ − 1) c–2/3 = 1.29 × 32/3. With these two conditions, there remain only two free parameters of the logistic function, namely h or s and η∞ or c. Here, we choose s and η∞ as remaining free parameters. Thus we have h = 2/(3s) while c follows from relation

$$c = \frac{1}{3}{{\left( {\frac{{{{\eta }_{\infty }} - 1}}{{1.29}}} \right)}^{{3/2}}}.$$
(32)

The logistic function from Eq. (29) then takes the form

$${{\eta }_{{2{\text{PL}}}}} = 1 + \frac{{{{\eta }_{\infty }} - 1}}{{{{{\left[ {1 + {{{\left( {\frac{{{{\eta }_{\infty }} - 1}}{{1.29}}} \right)}}^{{1/s}}}{{{\left( {3{\text{Ca}}} \right)}}^{{ - 2/(3s)}}}} \right]}}^{s}}}}.$$
(33)

For s = 1, Eq. (33) simplifies to

$${{\eta }_{{1{\text{PL}}}}} = 1 + \frac{{{{\eta }_{\infty }} - 1}}{{1 + \frac{{{{\eta }_{\infty }} - 1}}{{1.29}}{{{(3{\text{Ca}})}}^{{ - 2/3}}}}}.$$
(34)

with η∞ being the sole free parameter. The function in Eq. (34) is symmetric with respect to the inflection point. For F = FBZG =2.483, Eq. (28) yields η∞ = 2.8 so that Eq. (34) becomes

$$\eta = 1 + \frac{{1.8}}{{1 + 0.6708{\text{Ca}}_{{}}^{{ - 2/3}}}}.$$
(35)

Eq. (35) is in good agreement with the AQ-SFA curve in Fig. 2 only for Ca < 10−3.

A more accurate model for high values of Ca requires s ≠ 1 in order to account for the asymmetric behavior. To determine appropriate values for s and η∞ for the case of vanishing Reynolds number, we fit the data of LB [38] together with the data from Fig. 16a) in BZG [34] by function (33) using Origin. By regression analysis for in total 30 data points, we obtain s(Re = 0) = 0.474 and η∞(Re = 0) = 2.467. The latter value is well within the range reported in literature. Inserting both numerical values in Eq. (33) yields

$${{\eta }_{{{\text{Re}} \to 0}}} = 1 + \frac{{1.467}}{{{{{\left( {1 + 0.280{\text{Ca}}_{{}}^{{ - 1.408}}} \right)}}^{{0.474}}}}}.$$
(36)

Eq. (36) constitutes the present model for vanishing Reynolds number.

Flows with Inertia

In order to estimate the accuracy of the new model for vanishing and finite Reynolds numbers, we normalize the numerical data of BZG [34] and LB [38] by Eq. (36). Figure 3 shows the corresponding ratio as function of Ca. For Re = 0, the difference between Eq. (36) and the numerical data is less than 1% over the entire range of Ca. For Ca ≤ 0.01, the deviation is virtually zero due to the fact that the asymptotic behavior agrees with the theory of Bretherton [24].

For Re = 2, the difference between Eq. (36) and the numerical data of LB [38] is less than about 2% over the entire range of Ca. For Re ≤ 100, the deviation is less than about 2% only for Ca ≤ 0.025. For larger values of Ca, the ratio in Fig. 3 decreases with increase of Re from 0 to 100. At a value of Re ∼ 100, the ratio takes a minimum before it increases as Re increases up to 800.

Overall, Fig. 3 reveals that for the combination Ca > 0.025 and Re > 2 a refined model is required. Since for Re ≥ 200 only few numerical data points are available, we restrict the development of an improved model to the range 0 < Re ≤ 100. To that end, we follow the procedure from above and fit the numerical data of LB [38] for Re = 2, 10, 20, 40, 60 and 100 by Eq. (33) using Origin. By regression analysis, we obtain for each value of Re a combination of η∞ and s. In all cases, the coefficient of determination of the regression is larger than 0.9996. This value is close to the theoretical maximum of unity, indicating that the present model fits the data very well.

In Fig. 4 we show the values of η∞ and s for the above set of Re. In the range 20 ≤ Re ≤ 100, the upper asymptote is about constant with η∞ ∼ 2.3. The exponent s, instead, is slightly increasing over the entire range of Re. Figure 4 shows that one can well approximate the dependence of both parameters on Re by relations

$${{\eta }_{\infty }}({\text{Re}}) = 2.3 + 0.167 \times {{0.83}^{{{\text{Re}}}}}$$
(37)

and

$$s({\text{Re}}) = 0.884 - 0.41 \times {{0.968}^{{{\text{Re}}}}}.$$
(38)
Fig. 4.
figure 4

Parameters η∞ and s of the 2PL model versus Reynolds number.

Full size image

Equations (33), (37) and (38) constitute the present new model which we expect to be valid for capillary numbers up to Ca ∼ 10 and Reynolds numbers up to Re ∼ 100.

DISCUSSION

Model Accuracy in Comparison with Literature Data

We assess the accuracy of the new model by a parity plot in Fig. 5 which compares the values of η = η (Ca, Re) predicted by Eqs. (33), (37) and (38) with numerical data for η. The latter include in addition to the data from BZG [34] and LB [38] already used for model development the numerical data of Kurimoto et al. [39]. Figure 5 shows that for Re ≤ 200, the deviation between numerical data and model is within ±2% over the entire range of Ca. For Re = 200 and 400, the deviation is larger but still within ±5%.

Fig. 5.
figure 5

Parity plot comparing the present model with results from numerical simulations of Taylor flow [34, 38, 39].

Full size image

For further evaluation of the predictive capabilities of the new model, we show in Fig. 6 a second parity plot now comparing the model with the measurements listed in Table A1 of Kurimoto et al. [21]. The authors performed experiments in circular microchannels with four different diameters (D = 200, 320, 500, and 700 µm). They used three different liquids, namely water and two types of glycerol-water solutions with 64 and 52 wt % glycerol, respectively. The experiments encompass the ranges 0.005 ≤ Cab ≤ 0.235 and 6 ≤ Re ≤ 941 while η is in the range 1.1 − 1.6. Concerning measurements accuracy, the author give a relative error for the measured gas slug volume, which was estimated as less than ±3.0%.

Fig. 6.
figure 6

Parity plot comparing the present model with the experiments of Kurimoto et al. [21]. In the experiments with glycerol-water (GW) solutions, Re is in the range 6−34.3 (64 wt % glycerol) and 19.5−84.3 (52 wt % glycerol). For water, Re is in the range 139−941.

Full size image

The deviation between the present model and the experimental data in Fig. 6 is within ±10% for the diameter D = 200 µm. For the larger diameters D = 320 and 500 µm, the deviation is mostly in the range between 0 and −10%, meaning that the present model consistently underestimates the measurements. For the largest diameter D = 700 µm, the deviation is mostly in the range from −5 to −18%. Interestingly, the experiments with 52 wt % glycerol-water solution in the 200 µm channel is the only case were the present model consistently overestimates the measurements of Kurimoto et al. [21].

Limitations of Proposed Correlation

The comparison with experimental results in the previous subsection shows that the proposed model for the characteristic velocity ratio of Taylor flow may be considered sufficiently accurate with an error of ±10% for microchannels with diameter 500 µm and below and Reynolds number up to Re ∼ 400. For larger channel diameters and higher Reynolds numbers, the agreement is less good and refinement of the model is advisable.

The improvement of the model for high Reynolds number is hindered by the lack of reliable numerical and experimental data at large capillary numbers. Experimentally, it is quite hard to reach high Ca in capillaries (either by high velocities or by high viscosities) because it results in very high pressure-drops. While the utility of extending the model to large Ca may thus be limited for practical applications, it is nevertheless of academic interest.

The numerical simulations of LB [38] in Fig. 2 show that the value of η∞ depends on Re. For Re ≤ 100 the upper asymptote decreases with increase of Re. For Re ≥ 200, there are not sufficient data available at large Ca to allow for a reliable regression analysis with respect to the upper asymptote, as the maximum values of Ca in the simulations of LB [38] decrease with increase of Re, cf Fig. 2. In fact, the upper asymptotic behavior of η at large Re seems to be largely unknown and a quantitative relationship η∞(Re) is missing in literature.

This lack of information is related to the stability of Taylor bubbles. Goldsmith and Mason [11] found that the trailing end develops re-entrant cavities of the continuous liquid phase for high bubble speeds. For low Reynolds number, the corresponding re-entrant jet may cause bubble breakup at Ca ∼ 4−7 as experimentally observed by Olbricht and Kung [12] and confirmed by inertia-less numerical simulations by Lac and Sherwood [13], see also [50]. As the Reynolds number increases, the bubble might lose its axial symmetry at the rear. Water/nitrogen experiments in a 2 mm capillary by Asadolahi et al. [52] show that three-dimensional shape oscillations occur for Reynolds numbers above Re ∼ 951 even for capillary numbers as low as Ca ∼ 0.007.

Predicting Taylor Flow Hydrodynamics

Among the quantities that are related to the characteristic velocity ratio η are the mean liquid velocity, the relative velocity, the gas hold-up, the cross-sectional area of the partial bypass flow and recirculation flow regions, the non-dimensional recirculation time in the liquid slug, the thickness of the liquid film and the bubble diameter. Table 1 summarizes the mathematical relations of these and further quantities with the characteristic velocity ratio. When the pipe radius, the gas and liquid flow rates and the physical properties of the phases are known, then jT, β, Ca and Re are known as well. The correlation η = η(Ca, Re) given by Eqs. (33), (37) and (38) developed in this paper then links all priori unknown parameters in Tab. 1 with prior known parameters. Thus, the new model allows predicting a comprehensive set of hydrodynamic parameters characterizing gas-liquid Taylor flow in circular microchannels by one single relation.

Table 1. Relations between priori unknown hydrodynamic parameters of Taylor flow and the characteristic velocity ratio
Full size table

By means of the identities Cab = η Ca, Reb = η Re and Web = η2CaRe, the proposed correlation can also be used to estimate the liquid film thickness or the pressure drop from correlations relying on Cab, Reb and Web, cf. the section with literature relations. Furthermore, it is of benefit for modeling mass transfer in Taylor flow [53], as it allows estimating the streamline pattern in the liquid slug including the size of the recirculation area and the non-dimensional recirculation time, given in Eqs. (7) and (8), from prior known parameters.

The two-parameter logistic function in Eq. (33) with its asymptotic behavior at low capillary numbers agreeing with the theory of Bretherton [24], may also serve as basis for the development of correlations for a broader range of Taylor flow. While the present study is limited to gas-liquid flows, where the viscosity ratio λ approaches zero, the underlying approach could be applied to liquid-liquid flow as well. In literature, there exist already several numerical studies on liquid-liquid Taylor flows, which may serve as starting basis [34, 54–57]. Further potential extensions may concern larger/non-circular channels with upward/downward Taylor flow [18, 58]. In such cases, gravity/buoyancy forces are no longer negligible so that their influence on the characteristic velocity ratio should be taken into account by the Eötvös or Bond number.

CONCLUSIONS

Many hydrodynamic parameters of Taylor flow closely relate to the ratio between bubble velocity (ub) and total superficial velocity (jT). Correlations for this characteristic velocity ratio (η = ub/jT), which are valid in the entire range of capillary numbers, have been lacking so far. Using available theoretical, experimental and numerical results on gas-liquid Taylor flow in circular microchannels from literature, a correlation for η is proposed in terms of the capillary number (Ca) and Reynolds number (Re) both using jT as velocity scale.

As basis for the correlation a five parameter logistic function is selected which accounts for the lower and upper asymptotes of η for small and large values of Ca while allowing for asymmetry. At low Ca, the correlation adopts the theoretical asymptotic limit of Bretherton resulting in excellent agreement with literature data. By this asymptotic behavior, the number of free parameters is reduced to two. One parameter is the value of the upper asymptote while the other one accounts for the asymmetry of the logistic curve. Both remaining free parameters are obtained by regression analysis using numerical simulation data for η from literature. The new correlation is given by Eqs. (33), (37) and (38). The deviation between the correlation and numerical data for Re up to 800 is within ±5% over the entire range of Ca. In comparison with experimental data, the agreement is less good but still within ±18%.

For large values of Ca and Re, a further improvement of the new model is desirable. In literature there is, however, a relative large uncertainty concerning the upper asymptote of the characteristic velocity ratio for finite Reynolds number. Here, numerical studies where Ca and Re can be varied independently may be particularly useful to determine not only the upper asymptote but also the upper value of Ca where the Taylor bubble shape is stable for certain finite values of Re.

Since the proposed correlation relies on prior knowledge of physical properties and gas/liquid flow rates only, it should be particularly useful to predict hydrodynamic attributes of Taylor flow such as bubble velocity, mean liquid velocity, gas holdup, uniform liquid film thickness, bubble diameter, and streamline patterns in the liquid slug. Furthermore, the present model can be used in combination with models for liquid film thickness or pressure drop formulated in terms of non-dimensional groups being based on the bubble velocity instead of total superficial velocity. Finally, the developed two-parameter logistic function may also serve as prototype for similar correlations valid for non-circular capillary channels and liquid-liquid Taylor flow.

NOTATION

A

area, m2

α

void fraction (holdup)

Bo

Bond number

β

gas volumetric flow ratio (dynamic holdup)

c

parameter in 5PL function

Ca

capillary number based on total superficial velocity, Ca = jT µL/σ

Cab

capillary number based on bubble velocity, Cab = ubµL/σ

D

inner diameter of circular pipe, m

δ

uniform liquid film thickness, m

Eo

Eötvös number

F

constant parameter in Eq. (10)

g

gravitational acceleration, m s−2

h

parameter in 5PL function

j T

total superficial velocity, m s−1

λ

gas-to-liquid viscosity ratio

m

relative drift velocity

µ

dynamic viscosity, Pa s

η

characteristic velocity ratio, η = ub/jT

P

constant in Bretherton model, P = 1.3375

Q

volumetric flow rate, m3 s−1

R

pipe radius, m

R b

uniform bubble radius, m

Re

Reynolds number based on total superficial velocity, Re = ρLjTD/µL

Reb

Reynolds number based on bubble velocity, Reb = ρLubD/µL

s

parameter in 5PL function

ρ

density, kg m−3

S

slip ratio

σ

coefficient of surface tension, N m−1

τ

dimensionless recirculation time

u b

bubble velocity, m s−1

u d

drift velocity, m s−1

u L

mean liquid velocity, m s−1

w

wetting fraction

We

Weber number

SUBSCRIPTS

b

bubble

f

film

G

gas

L

liquid

s

slug

T

total

0

asymptotic value at zero capillary number

∞

asymptotic value at large capillary number

ABBREVIATIONS

5PL

five-parameter logistic (function)

CBF

complete bypass flow

ds

dividing streamline

SFA

stagnant film assumption