1 Introduction

With review of studies presented in the past two decades about cylindrical type of nano-structures composed of carbon atoms called carbon nanotubes (CNTs) that were discovered by Iijima (1991), strange and effective application of using CNTs can be seen in engineering and medicine nano-/microstructures such as energy conversion devices and biosensors (Baughman et al. 2002; Katz and Willner 2004), electronics (Arnold et al. 2006) and versatile drug delivery systems (Foldvari and Bagonluri 2008). Because of the different excellent properties of CNTs such as mechanical, thermal, fluid-transport and high elasticity and flexibility geometry, CNTs can also be used as fluid-conveying pipes in nanoscale.

Up to now, many studies have been carried out to investigate the mechanical properties of CNTs under buckling, bending and vibration. Firstly, by expanding molecular dynamics simulations of the fluid flow inside CNTs, the interaction between carbon nanotube and fluid is shown by Tuzun et al. (1996). Then, using an elastic Euler–Bernoulli beam model developed by Païdoussis and Li (1993) and Païdoussis (1998) to analysis of dynamics and stability of flexible pipes including flowing fluid, Yoon et al. (2005) investigated the effect of internal moving fluid on structural instability and vibration of CNTs for two boundary conditions (simply supported and clamped at both ends). They applied Galerkin method to demonstrate the dependence of vibration behavior of CNTs on the flow velocity and indicated that buckling phenomenon occurs when the velocity of flow reaches the critical value and frequency of CNTs becomes zero. In another work, based on the classic elasticity mechanics theory, Yoon et al. (2006) studied free vibration and flow-induced flutter instability phenomenon of cantilevered CNTs conveying fluid. They demonstrated when CNTs are embedded in stiff elastic medium the influence of velocity of internal fluid on structural instability of cantilevered CNTs significantly decreases. Based on the classic continuum theory, differential quadrature method (DQM) was used to discretize the equation of motion of carbon nanotubes conveying fluid by Wang and Ni (2008). Static and dynamic study of liquids inside CNTs was performed by Mattia and Gogotsi (2008). By taking into account the geometric nonlinearity and nonlinearity of van der Waals force, Chang (2013) developed a size-dependent model for thermomechanical vibration of double-walled carbon nanotubes. Based on the classical Euler–Bernoulli beam theory for modeling the nanotubes as a continuous structure, Khosravian and Rafii-Tabar (2007) put forwarded a model to viscous fluid flow in carbon nanotubes to investigate the fluid flow effects on the system stability. They showed that the nanotube-containing viscous flow is more stable than that with nonviscous flow. Also, the vibrational behavior of a viscous nano-flow-conveying carbon nanotube was investigated by Sadeghi-Goughari and Hosseini (2015). In their work, nonuniformity of the flow velocity distribution caused by the viscosity of fluid and the small-size effects on the flow field was considered. Ansari et al. (2016a), in the context of the von Karman hypothesis and Timoshenko beam theory, examined the effect of surface stress and internal moving fluid on the nonlinear free vibration and instability of embedded nanoscale pipes.

It is well known that the assumption of classical Euler–Bernoulli beam theory may be justified for macroscale beam structures. In other words, this assumption is less valid for nanoscale beam structures. In fact, ignoring the small-size effects in a nanoscale problem might generate erroneous results. In order to capture size effect relating to atoms and molecules that make up the materials of structures, higher-order continuum theories such as nonlocal elasticity theory were introduced by Eringen (1983), modified couple stress theory presented by Yang et al. (2002) and modified strain gradient theory developed by Lam et al. (2003). The significant effect of the Eringen’s nonlocal parameter on the elastic behavior of nano-structures has been demonstrably confirmed in the work of Ansari et al. (2015a); Ansari and Gholami (2016); Ansari et al. (2016c). In another work by Ansari et al. (2016b), nonlinear vibration response of fractional viscoelastic nano-beams has been investigated based on the nonlocal elasticity theory. Also, Ansari et al. (2015d) analyzed the dynamic stability of multi-walled carbon nanotubes resting on elastic foundation and subjected to the thermal environment effects. The effects of nano-size of both fluid flow and nanotube on vibration of a CNT conveying nano-flow embedded in biological soft tissue were considered by Hosseini et al. (2014). Wang (2010) showed that the natural frequencies and critical speeds of simply supported nanotube were significantly dependent on the nonlocal elasticity and the surface effects. Rafiei et al. (2012) investigated vibration analysis of fluid-conveying nonuniform carbon nanotubes resting on a viscoelastic medium. Fluid-induced flutter instability of cantilevered multi-walled CNT conveying fluid base on the classical Timoshenko and Euler beam theories was performed by Yun et al. (2012). They illustrated the effects of the radius ratio, transverse shear and van der Waals (vdW) forces on natural frequencies and flutter instability of the system. The influences of nonlocal effect, slip condition and structural damping coefficient on the dimensionless eigenvalues and flutter boundaries of the cantilever CNT conveying fluid were investigated by Bahaadini and Hosseini (2016). In microscale pipes, Xia and Wang (2010) analyzed the vibration and instability of fluid-conveying microscale pipes based on the nonclassical Timoshenko beam theory. Also, Ansari et al. (2014) studied nonlinear vibration response and instability behavior of fluid-conveying single-walled boron nitride nanotubes under thermal environment employing the theory of modified strain gradient elasticity. The size-dependent stability analysis of cantilever micro-pipes containing following flow investigated based on the modified strain gradient theory by Hosseini and Bahaadini (2016). In their work, the effects of the length scale parameter, outside diameter and aspect ratio on the natural frequencies and the flutter critical speeds were examined. Ansari et al. (2015b) used modified couple stress theory in conjunction with the classical first-order shear deformation shell model to investigate the vibration and instability characteristics of functionally graded micro-shells conveying fluid. The effect of material length scale parameter, nonuniform profile of the flow velocities and nonlinear electrostatical force on vibration and instability characteristics of the microbeam was also investigated by Dai et al. (2014).

Magnetically sensitive CNTs in external magnetic field have a wide applicability in the fields of NEMS, MEMS, spintronics and nano-composite (see, e.g., Murmu et al. 2012; Narendar et al. 2012; Wang et al. 2010). Therefore, it is vital to find the effect of the magnetic field on transverse vibration and stability of the magnetically sensitive CNTs. According to nonlocal beam theory, Narendar et al. (2012) studied the influence of longitudinal magnetic field on the ultrasonic wave dispersion properties of single-walled carbon nanotubes surrounded by the elastic Pasternak substrate. It was shown that with the increase in longitudinal magnetic field, the velocity of flexural wave in CNTs increases. Murmu et al. (2012) studied the effect of a longitudinal magnetic field on the transverse vibrations of double-walled CNTs and reported that with increasing magnetic field parameters, the natural frequency increases. Additionally, longitudinal magnetic field was found to be led to less nonlocal effects on double-walled nanotubes. Wang et al. (2010) evaluated wave propagation manner of elastic matrix embedded fluid-conveying CNTs under longitudinal magnetic field. They also studied the wave propagation velocity in CNTs along with longitudinal magnetic field exerted on the CNTs in some frequency regions. Ghorbanpour Arani et al. (2014) analyzed vibrations of double-bonded carbon nanotube conveying flow under longitudinal uniform magnetic field considering surface effect and visco-Pasternak foundation based on Euler–Bernoulli beam theory. They reported the effect of the longitudinal uniform magnetic field, Knudsen number, surface effect, visco-Pasternak foundation on the real and imaginary components of frequency and critical flow speed. By using Timoshenko and the third-order shear deformation beam theories, Ansari et al. (2015c, e) studied the nonlinear forced vibration of magneto-electro-thermo-elastic nano-beams. Amiri et al. (2016) studied the vibration and instability of micro-tube conveying fluid according to the magneto-electro-elasticity beam model. The free vibration analysis of CNTs conveying fluid under magnetic field was also addressed by Hosseini and Sadeghi-Goughari (2016).

The study of the elastic foundation effect on vibration and stability of CNTs conveying fluid is one of the main topics arousing a lot of interest. Chellapilla and Simha (2007) studied the flow critical speed of pipe containing fluid on Pasternak foundation for three simple boundary conditions. In their work, the influence of Pasternak foundation on the flow critical speed of pipe conveying fluid was shown. Pradhan and Murmu (2009) used both Winkler and Pasternak substrate models for vibration analysis of CNT. Additionally, they applied Eringen nonlocal elasticity and Timoshenko beam theory for the modeling of the continuous CNT. They showed the influence of the nonlocal parameters and Winkler and Pasternak modulus on the frequency of the system. Vibration and structural instability of fluid-conveying carbon nanotubes embedded in viscoelastic Winkler foundation regardless of the effect of nonlocal parameters are studied by Ghavanloo et al. (2010). They investigated damping and elastic properties of the foundation and fluid speed on the resonant frequencies. Soltani et al. (2010) studied nonlocal Euler–Bernoulli beam theory to predict transverse vibrations and buckling instability of single-walled carbon nanotubes containing viscous flow surrounded by visco-elastic medium and supported on both ends. They showed that the vibrational frequency and critical flow speed were dependent on the surrounding medium properties and boundary conditions.

The vibrational behavior of a cantilever CNT containing following flow is very different from CNTs under other boundary conditions, because former is a nonconservative system and its stability is lost by flutter. However, in comparison with the nonlocal cantilever CNT, a significant number of investigations have been conducted on the macroscale cantilever pipe conveying fluid. Benjamin (1961) was the first who derived the equation of motion using the Lagrangian equations to analyze dynamic behavior of cantilever pipe conveying fluid. Flutter of cantilevered pipes containing fluid flow was analyzed theoretically and experimentally by Gregory and Paidoussis (1966). Païdoussis and Issid (1974) addressed the dynamics and instability of pipe conveying fluid for both of steady and pulsatile flows. Hosseini and Fazelzadeh (2011) analyzed the stability of functionally graded cantilever pipe carrying fluid under axial end force and thermal field. Yu et al. (2013) studied the stability of the periodic cantilever pipe carrying fluid. Firouz-Abadi et al. (2013) analyzed the flutter instability of cantilevered pipe conveying fluid with an inclined terminal nozzle.

The foregoing literature survey shows that no case has been reported for the CNT conveying fluid based on the nonlocal elasticity theory and incorporating the effects of nonlocal parameter, longitudinal magnetic field and various boundary conditions on flutter and divergence instability. Therefore, the present study deals with the flutter and divergence instability of CNTs containing fluid lying on elastic substrate medium subjected to a magnetic field. The Eringen’s nonlocal constitutive relations are used to develop the equation of motion and boundary conditions via extended Hamilton’s principle. Then, application of the extended Galerkin’s method is used to transform the resulting equations into a general eigenvalue problem. Finally, having solved the resulting nonlocal magneto-structural-fluid eigenvalue system of equations, the effects of nonlocal parameter, longitudinal magnetic field, elastic substrate medium and boundary conditions on the instability region are investigated.

2 Mathematical modeling

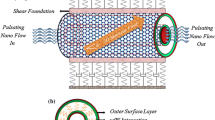
Consider a CNT model conveying fluid which is shown in Fig. 1. It is proposed to use the nonlocal beam model to analyze the dynamic behavior of the CNT conveying fluid with velocity \( U \). The CNT has geometric characteristic of length \( L \), outside diameter \( D \), the nanotube cross-sectional area \( A \), with bending rigid body of \( {\text{EI}} \). Its mass per unit length of the CNT and mass per unit length of fluid are \( m_{\text{c}} \) and \( m_{\text{f}} \), respectively. It is assumed that gravity effects and the externally imposed tension and pressure are disregarded in CNT.

Fig. 1
figure 1

Geometry of fluid-conveying CNT resting on elastic foundations subjected to an externally applied magnetic field

Full size image

According to Païdoussis (1998), Ryu et al. (2002), equations of motion and boundary conditions can be driven from extended Hamilton principle as shown in the following

$$ \delta \int_{{t_{1} }}^{{t_{2} }} {\left( {T_{\text{CNT}} + T_{\text{f}} - E_{\text{e}} + W_{\text{mf}} + W_{\text{b}} } \right){\text{d}}t - \int_{{t_{1} }}^{{t_{2} }} {m_{\text{f}} U\left( {\frac{{\partial w_{L} }}{\partial t} + U\frac{{\partial w_{L} }}{\partial x}} \right)\delta w_{L} } } = 0 $$
(1)

In which \( T_{\text{CNT}} \), \( T_{\text{f}} \) and \( E_{\text{e}} \) denote kinetic energy of CNTs, kinetic energy of fluid and potential energies, respectively. Also, \( W_{\text{mf}} \) and \( W_{\text{b}} \) represent the work done by the longitudinal magnetic field and elastic foundation, respectively. Moreover, \( ( \cdot )_{L} \) denotes the values of the corresponding quantities \( ( \cdot ) \) at \( x = L \). In addition, in the above equation, \( w_{L} \ne 0 \) for a cantilevered CNT and \( w_{L} = 0 \) for a fully supported CNT conveying fluid.

The first vibrational of kinetic energy of CNT and fluid is demonstrated in the following:

$$ \delta T_{\text{CNT}} = m_{\text{c}} \int_{0}^{L} {\frac{\partial w}{\partial t}\frac{\partial \delta w}{\partial t}{\text{d}}x} $$
(2)
$$ \delta T_{\text{f}} = m_{\text{f}} \int_{0}^{L} {\left[ {\frac{\partial w}{\partial t}\frac{\partial \delta w}{\partial t} + U\frac{\partial w}{\partial t}\frac{\partial \delta w}{\partial x} + U\frac{\partial w}{\partial x}\frac{\partial \delta w}{\partial t} + U^{2} \frac{\partial w}{\partial x}\frac{\partial \delta w}{\partial x}} \right]} {\text{d}}x $$
(3)

Also, the variation of strain energy is obtained by

$$ \delta E_{\text{e}} = \int_{0}^{L} {\int_{A} {\sigma_{xx} \delta \varepsilon_{xx} {\text{d}}A{\text{d}}x} } $$
(4)

where \( \sigma_{xx} \) and \( \varepsilon_{xx} \) represent nonlocal axial stress and strain in \( x \) direction, respectively. For a nanotube, nonlocal constitutive relation of linear elasticity in the one-dimensional case for homogeneous and isotropic material is expressed as (Eringen 1983):

$$ \sigma_{xx} - \left( {e_{0} a} \right)^{2} \frac{{\partial^{2} \sigma_{xx} }}{{\partial x^{2} }} = E\varepsilon_{xx} $$
(5)

where \( e_{0} \) is a material constant, \( a \) is an internal characteristic length and \( E \) is the Young’s modulus.

In addition, Lorentz magnetic force due to the presence of an externally applied longitudinal magnetic field can be obtained according to Maxwell equations. Murmu et al. (2012) define the variation of work of longitude magnetic field in \( z \) direction as

$$ \delta W_{\text{mf}} = \mathop \int \limits_{0}^{L} \delta w{\text{d}}x $$
(6)

where \( H_{x} \) and \( \eta_{\text{m}} = 4\pi \times 10^{ - 7} \) are magnetic field strength and magnetic field permeability, respectively.

It is well known that the components of the variational work of Winkler and Pasternak foundations model are written as:

$$ \delta W_{\text{b}} = \int_{0}^{L} { - K_{\text{w}} w\delta w{\text{d}}x} - \int_{0}^{L} {K_{\text{G}} \frac{\partial w}{\partial x}\delta \left( {\frac{\partial w}{\partial x}} \right){\text{d}}x} $$
(7)

where \( K_{\text{w}} \) is Winker’s substrate elasticity modulus and \( K_{\text{G}} \) is Pasternak substrate shear modulus.

Substituting Eqs. (2–4), (6) and (7) into Eq. (1), performing integration by parts and noticing that for every admissible variation (\( \delta w \)) the coefficient of this variation must be zero, one may find the governing equation of motion as

$$ 2m_{\text{f}} U\frac{{\partial^{2} w}}{\partial x\partial t} + m_{\text{f}} U^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }} - \eta_{\text{m}} AH_{x}^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }} - K_{\text{G}} \frac{{\partial^{2} w}}{{\partial x^{2} }} + K_{\text{w}} w + \left( {m_{\text{c}} + m_{\text{f}} } \right)\frac{{\partial^{2} w}}{{\partial t^{2} }} - \frac{{\partial^{2} M}}{{\partial x^{2} }} = 0 $$
(8)

Here, M is nonlocal bending moment about z-axis and can be obtained by the same method in (Kazemi-Lari et al. 2012) as:

$$ M = \int_{A} {\sigma_{xx} {\text{d}}A} = - {\text{EI}}\frac{{\partial^{2} w}}{{\partial x^{2} }} + \left( {e_{0} a} \right)^{2} \left[ {2m_{\text{f}} U\frac{{\partial^{2} w}}{\partial x\partial t} + m_{\text{f}} U^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }} - \eta_{\text{m}} AH_{x}^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }} - K_{\text{G}} \frac{{\partial^{2} w}}{{\partial x^{2} }} + K_{\text{w}} w + \left( {m_{\text{f}} + m_{\text{c}} } \right)\left. {\frac{{\partial^{2} w}}{{\partial t^{2} }}} \right]} \right. $$
(9)

The boundary conditions for nanotubes can be expressed as follows:

  1. (a)

    fully supported CNT

$$ \begin{aligned} & {\text{For}}\;{\text{P{-}P}}\;{\text{condition}} \\ & {\text{at}}\;x = 0,L\quad w = 0,\quad M = 0. \\ \end{aligned} $$
(10a)
$$ \begin{aligned} & {\text{For}}\;{\text{C{-}P}}\;{\text{condition}} \\ & {\text{at}}\;x = 0\quad w = 0,\quad \frac{\partial w}{\partial x} = 0, \\ & {\text{at}}\;x = L\quad w = 0,\quad M = 0. \\ \end{aligned} $$
(10b)
$$ \begin{aligned} & {\text{For}}\;{\text{C{-}C}}\;{\text{condition}} \\ & {\text{at}}\;x = 0,L\quad w = \frac{\partial w}{\partial x} = 0. \\ \end{aligned} $$
(10c)
  1. (b)

    cantilevered CNT

$$ {\text{at}}\;x = 0\quad w = 0,\quad \frac{\partial w}{\partial x} = 0, $$
$$ {\text{at}}\;x = L\quad M = 0,\quad \frac{\partial M}{\partial x} + K_{\text{G}} \frac{\partial w}{\partial x} = 0. $$
(11)

For convenience, the following dimensionless quantities are defined:

$$ \begin{aligned} & W = \frac{w}{L}\quad X = \frac{x}{L}\quad u = \left( {\frac{{m_{\text{f}} }}{\text{EI}}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} {\text{UL}}\quad \beta = \frac{{m_{\text{f}} }}{{m_{\text{f}} + m_{\text{c}} }} \\ & \psi = \eta_{\text{m}} AH_{x}^{2} \frac{{L^{2} }}{EI}\quad T = \frac{t}{{L^{2} }}\left( {\frac{\text{EI}}{{m_{\text{c}} + m_{\text{f}} }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} \quad k_{\text{w}} = \frac{{K_{\text{w}} L^{4} }}{EI}\quad k_{\text{G}} = \frac{{K_{\text{G}} L^{2} }}{EI} \\ \end{aligned} $$
(12)

By substituting Eq. (9) into Eq. (8) with regard to Eq. (12), the dimensionless equation of motion of the CNT is obtained as:

$$ \begin{aligned} & \frac{{\partial^{4} W}}{{\partial X^{4} }} + 2\beta^{1/2} u\frac{{\partial^{2} W}}{\partial X\partial T} + \left( {u^{2} - \psi - k_{\text{G}} } \right)\frac{{\partial^{2} W}}{{\partial X^{2} }} + k_{\text{w}} W + \frac{{\partial^{2} W}}{{\partial T^{2} }} \\ & \quad - \mu^{2} \left[ {2\beta^{1/2} u\frac{{\partial^{4} W}}{{\partial X^{3} \partial T}} + \left( {u^{2} - \psi - k_{\text{G}} } \right)\frac{{\partial^{4} W}}{{\partial X^{4} }}} \right. + k_{\text{w}} \frac{{\partial^{2} W}}{{\partial X^{2} }} + \left. {\frac{{\partial^{4} W}}{{\partial X^{2} \partial T^{2} }}} \right] = 0 \\ \end{aligned} $$
(13)

Consequently, the dimensionless boundary conditions are obtained as:

  1. (a)

    fully supported CNT

$$ \begin{aligned} & {\text{For}}\;{\text{P{-}P}}\;{\text{condition}} \\ & {\text{at}}\;X = 0,1\quad W = 0,\quad - \frac{{\partial^{2} W}}{{\partial X^{2} }} + \mu^{2} \left[ {2\beta^{1/2} u\frac{{\partial^{2} W}}{\partial X\partial T}} \right. + \left( {u^{2} - \psi - k_{\text{G}} } \right)\frac{{\partial^{2} W}}{{\partial X^{2} }} + k_{\text{w}} W + \left. {\frac{{\partial^{2} W}}{{\partial T^{2} }}} \right] = 0. \\ \end{aligned} $$
(14a)
$$ \begin{aligned} & {\text{For}}\;{\text{C{-}P}}\;{\text{condition}} \\ & {\text{at}}\;X = 0\quad W = 0,\quad \frac{\partial W}{\partial X} = 0, \\ & {\text{at}}\;X = 1\quad W = 0,\quad - \frac{{\partial^{2} W}}{{\partial X^{2} }} + \mu^{2} \left[ {2\beta^{1/2} u\frac{{\partial^{2} W}}{\partial X\partial T}} \right. + \left( {u^{2} - \psi - k_{\text{G}} } \right)\frac{{\partial^{2} W}}{{\partial X^{2} }} + k_{\text{w}} W + \left. {\frac{{\partial^{2} W}}{{\partial T^{2} }}} \right] = 0. \\ \end{aligned} $$
(14b)
$$ \begin{aligned} & {\text{For}}\;{\text{C{-}C}}\;{\text{condition}} \\ & {\text{at}}\;X = 0,1\quad W = 0,\quad \frac{\partial W}{\partial X} = 0. \\ \end{aligned} $$
(14c)
  1. (b)

    cantilevered CNT

$$ \begin{aligned} & {\text{at}}\;X = 0\quad W = 0,\quad \frac{\partial W}{\partial X} = 0, \\ & {\text{at}}\; \, X = 1\quad - \frac{{\partial^{2} W}}{{\partial X^{2} }} + \mu^{2} \left[ {2\beta^{1/2} u\frac{{\partial^{2} W}}{\partial X\partial T}} \right. + \left( {u^{2} - \psi - k_{\text{G}} } \right)\frac{{\partial^{2} W}}{{\partial X^{2} }} + k_{\text{w}} W + \left. {\frac{{\partial^{2} W}}{{\partial T^{2} }}} \right] = 0, \\ & \quad - \frac{{\partial^{3} W}}{{\partial X^{3} }} + k_{\text{G}} \frac{\partial W}{\partial X} + \mu^{2} \left[ {2\beta^{1/2} u\frac{{\partial^{3} W}}{{\partial x^{2} \partial t}}} \right. + \left( {u^{2} - \psi - k_{\text{G}} } \right)\frac{{\partial^{3} W}}{{\partial X^{3} }} + k_{\text{w}} \frac{\partial W}{\partial X} + \left. {\frac{{\partial^{3} W}}{{\partial X^{2} \partial T}}} \right] = 0. \\ \end{aligned} $$
(15)

It can be seen that when \( \mu = 0 \), above equation is reduced to equation of motion for classic Euler–Bernoulli beam carrying fluid flow.

3 Solution by extended Galerkin method

In this section, the extended Galerkin method is used to solve the governing equation. In this technique, we must choice weighting functions that are only essential to satisfy boundary conditions. The normalized transverse displacement \( W \) is approximated as:

$$ W\left( {X,T} \right) = \sum\limits_{r = 1}^{n} {q_{r} \left( T \right)\varphi_{r} \left( X \right)} $$
(16)

where \( q_{r} \left( T \right) \) and \( n \) are the generalized coordinates and the number of modes, respectively. Also, \( \varphi_{r} \left( X \right) \) represents free vibration natural modes of bending, which are expressed as (Reddy 1986):

$$ \varphi_{r} \left( X \right) = C_{1} \sin \sigma_{r} X + C_{2} \cos \sigma_{r} X + C_{3} \sinh \sigma_{r} X + C_{4} { \cosh }\sigma_{r} X $$
(17)

where \( \sigma_{r} \) represent \( r \) th dimensionless eigenvalue of the \( r \) th flexural mode \( \varphi_{r} (X) \) and \( C_{1} ,C_{2} ,C_{3} ,C_{4} \) are constant coefficients that obtained from the boundary conditions. By substituting the displacement field in the governing equation and using extended Galerkin method, the discretized form of the governing equation of motion for the CNT conveying fluid can be obtained as:

$$ [{\mathbf{M}}]\{ {\mathbf{\textit{\"{q}}}}(T)\} + [{\mathbf{C}}]\{ {\dot{\mathbf{q}}}(T)\} + [{\mathbf{K}}]\{ {\mathbf{q}}(T)\} = 0 $$
(18)

where {\( q(T) \)} is the vector of generalized coordinates and the dot notation refers to derivative with respect to time. \( \left[ {\mathbf{M}} \right] \), \( \left[ {\mathbf{C}} \right] \) and \( \left[ {\mathbf{K}} \right] \) correspond to the mass, damping and stiffness matrices of CNT conveying fluid, respectively, with the following elements:

$$ \begin{aligned} & M\left( {r,s} \right) = \int_{0}^{1} {\left[ {\varphi_{\text{r}} (X)\varphi_{\text{s}} (X) - \mu^{2} \varphi_{\text{r}}^{{\prime \prime }} (X)\varphi_{\text{s}} (X)} \right]} {\text{d}}X \\ & C\left( {r,s} \right) = \int_{0}^{1} {2\sqrt \beta u} \left[ {\varphi_{\text{r}}^{{\prime }} (X)\varphi_{\text{s}} (X) - \mu^{2} \varphi_{\text{r}}^{{{\prime \prime \prime }}} (X)\varphi_{\text{s}} (X)} \right]{\text{d}}X \\ & K\left( {r,s} \right) = \int_{0}^{1} {\varphi_{\text{r}}^{{\prime \prime }} (X)\varphi_{\text{r}}^{{\prime \prime }} (X){\text{d}}X + (u^{2} - \psi - k_{\text{G}} )(1 - \mu^{2} )\int_{0}^{1} {\left[ {\varphi_{\text{r}}^{{\prime \prime }} (X)\varphi_{\text{s}} (X) + \varphi_{\text{r}}^{(4)} (X)\varphi_{\text{s}} (X)} \right]{\text{d}}X} + k_{\text{w}} (1 - \mu^{2} )\int_{0}^{1} {\left[ {\varphi_{\text{r}} (X)\varphi_{\text{s}} (X) + \varphi_{\text{r}}^{{\prime \prime }} (X)\varphi_{\text{s}} (X)} \right]} {\text{d}}X} \\ \end{aligned} $$
(19)

The eigenfrequencies for this system are found by rewriting Eq. (16) in first-order form and solving the associate eigenvalue problem numerically. The stability and instability zones and type of instability can be examined based on the sign and magnitude of the real (\( \lambda \)) and imaginary (\( \varOmega \)) parts of the eigenvalues (Bahaadini and Hosseini 2016).

4 Numerical Results and Discussion

It is known that fluid-conveying cantilevers are nonconservative in nature, and no divergence can occur. Instead, they lose stability by flutter. However, for other boundary condition, CNT may experience both divergence and flutter instability when its fluid speed exceeds certain critical values. In this section, a parametric study is carried out to investigate the influence of various parameters on the vibration and instability behavior of a CNT conveying fluid with different boundary conditions. First of all, in Sect. 4.1, a model validation is performed. After that, Sect. 4.2 analyzes the effect of the nonlocal parameter and longitudinal magnetic field on the flutter instability of a cantilever (C–F) CNT conveying fluid. In Sect. 4.3, the effect of the elastic foundation on the stability region of a cantilever CNT is examined. Finally, Sect. 4.4 is devoted to consider the effects of end-boundary conditions on the stability region. As it will be shown, the latter investigation allows to found different stability behaviors between clamped–free boundary condition and other boundary conditions.

For numerical study, the outer radius and the aspect ratio of nanotube are assumed to be \( R_{\text{o}} = 3\;{\text{nm}} \) and \( \frac{L}{{2R_{\text{o}} }} = 50 \), respectively. The mass density of nanotube is \( \rho_{c} = 2300\;{\text{kg/m}}^{3} \) with Young’s modulus \( E = 3.4\;{\text{TPa}} \) (Murmu et al. 2012).

4.1 Model Validation

In order to assess the validation of the proposed model, the numerical results are presented to compare with those available in the literature. Also, eight number of modes (\( n = 8 \)) are taken to be used for analysis. The nonlocal effect, magnetic field and elastic Winkler and Pasternak foundations of the CNT are neglected for comparison with the results presented by Païdoussis and Li (1993) in Fig. 2. Also, the critical flow velocities of pipes conveying fluid with different boundary conditions obtained by Galerkin method are listed in Table 1 and compared with the results given by Païdoussis (1998) and Ni et al. (2011). In addition, the comparison of the frequencies without considering the magnetic field, the internal fluid and the elastic Winkler and Pasternak foundation effect of the cantilevered CNT is presented in Table 2 for different nonlocal parameters against results presented by Kazemi-Lari et al. (2012). It is clearly seen from Fig. 2, Tables 1 and 2 that the present model is actually in good agreement with previous models.

Fig. 2
figure 2

Comparison of the flutter instability boundary with Païdoussis and Li (1993) for \( \mu = \psi = k_{\text{G}} = k_{\text{w}} = 0 \)

Full size image
Table 1 Comparison of the divergence and couple mode flutter speeds obtained from the present model with the results presented in Païdoussis (1998) and Ni et al. (2011) for \( \mu = \psi = k_{\text{w}} = k_{\text{G}} = 0 \)
Full size table
Table 2 Comparison of the mode sequences obtained from the present model with the results presented in Kazemi-lari et al. (2012) for a cantilevered CNT with \( u = \psi = k_{\text{w}} = k_{\text{G}} = 0 \)
Full size table

4.2 Effect of the nonlocal parameter and longitudinal magnetic field

Preventing any vibration and instability of CNTs conveying fluid is an important requirement for the proper application of the nano-fluid systems and devices. Therefore, the study of vibration and stability of the CNTs containing fluid flow is of great importance.

Figure 3a, b, respectively, indicates real and imaginary components of eigenvalues as a function of flow velocity without considering Winkler and Pasternak foundations for different dimensionless magnetic fields with nonlocal parameter \( \mu = 0.05 \). The real part of eigenvalues is connected with the damping, and the imaginary part of eigenvalues is related to frequency. It can be seen that by increasing dimensionless magnetic field, natural frequency for both modes increases. Also, the second natural frequency increases more when compared to its first natural frequency. Results show that with increasing dimensionless magnetic field, the bifurcation point for the real parts of the first eigenvalue occurs at higher speeds. Therefore, with considering the dimensionless magnetic field, over-damping in CNT occurs in higher fluid speed. It means that the application of magnetic field makes the CNT stiffer.

Fig. 3
figure 3

Dimensionless two first eigenvalues in terms of dimensionless fluid velocities for various values of magnetic field parameters (\( k_{\text{G}} = k_{\text{w}} = 0, \mu = 0.05 \)): a imaginary part, b real part

Full size image

As mentioned before, cantilevered CNT carrying fluid is a nonconservative system and loses its stability via flutter at \( u = u_{\text{cr}} \). Critical flutter speed, \( u_{\text{cr}} \), occurs when the real part of the eigenvalue changes its sign from negative to positive and the imaginary part of the eigenvalue is not zero. For modeling the nonlocality effect, different values of nonlocal parameter for CNT have been reported by researchers. It was found that various parameters such as aspect ratio, mode shapes and boundary conditions have a considerable influence on the proper values of nonlocal parameter (Hu et al. 2011; Duan et al. 2007). Therefore, choice of the proper value for nonlocal parameter is crucial to calibrate the nonlocality effect. While there are no experiments conducted to determine the value of nonlocal parameter, one can use the discreet methods such as molecular dynamics/mechanics (MD/MM) to extract the proper values of nonlocal parameter (Ansari et al. 2012). In this paper, a conservative range of dimensionless nonlocal parameter \( 0 < \mu < 0.2 \) is used for analysis. Graphs shown in Fig. 4 illustrate critical flutter boundary of cantilever CNT conveying fluid with respect to mass ratio. These curves separating the stable area from unstable areas are called flutter instability boundary. At speed below the flutter speed any vibrations are damped, and at higher than the flutter speed any vibrations will grow rapidly. Figure 4a, b, respectively, shows dimensionless critical flutter fluid speed and dimensionless critical frequency for a set of nonlocal parameters \( \mu = 0,0.05,0.1,0.15 \) and \( \psi = k_{\text{w}} = k_{\text{G}} = 0 \). The dimensionless critical flutter speed and critical frequency of the cantilever CNT decrease by increasing nonlocal parameter which indicates a loss of stability region. In other words, the flutter speeds and stability regions given by the Eringen’s nonlocal model are smaller than those obtained by the local continuum results. This is because increasing the nonlocal parameter causes the interaction force between nanotube atoms decreases and makes structure more flexible than classical one. As seen from the figures, the curves for nonlocal parameter \( \mu = 0 \) have three S-shaped segments. These segments represent three different dynamic behaviors of CNT that is related to the instability–restabilization–instability sequence, which has previously been observed by Gregory and Paidoussis (1966). In addition, the curves in the figure 4(a) describe the relation between the dimensionless flutter speed and the critical mass ratio \( \beta_{\text{cr}} \) related to the transference of the two unstable modes. For example, for \( \mu = 0 \) in the range \( 0 < \beta < 0.3 \), flutter instability of cantilevered CNT occurs on the second eigenvalue mode. The mass ratio at which the transference of the instability occurs from the second to the third mode is \( \beta_{\text{cr}} \cong 0.3 \). In the range, \( 0.3 < \beta < 0.7 \), \( 0.7 < \beta < 0.92 \) and \( 0.92 < \beta < 1 \), flutter occurs on the third, fourth and fifth modes, respectively, and corresponding critical mass ratio at which transference of the instability modes occurs is shown to be β cr  ≅ 0.7 (for third to fourth mode) and β cr  ≅ 0.92 (for fourth to fifth mode). It is found from the figure that the decreases in the interaction force between nanotube atoms cause the system to become flexible and that S-shape segments occur at lower mass ratios with increase in nonlocal parameter.

Fig. 4
figure 4

Influence of nonlocal parameter \( \mu \) on the stability boundaries, as a function of nondimensional mass ratio \( \beta \) for \( \psi = k_{\text{G}} = k_{\text{w}} = 0 \): a dimensionless flutter speed, b dimensionless flutter frequency

Full size image

In order to better illustrate the effects of nonlocal parameter on the critical speed, similar calculation is also performed, and the corresponding result is depicted in Figs. 5a, b. In Fig. 5a, critical speeds of cantilever CNTs for three different mass ratios in terms of nonlocal parameter are shown. As it can be seen, for \( \mu < 0.18 \) the system is stable below a critical speed for different mass ratios. The results show that for \( \mu > 0.18 \) cantilever CNT containing fluid flow is unstable for low fluid flow. As it can be seen, there are two curves for each mass ratio, upper curve and lower curve. For \( \mu > 0.18 \), the stable region is further limited by these two curves. Thus, system is stable when parameters are in the region below the upper curve and above the lower curve. Outside of the stable region, except at the \( u = 0 \), CNT loses its stability by flutter. The results show that the starting point of the lower curve is approximately at \( \mu \cong 0.18 \), regardless of mass ratio. Figure 5b shows dimensionless critical fluid speed in terms of nonlocal parameter μ for various values of magnetic parameter \( \psi \). As is clear from this figure, regardless of the magnetic field parameter, after a certain value of nonlocal parameter system loses its stability through flutter for low fluid flow speed. One can see that the increase in the magnetic field intensity involves the increase in the critical flow speeds. Therefore, increasing the stability region of the CNT carrying fluid is caused by increasing the magnetic field parameter. This is also verified by Fig. 6, which shows the effects of varying the strength of the longitudinal magnetic field on the dimensionless critical speeds of a cantilever CNT conveying fluid for different values of nonlocal parameters. The strength of the magnetic field is considered varying from \( H_{x} = 10^{ - 4} \) to \( 5 \times 10^{8} \;({\text{A/m}}) \) with logarithmic scale on the horizontal axis. From this figure, it is observed that for the strength of the longitudinal magnetic field in the range \( 0 < H_{x} < 10^{7} \;{\text{A/m}} \), the flutter speeds are nearly constant versus \( H_{x} \), and the magnetic field is not effective on the flutter speeds. For \( 10^{7} < H_{x} < 10^{8} \;{\text{A/m}} \), the effects of magnetic field and nonlocal parameter on the flutter speed are significant, while by increasing \( H_{x} \) higher than \( 10^{8} \;{\text{A/m}} \) the effect of the magnetic field increases while the impact of nonlocal parameter decreases. This may be related to the coupling effect of vibrating CNTs and the longitudinal magnetic field.

Fig. 5
figure 5

Dimensionless critical speeds as a function of dimensionless nonlocal parameter for various values of: a mass ratio \( \beta \) (\( k_{\text{G}} = k_{\text{w}} = 0, \psi = 0 \)), b magnetic field \( \psi \) (\( k_{\text{G}} = k_{\text{w}} = 0, \beta = 0.1 \))

Full size image
Fig. 6
figure 6

Flutter speed as a function of magnetic field parameters for different nonlocal parameters \( \mu \) and for \( \beta = 0.5 \), \( k_{\text{G}} = k_{\text{w}} = 0 \)

Full size image

4.3 Effect of the elastic foundation

The effect of the elastic Winkler modulus and shearing modulus of Pasternak foundation on the stability analysis of a cantilever CNT conveying fluid is investigated in this section. Figure 7a, b shows the dimensionless critical flow velocities and the corresponding frequencies for flutter of a cantilever CNT conveying fluid, respectively. In these figures, flutter instability boundaries as a function of the elastic Winkler modulus are displayed for different values of mass ratio, i.e., \( \beta = 0.1,0.3,0.5,0.7 \), with \( \psi = 12 \), \( k_{\text{G}} = 0 \) and \( \mu = 0.05 \). The effect of foundation modulus is to increase the critical flutter fluid speed and the corresponding frequencies. This is due to the fact that increasing Winkler modulus increases the CNT stiffness, which, in turn, leads to greater system stability. In addition, the flutter instability occurs at \( \beta = 0.1 \) for second eigenvalue mode. For \( \beta = 0.7 \), flutter occurs on the third and fourth eigenvalue modes, and critical value of Winkler modulus at which transference of the instability modes occurs is \( k_{\text{w}}^{\text{cr}} \cong 220 \).

Fig. 7
figure 7

Influence of dimensionless mass ratio \( \beta \) on the stability boundaries, as a function of dimensionless Winkler foundation \( k_{\text{w}} \) for \( \mu = 0.05 \), \( \psi = 12 \), and \( k_{\text{G}} = 0 \): a dimensionless flutter speed, b dimensionless flutter frequency

Full size image

The effects of the nonlocal parameters on flutter speed and flutter frequency as a function of the elastic Winkler modulus are shown in Fig. 8a, b, respectively. As shown, a decrease in the number of S-shaped segments (and subsequently different instability modes) is observed at lower nonlocal parameters, such that the flutter occurs on the third eigenvalue mode for \( \mu = 0 \) and on third and fourth eigenvalue modes for \( \mu = 0.1 \).

Fig. 8
figure 8

Influence of nonlocal parameter μ on the stability boundaries, as a function of dimensionless Winkler modulus \( k_{\text{w}} \) for \( \psi = 12 \), \( \beta = 0.3 \) and \( k_{\text{G}} = 0 \): a dimensionless flutter speed, b dimensionless flutter frequency

Full size image

Figure 9a, b examines the flutter instability boundaries graph of cantilever CNT in the \( k_{\text{w}} - u_{\text{cr}} \) plane for different values of magnetic field parameter \( \psi = 0,12,48 \) with \( \beta = 0.5 \), \( k_{\text{G}} = 0 \) and \( \mu = 0.05 \). As expected, increasing the magnetic field parameter leads the stable region to become greater. In addition, it is remarkable to notice that the cantilevered CNT loses its flutter instability on the third and fourth eigenvalue modes for investigated parameters at this figure.

Fig. 9
figure 9

Influence of dimensionless magnetic parameter on the stability boundaries, as a function of dimensionless Winkler modulus \( k_{\text{w}} \) for \( \mu = 0.05 \), \( \beta = 0.5 \) and \( k_{\text{G}} = 0 \): a dimensionless flutter speed, b dimensionless flutter frequency

Full size image

Figure 10a presents the stability map of the CNT in the \( k_{\text{G}} - u_{\text{cr}} \) plane for different values of mass ratios and for \( \mu = 0 \), \( \psi = 48 \) and \( k_{\text{w}} = 600 \). Moreover, for all given values of \( k_{\text{G}} \), an increment of dimensionless flutter speed is noticeable under the influence of mass ratios. Figure 10b illustrates the stability curves for various values of nonlocal parameters and for \( \psi = 48 \), \( k_{\text{w}} = 600 \) and \( \beta = 0.5 \). Over the whole range of \( k_{\text{G}} \), the nondimensional critical speed decreases as the nonlocal parameter increases. In addition, the number of S-shape segments in the stability boundaries is reduced by increasing the nonlocal parameter. Figure 10c shows the nondimensional critical speed of a CNT as a function of \( k_{\text{G}} \), for different values of magnetic field and for \( \mu = 0.05 \), \( k_{\text{w}} = 150 \) and \( \beta = 0.5 \). The flutter speed increases with the increase in magnetic field, and the CNT becomes more stable. Further, as it can be seen from figure 10, by increasing the shearing modulus (\( k_{\text{G}} \)) the flutter velocity of cantilevered CNT increases. This physically implies that the influence of shearing modulus of the Pasternak foundation is to stiffen the CNT, and consequently, the critical speed and stability region increase. In addition, it is deduced that the influence of the shearing modulus of Pasternak foundation on the flutter velocity is more prominent compared to elastic Winkler modulus.

Fig. 10
figure 10

Flutter speed \( u_{\text{cr}} \) as a function of dimensionless shearing modulus of Pasternak foundation: a for different mass ratios and \( \mu = 0 \), \( \psi = 48 \), \( k_{\text{w}} = 600 \), b for different nonlocal parameters, and \( \psi = 12 \) \( k_{\text{w}} = 150 \), \( \beta = 0.5 \), c for different magnetic field parameters and \( k_{\text{w}} = 150 \), \( \mu = 0.05 \), \( \beta = 0.5 \)

Full size image

4.4 Effect of the boundary conditions

The critical velocity of CNT conveying fluid resting on elastic foundation under longitudinal magnetic field is shown as a function of the mass ratio in Fig. 11 for the P–P, C–P and C–C boundary conditions. Depending on the values of the fluid velocity and mass ratio, occurrence of divergence or flutter instability or both instabilities is possible. Critical flutter and divergence velocities are represented by solid lines and dashed lines, respectively. It is observed that the as mass ratio increases, the critical flutter velocities decrease until a certain mass ratio, after which flutter velocities increase. However, the critical divergence velocities are not changed by an increase in the mass ratio, because divergence instability is independent of the mass ratios. Also, it is observed that for fluid-conveying CNTs with P–P supported the stable region is smaller than the C–P and C–C boundary conditions because it is stiffer than other two boundary conditions. It was also demonstrated that increasing fluid velocity in CNTs with both ends supported causes first divergence and then flutter instability. The lower and upper divergence zones are associated with the first and second divergence modes, respectively. Consequently, divergence instability is more important for CNTs with both end supported.

Fig. 11
figure 11

Critical speed \( u_{\text{cr}} \) in terms of dimensionless mass ratios for \( \mu = 0.05 \), \( \psi = 12 \),\( k_{\text{w}} = 100 \) and \( k_{\text{G}} = 20 \): a for P–P, b for C–P, c for C–C boundary conditions

Full size image

5 Conclusion

In this paper, the vibration and stability characteristics of CNT carrying fluid on an elastic foundation under the magnetic field were studied. The equation of motion and boundary conditions were derived via extended Hamilton’s principle. The influence of some system physical parameter, such as the nonlocal effect, magnetic field, Winkler and Pasternak foundations and boundary conditions on the instability region is discussed. Having mentioned that, these parameters significantly affect the eigenvalues, critical speeds and frequencies. The major conclusions are as follows:

  • One can see that the nonlocal parameter plays a key role for stability of the cantilever CNT. The dimensionless critical speed and dimensionless critical frequency decrease as the nonlocal parameter increases. When the nonlocal parameter decreases, the stable region in \( \beta - u_{\text{cr}} \) stability plane is seen to increase. This indicates that the classical CNT is more stable. In other words, as nonlocal parameter increases, cantilever CNT loses its stability at low fluid velocities. So, for nonlocal parameters greater than a certain value even with infinitesimally small velocities flutter instability occurs.

  • Nondimensional critical speed (\( u_{\text{cr}} \)) and natural frequencies of the CNT with magnetic field are larger than that of CNT without magnetic field. Critical speed was increased significantly as strength of longitudinal magnetic field is between (\( 10^{7} < H_{x} < 5 \times 10^{8} \;{\text{A/m}} \)). Also, as a result of magnetic field effect, it has its greatest effect in enlarging the region of stability.

  • The foundation stiffness leads to increase in the fluid critical flutter speed and flutter frequency. Therefore, as the Winkler modulus and shearing modulus of Pasternak foundation increase, the region of stability increases. In addition, the effect of the Winkler modulus becomes less than the shearing modulus of Pasternak foundation.

  • It is also observed that the S-shape segments in the stability curves that related to the instability–restabilization–instability sequence disappear slowly, as the mass ratio decreases in both \( k_{\text{w}} - u_{\text{cr}} \) and \( \mu - u_{\text{cr}} \) stability planes. Also, the number of S-shaped segments is increased by increasing of nonlocal parameter in \( k_{\text{w}} - u_{\text{cr}} \) stability plane.

  • Also, number of S-shaped segments is reduced by increasing of nonlocal parameter in \( k_{\text{G}} - u_{\text{cr}} \) stability plane.

  • For CNTs with positively supported end, the system loses its stability first by divergence and then by flutter as fluid velocity increases. Thus, it can be interpreted that the fluid-conveying pipes with supported end can lose its stability by either divergence or flutter, whereas for cantilever CNT only flutter instability is observed.