1 Introduction

Composite stiffened panels, with the advantages of high specific strength and specific stiffness, are widely used in the fields of aircraft, aerospace, automobile and others [1,2,3,4]. However, structural deformation failure is still one of the most common failure modes, due to overloading, flutter and so on. Therefore, optimized design of composite stiffened panels has gained wide attention, aiming to improve structural stiffness and reduce structural weight at the same time [5, 6].

In the past decades, one common practice in optimization of composite stiffened panels is heuristic algorithm-based size optimization methods [7,8,9,10,11,12], such as genetic algorithm (GA) and ant colony algorithm (ACA). Lanzi and Giavotto [7] proposed a multi-objective optimization approach for composite stiffened panels considering post-buckling constraints. Moreover, a comparison was made between three global approximation methods, i.e., neural networks, radial basis function and Kriging approximation. Montemurro et al. [8] used GA to seek best stacking sequences for a wing box stiffened panel with nonidentical stiffeners. Fu et al. [9] integrated neural network with GA to minimize structural weight. Wang et al. [10] used ACA to investigate the optimal layup for maximizing the buckling load of T-shape stiffeners. In [11], the stacking sequences of stiffeners were optimized to maximize buckling and collapse loads based on evolutionary algorithms. Besides the aforementioned studies based on heuristic algorithm, a fractal branch and bound method was proposed by Todoroki and Eskishiro [13] for optimizing the stacking sequence of stiffeners. In size optimization [7,8,9,10,11,12,13], the optimized results can only be obtained from several presupposed stiffener configurations. There is no doubt that the amount of design variables could be significantly reduced by using size optimization and, therefore, save the computational cost during optimization. However, the mechanical properties of composite stiffened panels cannot be fully optimized by size optimization.

For simplicity, uniformly distributed stiffeners were adopted in some stiffener layout optimization methods [14,15,16,17]. Richards et al. [14] built surrogate models to optimize numbers of stiffeners to uniformly distributed stiffeners. Kaufmann et al. [15] proposed an optimization framework to minimize the direct cost of composite aircraft components, where the distance between two stiffeners is a continuous design variable. In [17], the location and size of stiffeners were optimized under mechanical and hygrothermal loads. Inspired by multiple intersected curved stiffeners in natural structures, Wang et al. [18] optimized the distribution of curved stiffener to further increase the structural mechanical properties. However, in the aforementioned studies, the mechanical properties of composite stiffened panels are still limited by the uniformly distributed design of stiffeners [14,15,16,17,18].

Topology optimization is another potential method to effectively search structural distribution with maximized properties. Compared with size optimization and shape optimization which would only change the geometric parameters or shape of stiffeners, topology optimization has tremendous potential to find the optimal stiffener layout by changing material layout [19,20,21,22]. A few studies have been reported concerning topology optimization of stiffener layout. An et al. [23] maximized the fundamental frequency of stiffened structures with displacement and manufacturing constraints based on the ground structure method. The optimization approach of solid isotropic material with penalization (SIMP) was adopted by Rais-Rohani and Lokits [24] to optimize the stiffener layout of a complex composite-advanced sail structure considering asymmetric loading. Niemann et al. [25] applied the SIMP method to determine the optimal orientation of stiffeners for next-generation lattice composite aircraft fuselage structures. In their study, Altair OptiStruct software was used to minimize the compliance of the fuselage under four critical flight load cases.

However, it is difficult for all the aforementioned approaches to obtain distinct stiffener layout, and the interpretation of topology concept is slightly subjective and unreasonable. Recently, an explicit topology optimization approach was proposed by Guo et al. [26], by which morphable components are used as basic building parts for forming structures with different topologies. Actually, components with various shapes are quite similar to the stiffeners of composite stiffened panels. In the present work, the authors will combine the MMCs approach with the composite stiffened panels and use explicit boundary evolution to find optimized configuration of composite stiffened panels, based on the equivalent stiffness method [27].

The rest of this manuscript is presented as follows. In Sect. 2, an equivalent stiffness model is introduced for composite stiffened panels. Optimization formulation of the composite stiffened panels is established based on MMCs. In Sect. 3, the corresponding sensitivity analysis is discussed in detail. In Sect. 4, several numerical examples, including two typical square panel examples and one aircraft flat pressure bulkhead example, are presented to demonstrate the capability of the proposed method. Finally, some concluding remarks are given.

2 Stiffener Layout Optimization Based on the MMCs Framework

2.1 Basic Idea

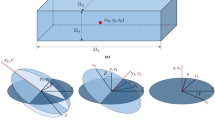
As shown in Fig. 1a, the composite stiffened panel is composed of skin and stiffeners. Application of stiffeners can enhance the overall bending stiffness and buckling ability of the structure remarkably at the cost of a slight increase in weight. This kind of panel, which represents a flat and partial idealization of fuselage, bodywork and hull structures, is frequently employed in the analysis and tests as a subcomponent.

An equivalent stiffness model [27] has been developed for general composite stiffened structures. According to these studies, the complete set of stress resultant equations for composite stiffened panels can be specified as follows:

$$\begin{aligned} {{\varvec{N}}}= & {} {{\varvec{A}}}_{\mathrm{eq}} {\varvec{\varepsilon }} +{{\varvec{B}}}_{\mathrm{eq}} {\varvec{\kappa }} , \nonumber \\ {{\varvec{M}}}= & {} {{\varvec{B}}}_{\mathrm{eq}} {\varvec{\varepsilon }} +{{\varvec{D}}}_{\mathrm{eq}} {\varvec{\kappa }} \end{aligned}$$
(1)

where \({{\varvec{N}}}, {{\varvec{M}}}, {\varvec{\varepsilon }}\) and \({\varvec{\kappa }}\) represent internal force, internal moment, strain and curvature vectors, respectively; \({{\varvec{A}}}_{\mathrm{eq}}, {{\varvec{B}}}_{\mathrm{eq}}\) and \({{\varvec{D}}}_{\mathrm{eq}}\) are the equivalent tensile, coupling and bending stiffness matrices, respectively, and

$$\begin{aligned} {{\varvec{A}}}_{\mathrm{eq}}= & {} {{\varvec{A}}}^{\mathrm{l}}+{{\varvec{A}}}^{\mathrm{s}},\nonumber \\ {{\varvec{B}}}_{\mathrm{eq}}= & {} {{\varvec{B}}}^{\mathrm{l}}+{{\varvec{B}}}^{\mathrm{s}},\nonumber \\ {{\varvec{D}}}_{\mathrm{eq}}= & {} {{\varvec{D}}}^{\mathrm{l}}+{{\varvec{D}}}^{\mathrm{s}} \end{aligned}$$
(2)

where the superscripts l and s denote the laminate skin and stiffeners, respectively. Readers can refer to [27] for details.

Fig. 1
figure 1

Schematic of the composite stiffened panel: a geometric model; b equivalent stiffness model; c description of stiffeners

Full size image

Based on the above equivalent stiffness theory, different materials can be adopted to represent skin and stiffeners, respectively [28]. Then, the problem of stiffener layout optimization can be considered as a topology optimization problem for two kinds of materials with different mechanical properties, as shown in Fig. 1b. In the present work, components with explicit geometric parameters are used to describe the stiffeners after equivalence. Furthermore, the characteristic function for the region of laminate skin and stiffeners can be interpolated as \([\bullet ]=[\bullet ]^{\mathrm{laminate}}+ H(\varPhi ^{s})[\bullet ]^{\mathrm{stiffeners}}\), where \(\varPhi ^{s}\) is the topology description function (TDF) for stiffeners, and H() is the Heaviside function.

2.2 Geometric Description of Stiffeners

Based on the MMCs approach, the distribution of stiffeners illustrated in Fig. 1 can be described by the following structural topology description:

$$\begin{aligned}&\varPhi ^{s}({{\varvec{x}}})>0,\quad \hbox { if }{{\varvec{x}}}\in \Omega ^{s}, \nonumber \\&\varPhi ^{s}({{\varvec{x}}})=0,\quad \hbox { if }{{\varvec{x}}}\in \partial \Omega ^{s}, \nonumber \\&\varPhi ^{s}({{\varvec{x}}})<0,\quad \hbox { if }{{\varvec{x}}}\in \hbox {D}\backslash (\Omega ^{s}\cup \partial \Omega ^{s}) \end{aligned}$$
(3)

where D denotes a prescribed design domain, and \(\Omega ^{s}\subset \hbox {D}\) represents the region occupied by stiffeners. Meanwhile, for thin plate structures, the following TDF \(\varPhi \) is employed in the present work:

$$\begin{aligned} \varPhi =1-\left( {\frac{x^{\prime } }{L_{x} }} \right) ^{p}-\left( {\frac{y^{\prime } }{f(x^{\prime } )}} \right) ^{p} \end{aligned}$$
(4)

with

$$\begin{aligned} \left\{ {{\begin{array}{*{20}c} {x^{\prime } } \\ {y^{\prime } } \\ \end{array} }} \right\} =\left[ {{\begin{array}{*{20}c} {\cos \theta } &{} {\sin \theta } \\ {-\sin \theta } &{} {\cos \theta } \\ \end{array} }} \right] \left\{ {{\begin{array}{*{20}c} {x-x_{0} } \\ {y-y_{0} } \\ \end{array} }} \right\} \end{aligned}$$
(5)

In Eq. (4), \(x^{\prime }\) and \(y^{\prime }\) are given for local component coordinate system \({O}^{\prime } -x^{\prime } -y^{\prime },\, p=6\) in the present study, and \(L_{x}\) and \(f(x^{\prime })\) stand for half-length and half-width of the component, respectively, as shown in Fig. 1c. In Eq. (5), (\(x_{0},y_{0})\) represents the coordinate of component center in global coordinate system, and \(\theta \) denotes the rotation angles of the local component coordinate system \({O}^{\prime }-x^{\prime } -y^{\prime }\) to the global coordinate system \({O}{-}x{-}y\), measured from the horizontal axis anti-clockwisely.

It should be pointed out that different types of stiffeners can be obtained owing to various geometric descriptions of components [29,30,31]. Specifically, rectangular components can obtain the simplest form of stiffeners. And if curvilinear stiffeners are required, components with quadratically varied width can be applied. Relatively complex geometric description may remarkably enhance the geometric building capability of components, which, however, will increase the computational cost. Considering the above factors, components with linearly changed width are used in this study, and the following form of \(f(x^{\prime } )\) is adopted:

$$\begin{aligned} f(x')=\frac{t_{1} +t_{2} }{2}+\frac{t_{2} -t_{1} }{2L_{x} }x' \end{aligned}$$
(6)

2.3 Problem Formulation

As shown in [26], a typical topology optimization problem can be formulated with the MMCs as follows:

$$\begin{aligned} \begin{array}{ll} \hbox {Find}&{}{{\varvec{V}}}=(({{\varvec{V}}}^{1})^{\mathrm{T}},...,({{\varvec{V}}}^{k})^{\mathrm{T}})^{\mathrm{T}}\\ \hbox {Min}&{}C=C({{\varvec{V}}}) \\ \hbox {s.t. }&{} g_{i}({{\varvec{V}}})\le 0,\quad i=1,...,m \\ &{}{{\varvec{V}}}\subset U({{\varvec{V}}}) \\ \end{array} \end{aligned}$$
(7)

where \({{\varvec{V}}}\) represents a composed design variable vector, which consists of the design variable vectors for all components \({{\varvec{V}}}^{j}=(x_{\mathrm{0j}}, y_{\mathrm{0j}}, L_{j}, t_{j}^{1}, t_{j}^{2},\theta _{j})^{\mathrm{T}}\), (\(j = 1,2,... k)\), and k is the number of components. \(C({{\varvec{V}}})\) and \(g_{i}({{\varvec{V}}})\) denote the objective function and constraint functions, respectively. For simplicity, only symmetrical laminate skin is considered here, and the composite stiffened panel is only subject to compressive load on the surface. Other types of loading would be transferred into the compressive load with certain distribution. To maximize structural stiffness, i.e., to minimize structural compliance, with the constraint of stiffener volume or mass, the optimization problem formulation for stiffener layout can be written as

$$\begin{aligned} \begin{array}{ll} \hbox {Find}&{} {{\varvec{V}}}=(({{\varvec{V}}}^{1})^{\mathrm{T}},..., ({{\varvec{V}}}^{k})^{\mathrm{T}})^{\mathrm{T}},\;\; w=w(x,y) \\ \hbox {Min}&{} C=\int _{\mathrm{D}} {q(x,y)w\hbox {d}A} \\ \hbox {s.t.}&{}\int _{\mathrm{D}} {{\nabla }^{2}w:(H(\varPhi ^{\mathrm{s}}({{\varvec{V}}})){\mathbb {D}}_{s} +{\mathbb {D}}_{l} ):{\nabla }^{2}\updelta w\hbox {d}A} =\int _{\mathrm{D}} {q(x,y)\updelta w\hbox {d}A} , \;\;\forall w\in \hbox {U}_{\mathrm{ad}},\\ &{}\int _{\mathrm{D}} {H(\varPhi ^{\mathrm{s}}({{\varvec{V}}})\hbox {d}A} \le {\overline{A}} , \\ &{}{{\varvec{V}}}\subset \hbox {U}({{\varvec{V}}}), \\ &{}w=w^{*} ,\quad \hbox { on }\Gamma _{w} \\ \end{array} \end{aligned}$$
(8)

where q is the compressive load on composite stiffened panel, subscript D denotes the design domain, w and \({\updelta }w\) represent the displacement field and virtual displacement field, respectively. \({\varvec{{\mathbb {D}}}}_{s} \) and \({\varvec{{\mathbb {D}}}}_{l}\) stand for the fourth-order elasticity tensor of the stiffeners and laminate skin, respectively. \(\varPhi ^{s}({{\varvec{V}}})\) is the TDF for stiffeners, \({\bar{A}}\) denotes the upper bound of middle surface area of stiffeners, and \(w^{*}\) represents the prescribed displacement on boundary \(\Gamma _{w}\). H(x) is the Heaviside function and is approximated in the following regularized form of \(H_{\varepsilon }(x)\)

$$\begin{aligned} H_{\varepsilon } (x)= \left\{ {{\begin{array}{lc} 1,&{}\hbox { if }\;\; x>\varepsilon \\ \frac{3}{4}\left( {\frac{x}{\varepsilon }-\frac{x^{3}}{3\varepsilon ^{3}}} \right) +\frac{1}{2},&{}\qquad \; \hbox { if }\; -\varepsilon \le x\le \varepsilon \\ 0, &{} \hbox { otherwise} \\ \end{array} }} \right. \end{aligned}$$
(9)

where \(\varepsilon \) is an approximation control parameter.

3 Sensitivity Analysis

The proposed method based on MMCs essentially conducts topology changes through changing shape and location of components. Therefore, the adjoint shape sensitivity analysis approach can be used for calculating the sensitivity of objective function. It is worth noting that deflection and rotation continuity at the material interface should be ensured. Under this circumstance, it is extremely necessary to deal with the jump of stress tensor at the material interface in a reasonable way. In the present work, by using generalized variational principle, the following function is constructed.

$$\begin{aligned} L= & {} \int _{\mathrm{D}} {qw\hbox {d}A} -\int _\Omega {{\nabla }^{2}w^{1}:({\mathbb {D}}_{s} +{\mathbb {D}}_{l} ):{\nabla }^{2}t^{1}\hbox {d}A} -\int _{\mathrm{D}\backslash \Omega } {\nabla }^{2}w^{2}:{\mathbb {D}}_{l} :{\nabla }^{2}t^{2}\hbox {d}A +\int _{\mathrm{D}} {qt\hbox {d}A}\nonumber \\&+\int _{\Gamma _{\mathrm{int}} } {({\nabla }t^{1}-{\nabla }t^{2})\cdot \lambda \hbox {d}s} \nonumber \\&+\int _{\Gamma _{\mathrm{int}} } {({\nabla }w^{1}-{\nabla }w^{2})\cdot \mu \hbox {d}s} +\int _{\Gamma _{\mathrm{int}} } {(t^{1}-t^{2})\alpha \hbox {d}s} +\int _{\Gamma _{\mathrm{int}} } {(w^{1}-w^{2})\beta \hbox {d}s} \end{aligned}$$
(10)

For simplicity, only one stiffener is considered here. In Eq. (10), w and t denote the actual and adjoint deflections, respectively. \(\mu \) is the adjoint moment, and \(\beta \) is the adjoint traction on \(\Gamma _{\mathrm{int}}\). Superscripts 1 and 2 denote the stiffeners and laminate skin, respectively. \(\Gamma _{\mathrm{int}}\) is the interface between two materials. The actual deflection w, interface moment \(\lambda \) and interface traction \(\alpha \) should satisfy

$$\begin{aligned}&\int _\Omega {{\nabla }^{2}w^{1}:({\mathbb {D}}_{s} +{\mathbb {D}}_{l} ):{\nabla }^{2}p^{1}\hbox {d}A} +\int _{\mathrm{D}\backslash \Omega }{{\nabla }^{2}w^{2}:{\mathbb {D}}_{l} :{\nabla }^{2}p^{2}\hbox {d}A} \nonumber \\&\quad =\int _{\mathrm{D}} {qp\hbox {d}A} +\int _{\Gamma _{\mathrm{int}} } {({\nabla }p^{1}-{\nabla }p^{2})\cdot \lambda \hbox {d}s} +\int _{\Gamma _{\mathrm{int}} } {({\nabla }w^{1}-{\nabla }w^{2})\cdot \eta \hbox {d}s}\nonumber \\&\qquad +\int _{\Gamma _{\mathrm{int}} } {(p^{1}-p^{2})\alpha \hbox {d}s} +\int _{\Gamma _{\mathrm{int}} } {(w^{1}-w^{2})\zeta \hbox {d}s} \end{aligned}$$
(11)

where p represents the adjoint displacement field defined on D. \(\eta \) and \(\zeta \) are adjoint moment field and adjoint traction field defined on \(\Gamma _{\mathrm{int}}\), respectively. According to the definition of Dirichlet boundary, we have \(V_{n}=0\) on \(\Gamma _{w}\). Choosing \(p=t^{\prime }\), \(p^{1}=t^{1\prime }\), \(p^{2}=t^{2\prime }\), \(\eta =\mu ^{\prime }\), \(\zeta =\beta ^\prime \), assuming that \(\mathbb {D}_{s}\), \(\mathbb {D}_{l}\) and q are all spatial invariants, and boundary \(\Gamma _{w}\) is fixed, the material derivative of L can be expressed as

$$\begin{aligned} \frac{\hbox {D}L}{\hbox {D}t}= & {} \int _{\mathrm{D}} {qw^{\prime } \hbox {d}A} -\int _\Omega {{\nabla }^{2}w^{1\prime } :(\mathbb {D}_{s} +\mathbb {D}_{l} ):{\nabla }^{2}t^{1}\hbox {d}A} -\int _{\mathrm{D}\backslash \Omega } {{\nabla } ^{2}w^{2^\prime } :\mathbb {D}_{l} :{\nabla }^{2}t^{2}\hbox {d}A} \nonumber \\&+\int _{\Gamma _{\mathrm{int}} } {{\nabla }^{2}w^{1}:(\mathbb {D}_{s} +\mathbb {D}_{l} ):{\nabla }^{2}t^{1}V_{n} \hbox {d}A} -\int _{\Gamma _{\mathrm{int}} } {{\nabla }^{2}w^{2}:\mathbb {D}_{l} :{\nabla }^{2}t^{2}V_{n} \hbox {d}A} \nonumber \\&+\int _{\Gamma _{\mathrm{int}} } {({\nabla } t^{1}-{\nabla } t^{2})\cdot \lambda ^{\prime } \hbox {d}s} +\int _{\Gamma _{\mathrm{int}} } {({\nabla } (({\nabla } t^{1}-{\nabla } t^{2})\cdot \lambda )\cdot {{\varvec{n}}}+\kappa _{\mathrm{c}} ({\nabla } t^{1}-{\nabla } t^{2})\cdot \lambda )V_{n} \hbox {d}s} \nonumber \\&+\int _{\Gamma _{\mathrm{int}} } {({\nabla } w^{1}-{\nabla } w^{2})^{\prime } \cdot \mu \hbox {d}s} +\int _{\Gamma _{\mathrm{int}} } {({\nabla } (({\nabla } w^{1}-{\nabla } w^{2})\cdot \mu )\cdot {{\varvec{n}}}+\kappa _{\mathrm{c}} ({\nabla } w^{1}-{\nabla } w^{2})\cdot \mu )V_{n} \hbox {d}s} \nonumber \\&+\int _{\Gamma _{\mathrm{int}} } {(t^{1}-t^{2})^{\prime } \alpha \hbox {d}s} +\int _{\Gamma _{\mathrm{int}} } {({\nabla } ((t^{1}-t^{2})\alpha )\cdot {{\varvec{n}}}+\kappa _{\mathrm{c}} (t^{1}-t^{2})\alpha )V_{n} \hbox {d}s}\nonumber \\&+\int _{\Gamma _{\mathrm{int}} } {(w^{1}-w^{2})\beta ^{\prime } \hbox {d}s} +\int _{\Gamma _{\mathrm{int}} } {({\nabla } ((w^{1}-w^{2})\beta )\cdot {{\varvec{n}}}+\kappa _{\mathrm{c}} (w^{1}-w^{2})\beta )V_{n} \hbox {d}s} \end{aligned}$$
(12)

where \(\hbox {D}(\bullet )/\hbox {D}t\) means the material derivative, \((\bullet )^{\prime } =\partial (\bullet )/\partial t\) denotes the partial derivative with respect to t, \({{\varvec{n}}}\) represents the normal vector of material interface, \(\kappa _{\mathrm{c}}\) is the curvature of material interface, and \(V_{n}\) is the velocity in the normal direction. Considering the symmetry of the elasticity tensors and strain tensor, Eq. (12) can be written as

$$\begin{aligned} \frac{\hbox {D}L}{\hbox {D}t}= & {} \int _{\mathrm{D}} {qw^{\prime } \hbox {d}A} -\int _\Omega {{\nabla }^{2}t^{1}:(\mathbb {D}_{s} +\mathbb {D}_{l} ):{\nabla } ^{2}w^{1^\prime } \hbox {d}A} -\int _{\mathrm{D}\backslash \Omega } {{\nabla } ^{2}t^{2}:\mathbb {D}_{l} :{\nabla }^{2}w^{2\prime } \hbox {d}A} \nonumber \\&+\int _{\Gamma _{\mathrm{int}} } {{\nabla } (w^{1}-w^{2})^{\prime } \cdot \mu \hbox {d}s} +\int _{\Gamma _{\mathrm{int}} } {{\nabla } (t^{1}-t^{2})\cdot \lambda ^{\prime } \hbox {d}s}\nonumber \\&+\int _{\Gamma _{\mathrm{int}} } {(t^{1}-t^{2})\alpha ^{\prime } \hbox {d}s} +\int _{\Gamma _{\mathrm{int}} } {(w^{1}-w^{2})^{\prime } \beta \hbox {d}s} \nonumber \\&+\int _{\Gamma _{\mathrm{int}} } {{\nabla } ^{2}w^{1}:(\mathbb {D}_{s} +\mathbb {D}_{l} ):{\nabla }^{2}p^{1}V_{n} \hbox {d}A} -\int _{\Gamma _{\mathrm{int}} } {{\nabla }^{2}w^{2}:\mathbb {D}_{l} :{\nabla } ^{2}p^{2}V_{n} \hbox {d}A} \nonumber \\&+\int _{\Gamma _{\mathrm{int}} } {({\nabla } ({\nabla } (t^{1}-t^{2})\cdot \lambda )\cdot {{\varvec{n}}}+\kappa _{\mathrm{c}} {\nabla } (t^{1}-t^{2})\cdot \lambda )V_{n} \hbox {d}s} \nonumber \\&+\int _{\Gamma _{\mathrm{int}} } {({\nabla } ({\nabla } (w^{1}-w^{2})\cdot \mu )\cdot {{\varvec{n}}}+\kappa _{\mathrm{c}} {\nabla } (w^{1}-w^{2})\cdot \mu )V_{n} \hbox {d}s} \nonumber \\&+\int _{\Gamma _{\mathrm{int}} } {({\nabla } ((t^{1}-t^{2})\alpha )\cdot {{\varvec{n}}}+\kappa _{\mathrm{c}} (t^{1}-t^{2})\alpha )V_{n} \hbox {d}s}\nonumber \\&+\int _{\Gamma _{\mathrm{int}} } {({\nabla } ((w^{1}-w^{2})\beta )\cdot {{\varvec{n}}}+\kappa _{\mathrm{c}} (w^{1}-w^{2})\beta )V_{n} \hbox {d}s} \end{aligned}$$
(13)

Letting t, \(\mu \) and \(\beta \) satisfies

$$\begin{aligned}&\int _\Omega {{\nabla }^{2}t^{1}:({\mathbb {D}}_{s} +{\mathbb {D}}_{l}):{\nabla }^{2}g^{1} \hbox {d}A} +\int _{\mathrm{D}\backslash \Omega }{{\nabla }^{2} t^{2}:{\mathbb {D}}_{l} :{\nabla }^{2}g^{2} \hbox {d}A} \nonumber \\&\quad =\int _{\mathrm{D}} {qg\hbox {d}A} +\int _{\Gamma _{\mathrm{int}} } {{\nabla }(t^{1}-t^{2})\cdot \varphi \hbox {d}s} +\int _{\Gamma _{\mathrm{int}} } {{\nabla }(g^{1}-g^{2})\cdot \mu \hbox {d}s}\nonumber \\&\qquad +\int _{\Gamma _{\mathrm{int}} } {(t^{1}-t^{2})\psi \hbox {d}s}+\int _{\Gamma _{\mathrm{int}} } {(g^{1}-g^{2})\beta \hbox {d}s} \end{aligned}$$
(14)

Choosing \(w^{1\prime } =g^{1}\), \(w^{2\prime } =g^{2}\), \(\lambda ^{\prime } =\varphi \), \(\alpha ^{\prime } =\psi \) in Eq. (14) leads to

$$\begin{aligned}&\int _\Omega {{\nabla }^{2}t^{1}:({\mathbb {D}}_{s} +{\mathbb {D}}_{l} ):{\nabla }^{2}w^{1\prime } \hbox {d}A} +\int _{\mathrm{D}\backslash \Omega } {{\nabla }^{2}t^{2}:{\mathbb {D}}_{l} :{\nabla }^{2}w^{2\prime } \hbox {d}A}\nonumber \\&\quad =\int _{\mathrm{D}} {qw^{\prime } \hbox {d}A} +\int _{\Gamma _{\mathrm{int}} } {{\nabla }(t^{1}-t^{2})\cdot \lambda ^{\prime } \hbox {d}s}\nonumber \\&\qquad +\int _{\Gamma _{\mathrm{int}} } {{\nabla }(w^{1\prime } -w^{2\prime } )\cdot \mu \hbox {d}s} +\int _{\Gamma _{\mathrm{int}} } {(t^{1}-t^{2})\alpha ^{\prime } \hbox {d}s} +\int _{\Gamma _{\mathrm{int}} } {(w^{1\prime } -w^{2\prime } )\beta \hbox {d}s} \end{aligned}$$
(15)

Substituting Eq. (15) into Eq. (13) results in

$$\begin{aligned} \frac{\hbox {D}L}{\hbox {D}t}= & {} \int _{\Gamma _{\mathrm{int}} } ({\nabla }^{2}w^{1}:({\mathbb {D}}_{s} +{\mathbb {D}}_{l}):{\nabla }^{2} p^{1}-{\nabla }^{2}w^{2}:{\mathbb {D}}_{l} :{\nabla }^{2}p^{2})V_{n} \hbox {d}A \nonumber \\&+\int _{\Gamma _{\mathrm{int}} } {({\nabla }({\nabla }(t^{1}-t^{2})\cdot \lambda )\cdot {{\varvec{n}}}+\kappa _{\mathrm{c}} {\nabla }(t^{1}-t^{2})\cdot \lambda )V_{n} \hbox {d}s} \nonumber \\&+\int _{\Gamma _{\mathrm{int}} } {({\nabla }({\nabla }(w^{1}-w^{2})\cdot \mu )\cdot {{\varvec{n}}}+\kappa _{\mathrm{c}} {\nabla }(w^{1}-w^{2})\cdot \mu )V_{n} \hbox {d}s} \nonumber \\&+\int _{\Gamma _{\mathrm{int}} } {({\nabla }((t^{1}-t^{2})\alpha )\cdot {{\varvec{n}}}+\kappa _{\mathrm{c}} (t^{1}-t^{2})\alpha )V_{n} \hbox {d}s} \nonumber \\&+\int _{\Gamma _{\mathrm{int}} } {({\nabla }((w^{1}-w^{2})\beta )\cdot {{\varvec{n}}}+\kappa _{\mathrm{c}} (w^{1}-w^{2})\beta )V_{n} \hbox {d}s} \end{aligned}$$
(16)

Comparing Eq. (14) with Eq. (11), it yields that \(t=w\), \(\mu =\lambda \) and \(\beta =\alpha \), since the solution of the corresponding boundary value problem is unique. Considering the fact that the displacement at material interface is continuous (\(w^{1}=w^{2}\), \(t^{1}=t^{2}\), \({\nabla } w^{1}= {\nabla } w^{2}\) and \({\nabla } t^{1}= {\nabla } t^{2}\) on \(\Gamma _{\mathrm{int}})\), Eq. (16) can be simplified into

$$\begin{aligned} \frac{\hbox {D}L}{\hbox {D}t}= & {} \int _{\Gamma _{\mathrm{int}} } {({\nabla }^{2}w^{1}:({\mathbb {D}}_{s} +{\mathbb {D}}_{l} ):{\nabla }^{2}w^{1}-{\nabla }^{2} w^{2}:{\mathbb {D}}_{l} :{\nabla }^{2}w^{2})V_{n} \hbox {d}A}\nonumber \\&+\,2\int _{\Gamma _{\mathrm{int}} } {({\nabla }({\nabla }(w^{1}-w^{2})\cdot \lambda )\cdot {{\varvec{n}}})V_{n} \hbox {d}s} \end{aligned}$$
(17)

In order to express concisely, (\({\mathbb {D}}{ }_{s}+{\mathbb {D}}_{l} )\) and \({\mathbb {D}}_{l} \) are set as \({\mathbb {D}}^{1}\) and \({\mathbb {D}}^{2}\), respectively. Because \({\nabla } w^{1}= {\nabla } w^{2}\) on \(\Gamma _{\mathrm{int}}\), we have

$$\begin{aligned} {\nabla }({\nabla }(w^{1}-w^{2})\cdot \lambda )\cdot {{\varvec{n}}}=\lambda \cdot {\nabla }^{2}(w^{1}-w^{2})\cdot {{\varvec{n}}} \end{aligned}$$
(18)

Considering the fact that the moment within a thin plate should be continuous at the interface \(\Gamma _{\mathrm{int}}\), the interface moment \(\lambda \) could be given as follows

$$\begin{aligned} \lambda =-{\varvec{\sigma }}^{1}\cdot {{\varvec{n}}}=-{\varvec{\sigma }}^{2}\cdot {{\varvec{n}}} \end{aligned}$$
(19)

and then, the right part of Eq. (18) follows that

$$\begin{aligned} \lambda \cdot {\nabla }^{2}(w^{1}-w^{2})\cdot {{\varvec{n}}}=-[({\varvec{\sigma }}^{1}\cdot {{\varvec{n}}})\cdot ({\nabla }^{2}w^{1}\cdot {{\varvec{n}}})-({\varvec{\sigma }}^{2}\cdot {{\varvec{n}}})\cdot ({\nabla }^{2}w^{2}\cdot {{\varvec{n}}})] \end{aligned}$$
(20)

From the above results, it can be finally concluded that

$$\begin{aligned} \frac{\hbox {D}L}{\hbox {D}t}=2\int _{\Gamma _{\mathrm{int}} } {{{\varvec{n}}}\cdot \left\{ {[\chi ^{1}{\varvec{\updelta }}-{\varvec{\sigma }}^{1}\cdot {\nabla }^{2}w^{1}]-[\chi ^{2}{\varvec{\updelta }} -{\varvec{\sigma }}^{2}\cdot {\nabla }^{2}w^{2}]} \right\} \cdot {{\varvec{n}}}V_{n} \hbox {d}s} =2\int _{\Gamma _{\mathrm{int}} } {{{\varvec{n}}}\cdot \left( {\varvec{\varSigma }}^{1} -{\varvec{\varSigma }}^{2} \right) \cdot {{\varvec{n}}}V_{n} \hbox {d}s} \end{aligned}$$
(21)

where \({\varvec{\varSigma }}^{i}=\chi ^{i}{\varvec{\updelta }} -{\varvec{\sigma }}^{i}\cdot {\nabla }^{2}w^{i}\), with \(\chi {}^{i}={\nabla }^{2}w^{i}: {\mathbb {D}}^{i}:{\nabla }^{2}w^{i}/2\) denoting the density of strain energy and \({\varvec{\updelta }}\) denoting the second-order identity tensor. In order to smear out the term in Eq. (21), the Ersatz material model is used for the finite element analysis in the present study [32]. Under this circumstance, the sensitivities of objective and constraint functions to a typical design variable a can be derived as

$$\begin{aligned} \frac{\partial C}{\partial a}=-{\nabla }^{2}w:\left( \sum \limits _{i=1}^k {\frac{\partial {\mathbb {D}}}{\partial \varPhi ^{s}}\frac{\partial \varPhi ^{s}}{\partial a}} \right) :{\nabla }^{2}\updelta w \end{aligned}$$
(22)

and

$$\begin{aligned} \frac{\partial V}{\partial a}=\frac{\partial }{\partial a}\int _{\mathrm{D}} {H_{\varepsilon } (\varPhi ^{s})\hbox {d}A} \end{aligned}$$
(23)

respectively. The corresponding derivation of \(\partial \varPhi ^{s}/\partial a\) is trivial, and readers can refer to [31] for details.

Fig. 2
figure 2

a Schematic of a stiffened panel with four fixed corners; b initial design of stiffeners; c optimized layout of stiffeners; d strain energy density of the optimized stiffened plane

Full size image
Fig. 3
figure 3

a Schematic of clamped composite panel; b initial design of stiffeners; c optimized stiffener layout for panel with twill-weave skin; d optimized stiffener layout for panel with unidirectional skin; e convergence history

Full size image

4 Numerical Examples

In this section, numerical examples of several typical stiffened panels are carried out to demonstrate the capability of the proposed topology optimization method. Four-node rectangular plate elements based on Kirchhoff’s theory are selected for the finite element analysis in all examples.

4.1 Panel with Four Fixed Corners

Firstly, a benchmark example of stiffener layout optimization is carried out to verify the proposed method. The material properties, compressive loads and geometric properties are dimensionless, following [33]. As shown in Fig. 2a, there is a compressive force q at the middle point of the panel. It is assumed that the skin and stiffeners are made from the same isotropic materials. The normalized mechanical properties and other geometric parameters of the stiffened panel are given as follows. The normalized Young’s modulus \(E=1\), Poisson’s ratio \(v=0.3\). The normalized length and thickness of skin are 1 and 0.01, respectively. The normalized height of stiffeners is 0.1, and the normalized compressive load \({q}=1\). The design domain is meshed by \(200\times 200\) uniform four-node elements, and the upper bound of the middle surface area of stiffeners \({\bar{A}}\) is set to be 0.15 A.

As shown in Fig. 2b, the initial stiffeners’ distribution consists of 32 components with 192 (i.e., \(32\times 6\)) design variables. The corresponding optimized stiffener layout is presented in Fig. 2c, and the corresponding optimized value of objective function value is 1684. It is discovered that the optimized stiffeners are distributed in “X” shape, connecting the loading point with the fixed corners, which is generally consistent with the optimized results in [33]. The numerical results in [33] illustrated that the optimized design searched by the adaptive growth technique is significantly affected by initial seeds. As shown in Fig. 6 of [33], three different configurations of initial seeds lead to three different optimized designs, with which the objective function value changes by about 16 times. The best optimized design is shown in Fig. 6c of [33], in which the width of stiffeners near the support points is wider than the portion farther away from the support points. Therefore, the present numerical results demonstrated that the proposed MMC-based method is capable of finding the reasonable optimized design without initiation dependence.

It is found that the components locating at the middle area of each side, where the strain energy density is relatively small, would shrink and merge simultaneously. The optimized stiffener layout with minimized area is beneficial to transfer the compressive load to the fixed corners. Besides, the optimized stiffener layout found by the proposed method does not contain any gray elements. It is discovered that the proposed method is capable of providing clear stiffener layout without any post-processing because the stiffener layout is described by explicit components, as shown in Fig. 2c. In addition, another important advantage of explicit geometric descriptions is that tiny and oversized structures, which are difficult to manufacture, can be simply avoided by setting lower and upper bounds of geometric design variables. Therefore, the proposed method can deal with stiffener layout optimization problems effectively.

4.2 Clamped Square Panel

A clamped anisotropic panel subject to five compressive loads is examined here, where each load q is normalized as 0.2. This example aims to design two comparative cases to analyze the numerical performance of the proposed method for different composite stiffened panels. Figure 3a shows the design domain, compressive load and boundary conditions of this example. In this example, the skin of stiffened panel is manufactured by twill-weave and unidirectional composites, respectively. The normalized mechanical properties and other geometric parameters of the stiffened panel are given as follows. On the one hand, the normalized Young’s moduli of twill-weave lamina are \(E_{1}=1\) and \(E_{2}=1\), respectively. The normalized shear modulus of twill-weave lamina is \(G_{12}=0.385\), and the Poisson’s ratio \(v_{21}=0.3\). The stacking sequence of twill-weave laminate skin is \([0^{\circ }]_{3}\) with the normalized layer thickness of \([0.0015]_{3}\). On the other hand, the normalized Young’s moduli of unidirectional lamina are \(E_{1}=1\) and \(E_{2}=0.001\), respectively. The normalized shear modulus of unidirectional lamina is \(G_{12}=0.385\times 10^{-3}\), and the Poisson’s ratio \(v_{21}=0.3\). The stacking sequence of unidirectional laminate skin is \([0^{\circ }/90^{\circ } ]_{\mathrm{s}}\) with the normalized layer thickness of \([0.0025/0.0025]_{\mathrm{s}}\). Other parameters, finite element mesh and the upper bound of middle surface area of stiffeners, are the same as those of the example in Sect. 4.1.

Similar to the example in Sect. 4.1, the initial stiffeners’ distribution is composed of 32 components, as shown in Fig. 3b. The optimized configuration of stiffeners is presented in Fig. 3b, c. It is found that the stiffeners are distributed in “X” shape at the center of the panel, connecting the five loading points. Then the “X” stiffeners are connected to the clamped boundary by thicker stiffeners. The optimized distribution of stiffeners is rational in view of mechanics. It is observed that the stiffeners tend to symmetrically connect the clamped boundary with the loading points to form the loading transferring path with minimized area.

Compared with Fig. 3c, it is discovered from Fig. 3d that the overall stiffener layouts are similar, since the stiffeners are primarily used to transfer external load to the clamped boundary. However, there are still some slight differences in detail. The stiffeners in Fig. 3d are more inclined to distribute along the 1-direction where flexural stiffness is higher. The stiffeners distributed along the 1-direction can be more conducive to restraining the bending deflection. Compared with size or shape optimization, the proposed method expands forms of stiffener layout, where stiffener layout is no longer limited by uniformly distributed design of stiffeners. Therefore, the mechanical properties of composite stiffened panels can be fully enhanced.

The iteration history of the objective function is shown in Fig. 3e. Considering the fact that insignificant changes in angle or location of components may lead to significant changes in structural topology, a relatively small step length is adopted during the optimization. Under this circumstance, it is still discovered that objective function converges within 200 iterations. Several obvious fluctuations can be discovered in the convergence history of unidirectional composites caused by the two following reasons. First, considering manufacturing cost, the profile of components is limited to linear width. Second, the jump of strain energy density on the material interface \(\Gamma _{\mathrm{int}}\) is ignored. From this example, it is found that both the total number of design variables (192) and the computational cost (within 200 iterations) are acceptable when the proposed method is used to optimize the stiffener layout.

4.3 Aircraft Flat Pressure Bulkhead

As shown in Fig. 4a, it is a simplified aircraft flat pressure bulkhead subject to pressure differential between cabin and the atmosphere. The bulkhead is composed of skin and stiffeners. The skin and stiffeners are made from laminated carbon/epoxy composite T300/5208 and steel, respectively. The bulkhead’s two opposite sides are clamped through adhesion, while other sides are connected to fuselage by riveting. The mechanical properties and geometric parameters of the bulkhead are given as follows. The moduli of T300/5208 lamina are \(E_{1}=180\) GPa, \(E_{2}=10\) GPa and \(G_{12}=7.2\) GPa, respectively. The Poisson’s ratio of T300/5208 lamina is \(v_{\mathrm{21}}=0.28\). The Young’s modulus and Poisson’s ratio of steel are \(E=200\) GPa and \(v=0.28\), respectively. The stacking sequence of T300/5208 laminate skin is \([0^{\circ }/90^{\circ }/\pm 45^{\circ }/0^{\circ }]_{\mathrm{s}}\) with the thickness of 1 mm for each layer. The length, width and rivet pitch for the aircraft flat pressure bulkhead are 2.0 m, 1.0 m and 0.2 m, respectively. The height of stiffeners is 0.1 m.

Fig. 4
figure 4

Simplified flat pressure bulkhead: a schematic of geometry and loads; b initial design of stiffeners; c optimized stiffener layout; d convergence history

Full size image

For simplicity, the out-of-plane pressure q is set to be 100 \(\hbox {kN/m}^{2}\), and the relatively small in-plane loads are ignored here. The design domain is meshed by \(400\times 200\) uniformly distributed four-node plate elements, while the upper bound of the middle surface area of stiffeners is \(0.15\,A\).

As shown in Fig. 4b, the initial stiffener layout, which is usually used in engineering, is composed of 72 components with 432 (\(72\times 6\)) design variables. The corresponding optimized design is presented in Fig. 4c. The iteration histories of the objective function and middle surface area of stiffeners are illustrated in Fig. 4d. It is demonstrated that both the objective function and the middle surface area converge within 100 iterations, yielding optimized objective function value of 10.6 J. For minimum compliance problems, stiffeners are usually distributed around the loading points and clamped boundary to restrain the local deformation. It is observed from Fig. 4c that fifteen thick straight stiffeners are regularly distributed on the bulkhead, which are used to transfer external load to the clamped boundary effectively. The joints between transverse stiffeners and longitudinal stiffeners are relatively small, due to the fact that the bending moment at the clamped edge is higher than the bending moment at the joint. Therefore, the conical-shape transverse stiffeners could provide proper overall reinforcement. For manufacturing, the joint zone needs extra reinforcement, indeed.

In traditional industrial design, grid-stiffened composite structures, whose design and manufacture are relatively simple, are widely used in aircraft flat pressure bulkhead. However, it is discovered from Fig. 4c that the transverse stiffeners in the middle of bulkhead are unnecessary. Therefore, removing distribution of transverse stiffeners in the middle region can reduce quality of the bulkhead, which, however, will not significantly increase deflection of the bulkhead. This example provides an eminently satisfactory design of the aircraft flat pressure bulkhead from the mechanical point of view.

It is also worthwhile to note that, in traditional implicit topology optimization framework, engineers only employed topology optimization method as a heuristic tool to find out potential optimal design. Engineers had to apply their knowledge to interpret topology concept and fulfill specific functions. Compared with implicit topology methods, however, the proposed method is capable of providing optimized stiffener layouts with explicit geometric descriptions, and these optimized stiffener layouts could be linked with the computer-aided design (CAD) system seamlessly. Therefore, the proposed method can be more conducive for engineers to industrial design.

5 Conclusion

In the present paper, a strategy for searching the optimized stiffener layout for composite stiffened panels is proposed based on the moving morphable components (MMCs). In the proposed method, the skin and stiffeners are considered as weak and strong materials with equivalent stiffness. Then the geometric components with linearly changed width are used to describe the distribution of stiffeners on the panel. The optimization formulation for stiffener layout based on MMCs is given to minimize structural compliance, with the constraint of stiffener volume or mass. Then the adjoint shape sensitivity analysis approach is used for calculating the sensitivity of objective function. The proposed method is verified by comparing with the numerical example in the literature. In addition, two different examples for composite stiffened panels are conducted to analyze the numerical performance of the proposed method. The numerical results indicate that the proposed method is capable of providing clear stiffener layout without any post-processing, which is not limited to uniform stiffener configurations. The optimized aircraft pressure bulkhead, which is insightful for engineering design, demonstrates practical significance of the proposed method.