Multiple criteria sorting models and methods—Part I: survey of the literature

Abstract

Multiple criteria sorting methods assign objects into ordered categories while objects are characterized by a vector of n attributes values. Categories are ordered, and the assignment of the object is monotonic w.r.t. to some underlying order on the attributes scales (criteria). Our goal is to offer a survey of the literature on multiple criteria sorting methods, since the origins, in the 1980s, focusing on the underlying models. Our proposal is organized into two parts. In Part I, we start by recalling two main models, one based on additive value functions (UTADIS) and the other on an outranking relation (Electre Tri). Then we draw a (structured) picture of multiple criteria sorting models and the methods designed for eliciting their parameters or learning them based on assignment examples. In Part II (to appear in a forthcoming issue of this journal), we attempt to provide a theoretical view of the field and position some existing models within it. We then discuss issues related to imperfect or insufficient information.

1 Introduction

Multiple Criteria Sorting (MCS) is about methods and models for assigning objects described by their evaluation w.r.t. to several criteria into ordered categories. Typical features of these models and methods include:

• Categories are known in advance; their number is fixed;

• The order on the categories represents the preference of the decision maker;

• There is a preference order on each criterion evaluation scale; the assignment rule is monotone w.r.t. these orders, i.e., an object that is equally or more preferred to another on all criteria is not assigned to a worse category than the other.

Examples Many real-life problems resort to MCS. Here are three examples from diverse horizons.

• Grading students According to their marks in their different courses, students may pass or fail. In this simple case, there are only two categories, and they are ordered by preference in an obvious way. A student having at least as good marks in all courses as another may not fail if the other passes. More detail in students’ classification can be added. For instance, a student may pass with or without honors or fail. Assigning students into one of these three clearly ordered categories must respect monotonicity w.r.t. marks.

• Country risk assessment Credit rating agencies evaluate countries as sovereign borrowers. Credit insurers like the French company COFACE rate countries in eight categories. The country rating reflects the risk of short-term non-payment for companies in the country. The categories are labelled A1, A2, A3, A4, B, C, D, and E, in increasing order of risk. The assessment follows a methodology elaborated within the company, which takes into account multiple economic indicators and relies on analysts’ expertise.

• ASA score The American Society of Anesthesiologists has established a classification into six categories of patients before going into surgery. It has been in use for 60 years. The patient categorization is made by the anesthesiologist based on an evaluation of the patient on several dimensions. The six categories correspond to increasing risk (although the perioperative risks cannot be predicted on the basis of the sole ASA score). The Society publishes guidelines and approved examples to help the clinician in her evaluation.

MCS within MCDM/A Many papers elaborated within the Multiple Criteria Decision Making or Aiding (MCDM/A) community have dealt with MCS methods and models since the 1980s. A possible candidate first paper could be Moscarola and Roy (1977), which describes a multiple criteria segmentation method in three categories. Two applications were presented. One of them aimed at sorting schools in three categories: those that deserve a better funding, those that should receive less funding and the intermediate category of schools for which the case is not clear (see also Roy 1981). This work can be viewed as an ancestor of the sorting methods based on outranking relations, as Electre Tri (Wei 1992).

Classically, MCDM/A has focused more on ranking objects or choosing among objects than sorting them into ordered categories. The theory of multi-attribute value functions (Keeney and Raiffa 1976), for example, builds an overall evaluation of objects, which allows to rank-order them. Such a model tells a Decision Maker (DM) which are the top-ranked actions, for instance, in a set of possible actions. It doesn’t tell the DM whether the top-ranked actions are good, excellent or poor. Ranking provides a relative evaluation of objects. In contrast, sorting in ordered categories may yield absolute evaluations provided categories correspond to standards for being good or excellent, for instance.

MCS and classification MCS has tight relationships with classification, more precisely, with monotone classification. The aim of both is to assign objects into ordered categories while respecting a preference order on each criterion or attribute scale. Traditionally, classification takes data as input and structures them into classes (unsupervised classification) or takes examples of objects assigned into classes and predicts the assignment of other objects (supervised classification). Monotone supervised classification, which is closely related to monotone machine learning or preference learning, is close to MCS. Nevertheless, the former focuses on learning a classifier from large datasets. In contrast, originally, MCS postulated an interaction process with a DM. The DM answers questions aiming to assign values to the parameters of a model (direct elicitation). Particular attention is paid to modelling the preferences of the DM, incorporating her values and goals into the model. Ideally, questions are asked by an expert in multiple criteria decision methods, who also selects a model appropriate to the case. The questioning process tailored to a particular model is sometimes implemented into a Decision Support System (DSS).

To avoid putting an excessive cognitive burden on the DM, or because of the limited availability of the DM for interaction, another approach has soon emerged, which consists of obtaining assignment examples from the DM (indirect elicitation). The latter way brings us closer to classification, with two main differences. In MCS, the set of assignment examples is typically small (a few dozen examples), and models are much more central; in particular, models condition the elicitation method because of the particular significance of parameters, such as criteria weights in each model.

In recent years, under the growing popularity of data mining, machine learning and artificial intelligence, the MCS community has emphasized models and learning methods that scale up to large datasets and aim to compete with machine learning algorithms. However, the MCS and the machine learning communities remain largely alien to each other.

In the sequel, we try to be consistent in using the terms direct elicitation, indirect elicitation, and learning as follows:

• Direct elicitation is used in the framework of a decision-aiding process in which appropriate questions are asked to the DM in order to elicit the parameters of a multiple criteria sorting model;

• Indirect elicitation is used in a decision-aiding context when relying on a small number of assignment examples to assign values to the parameters of an MCS model; a DM may be available (or not) to answer a small number of additional questions;

• Learning is used when the parameters of an MCS model are determined on the basis of large sets of assignment examples.

Sorting versus rating Rating is a very common activity in many application domains, such as finance (credit, country risk rating, etc.) or environmental and public policies assessment (vulnerability, resilience rating, etc.). Rating is mapping objects into a set of totally ordered labels. If this set is finite and only the labels’ order is considered (not values or value differences if labels are numerical), this is exactly what MCS does. Colorni and Tsoukiàs (2021) have argued in favor of changing terminology, abandoning the word “sorting”, and joining the community of people who do “rating”. Although Colorni and Tsoukiàs’s arguments make sense, some features of MCS distinguish it from rating. While rating methodologies aim at standardizing the evaluation process in specific domains (e.g., country risk rating) in view of making these evaluations as objective as possible, MCS, in contrast, highlights the modelling of a particular DM’s preferences. Rating methodologies hold themselves out as rational assessment procedures.

Goals The MCS domain has recently been reviewed (Alvarez et al. 2021). More than 160 papers were analyzed. The survey offers a global view of the scientific activity in the field, categorizing the methods, studying their main application areas, evaluating their bibliometric impact and identifying issues which require further development in the various approaches. The goal of the present work is different. We try to identify important trends and ideas driving scientific production in the field without aiming at exhaustivity. We organize our survey by focusing on the models underlying the reviewed methods. We believe that clearly defined and understood models are essential for settling decision-aiding on a firm basis, for making results explainable, and for designing methods that collect reliable information to specify the models’ parameters.

Models, procedures, methods Distinguishing between models and methods is not always easy. In the sequel, we try to use the terms “model” and “method” consistently. By “model”, we understand a synthetic way of representing the logic underlying the assignment of objects into categories. In Conjoint Measurement theory (Krantz et al. 1971), the notion of model is clearly defined. We have a set of objects and a primitive, here, an ordered partition of the set of objects into categories. The idea is to give a synthetic representation of the primitive and identify the properties of the primitive for which such a representation exists. In MCDM/A, and also in Machine Learning (ML), the notion of a model, is less formalized. A sorting model can be given, for instance, by a mathematical formula involving the evaluations of an object w.r.t. the different criteria and an assignment rule based on this formula. It is not often the case that such a model is fully characterized by properties of a primitive, i.e., the partition of objects into categories. This makes the interpretation of the model and its parameters (such as criteria weights, for instance) less precise, sometimes even relatively arbitrary.

Since the used models involve parameters, these need to be elicited. When the parameters of a model have been fixed, we talk of a “model instance”. What we call a “method” is composed of a model and a process for eliciting the value of the model’s parameters. A method may also include procedures for checking whether the model is suitable for representing the available assignment information, for dealing with imprecision, uncertainty, insufficiency of the available information, etc.

We sometimes use the term “sorting procedure” or “procedure” to designate how assignments are made. A sorting model defines a sorting procedure, but the term “procedure” may refer to a sequence of operations or an algorithm used for making the assignments. A sorting procedure may lack the synthetic character of a model.

Organisation of the paper The paper is published in two parts. Part I is composed of the present introduction followed by Sects.  2 to 4.

Section 2 presents the two historically most important sorting models: UTADIS, a method based on an additive value (or utility) function, and Electre Tri, which belongs to the family of outranking models.

In Sect. 3, we present methods for eliciting the parameters of the two main models on the basis of assignment examples (indirect elicitation). We discuss the different ideas for selecting a model instance among those that fit equally well the assignment examples. We introduce the “robust” and the stochastic ways of dealing with the indeterminacy of the model’s parameters.

A panorama of MCS models and methods is depicted in Sect. 4. We give a deliberately incomplete overview of sorting methods based on scores and on outranking relations. A trend in methods proposals is towards the sophistication of the underlying models. Another shifts towards simplification. We give an account of both trends. After revisiting the robust and stochastic approaches applied to sophisticated models, we discuss two approaches pertaining to the field of knowledge discovery (DRSA) and machine learning (choquistic regression). A subsection mentions various topics related to sorting.

The interested reader is referred to Appendices A, B and D for additional information on some points that are not developed in the main text. A list of abbreviations is available in Appendix C.

Part II (to appear in a forthcoming issue of this journal) has three main sections. One gives an overview of theoretical results characterizing several MCS models. It allows us to understand the relationships (inclusion, equivalence) between these models.

Another section discusses issues raised by imperfect information: How to deal with sets of assignment examples that are not fully compatible with a model? How to deal with insufficient, imprecise or uncertain information?

The third main section addresses issues related to the final phase of a decision-aiding process, such as: how to explain the recommendations and how to improve an object’s assignment.

The survey closes with some conclusions and research perspectives.

2 Two landmark models for multiple criteria sorting

In this section, we briefly describe, for the reader’s convenience, the first two models proposed for sorting objects into ordered categories on the basis of their evaluations w.r.t. several criteria. Their importance is not only historical. They have structured the field. Most developments since then have built upon one or the other of these two seminal models. Beforehand, we introduce the necessary notations and some conventions and formally define multiple criteria sorting procedures.

2.1 Multiple criteria sorting procedures

The objects to be sorted are described by a vector containing their evaluations w.r.t. n criteria. It is assumed throughout that only these evaluations intervene in sorting the objects so that objects will be identified with their evaluations vector. We assume that criterion i, for $i=1, \ldots , n$, takes its values from set $X_i$, which will be called the scale of criterion i. Therefore, the evaluation vector associated with an object is an element $x = (x_1, \ldots , x_i, \ldots , x_n)$ in the Cartesian product X of the criteria scales. We have $X = \Pi _{i=1}^n X_i$. Usually (unless otherwise stated), $X_i$ is a subset of the real numbers (which may be finite or infinite). If so, it is also generally the case that the natural ordering $>_i$ induced by the reals on the set $X_i$ is monotonically related to the DM’s preference¹. In other words, it will often be the case that the larger the value on a criterion scale, the better or, on the contrary, the smaller the value, the better. Unless otherwise mentioned, we shall assume that the preference increases with the value (the larger, the better). It may happen that only a subset of the Cartesian product X corresponds to evaluations of realistic objects. Nevertheless, sorting procedures are usually supposed to be able to sort all elements of X, do they correspond to realistic objects or not. Therefore, we shall refer to X as the set of objects (or the set of alternatives).

The dominance relation > on X is a partial order (asymmetric and transitive relation) on X defined as follows (assuming that the preference on the scale $X_i$ of each criterion does not decrease when the evaluation increases). Object $x \in X$ dominates object $y \in X$, denoted $x > y$, as soon as x is at least as good as y on all criteria and is strictly better on at least one criterion, i.e., $x_i \ge _i y_i$ for all i and $x_j > y_j$ for at least one $j \in \{1, \ldots , n\}$.

A Multiple Criteria Sorting (MCS) method assigns the objects in X into predefined ordered categories $C^1, \ldots , C^p$. We assume that categories are labelled in increasing order of preference, i.e., the objects assigned to category $C^h$ are preferred to those assigned to category $C^{h'}$ as soon as $h > h'$, for all $h, h' \in \{1, \ldots , p\}$. A further requirement on the assignment is that it is monotonic with respect to the dominance relation > on X, i.e., if x dominates y, x should be assigned to an at least as good category as y. Formally, $x \in C^h$, $y \in C^{h'}$ and $x>y$ imply that $h \ge h'$.

2.2 Sorting with an additive value function: UTADIS

UTADIS (UTilité Additive DIScriminante, in French) historically is the first proposed multiple criteria sorting method (Jacquet-Lagrèze and Siskos 1982). The underlying model is based on an additive value (or utility) function and thresholds. In the sequel, we refer to this model as the AVF model (AVF stands for “Additive Value Function”). A minimal utility value (threshold) $\lambda _h$ is associated with each category $C^h$. An object x is assigned to category $C^h$ if its value (or utility) u(x) is equal to or greater than the threshold $\lambda _h$ and is less than the threshold of the category $C^{h+1}$ (the latter condition only if category $C^{h+1}$ exists, i.e., if $h < p$).

Formally, it is assumed that u(x) is an additive value function that is compatible with the assignment of objects in X into categories. Thus there are marginal value functions $u_i : X_i \rightarrow {\mathbb {R}}$, with $u_i(x_i) \ge u_i(y_i)$ whenever $x_i >_i y_i$, and, for $x = (x_1, \ldots , x_i, \ldots , x_n) \in X$,

$$\begin{aligned} u(x) = \sum _{i=1}^n u_i(x_i). \end{aligned}$$

(1)

Let $\lambda _h$ be the threshold associated with category $C^h$, for $h=1, \ldots , p$. We have $\lambda _1< \ldots<\lambda _h< \ldots < \lambda _p$. We assume that $\lambda _1 \le u(x)$ for all $x \in X$ and we define $\lambda _{p+1}$ in such a way that $u(x) \le \lambda _{p+1}$ for all $x \in X$. The UTADIS assignment rule reads as follows: for all $x \in X$,

$$\begin{aligned} x \in C^h \quad \text {iff} \quad \lambda _h \le u(x) < \lambda _{h+1}, \end{aligned}$$

(2)

for all $h =1, \ldots , p$.

Remark UTADIS was briefly introduced in the final section of the paper by Jacquet-Lagrèze and Siskos (1982). The latter was mainly devoted to describing the UTA method, which aims at ranking objects by building an additive value function. We emphasize that UTA and UTADIS are methods, not only models. Both assign values to the model’s parameters by means of indirect elicitation. UTA uses a set of examples of pairs of objects belonging to an otherwise unknown ranking (which is the primitive in this case). UTADIS leans on a set of assignment examples to the categories (see below Sect. 3.1). In the case of UTADIS, the primitive is an ordered partition of X into categories.

2.3 Sorting with an outranking relation: Electre Tri

The second early example of a MCS model, Electre Tri, (Wei 1992; Roy and Bouyssou 1993) is based on an outranking relation and limiting profiles. The idea of outranking is the following. Assuming as before that each object is characterized by the vector of its evaluations w.r.t. n criteria, an object x outranks an object y if x is at least as good as y on a “sufficiently important” subset of criteria without being unacceptably worse than y on no criterion. These two conditions are referred to, respectively, as concordance and non-discordance conditions.

Several different versions of the idea of an outranking relation have been proposed and implemented, particularly in various Electre methods (Roy and Bouyssou 1993; Vincke 1992). The one in the original Electre Tri is the same as in the Electre-III ranking method (see Appendix A). A simpler and more easily interpretable version uses the outranking relation of Electre-I (see Appendix B). To present the method principles, it is not essential to know precisely how the outranking relation S is computed.

Let us assume that we are given an outranking relation S on X as well as $p-1$ special objects $b^2, \ldots , b^h, \ldots , b^p \in X$, which are called limiting profiles or boundary profiles. The coordinate $b_i^h$ of profile $b^h$ represents a minimal performance requirement for an object to be assigned to category $C_h$. These profiles are assumed to dominate one another, i.e., $b^h > b^{h-1}$ for all $h=3, \ldots , p$. There are two versions of the Electre Tri assignment rule, a pessimistic or pseudo-conjunctive one and an optimistic or pseudo-disjunctive one.

Pessimistic or pseudo-conjunctive rule Object x is assigned to category $C^h$ if x outranks the limiting profile $b^h$ and does not outrank the limiting profile $b^{h+1}$, i.e.,

$$\begin{aligned} x \in C^h \quad \text {if} \quad x S b^h \quad \text {and } \quad {\textit{Not}}[x S b^{h+1} ]. \end{aligned}$$

(3)

Optimistic or pseudo-disjunctive rule Object x is assigned to category $C_h$ if the limiting profile $b^{h+1}$ strictly outranks x and the limiting profile $b^h$ does not strictly outrank x, i.e.,

$$\begin{aligned} x \in C^h \quad \text {if} \quad b^{h+1} P x \quad \text {and } \quad {\textit{Not}}[b^{h} P x ], \end{aligned}$$

(4)

where P denotes the asymmetric part of S, i.e., xPy iff xSy and ${\textit{Not}}[ySx ]$.

Because limiting profiles dominate one another, the optimistic rule assigns any object to an at least as good category as the pessimistic rule does (Roy and Bouyssou 1993, pp. 392–396), hence their initial denomination (pessimistic/optimistic).

2.4 Direct elicitation

When a model has been chosen (e.g., UTADIS or Electre Tri), one issue is to assess the model’s parameters. One way, referred to as direct elicitation, requires the participation of the DM, whose preferences and values have to be incorporated into the model. Elicitation proceeds by asking the DM questions to set the required parameter values. Another way is known as indirect elicitation (or learning). The model parameters are inferred on the basis of assignment examples (in the case of sorting). We shall devote the next section to indirect elicitation. In the rest of the present section, we give a flavor of what could be a direct elicitation process for the models Electre Tri and AVF. Actually, we do not know of any published work devoted to presenting a formal direct elicitation method for MCS models.

Note that by “direct elicitation”, we do not mean questioning directly about the model’s parameter values. It has been abundantly argued in the literature (see Podinovskii 1994; Roy and Mousseau 1996; Bouyssou et al. 2006, §4.4.1) that questioning, for instance, about importance of criteria weights is bad practice. Ideally, the questions to the DM should be formulated in terms of the primitives only, i.e., here, in terms of objects assignments into categories.

Electre Tri Let us start with unveiling the intuition that supports the use of Electre Tri and the interpretation of its parameters. Eliciting such a model supposes determining the (lower) limiting profile $b^h$ of each category $C^h$. The value $b_i^h$ of $b^h$ on criterion i can be interpreted as a minimal requirement for an object to belong to $C^h$. If an object is at least as good as $b^h$ on all criteria, then it is certainly assigned to a category at least good as $C^h$. However, this is not a necessary condition. When applying the pseudo-conjunctive (pessimistic) approach, an object that is at least as good as $b^h$ on a “sufficiently important” subset of criteria is also assigned to category $C^h$ or better unless it is “unacceptably worse” than $b^h$ on some criteria. “Sufficiently important” subsets of criteria are usually determined by means of weights attached to the criteria and a threshold. If the sum of the weights attached to a subset of criteria passes the threshold, the subset of criteria is sufficient; otherwise, it is not. Values “unacceptably worse” than a profile $b^h$ on some criterion i are usually determined by means of a threshold $vt_i$ (called a veto threshold). If object x has a value $x_i$ that is worse than $b^h_i$ by at least the veto threshold, then x will be downgraded to a category worse than $C_h$. Such rules are commonly used in practice. Here is an example.

Example The following rule is used in some schools and universities to decide whether a student completes successfully or not her year. The minimal mark required in each subject is 10/20. A student who has at least 10/20 for all subjects succeeds. A student who fails to reach a mark of 10 in no more than two subjects also succeeds, provided their mark in these subjects is not less than 8/20. The category “succeed” is thus determined by a limiting profile $b^1$ defined by a mark of 10/20 for all subjects. Sets of subjects that are sufficiently important are all sets composed of all subjects but two. The veto threshold is 2 for all subjects: any mark less than $10-2=8$ means that the student does not successfully complete her year.

The fundamental parameters of Electre Tri are the limiting profiles, the criteria weights and the threshold aiming to define the “sufficiently important” subsets of criteria and the veto thresholds. When using the outranking relation in Electre-I (see Appendix B), no other parameters are required, and a direct elicitation is a feasible option, provided the DM is sufficiently involved in the process. Suppose we want to use Electre-III as an outranking relation (as is done in the classical version of Electre Tri). In that case, the above fundamental parameters have to be complemented by other thresholds that allow us to mitigate the all-or-nothing character of the method (see Appendix A). Eliciting these parameters adds complexity to the process.

The AVF sorting model UTADIS was described above as a method based on the AVF model and using indirect elicitation for assigning a value to the model’s parameters. Although it cannot be called “UTADIS”, it is possible to use direct methods to elicit the parameters of the AVF sorting model (described in Sect. 2.2) underlying UTADIS. One way would proceed in two steps. The first step consists of building an additive value function on the set of objects. The second step requires assigning value thresholds that separate the categories based on the object’s value, which was built in the first step. Many methods have been proposed to elicit an additive value function, from rigorous ones, such as the method of indifference judgments (von Winterfeldt and Edwards 1986, chap. 7) to less rigorous such as SMART (von Winterfeldt and Edwards 1986, chap. 8). Setting a category threshold amounts to finding the value below which an object cannot be assigned to the category. This can be done by exhibiting (or constructing) an object that is minimal in the category, i.e., the performances of which cannot be impaired without downgrading the object’s assignment to a worse category.

Note that the process in two steps outlined above is not entirely satisfactory. Indeed, the first step presupposes that the DM has a preference relation on the set of objects X, which can be represented by an additive value function. This process thus not only relies on the primitive of sorting models, i.e., an ordered partition of X in categories, but also on the primitive of ranking models, i.e., here, a complete preorder on X. However, referring to a preference relation can be avoided. A rigorous direct elicitation process is possible, based on Bouyssou and Marchant (2009). These authors gave an axiomatic characterization of ordered partitions representable in the AVF in case X is topologically connected. Since the representation is unique, it can be constructed, in principle, in a similar way as for the additive representation of a ranking, though using only assignment to a category as a primitive.

Conclusion Rigorous direct elicitation methods have not received much attention in the MCS context. There are several reasons for that. First, they require models that are axiomatically characterized and for which uniqueness of representation results have been obtained. Second, the questioning process leading to the elicitation of the unique representation (or a close approximation thereof) may involve assignment questions that the DM is unable to answer or is unsure about. Such a process requires a high level of involvement from the DM.

In real-world applications, it is often the case that non-rigorous or less rigorous direct elicitation is used. In order to avoid poor outcomes, questions to the DM must be carefully designed. Questioning directly about the model’s parameter values is not advisable. Ambiguous questions should be avoided, i.e., questions which could be wrongly interpreted by the DM and/or the answer to which does not lead to a clear interpretation in terms of the value of the model parameters. In any case, a deep understanding of the meaning of the parameters of the used model is certainly required from the consultant who drives the interactions with the DM.

3 Indirect elicitation of sorting models parameters

In this section, we discuss a number of methods used to determine parameters of the AVF and the Electre Tri models for which these models reproduce a set of assignment examples. We start with UTADIS (Sect. 3.1), which actually is a method for eliciting the parameters of an AVF model and the thresholds associated to the categories on the basis of assignment examples. In Sect. 3.2, we review some of the proposed indirect elicitation methods for Electre Tri and its simplified versions. Due to the usually limited size of the set of assignment examples, an important issue regarding indirect elicitation is that many model instances fit the examples. Two main attitudes show up in the literature. One is to select one of the compatible model instances, based on some heuristic principle (reviewed in Sect. 3.3 for the case of the AVF model). The other is to work with all compatible model instances (see Sect. 3.4).

Assume that the assignment of a subset of objects ${\mathcal {A}} \subseteq X$ is known or can be provided by the DM. Therefore, ${\mathcal {A}}$ is partitioned in a family of subsets ${\mathcal {A}}^h$, $h \in \{1, \ldots , p\}$ (some possibly empty) such that object $x \in {\mathcal {A}}$ is in ${\mathcal {A}}^h$ iff $x \in C^h$.

3.1 The UTADIS method

Given a set ${\mathcal {A}}$ of assignment examples, the UTADIS method proposes to elicit the parameters of an AVF sorting model by solving the following linear program (LP):

$$\begin{aligned} \begin{array}{lll} \min &{} \sum _{x \in {\mathcal {A}}} \sigma (x) &{} \\ &{}&{}\\ \text {s.t.} &{} u(x) \ge \lambda _h - \sigma (x) &{} \forall x \in {\mathcal {A}}^h, \forall h \\ &{} u(x) \le \lambda _{h+1} -\epsilon + \sigma (x) &{} \forall x \in {\mathcal {A}}^h, \forall h, \end{array} \end{aligned}$$

(5)

where u(x) is the sum of marginal value functions $u_i(x)$ (as in (1)). The positive number $\epsilon$ is a small quantity used to model strict inequalities. The variable $\sigma (x)$ is an error term associated with each object x in ${\mathcal {A}}$. The objective is to minimize the sum of error terms. If the minimal value of the objective is 0, it means that there are an AVF model and thresholds $\lambda _h$ that are compatible with all assignment examples. Otherwise, there is no AVF model that is able to restate all assignment examples. The LP selects one that minimizes the sum of the error terms needed to ensure that all assignment constraints are satisfied.

The variables in this LP are the category thresholds $\lambda _h$, the error terms $\sigma (x)$ and the variables that define the marginal value functions $u_i$. In case the criteria scales are finite and of sufficiently small cardinality, the values of $u_i$ at all points of the scale $X_i$ can be taken as variables. Otherwise, it is customary to divide the scale $X_i$ into intervals. The utility values at the interval endpoints are the variables and the marginal value of a point inside an interval is obtained by linear interpolation of the endpoint values. In this way, the marginal value functions are piecewise linear functions, that can approximate any marginal function shape with arbitrary accuracy by refining the division of the scale $X_i$ into intervals.

If the linear program (5) has a solution in which all error variables vanish, the program arbitrarily selects one AVF model and thresholds among those that restate all assignment examples. In case the LP has no solution in which all error terms vanish, different attitudes can be adopted. The objects unfaithfully assigned by the model may trigger interactions with the DM. In case piecewise linear marginals were used in the LP, the number of breaking points (i.e., interval endpoints) can be increased. One may also move from the UTADIS model towards a more general one.

Methods that elicit an additive value (or utility) function on the basis of holistic preference statements are referred to as ordinal regression and also as disaggregation methods. These terms are also used in the case of sorting although the suffix “DIS” in UTADIS refers to discriminant analysis, which is more appropriate than “regression” in this context (see Jacquet-Lagrèze and Siskos 2001, for historical details).

In contrast with the large data sets available in machine learning, the typical data sets used for eliciting multiple criteria sorting models are of small size. Therefore, a major issue is to deal with the indeterminacy of the model. This issue will be discussed in Sects. 3.3 and 3.4.

3.2 Indirect elicitation of the parameters of an Electre Tri model

Indirect elicitation of the parameters of an Electre Tri model is rather challenging. The first attempt to learn all model parameters simultaneously leads to a (non-linear) mathematical programming formulation (Mousseau and Słowiński 1998). This approach does not allow to deal with sufficiently large size problems within reasonable computing times.

Therefore, subsequent approaches have focused on eliciting subsets of parameters. Mousseau et al. (2001) consider the problem of finding the weights and the majority threshold of an Electre Tri model for which delimiting profiles are known beforehand. This can be done via a linear programming formulation. Ngo The and Mousseau (2002) propose a Mixed Integer Linear Programming (MILP) formulation to learn the profiles of an Electre Tri model for which the weights and the majority threshold are supposed to be known, i.e., the sufficient coalitions of criteria are known. Other linear and MILP formulations allowing to learn the vetoes of an Electre Tri model are presented by Dias et al. (2002).

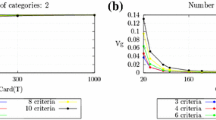
Doumpos et al. (2009) implemented a genetic algorithm to learn the parameters of an Electre Tri model. Such an approach can deal with large-size learning sets (up to 1000 assignments) and several criteria (up to 10). It was tested on artificial data generated by Electre Tri models.

The difficulty of eliciting the parameters of an Electre Tri model is related to the relatively large number of parameters, their discontinuous character (thresholds) and the interrelations between parameters (sufficient coalitions vs. veto effects). Bouyssou and Marchant (2007a, 2007b) have defined a model called the Non-Compensatory Sorting (NCS) model that captures the essence of Electre Tri while involving fewer parameters and allowing for a precise characterization. In this spirit, and also in view of the typically small size of the learning sets in MCDA, Leroy et al. (2011) have proposed to use a variant of the NCS model, known as MR-Sort (Majority Rule Sorting model). This model can also be described as a version of Electre Tri using the outranking relation of Electre  I without veto (see Appendix B). The parameters of an MR-Sort model can be elicited by solving a Mixed Integer Linear Program (MILP). This is a feasible approach for sets of assignment examples of sizes up to around 100. For larger sizes, a heuristic algorithm has been developed and tested (Sobrie et al. 2016, 2019). A formulation with (“coalitional”) veto is in Sobrie et al. (2017).

Eliciting the parameters of the more general NCS model² can be formulated as a satisfiability problem and solved by using a SAT or MaxSAT solver instead of resorting to mathematical programming. The latter approach seems more efficient (i.e., allows to deal with larger sets of assignment examples) than MILP solvers for MR-Sort (Belahcène et al. 2018).

3.3 Selecting model parameters

When several sets of model parameters fit equally well with a known set of assignment examples, which model instances should we use to predict the assignment of other alternatives? There have been two main different attitudes regarding this question. One is to implement a selection mechanism that usually relies on rational principles, for instance, selecting a model whose parameter values are “not extreme” in the region of parameter space corresponding to models restating the assignment examples correctly.

The other main attitude consists of considering all sets of parameters that make the model fit equally well with the set of known assignments. Conclusions, predictions, and recommendations are then drawn by taking into account all compatible model instances. We deal with the former attitude in the rest of this section and the latter in the next section.

The issue of selecting a model instance has given rise to many papers in the case of the AVF model, also with formulations allowing for errors. Note that this issue was mainly addressed in the framework of the ranking method UTA (Jacquet-Lagrèze and Siskos 1982). Nevertheless, the proposals made for UTA transpose mutatis mutandis to UTADIS and their features have also been studied in the sorting setup.

The major idea proposed as a selection principle is centrality. In mathematical programming formulations, the assignments from the set of examples give rise to constraints restricting the set of feasible values for the model’s parameters. The centrality principle amounts to pointing to a vector of parameters values located “in the middle” of the feasible region in parameter space. Since the centre of a set in a multidimensional space is not a well-defined notion, several implementations have been proposed. Here are a few examples.

• Post-optimality analysis for UTA and UTADIS, (Jacquet-Lagrèze and Siskos 1982; Siskos and Yannacopoulos 1985). In order to explore the feasible region in parameter space, one computes 2n “extreme” UTA models by respectively minimizing and maximizing the weight of each criterion (i.e., the maximal marginal value $u_i(x_i)$ on the scale of each criterion) under the constraints generated by the known examples. By averaging the parameters of the 2n extreme models, a feasible “central” model is obtained ;

• ACUTA (Bous et al. 2010). The proposed model is the analytic centre of the polytope defined by the constraints in parameter space; it is located as far as possible from the polytope boundaries and is obtained by maximizing a logarithmic potential function;

• Chebyshev centre (Doumpos et al. 2014). The proposed model is the Chebyshev centre of the polytope defined by the constraints in parameter space. It is defined as the centre of the sphere of maximal radius inscribed in the polytope.

Another selection rule is often referred to as the max-min approach (Zopounidis and Doumpos 2000). In case LP (5) has a solution in which error variables vanish, one subsequently solves the following LP:

$$\begin{aligned} \begin{array}{lll} \max &{} \delta &{} \\ &{}&{}\\ \text {s.t.} &{} u(x) \ge \lambda _h + \delta &{} \forall x \in {\mathcal {A}}^h, \forall h \\ &{} u(x) \le \lambda _{h+1} -\epsilon - \delta &{} \forall x \in {\mathcal {A}}^h, \forall h. \end{array} \end{aligned}$$

(6)

By maximizing $\delta$ one seeks to separate as much as possible the values of objects belonging to adjacent categories. The optimal value of $\delta$ provides an indication of how much constrained is the problem. A large value for $\delta$ is the sign that there are very different value functions that represent the assignment examples.

The properties of the formulations seeking for centrality as well as the max-min approach (6) are experimentally investigated and compared in Doumpos et al. (2014). Experiments are made using artificial data assigned by means of randomly generated UTA models. Models are elicited based on assignment examples and then used to predict other assignments generated by the same model (that form a test set). These experiments rank ACUTA in the top position in terms of prediction accuracy, closely followed by the Chebyshev centre and the max-min approach (6); then comes post-optimality. Other interesting results are obtained. We come back to them at the end of the next section.

A completely different approach to the selection of a particular value function leads to a notion termed representative value function (Greco et al. 2011; Kadziński and Tervonen 2013). This takes place in the so-called robust ordinal regression (ROR) approach that we describe in the next section.

Regarding the Electre Tri model, the issue of selecting a particular model has not been studied in depth. This is due to the greater complexity of the algorithms used to elicit the parameters of such models.

3.4 Computing “robust” results

The so-called robust approach considers all model instances (of a certain type, e.g., the additive value function model or the Electre Tri model) compatible with the available information, i.e., the set of assignment examples. Conclusions are drawn, taking all compatible model instances into account.

Such an approach was initiated in the context of sorting using an Electre Tri model by Dias et al. (2002). The authors propose an interactive approach in which preferential information is gradually obtained from a DM. The information may be directly provided in terms of constraints on the parameters values (e.g., an interval of possible values) or indirectly in terms of assignment examples. At some stages, for objects not yet assigned, one computes the best and worst possible assignments, given the available information. This may induce reactions from the DM, e.g., narrowing the range of possible assignments for some alternatives, hence reducing the feasible region in parameter space.

3.4.1 Robust ordinal regression (ROR)

A more systematic robust approach was developed in the framework of the additive value function model (UTA) for ranking (Greco et al. 2008) and for sorting (Greco et al. 2010). This approach is known as robust ordinal regression (ROR). The whole set of additive value functions u with monotone marginals $u_i$—not only the piecewise linear—that is compatible with the constraints are considered. The concept of necessary and possible assignments emerges. The assignment of an object to a category (or a category range) is necessary if all compatible models assign this object to this category (or category range). An assignment of an object to a category (or category range) is possible if there is a compatible model that assigns the object to this category (or category range). Given the available information, hence a set of feasible model parameters, it is possible to compute, for each object whose assignment is unknown, a set of necessarily assigned categories (which may be empty) and a set of possibly assigned categories (which may be vast), as observed by Kadziński and Tervonen (2013, p. 56). Providing such information in an interactive process may trigger the provision of additional preference statements by the DM.

3.4.2 Stochastic multicriteria acceptability analysis (SMAA)

Another manner of taking into account the whole set of model parameters compatible with the available information is through Monte Carlo simulation. In case the model parameters are not precisely determined but are known to belong to some region (e.g., as defined by a set of constraints), one may sample this region according to some probability distribution (e.g., a uniform distribution). It is then possible to compute the frequency with which an object is assigned to each category by the sampled models. The class acceptability index CAI(a, h) is the fraction of models in the sample that assign object a into category $C^h$. It provides an estimate for the corresponding probability. The initial paper introducing “Stochastic Multicriteria Acceptability Analysis” (SMAA) is Lahdelma et al. (1998). The methodology was subsequently developed and applied to a variety of situations (see Tervonen and Figueira 2008, for a survey), in particular, as a sorting method built on Electre Tri, named SMAA-TRI (Tervonen et al. 2009).

3.4.3 “Representative” value function

In the framework of ROR, Greco et al. (2011) have proposed a methodology for selecting a value function from the set of all compatible ones in an interactive process involving the DM. In the interactions, the DM has to specify her attitude (her “targets”). For instance, whenever an object a is assigned to at least as good a category as an object b by all compatible value functions, the DM may wish that the value difference $u(a) - u(b)$ is to be maximized. Using the constraints induced by the DM’s targets, the authors determine what they call “the most representative” value function.

Kadziński and Tervonen (2013) combine robust ordinal regression (ROR) and SMAA in sorting on the basis of the AVF. By uniformly sampling the set of feasible model parameters, they compute the share APWI(a, b) of compatible models that assign a into an at least as good category as b (for all pairs of objects a, b). By maximizing the difference $u(a)-u(b)$ for all pairs a, b such that $APWI(a,b) > APWI(b,a)$, they obtain a particular model instance that they call “representative” value function.

The possibility of interacting with the DM is a prerequisite for both of the above proposals.

3.4.4 Two robust assignment rules based on simulation; experimental results

In their experimental analysis already referred to in the previous section, Doumpos et al. (2014) describe two new assignment rules. Both rely on Monte-Carlo simulation, just like SMAA. The first rule assigns any object a to the category $C^h$ that maximizes the class acceptability index CAI(a, h). Note that, in general, no single value function model restates this rule assignment. The other rule uses the model that corresponds to the centroid of the feasible parameters polyhedron (i.e., its parameters are obtained by averaging those of the sampled models). The authors’ experimental study compares the behavior of their CAI-based assignment rule and the centroid rule with that of four “central” assignment rules, namely, ACUTA, Chebyshev, max-min and post-optimality. They conclude that the results obtained with the CAI-based and the centroid are very similar and that the performance of ACUTA and Chebyshev come close to their two “robust” rules. In particular, regarding classification accuracy (i.e., the percentage of correct assignments made by using a rule on a test set), the CAI-based rule shows the best performance. The centroid model assigns objects to a category different from that assigned by the CAI-based rule in about 1% of the cases in the test sets (on average). This is very close to the assignment accuracy obtained using ACUTA (1 to 2% lower than that of the CAI-based rule, on average). We are not aware of experimental results allowing to position the Kadziński and Tervonen “representative value function” w.r.t. the Doumpos et al. “robust” rules and the four “central” rules.

3.5 Discussion

The most recently published papers tend to emphasize “robust” methods, which take all compatible model instances into account. However, the robust approaches do not outdate methods based on parameter selection mechanisms. The latter assertion is backed by the following observations.

• Experimental studies (Doumpos et al. 2014) show that centrality parameters selection principles implicitly implement an idea of robustness.

• Robust conclusions, in terms of possible and necessary assignments, essentially depend on the more or less general character of the considered model. For a given set of assignment examples, the more general the model, the weaker the robust conclusions (less necessary and more possible assignments). Similarly, the assignment probabilities obtained using a SMAA approach depend on the – arbitrary – choice of a probability distribution on the set of feasible parameters.

In practice, it seems desirable to end up each step of the interaction process with the DM by exhibiting a tentative model instance (e.g., a central one) together with giving a sense of the variability of the model instances compatible with the examples (e.g., by using a robust and/or a stochastic approach). Note that this view was already present in the seminal paper by Jacquet-Lagrèze and Siskos (1982). The variability of the feasible instances was represented by the 2n extreme instances obtained in the post-optimal analysis. Averaging the parameters of the 2n extreme instances yields a feasible “central” instance. Note also that ending the interaction process by proposing a selected model instance may help the DM understand how assignments are made (e.g., in terms of the alternative values and category thresholds in the framework of the AVF model).

The above discussion has focused on the AVF model. Unfortunately, the literature relative to the indirect elicitation of the parameters of an Electre Tri model is much more limited (a notable contribution is Dias et al. (2002)).

The reader interested in a more detailed discussion is referred to Appendix D.1.

4 An overview of the literature related to multiple criteria sorting

Two reviews of multicriteria sorting methods have appeared in the literature. One by Zopounidis and Doumpos (2002) is ancient but presents a structured and complete overview of the field at the time of the publication and is still relevant nowadays (see also an expanded version in the book by Doumpos and Zopounidis 2002). This review also covers classification methods, in which the categories are not ordered (“nominal” categories, in the authors’ terminology). Among these were reviewed statistical methods (such as e.g., discriminant analysis) and machine learning methods (such as, e.g., neural networks).

A second, very recent review, by Alvarez et al. (2021), focuses on a bibliometric study of 164 papers devoted to multiple criteria sorting and published in journals (mainly obtained through searching in Web of Science and Scopus). The authors classify the methods in four categories (“full aggregation”, “outranking”, “goal, aspiration or reference-level”, “non classical”). They briefly describe the more cited paper in each category. All papers in each category are characterized by the variant of the method used or proposed, the type of contribution (e.g., a novel method, an extension of an existing method, an application-oriented paper), and the application domain.

In this section, we try to categorize the published papers related to MCS, without claiming to be complete. The first category consists of papers proposing either sorting methods based on different models or variations of the two main models analyzed above (Sects. 4.1, 4.2, 4.3). We then identify a stream of papers dealing with indeterminacy in the elicitation of model parameters, thus extending the robust and stochastic approach. Another set of papers proposes methods pertaining to fields such as data analysis, artificial intelligence or machine learning for sorting into ordered categories. Miscellaneous aspects linked with MCS are dealt with in the last set of papers. We close this section with a discussion.

4.1 Multiple criteria sorting methods

Most of the various published MCS methods either rely on a score or on an outranking relation.

4.1.1 Sorting based on scores

Almost all models and methods that were proposed for ranking objects have subsequently been complemented by a version for sorting objects into ordered categories. Such an adaptation is particularly straightforward for ranking methods relying on a score (value, utility, distance to an ideal object, etc.). The way it is usually done is by using thresholds that specify the minimal score value required for an object being assigned to each category.

Scores may result from aggregating the criteria values as, for example, in AHPsort (Ishizaka et al. 2012), MACBETHSort (Ishizaka and Gordon 2017) or the DEA-based sorting method of Karasakal and Aker (2017).

In other methods, they are computed as distances to an ideal point (to be minimized) and/or an anti-ideal point (to be maximized). Examples of that type are TOPSIS-Sort (Sabokbar et al. 2016), VIKORSORT (Demir et al. 2018) or the “case-based distance model for sorting” of Chen et al. (2007).

For more detail on these six examples, see Appendix D.2. Refer to Alvarez et al. (2021) for more examples of sorting methods derived from ranking methods³.

Remark The above methods suppose that a score was previously constructed on the set of objects. Such methods thus rely on the existence of preferences that allow to rank the objects. The DM must thus not only answer questions in terms of assignment to categories but also in terms of preferences between pairs of objects. Note that UTADIS is not a method of that sort. The indirect elicitation of the parameters is made on the sole basis of assignment examples. Hence the AVF function that is obtained is not supposed to represent preferences on pairs of objects. It should not be used to rank them.

4.1.2 Sorting based on an outranking relation

As apparent from our presentation of Electre Tri in Sect. 2.3, as soon as an outranking relation is available, it can be used in different ways (e.g., pessimistic or optimistic assignment procedure) to sort in ordered categories.

The share of papers based on outranking in the MCS literature analyzed by Alvarez et al. (2021) almost reaches one half (79/164), most of them being variants or extensions of Electre Tri.

Some methods are based on outranking relations different from those used in Electre. Examples based on the PROMETHEE method are ${\mathcal {F}}$low${\mathcal {S}}$ort (Nemery and Lamboray 2008), PromSort (Araz and Ozkarahan 2007) and PROMETHEE TRI (De Smet 2019; Figueira et al. 2004).

Other papers formulate general principles of assignment rules that can be applied to any valued (or fuzzy) preference relations, such as those built in Electre or Promethee methods. Papers of this type are Perny (1998) or Fernández and Navarro (2011).

For more detail on the cited examples, see Appendix D.3.

4.2 Sophisticating models

Recent literature shows a trend towards complexifying the underlying models and approaches both in the track of value function based and in the track of outranking based methods. The aim is to make the models more flexible, adapting them to a variety of situations and also propagating ideas that have been implemented in competing approaches.

Models with criteria interactions In such models, good performance on certain groups of criteria may be valued more or less than the weighted sum of the single criterion performances in the group. The Choquet integral (see Grabisch 2016), as a non-additive value function, has inspired several contributions. Marichal et al. (2005) proposed the TOMASO sorting method using the Choquet integral. Figueira et al. (2009a) generalize the concordance index by including criteria interactions.

Ranking methods based on a non-additive value function are in Angilella et al. (2010), and Greco et al. (2014). As the latter mentions, adapting them to the sorting context is straightforward.

Independently, Roy and Słowiński (2008), and Figueira et al. (2009a) suggested modifications of the concordance and discordance indices in Electre models in order to take into account the amplitude of evaluations differences on groups of criteria.

Models in which criteria are organized in a hierarchy Corrente et al. (2015, 2016) develop versions of the AVF and Electre Tri models, respectively, in which criteria are organized in a hierarchy (inspired from AHP (Saaty 1980)).

Electre Tri-like models with several limiting or central profiles per category Almeida-Dias et al. (2010) introduced Electre Tri-C, which sorts on the basis of a central profile in each category. Since then, Electre Tri has been referred to as Electre Tri-B (“B”, for “Boundary”). Subsequently, versions of Electre Tri using several limiting profiles, Electre Tri-nB (Fernández et al. 2017), or several central profiles, Electre Tri-nC (Almeida-Dias et al. 2012) have been published.

Indirect methods for eliciting the parameters of these extensions have been designed. For instance, Fernández et al. (2019) propose a genetic algorithm to elicit the (many) parameters of an Electre Tri-nB model. Kadziński et al. (2015b) revise the assignment rule in Electre Tri-C in order to obtain tractable linear programming formulations and find the parameters (except for the central profiles) of the models compatible with the (possibly imprecise⁴) assignment examples. Madhooshiarzanagh and Abi-Zeid (2021) adapt the previous paper to elicit the criteria weights and the credibility of outranking threshold of an Electre Tri-nC. This requires solving a MILP (the central profiles are supposed to be known; veto thresholds are not considered).

Interval versions of Electre Tri Fernández et al. (2019) have designed a version of Electre Tri-B, INTERCLASS, to deal with imperfectly known parameters and evaluations. The assignment rules of Electre Tri-B are adapted to deal with evaluations that are given as intervals of the real line; parameters, such as criteria weights, veto thresholds and credibility of outranking threshold, may also be given as intervals. The approach is extended to Electre Tri-nB and Electre Tri-nC in Fernández et al. (2020).

Combining several complexifications Arcidiacono et al. (2021) adapt the robust stochastic techniques to sorting with interacting criteria organized in a hierarchical structure; the Choquet integral is used to compute a value function. In the context of outranking methods, Fernández et al. (2022) adapt INTERCLASS to deal with several profiles per category and interacting criteria organized in a hierarchy.

4.3 Considering simpler models

In contrast to the complexification of models, we mentioned, in Sect. 3.2, a simplified version of Electre Tri-B, the Majority Rule Sorting model, MR-Sort (Leroy et al. 2011; Sobrie et al. 2019). This model arises from the characterization of an idealization of Electre Tri-B, called the Non-Compensatory Sorting (NCS) model by Bouyssou and Marchant (2007a, 2007b). With the latter model, an object is assigned to a category if it is at least as good as the lower limiting profile of the category on a sufficient coalition of criteria. At the same time, such a condition is not fulfilled w.r.t. to the upper limiting profile of the category. The set of profiles and the set of sufficient coalitions are the model’s parameters. The set of sufficient coalitions w.r.t. a profile is just a set of subsets of criteria that is closed by inclusion (i.e., a subset of criteria that contains a sufficient coalition is itself a sufficient coalition). The set of sufficient coalitions w.r.t. the lower limiting profile of a category contains the set of sufficient coalitions w.r.t. the profiles of any better category. A more general NCS model involving a veto has been characterized too.

To have an axiomatic characterization of a model at our disposal is essential. It permits us to know what are exactly the properties of the partitions that can be represented in the model. This allows to design rigorous direct elicitation procedures and also procedures for testing whether a model is suitable for reflecting the DM’s views. Simplifying a model to capture its essential characteristics (such as NCS w.r.t. Electre Tri) leads to models having a clear meaning for which rigorous elicitation methods can be proposed.

MR-Sort is a particular case of NCS, in which the set of sufficient coalitions can be determined by criteria weights and a majority threshold (which may be larger for being assigned into $C^{h+1}$ than into $C^h$). Other sub-models of NCS are described in Tlili et al. (2022). We come back to these models in Part II (Belahcène et al. 2022), Sect. 2.3. An experimental study of sets of sufficient coalitions that can–or cannot–be determined by weights and thresholds is in Ersek Uyanık et al. (2017).

It is worth noting that the parameters of the NCS model can be elicited on the basis of assignment examples by using a SAT formulation and a SAT solver instead of having recourse to MILP formulations (Belahcène et al. 2018). Such a formulation tends to be more efficient than MILP for finding an MR-Sort model compatible with the examples. In case no NCS model can fully fit the set of examples, such a logical formulation can be extended using MaxSAT to find a maximally consistent subset of assignment examples (Tlili et al. 2022).

4.4 Dealing with indeterminacy of model parameters

In case the parameters of an MCS model are to be elicited based on assignment examples, the available information is often too scarce to determine the model parameters with sufficient precision. Instead of focusing on finding a single (possibly representative) model compatible with a set of assignment examples, the “robust approach” deals with all models of a given type compatible with all the available information. This set of models is implicitly defined by the constraints on the model parameters generated by the input information. The whole set of models is used to formulate recommendations in terms, for instance, of possible assignments or, when non-void, of necessary assignments. Early developments of a robust approach have been outlined in Sect. 3.4, and discussed in Sect. 3.5.

These ideas have been systematically elaborated in recent years. Machinery that heavily relies on mathematical programming formulations and optimization techniques has been developed. It is intended to support the decision process and enrich the interactions with the DM. The preferential information used to specify a set of models has been extended. Individual assignment examples may be imprecise (e.g., an object assigned to a category interval). Information about relative pairwise category assignments may be accommodated (e.g., object x is to be assigned to a better category than object y; x should be assigned at least/at most k categories above y). Constraints on the cardinality of some categories may be expressed (e.g., the top class should not contain more than three objects). In counterpart to such an input, and relying on some selected model, one may compute possible and necessary assignments, a necessary or a possible binary relation on the assignment of pairs of objects (“all (resp. some) compatible models assign object $x'$ to a better category than object $y'$”), minimal and maximal category cardinality. The following are examples of work done in that research direction.

• Kadziński et al. (2015a) describe how such tools can be implemented for sorting on the basis of the additive value function model. The resulting integrated preference modeling framework is called ROR-UTADIS. Robust recommendations are obtained by solving linear or mixed integer linear programs. In addition to the type of information mentioned above, the DM may also express her preferences relative to the shape of the marginals (e.g., concave), to the values assigned to objects in some category or on the value differences between objects assigned to different categories, etc.

• Kadziński and Ciomek (2016) provide a similar framework for making robust recommendations in outranking-based multiple criteria sorting. The information given by the DM is translated into constraints on a generalized outranking relation. The adopted principle [previously introduced by Rocha and Dias (2008), Köksalan et al. (2009)] is that if x outranks y, then x should not be assigned to a worse category than y. The assignment rule should thus not only be monotone w.r.t. the dominance relation but also w.r.t. an outranking relation that contains it. Contraposing the above principle yields: if x is assigned to a worse category than y, then x does not outrank y. Such constraints thus define a set of feasible outranking relations. They do not specify a set of sorting models. For the particular cases of the Electre and the Promethee outranking relations, these constraints can be implemented in MILP formulations. The robust conclusions obtained take into account all feasible Electre or Promethee relations. For Electre in particular, note that these conclusions do not, in general, correspond to those obtained with a classical sorting model such as Electre Tri-B or Electre Tri-C.

• Kadziński and Martyn (2021) elicit the parameters of an Electre Tri-B model, assuming the limiting profiles are known. The available information can be of all the types described in the preamble of this section. A variety of conclusions are obtained, based either on the robust or the SMAA approach (category acceptability indices, in addition to the robust conclusions mentioned in preamble).

The “stochastic” approach, mainly the Stochastic Multicriteria Acceptability Analysis (SMAA) (see Pelissari et al. 2020, for a survey), introduced in Sect. 3.4.2, is entitled to be called a robust approach too. It shares with the latter the consideration of all model parameters compatible with the assignment examples. In contrast, the outputs are different (mainly, when using SMAA for sorting, the category acceptability index, i.e., the share of feasible models’ parameters assigning an object into each category). After the proposal of SMAA-TRI (Tervonen et al. 2009) in the outranking approach, Kadziński and Tervonen (2013) adapted SMAA to the additive value function approach and used it jointly with ROR for a robustness analysis of UTADIS. Since the above-cited paper, Kadziński and Martyn (2021) has applied the robust and the stochastic approaches for producing robust recommendations in sorting problems.

4.5 Alternative models or approaches

The following approaches position themselves in the field of artificial intelligence, machine learning or classification. The primary aim of all these approaches is to extract knowledge from data. They do not focus so much on representing preferences by a synthetic model. Usually, the size of the datasets is much larger than in MCDM/A. Eliciting an underlying model through interacting with a DM is irrelevant in these approaches (except in active learning, where data is collected in a sequential manner, and questions try to maximize the information gain conditionally on a particular model type).

4.5.1 Dominance-based rough set approach

The Dominance-based Rough Set Approach (DRSA) is a general method for inducing rules from a set of decision examples (“data table”). It implements the dominance principle (an object at least as good as another on all criteria is at least as preferred as the other). However, it allows for violations of this principle in the decision examples. Applied to sorting problems, DRSA induces several types of rules from a set of assignment examples (Greco et al. 2002, 2016). There are certain, possible and approximate rules. Certain rules read as follows:

If an object has evaluations at least (resp. at most) $r_i, i\in B$ on a subset of criteria B, Then the object is assigned to a category at least (resp. at most) as good as $C^h$.

Possible rules have the same structure, but the conclusion is weakened into “...Then the object is possibly assigned to ...”. Approximate rules assign objects to an interval of categories if they satisfy conditions of the type: the object has evaluations at least $r_i, i\in B$ on a subset of criteria B and at most $r'_i, i\in B'$ on a subset of criteria $B'$. Approximate rules arise from dominance violations in the assignment examples. They represent doubtful knowledge.

The algorithmic machinery for extracting such rules, respecting the dominance principle, has been adapted from that developed in the framework of rough sets theory previously applied to the classification of objects in unordered categories. The adaptation consists of substituting the indiscernibility principle by the dominance principle. Using all or part of the induced rules (e.g., only the “at least” rules, or only the “at most” rules), assignment rules to a single or a subset of categories can be derived.

This approach pertains to artificial intelligence, more specifically, to the field of knowledge discovery. It contrasts with the families of sorting methods considered previously by the technique used to extract preferential information from a set of assignment examples. The output is a preference model viewed as a set of rules instead of a functional model such as an additive value function. Note, however, that there is a very general functional model underlying this approach (Słowínski et al. 2002, Th. 2.1). We shall come back on this in Part II (Belahcène et al. 2022), Sect. 2.

DRSA has experienced quite a number of developments, complementing it in different ways. In particular, a robust approach based on generating all compatible minimal sets of rules was published in Kadziński et al. (2014). We refer to Greco et al. (2016) for a detailed presentation of DRSA and its developments up to 2016.

4.5.2 Interpretable classification in machine learning

Supervised machine learning (ML) consists of learning a parametric model from training examples. These examples are described by a number of features and are assumed to be sampled from a latent probability distribution. The learnt parameter is typically obtained with an efficient optimization procedure aiming at, e.g., maximizing the likelihood of the parameters given the observations or minimizing some loss function over validation examples. Typical tasks include regression and classification, and some ML systems are concerned explicitly with monotone classification, making them closely related to MCS. The underlying model, often called hypothesis class, allows to position those systems according to MCS methods.

Linear classifiers, such as the logistic regression, model the fitness of the objects after a weighted sum of the features, i.e., an AVF where the marginals are linear. Moreover, in logistic regression, this fitness is calibrated; in a sense, it can directly be interpreted as the probability ratio of belonging to one class rather than the other.

Generalized linear classifiers aim at learning simultaneously the marginal utilities and the aggregator of an AVF model, based on, e.g., the so-called “kernel trick” or specific assumptions about the underlying distribution, amounting to feeding a linear classifier with transformed objects features. Many models of marginal values have been proposed, from universal approximators (e.g., monotone piecewise linear functions, monotone polynomials, monotone neural networks, or monotone spline functions), to functions allowing to represent a specific decision stance, such as sigmoids or Choquet integrals (see Sect. 4.5.3 below for more detail on “choquistic regression”).

Tree models aim at fitting a factorized logical model, based on monotone rules of the form “if feature i is above level $x_i$ then assign to category at least $C^h$”, similar to DRSA, and possessing the non-compensatory property of the NCS model, a streamlined version of Electre Tri discussed in Sect. 4.3.

Those models are then fitted according to some specific loss function, usually augmented with a regularization term, which is a function penalizing model complexity, so as to promote simple models and reduce overfitting. Computation is generally performed inside the framework of smooth or convex optimization. In order to be able to deal with a large amount of data (number of training examples and/or features), the algorithmic machinery is geared towards efficiency, so as to quickly converge towards a model with good performance, as opposed to the mathematical programming solvers often used in MCDM/A that require more iterations but are guaranteed to converge towards a model with optimal performance. In order to achieve efficiency, ML frameworks often adapt the loss function, penalty function, and representation of the hypothesis class, so as to make the optimization problem easier to solve, usually by implementing smooth and convex approximations of those representations.

Optimizing a composite function $f_{obj} = \ell + \lambda \varphi$ combining a loss term $\ell$ and a regularization term $\varphi$ controlled by a Lagrange multiplier $\lambda$ theoretically allows to explore the set of supported solutions of the corresponding bi-objective problem where $\lambda$ is the price of complexity governing the trade-off between the two objectives. It is noteworthy that this hyperparameter $\lambda$ is almost always chosen so as to minimize the loss function $\ell$ over a validation set, rather than elicited from a DM.

Interpretable classification While neural networks or ensemble methods such as random forests have a reputation of inscrutability, ML approaches that put forward the underlying hypothesis class may yield interpretable classification models. Generalized linear classifiers implement the AVF model and can be described by plotting the marginal utilities. Classification trees, when kept shallow with pruning or regularization techniques, can be described with a limited number of logical decision rules. Note that this aptitude to be described in an intelligible manner should not be confused with explainability, where the aim is to justify the recommendation. This is indeed a difficult problem, even more so when the actual model is learned from massive data, results from a suboptimal optimization process and is actually taken from an approximation of the hypothesis class. Several recent works focus on learning an additive non-compensatory model, where the marginal utilities are stepwise. This hypothesis class, close to MR-Sort, is situated at the crossroad between AVFs and Electre Tri. The authors promote this class of models claiming superior interpretability because the learnt model is so simple it can be presented in a short table and operated by only performing summation of a small number of small integers. Sokolovska et al. (2018) show that learning such a model minimizing the mean squared error is NP-hard, and even computing a polynomial time approximation is difficult; therefore, they propose a greedy heuristic. Ustun and Rudin (2016) address the problem of minimizing the 0/1 loss with mixed integer linear programming when the learning set encompasses a few hundred examples. Ustun and Rudin (2019) learn a calibrated risk score with a cutting planes algorithm for integer non-linear programming. Alaya et al. (2019) propose a specific penalty function, called binarsity that favors using as few steps as possible and allows to attempt at learning an additive non-compensatory model via a proximal algorithm (which is typically much more efficient than MILP used for combinatorial optimization but much less efficient than the stochastic gradient descent algorithms used for the minimization of smooth convex functions).

4.5.3 Choquistic regression

We close this section by discussing choquistic regression, a method developed in a ML framework that has given rise to experimental comparisons with MCDA/M sorting methods. Preference Learning is a sub-field of machine learning considering monotone data (Fürnkranz and Hüllermeier 2010). In this perspective, Tehrani et al. (2012) have built on logistic regression, the well-established statistical method for probabilistic classification in two classes. In logistic regression, the logarithm of the probability ratio of the “good” category over the “bad” category is modeled as a linear function of the object evaluations. The authors substitute this linear function with a Choquet integral, which leads to “choquistic regression”. The maximal likelihood principle is applied to determine the model’s parameters, including the coefficients of the capacity used in the Choquet integral. This means that the selected model is one that maximizes the likelihood of the observed assignments. The method has been generalized to sorting in more than two classes under the name “ordinal choquistic regression” (Tehrani and Hüllermeier 2013). For each object, the model yields a probability of assignment in each category. The mode or the median of this probability distribution is used to predict the object category assignment. The mode (resp. the median) is the predictor that minimizes the risk w.r.t. the 0/1 loss (resp. the $L_1$ loss).

Tehrani et al. have tested their algorithm on a benchmark of 10 real datasets. Their size varies from 120 to 1728 objects, described by 4–16 criteria and assigned to 2 to 36 categories. Interestingly, Sobrie et al. (2019) have compared these results to those obtained by learning an MR-Sort model and an UTADIS model on the same data. The assignment accuracy (in generalization) is often better with choquistic regression, but none of the three models is best for all examples. This shows, in particular, that a simple model such as MR-Sort may have an expressivity comparable to that of UTADIS or choquistic regression. We briefly come back to this model in Part II (Belahcène et al. 2022), Sect. 3.1.4.

Note that Liu et al. (2020) have developed a framework based on additive value functions with various types of (monotone) marginals that aims to deal with large data sets. No comparison is available with Tehrani et al.’s results on a common benchmark.

4.6 Miscellaneous

We list below a number of special topics related to various peripheral aspects of sorting methods. We only briefly position these topics and refer the interested reader to Appendix D.4 for more details and for references.

• 1. Incremental elicitation/Active learning In a sequential elicitation process, some authors have proposed methods for selecting the next question for the DM in order to maximize the information obtained and make the elicitation process as efficient as possible.

• 2. Constrained sorting problems Constraints can be imposed on the size of the categories in MCS methods.

• 3. Group decision. A few papers deal with MCS in a group decision-making context.

• 4. Non-monotone criteria or attributes In applications, the preference on each attribute scale is not necessarily the natural order on the scale. If a DM is available for interactions, the attribute values can be transformed so that the natural order on the transformed scale reflects the DM’s preference. Some papers address this issue in the context of an indirect elicitation algorithm. Both the preference order on each scale and the parameters of a MCS model are thus induced from assignment examples.

• 5. Trichotomic forerunners A few papers have proposed multiple criteria methods for segmenting objects in three categories before or independently of Electre Tri. ABC analysis, used in inventory management, can be seen as another forerunner of MCS methods. Some recent papers explicitly use MCS methods to obtain ABC classifications.

• 6. Around MCS : clustering, nominal classification Several papers deviate from typical multiple criteria sorting into predefined and ordered categories. Some relate to clustering; the number of clusters may be fixed or not; there may be a relation (e.g., a partial order) between the clusters or no relation at all. Methods for classifying objects into unordered categories have also been proposed (nominal classification). See Appendices D.4.6, D.4.7, D.4.8 for a review.

4.7 Discussion

The picture of the field sketched above leads to some observations and raises some interrogations.

4.7.1 Choosing a model

Sections 4.1.1 and 4.1.2 indicate that many models designed for ranking objects have been adapted to monotone sorting in ordered categories [see also Appendices D.2, D.3 and Alvarez et al. (2021)]. In addition, many variants of the two main models, UTADIS and Electre Tri have been proposed.

The profusion of models that can be used for MCS raises the interrogation: how to make a choice among models?

• Are some models intrinsically better suited to some applications? The literature does not analyze this issue in depth. Often, applications simply serve as an illustration of a method. Some case studies involving DMs, consultants and methods designers show how a methodology can be applied in detail. Applying different approaches to the same situation is seldom put into practice, so it is difficult to compare how different models facilitate the decision-aiding process. The statistics connecting methods and applications fields in Alvarez et al. (2021, Figure 18) do not allow to go beyond the following simple facts: the application fields are quite diverse; the most frequently applied methods in the reviewed publications are Electre Tri (and variants) and UTADIS, respectively with 36 and 18 papers.

• In practice, the popularity of a method and the availability of implemented decision support tools may play a role. In a real decision-aiding process involving DM(s) and expert(s), it is likely that the choice of a model is mainly governed by the expert’s acquaintance with a particular method, the DM’s way of thinking about her problem and the semantics of the model. A pragmatic approach consists of selecting a MCS method out of the shelve that matches some desired features. A recent attempt by Cinelli et al. (2022) proposes a decision support system for guiding an expert in choosing an existing MCDM/A method based on a taxonomy of problem characteristics and a database of methods.

• Experimenting with real or artificial data is a manner of exploring the expressiveness of models. In a Machine Learning (ML) perspective, models can be experimentally compared in terms of their accuracy in generalization⁵. Such comparisons clearly make sense when large sets of assignment examples are used in the experiments, and it is recognized that assignment errors are made with some probability. Nothing precludes the use of MCS models in a ML context. Some (few) have been tested in this way. However, in an MCDM/A context, such comparisons make less sense. Small sets of assignment examples used for indirect elicitation often do not allow to discriminate between different models (in terms of accuracy in generalization, for instance). We don’t know of experimental comparison of different MCS models using indirect elicitation methods on small datasets.

• In a decision-aiding process, the choice of a model relies on (or should rely on) (i) a clear understanding of the semantics and underlying concepts of the candidate models, (ii) a clear interpretation of these models’ parameters, and (iii) an understanding of the way the DM views the decision problem.

  One should expect of models that it is possible to analyze them and determine what are the primitives which an elicitation process can lean on meaningfully. This is not the case for all models. For instance, methods using a score and thresholds for determining categories (see Sect. 4.1.1) can be criticized in this respect. What does the score actually represent for the DM in the framework of a sorting decision problem? An overall numerical evaluation? A preference ranking? How is it built, and for what purpose? How is it related to the sorting issue? Analyzing such methods cannot be done in terms of the sole legitimate primitive, which is a partition of the objects in ordered categories. There is at least another unformulated, primitive behind the construction of the score. Therefore, using such methods entails a certain degree of arbitrariness.

  In contrast, a clear understanding of a sorting model requires the characterization of the ordered partitions (i.e., the primitive, of MCS problems) that can be represented in the model. The distinctive properties of the model should be identified. Performing such an analysis for each model helps to better understand the global picture of the field of MCS models. Section 2 in Part II (Belahcène et al. 2022) aims at presenting such a picture.

4.7.2 Choosing a model variant of appropriate generality

As reported in Sect. 4.2, several recent papers have introduced more complex versions of the two main MCS models, often by incorporating popular ideas from other sectors of decision sciences. Variants of the AVF model and Electre Tri have been proposed, in which interactions between criteria can be modeled. Such extensions were fostered by the development of the Choquet and the Sugeno integrals in various areas of decision theory. Similarly, the popularity of AHP, and the fact that structuring criteria in a hierarchy is frequent in applications, has led to variants of the two dominant models. More general Electre Tri models have appeared, in particular, those using several limiting or central profiles for each category.

Very general models involving many degrees of freedom should not be considered from the outset in MCDM/A decision-aiding processes. They should be used only when appropriate. Here are a few reasons supporting this statement.

• In statistical learning, classification and machine learning, using over-parameterized models leads to overfitting, a phenomenon characterized by better performance in learning but worse in generalization. Preferring parsimonious models is a golden rule of statistical inference.

  The concept of overfitting is inappropriate as such in the context of a decision-aiding process. Yet, a phenomenon of the same order occurs when using indirect elicitation to find a model’s parameter values compatible with a small set of assignment examples. In a “robust” approach, assignment recommendations are based on all the model instances compatible with the assignment examples. The more general the model, the larger the variety of model parameters compatible with the set of assignment examples (or fitting them equally well). Therefore, working with more general models typically leads to weaker recommendations for a given set of assignment examples.

• Indirect elicitation methods have been developed for increasingly complex value function models in the so-called robust ordinal regression (ROR) and the stochastic multicriteria acceptability analysis (SMAA) frameworks (see Sect. 3.4.1). In order to reduce the set of model instances to be taken into account in computing recommendations, the authors consider using information other than assignment examples. Their methods enable them to incorporate, for instance, statements about positive or negative interactions between criteria, the number of categories separating the assignments of a pair of objects, typical values of objects in a category, etc. It is unclear whether such statements made by the DM should be relied upon. It is especially the case with statements about the value of some model parameters because the DM may misinterpret the significance of such parameters in a model, see Podinovskii (1994), Roy and Mousseau (1996), Bouyssou et al. (2006, §4.4.1).

• The expressive power of simple models may be considerable. No systematic experiments have assessed the effect of using more or less general versions of models such as AVF or Electre Tri in a machine learning context. However, the experiments in Sobrie et al. (2019) show that a simple version of Electre Tri, MR-Sort, is competitive with UTADIS on a benchmark of large real data sets. This is all the more true when an indirect elicitation method for a simple MCS model is used with small sets of assignment examples in a decision-aiding process.

Instead of resorting a priori to general models, we believe that the simplest possible models should be used for decision-aiding. Models are structured in families. For instance, the multi-attribute value function family contains the weighted sum as a simple case; the AVF is more complex; still more complex are the Choquet integral or the multilinear model (Keeney and Raiffa 1976; Pelegrina et al. 2020). After having chosen a family of models, a sensible methodological practice consists of starting the decision-aiding process with a simple version of a model in the family and to move to a more complex model only in case the preferences of the decision maker cannot be taken into account in the simpler version. The sign that a model version is not adequate is that the DM does not agree with some assignment recommendations. Such disagreements usually result in new assignment examples and trigger another step in the decision-aiding process (see, e.g., Labreuche et al. 2015). Vague statements, for instance, about criteria importance or interactions, should be handled with great caution.

4.7.3 Remarks

We formulate below additional remarks on particular aspects.

Regularization in MCDM/A A classical way of handling overfitting in statistical learning is by adding a regularization term in the objective function. Such a term penalizes complex models, e.g., by tending to minimize the number of non-null parameters in the model⁶. This technique has been imported in MCDM/A, in particular in MCS methods like UTADIS (Doumpos and Zopounidis 2007) and models based on non-additive value functions (Liu et al. 2019). Dembczyński et al. (2006) compute AVFs that approach the lower and upper approximations of categories obtained by DRSA. The piecewise linear marginals in these AVF models are obtained by solving a regularized optimization problem. The regularization term aims at minimizing a measure of complexity of the marginals. In the framework of the multilinear model, Pelegrina et al. (2020) use a regularization technique to identify a simpler 2-additive capacity.

Few papers on MCS methods incorporate a regularization term when learning models. This is probably due to the emphasis on considering all compatible models, even complex, in the–much developed–robust ordinal regression approach.

Indirect elicitation algorithms complexity Indirect elicitation of the parameters of an AVF model (or a variant thereof) generally relies on an LP formulation. In contrast, eliciting the parameters of an Electre Tri model (or a variant thereof) requires solving a MILP formulation or, alternatively, a SAT formulation. Indeed, the latter requires modelling the fact that the evaluation of an object on each criterion is–or is not–at least as good as a profile value. This gives a strong computational advantage to dealing with the models in the AVF family over those in the outranking family. Indirect elicitation methods and robust methods for Electre Tri models are less developed. Usually, either it is assumed that some parameters are known, e.g., the profiles (as in Kadziński and Martyn 2021), or they are based on a modified model (as in Kadziński and Ciomek 2016).

Recommendation-oriented approaches The robust and the stochastic approaches, although based on a model, do not focus on identifying a particular instance of the model. Instead, they are recommendation-oriented. The robust approach initially aims at telling the DM what is true, possible or impossible in terms of assignments. The stochastic approach aims at saying what is more or less likely. We already noted in the discussion Sect. 3.5 that the recommendations resulting from a robust or a stochastic approach depend on the more or less general character of the model chosen. The more general the model, the less precise the robust recommendations.

Appendices

Appendix A: The outranking relation in Electre  III

We give below, for the reader’s convenience a definition of the outranking relation used in Electre  III, which is the one involved in the classical version of Electre Tri (Roy and Bouyssou 1993).

Its definition involves the computation of a concordance index, a discordance index and a degree of credibility of outranking.

Let x, y be two objects whose evaluations on criterion i are, respectively, $x_i, y_i$ for $i=1, \ldots , n$. The concordance index c(x, y) is defined by $c(x,y) = \sum _{i=1}^{n} w_i c_i(x_i, y_i)$, where $w_i \ge 0$ is the importance weight of criterion i (we assume w.l.o.g. that weights sum up to 1) and $c_i(x_i, y_i)$ is a function represented in Fig. 1. Its definition involves the determination of $q_i$ (resp. $p_i$), the indifference (resp. preference) threshold.

Fig. 1

Shapes of the single criterion concordance index $c_i(x_i, y_i)$ and the discordance index $d_i(x_i, y_i)$ in Electre III and Electre Tri

The discordance index $d_i(x_i, y_i)$, also represented in Fig. 1, uses an additional parameter $v_i$, the veto threshold⁷.

The outranking credibility index $\sigma (x,y)$ is computed as follows:

$$\begin{aligned} \sigma (x,y)= c(x,y) \prod _{i: d_i(x_i, y_i) > c(x,y)} \frac{1-d_i(x_i, y_i)}{1-c(x,y)}. \end{aligned}$$

(7)

The outranking relation S can now be defined. Object x outranks object y, i.e., xSy, if $\sigma (x,y) \ge \lambda$, with the threshold $\lambda$ verifying $.5 \le \lambda \le 1$.

In order that x outranks y, c(x, y) has to be greater than or equal to $\lambda$. This index is “locally compensatory” in the sense that, for each i, there is an interval (namely, $[-p_i, -q_i]$) for the differences $x_i - y_i$ on which the single criterion concordance index increases linearly and these indices are aggregated using a weighted sum. Discordance also is gradual in a certain zone (namely $[-v_i, -p_i]$); it comes into play only when the discordance index $d_i(x_i , y_i)$ is greater than the overall concordance index c(x, y).

Appendix B: The outranking relation in Electre  I

A simpler, more ordinal, version of the construction of an outranking relation stands in the spirit of Electre I. It is the version used in MR-Sort (which does not use vetoes). It differs from the outranking relation in Electre  III mainly by the shapes of the single criterion concordance and discordance indices.

Fig. 2

Shapes of the single criterion concordance index $c_i(x_i ,y_i)$ and the discordance index $d_i(x_i,y_i)$ in the style of Electre I. Empty (resp. filled) circles indicate excluded (resp. included) values

The preference and indifference thresholds are confounded, which implies that there is no linear “compensatory” part in $c_i(x_i ,y_i)$; discordance only occurs in an all-or-nothing manner. The overall concordance index is defined by $c(x,y) = \sum _{i=1}^{n} w_i c_i(g_i(x) ,g_i(y))$, as above. In this construction, x outranks y, i.e., xSy, if $\sigma (x,y) \ge \lambda$, with

$$\begin{aligned} \sigma (x,y)= c(x,y) \prod _{i=1}^{n} (1-d_i(x_i ,y_i)), \end{aligned}$$

(8)

i.e., xSy if $c(x,y) \ge \lambda$ and $d_i(x_i ,y_i) =0$, for all i. Note that

$$\begin{aligned} c(x,y) = \sum _{i:x_i \ge y_i-q_i} w_i. \end{aligned}$$

We thus have $c(x,y) \ge \lambda$ if the sum of the weights of the criteria on which x is indifferent or strictly preferred to y is at least equal to $\lambda$.

Appendix C: List of abbreviations

For the reader’s convenience, we list below, in alphabetic order, the acronyms used in the text, except for acronyms of sorting methods.

• AVF: Additive Value Function

• CAI: Class Acceptability Index

• DM: Decision Maker

• DRSA: Dominance based Rough Sets Approach

• LP: Linear Program

• MCDM/A: Multiple Criteria Decision Making / Aiding

• MCS: Multiple Criteria Sorting

• MILP: Mixed Integer Linear Program

• ML: Machine Learning

• MOP: Monotone Ordered Partition

• PL: Preference Learning

• ROR: Robust Ordinal Regression

• SMAA: Stochatic Multicriteria Acceptability Analysis

• VF: Value Function

Appendix D: Complements

1.1 D.1 Complements to Sect. 3.5

Selecting a “central” model in the set of models compatible with assignment examples is a default rule that is supported by intuition. Experimental studies (Doumpos et al. 2014) show that the “centrality option” implicitly implements an idea of robustness. For a model, being “central” means that its parameters are far from violating the constraints induced by the assignment examples. However, this default option is not univocally defined (because centrality is not a totally clear notion) and sounds partly arbitrary (because the robustness principle is not made explicit).

In contrast, the principle of the robust approaches is to take into account all compatible models and to qualify the recommended assignments as being shared by all compatible models (necessary assignments), by some of these models (possible assignments) or by a fraction of them (probabilistic assignments). Although these ideas of robustness are appealing and likely useful in practice, they are not as unquestionable as they look at first glance. The following observations are in order.

Regarding the possibility/necessity approach, note that:

• Relying only on possible and necessary assignments for the recommendations will often be inefficient in practice (because, often, the range of possible assignments is large, and the set of necessary assignments may be empty). Using Greco et al. “representative value function” requires interactions with a DM, while the behavior of Kadziński and Tervonen’s representative model, which does not require interaction, has not been tested experimentally.

• The sets of possible and necessary assignments depend on the more or less general character of the model considered. They differ when we restrict the additive value function model to have linear marginals (i.e., when the model is a weighted sum) or to have piecewise linear marginals with a fixed number of segments or if we do not impose any restriction on the marginals. Obviously, the more general the model considered in the indirect elicitation process, the larger the set of possible assignments and the smaller the necessary assignments (for a given set of assignment examples). Therefore, the idea of necessary and possible assignments is not self-evident and should never be discussed without explicitly mentioning the precise underlying model.

Regarding the probabilistic approach to robustness (SMAA), in addition to being dependent on the general character of the model, there is an additional dependence of the simulation results on the choice of a probability distribution on the set of feasible parameters. Doumpos et al. (2014) postulate a uniform distribution and make their simulations accordingly. They experiment with the elicitation of an AVF with linear marginals and of the more general model using piecewise linear marginals (while the set of assignment examples and the test sets are generated by random models with linear marginals). They observe that the assignment accuracy degrades for all rules, including the two rules based on simulation (CAI-based and centroid) when a more general model (using piecewise linear marginals) is used.

From a purely experimental point of view, Doumpos et al.’s study tends to establish that the CAI-based and centroid rules (resulting from simulation with uniform distribution) show (slightly) better performance than the models implementing the centrality paradigm, in particular w.r.t. assignment accuracy on test sets. However, the following reservations can be made.

• In general, there is no single Additive Value Function (AVF) model producing the same assignments as the CAI-based rule. Therefore, assignment accuracy comparisons with rules corresponding to such a model are biased. The performance of the centroid rule is close to that of the CAI rule, but there is no clearcut experimental evidence that the centroid model beats the most accurate central rules. Experimental comparisons involving the “representative value function” are not available to date.

• Doumpos et al. (2014) conclusions rely on artificial assignment data generated by random additive value functions with linear marginals. One may wonder whether the same conclusions would emerge from experiments based on real assignment data, artificial data generated by another model, or noisy artificial data (i.e., assignments generated by a known model subsequently altered by random errors).

From a practical point of view, if a DM is available for interactions, the model instance elicited on the basis of assignments known or provided by the DM can be useful for triggering DM’s reactions and providing additional information. Elements such as possible and necessary assignments or indices such as CAI may help too. However, there is no evidence that proposing “representative” additive value function models would stimulate interactions more efficiently or accurately than the central or centroid models. Obtaining such evidence appears to be quite challenging.

Ending up an interactive process with a singled out model aiming to reflect the DM’s assignment mechanism is desirable. Such a model provides a compact representation of the assignment rule used by the DM and allows the generation of new assignments. It also provides a form of explanation or justification for the assignments (e.g., “this object is assigned to that category because its value is good enough for that; to be assigned to a better category, its value should be improved by at least this amount”). This is an advantage compared to a rule, such as the CAI-based rule, whose interpretation is more opaque to the DM.

The above discussion has focused on the additive value function model. The investigations relative to the Electre Tri model are much more limited, probably due to the algorithmic complexity eliciting the parameters of such a model. Note that the idea of robust assignment, in the guise of a range of possible assignments, was already present in Dias et al. (2002).

1.2 D.2 Complements to Sect. 4.1.1

Three examples of a sorting method derived from a ranking method:

• AHPsort (Ishizaka et al. 2012) builds on AHP, the “Analytic Hierarchy Process”, Saaty (1977, 1980)). AHP is a method for evaluating multi-dimensional objects using pairwise comparison judgments. These are supposed to be made in reference to underlying ratio scales of measurement (for assessing objects w.r.t. criteria and the relative importance of criteria). The result of the procedure is an evaluation, called priority, of each object in the form of a weighted sum of measurements on each criterion⁸. AHPSort characterizes categories either by limiting profiles or by central profiles. In both cases, for each object, the priorities of the object and all the profiles are computed through pairwise comparisons. The priorities of the limiting profiles define intervals of the real line. Each object is assigned to the category corresponding to the interval where its priority belongs. When using central profiles, the central profile having its priority closest to that of the object determines the category assigned to the object.

• MACBETHSort (Ishizaka and Gordon 2017) elaborates on the ranking method MACBETH (Bana e Costa and Vansnick 1994; Bana e Costa et al. 2005). The latter is a method for building an additive value function that is cardinal, i.e., the value differences represent the difference of preferences. In contrast, the value function used in UTADIS is ordinal because it allows one to rank the objects but not to assess the difference of preference between them. The model underlying MACBETH is thus much more constrained (i.e., a particular case of the additive value function model). MACBETHSort uses either limiting or central profiles. The MACBETH method is used to assess objects and profiles by an additive value function. The assignment to categories follows the same idea as in AHPSort.

• DEA-based sorting (Karasakal and Aker 2017) is a more complex proposal mixing techniques from AHP and DEA (Data Envelopment Analysis). A version of AHP using interval evaluations in pairwise comparisons yields interval values for criteria weights. One idea taken from DEA is to assess objects by using the set of weight values that is most favorable for them. Reference profiles are used for sorting. DEASort (Ishizaka et al. 2018) seems to have been developed independently. It is based on similar ideas (AHP and DEA). Classification thresholds on object evaluations are obtained by training a decision tree on reference assignments.

Three examples of sorting methods derived from an ideal point ranking method:

• TOPSIS-Sort (Sabokbar et al. 2016) adapts TOPSIS (Hwang and Yoon 1981) to sorting. TOPSIS ranks objects by computing their (Euclidean) distance to an ideal point and from an anti-ideal point. The closest to the ideal and the farthest to the anti-ideal, the better. Computing these distances for limiting profiles allows sorting objects in ordered categories (same way as in AHPSort).

• VIKORSORT (Demir et al. 2018) builds upon the ranking method VIKOR (Opricovic and Tzeng 2004; Duckstein and Opricovic 1980) relying on compromise programming (Zeleny 1973). VIKOR establishes a “compromise ranking” through the use of (a mixture of) two different distances (L$_1$, L$_{\infty }$) of objects from an ideal point. The assignment rule in VIKORSORT assigns objects to categories by comparing them to limiting profiles in terms of distance to an ideal point.

• The “case-based distance model for sorting” (Chen et al. 2007) requires that the DM provides assignment examples (cases) for each category. The centroid of the cases assigned to the best category furnishes an ideal point. The idea is that the cases assigned to the same category should be approximately equidistant from the ideal point, and the closer the category is to the ideal point, the better the category. The method aims at finding criteria weights and thresholds on the weighted (Euclidean) distance to the ideal point such that objects are assigned to the same category whenever their distance to the ideal point falls between two consecutive thresholds. The preference order on the categories is the succession order of the intervals between consecutive thresholds. Criteria weights and distance thresholds are obtained by solving an optimization problem that minimizes the sum of slack variables needed to enforce the application of the assignment rule on the set of available cases. This method is much in the spirit of UTADIS. The underlying model assumes that categories can be defined as the sets of objects whose distance from an ideal point is comprised between two thresholds. The method consists of eliciting the parameters of such a model based on assignment examples.

1.3 D.3 Complements to Sect. 4.1.2

Examples of PROMETHEE-based sorting methods PROMETHEE (Brans and Vincke 1985) is a ranking method based on a valued outranking relation $\sigma (x,y)$ ($x,y \in A$, where A is a finite set of objects). The $\sigma$ values are computed in a different way as in Electre. They represent the intensity of preference of x over y. Using matrix $\sigma$, three scores can be obtained. The out-flow (resp. in-flow) of object x is the sum in row (resp. column) of matrix $\sigma$, i.e., the sum over y of the values $\sigma (x,y)$ (resp. $\sigma (y,x)$). The net-flow is defined as the out-flow minus the in-flow. The following rule obtains a partial preorder on the objects in A: x is at least as preferred as y if the out-flow of x is not smaller than the out-flow of y and the other way around for their in-flows (PROMETHEE I). A complete preorder is obtained using the net flow (PROMETHEE II).

FlowSort (Nemery and Lamboray 2008) uses either limiting or central profiles. For each object x, one considers the set A containing x and all the profiles. Computing the three flows and using them as scores allows sorting objects in categories based on the profiles’ scores. The net flow score assigns objects to a category in-between those assigned by the in-flow and the out-flow. PromSort (Araz and Ozkarahan 2007) and PROMETHEE TRI (De Smet 2019; Figueira et al. 2004) also rely on the PROMETHEE flows. They differ by the way they use them in assignment rules.

Assignment rules applicable to valued preference relations Some papers formulate principles of assignment rules that can be applied to valued (or fuzzy) preference relations, such as those built in Electre or Promethee methods. Perny (1998) assigns an object to the category that maximizes a membership degree. The latter combines, by means of fuzzy logic operators, degrees of concordance and non-discordance of an object w.r.t. to limit profiles of the categories.

THESEUS (Fernández and Navarro 2011) starts from an unspecified valued binary relation $\sigma (x,y)$ and a threshold $\lambda$. The valued (or fuzzy) relation $\sigma$ may be constructed as in Electre or in Promethee, or otherwise. Five crisp binary relations are defined using $\sigma$ and $\lambda$ (outranking, strict preference, weak preference, indifference and incomparability). A set of reference profiles (at least one per category, possibly many) is assumed to be available. THESEUS assigns an object by taking into account the five possible relations between the object and all reference profiles.

1.4 D.4 Complements to Sect. 4.6

1.4.1 D.4.1 Incremental elicitation/active learning

In case the parameters of a model (in particular, a sorting model) have to be elicited by asking questions to a DM, it is of interest to optimize the sequence of questions. This generally means maximizing the expected information obtained from each question (which consists of asking the DM to assign an object to a category). Benabbou et al. (2017) apply a min max regret approach to elicit a capacity for models based on the Choquet integral in choice, ranking and sorting problems.

In the framework of AVF model with thresholds, Kadziński and Ciomek (2021) propose and test empirically a number of heuristic strategies to choose the next object that the DM will be asked to assign. The DM may answer by assigning the object to a category interval. After each answer, the “robust approach” is applied in order to determine the set of possible category assignments for each object. The SMAA approach is possibly also applied to compute each object’s class acceptability index (CAI). One of the tested heuristics selects an object whose current assignment is maximally imprecise; another chooses an object for which the entropy of the CAI probability distribution is maximal. The general idea of these heuristics is to reduce as much as possible the assignment indeterminacy at each step.

1.4.2 D.4.2 Constrained sorting problems

Constraints on the cardinality of categories have already been considered in Sect. 4.4. Besides modelling possible wishes of the DM, it is also a means for limiting the indeterminacy of the model in order to obtain more precise assignments in the robust approach. Kadziński and Słowiński (2013), Köksalan et al. (2017) deal with such constraints in the framework of the additive value function model; Özpeynirci et al. (2018) do the same for MRSort and the additive value function model too.

1.4.3 D.4.3 Group decision

For addressing multiple criteria sorting problems in a group decision-making context, it is pretty natural to start by building sorting models reflecting the views of each group member. In the second step, tools aiding in reaching a consensus are developed.

Damart et al. (2007) and Greco et al. (2012) do so in the framework of the AVF model. The group members provide assignment examples. In both papers, the consensus-seeking process takes advantage of the fact that the provided assignment examples do not fully determine the group members’ AVF models. Assignments to category intervals (Damart et al. 2007) or necessary and possible assignments (Greco et al. 2012) computed for each group member help in building a consensus.

de Morais Bezerra et al. (2017) elicit an Electre Tri model for each group member. They use a graphical interface (VICA) to compare the assignments produced by the group members sorting models. They try to reach a consensus by identifying assignments supported by a majority of the group members.

Chen et al. (2011) rely on assignment examples provided by each group member. They use DRSA to induce rules from the assignment examples and Dempster-Shafer theory of evidence to aggregate these rules. The most plausible assignments based on aggregated rules are selected.

Contributions to group decision for sorting are relatively scarce. Some further references are listed in Alvarez et al. (2021).

1.4.4 D.4.4 Non-monotone criteria or attributes

The preference is not always monotone (nondecreasing or nonincreasing) with the evaluations. For instance, in evaluating patients before surgery, the doctors’ preference about glycemia is neither “the more, the better” nor “, the less, the better”. There is an optimal value range; preference decreases above and below it. The assignment may not be monotone w.r.t. the value of some evaluations. However, in the case considered here, it is possible to reorder or re-code the evaluations in such a way that the assignment is monotone w.r.t. re-coded evaluations.

Guo et al. (2019) propose a method for progressively constructing an AVF sorting model with non-necessarily monotonic marginals. The non-monotone dimensions are single-peaked. The DM is asked to reveal her most preferred value on the scale. The first approximation of the corresponding marginal is linear nondecreasing up to the most preferred value and nonincreasing thereafter. The shape of the marginal is further refined in the following steps. In the same framework of AVF-based sorting models, Liu et al. (2019) learn non necessarily monotonic piecewise linear marginals. In order to limit overfitting, they add a regularization term to the loss function they want to minimize. Such a term may for instance aim at minimizing the slope variations at the breakpoint of the piecewise linear marginals.

Minoungou et al. (2022) address non-monotone criteria in outranking-based sorting, namely, using the MR-Sort model. They propose a MIP formulation for eliciting the parameters of MR-Sort based on assignment examples with non-necessarily monotone criteria. Their formulation recognizes cost, gain, single-peaked and single-valley criteria.

We come back on this, at the end of Sect. 2.1 in Part II (Belahcène et al. 2022), situating the criteria non-monotonicity issue in a general picture of sorting models.

1.4.5 D.4.5 Trichotomic forerunners

Sorting in three ordered categories (sometimes called trichotomic segmentation) has attracted particular attention before general MCS methods started to develop. Sorting requests for credit in a bank is an often cited example. Banks may want to make an initial rough rating of loan applicants by categorizing them into three categories: acceptable, refused and an intermediate category for which there is an hesitation on the decision, thus requiring further inquiry. The papers by Moscarola and Roy (1977) and Roy (1981), relying on an outranking relation à la Electre, were already cited in Sect. 1. In a similar vein, relying on an Electre-III outranking relation, Massaglia and Ostanello (1991) proposed nTOMIC, a method for segmenting objects in three categories with further refinement of the intermediate categories in five subcategories. The method was implemented in a software tool supporting all stages of the segmentation process (including the reference profiles, i.e., limiting profiles as in Electre Tri⁹.)

ABC analysis Another segmentation in three categories has been used for a long in inventory management, known as ABC analysis. The principle of classifying goods in storage into three categories is inspired by the famous 80–20 Pareto rule, in which a small percentage of a country’s population (typically 20%) generates the largest part of its output (typically 80%). Applied to inventory management, this idea leads to apply of tight control on goods in category A, which contains a small percentage (10 to 20%) of the inventory responsible for 60 to 80% of the total dollar usage (the annual dollar usage of a good is its cost time the annual volume of the demand). Category B (resp. C) is constituted of the goods responsible for about 30% (resp. 5 to 15%) of the total dollar usage; they represent 20 to 25% (resp. 50 to 60%) of the inventory. Category B receives less control than category A, and category C receives low control.

It was soon realized that dollar usage was not the sole criterion to take into account to assign goods into categories A, B or C. For instance, flexibility in production, scheduling, and reducing costs including costs of shortage and storage, may be important factors. Starting with Flores and Whybark (1986), a number of methods have been proposed to classify items in categories A, B or C, taking into account several criteria. Many MCS models have been adapted to that particular context, in which category A should collect a small number of items the control of which is crucial and category C a large number of items whose control may be relaxed (such requirements echo constraints on category cardinality, see Sect. D.4.2). Papers on ABC classification based on MCDM/A methods include e.g., Liu et al. (2016), based on Electre-III, and Kheybari et al. (2019), based on TOPSIS and goal programming (see also the references therein). Chen et al. (2008) propose a method for eliciting an ABC categorization on the basis of assignment examples (“case-based learning”). They use their “case-based distance model for sorting” (see last item in Sect. D.2).

1.4.6 D.4.6 Around sorting

Multiple Criteria Sorting (MCS) is a particular case of classification in which (i) categories are known a priori, in particular, their number is fixed, (ii) categories are totally ordered in terms of preference, (iii) assignment to categories respects the dominance relation, i.e., an object at least as good as another w.r.t. all criteria is not assigned to a worse category. This specification makes MCS close to Monotone Classification. However, the notion of a model is more central in MCS. Historically, model parameters had to be elicited by questioning a DM. In contrast, learning from cases is typical of (monotone) classification. Therefore, classification literature focuses on algorithms. A recent review on monotonic classification (Cano et al. 2019) does not mention any model within the two main families analyzed in the present paper (i.e., AVF- and outranking-based); only DRSA and the methods in Sect. 4.5.3 are discussed.

Some work done in the MCDA community falls within the field of classification or clustering but departs from MCS. Some of these relate to clustering. Usually, clustering algorithms are unsupervised techniques that form clusters of objects characterized by a n-tuple of attribute values. A cluster contains objects that are similar and as dissimilar as possible from the objects in the other clusters. The number of clusters may be fixed or not.

1.4.7 D.4.7 Multiple-criteria clustering

In Multiple Criteria Clustering (MCC), there is a preference direction on all attributes. Rosenfeld et al. (2021) distinguish three types of MCC : nominal, relational or ordered.

An early example of nominal clustering (De Smet and Montano Guzmán 2004) is based on a binary preference relation (neither necessarily complete nor transitive, such as a crisp outranking relation). A distance is defined: for any pair of objects, the more similar the sets of other objects they are preferred to, the smaller their distance. Based on such a distance, clusters are formed using a k-means algorithm.

De Smet et al. (2012) present an example of ordered clustering algorithm. The number of clusters is fixed, and the result is an ordered partition (yet it is not made clear whether the clustering algorithm always respects the dominance relation). Given a valued preference relation on objects (as those obtained using Promethee or Electre  III, for instance), an inconsistency matrix is associated with each ordered partition (into a fixed number of categories). The clustering algorithm finds an ordered partition minimizing inconsistency in a certain (lexicographic) sense.

In the intermediate type of MCC, i.e., relational clustering, a binary relation on clusters is obtained, which is a partial order. Eppe et al. (2014), Rocha et al. (2012) are examples of papers in that vein.

MCC exhibits characteristics that contrast with MCS, even in case the clusters are totally ordered. MCC pertains to data analysis. Existing MCC methods identify groups in a given dataset (with the peculiarity that there is a preference order on the attributes scales). They do not end up with a model that could predict the assignment of new objects to one of the clusters.

1.4.8 D.4.8 Nominal classification

Some methods for assigning objects to predefined unordered categories have been proposed within the MCDA community.

Multicriteria filtering We referred to Perny (1998) in Sect. 4.1.2. The principles exposed in this paper apply to ranking, sorting in ordered categories and assigning to unordered categories on the basis of fuzzy relations, implementing a concordance and non-discordance principle (as in the ELECTRE methods). In case of assigning to unordered categories, the fuzzy relation models indifference between an object and prototypes in each category. The membership of an object to a category is obtained by taking the maximum of the indifference degrees between the object and the prototypes characterizing the category (or more generally, by applying a t-conorm operator to these indifference degrees).

PROAFTN While Perny (1998) mainly describes and illustrates principles, Belacel (2000) proposes an instantiation of these principles in a method called PROAFTN. A valued indifference degree between objects and prototypes is built in the spirit of the outranking relation in Electre III. The degree of membership of an object to a category is the largest indifference degree between the object and the prototypes in the category. Each object is assigned to the category maximizing its membership degree.

In contrast with nominal clustering (e.g., De Smet and Montano Guzmán 2004), PROAFTN builds a model allowing to assign any new object. Originally, the user had to set the parameters defining the valued indifference degree (weights and thresholds). Several approaches for eliciting the model parameters have been proposed since then (see, e.g., Belacel et al. (2007), who design a variable neighborhood search heuristic).

CAT-SD As compared to PROAFTN, Costa et al. (2018) propose a more general way of constructing a membership degree (called degree of likeness) of an object to a category. This membership degree combines (again, in the style of ELECTRE III) an overall similarity and an overall dissimilarity functions¹⁰. Interactions between criteria can be modelled. The category assigned to an object is not necessarily unique. An object is assigned to all categories in which it has a membership degree above some threshold (such an assignment rule was already in Perny (1998). The resulting method is called CAT-SD. Costa et al. (2020) add further ingredients: a hierarchical structure of the criteria and the application of a SMAA methodology to obtain assignment probabilities. A deterministic assignment rule minimizing a loss function is also computed.