A theoretical look at Electre Tri-nB and related sorting models

Abstract

Electre Tri is a set of methods designed to sort alternatives evaluated on several criteria into ordered categories. In these methods, alternatives are assigned to categories by comparing them with reference profiles that represent either the boundary or central elements of the category. The original Electre Tri-B method uses one limiting profile for separating a category from the category below. A more recent method, Electre Tri-nB, allows one to use several limiting profiles for the same purpose. We investigate the properties of Electre Tri-nB using a conjoint measurement framework. When the number of limiting profiles used to define each category is not restricted, Electre Tri-nB is easy to characterize axiomatically and is found to be equivalent to several other methods proposed in the literature. We extend this result in various directions.

1 Introduction

Electre Tri¹ is a family of methods for sorting alternatives evaluated on several criteria into ordered categories. The principle of these methods is that they assign an alternative to a category by comparing it with profiles specifying levels on each criterion. Comparisons are made by using an outranking relation which is typical of the Electre methods. In its original version, ETri-B (Yu 1992; Roy and Bouyssou 1993), each profile represents the limit between a category and the category below. Therefore, they are called limiting profiles. In contrast, in ETri-C (Almeida-Dias et al. 2010), each category is represented by a typical profile, therefore called central profile.

For an introduction to the Electre methods, we refer the reader to Belton and Stewart (2001)[Ch. 8]. Overviews of these methods can be found in Roy and Bouyssou (1993)[Ch. 5 & 6], Figueira et al. (2010, 2013, 2016).

Recently, Fernández et al. (2017) proposed a method called Electre Tri-nB. It is an extension of ETri-B, and, thus, uses limiting profiles. Whereas ETri-B uses one limiting profile per category, ETri-nB allows one to use several limiting profiles for each category.

ETri-nB deserves close attention for at least two reasons. First, as explained in Bouyssou and Marchant (2015), ETrican be considered as a real success story within the Electre family of methods. A closely related model, the NonCompensatory Sorting (NCS) model, has received a fairly complete axiomatic analysis in Bouyssou and Marchant (2007a, 2007b). ETrihas been applied to a large variety of real world problems (see the references in Almeida-Dias et al. 2010, Sect. 6, as well as Bisdorff et al. 2015, Ch. 6, 10, 12, 13, 15, 16). Many techniques have been proposed for the elicitation of the parameters of this method (see the references in Bouyssou and Marchant 2015, Sect. 1).

Second, the extension presented with ETri-nB is most welcome. Since outranking relations are not necessarily complete, one may easily argue that it is natural to try to characterize a category using several limiting profiles, instead of just one. Moreover, compared to ETri-B, ETri-nB gives more flexibility to the decision-maker to define categories using limiting profiles, as observed by Fernández et al. (2017)[Remark 3, p. 217] ².

In this paper, we analyze ETri-nB from a theoretical point of view. Our aim is to give a complete characterization of this method without any supplementary hypotheses. This is, in a sense, in contrast with Bouyssou and Marchant (2007a, 2007b) who characterize a model close to ETri-B, which is not exactly ETri-B (it differs from it, in particular, by considering “quasi-criteria” instead of the more general “pseudo-criteria” used in ETri-B, see Roy and Bouyssou,1993, pp. 55–56, for definitions). As far as we know, this is the first time that an axiomatic foundation is provided for a complete outranking method (encompassing the construction of the outranking relation and the exploitation phase). The usefulness of such axiomatic analyses has been discussed elsewhere and will not be repeated here (Bouyssou and Pirlot 2015; Dekel and Lipman 2010; Gilboa et al. 2019). Our main finding is that, if the number of profiles used to delimit each category is not restricted, the axiomatic analysis of ETri-nB is easy and rests on a condition, linearity, that is familiar in the analysis of sorting models (Goldstein 1991; Bouyssou and Marchant 2007a, b, 2010; Greco et al. 2004; Słowiński et al. 2002; Greco et al. 2001b). Our simple result shows the equivalence between ETri-nB  and many other sorting models proposed in the literature. It could also allow one to use elicitation or learning techniques developed for these other models for the application of ETri-nB. This is useful since Fernández et al. (2017) did not propose any elicitation technique (an elicitation technique was suggested afterwards in Fernández et al. 2019).

The rest of this text is organized as follows. In the next section, we recall the definitions of ETri-B and ETri-nB. We motivate the theoretical investigation that follows by analyzing an example of an ETri-nB  model. Section 3 introduces our notation and framework. Section 4 presents our main results about the pseudo-conjunctive version of ETri-nB. Section 5 presents various extensions of these results. A final section discusses our findings. An appendix, containing supplementary material to this paper, will allow us to keep the text of manageable length. Its content will be detailed when needed.

2 ETri-nB: definitions and examples

For the ease of future reference, we first recall the definitions of ETri-B and ETri-nB. For keeping it simple, we limit ourselves to sorting alternatives into two categories, say the “acceptable” and the “unacceptable”. For a more detailed description, we refer the reader to Yu (1992); Roy and Bouyssou (1993); Mousseau et al. (2000); Fernández et al. (2017). We refer to Bouyssou and Marchant (2015) for an analysis of the importance of the various Electre Tri methods within the set of all Electre methods.

In the second subsection, we informally analyze an example of an ETri-nB model in order to motivate the theoretical investigation conducted in the rest of the paper.

2.1 ETri-B and ETri-nB

All Electre Tri methods are based on the definition of an outranking relation. There are several ways of defining such a relation.

2.1.1 The outranking relations in Electre III and in Electre I

A crisp outranking relation S (with asymmetric part P) comparing pairs of alternatives as in Electre III (see Roy and Bouyssou 1993, pp. 284–289) is built by cutting a valued relation $\sigma$ at a certain level $\lambda$. The value associated to each pair in the relation $\sigma$ is called the outranking credibility index. It implements (see formula (1) below) the principle of outranking, i.e.,  an alternative x outranks an alternative y if x is at least as good as y on a sufficiently important set of criteria (concordance) and x is unacceptably worse than y on no criterion (non-discordance). Let x, y be two alternatives respectively represented by their evaluations $(g_1(x), \ldots g_i(x), \ldots g_n(x))$, $(g_1(y), \ldots , g_i(y), \ldots , g_n(y))$ w.r.t. n criteria. For all $i=1, \ldots , n$, $g_i$ is a real valued function defined on the set of alternatives.

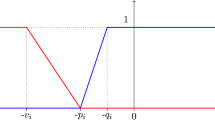
The concordance index $c(x,y) = \sum _{i=1}^{n} w_i c_i(g_i(x), g_i(y))$, where $w_i \ge 0$ is the importance weight of criterion i (we assume w.l.o.g.  that weights sum up to 1) and $c_i(g_i(x), g_i(y))$ is a function represented in Fig. 1. Its definition involves the determination of $qt_i$ (resp. $pt_i$), the indifference (resp. preference) threshold. These two thresholds are nonnegative and such that $pt_{i} \ge qt_{i}$.

Fig. 1

Shapes of the single criterion concordance index $c_i(g_i(x), g_i(y))$ (gray) and the discordance index $d_i(g_i(x), g_i(y))$ (black dashed) in Electre III. The two indices are a function of the difference $g_i(x) - g_i(y)$ and the three nonnegative thresholds: $vt_{i} \ge pt_{i} \ge qt_{i} \ge 0$.

The discordance index $d_i(g_i(x), g_i(y))$, also represented in Fig. 1, uses an additional parameter $vt_i$, the veto threshold³ (that is such that $vt_{i} \ge pt_{i}$, so that we have $vt_{i} \ge pt_{i} \ge qt_{i} \ge 0$).

The outranking credibility index $\sigma (x,y)$ is computed as follows:

$$\begin{aligned} \sigma (x,y)= c(x,y) \prod _{i: d_i(g_i(x) ,g_i(y)) > c(x,y)} \frac{1-d_i(g_i(x) ,g_i(y))}{1-c(x,y)}. \end{aligned}$$

(1)

Alternative x outranks alternative y, i.e.,  xSy, if $\sigma (x,y) \ge \lambda$, with $.5 \le \lambda \le 1$.

In order that x outranks y, c(x, y) has to be greater than or equal to $\lambda$. This index is “locally compensatory” in the sense that, for each i, there is an interval (namely, $[-pt_i, -qt_i]$) for the differences $g_i(x) - g_i(y)$ on which the single criterion concordance index increases linearly and these indices are aggregated using a weighted sum. Discordance also is gradual in a certain zone (namely $[-vt_i, -pt_i]$); it comes into play only when the discordance index $d_i(g_i(x) ,g_i(y))$ is greater than the overall concordance index c(x, y).

A simpler, more ordinal, version of the construction of an outranking relation stands in the spirit of Electre I. It is also more amenable to theoretical investigation: see the characterization of outranking relations (Bouyssou and Pirlot 2016) and the analysis of the noncompensatory sorting model (Bouyssou and Marchant 2007a, b). It differs from the above mainly by the shapes of the single criterion concordance and discordance indices (see Fig. 2).

Fig. 2

Shapes of the single criterion concordance index $c_i(g_i(x) ,g_i(y))$ (gray) and the discordance index $d_i(g_i(x) ,g_i(y))$ (black dashed) in the style of Electre I. The two indices are a function of the difference $g_i(x) - g_i(y)$ and the three nonnegative thresholds: $vt_{i} \ge pt_{i} \ge qt_{i} \ge 0$ Filled (resp. empty) circles indicate included (resp. excluded) values

The preference and indifference thresholds are confounded, which implies that there is no linear “compensatory” part in $c_i(g_i(x) ,g_i(y))$; discordance only occurs in an all-or-nothing manner. The overall concordance index $c(x,y) = \sum _{i=1}^{n} w_i c_i(g_i(x) ,g_i(y))$, as above. In this construction, x outranks y, i.e.,  xSy, if $\sigma (x,y) \ge \lambda$, with

$$\begin{aligned} \sigma (x,y)= c(x,y) \prod _{i=1}^{n} (1-d_i(g_i(x) ,g_i(y))), \end{aligned}$$

(2)

i.e.,  xSy if $c(x,y) \ge \lambda$ and $d_i(g_i(x) ,g_i(y)) =0$, for all i. Note that

$$\begin{aligned} c(x,y) = \sum _{i:g_i(x) \ge g_i(y)-qt_i} w_i. \end{aligned}$$

We thus have $c(x,y) \ge \lambda$ if the sum of the weights of the criteria on which x is indifferent or strictly preferred to y is at least equal to $\lambda$. Subsets of criteria of which the sum of the weights is at least $\lambda$ will be called winning coalitions (of criteria).

Notice that both the Electre III outranking relation defined by means of (1) and the Electre I outranking relation defined by means of (2) respect the dominance relation⁴$\ge$. This is easily seen by observing that both formulae (1) and (2) are nondecreasing in $g_i(x)$ and nonincreasing in $g_i(y)$, for all i. We note this fact in the following proposition for further reference.

Proposition 1

Let S denote an outranking relation of Electre III or Electre I type. The relation S respects the dominance relation $\ge$, i.e.,  for all alternatives x, y, z, w,

$$\begin{aligned}{}[xSy, z\ge x \ \text {and} \ y \ge w] \quad \Rightarrow \quad zSw. \end{aligned}$$

2.1.2 ETri-B

The sorting of an alternative x into category $\mathcal {A}$ (acceptable) or $\mathcal {U}$ (unacceptable) is based upon the comparison of x with a limiting profile  p using the relation $\mathrel {S}$.

In the pessimistic version of ETri-B, now known, following Almeida-Dias et al. (2010), as the pseudo-conjunctive version (ETri-B-pc  ), we have, for all $x \in X$,

$$\begin{aligned} x \in \mathcal {A}\Leftrightarrow x \mathrel {S}p. \end{aligned}$$

In the optimistic version of Electre Tri, now known as the pseudo-disjunctive version (ETri-B-pd  ), we have, for all $x \in X$,

$$\begin{aligned} x \in \mathcal {A}\Leftrightarrow {\textit{Not}}[p \mathrel {P}x ], \end{aligned}$$

where $\mathrel {P}$ is the asymmetric part of $\mathrel {S}$. Consequently, we have $x \in \mathcal {U}\iff p \mathrel {P}x$.

2.1.3 ETri-nB

We now have a set of k limiting profiles $\mathcal {P}= \{p^{1}, p^{2}, \dots , p^{k}\}$. This set of limiting profiles must be such that, for all $p, q \in \mathcal {P}$, we have ${\textit{Not}}[p \mathrel {P}q ]$.

In the pseudo-conjunctive version of ETri-nB (ETri-nB-pc, for short), we have that

$$\begin{aligned} x \in \mathcal {A}\Leftrightarrow {\left\{ \begin{array}{ll} x \mathrel {S}p &{} \quad \text { for some } p \in \mathcal {P}, \text { and}\\ {\textit{Not}}[q \mathrel {P}x ] &{} \quad \text { for all } q \in \mathcal {P}, \end{array}\right. } \end{aligned}$$

and $x \in \mathcal {U}$, otherwise.

In the pseudo-disjunctive version of ETri-nB (ETri-nB-pd  , for short), we have that

$$\begin{aligned} x \in \mathcal {U}\Leftrightarrow {\left\{ \begin{array}{ll} p \mathrel {P}x &{} \quad \text { for some } p \in \mathcal {P}, \text { and}\\ {\textit{Not}}[x \mathrel {P}q ] &{} \quad \text { for all } q \in \mathcal {P}, \end{array}\right. } \end{aligned}$$

and $x \in \mathcal {A}$, otherwise.

ETri-B-pc  and ETri-B-pd  are particular cases of ETri-nB-pc and ETri-nB-pd  , respectively. In this section, we consider only ETri-nB-pc and omit the suffix “pc”. We shall only turn back, briefly, to ETri-nB-pd  in Sect. 5.6. Following Fernández et al. (2017), unless otherwise mentioned, we use the Electre III outranking relation S defined by means of (1). The version of ETri-nB using the Electre I outranking relation S defined via (2) will be referred to as ETri-nB-I.

Remark 1

Using Proposition 1, it is easy to see that ETri-nB and ETri-nB-I respect the dominance relation $\ge$, i.e.,  are monotone w.r.t. this relation. In particular, if y dominates the acceptable  alternative x, then y is acceptable  . Symmetrically, if x is unacceptable  and dominates y, then y is unacceptable.

2.1.4 The family of Electre Tri methods

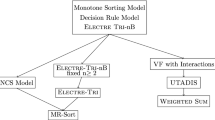
To ease the reading, we summarize the different variants of the ETri methods considered in the sequel as well as their interrelationships.

The variants of ETri-nB appear in Table 1 on the left. Their version using only one limiting profile, i.e.,  the different variants of ETri-B, appear on the right of the same table.

Table 1 Variants of ETri-nB  and ETri-B

Model (a) contains model (b), which contains model (d). Model (c) (resp. (d)) differs from model (a) (resp. (b)) in that it uses the outranking relation in Electre I instead of Electre III.

The relationships between the ETri-B models are the same as between the homologous ETri-nB models. The NonCompensatory Sorting (NCS) model analyzed by Bouyssou and Marchant (2007a, 2007b) generalizes (h), while the NCS model with veto generalizes (g). In both cases, the generalization lies in that the winning coalitions of criteria are not necessarily determined by means of additive weights. Model (h) is called the Majority Rule sorting model (MR-Sort) in the literature (Leroy et al. 2011; Sobrie et al. 2019).

Note that another type of ETrimethods has been proposed, namely ETri-C  (Almeida-Dias et al. 2010) and ETri-nC  (Almeida-Dias et al. 2012). These are based on a different logic (using central profiles instead of limiting profiles) as analyzed in Bouyssou and Marchant (2015). We shall not consider them in this paper for lack of place.

2.2 An example of an ETri-nB model

Consider alternatives evaluated on three criteria. Each criterion value belongs to the [0, 10] interval. In practice, such evaluations have a limited precision. Let us assume that evaluations are integers or half-integers.

Assume that the alternatives are partitioned into two classes $\mathcal {A}$ and $\mathcal {U}$ by an ETri-nB model with 2 limiting profiles. Let these profiles be $p^1 = (8,7,5)$ and $p^2=(5,6,8)$. The indifference, preference and veto thresholds are, respectively, $qt_i=1$, $pt_i=2$ and $vt_i=4$, the same for all criteria $i=1,2,3$. All criteria have the same weight $w_i=\frac{1}{3}$ and the cutting threshold $\lambda = .6$. It is readily verified that ${p^1 S p^2}$ and ${p^2 S p^1}$ so that none of the profiles strictly outranks the other.

2.2.1 Minimally acceptable  alternatives

Let us apply the above model. The set of possible evaluations for criterion i is $X_i = \{0, .5, 1, 1.5,$ $\ldots , 9.5, 10\}$, for $i=1,2,3$, and the set of all possible alternatives is $X=\prod _{i=1}^{3} X_i$. Each alternative is thus represented by an evaluation vector: for any $x \in X$, $x=(x_1, x_2, x_3)$, with $x_i = g_i(x)$, $i=1, 2, 3$. Since each alternative is identified with its evaluation vector, the dominance relation $\ge$ on X is antisymmetric. Therefore, it is a partial order.

Since ETri-nB is monotone w.r.t. the dominance relation $\ge$, which is a partial order on X, and since there are finitely many alternatives, the set $\mathcal {A}$ of acceptable  alternatives has a finite number of minimal elements $\mathcal {A}_{*}$ that we shall call minimally acceptable  alternatives (see Sect. 4.2 for further justification). The set $\mathcal {A}$ is the set of alternatives that dominate at least one alternative in $\mathcal {A}_{*}$. It contains $\mathcal {A}_{*}$. Decreasing the performance of a minimally acceptable  alternative by any amount on any criterion produces an unacceptable  alternative.

Let us determine the set $\mathcal {A}_{*}$. We first focus on $p^1$. Given the granularity of the evaluations, for satisfying $c(x,p^1)\ge .6$, the index $c_i(x_i, p^1_i)$, which takes only the values 0, .5 and 1,

• must be 1 for two criteria $i \in \{1,2,3\}$; it can be 0 for the third one,

• or must be 1 for one criterion and take the value .5 on the other two.

Consider the alternatives of the form $x=(7,6,x_3)$. For them, $c(x, p^1) \ge \frac{2}{3} > .6$. We have $d_3(x_3, p^1_3) = .75$ if $x_3 = 1.5$ and $d_3(x_3, p^1_3) = .5$ if $x_3 = 2$. Therefore $\sigma (7,6,1.5) = \frac{2}{3}\times \frac{1/4}{1/3}= .5 < .6$ and $\sigma (7,6,2) = \frac{2}{3}>.6$ since $d_3(2, p^1_3) = .5 < c(x,p^1)$. Therefore, (7, 6, 2) is minimal in $\mathcal {A}$ and, by a similar reasoning, we have that (7, 4, 4) and (5, 6, 4) are also minimal.

Consider now the second type of minimal alternatives. For example, for $x=(7, 5.5, 3.5)$, we have $\sigma (x,p^1) = c(x,p^1)= 1 \times 1/3 + 1/2 \times 1/3 + 1/2 \times 1/3 = 2/3 > 0.6$. Clearly, none of the performances of x can be decreased by .5 without resulting in an unacceptable  alternative. Therefore, (7, 5.5, 3.5) is minimal and, by a similar reasoning, we see that (6.5, 6, 3.5) and (6.5, 5.5, 4) are minimal too.

Applying the same analysis to the second profile $p^2$, yields the complete description of the set $\mathcal {A}_{*}$ of minimally acceptable  elements displayed in Table 2 (the first (resp. second) row corresponds to profile $p^1$ (resp. $p^2))$.

Table 2 List of minimally acceptable  alternatives in case evaluations are integers or half-integers

None of these 12 alternatives dominates another. The number of elements in $\mathcal {A}_{*}$ is thus 12.

Remark 2

Let us briefly discuss the consequences of using a similar ETri-nB-I model, using the Electre I outranking relation, instead of the more classical version above. We keep the same two limiting profiles $p^1, p^2$ and the same parameters except for $qt_i$ and $pt_i$ that we both set equal to 1 and $vt_i$ that we set to 3. It is easy to see that there are three minimally acceptable  alternatives w.r.t. $p^1$ which are (7, 6, 2), (7, 4, 4) and (5, 6, 4). The minimally acceptable  alternatives w.r.t. $p^2$ are (4, 5, 5), (4, 3, 7) and (2, 5, 7). The number of minimally acceptable  alternatives is half the one in Table 2. The minimally acceptable  alternatives in this simplified model are identical to the first three ones in each row of Table 2. The last three ones in each row are not “represented” in the simplified model. They correspond to alternatives for which the distinction between thresholds $pt_i$ and $qt_i$ plays an important role.

2.2.2 Observations

We emphasize the following observations supported by the above example.

• 1. From the analysis of the above example, it results that an alternative is assigned to $\mathcal {A}$ by the ETri-nB model iff it is equal or dominates one of the twelve alternatives listed in Table 2. Therefore, this model is equivalent to another ETri-nB model with different parameters. The latter has the 12 alternatives $\mathcal {P}' = \{{p'}^{1}, \ldots , {p'}^{j}, \dots , {p'}^{12}\}$ listed in Table 2 as limiting profiles. For all $i=1,2,3$, $w_i'=1/3$, $pt_i' = qt_i'=0$ and $vt_i'$ is a large number, e.g.,  $vt_i'=10$. We set $\lambda ' = 1$. With this model, $c'(x,{p'}^j) \ge \lambda ' =1$ iff $x_i \ge {p'}_i^{j}$ for all i. There is no veto effect since $d_i(x_i, {p'}_i^j) \le c'(x,{p'}^j)$ whenever the condition $c'(x,{p'}^j) \ge \lambda '$ is fulfilled and whatever the value of $vt'_i$. We call such a model an unanimous ETri-nB model in the sequel.

• 2. While the scale $X_i$ of each criterion $i=1, 2, 3$ has 21 levels (all integers and half integers between 0 and 10), only 6 of them are distinguished by appearing as distinct values of the ith coordinate in the 12 minimally acceptable  alternatives listed in Table 2. The ETri-nB model distinguishes only the 7 classes of equivalent evaluations that are delimited by these 6 values. For instance, on the scale of criterion $i=1$, the 6 values that make a difference are 7, 6.5, 5, 3, 2.5, 1. They are the different values taken by the first coordinate of the alternatives in Table 2. This means that the model’s assignments to $\mathcal {A}$ or $\mathcal {U}$ induce a weak order $\succsim _1$ on $X_1$ that is coarser than the natural order on the set of integers and half-integers in [0, 1]. This weak order $\succsim _1$ (with its asymmetric part denoted $\succ _1$ and its symmetric part $\sim _1$) on $X_1$ is as follows:

  $$\begin{aligned}{}[10 \sim _1 9.5 \sim _1 9 \sim _1 8.5 \sim _1 8 \sim _1 7.5 \sim _1 7] \succ _1 6.5 \succ _1 [6 \sim _1 5.5 \sim _1 5] \\ \succ _1 [4.5 \sim _1 4 \sim _1 3.5 \sim _1 3] \succ _1 2.5 \succ _1 [ 2 \sim _1.5 \sim _1 1] \succ _1 [0.5 \sim _1 0]. \end{aligned}$$

  This implies, for example, the following. If the evaluation of x on the first criterion is 6, decreasing it to 5 does not change the assignment of the alternative. Such a weak order with 7 equivalence classes is defined on each criterion by the model.

• 3. In the process of aiding a decision maker (DM) to make a decision by eliciting her preference in a question-and-answer session, ETri-nB may be a useful tool because the principle of concordance/non-discordance at the root of the method is intuitively appealing. The perspective is different when the parameters of the method are not elicited through actual interaction with a DM but have to be learned on the basis of an (often limited) number of assignment examples. The minimal number of examples that allows us to determine a sorting model is important whenever learning the model is the issue. Assume that an oracle tells you that ETri-nB is the model used by the DM for sorting the alternatives into two categories $\mathcal {A}$ and $\mathcal {U}$. The oracle gives you the values of all the model’s parameters including the number and the definition of limiting profiles. What is the minimal number of assignment questions you have to ask the DM just to verify that the oracle is not cheating on you? The most efficient questioning strategy is asking the decision maker to assign all minimally acceptable  alternatives (that can be determined according to the model indicated by the oracle). If the DM assigns them all to $\mathcal {A}$, then it is still necessary to ask her to assign all maximally unacceptable  alternatives. If the DM assigns them all to $\mathcal {U}$, then the oracle’s model is the right one. So, in particular, the number of minimally acceptable  alternatives (i.e.,  the limiting profiles of the unanimous ETri-nB equivalent model) is important in a learning context. From this point of view, ETri-nB appears as rather complex since the set of minimally acceptable  alternatives it induces tends to be large. In the above example with 3 criteria, 2 limiting profiles and criteria scales composed of integers and half-integers, this number is 12. It grows rapidly, for instance, with the criteria scales precision. If we apply the same model to the case the criteria scales are rational numbers with one decimal digit ranging in [0,10] (i.e.,  101 levels on each criterion scale instead of 21), the number of minimally acceptable  alternatives grows up to 192 (see Supplementary material, Appendix C). Therefore, in a learning perspective, the question of approximating an ETri-nB model by a simpler one, i.e.,  a model determining relatively few minimally acceptable  alternatives is important.

2.3 Goal of the paper

In Sects. 3 and 4, we analyze, in a conjoint measurement framework ( Krantz et al. 1971, Ch. 6 and 7), an assignment model, Model $(E)$, that is closely related to the ETri-nB-I method presented above. Just as ETri-nB generalizes ETri-B, Model $(E)$ generalizes the noncompensatory sorting model studied by Bouyssou and Marchant (2007a, 2007b) to the case in which several limiting profiles are used to sort the alternatives.

We place ourselves in a conjoint measurement framework because it is the usual one in decision theory and it has been used in previous works analyzing the Electre methods. Analyzing sorting methods in this framework means that any alternative in a Cartesian product can be sorted into categories and that an a priori linear ordering of each criterion scale is not postulated. A weak order on each criterion scale, if it exists, will be revealed by the partition. Working in such a framework does not restrict the generality of the study. Indeed, in case each criterion scale is linearly ordered and a partition respects the dominance relation determined by these orders, then the partition does reveal a weak order on each scale, possibly coarser than the a priori linear orders, but compatible with them. This was illustrated in item 2 of Sect. 2.2.2.

Our main finding is that, if the number of limiting profiles is not bounded above, the axiomatic analysis of Model $(E)$ is easy and rests on a condition, linearity, that is familiar in the analysis of sorting models (Goldstein 1991; Bouyssou and Marchant 2007a, b, 2010; Greco et al. 2004; Słowiński et al. 2002; Greco et al. 2001b). Our simple result shows the equivalence between Model $(E)$ and several other sorting models, in particular, the unanimous model introduced above in the example.

We prove, in Sect. 5.2, that the ETri-nB model, which uses the Electre III outranking relation, is equivalent to the ETri-nB-I model and to the decomposable model (D1) (that will be defined below, in Sect. 3.2). By “equivalent”, we mean that, for all particular ETri-nB model, there is an ETri-nB-I model that determines the same partition. The parameters of these equivalent models are possibly different. In particular, we emphasize that the sets of limiting profiles used in equivalent models usually differ, also in cardinality. Our theoretical analysis gives insight into the issue of learning such models on the basis of assignment examples (see Sect. 6.2).

3 Notation and framework

Although the analyses presented in this paper can easily be extended to cover the case of several ordered categories, we will mostly limit ourselves to the study of the case of two ordered categories. This will allow us to keep things simple, while giving us a sufficiently rich framework to present our main points.

Similarly, we suppose throughout that the set of objects to be sorted is finite. This is hardly a limitation with applications of sorting methods in mind. The extension to the general case is not difficult but calls for developments that would obscure our main messages⁵.

3.1 The setting

Let $n\ge 2$ be an integer and $X= X_{1} \times X_{2} \times \cdots \times X_{n}$ be a finite set of objects⁶. Elements $x, y, z,\ldots$ of $X$ will be interpreted as alternatives evaluated on a set $N= \lbrace 1, 2, \ldots , n \rbrace$ of attributes⁷. Any element $x \in X$ is thus an n-dimensional vector $x=(x_1, \ldots , x_i, \ldots , x_n)$, with $x_i \in X_i$, for all $i \in N$. For all $x, y \in X$ and $i \in N$, we denote by $(x_i, y_{-i})$ the element $w \in X$ such that $w_i = x_i$ and, for all $j \ne i$, $w_j = y_j$. In other words, $w=(x_i, y_{-i})$ is obtained by replacing the ith component of y, i.e.,  $y_i$, by $x_i$.

Our primitives consist in a twofold partition $\langle \mathcal {A},\mathcal {U}\rangle$ of the set $X$. This means that the sets $\mathcal {A}$ and $\mathcal {U}$ are nonempty and disjoint and that their union is the entire set $X$. Our central aim is to study various models allowing to represent the information contained in $\langle \mathcal {A},\mathcal {U}\rangle$. We interpret the partition $\langle \mathcal {A},\mathcal {U}\rangle$ as the result of a sorting method applied to the alternatives in $X$. Although the ordering of the categories is not part of our primitives, it is useful to interpret the set $\mathcal {A}$ as containing Acceptable  objects, while $\mathcal {U}$ contains Unacceptable  ones.

We say that an attribute $i \in N$ is influential for $\langle \mathcal {A},\mathcal {U}\rangle$ if there are $x_{i}, y_{i}\in X_{i}$ and $a_{-i}\in X_{-i}$ such that $(x_{i}, a_{-i}) \in \mathcal {A}$ and $(y_{i}, a_{-i}) \in \mathcal {U}$. We say that an attribute is degenerate if it is not influential. Note that the fact that $\langle \mathcal {A},\mathcal {U}\rangle$ is a partition implies that there is at least one influential attribute in $N$. A degenerate attribute has no influence whatsoever on the sorting of the alternatives and may be suppressed from $N$. Hence, we suppose henceforth that all attributes are influential for $\langle \mathcal {A},\mathcal {U}\rangle$.

A twofold partition $\langle \mathcal {A},\mathcal {U}\rangle$ induces on each $i \in N$ a binary relation defined letting, for all $i \in N$ and all $x_{i}, y_{i} \in X_{i}$,

$$\begin{aligned} x_{i} \sim _{i}y_{i} \text { if }\big [\forall a_{-i} \in X_{-i}, (y_{i},a_{-i}) \in \mathcal {A}\iff (x_{i},a_{-i}) \in \mathcal {A}\big ]. \end{aligned}$$

(3)

This relation is always reflexive, symmetric and transitive, i.e.,  is an equivalence. We omit the simple proof of the following (see Bouyssou and Marchant 2007a, Lemma 1, p. 220).

Lemma 1

For all $x, y \in X$ and all $i \in N$,

• 1. labelit1:lemma1:Gold $[y \in \mathcal {A}$ and $x_{i}\sim _{i}y_{i}]$ $\Rightarrow$ $(x_{i}, y_{-i}) \in \mathcal {A}$,

• 2. $[x_{j} \sim _{j} y_{j}$, for all $j \in N]$ $\Rightarrow$ $[x \in \text{\AA} \Leftrightarrow y \in \mathcal {A}]$.

This lemma will be used to justify the convention made later in Sect. 4.1.

3.2 A general measurement framework

Goldstein (1991) suggested the use of conjoint measurement techniques for the analysis of twofold and threefold partitions of a set of multi-attributed alternatives. His analysis was rediscovered and developed in Greco et al. (2001b) and Słowiński et al. (2002). We briefly recall here the main points of the analysis in the above papers for the case of twofold partitions. We follow Bouyssou and Marchant (2007a).

Let $\langle \mathcal {A},\mathcal {U}\rangle$ be a partition of $X$. Consider a measurement model, henceforth the Decomposable model, in which, for all $x \in X$,

where $u_{i}$ is a real-valued function on $X_{i}$ and F is a real-valued function on $\prod _{i=1}^{n}u_{i}(X_{i})$ that is nondecreasing in each argument⁸. The special case of Model (D1) in which F is supposed to be increasing in each argument, is called Model (D2). Model (D2) contains as a particular case the additive model for sorting in which, for all $x \in X$,

that is at the heart of the UTADIS technique (Jacquet-Lagrèze 1995) and its variants (Zopounidis and Doumpos 2000a, b; Greco et al. 2010). It is easy to check⁹ that there are twofold partitions that can be obtained in Model (D2) but that cannot be obtained in Model (Add) (see Supplementary material, Appendix E).

In order to analyze Model (D1), we define on each $X_{i}$ the binary relation $\succsim _{i}$ letting, for all $x_{i}, y_{i}\in X_{i}$,

$$\begin{aligned} x_{i} \succsim _{i}y_{i} \text { if }[\text{ for } \text{ all } a_{-i} \in X_{-i}, (y_{i}, a_{-i}) \in \mathcal {A}\Rightarrow (x_{i}, a_{-i}) \in \mathcal {A}]. \end{aligned}$$

(4)

It is not difficult to see that, by construction, $\succsim _{i}$ is reflexive and transitive. We denote by $\succ _{i}$ (resp. $\sim _{i}$) the asymmetric (resp. symmetric) part of $\succsim _{i}$ (hence, the relation $\sim _{i}$ coincides with the one defined by (3)).

We say that the partition $\langle \mathcal {A},\mathcal {U}\rangle$ is linear  on attribute $i \in N$ (condition $i$-linear  ) if, for all $x_{i}, y_{i} \in X_{i}$ and all $a_{-i}, b_{-i}\in X_{-i}$,

The partition is said to be linear  if it is $i$-linear  , for all $i \in N$. This condition was first proposed in Goldstein (1991), under the name “context-independence”, and generalized in Greco et al. (2001b) and Słowiński et al. (2002) (these authors call it “cancellation property”). The adaptation of this condition to the study of binary relations, adaptation first suggested by Goldstein (1991), is central in the analysis of the nontransitive decomposable models presented in Bouyssou and Pirlot (1999, 2002, 2004).

The following lemma takes note of the consequences of condition $i$-linear  on the relation $\succsim _{i}$ and shows that linearity is necessary for Model (D1). Its proof can be found in Bouyssou and Marchant (2007a, Lemma 5, p. 221).

Lemma 2

• 1. Condition $i$-linear  holds iff $\succsim _{i}$ is complete,

• 2. If a partition $\langle \mathcal {A},\mathcal {U}\rangle$ has a representation in Model (D1) then it is linear.

The following proposition is due to Goldstein (1991, Theorem 2) and Greco et al. (2001b, Theorem 2.1, Part 2).

Proposition 2

Let $\langle \mathcal {A},\mathcal {U}\rangle$ be a twofold partition of a set $X$. Then:

• (i) there is a representation of $\langle \mathcal {A},\mathcal {U}\rangle$ in Model (D1) iff it is linear  ,

• (ii) if $\langle \mathcal {A},\mathcal {U}\rangle$ has a representation in Model (D1), it has a representation in which, for all $i \in N$, $u_{i}$ is a numerical representation of $\succsim _{i}$,

• (iii) moreover, Models (D1) and (D2) are equivalent.

Proof

See, e.g.,  Bouyssou and Marchant (2007a, Proposition 6, p. 222). $\square$

3.3 Partitions respecting a dominance relation

Footnote 6 has emphasized that it is not necessarily the case that $X_i$ is a subset of the reals and the range of a function $g_i$ evaluating the alternatives w.r.t. criterion i, for all $i \in N$. In the case a partition respects the dominance relation determined by pre-existing linear orderings of the criteria scales (see Remark 1, for a definition), we note the following result.

Proposition 3

Let $X = \prod _{i=1}^{n} X_i$, where the finite set $X_i$ is endowed with a linear order $\ge _i$, for all i. Let $\langle \mathcal {A},\mathcal {U}\rangle$ be a twofold partition of X which respects the dominance relation $\ge$ determined by the linear orders $\ge _i$. Then $\langle \mathcal {A},\mathcal {U}\rangle$ is linear and the weak order $\succsim _i$ induced by the partition is compatible with the linear order $\ge _i$, for all i, i.e.,  for all $x_i, y_i \in X_i$, $x_i \ge _i y_i$ entails $x_i \succsim _i y_i$.

Proof

If $x_i \ge _i y_i$, condition (4) is fulfilled, since the partition respects dominance, and therefore $x_i \succsim _i y_i$. Since $\ge _i$ is complete, so is $\succsim _i$, for all i. Therefore $\langle \mathcal {A},\mathcal {U}\rangle$ is linear (Lemma 2.1). $\square$

The fact that, in general, $\succsim _i$ does not distinguish (i.e.,  considers as equivalent) some pairs that are strictly ordered by $\ge _i$ is illustrated in Sect. 2.2.2, item 2.

We noticed in Remark 1, that ETri-nB-pc and ETri-nB-I-pc respect the dominance relation. Therefore, we have the following corollary of Proposition 3.

Corollary 1

The twofold partitions determined by ETri-nB-pc and ETri-nB-I-pc are linear.

3.4 Interpretations of the decomposable model (D1)

The framework offered by the decomposable model (D1) is quite flexible. It contains many other sorting models as particular cases. We already observed that it contains Model (Add) as a particular case. Bouyssou and Marchant (2007a) have reviewed various possible interpretations of Model (D1). They have shown that both the pseudo-conjunctive and the pseudo-disjunctive variants of ETri-B-I (see Table 1) enter into this framework. In particular, they have characterized, within the decomposable model, the NCS model, which is a generalization (without additive weights) of ETri-B-I (pseudo-conjunctive).

Greco et al. (2001b, Theorem 2.1, Parts 3 and 4) (see also Slowinski et al., 2002, Theorem 2.1) have proposed two equivalent reformulations of the decomposable model (D1). The first one uses “at least” decision rules. The second one uses a binary relation to compare alternatives to a profile. We refer to Bouyssou and Marchant (2007a) and to the original papers for details.

4 Main results

4.1 Definitions

The following definition synthesizes the main features of ETri-nB-I-pc, the version of ETri-nB-pc using the Electre I outranking relation (see Sect. 2.1). The main differences w.r.t. ETri-nB-I-pc are that: (i) we do not suppose that the real-valued functions $g_{i}$ are given beforehand and (ii) we do not use additive weights combined with a threshold to determine the winning coalitions. Actually, the model defined below is a multi-profile version of the noncompensatory sorting model with veto analyzed in Bouyssou and Marchant (2007a), exactly in the same way as ETri-nB is a multi-profile version of ETri-B. For notational simplicity, we shall refer to it as Model $(E)$ (“E”, for Electre Tri) in the sequel.

Definition 1

We say that a partition $\langle \mathcal {A},\mathcal {U}\rangle$ has a representation in Model $(E)$ if:

• for all $i \in N$, there is a semiorder $\mathrel {S_{i}}$ on $X_{i}$ (with asymmetric part $\mathrel {P_{i}}$ and symmetric part $\mathrel {I_{i}}$),

• for all $i \in N$, there is a strict semiorder $\mathrel {V_{i}}$ on $X_{i}$ that is included in $\mathrel {P_{i}}$ and is the asymmetric part of a semiorder $\mathrel {U_{i}}$,

• $(\mathrel {S_{i}}, \mathrel {U_{i}})$ is a homogeneous nested chain of semiorders and ${\mathrel {W_{i}}} = {\mathrel {S}_{i}^{wo}} \cap {\mathrel {U}_{i}^{wo}}$ is a weak order that is compatible with both $\mathrel {S_{i}}$ and $\mathrel {U_{i}}$,

• there is a set of subsets of attributes $\mathcal {F}\subseteq 2^{N}$ such that, for all $I, J \in 2^{N}$, $[I \in \mathcal {F}$ and $I \subseteq J]$ $\Rightarrow J \in \mathcal {F}$,

• there is a binary relation $\mathrel {S}$ on X (with symmetric part $\mathrel {I}$ and asymmetric part $\mathrel {P}$) defined by

  $$\begin{aligned} x \mathrel {S}y \iff \left[ S(x,y) \in \mathcal {F}\text { and } V(y,x) = \varnothing \right] , \end{aligned}$$

• there is a set $\mathcal {P}= \{p^{1}, \ldots , p^{k}\} \subseteq X$ of k limiting profiles, such that for all $p, q \in \mathcal {P}$, ${\textit{Not}}[p \mathrel {P}q ]$,

such that

where

$$\begin{aligned} S(x, y) = \{i \in N: x_{i} \mathrel {S_{i}}y_{i}\}, \end{aligned}$$

and

$$\begin{aligned} V(x, y) = \{i \in N: x_{i} \mathrel {V_{i}}y_{i}\}. \end{aligned}$$

We then say that $\langle (\mathrel {S_{i}}, \mathrel {V_{i}})_{i\in N}, \mathcal {F}, \mathcal {P}\rangle$ is a representation of $\langle \mathcal {A},\mathcal {U}\rangle$ in Model $(E)$. Model $(E^{c})$ is the particular case of Model $(E)$, in which there is a representation that shows no discordance effects, i.e.,  in which all relations $\mathrel {V_{i}}$ are empty. Model $(E^{u})$ is the particular case of Model $(E)$, in which there is a representation that requires unanimity, i.e.,  such that $\mathcal {F}= \{N\}$.

Table 3 Model $(E)$ and its variants

Table 3 summarizes the models defined above. It should be clear that $(E)$ is closely related to ETri-nB-I-pc (see Remark 3 below). It does not use criteria but uses attributes, as is traditional in conjoint measurement. Moreover, it does not use an additive weighting scheme combined with a threshold to determine winning coalitions but uses instead a general family $\mathcal {F}$ of subsets of attributes that is compatible with inclusion (see also Bouyssou and Marchant 2007a). Note that, when the set of limiting profiles $\mathcal {P}$ is restricted to be a singleton, Model $(E)$ is exactly the noncompensatory sorting model (NCS) studied by Bouyssou and Marchant (2007a).

Remark 3

Any partition determined by an ETri-nB-I-pc model has a representation in Model $(E)$. We illustrate this fact using the example of the ETri-nB-I-pc model described in Remark 2. Note that this way of constructing a representation in Model $(E)$ is applicable to any ETri-nB-I-pc model.

For all $i=1, 2, 3$, $X_i$ is the set of integers and half-integers between 0 and 10. The semiorder $S_i$ on $X_i$ is defined using the threshold $pt_i = qt_i =1$, i.e.,  for all $x_i, y_i \in X_i$, $x_i S_i y_i$ iff $x_i \ge y_i - 1$. We have $x_i S_i y_i$ iff $c_i(x_i,y_i) =1$. Similarly, the strict semiorder $V_i$ is defined using the threshold $vt_i =3$ by $x_i V_i y_i$ iff $x_i > y_i + 3$. We have $x_i V_i y_i$ iff $d_i(y_i, x_i) = 1$. The subsets of attributes in $\mathcal {F}$ are all sets of two or three attributes since $c(x,y) \ge .6$ if and only if, for at least two criteria, $x_i S_i y_i$ and, therefore, $|S(x,y)| \ge 2$. The pair (x, y) belongs to the outranking relation S iff $|S(x,y)| = |\{i: x_i S_i y_i\}| \ge 2$ and $V(y,x) = \{i: y_i V_i x_i\} = \varnothing$, i.e.,  it is never the case that $y_i \ge x_i + 3.5$. With these definitions of $S_i, V_i$ and $\mathcal {F}$, the acceptable alternatives in the example are exactly these which satisfy $(E)$.

It is easy to see that the model in the example is equivalent to a model based on unanimity, i.e.,  a model ($E^{u}$), using as limiting profiles the three first alternatives in each row of Table 2 and the natural order $\ge$ as the relation $S_i$ on $X_i$.

Remark 4

It is clear that Model $(E^{u})$ is a particular case of Model $(E^{c})$: if unanimity is required to have $x \mathrel {S}y$, the veto relations $\mathrel {V_{i}}$ play no role and can always be taken to be empty.

The following lemma takes note of elementary consequences of the fact that $(\mathrel {S_{i}}, \mathrel {U_{i}})$ is a homogeneous nested chain of semiorders (we remind the reader that the necessary definitions are recalled in Appendix A, as supplementary material).

Lemma 3

Let $\langle \mathcal {A}, \mathcal {U}\rangle$ be a twofold partition of X. If $\langle \mathcal {A}, \mathcal {U}\rangle$ is representable in $(E)$ then, for all $a = (a_{i}, a_{-i})$, $b=(b_{i}, b_{-i}) \in X$, all $i \in N$ and all $c_{i} \in X_{i}$,

$$\begin{aligned} a \mathrel {S}b \text { and } b_{i} \mathrel {W_{i}}c_{i}&\Rightarrow a \mathrel {S}(c_{i}, b_{-i}), \end{aligned}$$

(5a)

$$\begin{aligned} a \mathrel {P}b \text { and } b_{i} \mathrel {W_{i}}c_{i}&\Rightarrow a \mathrel {P}(c_{i}, b_{-i}), \end{aligned}$$

(5b)

$$\begin{aligned} a \mathrel {S}b \text { and } c_{i} \mathrel {W_{i}}a_{i}&\Rightarrow (c_{i},a_{-i}) \mathrel {S}b, \end{aligned}$$

(5c)

$$\begin{aligned} a \mathrel {P}b \text { and } c_{i} \mathrel {W_{i}}a_{i}&\Rightarrow (c_{i},a_{-i}) \mathrel {P}b, \end{aligned}$$

(5d)

where $\mathrel {W_{i}}$ denotes a weak order that is compatible with the homogeneous nested chain of semiorders $(\mathrel {S_{i}}, \mathrel {U_{i}})$.

Proof

Let $a' = (c_{i},a_{-i})$ and $b' = (c_{i}, b_{-i})$. Let us show that (5a) holds. Suppose that $a \mathrel {S}b$, so that $S(a, b) \in \mathcal {F}$ and $V(b,a) = \varnothing$. Because $b_{i} \mathrel {W_{i}}c_{i}$, we know that $S(a, b') \supseteq S(a, b)$. Hence, we have $S(a, b') \in \mathcal {F}$. Similarly, we know that $V(b,a) = \varnothing$, so that ${\textit{Not}}[b_{i} \mathrel {V_{i}}a_{i} ]$. It is therefore impossible that $c_{i} \mathrel {V_{i}}a_{i}$ since $b_{i} \mathrel {W_{i}}c_{i}$ would imply $b_{i} \mathrel {V_{i}}a_{i}$, a contradiction. Hence, $V(b', a) = \varnothing$ and we have $a \mathrel {S}b'$.

Let us show that (5b) holds. Because $a \mathrel {P}b$ implies $a \mathrel {S}b$, we know from (5a) that $a \mathrel {S}b'$. Suppose now that $b' \mathrel {S}a$ so that $S(b', a) \in \mathcal {F}$ and $V(a, b') = \varnothing$. Because $b_{i} \mathrel {W_{i}}c_{i}$, $c_{i} \mathrel {S_{i}}a_{i}$ implies $b_{i} \mathrel {S_{i}}a_{i}$, so that $S(b, a) \supseteq S(b', a)$, implying $S(b, a) \in \mathcal {F}$. Similarly, we know that $V(a, b') = \varnothing$, so that ${\textit{Not}}[a_{i} \mathrel {V_{i}}c_{i} ]$. It is therefore impossible that $a_{i} \mathrel {V_{i}}b_{i}$, since $b_{i} \mathrel {W_{i}}c_{i}$ would imply $a_{i} \mathrel {V_{i}}c_{i}$, a contradiction. Hence, we must have $V(a, b) = \varnothing$, so that we have $b \mathrel {S}a$, a contradiction.

The proof of (5c) and (5d) is similar. $\square$

The next lemma shows that Model $(E)$ implies linearity.

Lemma 4

Let $\langle \mathcal {A},\mathcal {U}\rangle$ be a twofold partition of $X= \prod _{i=1}^{n} X_{i}$. If $\langle \mathcal {A},\mathcal {U}\rangle$ has a representation in Model $(E)$ then it is linear.

Proof

Suppose that we have $(x_{i}, a_{-i}) \in \mathcal {A}$, $(y_{i}, b_{-i}) \in \mathcal {A}$. Defining the relations $W_i$ as in Lemma 3, we have either $x_{i} \mathrel {W_{i}}y_{i}$ or $y_{i} \mathrel {W_{i}}x_{i}$. Suppose that $x_{i} \mathrel {W_{i}}y_{i}$. Because $(y_{i}, b_{-i}) \in \mathcal {A}$, we know that $(y_{i}, b_{-i}) \mathrel {S}p$, for some $p \in \mathcal {P}$, and ${\textit{Not}}[q \mathrel {P}(y_{i}, b_{-i}) ]$ for all $q \in \mathcal {P}$, Lemma 3 implies that $(x_{i}, b_{-i}) \mathrel {S}p$ and ${\textit{Not}}[q \mathrel {P}(x_{i}, b_{-i}) ]$ for all $q \in \mathcal {P}$. Hence, $(x_{i}, b_{-i}) \in \mathcal {A}$. The case $y_{i} \mathrel {W_{i}}x_{i}$ is similar: we start with $(x_{i}, a_{-i}) \in \mathcal {A}$ to conclude that $(y_{i}, a_{-i}) \in \mathcal {A}$. Hence, linearity holds. $\square$

In view of Lemma 4, we therefore know from Lemma 2 that in Model $(E)$ there is, on each attribute $i \in N$, a weak order $\succsim _{i}$ on $X_{i}$ that is compatible with the partition $\langle \mathcal {A},\mathcal {U}\rangle$.

Convention

For the analysis of $\langle \mathcal {A},\mathcal {U}\rangle$ on $X= \prod _{i=1}^{n} X_{i}$, it is not useful to keep in $X_{i}$ elements that are equivalent w.r.t. the equivalence relation $\sim _{i}$. Indeed, if $x_{i} \sim _{i}y_{i}$ then $(x_{i}, a_{-i}) \in \mathcal {A}$ iff $(y_{i}, a_{-i}) \in \mathcal {A}$ (see Lemma 1).

In order to simplify the analysis, it is not restrictive to suppose that we work with $\mathord {X_{i}}/\mathord {\sim _{i}}$ (i.e.,  the set of equivalence classes in $X_{i}$ for the equivalence $\sim _{i}$) instead of $X_{i}$ and, thus, on $\prod _{i=1}^{n} [\mathord {X_{i}}/\mathord {\sim _{i}}]$ instead of $\prod _{i=1}^{n} X_{i}$. This amounts to supposing that the equivalence $\sim _{i}$ becomes the identity relation. We systematically make this hypothesis below. This is w.l.o.g.  since the properties of a partition on $\prod _{i=1}^{n} [\mathord {X_{i}}/\mathord {\sim _{i}}]$ can immediately be extended to a partition on $\prod _{i=1}^{n} X_{i}$ (see Lemma 1) and is done for convenience only. In order to simplify notation, we suppose below that we are dealing with partitions on $\prod _{i=1}^{n} X_{i}$ for which all relations $\sim _{i}$ are trivial. Our convention implies that each relation $\succsim _{i}$ is antisymmetric, so that the sets $X_{i}$ are linearly ordered by $\succsim _{i}$.

Let us define the relation $\succsim$ on $X$ letting, for all $x,y \in X$,

$$\begin{aligned} x \succsim y \iff x_{i} \succsim _{i}y_{i}, \text { for all } i \in N. \end{aligned}$$

It is clear that the relation $\succsim$ plays the role of a dominance relation in our conjoint measurement framework. It is a partial order on $X$, being reflexive, antisymmetric, and transitive. This partial order is obtained as a “direct product of chains” (the relations $\succsim _{i}$ on each $X_{i}$) as defined in Caspard et al. (2012, p. 119).

Before we turn to our main results, it will be useful to take note of a few elementary observations about maximal and minimal elements in partially ordered sets (posets), referring to Davey and Priestley (2002), for more details.

4.2 Minimal and maximal elements in posets

Let $\mathrel {T}$ be a binary relation on a set Z. An element $x \in B \subseteq Z$ is maximal (resp. minimal) in B for $\mathrel {T}$ if there is no $y \in B$ such that $y \mathrel {\mathrel {T}^{\alpha }}x$ (resp. $x \mathrel {\mathrel {T}^{\alpha }}y$), where $\mathrel {\mathrel {T}^{\alpha }}$ denotes the asymmetric part of $\mathrel {T}$. The set of all maximal (resp. minimal) elements in $B \subseteq Z$ for $\mathrel {T}$ is denoted by ${\text {Max}}(\mathrel {T}, B)$ (resp. ${\text {Min}}(\mathrel {T}, B)$).

For the record, the following proposition recalls some well-known facts about maximal and minimal elements of partial orders on finite sets ( Davey and Priestley 2002, p. 16). We sketch its proof in Appendix B for completeness.

Proposition 4

Let $\mathrel {T}$ be a partial order (i.e.,  a reflexive, antisymmetric and transitive relation) on a nonempty set Z. Let B be a finite nonempty subset of Z. Then the set of maximal elements, ${\text {Max}}(\mathrel {T}, B)$, and the set of minimal elements, ${\text {Min}}(\mathrel {T}, B)$, in B for $\mathrel {T}$ are both nonempty. For all $x,y \in {\text {Max}}(\mathrel {T}, B)$ (resp. ${\text {Min}}(\mathrel {T}, B)$) we have ${\textit{Not}}[x \mathrel {\mathrel {T}^{\alpha }}y ]$. Moreover, for all $x \in B$, there is $y \in {\text {Max}}(\mathrel {T}, B)$ and $z \in {\text {Min}}(\mathrel {T}, B)$ such that $y \mathrel {T}x$ and $x \mathrel {T}z$.

We will apply the above proposition to the proper nonempty subset $\mathcal {A}$ of the finite set $X= \prod _{i=1}^{n} X_{i}$, partially ordered by $\succsim$.

4.3 A characterization of model $(E)$

We know that $\succsim$ is a partial order on $X= \prod _{i=1}^{n} X_{i}$. Because $\langle \mathcal {A},\mathcal {U}\rangle$ is a twofold partition of $X$, we know that $\text{\AA} \ne \varnothing$. Because we have supposed $X$ to be finite, so is $\mathcal {A}$. Hence, we can apply Proposition 4 to conclude that the set $\mathcal {A}_{*}= {\text {Min}}(\succsim , \mathcal {A})$ is nonempty.

We are now fully equipped to present our main result.

Theorem 1

Let $X= \prod _{i=1}^{n} X_{i}$ be a finite set and $\langle \mathcal {A},\mathcal {U}\rangle$ be a twofold partition of $X$. The partition $\langle \mathcal {A},\mathcal {U}\rangle$ has a representation in Model $(E)$ iff it is linear. This representation can always be taken to be $\langle ({\succsim _{i}}, {\mathrel {V_{i}}} = \varnothing )_{i \in N}, \mathcal {F}= \{N\}, \mathcal {P}= \mathcal {A}_{*}\rangle$.

Proof

We know from Lemma 4 that Model $(E)$ implies linearity. Let us prove the converse implication. Take, for each $i \in N$, ${\mathrel {S_{i}}} = {\succsim _{i}}$ and ${\mathrel {V_{i}}} = \varnothing$. Take $\mathcal {F}= \{N\}$. Hence, we have ${\mathrel {S}} = {\succsim }$. Take $\mathcal {P}= \mathcal {A}_{*}$. Using Proposition 4, we know that $\mathcal {A}_{*}$ is nonempty and that, for all $p, q \in \mathcal {A}_{*}$, we have ${\textit{Not}}[p \succ q ]$. Hence, taking $\mathcal {P}= \mathcal {A}_{*}$ leads to an admissible set of profiles in Model $(E)$.

If $x \in \mathcal {A}$, we use Proposition 4 to conclude that there is $y \in \mathcal {A}_{*}$ such that $x \succsim y$, so that we have $x \succsim p$, for some $p \in \mathcal {P}$. Suppose now that, for some $q \in \mathcal {P}$, we have $q \succ x$. Using the fact that $\succsim$ is a partial order, we obtain $q \succ p$, contradicting the fact that $p, q \in \mathcal {A}_{*}$, in view of Proposition 4. Suppose now that $x \in \mathcal {U}$. Supposing that $x \succsim p$, for some $p \in \mathcal {P}= \mathcal {A}_{*}$, would lead to $x \in \mathcal {A}$, a contradiction. This completes the proof. $\square$

Remark 5

In the representation in Model $(E)$ built in Theorem 1, the relation $\mathrel {S}$ is a partial order. When this is so, the condition stating that ${\textit{Not}}[q \mathrel {P}x ] \text { for all } q \in \mathcal {P}$ and all $x \in \mathcal {A}$, is automatically verified. Indeed, suppose that, for some $q \in \mathcal {P}$ and some $x \in \mathcal {A}$, we have $q \mathrel {P}x$. Because $x \in \mathcal {A}$, there is $p \in \mathcal {P}$ such that $x \mathrel {S}p$. Transitivity leads to $q \mathrel {P}p$, violating the condition on the set of profiles.

Remark 6

Under our convention that $\succsim _{i}$ is antisymmetric, for all $i \in N$, it is clear that, if we are only interested in representations with $\mathcal {F}= \{N\}$, the set $\mathcal {P}$ must be taken equal to $\mathcal {A}_{*}$. Hence, the representation built above is unique, under our convention about antisymmetry and the constraint that $\mathcal {F}= \{N\}$. Without the constraint that $\mathcal {F}= \{N\}$, uniqueness does not obtain any more, as shown, e.g.,  by Example 1 below. Since this is not important for our purposes, we do not investigate this point further in this text.

4.4 Example

We illustrate the construction of the representation in Theorem 1 with the example below.

Example 1

Let $X = \prod _{i=1}^{3} X_{i}$ with $X_{1} = X_{2} = X_{3} = \{39, 37, 34, 30, 25\}$. Hence, X contains $5^{3} = 125$ objects.

Define the twofold partition $\langle \mathcal {A},\mathcal {U}\rangle$ letting:

$$\begin{aligned} (x_{1}, x_{2}, x_{3}) \in \mathcal {A}\iff x_{1} + x_{2} + x_{3} \ge 106. \end{aligned}$$

In this twofold partition, the set $\mathcal {A}$ contains 32 objects, while $\mathcal {U}$ contains the remaining 93 objects.

It is easy to check that all attributes are influential for this partition and that, on each attribute $i \in N$, we have $39 \succ _{i}37 \succ _{i}34 \succ _{i}30 \succ _{i}25$. For instance, for attribute 1, we have:

$$\begin{aligned} \begin{aligned}&(39, 37, 30) \in \mathcal {A}&\quad&(37, 37, 30) \notin \mathcal {A},\\&(37, 39, 30) \in \mathcal {A}&\quad&(34, 39, 30) \notin \mathcal {A},\\&(34, 39, 34) \in \mathcal {A}&\quad&(30, 39, 34) \notin \mathcal {A},\\&(30, 39, 37) \in \mathcal {A}&\quad&(25, 39, 37) \notin \mathcal {A}. \end{aligned} \end{aligned}$$

This twofold partition has an obvious representation in Model (Add). Hence it is linear  and also has a representation in Model $(E)$. Considering the representation built in Theorem 1 with ${\mathrel {S_{i}}} = {\succsim _{i}}$, ${\mathrel {V_{i}}} = {\varnothing }$, $\mathcal {P}= \mathcal {A}_{*}$ and $\mathcal {F}= \{N\}$, we obtain¹⁰ a representation that uses the following 12 profiles:

$$\begin{aligned} \begin{aligned}&(37, 37, 34)&\quad&(39, 34, 34)&\quad&(39, 37, 30)&\quad&(37, 30, 39)\\&(37, 34, 37)&\quad&(34, 39, 34)&\quad&(39, 30, 37)&\quad&(30, 39, 37)\\&(34, 37, 37)&\quad&(34, 34, 39)&\quad&(37, 39, 30)&\quad&(30, 37, 39). \end{aligned} \end{aligned}$$

(6)

It is clear that these twelve profiles are pairwise incomparable w.r.t. ${\mathrel {S}} = {\succsim }$.

For instance, the object (39, 30, 39) belongs to $\mathcal {A}$, because $39+30+39 = 108 \ge 106$. This object outranks (meaning here, dominates) the two profiles (39, 30, 37) and (37, 30, 39), but no other.

Notice that this twofold partition is also determined by an ETri-nB-pc model with a single limiting profile $p^1 = (39, 39, 39)$, thresholds $qt_i = 0$, $pt_i = 9$, $vt_i=14$, for $i=1, 2, 3$ and $\lambda = 16/27$.

5 Remarks and extensions

5.1 Positioning model $(E)$ w.r.t. other sorting models

Theorem 1 gives a simple characterization of Model $(E)$. It makes no restriction on the size of the set of profiles $\mathcal {P}$, except that it is finite.

The proof of Theorem 1 builds a representation of any partition $\langle \mathcal {A},\mathcal {U}\rangle$ satisfying linearity in a special case of Model $(E)$, Model $(E^{u})$. This shows that Models $(E^{u})$ and $(E)$ are equivalent. Because, $(E^{u})$ is a particular case of Model $(E^{c})$, this also shows that Models $(E)$, $(E^{u})$ and $(E^{c})$ are equivalent.

In view of Proposition 2, Model $(E)$ is equivalent to Model (D1) and, hence, to Model (D2). However, Model (Add) is not equivalent to Model $(E)$. An example of a linear partition that is not representable in Model (Add) is given in Appendix E, as supplementary material. Note also that a characterization of Model (Add) in case X is a finite set is known but requires a countably infinite scheme of axioms (see Bouyssou and Marchant 2008, Appendix B, and especially, Remark 31, p. 32).

Because Model (D2) contains Model (Add) as a particular case, the same is true for Model $(E)$.

We summarize our observations in the following.

Proposition 5

• 1. Models $(E)$, $(E^{c})$, and $(E^{u})$ are equivalent.

• 2. Models $(E)$, (D1), and (D2) are equivalent.

• 3. Model (Add) is a particular case of Model $(E)$ but not vice versa.

The above proposition allows us to position rather precisely Model $(E)$ within the family of all sorting models.

Remark 7

As observed in Sect. 4.1, when the set $\mathcal {P}$ of limiting profiles is restricted to a singleton, Model $(E)$ is the noncompensatory sorting model. The twofold partitions $\langle \mathcal {A},\mathcal {U}\rangle$ that can be represented in this model have been characterized as being linear and 3v-graded (see Bouyssou and Marchant 2007a). The latter property implies that the weak order $\succsim _i$ induced by the partition on $X_i$, for all i, distinguishes at most three equivalence classes of evaluations on criterion i. In case there is no veto effect, $\succsim _i$ distinguishes at most two equivalence classes on $X_i$ (2-graded). This result characterizes the twofold partitions representable in the noncompensatory sorting model within the set of linear twofold partitions. In other words, it characterizes the particular case of Model $(E)$ with one limiting profile within the general Model $(E)$.

5.2 Model $(E)$ versus ETri-nB-pc

In order to position Model $(E)$ w.r.t. ETri-nB-pc, we assume that, for all i, $X_i$ is the range of a real-valued function $g_i$ evaluating the alternatives w.r.t. criterion i. We know that Model $(E)$ is equivalent to Model $(E^{u})$. These models are characterized by linearity. But all partitions obtained with the original method ETri-nB-pc satisfy linearity (by Corollary 1). Therefore, ETri-nB-pc is a particular case of Model $(E)$.

Conversely, Model $(E^{u})$ is a particular case of ETri-nB-pc that is obtained taking the cutting level $\lambda$ to be 1 and, on all criteria, the preference and indifference thresholds to be equal. Since unanimity is required, veto thresholds play no role. Since Model $(E^{u})$ is equivalent to Model $(E)$, Model $(E)$ is a particular case of ETri-nB-pc.

The same can be said of ETri-nB-I-pc, since this model also satisfies linearity (by Corollary 1) and contains the unanimous model $(E^{u})$. This is also true of the versions without veto of ETri-nB-pc and ETri-nB-I-pc. Therefore, $(E)$ and all four models in the left part of Table 1 are equivalent models.

We take note of this in the next proposition.

Proposition 6

Models $(E)$, ETri-nB-pc (with or without veto) and ETri-nB-I-pc (with or without veto) are equivalent models¹¹.

The relationship of $(E)$ with ETri-nB-I-pc is however tighter than with ETri-nB-pc. Indeed, as shown in Remark 3, any ETri-nB-I-pc model has a straightforward representation in Model $(E)$ that does not make use of the unanimous model.

5.3 Unanimous representations

The reader may be perplexed by the fact that the proof of Theorem 1 builds a representation in Model $(E)$ in which $\mathcal {F}=\{N\}$. This is indeed a very particular form of representation. Notice that there are linear partitions of which the sole representation in Model $(E)$ is a unanimous one, i.e.,  with $\mathcal {F}=\{N\}$. The curious reader will find such an example in Appendix D, as supplementary material. Hence, representations with $\mathcal {F}=\{N\}$ are sometimes quite useful and even, may be the only possible ones. We show below that obtaining such a representation from a representation based on concordance, i.e.,  in Model $(E^{c})$, is easy.

Any representation in Model $(E)$ can be transformed into a representation with $\mathcal {F}=\{N\}$. This is a direct consequence of Theorem 1. When the representation is without discordance, we show below that the process of building $\mathcal {A}$ and then deriving $\mathcal {A}_{*}$ can be avoided.

Suppose we know a representation $\langle (\mathrel {S}_{i}, \varnothing )_{i \in N}, \mathcal {F}, \mathcal {P}\rangle$ of the partition $\langle A, U \rangle$ in $(E)$ (in fact, in $(E^{c})$) and that $\mathcal {F}\ne \{N\}$.

We want to find a representation such that $\mathcal {F}= \{N\}$. Theorem 1 ensures that such a representation exists. It can be built quite efficiently, independently of the construction used in Theorem 1.

Let $\mathcal {F}_{*}= {\text {Min}}(\supseteq , \mathcal {F})$, the set of minimal elements in $\mathcal {F}$ w.r.t. inclusion. For each $i \in N$, let $x^{0}_{i}$ be the unique element in $X_{i}$ that is minimal for the linear order $\succsim _{i}$. Define $x^{0}$ accordingly. Moreover, let:

$$\begin{aligned} \mathcal {P}' = \{ (x^{0}_{-I},p_{I}), \text { for all } p \in \mathcal {P}\text { and } I \in \mathcal {F}_{*}\}. \end{aligned}$$

It is clear that $\langle ({\mathrel {S}_{i}}, \varnothing )_{i \in N}, \{N\}, \mathcal {P}' \rangle$ is a representation of the partition $\langle A, U \rangle$ in $(E)$.

5.4 Variable set of winning coalitions $\mathcal {F}$

A rather natural generalization of Model $(E)$, called $(\widetilde{E})$, is as follows. Instead of considering a single family of winning coalitions $\mathcal {F}$ that is used to build the relation $\mathrel {S}$ and compare each alternative in $X$ to all profiles in $\mathcal {P}$, we could use a family $\mathcal {F}^{p}$ that would be specific to each profile $p \in \mathcal {P}$, with a relation $\mathrel {S}^{p}$ that now depends on the profile.

The analysis of Model $(\widetilde{E})$ is easy. It is simple to check that Model $(\widetilde{E})$ implies linearity. Indeed, for each relation $\mathrel {S}^{p}$, Lemma 3 holds and, hence, linearity cannot be violated. This shows that Model $(\widetilde{E})$ is a particular case of Model $(E)$ and, hence, is equivalent to it.

5.5 More than two categories

Our analysis of Model $(E)$ can easily be extended to cover the case of an arbitrary number of categories. Because this would require the introduction of a rather cumbersome framework, without adding much to the analysis of two categories, we do not formalize this point. We briefly indicate how this can be done, leaving the details to the interested readers.

Linearity has been generalized to cope with more than two categories. This is done in Słowiński et al. (2002) and Bouyssou and Marchant (2007b). The intuition behind this generalization is simple. It guarantees that there is a weak order on each attribute that is compatible with the ordered partition.

When $X$ is finite, this condition is necessary and sufficient to characterize the obvious generalization of Model (D1) that uses more than one threshold, instead of the single threshold 0 (see, e.g.,  Bouyssou and Marchant 2007b, Prop. 7, p. 250). Moreover, it is easy to check that this condition is satisfied by the natural generalization of Model $(E)$ that uses more than two categories (this involves working with of a set of profiles $\mathcal {P}$ for each of the induced twofold partitions).

Now, the technique used in the proof of Theorem 1 easily allows one to define a family of profiles for each of the induced twofold partitions. It just remains to check that these families of profiles satisfy the constraints put forward in Fernández et al. (2017, Condition 1, p. 216). This is immediate.

5.6 Pseudo-disjunctive ETri-nB

Up to this point, we have investigated the properties of Model $(E)$ which is closely linked to ETri-nB-pc and some of its variants. We now briefly examine ETri-nB-pd  (defined in Sect. 2.1.3).

Let us first observe, as in Remark 1, that ETri-nB-pd  and ETri-nB-I-pd  respect the dominance relation. Therefore, by Proposition 3, we have that these models satisfy linearity. Hence all partitions determined either by ETri-nB-pd  or by ETri-nB-I-pd  have a representation in Model $(E)$.

Whether or not these models are equivalent to Model $(E)$ is still unclear. The interested reader may refer to Bouyssou et al. (2020, Section 5), for a theoretical look at ETri-nB-pd  . This reference contains examples showing that the study of this model is more complex than that of the pseudo-conjunctive version. These examples suggest that ETri-nB-pd  might be strictly included in Model $(E)$, but this question remains open.

The extra complexity involved in studying the pseudo-disjunctive model was already pointed out by Bouyssou and Marchant (2015) in the case of ETri-B-pd  . Their analysis concludes that this is mainly due to the fact that ETri-B-pc  and ETri-B-pd  are not dual of each other (see Bouyssou et al. 2020, Section 5.3, for more detail).

6 Discussion

6.1 Summary

Using classical tools from conjoint measurement, we have proposed a new interpretation of the decomposable model (D1) introduced by Goldstein , i.e.,  of linear twofold partitions of a finite product set $X = \prod _{i=1}^{n} X_i$. Any such partition can be represented in Model $(E)$ using an appropriate set of limiting profiles. It can also always be represented in Model $(E^{u})$, the unanimous model, using as limiting profiles the set of minimally acceptable elements in X. Some linear twofold partitions have a unique representation in Model $(E)$. It is then a unanimous one. Some other linear twofold partitions have several representations in model $(E)$, one of which is unanimous.

In case $X_i$ is a finite subset endowed with a linear ordering $\ge _i$ (e.g.,  $X_i$ is the range of the real-valued evaluation function $g_i$ w.r.t. criterion i) and the partition $\langle \mathcal {A},\mathcal {U}\rangle$ of $X=\prod _{i=1}^{n}X_i$ respects dominance, then it is linear w.r.t. the weak order $\succsim _i$ on $X_i$ that is compatible with the linear order $\ge _i$ on $X_i$. Any such twofold partition is representable in Model ETri-nB-pc using an appropriate set of limiting profiles and other model parameters (thresholds, additive criteria weights). It can also be represented in model ETri-nB-I-pc (again with appropriate, possibly different, limiting profiles and parameters). Of course, it can also be represented in Models (D1) or in Model $(E)$ (possibly using a set of winning coalitions $\mathcal {F}$ that cannot be represented by additive weights and a threshold). Since all these models contain as a particular case the unanimous model $(E^{u})$, it may happen that the sole representation of the twofold partition in these models is the unanimous one. In some cases, but not always, there exists a more synthetic representation with fewer limiting profiles and a nontrivial set of winning coalitions.

Note that any sorting model producing partitions respecting dominance and able to determine any partition generated by the unanimous model is equivalent to Model (D1). Not all sorting models respecting dominance however are able to determine any partition produced by the unanimous model. For example, the additive model (Add) is strictly included in Model (D1).

Somewhat surprisingly, while Bernard Roy had always championed outranking approaches as an alternative to the classical additive value function model, it turns out that the last Electre method that he published before he passed away, Electre Tri-nB,  contains the additive value function model for sorting as a particular case. We think that this unexpected conclusion is a plea for the development of axiomatic studies in the field of decision with multiple attributes, as already advocated in Bouyssou et al. (1993), more than 25 years ago.

6.2 Perspectives for elicitation and learning

As a preliminary remark, let us observe the following. We have established that Electre Tri sorting models with multiple limiting profiles have the same expressive power be they based on Electre I (ETri-nB-I) or Electre III (ETri-nB) outranking relations. This does not imply that one should systematically opt for the simpler model based on Electre I (ETri-nB-I) in an elicitation or a learning process. In such a process, the crisp preference thresholds in Electre I may not fit with the decision maker’s insights, while she may be receptive to the more gradual preference model in Electre III. Similarly, learning a model based on Electre III may be at an advantage even though the model has more parameters and assignment examples are scarce. The more “continuous” character of the preferences in Electre III may allow for different optimization techniques (especially with the variant of Electre III proposed by Mousseau and Dias, 2004). In any case, since assignment examples or other preference information are typically scarce in MCDA, model indeterminacy is generally an issue. Therefore, attention should be paid to not using exceedingly general models. In particular, the number of limiting profiles considered should be kept to a minimum (using a model based on Electre I or on Electre III).

In the rest of this section, we focus on situations in which a model of assignment respecting dominance has to be learned solely on the basis of assignment examples. We thus assume that either we do not have the opportunity to interact with a decision maker or, if such a possibility exists, we decided to only ask her questions in terms of assignments to the classes of the partition. In such a perspective, the intuitive content of the underlying models plays no role, while mastering the complexity of these models is important as observed in Sect. 2.2.2, item 3.

ETri-nB-pc is equivalent to Model $(E)$, which is equivalent to the decomposable model (D1) and thus to the model based on “at least” decision rules (see Sect. 3.4). Techniques have been proposed to learn a decision rule model (see Greco et al. 1999, 2001a, c; Słowiński et al. 2002; Greco et al. 2016, and, for a recent application of these techniques, Abastante et al. 2014). A large scale recent application to the detection of frauds in car loans applications is described in Błaszczyński et al. (2021). The dataset involves 26 187 loans among which 405 were fraudulently obtained. The dominance-based rough set approach (DRSA) is applied. It determines “at least” decision rules, which approximately reproduce the partition in fraudulent and non-fraudulent loans. The approach outperforms two classical machine learning techniques (random forest and support vector machine). Methods such as DRSA can directly be used to learn an ETri-nB-pc model since a limiting profile can immediately be deduced from any “at least” decision rule d. Indeed, the latter specifies minimal levels to be attained on a subset $N_d \subseteq N$ of criteria in order to be assigned to category $\mathcal {A}$. A minimally acceptable element associated to such a rule is the n-tuple whose components corresponding to the criteria in $N_d$ are set to the minimal levels specified in the rule. The components corresponding to any criterion $i \not \in N_d$ are set to the minimal element in $X_i$ (w.r.t. the linear order $\ge _i$). An alternative satisfies rule d iff it is at least as good as the minimally acceptable element associated to the rule. This correspondence between rules and minimally acceptable elements provides a description of the partition in the unanimous model $E^{u}$.

Because Model (D1) is quite general and the learning sets of assignment examples usually of limited size, using these techniques is not entirely straightforward and, e.g.,  may lead, in the decision rule model, to a large number of rules. Moreover, these techniques, when used for learning an ETri-nB-pc model, produce indeed an ETri-nB-pc model but under the form of a unanimous model, i.e.,  in terms of a set of minimally acceptable alternatives, not under a more compact form, even when there is one.

Having at hand alternative descriptions of Model (D1) may offer an opportunity to control the complexity of the learned models. It is therefore important to investigate particular cases of Model $(E)$, in which the cardinality of the set of profiles $\mathcal {P}$ is restricted. Unfortunately, the problem seems to be difficult. This is the subject of a companion paper that deals with these more technical issues (Bouyssou et al. 2021a). This companion paper only analyzes the particular case of two profiles coupled with unanimity. Even in this apparently simple case, the problem is not easy. Hence, our analysis also leaves open the study of the gain of expressiveness brought by increasing the size of the set of profiles. Going from a single profile, the case studied in Bouyssou and Marchant (2007a), to an arbitrarily large number of profiles, the case implicitly studied in Sect. 4, leads to a huge gain in expressiveness. Is this gain already present when going from a single profile to a small number of profiles? This question is clearly important as a guide to learning the parameters of ETri-nB. Our analysis of the case of two profiles coupled with unanimity shows that it is unlikely that a purely axiomatic investigation will allow us to obtain clear answers to this question. Hence, this is also a plea to combine axiomatic work with other types of work, e.g.,  based on computer simulations.

Instead of constraining the number of limiting profiles in the unanimous model, an alternative approach would consist of exploring ETri-nB-pc or ETri-nB-I-pc with restricted number of limiting profiles¹². Models ETri-nB-I-pc and $(E)$ with one limiting profile are well-known. Model $(E)$ with one limiting profile is the noncompensatory sorting (NCS) model characterized by Bouyssou and Marchant (2007a). The particular case in which the winning coalitions can be represented by additive weights and a majority threshold corresponds to model ETri-nB-I-pc with one limiting profile. In the absence of veto, this model is known as MR-Sort (Leroy et al. 2011; Sobrie et al. 2019)

Several methods have been proposed for learning Model $(E)$ with one limiting profile (Belahcène et al. 2018) or its particular case Model ETri-nB-I-pc with one limiting profile (Leroy et al. 2011; Sobrie et al. 2017, 2019). These methods rely on various techniques such as mixed integer programming (MIP), Boolean satisfiability algorithms (SAT, MaxSAT) or metaheuristics. The size of sets of assignment examples that exact methods (such as MIP, SAT or MaxSAT) can deal with is limited. In contrast, the metaheuristic designed by Sobrie et al. (2013, 2019) or that by Olteanu and Meyer (2014) competes with state-of-the-art machine learning algorithms on real datasets (Tehrani et al. 2012b, a). The size of these datasets, which are benchmarks commonly used in machine learning, ranges from 120 to 1728 alternatives, the number of attributes, from 3 to 8 and the number of categories, from 2 to 9.

Characterizing Model $(E)$ with a fixed small number (e.g.,  2 or 3) of limiting profiles seems very difficult. The only thing that can easily be provided is an upper bound on the number of equivalence classes of the relations $\succsim _i$ induced by the corresponding twofold partition on the scale $X_i$ of each criterion (see Observation 2 in Sect. 2.2.2, for an illustration) and correlatively, an upper bound on the maximal number of minimally acceptable alternatives (see footnote 14). Extending the approaches referred to above for learning models with more than one limiting profile has not been done yet and does not seem straightforward either. In case a formulation for learning such models when the number of limiting profiles is limited to 2 or 3 would prove operational, then an incremental learning approach could be envisaged. Start with fitting Model $(E)$ with one limiting profile to the data. If assignment accuracy is not satisfactory, proceed with fitting a model with two profiles, etc.

Turning to the learning of an ETri-nB-pc model (using an Electre III outranking relation), observe first that the case with one limiting profile corresponds to the classical Electre Tri-pc model. Much effort has been devoted to develop learning methods for this model (e.g.,  Mousseau and Słowiński 1998; Ngo The and Mousseau 2002; Doumpos et al. 2009). The genetic algorithm proposed by Doumpos et al. (2009) has been tested on a real dataset (in the banking sector) involving 100 alternatives evaluated on 7 criteria and assigned to 3 categories. It has also been tested on artificial datasets, involving up to 1000 alternatives in the learning set, assigned to categories using randomly generated ETri models. No exact methods have been developed to date to learn ETri-nB-pc. The genetic algorithm proposed by Fernández et al. (2019) for learning ETri-nB-pc has shown good performance on a real case study involving 81 assignment examples (R & D projects) evaluated on 4 criteria assigned to 8 categories. It has also been tested on artificial datasets assigned to categories by randomly generated ETri-nB-pc (using 5 limiting profiles in each category boundary).

In conclusion, the general approach, based on the decision rule model and techniques, without restrictions on the generality of Model (D1), is available but does not allow to easily control the simplicity of the learned model (see Greco et al. 2000; Dembczyński et al. 2003). Current methods, such as the genetic algorithm proposed by Fernández et al. (2019) are usable. Unfortunately, the scalability of these algorithms is difficult to assess since they have not been tested on common benchmark datasets¹³.

Alternative approaches remain to be developed. Ideally, they should fulfill the following three requirements.

• 1. Focus on a well-defined, preferably characterized, family of assignment models forming a proper subset of all assignment models (D1) respecting the linearity property or the dominance relation.

• 2. The models in this family should have a compact description, i.e.,  there should be a synthetic, interpretable, manner of describing the set of minimally acceptable alternatives.

• 3. Learning these models should be computationally tractable, i.e.,  there should be an algorithm able to fit, in reasonable computing time, a model in the family to a set of assignment examples involving several hundreds up to a few thousands assignments.

Model $(E)$ and ETri-nB-pc with a restricted number of limiting profiles fulfill the first requirement and the second but not the third (except perhaps for Model $(E)$ with one limiting profile). The additive model (Add) is a candidate that checks all three boxes. It is closely related with the UTADIS technique and its variants (as already mentioned in Sect. 3.2). However, its interpretation is quite at a distance from that of Electre based models, which rely on the idea of one or several limiting profiles and outranking relations. These are interpreted as expressing requirements on each criterion that an alternative should ideally fulfill in order to be acceptable. A challenging research issue is thus to define a family of models within the decomposable model (D1) that are in the spirit of the Electre methods and fulfills the above three requirements.

6.3 Future research and work in progress

Theorem 1 is a simple result that establishes the equivalence of the decomposable model (D1) with ETri-nB-pc and related models in the spirit of Electre Tri. Besides issues related to learning, this result leaves open a number of interesting problems that we intend to deal with in later studies. Among them, let us mention the following sets of questions.

Algorithmic questions. Is it easy to test whether a partition $\langle \mathcal {A},\mathcal {U}\rangle$ satisfies linearity? Are there efficient algorithms to find a linear partition close to a partition that is not linear? Is it easy to test whether it is possible to build a linear partition on the basis of partial information about $\mathcal {A}$ and $\mathcal {U}$? Similar questions arise, when there is a supplementary constraint on the size of the set of profiles.

Combinatorial questions. Given a set $X = \prod _{i=1}^{n} X_{i}$, can we devise (easy to evaluate) formulae for the maximal number of objects in $\mathcal {A}_{*}$ (this is related to the size of the largest antichain¹⁴ in a direct product of chains, see Sander, 1993, for the case of the direct product of chains of the same length)? What is the number of twofold partitions of $X = \prod _{i=1}^{n} X_{i}$ that can be represented in Model $(E)$ this is related to the famous problem of Dedekind numbers, see Kahn (2002), Kisielewicz (1988), Ersek Uyanık et al. (2017)

Questions linked to the number of profiles. Given a learning set of assignment examples that is compatible with Model (D1), what is the minimal number of limiting profiles of a unanimous model (or of a Model $(E)$ or of an ETri-nB-pc model) that exactly restores the assignments?