1 Introduction

Firms and factories in the world, no matter how small they are, may keep an amount of goods as inventory in storage [1]. The number and variety of goods increase with increased demand and corporate activity. These items are generally divided into three categories: raw materials, semi-manufactured products, and finished goods. Inventories are usually kept with many goals such as flexibility in production, scheduling, and reducing costs including the cost of shortages and storage [2].

For organizations that keep thousands of items of inventory, paying equal attention to all items is irrational. Managers need classification to better control these items. ABC analysis is a widely used and the most comprehensive classification technique of inventory [3]. The main purpose of ABC analysis is to focus on tight control of class A items, less control of class B items, and very low control of class C items [4]. Conventional ABC analysis follows the 80/20 law of Pareto [5]. According to this law, class A is the mostly valued class by having 60–80% of the total value with 10–20% of inventory; class C with the value between 5 and 15% while having 50–60% of inventory has the least significance among the classes. From 20 to 25% of items belonging to class B, values close to 30% can be achieved [6].

In traditional classification, items are classified based on annual dollar usage. However, in addition to the value of annual consumption, there are other measures important in inventory management. Among these, lead-time, obsolescence, and availability can be pointed out [6,7,8]. As the number of criteria increases, so does the need to use multi-criteria decision-making (MCDM) methods to classify items [9]. So far, many studies with different methods and criteria have been carried out for ABC analysis. All previous studies conducted on ABC analysis have focused their attention on two issues, namely using different qualitative and quantitative criteria as well as increasing accuracy in calculating the value of each item. The base of these studies is calculating the value of each item according to different parameters and the final classification based on the resulting value.

In addition to these two issues, determining the number and value of each class of the classification is of the requirements of ABC analysis. In most research conducted in this field, items related to each class are determined qualitatively. This means that after the score is calculated for each item, according to various criteria, the decision makers, based on experience, determine the percentage of items related to each class and rank them. This kind of classification ignores the limitation of the number of items and the total value in Pareto’s principle. This means that in final classifications, one of the two mentioned criteria usually becomes the base and classification is performed on that basis. With this purpose, in this study, it is attempted to offer a model by combining MCDM methods so that, in addition to calculating the value of each item with different qualitative and quantitative criteria, it has the ability to satisfy Pareto’s law limitations.

The reminder parts of this paper are organized based on the description below. In Sect. 2, the literature is reviewed. In Sect. 3, the methods used in this study are described and the mathematical model which classifies inventory items is presented. In Sect. 4, using the information of some studies, the proposed model is run and evaluated, and finally in Sect. 5, the conclusion and future research are presented.

2 Literature review

For the first time, Flores and Whybark [6, 10], using the joint criteria matrix, raised the issue of the multi-attribute inventory classification. The suggested method is appropriate when two criteria are considered for classification. Flores et al. [11] propounded an approach that merged the clustering method with operations constraints. Partovi and Hopton [12] as well as Gajpal et al. [13] presented the analytical hierarchy process (AHP) method to address ABC inventory analysis. Considering different qualitative and quantitative parameters and not requiring plenty of measurements are the advantages of this methodology. Ramanathan [3] proposed a weighted linear optimization model to classify inventory items. In this research, a weighted additive function was used to obtain the score of the performance of inventory items. Ng [7] proposed a linear optimization model for the multiple criteria inventory classification (MCIC). The proposed model converts all the criteria of inventory items into a scalar score. Bhattacharya et al. [14] used TOPSIS to classify inventory items in a company in India. They determined the effectiveness of the proposed method by the analysis of variance (ANOVA) technique. Zhou and Fan [15] proposed the R-model for classification of inventory items. This model that is the improved version of Ramanathan’s model uses two sets of weights for each item.

Tsai and Yeh [16] suggested the particle swarm optimization (PSO) algorithm for the inventory classification. They considered three objectives including minimizing costs, maximizing inventory turnover ratios and maximizing inventory correlation for classification of inventory items. Chu et al. [17] proposed a new inventory control approach called the ABC-fuzzy classification (ABC-FC). The strengths of this approach are the ability to handle variables with either nominal or non-nominal attribute and its easy application. Rezaie [18], to improve the model provided by Ramanathan [3], developed a model that is able to rank items with an optimal score of 1 using a cross-efficiency technique. Hadi-Vancheh [19] conducted a study to extend the Ng-model [7] for classifying inventory items. The extended model, that is a nonlinear programming, determined the most favorable weights within the feasible region for each item. Hadi-Vancheh and Mohamadghasemi [1] in their study proposed the fuzzy analytical hierarchy process (FAHP) and data envelopment analysis (DEA) to calculate weights of criteria and scores of items, respectively. Inventory items in this study were classified under four criteria including annual dollar usage, limitation of warehouse space, average lot cost and lead time. Xiao et al. [20] presented an algorithm which classifies inventors into three classes using the lost profit of item/itemset. Chen [9] proposed an alternative approach to MCIC. He first compared all real items with two virtual items, i.e. the positive ideal item (PII) and negative ideal item (NII), and then calculated an overall performance index for classification of inventory items using relative closeness (RC) index derived from TOPSIS.

Torabi et al. [21] presented a DEA-like model for the ABC inventory classification. The proposed model can consider both quantitative and qualitative criteria. Annual dollar usage, average unit cost, critical factor and lead time are the four criteria used in this research. Kabir and Akhtar Hasin [22] proposed an FAHP approach which determines the weight of criteria in MCIC problems. To accredit the proposed model, 351 raw materials of the switch gear section of Energypac engineering limited (EEL), a large power engineering company in Bangladesh, were classified in their study. Kiris [23] applied the fuzzy analytical network process (FANP) and simple additive weighting (SAW) for the MCIC problem. They categorized inventory items based on 16 criteria categorized into five categories including price, criticality, storage ability, procurement process, and maintenance. Kabir and Akhtar Hasin [24] proposed a hybrid model including FAHP and ANN for classification of inventory items. Unit price, annual demand, criticality, last use date and durability are the criteria used in their study. Lolli et al. [25] introduced a new hybrid MCIC method for the inventory classification based on AHP and the K-means algorithm. Annual dollar usage, critical factor and replenishment lead time are the three factors used in their study. Soyla and Akyol [26] used a classification scheme based on a linear utility function to classify inventory items. For this purpose, a linear programming (LP) was presented with the objective of minimizing average classification errors over the reference set. Park et al. [27] used the cross-evaluation-based weighted linear optimization (CL-WLO) model for classification of inventory items. They classified 47 items based on three criteria including average unit cost, annual dollar usage, and lead time.

Hatefi and Torabi [28] applied a novel methodology which used the concept of the common weight linear optimization model for solving the MCIC problem. The proposed method reduced the number of required LP models for the ABC inventory items classification problem. Kaabi and Jabeur [29] used two TOPSIS models with two different distance metrics (first order and second order metrics) and a combination of the weights of subjective–objective criteria for the inventory classification. They used the variable neighborhood search (VNS) and AHP to calculate the weights of the two types of criteria. Kartal et al. [30] applied three MCDM methods (SAW, AHP and Visekriterijumsko Kompromisno Rangiranje (VIKOR) integrated with machine learning for solving the MCIC problem. Douissa and Jabeur [31] used Elimination and Choice Expressing Reality III (ELECTRE III), as well as entropy and continuous variable neighborhood search (CVNS) techniques for classification of inventory items. Accordingly, the ELECTRE III method was used to compute the global score of each item, CVNS estimated the ELECTRE III parameters and the entropy method was applied to calculate the criteria weights. Kaabi and Alsulimani [32] suggested a hybrid multi objective genetic algorithm TOPSIS (MOGA-TOPSIS) approach for the inventory classification. Through the proposed approach, first, a set of feasible optimal solutions was generated and then, using TOPSIS, an optimal solution was selected. Hadi-vencheh et al. [33] proposed a hybrid model including TOPSIS and Gaussian interval type-2 fuzzy sets (GIT2FSs) for the ABC inventory classification. They used two linear programs to determine the weights of criteria in this research. Rauf et al. [34] applied the TOPSIS method for solving the MCIC problem. Four criteria including average unit cost, average annual usage, critical factor and lead time were used in this research for classification of inventory items.

In general, the conducted studies can be categorized into two groups: MCDM and multi objective decision making (MODM). MCDM methods such as AHP, ANP, TOPSIS, and ELECTRE III were used for (1) increasing the accuracy of classification in compared to the previous methods, (2) considering various quantitative and qualitative criteria, (3) considering the trade-off between criteria, and (4) considering linguistic variables in the weighting process of criteria. By reviewing studies on MODM, we can point out that they were used to (1) increase the accuracy of previous models, (2) optimize the number of items and (3) minimize the error values in each item by using combination methods and paying attention to the impact of items on each other.

As the literature review reveals, simultaneously considering the value and number of items in the problem of classifying inventory items is a main issue which has been neglected in previous studies. In this study, for the first time, a hybrid methodology is presented which solves the MCIC problem so that the maintained issue, Pareto’s principle, is covered as much as possible.

3 Methods used in the study

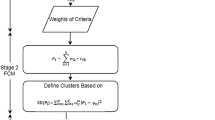
The present study is conducted to provide an appropriate model for ABC analysis. Components of the proposed model are shown in Fig. 1. The first step in the proposed model is to determine criteria related to ABC analysis. The important criteria are determined according to the decision-making environment and decision makers’ ideas. The second step is to determine the weight of each criterion. In the proposed model, the weight of each criterion is determined by Shannon’s entropy.

Fig. 1
figure 1

Methods used in this study

Full size image

The third step is to determine the value of each item according to various quantitative and qualitative criteria. In this step, using TOPSIS, all items are evaluated and ranked. After the value of each item is determined, items require to be classified. Classification should be based on Pareto’s law and taking into account both the number and value of the criteria. The need to have a minimum deviation of the quantity of each criterion on each floor leads to the use of goal programming for this purpose. Thus, in the fourth step, items are classified using goal programming in three classes of A, B and C. The proposed goal-programming model is presented below.

3.1 Shannon’s entropy

In MCDM problems, knowing the relative weight of the existing criteria is a major step forward in the process of problem solving. Among the methods available, Shannon’s entropy is one of the most popular methods for calculating the weight of criteria [35]. Entropy in the social sciences, physics, and information theory is a concept used to measure uncertainties. As the entropy of information becomes more, its value will be less and vice versa. Entropy is also used in decision-making in the same sense. Thus, as a criterion has more uncertainty (or less entropy), it has more weight and importance. Therefore, by calculating the uncertainty in criteria, one can determine the weight of criteria. Among the properties of Shannon’s entropy is its flexibility in acceptance or non-acceptance of sometimes contradictory comments made by decision makers. Steps necessary to calculate the weight of each criterion using the entropy technique are given below [36, 37].

3.1.1 Step one: normalization

One multi-attribute problem can be fully defined in form of a matrix. Suppose that there are m items and n evaluation criteria. The decision matrix (D) is an m × n matrix whose xij element represents the value of the j-th criteria for the i-th item

$$ D = \left( {\begin{array}{*{20}c} {x_{11} } \\ {x_{21} } \\ \ldots \\ {x_{m1} } \\ \end{array} \begin{array}{*{20}c} {x_{12} } \\ {x_{22} } \\ \ldots \\ {x_{m2 } } \\ \end{array} \begin{array}{*{20}c} { \ldots } \\ \ldots \\ \ldots \\ \ldots \\ \end{array} \begin{array}{*{20}c} {x_{1n} } \\ {x_{2n} } \\ \ldots \\ { x_{mn} } \\ \end{array} } \right). $$
(1)

To normalize the elements of the matrix, Eq. 2 is used

$$ P_{ij} = \frac{{x_{ij} }}{{\mathop \sum \nolimits_{i = 1}^{m} x_{ij} }}\quad \forall \, i\quad and\quad j. $$
(2)

3.1.2 Step two: determining the value of entropy for each criterion

After normalizing the decision matrix, the value of entropy (ej) for each criterion is obtained by Eq. 3

$$ e_{j} = - k\mathop \sum \limits_{i = 1}^{m} P_{ij} \cdot Ln\left( { P_{ij} } \right) \quad \forall j. $$
(3)

In the above equation, K is equal to:

$$ k = \frac{1}{Ln\,m}. $$
(4)

3.1.3 Step three: calculating the amount of deviation for each criterion

By determination of entropy for each criterion, the criterion deviation of j-th (dj) can be achieved from Eq. 5:

$$ d_{j} = 1 - e_{j} . $$
(5)

3.1.4 Step four: calculating the weight of each criterion

The weight of the j-th criterion (wj) is obtained from Eq. 6

$$ w_{j} = \frac{{d_{j} }}{{\mathop \sum \nolimits_{j = 1}^{n} d_{j} }} \quad\forall j. $$
(6)

The number obtained from the above equations is a parameter that describes the degree of importance of each criterion. As is clear, higher amount of criterion entropy causes the criterion to have much less importance. If a decision-maker considers a special weight (λj) beforehand based on experience or based on the existing methods such as AHP for the j-th criterion, then, the new weight wj′ is calculated as follows

$$ w_{j}^{{\prime }} = \frac{{\lambda_{j} w_{j} }}{{\mathop \sum \nolimits_{j = 1}^{n} w_{j} \lambda_{j} }} \quad \forall j. $$
(7)

3.2 TOPSIS

TOPSIS is a widely used method in multi-attribute decision-making that ranks m alternatives according to n criteria. Hwang presented TOPSIS for the first time. In this method, alternatives are assessed based on proximity to positive and negative ideal points and then an alternative with maximum proximity to the positive ideal point and maximum distance from the negative ideal point is selected [38]. Among the advantages of using this method are simplicity and producing solution compatible with prioritization (ability to yield an indisputable preference order) [39]. Steps required to prioritize alternatives by TOPSIS are given below.

3.2.1 Step one: normalizing the decision matrix

Consider the decision matrix (D) in the previous section. To normalize the elements of this matrix (rij), Eq. 8 is used

$$ r_{ij} = \frac{x_{ij}}{\left(\mathop{\sum}\nolimits_{i = 1}^{m} x_{ij}^{2} \right)^{1/2}}\, \quad \forall \, i\,{\it and}\,j. $$
(8)

In normalizing the decision matrix (D) elements, the normalized matrix R is obtained (see Eq. 9)

$$ R = \left( {\begin{array}{*{20}c} {r_{11} } \\ {r_{21} } \\ \ldots \\ {r_{m1} } \\ \end{array} \begin{array}{*{20}c} {r_{12} } \\ {r_{22} } \\ \ldots \\ {r_{m2 } } \\ \end{array} \begin{array}{*{20}c} { \ldots } \\ \ldots \\ \ldots \\ \ldots \\ \end{array} \begin{array}{*{20}c} { r_{1n} } \\ {r_{2n} } \\ \ldots \\ { r_{mn} } \\ \end{array} } \right). $$
(9)

3.2.2 Step two: weighting the normalized matrix

In order to enter the importance of criteria in the evaluation process, the predetermined weight of each criterion (wi) using Eq. 10 is multiplied in the elements of the R matrix. The result is the normalized weighted matrix (Y) below

$$ y_{ij} = w_{j} \cdot r_{ij} \quad\forall \, i\,and\,j $$
(10)
$$ Y = \left( {\begin{array}{*{20}c} {y_{11} } \\ {y_{21 } } \\ \ldots \\ {y_{m1} } \\ \end{array} \begin{array}{*{20}c} {y_{12} } \\ {y_{22} } \\ \ldots \\ {y_{m2 } } \\ \end{array} \begin{array}{*{20}c} { \ldots } \\ \ldots \\ \ldots \\ \ldots \\ \end{array} \begin{array}{*{20}c} {y_{1n} } \\ {y_{2n} } \\ \ldots \\ { y_{mn} } \\ \end{array} } \right). $$
(11)

3.2.3 Step three: determining positive and negative ideal solutions

The positive ideal point (\( A_{i}^{ + } ;i = 1,2, \ldots , n \)) \( A^{ + } \) is obtained from the maximum amount of alternatives in each positive criterion (or from the least value in each negative criterion) in the matrix Y. The negative ideal point A− (\( A_{i}^{ - } ;i = 1,2, \ldots , n \)) is obtained from the minimum amount of alternatives in each positive criterion (or from the maximum value in each negative criterion) in the matrix Y. Equations 12 and 13 show how to calculate either of the amount listed

$$ A_{j}^{+} = \left\{{\left({\mathop {\min}\limits_{i} y_{ij} |j \epsilon C} \right),\quad \left({\mathop {\max}\limits_{i} y_{ij} |j \epsilon B} \right)| i = 1, 2, \ldots,m} \right\} $$
(12)
$$ A_{j}^{-} = \left\{{\left({\mathop {\max}\limits_{i} y_{ij} |j \epsilon C} \right),\quad \left({\mathop {\min}\limits_{i} y_{ij} |j\epsilon B} \right)| i = 1, 2, \ldots,m} \right\}. $$
(13)

In the above equation, B and C denote the set of positive and negative criteria, respectively.

3.2.4 Step four: obtaining the value of distances

At this stage, distance from each positive and negative ideal point (\( {\text{S}}_{i}^{ - } \) and \( {\text{S}}_{i}^{*} \)) is obtained from Eqs. 14 and 15, respectively

$$ {\text{S}}_{i}^{*} = \left[ {\mathop \sum \limits_{j = 1}^{n} (y_{ij} - A_{j}^{ + } )^{2} } \right]^{1/2}\quad \forall i $$
(14)
$$ {\text{S}}_{i}^{ - } = \left[ {\mathop \sum \limits_{j = 1}^{n} (y_{ij} - A_{j}^{ - } )^{2} } \right]^{1/2}\quad \forall i. $$
(15)

3.2.5 Step five: calculating how near the options are to the ideal solution

This step solves the similarities to an ideal solution by Eq. 16:

$$ Cl_{i} = \frac{{d_{i}^{ - } }}{{d_{i}^{ - } + d_{i}^{ + } }}\quad \forall i. $$
(16)

3.3 Goal programming

Goal programming is a prominent planning tool for multi-objective decision analysis with features such as achieving several goals simultaneously based on the priority-rating [40]. Charnes and Cooper introduced this programming for the first time. Goal programming attempts to combine the logic of optimization with the requirements of decision-makers to satisfy several goals. This model includes several goals simultaneously and is set based on minimizing deviations from the targets. The main advantage of goal programming is in removing or fading weak human argument during programming and decision-making [41]. The mathematical formula of goal programming is presented below:

$$ \begin{aligned} Minimize & \mathop \sum \limits_{k = 1}^{m} \left| {f_{k} \left( x \right) - g_{k} } \right| \\ & Subject\,to :\,X\epsilon F,{\mkern 1mu} \left( {F{\mkern 1mu} is\,a\,feasible\,set} \right) \\ \end{aligned} $$
(17)

where fk (x) is the function of the k-th goal, and gk is the aspiration level of the k-th goal.

For classification of inventory items based on value and quantity, we present a goal programing mode which uses the result of Shannon’s entropy and TOPSIS as parameter. The mathematical model determines the class of each item. All the parameters and decision variables applied in the proposed model are presented in Table 1. The proposed model including explanation is presented as follows:

Table 1 The criteria, parameters, and decision variables used in the model
Full size table

3.3.1 Objective function

In the proposed model, the objective function (Eq. 18) refers to minimizing deviations from the goals

$$ Min \, d_{1}^{ - } + d_{1}^{ + } + d_{2}^{ - } + d_{2}^{ + } + d_{3}^{ - } + d_{3}^{ + } + d_{4}^{ - } + d_{4}^{ + } + d_{5}^{ - } + d_{5}^{ + } + d_{6}^{ - } + d_{6}^{ + } . $$
(18)

3.3.2 Constraints

The set of constraints considered in the proposed method is as follows:

3.3.2.1 The total value of items belonging to each class

Constraints 19–21 decrease the deviation of value that belongs to each class. Based on Eqs. 19–21, the ideal value belonging to classes A, B and C is respectively TPA, \( TP_{B} , \) and TPC percent of the total value of inventory items, which is satisfied by minimizing the amount of \( d_{1}^{ - } ,d_{2}^{ - } , d_{3}^{ - } , d_{2}^{ + } , d_{2}^{ + } \,{\text{and}}\,d_{3}^{ + } \) in the objective function

$$ \mathop \sum \limits_{i = 0}^{N} n_{N - i} \times p_{N - i} \times A_{N - i} + d_{1}^{ - } - d_{1}^{ + } = TP_{A} \mathop \sum \limits_{i = 1}^{N} n_{i} \times p_{i} $$
(19)
$$ \mathop \sum \limits_{i = 1}^{N} n_{i} \times p_{i} \times B_{i} + d_{2}^{ - } - d_{2}^{ + } = TP_{B} \mathop \sum \limits_{i = 1}^{N} n_{i} \times p_{i} $$
(20)
$$ \mathop \sum \limits_{i = 1}^{N} n_{i} \times p_{i} \times C_{i} + d_{3}^{ - } - d_{3}^{ + } = TP_{C} \mathop \sum \limits_{i = 1}^{N} n_{i} \times p_{i} . $$
(21)
3.3.2.2 The number of items belonging to each class

Constraints 22 and 23 guarantee that the number of items belonging to each class have the minimum deviation from their aspirations, i.e. \( TN_{A} , TN_{B} , \,and\,TN_{C} \) for classes \( A, B,\,and\,C, \) respectively. These concepts are satisfied by minimizing \( d_{4}^{ - } ,d_{5}^{ - } , d_{6}^{ - } , d_{4}^{ + } , d_{5}^{ + } \,{\text{and}}\,d_{6}^{ + } \) in the objective function

$$ \mathop \sum \limits_{i = 0}^{N} n_{N - i} \times A_{N - i} + d_{4}^{ - } - d_{4}^{ + } = TN_{A} \mathop \sum \limits_{i = 1}^{N} n_{i} $$
(22)
$$ \mathop \sum \limits_{i = 1}^{N} n_{i} \times B_{i} + d_{5}^{ - } - d_{5}^{ + } = TN_{B} \mathop \sum \limits_{i = 1}^{N} n_{i} $$
(23)
$$ \mathop \sum \limits_{i = 1}^{N} n_{i} \times C_{i} + d_{6}^{ - } - d_{6}^{ + } = TN_{C} \mathop \sum \limits_{i = 1}^{N} n_{i} . $$
(24)
3.3.2.3 Classification rules

The value of each item categorized into class A should be greater than or equal to the value of each item in class B; moreover, the value of each item categorized in class C should be less than or equal to each item in class B. Constraints 25–27 satisfy the maintained rules.

Subject to:

$$ A_{i} \le A_{i + 1}\quad \forall i $$
(25)
$$ C_{i} \ge C_{i + 1 } \quad\forall i $$
(26)
$$ A_{i} + B_{i} + C_{i} = 1\quad \forall i $$
(27)
$$ A,B\,and\quad C\epsilon \left\{ {0,1} \right\} $$
(28)

4 Numerical analysis

Numerical analysis of the model is performed in two separate parts. The first part is related to the validation of the model in terms of percentage of similarity of the carried out classification compared with other research. To this end, the information of the article by Yu [5] is used. The mentioned study has examined 47 items according to the four criteria including average unit cost, annual dollar usage, critical factor, and lead-time data. Information on the items in any of the listed parameters is provided in Table 2. According to the availability of the criteria, the first step to use the proposed model is to calculate the weight of each criterion.

Table 2 The performance of the 47 items in the four criteria
Full size table

Based on the output from Shannon’s entropy, the greatest weight is for critical factor whereas the least weight belongs to the lead-time criterion (see Table 3). After calculating the weight, it is time to evaluate the items according to the four criteria listed.

Table 3 The weight of the criteria
Full size table

TOPSIS is used for this purpose. The value obtained by TOPSIS for each item is rounded to four decimal numbers and set in Table 4. Since the items with the same value should be placed in one class, a column called the number of repetitions is considered in Table 4.

Table 4 Ranking the items and their value
Full size table

The number shown in this column means the number of items with the same value. In order to determine the scope of each class according to Pareto’s law, goal programming is used. Information on the model parameters is set in Table 5.

Table 5 The goal programming model’s parameters
Full size table

Based on the carried-out classification, of the 47 items available, 10 items are in class A, 11 items in class B and 26 items in class C (see Table 6).

Table 6 Classification of the items
Full size table

After classification, it is time for validation of the model. Validity of the proposed model is evaluated in three ways. The first method is the use of the multivariate analysis of variance (MANOVA) and discriminant analysis (DA). These two tests are carried out with the purpose of assessing whether the separation between the items is statistically significant. In MANOVA, the hypothesis is investigated regarding the equality of the vector of the means of the three obtained categories. In Table 7, MANOVA results are listed based on the values of Wilkes, Hotelling and the largest root. According to the results of this test, the aforementioned hypothesis is rejected. Thus, at least one of the existing categories has an acceptable difference in terms of the mean of one or more criteria of the surveys compared to the other categories.

Table 7 Results of MANOVA
Full size table

In DA, presence or absence of difference between classes is examined based on values obtained by the items in the criteria. In fact, in DA, function or functions of the variables on which the classification is based are presented, and then the statistical significance of this function or functions is investigated. If significant, at least one of the extracted functions can refer to the existence of distinction between the categories. According to the description given, of the two functions extracted, the first function with statistic value is significant (P value), meaning that a proper distinction is created between the categories (see Table 8).

Table 8 Results of DA
Full size table

The second method determines the degree of overlap between the results of the model and those of other methods and compares them with each other. For this purpose, the classification presented in this study is compared with the classification of four other methods (see Table 9) in terms of similarities.

Table 9 Classification of the items according to different methods
Full size table

The method is to evaluate the percent of similarity with other methods and then compare the similarity of the proposed method with the other methods of the groups. Table 10 shows the results of similarity compared to the other methods.

Table 10 Percentage of similarity in different methods
Full size table

It should be noted that each of these four methods, using different criteria, classifies items listed in Table 2. In 10 comparisons carried out, the number of times to which the proposed method had more similarity was 8, and only in one case, with difference of only 9%, the proposed method had less percent of similarity.

The third section is devoted to the validation of knowledge in terms of number and value of each class. According to Table 11, class A valued at more than 51% of 21% of the total items is in the first place, followed by class B with values close to 28% from 23% of the items and class C with values of 20% of more than 55%.

Table 11 Fractional analysis of each class
Full size table

In the proposed model, it is attempted to take into account Pareto’s law as much as possible. On this basis, regarding the class number criterion, class B, A and C have the minimum deviations of zero, 1.2, and 5%, respectively. Regarding the value criterion, classes C, B and A with deviations of zero, 0.2 and 9.7% are in the position from one to three, respectively. This classification has less deviation compared to similar studies. To illustrate this claim, the classification in the study by Bhattacharya et al. [14] using TOPSIS can be noted, and its results can be compared with the classification of the proposed model. Table 12 shows the criteria and performance of 50 alternatives used in Bhattacharya et al.’s study.

Table 12 Bhattacharya et al.’s study information
Full size table

In the study by Bhattacharya et al., classes A, B and C with 20, 40, and 40% have the value of 26, 44.71 and 40%, respectively (see Table 13). This is while, using the proposed model, class A has 16% of the items with a value of 61%, class B has 28% of the items with a value of 23%, and class C has 54% of the items with a value of 15%. As is evident, the existing deviations in the classification with Bhattacharya et al.’s method have far greater value and number than the model proposed in this study (see Table 14).

Table 13 Classification of the items by the two methods
Full size table
Table 14 Classification analysis of the two methods in terms of percent using Bhattacharya et al.’s method and the proposed model
Full size table

5 Conclusions and future research

The ABC multi-criteria classification can be useful for companies that are faced with a large number of various inventory items. Regarding the ABC classification, many models have been proposed. However, in most of these models, either the final classification is based on the number of factors or the value belongs to each class. This is while taking into account both the listed criteria is of the requirements of the ABC classification. This article has attempted to use methods that provide a multi-attribute model in the classification of items to cover both the mentioned criteria to the extent possible. The first step is to calculate the value of each item in the model using Shannon’s entropy. The second step is to determine the value of each item and rank it using TOPSIS. Simultaneous use of Shannon’s entropy and TOPSIS for weighting and evaluating alternatives leads to ranking of items with correct distance from each other. After determining the value of each item, they should be classified. The final classification is carried out using goal programming. In order to assess the proposed model, three methods of statistical analysis are used to determine the similarity in classification compared with other methods as well as bit-to-bit analysis in each class. Given that the proposed model performs classification in terms of Crisp state, the use of fuzzy logic in any part of the model to enhance the accuracy of the results is suggested as future activities in undertaking research in this area.