Volatility versus downside risk: performance protection in dynamic portfolio strategies

Abstract

Volatility-based and volatility targeting approaches have become popular among equity fund managers after the introduction in 1993 of the VIX, the implied volatility index on the S&P500 at the Chicago Board of Exchange (CBOE), followed, in 2004, by futures and option contracts on the VIX: since then we have assisted to an increasing interest in risk control strategies based on market signals. In January 2000 also the FTSE implied volatility index (FTSEIVI) was introduced at the London Stock Exchange. As a result, specifically in the US, portfolio strategies based on combinations of market indices and derivatives have been proposed by Stock Exchanges and investment banks: one such example is the S&P500 protective put index (PPUT). Early in 2016, relevant to the definition of optimal bond-equity strategies, CBOE launched an Index called TYVIX/VIX featuring an investment rotation strategy based jointly on signals coming from the VIX and the 10-year Treasury Yield implied volatility (TYVIX). All these are rule-based portfolio strategies in which no optimization methods are involved. While rather effective in reducing the downside risk, those index-based portfolio approaches do not allow an optimal risk-reward trade-off and may not be sufficient to control financial risk originated by extreme market drops. To overcome these limits we propose an optimization-based approach to portfolio management jointly focusing on volatility and tail risk controls and able to accommodate effectively the return payoffs associated with option strategies, whose cost as market volatility increases may become excessive. The model is based on a mean absolute deviation formulation and tested in the US equity market over the 2000–2016 period and with a focus on three periods of high volatility, in 2000, 2001 and 2008. The results confirm that optimal volatility controls produce better risk-adjusted returns if compared with rule-based approaches. Moreover the portfolio return distribution is dynamically shaped depending on the adopted risk management approach.

1 Introduction

Since the start of this century, due either to an endogenous increase of systemic risk or to exogenous political events, global financial markets are experiencing a prolonged period of very volatile returns, sometimes leading to financial turmoils, and an overall reduction of investment horizons induced by deteriorating economic expectations. Not only sovereign and corporate bond markets but commodity and equity markets alike, amid a widespread negative economic cycle, have gone in Europe and the US through prolonged negative phases. Those market conditions, as well known, are by no means new to global and equity markets, in particular (Consigli et al. 2009), and they represent one of the factors underlying the persistent growth of selected (when also considering credit derivatives and structured product markets) derivative markets.

Over the last few years, several portfolio management approaches have been put forward treating volatility as an asset class (Chen et al. 2011), or add overlays to risky portfolios through derivatives based on the volatility (Benson et al. 2013). For an extended analysis of the use of volatility derivatives in equity portfolio management we also refer to (Guobuzite and Martinelli 2012). The inclusion of volatility-based financial payoffs within investment portfolios for diversification purposes relies on the inverse relationship between equity returns and their volatility. Moreover, such negative correlation patterns seem to be stronger in periods of market downturns. For empirical evidence and economic foundations see, for example, (Christie 1982; Dopfel and Ramkumar 2013; Schwert 1989). The importance of volatility in investment decisions is discussed also in Dempster et al. (2007, 2008), Fleming et al. (2001), Xiong et al. (2014). In 2016 the CBOE launched the TYVIX/VIX index to propose a market instrument capturing jointly volatility signals from the Treasury and the equity markets and their inherent trade-offs to determine an effective bond-equity portfolio composition.

In the above financial scenario, many investment institutions have indeed successfully proposed over the last twenty years or so over the counter (OTC) products based on volatility strategies or volatility targeting approaches. In extreme summary, these strategies are designed to keep a desired and fixed level of volatility, that is a constant level of risk exposure through time. Recently, several authors advocated the benefits of constant volatility approaches to investment. Among them, Hocquard et al. Hocquard et al. (2013) have proposed an approach to target constant level of portfolio volatility consistent with multivariate normal returns. Thomas and Shapiro (2009) argued that equity strategies that maximize return while targeting low levels of volatility are increasingly interesting for insurance companies and institutional investors for their ability to produce better risk-return profiles. Dopfel and Ramkumar Dopfel and Ramkumar (2013) discussed the advantages of managed volatility strategies in response to the presence of volatility regimes.

Fig. 1

S&P500, VIX, PPUT index. Weekly data: January 5, 1990–June 10, 2016

When analysing volatility dynamics, as shown in Fig. 1, an important difference is related to the underlying source of volatility: we distinguish between volatility increases due to (increasing) continuous squared returns with an impact on the fourth (the kurtosis) but not the third central moment (the skewness), and those due to market jumps leading to severe asymmetries of the return distribution. In this article, without introducing any parametric assumption on the return process, we present an optimization approach able to capture hedging and speculative strategies specifically for equity portfolios based on implied volatility signals. Despite its generality, the model is motivated and developed considering the US equity market in particular. We consider a fund manager with a short planning horizon (1-month) whose investment policy focuses on volatility control and tail risk protection in specific periods while tracking a market portfolio during positive phases. Index-based portfolio strategies and signals coming from (1-month) implied volatility also influence the fund manager strategy.

Hedging against tail risk is in general quite a complex task and a full protection can be highly expensive either due to the costs of the insurance, or due to the implementation of a too defensive investment strategy. Derivative-based strategies, such as protective put and option-based portfolio insurance, suffer from the first problem; while, active equity management strategies, such as defensive equity, low-beta alternative investments, constant-proportion portfolio insurance and stop-loss strategies, may fail to provide interesting returns during bull market periods. Moving from the observations that tail events are typically associated with a heightened volatility, and that a high volatile environment increases the costs of risk protection strategies we support the idea of using volatility for tail risk mitigation. With the purpose of benchmarking index-based portfolio strategies and derivatives-based strategies, we propose here below an approach to integrate volatility and tail risk controls in a portfolio optimization model. We tackle the problem from a dynamic portfolio management perspective and the model is built on a well-known approach in portfolio management, the mean absolute deviation (MAD) approach.

The use of absolute deviation measures in portfolio modeling was introduced in 1991 by Konno and Yamazaki (1991) and, since then, extensively studied. For the static case, we refer, for example, to (Dembo and Rosen 1999; King 1993; Michalowski and Ogryczak 2001; Rudolf et al. 1999; Worzel et al. 1993; Zenios and Kang 1993). For dynamic replication problems see (Barro and Canestrelli 2009; Dempster and Thompson 2002; Gaivoronski et al. 2005). We refer to (Zenios 2007) for a detailed discussion on mean absolute deviation models in stochastic programming problems. In this article we extend (Barro and Canestrelli 2014) by formulating a multistage stochastic program (MSP) based on three interacting goals: the first one based on index-tracking, the second related to volatility control, the third to tail risk protection. Thus, the model can be interpreted in terms of different layers of protection to respond to risky market conditions. The approach is inspired by asset management models (Zenios and Ziemba 2006; Mitra et al. 2011; Consigli et al. 2015) carrying several decision criteria and a stochastic tracking component which is tested over recent periods in the US equity market. The article carries three relevant contributions: (i) the formulation of an optimal risk control problem based on a set of commonly used derivative-based payoff functions; (ii) the benchmarking of the resulting optimal strategies against derivatives-based market indices. The two lead to (iii) the study of the relationship between volatility regimes, as reflected in derivatives’ implied volatility signals, the selection of a given portfolio rule and the resulting performance. From a methodological viewpoint the development of a MAD model integrating in a MSP framework well-known derivatives payoffs (without including those derivatives as investment classes) and forward volatility signals in a data-driven optimization approach is also relevant. MSP approaches have been widely applied to long-term financial planning problems (Bertocchi et al. 2011) while hardly on short-term decision problems such as those characterizing portfolio managers, specifically under risky market conditions. From an operational viewpoint, furthermore, we are not aware of any attempt to benchmark index-based portfolio policies and derivatives-based insurance approaches with an optimization model based on asymmetric payoff functions. Throughout the paper we take the view of a fund manager with long equity positions and negligible transaction costs, assumed to be fully compensated by management fees.

The paper is organized as follows. In Sect. 1 we analyse the rationale of risk control strategies starting from recent US market history and relate those controls to the payoffs of specific derivatives’ portfolios. In Sect. 2 those payoffs are considered in relation to an optimal risk control problem, which can be formulated as a stochastic linear program (SLP) and compared to an index-based portfolio policy as clarified in Sect. 3.

In Sect. 4 the mathematical instance of a portfolio model for optimal risk control is introduced as a dynamic stochastic program whose solution will depend on the input volatility and tail risk tolerances and on the postulated underlying uncertainty. This, as common in discrete decision problems, is introduced through an event tree whose nodal values are generated by sampling from data history. A non-parametric model for scenario generation is briefly described. In Sect. 5 we present the results of an application to real market data. We finally delimit the scope of the proposed modeling framework in Sect. 6, before concluding in Sect. 7. An appendix with a more extended set of evidences corresponding to several global financial crises is included at the end.

2 Market regimes and volatility signals

Equity portfolio managers and, increasingly, fund managers operating in risky markets aim at achieving and preserving over time a positive risk-adjusted performance with a premium over prevailing money-market, non risky allocations (Zenios 2007). Historically, the adoption of global market indices, such as the S&P500 index, as portfolio benchmarks in passive portfolio management, originated from its postulated market efficiency in the sense of modern portfolio theory. In periods of increasing volatility, thus decreasing risk-adjusted returns a common form of performance protection was based on option strategies. Target volatility strategies originate from the introduction after 1993 of implied volatility indices such as the VIX at the Chicago Board of Exchange (CBOE). Financial engineers have developed several approaches to incorporate volatility-based portfolio management within financial products for investors and portfolio managers (Hill 2011). More recently, still outside optimization approaches, simulation-based investment policy evaluations have been considered to enhance portfolio performance (Mulvey et al. 2016). The introduction of the VIX, as the subsequent development of an associated derivative market, provides on one side a direct instrument for risk control in the largest equity market in the world and, on the other side, represents maybe the most common information vehicle to evaluate financial agents expectations over the months ahead. We are here primarily interested in this second feature and relying on it as early warning signal (EWS) we propose a VIX-based adaptive investment approach.

Implied volatility signals from derivatives markets are known to be consistent with market returns fat-tails and/or increasing negative skewness. The adoption of semi-variance and MAD semi-deviation (Mansini et al. 2014) as risk measures in optimization approaches respond as well to both asymmetric risk and tail-risk control objectives and their payoffs can be analysed from a financial engineering perspective.

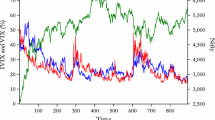
To further clarify the financial motivation of a (market) regime-dependent risk control approach, consider in Fig. 1 the S&P index data history since 1990, together with the VIX and the S&P-based protective put index (PPUT).¹ The US stock market went over several phases and indeed the need for volatility control and downside protection emerged many times during the 1990–2016 period. From Fig. 1, in which actual index values are reported (on the left Y axis the S&P and the PPUT and on the right Y axis the VIX), we see that when replicating the equity index with a put protection, the investor would greatly constrain the market volatility and both up- and down-sides. The inverse relationship between equity returns and historic volatility in this market is confirmed by the data in Fig. 2 where we summarize the S&P500 annualized volatility and returns computed on a 52-weeks moving window.

Fig. 2

S&P500—Annualized returns and Annualized volatilities (computed using 52-observation moving windows—Weekly data January 4, 1991–June 10, 2016)

From Figs. 1 and 2 we can infer the behaviour over time of the maximum drawdown (MaxDD) and maximum implied volatility (MaxVIX) series: these are computed from 52-weeks moving windows between 1991 and 2016 with weekly steps. The MaxDD level is defined as the difference between the highest and lowest S&P values over the past 1-year moving window, while the MaxVIX value is just the maximum VIX over the same period. We can in this way identify a VIX time-varying moving average (Average VIX). These series are plotted and compared in Fig. 3. The horizontal lines are computed ex-post to identify the VIX threshold corresponding to the long-run mean plus one standard deviation. We recall that volatility units are in percentage and a volatility index at x is equivalent to an implied annual volatility of $x\%$.

Fig. 3

S&P500—Max DD, Max VIX and average VIX (computed using 52-observation moving windows—Weekly data January 4, 1991–June 10, 2016). The horizontal line identifies the VIX threshold corresponding to the long run mean plus one standard deviation

Consistently with stylised financial evidence, Fig. 3 helps clarifying the nature of the relationship between the implied volatility and the market phase: a VIX above the threshold is constantly coupled with a stepwise increase of the maximum drawdown while periods of market recovery are typically associated with decreasing VIX and MaxVIX series.

The following sub-periods are considered as particularly relevant for model validation:

• 1. From January 07, 2000 to December 29, 2000: this is the period including the dot.com speculative bubble; we have sustained volatility and limited downside (with average VIX value of 22.98 and maximum VIX value of 33.5). It is an example of market instability which originates within the market after a prolonged period of growth: the risk source is endogenous and ex-post year 2000 has been recorded as originating from a fundamental distortion between equity and fixed income returns.

• 2. From February 09, 2001 to January 25, 2002: the period preceding and following the 9/11 terrorist attack: from a financial standpoint this can be recorded as a period of high volatility and relevant maximum drawdown (with average VIX value of 25.23 and maximum VIX value of 42.66) not entirely due to that attack, however, as we will see below. Unlike in the first example, here, we have though, a relevant exogenous shock source, hardly predictable by any EWS.

• 3. From January 04, 2008 to December 26, 2008: this is the period associated with the global financial crisis which originated in the US before spreading globally with long-term market and economic consequences. This is a period with relevant market instability and dramatic downside (with average VIX value of 32.79 and maximum VIX value as high as 79.13) that will last for long.

We show below that indeed when the MAD functional is adopted to characterize agents’ risk preferences a relevant set of contingent claim payoffs emerges in the formulation of the portfolio optimization problems. When confronted with the described market conditions the following strategies may prove of interest to a portfolio manager and should be compared with derivatives-based or index-based market strategies:

• An effective replication of the equity benchmark within a passive fund management strategy: the outcome corresponds to a tracking error control strategy.

• A downside risk control also based on a tracking error criterion, in which however the replication strategy is suspended during negative market phases.

• A local volatility control in which, upon exceedance of a given threshold a volatility corridor with fixed width over a limited time period will determine the portfolio rebalancing dynamics.

• A target volatility strategy based on the definition of a volatility target and a portfolio strategy based on periodic rebalancing between a risky and a riskfree portfolios over the entire data-history.

• A tail-risk control strategy based on the definition of a negative return threshold and the control of shortfalls with respect to that threshold.

The above strategies reflect a defensive approach to portfolio management, they are not meant to be exhaustive but, as shown next, help spanning a large range of risk-aversion degrees. We consider next the formulation of an optimization problem and analyze its distinctive elements relative to index-driven decision policies.

3 Optimal strategies and decision policies

Denote by $x_t$ the value at time t of a portfolio invested in the $S \& P500$ and the managed portfolio value by $y_t$, where $t \in \mathcal{T}$ and $\mathcal{T}=\left\{ 0, \Delta t, 2 \Delta t, ..., n \Delta t=T \right\}$ corresponds to a discrete and countable time set. Assume a bi-weekly portfolio revision with time step $\Delta t$. Associated with $y_t$ is an investment universe $\mathcal{Y}$ which, as further detailed below, is assumed to include a set of S&P500 sub-indices. We assume that the initial value of the two portfolios coincide, that is $x_0=y_0$.

Tracking error strategy At $t=0,\Delta t,..,(n-1) \Delta t$ construct a portfolio $y_t$, so that prior to further revision, at $t+\Delta t$, $\frac{y_{t+\Delta t}}{x_{t+\Delta t}}=1$ as close as possible. Such goal can be expressed by $|y_t-x_t|=0$ in absolute value for $t \ge 0$. If the downside only is considered we would have $\max \{0,x_t-y_t\}$ associated with an asymmetric payoff function $|y_t-x_t|^-$. The absolute downside deviation formulation is equivalent to the payoff a put option with strike equal to $x_t$ and maturity in two weeks time. Whereas the MAD functional can be seen as a combination of the payoffs of a call and a put on the same strike, given by the stochastic benchmark value. A long call position and a short put, in particular, will replicate the underlying index.

Local volatility and target volatility strategies Over the same timeframe and time discretization consider a portfolio corridor defined by $z^{d}_t=y_{t-\Delta t}(1-\sigma )$ and $z^{u}_t=y_{t-\Delta t}(1+\sigma )$. Then, at the beginning of each time period the payoffs $\max \{0,z^{d}_t-y_t\}=|y_t-z^{d}_t|^-$ and $\max \{0,y_t-z^{u}_t\}=|z^{u}_t-y_t|^-$ will generate a local volatility control driven by the parameter $\sigma$. A portfolio strategy based on volatility control, implies an objective function in the MAD formulation that is equivalent to the payout function of a long call with strike on the upper volatility and long put option with strike on the portfolio lower-bound. Such local volatility strategy is typically employed on specific time periods where forward volatility is signaling a forthcoming instability.

A target volatility strategy leads, instead, to portfolio rebalancing between a risky and a riskfree portfolio where the exposure to the risky market is determined over time by a ratio between a target volatility $\tilde{\sigma }$ and the one-period-ahead forecasted volatility. Target volatility strategies may be employed actively with the definition of a less risky or even risk-free allocation or just investing in a synthetic index which, as in the case of the protecting put index, will replicate that strategy. In this paper we consider both options.

Tail risk control Under the same assumptions we may consider a rich set of payoffs, whose rationale is strictly related with portfolio protection from tail events. Let $\rho$ be a tolerable percentage tail loss on the given portfolio position $y_t$ for $t \le T$. Then $y_{t-\Delta t}(1-\rho )$ will represent a price loss to be controlled at t resulting in the asymmetric payoff $\max \{0,y_{t-\Delta t}(1-\rho )-y_t\}=|y_t-\rho ^y_t|^-$ at the end of each period, which, again, in the MAD formulation captures the payoff of a put contract.

We consider here the potentials in terms of risk-control effectiveness, of an MSP formulation whose objective function is defined taking a linear combination of the above set of symmetric and asymmetric payoffs. The type of control strategy will however be determined adaptively through a VIX-based feedback rule. In the sequel we first test in Sect. 3 the effectiveness of the proposed approach in providing the desired risk control in a one-period static optimization model, and then we extend the model to a 2-stage setting to allow for a recourse portfolio decision still facing a residual, one-period, uncertainty. The proposed optimization approaches are validated against a set of well-established policy rules: namely based on a target volatility decision model, on a perfectly diversified portfolio model, and on a fix-mix strategy.

4 Risk controls’ LP characterization

In Sect. 2, we considered different risk control approaches resulting, thanks to the MAD functional, into linear programming (LP) formulations of the associated optimization problems. We consider next the labeling convention adopted to describe discrete event tree processes then we formulate the optimization problems associated with the risk control approaches previously discussed.

We consider a planning horizon $\mathcal{T}$ specified as a discrete set of decision stages. The beginning of the decision horizon coincides with the current time $t=0$, while T will denote the end of the decision horizon. A reference period $0-$, prior to 0 is introduced in the model to define holding returns to be evaluated at time 0. Consistently with a stochastic programming formulation, random dynamics are modeled through a discrete tree process with non-recombining sample paths in a probability space $(\Omega , \mathcal{F}, \mathbb {P})$ (Consigli et al. 2012). Nodes along the tree, for $t \in \mathcal{T}$, are denoted by $n \in \mathcal{N}_t$ and for $t=0$ the root node is labeled $n=0$. The root node is associated with the partition $\mathcal{N}_0 = \{\Omega , \emptyset \}$ corresponding to the entire probability space. Leaf nodes $n \in \mathcal{N}_T$ correspond one-to-one to the atoms $\omega \in \Omega$. For $t > 0$ every $n \in \mathcal{N}_t$ has a unique ancestor $n-$ and for $t < T$ a non-empty set of children nodes $n+$. We denote with $N_t$ the number of nodes or height of the tree in stage t and with $t_n$ the time period associated with node n: $t_n-t_{n-}$ will then denote the time length between node $n-$ and node n. The set of all predecessors of node n: $n-, n--, ..,0$ is denoted by $\mathcal{P}_n$. We define the probability distribution $\mathbb {P}$ on the leaf nodes of the scenario tree so that $\sum _{n \in \mathcal{N}_T} \pi _n=1$ and for each non-terminal node $n \in \mathcal{N}_t$ with $t \le T-1$ we have unconditional probabilities $\pi _n=\sum _{m \in n+} \pi _m$. With each branch being equally probable along the tree we can derive the conditional probability to reach node n from $n-$ as $\pi _n=\frac{n}{\#n+}$ where $\#n+$ will denote the cardinality of descending nodes. We denote with ${\mathbb {E}}_{\mathcal{F}_t}$ the conditional expectation with respect to information available in t. A scenario is a path from the root to a leaf node and represents a joint realization of the random variables along the path to the planning horizon. We shall denote by $S=N_T$ the number of scenarios or sample paths from the root node to the leafs. In this study the tree structure will be particularly simple with two equal 2-week periods spanning one month and a symmetric scenario tree: all scenarios will carry equal probability.

We can now specify the set of variables associated with the risk controls introduced in Sect. 2. Let $\theta _{n}^{+}=|y_n-x_n|^{+}$ and $\theta _{n}^{-}=|y_n-x_n|^{-}$ denote respectively positive and negative deviations of the managed portfolio $y_n$ from the benchmark portfolio $x_n$. We use $\eta _n^{-}=|y_n-z_n^{d}|^-$ and $\eta _n^{+}=|y_n-z_n^{u}|^+$ to denote deviations associated with volatility control, where we recall $z_n^u=y_{n-}(1+ \sigma )$, $z_n^d=y_{n-}(1-\sigma )$. Finally $\nu _n^-=|y_n-\rho ^y_n|^-$ is used to characterize the control of tail risk.

Risk control strategies and derivative payoffs

In the following we discuss the connections between the proposed risk control strategies and a set of derivatives’ portfolios’ payoffs:

• 1. A passive portfolio manager seeking a market benchmark tracking will act as a derivative trader long a call option with strike set by the index and short a put option with the same strike. Indicating the benchmark with $x_n$ and the managed portfolio with $y_n$, we have: $\theta _{n}^+ -\theta _{n}^- = y_{n}-x_{n}$.

• 2. By the same reasoning we can consider a portfolio manager applying volatility control as one carrying an objective function equivalent to the payout function of two long option positions, so to keep the portfolio value within a prescribed corridor: a long call with strike $z_n^u$ and a long put with strike $z_n^d$. By setting $\eta _{n}^- \ge z_n^d-y_{n}$ and $\eta _{n}^+ \ge y_{n}-z_n^u$ we treat the two auxiliary variables, that has to be minimized, as upper bounds on in-the-money (ITM) option values.

• 3. When however the implied volatility exceeds a certain threshold, the equity market is actually often experiencing sequences of negative shocks resulting into returns’ outliers and increasing tail risk: $\nu _n^-=|y_n-\rho ^y_n|^-$ defines the payoff of a put option with strike $\rho ^y_n$. By setting $\nu _{n}^- \ge \rho ^y_n - y_{n}$ we can introduce an auxiliary variable for the positive payoff associated with an ITM option.

In Table 1 we summarize the risk controls introduced in the objective function and their representations in the MAD framework.

Table 1 Risk controls, their representations in the MAD framework

The above risk control strategies can be analysed from the perspective of derivative contracts’ hedging properties. To discriminate between each risk control type, we consider risk controls activated separately through the choice of the coefficients $\alpha _j$, $j=1,2,3$ in the objective function in (1) here below.

First, in normal market period—the VIX is below a certain thereshold—the manager is assumed to track the market portfolio. The tracking error strategy minimizes both positive and negative deviations from the benchmark, which in the objective function (1) below, will generate a straddle-type of payoff with a strike identified by the value of the benchmark.

Second, when instead the VIX signals a future increase of equity volatility, the manager is assumed to minimize portfolio dynamics outside a given corridor and this is the situation in which a short position in a strangle is profitable. Finally, when VIX values are above a given threshold, we assume relevant forward market instability and a portfolio manager seeking minimal downside deviations from a maximum acceptable loss level. This corresponds to a situation in which a long put is used to hedge the portfolio value.

The proposed portfolio management approach aims at generating a portfolio profit and loss distribution as the one that could be obtained by combining the market benchmark and the derivatives. Consider, for instance, a Protective Put strategy obtained buying the underlying and a long out-of-the-money (OTM) put contract. The payoff of such portfolio may be replicated by tracking the benchmark when the market is calm (and there is a positive outlook) and switching to a tail risk control when the volatility signal anticipates a negative downturn of the market. Along the same line, a strangle payoff provides protection against sharp movements of the underlying. When there is an increase in the expected volatility the manager can switch to a volatility controlled portfolio with the aim of limiting the losses associated with huge movements of the market.

Finally, in the case of a stable market situation, the manager is assumed to track the benchmark and the payoff of this strategy could be obtained with a long call and a short put with the advantage of allowing for a stochastic benchmark rather than a fixed strike level. The suggested formulation does not replicate a derivative contract, per se, in the sense of providing the same payoff. However, the combination of different risk controls will lead to portfolio dynamics that resemble the behaviour of a portfolio hedged with derivative overlays without the need to enter into derivative contracts and with a more flexible risk control policy, driven by the implied volatility signals.

We can now define the cost functions associated with each type of control. For $t \in \mathcal{T}, n \in \mathcal{N}_t$, $\theta _n^+ + \theta _n^-$ defines a positive cone pointed at $x_n$ which is the minimum of the function. Similarly $\eta _n^+ + \eta _n^-$ defines a stepwise positive function which is decreasing for $y_n \le z_n^d$, constant at 0 between $z_n^d$ and $z_n^u$ and increasing for $y_n \ge z_n^u$. Finally $\nu _n^-$ is constant at 0 for $y_n \ge \rho ^y_n$ and nonegative for $y_n \le \rho ^y_n$. Summing up the following formulation translates all the above payoffs in a stochastic linear program which can be solved with standard methods, e.g. dual simplex for instance, over a single period. Let $t=\{0,1\}$, with $n \in \mathcal{N}_1$ at the end of the period, we write:

$$\begin{aligned} \min _{q_{1\,0}\,\ldots q_{I\,0},l_0}&{\mathbb {E}}_{\mathcal{F}_0} \{ \alpha _1\left( \theta _n^+ + \theta _n^- \right) + \alpha _2\left( \eta _n^+ + \eta _n^- \right) + \alpha _3 \nu _n^- \} \end{aligned}$$

(1)

$$\begin{aligned}&\text {s.t.} \nonumber \\&l_{0}+\sum _{i=1}^{I}q_{i\,0}=\bar{y} \end{aligned}$$

(2)

$$\begin{aligned}&y_{n}=(1+r_{l\,n})l_{0}+\sum _{i=1}^{I}(1+r_{i\,n})q_{i\,0}\end{aligned}$$

(3)

$$\begin{aligned}&\theta _{n}^+ -\theta _{n}^- = y_{n}-x_{n}\end{aligned}$$

(4)

$$\begin{aligned}&\eta _{n}^- \ge z_n^d - y_n \end{aligned}$$

(5)

$$\begin{aligned}&\eta _{n}^+ \ge y_{n}-z_n^u \end{aligned}$$

(6)

$$\begin{aligned}&\nu _{n}^- \ge \rho ^y_n - y_n \end{aligned}$$

(7)

$$\begin{aligned}&q_{i\,0} \ge 0 \ \ i=1,\ldots ,I \end{aligned}$$

(8)

$$\begin{aligned}&\theta _{n}^+,\, \theta _{n}^- ,\, \eta _{n}^+,\, \eta _{n}^-,\, \nu _{n}^- \ge 0 \ \ n \in \mathcal{N}_1 \end{aligned}$$

(9)

The vector $(q_{1\,0},\ldots ,q_{I\,0},l_{0})$ denotes the portfolio composition to be determined in the root node, where $q_{i}$, $i=1,\ldots ,I$ represents the amount invested in the risky asset i with return $r_{i,n}$, and l denotes the money market account for which an interest rate $r_l=0.5\%$, constant over the year, is assumed; $\bar{y}$ denotes the initial portfolio endowment. According to model (1)–(9) with $\sum _{j=1,2,3} \alpha _j=1$ over a single period, the fund manager would control jointly different risk sources: through $\theta _n^{+/-}$ the risk of under or overperforming the market benchmark $x_n$,through $\eta _n^{+/-}$ the risk of exceeding a certain volatility and through $\nu _n^{-}$ the risk of loosing more than a certain value in extremely unstable market conditions. We are interested to analyse every VIX-based control problem separately to validate the adopted model formulation with only one $\alpha _j=1$ for $j=1,2,3$. The extension to weighted combinations of controls leading to the activation of mixed strategies is also possible and straightforward in the adopted model formulation. When assessing ex-ante the preferable form of risk control the current VIX value, associated with 1-month forward market volatility expectations, will provide an important source of information. We consider here the case in which ex-ante the fund manager will determine subjectively constant volatility thresholds discriminating between the different approaches. In Sect. 5.2.2 we test a path-dependent signal updates.

Table 2 summarizes the coefficients set in the objective function at each step as a function of the at-the-time prevailing VIX value.

• 1. If the current level of the VIX Index is below 20 we assume we are in normal market conditions and we activate a (symmetric) tracking goal;

• 2. For observed values of the VIX Index between 20 and 45 there are signals of increased volatility in the market and the corresponding volatility control goal is activated ($\sigma =0.01$);

• 3. Whereas if the VIX Index is above 45 we assume this is a signal of instability and the shortfall control goal is activated ($\rho ^y=0.05$).

The introduced 20 and $45\%$ thresholds on stock market volatilities have been determined analysing the behaviour of US equity market volatility indices: to derive reliable long-term volatility thresholds we consider not only the VIX index but also the VXO index, computed since 1983 on the S&P 100 options. The values correspond to the long-run mean and a tail quantile of the VXO distribution for the period 02/01/1986–31/12/1999, and they are coherent with the values of the VIX index in the entire sample 05/01/1990–10/06/2016 taken into account. They can be regarded as subjective assessments of high volatility regimes versus financial turmoils typically adopted in financial practice (Consigli et al. 2009).

The parameters $\sigma =0.01$ and $\rho =0.05$ are subjectively chosen and characterize a risk tolerance level in which a loss threshold of $5\%$ and a corridor width for portfolio variations of $1\%$ on a biweeekly basis are assumed.

Table 2 Investment risk control type according to observed values of the VIX Index

We test model (1)–(9) in the three sample periods corresponding to different market crises.² We are here primarily interested in validating the adopted problem formulation and clarify the impact of the introduced volatility thresholds on the adopted control strategy and its hedging effectiveness.

Table 3 reports details on the three periods considered along with the average and maximum VIX values during those periods.

Table 3 Market crises and bear periods considered in the experiments

The following settings define the experiment: the S&P500 is the equity benchmark, its initial value is set to 1000 as the input portfolio value.

We adopt as investment universe the set of S&P sub-indices reported in Table 4,³ which includes also a summary of descriptive statistics, and a money market account.

Table 4 Descriptive statistics (mean, standard deviation, skewness and excess of kurtosis) for the index and the sub-indices, for the period 05/01/1990–10/06/2016, weekly data

The volatility target over the 2 weeks is set at $1\%$ and the problem is solved over 400 possible scenarios at the end of the 2-week investment period. The scenario tree for the returns of the benchmark and of the sub-indices are generated using a bootstrapping procedure from past data realizations. The returns’ trees are then applied to the initial value of the portfolio and of the benchmark to compute the MAD functions and payoffs. To guarantee consistency not only in the first but also in subsequent steps of the simulation, the values of the benchmark portfolio in each node of the scenario tree are computed as $x_n=(1+r_n^x)y_0 \ \ n \in \mathcal{N}_1$, where $y_0$ is the initial endowment of the portfolio, either 1000 at the first step or the market value of the portfolio at subsequent steps of the experiment.

Each experiment is carried out spanning the entire reference year: we solve 26 (bi-weekly) optimization problems setting, at the beginning of each run and depending on the current VIX value, one $\alpha _j=1$, $j=1,2,3$. Depending on the adopted risk control approach the redundant constraints in model (1)–(9) are not considered. At the end of each 2-week investment problem the outcome of the optimal portfolio is compared ex-post, thus out-of-sample, with the value of the portfolio corresponding to the S&P500, the PPUT Index and a target volatility strategy. The latter, as mentioned, represents a policy rule under which the switching from the S&P500 to a riskfree portfolio and viceversa is determined by the ratio between a target and the current forward volatility. The results are presented in the Figs. 4, 5, 6, 7 and 8. By considering these three periods, we aim at both validating the model formulation and analysing the effectiveness of the volatility signal and the derived optimal controls within a static one-period model. The analysis is then extended in Sect. 4 to a multi-period setting.

Consider the 2000 dot.com crisis first.

The sequence of optimal portfolios is determined by the prevailing volatility signal: at each run the input portfolio value is preserved and we show in Fig. 4 the 2-week return that, given the initial portfolio allocation would have been generated by the observed market dynamics. The peak of the speculative bubble in the Nasdaq was at the beginning of the year and afterwards the crisis spreaded to the S&P market. The VIX signals (bottom plot) lead to the sequence of controls displayed in the intermediate plot and then to the results shown in the upper plot of Fig. 4. Given the introduced volatility thresholds we see that the strategy switches few times over the year from tracking error to volatility control and indeed the managed portfolio is very well immunized against market volatility.

Table 5 presents the statistics of the returns’ distribution over the test period for the optimal portfolio and for the other strategies. We observe that the introduction of the volatility control succeeds in reducing not only the variability but also the negative skewness of the distribution. As a consequence of the consistent reduction of the standard deviation, induced by the VC, we obtain a highly concentrated distribution of returns with associated kurtosis markedly higher if compared with the other strategies. The optimal portfolio allocation leads also to a consistent reduction of the maximum drawdown. The returns’ histograms generated by the different strategies are presented in Fig. 5 and they help analysing some of the strategies implications. The optimal controls generate over the year a positively skewed, highly concentrated portfolio return distribution, since the VIX increases at the end of the first quarter and during the fall do actually anticipate a sequence of market drops, while VIX reductions do correspond to positive market phases: those signals thus jointly lead to timely and effective hedging and index-tracking strategies. To evaluate the performance of the proposed strategies we consider risk-adjusted performance measures. We compute the Sharpe ratio, the Sortino ratio and the Omega ratio⁴ to better evaluate the implications of the control strategies.

Fig. 4

Dot-com bubble. Comparison of optimal hedging portfolio with the S&P500 and the target volatility portfolio (target volatility level 0.01)—bi-weekly data 07/01/2000–29/12/2000

Table 5 Dot-com bubble

Fig. 5

Dot-com bubble. Comparison of the histograms for the S&P500 (top left), the optimal hedging portfolio (top right), the target volatility portfolio (target volatility level 0.01) (bottom left) and the Protective Put Index (bottom right)— bi-weekly data 07/01/2000–29/12/2000

Fig. 6

September, 2001. Comparison of optimal hedging portfolio with the S&P500 and target volatility portfolio (target volatility level 0.01)—bi-weekly data 09/02/2001–25/01/2002

Fig. 7

September, 2001. Comparison of the histograms for the S&P500 (top left), the optimal hedging portfolio (top right), the target volatility portfolio (target volatility level 0.01) (bottom left) and the Protective Put Index (bottom right)—bi-weekly data 09/02/2001–25/01/2002

As shown in Table 5, optimal portfolios provide better risk-adjusted performances and outperforms all competing strategies, for all measures considered. The improvement is due to a reduction of the volatility, of the negative skewness and to an increase of the right tail of the distribution as can be seen by comparing the corresponding histograms in Fig. 5. Finally, we consider the Information Ratio (IR) and the Tracking Error Volatility (TEV) to compare the considered strategies with the benchmark portfolio (S&P500), the optimized portfolios exhibit the highest IR motivated by a considerable reduction in the standard deviation of the associated distribution.

Unlike the dot.com crisis which was endogenous and determined by a fundamental departure of conditional market expectations from justifiable equity values in the US market, the 2001 crisis came relatively unexpected at the time of the September 11 terrorist attack. The S&P500 was at the time already going through a period of relatively high volatility and negative expectations: we consider this period as interesting, however, given that in correspondence with the terrorist attack the market experienced a relevant peak of the VIX which was not entirely attributable to current market conditions at that time. As shown in Fig. 6, when employing the VIX-based control rule, the resulting optimal portfolio value is generated throughout the year by a VC strategy, with two noticeable reductions of the VIX below the threshold of 20. During the September market shock the VIX does not exceed the 45 value and the TR control is never active. At the time of decreasing VIX however the market is still experiencing a negative phase which is reflected in the optimal portolio negative returns between September and October. The optimal portfolio return distribution in Fig. 7 displays accordingly a bimodal profile which is reflected in the statistics reported in Table 6. Interestingly, during the last part of the year, at the time in which the market started recovering both the protective Put and the target volatility strategies generated a positive return, while the optimal portfolio was unable to capture the market inversion as it is documented by the comparison of the performance measures in Table 6.

Table 6 September, 2001 Comparison of optimal hedging portfolio with the S&P500 the target volatility portfolio (target volatility level 0.01) and the Protective Put Index

Table 7 September 2008 Financial Crisis

Fig. 8

September 2008 Financial crisis. Comparison of optimized adapted portfolio with the S&P500 and target volatility portfolio (target volatility level 0.01)—bi-weekly data 04/01/2008–26/12/2008

Table 6 shows the statistics of the returns distributions for different strategies, over the considered period. We observe that the introduction of the volatility control succeeds in reducing the variability but limits the portfolios’ upside. Indeed, in the last part of the period we can observe a progressive reduction of the VIX associated with a recovery phase of the market, however, according to the adopted thresholds, the values of the VIX still signal a high volatility condition and thus the portfolio persists in a volatility control strategy. The reduction of the variability impacts also on the level of kurtosis which is sensitive to the location and frequency of tail outliers.

Figure 7 displays the returns’ histograms generated by the introduced strategies.

Finally, during 2008, the adaptive approach based on incoming VIX information turns out to be very effective in controlling the downside and preserve the portfolio value during prolonged phases of extremely relevant market falls.

The depth of the market adjustment experienced by the S&P500 during 2008 is relevant and it will be remembered as a period of previously unknown systemic risk. The VIX signals are frequent in particular after the Summer and the strategy switches from VC to TR control with overall an effective outcome. Table 7 shows, for different strategies, the returns’ distributions and the performance measures over the considered period.

Figure 9 presents the histograms of the returns associated with each strategy.

In summary, taking all three periods into account, we can conclude that the introduced model specifications do actually generate effective and timely hedging strategies and dominate two popular index-based protection schemes. A limited drawback of the introduced approach may be associated with the persistence of relatively high VIX values at times in which the market was actually recovering, in this way leading to a volatility control or a tail-risk control (rather than a tracking error approach) or, on the contrary, VIX reductions during negative market phases, resulting into tracking error minimisation rather than risk control.

In Sect. 4 we extend the analysis beyond the one-period, myopic case and formulate an optimal selection problem for short-term portfolio management based on a two stage model with by-weekly rebalancing.

Fig. 9

Financial Crisis 2007–2008. Comparison of the histograms for the S&P500 (top left), the optimal hedging portfolio (top right), the target volatility portfolio (target volatility level 0.01)(bottom left) and the Protective Put Index (bottom right)— bi-weekly data 04/01/2008–26/12/2008

5 Volatility-based portfolio management

We extend program (1)–(9) to a dynamic setting by introducing the canonical inventory balance and cash balance constraints to track ongoing portfolio revisions and associated cash-inflows and out-flows. Unlike in the previous section we span here an extended 17-year period including the three financial turmoils above but others as well (see the report in appendix). From a modeling viewpoint, starting at $t=0$, the associated $\sigma$-algebra $\mathcal{N}_0$ reflects current market conditions and in particular the current VIX value, from which a given optimal control problem will result. The decision vector includes a money market account and the 10 $S \& P$ sub-indices: we indicate with $q_{i,n}, a_{i,n}$ and $v_{i,n}$ the amounts held, bought and sold, respectively, of risky asset i in node n, and with $l_n$ the position in the money market account in node n. The analysis is simplified by assuming transaction costs compensated over time by management fees.

The portfolio manager, starting in 0 and with $t=\Delta t, 2 \Delta t, ...,n \Delta t$, $\Delta t=2$ weeks and $n \in \mathcal{N}_t$, will face a sequence of 2-stage problems:

$$\begin{aligned} \min _{q_{i,n},a_{i,n},v_{i,n}} \ \ \&\sum _{\tau =t}^{t+\Delta t} {\mathbb {E}}_{\mathcal{N}_{\tau }} \left[ \alpha _{1} \left( \theta _{n}^+ + \theta _{n}^- \right) +\alpha _{2} \left( \eta _{n}^-+\eta _{n}^+\right) + \alpha _{2}\,\, \nu _{n}^-\right] \end{aligned}$$

(11)

$$\begin{aligned}&q_{i\,n}=(1+r_{i\,n})\left[ q_{i\,n^{-}}\, +\, a_{i\,n^{-}} \,-\, v_{i\,n^{-}} \right] \ \ i=1,\ldots , I\end{aligned}$$

(12)

$$\begin{aligned}&l_{n}=(1+r_{l\,n})\left[ l_{n^{-}}\, -\, \sum _{i=1}^{I}\, a_{i\,n^{-}} +\, \sum _{i=1}^{I} v_{i\,n^{-}}\right] \end{aligned}$$

(13)

$$\begin{aligned}&y_{n}=l_{n}+\sum _{i=1}^{I} q_{i\,n}\end{aligned}$$

(14)

$$\begin{aligned}&l_{n} \ge 0 \ \ q_{i\,n} \ge 0 \ \ a_{i\,n} \ge 0\ \ v_{i\,n} \ge 0\end{aligned}$$

(15)

$$\begin{aligned}&\theta _{n}^+ -\theta _{n}^- = y_{n}-x_{n}\end{aligned}$$

(16)

$$\begin{aligned}&\eta _{n}^- \ge z_{n}^{d} -y_{n} \end{aligned}$$

(17)

$$\begin{aligned}&\eta _{n}^+ \ge y_{n}-z_{n}^{u} \end{aligned}$$

(18)

$$\begin{aligned}&\nu _{n}^- \ge \rho _{n}^{y}- y_{n} \end{aligned}$$

(19)

$$\begin{aligned}&\theta _{n}^+,\, \theta _{n}^- ,\, \eta _{n}^+,\, \eta _{n}^-,\, \nu _{n}^- \ge 0 \end{aligned}$$

(20)

where ${\mathbb {E}}_{\mathcal{N}_t}\left[ \omega _t\right] :=\sum _{n \in {\mathcal {N}}_t} \left[ \pi _{n} \omega _n \right]$, with $\pi _n$ being the conditional probabilities of moving to node $n \in N_t$ from the ancestor $n- \in N_{t-1}$. The initial endowments for the liquidity component and the risky assets are $l_0 \ge 0$ and $q_{i,0}\ge 0$, $i=1,..,n$, and they determine the value of the portfolio at time $t=0$, $y_0=l_0+\sum _{i=1}^{n} q_{i\,0}$.

As shown below, we formulate and solve in each period a sequence of 2-stage, 2 periods optimization problems, following formulation (11)–(20), and report their outcome again benchmarking out-of-sample the dynamic of the resulting optimal portfolio against the market benchmark, the protective put index, a synthetic target volatility strategy, a constant proportion fix-mix portfolio and the 1 / n portfolio.

At every iteration the previous portfolio value is input as initial portfolio in the following optimization problem. Unlike in the static, one-period case described in Sect. 2, here we solve a recourse problem with optimal non-anticipative investment strategies at $\tau =t,t+\Delta t$ for each t over the validation period. The first stage decision is then actually implemented and revised at the subsequent run, while the recourse decisions are discarded and not considered for policy validation purposes.

We consider the S&P500 as benchmark and the S&P sector indices as elements of the investment universe plus a liquidity component in the form of a money account. We proceed as follows:

• VIX-based adaptive portfolio management simulation scheme.

• Step 0 Let $t \in \{0, \Delta t, 2 \Delta t, ...,n \Delta t=T\}$, set $\tau =t$. $\Delta t$ corresponds to 2 weeks.

• Step 1 Generate a two-period scenario tree using data up to t with branching degree $\{40^1,10^1\}$ resulting in 400 scenarios over the forthcoming month: between $\tau$ and $\tau +2 \Delta t$.

• Step 2 Collect the current VIX value and identify the appropriate decision criterion,

• Step 3 Formulate the objective function and constraints accordingly and solve problem (11)–(20) using scenario tree created at Step 1.

• Step 4 Adopt the first period optimal decision obtained in step 2.

• Step 5 Evaluate the portfolio in step 4 using market realised returns at time $\tau +\Delta t$: this value represents the new budget available for investment at the beginning of next period ($[\tau +\Delta t,\tau +2 \Delta t]$).

• Step 6 Set $\tau =t+\Delta t$. If $t\le T-2\Delta t$ go to step 1, otherwise exit.

The model validation is entirely carried out out-of-sample and the optimal portfolios are evaluated using realized returns in the market.

6 Empirical study

Aim of this section is to assess the VIX-based portfolio management approach and check its effectiveness over an extended time period against other commonly adopted investment policies. We test the adaptive scheme over the period January 2000-December 2016. We take the view of an equity fund manager with a short 1-month decision horizon and a rebalancing frequency of 2 weeks. It is also of interest to analyse the effectiveness of this approach for hedging purposes. Every fortnight, as mentioned, the portfolio manager will reformulate and solve a new optimization problem always using 1 month forward implied volatility information and defining an optimal policy based on the current implementable, here-and-now decision and a forward recourse decision. The managed portfolio generated by the investment decisions $\{q_n,a_n,v_n\}$ in problem (11)–(20), is based on 10 S&P500 sub-indices and the money market account. In Sect. 5.2 we provide evidence on the portfolios’ dynamic compositions and the resulting value dynamics. At the time the portfolio is revised the market uncertainty characterising the problem is defined through a rich scenario tree with 400 scenarios over the next 2 periods generated relying on a bootstrapping method and 10 year of data history. In Sect. 5.1 we summarise the steps adopted to generate the event tree, following a very easy data-driven approach. Relying on a sequence of scenario trees, we evaluate two possible adaptive portfolio schemes, based on constant long-term volatility thresholds or on time-varying thresholds leading to market-dependent risk controls.

6.1 Scenario generation and historical out-of-sample simulation

When formulating problem (11)–(20) the issue of introducing the coefficient tree process needed to implement and solve the problem comes about. We intend to validate a set of regime-dependent optimal policies relying on actual market data and avoiding parametric assumptions on the return distributions, recently reported to have led to significant model risk. The use of a multistage stochastic optimization approach for very short-term investment management is here motivated primarily by the effort to control emerging risky conditions in the market and rely on implied 1-month forward information on the stock market volatility as captured by the VIX.

We describe briefly the approach adopted to generate a 2-period scenario tree with 40 branches at the root node and for each descending node additional 10 branches. The expectation is taken giving to every scenario equal probability of occurrence. In every node of the scenario tree we need to specify all the assets returns $r_n$ and the S&P return $r^x_n$.

The coefficient scenarios are generated through a bootstrapping procedure from past data realizations (Brandimarte 2014; Calafiore 2016; Çetinkaya and Thiele 2015). At the beginning of year 2000 a 10 year data history is considered for the S&P equity benchmark, the VIX and all sub-indices. The current VIX value will be the first volatility reference to determine the risk control rule within the first iteration. The 10-year data history is then preserved via a rolling window until the last 400 scenario tree and associated optimal strategy are determined. A 2-week time update is adopted and the return vector is sampled at random from the past 10 year history. The multidimensional character of the data and the dependence among time series are preserved through simultaneous sampling from all the series involved, while we do not account for autocorrelation or serial dependence since the returns for each node in the scenario tree are randomly sampled from past realizations.

The benchmark itself is stochastic. For each node of the tree we generate jointly the returns for the market benchmark and the sub-indices. The returns’ trees are then applied to the initial value of the portfolio and of the benchmark to jointly determine the MAD functions and associated returns payoffs. To avoid inconsistencies between the portfolio value and the $S \& P500$ evolutions, at the beginning of the experiment, the initial values of the portfolio and of the benchmark are both set at 1000. In order to guarantee consistency also at each subsequent step of the simulation, the scenario trees for portfolio values and benchmark values, are obtained from the initial market value of the portfolio, applying the bootstrapped returns from the assets’ return distribution and from the S&P500 distribution, respectively. In detail, let $r^x_n$ denotes the benchmark return bootstrapped for node n, the benchmark values along the tree are computed as follows:

$$\begin{aligned} x_n=(1+r^x_n) \ y_0 \ \ \ n \in \mathcal{N}_1 \qquad \qquad x_n=(1+r^x_n) \ x_n^{-} \ \ \ n\in \mathcal{N}_2 \end{aligned}$$

where $y_0$ is the initial endowment of the portfolio, either 1000 at the first step or the market value of the portfolio at subsequent steps of the simulation. These positions guarantee that the tracking errors are computed in terms of differences in the returns at each step.

The bootstrapping approach is opposed to a model-based one in which a (multivariate) stochastic model for the stochastic components is introduced and estimated on the historical data in order to be subsequently used to generate the data for the scenario tree. In extreme summary what are the implications of such method? That can be roughly regarded as an extension of common historial simulation methods for risk management into a multiperiod portfolio optimization context. Among the pros’:

• No need of any parametric assumption and thus lack of any source of model risk,

• Through the bootstrapping, the generation of robust optimal decisions relative to alternative data samples: this is what we refer to as in-sample stability of the optimal decision,

• Easy implementation and consistency with past market data and associated statistical properties,

• Event study selection and dedicated filtering approaches on past data.

In summary these are well-known positive properties of generic data-driven approaches (Consigli et al. 2017). From which few cons’ can also be deduced: the lack of serial dependence when needed, the persistence of tail events within the sample space that may influence the risk control accuracy, the impossibility to carry I/O what-if analysis commonly adopted with respect to alternative statistical assumptions in input data. As for a MSP set-up, the forced limitation of the tree process depth with respect to the adopted planning horizon and often a cumbersome derivation of time-dependent coefficients within the optimization model.

The output of the scenario tree generation is represented by the coefficient specification of the stochastic programme: in the next section we consider alternative risk control rules and analyze their effectiveness over an extended 16 years period in the US equity market. The collected evidences can provide a benchmark for studies in other equity markets, such as the European or the far East and the UK, also very developed and endowed with implied volatility benchmarks. A further relevant extension is represented by the introduction of early-warning-signals other than or together with the implied volatility, see (Consigli et al. 2009).

6.2 Volatility regime switches and optimal portfolio policy

In Sect. 3 the definition of different investment rules and hedging strategies was given a mathematical characterization in terms of MAD risk measures. Depending on the VIX information, either one of the policies was activated: a passive tracking error (TE) minimization problem for low current values of the implied volatility, an active volatility control (VC) policy within a corridor for VIX values within a lower and upper bounds, and finally for values beyond a certain threshold a tail risk (TR) control strategy. The three types of risk control are determined by two volatility bounds. Among these 3 classical investment approaches the second and the third are expected to lead to an effective limitation of the portfolio downside but they might jeopardise extra returns at times in which the market is growing. The first criterion instead is consistent with a risk-neutral investor and, depending, on the equity benchmark is expected to generate positive returns as well as negative returns. The definition of the input volatility bounds, leading to different risk control problems, will reflect indirectly the risk-attitude of the portfolio manager. The above market characterization does not consider the possibility of aggressive risk-seeking investment policies, which may be of interest. We focus instead on the feedback of a volatility signal coming from the option market into a limited set of risk control types.

The different controls have been introduced as alternative to each other: only pure, rather than mixed, TE, VC and TR strategies were considered in section and the volatility thresholds were assumed constant over time, see Table 2. In what follows, we relax such assumption to analyse how the optimal control will evolve under different specifications of the volatility signal: constant or time-varying.

To evaluate the effectiveness of the strategies in the long run with multiple switches to different market conditions we consider a 16 year period, starting in January 2000 until December 2015. The aim is here both to further validate the adopted modeling approach (in terms of effective replication of option strategies) and analyse how different assumptions on the feedback rule (from implied volatility to risk control) translate into alternative portfolio policies and their market potential. From a decision-making viewpoint the proposed modeling approach, integrating an implied market signal with the derivation of an optimal risk control, provides an effective framework to consider other types of signals and other replicating portfolio rules. In this work we have paid a primary attention to hedging portfolios and downside protection rather than allowing for more aggressive strategies. Risk controls based on a convex combination of the three criteria are also practical and would in general reflect investors risk attitudes even more effectively. In what follows, however, we will focus as mentioned on pure strategies, to derive the necessary modeling and policy implications.

6.2.1 Constant volatility thresholds

We indicate the VIX at time t with $\sigma _t$: $\sigma ^u$ and $\sigma _l$ are constant volatility upper and lower bounds. These are inputs by the portfolio manager relying on a given data history and they will determine the adopted policy throughout the 2000–2016 period. Consider again the set of volatility bounds introduced in Table 2: let $\sigma _l=20\%$ and $\sigma _u=45\%$. Below 20 a TE will be activated, above 45 a TR control and within the two bounds the VC policy. As noted in Sect. 3 these values are determined ex-ante analysing the behaviour of the US equity market volatility indices over a prolonged period and assumed to reflect different volatility regimes. Once a form of control holds, its quality will depend on two parameters associated with each one of the two: we indicate with $+/- \tilde{\sigma }$ the positive and negative volatility increments needed to specify the corridor associated with VC and with $\rho ^y$ the maximum tolerable negative market movement before activating TR. We show here next graphical evidence of the sensitivity of the policy rules to the settings $\tilde{\sigma }=1\%$ and $\rho ^y=5\%$.

Fig. 10

Comparison of optimal adaptive policy against the S&P500, the PPUT, a target volatility portfolio (target volatility level 0.01), a fixed-mix market-weighted portfolio and the equally-weighted 1 / n portfolio. Regime switching frequency and VIX behaviour—bi-weekly data 07/01/2000–10/06/2016

Figure 10 displays the outcome of the introduced policies, the frequency of the control switches over the 16 years and at the bottom the behaviour of the VIX during the period. We focused in the previous sections on three subperiods and we have shown that across those periods the introduced controls were effective in a static model. Here we evaluate the control policy within a recourse model over an extended 16 years’ test-period. According to the chosen thresholds, along this period, the market results to be in an instability condition, with the activation of tail risk control, only during the 2008 Financial Crisis. While, volatility control and tracking error alternate along the remaining periods. We observe that, when the market is in a positive phase associated with low volatility levels the tracking error strategy allows to follow the market. However, the signal is not able to recognize periods in which the market experiences losses in a low volatility setting and thus it is not able to avoid associated losses. The volatility control is rather effective and allows to avoid the most relevant downturns in the period.

Figure 11 displays in colour the optimal portfolio composition as a result of the introduced feedbacks: we present in dark blue the investment in the money market and then a range of colours spans the 10 S&P sub-indices.

Fig. 11

Optimal here-and-now portfolios composition over the test-period, sequence of 2-stage problems with bi-weekly data 07/01/2000–10/06/2016

Table 8 Comparison of optimal adaptive policy against the S&P500, the PPUT, a target volatility portfolio (target volatility level 0.01), a fixed-mix market-weighted portfolio and the equally-weighted 1 / n portfolio

Fig. 12

Comparison of the histograms for the S&P500 (top left), the optimal hedging portfolio (top right), the target volatility portfolio (target volatility level 0.01)(middle left), the Protective Put Index (middle right), the equally-weighted 1 / n portfolio (bottom left) and a fix-mix market-weighted portfolio (bottom right)—bi-weekly data 07/01/2000–10/06/2016

A good portfolio diversification characterizes the optimal portfolio allocation under the tracking error minimisation rule, a partial diversification is introduced under the tail risk control, while the money market allocation is prevalent under the volatility control rule. It must be pointed out that both $\alpha _2=1$ and $\alpha _3=1$ penalize portfolio returns outside the given $1\%$ volatility corridor and below the $5\%$ tail risk threshold: any portfolio satisfying those conditions would work and indeed be optimal under the given model specification. In market practice, portfolio revisions will likely be determined by policy and turnover constraints as well and, as mentioned, mixed strategies will prevail.

Table 8 displays the statistics associated with the returns’ distributions generated by each strategy over the considered period. Optimal portfolios are shown to dominate all other portfolios according to all three performance ratios. Furthermore, to measure the distance of the different strategies with respect to the benchmark, we consider the Information Ratio (IR) and the Tracking Error Volatility (TEV).

Figure 12, finally, presents the returns histograms generated by each strategy over the test-period.

The histograms in Fig. 12 display the return frequency distribution generated ex-post by actual market returns: at first glance the optimal portfolio return distribution top right dominates the other distributions.

The risk controls considered aim at shaping the resulting returns’ distribution according to different risk preferences. In particular, the TE control determines a returns’ distribution that resembles the one of the benchmark, the VC aims at shrinking the dispersion of the returns’ distribution obtaining a more concentrated distribution around the mean value, finally in the TR control the goal is the reduction of the tail of the distribution.

In Table 9 the statistics and performance measures computed with reference to Tracking error, Volatility control and Tail risk control periods, separately.

By disaggregating the analysis with respect to the adopted risk control type, we can evaluate each strategy. In particular, by comparing the distributions of the optimal portfolio against the others during the period in which the Tracking error was active (top section in Table 9) we observe that the return distribution of the optimal portfolio closely resembles the statistical features of the benchmark. This is confirmed by the Information Ratio and the Tracking Error Volatility in the last two rows of the table.

In the Volatility control case (middle part of Table 9) we can confirm its effectiveness, as witnessed by the return distribution minimal dispersion w.r.t the distribution of the benchmark, this determines also the higher value reported for the kurtosis given that even small deviations from the mean are thus relevant for the measure of tails. In the Tail risk control case (bottom section in Table 9) we can observe a considerable reduction of the maximum drawdown.

6.2.2 Path-dependent volatility thresholds

We consider now the evidence collected when including in the model time-varying thresholds $\sigma ^l_t$ and $\sigma ^u_t$ to discriminate between different policies. The fund manager is assumed to revise regularly the volatility thresholds to capture changing market conditions. We introduce a VIX moving average $\mu ^{\sigma }_t$ computed over the preceding year $\left[ t-52, t\right]$ as t evolves from 2000 until 2016 with weekly observations. Over the same period let $\sigma ^{\sigma }_t$ be the estimated so-called volvol process, i.e. the volatility of the implied volatility: it was shown already in Fig. 1 that indeed the VIX has gone over the last 20 years or so through several relevant breaking points. Here we do overlook such phenomenon and just test how alternative time-varying volatility thresholds influence the policy switches across the three introduced policies: TE, VC and TR.

Table 9 Comparison of optimal adaptive policy against the S&P500, the PPUT, a target volatility portfolio (target volatility level 0.01), a fixed-mix market-weighted portfolio and the equally-weighted 1 / n portfolio disaggregated for risk control

Figures 1 and 10 support at first sight the stylized evidence that the S&P500 carries a fat-tailed and asymmetric return distribution and indeed even stochastic volatility processes such as the celebrated GARCH model may be unsuitable to capture the volatility regime switches and their intensity. With this in mind we evaluate the feedback from volatility signals to control actions by considering the following thresholds specifications. For $\sigma _l(t)=\mu _t^{\sigma }-k \sigma _t^{\sigma }$ with $k=2,1.5,1,0.5$ we consider different time-varying thresholds discriminating the adoption of TE (below those values) and VC (above those values). Instead we keep $\sigma ^u_t=\mu _t^{\sigma }+2 \sigma _t^{\sigma }$ to discriminate between a VC policy and a TR control policy (above the threshold). Alternative threshold definitions may very well be adopted in search of superior portfolio performances: here, however, we are only interested to generalize the adaptive scheme and evaluate its hedging effectiveness when explicitly considering evolving market conditions.

Under the given definition of $\sigma ^u_t$ a tail risk control policy will become active only for sufficiently high VIX values. This quantile will change over time but remaining always on the extreme tail of the VIX distribution. Given such threshold, consider for $k=0.5,1,1.5$ and 2 the cases of increasing expansion/reduction TE/VC policy areas. As before it is of interest here to evaluate the associated frequency of policy rule changes and the quality of the introduced forms of control.

Fig. 13

Comparison of optimal adaptive policy against the S&P500, the PPUT, a target volatility portfolio (target volatility level 0.01), a fix-mix market-weighted portfolio and the equally-weighted 1 / n portfolio. Time varying volatility bounds—bi-weekly data 08/01/2000–10/06/2016. Top left $\sigma ^l_t= \mu ^{\sigma }_t-2\sigma ^{\sigma }_t$ and $\sigma ^u_t= \mu ^{\sigma }_t+2\sigma ^{\sigma }_t$. Top right $\sigma ^l_t= \mu ^{\sigma }_t-1.5\sigma ^{\sigma }_t$ and $\sigma ^u_t= \mu ^{\sigma }_t+2\sigma ^{\sigma }_t$. Bottom left $\sigma ^l_t= \mu ^{\sigma }_t-\sigma ^{\sigma }_t$ and $\sigma ^u_t= \mu ^{\sigma }_t+2\sigma ^{\sigma }_t$. Bottom right $\sigma ^l_t= \mu ^{\sigma }_t-0.5\sigma ^{\sigma }_t$ and $\sigma ^u_t= \mu ^{\sigma }_t+2\sigma ^{\sigma }_t$

Figure 13 displays the optimal portfolio dynamics relative to the introduced set of benchmarks for decreasing k: on the top left we have $k=2$, then right $k=1.5$ on the bottom left plot $k=1$ and finally $k=0.5$ on the bottom right plot. We see that in the top-left plot with $\sigma ^l_t= \mu ^{\sigma }_t-2\sigma ^{\sigma }_t$ and $\sigma ^u_t= \mu ^{\sigma }_t+2\sigma ^{\sigma }_t$ the VC area is so large that the resulting optimal strategy is always targeting a portfolio with almost null volatility and indeed as outcome we see that this strategy provides a perfect protection throughout the 16 years. For $k=1.5,1$ and 0.5 the area for index tracking expands and the resulting strategy will progressively focus on an optimal S&P replication. In parallel, the switches from VC to TE minimization will become significantly more frequent as shown here next in Fig. 14.

Fig. 14

Comparison of the activated controls for varying volatility thresholds—bi-weekly data 08/01/2000–10/06/2016. Top left $\sigma ^l_t= \mu ^{\sigma }_t-2\sigma ^{\sigma }_t$ and $\sigma ^u_t= \mu ^{\sigma }_t+2\sigma ^{\sigma }_t$. Top right $\sigma ^l_t= \mu ^{\sigma }_t-1.5\sigma ^{\sigma }_t$ and $\sigma ^u_t= \mu ^{\sigma }_t+2\sigma ^{\sigma }_t$. Bottom left $\sigma ^l_t= \mu ^{\sigma }_t-\sigma ^{\sigma }_t$ and $\sigma ^u_t= \mu ^{\sigma }_t+2\sigma ^{\sigma }_t$. Bottom right $\sigma ^l_t= \mu ^{\sigma }_t-0.5\sigma ^{\sigma }_t$ and $\sigma ^u_t= \mu ^{\sigma }_t+2\sigma ^{\sigma }_t$

Notice that in both cases, here above and in the previous experiment based on constant thresholds, we apply the same discriminating rule throughout the 16 years: the evidence presented in Fig. 13 supports however the need to adapt not only the thresholds but also such discriminating rule over time as the statistical properties of the VIX distribution change. Surely an asymmetric upper and lower deviation from the mean appears necessary to achieve a good hedging performance. We complete the analysis of this case of continuously evolving volatility thresholds by showing the associated optimal root-node portfolio allocations over the 2000–2016 period.

Fig. 15

Comparison of optimal first stage portfolio compositions for varying volatility thresholds—bi-weekly data 08/01/2000–10/06/2016. Top left $\sigma ^l_t= \mu ^{\sigma }_t-2\sigma ^{\sigma }_t$ and $\sigma ^u_t= \mu ^{\sigma }_t+2\sigma ^{\sigma }_t$. Top right $\sigma ^l_t= \mu ^{\sigma }_t-1.5\sigma ^{\sigma }_t$ and $\sigma ^u_t= \mu ^{\sigma }_t+2\sigma ^{\sigma }_t$. Bottom left $\sigma ^l_t= \mu ^{\sigma }_t-\sigma ^{\sigma }_t$ and $\sigma ^u_t= \mu ^{\sigma }_t+2\sigma ^{\sigma }_t$. Bottom right $\sigma ^l_t= \mu ^{\sigma }_t-0.5\sigma ^{\sigma }_t$ and $\sigma ^u_t= \mu ^{\sigma }_t+2\sigma ^{\sigma }_t$

The four plots in Fig. 15 help understanding, in case of very tight volatility control, the preference for risk-free money market allocation. As the space for portfolio tracking and relaxed volatility control increases the optimal portfolio strategy starts diversifying. By only considering the top left plot and the bottom right plot, based on the $\{+2,-2\}$ and $\{+2,-0.5\}$ threshold definitions, respectively, we present here next the associated out-of-sample performance evidence.

Table 10 Comparison of optimal adaptive policy against the S&P500, the PPUT, a target volatility portfolio (target volatility level 0.01), a fixed-mix market-weighted portfolio and the equally-weighted 1 / n portfolio

The results in Table 10 highlight the optimal portfolio returns’ distributions under the adopted threshold specifications against the benchmark policies. In the top table, based on $\{+\,2,-\,2\}$ threshold definition in which there is a prevalence of the VC, the returns’ distribution is extremely concentrated around the mean and negatively skewed. In the bottom table, based on the $\{+\,2,-\,0.5\}$ case with a more relevant presence of TE periods, the distribution is less negatively skewed but the threshold specification in this case inhibits the consistent upward movement of the market when associated with high levels of volatility thus resulting in a worsening of the risk adjusted performance indicators. The strategies’ outcome is determined by both the specification of k and by the length of the adopted moving window, in our case of 1 year.

Overall we may summarise that under a path-dependent thresholds definition, the optimal policy will adapt consistently to the varying hedging constraints, however considering prolonged periods the opportunity to introduce regime-based discriminating rules appears relevant.

7 Volatility signals and risk control: a summary

In Sects. 5.2.1 and 5.2.2 we gave evidence of the quality of the optimal controls induced by different model specifications. From a decision-paradigm viewpoint we may regard the adopted approach as a 4-legs decision process based on (1) a volatility signal from the derivative market, (2) the definition of the appropriate hedging or policy rule, (3) the subsequent derivation of an optimal portfolio replication within a recourse model and (4) its out-of-sample validation based on market data. Step (4) may lead over time to a refinement of (1) and so forth.

The (non trivial) relationship between (2) and (3) represents the main focus of the analysis and motivates a core part of this research. We believe that the collected evidences are sufficient to validate the adopted problem formulation (11)–(20). The tests were limited to relatively common and simple derivatives-based hedging policies, thus assuming a risk-averse decision maker primarily concerned with downside portfolio protection. The representation as MAD functionals for the cases in which short positions and long positions are jointly present is problematic. This represents a limitation of the proposed optimization approach and a task for future research.

The elements for other types of maybe bullish and speculative option strategies have been introduced in Sect. 4 and are definitely worth considering to extend the scope and practical applicability of the method. In market practice, a fund manager would hardly stick to only 3 risk management rules and depending on the market phase other portfolio payoffs may be appropriate. In our setting we didn’t discriminate at a macro-level between volatility regimes: between 1990 and 2016 it is widely acknowledged that the US equity market went through several volatility breaks (e.g. in 1998, 2007). Such evidence once statistically validated should lead to a revision of policy rules and signals across volatility macro-regimes. It must be finally recalled that the analysis has been developed under the simplifying, though realistic, assumption of no transaction costs and no management fees, assumed compensating one another.

The relationship between (1) and (2), being associated with the quality of forward signals collected in derivatives markets and their mapping into different types of regime-dependent policies, is also extremely relevant for portfolio managers. The continuous growth of volatility-based market indices employing an automatic revision of model portfolios further qualifies the search of effective feedback criteria to span agents’ risk preferences. Of particular interest and not treated in this article, the signals generated by indices or hidden market variables other than the VIX: in Consigli et al. (2009) we studied for the US equity market the ratio between the 10-year bond yield and the equity yield and develop a risk indicator. Increasing markets’ information efficiency is primarily reflected into growing and liquid derivatives markets and the adoption both for risk management and policy making objectives of implied information. This research stream was recently consolidated by the launch at CBOE of the TYVIX/VIX index and fits naturally in the proposed methodology, resulting in the definition of more comprehensive optimal portfolio replication problems. Other market signals may also be proposed and associated with desirable portfolio return profiles. The introduction of a weighted combinations of risk controls, obtained allowing $\alpha _{j}\ne 0$ for more than one j, results in the activation of mixed hedging strategies and represents a possible extension of the adopted model. Preliminary evidences, however, suggest that the relationships among the risk preferences of the decision maker, the market signals and thresholds used to activate the risk controls and the resulting optimal policies require further investigations.

Specifically from a methodological viewpoint the adoption of a data-driven short-term portfolio optimization model based on a 2-stage recourse program is new: we consider a fund manager with a 1 month horizon and as such employing 1-month forward implied market information and facing an uncertainty associated with a scenario tree representation of the problem. The performances reported in the preceding sections qualify the use of portfolio optimization approaches relative to automatic volatility trading rules and index-based strategies. The proposed framework is contiguous but substantially different from the stream of policy rule optimization approaches (Powell 2014) seeking through intensive Monte Carlo methods and heuristics, optimal policy rules over medium to long-term horizons. Here we only discriminate between different rules (TE or VC or TR) depending on a volatility signal and then solve an optimal portfolio replication problem given the rule. From a financial management viewpoint the adopted approach is close to so-called contingency approaches in which upon specific market conditions, likely to jeopardise ongoing optimal investment strategies, the portfolio manager protects the portfolio risk-adjusted performance over very short horizons.

8 Conclusion

This article’s ambitious contributions, broadly speaking, include: (i) the formulation of a recourse stochastic linear program, which replicates a set of option strategies commonly adopted for hedging purposes in equity markets, (ii) the validation of the associated policies when a derivative-market EWS, such as the implied volatility, is adopted over an extended time period, and (iii) the formulation of a stochastic programming model for short-term hedging purposes relying on a data-driven approach to model uncertainty.

For (i), in the first part of the article we have clarified the rationale for adopting an optimization approach rather than a direct derivative-based portfolio or a composite market benchmark: the effectiveness of the MAD formulation has been tested over three periods of market instability relying on a static one-period framework. After assessing the accuracy of the MAD formulation, with evidence on three risk control models—for tracking error minimization with respect to a benchmark, volatility control within a volatility corridor and tail risk control—we have extended the model to a two-stage formulation which has been implemented and tested out-of-sample over an extended 17 years period, between January 2000 and December 2016 under two possible volatility-based hedging schemes.

The model formulation and methodology relies entirely on market data without introducing any parametric assumption on returns distributions. The collected evidence supports the effectiveness of the adopted model formulation for hedging purposes, particularly during periods of high volatility in equity markets and illiquid and extremely expensive derivative contracts. The adoption of a data-driven characterization of the uncertainty is consistent with a decision model for short-term portfolio management as generally adopted in derivatives markets and fund management: as such the inclusion of an implied volatility signal based on 1 month derivative expiries coincides with the portfolio manager planning horizon. The extension of the proposed methodology to a full multistage setting, still relying on non parametric, market based scenario returns, must thus be taken with care. To infer the general properties of each type of policy, in this article we have limited the analysis to risk control strategies treated as alternative one another: the adoption of mixed strategies based on a multi-criteria approach appears desirable in practice and likely to induce superior portfolio performances.

Appendix A: List of crisis periods

In Table 11 recent stock market crashes and bear market periods in the period 2000-2016 are listed. For each period we test model (1)–(7) to validate the adopted problem formulation under different market conditions. The settings used in the experiments are the same presented in Sect. 3. Each experiment spans a period of 1 year and we solve 26 (bi-weekly) optimization problems.

Results of the management experiments for the Dot-com bubble, the September 11, 2001 attacks and the 2008 Financial Crisis are presented in Sect. 3 in the paper while results for the remaining periods are presented in Figs. 16, 17, 18, 19, 20 and 21.

Evidences obtained in different bear market periods confirm that the introduced model and the associated optimal hedging strategies are overall effective in providing protection from downside with the relevant exceptions of the Chinese stock bubble of 2007 and the Chinese stock market crash of June 2015 periods for which the signal seems to be too delayed and is thus not effective in activating the proper risk control. In these two periods the VIX crosses the lower threshold several times thus activating alternatively the VC and the TE strategies. A second limitation of the model confirmed by the Dubai debt crisis period is the inability of the model to capture and follow upward trends in the market when they are associated with high volatility levels signalled by levels of the VIX that are in the VC zone.

Table 11 List of major stock market crashes and bear markets in the period 2000–2016

Fig. 16

October, 2002 downturn. Comparison of optimized adapted portfolio with the benchmark portfolio (S&P500) and target volatility portfolio (target volatility level 0.01)—bi-weekly data 23/08/2002–08/08/2003

Fig. 17

Chinese stock bubble and US bear market, 2007. Comparison of optimized adapted portfolio with the benchmark portfolio (S&P500) and target volatility portfolio (target volatility level 0.01)—bi-weekly data 30/03/2007–14/03/2008

Fig. 18

November, 2009– Dubai debt crisis. Comparison of optimized adapted portfolio with the benchmark portfolio (S&P500) and target volatility portfolio (target volatility level 0.01)—bi-weekly data 13/02/2009–05/02/2010

Fig. 19

2010—European sovereign debt crisis. Comparison of optimized adapted portfolio with the benchmark portfolio (S&P500) and target volatility portfolio (target volatility level 0.01)—bi-weekly data 08/01/2010–24/12/2010

Fig. 20

August 2011—Stock market fall. Comparison of optimized adapted portfolio with the benchmark portfolio (S&P500) and target volatility portfolio (target volatility level 0.01)—bi-weekly data 08/04/2011–23/03/2012

Fig. 21

June, 2015—Chinese stock market crash. Comparison of optimized adapted portfolio with the benchmark portfolio (S&P500) and target volatility portfolio (target volatility level 0.01)—bi-weekly data 06/02/2015–22/01/2016