1 Introduction

From experiments it is known that the force after a stretch of a tetanically activated skeletal muscle/muscle fibre/myofibril/sarcomere/half-sarcomere is higher than the force resulting from an isometric tetanic contraction at the same (final) length (cf. e. g. Abbott and Aubert 1952; Edman et al. 1978; Joumaa et al. 2007). This phenomenon is known as force enhancement. A number of mechanisms have been proposed to contribute to force enhancement (for reviews see Edman 2012; Campbell and Campbell 2011). While some researchers explain this phenomenon with classical theories of contraction, for example, half-sarcomere inhomogeneities (Morgan et al. 1982) or altered cross-bridge dynamics (Walcott and Herzog 2008), others relate force enhancement to a non-cross-bridge, semi-active contribution of the titin filament (Noble 1992; Rode et al. 2009; Till et al. 2010; Leonard and Herzog 2010; Nishikawa et al. 2012).

Titin links the thick (myosin) filament to the Z-disc, where it attaches near a thin (actin) filament (Prado et al. 2005). In passive muscle, titin acts like a nonlinear spring, restoring the resting length of the half-sarcomere after stretch. In the presence of calcium, i.e. during activation, titin can alter its stiffness (Labeit et al. 2003) and, more importantly, can attach to the thin filament (Powers et al. 2014; Bianco et al. 2007; Kellermayer and Granzier 1996). Through this attachment, titin’s free molecular spring length is dramatically reduced. This leads to vastly increased titin forces during and after active muscle stretch.

Force enhancement plays an important role during and after lengthening contractions, i. e., when muscles act as brakes. Moreover, it might reduce the neural control effort (Häufle et al. 2014; Müller et al. 2012), improve the muscle’s efficiency in cyclic stretch-shortening situations (Rode et al. 2009; Nishikawa et al. 2012), and might provide stability when the muscle works in a length range corresponding to the descending limb of the muscle’s isometric force–length relation (Morgan 1990). Thus, neglecting this phenomenon in computational models might lead to inaccurate model predictions.

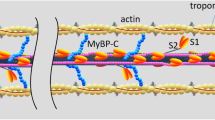
Rode et al. (2009) proposed a biophysical, molecular model of titin’s semi-active behaviour. Their ‘sticky-spring’ mechanism assumes that the PEVK region (rich in proline (P), glutamic acid (E), valine (V), and lysine (K)) of titin’s molecular spring region attaches in the presence of calcium (Kulke et al. 2001; Nagy et al. 2004; Bianco et al. 2007) to available myosin-binding sites on the actin filaments (Niederländer et al. 2004), see Fig. 1. By modelling this actin–titin interaction through a ‘sticky-spring’ model, they could predict experimentally observed phenomena related to force enhancement that cannot be explained by classic theories of contraction.

Fig. 1
figure 1

Schematic drawing of a half-sarcomere in lateral view (left) and axial view (right). For the sake of readability, the fibre direction is assumed to be aligned with the \(\varvec{e}_1\)-direction. The lengths of the projections in the \(\varvec{e}_1\)-direction of the entire titin filament, its distal Ig region, its PEVK region, and its proximal Ig region are denoted by \(l_\mathrm{Titin}\), \(l_\mathrm{distIg}\), \(l_\mathrm{PEVK}\), and \(l_\mathrm{proxIg}\), respectively. Further, \(d_\mathrm{AM}\) is the distance between the thin and thick filaments, and \(\phi \) denotes the angle between the \(\varvec{e}_2\)-direction and the origin of a titin filament in the plane normal to the \(\varvec{e}_1\)-direction. Left The upper titin filament is in the passive state, i. e., titin’s entire molecular spring region acts as a spring. The lower titin filament is in the active state, i. e., its PEVK region is connected to the thin filament at myosin binding sites reducing the effective molecular spring region to titin’s distal Ig region. Right We assume that six titin filaments connect each thick filament to the origin of each of six surrounding thin filaments

Full size image

Rode et al. (2009) implemented their biophysical model of force enhancement and force depression within a simple Hill-type muscle model. Depending on the application, Hill-type models, however, can be of limited use, since they lump functional and spatially heterogeneous muscle properties together to a few parameters (Siebert and Rode 2014). Further, Hill-type models neglect muscle mass effects (Günther et al. 2012), and assume that the calculated force only acts along a predefined line of action (Hill 1938). For muscles with complex geometries, Hill-type models also exhibit difficulties in accurately predicting muscle force directions and magnitudes (Röhrle and Pullan 2007).

To overcome these limitations, finite element models based on the theory of finite deformations of continuum mechanics have been proposed (Blemker et al. 2005; Röhrle et al. 2008). While continuum-mechanical models can, for example, account for complex muscle fibre distributions (Blemker and Delp 2005), regional activation properties (Heidlauf and Röhrle 2014), a dynamically generated line of action (Röhrle and Pullan 2007), as well as transverse forces (Siebert et al. 2012), they usually neglect force enhancement. Indeed, to the best knowledge of the authors, the model of Lemos et al. (2001) is the only continuum-mechanical muscle model that aims to model force enhancement. In Lemos et al. (2001), the nonlinear active force–length relationship of the muscle is replaced by a linear model when stretch of an activated muscle starts. This approach is purely phenomenological and leads to a velocity dependence of force enhancement during stretch, which is in contrast to experiments (Till et al. 2008; Edman et al. 1978).

To account for force enhancement in a continuum-mechanical muscle model, the present contribution extends the multi-scale chemo-electro-mechanical model of Heidlauf and Röhrle (2013, 2014). To this end, the continuum-mechanical stress tensor needs to be extended by terms describing the semi-active behaviour of the titin filaments. The stress contributions induced by titin filaments are derived from the biophysical ‘sticky-spring’ model of Rode et al. (2009). To bridge the gap between the half-sarcomere level and the macroscopic entire skeletal muscle level, the microscopic, half-sarcomere-based titin stress contributions need to be homogenised. Further, to be able to simulate submaximal contractions, in addition to passive and fully activated half-sarcomeres, the model of Rode et al. (2009) needs to be extended. Titin-induced stress contributions are hereby modelled to be dependent on the activation level of the half-sarcomeres. This approach accounts for the fact that during submaximal contractions fewer myosin binding sites on actin are available for titin attachment. Moreover, to describe the entire three-dimensional (3D) stress state of the muscle, it is necessary to account also for titin-induced stresses in the muscle’s cross-fibre (XF) directions. Although these terms result from purely geometrical considerations (trigonometry), none of the previous models of force enhancement (Rode et al. 2009; Lemos et al. 2001; Nishikawa et al. 2012) have considered this. It is noteworthy that the presented model does not require any parameters in addition to those of the models of Rode et al. (2009) and Heidlauf and Röhrle (2013, 2014).

2 Material and Methods

This work is based on the biophysical force enhancement model of Rode et al. (2009) and the chemo-electro-mechanical 3D skeletal muscle model of Heidlauf and Röhrle (2013, 2014). Before introducing the embedding of the force enhancement model within the continuum-mechanical skeletal muscle model, the model of Rode et al. (2009) is briefly reviewed.

2.1 Titin Model of Rode et al. (2009)

Rode et al. (2009) consider in their model one half-sarcomere and attribute all passive forces in the half-sarcomere to the titin filaments. Further, all forces are normalised with respect to the maximum isometric active force of the half-sarcomere. Titin properties reported by Linke et al. (1998a, b) are used to obtain required force–elongation relationships of the relevant titin regions.

Titin force depends on the state of the half-sarcomere. In the passive, low calcium concentration state, titin is not bound to the thin filament. Its normalised force, \(\theta _{\mathrm{Titin}}^\mathrm{unbound}\), depends only on the actual half-sarcomere length, \(l_{\mathrm{hs}}\). In the active, high calcium concentration state, the pre-stretched PEVK region of the titin filament is attached to myosin binding sites on the actin filament, cf. Fig. 1. During a subsequent stretch of the half-sarcomere, the PEVK region elongates along the actin filament by subsequently breaking bonds and immediately reattaching to the actin filament leading to opposed gradients of force in the PEVK region and in the actin filament. This behaviour can be approximated phenomenologically by a linear spring that extends due to force in excess of the passive force at the initial length. Its stiffness, \(k_{\mathrm{PEVK}}^\mathrm{bound}\), increases with increasing pre-stretch of the unbound PEVK region, i. e., with increasing initial length, \(l_{\mathrm{hs[0]}}\), at which the sarcomere is activated. Therefore, the force in bound titin, \(\theta _{\mathrm{Titin}}^\mathrm{bound}\), depends on \(l_{\mathrm{hs}}\) and \(l_{\mathrm{hs[0]}}\).

As a consequence of the serial arrangement of the PEVK and distal Immunoglobulin (Ig) regions, the following equations have to be satisfied:

$$\begin{aligned} \begin{aligned}&0\, =\ \theta _\mathrm{distIg}(l_\mathrm{distIg}) - \theta _\mathrm{PEVK}^\mathrm{bound}\left( l_\mathrm{hs[0]}, \Delta l_\mathrm{PEVK}^\mathrm{bound}\right) \\&\quad =\ \theta _\mathrm{distIg}(l_\mathrm{distIg}) - \left[ \theta _{\mathrm{Titin}}^\mathrm{unbound}(l_\mathrm{hs[0]}) \,+ \right. \\&\qquad \left. \ +\, \Delta l_\mathrm{PEVK}^\mathrm{bound} \cdot k_\mathrm{PEVK}^\mathrm{bound}(l_\mathrm{hs[0]})\right] , \end{aligned} \end{aligned}$$
(1)
$$\begin{aligned} \Delta l_\mathrm{distIg} = \Delta l_{\mathrm{hs}} - \Delta l_\mathrm{PEVK}^\mathrm{bound}. \end{aligned}$$
(2)

Therein, \(\theta _{\mathrm{PEVK}}^\mathrm{bound}\) and \(\theta _{\mathrm{distIg}}\) denote the forces in the PEVK and distal Ig regions, respectively, \(\theta _\mathrm{Titin}^\mathrm{unbound}(l_{\mathrm{hs}[0]})\) is the titin force at the beginning of the activation, \(\Delta l_{\mathrm{PEVK}}^\mathrm{bound}\) and \(\Delta l_\mathrm{distIg}\) are the elongations of the PEVK and distal Ig regions, respectively, and \(\Delta l_{\mathrm{hs}}\) denotes the elongation of the activated half-sarcomere, i. e., \(\Delta l_{\mathrm{hs}} = l_\mathrm{hs} - l_\mathrm{hs[0]}\). Note that \(\theta _{\mathrm{PEVK}}^\mathrm{bound}\) is measured at the distal end of the PEVK region, and consists of two components. Its first component, \(\theta _{\mathrm{Titin}}^\mathrm{unbound}(l_\mathrm{hs[0]})\), is transmitted via the proximal Ig region to the Z-disc, its second component, the cumulated force of actin–titin attachments modelled by a linear spring, is transmitted to the actin filament. The actual length of the distal Ig region, \(l_\mathrm{distIg}\) can be determined from its length at the beginning of the activation, \(l_\mathrm{distIg[0]}\), and its elongation, i. e., \(l_\mathrm{distIg}=l_\mathrm{distIg[0]} + \Delta l_\mathrm{distIg}\).

Inserting (2) into this relation and substituting the resulting equation into (1) yields

$$\begin{aligned} \begin{aligned} 0\,&=\ \,\theta _\mathrm{distIg}(l_\mathrm{distIg[0]} + \Delta l_\mathrm{hs} - \Delta l_\mathrm{PEVK}^\mathrm{bound}) \\&\quad \ - \left[ \theta _\mathrm{Titin}^\mathrm{unbound}(l_\mathrm{hs[0]}) + \quad \Delta l_\mathrm{PEVK}^\mathrm{bound} \cdot k_\mathrm{PEVK}^\mathrm{bound}(l_\mathrm{hs[0]})\right] . \end{aligned} \end{aligned}$$
(3)

Solving the nonlinear Eq. (3) for \(\Delta l_\mathrm{PEVK}^\mathrm{bound}\) with e. g. Newton’s method, \(\theta _{\mathrm{Titin}}^\mathrm{bound}\) is given by the force equilibrium \(\theta _{\mathrm{Titin}}^\mathrm{bound} = \theta _\mathrm{distIg} = \theta _\mathrm{PEVK}^\mathrm{bound}\).

2.2 The Extended Continuum-Mechanical Muscle Model

Having introduced the titin forces in the passive and active states, the model of Rode et al. (2009) is now extended to account for submaximal activation levels. This is done by introducing an activation parameter \(\gamma \in [0,1]\) describing the probability that a titin filament is bound to a thin filament. Assuming that this probability depends on the calcium concentration (cf. Sect. 2.2), the titin force in a passive (\(\gamma =0\)), fully activated (\(\gamma =1\)), or submaximally activated (\(0<\gamma <1\)) half-sarcomere is given by

$$\begin{aligned} \begin{aligned} \theta _{\mathrm{Titin}} (l_\mathrm{hs},l_\mathrm{hs[0]},\gamma ) \,=&\ \gamma \,\theta _{\mathrm{Titin}}^\mathrm{bound} (l_\mathrm{hs},l_\mathrm{hs[0]}) \,+ \\&\ +\, (1-\gamma )\,\theta _{\mathrm{Titin}}^\mathrm{unbound} (l_\mathrm{hs}). \end{aligned} \end{aligned}$$
(4)

The normalised force, \(\theta \), can also be interpreted as a normalised nominal stress due to the definition of the nominal stress (force per referential surface element). Thus, from now on \(\theta \) denotes a normalised nominal stress.

To account for force enhancement, the continuum-mechanical multi-scale skeletal muscle model of Heidlauf and Röhrle (2013, 2014) needs to be extended. For the sake of brevity, we omit a general introduction to continuum mechanics, which can be found e. g. in Holzapfel (2000). Instead, we focus on the underlying modelling assumptions and the resulting stress tensor. The proposed method neglects body and inertia forces, and models the muscle tissue as a transversely isotropic, incompressible, and hyperelastic material.

The second Piola–Kirchhoff stress tensor in this contribution is additively split into passive, active, and titin-related components. The titin-related components account for the stiffness induced by the titin filaments (which can be in the bound or unbound state), the passive components describe the transversely isotropic behaviour of the other passive structures of the muscle tissue (Prado et al. 2005; Van Loocke et al. 2006), and the active component aims to describe the tension generated due to electrical stimulation. Thus, the second Piola–Kirchhoff stress tensor is given by

$$\begin{aligned} \begin{aligned} \varvec{S} \,=\&- p\,J\, \varvec{C}^{-1} + \varvec{S}_{\mathrm{Passive}}^\mathrm{{iso}}+ \varvec{S}_{\mathrm{Passive}}^\mathrm{{ani}}+ \varvec{S}_{\mathrm{Active}}\,+ \\&+ \varvec{S}_{\mathrm{Titin}}+ \varvec{S}_{\mathrm{Titin,XF}}, \end{aligned} \end{aligned}$$
(5)

where, \(J:={\text {det}}\varvec{F}\) denotes the Jacobian determinant (the determinant of the material deformation gradient tensor \(\varvec{F}\)), and p is the hydrostatic pressure, which enters the equation as a Lagrange multiplier due to the incompressibility condition. Furthermore, the passive anisotropic mechanical behaviour of skeletal muscle tissue (except for the contribution of titin) is described by the sum of an isotropic Mooney–Rivlin part,

$$\begin{aligned} \varvec{S}_{\mathrm{Passive}}^\mathrm{{iso}} \,=\, 2\, c_{10}\, \varvec{I} + 2\, c_{01} \left[ {\text {tr}} (\varvec{C}) \varvec{I} - \varvec{C} \right] , \end{aligned}$$
(6)

and an anisotropic part, which acts only upon stretch in fibre direction (\(\lambda _\mathrm{f}>1\)) and is given by

$$\begin{aligned} \varvec{S}_{\mathrm{Passive}}^\mathrm{{ani}} \,=\, b_1\big [\lambda _\mathrm{f}^{d_1-2}-\lambda _\mathrm{f}^{-2}\big ] \varvec{a}_0 \otimes \varvec{a}_0 . \end{aligned}$$
(7)

The parameters \(c_{10}, c_{01}, b_1\), and \(d_1\) in (6) and (7) are material parameters, \(\varvec{I}\) is the second-order identity tensor, \(\lambda _\mathrm{f}\) is the fibre stretch, which is the square root of the fourth (mixed) invariant, i. e., \(\lambda _\mathrm{f}=\sqrt{I_4}=\sqrt{\varvec{F}\varvec{a}_0 \cdot \varvec{F}\varvec{a}_0}\), and \(\varvec{a}_0\) is a unit vector pointing in the referential fibre direction. Note the relation between the fibre stretch and the half-sarcomere length \(\lambda _\mathrm{f}=l_\mathrm{hs}/l_\mathrm{hs}^\mathrm{ref}\), where \(l_\mathrm{hs}^\mathrm{ref}=1.0\,\upmu \)m denotes the half-sarcomere length in the resting state (reference configuration; Edman 1979).

The active part of the second Piola–Kirchhoff stress tensor reflects the muscle’s ability to generate tension by transforming chemically stored energy into mechanical work and is given by

$$\begin{aligned} \varvec{S}_{\mathrm{Active}} \,=\, \gamma (f_\mathrm{stim}, t, \varvec{x})\,f_\mathrm{l}(l_\mathrm{hs})\,{P_\mathrm{max}}\,{\lambda _\mathrm{f}}^{-1} \,\varvec{a}_0 \otimes \varvec{a}_0 . \end{aligned}$$
(8)

Here, \(P_\mathrm{max}\) is the maximum isometric stress, \(f_\mathrm{l}(l_\mathrm{hs})\) denotes the sarcomere’s normalised force–length relation taken from Gordon et al. (1966), t is the time, and \(f_\mathrm{stim}\) denotes the stimulation frequency. Moreover, \(\gamma (f_\mathrm{stim}, t, \varvec{x})\) denotes the normalised, sarcomere-based, activation parameter, which is also used to interpolate between the unbound and bound titin stresses, cf. (4). The activation parameter is normalised using its value due to tetanic stimulation (50 Hz).

In the multi-scale chemo-electro-mechanical skeletal muscle model of Heidlauf and Röhrle (2013), Heidlauf and Röhrle (2014), \(\gamma \) is determined from the biophysical model of Shorten et al. (2007). The model of Shorten et al. (2007) describes biophysically the excitation–contraction coupling in a half-sarcomere by coupling models of the membrane electrophysiology (Wallinga et al. 1999), calcium dynamics (Baylor and Hollingworth 1998, 2003), and force generation via cross-bridge cycling (Razumova et al. 1999) at a point in space, i. e. in a single half-sarcomere. The individual half-sarcomere models (Shorten et al. 2007) belonging to a muscle fibre are linked to each other via a diffusion equation, the so-called monodomain equation, representing the propagation of action potentials (Keener and Sneyd 2009). Similar to the model of the excitation–contraction coupling (Shorten et al. 2007), the force–length relation is also included at the half-sarcomere level, which justifies the use of the sarcomere-based relation of Gordon et al. (1966). In the multi-scale model, the product of the force–length relation and \(\gamma \) is homogenised to the macroscopic continuum-mechanical scale (see Heidlauf and Röhrle 2014 for details).

Thus, in the chemo-electro-mechanical model, the activation parameter, \(\gamma \), depends on the stimulation frequency, \(f_\mathrm{stim}\), the time, t, and the position of the half-sarcomere, \(\varvec{x}\).

Figure 2 shows the relation between \(\gamma \) and \(f_\mathrm{stim}\) for a single half-sarcomere. Under conditions of not completely fused twitches, the range between the minimum and maximum values of the activation parameter is depicted.

Fig. 2
figure 2

Force–frequency relation of a half-sarcomere. Under conditions of not completely fused twitches, the range between the minimum and maximum values of the active force is shown

Full size image

Note that in Heidlauf and Röhrle (2014) the half-sarcomere-based activation parameter, \(\gamma \), depends also on the contraction velocity, cf. Hill (1938). The present work, however, omits this otherwise important muscle property in order to isolate the titin-induced effects present within the newly proposed model. The advantage of omitting the force–velocity relation is that the material behaves purely hyperelastic, i. e., it does not show time- or velocity-dependent behaviour, and no force transients exist during stretch. In combination with neglecting inertia terms, this leads to the fact that at each instant in time, the model predicts the steady-state forces at the corresponding length, and hence, all observed enhanced muscle forces can be attributed to actin–titin binding.

Further, in (5), \(\varvec{S}_{\mathrm{Titin}}\) and \(\varvec{S}_{\mathrm{Titin,XF}}\) represent the stresses induced by the titin filaments in the muscle fibre and XF directions, respectively. The titin-induced stress in fibre direction is given by

$$\begin{aligned} \varvec{S}_{\mathrm{Titin}} \,=\, \theta _\mathrm{Titin}(l_\mathrm{hs[0]},l_\mathrm{hs},\gamma )\,{P_\mathrm{max}}\,{\lambda _\mathrm{f}}^{-1}\, \varvec{a}_0 \otimes \varvec{a}_0, \end{aligned}$$
(9)

where \(\theta _\mathrm{Titin}\) directly follows from (4). Further, the titin-induced stress in XF direction is given by

$$\begin{aligned} \varvec{S}_{\mathrm{Titin,XF}} \,=\, \theta _\mathrm{Titin,XF}(l_{hs[0]},l_{hs},\gamma )\,P_\mathrm{max}\,\lambda _\mathrm{f}^{-1} [\varvec{I} - \varvec{a}_0 \otimes \varvec{a}_0]. \end{aligned}$$
(10)

The normalised stress in XF direction, \(\theta _\mathrm{Titin,XF}\), will be specified in the following.

Titin’s free molecular spring part is not aligned with the fibre direction but spans from an attachment site on the Z-disc close to a thin filament to the beginning of the thick filament, cf. Fig. 1. Thus, the titin filament induces stresses not only in the muscle fibre direction but also in the XF directions (normal to the muscle fibre direction). The detailed arrangement and the exact number of titin filaments per myosin filament are not known. We assume six titin filaments per thick filament, which connect hexagonally to the Z-disc. It is assumed that each titin filament is loaded by 1 / 6 of the total titin stress of the respective thick filament. Given the titin stress in fibre direction in a half-sarcomere, the average XF stress of a single titin filament can be calculated from geometric considerations (trigonometry) of the forces acting in a half-sarcomere and are given by

$$\begin{aligned} \begin{aligned} \bar{\theta }_\mathrm{singleTitin,XF}&\,=\, \gamma \, \theta _\mathrm{singleTitin,XF}^\mathrm{bound}(l_\mathrm{hs},l_\mathrm{hs[0]})\,+ \\&\qquad + (1-\gamma ) \, \theta _\mathrm{singleTitin,XF}^\mathrm{unbound} (l_\mathrm{hs}) \\&\,=\, \frac{1}{6} \Big [\gamma \, \theta _{\mathrm{Titin}}^\mathrm{bound} (l_\mathrm{hs},l_\mathrm{hs[0]}) \frac{d_\mathrm{AM}}{l_\mathrm{distIg}} \,+ \\&\qquad + (1-\gamma ) \, \theta _{\mathrm{Titin}}^\mathrm{unbound} (l_\mathrm{hs}) \frac{d_\mathrm{AM}}{l_\mathrm{Titin}} \Big ]. \end{aligned} \end{aligned}$$
(11)

Therein, \(l_\mathrm{Titin}\) is the length of titin’s molecular spring region, and \(l_\mathrm{distIg}\) is the length of the distal Ig region. The distance between the thin and thick filaments, \(d_\mathrm{AM}\), is assumed to be independent of the macroscopic deformation of the muscle (e. g. in XF direction). Thus, \(d_\mathrm{AM}(l_\mathrm{hs})\) depends only on the length of the half-sarcomere. This relation is determined from the experimental data of mammalian muscle of Elliott et al. (1963).

For a continuum-mechanical treatment, the discrete titin XF stress values, \(\bar{\theta }_\mathrm{singleTitin,XF}\), have to be homogenised towards the coefficient \({\theta }_\mathrm{Titin,XF}\) of the stress tensor \(\varvec{S}_{\mathrm{Titin,XF}}\) in (10). Owing to the structural filament arrangement as depicted on the right-hand side of Fig. 1, the filament XF stresses act in a hexagonal manner in a plane normal to the fibre direction, \(\varvec{a}_0\). Hence, for each of the six filaments an individual stress tensor \(\varvec{S}_{\mathrm{singleTitin,XF}} = \bar{\theta }_\mathrm{singleTitin,XF}\,{P_\mathrm{max}}\,{\lambda _\mathrm{f}}^{-1}\,\varvec{t}_n\otimes \varvec{t}_n\) can be formulated, where the unit vectors \(\varvec{t}_n\) are given by

$$\begin{aligned} \varvec{t}_n \,=\, \begin{bmatrix}0 \\ \hbox {cos}(\phi \,+\,(n-1)\,\frac{\pi }{3}) \\ \hbox {sin}(\phi \,+\,(n-1)\,\frac{\pi }{3}) \end{bmatrix} \varvec{e}_i, \end{aligned}$$
(12)

for \(n\in \{1,2,3,4,5,6\}\). Note that, without loss of generality, the relation \(\varvec{a}_0=\varvec{e}_1\) is applied for the sake of readability. Moreover, the angle \(\phi \in [0, 2\pi )\) in (12) is included due to the non-uniqueness of the coordinate vectors \(\varvec{e}_2\) and \(\varvec{e}_3\). The overall XF stress tensor, \(\varvec{S}_{\mathrm{Titin,XF}}\), is now derived by a summation of the individual stresses via

$$\begin{aligned} \begin{aligned} \varvec{S}_{\mathrm{Titin,XF}}&\,= \,\sum _{n=1}^6 \varvec{S}_{\mathrm{singleTitin,XF}} \\&\,= \, \bar{\theta }_\mathrm{singleTitin,XF}\, {P_\mathrm{max}}\, {\lambda _\mathrm{f}}^{-1} \sum _{n=1}^6 \varvec{t}_n\otimes \varvec{t}_n, \end{aligned} \end{aligned}$$
(13)

where

$$\begin{aligned} \sum _{n=1}^6\,\varvec{t}_n\otimes \varvec{t}_n \,=\, 3\,[\varvec{I}-\varvec{a}_0\otimes \varvec{a}_0]. \end{aligned}$$
(14)

This result is valid for any choice of the fibre direction, \(\varvec{a}_0\), and is independent of the angle \(\phi \), since the overall stress induced by the six individual filament stresses in the transverse plane is invariant to rotations about the fibre direction, \(\varvec{a}_0\). Finally, the scalar coefficients \({\theta }_\mathrm{Titin,XF}\) in (10) are identified to \({\theta }_\mathrm{Titin,XF} = 3\, \bar{\theta }_\mathrm{singleTitin,XF}\).

Within the multi-scale model, the titin model of Rode et al. (2009) is implemented on the half-sarcomere level, just like the model of the excitation–contraction coupling of Shorten et al. (2007). Hence, the computational muscle fibres embedded in the 3D muscle geometry consist now of series-arranged half-sarcomere models describing both the excitation–contraction coupling (including the generation of the activation parameter, \(\gamma \), due to cross-bridge cycling) and the titin-induced stresses. Due to computational limitations, different finite element discretisations are used for the 1D muscle fibres and the 3D muscle geometry. The 1D muscle fibre meshes are only used to solve the monodomain equation (including the biophysical half-sarcomere model of Shorten et al. 2007 and the titin model at each discretisation point). The coarser 3D mesh of the muscle geometry is used to solve the continuum-mechanical model. Due to the occurrence of different meshes within the model, transfer operations are required. In detail, the sarcomere-based activation parameter and the titin stress need to be homogenised, before they can be used within the continuum-mechanical constitutive equation. For further details, the reader is referred to Heidlauf and Röhrle (2013), Heidlauf and Röhrle (2014).

As mentioned above, the terms \(\varvec{S}_{\mathrm{Passive}}^\mathrm{{iso}}\) and \(\varvec{S}_{\mathrm{Passive}}^\mathrm{{ani}}\) now represent only the mechanical behaviour of the extracellular connective tissue. Hence, the more compliant behaviour of the extracellular connective tissue in comparison to the entire muscle tissue (Prado et al. 2005; Gillies and Lieber 2011) is modelled by choosing material parameters describing lower stiffness. The material parameters of the presented continuum-mechanical model are summarised in Table 1. The data required for the titin model, i. e., the force–elongation relations of the distinct titin regions and the PEVK stiffness depending on the initial half-sarcomere length preceding stretch are taken from Figures 2 and B1A of Rode et al. (2009), respectively.

Table 1 Material parameters
Full size table

The presented equations have been implemented into the open-source software library OpenCMISS (Bradley et al. 2011; Heidlauf and Röhrle 2013).

3 Results

The aim of this section is to present simulation results of force enhancement, first, on the microscopic half-sarcomere level, then on the muscle fibre level (mesoscale), and, finally, on the macroscopic whole muscle level.

3.1 Force Enhancement on the Half-Sarcomere Level

Figure 3 shows the dependence of the titin-induced stresses of a single half-sarcomere, \({\theta }_\mathrm{Titin}(l_\mathrm{hs}, l_\mathrm{hs[0]}, \gamma )\), on the activation parameter, \(\gamma \), and the elongation of the half-sarcomere, \(\Delta l_\mathrm{hs}\). There, the combinations of 10 uniformly spaced activation levels and 20 different stretch lengths are depicted for three initial half-sarcomere lengths (\(l_\mathrm{ls[0]}=1, \)1.2, \(1.4\,\upmu \)m).

Fig. 3
figure 3

Half-sarcomere-based titin stresses, \({\theta }_\mathrm{Titin}(l_\mathrm{hs}, l_\mathrm{hs[0]}, \gamma )\), versus activation, \(\gamma \), and half-sarcomere elongation, \(\Delta l_\mathrm{hs}\), for stretches starting from \(1\,\upmu \)m (left), \(1.2\,\upmu \)m (middle), and \(1.4\,\upmu \)m (right)

Full size image

In the passive state (\(\gamma =0\)), the titin-induced stresses are very small at short to medium initial half-sarcomere lengths (\(l_\mathrm{hs[0]}=1.0\) and \(1.2\,\upmu \)m), and significantly increase only at longer lengths (\(l_\mathrm{hs[0]}=1.4\,\upmu \)m). In the fully activated state (\(\gamma =1\)), the titin-induced stresses are much more pronounced as a result of actin–titin binding, and the stresses increase linearly with stretch and have similar slope for the different initial half-sarcomere lengths. Besides the passive and fully activated states, Fig. 3 also shows the resulting titin stress due to submaximal activation levels. Note that each point on the surfaces indicates the resulting steady-state stress induced exclusively by the titin filaments.

3.2 Force Enhancement on the Muscle Fibre Level

To demonstrate the effect of force enhancement on the muscle fibre level, an 8-cm-long fibre model consisting of 301 discrete half-sarcomere models, i. e., models of the excitation–contraction coupling (Shorten et al. 2007), is considered. Since myofibrils within a muscle are laterally connected to each other at the Z-discs, homogeneous conditions within the cross section of a muscle fibre are assumed. Hence, only in-series-arranged half-sarcomeres are considered.

The fibre model is first passively stretched to an average half-sarcomere length of 1.3 \(\upmu \)m (\(\lambda _\mathrm{f}^\mathrm{init}=1.3\)). Then, the leftmost half-sarcomere is stimulated with 25 Hz and the muscle fibre is stretched with a constant velocity of \(v=4\,\)cm/s. The propagating action potentials represented by the monodomain equation successively activate the other half-sarcomere models.

Figure 4 shows the distribution of the titin stresses in the computational muscle fibre at times \(t=170\) ms (top), \(t=180\) ms (middle), and \(t=190\) ms (bottom). Since the action potential propagation velocity is relatively low in skeletal muscle (about 2–6 m/s), the activation parameter, \(\gamma \), and the titin stress, \(\theta _{\mathrm{Titin}}\), [which depends on \(\gamma \), cf. (4)] are non-uniformly distributed within the fibre.

Fig. 4
figure 4

Distribution of titin stresses in an 8-cm-long muscle fibre at times \(t=170\) ms (top), \(t=180\) ms (middle), and \(t=190\) ms (bottom)

Full size image

The non-uniform distribution of the titin-induced stress in the muscle fibre is clearly visible at all three considered time steps.

3.3 Force Enhancement on the Whole Muscle Level

This section investigates force enhancement on the macroscopic muscle level. To exclude geometrical effects, a cubic geometry with edge length \(l=1\) cm is considered. The cube has been discretised using 8 tri-quadratic/tri-linear Lagrange finite elements. Further, 36 parallel-aligned muscle fibres have been embedded within the cube, cf. Heidlauf and Röhrle (2013). The boundary conditions have been chosen such that all the displacement degrees of freedom (DOFs) on the surfaces normal to the fibre direction are constrained in fibre direction. Further, symmetric boundary conditions are assumed at two other non-parallel sides of the cube.

Unless otherwise stated, the numerical experiments presented in this section are performed as described in the following. First, the sample is passively stretched in fibre direction from \(L_0=1.0\) cm to a certain length \(L=\lambda _\mathrm{f}^\mathrm{init} L_0\). Under fixed-length conditions the muscle is then fully activated for 500 ms, i. e. the half-sarcomere model located in the middle of each computational muscle fibre is tetanically stimulated at a frequency of \(f_\mathrm{stim}=50\) Hz. This stimulation frequency leads to activation parameters, \(\gamma \), that are essentially uniformly equal to 1 within the muscle geometry. After 500 ms the activated muscle is stretched with constant velocity \(v=4\) cm/s. Note that the material response is essentially independent of the stretching velocity. This results from neglecting inertia effects, and from omitting the force–velocity relation (i. e., a purely elastic material model is used).

3.3.1 Skeletal Muscle Force Enhancement at Tetanic Stimulation

First, stretch simulations with different starting lengths, i. e., \(\lambda _\mathrm{f}^\mathrm{init}=1.0\), 1.1, 1.2, 1.3, and 1.4, were performed. Stretching the muscle while maintaining the level of activation resulted in enhanced muscle forces due to actin–titin binding compared to the isometric force–stretch relation. Figure 5 depicts the nominal stresses derived from the reaction forces in fibre direction for the five initial muscle lengths described above (red lines). Note that due to neglecting the force–velocity relation, the enhancement in muscle forces above the level of isometric forces can be completely attributed to actin–titin interactions. Additionally, Fig. 5 depicts the passive, active, and total isometric stress–stretch relations (black lines). All stresses have been normalised with respect to the maximum isometric active stress of the muscle. Despite different muscle starting lengths, the simulated stress-stretch responses were, after an initial transient phase, almost linear and nearly parallel to each other.

Fig. 5
figure 5

Simulation of active stretches (red) for different muscle lengths at activation (\(\lambda _\mathrm{f}^\mathrm{init}\in \{1.0, 1.1, 1.2, 1.3, 1.4\}\)). Additionally, the isometric stress-stretch relations, as determined from the continuum-mechanical model, are depicted (black). Because there is no serial elasticity, the active stresses are obtained in a straightforward manner by subtracting the passive stresses from the total isometric stresses. The total stress during the stretch (red) is characterised by an initial transient phase, which stems from the nonlinear elasticity of the distal Ig region

Full size image

For the simulation in which the muscle has initially been stretched to \(\lambda _\mathrm{f}^\mathrm{init}=1.1\), Fig. 6 displays the cubic muscle specimen including the 36 embedded computational muscle fibres. The muscle is shown at three different muscle lengths, i. e., at \(\lambda _\mathrm{f}=1.132\) (left), \(\lambda _\mathrm{f}=1.292\) (middle), and \(\lambda _\mathrm{f}=1.452\) (right). In each muscle, the thick black lines refer to the undeformed reference configuration and the thin black lines indicate the deformed configuration of the muscle specimen. At each computational half-sarcomere, the top row depicts the calcium concentration, i. e., Ca\(^{2+}\), the middle row indicates the stresses induced by titin in the unbound state, i. e., \(\theta _{\mathrm{Titin}}^\mathrm{unbound}\), and the bottom row shows the stresses induced by titin in the bound state, i. e., \(\theta _{\mathrm{Titin}}^\mathrm{bound}\).

Fig. 6
figure 6

For three different muscle lengths, the 3D cube-shaped muscle geometry and the embedded 1D muscle fibres are depicted. The top row shows the calcium concentration, Ca\(^{2+}\) in [\(\upmu \)M], the middle row shows the stresses induced by unbound titin filaments, \(\theta _{\mathrm{Titin}}^\mathrm{unbound}\), and the bottom row shows the stresses induced by bound titin filaments, \(\theta _{\mathrm{Titin}}^\mathrm{bound}\), at each computational half-sarcomere

Full size image

The stretches depicted in Fig. 6 have been selected such that a calcium spike propagating from the neuromuscular junction at the middle of the muscle fibres towards their ends, can be observed at each stretch. Unlike the calcium concentration, the activation parameters, \(\gamma \), are due to the tetanic stimulation almost uniformly equal to 1 during the entire active stretch (result not shown). One can conclude from \(\gamma =1\) and (4) that \(\theta _\mathrm{Titin}=\theta _\mathrm{Titin}^\mathrm{bound}\) holds for the results depicted in Fig. 6.

3.3.2 Force Enhancement Simulations at Submaximal Stimulation Levels

In order to demonstrate the effect of submaximal activations, simulations are conducted for different stimulation frequencies. The muscle is passively stretched to \(\lambda _\mathrm{f}^\mathrm{init}=1.1\), before it is tetanically stimulated. Then, 500 ms after the start of the stimulation, the muscle is stretched with a constant velocity of \(v=1\) cm/s.

In the isometric phase, the reaction force in muscle fibre direction increases with the stimulation frequency (Fig. 7). At 50 Hz stimulation (blue curve in Fig. 7) the muscle generates an almost fused contraction (\(\gamma \approx 1\)). Stretching the fully activated muscle results in an almost linear increase in the muscle force. For non-tetanic stimulations, i. e. stimulation frequencies \(f_\mathrm{stim}<50\) Hz, the force traces vary with respect to the stimulation frequency. Without actin–titin interactions, the model would predict decreasing total stresses due to the descending limb of the force–length relation.

Fig. 7
figure 7

Simulations with different stimulation frequencies (5, 10, 20, 50 Hz). The muscle specimen is first passively stretched to \(\lambda _\mathrm{f}^\mathrm{init}=1.1\) (time \(t=0\)) and then stimulated under fixed-length conditions for 500 ms. After 500 ms the sample is actively stretched with a constant velocity of \(v=1\) cm/s. The nominal stresses derived from the total reaction forces in muscle fibre direction are shown

Full size image

3.3.3 Influence of Titin’s Cross-Fibre Component

To investigate the influence of the titin XF component on the total mechanical behaviour of the muscle, the titin XF model is included or omitted (\(\varvec{S}_\mathrm{Titin,XF}=0\)) in the simulations. The uniaxial tests presented in the previous sections are not suitable to reveal the differences between these two models, since XF stress components do not significantly influence the stresses in fibre direction. Therefore, biaxial tests are employed. Hence, the cube-shaped model introduced at the beginning of Sect. 3.3 is modified in such a way that, in addition to the two surfaces normal to the fibre direction (direction \(\varvec{a}_0\)), two parallel surfaces that are parallel to the fibre direction are constrained. In the third direction, symmetric boundary conditions are applied at one side of the specimen. First, the muscle specimen is passively stretched in both the muscle fibre direction and the constrained XF direction. After stimulating the muscle under fixed-length conditions with 50 Hz for 500 ms, the muscle is actively stretched in fibre direction.

The resulting nominal stresses in fibre direction (Normalised Nominal Stress, top) and XF direction (Normalised XF Nominal Stress, bottom) are shown in Fig. 8 for different initial stretches in fibre direction (\(\lambda _\mathrm{f}^\mathrm{init}=1\) left; \(\lambda _\mathrm{f}^\mathrm{init}=1.2\) right) and XF directions (\(\lambda _\mathrm{XF}=1.0, 1.1, 1.2\), and 1.3). The stresses without the titin XF model are shown as coloured lines, while their counterparts with the XF model are shown as dashed black lines.

Fig. 8
figure 8

Comparison between the reaction forces for simulations with and without the cross-fibre model in fibre direction (top) and XF direction (bottom). Before the muscle was stimulated, it was stretched to an initial length of \(\lambda _\mathrm{f}^\mathrm{init}=1.0\) (left) or 1.2 (right)

Full size image

In fibre direction, the relative difference between the reaction forces of the two models is less than 1 %. In the XF direction, the difference is less than 5 %.

4 Discussion

4.1 Comparison with Experimental Findings and Functional Relevance of Force Enhancement

The continuum-mechanical muscle model is able to reproduce a series of experimental findings. As observed by Abbott and Aubert (1952), model simulations yielded enhanced muscle forces (forces that exceeded the maximum isometric force) during and after active stretch. Binding of titin to actin during activation reduces the titin length dramatically. This leads to increased titin forces when the muscle is stretched, and thus to force enhancement. Simulated force enhancements were up to 40 % of the maximum isometric stress for stretches of about 30 % (Fig. 5). This corresponds to the upper range of experimental observations on muscles (Morgan et al. 2000; Lee and Herzog 2002; Abbott and Aubert 1952; Siebert et al. 2015). As the proposed actin–titin binding needs no additional energy (ATP), the mechanism enables the muscle to withstand high forces during lengthening contractions contributing to low metabolic cost of lengthening contractions (e. g.Hill 1938; Curtin and Davies 1975). A quantitative prediction of the metabolic cost associated with a certain contraction, however, is not possible with the current model, as it does not include a description of ATP hydrolysis.

The model predicts almost linear force–stretch responses for lengthening contractions starting from different muscle lengths (Fig. 5). This model prediction is in agreement with eccentric experiments performed on rat gastrocnemius medialis muscle (Till et al. 2008, 2010). In these experiments, the muscle responded with constant stiffness to active stretches, independent of its starting length (i. e. the starting position on the muscle’s force–length relation). This behaviour may be functionally relevant regarding the reduction of neural effort during eccentric muscle stretches (e. g. in cyclic locomotion), as the muscle reacts like a linear spring. Reduced central nervous system control is an important design criterion for neuro-muscular systems during cyclical locomotion (Blickhan et al. 2007) and a linear dependence of muscle force might reduce the neural effort (Müller et al. 2012; Häufle et al. 2014). Titin-induced force enhancement might also improve the muscle’s efficiency in cyclic stretch-shortening situations by temporarily storing and subsequently releasing elastic strain energy. In addition to energy savings in series (Biewener and Baudinette 1995), this would be a further possibility of energy recovery during cyclical locomotion.

The stiffness of bound titin increases with increasing initial length in our model (Fig. 5) leading to increased absolute force enhancement with increasing initial length. This behaviour is partly in agreement and partly in contradiction with experimental data. While force enhancement on the ascending limb, the plateau, and the upper part of the descending limb of the active force–length relationship increased with initial length (Lee and Herzog 2008; Peterson et al. 2004; Herzog and Leonard 2002; Joumaa et al. 2008), for very long initial half-sarcomere lengths force enhancement was lower (Leonard and Herzog 2010). It is conceivable that increased passive tension in titin before activation leads to hampered actin–titin binding resulting in a lower fraction of bound titin. Alternatively, the titin model by Nishikawa et al. (2012) predicts decreased stiffness of titin with decreasing active force. However, this model would have difficulty in predicting the mentioned increasing force enhancement in other ranges of the force–length relationship (Lee and Herzog 2008).

As it is well known from experiments, the multi-scale continuum-mechanical model predicts the complete fusion of the twitch force under tetanic stimulation (Fig. 7). At the same stimulation frequency, the model predicts that unfused peaks of high amplitude occur in the local calcium concentration (Fig. 6), which is in agreement with the experimental data of Baylor and Hollingworth (2003). Due to the fact that modelled actin–titin binding scales with activation, absolute force enhancement decreases with decreasing muscle activation (Fig. 7), which is in accordance with experiments on maximally (stimulation frequency 80 Hz) and submaximally (stimulation frequency 30 Hz) stimulated rat medial gastrocnemius muscle (Meijer 2002).

4.2 Model Implications and Limitations

Continuum-mechanical muscle models can potentially predict the 3D geometrical deformation of the muscle and the muscle’s influence on other muscle forces (Maas et al. 2001; Yucesoy et al. 2007; Blemker et al. 2005). So far, the substantial effects of force enhancement have largely been ignored in continuum-mechanical muscle models. Here, we present the first continuum-mechanical muscle model that comprises physiologically motivated mechanisms describing actin–myosin (Huxley 1957) and actin–titin interactions (Noble 1992; Kulke et al. 2001; Bianco et al. 2007; Kellermayer and Granzier 1996) during isometric contractions and active stretch. These mechanisms work in parallel; the sliding filament (Huxley and Niedergerke 1954; Huxley and Hanson 1954) and cross-bridge (Huxley 1957) theories of muscle contraction remain unchanged.

The implemented sticky-spring mechanism (Rode et al. 2009) is one of three (Nishikawa et al. 2012; Schappacher-Tilp et al. 2015) biophysical models published so far aiming at modelling actin–titin interactions. All three models lead to increased titin forces during active stretch due to actin–titin binding. Binding of titin to actin filaments may be facilitated by actin rotation (Nishikawa et al. 2012). When stretching the activated muscle on the descending limb of the active force–length relationship, the models by  Schappacher-Tilp et al. (2015) and by Nishikawa et al. (2012) transmit the accumulating titin tension via one actin–titin binding site. In contrast, the model of Rode et al. (2009) transmits this force via multiple binding sites simultaneously, developing a force gradient in the PEVK region during active stretch. This seems to be important due to the limited average PEVK-actin binding force of 8 pN (Bianco et al. 2007). Stretching activated myofibrils to lengths of no actin–myosin overlap, Leonard and Herzog (2010) reported force enhancement of 200 % of the maximal isometric force, and if this force is carried by titin then this force exceeds 8 pN per titin by an order of magnitude (Rode et al. 2009). Moreover, the titin model by Rode et al. (2009) already includes a mathematical description of the behaviour of titin during active shortening which can be seamlessly implemented in the presented 3D model in the future. For these and other reasons (Siebert and Rode 2014) we chose to implement the biophysical model of Rode et al. (2009).

The continuum-mechanical muscle model employed in this work, is the multi-scale chemo-electro-mechanical model of Heidlauf and Röhrle (2013). This model unifies a biophysical description of the excitation–contraction coupling at the half-sarcomere level (Shorten et al. 2007), the subsequent activation of sarcomeres within a muscle fibre through propagating action potentials (Heidlauf and Röhrle 2014; Mordhorst et al. 2015), and a description of the transversely isotropic and incompressible behaviour of the muscle tissue. The results obtained with the 3D continuum-mechanical model are in agreement with simulations of the 1D ‘sticky-spring’ model of Rode et al. (2009). Thus, the half-sarcomere-based titin model of Rode et al. (2009) can be transferred to the macroscopic whole muscle level.

Force predictions of our generic multi-scale model depend, for example, on the chosen force–length relationship and the model and data describing the titin properties, which change from muscle to muscle (even in the same species, Prado et al. 2005). We used the force–length relationship of a frog muscle by Gordon et al. (1966), titin data from rabbit psoas (Linke et al. 1998a, b), and the titin model of Rode et al. (2009). By our model’s modular organisation, these properties can be straightforwardly replaced if necessary. Predicted steady-state force enhancements are of the right order of magnitude. If the goal is to arrive at realistic force predictions for a specific muscle, it is important to implement the corresponding properties in the model.

Some doubt remains concerning the extensibility of the distal immunoglobulin region of the titin filament (Fig. 1). While some researchers report an essentially non-extensible distal Ig region (e. g. Tskhovrebova and Trinick 2003; Linke and Krüger 2010), others dispute that notion (Bianco et al. 2015) based on single titin molecule studies. We derived the force–elongation data of this region from experimental data obtained from isolated titin filaments (Linke et al. 1998a, b). It should however be noted that the predictions of the applied titin model remain relatively similar when a more stiff distal Ig region is assumed because a large portion of the total compliance stems from the bound but extending PEVK region (Rode et al. 2009).

While neglecting the increase in the titin stiffness by about 25 % in the presence of calcium (cf. Labeit et al. 2003), the presented model accounts for the more important effect of actin–titin binding. Unfortunately, the binding and dissociation rates of titin to actin are currently unknown (Schappacher-Tilp et al. 2015). Once these parameters have been determined, this process can be directly and biophysically modelled within the presented muscle model due to the fact that the multi-scale chemo-electro-mechanical model includes a description of calcium dynamics (Baylor and Hollingworth 1998) within the half-sarcomere model(Shorten et al. 2007). Hence, including the titin model within the multi-scale model provides an advantage over linking it to a purely continuum-mechanical muscle model that does not include a description of calcium dynamics. For lack of data on binding rates a simplified approach is used, which assumes that the binding kinetic of titin’s PEVK region to the thin filament is similar to the binding kinetic of the myosin heads to the thin filaments. Following this, the activation parameter is used to interpolate between the stresses induced by the unbound and bound titin filaments (cf. Eq. 4). This simplification, however, imposes an important limitation on the current model. Passive force enhancement is observed in real muscle after deactivation, when the calcium concentration in the myoplasm returned to its resting level (Joumaa et al. 2007). The existence of passive force enhancement suggests that the dissociation rate of titin from actin is significantly lower than the dissociation rate of myosin from actin, at least when titin is tensed. Details on the binding and dissociation kinetics are needed to include these effects in the model.

In contrast to one-dimensional models (Rode et al. 2009; Nishikawa et al. 2012; Schappacher-Tilp et al. 2015) and the only existing continuum-mechanical model of force enhancement (Lemos et al. 2001), the presented chemo-electro-mechanical muscle model also predicts titin-induced stresses in the muscle’s XF directions. As expected, the additional term describing titin stresses in XF directions provides additional stiffness, which results in higher reaction forces in XF direction for all simulations (Fig. 8). The fact that the additional stiffness in XF direction is relatively small (less than 5 %) can be explained by the pointed angle between the muscle fibre direction and the direction of the titin filaments. This applies even when titin’s PEVK region is bound to the actin filament. The influence of the additional stiffness in XF direction on the stress in fibre direction is negligibly small (less than 1 %). This is expected, as the fibre and the XF directions remain perpendicular during the deformation, and hence, additional stress components in XF directions do not influence the reaction forces in the fibre direction.

For the derivation of the XF components, six titin filaments per thick filament were assumed. There is some indication, however, that there are only four titin filaments per thick filament (Zou et al. 2006). Assuming four titin filaments per thick filament does not significantly change the model. As a result, even lower XF titin stresses are expected. A stronger influence on the contractile forces is expected from considering XF components for the active stress, as suggested e. g. by Usyk et al. (2000) for the myocardium. These terms, however, require additional material parameters, which are not available from the literature, neither for heart nor for skeletal muscle. In contrast to this, the terms describing the XF components of the titin stress within this work are completely derived from geometrical considerations and do not require additional material parameters.

To exclude effects resulting from complex geometries (Zuurbier and Huijing 1992; Blemker et al. 2005), a cube was used for the analysis. As the presented multi-scale model is based on the finite element method, which is appreciated by its users for its geometric flexibility, modelling a more complex geometry is feasible (Heidlauf and Röhrle 2013; Mordhorst et al. 2015). The effect of force enhancement based on actin–titin interaction, however, can be similarly well appreciated on a simple geometry, without the problem of separating these effects from effects induced through a complex geometry. Future studies investigating muscle function in dynamic situations, however, should account for complex muscle geometries as well as the force–velocity relation.

4.3 Conclusion

This work presented a biophysically based continuum-mechanical model that, in addition to actin–myosin interactions, also comprises actin–titin interactions that contribute to force in a semi-active way. Representative simulations revealed that the model is capable of simulating a number of phenomena related to force enhancement during and after stretch under maximal and submaximal stimulations. While the model predicted significantly higher stresses in the muscle fibre direction, the titin-induced stress contributions in the cross-fibre direction were rather small. This may, however, change when considering more realistic muscle architectures. The inclusion of actin–titin interactions in our continuum-mechanical model provides the basis for such investigations. For example, the model can be used to assess transverse forces exerted by the muscle to adjacent structures like joints, bones, or prostheses.