A mechanical model of the half-sarcomere which includes the contribution of titin

Abstract

The evidence, in both resting and active muscle, for the presence of an I-band spring element like titin that anchors the Z line to the end of the thick filament did not yet produce a proper theoretical treatment in a complete model of the half-sarcomere. The textbook model developed by A. F. Huxley and his collaborators in 1981, which provides that the half-sarcomere (hs) compliance is due to the contribution of the compliances of the thin and thick filaments and actin-attached myosin motors, predicts that at any sarcomere length (SL) the absence of attached motors results in an infinite half-sarcomere compliance, in contrast with the observations. Growing evidence for the presence of a titin-like I-band spring urges the 1981 model to be implemented to include the contribution of this element in the mechanical model of the half-sarcomere. The model described here represents a tool for the interpretation of measurements of hs stiffness at increasing SL, which is important either in relation to the mechanism of stabilisation of SL against the consequence of sarcomere inhomogeneity in active force generation, or for investigations on the role of titin as mechano-sensor in thick filament regulation. Moreover the model opens the possibility for understanding the functional differences related to the titin isoform of various muscle types and the mechanism by which mutations in titin gene lead to myopathies.

Introduction

In the striated (skeletal and cardiac) muscle, the contractile proteins myosin and actin are organized respectively in well-ordered thick and thin filaments in the sarcomere, the ca 2 µm long structural unit of muscle in which bipolar arrays of myosin II motors emerging from the thick filaments overlap with the thin filaments originating from the Z line bounding the sarcomere. Force and shortening during muscle contraction are due to cyclical ATP-driven interactions of the globular portion (the head) of the motors with the nearby actin monomers in the thin filaments. In each half-sarcomere (hs), the myosin motors are mechanically coupled as parallel force generators via their attachment to the thick filament, constituting, together with the interdigitating thin filaments and other cytoskeleton and regulatory proteins, the basic functional unit of muscle (Fig. 1). Stiffness measurements at the level of the half-sarcomere directly inform on the stiffness and the number of actin-attached motors (cross-bridges) under the condition that their elasticity is linear and they are the only source of compliance in the half-sarcomere (Huxley and Simmons 1971; Ford et al. 1977). In contrast to the second of these assumptions, X-ray diffraction experiments indicated that thin and thick filaments under stress (Huxley et al. 1994, 2006; Wakabayashi et al. 1994; Reconditi et al. 2004; Piazzesi et al. 2007) extend by 0.23–0.26% for a force change equivalent to T₀, the maximal force developed in an isometric tetanic contraction. Under these condition and provided that both the cross-bridge stiffness and the stiffnesses of the actin and myosin filaments are constant independent of force (Ford et al. 1977; Brunello et al. 2014), the contribution of actin-attached cross-bridges and myofilaments to half-sarcomere compliance (C_hs) can be defined, in the framework of the model developed by Ford and colleagues (Ford et al. 1981; FHS1981 hereafter). The arguments recently risen against the constraint that the sarcomere elements have linear elasticity, either related to cross-bridges (Kaya and Higuchi 2010) or to myofilaments (Ma et al. 2018), cannot sustain a rigorous analysis of the different conditions in which the measurements have been done: for the cross bridges, the nonlinear elasticity observed in vitro is likely related the loss of the native filament lattice; for the myosin filament the nonlinear elasticity reported from measurements of spacing changes in X-ray myosin based meridional reflections in the active muscle is the results of the inadequate time resolution of the measurement that makes the compliance of the myosin filament to be contaminated by the ten times larger activation-dependent structural changes (Linari et al. 2015; Reconditi et al. 2019).

Fig. 1

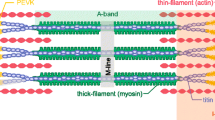
Schematic representation of the half-sarcomere protein assembly. On the thin filament (yellow, formed by the actin monomer polymerization in a double helix with a period of 73 nm) are shown the regulatory proteins tropomyosin (red) and troponin complex (light and dark gray and brown). On the thick filament (dark blue) the S1 globular head domains of myosin (orange) emerge with a three stranded helical symmetry with 43 nm periodicity. The Myosin Binding Protein C (MyBP-C, blue) lies on the proximal 1/3 of the thick filament with the C-terminus and extends to thin filament with the N-terminus. Titin (pink) in the I-band connects the Z line at the end of the sarcomere (green) to the tip of the thick filament and in the A-band runs on the surface of the thick filament up to the M-line at the centre of the sarcomere. To see this figure in color, go online

Under the constraint that the myofilament and cross-bridges have linear elasticities and assuming that the compliance of the array of cross-bridges is not smaller than the cumulative compliance of the actin and myosin filaments, C_hs can be calculated by the sum of the equivalent compliances of the three elements (see Methods). The simple useful formulation of this equation is:

$${C_{{\text{hs}}}}={C_{\text{f}}}+\frac{1}{{{k_{\text{c}}}{{{\upzeta}}}}},$$

(1)

where C_f is the equivalent filament compliance, k_c is the stiffness per unit length of the array of the cross-bridges and is the length of overlap of thin filament with the cross-bridges array in each half-sarcomere.

More recently, hs stiffness measurements by means of fast (4 kHz) length oscillations applied to single muscle fibres during the development of an isometric tetanus have shown that at low forces, when the number of attached motors is relatively low (Brunello et al. 2006), a significant contribution to emerges from another elastic element the compliance of which, C_p, is functionally in parallel with that of the attached motors (Colombini et al. 2010; Fusi et al. 2014, 2017). The value of C_p was somewhat controversial depending on the protocols used to estimate it. When stiffness measurements were made at the level of a selected population of sarcomeres in an isometrically contracting single frog fibre at 4 °C (plateau force T₀ ~ 150 kPa), it resulted to be 200–300 nm/MPa (Fusi et al. 2014, 2017), that is ~ 20 times larger than the compliance of the array of motors attached at T₀ (11.5 nm/MPa). Such a relatively large compliance of the parallel elasticity explains why its contribution emerges only at low forces, when the number of motors is low and the stiffness of the motor array becomes comparable to that of the parallel element. To consider the contribution of this element to the C_hs requires only a slight modification of the FHS1981 model. Namely, C_hs can be interpreted as the series of the filament compliance, C_f, and the compliance resulting from the parallel arrangement of the force-generating cross-bridges and the new element:

$${C_{{\text{hs}}}}={C_{\text{f}}}+\frac{{{C_p}}}{{1+{C_p}{k_{\text{c}}}{{{\upzeta}}}}}.$$

(2)

This element could be associated to the presence of links connecting the thin and thick filaments in the A-band, like either a fraction of weakly bound, no-force generating motors (Colombini et al. 2010; Fusi et al. 2017), or the thick filament accessory protein myosin-binding protein C (MyBP-C) (Fig. 1), which has shown to undergo dynamic interactions with the thin filament (Offer et al. 1973; Moos 1981; Yamamoto 1986; Squire et al. 2004; Luther et al. 2011; Rybakova et al. 2011; Pfuhl and Gautel 2012). Alternatively, a similar role of parallel elasticity could be played by an I-band spring, like the gigantic protein titin that spans the whole half-sarcomere, connecting the Z line at the end of the sarcomere with the tip of the thick filament and running bound to the surface of the thick filament up to the M-line at the centre of the sarcomere (Fig. 1; Maruyama et al. 1977; Wang et al. 1979; Fürst et al. 1988; Linke et al. 2002; Granzier and Labeit 2004). Titin, as an I-band spring, is the only element able to transmit the stress to thick filament also in the resting sarcomere, when no motors are attached to actin, which explains the passive force developed by a resting sarcomere when it is stretched. In frog skeletal muscle, this happens for sarcomere length (SL) > 2.50 µm and reaches ca 0.7 T₀ for SL ~ 3.4 µm (Reconditi et al. 2014). In this respect it must be noted that the cord compliance that can be calculated from the passive force—SL relation is (0.45 µm/(0.7⋅150 kPa) =) 4300 nm/MPa per hs, ~ 20 times larger than C_p determined at full overlap (200–300 nm/MPa; Fusi et al. 2014, 2017).

If the contribution to C_hs of the elasticity in parallel with the motor array were due to either weakly bound cross-bridges or MyBP-C links, the stiffness of the active muscle should reduce at long SL with the reduction of filament overlap. A more complex behaviour is expected in the case of a titin-like I-band spring, as in this case the stiffness of the spring may vary with the large changes in its length accompanying the changes in SL. In this respect it is worth to note that, using large stretches, Bagni and co-workers (Bagni et al. 2002) identified an elastic element in parallel with the cross-bridges, defined as a ‘static stiffness’, which rises abruptly upon activation independent of motor attachment and increases with the increase of sarcomere length up to 2.8 µm. Even if the large stretch is a somewhat less direct mean for estimating stiffness changes, as the attached motors are brought into a regime which may imply also rapid detachment–attachment kinetics (Lombardi and Piazzesi 1990), the results are intriguing and suggestive of a role of titin in active contraction. A further support to this idea derives from the finding that in vitro titin stiffness increases in the presence of Ca²⁺ (Labeit et al. 2003). Recent experiments that overcome the limits in the work of Bagni et al. (2002) by measuring the SL-dependence of C_hs with small 4 kHz oscillation during isometric force development indeed confirm the role of titin showing that the stiffness of the additional elasticity increases with the increase in SL (Powers et al. 2017).

The finding that a titin-like I-band spring has an instantaneous stiffness one–two orders of magnitude larger than the “static” cord stiffness calculated from the passive force-SL relation may find a molecular explanation in the in vitro mechanical studies that allowed the definition of the load dependent structural dynamics of titin (Mártonfalvi et al. 2014; Rivas-Pardo et al. 2016). According to those experiments, titin extensibility is modulated in time by the load-dependent equilibrium between folding-unfolding of its immunoglobulin (Ig) domains. This finding suggests that the role of titin as I-band spring in parallel to the array of motors can be much more relevant than that of a static elastic element that adds its contribution to force in the extreme condition of a weak half-sarcomere which has undergone a large stretch (Rassier et al. 2005, 2015; Cornachione et al. 2016). Rather, titin may work as a dynamic spring that provides a substantial contribution of force to prevent a weak half-sarcomere to give during contraction.

FHS 1981 model assumes that, at any SL, the absence of cross-bridges results in an infinite half sarcomere compliance. In this respect the evidence of an I-band spring element like titin that anchors the Z line to the end of the thick filament and, at long but still physiological SL, provides a dynamic stiffness that can influence cross-bridge action in contracting muscle, makes FHS 1981 model no longer valid and urges its implementation. The attempts to consider the effect of titin on the dynamics of the half-sarcomere done so far have used the simplified assumption that titin spring is in parallel with the force generating cross-bridges (Rice et al. 2008; Campbell et al. 2018). However, an I-band spring as titin is neither in parallel (sharing the same length change) nor in series (sharing the same force change) with any other element in the hs.

Here we integrate the FHS1981 model to include for the first time the contribution of an I-band spring to the half sarcomere compliance in its proper configuration. The model represents a tool for the interpretation of measurements of hs stiffness at increasing SL, which is important either in relation to the mechanism of stabilisation of SL against the consequence of sarcomere inhomogeneity in active force generation, or for investigations on the role of titin as mechano-sensor in thick filament regulation (Linari et al. 2015; Reconditi et al. 2017; Piazzesi et al. 2018). Moreover, the model opens the possibility for understanding the functional differences related to titin isoforms and the mechanism by which mutations in titin gene lead to myopathies.

Methods

In the FHS 1981 model the compliance of the half sarcomere is calculated as:

$$\begin{aligned} {C_{{\text{hs}}}} & ={c_{\text{A}}}\left( {{l_{\text{A}}} - {{{\upzeta}}}} \right)+{c_{\text{M}}}\left( {{l_{\text{M}}} - {{{\upzeta}}}} \right) \\ & \quad +\frac{{{c_{\text{A}}}{c_{\text{M}}}}}{{{c_{\text{A}}}+{c_{\text{M}}}}}{{{\upzeta}+}}\frac{{{c_{{\text{A}}+}}{c_{\text{M}}}}}{{2\mu }}\left\{ {\coth \left( {\frac{{\mu {{{\upzeta}}}}}{2}} \right)+{{\left( {\frac{{{c_{\text{A}}} - {c_{\text{M}}}}}{{{c_{\text{A}}}+{c_{\text{M}}}}}} \right)}^2}\tanh \left( {\frac{{\mu {{{\upzeta}}}}}{2}} \right)} \right\}+{C_{\text{Z}}}, \\ \end{aligned}$$

(3)

where c_A and c_M are the compliances per unit length of the thin and thick filaments respectively, k_c is the stiffness per unit length of the array of the cross-bridges, C_Z is the compliance of the Z line, l_A and l_M are the length of the thin and thick filament respectively, ${{{\upzeta}}}$ is the length of overlap of thin and thick filaments in each half-sarcomere and $\mu ~\left( {={{({k_{\text{c}}}\left( {{c_{\text{A}}}+{c_{\text{M}}}} \right))}^{\frac{1}{2}}}} \right)$ is a parameter that increases as the cumulative compliance of the filaments increases relative to that of the motor array (1/k_c).

Provided that $\mu {{{\upzeta}}}/2$ is not too large, which is equivalent to assume that the compliance of the array of cross-bridges is not smaller than the cumulative compliance of the actin and myosin filaments, Eq. 1 simplifies to:

$${C_{{\text{hs}}}}={c_{\text{A}}}\left( {{l_{\text{A}}} - \frac{2}{3}{{{\upzeta}}}} \right)+{c_{\text{M}}}\left( {{l_{\text{M}}} - \frac{2}{3}{{{\upzeta}}}} \right)+\frac{1}{{{k_{\text{c}}}{{{\upzeta}}}}}+{C_{\text{Z}}}.$$

(4)

Given the small axial extension of the Z line (~ 30–50 nm in the fast skeletal muscles; Luther 2009), its contribution C_Z to C_hs will be neglected hereafter. Estimates of c_A, c_M and k_c obtained from both X-ray diffraction and mechanical measurements (Huxley et al. 1994, 2006; Wakabayashi et al. 1994; Reconditi et al. 2004; Piazzesi et al. 2007; Fusi et al. 2014; Brunello et al. 2014) indicate that the condition $\mu {{{\upzeta}}}/2$ < 1 is fulfilled. Consequently, according to the model, ${C_{{\text{hs}}}}$ can be considered functionally as the series of two compliances: the myofilament compliance, $~{C_{\text{f}}}={c_{\text{A}}}\left( {{l_{\text{A}}} - \frac{2}{3}{{{\upzeta}}}} \right)+{c_{\text{M}}}\left( {{l_{\text{M}}} - \frac{2}{3}{{{\upzeta}}}} \right)$ and the motor compliance, $1/{k_{\text{c}}}{{{\upzeta}}}$.

According to the model of FHS1981 (Fig. 2), an external force T applied to the hs is entirely born by the thick and thin filaments in the regions that do not overlap and is shared between the two filaments in the overlap region, where the cross-bridges transfer force between the two filaments. At any axial position the force born by the thin filament, T_A, and that born by the thick filament, T_M, add to give the total force T applied to the hs. Taking ξ as the axial distance measured from the centre of the overlap zone, and positive toward the Z line, the difference dT_A(ξ) = T_A(ξ + d ξ) − T_A(ξ) in the force born by the thin filament along a small axial distance dξ at the coordinate ξ is k_c dξ x(ξ), where k_c dξ is the stiffness of the small cross-bridge segment dξ and x(ξ) is the distortion of the cross-bridge array at that coordinate, taken positive for stretches (Fig. 3, upper panel). In the same way, for the thick filament dT_M(ξ) = − k_cdξ x(ξ), consistent with the fact that force is transferred between the two filaments through the cross-bridge array and, in each point along the hs, is the same and shared between the filaments in the overlap region. This leads to Eq. A1 of FHS1981:

Fig. 2

(adapted from Ford et al. 1981)

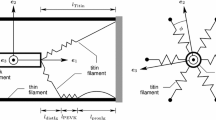
Diagram indicating the arrangement of the thick and thin filaments and the cross-bridges in the half-sarcomere. The half-thick filament (length l_M; black, where myosin motors are present; dashed, bare zone, where no myosin motors are present) extends from the M line, at the centre of the sarcomere. The grey band represents the cross-bridges in the region (length ζ) that overlaps with the thin filament (white; length l_A) that extends from the Z line. Motors attaching to the thin filament (cross-bridges) contribute to the compliance of the half-sarcomere. ξ is the axial coordinate, with the origin in the middle of the overlap region

Fig. 3

Schematic of the half sarcomere strained by an external force T. x_A and x_B are the cross-bridge distortion at the point A and B along the half-sarcomeres, at coordinate ξ = -ζ/2 and ξ = +ζ/2 respectively. Upper panel: the expanded region around the generic coordinate ξ shows that the force in a small region dξ is transmitted between the thick and thin filament through a distortion $x({{{\upxi})}}$ of the cross-bridge array segment ${{\text{d}{\upxi}}}$ wide and ${k_{\text{c}}}{{\text{d}{\upxi}}}$ stiff. Lower panel: in the expanded region is now indicated the different distortion x of the cross-bridge array over a small axial distance ${{\text{d}}{\upxi}}$

$$\frac{{{\text{d}}{T_{\text{A}}}}}{{{{\text{d}{\upxi}}}}}=-\frac{{\text{d}{T_{\text{M}}}}}{{{{\text{d}{\upxi}}}}}={k_{\text{c}}}x\left({{{\upxi}}} \right).$$

(5)

Over a small axial distance ${{\text{d}{\upxi},}}$ the distortion of the cross-bridges differs by a quantity ${\text{d}}x\left( {{{\upxi}}} \right)=x\left( {{{\upxi}}}+{{\text{d}{\upxi}}} \right) - x\left( {{{\upxi}}} \right)$ that results from the different strain in the thin and thick filaments (Fig. 3, lower panel), so that:

$${\text{d}}x\left( {{{\upxi}}} \right)={T_{\text{A}}}\left( {{{\upxi}}} \right)~{c_{\text{A}}}{{\text{d}{\upxi}}} - {T_{\text{M}}}\left( {{{\upxi}}} \right)~{c_{\text{M}}}{{\text{d}{\upxi},}}$$

(6)

and thus:

$${\text{d}}x/{{\text{d}{\upxi}}}={T_{\text{A}}}\left( {{{\upxi}}} \right){c_{\text{A}}} - {T_{\text{M}}}\left( {{{\upxi}}} \right){c_{\text{M}}}=\left( {{c_{\text{A}}}+{c_{\text{M}}}} \right){T_{\text{A}}}\left( {{{\upxi}}} \right) - {c_{\text{M}}}T,$$

(7)

that is Eq. A2 of FHS1981.

Differentiating (7) and substituting for ${\text{d}}{T_{\text{A}}}/{{\text{d}{\upxi}}}$ from Eq. 5 gives

$${\text{d}^2}x/{\text{d}}{{{{\upxi}}}^2}={k_{\text{c}}}\left( {{c_{\text{A}}}+{c_{\text{M}}}} \right)x\left( {{{\upxi}}} \right),$$

(8)

whose solution (Eq. A4a of FHS81) is

$$x\left( {{{\upxi}}} \right)={x_0}\cosh \left( {\mu \left( {{{{\upxi}}} - {{{{\upxi}}}_0}} \right)} \right),$$

(9a)

where

$$\mu ={({k_{\text{c}}}\left( {{c_{\text{A}}}+{c_{\text{M}}}} \right))^{1/2}},$$

(9b)

The presence of an elastic link between the end of the thick filament and the Z line, which is the role played by titin in the I band, changes the boundary conditions with respect to FHS1981 model, and in turns affects the expressions for ${x_0}$ and ${\xi _0}$. In the original model, at point A (Fig. 2) ${{{\upxi}}}= - \frac{{{{\upzeta}}}}{2}$ and ${T_{\text{A}}}\left( { - \frac{{{{\upzeta}}}}{2}} \right)=0$ and at point B ${{{\upxi}}}=+\frac{{{{\upzeta}}}}{2}$ and ${T_{\text{M}}}\left( {+\frac{{{{\upzeta}}}}{2}} \right)=0$.

In the presence of titin link, the force on the thick filament at B, i.e. at the end of the filament, is the same as that, ${T_{\text{T}}}$, born by titin in the I band. This force, added to ${T_{\text{A}}}$ in the I band, gives the full force T found at the Z line:

$${T_{\text{T}}}+{T_{\text{A}}}=T.$$

(10)

Thus, to determine the boundary condition at B, one must first determine how T is distributed between thin filament and titin in the I band. To do that, we consider that under a force T on the hs, in the I band the strain of titin, ${c_{\text{T}}}\left( {{l_{\text{A}}} - {{{\upzeta}}}} \right){T_{\text{T}}}$, where c_T indicates the compliance of titin per unit length, must be the same as the strain of the thin filament, ${c_{\text{A}}}\left( {{l_{\text{A}}} - {{{\upzeta}}}} \right){T_{\text{A}}}$, plus the strain of the cross-bridges at B, ${x_{\text{B}}}$ (Fig. 4):

Fig. 4

Diagram of the half-sarcomere incorporating the titin (dark grey band, extending from the Z line to the edge of the thick filament). When an axial force is applied to the half-sarcomere, the strain of the titin is equal to the strain of the thin filament in the I band plus the strain of the cross-bridge array at B, ${x_{\text{B}}}$

$${c_{\text{T}}}\left( {{l_{\text{A}}} - {{{\upzeta}}}} \right){T_{\text{T}}}={c_{\text{A}}}\left( {{l_{\text{A}}} - {{{\upzeta}}}} \right){T_{\text{A}}}+{x_{\text{B}}}.$$

(11)

Equations 10, 11 provide the expression for ${T_{\text{A}}}$ and ${T_{\text{T}}}$ in the I band (and thus their values in B) as:

$${T_{\text{A}}}=\frac{{{c_{\text{T}}}}}{{{c_{\text{A}}}+{c_{\text{T}}}}}\left\{ {T - \frac{{{x_{\text{B}}}}}{{{c_{\text{T}}}\left( {{l_{\text{A}}} - {{{\upzeta}}}} \right)}}} \right\},$$

(12)

$${T_{\text{T}}}=T - {T_{\text{A}}}=\frac{{{c_{\text{A}}}}}{{{c_{\text{A}}}+{c_{\text{T}}}}}\left\{ {T+\frac{{{x_{\text{B}}}}}{{{c_{\text{A}}}\left( {{l_{\text{A}}} - {{{\upzeta}}}} \right)}}} \right\},$$

(13)

With this, the boundary conditions in A and B become respectively:

$$- {c_{\text{M}}}T={\left( {\frac{{\text{d}x}}{{\text{d}{\upxi}}}} \right)}_{\text{A}}=\mu {x_0}\sinh \left( {\mu \left( { - \frac{{{{\upzeta}}}}{2} - {{{\upxi_0}}}} \right)} \right),$$

(14)

and

$$+ c_{{\text{A}}} T_{{\text{A}}} - c_{{\text{M}}} T_{{\text{T}}} = \left( {\frac{{{\text{d}}x}}{{{\text{d}}{\upxi }}}} \right)_{B} = \mu x_{0} \sinh \left( {\mu \left( { + \frac{{\upzeta }}{2} - {\upxi_0}} \right)} \right),$$

(15)

By using Eq. 11 and Eq. 12, Eq. 15 can be rearranged to:

$$+ c_{A} \cdot T = \frac{{\left( {\frac{{\rm{d}x}}{{\rm{d}}\upxi }} \right)_{B} \left( {c_{{\text{A}}} + c_{{\text{T}}} } \right)\left( {l_{{\text{A}}} - {\upzeta }} \right) + x_{{\text{B}}} \left( {c_{{\text{A}}} + c_{{\text{M}}} } \right)}}{{\left( {c_{{\text{T}}} - c_{{\text{M}}} } \right)\left( {l_{A} - {\upzeta }} \right)}} = x_{0} \frac{{\mu \sinh \left( {\mu \left( { + \frac{{\upzeta }}{2} - {\upxi_0 }} \right)} \right)\left( {c_{{\text{A}}} + c_{{\text{T}}} } \right)\left( {l_{{\text{A}}} - {\upzeta }} \right) + \cosh \left( {\mu \left( { + \frac{\upzeta }{2} - \upxi_0} \right)} \right)\left( {c_{{\text{A}}} + c_{{\text{M}}} } \right)}}{{\left( {c_{{\text{T}}} - c_{{\text{M}}} } \right)\left( {l_{{\text{A}}} - \upzeta } \right)}}.$$

(16)

Equations 14, 16 are then equivalent to Eq. A5a and Eq. A5b of FHS1981 respectively.

Equating Eqs. 14, 16 for T leads to:

$$\tanh \left( {\mu {{{\upxi}0}}} \right)=\frac{{{c_{\text{M}}}\left( {{c_{\text{A}}}+{c_{\text{M}}}} \right)+\mu \left( {{l_{\text{A}}} - {{{\upzeta}}}} \right)\left[ {{c_{\text{T}}}\left( {{c_{\text{M}}} - {c_{\text{A}}}} \right)+2{c_{\text{M}}}{c_{\text{A}}}} \right]\tanh \left( {\mu \frac{{{{\upzeta}}}}{2}} \right)}}{{\mu \left( {{l_{\text{A}}} - {{{\upzeta}}}} \right){c_{\text{T}}}\left( {{c_{\text{A}}}+{c_{\text{M}}}} \right)+{c_{\text{M}}}\left( {{c_{\text{A}}}+{c_{\text{M}}}} \right)\tanh \left( {\mu \frac{{{{\upzeta}}}}{2}} \right)}}.$$

(17)

Subtracting Eq. 14 from Eq. 16 gives:

$${x_0}=\frac{{\left( {{c_{\text{T}}} - {c_{\text{M}}}} \right)\left( {{c_{\text{A}}}+{c_{\text{M}}}} \right)\left( {{l_{\text{A}}} - {{{\upzeta}}}} \right)T}}{{\mu \left( {{l_{\text{A}}} - {{{\upzeta}}}} \right)\left( {2{c_{\text{T}}}+{c_{\text{A}}} - {c_{\text{M}}}} \right)\sinh \left( {\mu \frac{{{{\upzeta}}}}{2}} \right)\cosh \left( {\mu {{{\upxi_0}}}} \right)+\left( {{c_{\text{A}}}+{c_{\text{M}}}} \right)\left[ {\cosh \left( {\mu \frac{{{{\upzeta}}}}{2}} \right)\cosh \left( {\mu {{{\upxi_0}}}} \right) - \sinh \left( {\mu \frac{{{{\upzeta}}}}{2}} \right)\sinh \left( {\mu {{{\upxi_0}}}} \right)} \right] - \mu \left( {{l_{\text{A}}} - {{{\upzeta}}}} \right)\left( {{c_{\text{A}}}+{c_{\text{M}}}} \right)\cosh \left( {\mu \frac{{{{\upzeta}}}}{2}} \right)\sinh \left( {\mu {{{\upxi_0}}}} \right)}}.$$

(18)

Equations 17, 18 are equivalent to Eqs. A6 and A7 of FHS1981 respectively.

The compliance per half sarcomere, C_hs, is obtained by calculating the total strain S_hs that an external force T induces on the half-sarcomere, and dividing the result by T, according to the relation C_hs= S_hs/T.

Going from the M line to the Z line there are four possible paths to calculate S_hs, and of course the results are the same.

The same path as in FHS1981 (where the possible paths are just two, since there is no titin link) is followed here. S_hs is given by the sum of the strain of the thick filament within the H zone (from the M line to the beginning of the overlap with the thin filament), the displacement of tip of the thin filament with respect to thick filament (or the strain of cross-bridges array at A, x_A), the extension of the thin filament in the overlap region, and the extension of thin filament within the I-band (Fig. 4):

$${S_{{\text{hs}}}}={c_{\text{M}}}\left( {{l_{\text{M}}} - {{{\upzeta}}}} \right)T+{x_{\text{A}}}+{c_{\text{A}}}\mathop \smallint \limits_{{ - \frac{{{{\upzeta}}}}{2}}}^{{+\frac{{{{\upzeta}}}}{2}}} {T_{\text{A}}}\left( {{{\upxi}}} \right){{\text{d}{\upxi}}}+{c_{\text{A}}}\left( {{l_{\text{A}}} - {{{\upzeta}}}} \right)\frac{{{c_{\text{T}}}}}{{{c_{\text{A}}}+{c_{\text{T}}}}}\left\{ {T - \frac{{{x_{\text{B}}}}}{{{c_{\text{T}}}\left( {{l_{\text{A}}} - {{{\upzeta}}}} \right)}}} \right\}.$$

(19)

Equation 15 is equivalent to Eq. A8 in FHS1981, and similarly, from Eq. 7:

$$T_{{\text{A}}} = \frac{{\frac{{{\text{d}}x}}{{{\text{d}}{\upxi }}} + c_{{\text{M}}} T}}{{c_{{\text{A}}} + c_{{\text{M}}} }},$$

and the integral in Eq. 19 becomes:

$$\mathop \smallint \limits_{{ - \frac{{{{\upzeta}}}}{2}}}^{{+\frac{{{{\upzeta}}}}{2}}} {T_{\text{A}}}\left( {{{\upxi}}} \right){{\text{d}{\upxi}}}=\frac{{{x_{\text{B}}} - {x_{\text{A}}}}}{{{c_{\text{A}}}+{c_{\text{M}}}}}+\frac{{{c_{\text{M}}}T}}{{{c_{\text{A}}}+{c_{\text{M}}}}}{{{\upzeta}}}{\text{.}}$$

(20)

Thus:

$$\begin{aligned} ~{C_{{\text{hs}}}} & ={c_{\text{M}}}\left( {{l_{\text{M}}} - {{{\upzeta}}}} \right)+\frac{{{x_{\text{A}}}}}{T}+\frac{{{c_{\text{A}}}}}{{{c_{\text{A}}}+{c_{\text{M}}}}}\frac{{{x_{\text{B}}} - {x_{\text{A}}}}}{T}+\frac{{{c_{\text{A}}}{c_{\text{M}}}}}{{{c_{\text{A}}}+{c_{\text{M}}}}}{{{\upzeta}}}+\left( {{l_{\text{A}}} - {{{\upzeta}}}} \right)\frac{{{c_{\text{A}}}{c_{\text{T}}}}}{{{c_{\text{A}}}+{c_{\text{T}}}}} - \frac{{{c_{\text{A}}}}}{{({c_{\text{A}}}+{c_{\text{T}}})}}\frac{{~{x_{\text{B}}}}}{T} \\ & ={c_{\text{M}}}\left( {{l_{\text{M}}} - {{{\upzeta}}}} \right)+\frac{{{c_{\text{A}}}{c_{\text{M}}}}}{{{c_{\text{A}}}+{c_{\text{M}}}}}{{{\upzeta}}}+\frac{{{c_{\text{A}}}{c_{\text{T}}}}}{{{c_{\text{A}}}+{c_{\text{T}}}}}\left( {{l_{\text{A}}} - {{{\upzeta}}}} \right)+\frac{{{x_{\text{A}}}}}{T}+\frac{{{c_{\text{A}}}}}{{{c_{\text{A}}}+{c_{\text{M}}}}}\frac{{{x_{\text{B}}} - {x_{\text{A}}}}}{T} - \frac{{{c_{\text{A}}}}}{{({c_{\text{A}}}+{c_{\text{T}}})}}\frac{{~{x_{\text{B}}}}}{T} \\ & ={c_{\text{M}}}\left( {{l_{\text{M}}} - {{{\upzeta}}}} \right)+\frac{{{c_{\text{A}}}{c_{\text{M}}}}}{{{c_{\text{A}}}+{c_{\text{M}}}}}{{{\upzeta}}}+\frac{{{c_{\text{A}}}{c_{\text{T}}}}}{{{c_{\text{A}}}+{c_{\text{T}}}}}\left( {{l_{\text{A}}} - {{{\upzeta}}}} \right)+\frac{{{x_{\text{A}}}}}{T}\left( {\frac{{{c_{\text{M}}}}}{{{c_{\text{A}}}+{c_{\text{M}}}}}} \right)+\frac{{~{x_{\text{B}}}}}{T}\left[ {\frac{{{c_{\text{A}}}({c_{\text{T}}} - {c_{{\text{M}})}}}}{{({c_{\text{A}}}+{c_{\text{M}}})({c_{\text{A}}}+{c_{\text{T}}})}}} \right]. \\ \end{aligned}$$

(21)

Finally, substituting ${x_{\text{A}}}$ and ${x_{\text{B}}}$ with ${x_0}\cosh \left( {\mu \left( {{\text{-}}\frac{{{{\upzeta}}}}{2} - {{{{\upxi}}}_0}} \right)} \right)$ and ${x_0}\cosh \left( {\mu \left( {{\text{+}}\frac{{{{\upzeta}}}}{2} - {{{{\upxi}}}_0}} \right)} \right)$ respectively, and using Eq. 17 and Eq. 18 lead to:

$$\begin{aligned} {C_{{\text{hs}}}} & ={c_{\text{M}}}\left( {{l_{\text{M}}} - {{{\upzeta}}}} \right)+\frac{{{c_{\text{A}}}{c_{\text{T}}}}}{{{c_{\text{A}}}+{c_{\text{T}}}}}\left( {{l_{\text{A}}} - {{{\upzeta}}}} \right)+\frac{{{c_{\text{A}}}{c_{\text{M}}}}}{{{c_{\text{A}}}+{c_{\text{M}}}}}{{{\upzeta}}} \\ & \quad +\frac{{\mu \frac{{{c_{\text{T}}}^{2}}}{{{c_{\text{A}}}+{{\text{c}}_{\text{T}}}}}\left( {{l_{\text{A}}} - {{{\upzeta}}}} \right)+2\tanh \left( {\frac{{\mu {{{\upzeta}}}}}{2}} \right)\frac{{{c_{\text{M}}}^{2}}}{{{c_{\text{A}}}+{c_{\text{M}}}}}+\mu \tanh {{\left( {\frac{{\mu {{{\upzeta}}}}}{2}} \right)}^2}\left( {{l_{\text{A}}} - {{{\upzeta}}}} \right)\frac{{{{\left[ {{c_{\text{T}}}\left( {{c_{\text{M}}} - {c_{\text{A}}}} \right)+2{c_{\text{A}}}{c_{\text{M}}}} \right]}^2}}}{{{{\left( {{c_{\text{M}}}+{c_{\text{A}}}} \right)}^2}\left( {{c_{\text{T}}}+{c_{\text{A}}}} \right)}}}}{{\mu \left[ {1+2\mu \tanh \left( {\frac{{\mu {{{\upzeta}}}}}{2}} \right)\frac{{{c_{\text{A}}}+{c_{\text{T}}}}}{{{c_{\text{A}}}+{c_{\text{M}}}}}\left( {{l_{\text{A}}} - {{{\upzeta}}}} \right)+\tanh {{\left( {\frac{{\mu {{{\upzeta}}}}}{2}} \right)}^2}} \right]}}. \\ \end{aligned}$$

(22)

Provided that $\mu {{{\upzeta}}}/2$ is not too large, dividing both numerator and denominator of the last term for $\tanh \left( {\mu {{{\upzeta}}}/2} \right)~$ and using the approximations:

$$\tanh \left( {\frac{{\mu {{{\upzeta}}}}}{2}} \right) \approx \frac{{\mu {{{\upzeta}}}}}{2},$$

and

$${\text{coth}}\left( {\frac{{\mu {{{\upzeta}}}}}{2}} \right) \approx \frac{2}{{\mu {{{\upzeta}}}}}+\frac{1}{3}\frac{{\mu {{{\upzeta}}}}}{2},$$

Equation 22 can be approximated by:

$$\begin{aligned} {C_{{\text{hs}}}} & ={c_{\text{M}}}\left( {{l_{\text{M}}} - {{{\upzeta}}}} \right)+\frac{{{c_{\text{A}}}{c_{\text{T}}}}}{{{c_{\text{A}}}+{c_{\text{T}}}}}\left( {{l_{\text{A}}} - {{{\upzeta}}}} \right)+\frac{{{c_{\text{A}}}{c_{\text{M}}}}}{{{c_{\text{A}}}+{c_{\text{M}}}}}{{{\upzeta}}} \\ & \quad +\frac{{\frac{{{c_{\text{T}}}^{2}}}{{{c_{\text{A}}}+{{\text{c}}_{\text{T}}}}}\left( {{l_{\text{A}}} - {{{\upzeta}}}} \right)+\frac{{{c_{\text{M}}}^{2}}}{{{c_{\text{A}}}+{c_{\text{M}}}}}{{{\upzeta}}}+\frac{{{k_{\text{c}}}{{{{\upzeta}}}^2}\left( {{l_{\text{A}}} - {{{\upzeta}}}} \right)}}{{12({c_{\text{A}}}+{c_{\text{T}}})}}\left\{ {{c_{\text{T}}}^{2}\left( {{c_{\text{M}}}+{c_{\text{A}}}} \right)+\frac{{3{{\left[ {{c_{\text{T}}}\left( {{c_{\text{M}}} - {c_{\text{A}}}} \right)+2{c_{\text{A}}}{c_{\text{M}}}} \right]}^2}}}{{{c_{\text{M}}}+{c_{\text{A}}}}}} \right\}}}{{1+\frac{{{k_{\text{c}}}{{{\upzeta}}}}}{3}\left[ {{{{\upzeta}}}\left( {{c_{\text{A}}}+{c_{\text{M}}}} \right)+3\left( {{l_{\text{A}}} - {{{\upzeta}}}} \right)({c_{\text{A}}}+{c_{\text{T}}}} \right)]}}. \\ \end{aligned}$$

(23)

where the dependence of C_hs on ${k_{\text{c}}}$, the stiffness per unit length of the motor array, is made explicit.

Results

When ${c_{\text{T}}} \to \infty$, Eq. 22 and Eq. 23 reduce to Eqs. A9 and A10 of FHS1981, as expected. On the contrary, when ${k_{\text{c}}}$, and then µ, $\to 0$ or ${c_{\text{A}}} \to \infty$, while FHS1981 predicts ${C_{{\text{hs}}}} \to \infty$, Eq. 22 predicts ${C_{{\text{hs}}}}=$${c_{\text{M}}}{l_{\text{M}}}+{c_{\text{T}}}\left( {{l_{\text{A}}} - {{{\upzeta}}}} \right)$, i.e. the series of thick filament and I-band titin compliances. These results are consistent with the structural/mechanical models drawn in Figs. 2 and 4 respectively.

The main difference introduced by the I-band spring that links the edge of the thick filament to the Z line is that in this case the compliance of the half-sarcomere cannot any longer be thought as the sum of compliances in series, even within the approximation that leads to Eq. A10 of FHS1981. Thus, while FHS1981 allowed to define an equivalent filament compliance C_f contributing to C_hs, as represented by Eq. 3, when the contribution of titin is considered, the concept of equivalent filament compliance is no longer applicable.

Experimentally, the values of the parameters c_A, c_M, c_T, k_c can be estimated, for example, by applying fast (4 kHz) length oscillations to a muscle fibre during the rise of an isometric tetanus (Fusi et al. 2014) to measure C_hs at several force levels during the rise of an isometric tetanus. The number of attached motors (n_A) varies linearly with force (Piazzesi et al. 2018), and so does their stiffness: ${k_{\text{c}}}{{{\upzeta}=}}{k_{{\text{c}}0}}{{{\upzeta}T}}$, where ${k_{{\text{c}}0}}$ is the stiffness per unit length of the cross-bridge array at the maximal isometric force T₀, and T is the force during the tetanus rise expressed in T₀ units. In this way, the values of C_hs at different T can be fitted by Eq. 22 or Eq. 23 to determine the different parameters.

As an example, to evaluate the possible contribution of titin to the half-sarcomere compliance, we have calculated how C_hs from Eq. 22 should vary during the tetanus rise with the values for c_A, c_M and k_c0 as estimated in Brunello et al. (2014), and with different values for c_T. Here we neglect the possible contribution of the compliance in parallel with the cross-bridges in the A-band (C_p). In Brunello et al. (2014) the myofilament compliances are estimated by means of X-ray diffraction measurements, and their values are 16.8 pm/pN/µm and 10.3 pm/pN/µm for a single thin and thick filament respectively. With an isometric force T₀ = 183 kPa (Brunello et al. 2014), and considering the myofilament lattice geometry, these values reflects on c_A = 2.29 nm/T₀/µm and c_M = 2.80 nm/T₀/µm, and, by comparing these results with mechanical measurements, k_c0 is calculated to be 0.806 T₀/nm/µm. The results are reported in Fig. 5, where C_hs as a function of T is plotted for different c_T (1, 10, 100 and 1000 nm/T₀/µm) at four different sarcomere lengths (SL), 2.15 (A), 2.5 (B), 2.7 (C) and 2.90 µm (D) (and correspondingly different ${{{\upzeta}}}$ from 0.7 to 0.325 µm, having taken l_A=0.975 µm and l_M=0.8; Brunello et al. 2014). It can be seen that the presence of a titin-like compliance with c_T of 10 nm/T₀/µm or less (dotted lines) is not compatible with the observed C_hs-T relation at 2.15 µm (open circles from Fig. 3d in Fusi et al. 2014). In fact, in this case, unlike what observed, C_hs at forces < 0.5 T₀ is systematically reduced with respect to the value in the absence of the titin-like spring, as it does not increase with the reduction of isometric force (and thus the number of attached motors n_A) but it remains constant independent of isometric force. Instead, for higher c_T values (100 nm/T₀/µm, short-dashed lines, or larger), C_hs at high forces (or n_A) is unaffected, while at low forces it is reduced by an extent that is larger at smaller forces in agreement with experimental results at SL 2.15 µm (open circles) and, at any force, is larger at longer SL. It can be seen that the experimental relation almost coincides with the relation predicted by the model with a c_T of 100 nm/T₀/µm (short dashed line). A detailed comparison between titin compliance and the compliances of the various elements contributing to the half-sarcomere compliance is reported in Table 1 with the actual value contributed in the haf-sarcomere at full overlap (${{{\upzeta}}}$ = 0.7 µm). Noteworthy, with c_T = 1000 nm/T₀/µm (long dashed line), ten times larger than that of the instantaneous elasticity of titin and of the order of the static compliance responsible for the passive force, the C_hs—force relation almost superposes on that of the half-sarcomere without titin (continuous line), rising to infinite as the isometric force approaches to zero.

Fig. 5

Compliance of the half sarcomere C_hs calculated as a function of force T during the rise of an isometric tetanus for different values of titin compliance per unit length (c_T, as in the inset) and at four different sarcomere lengths (A SL = 2.15 µm; B SL = 2.50 µm; C SL = 2.70 µm; D SL = 2.90 µm), with superimposed, for SL = 2.15 µm (A), the data from Fig. 3d in Fusi et al. 2014 (grey symbols). T₀ is the maximal tetanic force developed in isometric contraction at SL = 2.15 µm. c_A, c_M and k_c from Brunello et al. 2014 (see text). l_A = 0.975 µm, l_M = 0.8 µm

Table 1 Compliance of the different elements contributing to the compliance of the half sarcomere at SL = 2.15 µm and force T₀

Superimposed C_hs-force relations at the four SL are shown in Fig. 6 in the absence of a titin-like spring (A, B) and with a titin-like spring with c_T 100 nm/T₀/µm (C, D). In the expanded scale (right column) it can be better appreciated that in the absence of titin (B) the increase in C_hs with the reduction of force is larger than with c_T 100 nm/T₀/µm (D), as a consequence of the fact that in the absence of titin C_hs tends to ∞ as n_A tends to zero. Accordingly, in the presence of the titin spring with c_T 100 nm/T₀/µm, the SL-dependent upward shift in C_hs remains at any force, as at low force the contribution of titin to C_hs takes over that of n_A.

Fig. 6

Compliance of the half-sarcomere C_hs calculated as a function of force T during the rise of an isometric tetanus at different sarcomere lengths (SL, as in the inset) in the absence (A, B) or in the presence (C, D) of titin with a compliance per unit length c_T = 100 nm/T₀/µm

Discussion

Mechanical experiments on active muscle fibres provided evidence that an additional elastic element in parallel to the attached myosin motors is present in the activated half-sarcomere (Bagni et al. 2002; Colombini et al. 2010; Fusi et al. 2014). Studies that use stiffness measurements with small 4 kHz oscillation during the rise of the isometric tetanus found that the compliance of this additional elastic element is 200–300 nm/MPa (Fusi et al. 2014, 2017), that is ∼ 20 times the compliance of the array of the attached myosin motors at T₀ and comparable to the compliance of the array of the myosin motors attached early during the tetanus rise, when the isometric force is ∼ 0.1 T₀. This is because at this low force the number of attached motors n_A is relatively small and the contribution of the additional elastic element becomes comparable to that of the attached motors. There are evidences that this additional elasticity increases with SL (Bagni et al. 2002; Powers et al. 2017), which indicates that it is due at least in part to a titin-like I-band spring. In this respect, however, it must be noted that the stiffness of the additional elasticity is at least one order of magnitude larger than that estimated from the force-extension relation responsible for the passive force of the fibre and attributed to the static elasticity of titin. It is likely that titin structural dynamics described with in vitro mechanical measurements on titin (Mártonfalvi et al. 2014) or on its Ig-domain construct (Rivas-Pardo et al. 2016) are responsible of the relaxation processes that account for the large difference between instantaneous and static titin stiffness.

The application of the mechanical model with the additional elastic element in the I-band shows in detail how the presence of an I-band spring prevents C_hs to rise to infinite as the isometric force (and thus n_A) approaches zero (compare B and D panels in Fig. 5). The reduction of C_hs is larger if the compliance of the titin-like element (c_T) is smaller and, for a given value of c_T, is larger at lower forces. This is emphasised in Fig. 7A, where the points (extracted by the relations in Fig. 5) indicate the relation between C_hs and c_T at 0.5 T₀ (triangles) and 0.1 T₀ (circles). The reduction in C_hs produced by introducing a titin-like spring with a c_T of 100 nm/T₀/µm (similar to that necessary to fit the experimental C_hs-force relation at SL 2.15 µm; short dashed line and circles in Fig. 5A) is estimated at 0.1 T₀ and at 0.5 T₀ by the length of the segment m and n respectively, showing that the effect of titin is 12 times larger at 0.1 than at 0.5 T₀. In this respect the contribution of an I-band spring like titin is similar to that of an A-band spring as that represented by a fraction of no-force generating or weakly-bound motors in parallel with the array of force generating motors (Colombini et al. 2010; Fusi et al. 2017).

Fig. 7

A Compliance of the half-sarcomere C_hs calculated as a function of titin compliance per unit length, c_T, at SL 2.15 µm at forces 0.1 T₀ (circles) and 0.5 T₀ (triangles) during the rise of an isometric tetanus. The vertical grey lines indicate the reduction in C_hs caused by introducing an I-band spring with c_T = 100 nm/T₀/µm at either 0.1 T₀ (m) or 0.5 T₀ (n). B Compliance of the half-sarcomere C_hs calculated as a function of SL at 0.1 T₀. Circles: C_hs contributed only by the myofilaments and cross-bridges; squares: effect of a parallel elastic element with compliance C_p as described in the text; triangles, reverse triangles and diamonds: effect of titin-like I-band spring with compliance c_T = 100 nm/T₀/µm, 50 nm/T₀/µm and 10 nm/T₀/µm respectively. See text for filled symbols

The effect on C_hs of an I-band spring like titin with respect to that of an A-band spring may become quite more specific in relation to changes in sarcomere length. The question is analysed in Fig. 7B by comparing the relations between C_hs and SL at force 0.1 T₀, at which both an I-band and an A-band spring produce a large effect, obtained either with the contribution of cross-bridges in the absence of any added spring (squares) or in the presence of either an A-band spring like that determined in Fusi et al. (2014) (grey circles, C_p = 29 nm/T₀) or an I-band spring with c_T of 100 nm/T₀/µm (triangles), 50 nm/T₀/µm (reverse triangles) and 10 nm/T₀/µm (diamonds). At SL 2.15 µm an A-band spring with C_p 29 nm/T₀ decreases C_hs by almost the same amount (~ 35%) as an I-band spring with c_T 100 nm/T₀/µm. In fact, taking into account the length of the I-band spring (SL/2 – l_M = 0.275 µm), the actual I-band spring compliance C_T is (100 nm/T₀/µm·0.275 µm =) 27 nm/T₀, not significantly different from C_p of the A-band spring determined in Fusi et al. (2014) at SL 2.15 µm. Thus, both the I-band and the A-band springs with constant stiffness do contribute to increase C_hs with the increase in SL, as demonstrated by the finding that the slopes of both C_hs-SL relations identified by grey circles and triangles are larger than the slope of the C_hs—SL relation calculated with the contribution of cross-bridges without any added spring (squares). The C_hs-SL relation is shifted progressively downward with the reduction of c_T to 50 nm/T₀/µm (reverse triangles) and 10 nm/T₀/µm (diamonds).

It must be noted that the relations in Fig. 7B represent the theoretical predictions of the effect on C_hs of springs that have a constant compliance per unit length. To apply these predictions to the contribution to C_hs of a titin-like I-band spring in situ, we need to take into account the experimental evidence [first of all the passive force-SL relation, but also the response of active muscle to sudden larger stretch (Bagni et al. 2002) and eventually the first experiments performed with small length perturbation in the ≥ 4 kHz frequency domain (Powers et al. 2017)] showing that C_hs reduces at larger SL, suggesting a reduction in titin compliance per unit length as the SL and thus the overall length of I-band spring increases. In vitro measurements of length dependence of titin stiffness cannot be done with the time resolution necessary to prevent the confounding effects of the relaxation processes related to titin structural dynamics (Kellermayer et al. 1997; Martonfalvi et al. 2014; Rivas-Pardo et al. 2016). On the other hand, it looks likely from first in situ measurements (Powers et al. 2017) that in the active muscle the instantaneous stiffness of titin, which is one–two orders of magnitude larger that the passive “static” stiffness, increases with increase in SL so as to explain the reduction of C_hs. Under these conditions the relations in Fig. 7B provide a fundamental tool to interpret the changes in C_hs with SL in terms of the contribution of a titin-like I-band spring. As an example, let’s assume that c_T at SL 2.15 µm is 100 nm/T₀/µm and compare the C_hs attained at SL 2.7 µm with c_T 100 nm/T₀/µm (triangle) to that with c_T 50 nm/T₀/µm (reverse triangle). If c_T does not change with the increase in SL, C_hs at 2.7 µm (triangle) increases by 25%, as the result of both the reduction of n_A (due to the reduction of filament overlap by 0.25 nm) and doubling of the length of the I-band spring, (SL/2 – l_M), from 0.275 to 0.55 µm. However, if we assume that titin is a tuneable spring which maintains constant its stiffness neutralising the large changes in the I-band length, its c_T would be halved when its length is doubled. In this case, the increase in SL from 2.15 to 2.7 µm would not produce the increase in C_hs expected from a constant c_T of 100 nm/T₀/µm (open triangle at 2.7 µm), as the Chs–SL point at 2.7 µm would have shifted to the relation with c_T 50 nm/T₀/µm (reverse triangles), as indicated by the filled reverse triangle at SL 2.7 µm.