Abstract
This work introduces the StoMADS-PB algorithm for constrained stochastic blackbox optimization, which is an extension of the mesh adaptive direct-search (MADS) method originally developed for deterministic blackbox optimization under general constraints. The values of the objective and constraint functions are provided by a noisy blackbox, i.e., they can only be computed with random noise whose distribution is unknown. As in MADS, constraint violations are aggregated into a single constraint violation function. Since all function values are numerically unavailable, StoMADS-PB uses estimates and introduces probabilistic bounds for the violation. Such estimates and bounds obtained from stochastic observations are required to be accurate and reliable with high, but fixed, probabilities. The proposed method, which allows intermediate infeasible solutions, accepts new points using sufficient decrease conditions and imposing a threshold on the probabilistic bounds. Using Clarke nonsmooth calculus and martingale theory, Clarke stationarity convergence results for the objective and the violation function are derived with probability one.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Blackbox optimization (BBO) is concerned with optimization problems in which the functions defining the objective and the constraints are given by a process called a blackbox which returns an output when provided an input but whose inner workings are analytically unavailable [12]. Mesh adaptive direct-search (MADS) [8, 9] with progressive barrier (PB) is an algorithm for deterministic BBO. The present work considers the following constrained stochastic BBO problem
where \({\mathcal {D}}=\{x\in {\mathcal {X}}: c(x)\le 0\}\subset {\mathbb {R}}^n\) is the feasible region, \(c = (c_1,c_2,\dots , c_m)^{\top }\), \({\mathcal {X}}\) is a subset of \({\mathbb {R}}^n\), \(f(x)={\mathbb {E}}_{\Theta _0}\left[ f_{\Theta _0}(x)\right] \) with \(f:{\mathcal {X}}\mapsto {\mathbb {R}}\), and \(c_j(x)={\mathbb {E}}_{\Theta _j}\left[ c_{\Theta _j}(x)\right] \) with \(c_j:{\mathcal {X}}\mapsto {\mathbb {R}}\) for all \(j\in J:=\{{1},2,\dots ,m\}\). \({\mathbb {E}}_{\Theta _{j}}\) denotes the expectation with respect to the random variable \(\Theta _j\) for all \({j \in J\cup \{0\}}\), which are supposed to be independent with unknown, possibly different, distributions. \(f_{\Theta _0}(\cdot )\) denotes the noisy computable version of the numerically unavailable objective function \(f(\cdot )\), while for all \(j\in J\), \(c_{\Theta _j}(\cdot )\) denotes the noisy computable version of the numerically unavailable constraint \(c_j(\cdot )\). Note that the noisy objective function \(f_{\Theta _0}\) and the constraints \(c_{\Theta _j}, j\in J,\) are the outputs of a blackbox. By means of some useful terminology, constraints that must always be satisfied, such as those defining \({\mathcal {X}}\), are differentiated from those that need only to be satisfied at the solution, such as \(c(x)\le 0\). The former will be called unrelaxable non-quantifiable constraints and the latter, relaxable quantifiable constraints [41].
Solving stochastic blackbox optimization problems such as Problem (1), which often arise in signal processing and machine learning [27], has recently been a topic of intense research. Most methods for solving such problems borrow ideas from the stochastic gradient method [49]. Several works have also attempted to transfer ideas from deterministic DFO methods to the stochastic context. However, most of such proposed methods are restricted to unconstrained optimization. Indeed, after [18] which is among the first to propose a stochastic variant of the deterministic Nelder-Mead (NM) method [3, 47] also considered the optimization of functions whose evaluations are subject to random noise and proposed an algorithm which is shown to have convergence properties, based on Markov chain theory [32]. Another stochastic variant of NM was recently proposed in [22] and was proved to have global convergence properties with probability one. Using elements from [17, 23, 40] proposed STORM, a trust-region algorithm designed for stochastic optimization problems, with almost sure global convergence results. Additional research that extends the traditional deterministic trust-region method to stochastic setting have been conducted in [28, 52]. In [48], a classical backtracking Armijo line search method [5] has been adapted to the stochastic optimization setting and was shown to have first-order complexity bounds. Robust-MADS, a kernel smoothing-based variant of MADS [8], was proposed in [13] to approach the minimizer of an objective function whose values can only be computed with random noise, and was shown to possess zeroth-order [10] convergence properties. Another stochastic variant of MADS was proposed in [2] for BBO, where the noise corrupting the blackbox was supposed to be Gaussian. Convergence results of the proposed method have been derived, making use of statistical inference techniques. The StoMADS algorithm [11] is another stochastic optimization approach using estimates of function values obtained from stochastic observations and an algorithmic framework similar to that of MADS. By assuming that such estimates satisfy a variance condition and are sufficiently accurate with a large but fixed probability conditioned to the past, a Clarke [25] stationarity convergence result of StoMADS has been derived with probability one, using martingale theory. A general framework for stochastic directional direct-search [26] methods was introduced in [33] with expected complexity analysis.
All the above stochastic optimization methods are restricted to unconstrained problems and most of them use estimated gradient information to seek an optimal solution. When the gradient does not exist or is computationally expensive to estimate, heuristics such as simulated annealing methods, genetic algorithms [39], and tabu/scatter search [38], are also used for problems with noisy constraints but do not present any convergence theory. Surrogate model-based methods for constrained stochastic BBO have also been a topic of intense research, including the response surface methodology with stochastic constraints [4] developed for expensive simulation. In [16], the capabilities of the deterministic constrained trust-region algorithm NOWPAC [15] are generalized to the optimization of blackboxes with inherently noisy evaluations of the objective and constraint functions. To mitigate the noise in function evaluations, the resulting gradient-free method SNOWPAC utilizes a Gaussian process surrogate combined with local fully linear surrogate models. Another surrogate-based approach that has gained in popularity in various research fields is Bayesian optimization [45]. Various Bayesian optimization methods for constrained stochastic BBO have been demonstrated to be efficient in practice [42, 54].
Developing direct-search methods for BBO has received renewed interest since such methods are generally known to be reliable and robust in practice [6], thereby appearing as the most promising approach in most of real applications where the gradient does not exist or is computationally expensive to estimate. However, there is relatively scarce research on developing direct-search methods for constrained stochastic BBO, especially when noise is present in the constraint functions. A pattern search and implicit filtering algorithm (PSIFA) [29, 30] was recently developed for linearly constrained problems with a noisy objective function, and was shown to have global convergence properties. A class of direct-search methods for solving smooth linearly constrained problems was also studied in [34] but even though using a probabilistic feasible descent based approach, this work assumes the objective and constraints function values to be exactly computed without noise.
The present work introduces StoMADS-PB, a stochastic variant of the mesh adaptive direct-search with progressive barrier [9], using elements from [8, 9, 11, 17, 23, 48] and is, to the best of our knowledge, the first to propose a directional direct-search [26] stochastic BBO algorithm, capable of handling general noisy constraints without requiring any feasible initial point. Its main contribution is the analysis of the resulting new framework with fully supported theoretical results. StoMADS-PB uses no (approximate) gradient information to find descent directions or to improve feasibility, compared to prior work. Rather, it uses so-called probabilistic estimates [23] of the objective and constraint function values and also introduces probabilistic bounds on constraint violation function values. The reliability of such bounds is assumed to hold with a high, but fixed, probability. Moreover, although no distributions are assumed on the estimates and no assumption is made about the way the estimates are generated, they are required to be sufficiently accurate with large, but fixed, probabilities and satisfy some variance conditions.
The manuscript is organized as follows. Section 2 presents the general framework of the proposed StoMADS-PB algorithm. Section 3 explains how the proposed method results in a stochastic process and discusses requirements on random estimates to guarantee convergence. Section 4 presents the main convergence results. Section 5 shows how random estimates and bounds can be constructed in practice. Computational results are also reported in Sect. 5 followed by a discussion and suggestions for future work. Additional results are provided in the appendix.
2 The StoMADS-PB algorithm
StoMADS-PB is based on an algorithmic framework similar to that of MADS with PB [9]. For the convergence analysis of Sect. 4, deterministic constraint violations are aggregated into a single function h called the constraint violation function, defined using the \(\ell _1\)-norm. This in contrast to [9] where an \(\ell _2\)-norm was employed.
According to this definition, \(h:{\mathbb {R}}^n\rightarrow {\mathbb {R}}\cup \{+\infty \}\) and \(x\in {\mathcal {D}}\), i.e., x is feasible with respect to the relaxable constraints if and only if \(h(x)=0\). Moreover, if \(0<h(x)<+\infty \), then x is called infeasible and satisfies the unrelaxable constraints but not the relaxable ones. Notice that \(h(x)=\infty \) when x does not satisfy the unrelaxable constraints.
In MADS with PB, feasibility improvement is achieved by decreasing h, specifically by comparing its function value at a current point \(x^k\) to that of a trial point \(x^k+s^k\), where \(s^k\) denotes a trial step around \(x^k\). Likewise, to decrease f, MADS with PB uses objective function values since they are available in the deterministic setting.
For the StoMADS-PB algorithm, one must guarantee some form of decrease in both f and h, using only noisy information provided by the noisy blackbox outputs \(f_{\Theta _0}\) and \(c_{\Theta _j}\), \(j\in J\). This section shows how this can be achieved, making use of \(\varepsilon \)-accurate estimates introduced in [23] and then presents the general framework of the proposed method.
2.1 Feasibility and objective function improvements
At iteration k, let \(x^k\) and \(x^k+s^k\) be two points in \({\mathcal {X}}\). Since the constraint function values \(c_j(x^k)\) and \(c_j(x^k+s^k)\), \(j\in J=\{1,2,\dots ,m\}\), are numerically unavailable, their corresponding estimates are respectively constructed using evaluations of the noisy blackbox outputs \(c_{\Theta _j}\), \(j\in J\). In general for the remainder of the manuscript, unless otherwise stated, given a function \(g:{\mathcal {X}}\rightarrow {\mathbb {R}}\), an estimate of \(g(x^k)\) is denoted by \(g_0^k(x^k)\) (or simply by \(g_0^k\) if there is no ambiguity) while an estimate of \(g(x^k+s^k)\) is denoted by \(g_s^k(x^k+s^k)\) or \(g_s^k\). In StoMADS-PB, the violations of the estimates \(c^k_{j,0}(x^k)\) and \(c^k_{j,s}(x^k+s^k)\) of \(c_j(x^k)\) and \(c_j(x^k+s^k)\), respectively, are aggregated in estimated violations \(h^k_0(x^k)\) and \(h^k_s(x^k+s^k)\) defined as
In order for such estimated constraint violations to be reliable enough to determine whether \(h(x^k\!\!+\!\!s^k)<h(x^k)\), the estimates \(c^k_{j,0}(x^k)\) and \(c^k_{j,s}(x^k+s^k)\) need to be sufficiently accurate. The following definition, similar to that of [11], is adapted from [23].
Definition 2.1
Let \(\varepsilon >0\) be a constant and \(\delta ^k_p\) be a nonnegative real number. For a given function \(g:{\mathcal {X}}\mapsto {\mathbb {R}}\) and \(y^k\in {\mathcal {X}}\), let \(g^k\) be an estimate of \(g(y^k)\). Then \(g^k\) is said to be an \(\varepsilon \)-accurate estimate of \(g(y^k)\) for the given \(\delta ^k_p\), if
As in [11], the role of \(\delta ^k_p\) will be played by the poll size parameter introduced later in Sect. 2.2. The following result provides bounds on \(h(x^k)\) and \(h(x^k+s^k)\), respectively, which will allow, later in Proposition 2.4, a decrease in the constraint violation function h by means of a sufficient decrease condition on the estimated violations \(h^k_0\) and \(h^k_s\).
Proposition 2.2
Let \(c^k_{j,0}\) and \(c^k_{j,s}\) be \(\varepsilon \)-accurate estimates of \(c_j(x^k)\) and \(c_j(x^k+s^k)\), respectively, for the given \(\delta ^k_p\), with \(x^k\) and \(x^k+s^k\in {\mathcal {X}}\). Then the following hold:
and
Proof
The result is shown for \(h(x^k)\) but the proof for \(h(x^k+s^k)\) is the same. Since \(c^k_{j,0}\) is an \(\varepsilon \)-accurate estimate of \(c_j(x^k)\) for all \(j\in J\), it follows from Definition 2.1 that
which implies that
Finally, summing each term of (5) from \(j=1\) to m leads to (4). \(\square \)
Definition 2.3
The estimates \(\ell ^k_0(x^k)\) and \(u^k_0(x^k)\) of Proposition 2.2, satisfying \(\ell ^k_0(x^k)\le h(x^k)\le u^k_0(x^k)\), are said to be \(\varepsilon \)-reliable bounds for \(h(x^k)\). Similarly, the estimates \(\ell ^k_s(x^k+s^k)\) and \(u^k_s(x^k+s^k)\) satisfying \(\ell ^k_s(x^k+s^k)\le h(x^k+s^k)\le u^k_s(x^k+s^k)\) are said to be \(\varepsilon \)-reliable bounds for \(h(x^k+s^k)\).
The following result provides sufficient conditions to identify a decrease in h and will be also used to determine an iteration type later in Sect. 2.2.
Proposition 2.4
Let \(h^k_0\) and \(h^k_s\) be the estimated constraint violations at \(x^k\) and \(x^k+s^k\in {\mathcal {X}}\), respectively, that are constructed using of \(\varepsilon \)-accurate estimates \(c^k_{j,0}\) and \(c^k_{j,s}\). Let \(\gamma >2\) be a constant. Then the following holds:
Proof
It follows from Proposition 2.2 that
By noticing that
and
it follows from (7) that
where the last inequality follows from the assumption that \(h^k_s-h^k_0\le -\gamma m\varepsilon (\delta ^k_p)^2\). The proof is complete by noticing that \(\gamma >2\). \(\square \)
Remark 2.5
The result of Proposition 2.4 is very important since it allows to identify a decrease in h making use of the estimated violations \(h^k_0\) and \(h^k_s\). However, it can be observed that deriving easily Inequalities (8) and (9) in order to prove (6) is greatly favored by the use of an \(\ell _1\)-norm in the definitions of h and both \(h^k_0\) and \(h^k_s\). Indeed, proving a result similar to (6) when an \(\ell _2\)-norm is used should not be as easy as it is in the latter proof. This observation motivates in fact the definition of the progressive barrier function h (and consequently the definitions of \(h^k_0\) and \(h^k_s\)) using an \(\ell _1\)-norm unlike [9] where an \(\ell _2\)-norm was preferred for the analysis of MADS with PB.
The \(\varepsilon \)-reliable upper bound \(u^k_0(x^k)\) previously obtained for \(h(x^k)\) also allows one to determine the feasibility with respect to the relaxable constraints of a given trial point \(x^k\in {\mathcal {X}}\). Indeed, it obviously follows from (4) that \(h(x^k)=0\) if \(u^k_0(x^k)=0\), which is satisfied provided that \(c^k_{j,0}(x^k)\le -\varepsilon (\delta ^k_p)^2\), for all \(j\in J\). This means that in order for \(h(x^k)=0\) to hold, all the estimates of constraint function values must be sufficiently negative and not simply zero. By means of the following definition, StoMADS-PB partitions the trial points into \(\varepsilon \)-feasible and \(\varepsilon \)-infeasible points making use of a nonnegative barrier threshold \(h^k_{\max }\) which is introduced in the present research, inspired by [9]
Definition 2.6
Let \(x^k\in {\mathcal {X}}\) be any trial point and let \(u^k_0(x^k)\) be an \(\varepsilon \)-reliable upper bound for \(h(x^k)\). Then \(x^k\) is called \(\varepsilon \)-feasible if \(u^k_0(x^k)=0\), and it is called \(\varepsilon \)-infeasible if \(\ 0<u^k_0(x^k)\le h^k_{\max }\). Similarly, \(x^k+s^k\in {\mathcal {X}}\) is called \(\varepsilon \)-feasible if \(u^k_s(x^k+s^k)=0\), and it is called \(\varepsilon \)-infeasible if \(\ 0<u^k_s(x^k+s^k)\le h^k_{\max }\).
StoMADS-PB does not require that the starting point be \(\varepsilon \)-feasible. The algorithm can be applied to any problem satisfying only the following assumption adapted from [9].
Assumption 1
There exists some point \(x^0\in {\mathcal {X}}\) such that \(f^0_0(x^0)\) and \(u^0_0(x^0)\) are both finite, and \(u^0_0(x^0)\le h^0_{\max }\).
The next result similar to that in [11] provides a sufficient condition to identify a decrease in f and also allows one to determine an iteration type in Sect. 2.2.
Proposition 2.7
Let \(f_0^k\) and \(f_s^k\) be \(\varepsilon \)-accurate estimates of \(f(x^k)\) and \(f(x^k+s^k)\), respectively, for \(x^k\) and \(x^k+s^k\in {\mathcal {X}}\). Let \(\gamma >2\) be a constant. Then the following holds:
Proof
The proof follows from Definition 2.1 and the equality
\(\square \)
The incumbent solutions \(x^k_{\text {inf}}\) and \(x^k_{\text {feas}}\) at the start of a given iteration k are defined in Definition 2.9 after ranking the trial mesh points of \({\mathcal {X}}\), making use of the following dominance notion inspired by [9].
Definition 2.8
The \(\varepsilon \)-feasible point \(x^k+s^k\) is said to dominate the \(\varepsilon \)-feasible point \(x^k\), denoted \(x^k+s^k \prec _{f;\varepsilon }x^k\), provided \(f^k_s-f^k_0\le -\gamma \varepsilon (\delta ^k_p)^2\) and \(u^k_s(x^k+s^k)=0\).
The \(\varepsilon \)-infeasible point \(x^k+s^k\) is said to dominate the \(\varepsilon \)-infeasible point \(x^k\), denoted \(x^k+s^k \prec _{h;\varepsilon }x^k\), provided \(f^k_s-f^k_0\le -\gamma \varepsilon (\delta ^k_p)^2\), \(h^k_s-h^k_0\le -\gamma m\varepsilon (\delta ^k_p)^2\) and \(\ 0<u^k_s(x^k+s^k)\le h^k_{\max }\).
Definition 2.9
Let \({\mathscr {E}}_k\) be the set of points where the objective and constraint functions have been evaluated at a given iteration k. If no \(\varepsilon \)-feasible point is generated by Algorithm 2, then there is no \(\varepsilon \)-feasible solution. Otherwise, let \(t\ge 1\) be such that \(t-1\) is the iteration where a first \(\varepsilon \)-feasible point is found. Then \(x^{t}_{\text {feas}}\in \left\{ x^{t-1}+s^{t-1}\in {\mathscr {E}}_{t-1}:u_s^{t-1}(x^{t-1}+s^{t-1})=0\right\} \) is an \(\varepsilon \)-feasible incumbent solution at the start of iteration t. Define \({\mathscr {F}}_k(y)=\{x^k+s^k\in {\mathscr {E}}_k:u^k_s(x^k+s^k)=0\ \text {and}\ x^k+s^k \prec _{f;\varepsilon }y\}\) for all \(k\ge t\) with \({\mathscr {F}}_k(y)=\emptyset \) if \(k\le {t-1}\). Define the sets \({\mathscr {D}}_k(x^k)=\left\{ x^k+s^k\in {\mathscr {E}}_k:x^k+s^k \prec _{h;\varepsilon }x^k\right\} \) and \({\mathscr {I}}_k(x^k)= \Big \{ x^k+s^k\in {\mathscr {E}}_k:h^k_s(x^k+s^k)-h^k_0(x^k)\le -\gamma m\varepsilon (\delta ^k_p)^2\Big \}\) for all \(k\ge 0\). Let \(x^0_{\text {inf}}\in {\mathcal {X}}\) be a starting point. For all \(k\ge t\), an \(\varepsilon \)-feasible incumbent solution at iteration \(k+1\) is defined as:
For all \(k\ge 0\), an \(\varepsilon \)-infeasible incumbent solution at iteration \(k+1\) is defined as:
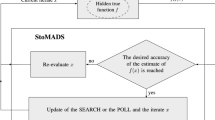
2.2 The StoMADS-PB algorithm and parameter update
Recall first that MADS with PB is an iterative algorithm where every iteration is comprised of two main steps: an optional step called the SEARCH [9, 12], and the POLL. The SEARCH which typically consists of a global exploration may use a plethora of strategies like those based on interpolation models, heuristics and surrogate functions or simplified physics models [9] to explore the variables space. Each iteration of StoMADS-PB can also allow a SEARCH step, but it is not shown here for simplicity. Similarly to MADS with PB, the POLL step of StoMADS-PB is more rigidly defined, unlike the freedom of the SEARCH, and consists of a local exploration. During each of these two steps, a finite number of trial points is generated on an underlying mesh \({\mathcal {M}}^k\). The mesh is a discretization of the variable space, whose coarseness or fineness is controlled by a mesh size parameter \(\delta ^k_m\), thus deviating from the notation \(\Delta ^m_k\) from [9], since uppercase letters will be used to denote random variables. For the remainder of the manuscript, \(s^k=\delta ^k_md^k\) where \(d^k\) is a nonzero direction. The POLL step is governed by the poll size parameter \(\delta ^k_p\) which is linked to \(\delta ^k_m\) by \(\delta ^k_m=\min \{\delta ^k_p,(\delta ^k_p)^2\}\) [12]. As specified earlier, \(\{\delta ^k_p\}_{k\in {\mathbb {N}}}\) will play the role of the sequence of nonnegative real numbers introduced in Definition 2.1. Let \({\hat{z}}\in {\mathbb {N}}\) be a large fixed integer and \(\tau \in (0,1)\cap {\mathbb {Q}}\) be a fixed rational constant. For the needs of Sect. 4, note also that as in [11], \(\delta ^k_p\) is supposed to be bounded above by the positive and fixed constant \(\tau ^{-{\hat{z}}}\) in order for the random poll size parameter \(\Delta ^k_p\) introduced later in Sect. 3 to be integrable. The notion of a positive spanning set introduced in the following definition from [12] is required to define the mesh \({\mathcal {M}}^k\) and the POLL set \({\mathcal {P}}^k\).
Definition 2.10
The positive span of a set \({\mathbb {D}}\subseteq {\mathbb {R}}^n\), denoted \(pspan ({\mathbb {D}})\), is the set of all nonnegative linear combinations of vectors in \({\mathbb {D}}:\)
The set \({\mathbb {D}}\) is a positive spanning set for \({\mathbb {R}}^n\) if and only if \(pspan ({\mathbb {D}})={\mathbb {R}}^n\).
The definitions of the mesh \({\mathcal {M}}^k\) and the POLL set \({\mathcal {P}}^k\) inspired by [9] are given next.
Definition 2.11
Let \({\mathbf {D}}\in {\mathbb {R}}^{n\times p}\) be a matrix, with columns denoted by the set \({\mathbb {D}}\), which form a positive spanning set. At the beginning of iteration k, let \(x^k_{\text {inf}}\) and \(x^k_{\text {feas}}\) denote respectively the \(\varepsilon \)-infeasible and the \(\varepsilon \)-feasible incumbent solutions (there might be only one), and let \({\mathcal {V}}^k:=\{x^k_{\text {inf}},x^k_{\text {feas}}\}\) be the set of such incumbents. The mesh \({\mathcal {M}}^k\) and the POLL set \({\mathcal {P}}^k\) are respectively
where \(\forall x^k\in {\mathcal {M}}^k\cap {\mathcal {X}}\), \({\mathcal {P}}^k(x^k)=\{x^k+\delta ^k_md^k\in {\mathcal {M}}^k\cap {\mathcal {X}}: \delta ^k_m{\left\Vert d^k\right\Vert }_{\infty }\le \delta ^k_pb,\ d^k\in {\mathbb {D}}^k_p(x^k)\}\) is called a frame around \(x^k\), with \(b=\max \left\{ {\left\Vert d'\right\Vert }_{\infty }, d'\in {\mathbb {D}}\right\} \). \({\mathbb {D}}^k_p(x^k)\) is a positive spanning set which is said to be a set of frame directions used for polling around \(x^k\). The set \({\mathbb {D}}^k_p\) of all polling directions at iteration k is defined by \({\mathbb {D}}^k_p:={\mathbb {D}}^k_p(x^k_{\text {inf}})\cup {\mathbb {D}}^k_p(x^k_{\text {feas}})\). When there is no incumbent \(\varepsilon \)-feasible solution \(x^k_{\text {feas}}\), then the set \({\mathcal {V}}^k\) is reduced to \(\{x^k_{\text {inf}}\}\), in which case \({\mathcal {P}}^k = {\mathcal {P}}^k(x^k_{\text {inf}})\) and \({\mathbb {D}}^k_p={\mathbb {D}}^k_p(x^k_{\text {inf}})\).
The set \({\mathbb {D}}^k_p(x^k)\) of directions used for polling in Algorithm 2 can be created using Algorithm 1 [11, 12]. A definition of the \(\text {round}(\cdot )\) function used in the latter algorithm can be found in [11].

After the POLL step is completed, StoMADS-PB computes not only estimates \(f^k_0\), \(f^k_s\), \(h^k_0\) and \(h^k_s\) of \(f(x^k)\), \(f(x^k+s^k)\), \(h(x^k)\) and \(h(x^k+s^k)\), respectively at trial points \(x^k\in {\mathcal {V}}^k\) and \(x^k+s^k\in {\mathcal {P}}^k\), but also upper bounds \(u^k_s(x^k+s^k)\) and \(u^k_0(x^k_{\text {inf}})\), respectively for \(h(x^k+s^k)\) and \(h(x^k_{\text {inf}})\). The values of such estimates and bounds determine the iteration type of the algorithm and govern the way \(\delta ^k_p\) is updated. Adapting the terminologies from [9] and depending on the values of the aforementioned estimates and bounds, there are four StoMADS-PB iteration types: an iteration can be either f-Dominating, h-Dominating (the former and the latter are referred to as Dominating iterations), Improving, or Unsuccessful. During a Dominating iteration, either the algorithm has evaluated its first \(\varepsilon \)-feasible point or a trial point that dominates an incumbent is generated. An iteration which is Improving is not Dominating but it aims to improve the feasibility of the \(\varepsilon \)-infeasible incumbent. Unsuccessful iterations are those that are neither Dominating nor Improving.
-
At the beginning of iteration k, if no available \(\varepsilon \)-feasible solution has been evaluated yet, then the iteration is called f-Dominating if for \(x^k\in {\mathcal {V}}^k\), a trial point \(x^k+s^k\in {\mathcal {P}}^k\) satisfying \(u^k_s(x^k+s^k)=0\) is found, in which case \(h(x^k+s^k)=0\) due to Proposition 2.2, meaning that \(x^k+s^k\) is \(\varepsilon \)-feasible. Otherwise, if an \(\varepsilon \)-feasible point that dominates the incumbent is generated, i.e., \(x^k+s^k \prec _{f;\varepsilon }x^k_{\text {feas}}\) for some \(x^k\in {\mathcal {V}}^k\), then the inequality \(f^k_s(x^k+s^k)-f^k_0(x^k_{\text {feas}})\le -\gamma \varepsilon (\delta ^k_p)^2\) leads to a decrease in f due to Proposition 2.7. In either case, \(x^{k+1}_{\text {feas}}:=x^k+s^k\) and \(\delta _p^{k+1}= \min \{\tau ^{-1}\delta ^k_p,\tau ^{-{\hat{z}}}\}\). The \(\varepsilon \)-infeasible incumbent \(x^k_{\text {inf}}\) is not updated, since there is no feasibility improvement.
-
Iteration k is said to be h-Dominating whenever an \(\varepsilon \)-infeasible point that dominates the incumbent is generated, i.e., \(x^k_{\text {inf}}+s^k \prec _{h;\varepsilon }x^k_{\text {inf}}\), which means that both inequalities \(f^k_s(x^k_{\text {inf}}+s^k)-f^k_0(x^k_{\text {inf}})\le -\gamma \varepsilon (\delta ^k_p)^2\) and \(h^k_s(x^k_{\text {inf}}+s^k)-h^k_0(x^k_{\text {inf}})\le -\gamma m\varepsilon (\delta ^k_p)^2\) hold. Consequently, it follows from Propositions 2.4 and 2.7 that decreases occur both in f and h. In this case, \(x^{k+1}_{\text {feas}}=x^k_{\text {feas}}\) and since feasibility is improved, \(x^{k+1}_{\text {inf}}\) is set to equal \(x^k_{\text {inf}}+s^k\) while the poll size parameter is updated as in f-Dominating iterations.
-
Iteration k is said to be Improving if it is not Dominating but at least one \(\varepsilon \)-infeasible point \(x^k_{\text {inf}}+s^k\) is evaluated satisfying \(h^k_s(x^k_{\text {inf}}+s^k)-h^k_0(x^k_{\text {inf}})\le -\gamma m\varepsilon (\delta ^k_p)^2\). Indeed, this means that \(x^k_{\text {inf}}+s^k\) improves the feasibility of the \(\varepsilon \)-infeasible incumbent \(x^k_{\text {inf}}\) since the previous inequality leads to a decrease in h due to Proposition 2.4. In this case, \(\delta ^k_p\) is updated as in Dominating iterations, \(x^{k+1}_{\text {feas}}=x^k_{\text {feas}}\) while the \(\varepsilon \)-infeasible incumbent is updated according to
$$\begin{aligned} x^{k+1}_{\text {inf}}\in \underset{{x^k_{\text {inf}}+s^k}}{\arg \!\min } \left\{ u^k_s(x^k_{\text {inf}}+s^k): h^k_s(x^k_{\text {inf}}+s^k)-h_0^k(x^k_{\text {inf}})\le -\gamma m\varepsilon (\delta ^k_p)^2\right\} . \end{aligned}$$ -
Finally, an iteration is called Unsuccessful if it is neither Dominating nor Improving. In this case, \(\delta _p^{k+1}=\tau \delta ^k_p\) while neither \(x^k_{\text {inf}}\) nor \(x^k_{\text {feas}}\) are updated.
While \(x^k_{\text {inf}}\) is updated at the end of each iteration of StoMADS-PB, the barrier threshold is computed at the beginning of each iteration according to \(h^k_{\max }=u^k_0(x^k_{\text {inf}})\) in order to avoid keeping its possibly inaccurate values from one iteration to another. In fact, estimates in StoMADS-PB are always computed at the beginning of each iteration and their accuracies are improved compared to previous iterations as will be seen in Sect. 5.1. Consequently, even though the sequence \(\{h^k_{\max }\}_{k\in {\mathbb {N}}}\) has a decreasing tendency, it can possibly increase between successive iterations, unlike in the deterministic setting. The goal of StoMADS-PB is to accept only trial points satisfying \(h(x^k)\le h^k_{\max }\). Any trial point \(x^k\) for which the inequality \(u^k_0(x^k)\le h^k_{\max }\) does not hold is discarded since such an inequality implies that \(h(x^k)\le h^k_{\max }\) due to (4). However, this is a sufficient acceptance condition since \(u^k_0(x^k)>h^k_{\max }\) does not necessarily imply that \(h(x^k)\le h^k_{\max }\) does not hold, but rather leads to a situation of uncertainty which is not explicitly distinguished in the present manuscript for the sake of simplicity.
Remark 2.12
Let \(t\ge 1\) be such that \({t-1}\) is the index of the first f-Dominating iteration of Algorithm 2 and assume that \(t<+\infty \). Then in Algorithm 2, \(x^k_{\text {feas}}=x^0_{\text {inf}}\) for all \(k=0,1,\dots ,{t-1}\) while \(x^{t}_{\text {feas}}=x^{(t-1)+1}_{\text {feas}}\ne x^0_{\text {inf}}\). Moreover, even though estimates \(f^k_0(x^k_{\text {feas}})\), \(f^k_s(x^k_{\text {feas}}+s^k)\), \(h^k_0(x^k_{\text {feas}})\) and \(h^k_s(x^k_{\text {feas}}+s^k)\) are computed at \(x^k_{\text {feas}}\) and \(x^k_{\text {feas}}+s^k\in {\mathcal {P}}^k\) respectively for all \(k\le {t-1}\), they are not used by the algorithm until the end of iteration \({t-1}\) and one can even notice that for all \(k\le {t-1}\), \(x^k_{\text {feas}}\) is not an \(\varepsilon \)-feasible point in the sense of Definition 2.9. Furthermore, no point in \({\mathcal {P}}^k\) generated using \({\mathbb {D}}^k_p(x^k_{\text {feas}})\) is evaluated until the end of iteration \({t-1}\). In fact, setting \(x^0_{\text {feas}}\) to equal \(x^0_{\text {inf}}\) as is done in Algorithm 2 and then computing the latter estimates are not necessary in practice. However, doing so allows simply the aforementioned estimates to be defined for all \(k\ge 0\) for theoretical needs, specifically the construction of the \(\sigma \)-algebra \({\mathcal {F}}^{C\cdot F}_{k-1}\) in Sect. 3. As emphasized in Definition 2.11, observe that for all \(k\le {t-1}\), there is only one incumbent (\(\varepsilon \)-infeasible) solution \(x^k_{\text {inf}}\) according to Definition 2.9.
2.3 Frame center selection rule
Before describing the frame center selection rule, recall the set \({\mathcal {V}}^k\) of incumbent solutions introduced in Definition 2.11 and the fact that POLL trial points are generated inside frames around such incumbents. At a given iteration, there are either one or two frame centers in \({\mathcal {V}}^k\). When \({\mathcal {V}}^k\) contains only one point, then using terminologies from [9], that point is called the primary frame center. In the event that there are two incumbent solutions \(x^k_{\text {inf}}\) and \(x^k_{\text {feas}}\), one of them is chosen as the primary frame center while the other one is the secondary frame center. Because of the unavailability of f function values for StoMADS-PB, a specific frame center selection strategy (inspired by Section 2.5 of [9]) using estimates of such function values is proposed and relies on the following result.
Proposition 2.13
Let \(f^k_0(x^k_{\text {feas}})\) and \(f^k_0(x^k_{\text {inf}})\) be \(\varepsilon \)-accurate estimates of \(f(x^k_{\text {feas}})\) and \(f(x^k_{\text {inf}})\) respectively. Let \(\rho >0\) be a scalar.
Proof
Assume that \(f^k_0(x^k_{\text {feas}})-\rho >f^k_0(x^k_{\text {inf}})+2\varepsilon (\delta ^k_p)^2\). Then, it follows from the \(\varepsilon \)-accuracy of \(f^k_0(x^k_{\text {feas}})\) and \(f^k_0(x^k_{\text {inf}})\) that
\(\square \)
Based on the result of Proposition 2.13, \(x^k_{\text {feas}}\) is always chosen as the StoMADS-PB primary frame center unless the estimates \(f^k_0(x^k_{\text {feas}})\) and \(f^k_0(x^k_{\text {inf}})\) satisfy the sufficient decrease condition in (11) leading to the inequality \(f(x^k_{\text {feas}})-\rho >f(x^k_{\text {inf}})\), which as in [9] allows the choice of the infeasible incumbent solution as primary frame center.
3 Stochastic process generated by StoMADS-PB
The stochastic quantities in the present work are all defined on the same probability space \((\Omega ,{\mathcal {G}},{\mathbb {P}})\). The nonempty set \(\Omega \) is referred to as the sample space and its subsets are called events. The collection \({\mathcal {G}}\) of such events is called a \(\sigma \)-algebra or \(\sigma \)-field and \({\mathbb {P}}\) is a finite measure satisfying \({\mathbb {P}}(\Omega )=1\), referred to as probability measure and defined on the measurable space \((\Omega ,{\mathcal {G}})\). Each element \(\omega \in \Omega \) is referred to as a sample point. Let \({\mathcal {B}}({\mathbb {R}}^n)\) be the Borel \(\sigma \)-algebra of \({\mathbb {R}}^n\), i.e., the one generated by its open sets. A random variable X is a measurable map defined on \((\Omega ,{\mathcal {G}},{\mathbb {P}})\) into the measurable space \(({\mathbb {R}}^n,{\mathcal {B}}({\mathbb {R}}^n))\), where measurability means that each event \(\{X\in B \}:=X^{-1}(B)\) belongs to \({\mathcal {G}}\) for all \(B\in {\mathcal {B}}({\mathbb {R}}^n)\) [20, 33].
The estimates \(f^k_0(x^k)\), \(f^k_s(x^k+s^k)\), \(c^k_{j,0}(x^k)\) and \(c^k_{j,s}(x^k+s^k)\), for \(j=1,2,\dots ,m\), \(x^k\in \{x^k_{\text {inf}},x^k_{\text {feas}}\}\) and \(x^k+s^k\in {\mathcal {P}}^k\), of function values are computed at every iteration of Algorithm 2 using the noisy blackbox evaluations. Because of the randomness of the blackbox outputs, such estimates can respectively be considered as realizations of random estimates \(F^k_0(X^k)\), \(F^k_s(X^k+S^k)\), \(C^k_{j,0}(X^k)\) and \(C^k_{j,s}(X^k+S^k)\), for \(j=1,2,\dots ,m\). Since each iteration k of Algorithm 2 is influenced by the randomness stemming from such random estimates, Algorithm 2 results in a stochastic process. For the remainder of the manuscript, uppercase letters will be used to denote random quantities while their realizations will be denoted by lowercase letters. Thus, \(x^k=X^k(\omega )\), \(x^k_{\text {inf}}=X^k_{\text {inf}}(\omega )\), \(x^k_{\text {feas}}=X^k_{\text {feas}}(\omega )\), \(s^k=S^k(\omega )\), \(\delta ^k_p=\Delta ^k_p(\omega )\) and \(\delta ^k_m=\Delta ^k_m(\omega )\) denote respectively realizations of \(X^k\), \(X^k_{\text {inf}}\), \(X^k_{\text {feas}}\), \(S^k\), \(\Delta ^k_p\) and \(\Delta ^k_m\). Similarly, \(f^k_0(x^k)=F^k_0(X^k)(\omega )\), \(f^k_s(x^k+s^k)=F^k_s(X^k+S^k)(\omega )\), \(c^k_{j,0}(x^k)=C^k_{j,0}(X^k)(\omega )\), \(c^k_{j,s}(x^k+s^k)=C^k_{j,s}(X^k+S^k)(\omega )\), \(h^k_0(x^k)=H^k_0(X^k)(\omega )\), \(h^k_s(x^k+s^k)=H^k_s(X^k+S^k)(\omega )\), \(\ell ^k_0(x^k)=L^k_0(X^k)(\omega )\), \(\ell ^k_s(x^k+s^k)=L^k_s(X^k+S^k)(\omega )\), \(u^k_0(x^k)=U^k_0(X^k)(\omega )\) and \(u^k_s(x^k+s^k)=U^k_s(X^k+S^k)(\omega )\). When there is no ambiguity, \(F^k_0\) will be used instead of \(F^k_0(X^k)\), etc. In general, following the notations in [11, 21, 23, 33, 48], \(F^k_0\), \(F^k_s\), \(H^k_0\) and \(H^k_s\) are respectively the estimates of \(f(X^k)\), \(f(X^k+S^k)\), \(h(X^k)\) and \(h(X^k+S^k)\). Moreover, as highlighted in [11], the notation “\(f(X^k)\)” is used to denote the random variable with realizations \(\left\{ f(X^k(\omega )):\omega \in \Omega \right\} \).
The present research aims to show that the stochastic process \(\Big \{X^k_{\text {inf}},X^k_{\text {feas}},\Delta ^k_p,\Delta ^k_m,F^k_0,F^k_s,H^k_0,H^k_s,L^k_0,U^k_0,L^k_s,U^k_s\Big \}\) resulting from Algorithm 2 has desirable convergence properties with probability one under some assumptions on the estimates \(F^k_0\), \(F^k_s\), \(C^k_{j,0}\), \(C^k_{j,s}\), \(H^k_0\), \(H^k_s\) and on the bounds \(L^k_0\), \(U^k_0\), \(L^k_s\), \(U^k_s\). In particular, the estimates \(F^k_0,F^k_s,C^k_{j,0}\) and \(C^k_{j,s}\) will be assumed to be \(\varepsilon \)-accurate while the bounds will be assumed to be \(\varepsilon \)-reliable, with sufficiently high, but fixed, probabilities conditioned on the past.
3.1 Probabilistic bounds and probabilistic estimates
The notion of conditioning on the past is formalized following [11, 21, 23, 33, 48]. Denote by \({\mathcal {F}}^{C\cdot F}_{k-1}\) the \(\sigma \)-algebra generated by \(F_0^{\ell }(X^{\ell })\), \(F_s^{\ell }(X^{\ell }+S^{\ell })\), \(C_{j,0}^{\ell }(X^{\ell })\) and \(C_{j,s}^{\ell }(X^{\ell }+S^{\ell })\), for \(j=1,2,\dots ,m\), for \(X^{\ell }\in \left\{ X^{\ell }_{\inf },X^{\ell }_{\text {feas}}\right\} \) and for \(\ell =0,1,\dots ,k-1\). For completeness, \({\mathcal {F}}^{C\cdot F}_{-1}\) is set to equal \(\sigma (x^0)=\sigma (x^0_{\text {inf}})\). Thus, \(\{{\mathcal {F}}^{C\cdot F}_k\}_{k\ge -1}\) is a filtration, i.e., a sequence of increasing \(\sigma \)-algebras of \({\mathcal {G}}\).
Sufficient accuracy of function estimates is measured using the poll size parameter and is formalized, following [11, 21, 23, 33, 48], by means of the definitions below.
Definition 3.1
A sequence of random estimates \(\{F^k_0,F^k_s\}\) is said to be \(\beta \)-probabilistically \(\varepsilon \)-accurate with respect to the sequence \(\{X^k, S^k, \Delta ^k_p\}\) if the events
satisfy the submartingale-like condition
where \(\mathbb {1}_{J_k}\) denotes the indicator function of the event \(J_k\), i.e., \(\mathbb {1}_{J_k}=1\) if \(\omega \in J_k\) and \(\mathbb {1}_{J_k}=0\) otherwise. The estimates are called “good” if \(\mathbb {1}_{J_k}=1\). Otherwise they are called “bad”.
Definition 3.2
A sequence of random estimates \(\{C^k_{j,0},C^k_{j,s}\}\) is said to be \(\alpha ^{1/m}\)-probabilistically \(\varepsilon \)-accurate for some \(j=1,2,\dots ,m\) with respect to the corresponding sequence \(\{X^k, S^k, \Delta ^k_p\}\) if the events
satisfy the submartingale-like condition
Recall the \(\varepsilon \)-reliable bounds \(\ell ^k_0, u^k_0\) for \(h(x^k)\), and \(\ell ^k_s, u^k_s\) for \(h(x^k+s^k)\) provided by Proposition 2.2 making use of \(\varepsilon \)-accurate estimates \(c^k_{j,0}\) and \(c^k_{j,s}\), for all \(j\in J\). Since Algorithm 2 results in a stochastic process introducing random bounds \(L^k_0, U^k_0, L^k_s\) and \(U^k_s\) with realizations \(\ell ^k_0, u^k_0, \ell ^k_s\) and \(u^k_s\) respectively, the reliability of such random bounds has to be quantified probabilistically, using Definition 3.2 and inspired by Definition 3.1. Indeed, in order to show later in Sect. 4 that the stochastic process resulting from Algorithm 2 has desirable convergence properties, the reliability of the random bounds will be required to hold with sufficiently high probability. This notion of sufficient reliability introduced in the present work is formalized next.
Definition 3.3
A sequence of random bounds \(\{L^k_0, U^k_0,L^k_s, U^k_s\}\) is said to be \(\alpha \)-probabilistically \(\varepsilon \)-reliable with respect to the corresponding sequence \(\{X^k, S^k, \Delta ^k_p\}\) if the events
satisfy the submartingale-like condition
The bounds are called “good” if \(\ \mathbb {1}_{I_k}=1\). Otherwise, \(\ \mathbb {1}_{I_k}=0\) and they are called “bad”.
The p-integrability of random variables [11, 20] is defined below and will be useful for the analysis of Algorithm 2.
Definition 3.4
Let \((\Omega ,{{\mathcal {G}}},{\mathbb {P}})\) be a probability space and let \(p\in [1,+\infty )\) be an integer. Then the space \({{\mathbb {L}}}^p(\Omega ,{\mathcal {G}},{\mathbb {P}})\) of so-called p-integrable random variables is the set of all real-valued random variables X such that
As in [11], the following is assumed in order for the random variables \(f(X^k)\), \(h(X^k)\) and \(c_j(X^k)\), \(j\!\!\in \!\! J\), to be integrable so that the conditional expectations \({\mathbb {E}}\left( f(X^k)|{\mathcal {F}}^{C\cdot F}_{k-1}\right) \), \({\mathbb {E}}\left( c_j(X^k)|{\mathcal {F}}^{C\cdot F}_{k-1}\right) \), \(j\in J\) and \({\mathbb {E}}\left( h(X^k)|{\mathcal {F}}^{C\cdot F}_{k-1}\right) \) are well-defined [20].
In the assumption below, f and h are assumed to be locally Lipschitz. In general, a function \(g:{\mathcal {X}}\rightarrow {\mathbb {R}}\) is called locally Lipschitz if it is Lipschitz with a finite constant in some nonempty open neighborhood intersected with \({\mathcal {X}}\) [9].
Assumption 2
The objective function f and the constraint violation function h are locally Lipschitz with constants \(\lambda ^f>0\) and \(\lambda ^h>0\), respectively. The constraint functions \(c_j\), \(j\in J\), are continuous on \({\mathcal {X}}\). The set \({\mathcal {U}}\subset {\mathcal {X}}\) containing all incumbents realizations is compact.
Proposition 3.5
Under Assumption 2, there exists a finite constant \(\kappa ^f_{\max }\) satisfying \(\left|f(x^k)\right|\le \kappa ^f_{\max }\ \) for all \(x^k\in {\mathcal {U}}\). Moreover, the random variables \(f(X^k)\), \(h(X^k)\), \(c_j(X^k)\) and \(\Delta ^k_p\) belong to \({\mathbb {L}}^1(\Omega ,{\mathcal {G}},{\mathbb {P}})\), for all \(j\in J\) and for all \(k\ge 0\).
Proof
Since f is locally Lipschitz on the compact set \({\mathcal {U}}\), f is bounded on \({\mathcal {U}}\). Consequently, there exists a finite constant \(\kappa ^f_{\max }\) such that \(\left|f(x^k)\right|\le \kappa ^f_{\max }\ \) for all \(x^k\in {\mathcal {U}}\). Similarly, there exist \(\kappa ^h_{\max }\) satisfying \(\left|h(x^k)\right|\le \kappa ^h_{\max } \) and \(\kappa ^c_{\max }\) such that \(\left|c_j(x^k)\right|\le \kappa ^c_{\max }\ \) for all \(j\in J\) and all \(x^k\in {\mathcal {U}}\) since h is locally Lipschitz and \(c_j\) is continuous on \({\mathcal {U}}\). Thus, \({\mathbb {E}}\left( \left|f(X^k)\right|\right) :=\int _{\Omega }\left|f(X^k(\omega ))\right| {\mathbb {P}}(d\omega )\le \kappa ^f_{\max }<+\infty \). Similarly, \({\mathbb {E}}\left( \left|h(X^k)\right|\right) \le \kappa ^h_{\max }\le +\infty \) and for all \(j\in J\), \({\mathbb {E}}\left( \left|c_j(X^k)\right|\right) \le \kappa ^c_{\max }\le +\infty \). Finally, the integrability of \(\Delta ^k_p\) follows from the fact that \(\Delta ^k_p(\omega )\le \tau ^{-{\hat{z}}}\) for all \(\omega \in \Omega \), which implies that \({\mathbb {E}}\left( \left|\Delta ^k_p\right|\right) :=\int _{\Omega }\left|\Delta ^k_p(\omega )\right| {\mathbb {P}}(d\omega )\le \tau ^{-{\hat{z}}}<+\infty \). \(\square \)
Next are stated some key assumptions on the stochastic variables in Algorithm 2, some of which are made in [11] and will be useful for the convergence analysis in Sect. 4. Approaches for computing random estimates and bounds satisfying these assumptions in a simple random noise framework are discussed in Sect. 5.1.
Assumption 3
For fixed \(\alpha , \beta \in (0,1)\), the following hold for the random quantities generated by Algorithm 2 at iteration k.
-
(i)
The sequence of estimates \(\{F^k_0,F^k_s\}\) generated by Algorithm 2 is \(\beta \)-probabilistically \(\varepsilon \)-accurate.
-
(ii)
The sequence of estimates \(\{F^k_0,F^k_s\}\) generated by Algorithm 2 satisfies the following variance condition for all \(k\ge 0\) :
$$\begin{aligned} \begin{aligned}&{\mathbb {E}}\left( \left|F^k_s-f(X^k+S^k)\right|^2 |\ {\mathcal {F}}^{C\cdot F}_{k-1}\right) \le \varepsilon ^2(1-\sqrt{\beta })(\Delta ^k_p)^4\\&\quad \text {and}\quad {\mathbb {E}}\left( \left|F^k_0-f(X^k)\right|^2 |\ {\mathcal {F}}^{C\cdot F}_{k-1}\right) \le \varepsilon ^2(1-\sqrt{\beta })(\Delta ^k_p)^4. \end{aligned} \end{aligned}$$(12) -
(iii)
For all \(j=1,2,\dots ,m\), the sequence of estimates \(\{C^k_{j,0},C^k_{j,s}\}\) is \(\alpha ^{1/m}\)-probabilistically \(\varepsilon \)-accurate.
-
(iv)
For all \(j=1,2,\dots ,m\), the sequence of estimates \(\{C^k_{j,0},C^k_{j,s}\}\) satisfies the following variance condition for all \(k\ge 0\) :
$$\begin{aligned} \begin{aligned}&{\mathbb {E}}\left( \left|C^k_{j,s}-c_j(X^k+S^k)\right|^2 |\ {\mathcal {F}}^{C\cdot F}_{k-1}\right) \le \varepsilon ^2\left( 1-\alpha ^{1/2m}\right) (\Delta ^k_p)^4\\&\quad \text {and}\quad {\mathbb {E}}\left( \left|C^k_{j,0}-c_j(X^k)\right|^2 |\ {\mathcal {F}}^{C\cdot F}_{k-1}\right) \le \varepsilon ^2\left( 1-\alpha ^{1/2m}\right) (\Delta ^k_p)^4. \end{aligned} \end{aligned}$$(13) -
(v)
The sequence of random bounds \(\{L^k_0, U^k_0,L^k_s, U^k_s\}\) is \(\alpha \)-probabilistically \(\varepsilon \)-reliable.
An iteration k for which \(\mathbb {1}_{I_k}\mathbb {1}_{J_k}=1\), i.e., for which the events \(I_k\) and \(J_k\) both occur, will be called “true”. Otherwise, k will be called “false”. Even though the present algorithmic framework does not allow one to determine which iterations are true or false, Theorem 3.6 shows that true iterations occur infinitely often. Theorem 3.6 will also be useful for the convergence analysis of Algorithm 2, more precisely in Sect. 4.3.
Theorem 3.6
Assume that Assumption 3 holds for \(\alpha \beta \in (1/2,1)\). Then true iterations of Algorithm 2 occur infinitely often.
Proof
Consider the random walk
Then, since \(W_k\) is a submartingale with bounded increments (and, as such, cannot converge), the result follows from the fact that \(\left\{ \underset{k\rightarrow +\infty }{\limsup }\ W_k=+\infty \right\} \) occurs almost surely, the proof of which can be derived from that of Theorem 4.16 in [23], where a similar random walk was studied. Indeed, the latter result means that
which implies that \(\mathbb {1}_{I_i}\mathbb {1}_{J_i}=1\) infinitely often. \(\square \)
The following lemma will be useful later in the analysis of StoMADS-PB. In fact, for a given realization of Algorithm 2, the inequality \(h^k_s-h^k_0\le -\gamma m\varepsilon (\delta ^k_p)^2\) leads to a decrease in h at iteration k as was shown in Proposition 2.4 if the event \(I_k\) occurs, i.e., when the bounds are \(\varepsilon \)-reliable. But when the bounds are not \(\varepsilon \)-reliable, the algorithm can accept a step which leads to an increase in h. Later in the proof of Theorem 4.2, such an increase will be controlled in expectation by making use of (15).
Lemma 3.7
Let Assumption 3-(iv) hold for \(\alpha \in (0,1)\). The sequence of random estimated violations \(\{H^k_0,H^k_s\}\) satisfies
Proof
Before showing (15), observe that
where the last inequality in (16) follows from the inequality \(\left|\max \{x,0\} - \max \{y,0\}\right|\le \left|x-y\right|\), for all \(x,y\in {\mathbb {R}}\). Moreover, it follows from the conditional Cauchy-Schwarz inequality [20] that for all \(j\in J\),
where the first inequality in (17) follows from (13). Thus, taking the conditional expectation with respect to \({\mathcal {F}}^{C\cdot F}_{k-1}\) in (16) and then using (17) yield
\(\square \)
4 Convergence analysis
Using ideas inspired by [9, 11, 23, 40, 48], this section presents convergence results of StoMADS-PB, most of which are stochastic variants of the convergence results in [9]. It introduces the random time T at which Algorithm 2 generates a first \(\varepsilon \)-feasible solution. Then assuming that T is either almost surely finite or almost surely infinite, a so-called zeroth-order result [10, 11] is derived showing that there exists a subsequence of Algorithm 2-generated random incumbents with mesh realizations becoming infinitely fine and which converges with probability one to a limit. This is achieved by showing, by means of Theorem 4.2, that the sequence of random poll size parameters converges to zero with probability one. Section 4.2 analyzes the function h and the random \(\varepsilon \)-infeasible incumbents generated by Algorithm 2. In particular, it gives conditions under which an almost sure limit of a subsequence of such incumbents is shown in Theorem 4.10 to satisfy a first-order necessary optimality condition via the Clarke generalized derivative of h with probability one. Then, a similar result for f and the sequence of \(\varepsilon \)-feasible incumbents is derived in Theorem 4.14 of Sect. 4.3. The proofs of the main results of this section are presented in the Appendix. For the sake of clarity in the presentation, the following definition is introduced.
Definition 4.1
A sequence \(\left\{ X^k\right\} _{k\in {\mathbb {N}}}\) of StoMADS-PB random incumbents is either a sequence \(\left\{ X^{k\vee T}_{\text {feas}}\right\} _{k\in {\mathbb {N}}}\) of random \(\varepsilon \)-feasible incumbents provided \(T<+\infty \) almost surely, or a sequence \(\left\{ X^k_{\text {inf}}\right\} _{k\in {\mathbb {N}}}\) of random \(\varepsilon \)-infeasible incumbents. A similar definition is considered for the sequences of realizations \(\left\{ x^k\right\} _{k\in {\mathbb {N}}}\), \(\left\{ x^{k\vee t}_{\text {feas}}\right\} _{k\in {\mathbb {N}}}\) and \(\left\{ x^k_{\text {inf}}\right\} _{k\in {\mathbb {N}}}\) of \(\left\{ X^k\right\} _{k\in {\mathbb {N}}}\), \(\left\{ X^{k\vee T}_{\text {feas}}\right\} _{k\in {\mathbb {N}}}\) and \(\left\{ X^k_{\text {inf}}\right\} _{k\in {\mathbb {N}}}\) respectively, where t denotes a realization of T.
4.1 Zeroth-order convergence
Recall Remark 2.12 and denote by \({\mathscr {S}}^k_X=\{X^{\ell }_{\text {feas}}:X^{\ell }_{\text {feas}}\ne x^0_{\text {inf}},\ \ell \le k\}\) the set of all random \(\varepsilon \)-feasible incumbents generated by Algorithm 2 until the beginning of iteration k. Consider the random time T defined by
Then, \(T\ge 1\) and for all \(k\ge 1\), the occurrence of the event \(\{T\le k\}\) is determined by observing the random quantities generated by Algorithm 2 until the iteration \(k-1\), which means that T is a stopping time [32] for the stochastic process generated by Algorithm 2. For a given \(\omega \in \Omega \), \(t=T(\omega )\) is the number of iterations required by Algorithm 2 to find a first point which is \(\varepsilon \)-feasible in the sense of Definition 2.6. Just as a BBO method in a deterministic framework is not always guaranteed to find feasible points even though the feasible region \({\mathcal {D}}\) is nonempty, the algorithmic framework proposed in the present manuscript does not guarantee that t will always be finite for every realization of the stochastic process generated by Algorithm 2 even when \({\mathcal {D}}\) is nonempty. Thus, T could either be finite almost surely depending on the optimization problem or satisfy \({\mathbb {P}}\left( T<+\infty \right) \le 1-\zeta \) for some \(\zeta \in (0, 1]\). In the latter case, the algorithm will fail to generate \(\varepsilon \)-feasible incumbents with a probability of at least \(\zeta \), in which case an almost sure convergence result related to such incumbents cannot be derived. The following is therefore assumed for the remainder of the analysis.
Assumption 4
The stopping time T associated to the stochastic process generated by Algorithm 2 is either almost surely finite or almost surely infinite.
The next result implies that the sequence \(\{\Delta ^k_p\}_{k\in {\mathbb {N}}}\) of random frame size parameters converges to zero with probability one and will be useful for the Clarke stationarity results of Sects. 4.2 and 4.3. It holds under the assumption below.
Assumption 5
The objective function f is bounded from below, i.e., there exists \(\kappa ^f_{\min }\in {\mathbb {R}}\) such that \(-\infty <\kappa ^f_{\min }\le f(x)\), for all \(x\in {\mathbb {R}}^n\).
Theorem 4.2
Let Assumptions 1, 2, 4 and 5 be satisfied. Let \(\gamma >2\) and \(\tau \in (0,1)\cap {\mathbb {Q}}\). Let \(\nu \in (0,1)\) be chosen such that
Assume further that Assumption 3 holds for \(\alpha \) and \(\beta \) chosen such that
Then, the sequence \(\{\Delta ^k_p\}_{k\in {\mathbb {N}}}\) of frame size parameters generated by Algorithm 2 satisfies
The following result is an immediate consequence of Theorem 4.2. It shows that the sequences \(\{\Delta ^k_m\}_{k\in {\mathbb {N}}}\) and \(\{\Delta ^k_p\}_{k\in {\mathbb {N}}}\) converge to zero almost surely respectively.
Corollary 4.3
The following hold under all the assumptions made in Theorem 4.2
The next result shows that, with probability one, the differences between the estimates and their corresponding true function values converge to zero. This means that Algorithm 2 behaves like an exact deterministic method asymptotically. This result will also be useful in Sect. 4.3 for the proof of Theorem 4.13.
Corollary 4.4
Let all assumptions that were made in Theorem 4.2 hold. Then,
Likewise, \(\left|H^k_s-h(X^k+S^k)\right|\) and \(\left|F^k_s-f(X^k+S^k)\right|\) respectively.
Definition 4.5
A convergent subsequence \(\{x^k\}_{k\in {\mathcal {K}}}\) of Algorithm 2 incumbents, for some subset of indices \({\mathcal {K}}\), is called a refining subsequence if and only if the corresponding subsequence \(\{\delta ^k_m\}_{k\in {\mathcal {K}}}\) converges to zero. The limit \({\hat{x}}\) is called a refined point.
Corollary 4.3, along with the compactness hypothesis of Assumption 2 was shown in the proof of Theorem 2 in [11] to be enough to ensure the existence of refining subsequences. Indeed, conditioned on the event \(E_0 = \left\{ \omega \in \Omega : \lim _{k\rightarrow +\infty }\Delta ^k_m(\omega )=0\right\} \) which is almost sure due to Corollary 4.3, the aforementioned proof applies to the next theorem.
Theorem 4.6
Let the assumptions that were made in Corollary 4.3 hold. Then there almost surely exists at least one refining subsequence \(\{X^k\}_{k\in K}\) (where K is a sequence of random variables) that converges to a refined point \({\hat{X}}\).
4.2 Nonsmooth optimality conditions: Results for h
This subsection aims to show that there almost surely exists a refining subsequence \(\{X^k_{\text {inf}}\}_{k\in K}\) generated by StoMADS-PB that converges to a refined point \({\hat{X}}_{\inf }\) which satisfies a necessary optimality condition via the Clarke generalized derivative of h with probability one. As in [11], this optimality result strongly relies on the requirement that the polling directions \(d^k\in {\mathbb {D}}^k_p(x^k_{\text {inf}})\) of Algorithm 2 are such that \(\delta ^k_p{\left\Vert d^k\right\Vert }_{\infty }\) never approaches zero for all k. The way such a requirement can be met is discussed in [11]. Indeed, by choosing the columns of the matrix \({\mathbf {D}}\) used in the definition of the mesh \({\mathcal {M}}^k\) to be the 2n positive and negative coordinate directions, \(\delta _p^0=1\) and \(\tau =1/2\), the directions \(\delta ^k_pd^k\) were shown in [11] to satisfy \(\delta ^k_p{\left\Vert d^k\right\Vert }_{\infty }\ge 1\) whenever \(d^k\) is constructed by means of Algorithm 1. The latter key result which holds under conditions that can also be found in Theorem 8.5 of [12], is in fact proved in [11], inspired by the proof of the latter theorem, making use of the \(\ell _{\infty }\) norm \({\left\Vert \cdot \right\Vert }_{\infty }\), for the polling directions. This motivates in particular the use of an \(\ell _{\infty }\) norm in the analysis of StoMADS-PB and later in Definition 4.8 of refining directions unlike [9] where an \(\ell _2\) norm (i.e., the euclidean norm) was used for the analysis of MADS with PB. The following assumption is made for the remainder of the analysis.
Assumption 6
Let \(d^k\in {\mathbb {D}}^k_p\) be any polling direction used by Algorithm 2 at iteration k. Then there exists a constant \(d_{\min }>0\) such that \(\delta ^k_p{\left\Vert d^k\right\Vert }_{\infty }\ge d_{\min }\ \) for all \(k\ge 0\).
The main result of this subsection relies on the properties of the random function \(\Psi _k^h\) introduced next, similar to the one used in [11].
Lemma 4.7
Let the same assumptions that were made in Theorem 4.2 hold and assume in addition to (20) that \(\alpha \beta \in (1/2,1)\). Consider the random function \(\Psi _k^h\) with realizations \(\psi _k^h\) defined by
where \(d^k\in {\mathbb {D}}^k_p(x^k_{\text {inf}})\). Then,
The following definition of refining directions [8, 12] will be useful in the analysis.
Definition 4.8
Let \({\hat{x}}\) be the refined point associated with a convergent refining subsequence \(\{x^k\}_{k\in {\mathcal {K}}}\). A direction v is said to be a refining direction for \({\hat{x}}\) if and only if there exists an infinite subset \({\mathcal {L}}\subseteq {\mathcal {K}}\) with polling directions \(d^k\in {\mathbb {D}}^k_p(x^k)\) such that \(v=\underset{k\in {\mathcal {L}}}{\lim }\frac{d^k}{{\left\Vert d^k\right\Vert }_{\infty }}\).
The analysis in this subsection also relies on the following definitions [9]. The Clarke generalized derivative \(h^{\circ }({\hat{x}};v)\) of h at \({\hat{x}}\in {\mathcal {X}}\) in the direction \(v\in {\mathbb {R}}^n\) is defined by
As highlighted in [9], this definition from [36] is a generalization of the original one by Clarke [25] to the case where the constraint violation function h is not defined outside \({\mathcal {X}}\).
The analysis involves a specific cone \(T^H_{{\mathcal {X}}}({\hat{x}}_{\inf })\) called the hypertangent cone [50] to \({\mathcal {X}}\) at \({\hat{x}}_{\inf }\). The hypertangent cone to a subset \({\mathcal {O}}\subseteq {\mathcal {X}}\) at \({\hat{x}}\) is defined by
The next lemma from elementary analysis [9] will be useful in the present analysis.
Lemma 4.9
If \(\{a_k\}\) is a bounded real sequence and \(\{b_k\}\) is a convergent real sequence, then
The next result which is a stochastic variant of Theorem 3.5 in [9] presents a necessary optimality condition (see e.g. Theorem 6.10 of [12]) based on the hypertangent cone definition. It states that almost surely, the refined point \({\hat{X}}_{\inf }\) of a convergent \(\varepsilon \)-infeasible refining subsequence \(\{X^k_{\text {inf}}\}_{k\in K}\) is a hypertangent stationary point of h over \({\mathcal {X}}\). Since the inequality \(h(x^k_{\text {inf}}+\delta ^k_md^k)-h(x^k_{\text {inf}})\ge 0\), on which relies the proof of Theorem 3.5 in [9] does not hold in the present stochastic setting, the proof of this novel result uses the random function \(\Psi _k^h\) and the result of Lemma 4.7.
Theorem 4.10
Let Assumptions 1, 6 and all the assumptions made in Theorem 4.2 and Lemma 4.7 hold. Then there almost surely exists a convergent \(\varepsilon \)-infeasible refining subsequence \(\{X^k_{\text {inf}}\}_{k\in K}\) generated by Algorithm 2, for some sequence \(K\subseteq K'\) of random variables satisfying \(\lim _{K'} \Psi _k^h\le 0\) almost surely, such that if \({\hat{x}}_{\inf }\in {\mathcal {X}}\) is a refined point for a realization \(\{x^k_{\text {inf}}\}_{k\in {\mathcal {K}}}\) of \(\{X^k_{\text {inf}}\}_{k\in K}\) for which the events \(\Delta ^k_p\rightarrow 0\) and \(\lim _{K'} \Psi _k^h\le 0\) both occur, and if \(v\in T^H_{{\mathcal {X}}}({\hat{x}}_{\inf })\) is a refining direction for \({\hat{x}}_{\inf }\), then \(h^{\circ }({\hat{x}}_{\inf };v)\ge 0\). In particular, this means that
Next is stated a stochastic variant of a result in [9], showing that Clarke stationarity is guaranteed with probability one when the set of refining directions is dense in a nonempty hypertangent cone to \({\mathcal {X}}\).
Corollary 4.11
Let all assumptions that were made in Theorem 4.10 hold. Let \(\{X^k_{\text {inf}}\}_{k\in K}\) be the \(\varepsilon \)-infeasible refining subsequence of Theorem 4.10 for some sequence \(K\subseteq K'\) satisfying \(\lim _{K'} \Psi _k^h\le 0\) almost surely. If \({\hat{x}}_{\inf }\in {\mathcal {X}}\) is a refined point for a realization \(\{x^k_{\text {inf}}\}_{k\in {\mathcal {K}}}\) of \(\{X^k_{\text {inf}}\}_{k\in K}\) for which the events \(\Delta ^k_p\rightarrow 0\) and \(\lim _{K'} \Psi _k^h\le 0\) both occur, and if the set of refining directions for \({\hat{x}}_{\inf }\) is dense in \(T^H_{{\mathcal {X}}}({\hat{x}}_{\inf })\ne \emptyset \), then \({\hat{x}}_{\inf }\) is a Clarke stationary point for the problem \(\ \displaystyle {\min _{x\in {\mathcal {X}}}h(x)}\).
4.3 Nonsmooth optimality conditions: Results for f
The analysis presented in this subsection assumes that Algorithm 2 generates infinitely many \(\varepsilon \)-feasible points. It aims to show that there almost surely exists a refining subsequence \(\{X^k_{\text {feas}}\}_{k\in K}\) generated by StoMADS-PB that converges to a refined point \({\hat{X}}_{\text {feas}}\) which satisfies a necessary optimality condition via the Clarke derivative of f with probability one. The following lemma will be useful in the analysis.
Lemma 4.12
Let the same assumptions that were made in Theorem 4.2 hold and assume in addition to (20) that \(\alpha \beta \in (1/2,1)\). Assume that the random time T with realizations t is finite almost surely. Consider the random function \(\Psi _k^{f,T}\) with realizations \(\psi _k^{f,t}\) defined by
where \(k\vee t:=\max \{k,t\}\) and \(d^k\in {\mathbb {D}}^k_p(x^{k\vee t}_{\text {feas}})\) denotes any polling direction at iteration k. Then,
The next theorem shows that the almost sure limit \({\hat{X}}_{\text {feas}}\) of any convergent refining subsequence of \(\varepsilon \)-feasible incumbents which drives the random estimated violations \(H^k_0(X^k_{\text {feas}})\) to zero almost surely, satisfies \({\mathbb {P}}\left( {\hat{X}}_{\text {feas}}\in {\mathcal {D}}\right) =1\). First, the existence of such a refining subsequence can be assumed. Indeed, it is known from Theorem 3.6 that true iterations occur infinitely often provided the estimates and bounds are sufficiently accurate. In addition, every \(\varepsilon \)-feasible point \(x^k_{\text {feas}}\) accepted by Algorithm 2 satisfies \(u^k_0(x^k_{\text {feas}}) = 0 \le h^k_0(x^k_{\text {feas}})+m\varepsilon (\delta ^k_p)^2\), which implies \({\ell ^k_0(x^k_{\text {feas}})=0\ge h^k_0(x^k_{\text {feas}})-m\varepsilon (\delta ^k_p)^2}\) (see e.g. (8) and (9)), and consequently \(-m\varepsilon (\delta ^k_p)^2\le h^k_0(x^k_{\text {feas}})\le m\varepsilon (\delta ^k_p)^2\), thus leading to the overall conclusion that \(\underset{k\rightarrow +\infty }{\liminf }\ H^k_0(X^k_{\text {feas}})=0\) almost surely, which is implicitly assumed in the next theorem.
Theorem 4.13
Let all the assumptions of Lemma 4.12 hold. Let \({\hat{X}}_{\text {feas}}\) be the almost sure limit of a convergent \(\varepsilon \)-feasible refining subsequence \(\{X^{k\vee T}_{\text {feas}}\}_{k\in K}\), for which \(\underset{k\in K}{\lim } H^k_0(X^{k\vee T}_{\text {feas}})=0\) almost surely. Then
The following result which is a stochastic variant of Theorem 3.3 in [9] presents a necessary optimality condition based on the hypertangent cone definition. It states that the limit \({\hat{X}}_{\text {feas}}\) of an almost surely convergent \(\varepsilon \)-feasible refining subsequence \(\{X^k_{\text {feas}}\}_{k\in K}\) is a hypertangent stationary point of f over the feasible region \({\mathcal {D}}\), with probability one.
Theorem 4.14
Let Assumptions 1, 6 and all assumptions that were made in Theorem 4.2 and Lemma 4.12 hold. Let \(\{X^{k\vee T}_{\text {feas}}\}_{k\in K}\) be an almost surely convergent \(\varepsilon \)-feasible refining subsequence, for some sequence K of random variables satisfying \(\lim _{K} \Psi _k^{f,T}\le 0\) and \(\lim _K H^k_0(X^{k\vee T}_{\text {feas}})=0\) almost surely. If \({\hat{x}}_{\text {feas}}\in {\mathcal {D}}\) is a refined point for a realization \(\{x^{k\vee t}_{\text {feas}}\}_{k\in {\mathcal {K}}}\) of \(\{X^{k\vee T}_{\text {feas}}\}_{k\in K}\) for which the events \(\Delta ^k_p\rightarrow 0\), \(\lim _{K} \Psi _k^{f,T}\le 0\) and \(\lim _K H^k_0(X^{k\vee T}_{\text {feas}})=0\) occur, and if \(v\in T^H_{{\mathcal {D}}}({\hat{x}}_{\text {feas}})\) is a refining direction for \({\hat{x}}_{\text {feas}}\), then \(f^{\circ }({\hat{x}}_{\text {feas}};v)\ge 0\). In particular, this means that
Next is stated a stochastic variant of a result in [9] showing that Clarke stationarity is guaranteed with probability one when the set of refining directions is dense in a nonempty hypertangent cone to \({\mathcal {D}}\).
Corollary 4.15
Let all assumptions that were made in Theorem 4.14 hold. Let \(\{X^{k\vee T}_{\text {feas}}\}_{k\in K}\) be the \(\varepsilon \)-feasible refining subsequence of Theorem 4.14 where K is the sequence of random variables satisfying \(\lim _{K} \Psi _k^{f,T}\le 0\) and \(\lim _K H^k_0(X^{k\vee T}_{\text {feas}})=0\) almost surely. If \({\hat{x}}_{\text {feas}}\in {\mathcal {D}}\) is a refined point for a realization \(\{x^{k\vee t}_{\text {feas}}\}_{k\in {\mathcal {K}}}\) of \(\{X^{k\vee T}_{\text {feas}}\}_{k\in K}\) for which the events \(\Delta ^k_p\rightarrow 0\), \(\lim _{K} \Psi _k^{f,T}\le 0\) and \(\lim _K H^k_0(X^{k\vee T}_{\text {feas}})=0\) occur, and if the set of refining directions for \({\hat{x}}_{\text {feas}}\) is dense in \(T^H_{{\mathcal {D}}}({\hat{x}}_{\text {feas}})\ne \emptyset \), then \({\hat{x}}_{\text {feas}}\) is a Clarke stationary point for (1).
5 Estimates computation and computational experiments
Section 5.1 discusses approaches for computing \(\varepsilon \)-accurate random estimates and \(\varepsilon \)-reliable bounds satisfying Assumption 3 in a simple random noise framework, and hence how corresponding deterministic estimates can be obtained using evaluations of the stochastic blackbox. These approaches strongly rely on the computation of \(\alpha ^{1/m}\)-probabilistically \(\varepsilon \)-accurate estimates \(\{C^k_{j,0},C^k_{j,s}\}\), using techniques derived in [23]. Computational experiments comparing StoMADS-PB to MADS with PB are then presented in Sect. 5.2.
5.1 Computation of probabilistically accurate estimates and reliable bounds
Consider the following typical noise assumption often made in the stochastic optimization literature:
where \(V_i>0\) is a constant for all \(i=0,1,\dots ,m\). Let \(V=\max \{V_0,V_1,\dots ,V_m\}\).
For some fixed \(j\in J\), let \(\Theta _j^0\) and \(\Theta _j^s\) be two independent random variables following the same distribution as \(\Theta _j\). Let \(\Theta ^0_{j,\ell },\ \ell =1,2,\dots ,p^k_j\) and \(\Theta ^s_{j,\ell },\ \ell =1,2,\dots ,p^k_j\) be independent random samples of \(\Theta _j^0\) and \(\Theta _j^s\) respectively, where \(p_j^k\ge 1\) is an integer denoting the sample size. In order to satisfy Assumption 3-(iii), define \(C^k_{j,0}\) and \(C^k_{j,s}\) respectively by
Since \({\mathbb {E}}\left( C^k_{j,0}\right) =c_j(x^k)\) and that \({\mathbb {V}}\left( C^k_{j,0}\right) \le \frac{V}{p^k_j}\) for all j, it follows from the Chebyshev inequality that
Thus, choosing \(p^k_j\) such that
ensures that \(\frac{V}{p^k_j \varepsilon ^2(\delta ^k_p)^4}\le 1-\alpha ^{1/2m}\). Then, combining (30) and (31) yields, for all \(j\in J\),
and similarly, \({\mathbb {P}}\left( \left|C^k_{j,s}-c_j(x^k+s^k)\right|\le \varepsilon (\delta ^k_p)^2\right) \ge \alpha ^{1/2m}\). It follows from the independence of the random variables \(\Theta _j^0\) and \(\Theta _j^s\) and both previous inequalities that
which means that Assumption 3-(iii) holds. Estimates \(c^k_{j,0}=C^k_{j,0}(\omega )\) and \(c^k_{j,s}=C^k_{j,s}(\omega )\), obtained by averaging \(\, p^k_j\) realizations of \(c_{\Theta _j}\) resulting from the evaluations of the stochastic blackbox, respectively at \(x^k\) and \(x^k+s^k\), are obviously \(\alpha ^{1/m}\)-probabilistically \(\varepsilon \)-accurate.
In order to satisfy Assumption 3-(v), notice that the independence of the random variables \(\Theta _j, j\in J\) combined with (32) implies
Define the random bounds \(L^k_0(x^k)\), \(\ L^k_s(x^k+s^k)\), \(\ U^k_0(x^k)\ \) and \(\ U^k_s(x^k+s^k),\ \) respectively by
Define the events \(E_0^k\) and \(E_s^k\) respectively by
Because
and
combining respectively (34) and (37), and (35) and (38), lead to
It follows from the independence of the random variables \(\Theta ^0_{j,\ell }\) and \(\Theta ^s_{j,\ell }\), for all \(j\in J\) and for all \(\ell =1,2,\dots ,p^k_j\), that the events \(E_0^k\) and \(E_s^k\) are also independent. Hence, inequalities (39) and (40) imply that
which shows that Assumption 3-(v) holds.
In order to show that Assumption 3-(iv) holds, notice that \({\mathbb {E}}\left( C^k_{j,0}-c_j(x^k)\right) =0\) for all \(j\in J\), which implies that for all \(j\in J\),
where the last inequality in (41) follows from (31). Similarly, since \(\Big (C^k_{j,s}-c_j(x^k+s^k)\Big )=0\) for all \(j\in J\), then
which shows that Assumption 3-(iv) holds.
Finally, in order to compute estimates \(F^k_0\) and \(F^k_s\) that satisfy Assumption 3-(i) and (ii), let \(\Theta _0^0\) and \(\Theta _0^s\) be two independent random variables following the same distribution as \(\Theta _0\). Let \(\Theta ^0_{0,\ell },\ \ell =1,2,\dots ,p^k_0\) and \(\Theta ^s_{0,\ell },\ \ell =1,2,\dots ,p^k_0\) be independent random samples of \(\Theta _0^0\) and \(\Theta _0^s\) respectively, where \(p_0^k\ge 1\) denotes the sample size. Define \(F^k_0\) and \(F^k_s\) respectively by
Then \({\mathbb {E}}\left( F^k_0\right) =f(x^k)\), which implies that \({\mathbb {V}}\left( F^k_0\right) \le \frac{V}{p^k_0}\). Thus, it is easy to notice that the proof of Assumption 3-(i) follows that of Assumption 3-(iii). More precisely, the following inequality holds:
provided that
Estimates \(f^k_0=F^k_0(\omega )\) and \(f^k_s=F^k_s(\omega )\), obtained by averaging \(\, p^k_0\) realizations of \(f_{\Theta _0}\), respectively at \(x^k\) and \(x^k+s^k\), are obviously \(\beta \)-probabilistically \(\varepsilon \)-accurate. The proof of Assumption 3-(ii) follows that of Assumption 3-(iv). Specifically,
provided \(p^k_0\) is chosen according to (45).
5.2 Computational experiments
This section illustrates the performance and the efficiency of StoMADS-PB using noisy variants of 42 continuous constrained problems from the optimization literature. The sources and characteristics of these problems are summarized in Table 1. The number of variables ranges from \(n=2\) to \(n=20\), where every problem has at least one constraint (\(m>0\)) other than bound constraints. In order to show the capability of StoMADS-PB to cope with noisy constrained problems compared to MADS with PB [9], referred to as MADS-PB, two variants of the latter algorithm are compared to several variants of StoMADS-PB. For all computational investigations of both algorithms, only the POLL step is used, i.e., no SEARCH step is involved. Based on the result of Proposition 2.13, the \(\varepsilon \)-feasible incumbent solution is always chosen as the StoMADS-PB primary frame center unless the estimates \(f^k_0(x^k_{\text {feas}})\) and \(f^k_0(x^k_{\text {inf}})\) satisfy the sufficient decrease condition in (11), in which case the choice of the infeasible incumbent solution as primary frame center is preferred. As in [9], StoMADS-PB places less effort in polling around the secondary frame center than the primary one. Specifically, as default strategy, a maximal positive basis [12] is used for the primary frame center while only two directions, with one being the negative of the first, are used for the secondary frame center. The OrthoMADS-2n directions [1] are used for the POLL which is ordered by means of an opportunistic strategy [12], i.e., trial points around the primary frame center are evaluated first. Then, all the points around a given frame center are sorted relatively to the successful direction from the last h-Dominating iteration in StoMADS-PB, while in MADS-PB, they are sorted relatively to the last successful direction both in the noisy objective and constraint violation functions. MADS-PB and all the proposed variants of StoMADS-PB are implemented in MATLAB.
The stochastic variants of the 42 deterministic constrained optimization problems are solved using three different infeasible initial points for a total of 126 problem instances. Inspired by [11], the stochastic variants are constructed by additively perturbing the objective f by a random variable \(\Theta _0\) and by additively perturbing each constraint \(c_j, j=1,2,\dots ,m\) by a random variable \(\Theta _j\). That is,
where \(\Theta _0\) is uniformly generated in the interval \(I(\sigma ,x^0,f)=\left[ -\sigma \left|f(x^0)-f^*\right|, \sigma \left|f(x^0)-f^*\right|\right] \) and \(\Theta _j\) is uniformly generated in \(I(\sigma ,x^0,c_j)=\left[ -\sigma \left|c_j(x^0)\right|, \sigma \left|c_j(x^0)\right|\right] \). The scalar \(\sigma >0\) is used to define different noise levels, \(x^0\) denotes an initial point and \(f^*\) is the best known feasible minimum value of f. Thus, the test set used during the experiments is representative of real-world applications, since consisting of a collection of more than 20 stochastically noisy test problems (see e.g. [12], appendix A.1.) The bounds of \(I(\sigma ,x^0,f)\) and \(I(\sigma ,x^0,c_j)\) are respectively expressed in terms of \(\left|f(x^0)-f^*\right|\) and \(\left|c_j(x^0)\right|\) in order to take into account the effort of a given algorithm when reducing the value of the objective function from \(f(x^0)\) to \(f^*\), and when reducing the values of the constraints from \(c_j(x^0)\) to zero (whenever \(c_j(x^0)>0\)), for a given problem. The random variables \(\Theta _0, \Theta _1,\dots ,\Theta _m\) are independent. For the remainder of the study, the process which returns the vector \(\left[ f_{\Theta _0}(x), c_{\Theta _1}(x), c_{\Theta _2}(x),\dots ,c_{\Theta _m}(x) \right] \) when provided the input x will be referred to as the noisy blackbox.
The MADS-PB algorithm [9], of which StoMADS-PB is a stochastic variant, and to which the latter is compared is an iterative direct-search method originally developed for deterministic constrained blackbox optimization. In MADS-PB, feasibility is sought by progressively decreasing a threshold imposed on a constraint violation function into which all the constraint violations are aggregated. Any trial point with a constraint violation value greater than that threshold is rejected. A full description of MADS-PB iterations and its behavior can also be found in [12].
The relative performance and efficiency of algorithms are assessed by performance profiles [31, 46] and data profiles [46], which require the definition of a convergence test for a given problem instance. For each of the 126 problem instances (defined by the 42 functions f, minimized using three different initial points), denote by \(x^N\) the best feasible point found after N evaluations of the noisy blackbox and let \(x^*\) be the best feasible point of f obtained by the six compared algorithms (described later) on the three stochastic problem instances involving f. This means that for a given objective function f, the value of \(x^*\) is the best among eighteen, which can be considered significant and representative in an expensive-to-evaluate BBO framework. The convergence test from [14] used for the experiments is defined as
where \(\tau \in [0,1]\) is the convergence tolerance and \({\bar{f}}_{\text {f}eas}\) is a reference value obtained by taking the average of the available first feasible f values over all instances of a given problem over all algorithms. If no feasible point is found, then the convergence test fails. Otherwise, a problem is said to be successfully solved within the tolerance \(\tau \) if (47) holds. As highlighted in [14], \({\bar{f}}_{\text {f}eas}=f(x^0)\) for unconstrained problems, where \(x^0\) denotes the initial point.
Inspired by [31], the number of noisy objective function evaluations is chosen as performance measure. The horizontal axis of the performance profiles shows a ratio of the performance on a given problem by a given algorithm to the best performance by any algorithm on that problem, while the fraction of problems solved within the convergence tolerance \(\tau \) is shown on the vertical axis. On the horizontal axis of the data profiles is shown the number of function calls to the noisy blackbox divided by \((n+1)\)Footnote 1 while the vertical axis shows the proportion of problems solved by all instances of a given algorithm within a tolerance \(\tau \). As emphasized in [12], performance profiles show information concerning speed of convergence (i.e., the quality of a given algorithm’s output in terms of the number of objective function evaluations) and robustness (i.e., the fraction of problems solved) in a compact graphical format, while data profiles also examine the robustness and efficiency from a different perspective.
Recall that in StoMADS-PB, according to Sect. 5.1, specifically (29) and (43), the noisy blackbox needs to be evaluated many times at a given point in order to compute function estimates unlike the MADS-PB method, in which it is evaluated only once at each point. Thus, the limited budget of \(1000(n+1)\) noisy blackbox evaluations allocated to all the algorithms during the computational experiments should not be exhausted too quickly by doing replications at a given current point when computing estimates for StoMADS-PB. However, given that such estimates are required to be sufficiently accurate in order for the solutions to be satisfactory, a procedure inspired by [11] aimed at improving the estimates accuracy by making use of available samples at a given current point is proposed. The following computation scheme is described only for \(f^k_0(x^k)\) but is the same for \(f^k_s(x^k+s^k)\), \(c^k_{j,0}(x^k)\) and \(c^k_{j,s}(x^k+s^k)\), for all \(j\in J\). During the optimization, all trial points \(x^k\) used by StoMADS-PB and all corresponding values \(f_{\Theta _0}(x^k)\) are stored in a cache. When constructing an estimate of \(f(x^k)\) at the iteration \(k\ge 1\), denote by \(a^k(x^k)\)Footnote 2 the number of sample values of \(f_{\Theta _0}(x^k)\) available in the cache from previous blackbox evaluations until iteration \(k-1\). Since all the values of the noisy objective function \(f_{\Theta _0}\) are always computed independently of each other, the aforementioned sample values can be considered as independent realizations \(f_{\theta _{0,1}}(x^k), f_{\theta _{0,2}}(x^k),\dots ,f_{\theta _{0,a^k(x^k)}}(x^k)\) of \(f_{\Theta _0}(x^k)\), where for all \(\ell =1,2,\dots ,a^k(x^k)\), \(\theta _{0,\ell }\) is a realization of the random variable \(\Theta _{0,\ell }\) following the same distribution as \(\Theta _0\). Now let \(n^k\ge 1\) be the number of blackbox evaluations at \(x^k\) and consider the independent realizations \(\theta _{0,a^k(x^k)+1}, \theta _{0,a^k(x^k)+2},\dots , \theta _{0,a^k(x^k)+n^k}\) of \(\Theta _0\). Then using (43), an estimate \(f^k_0(x^k)\) of \(f(x^k)\) is computed according to
where \(p^k=n^k+a^k(x^k)\) is the sample size. Note that this computation procedure is very efficient in practice as highlighted in [11] even though it is inherently biased.
The same values are used to initialize most of the common parameters to StoMADS-PB and MADS-PB. Specifically, the mesh refining parameter \(\tau =1/2\), the frame center trigger \(\rho =0.1\) and \(\delta _m^0=\delta _p^0=1\) are common to both methods. However, in MADS-PB, the initial barrier threshold is set equal its default value, i.e., \(h^0_{\max }\!\!=\!\!+\infty \) [9]while in StoMADS-PB it equals \(u^0_0(x^0_{\text {inf}})\), with \(u^k_0(x^k)\) defined in (4) for all \(k\in {\mathbb {N}}\). The default values of Algorithm 2 parameters \(\gamma >2\) and \(\varepsilon >0\)Footnote 3 are borrowed from [11], that is, \(\gamma =17\) and \(\varepsilon =0.01\).
Four variants of StoMADS-PB corresponding to \(n^k \in \{1,2, 3, 4\}\) are compared to two variants of MADS-PB : a variant referred to as \(\ell _1\)-MADS-PB using an \(\ell _1\)-norm (as in StoMADS-PB) for the definition of the barrier function h, and a second one, \(\ell _2\)-MADS-PB, which uses the euclidean norm as in [9]. The data and performance profiles used for the comparisons are depicted in Figs. 2, 4 and 6 and Figs. 3, 5 and 7. Three levels of noise are used during the experiments, which correspond to \(\sigma =0.01\), \(\sigma =0.03\) and \(\sigma =0.05\). For each of the three levels of noise, since each of the six compared algorithms were applied to the stochastic variants of the 126 problem instances, a total of \(3\times 6 \times 126 = 2268\) algorithm runs were necessary to obtain the data and performance profiles. For a given algorithm, the percentage of problems solved after \(1000(n+1)\) noisy blackbox evaluations for each noise level within a convergence tolerance \(\tau \) are reported in Table 2.
The data and performance profiles show that when given sufficient budget, StoMADS-PB generally outperforms MADS-PB. They also show that MADS-PB is very efficient for moderate values of the noise level \(\sigma \), but its performance degrades quickly as \(\sigma \) increases. As expected, \(\ell _2\)-MADS-PB outperforms \(\ell _1\)-MADS-PB since the latter should introduce some nondifferentiability in the deterministic minimization problem as discussed in [12]. Moreover as in [11], varying the value of the convergence tolerance \(\tau \) in the data profiles does not significantly alter the conclusions drawn from the performance profiles. Indeed, as expected, it can be easily observed from Table 2 that the higher the tolerance parameter \(\tau \), the larger the percentage of problems solved by all algorithms for a fixed noise level \(\sigma \). Notice that while for a given \(\tau \), the fraction of problems solved by each variant of MADS-PB has a decreasing tendency when the noise level increases from \(\sigma =0.01\) to \(\sigma =0.05\), this seems not to be the case for StoMADS-PB variants. Before giving an insight as to why, recall that in the present constrained framework, the success or failure of the convergence test (47) depends not only on the values of the objective function f but also on whether a feasible point is found or not, unlike the framework of [11] where no constraints are involved. In fact, as highlighted in [11] from which the scheme (48) was inspired, even though the robustness and efficiency of each StoMADS-PB variant depends on the number \(n^k\) of noisy blackbox evaluations which is constant for all k, the quality of the solutions is influenced by the sample size \(p^k=n^k+a^k(x^k)\), which is not constant. On one hand, this is the reason why for \(n^k=1\), StoMADS-PB does not have the same behavior as \(\ell _1\)-MADS-PB. On the other hand, (48) naturally favors StoMADS-PB by improving the accuracy of the estimates of the constraint functions, thus allowing it to find a higher amount of feasible solutions compared to MADS-PB and consequently possibly solve a larger fraction of problems when the noise level increases for a fixed tolerance parameter \(\tau \).
Based on Table 2, observe that for a given convergence tolerance \(\tau \), varying \(\sigma \) seems not to have a significant influence on the fraction of problems solved by the StoMADS-PB variants corresponding to \(n^k=1, n^k=2\) and \({n^k=4}\). Moreover, even though for the lowest noise level studied, \(\sigma =0.01\), StoMADS-PB with \(n^k=3\) solved the most problems, the corresponding percentage is not significantly larger than those of StoMADS-PB with \(n^k=2\) and \(n^k=4\). For all these reasons, the variant with \(n^k=2\) seems preferable for constrained stochastic blackbox optimization problems with limited budget while the variant \(n^k=4\) should be preferred for stochastic blackbox optimization problems with higher evaluations budgets. Finally, recall that \(\ell _2\)-MADS-PB outperforms \(\ell _1\)-MADS-PB in the present stochastic framework. Thus, given that even in a deterministic BBO context, squared violations were shown in [7] to perform better (thus motivating the use of an \(\ell _2\) barrier function h in [9]), one could expect a StoMADS-PB variant using an \(\ell _2\) barrier function to outperform the one analyzed in the present manuscript even though the convergence of this \(\ell _2\) variant is not yet demonstrated.
6 Concluding remarks
The StoMADS-PB algorithm introduced in the present work is developed for constrained stochastic blackbox optimization. The proposed method, which uses an algorithmic framework similar to that of MADS, considers the optimization of objective and constraint functions whose values can only be accessed through a stochastically noisy blackbox. It treats constraints using a progressive barrier approach, by aggregating their violations into a single function. It does not use any model or approximate gradient information to find descent directions or improve feasibility unlike prior works. Instead, StoMADS-PB uses function estimates and introduces probabilistic bounds on which sufficient decrease conditions are imposed. By requiring the accuracy of such estimates and bounds to hold with sufficiently high, but fixed, probabilities, convergence results for StoMADS-PB are derived, most of which are stochastic variants of those of MADS.
Computational experiments conducted on several variants of StoMADS-PB on a collection of constrained stochastically noisy problems showed the proposed method eventually outperforms MADS, and show some of its variants to be almost robust to random noise despite the use of very inaccurate estimates.
This research is, to the best of our knowledge, the first to propose a stochastic directional direct-search algorithm for BBO, developed to cope with both a stochastically noisy objective and constraints.
Future research could focus on improving the proposed method to handle large-scale machine learning problems, making use, for example, of parallel space decomposition.
Notes
References
Abramson, M.A., Audet, C., Dennis, J.E., Jr., Le Digabel, S.: OrthoMADS: a deterministic MADS instance with orthogonal directions. SIAM J. Optim. 20(2), 948–966 (2009)
Alarie, S., Audet, C., Bouchet, P.-Y., Le Digabel, S.: Optimization of noisy blackboxes with adaptive precision. SIAM J. Optim. 31(4), 3127–3156 (2021)
Anderson, E.J., Ferris, M.C.: A direct search algorithm for optimization with noisy function evaluations. SIAM J. Optim. 11(3), 837–857 (2001)
Angün, E., Kleijnen, J., den Hertog, D., Gürkan, G.: Response surface methodology with stochastic constraints for expensive simulation. J. Oper. Res. Soc. 60(6), 735–746 (2009)
Armijo, L.: Minimization of functions having Lipschitz continuous first partial derivatives. Pac. J. Math. 16(1), 1–3 (1966)
Audet, C.: A survey on direct search methods for blackbox optimization and their applications. In: Pardalos, P.M., Rassias, T.M. (eds.) chapter 2 Mathematics Without Boundaries: Surveys in Interdisciplinary Research, pp. 31–56. Springer (2014)
Audet, C., Dennis, J.E., Jr.: A pattern search filter method for nonlinear programming without derivatives. SIAM J. Optim. 14(4), 980–1010 (2004)
Audet, C., Dennis, J.E., Jr.: Mesh adaptive direct search algorithms for constrained optimization. SIAM J. Optim. 17(1), 188–217 (2006)
Audet, C., Dennis, J.E., Jr.: A progressive barrier for derivative-free nonlinear programming. SIAM J. Optim. 20(1), 445–472 (2009)
Audet, C., Dennis, J.E., Jr., Le Digabel, S.: Parallel space decomposition of the mesh adaptive direct search algorithm. SIAM J. Optim. 19(3), 1150–1170 (2008)
Audet, C., Dzahini, K.J., Kokkolaras, M., Le Digabel, S.: Stochastic mesh adaptive direct search for blackbox optimization using probabilistic estimates. Comput. Optim. Appl. 79(1), 1–34 (2021)
Audet, C., Hare, W.: Derivative-Free and Blackbox Optimization. Springer Series in Operations Research and Financial Engineering. Springer (2017)
Audet, C., Ihaddadene, A., Le Digabel, S., Tribes, C.: Robust optimization of noisy blackbox problems using the Mesh Adaptive Direct Search algorithm. Optim. Lett. 12(4), 675–689 (2018)
Audet, C., Le Digabel, S., Tribes, C.: The mesh adaptive direct search algorithm for granular and discrete variables. SIAM J. Optim. 29(2), 1164–1189 (2019)
Augustin, F., Marzouk, Y.M.: NOWPAC: A provably convergent derivative-free nonlinear optimizer with path-augmented constraints. Technical report, arXiv (2014)
Augustin, F., Marzouk, Y.M.: A trust-region method for derivative-free nonlinear constrained stochastic optimization. Technical Report 1703.04156, arXiv (2017)
Bandeira, A.S., Scheinberg, K., Vicente, L.N.: Convergence of trust-region methods based on probabilistic models. SIAM J. Optim. 24(3), 1238–1264 (2014)
Barton, R.R., Ivey, J.S., Jr.: Nelder-Mead simplex modifications for simulation optimization. Manag. Sci. 42(7), 954–973 (1996)
Bertsimas, D., Nohadani, O., Teo, K.M.: Nonconvex robust optimization for problems with constraints. Informs J. Comput. 22(1), 44–58 (2010)
Bhattacharya, R.N., Waymire, E.C.: A basic course in probability theory, vol. 69. Springer (2007)
Blanchet, J., Cartis, C., Menickelly, M., Scheinberg, K.: Convergence Rate Analysis of a Stochastic Trust Region Method via Submartingales. Informs J. Optim. 1(2), 92–119 (2019)
Chang, K.H.: Stochastic nelder-mead simplex method—a new globally convergent direct search method for simulation optimization. Eur. J. Oper. Res. 220(3), 684–694 (2012)
Chen, R., Menickelly, M., Scheinberg, K.: Stochastic optimization using a trust-region method and random models. Math. Program. 169(2), 447–487 (2018)
Chen, X., Wang, N.: Optimization of short-time gasoline blending scheduling problem with a DNA based hybrid genetic algorithm. Chem. Eng. Process. 49(10), 1076–1083 (2010)
Clarke, F.H.: Optimization and Nonsmooth Analysis. John Wiley and Sons, New York (1983). Reissued in 1990 by SIAM Publications, Philadelphia, as Vol. 5 in the series Classics in Applied Mathematics
Conn, A.R., Scheinberg, K., Vicente, L.N.: Introduction to Derivative-Free Optimization. MOS-SIAM Series on Optimization. SIAM, Philadelphia (2009)
Curtis, F.E., Scheinberg, K.: Adaptive stochastic optimization: A framework for analyzing stochastic optimization algorithms. IEEE Signal Process. Mag. 37(5), 32–42 (2020)
Curtis, F.E., Scheinberg, K., Shi, R.: A stochastic trust region algorithm based on careful step normalization. Informs J. Optim. 1(3), 200–220 (2019)
Diniz-Ehrhardt, M.A., Ferreira, D.G., Santos, S.A.: A pattern search and implicit filtering algorithm for solving linearly constrained minimization problems with noisy objective functions. Optim. Methods Softw. 34(4), 827–852 (2019)
Diniz-Ehrhardt, M.A., Ferreira, D.G., Santos, S.A.: Applying the pattern search implicit filtering algorithm for solving a noisy problem of parameter identification. Comput. Optim. Appl. 1–32 (2020)
Dolan, E.D., Moré, J.J.: Benchmarking optimization software with performance profiles. Math. Program. 91(2), 201–213 (2002)
Durrett, R.: Probability: Theory and Examples. Cambridge University Press (2010)
Dzahini, K.J.: Expected complexity analysis of stochastic direct-search. Comput. Optim. Appl. 81(1), 179–200 (2022)
Gratton, S., Royer, C.W., Vicente, L.N., Zhang, Z.: Direct search based on probabilistic feasible descent for bound and linearly constrained problems. Comput. Optim. Appl. 72(3), 525–559 (2019)
Hock, W., Schittkowski, K.: Test Examples for Nonlinear Programming Codes. Lecture Notes in Economics and Mathematical Systems, vol. 187. Springer (1981)
Jahn, J.: Introduction to the Theory of Nonlinear Optimization. Springer (1994)
Kitayama, S., Arakawa, M., Yamazaki, K.: Sequential approximate optimization using radial basis function network for engineering optimization. Optim. Eng. 12(4), 535–557 (2011)
Klassen, K.J., Yoogalingam, R.: Improving performance in outpatient appointment services with a simulation optimization approach. Prod. Oper. Manag. 18(4), 447–458 (2009)
Lacksonen, T.: Empirical comparison of search algorithms for discrete event simulation. Comput. Ind. Eng. 40(1–2), 133–148 (2001)
Larson, J., Billups, S.C.: Stochastic derivative-free optimization using a trust region framework. Comput. Optim. Appl. 64(3), 619–645 (2016)
Le Digabel, S., Wild, S.M.: A Taxonomy of Constraints in Simulation-Based Optimization. Technical Report G-2015-57, Les cahiers du GERAD (2015)
Letham, B., Karrer, B., Ottoni, G., Bakshy, E.: Constrained Bayesian optimization with noisy experiments. Bayesian Anal. 14(2), 495–519 (2019)
Lukšan, L., Vlček, J.: Test problems for nonsmooth unconstrained and linearly constrained optimization. Technical Report V-798, ICS AS CR (2000)
Mezura-Montes, E., Coello, C.A.: Useful Infeasible Solutions in Engineering Optimization with Evolutionary Algorithms. In: Proceedings of the 4th Mexican International Conference on Advances in Artificial Intelligence, MICAI’05, pp. 652–662, Springer (2005)
Mockus, J.: Bayesian approach to global optimization: theory and applications, volume 37 of Mathematics and Its Applications. Springer (2012)
Moré, J.J., Wild, S.M.: Benchmarking derivative-free optimization algorithms. SIAM J. Optim. 20(1), 172–191 (2009)
Nelder, J.A., Mead, R.: A simplex method for function minimization. Comput. J. 7(4), 308–313 (1965)
Paquette, C., Scheinberg, K.: A stochastic line search method with expected complexity analysis. SIAM J. Optim. 30(1), 349–376 (2020)
Robbins, H., Monro, S.: A stochastic approximation method. Ann. Math. Stat. 22(3), 400–407 (1951)
Rockafellar, R.T.: Generalized directional derivatives and subgradients of nonconvex functions. Canad. J. Math. 32(2), 257–280 (1980)
Rodríguez, J.F., Renaud, J.E., Watson, L.T.: Trust region augmented lagrangian methods for sequential response surface approximation and optimization. J. Mech. Des. 120(1), 58–66 (1998)
Shashaani, S., Hashemi, F.S., Pasupathy, R.: ASTRO-DF: a class of adaptive sampling trust-region algorithms for derivative-free stochastic optimization. SIAM J. Optim. 28(4), 3145–3176 (2018)
Tao, J., Wang, N.: DNA double helix based hybrid GA for the gasoline blending recipe optimization problem. Chem. Eng. Technol. 31(3), 440–451 (2008)
Wang, Z., Ierapetritou, M.: Constrained optimization of black-box stochastic systems using a novel feasibility enhanced Kriging-based method. Comput. Chem. Eng. 118, 210–223 (2018)
Zhao, J., Wang, N.: A bio-inspired algorithm based on membrane computing and its application to gasoline blending scheduling. Comput. Chem. Eng. 35(2), 272–283 (2011)
Acknowledgements
The authors are grateful to Charles Audet from Polytechnique Montréal for valuable discussions and constructive suggestions. This work is supported by the NSERC CRD RDCPJ 490744-15 grant and by an InnovÉÉ grant, both in collaboration with Hydro-Québec and Rio Tinto, and by a FRQNT fellowship.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
This appendix presents the proofs of a series of results stated in Sect. 4.
1.1 Proof of Theorem 4.2
Proof
This theorem is proved using ideas from [11, 21, 23, 33, 40, 48] and conditioning on the disjoint events \(\left\{ T=+\infty \right\} \) and \(\left\{ T<+\infty \right\} \) that are almost sure due to Assumption 4. The proof considers two different parts. Part 1 considers two separate cases conditioned on the event \(\left\{ T=+\infty \right\} \) (i.e., no \(\varepsilon \)-feasible point is found by Algorithm 2): “good bounds” and “bad bounds”, each of which is separated into whether an iteration is h-Dominating, Improving or Unsuccessful. Part 2 considers three separates cases conditioned on the event \(\left\{ T<+\infty \right\} \): “good estimates and good bounds”, “bad estimates and good bounds” and “bad bounds”, each of which is separated into whether an iteration is f-Dominating, h-Dominating, Improving or Unsuccessful.
In order to show (21), the goal of Part 1 is to show that there exists a constant \(\eta >0\) such that conditioned on the almost sure event \(\{T=+\infty \}\), the following holds for all \(k\in {\mathbb {N}}\):
where \(\Phi _k\) is the random function defined by
Indeed, assume that (49) holds. Since \(\Phi _k>0\) for all \(k\in {\mathbb {N}}\), then summing (49) over \(k\in {\mathbb {N}}\) and taking expectations on both sides lead to
That is, (21) holds. Then, Part 2 aims to show that for the same previous constant \(\eta \), conditioned on the almost sure event \(\{T<+\infty \}\) and making use of the following random function
where \(k\vee T:=\max \{k,T\}\), the following holds for all \(k\in {\mathbb {N}}\):
Indeed, assume that (53) holds. Since \(\Phi _k^T>0\) for all \(k\ge 0\), then summing (53) over \(k\in {\mathbb {N}}\) and taking expectations on both sides, yields
where the last inequality in (54) follows from the inequality \(f(X^k_{\text {feas}})\le \kappa ^f_{\max }\) for all \(k\ge 0\), due to Proposition 3.5, and the fact that T is finite almost surely.
The remainder of the proof is devoted to showing that (49) and (53) hold. The following events are introduced for the sake of clarity in the analysis.
Part 1 (\(\varvec{T=+\infty }\) almost surely). The random function \(\Phi _k\) defined in (50) will be shown to satisfy (49) with \(\eta =\frac{1}{2}\alpha \beta (1-\nu )(1-\tau ^2)\), regardless of the change in the objective function f on the \(\varepsilon \)-infeasible incumbents encountered by Algorithm 2. Moreover, since T is infinite almost surely, then no iteration of Algorithm 2 can be f-Dominating. Two separate cases are distinguished and all that follows is conditioned on the almost sure event \(\{T=+\infty \}\).
Case 1 (Good bounds, \(\varvec{\mathbb {1}_{I_k}=1}\)). No matter the type of iteration which occurs, the random function \(\Phi _k\) will be shown to decrease and the smallest decrease is shown to happen on Unsuccessful iterations, thus yielding
-
(i)
The iteration is h-Dominating (\(\mathbb {1}_{{\mathcal {D}}_h}=1\)). The iteration is h-Dominating and the bounds are good, so a decrease occurs in h according to (6), i.e.,
$$\begin{aligned} \mathbb {1}_{I_k}\mathbb {1}_{{\mathcal {D}}_h}\frac{\nu }{m\varepsilon } (h(X^{k+1}_{\text {inf}})-h(X^k_{\text {inf}}))\le -\mathbb {1}_{I_k}\mathbb {1}_{{\mathcal {D}}_h}\nu (\gamma -2)(\Delta ^k_p)^2{.} \end{aligned}$$(56)The frame size parameter is updated according to \(\Delta ^{k+1}_p=\min \{\tau ^{-1}\Delta ^k_p,\delta _{\max }\}\), which implies that
$$\begin{aligned} \mathbb {1}_{I_k}\mathbb {1}_{{\mathcal {D}}_h}(1-\nu )[(\Delta ^{k+1}_p)^2-(\Delta ^k_p)^2]\le \mathbb {1}_{I_k}\mathbb {1}_{{\mathcal {D}}_h}(1-\nu )(\tau ^{-2}-1)(\Delta ^k_p)^2. \end{aligned}$$(57)Then, by choosing \(\nu \) according to (19), the right-hand side of (56) dominates that of (57). That is,
$$\begin{aligned} -\nu (\gamma -2)(\Delta ^k_p)^2 + (1-\nu )(\tau ^{-2}-1)(\Delta ^k_p)^2 \le -\frac{1}{2}\nu (\gamma -2)(\Delta ^k_p)^2. \end{aligned}$$(58)Combining (56), (57) and (58) leads to
$$\begin{aligned} \mathbb {1}_{I_k}\mathbb {1}_{{\mathcal {D}}_h}(\Phi _{k+1}-\Phi _k)\le -\mathbb {1}_{I_k}\mathbb {1}_{{\mathcal {D}}_h}\frac{1}{2}\nu (\gamma -2)(\Delta ^k_p)^2. \end{aligned}$$(59) -
(ii)
The iteration is Improving (\(\mathbb {1}_{{\mathcal {I}}}=1\)). The iteration is Improving and the bounds are good, so again, a decrease occurs in h according to (6). Moreover, \(\Delta ^k_p\) is updated as in h-Dominating iterations. Thus, the change in \(\Phi _k\) follows from (59) by replacing \(\mathbb {1}_{{\mathcal {D}}_h}\) by \(\mathbb {1}_{{\mathcal {I}}}\). Specifically,
$$\begin{aligned} \mathbb {1}_{I_k}\mathbb {1}_{{\mathcal {I}}}(\Phi _{k+1}-\Phi _k)\le -\mathbb {1}_{I_k}\mathbb {1}_{{\mathcal {I}}}\frac{1}{2}\nu (\gamma -2)(\Delta ^k_p)^2. \end{aligned}$$(60) -
(iii)
The iteration is Unsuccessful (\(\mathbb {1}_{{\mathcal {U}}}=1\)). The value of h is unchanged while the frame size parameter is decreased. Consequently,
$$\begin{aligned} \mathbb {1}_{I_k}\mathbb {1}_{{\mathcal {U}}}(\Phi _{k+1}-\Phi _k)=-\mathbb {1}_{I_k}\mathbb {1}_{{\mathcal {U}}}(1-\nu )(1-\tau ^{2})(\Delta ^k_p)^2 \end{aligned}$$(61)Because \(\nu \) satisfies (19) and because \(1-\tau ^2<\tau ^{-2}-1\), Unsuccessful iterations, vis a vis (61), provide the worst case decrease when compared to (59) and (60). That is,
$$\begin{aligned} -\frac{1}{2}\nu (\gamma -2)(\Delta ^k_p)^2\le -(1-\nu )(1-\tau ^{2})(\Delta ^k_p)^2. \end{aligned}$$(62)Thus, it follows from (59), (60), (61) and (62) that the change in \(\Phi _k\) is bounded like
$$\begin{aligned} \mathbb {1}_{I_k}(\Phi _{k+1}-\Phi _k)= & {} \mathbb {1}_{I_k}(\mathbb {1}_{{\mathcal {D}}_h}+\mathbb {1}_{{\mathcal {I}}}+\mathbb {1}_{{\mathcal {U}}})(\Phi _{k+1}-\Phi _k)\nonumber \\\le & {} -\mathbb {1}_{I_k}(1-\nu )(1-\tau ^{2})(\Delta ^k_p)^2. \end{aligned}$$(63)
Since Assumption 3 holds, taking conditional expectations with respect to \({\mathcal {F}}^{C\cdot F}_{k-1}\) on both sides of the inequality in (63) leads to (55).
Case 2 (Bad bounds, \(\varvec{\mathbb {1}_{\bar{I_k}}=1}\)). Since the bounds are bad, Algorithm 2 can accept a step which leads to an increase in h and \(\Delta ^k_p\), and hence in \(\Phi _k\). Such an increase in \(\Phi _k\) is controlled by making use of (15). Then, the probability of \(\bar{I_k}\) is chosen to be sufficiently small so that \(\Phi _k\) can be reduced sufficiently in expectation. More precisely, the next result will be proved
-
(i)
The iteration is h-Dominating (\(\mathbb {1}_{{\mathcal {D}}_h}=1\)). The change in h is bounded like
$$\begin{aligned}&\mathbb {1}_{\bar{I_k}}\mathbb {1}_{{\mathcal {D}}_h}\frac{\nu }{m\varepsilon } (h(X^{k+1}_{\text {inf}})-h(X^k_{\text {inf}})) \nonumber \\&\quad \le \mathbb {1}_{\bar{I_k}}\mathbb {1}_{{\mathcal {D}}_h}\frac{\nu }{m\varepsilon } \left[ (H^k_s-H^k_0)+\left|h(X^{k+1}_{\text {inf}}) -H^k_s\right|+\left|h(X^k_{\text {inf}})-H^k_0\right|\right] \nonumber \\&\quad \le \mathbb {1}_{\bar{I_k}}\mathbb {1}_{{\mathcal {D}}_h}\nu \left[ -\gamma (\Delta ^k_p)^2+\frac{1}{m\varepsilon }\left( \left|h(X^{k+1}_{\text {inf}}) -H^k_s\right|+\left|h(X^k_{\text {inf}})-H^k_0\right|\right) \right] , \end{aligned}$$(65)where (65) follows from \(H^k_s-H^k_0\le -\gamma m\varepsilon (\Delta ^k_p)^2 \) which is satisfied in every h-Dominating iteration. Moreover, the change in \(\Delta ^k_p\) can be obtained simply by replacing \(\mathbb {1}_{I_k}\) by \(\mathbb {1}_{\bar{I_k}}\) in (57). That is,
$$\begin{aligned} \mathbb {1}_{\bar{I_k}}\mathbb {1}_{{\mathcal {D}}_h}(1-\nu )[(\Delta ^{k+1}_p)^2-(\Delta ^k_p)^2]\le \mathbb {1}_{\bar{I_k}}\mathbb {1}_{{\mathcal {D}}_h}(1-\nu )(\tau ^{-2}-1)(\Delta ^k_p)^2. \end{aligned}$$(66)Because \(\nu \) satisfies (19), \(-\nu \gamma (\Delta ^k_p)^2+(1-\nu )(\tau ^{-2}-1)(\Delta ^k_p)^2\le 0\). Combining (65) and (66),
$$\begin{aligned} \mathbb {1}_{\bar{I_k}}\mathbb {1}_{{\mathcal {D}}_h}(\Phi _{k+1}-\Phi _k)\le \mathbb {1}_{\bar{I_k}}\mathbb {1}_{{\mathcal {D}}_h}\frac{\nu }{m\varepsilon } \left( \left|h(X^{k+1}_{\text {inf}})-H^k_s\right|+\left|h(X^k_{\text {inf}})-H^k_0\right|\right) .\nonumber \\ \end{aligned}$$(67) -
(ii)
The iteration is Improving (\(\mathbb {1}_{{\mathcal {I}}}=1\)). \(\Delta ^k_p\) is updated as in h-Dominating iterations. The increase in h is bounded as in (65). Thus, the bound on the change in \(\Phi _k\) can be obtained by replacing \(\mathbb {1}_{{\mathcal {D}}_h}\) by \(\mathbb {1}_{{\mathcal {I}}}\) in (67). That is,
$$\begin{aligned} \mathbb {1}_{\bar{I_k}}\mathbb {1}_{{\mathcal {I}}}(\Phi _{k+1}-\Phi _k)\le \mathbb {1}_{\bar{I_k}}\mathbb {1}_{{\mathcal {I}}}\frac{\nu }{m\varepsilon } \left( \left|h(X^{k+1}_{\text {inf}})-H^k_s\right|+\left|h(X^k_{\text {inf}})-H^k_0\right|\right) .\nonumber \\ \end{aligned}$$(68) -
(iii)
The iteration is Unsuccessful (\(\mathbb {1}_{{\mathcal {U}}}=1\)). The value of h is unchanged and \(\Delta ^k_p\) is decreased. Thus, the change in \(\Phi _k\) follows from (61) by replacing \(\mathbb {1}_{I_k}\) by \(\mathbb {1}_{\bar{I_k}}\) and is trivially bounded like
$$\begin{aligned} \mathbb {1}_{\bar{I_k}}\mathbb {1}_{{\mathcal {U}}}(\Phi _{k+1}-\Phi _k) \le \mathbb {1}_{\bar{I_k}}\mathbb {1}_{{\mathcal {U}}}\frac{\nu }{m\varepsilon } \left( \left|h(X^{k+1}_{\text {inf}})-H^k_s\right|+\left|h(X^k_{\text {inf}})-H^k_0\right|\right) .\nonumber \\ \end{aligned}$$(69)It follows from (67), (68), (69) and the inequality \(\mathbb {1}_{\bar{I_k}}\le 1\), that
$$\begin{aligned} \mathbb {1}_{\bar{I_k}}(\Phi _{k+1}-\Phi _k) \le \frac{\nu }{m\varepsilon }\left( \left|h(X^{k+1}_{\text {inf}})-H^k_s\right|+\left|h(X^k_{\text {inf}})-H^k_0\right|\right) {.} \end{aligned}$$(70)Taking conditional expectations with respect to \({\mathcal {F}}^{C\cdot F}_{k-1}\) on both sides of (70) and using the inequalities (15) of Lemma 3.7, leads to (64).
Combining (55) and (64) yields,
Choosing \(\alpha \) according to (20) implies that \(\displaystyle {\alpha \ge \frac{4\nu (1-\alpha )^{1/2}}{(1-\nu )(1-\tau ^2)}}\), which ensures
Thus, (49) follows from (71) and (72) with \(\eta =\frac{1}{2}\alpha \beta (1-\nu )(1-\tau ^2)\).
Part 2 (\(\varvec{T<+\infty }\) almost surely). In order to show that the random function \(\Phi _k^T\) defined by
satisfies (53) with the same constant \(\eta \) derived in Part 1, notice that whenever the event \(\{T>k\}\) occurs, then \(f(X^{(k+1)\vee T}_{\text {feas}})-f(X^{k\vee T}_{\text {feas}})=0\) since \(\max \{k,T\}:=k\vee T=(k+1)\vee T=T\). Thus, on the event \(\{T>k\}\), the random function \(\Phi _k\) used in Part 1 has the same increment as \(\Phi _k^T\). Specifically,
Moreover, it follows from the definition of the stopping time T that no iteration can be f-Dominating when the event \(\{T>k\}\) occurs. Consequently, it easily follows from the analysis in Part 1 and the fact that the random variable \(\mathbb {1}_{\{T> k\}}\) is \({\mathcal {F}}^{C\cdot F}_{k-1}\)-measurable that,
The remainder of the proof is devoted to showing that
since combining (73) and (74) leads to (53), which is the overall goal. In all that follows, it is assumed that the event \(\{T\le k\}\) occurs.
Case 1 (Good estimates and good bounds, \(\varvec{\mathbb {1}_{I_k}\mathbb {1}_{J_k}=1}\)). Regardless of the iteration type, the smallest decrease in \(\Phi _k^T\) will be shown to happen on Unsuccessful iterations, and it will be shown that
-
(i)
The iteration is f-Dominating (\(\mathbb {1}_{{\mathcal {D}}_f}=1\)). The iteration is f-Dominating and the estimates are good, so a decrease occurs in f according to (10). That is,
$$\begin{aligned}&\mathbb {1}_{\{T\le k\}}\mathbb {1}_{I_k}\mathbb {1}_{J_k}\mathbb {1}_{{\mathcal {D}}_f}\frac{\nu }{\varepsilon }(f(X^{(k+1)\vee T}_{\text {feas}})-f(X^{k\vee T}_{\text {feas}}))\nonumber \\&\quad \le -\mathbb {1}_{\{T\le k\}}\mathbb {1}_{I_k}\mathbb {1}_{J_k}\mathbb {1}_{{\mathcal {D}}_f}\nu (\gamma -2)(\Delta ^k_p)^2. \end{aligned}$$(76)Since the \(\varepsilon \)-infeasible incumbent is not updated, The value of h is unchanged. The frame size parameter is updated according to \(\Delta ^{k+1}_p=\min \{\tau ^{-1}\Delta ^k_p,\delta _{\max }\}\), thus implying that
$$\begin{aligned}&\mathbb {1}_{\{T\le k\}}\mathbb {1}_{I_k}\mathbb {1}_{J_k}\mathbb {1}_{{\mathcal {D}}_f}(1-\nu )[(\Delta ^{k+1}_p)^2-(\Delta ^k_p)^2]\nonumber \\&\quad \le \mathbb {1}_{\{T\le k\}}\mathbb {1}_{I_k}\mathbb {1}_{J_k}\mathbb {1}_{{\mathcal {D}}_f}(1-\nu )(\tau ^{-2}-1)(\Delta ^k_p)^2. \end{aligned}$$(77)Because \(\nu \) satisfies (19), (58) holds, which implies that the right-hand side of (76) dominates that of (77), leading to the inequality
$$\begin{aligned} \mathbb {1}_{\{T\le k\}}\mathbb {1}_{I_k}\mathbb {1}_{J_k}\mathbb {1}_{{\mathcal {D}}_f}(\Phi _{k+1}^T-\Phi _k^T) \le -\mathbb {1}_{\{T\le k\}}\mathbb {1}_{I_k}\mathbb {1}_{J_k}\mathbb {1}_{{\mathcal {D}}_f}\frac{1}{2} \nu (\gamma -2)(\Delta ^k_p)^2.\nonumber \\ \end{aligned}$$(78) -
(ii)
The iteration is h-Dominating (\(\mathbb {1}_{{\mathcal {D}}_h}=1\)). The value of f is unchanged since \(X^k_{\text {feas}}\) is not updated. Thus, the bound on the change in \(\Phi _k^T\) follows from multiplying both sides of (59) by \(\mathbb {1}_{\{T\le k\}}\mathbb {1}_{J_k}\), and replacing \(\Phi _k\) by \(\Phi _k^T\). That is,
$$\begin{aligned}&\mathbb {1}_{\{T\le k\}}\mathbb {1}_{I_k}\mathbb {1}_{J_k}\mathbb {1}_{{\mathcal {D}}_h}(\Phi _{k+1}^T-\Phi _k^T) \le -\mathbb {1}_{\{T\le k\}}\mathbb {1}_{I_k}\mathbb {1}_{J_k}\mathbb {1}_{{\mathcal {D}}_h}\frac{1}{2}\nu (\gamma -2)(\Delta ^k_p)^2.\nonumber \\ \end{aligned}$$(79) -
(iii)
The iteration is Improving (\(\mathbb {1}_{{\mathcal {I}}}=1\)). Again, the value of f is unchanged. Thus, the bound on the change in \(\Phi _k^T\) follows from multiplying both sides of (60) by \(\mathbb {1}_{\{T\le k\}}\mathbb {1}_{J_k}\), and replacing \(\Phi _k\) by \(\Phi _k^T\). That is,
$$\begin{aligned}&\mathbb {1}_{\{T\le k\}}\mathbb {1}_{I_k}\mathbb {1}_{J_k}\mathbb {1}_{{\mathcal {I}}}(\Phi _{k+1}^T-\Phi _k^T) \le -\mathbb {1}_{\{T\le k\}}\mathbb {1}_{I_k}\mathbb {1}_{J_k}\mathbb {1}_{{\mathcal {I}}}\frac{1}{2}\nu (\gamma -2)(\Delta ^k_p)^2.\nonumber \\ \end{aligned}$$(80) -
(iv)
The iteration is Unsuccessful (\(\mathbb {1}_{{\mathcal {U}}}=1\)). The value of f and h is unchanged since no incumbent is updated, while \(\Delta ^k_p\) is decreased. Consequently, the bound on the change in \(\Phi _k^T\) follows from multiplying both sides of (61) by \(\mathbb {1}_{\{T\le k\}}\mathbb {1}_{J_k}\), and replacing \(\Phi _k\) by \(\Phi _k^T\). That is,
$$\begin{aligned} \mathbb {1}_{\{T\le k\}}\mathbb {1}_{I_k}\mathbb {1}_{J_k}\mathbb {1}_{{\mathcal {U}}}(\Phi _{k+1}^T-\Phi _k^T)=-\mathbb {1}_{\{T\le k\}}\mathbb {1}_{I_k}\mathbb {1}_{J_k}\mathbb {1}_{{\mathcal {U}}}(1-\nu )(1-\tau ^{2})(\Delta ^k_p)^2.\nonumber \\ \end{aligned}$$(81)Combining (78), (79), (80), (81) and (62) yields
$$\begin{aligned} \mathbb {1}_{\{T\le k\}}\mathbb {1}_{I_k}\mathbb {1}_{J_k}(\Phi _{k+1}^T-\Phi _k^T) \le -\mathbb {1}_{\{T\le k\}}\mathbb {1}_{I_k}\mathbb {1}_{J_k}(1-\nu )(1-\tau ^2)(\Delta ^k_p)^2. \end{aligned}$$(82)
The following holds under Assumption 3: \({\mathbb {E}}\left( \mathbb {1}_{I_k}\mathbb {1}_{J_k}|{\mathcal {F}}^{C\cdot F}_{k-1}\right) \ge \alpha \beta \). Then, taking expectations with respect to \({\mathcal {F}}^{C\cdot F}_{k-1}\) on both sides of (82) and using the \({\mathcal {F}}^{C\cdot F}_{k-1}\)-measurability of the random variables \(\mathbb {1}_{\{T\le k\}}\) and \(\Delta ^k_p\) leads to (75).
Case 2 (Bad estimates and good bounds, \(\varvec{\mathbb {1}_{I_k}\mathbb {1}_{\bar{J_k}}=1}\)). An increase in the difference of \(\Phi _k^T\) may occur since good bounds might not provide enough decrease to cancel the increase which occurs in f whenever Algorithm 2 wrongly accepts an incumbent due to bad estimates. Specifically, the f-Dominating case dominates the worst-case increase in the change of \(\Phi _k^T\), leading to
-
(i)
The iteration is f-Dominating (\(\mathbb {1}_{{\mathcal {D}}_f}=1\)). Whenever bad estimates occur and the iteration is f-Dominating, the change in f is bounded like
$$\begin{aligned} \begin{aligned}&\mathbb {1}_{\{T\le k\}} \mathbb {1}_{I_k}\mathbb {1}_{\bar{J_k}}\mathbb {1}_{{\mathcal {D}}_f}\frac{\nu }{\varepsilon }(f(X^{(k+1)\vee T}_{\text {feas}})-f(X^{k\vee T}_{\text {feas}}))\\&\quad \le \mathbb {1}_{\{T\le k\}}\mathbb {1}_{I_k}\mathbb {1}_{\bar{J_k}}\mathbb {1}_{{\mathcal {D}}_f}\frac{\nu }{\varepsilon } \left[ (F^k_s-F^k_0) +\left|f(X^{k+1}_{\text {feas}})-F^k_s\right|+\left|f(X^k_{\text {feas}})-F^k_0\right|\right] \\&\quad \le \mathbb {1}_{\{T\le k\}}\mathbb {1}_{I_k}\mathbb {1}_{\bar{J_k}}\mathbb {1}_{{\mathcal {D}}_f}\nu \left[ -\gamma (\Delta ^k_p)^2 +\frac{1}{\varepsilon }\left( \left|f(X^{k+1}_{\text {feas}})-F^k_s\right|+\left|f(X^k_{\text {feas}})-F^k_0\right|\right) \right] \end{aligned}\nonumber \\ \end{aligned}$$(84)where the last inequality in (84) follows from \(F^k_s-F^k_0\le -\gamma \varepsilon (\Delta ^k_p)^2 \) which is satisfied for every f-Dominating iteration. While the value of h remains unchanged since \(X^k_{\text {inf}}\) is not updated, the change in \(\Delta ^k_p\) follows (77) by replacing \(\mathbb {1}_{J_k}\) by \(\mathbb {1}_{\bar{J_k}}\). That is,
$$\begin{aligned}&\mathbb {1}_{\{T\le k\}}\mathbb {1}_{I_k}\mathbb {1}_{\bar{J_k}}\mathbb {1}_{{\mathcal {D}}_f}(1-\nu )[(\Delta ^{k+1}_p)^2-(\Delta ^k_p)^2] \le \mathbb {1}_{\{T\le k\}}\mathbb {1}_{I_k}\mathbb {1}_{\bar{J_k}}\mathbb {1}_{{\mathcal {D}}_f}(1-\nu )(\tau ^{-2}-1)(\Delta ^k_p)^2. \nonumber \\ \end{aligned}$$(85)Then, (84), (85), (19) and the inequality \(-\nu \gamma (\Delta ^k_p)^2+(1-\nu )(\tau ^{-2}-1)(\Delta ^k_p)^2\le 0\) yield
$$\begin{aligned} \begin{aligned}&\mathbb {1}_{\{T\le k\}}\mathbb {1}_{I_k}\mathbb {1}_{\bar{J_k}}\mathbb {1}_{{\mathcal {D}}_f}( \Phi _{k+1}^T-\Phi _k^T)\\&\quad \le \mathbb {1}_{\{T\le k\}}\mathbb {1}_{I_k}\mathbb {1}_{\bar{J_k}}\mathbb {1}_{{\mathcal {D}}_f}\frac{\nu }{\varepsilon }\left( \left|f(X^{k+1}_{\text {feas}}) -F^k_s\right|+\left|f(X^k_{\text {feas}})-F^k_0\right|\right) . \end{aligned} \end{aligned}$$(86) -
(ii)
The iteration is h-Dominating (\(\mathbb {1}_{{\mathcal {D}}_h}=1\)). The bound on the change in \(\Phi _k^T\), which can be obtained by replacing \(\mathbb {1}_{J_k}\) by \(\mathbb {1}_{\bar{J_k}}\) in (79), is trivially bounded like
$$\begin{aligned}&\mathbb {1}_{\{T\le k\}}\mathbb {1}_{I_k}\mathbb {1}_{\bar{J_k}}\mathbb {1}_{{\mathcal {D}}_h}\quad (\Phi _{k+1}^T-\Phi _k^T)\nonumber \\&\quad \le \mathbb {1}_{\{T\le k\}}\mathbb {1}_{I_k}\mathbb {1}_{\bar{J_k}}\mathbb {1}_{{\mathcal {D}}_h}\frac{\nu }{\varepsilon }\left( \left|f(X^{k+1}_{\text {feas}}) -F^k_s\right|+\left|f(X^k_{\text {feas}})-F^k_0\right|\right) . \end{aligned}$$(87) -
(iii)
The iteration is Improving (\(\mathbb {1}_{{\mathcal {I}}}=1\)). Again, the change in \(\Phi _k^T\) which can be obtained by replacing \(\mathbb {1}_{J_k}\) by \(\mathbb {1}_{\bar{J_k}}\) in (80), is trivially bounded like
$$\begin{aligned}&\mathbb {1}_{\{T\le k\}}\mathbb {1}_{I_k}\mathbb {1}_{\bar{J_k}}\mathbb {1}_{{\mathcal {I}}}\quad (\Phi _{k+1}^T-\Phi _k^T)\nonumber \\&\quad \le \mathbb {1}_{\{T\le k\}}\mathbb {1}_{I_k}\mathbb {1}_{\bar{J_k}}\mathbb {1}_{{\mathcal {I}}}\frac{\nu }{\varepsilon }\left( \left|f(X^{k+1}_{\text {feas}}) -F^k_s\right|+\left|f(X^k_{\text {feas}})-F^k_0\right|\right) . \end{aligned}$$(88) -
(iv)
The iteration is Unsuccessful (\(\mathbb {1}_{{\mathcal {U}}}=1\)). Because of the decrease of the frame size parameter and hence the decrease in \(\Phi _k^T\), the bound on the change in \(\Phi _k^T\) follows
$$\begin{aligned} \begin{aligned}&\mathbb {1}_{\{T\le k\}}\mathbb {1}_{I_k}\mathbb {1}_{\bar{J_k}}\mathbb {1}_{{\mathcal {U}}}( \Phi _{k+1}^T-\Phi _k^T)\\&\quad \le \mathbb {1}_{\{T\le k\}}\mathbb {1}_{I_k}\mathbb {1}_{\bar{J_k}}\mathbb {1}_{{\mathcal {U}}}\frac{\nu }{\varepsilon }\left( \left|f(X^{k+1}_{\text {feas}}) -F^k_s\right|+\left|f(X^k_{\text {feas}})-F^k_0\right|\right) . \end{aligned} \end{aligned}$$(89)Then, combining (86), (87), (88) and \(\mathbb {1}_{I_k}\mathbb {1}_{\bar{J_k}}\le 1\), yields
$$\begin{aligned}&\mathbb {1}_{\{T\le k\}}\mathbb {1}_{I_k}\mathbb {1}_{\bar{J_k}}(\Phi _{k+1}^T-\Phi _k^T)\nonumber \\&\quad \le \mathbb {1}_{\{T\le k\}}\frac{\nu }{\varepsilon }\left( \left|f(X^{k+1}_{\text {feas}})-F^k_s\right|+\left|f(X^k_{\text {feas}})-F^k_0\right|\right) . \end{aligned}$$(90)Since Assumption 3 holds, it follows from the conditional Cauchy-Schwarz inequality [20] that
$$\begin{aligned} {\mathbb {E}}\left( \left|f(X^k_{\text {feas}})-F^k_0\right||{\mathcal {F}}^{C\cdot F}_{k-1}\right)\le & {} {\mathbb {E}}\left( 1|{\mathcal {F}}^{C\cdot F}_{k-1}\right) ^{1/2} \left[ {\mathbb {E}}\left( \left|f(X^k_{\text {feas}}) -F^k_0\right|^2|{\mathcal {F}}^{C\cdot F}_{k-1}\right) \right] ^{1/2}\nonumber \\\le & {} \varepsilon (1-\beta )^{1/2}(\Delta ^k_p)^2, \end{aligned}$$(91)where (91) follows from (12) and the fact that \({\mathbb {E}}\left( 1|{\mathcal {F}}^{C\cdot F}_{k-1}\right) =1\). Similarly,
$$\begin{aligned} {\mathbb {E}}\left( \left|f(X^{k+1}_{\text {feas}})-F^k_s\right||{\mathcal {F}}^{C\cdot F}_{k-1}\right) \le \varepsilon (1-\beta )^{1/2}(\Delta ^k_p)^2. \end{aligned}$$(92)
Taking expectations with respect to \({\mathcal {F}}^{C\cdot F}_{k-1}\) on both sides of (90) and then using (91), (92) and the \({\mathcal {F}}^{C\cdot F}_{k-1}\)-measurability of the random variables \(\mathbb {1}_{\{T\le k\}}\) and \(\Delta ^k_p\), leads to (83).
Case 3 (Bad bounds, \(\varvec{\mathbb {1}_{\bar{I_k}}=1}\)). The difference in \(\Phi _k^T\) may increase since even though good estimates of f values occur, they might not provide enough decrease to cancel the increase in h whenever Algorithm 2 wrongly accepts an incumbent due to bad bounds. It will be shown that
-
(i)
The iteration is f-Dominating (\(\mathbb {1}_{{\mathcal {D}}_f}=1\)). The change in \(\Phi _k^T\) is bounded, taking into account the possible increase in f. Since the value of h is unchanged, the bound on the change in \(\Phi _k^T\) can be derived from (86) by replacing \(\mathbb {1}_{I_k}\mathbb {1}_{\bar{J_k}}\) by \(\mathbb {1}_{\bar{I_k}}\). That is,
$$\begin{aligned} \begin{aligned}&\mathbb {1}_{\{T\le k\}}\mathbb {1}_{\bar{I_k}}\mathbb {1}_{{\mathcal {D}}_f}( \Phi _{k+1}^T-\Phi _k^T)\\&\quad \le \mathbb {1}_{\{T\le k\}}\mathbb {1}_{\bar{I_k}}\mathbb {1}_{{\mathcal {D}}_f}\frac{\nu }{\varepsilon }\left( \left|f(X^{k+1}_{\text {feas}})-F^k_s\right|+\left|f(X^k_{\text {feas}})-F^k_0\right|\right) . \end{aligned} \end{aligned}$$(94) -
(ii)
The iteration is h-Dominating (\(\mathbb {1}_{{\mathcal {D}}_h}=1\)). Since the value of f is unchanged, the bound on the change in \(\Phi _k^T\) is obtained by multiplying both sides of (67) by \(\mathbb {1}_{\{T\le k\}}\) and replacing \(\Phi _k\) by \(\Phi _k^T\). That is,
$$\begin{aligned} \mathbb {1}_{\{T\le k\}}\mathbb {1}_{\bar{I_k}}\mathbb {1}_{{\mathcal {D}}_h}(\Phi _{k+1}-\Phi _k)\le \mathbb {1}_{\{T\le k\}}\mathbb {1}_{\bar{I_k}}\mathbb {1}_{{\mathcal {D}}_h}\frac{\nu }{m\varepsilon }\left( \left|h(X^{k+1}_{\text {inf}})-H^k_s\right|+\left|h(X^k_{\text {inf}})-H^k_0\right|\right) .\nonumber \\ \end{aligned}$$(95) -
(iii)
The iteration is Improving (\(\mathbb {1}_{{\mathcal {I}}}=1\)). The frame size parameter is updated as in h-Dominating iterations and the value of f is unchanged. Thus, the bound on the change in \(\Phi _k^T\) follows from (95) by replacing \(\mathbb {1}_{{\mathcal {D}}_h}\) by \(\mathbb {1}_{{\mathcal {I}}}\). That is, follows
$$\begin{aligned} \mathbb {1}_{\{T\le k\}}\mathbb {1}_{\bar{I_k}}\mathbb {1}_{{\mathcal {I}}}(\Phi _{k+1}-\Phi _k)\le \mathbb {1}_{\{T\le k\}}\mathbb {1}_{\bar{I_k}}\mathbb {1}_{{\mathcal {I}}}\frac{\nu }{m\varepsilon }\left( \left|h(X^{k+1}_{\text {inf}})-H^k_s\right|+\left|h(X^k_{\text {inf}})-H^k_0\right|\right) .\nonumber \\ \end{aligned}$$(96) -
(iv)
The iteration is Unsuccessful (\(\mathbb {1}_{{\mathcal {U}}}=1\)). Because of the decrease of the frame size parameter and hence the decrease in \(\Phi _k^T\), the bound on the change in \(\Phi _k^T\) is
$$\begin{aligned} \begin{aligned}&\mathbb {1}_{\{T\le k\}}\mathbb {1}_{\bar{I_k}}\mathbb {1}_{{\mathcal {U}}}( \Phi _{k+1}^T-\Phi _k^T)\\&\quad \le \mathbb {1}_{\{T\le k\}}\mathbb {1}_{\bar{I_k}}\mathbb {1}_{{\mathcal {U}}}\nu \left[ \frac{1}{\varepsilon }\left( \left|f(X^{k+1}_{\text {feas}})-F^k_s\right|+\left|f(X^k_{\text {feas}})-F^k_0\right|\right) \right. \\&\qquad \left. +\frac{1}{m\varepsilon }\left( \left|h(X^{k+1}_{\text {inf}})-H^k_s\right|+\left|h(X^k_{\text {inf}})-H^k_0\right|\right) \right] \end{aligned} \end{aligned}$$(97)
Since (97) dominates (94), (95) and (96), combining all four cases leads to
Taking expectations with respect to \({\mathcal {F}}^{C\cdot F}_{k-1}\) on both sides of (98) and using (15), (91) and (92) lead to (93). Combining the main results of Case 1, Case 2 and Case 3 of Part 2, specifically (75), (83) and (93),
Choosing \(\alpha \) and \(\beta \) according to (20) ensures that
and (74) follows from (99) and (100) with the same constant \(\eta =\frac{1}{2}\alpha \beta (1-\nu )(1-\tau ^2)\) as Part 1, which completes the proof. \(\square \)
1.2 Proof of Corollary 4.4
Proof
Only (22) is proved but the proof also applies for \(\left|H^k_s-h(X^k+S^k)\right|\) and \(\left|F^k_s-f(X^k+S^k)\right|\). According to Assumption 3(vi), \({\mathbb {E}}\left( \left|H^k_0-h(X^k)\right| |\ {\mathcal {F}}^{C\cdot F}_{k-1}\right) \le m\varepsilon (1-\alpha )^{1/2}(\Delta ^k_p)^2\), which implies that
By summing each side of (101) over k from 0 to N, and observing that

it follows from the monotone convergence theorem (see e.g. Theorem 1.6.6 in [32]) that
where \(\mu \) is from (54). This means that \(\displaystyle {\sum _{k=0}^{+\infty }\left|H^k_0-h(X^k)\right|<+\infty }\) almost surely, which implies the first result of (22). The proof for \(\left|F^k_0-f(X^k)\right|\) is similar by observing that (see (91))
\(\square \)
1.3 Proof of Lemma 4.7
Proof
The proof uses ideas from [11, 23]. The result is proved by contradiction conditioned on the almost sure event \(E_1=\{\Delta ^k_p\rightarrow 0\}\). All that follows is conditioned on the event \(E_1\). Assume that with nonzero probability, there exists a random variable \({\mathcal {E}}'>0\) such that
that is,
Let \(\{x^k_{\text {inf}}\}_{k\in {\mathbb {N}}}\), \(\{s^k\}_{k\in {\mathbb {N}}}\), \(\{\delta ^k_p\}_{k\in {\mathbb {N}}}\) and \(\epsilon '>0\) be realizations of \(\{X^k_{\text {inf}}\}_{k\in {\mathbb {N}}}\), \(\{S^k\}_{k\in {\mathbb {N}}}\), \(\{\Delta ^k_p\}_{k\in {\mathbb {N}}}\) and \({\mathcal {E}}'\), respectively for which \(\psi _k^h\ge \epsilon '\), for all \(k\in {\mathbb {N}}\). Let \({\hat{z}}\) be the parameter of Algorithm 2 satisfying \(\delta ^k_p\le \tau ^{-{\hat{z}}}\) for all \(k\ge 0\). Since \(\delta ^k_p\rightarrow 0\) due to the conditioning on \(E_1\), there exists \(k_0\in {\mathbb {N}}\) such that
Consequently and since \(\tau <1\), the random variable \(R_k\) with realizations \(r_k:=-\log _{\tau }\left( \frac{\delta ^k_p}{\lambda }\right) \) satisfies \(r_k<0\) for all \(k\ge k_0\). The main idea of the proof is to show that such realizations occur only with probability zero, thus leading to a contradiction. First \(\{R_k\}_{k\in {\mathbb {N}}}\) is shown to be a submartingale. Let \(k\ge k_0\) be an iteration for which the events \(I_k\) and \(J_k\) both occur, which happens with probability at least \(\alpha \beta >1/2\). Then, it follows from the definition of the event \(I_k\) (see Definition 3.3) that
where the first inequality in (107) follows from (102), (105) and (106) while the last inequality follows from (104). Consequently, iteration k of Algorithm 2 cannot be Unsuccessful. Thus, the frame size parameter is updated according to \(\delta _p^{k+1}=\tau ^{-1}\delta ^k_p\) since \(\delta ^k_p<\tau ^{1-{\hat{z}}}\). Hence, \(r_{k+1}=r_k+1\).
Let \({\mathcal {F}}^{I\cdot J}_{k-1}=\sigma (I_0,I_1,\dots ,I_{k-1})\cap \sigma (J_0,J_1,\dots ,J_{k-1})\). For all other outcomes of \(I_k\) and \(J_k\), which will occur with a total probability of at most \(1-\alpha \beta \), the inequality \(\delta _p^{k+1}\ge \tau \delta ^k_p\) always holds, thus implying that \(r_{k+1}\ge r_k-1\). Hence,
Thus, \({\mathbb {E}}\left( R_{k+1}-R_k|{\mathcal {F}}^{I\cdot J}_{k-1}\right) \ge 2\alpha \beta -1>0\), implying that \(\{R_k\}\) is a submartingale. The remainder of the proof is almost identical to that of the proof of the \(\liminf \)-type first-order result in [23].
Next is constructed a random walk \(W_k\) with realizations \(w_k\) on the same probability space as \(R_k\), which will serve as a lower bound on \(R_k\). Define \(W_k\) as in (14) by
where the indicator random variables \(\mathbb {1}_{I_i}\) and \(\mathbb {1}_{J_i}\) are such that \(\mathbb {1}_{I_i}=1\) if \(I_i\) occurs, \(\mathbb {1}_{I_i}=0\) otherwise, and similarly, \(\mathbb {1}_{J_i}=1\) if \(J_i\) occurs while \(\mathbb {1}_{J_i}=0\) otherwise. Then following the proof of Theorem 3.6, observe that \(\{W_k\}\) is a \({\mathcal {F}}^{I\cdot J}_{k-1}\)-submartingale with bounded (nonzero) increments (and, as such, cannot converge to any finite value; see also [23] for the same result), thus leading to the conclusion that the event \(\left\{ \underset{k\rightarrow +\infty }{\limsup }\ W_k=+\infty \right\} \) occurs almost surely. Since by construction
then with probability one, \(R_k\) is positive infinitely often. Thus, the sequence of realizations \(r_k\) such that \(r_k<0\) for all \(k\ge k_0\) occurs with probability zero. Thus, the assumption that (103) holds is false. This implies that
which means that (23) holds. \(\square \)
1.4 Proof of Theorem 4.10
Proof
The theorem is proved using ideas from [9, 11]. Define the events \(E_1\) and \(E_2\) by
Then \(E_1\) and \(E_2\) are almost sure due to Corollary 4.3 and (23) respectively. Let \(\omega \in E_1\cap E_2\) be an arbitrary outcome and note that the event \(E_1\cap E_2\) is also almost sure as a countable intersection of almost sure events. Then \(\lim _{K'(\omega )}\Delta ^k_p(\omega )=0\). It follows from the compactness hypothesis of Assumption 2 that there exists \(K(\omega )\subseteq K'(\omega )\) for which the subsequence \(\{X^k_{\text {inf}}(\omega )\}_{k\in K(\omega )}\) converges to a limit \({\hat{X}}_{\inf }(\omega )\). Specifically, \({\hat{X}}_{\inf }(\omega )\) is a refined point for the refining subsequence \(\{X^k_{\text {inf}}(\omega )\}_{k\in K(\omega )}\). Let \(v\in T^H_{{\mathcal {X}}}({\hat{X}}_{\inf }(\omega ))\) be a refining direction for \({\hat{X}}_{\inf }(\omega )\). Denote by V the random vector with realizations v, i.e., \(v=V(\omega )\), and let \({\hat{x}}_{\inf }={\hat{X}}_{\inf }(\omega )\), \(x^k_{\text {inf}}=X^k_{\text {inf}}(\omega )\), \(\delta ^k_p=\Delta ^k_p(\omega )\), \(\delta ^k_m=\Delta ^k_m(\omega )\), \(\psi _k^h=\Psi _k^h(\omega )\) and \({\mathcal {K}}=K(\omega )\). Since v is a refining direction, there exists \({\mathcal {L}}\subseteq {\mathcal {K}}\) and polling directions \(d^k\in {\mathbb {D}}^k_p(x^k_{\text {inf}})\) such that \(v=\underset{k\in {\mathcal {L}}}{\lim }\frac{d^k}{{\left\Vert d^k\right\Vert }_{\infty }}\). For each \(k\in {\mathcal {L}}\), define
where the fact that \(t_k\rightarrow 0\) follows from Definition 2.11, specifically the inequality \(\delta ^k_m{\left\Vert d^k\right\Vert }_{\infty }\le \delta ^k_pb\). Since h is \(\lambda ^h\)–locally Lipschitz,
which shows that Lemma 4.9 applies to both subsequences \(\{a_k\}_{k\in {\mathcal {L}}}\) and \(\{b_k\}_{k\in {\mathcal {L}}}\). Moreover, combining the inequality \(\lim _{{\mathcal {L}}}\psi _k^h\le 0\) and Assumption 6 (the fact that \(\delta ^k_p{\left\Vert d^k\right\Vert }_{\infty }\ge d_{\min }>0\)), yields
where the equality in (109) follows from \(\delta ^k_m=(\delta ^k_p)^2\) for sufficiently large k. Thus, by adding and subtracting \(h(x^k_{\text {inf}})\) to the numerator of the definition of the Clarke derivative, and using the fact that \(x^k_{\text {inf}}+\delta ^k_md^k\in {\mathcal {X}}\) for sufficiently large \(k\in {\mathcal {L}}\) since v is a hypertangent direction,
where the last inequality follows from (109). Every outcome \(\omega \) arbitrarily chosen in \(E_1\cap E_2\) therefore belongs to the event
thus implying that \(E_1\cap E_2\subseteq E_3\). Then the proof is complete since \({\mathbb {P}}\left( E_1\cap E_2\right) =1\).
\(\square \)
1.5 Proof of Corollary 4.11
Proof
The proof is almost identical to the proof of a similar result (Corollary 3.6) in [9]. Recall the sequence \(K'\) of random variables and the almost sure event \(E_1\cap E_2\) in the proof of Theorem 4.10 and let \(\omega \in E_1\cap E_2\). Following the latter proof, there exists \(K(\omega )\subseteq K'(\omega )\) such that \(\lim _{K(\omega )}X^k_{\text {inf}}(\omega )={\hat{X}}_{\inf }(\omega )={\hat{x}}_{\inf }\). Moreover, it follows from Theorem 4.10 that \(h^\circ ({\hat{x}}_{\inf }; v)=h^\circ ({\hat{X}}_{\inf }(\omega ); V(\omega ))\ge 0\) for a set of refining directions v which is dense in the closure \(\ {\text {cl}}\left( T^H_{{\mathcal {X}}}({\hat{x}}_{\inf })\right) \) of \(T^H_{{\mathcal {X}}}({\hat{x}}_{\inf })\). Then the proof is complete by noticing that \(\ {\text {cl}}\left( T^H_{{\mathcal {X}}}({\hat{x}}_{\inf })\right) =T^{Cl}_{{\mathcal {X}}}({\hat{x}}_{\inf })\) wherever \(T^H_{{\mathcal {X}}}({\hat{x}}_{\inf })\ne \emptyset \) [50], with \(T^{Cl}_{{\mathcal {X}}}({\hat{x}}_{\inf })\) denoting the Clarke tangent cone to \({\mathcal {X}}\) at \({\hat{x}}_{\inf }\). \(\square \)
1.6 Proof of Lemma 4.12
Proof
The proof is almost identical to those of Lemma 4.7 and a similar result in [11]. Hence, full details are not provided here again. Unless otherwise stated, all the sequences, events and constants considered are defined as in the proof of Lemma 4.7. The result is proved by contradiction and all that follows is conditioned on the almost sure event \(E_1\cap \{T<+\infty \}\). Assume that with nonzero probability there exists a random variable \({\mathcal {E}}''>0\) such that
Let \({t,}\ \{x^{k\vee t}_{\text {feas}}\}_{k\in {\mathbb {N}}}\), \(\{s^k\}_{k\in {\mathbb {N}}}\), \(\{\delta ^k_p\}_{k\in {\mathbb {N}}}\) and \(\epsilon ''>0\) be realizations of \({T,}\ \{X^{k\vee T}_{\text {feas}}\}_{k\in {\mathbb {N}}}\), \(\{S^k\}_{k\in {\mathbb {N}}}\), \(\{\Delta ^k_p\}_{k\in {\mathbb {N}}}\) and \({\mathcal {E}}''\), respectively for which \(\psi _k^{f,t}\ge \epsilon ''\) for all \(k\ge 0\). Let \({\bar{k}}_0\in {\mathbb {N}}^*\) be such that
The key element of the proof is to show that an iteration \(k\ge k_0:=\max \{{\bar{k}}_0,t\}\) for which the events \(I_k\) and \(J_k\) both occur cannot be Unsuccessful, and hence \(\{R_k\}\) is a submartingale.
It follows from (110) and (111) that
which implies that the iteration \(k\ge k_0\) of Algorithm 2 cannot be Unsuccessful. The rest of the proof follows that of Lemma 4.7. \(\square \)
1.7 Proof of Theorem 4.13
Proof
The proof follows from Corollary 4.4 and the assumption \(\lim _{k\in K}H^k_0(X^{k\vee T}_{\text {feas}})= 0\) almost surely, by observing that for any outcome \(\omega \) in the almost sure event
the inequalities
and the continuity of \(y\mapsto \left|y\right|\), yield
This means that
since h is nonnegative, where the first equality in (112) follows from the continuity of h in \({\mathcal {X}}\). Consequently,
\(\square \)
1.8 Proof of Theorem 4.14
Proof
First, \({\mathbb {P}}\left( {\hat{X}}_{\text {feas}}\in {\mathcal {D}}\right) =1\) follows from Theorem 4.13. The proof follows from that of Theorem 4.10, by replacing h by f, \({\hat{x}}_{\inf }={\hat{X}}_{\inf }(\omega )\) by \({\hat{x}}_{\text {feas}}={\hat{X}}_{\text {feas}}(\omega )\), \(x^k_{\text {inf}}=X^k_{\text {inf}}(\omega )\) by \(x^{k\vee t}_{\text {feas}}=X^{k\vee T}_{\text {feas}}(\omega )\), \(\psi _k^h=\Psi _k^h(\omega )\) by \(\psi _k^{f,t}=\Psi _k^{f,T}(\omega )\) with \(t=T(\omega )\) and \(T^H_{{\mathcal {X}}}(\cdot )\) by \(T^H_{{\mathcal {D}}}(\cdot )\), for \(\omega \) fixed and arbitrarily chosen in the almost sure event \(E_1\cap E_5\cap \{T<+\infty \}\), where
\(\square \)
1.9 Proof of Corollary 4.15
Proof
The proof is almost identical to the proof of a similar result (Corollary 3.4) in [9]. Let \(\omega \) be arbitrarily chosen in the almost sure event \(E_1\cap E_5\cap \{T<+\infty \}\). It follows from Theorem 4.14 that \(f^\circ ({\hat{x}}_{\text {feas}}; v)=f^\circ ({\hat{X}}_{\text {feas}}(\omega ); V(\omega ))\ge 0\) for a set of refining directions v which is dense in the closure of \(T^H_{{\mathcal {D}}}({\hat{x}}_{\text {feas}})\). Then the proof is complete by noticing that the closure of the hypertangent cone coincides with the Clarke tangent cone wherever the hypertangent cone is nonempty [9, 50]. \(\square \)
Rights and permissions
About this article
Cite this article
Dzahini, K.J., Kokkolaras, M. & Le Digabel, S. Constrained stochastic blackbox optimization using a progressive barrier and probabilistic estimates. Math. Program. 198, 675–732 (2023). https://doi.org/10.1007/s10107-022-01787-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-022-01787-7