1 Optimization with noisy functions

This work studies the unconstrained optimization problem

$$\begin{aligned} \begin{array}{rl} \displaystyle \min _{x \in {\mathbb {R}}^n} &{} f(x) \\ \end{array} \end{aligned}$$
(1)

in which the objective function \(f: {\mathbb {R}}^n \rightarrow {\mathbb {R}}\cup \{+\infty \}\) is computed by a blackbox simulation, contaminated with deterministic or stochastic noise. An objective function with a deterministic noise component may be written as:

$$\begin{aligned} \begin{array}{rl} \displaystyle \ f(x) = \left( 1+ \phi (x) \right) z(x) \end{array} \end{aligned}$$
(2)

where \(z: {\mathbb {R}}^n \rightarrow {\mathbb {R}}\cup \{+\infty \}\) is a smoother function, but is unknown in practice, and \(\phi : {\mathbb {R}}^n \rightarrow {\mathbb {R}}\) is a noise function that depends on x. In stochastic problems, \(\phi \) is a random variable whose distribution may be independent of x or not.

The proposed robust optimization algorithm aims to approach a minimizer of z(x) when only having access to the noisy function values f(x). In the algorithms proposed in [8, 14, 19, 25] quadratic models are constructed with regression techniques using previous evaluations of the noisy function values. The models are built on a trust-region and weighted according to the evaluation uncertainty [8]. Repeated function evaluations reduce the quadratic model variance and increase the accuracy of the model parameters [25]. Several strategies for minimizing the quadratic model have been tested in previous work: a trust-region algorithm in [10, 19], a modified version of the DIRECT algorithm in [17, 23] or a variant of the BOBYQA algorithm [25] to solve the stochastic problems [12]. Another technique for stochastic system optimization is described in [28], in which a ranking and selection strategy is used to determine the number of replicated responses to produce a sampling mean that satisfies a probability of correct selection. On the one hand, this procedure allows to determine the size of the sample which ensures obtaining a good estimation of the objective value. On the other hand, this classification allows to select the point having the minimum objective value. Furthermore, in [30] the smoothing function is constructed by elimination of all local optimal solutions worse than the best solution.

In [22], a smoothing technique approximates f by a smooth function \({\widetilde{f}}(x)\), constructed by the convolution with the probability density function v of the random variable that represents the noise:

$$\begin{aligned} \begin{array}{rl} \displaystyle {\widetilde{f}}(x) = \int _{{\mathbb {R}}^{n}} f(x+u) v(u) du. \end{array} \end{aligned}$$

An application of a smoothing technique on the energy function of a molecular model is described in [27]. The idea is to replace the value of the function at each point by a weighted average of nearby values. A Gaussian distribution is used to determine the weights:

$$\begin{aligned} \begin{array}{rl} \displaystyle {\widetilde{f}}_s(x) = \int _{{\mathbb {R}}^n} H(f(u),s) \exp \left( \frac{- \Vert x-u\Vert ^2}{ \sigma ^2 } \right) du, \end{array} \end{aligned}$$

where the standard deviation \(\sigma \) and s are the smoothing parameters, H is the function used to make the function f integrable, by using the energetic system transformation [31] based on the average value of f, or it can be also obtained by the diffusion equation method [18]. The motivation is to assign a low weight for values of f whose corresponding points are distant from the point x, and a high weight to values whose points are close to x.

In practice only a finite set of function values f is available for smoothing in blackbox optimization. Hence, the function \(\widetilde{f}\) can be approximated by a discrete weighted sum of a set of observations. The function smoothing considered in this work is commonly known as a kernel regression. It is also used in [13] to estimate the convolution product.

The present work takes advantage of the function evaluations required by the optimization process to dynamically smooth out the objective function. The document is structured as follows. Section 2 proposes an algorithmic approach called Robust-MADS that dynamically smoothes the objective function by using newly obtained function evaluations, followed by a succinct convergence analysis. Section 3 illustrates its performance on a collection of test problems and on a blackbox problem from the literature.

2 Algorithmic approach

Our algorithm is designed to perform a robust optimization of Problem (1) by smoothing the noisy objective function. The approach is named Robust-MADS because it is embedded into the Mesh Adaptive Direct Search (MADS) blackbox optimization algorithm.

2.1 Mesh Adaptive Direct Search

MADS  [3] is an iterative algorithm designed for a class of problems including unconstrained optimization of the form (1). The algorithm generates a sequence of trial points at which the objective function is evaluated. Each trial point is located on a mesh, a discretization of the space of variables, whose coarseness varies as the algorithm unfolds. The mesh becomes coarser when a better solution is found, and gets refined when local polling around the current best point fails to produce a better solution. The typical presentation of the MADS algorithm involves an iteration counter k that is incremented every time the mesh size parameter is updated.

The present work does not go into the details of how the trial points are generated, and simply considers the sequence of candidate points at which the objective function is evaluated. The reader is invited to consult [1, 6, 26, 29] for a thorough description of the way MADS may generate trial points.

Let \(x^0 \in {\mathbb {R}}^n\) be the initial point, and denote \(x^\ell \) the \(\ell \)-th candidate point at which f is evaluated. In addition, \(V^\ell = \{ x^0, x^1, \ldots , x^\ell \}\) denotes the set of all trial points up to \(x^\ell \) for which f has been successfully evaluated. Later, we will use the information \((V^\ell , f(V^\ell ))\) to construct a smoothed version of the function f. For a given value of \(\ell \), we call \(x^\ell _{\mathrm{best}}\in \mathop {\mathrm {argmin}}\{ f(v) : v \in V^\ell \}\) the incumbent solution, i.e., the best known solution. In the unlikely case that there are more than one candidate for the incumbent solution, we select the one that is the closest to the previous incumbent \(x^{\ell -1}_{\mathrm{best}}\).

The mesh \(M^k\) is updated at each iteration and is defined as follows. Let k be an iteration number, and let \(\ell \) be the number of evaluations of f done by the start of iteration k. The mesh is

$$\begin{aligned} M^k= & {} V^\ell + \left\{ \delta ^k Dz \ : \ z \in {\mathbb {Z}}^m\right\} \end{aligned}$$
(3)

where D is a \(n \times m\) matrix whose columns form a positive spanning set, and \(\delta ^k\in {\mathbb {R}}_+\) is called the mesh size parameter. At iteration k, trial points are generated during two separate steps, one global and one local, called the search and the poll. While search trial points can be constructed using any technique as long as they remain on the mesh, poll trial points are selected in a region around the incumbent \(x^\ell _{\mathrm{best}}\), at a distance of at most \(\varDelta ^k\): \(\{ x \in M^k : \Vert x - x^\ell _{\mathrm{best}}\Vert _\infty \le \varDelta ^k \}\). The poll size parameter \(\varDelta ^k\) is such that \(\varDelta ^k \ge \delta ^k\).

Typical values of the MADS parameters are to set the columns of \(D \in {\mathbb {R}}^{n \times 2n}\) to be the positive and negative coordinate directions. When either the search or poll step is successful at improving the incumbent solution, the poll size parameter is doubled: \(\varDelta ^{k+1} = 2 \varDelta ^k\), and when the iteration is unsuccessful, the poll size parameter is halved: \(\varDelta ^{k+1} = \frac{1}{2} \varDelta ^k\). The mesh size parameter is set to \(\delta ^{k+1} = \min \{ (\varDelta ^{k+1})^2, \varDelta ^{k+1}\}\). This way, the mesh size parameter will go to zero much faster than the poll size parameter.

In Robust-MADS we introduce a smoothed function \(\widetilde{f}\) to identify the incumbent solutions whereas MADS uses the original function f.

2.2 Function smoothing

We define the function \({\widetilde{f}}^\ell : {\mathbb {R}}^n \mapsto {\mathbb {R}}\) that uses the values \((V^\ell , f(V^\ell ))\) to smooth f using a kernel function. For any \(x \in {\mathbb {R}}^n\), we set

$$\begin{aligned} {\widetilde{f}}^\ell (x) = \frac{1}{P^\ell (x)} \sum _{v \in V^\ell } \psi ( x,v) f(v) \quad \text{ where } \quad P^\ell (x) \ = \ \sum _{v \in V^\ell }\psi ( x,v) \end{aligned}$$
(4)

and \(\psi \) is a kernel function. There are many kernel functions, for example, the Epanechnikov [15] or Gaussian functions. Here \(\psi \) is chosen to be a Gaussian function for a random variable with average \(\mu = 0 \) and variance \( \sigma ^2\). The kernel function is given by:

$$\begin{aligned} \psi (x,v) = \frac{1}{\sqrt{2\pi \sigma ^2}} e^{\frac{-\Vert x - v \Vert ^2}{2\sigma ^2}} \end{aligned}$$
(5)

where \(\Vert x - v \Vert \) is the Euclidean distance between x and v. In this work, the smoothing is dynamically adapted by setting the standard deviation as a multiple of the poll size parameter when the trial point x is generated at iteration k: \(\sigma (x)= \beta \varDelta ^k\), where \(\beta >0\) is a fixed constant. The value \(\sigma (x)\) is tied to the poll size \(\varDelta ^k\) when x was generated and remains unchanged at ulterior iterations. Hence, \(\psi (x,v)\) and \(\psi (v,x)\) have the same value only if x and v have been produced with the same poll size \(\varDelta ^k\). Tying the standard deviation to the poll size ensures that as the algorithm unfolds and \(\varDelta ^k\) gets small, more weight will be given to the neighbors of new trial points.

2.3 Updating the smoothed function

After evaluating f at a new trial point x and adding it to the set \(V^\ell \), the smoothed function \({\widetilde{f}}^{\ell }(x)\) is evaluated using (4).

The smoothed function needs to be recalculated for all points in \(V^{\ell -1}\) when new information is available and the smoothed function quality increases.

Proposition 1

Having a newly evaluated trial point x, the function \({\widetilde{f}}^{\ell }\) with \(\ell >1\) is calculated for each point \(v \in V^{\ell -1}\) as follows:

$$\begin{aligned} {\widetilde{f}}^{\ell }(v) \ = \ \frac{1}{P^{\ell }(v)} \left( P^{\ell -1}(v) {\widetilde{f}}^{\ell -1}(v) + \psi (v,x) f(x) \right) \end{aligned}$$
(6)

where \(P^{\ell }(v) \ = \ P^{\ell -1} (v) + \psi (v,x)\).

Proof

For each point \(v \in V^{\ell -1} = V^\ell {\setminus } \{x\}\),

$$\begin{aligned} {\widetilde{f}}^{\ell }(v)&= \frac{1}{P^\ell (v)} \sum _{w \in V^\ell } \psi (v,w) f(w) \\&= \frac{1}{P^\ell (v)} \left( \sum _{w \in V^\ell {\setminus } \{x\} } \psi (v,w) f(w) + \psi (v,x) f(x) \right) . \end{aligned}$$

The function \({\widetilde{f}}^{\ell -1}\) has already been evaluated at v, and substituting the sum by \(P^{\ell -1}(v) {\widetilde{f}}^{\ell -1}(v)\) in the previous equality gives (6). The quantity \(P^{\ell }(v)\) is obtained by adding the weight corresponding to (v, x) to the previous weight \(P^{\ell -1}(v)\). \(\square \)

In a blackbox optimization context, this updating technique reduces the computational effort by storing the values \({\widetilde{f}}^{\ell -1}\) and \(P^{\ell -1}\) in a cache.

2.4 The Robust-MADS algorithm

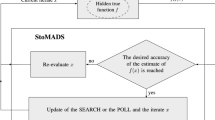
The Robust-MADS algorithm proceeds as follows. At each iteration, denoted by k, the standard MADS algorithm generates a finite list \(X^k\) of search and poll trial points located on the mesh \(M^k\). Then, the blackbox function f is evaluated at trial points in \(X^k\). Due to hidden constraints [11, 21], the evaluation of f may fail, and the corresponding point is simply discarded. When the evaluation succeeds, the smoothed function \({\tilde{f}}^\ell \) is constructed and evaluated at each point of the set \(V^\ell \) and the incumbent solution \(x^\ell _{\mathrm{best}}\) is determined. If the incumbent coincides with the last point where f was evaluated, then the iteration ends and is called successful. The poll and mesh size parameters are increased. Otherwise, the situation where the incumbent \(x^\ell _{\mathrm{best}}\) differs from \(x^{\ell -1}_{\mathrm{best}}\) is called a cache success because a previously evaluated trial point becomes the incumbent solution. This is due to the new smoothing function. The iteration is terminated, and the poll and mesh size parameters remain at their previous values. In both cases of success, all trial points in \(X^k\) may not be evaluated at iteration k. This is referred to as an opportunistic strategy. Finally, if \(x^\ell _{\mathrm{best}}= x^{\ell -1}_{\mathrm{best}}\) then the algorithm proceeds to the next trial point. Algorithm 1 shows the pseudo-code of Robust-MADS. Figure 1 illustrates the \({\tilde{f}}^\ell (V^\ell )\) evaluation for a given \(x \in X^k\).

figure a
Fig. 1
figure 1

Function smoothing of a new point and all cache points in Robust-MADS

Full size image

2.5 Convergence analysis of Robust-MADS

The convergence analysis of Robust-MADS is similar to that of MADS  [2]. The cornerstone of the analysis states that if the set of trial points generated by a MADS instance belongs to a bounded set, then the poll and mesh size parameters satisfy

$$\begin{aligned} \displaystyle \liminf _{k \rightarrow \infty } \delta ^{k} = \displaystyle \liminf _{k \rightarrow \infty } \varDelta ^{k} = 0. \end{aligned}$$

The requirement that the trial points belong to a bounded set is satisfied in particular when the level sets of f are bounded. The proof of the result relies on the fact that the mesh \(M^k\) contains finitely many points inside the bounded set. Consequently, the result trivially holds when MADS is replaced by Robust-MADS.

The mesh and poll size parameters are only reduced at unsuccessful iterations, i.e., when the incumbent solution remains unchanged after completing an iteration. The incumbent is then said to be a mesh local optimizer.

Definition 1

A convergent subsequence of mesh local optimizers, \(\{x^k\}_{k \in K}\) (for some subset of indices K), is said to be a refining subsequence if \(\{\varDelta ^k\}_{k \in K}\) converges to zero.

It is shown in [2] that if the trial points generated by a MADS instance belong to a bounded set, then refining subsequences exist and the following hierarchy of convergence results hold. Let \({\hat{x}}\) be the limit of a refining subsequence. If f is strictly differentiable near \({\hat{x}}\), then \(\nabla f({\hat{x}}) = 0\); if f is regular near \({\hat{x}}\) then \(f'({\hat{x}}; d) \ge 0\) for all \(d \in {\mathbb {R}}^n\); if f is Lipschitz near \({\hat{x}}\) then \(f^\circ ({\hat{x}}; d) \ge 0\) for all \(d \in {\mathbb {R}}^n\) (\(f^\circ \) is the Clarke Generalized derivative); if f is lower semi-continuous (lsc) at \({\hat{x}}\) then \(f({\hat{x}}) \le f(x^k)\) for all k; and if none of the above hold, then \(\hat{x}\) is the limit of mesh local optimizers on meshes that get infinitely fine. This last result is called the zeroth order result [5] because it does not assume anything on the objective function f. In the present context, the objective function f is noisy and therefore it does not satisfy any of the continuity assumptions (lsc, Lipschitz, regular, strictly differentiable), and consequently, the only part of the convergence analysis that remains valid is the zeroth order result.

3 Computational study

We first analyze the performance of Robust-MADS on a collection of artificially created unconstrained deterministic noisy problems from the derivative-free optimization literature [24], in the form of Eq. (2).

Second, we consider the blackbox optimization problem proposed and studied in [7]. The objective function of this problem returns the CPU time required by a trust-region algorithm to solve a collection of test problems. The variables of the blackbox problem are the four trust-region parameters. Each blackbox evaluation is time-consuming and the objective function value is contaminated by numerical noise because it consists of a CPU time. In fact, evaluating it twice with the same parameter values produces slightly different values.

For both deterministic and blackbox problems we study the effect of different values of the kernel function standard deviation factor \(\beta \) with respect to noise level.

Both Robust-MADS and MADS are available in the freely available NOMAD  [20] software package (version 3.8.0) using the OrthoMADS 2n directions of MADS with quadratic models and anisotropic mesh disabled. The stopping criteria of NOMAD are set to be a maximal number of evaluations and a minimal mesh size parameter value of \(10^{-13}\).

3.1 Analytical problems

The analytical problems are generated from the 22 different CUTEst [16] functions used in [24] with different starting points giving a total of 53 smooth problems with the dimension n ranging from 2 to 12. Note that for 8 problems, some variables are constrained by a lower bound of zero. For these, infeasible trial points are simply rejected. We consider the deterministic noisy variant of these functions in the form (2). The parameter \(\alpha \in {\mathbb {R}}^+\cup \{0\}\) controls the noise amplitude:

$$\begin{aligned} \phi (x)=\alpha T_3(\kappa (x)) \end{aligned}$$

where \(\kappa (x)=0.9 \sin (100 \Vert x\Vert _1) \cos (100 \Vert x\Vert _\infty ) + 0.1 \cos ( \Vert x\Vert _2)\) and \(T_3(x)=4x^3-3x\) is the cubic Chebyshev polynomial.

We study the influence of the noise level on the performance of the algorithm by considering other values than the default value (\(\alpha =0.001\)) given in [24] which corresponds to a very weak noise. On the low end side of the noise level we obtain smooth functions \(f(x)=z(x)\) for \(\alpha =0\). For the deterministic noise, above \(\alpha \simeq 0.8\) the noise amplitude is so large that it dominates the variations of f(x) due to z(x) and the algorithms stop near the starting point. For this reason, we consider that \(\alpha =0.7\) corresponds to the strongest noise level worth studying.

Fig. 2
figure 2

Data profiles obtained with MADS and Robust-MADS for a convergence tolerance of \(\tau =10^{-3}\) with test problems of various noise levels (\(\alpha =0\) is smooth and \(\alpha = 0.7\) is the noisiest). (a) smooth (\(\alpha = 0\)) (b) \(\alpha =0.1\) (c) \(\alpha =0.4\) (d) \(\alpha =0.7\)

Full size image

Ten optimization runs are reported for each function with 10 different pseudo-random number generator seeds that influence the selection of candidate points in MADS and Robust-MADS. Having a large enough set of problems allows the presentation of results with data profiles [24] using the following convergence test with respect to the smooth objective function: \(z(x^0)-z(x^e) \ge (1-\tau ) \left( z(x^0)-z^* \right) \), where \(x^0\) denotes the starting point, \(x^e\) corresponds to the best point obtained after e evaluations on one of the problems for all the compared methods and seed, \(\tau \) is the convergence tolerance, and \(z^*\) is the smooth objective function value of the best solution obtained by all the methods for all the runs of the considered problem.

In the figures, the horizontal axis is the number of evaluations divided by \(n+1\), and the vertical axis corresponds to the proportion of problems solved according to a given \(\tau \). Each variant of MADS corresponds to one curve, so that graphic comparison of the performance is easy.

The data profiles of Fig. 2 show that for problems with relatively low noise level (\(\alpha =0\) and \(\alpha =0.1\)), MADS tends to perform better than Robust-MADS, as expected. However, Robust-MADS is less sensitive to the noise level, and for \(\alpha \ge 0.4\) it tends to become more effective than MADS. The parameter \(\beta \) that controls the smoothing intensity impacts the performance of Robust-MADS. The small value \(\beta = 0.1\) makes Robust-MADS similar to MADS. For \(\beta =4\) the performance of Robust-MADS is not as good as for smaller values of \(\beta \). Based on these preliminary results, \(\beta =2\) appears to be an adequate compromise for noisy problems.

Fig. 3
figure 3

Convergence history plots for the blackbox optimization problem using NOMAD and SNOBFIT (a) Robust-MADS \(\beta =0.1\) (b) Robust-MADS \(\beta =1\) (c) Robust-MADS \(\beta =2\) (d) Robust-MADS \(\beta =3\) (e) MADS (f) SNOBFIT

Full size image

3.2 Tuning trust-region parameters

The blackbox problem is taken from [7], and consists in finding values of a set of continuous parameters of a trust-region (TR) algorithm:

$$\begin{aligned} p=(\eta _1,\eta _2,\alpha _1,\alpha _2) \in \varOmega = \{ p \in {\mathbb {R}}^4 \; | \; 0 \le \eta _1< \eta _2 \; \text {and} \; 0< \alpha _1< 1 < \alpha _2 \le 10 \}. \end{aligned}$$
Table 1 Post-optimization statistics for the blackbox parameter tuning problem using NOMAD and SNOBFIT
Full size table

The objective is to minimize the computational time required by TR to solve a collection of 55 test problems. The CPU time reported in [7] for solving these problems is 3 hours and 45 minutes with the parameter values \(p=(\frac{1}{4},\frac{3}{4},\frac{1}{2},2)\), but is now 5 minutes and 40 secondes with newer machines (Intel(R) Core(TM) i7 CPU 3.40GHz with 6 processors). The best solution reported in [7] is \(p_o^*=(0.22125,\, 0.94457031,\) \(\, 0.37933594, \, 2.3042969)\) with corresponding CPU time just under 2 hours and 50 minutes, an improvement of approximately \(25\%\). The newer machines requires 4 minutes, a \(29\%\) improvement. The two relative improvements are comparable.

The objective function value f(p) returns the CPU time consumed by TR to solve the problems with parameter values \(p \in \varOmega \). The value f(p) is set to infinity if \(x \not \in \varOmega \). Furthermore, if TR fails to converge within ten minutes for any of the 55 problems, f(p) is once again set to infinity. Consequently, these trial points are rejected by the optimization method. A maximum budget of 500 evaluations is considered during the optimization in addition to the default minimum mesh size convergence criterion of NOMAD. Each optimization run requires approximately \(500 \times 4\) min \(\approx 33\) h of CPU time. The duration of a single evaluation depends on the workload of the computer, and to limit the impact of this factor on the optimization, a single optimization is conducted at a time with no other significant workload.

A total of six optimization runs were performed. Four of them are done with Robust-MADS, and for comparisons, one of them is done with the standard MADS algorithms (without any robustness treatment) and another one is done with the MATLAB implementation of SNOBFIT  [9] (Stable Noisy Optimization by Branch and FIT). This last algorithm is designed for the robust and fast solution of noisy optimization problems. All tests were conducted with default algorithmic parameters, on the same computer with the same type of workload.

Figure 3a–f show the convergence history plots for each optimization. The small dots represent the finite objective function value f. In Fig. 3a–d, the other symbols represent the smoothed function \({\widetilde{f}}\) constructed by Robust-MADS to identify successes during optimization. Robust-MADS produces many more successes than MADS and the mesh size parameter is not reduced as quickly. The dispersion of the objective function value is more important at the beginning of the optimization process and tends to decrease toward the end. This is more obvious with the MADS optimization in Fig. 3e where a small dispersion of f at the end of the optimization reduces to the stochastic variation of the CPU time for a given evaluation for some trust-region parameters that are in practice identical. The dispersion seen in Fig. 3f shows that SNOBFIT has the opposite behavior.

The larger circles in Fig. 3a–d represent the smoothed objective function value at every successful iteration. These values are not monotone because the smoothed function is recalibrated at every iteration. The triangles represent the smoothed value where a previously evaluated trial point was re-established as an incumbent solution: A cache success. The decrease in the smoothed objective function value is more apparent for Robust-MADS with \(\beta =2\) and 3 which also leads to better objective function value (see Table 1). As observed when running the analytical problems, a value of \(\beta \) larger than 3 seems not beneficial when considering the final objective function value.

Table 1 proposes another way to evaluate the quality of the solutions produced by MADS, Robust-MADS with the four values of \(\beta \), and SNOBFIT. The second column lists \(f(p^*)\), the objective function value at the final point produced by the optimization methods. Because of the smoothing techniques, this point is not the point that produced the lowest value of f. In addition, and in order to quantify the stability of that solution, the objective function value was evaluated at 16 additional neighbouring points of each \(p^*\). These 16 post-optimization points are obtained by rounding-up and rounding-down each of the four components of \(p^*\) to the third decimal. The column labelled Failures indicates the number out of these 16 solutions where the evaluation of f failed. The minimal, maximal, range and mean values are reported in the table. The last column of the table gives the smoothed value \(\widetilde{f}(p^*)\) produced by Robust-MADS.

Worst-case analysis of the table suggests that the best strategy is Robust-MADS with \(\beta =2\). The corresponding value \(\max f(p^*_i) = 218.14\) is less than \(f(p^*)\) and \(\min f(p^*_i)\) for all other values of \(\beta \) and for MADS.

SNOBFIT produced a solution with \(f(p^*) =205.41\). At first glance, this might appear to be interesting, but notice that the evaluation of f failed at 4 out of the 16 neighbouring solutions. This means that for these nearby values, the trust-region algorithm failed to converge within the allotted time. The range of the SNOBFIT solution values \(\text {range} f(p^*_i) = 34.87\) is much larger than that of all Robust-MADS runs. Furthermore, Robust-MADS with \(\beta =2\) produced a trial point with \(f(x) = 183.76\), but not considered as a success because the value of f increases significantly for small perturbations on x.

In both the analytical and the blackbox problem, we recommend to set the standard deviation of the Gaussian distribution used to determine the Robust-MADS weights as twice (\(\beta = 2\)) the value of the poll size parameter.

4 Discussion

We have proposed a straightforward way to smooth out an objective function by means of a weighted average involving a kernel function parameterized by the current poll size parameter. This means that as the algorithm generates points that converge to some region in the space of variables, the objective function is sampled more and more in that region, thereby increasing the number of sampling points. There are no additional mechanism to resample extra points. The method was tested on a collection of analytical test problems, and on a real noisy black parameter-tuning problem.

Future work will focus on extending this approach to constrained blackbox optimization, using the progressive barrier [4].