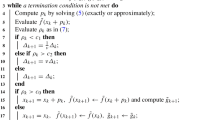Abstract
In this paper, we propose and analyze a trust-region model-based algorithm for solving unconstrained stochastic optimization problems. Our framework utilizes random models of an objective function f(x), obtained from stochastic observations of the function or its gradient. Our method also utilizes estimates of function values to gauge progress that is being made. The convergence analysis relies on requirements that these models and these estimates are sufficiently accurate with high enough, but fixed, probability. Beyond these conditions, no assumptions are made on how these models and estimates are generated. Under these general conditions we show an almost sure global convergence of the method to a first order stationary point. In the second part of the paper, we present examples of generating sufficiently accurate random models under biased or unbiased noise assumptions. Lastly, we present some computational results showing the benefits of the proposed method compared to existing approaches that are based on sample averaging or stochastic gradients.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Derivative free optimization (DFO) [8] has recently grown as a field of nonlinear optimization which addresses optimization of black-box functions, that is functions whose value can be (approximately) computed by some numerical procedure or an experiment, while their closed-form expressions and/or derivatives are not available and cannot be approximated accurately or efficiently. Although the role of derivative-free optimization is particularly important when objective functions are noisy, traditional DFO methods have been developed primarily for deterministic functions. The fields of stochastic optimization [22, 29] and stochastic approximation [33] on the other hand focus on optimizing functions that are stochastic in nature. Much of the focus of these methods depend on the availability and use of stochastic derivatives; however, some work has addressed stochastic black box functions, typically by some sort of a finite differencing scheme [18].
In this paper, using methods developed for DFO, we aim to solve
where f(x) is a function which is assumed to be smooth and bounded from below, but the value of which can only be computed with some noise. Let \(\tilde{f}\) be the noisy computable version of f, which takes the form
where the noise \(\varepsilon \) is a random variable.
In recent years, some DFO methods have been extended to and analyzed for stochastic functions [10, 20]. Additionally, stochastic approximation methodologies started to incorporate techniques from the DFO literature [5]. The analysis in all that work assumes some particular structure of the noise, including the assumption that the noisy function values give an unbiased estimator of the true function value.
There are two main classes of methods in this setting of stochastic optimization: stochastic gradient (SG) methods (such as the well known Robbins–Monro method) and sample average approximation (SAA) methods. The former (SG) methods work roughly as follows: they obtain a realization of an unbiased estimator of the gradient at each iteration and take a step in the direction of the negative gradient. The step sizes progressively diminish and the iterates are averaged to form a sequence that converges to a solution. These methods typically have very inexpensive iterations, but exhibit slow convergence, with the convergence rate being strongly dependent on the choice of algorithmic parameters, particularly the sequence of step sizes. Many variants exist that average the gradient information from past iterations and are able to accept sufficiently small, but nondecreasing step sizes [1, 17]. The SG type of method has gained very high popularity with their application in the field of machine learning (e.g., see an extensive survey on the subject [4]). Many sophisticated variants, that involve acceleration and other techniques have been developed and shown to be efficient in practice, [14, 19, 24]. However, the majority of these methods aim exclusively at convex functions and may not converge in non convex settings. Variance reduction techniques, such as [9, 16] have been proposed for the cases when f(x) is a finite sum of convex functions, which is a much more restrictive than what we consider here. While some variants of the above methods exists for nonconvex problems (e.g. [13]), the convergence remains slow, and parameter tuning remains necessary in most cases.
The second class of methods, (SAA), is based on sample averaging of the function and gradient estimators, which is applied to reduce the variance of the noise. These methods repeatedly sample the function value at a set of points in hopes to ensure sufficient accuracy of the function and gradient estimates. For a thorough introduction and references therein, see [25]. The optimization method and sampling process are usually tightly connected in these approaches; hence, again, algorithmic parameters need to be specially chosen and tuned. These methods tend to be more robust with respect to parameters and enjoy faster convergence at a cost of more expensive iterations. Practical success has been demonstrated for specially designed methods for problems of particular structure (see, e.g. [21]). However, very few sample averaging methods have been developed specifically for trust region methods and general nonconvex problems. Moreover, none of the methods mentioned above are applicable in the case of biased noise and they suffer significantly in the presence of outliers.
The goal of this paper is to show that a standard, efficient, unconstrained optimization method, such as a trust region method, can be applied, with very small modifications, to stochastic nonlinear (not necessarily convex) functions and can be guaranteed to converge to first order stationary points as long as certain conditions are satisfied. We present a general framework, where we do not specify any particular sampling technique. The framework is based on the trust region DFO framework [8], and its extension to probabilistic models [2]. In terms of this framework and the certain conditions that must be satisfied, we essentially assume that
-
the local models of the objective function constructed on each iteration satisfy some first order accuracy requirement with sufficiently high probability,
-
and that function estimates at the current iterate and at a potential next iterate are sufficiently accurate with sufficiently high probability.
The main novelty of this work is the analysis of the framework and the resulting weaker, more general, conditions for convergence compared to prior work. In particular,
-
We do not assume that the probabilities of obtaining sufficiently accurate models and estimates are increasing (they simply need to be above a certain constant) and
-
We do not assume any distribution of the random models and estimates. In other words, if a model or estimate is inaccurate, it can be arbitrarily inaccurate, i.e. the noise in the function values can have nonconstant bias.
It is also important to note that while our framework and model requirements are borrowed from prior work in DFO, this framework applies to derivative-based optimization as well. Later in the paper we will discuss different settings which will fit into the proposed framework.
This paper consists of two main parts. In the first part, we propose and analyze a trust region framework, which utilizes random models of f(x) at each iteration to compute the next potential iterate. It also relies on (random, noisy) estimates of the function values at the current iterate and the potential iterate to gauge the progress that is being made. The convergence analysis then relies on requirements that these models and these estimates are sufficiently accurate with sufficiently high probability. Beyond these conditions, no assumptions are made about how these models and estimates are generated. The resulting method is a stochastic process that is analyzed with the help of martingale theory. The method is shown to converge to first order stationary points with probability one.
In the second part of the paper, we consider various scenarios under different assumptions on the noise-inducing component \(\varepsilon \) and discuss how sufficiently accurate random models can be generated. In particular, we show that in the case of unbiased noise, that is when \( \mathbb {E}[{f}(x,\varepsilon )] = f(x)\) and \(\mathrm{Var}[f(x,\varepsilon )]\le \sigma ^2< \infty \) for all x, sample averaging techniques give us sufficiently accurate models. Although we will prove convergence under the mentioned framework that essentially says we have the ability to compute both sufficiently accurate models and estimates with constant, separate probabilities, it is not necessarily easy to estimate what these probabilities ought to be for a given problem. While we provide some guidance on the selection of sampling rates in an unbiased noise setting in Sect. 5, our numerical experiments show that the bounds on probabilities suggested by our theory to be necessary for almost sure convergence are far from tight.
We also discuss the case where \( \mathbb {E}[{f}(x,\varepsilon )] \ne f(x)\), and where the noise bias may depend on x or on the method of computation of the function values. One simple setting, which is illustrative, is as follows. Suppose we have an objective function, which is computed by a numerical process, whose accuracy can be controlled (for instance by tightening some stopping criterion within this numerical process). Suppose now that this numerical process involves some random component (such as sampling from some large data and/or utilizing a randomized algorithm). It may be known that with sufficiently high probability this numerical process produces a sufficiently accurate function value—however, with some small (but nonzero) probability the numerical process may fail and hence no reasonable value is guaranteed. Moreover, such failures may become more likely as more accurate computations are required (for instance because an upper bound on the total number of iterations is reached inside the numerical process). Hence the probability of failure may depend on the current iterate and state of the algorithm. Here we simply assume that such failures do not occur with probability higher than some constant (which will be specified in our analysis), conditioned on the past. However, we do not assume anything about the magnitude of the inaccurate function values. As we will demonstrate later in this paper, in this setting, \(\mathbb {E}[{f}(x,\varepsilon )] \ne f(x)\).
1.1 Comparison with related work
There is a very large volume of work on SAA and SG, most of which is quite different from our proposed analysis and method. However, we will mention a few works here that are most closely related to this paper and highlight the differences. The three methods existing in the literature we will compare with are by Deng and Ferris [10], SPSA (simultaneous perturbations stochastic approximation) [31, 32], and SCSR (sampling controlled stochastic recursion) [15]. These three settings and methods are most closely related to our work because they all rely on using models of the (possibly non convex) objective function that can both incorporate second-order information and whose accuracy with respect to a “true” model can be dynamically adjusted. In particular, Deng and Ferris apply the trust-region model-based derivative free optimization method UOBYQA [26] in a setting of sample path optimization [28]. In [31, 32], the author applies an approximate gradient descent and Newton method, respectively, with gradient and Hessian estimates computed from specially designed finite differencing techniques, with a decaying finite differencing parameter. In [15] a very general scheme is presented, where various deterministic optimization algorithms are generalized as stochastic counterparts, with the stochastic component arising from the stochasticity of the models and the resulting step of the optimization algorithm. We now compare some key components of these three methods with those of our framework, which we hereforth refer to as STORM (STochastic Optimization with Random Models).
Deng and Ferris The assumptions of the sample path setting are roughly as follows: on each iteration k, given a collection of points \(X^k=\{ x_1^k, \ldots , x_p^k\}\) one can compute noisy function values \(f(x_1^k, \varepsilon ^k),\ldots , f(x_p^k, \varepsilon ^k) \). The noisy function values are assumed to be realizations of an unbiased estimator of true values \(f(x_1^k),\ldots , f(x_p^k)\). Then, using multiple, say \(N_k\), realizations of \(\varepsilon ^k\), average function values \(f^{N_k}(x_1^k),\ldots , f^{N_k}(x_p^k) \) can be computed. A quadratic model \(m^{N_k}_k(x)\) is then fit into these function values, and so a sequence of models \(\{m^{N_k}_k(x)\}\) is created using a nondecreasing sequence of sampling rates \(\{N_k\}\). The assumption on this sequence of models is that each of them satisfies a sufficient decrease condition (with respect to the true model of the true function f) with probability \(1-\alpha _k\), such that \(\sum _{k=1}^\infty \alpha _k< \infty \). The trust region maintenance follows the usual scheme like that in UOBYQA, hence the steps taken by the algorithm can be increased or decreased depending on the observed improvement of the function estimates.
SPSA The first order version of this method assumes that \(f(x,\varepsilon )\) is an unbiased estimate of f(x), and the second order version, 2SPSA, assumes that an unbiased estimate of \(\nabla f(x)\), \(g(x,\varepsilon )\in \mathbf{R}^n\), can be computed. Gradient (in the first order case) and Hessian (in the second order case) estimates are constructed using an interesting randomized finite differencing scheme. The finite difference step is assumed to be decaying to zero. An approximate steepest descent direction or approximate Newton direction are then constructed and a step of length \(t_k\) is taken along this direction. The sequence \(\{t_k\}\) is assumed to be decaying in the usual Robbins–Monro way, that is \(t_k\rightarrow 0\), \(\sum _k t_k =\infty \). Hence, while no increase in accuracy of the models is assumed (they only need to be accurate in expectation), the step size parameter and the finite differencing parameter need to be tuned. Decaying step sizes often lead to slow convergence, as has been observed often in stochastic optimization literature.
SCSR This is a very general scheme which can include multiple optimization methods and sampling rates. The key ingredients of this scheme are a deterministic optimization method, and a stochastic variant that approximates it. The stochastic step (recursion) is assumed to be a sufficiently accurate approximation of the deterministic step with increasing probability (the probabilities of failure for each iteration are summable). This assumption is stronger than the one in this paper. In addition, another key assumption made for SCSR is that the iterates produced by the base deterministic algorithm converge to the unique optimal minimizer \(x^*\). Not only we do not assume here that the minimizer/stationary point is unique, but we also do not assume a priori that the iterates form a convergent sequence, since they may not do so in a nonconvex setting, while every iterate subsequence converges to a stationary point.
STORM Like the Deng and Ferris method, we utilize a trust-region, model-based framework, where the size of the trust region can be increased or decreased according to empirically observed function decrease and the size of the observed approximate gradients. The desired accuracy of the models is tied only to the trust region radius in our case, while for Deng and Ferris, it is tied to both the radius and the size of true model gradients (the second condition is harder to ensure). In either method, this desired accuracy is assumed to hold with some probability—in STORM, this probability remains constant throughout the progress of the algorithm, while for Deng and Ferris it has to converge to 1 sufficiently rapidly.
There are three major advantages to our results. First of all, in the case of unbiased noise, the sampling rate is directly connected to the desired accuracy of the estimates and the probability with which this accuracy is achieved. Hence, for the STORM method, the sampling rate may increase or decrease according to the trust region radius, eventually increasing only when necessary, i.e. when the noise becomes dominating. For all the other methods listed here, the sampling rate is assumed to increase monotonically. Secondly, in the case of biased noise, we can still prove convergence of our method, as long as the desired accuracy is achieved with a fixed probability. In other words, we allow for the noise to be arbitrarily large with a small, but fixed, probability on each iteration. This allows us to consider new models of noise which cannot be handled by any of the other methods discussed here. In addition, STORM incorporates first and second order models without changing the algorithm—the step size parameter (i.e., the trust region radius) and other parameters of the method are chosen almost identically to the standard practices of the trust region methods, which have proved to be very effective in practice for unconstrained nonlinear optimization. In Sect. 6 we show that the STORM method is very effective in different noise settings and is very robust with respect to sampling strategies.
Finally, we want to point to [20], which proposes a very similar method to the one in this paper. Both methods were developed based on the trust region DFO method with random models for deterministic functions analyzed in [2] and extended to the stochastic setting. Some of the assumptions in this paper were inspired by an early version of [20]. However, the assumptions and the analysis in [20] are quite different from what appears in this paper. In particular, they rely on the assumption that \(f(x,\varepsilon )\) is an unbiased estimate of f(x), hence their analysis does not extend to the biased case. Also they assume that the probability of having an accurate model at the k-th iteration is at least \(1-\alpha _k\), such that \(\alpha _k\rightarrow 0\), while for our method this probability can remain bounded away from zero. Similarly, they assume that the probability of having accurate function estimates at the k-th iteration also converges to 1 sufficiently rapidly, while in our case it is again constant. Their analysis, as a result, is very different from ours, and does not generalize to various stochastic settings (they only focus on the derivative free setting with additive noise). The advantage of their method is that they do not need to put a restriction on acceptable step sizes when the norm of the gradient of the model is small. We, on the other hand, impose such a restriction in our method and use it in the proof of our main result. However, as we discuss later in the paper this restriction can be relaxed at the cost of a more complex algorithm and analysis. In practice, we do not implement this restriction, hence our basic implementation is virtually identical to that in [20] except that we implement a variety of model building strategies, while only one such strategy (regression models based on randomly rotated orthogonal samples sets) is implemented in [20]. Thus we do not directly compare the empirical performance of our method with the method in [20] since we view it as more or less the same method.
We conclude this section by introducing some frequently used notations and their meanings. The rest of the paper is organized as follows. In Sect. 2 we introduce the trust region framework, followed by Sect. 3, where we discuss the requirements on our random models and function estimates. The main convergence results are presented in Sect. 4. In Sect. 5 we discuss various noise scenarios and how sufficiently accurate models and estimates can be constructed in these cases. Finally, we present computational experiments based on these various noise scenarios in Sect. 6.
Notations Let \(\Vert \cdot \Vert \) denote the Euclidean norm and \(B(x, \Delta )\) denote the ball of radius \(\Delta \) around x, i.e., \(B(x, \Delta ): \{y:\Vert x-y\Vert \le \Delta \}\). Probability sample spaces are denoted by \(\Omega \), according to the context, and a sample from that space is denoted by \(\omega \in \Omega \). As a rule, when we describe a random process within the algorithmic framework, uppercase letters, e.g. the k-th iterate \(X_k\), will denote random variables, while lowercase letters will denote realizations of the random variable, e.g. \(x_k=X_k(\omega )\) is the k-th iterate for a particular realization of our algorithm.
We also list here, for convenience, several constants that are used in the paper to bound various quantities. These constants are denoted by \(\kappa \) with subscripts indicating quantities that they are meant to bound.
2 Trust region method
We consider the trust-region class of methods for minimization of unconstrained functions. They operate as follows: at each iteration k, given the current iterate \(x_k\) and a trust-region radius \(\delta _k\), a (random) model \(m_k(x)\) is built, which serves as an approximation of f(x) in \(B(x_k, \delta _k)\). The model is assumed to be of the form
It is possible to generalize our framework to other forms of models, as long as all conditions on the models, described below, hold. We consider quadratic models for simplicity of the presentation and because they are the most common. The model \(m_k(x)\) is minimized (approximately) in \(B(x_k, \delta _k)\) to produce a step \(s_k\) and (random) estimates of \(f(x_k)\) and \(f(x_k+s_k)\) are obtained, denoted by \(f_k^0\) and \( f_k^s\) respectively. The achieved reduction is measured by comparing \(f_k^0\) and \(f_k^s\) and if reduction is deemed sufficient, then \(x_k+s_k\) is chosen as the next iterate \(x_{k+1}\). Otherwise the iterate remains \(x_k\). The trust-region radius \(\delta _{k+1}\) is then chosen by either increasing or decreasing \(\delta _k\) according to the outcome of the iteration. The details of the algorithm are presented in Algorithm 1.

The trial step computed on each iteration has to provide sufficient decrease of the model; in other words it has to satisfy the following standard fraction of Cauchy decrease condition:
Assumption 2.1
For every k, the step \(s_k\) is computed so that
for some constant \(\kappa _{fcd}\in (0,1].\)
If progress is achieved and a new iterate is accepted in the k-th iteration then we call this a successful iteration. Otherwise, the iteration is unsuccessful (and no step is taken). Hence a successful iteration occurs when \(\rho _k\ge \eta _1\) and \( \Vert g_k\Vert \ge \eta _2 \delta _k \). However, a successful iteration does not necessarily yield an actual reduction in the true function f. This is because the values of f(x) are not accessible in our stochastic setting and the step acceptance decision is made merely based on the estimates of \(f(x_k)\) and \(f(x_k+s_k)\). If these estimates, \(f_k^0\) and \(f_k^s\), are not accurate enough, a successful iteration can result in an increase of the true function value. Hence we consider two types of successful iterations - those where f(x) is in fact decreased proportionally to \(f_k^0-f_k^s\) which we call true successful iterations, and all other successful iterations, where the decrease of f(x) can be arbitrarily small or even negative, which we call false successful iterations. Our setting and algorithmic framework do not allow us to determine which successful iterations are true and which ones are false; however, we will be able to show that true successful iterations occur sufficiently often for convergence to hold if the random estimates \(f_k^0\) and \(f_k^s\) are sufficiently accurate.
A trust region framework based on random models was introduced and analyzed in [2]. In that paper, the authors introduced the concept of probabilistically fully-linear models to determine the conditions that random models should satisfy for convergence of the algorithm to hold. However, the randomness in the models in their setting arises from the construction process, and not from the noisy objective function. It is assumed in [2] that the function values at the current iterate and the trial point can be computed exactly and hence all successful iterations are true in that case. In our case, it is necessary to define a measure for the accuracy of the estimates \(f_k^0\) and \(f_k^s\) (which, as we will see, generally has to be tighter than the measure of accuracy of the model). We will use a modified version of the probabilistic estimates introduced in [20].
3 Probabilistic models and estimates
The models in this paper are functions which are constructed on each iteration, based on some random samples of stochastic function \(\tilde{f}(x)\). Hence, the models themselves are random and so is their behavior and influence on the iterations. Hence, \(M_k\) will denote a random model in the k-th iteration, while we will use the notation \(m_k=M_k(\omega )\) for its realizations. As a consequence of using random models, the iterates \(X_k\), the trust-region radii \(\Delta _k\) and the steps \(S_k\) are also random quantities, and so \(x_k=X_k(\omega )\), \(\delta _k = \Delta _k(\omega )\), \(s_k=S_k(\omega )\) will denote their respective realizations. Similarly, let random quantities \(\{F_k^0,F_k^s\}\) denote the estimates of \(f(X_k)\) and \(f(X_k+S_k)\), with their realizations denoted by \(f_k^0=F_k^0(\omega )\) and \(f_k^s=F_k^s(\omega )\). In other words, Algorithm 1 results in a stochastic process \(\{M_k,X_k,S_k, \Delta _k, F_k^0, F_k^s\}\). Our goal is to show that under certain conditions on the sequences \(\{M_k\}\) and \(\{F_k^0, F_k^s\}\) the resulting stochastic process has desirable convergence properties with probability one. In particular, we will assume that models \(M_k\) and estimates \(F_k^0, F_k^s\) are sufficiently accurate with sufficiently high probability, conditioned on the past.
To formalize conditioning on the past, let \(\mathcal {F}_{k-1}^{M\cdot F}\) denote the \(\sigma \)-algebra generated by \(M_0,\ldots , M_{k-1}\) and \(F_0,\ldots ,F_{k-1}\) and let \(\mathcal {F}_{k-{1}/{2}}^{M\cdot F}\) denote the \(\sigma \)-algebra generated by \(M_0,\ldots , M_{k}\) and \(F_0,\ldots ,F_{k-1}\).
To formalize sufficient accuracy, let us recall a measure for the accuracy of deterministic models introduced in [7, 8] (with the exact notation introduced in [3]).
Definition 3.1
Suppose \(\nabla f\) is Lipschitz continuous. A function \(m_k\) is a \(\kappa \)-fully linear model of f on \(B(x_k,\delta _k)\) provided, for \( \kappa = (\kappa _{ef}, \kappa _{eg})\) and \(\forall y \in B\),
In this paper we extend the following concept of probabilistically fully-linear models which is proposed in [2].
Definition 3.2
A sequence of random models \(\{ M_k \}\) is said to be \(\alpha \)-probabilistically \(\kappa \)-fully linear with respect to the corresponding sequence \(\{ B(X_k,\Delta _k)\}\) if the events
satisfy the condition
where \(\mathcal {F}^M_{k-1}\) is the \(\sigma \)-algebra generated by \(M_0,\ldots , M_{k-1}\).
These probabilistically fully-linear models have the very simple properties that they are fully-linear (i.e., accurate enough) with sufficiently high probability conditioned on the past, and they can be arbitrarily inaccurate otherwise. This property is somewhat different from the properties of models typical to stochastic optimization (such as, for example, stochastic gradient-based models), where assumptions on the expected value and the variance of the models is imposed. We will discuss this in more detail in Sect. 5.
In this paper, aside from sufficiently accurate models, we require estimates of the function values \(f(x_k)\), \(f(x_k+s_k)\) that are sufficiently accurate. This is needed in order to evaluate whether a step is successful, unlike the case in [2] where the exact values \(f(x_k)\) and \(f(x_k+s_k)\) are assumed to be available. The following definition of accurate estimates is a modified version of that used in [20].
Definition 3.3
The estimates \(f_k^0\) and \(f_k^s\) are said to be \(\epsilon _F\)-accurate estimates of \(f(x_k)\) and \(f(x_k+s_k)\), respectively, for a given \(\delta _k\) if
We now modify Definitions 3.2 and 3.3 and introduce definitions of probabilistically accurate models and estimates which we will use throughout the remainder of the paper.
Definition 3.4
A sequence of random models \(\{ M_k \}\) is said to be \(\alpha \)-probabilistically \(\kappa \)-fully linear with respect to the corresponding sequence \(\{ B(X_k,\Delta _k)\}\) if the events
satisfy the condition
where \(\mathcal {F}^{M\cdot F}_{k-1}\) is the \(\sigma \)-algebra generated by \(M_0,\ldots , M_{k-1}\) and \(F_0,\ldots ,F_{k-1}\).
Definition 3.5
A sequence of random estimates \(\{F_k^0,F_k^s\}\) is said to be \(\beta \)-probabilistically \(\epsilon _F\)-accurate with respect to the corresponding sequence \(\{X_k,\Delta _k,S_k\}\) if the events
satisfy the condition
where \(\epsilon _F\) is a fixed constant and \(\mathcal {F}_{k-{1}/{2}}^{M\cdot F}\) is the \(\sigma \)-algebra generated by \(M_0,\ldots , M_{k}\) and \(F_0,\ldots ,F_{k-1}\).
Motivated by Definitions 3.4 and 3.5, we will make later an assumption in our analysis that our method has access to a sequence of \(\alpha \)-probabilistically \(\kappa \)-fully linear models, for some fixed \( \kappa = (\kappa _{ef}, \kappa _{eg})\) and to a sequence of \(\beta \)-probabilistically \(\epsilon _F\)-accurate estimates, for some fixed, sufficiently small \(\epsilon _F\). This will imply that the model and the estimate accuracy are both assumed to be proportional to \(\delta _k^2\) (with some probability); we remark now that the condition on the estimates will be somewhat tighter due to an upper bound on \(\epsilon _F\). However, we will see that this upper bound is not too small.
Procedures for obtaining probabilistically fully-linear models and probabilistically accurate estimates under different models of noise are discussed in Sect. 5.
4 Convergence analysis
We now present first-order convergence analysis for the general framework described in Algorithm 1. Towards that end, we assume that the function f and its gradient are Lipschitz continuous in regions considered by the algorithm realizations.
Assumption 4.1
(Assumptions on f) Let \(x_0\) and \(\delta _{\max }\) be given. Let \(\mathcal{L}(x_0)\) define the set in \(\mathbb {R}^n\) which contains all iterates of our algorithm. Assume that f is bounded from below on \(\mathcal{L}(x_0)\). Assume also that the function f and its gradient \(\nabla f\) are L-Lipschitz continuous on the set \(\mathcal{L}_{enl}(x_0)\), where \(\mathcal{L}_{enl}(x_0)\) defines the region considered by the algorithm realizations
Remark 4.2
In the case of deterministic functions \(\mathcal{L}(x_0)=\{ x\in \mathbb {R}^n:\, f(x)\le f(x_0) \}\), because algorithm iterates never increase the objective function value, hence they do not step outside the initial level set. However, here we allow iterates to increase the function value, because the true function value is not known. Such iterates, as we will see, may happen with some (relatively small) probability, hence the algorithm can venture outside the initial level set. Hence we choose to make the assumption above, which of course depends on the algorithmic behavior. Clearly, if we assume a global Lipschitz constant and global lower bound, then the above assumption always holds. If we prefer to weaken this assumption, then there are several algorithmic remedies possible; however, they will make our analysis more complicated and we choose to leave it for future work.
The second assumption provides a uniform upper bound on the model Hessian.
Assumption 4.3
There exists a positive constant \(\kappa _{bhm} \) such that, for every k, the Hessian \(H_k\) of all realizations \(m_k\) of \(M_k\) satisfy
Note that since we are concerned with convergence to a first order stationary point in this paper, the bound \(\kappa _{bhm}\) can be chosen to be any nonnegative number, including zero. Allowing a larger bound will give more flexibility to the algorithm and may allow better Hessian approximations, but as we will see in the convergence analysis, this imposes restrictions on the trust region radius and some other algorithmic parameters.
We now state the following result from martingale literature [12] (see Exercise 5.3.1) that will be useful later in our analysis.
Theorem 4.4
Let \(G_k\) be a submartingale, i.e., a sequence of random variables which, for every k,
where \(\mathcal {F}_{k-1}^G=\sigma (G_0,\ldots ,G_{k-1})\) is the \(\sigma \)-algebra generated by \(G_0,\ldots , G_{k-1}\), and \(E[G_k|\mathcal {F}_{k-1}^G]\) denotes the conditional expectation of \(G_k\) given the past history of events \(\mathcal {F}_{k-1}^G\).
Assume further that \(G_k-G_{k-1}\le M<\infty \), for every k. Then,
We now prove some auxiliary lemmas that provide conditions under which decrease of the true objective function f(x) is guaranteed. The first lemma states that if the trust region radius is small enough relative to the size of the model gradient and if the model is fully linear, then the step \(s_k\) provides a decrease in f(x) proportional to the size of the model gradient. Note that the trial step may still be rejected if the estimates \(f_k^0\) and \(f_k^s\) are not accurate enough.
Lemma 4.5
Suppose that a model \(m_k\) of the form (2) is a \((\kappa _{ef},\kappa _{eg})\)-fully linear model of f on \(B(x_k,\delta _k)\). If
then the trial step \(s_k\) leads to an improvement in \(f(x_k+s_k)\) such that
Proof
Using the Cauchy decrease condition, the upper bound on model Hessian and the fact that \(\Vert g_k\Vert \ge \kappa _{bhm}\delta _k\), we have
Since the model is \(\kappa \)-fully linear, one can express the improvement in f achieved by \(s_k\) as
where the last inequality is implied by \(\delta _k\le \frac{\kappa _{fcd}}{8\kappa _{ef}} \Vert g_k\Vert \).
The next lemma shows that for \(\delta _k\) small enough relative to the size of the true gradient \(\nabla f(x_k)\), the guaranteed decrease in the objective function, provided by \(s_k\), is proportional to the size of the true gradient.
Lemma 4.6
Under Assumption 4.3, suppose that a model is \((\kappa _{ef},\kappa _{eg})\)-fully linear on \(B(x_k,\delta _k)\). If
then the trial step \(s_k\) leads to an improvement in \(f(x_k+s_k)\) such that
where \(C_1=\frac{\kappa _{fcd}}{4}\cdot \max \left\{ \frac{\kappa _{bhm}}{\kappa _{bhm}+\kappa _{eg}},\frac{8\kappa _{ef}}{8\kappa _{ef}+\kappa _{fcd}\kappa _{eg}}\right\} .\)
Proof
The definition of a \(\kappa \)-fully-linear model yields that
Since condition (11) implies that \(\Vert \nabla f(x_k) \Vert \ge \max \left\{ \kappa _{bhm}+\kappa _{eg},\frac{8\kappa _{ef}}{\kappa _{fcd}}+\kappa _{eg}\right\} \delta _k \), we have
Hence, the conditions of Lemma 4.5 hold and we have
Since \(\Vert g_k\Vert \ge \Vert \nabla f(x)\Vert -\kappa _{eg}\delta _k\) in which \(\delta _k\) satisfies (11), we also have
Combining (13) and (14) yields (12).
We now prove a lemma that states that if a) the estimates are sufficiently accurate, b) the model is fully-linear, and c) the trust-region radius is sufficiently small relative to the size of the model gradient, then a successful step is guaranteed.
Lemma 4.7
Under Assumption 4.3, suppose that \(m_k\) is \((\kappa _{ef},\kappa _{eg})\)-fully linear on \(B(x_k,\delta _k)\) and the estimates \(\{ f_k^0,f_k^s \}\) are \(\epsilon _F\)-accurate with \(\epsilon _F\le \kappa _{ef}\). If
then the k-th iteration is successful.
Proof
Since \( \delta _k \le \frac{\Vert g_k \Vert }{\kappa _{bhm}}\), the Cauchy decrease condition and the uniform bound on \(H_k\) immediately yield that
The model \(m_k\) being \((\kappa _{ef},\kappa _{eg})\)-fully linear implies that
Since the estimates are \({\epsilon }_F\)-accurate with \(\epsilon _F\le \kappa _{ef}\), we obtain
We have
which, combined with (16)–(19), implies
where we have used the assumption \(\delta _k \le \frac{ \kappa _{fcd}(1-\eta _1) }{ 8\kappa _{ef} } \Vert g_k \Vert \) to deduce the last inequality. Hence, \(\rho _k\ge \eta _1\). Moreover, since \(\Vert g_k\Vert \ge \eta _2\delta _k\), the k-th iteration is successful.
Finally, we state and prove a lemma which guarantees an amount of decrease of the objective function on a true successful iteration.
Lemma 4.8
Under Assumption 4.3, suppose that the estimates \(\{f_k^0,f_k^s \}\) are \({\epsilon }_F\)-accurate with \({\epsilon }_F< \frac{1}{4}\eta _1\eta _2 \kappa _{fcd}\min \left\{ \frac{\eta _2}{\kappa _{bhm}},1 \right\} \). If a trial step \(s_k\) is accepted (a successful iteration occurs), then the improvement in f is bounded below as follows
where \(C_2 =\frac{1}{2}\eta _1\eta _2 \kappa _{fcd}\min \left\{ \frac{\eta _2}{\kappa _{bhm}},1 \right\} -2\epsilon _F>0\).
Proof
An iteration being successful indicates that \(\Vert g_k\Vert \ge \eta _2 \delta _k\) and \(\rho \ge \eta _1\). Thus,
Then, since the estimates are \(\epsilon _F\)-accurate, we have that the improvement in f can be bounded as
where \(C_2 =\frac{1}{2}\eta _1\eta _2 \kappa _{fcd}\min \left\{ \frac{\eta _2}{\kappa _{bhm}},1 \right\} -2\epsilon _F>0\).
To prove convergence of Algorithm 1 we will need to assume that models \(\{M_k\}\) and estimates \(\{F_k^0, F_k^s\}\) are sufficiently accurate with sufficiently high probability.
Assumption 4.9
Given values of \(\alpha ,\beta \in (0,1)\) and \(\epsilon _F>0\), there exist \(\kappa _{eg}\) and \(\kappa _{ef}\) such that the sequence of models \(\{M_k\}\) and estimates \(\{F_k^0, F_k^s\}\) generated by Algorithm 1 are, respectively, \(\alpha \)-probabilistically \((\kappa _{ef}, \kappa _{eg})\)- fully-linear and \(\beta \)-probabilistically \(\epsilon _F\)-accurate.
Remark 4.10
Note that this assumption is a statement about the existence of constants \(\kappa =(\kappa _{ef},\kappa _{eg})\) given an \(\alpha \), \(\beta \) and \(\epsilon _F\) - we will determine exact conditions on \(\alpha \), \(\beta \) and \(\epsilon _F\) in Theorem 4.11 and Lemma 4.12 below.
The following theorem states that the trust-region radius converges to zero with probability 1.
Theorem 4.11
Let Assumptions 4.1 and 4.3 be satisfied and assume that in Algorithm 1 the following holds.
-
The step acceptance parameter \(\eta _2\) is chosen so that
$$\begin{aligned} \eta _2\ge & {} \max \left\{ \kappa _{bhm}, \frac{8\kappa _{ef}}{\kappa _{fcd}(1-\eta _1)} \right\} .\end{aligned}$$(21) -
The accuracy parameter of the estimates satisfies
$$\begin{aligned} \epsilon _F\le & {} \min \left\{ \kappa _{ef}, \frac{1}{8}\eta _1\eta _2 \kappa _{fcd} \right\} . \end{aligned}$$(22)
Then \(\alpha \) and \(\beta \) can be chosen so that, if Assumption 4.9 holds for these values, then the sequence of trust-region radii, \(\{\Delta _k\}\), generated by Algorithm 1 satisfies
almost surely.
Proof
We base our proof on properties of the random function \(\Phi _k =\nu f(X_{k})+(1-\nu )\Delta _{k}^2 \), where \(\nu \in (0,1)\) is a fixed constant, which is specified below. A similar function is used in the analysis in [20], but the analysis itself is different. The overall goal is to show that there exists a constant \(\sigma >0\) such that for all k
Since f is bounded from below and \(\Delta _k>0\), we have that \(\Phi _{k}\) is bounded from below for all k; hence if (24) holds on every iteration, then by summing (24) over \(k\in (1,\infty )\) and taking expectations on both sides we can conclude that (23) holds with probability 1. Hence, to prove the theorem we need to show that (24) holds on each iteration.
Let us pick some constant \(\zeta \) which satisfies
We now consider two possible cases: \(\Vert \nabla f(x_k) \Vert \ge \zeta \delta _k \) and \(\Vert \nabla f(x_k) \Vert < \zeta \delta _k\). We will show that (24) holds in both cases and hence it holds on every iteration. Given \(\zeta \) we now select \(\nu \in (0,1)\) such that
with \(C_1\) defined as in Lemma 4.6.
As usual, let \(x_k\), \(\delta _k\), \(s_k\), \(g_k\), and \(\phi _k\) denote realizations of random quantities \(X_k\), \(\Delta _k\), \(S_k\), \(G_k\), and \(\Phi _k\), respectively.
Let us consider some realization of Algorithm 1. Note that on all successful iterations, \(x_{k+1}=x_k+s_k\) and \(\delta _{k+1}=\min \{\gamma \delta _k, \delta _{max}\}\) with \(\gamma >1\), hence
On all unsuccessful iterations, \(x_{k+1}=x_k\) and \(\delta _{k+1}=\frac{1}{\gamma } \delta _k\), i.e.
For each iteration and each of the two cases we consider, we will analyze the four possible combined outcomes of the events \(I_k\) and \(J_k\) as defined in (7) and (8), respectively.
Before presenting the formal proof let us outline the key ideas. We will show that, unless both the model and the estimates are bad on iteration k, we select \(\nu \in (0,1)\) sufficiently close to 1, so that the decrease in \(\phi _k\) on a successful iteration is greater than the decrease on an unsuccessful iteration (which is equal to \(b_1\), according to (28)). When the model and the estimates are both bad, an increase in \(\phi _k\) may occur. This increase is bounded by a value proportional to \(\delta _k^2\) when \(\Vert \nabla f(x_k)\Vert < \zeta \delta _k\). When \(\Vert \nabla f(x_k) \Vert \ge \zeta \delta _k\), though, the increase in \(\phi _k\) may be proportional to \(\Vert \nabla f(x_k)\Vert \delta _k\). However, since iterations with good models and good estimates will provide decrease in \(\phi _k\) also proportional to \(\Vert \nabla f(x_k)\Vert \delta _k\), then by choosing values of \(\alpha \) and \(\beta \) close enough to 1, we can ensure that in expectation \(\phi _k\) decreases.
We now present the proof.
Case 1: \(\Vert \nabla f(x_k) \Vert \ge \zeta \delta _k \).
-
(a)
\(I_k\) and \(J_k\) are both true, i.e., both the model and the estimates are good on iteration k. From the definition of \(\zeta \), we know
$$\begin{aligned} \Vert \nabla f(x_k)\Vert \ge \left( \kappa _{eg}+ \max \left\{ \eta _2, \frac{8\kappa _{ef}}{\kappa _{fcd}(1-\eta _1)}\right\} \right) \delta _k. \end{aligned}$$Then since the model \(m_k\) is \(\kappa \)-fully linear and, from \(\eta _2>\kappa _{bhm}\), \({\epsilon }_F\le \kappa _{ef}\) and \(0<\eta _1<1\), it is easy to show that the condition (11) in Lemma 4.6 holds. Therefore, the trial step \(s_k\) leads to a decrease in f as in (12).
Moreover, since
$$\begin{aligned} \Vert g_k\Vert \ge \Vert \nabla f(x_k)\Vert -\kappa _{eg}\delta _k\ge (\zeta -\kappa _{eg})\delta _k\ge \max \left\{ \eta _2, \frac{8\kappa _{ef}}{\kappa _{fcd}(1-\eta _1)} \right\} \delta _k, \end{aligned}$$and the estimates \(\{ f_k^0,f_k^s \}\) are \({\epsilon }_F\)-accurate, with \({\epsilon }_F\le \kappa _{ef}\), the condition (15) in Lemma 4.7 holds. Hence, iteration k is successful, i.e. \(x_{k+1}=x_k+s_k\) and \(\delta _{k+1}=\gamma \delta _k\).
Combining (12) and (27), we get
$$\begin{aligned} \phi _{k+1}-\phi _k\le -\nu C_1\Vert \nabla f(x_k)\Vert \delta _k +(1-\nu )(\gamma ^2-1)\delta _k^2\equiv b_2, \end{aligned}$$(29)with \(C_1\) defined in Lemma 4.6. Since \(\Vert \nabla f(x_k) \Vert \ge \zeta \delta _k\) we have
$$\begin{aligned} b_2\le [-\nu C_1 \zeta +(1-\nu )(\gamma ^2-1)]\delta _k^2<0, \end{aligned}$$(30)for \(\nu \in (0,1)\) satisfying (26).
-
(b)
\(I_k\) is true and \(J_k\) is false, i.e., we have a good model and bad estimates on iteration k.
In this case, Lemma 4.6 still holds, that is \(s_k\) yields a sufficient decrease in f; hence, if the iteration is successful, we obtain (29) and (30). However, the step can be erroneously rejected, because of inaccurate probabilistic estimates, in which case we have an unsuccessful iteration and (28) holds. Since (26) holds, the right hand side of the first relation in (30) is strictly smaller than the right hand side of the first relation in (28) and therefore, (28) holds whether the iteration is successful or not.
-
(c)
\(I_k\) is false and \(J_k\) is true, i.e., we have a bad model and good estimates on iteration k. In this case, iteration k can be either successful or unsuccessful. In the unsuccessful case (28) holds. When the iteration is successful, since the estimates are \({\epsilon }_F\)-accurate and (22) holds then by Lemma 4.8 (20) holds with \(C_2\ge \frac{1}{4}\eta _1\eta _2\kappa _{fcd}\). Hence, in this case we have
$$\begin{aligned} \phi _{k+1}-\phi _k\le [-\nu C_2+(1-\nu )(\gamma ^2-1)]\delta _k^2. \end{aligned}$$(31)Again, due to the choice of \(\nu \) satisfying (26) we have that, as in case (b), (28) holds whether the iteration is successful or not.
-
(d)
\(I_k\) and \(J_k\) are both false, i.e., both the model and the estimates are bad on iteration k.
Inaccurate estimates can cause the algorithm to accept a bad step, which may lead to an increase both in f and in \(\delta _k\). Hence in this case \(\phi _{k+1}-\phi _{k}\) may be positive. However, combining the Taylor expansion of \(f(x_k)\) at \(x_k+s_k\) and the Lipschitz continuity of \(\nabla f(x)\) we can bound the amount of increase in f, hence bounding \(\phi _{k+1}-\phi _{k}\) from above. By adjusting the probability of outcome (d) to be sufficiently small, we can ensure that in expectation \(\Phi _k\) is sufficiently reduced. In particular, from Taylor’s Theorem and the L-Lipschitz continuity of \(\nabla f(x)\) we have, respectively,
$$\begin{aligned} f(x_k)-f(x_k+s_k)\ge & {} \nabla f(x_k+s_k)^T(-s_k)-\dfrac{1}{2}L\delta _k^2, \text{ and } \\ \Vert \nabla f(x_k+s_k)-\nabla f(x_k) \Vert\le & {} Ls_k\le L\delta _k. \end{aligned}$$From this we can derive that any increase of \(f(x_k)\) is bounded by
$$\begin{aligned} f(x_k+s_k)-f(x_k)\le C_3 \Vert \nabla f(x_k)\Vert \delta _k, \end{aligned}$$where \(C_3=1+\frac{3L}{2\zeta }\). Hence, the change in function \(\phi \) is bounded:
$$\begin{aligned} \phi _{k+1}-\phi _k\le \nu C_3 \Vert \nabla f(x_k)\Vert \delta _k+(1-\nu )(\gamma ^2-1)\delta _k^2\equiv b_3. \end{aligned}$$(32)
Now we are ready to take the expectation of \(\Phi _{k+1}-\Phi _{k}\) for the case when \(\Vert \nabla f(X_k) \Vert \ge \zeta \Delta _k\). We know that case (a) occurs with a probability at least \(\alpha \beta \) (conditioned on the past) and in that case \(\phi _{k+1}-\phi _{k}=b_2<0\) with \(b_2\) defined in (29). Case (d) occurs with probability at most \((1-\alpha )(1-\beta )\) and in that case \(\phi _{k+1}-\phi _{k}\) is bounded from above by \(b_3>0\). Cases (b) and (c) occur otherwise and in those cases \(\phi _{k+1}-\phi _{k}\) is bounded from above by \(b_1<0\), with \(b_1\) defined in (28). Finally we note that \(b_1>b_2\) due to our choice of \(\nu \) in (26).
Hence, we can combine (28), (29), (31), and (32), and use \(B_1\), \(B_2\), and \(B_3\) as random counterparts of \(b_1\), \(b_2\), and \(b_3\), to obtain the following bound
Rearranging the terms we obtain
where the last inequality holds because \(\alpha \beta - \frac{1}{\gamma ^2}(\alpha (1-\beta )+(1-\alpha )\beta ) +(1-\alpha )(1-\beta )\le [\alpha +(1-\alpha )][(\beta +(1-\beta )]=1.\)
Let us choose \(0<\alpha \le 1\) and \(0<\beta \le 1\) so that they satisfy
which implies
where the last inequality is the result of (26). We note that the quantity \(\frac{1}{2}\) in the numerator of (33) was chosen so that the first inequality of the above expression holds: see Remark 4.15 following the proof for a brief discussion about this choice.
Recall that \(\Vert \nabla f(X_k)\Vert \ge \zeta \Delta _k\), hence
In summary, we have
and
For the purposes of this lemma and the liminf-type convergence result, which will follow, bound (35) is sufficient. We will use bound (34) in the proof of the \(\lim \)-type convergence result.
Case 2: Let us consider now the iterations when \(\Vert \nabla f(x_k) \Vert < \zeta \delta _k \). First we note that if \(\Vert g_k \Vert <\eta _2\delta _k\), then we have an unsuccessful step and (28) holds. Hence, we now assume that \(\Vert g_k \Vert \ge \eta _2\delta _k\) and again consider four possible outcomes. We will show that in all situations, except when both the model and the estimates are bad, (28) holds. In the remaining case, because \(\Vert \nabla f(x_k) \Vert < \zeta \delta _k \), the increase in \(\phi _k\) can be bounded from above by a multiple of \(\delta _k^2\). Hence by selecting appropriate values for probabilities \(\alpha \) and \(\beta \) we will be able to establish the bound on expected decrease in \(\Phi _k\) as in Case 1.
-
(a)
\(I_k\) and \(J_k\) are both true, i.e., both the model and the estimates are good on iteration k.
The iteration may or may not be successful, even though \(I_k\) is true. On successful iterations, the good model ensures reduction in f. Applying the same argument as in the case 1(c) we establish (28).
-
(b)
\(I_k\) is true and \(J_k\) is false, i.e., we have a good model and bad estimates on iteration k.
On unsuccessful iterations, (28) holds. On successful iterations, \(\Vert g_k \Vert \ge \eta _2\delta _k\) and \(\eta _2\ge \kappa _{bhm}\) imply that
$$\begin{aligned} m_k(x_k)-m_k(x_k+s_k)\ge & {} \frac{\kappa _{fcd}}{2} \Vert g_k \Vert \min \left\{ \frac{\Vert g_k\Vert }{\Vert H_k \Vert } ,\delta _k\right\} \\\ge & {} \eta _2\frac{\kappa _{fcd}}{2}\delta _k^2. \end{aligned}$$Since \(I_k\) is true, the model is \(\kappa \)-fully-linear, and the function decrease can be bounded as
$$\begin{aligned}&f(x_k)-f(x_k+s_k)\nonumber \\&\quad =f(x_k)-m_k(x_k)+m_k(x_k)-m_k(x_k+s_k)+m_k(x_k+s_k)-f(x_k+s_k)\nonumber \\&\quad \ge (\eta _2\frac{\kappa _{fcd}}{2}-2\kappa _{ef})\delta _k^2 \ge \kappa _{ef}\delta _k^2 \end{aligned}$$due to (21).
It follows that, if the k-th iterate is successful, then
$$\begin{aligned} \phi _{k+1}-\phi _k\le [-\nu \kappa _{ef}+(1-\nu )(\gamma ^2-1)]\delta _k^2 . \end{aligned}$$(36)Again by choosing \(\nu \in (0,1)\) so that (26) holds, we ensure that the right hand side of (36) is strictly smaller than that of (28), hence (28) holds, whether the iteration is successful or not.
Remark \(\eta _2\) may need to be a relatively large constant to satisfy (21). This is due to the fact that the model has to be sufficiently accurate to ensure decrease in the function if a step is taken, since the step is accepted based on poor estimates. Note that \(\eta _2\) restricts the size of \(\Delta _k\), which is used both as a bound on the step size and the control of the accuracy. In general it is possible to have two separate quantities (related by a constant)—one to control the step size and another to control the accuracy. Hence, it is possible to modify our algorithm to accept steps larger than \(\Vert g_k\Vert /\eta _2\). This will make the algorithm more practical, but the analysis much more complex. In this paper, we choose to stay with the simplest version, but keep in mind that the condition (26) is not terminally restrictive.
-
(c)
\(I_k\) is false and \(J_k\) is true, i.e., we have a bad model and good estimates on iteration k.
This case is analyzed identically to the case 1(c).
-
(d)
\(I_k\) and \(J_k\) are both false, i.e., both the model and the estimates are bad on iteration k.
Here we bound the maximum possible increase in \(\phi _k\) using the Taylor expansion and the Lipschitz continuity of \(\nabla f(x)\).
$$\begin{aligned} f(x_k+s_k)-f(x_k)\le \Vert \nabla f(x_k)\Vert \delta _k+\frac{1}{2}L\delta _k^2<C_3\zeta \delta _k^2. \end{aligned}$$Hence, the change in function \(\phi \) is
$$\begin{aligned} \phi _{k+1}-\phi _k\le \left[ \nu C_3\zeta +(1-\nu )(\gamma ^2-1)\right] \delta _k^2. \end{aligned}$$(37)
We are now ready to bound the expectation of \(\phi _{k+1}-\phi _{k}\) as we did in Case 1, except that in Case 2 we simply combine (37), which holds with probability at most \((1-\alpha )(1-\beta )\), and (28), which holds otherwise:
If we choose probabilities \(0<\alpha \le 1\) and \(0<\beta \le 1\) so that the following holds,
then
In conclusion, combining (35) and (39), and noting that \(1-\frac{1}{\gamma ^2}<\gamma ^2-1\) we have
which implies that (24) holds with \(\sigma = - \frac{1}{2}(1-\nu )(1-\frac{1}{\gamma ^2}-1)<0\). This concludes the proof of the theorem.
To summarize the conditions on the probabilities involved in Theorem 4.11 to ensure that the theorem holds, we state the following additional lemma.
Corollary 4.12
Let all assumptions of Theorem 4.11 hold. The statement of Theorem 4.11 holds if the \(\alpha \) and \(\beta \) are chosen to satisfy the following conditions:
and
with \(C_1 =\frac{\kappa _{fcd}}{4}\cdot \max \left\{ \frac{\kappa _{bhm}}{\kappa _{bhm}+\kappa _{eg}},\frac{8\kappa _{ef}}{8\kappa _{ef}+\kappa _{fcd}\kappa _{eg}}\right\} \) and \(\zeta =\kappa _{eg}+\eta _2.\)
Proof
The proof follows simply from combining the expression for \(C_3\) and condition (26) with (33) and (38).
Clearly, choosing \(\alpha \) and \(\beta \) sufficiently close to 1 will satisfy this condition.
Remark 4.13
We will briefly illustrate through a simple example how these algorithmic parameters scale with problem data.
Recall that L is the Lipschitz constant of the gradient of f and of f over \(\mathcal{L}_{enl}(x^0)\). It is reasonable to expect that \(\kappa _{ef}\) and \(\kappa _{eg}\) are quantities that scale with L, since Taylor models satisfy this condition, as do polynomial interpolation and regression models based on well-poised data sets [8]. Let us assume for the sake of an example that \(\kappa _{ef}=\kappa _{eg}=10L\). The bound on model Hessians \(\kappa _{bhm}\) can be chosen to be arbitrarily small, at the expense of limiting the class of models; however, it is clearly reasonable to choose \(\kappa _{bhm}\) as something that scales with L if this information is available. Let us assume that \(\kappa _{bhm}=10L\), as well. In a standard trust region method, a common choice of algorithmic parameters would use \(\kappa _{fcd}=\frac{1}{2}\), \(\gamma =2\), and \(\eta _1=\frac{1}{2}\).
The reader can easily verify that with these parameter choices and previous assumptions, Lemma 4.12 states that we must choose \(\eta _2\ge 32L\). The intermediate constants satisfy \(\zeta \ge 42L\) and \(C_1=\frac{2}{17}\). Without loss of generality, we will simply accept \(\zeta =42L\).
From observing that, given the above values of the constants,
we have
and
We note that as \(\eta _1\) and \(\kappa _{fcd}\) constants are driven closer to 1, the constant 440 can be reduced by up to a factor of 4.
Supposing that \(\kappa _{ef},\kappa _{eg}\), and \(\kappa _{bhm}\) scale linearly with L, then \(\eta _2\), \(\epsilon _F\), and the expressions relating to \(\alpha \) and \(\beta \) in Corollary 4.12 are all functions in L satisfying
and
where we use the notation \(\Theta (\cdot )\) to indicate the \(O(\cdot )\) relationship with moderate constants.
Remark 4.14
Recall our remark made earlier in Theorem 4.11, case 2b, on how \(\eta _2\) bounds our step sizes. Indeed, if \(\eta _2\ge \Theta (L)\) has to be imposed this may force the algorithm to take small step sizes throughout. However, as mentioned earlier, the analysis of Theorem 4.11 can be modified by introducing a tradeoff between the size of \(\eta _2\) and the accuracy parameters \(\epsilon _F\) and \(\kappa _{ef}\) (as both of these constant parameters can be made smaller). It also may be advantageous to choose \(\eta _2\) dynamically. Exploring this is a subject for future work. In the practical implementations that we will discuss in Sect. 6, we do not make use of the algorithmic parameter \(\eta _2\) at all, and so even though \(\eta _2\) is effectively arbitrarily close to 0, the algorithm still works.
Remark 4.15
Note that if \(\beta =1\), then \(\Delta _k\rightarrow 0\) for \(\alpha \ge \frac{1}{2}\), which is the case shown in [2]. This is because, in our discussion of Case 1, the condition (33) via an appropriate adjustment to (26) could be written as
where \(\theta _1\) is positive and arbitrarily close to zero and \(\theta _2>1\) is arbitrarily close to one. In the proof we provided, we chose values of \(\theta _1=\frac{1}{2}\) and \(\theta _2=2\) for simplicity of the presentation.
4.1 The liminf-type convergence
We are ready to prove a liminf-type first-order convergence result, i.e., that a subsequence of the iterates drive the gradient of the objective function to zero. The proof follows closely that in [2], the key difference being the assumption on the function estimates that are needed to ensure that a good step gets accepted by Algorithm 1.
Theorem 4.16
Let the assumptions of Theorem 4.11 and Corollary 4.12 hold.
Then the sequence of random iterates generated by Algorithm 1, \(\{X_k\}\), almost surely satisfies
Proof
We prove this result by contradiction conditioned on the almost sure event \(\Delta _k \rightarrow 0\). Let us thus assume that there exists \( \epsilon '\) such that, with positive probability, we have
Let \( \{x_k\}\) and \(\{\delta _k\}\) be realizations of \(\{X_k\}\) and \(\{\Delta _k\}\), respectively for which \(\Vert \nabla f(x_k)\Vert \ge \epsilon ',\quad \forall k.\) Since \(\lim \limits _{k\rightarrow \infty }\delta _k=0\) (because we conditioned on \(\Delta _k \rightarrow 0\)), there exists \(k_0\) such that for all \(k\ge k_0\),
We define a random variable \(R_k\) with realizations \(r_k=\log _{\gamma }\left( \dfrac{\delta _k}{b} \right) \). Then for the realization \(\{ r_k \}\) of \(\{ R_k\}\), \(r_k<0\) for \(k\ge k_0\). The main idea of the proof is to show that such realizations occur only with probability zero, hence obtaining a contradiction with the initial assumption of \(\Vert \nabla f(x_k)\Vert \ge \epsilon '\) \(\forall k\).
We first show that \(R_k\) is a submartingale. Recall the events \(I_k\) and \(J_k\) in Definitions 3.2 and 3.5. Consider some iterate \(k\ge k_0\) for which \(I_k\) and \(J_k\) both occur, which happens with probability \(P(I_k\cap J_k)\ge \alpha \beta \). Since (48) holds we have exactly the same situation as in Case 1(a) in the proof of Theorem 4.11. In other words, we can apply Lemmas 4.6 and 4.7 to conclude that the k-th iteration is successful, hence, the trust-region radius is increased. In particular, since \(\delta _k\le \frac{\delta _{\max }}{\gamma }\), \(\delta _{k+1}=\gamma \delta _{k}\). Consequently, \(r_{k+1}=r_k+1\).
Let \(\mathcal {F}_{k-1}^{I\cdot J}=\sigma ({I_0},\ldots , {I_{k-1}})\cap \sigma ({J_0},\ldots , J_{k-1})\). For all other outcomes of \(I_k\) and \(J_k\), which occur with total probability of at most \(1-\alpha \beta \), we have \(\delta _{k+1}\ge \gamma ^{-1}\delta _{k}\). Hence
because \(\alpha \beta > 1/2\) as a consequence of the assumptions from Corollary 4.12. This implies that \(R_k\) is a submartingale.
Now let us construct another submartingale \(W_k\), on the same probability space as \(R_k\) which will serve as a lower bound on \(R_k\) and for which \(\left\{ \underset{k\rightarrow \infty }{\lim \sup }\ W_k=\infty \right\} \) holds almost surely. Define indicator random variables \(\mathbf 1 _{I_k}\) and \(\mathbf 1 _{J_k}\) such that \(\mathbf 1 _{I_k}=1\) if \(I_k\) occurs, \(\mathbf 1 _{I_k}=0\) otherwise, and similarly, \(\mathbf 1 _{J_k}=1\) if \(J_k\) occurs, \(\mathbf 1 _{J_k}=0\) otherwise. Then define
Notice that \(W_k\) is a submartingale since
where the last inequality holds because \(\alpha \beta \ge 1/2\). Since \(W_k\) only has \(\pm 1\) increments, it has no finite limit. Therefore, by Theorem 4.4, we have \(\left\{ \underset{k\rightarrow \infty }{\lim \sup }\ W_k=\infty \right\} \).
By the construction of \(R_k\) and \(W_k\), we know that \(r_k-r_{k_0}\ge w_k -w_{k_0}\). Therefore, \(R_k\) has to be positive infinitely often with probability one. This implies that the sequence of realizations \(r_k\) such that \(r_k<0\) for \(k\ge k_0\) occurs with probability zero. Therefore our assumption that \( \Vert \nabla f(X_k) \Vert \ge \epsilon '\) holds for all k with positive probability is false and
holds almost surely.
4.2 The lim-type convergence
In this subsection we show that \(\lim _{k\rightarrow \infty } \Vert \nabla f(X_k) \Vert =0\) almost surely.
We now state an auxiliary lemma, which is similar to the one in [2], but requires a different proof because in our case the function values \(f(X_k)\) can increase with k, while in the case considered in [2], function values are monotonically nonincreasing.
Lemma 4.17
Let the same assumptions that were made in Theorem 4.16 hold. Let \(\{ X_k \}\) and \(\{ \Delta _k \}\) be sequences of random iterates and random trust-region radii generated by Algorithm 1. Fix \(\epsilon >0\) and define the sequence \(\left\{ K_\epsilon \right\} \) consisting of the natural numbers k for which \(\Vert \nabla f(X_k)\Vert >\epsilon \) (note that \(K_\epsilon \) is a sequence of random variables). Then,
almost surely.
Proof
From Theorem 4.11 we know that \(\sum \Delta _k^2 <\infty \) and hence \(\Delta _k\rightarrow 0\) almost surely. For each realization of Algorithm 1 and a sequence \(\{\delta _k\}\), there exists \(k_0\) such that \(\delta _k\le \epsilon /\zeta \), \(\forall k\ge k_0\), where \(\zeta \) is defined as in Theorem 4.11. Let \(K_0\) be the random variable with realization \(k_0\) and let K denote the sequence of indices k such that \(k\in K_\epsilon \) and \(k\ge K_0\). Then for all \(k\in K\), Case 1 of Theorem 4.11 holds, i.e., \(\Vert \nabla f(X_k) \Vert \ge \zeta \Delta _k\), since \( \Vert \nabla f(X_k) \Vert \ge \epsilon \) for all \(k\in K\). From this and from (34) we have
Recall that \(\Phi _{k}\) is bounded from below. Hence, summing up the above inequality for all \(k\in K\) and taking the expectation, we have that
almost surely. Since \(K_\epsilon \subseteq K\cup \{k: k\le K_0\}\) and \(K_0\) is finite almost surely then the statement of the lemma holds.
We are now ready to state the \(\lim \)-type result.
Theorem 4.18
Let the same assumptions as in Theorem 4.16 hold. Let \(\{ X_k \}\) be a sequence of random iterates generated by Algorithm 1. Then, almost surely,
Proof
The proof of this result is almost identical to the proof of the same theorem in [2]; hence we will not present the proof here. The key idea of the proof is to show that if the theorem does not hold, then with positive probability
with \(K_\epsilon \) defined as in Lemma 4.17. This result is shown using Lipschitz continuity of the gradient and does not depend on the stochastic nature of the algorithm. Since this result contradicts the almost sure result of Lemma 4.17, we can conclude that the statement of the theorem holds almost surely.
5 Constructing models and estimates in different stochastic settings
We now discuss various settings of stochastic noise in the objective function and how \(\alpha \)-probabilistically \(\kappa \)-fully linear models and \(\beta \)-probabilistically \(\epsilon _F\)-accurate estimates can be obtained in these settings.
Recall that we assume that for each x we can compute the value of \(\tilde{f}(x)\), which is the noisy version of f,
where \(\omega \) is a random variable which induces the noise.
Simple stochastic noise. The example of noise which is typically considered in stochastic optimization is the “i.i.d.” noise, that is noise with distribution independent of the function values. Here we consider a somewhat more general setting, where the noise is unbiased for all f, i.e.,
and
This is the typical noise assumption in stochastic optimization literature. In the case of unbiased noise as above, constructing estimates and models that satisfy our assumptions is fairly straight-forward. First, let us consider the case when only the noisy function values are available (without any gradient information), where we want to construct a model that is \(\kappa \)-fully linear in a given trust region \(B(x^0, \delta )\) with some sufficiently high probability, \(\alpha \).
One can employ standard sample averaging approximation techniques to reduce the variance of the function evaluations. In particular, let \(\bar{f}_p(x,\omega )= \frac{1}{p} \sum _{i=1}^p{f}(x,\omega _i)\), where \(\omega _i\) are the i.i.d. realizations of the noise \(\omega \). Then, by Chebyshev inequality, for any \(v>0\),
In particular, we want \(v= \kappa ^\prime _{ef}\delta ^2\) for some \(\kappa ^\prime _{ef}>0\) and \(\frac{V}{pv^2}\le 1-\alpha ^\prime \) for some \(\alpha ^\prime \), which can be ensured by choosing \(p\ge \frac{V}{(\kappa ^\prime _{ef})^2(1-\alpha ^\prime ) \delta ^4}\).
We now construct a fully linear model as follows: given a well-poised setFootnote 1 Y of \(n+1\) points in \(B(x^0, \delta )\), at each point \(y^i\in Y\), we compute \(\bar{f}_p(y^i, \omega )\) and build a linear interpolation model m(x) such that \(m(y^i)=\bar{f}_p(y^i, \omega )\), for all \(i=1, \ldots , n+1\). Hence, for any \(y^i\in Y\), we have
Moreover, the events \(\{|m(y^i)-f(y^i)]| > \kappa ^\prime _{ef} \delta ^2\}\) are independent, hence
It is easy to show using, for example, techniques described in [8], that m(x) is a \(\kappa \)-fully linear model of \(E_\omega [{f}(x,\omega )] \) in \(B(x^0, \delta )\) for appropriately chosen \(\kappa =(\kappa _{eg}, \kappa _{ef})\), with probability at least \(\alpha =(\alpha ^\prime )^{n+1}\).
Computing the \(\beta \)-probabilistically \(\epsilon _F\)-accurate estimates of \(f(x, \omega )\) can be done analogously to the construction of the models described above.
The majority of stochastic optimization and sample average approximation methods focus on derivative based optimization where it is assumed that, in addition to \(f(x, \omega )\), \(\nabla _x f(x, \omega )\) is also available, and that the noise in the gradient computation is also independent of x, that is
and
(in general the variance of the gradient and the function value are not the same, but here for simplicity we bound both by V).
In the case where the noisy gradient values are available, the construction of fully linear models in \(B(x^0, \delta )\) is simpler. Let \(\bar{\nabla }{f}_p(x,\omega )= \frac{1}{p} \sum _{i=1}^p{\nabla f}(x,\omega _i)\). Again, by an extension of the Chebyshev inequality, for p such that
and
Hence the linear expansion \(m(x)=\bar{f}_p(x^0,\omega )+\bar{\nabla }f_p(x^0, \omega )^T(x-x^0)\) is a \(\kappa \)-fully linear model of \(f(x)=E_\omega [{f}(x,\omega )] \) on \(B(x^0, \delta )\) for appropriately chosen \(\kappa =(\kappa _{eg}, \kappa _{ef})\), with probability at least \(\alpha =(\alpha ^\prime )^2\).
In [20] it is shown that least squares regression models based on sufficiently large strongly poised [8] sample sets are \(\alpha \)-probabilistically \(\kappa \)-fully linear models.
There are many existing methods and convergence results using sample average approximations and stochastic gradients for stochastic optimization with i.i.d. or unbiased noise. Some of these methods have been shown to achieve optimal sampling rate [15], that is they converge to the optimal solution while sampling the gradient at the best possible rate. We do not provide convergence rates in this paper (it is a subject for future research), hence it remains to be seen if our algorithm can achieve the optimal rate. Our contribution here is the method which applies beyond the i.i.d. case, as we will discuss below. In Sect. 6, however, we demonstrate that our method can have superior numerical behavior compared to standard sample averaging even in the case of i.i.d. noise, so it is at least competitive in practice.
Function computation failures Now, let us consider a more complex noise case. Suppose that the function f(x) is computed (as it often is, in black-box optimization) by some numerical method that includes a random component. Such examples are common in machine learning applications, for instance, where x is the vector of hyperparameters of a learning algorithm and f(x) is the expected error of the resulting classifier. In this case, for each value of x, the classifier is obtained by solving an optimization problem, up to a certain accuracy, on a given training set. Then the classifier is evaluated on the testing set. If a randomized coordinate descent or a stochastic gradient descent is applied to train the classifier for a given vector x, then the resulting classifier is sufficiently close to the optimal classifier with some known probability. However, in the case when the training of the classifier fails to produce a sufficiently accurate solution, the resulting error is difficult to estimate. Usually, it is possible to know the upper bound on the value of this inaccurate objective function but nothing else may be known about the distribution of this value. Moreover, it is likely that the probability of the accurate computation depends on x; for example, after k iterations of randomized coordinate descent, the error between the true f(x) and the computed \(\tilde{f}(x)\) is bounded by some value, with probability \(\alpha \), where the value depends on \(\alpha \), k, and x [27].
Another example is solving a system of nonlinear black-box equations. Assume that we seek x such that \(\sum _i (f_i(x))^2=0\), for some functions \(f_i(x)\), \(i=1, \ldots , m\) that are computed by numerical simulation, with noise. As is often done in practice (and is supported by our theory) the noise in the function computation is reduced as the algorithm progresses, for example, by reducing the size of a discretization, step size, or convergence tolerance within the black-box computation. These adjustments for noise reduction usually increase the workload of the simulation. With the increase of the workload, there is an increased probability of failure of the code. Hence, the smaller the values of \(f_i(x)\), the more likely the computation of \(f_i(x)\) will fail and some inaccurate value is returned.
These two examples show that the noise in \(\tilde{f}(x)\) may be large with some positive probability, which may depend on x. Hence, let us consider the following, idealized, noise model
where \(\sigma (x)\) is the probability with which the function f(x) is computed inaccurately, and \(\omega (x)\) is some random function of x, for which only an upper bound V is known. This case is idealized, because we assume that with probability \(1-\sigma (x)\), f(x) is computed exactly. It is trivial to extend this example to the case when f(x) is computed with an error, but this error can be made sufficiently small.
For this model of function computation failures we have
and it is clear, that for any \(\sigma (x)>0\), unless \(E[\omega (x)]\equiv \text {some constant}\), optimizing \(E_\omega [{f}(x,\omega )]\) does not give the same result as optimizing f(x). Hence applying Monte-Carlo sampling within an optimization algorithm solving this problem is not a correct approach.
We now observe that constructing \(\alpha \)-probabilistically \(\kappa \)-fully linear models and \(\beta \)-probabilistically \(\epsilon _F\)-accurate estimates is trivial in this case, assuming that \(\sigma (x)\le \sigma \) for all x, when \(\sigma \) is small enough. In particular, given a trust region \(B(x^0, \delta )\), sampling a function f(x) on a sample set \(Y\subset B(x^0, \delta )\) well-poised for linear interpolation will produce a \(\kappa \)-fully linear model in \(B(x^0, \delta )\) with probability at least \((1-\sigma )^{|Y|}\), since with this probability all of the function values are computed exactly. Similarly, for any \(s\in B(x^0, \delta )\), the function estimates \(F^0\) and \(F^s\) are both correct with probability at least \((1-\sigma )^2\). Assuming that \((1-\sigma )^{|Y|}\ge \alpha \) and \((1-\sigma )^2\ge \beta \), where \(\alpha \) and \(\beta \) satisfy the assumptions of Theorem 4.11 and Lemma 4.12 and \(\alpha \beta \ge \frac{1}{2}\) as in Theorem 4.16, we observe that the resulting models satisfy our theory.
Remark 5.1
We assume here that the probability of failure to compute f(x) is small enough for all x. In the machine learning example above, it is often possible to control the probability \(\sigma (x)\) in the computation of f(x), for example by increasing the number of iterations of a randomized coordinate descent or stochastic gradient method. In the case of the black-box nonlinear equation solver, the probability of code failure is expected to be quite small. There are, however, examples of black box optimization problems where the computation of f(x) fails all the time for specific values of x. This is often referred to as hidden constraints [23]. Clearly our theory does not apply here, but we believe there is no local method that can provably converge to a local minimizer in such a setting without additional information about these specific values of x.
6 Computational experiments
In this section, we will discuss the performance of several variants of our proposed method (varied in the way the models are constructed), henceforth only referred to as STORM (STochastic Optimization using Random Models), that target various noisy situations discussed in the previous section. We note that a comparison of STORM to the SPSA method of [31] and the classical Kiefer–Wolfowitz method in [18] has been reported in [6] and shows that STORM significantly outperformed these two methods, while no special tuning of SPSA or Kiefer–Wolfowitz was applied. Since a trust-region based method, which is able to use second order information is likely to outperform stochastic gradient-like methods in many settings, we omit such comparison here.
Throughout this section, all proposed algorithms were implemented in Matlab and all experiments were performed on a laptop computer running Ubuntu 14.04 LTS with an Intel Celeron 2955U @ 1.40GHz dual processor.
6.1 Simple stochastic noise
In these experiments, we used a set of 53 unconstrained problems adapted from the CUTEr test set, each being in the form of a sum of squares problem, i.e.
where for each \(i\in \{1,\dots ,m\}\), \(f_i(x)\) is a smooth function. Two different types of noise will be used in this first subsection, which we will refer to as multiplicative noise and additive noise. In the multiplicative noise case, for each \(i\in \{1,\dots ,m\}\), we generate some \(\omega _i\) from the uniform distribution on \([-\sigma ,\sigma ]\) for some parameter \(\sigma >0\), and then compute the noisy function
The key characteristic of this noise is that for each x, we have \(E_{\omega }[f(x,\omega )] = f(x)\), however the variance is nonconstant over x and scales with the magnitudes of the components \(f_i(x)\). Thus, one should expect that if an algorithm is minimizing a function of the form (50), the accuracy of the estimates of f(x) based on a constant number of samples of \(\tilde{f}(x,\omega )\) should increase, assuming that the algorithm produces a decreasing sequence \(\{f(x^k)\}_{k=1}^\infty \). While this behavior is not supported by theory, because we do not know how quickly \(f(x^k)\) decreases, our computational results show that a constant number of samples is indeed sufficient for convergence.
The other type of noise we will test is additive, i.e. we additively perturb each component in (49) by some \(\omega _i\) uniformly generated in \([-\sigma ,\sigma ]\) for some parameter \(\sigma >0\). That is,
Note that the noise is additive only in terms of the component functions, but not in terms of the objective function, moreover \(E_{\omega }[f(x,\omega )] = f(x)+\sum _{i}^mE(\omega _i)^2\). However, the constant bias term does not affect optimization results, since \(\min _x E_{\omega }[f(x,\omega )] = \min _x f(x)\).
In our first set of experiments for these two noisy settings, we compare a version of STORM to a version of sample average based trust region algorithms, which we will call “TR-SAA”, and which is similar to a trust-region algorithm presented in [10]. A similar method, with convergence guarantees, has been recently proposed in [30]. In their work, they use a Bayesian scheme to select a sufficiently large sample complexity for computing average function values at a current interpolation set. Here, in TR-SAA, we simplify this approach, by increasing sample complexity in each iteration proportionally to the decrease of the trust region radius \(\delta _k\). A description of TR-SAA is given in Algorithm 2 in the “Appendix”.
There are two particular aspects of TR-SAA that we would like to draw attention to: in the estimate calculation step, the computation of \(f_k^0\) is performed before the model \(m_k\) is constructed, and \(m_k\) is built to interpolate \(f_k^0\), hence the quality of estimate \(f_k^0\) and that of the model \(m_k\) are dependent. Additionally, the quality of the model \(m_k\) is dependent on that of \(m_{k-1}\) because the samples are reused. Both of these aspects are violations of the typical assumptions of STORM. Thus, we also propose TR-SAA-resample, which is the same algorithm as TR-SAA except that at each iteration, the function value at every interpolation point is recomputed as an average of function evaluations, independent of past function evaluations. While TR-SAA-resample may overcome some of the problems of the dependence of \(m_k\) on \(m_{k-1}\), it still doesn’t satisfy the assumptions of STORM because of the dependence of \(f_k^0\) on \(m_k\).
Thus, in Algorithm 3, stated in the “Appendix”, we propose a version of STORM, comparable to TR-SAA in terms of sample sizes. In Algorithm 3, the models \(m_k\) and \(m_{k-1}\) are entirely independent since a new regression set is drawn in each iteration. Additionally, in the estimates calculation step, the computations of \(f_k^0\) and \(f_k^s\) are completely independent of the model \(m_k\). For these reasons, Algorithm 3 is more in line with the theory analyzed in this paper than a sample average approximation scheme like in Algorithm 2.
For each of the 53 problems, the best known value of the noiseless f(x) obtained by a solver is recorded as \(f^*\). We recorded the number of function evaluations required by a solver to obtain a function value \(f(x^k) < f'\) such that
This number was averaged over 10 runs for each problem. In the profiles shown in Fig. 1 for the multiplicative noise case \(\tau =10^{-3}\). In all the experiments, a budget of \(1000(n+1)\) noisy function evaluations was set. For the choice of initialization, the same parameters were used in all of TR-SAA, TR-SAA-resample, and STORM-unbiased: \(\delta _{\max } = 10, \delta _0=1, \gamma =2,\eta _1=0.1,\eta _2=0.001,p_{\min } = 10.\)
Note that even though we have ignored the theoretical prescription derived in the previous section that sample rate should scale with \(1/\delta _k^4\), we note that STORM-unbiased performs extremely well compared to the TR-SAA method. Although we chose to sample at a rate so that \(p_k\) was on the order of \(1/\delta _k\), this particular sample rate was chosen after testing various other rates on the same set of test functions, and seemed to work relatively well for both STORM-unbiased and TR-SAA.
Function computation failures In these experiments, we used the same 53 sum of squares problems as in the unbiased noise experiments described above, but introduced biased noise. For each component in the sum in (49), if \(|f_i(x)| < \epsilon \) for some parameter \(\epsilon >0\), then \(f_i(x)\) is computed as
for some parameter \(\sigma >0\) and for some “garbage value” V. If \(f_i(x)\ge \epsilon \), then it is deterministically computed as \(f_i(x)\). This noise is biased, with bias depending on x, and we should not expect any sort of averaging approximation to work well here. This is indeed indicated in our experiments, where various levels of \(\sigma \) and \(\epsilon \) are shown below. There choice of V did not significantly affect the results, and in the experiments illustrated below \(V=-10{,}000\) was used. Obviously, the intention here is that such a large negative value will cause STORM to see a trial step as promising, when it may, in fact, yield an increase in function value if taken. We propose the version of STORM presented as Algorithm 4 in the “Appendix”.
The key feature of Algorithm 4 is that on each iteration, the interpolation set changes minimally as in a typical DFO trust region method, but the interpolated function values are computed afresh. Intuitively, this is the right thing to do, since if a “garbage value” is computed at some point in the algorithm to either construct a model or provide a function value estimate, we do not want its presence to affect the computation of models in subsequent iterations. No averaging is performed, as it can only cause harm in the setting.
Since we are not aware of any other optimization algorithm that is designed for this case of noise, we performed no comparisons, but experiment to discover how the method works as a function of the probability of failure. On the test set of 53 problems, we ran Algorithm 4 30 times and report the average percentage of instances that are solved in the sense of (52) with \(\tau =10^{-3}\) within a budget of \(10{,}000(n+1)\) function evaluations, where \(f^*\) was computed by Algorithm 4 with \(\sigma =0\). In order to standardize the probability of failure over the test set, we define the probability of success \(p_s\) and then take \(\sigma \) on a function with m component to be \(\sigma = 1-p_s^{(1/m)}\). The results are summarized in Fig. 2.
This experiment suggests that the practical threshold at which STORM fails to make progress may be looser than that suggested by theory. We will illustrate this idea through a simple example. Consider the minimization of the simple quadratic function
The minimizer uniquely occurs at the vector of all 1s. Now consider the minimization of this function under our setting of computation failure where we vary the probability parameter \(\sigma \) and fix \(\epsilon = 0.1\). Suppose on each iteration of STORM, the interpolation set contains \((n+1)(n+2)/2\) points. Then, the probability of obtaining the correct quadratic model in the worst case where for all i, \(|x_i-1|<\epsilon \) is precisely \(\alpha = ((1-\sigma )^n)^{\frac{(n+1)(n+2)}{2}}\). Likewise, the probability of obtaining the correct function evaluation for \(F_0\) and \(F_s\) on each iteration in the worst case is \(\beta = ((1-\sigma )^n)^2\). Now, supposing we initialize STORM with the zero vector in \(\mathbb {R}^n\), it is reasonable to assume that all iterates will occur near the unit cube \([0,1]^n\), and so we can use simple calculus to estimate a Lipschitz constant of the function over the relevant domain as \(2\sqrt{n}\), and the Lipschitz constant of the gradient is constantly 2. These also serve as reasonable estimates of \(\kappa _{ef}\) and \(\kappa _{eg}\), respectively. Using parameter choices \(\gamma =2\), \(\eta _1=0.1\), \(\eta _2=1\), we can use the bounds in (40) and (41) to solve for the smallest allowable \((1-\sigma )\) for which our algorithm can guarantee convergence. For \(n=2\), our theory suggests that we can safely lower bound \((1-\sigma ) > 0.9592\) (which implies \(\alpha \approx 0.6069\) and \(\beta \approx 0.8467\)), and for \(n=10\), we can lower bound \((1-\sigma ) > 0.9990\) (which implies \(\alpha \approx 0.5233\) and \(\beta \approx 0.9806\)).
In Fig. 3 for \(n=2,10\), we plot an indicated level of \((1-\sigma )\) on the x-axis against the proportion of 100 randomly seeded instances with that level of \((1-\sigma )\) that Algorithm 4 managed to find a solution \(x^*\) satisfying \(f(x^*)< 10^{-5}\) within \(10^4\) many function evaluations using the discussed parameter choices. The red line shows the level of \((1-\sigma )\) that our theory predicted in the previous paragraph. As we can see, \((1-\sigma )\) can be quite smaller than predicted by our theory before the failure rate becomes unsatisfactory. As a particular example, in the \(n=10\) case, when \((1-\sigma ) = .998\), the corresponding probabilities are \(\alpha \approx 0.266782\) and \(\beta \approx 0.960751\), and yet \(100\%\) of the instances were solved to the required level of accuracy. In other words, even though the models are eventually only accurate on roughly \(27\%\) of the iterations, we still see satisfactory performance.
6.2 Stochastic gradient based method comparison
In this subsection, we show how STORM applies to empirical risk minimization in machine learning. Consider a training dataset of N samples, \(\{(x_i,y_i)\}_{i=1\dots N}\), where \(x_i\in \mathbb {R}^m\) is a vector of m real-valued and \(y_i\in \{-1,1\}\) indicates a positive or negative label respectively. We will train a linear classifier and bias term \((w,\beta )\in \mathbb {R}^{m+1}\) by minimizing the smooth (convex) regularized logistic loss
As in the typical machine learning setting, we will assume that \(N>> m\) and computing \(f(w,\beta )\) as well as \(\nabla f(w,\beta )\) and \(\nabla ^2 f(w,\beta )\) is prohibitive. Hence we will only compute estimates of these quantities by considering a sample \(I \subset \{1,\dots ,N\}\) of size \(|I| = n<< N\), yielding
Thus we can construct models based on sample gradient and Hessians information and we present the appropriate variant of STORM as Algorithm 5 in the “Appendix”.
We compare Algorithm 5 with the well-known implementation of Adagrad described in [11] from the Ada-whatever package. We compare against this particular solver because it is a well-understood stochastic gradient method used by the machine learning community that, like our algorithm, takes adaptive step sizes, but unlike our algorithm, does not compute estimates of the loss function, but only computes averaged stochastic gradients. For the choice of initialization in Algorithm 5, the following parameters were used: \(\delta _{\max } = 10, \delta _0=1, x_0 = 0, \gamma =2,\eta _1=0.1,\eta _2=0.001,p_{\min } = m + 2, p_{\max } = N\). Adagrad was also given the same initial point and an initial step size of \(\delta _0=1\).
We implemented two versions of Algorithm 5: one which uses stochastic Hessians, and a second where we do not compute stochastic Hessians, effectively setting \(H_k=0\) on each iteration, yielding a trivial subproblem in the step calculation.
We set the maximum budget of data evaluations for each solver equal to the size of the training set, thus comparing various solvers’ performance with a budget of roughly one full pass through the dataset. For the two implementations of STORM, we plot in Fig. 4 the true training loss function value at the end of each successful iteration, while for Adagrad, we simply plot the true training loss function value over an evenly spaced array of function value counts.
Notice that, as expected, the true function values produced by Adagrad can vary widely over this horizon, but implementations of STORM tend to yield fairly stable decreasing trajectories over its successful iterations.
Notes
See [8] for details on well-poised sets and how they can be obtained.
References
Bach, F., Moulines, E.: Non-asymptotic analysis of stochastic approximation algorithms for machine learning. In: Advances in Neural Information Processing Systems 24: 25th Annual Conference on Neural Information Processing Systems 2011. Proceedings of a Meeting Held 12–14 December 2011, Granada, Spain, pp. 451–459 (2011)
Bandeira, A.S., Scheinberg, K., Vicente, L.N.: Convergence of trust-region methods based on probabilistic models. SIAM J. Optim. 24(3), 1238–1264 (2014)
Billups, S.C., Graf, P., Larson, J.: Derivative-free optimization of expensive functions with computational error using weighted regression. SIAM J. Optim. 23(1), 27–53 (2013)
Bottou, L., Curtis, F.E., Nocedal, J.: Optimization methods for large-scale machine learning. Technical report. arXiv:1606.04838 (2016)
Chang, K.H., Li, M.K., Wan, H.: Stochastic trust-region response-surface method (strong)—a new response-surface framework for simulation optimization. INFORMS J. Comput. 25(2), 230–243 (2013)
Chen, R.: Stochastic derivative-free optimization of noisy functions. PhD thesis, Department of Industrial and Systems Engineering, Lehigh University, Bethlehem, USA (2015)
Conn, A.R., Scheinberg, K., Vicente, L.N.: Global convergence of general derivative-free trust-region algorithms to first- and second-order critical points. SIAM J. Optim. 20(1), 387–415 (2009)
Conn, A.R., Scheinberg, K., Vicente, L.N.: Introduction to Derivative-Free Optimization. Society for Industrial and Applied Mathematics, Philadelphia (2009)
Defazio, A., Bach, F., Lacoste-Julien, S.: Saga: a fast incremental gradient method with support for non-strongly convex composite objectives. In: Ghahramani, Z., Welling, M., Cortes, C., Lawrence, N.D., Weinberger, K.Q. (eds.) Advances in Neural Information Processing Systems, vol. 27, pp. 1646–1654. Curran Associates Inc, Red Hook (2014)
Deng, G., Ferris, M.C.: Variable-number sample-path optimization. Math. Program. 117, 81–109 (2009)
Duchi, J., Hazan, E., Singer, Y.: Adaptive subgradient methods for online learning and stochastic optimization. J. Mach. Learn. Res. 12, 2121–2159 (2011)
Durrett, R.: Probability: Theory and Examples. Cambridge Series in Statistical and Probabilistic Mathematics, p. 105. Cambridge University Press, Cambridge (2010)
Ghadimi, S., Lan, G.: Accelerated gradient methods for nonconvex nonlinear and stochastic programming. Math. Program. 156(1), 59–99 (2016)
Ghadimi, S., Lan, G.: Stochastic first- and zeroth-order methods for nonconvex stochastic programming. SIAM J. Optim. 23(4), 2341–2368 (2013)
Ghosh, S., Glynn, P.W., Hashemi, F., Pasupathy, R.: On sampling roles in stochastic recursion. SIAM J. Optim. (under review)
Johnson, R., Zhang, T.: Accelerating stochastic gradient descent using predictive variance reduction. In: Burges, C.J.C., Bottou, L., Welling, M., Ghahramani, Z., Weinberger, K.Q. (eds.), Advances in Neural Information Processing Systems (NIPS 2013), vol. 26, pp. 315–323 (2013)
Juditsky, A.B., Polyak, B.T.: Acceleration of stochastic approximation by averaging. SIAM J. Control Optim. 30(4), 838–855 (1992)
Kiefer, J., Wolfowitz, J.: Stochastic estimation of the maximum of a regression function. Ann. Math. Stat. 22(3), 462–466 (1952)
Lan, G.: An optimal method for stochastic composite optimization. Math. Program. 133, 365397 (2012)
Larson, J., Billups, S.C.: Stochastic derivative-free optimization using a trust region framework. Comput. Optim. Appl. 64(3), 619645 (2016)
Linderoth, J., Shapiro, A., Wright, S.: The empirical behavior of sampling methods for stochastic programming. Ann. Oper. Res. 142(1), 215–241 (2006)
Monro, S., Robbins, H.: A stochastic approximation method. Ann. Math. Stat. 22(3), 400–407 (1951)
Moré, J.J., Wild, S.M.: Benchmarking derivative-free optimization algorithms. SIAM J. Optim. 20(1), 172–191 (2009)
Nemirovski, A., Juditsky, A., Lan, G., Shapiro, A.: Robust stochastic approximation approach to stochastic programming. SIAM J. Optim. 19(4), 1574–1609 (2009)
Pasupathy, R., Ghosh, S.: Simulation optimization: a concise overview and implementation guide. In: Topaloglu, H., Smith, J. C. (eds.) TutORials in Operations Research, chapter 7, pp. 122–150. INFORMS, Catonsville (2013)
Powell, M.J.D.: UOBYQA: unconstrained optimization by quadratic approximation. Math. Program. 92(3), 555–582 (2002)
Richtarik, P., Takac, M.: Iteration complexity of randomized block-coordinate descent methods for minimizing a composite function. Math. Program. 144(1,2), 1–38 (2014)
Robinson, S.M.: Analysis of sample-path optimization. Math. Oper. Res. 21(3), 513–528 (1996)
Ruszczynski, A., Shapiro, A. (eds.): Stochastic Programming. Handbooks in Operations Research and Management Science, vol. 10. Elsevier, Amsterdam (2003)
Shashaani, S., Hashemi, F.S., Pasupathy, R.: Astro-DF: a class of adaptive sampling trust-region algorithms for derivative-free simulation optimization (2015) (under review)
Spall, J.C.: Multivariate stochastic approximation using a simultaneous perturbation gradient approximation. IEEE Trans. Autom. Control 37, 332–341 (1992)
Spall, J.C.: Adaptive stochastic approximation by the simultaneous perturbation method. IEEE Trans. Autom. Control 45(10), 1839–1853 (2000)
Spall, J.C.: Introduction to Stochastic Search and Optimization: Estimation, Simulation, and Control. Wiley Series in Discrete Mathematics and Optimization. Wiley, London (2005)
Author information
Authors and Affiliations
Corresponding author
Additional information
R. Chen: The work of this author was partially supported by NSF Grant CCF-1320137 and AFOSR Grant FA9550-11-1-0239. M. Menickelly: The work of this author is partially supported by NSF Grants DMS 13-19356 and CCF-1320137. K. Scheinberg: The work of this author is partially supported by NSF Grants DMS 10-16571, DMS 13-19356, CCF-1320137, AFOSR Grant FA9550-11-1-0239, and DARPA Grant FA 9550-12-1-0406 negotiated by AFOSR.
Rights and permissions
About this article
Cite this article
Chen, R., Menickelly, M. & Scheinberg, K. Stochastic optimization using a trust-region method and random models. Math. Program. 169, 447–487 (2018). https://doi.org/10.1007/s10107-017-1141-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-017-1141-8