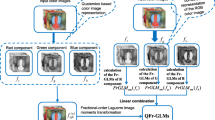
Abstract
Orthogonal moments have become a powerful tool for object representation and image analysis. Radial harmonic Fourier moments (RHFMs) are one of such image descriptors based on a set of orthogonal projection bases, which outperform other moments because of their computational efficiency. However, the conventional computational framework of RHFMs produces geometric error and numerical integration error, which will affect the accuracy of RHFMs, thus degrading the image reconstruction performance. To overcome this shortcoming, we propose a new computational framework of RHFMs, namely accurate quaternion radial harmonic Fourier moments (AQRHFMs), for color image processing, and also analyze the properties of AQRHFMs. Firstly, we propose a precise computation method of RHFMs to reduce the geometric and numerical errors. Secondly, by using the algebra of quaternions, we extend the accurate RHFMs to AQRHFMs in order to deal with the color images in a holistic manner. Experimental results show the proposed AQRHFMs achieve promising performance in image reconstruction and object recognition in both noise-free and noisy conditions.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Description of objects invariant to geometric transformation such as translation, scale, and rotation is useful in pattern recognition and other similar applications. A popular class of invariant features is based on the moment techniques including geometric moments, rotational moments, complex moments, and orthogonal moments [1, 2]. However, geometric moments and their extensions in the form of complex moments and rotational moments are not orthogonal. It has a certain degree of information redundancy and high sensitivity to noise. Consequently, reconstruction of images from these moments is quite difficult and computationally expensive.
To overcome this shortcoming, Khotanzad et al. [3] proposed using orthogonal moments—Zernike moments (ZMs)—in object recognition task. Chong et al. [4] used a new set of translation and scale invariants of orthogonal Legendre moments to recognize English, Chinese, and Latin characters. Teh et al. [5] commented the description performance and noise sensibility of various image moments. They found that the orthogonal moments have a superior performance over other types of moments. Other orthogonal moments, such as Krawtchouk moments (KMs) [6], pseudo-Zernike moments (PZMs) [5], Chebyshev–Fourier moments (CHFMs) [7], Bessel–Fourier moments (BFMs) [8], orthogonal Fourier–Mellin moments (OFMMs) [9], exponent-Fourier moments (EFMs) [10], polar harmonic transforms (PHTs) [11], and radial harmonic Fourier moments (RHFMs) [12, 13], were proposed, as well.
RHFMs are better rated and offer a better depiction of the image in comparison with other orthogonal moments, which make them more suitable for image analysis and object recognition [14,15,16]. However, the conventional computation of RHFMs produces geometric error and numerical integration error, which is a common problem with the orthogonal moments [17, 18]. The geometric error is caused when a square image is mapped into a unit circular disk, which cannot exactly match the square domain. The numerical integration error is caused when the integration is approximated by zeroth-order summation. These errors are reflected through the image reconstruction error which is visible in the neighborhood of the center of the circular disk and the presence of numerical instability even at low orders of transform. Since the traditional computation method of RHFMs has obvious shortcomings, Singh et al. [15] presented an accuracy and efficiency computational framework for RHFMs. In this work, higher accuracy of RHFMs is achieved by the Gaussian quadrature technique [14] for numerical integration of kernel functions that reduces geometric and numerical integration errors. In addition, the speed is accelerated by the fast recursive algorithms for the radial and angular functions of RHFMs and their 8-way symmetry/anti-symmetry properties. Although this paper has improved the computational speed of RHFMs, the time complexity did not change essentially. Moreover, it does not analyze the relationship between reconstruction performance and the number of used RHFMs. To improve the computation accuracy and reduce the time complexity, Wang et al. [16] proposed a fast and precise method to compute RHFMs based on FFT. In this method, a Cartesian coordinate image of size M × M is mapping into a polar coordinate image with a size of 4M × 4M. Although FFT can be used to speed up the computation of RHFMs, the computational complexity of the reconstruction process is still very high, which is O(16M2). To solve this problem, we will reconstruct RHFMs obtained by FFT in Cartesian coordinate system instead of polar coordinate system, in which the reconstruction complexity has been reduced by a factor of 16. In addition, the experimental results show that the proposed computing method for RHFMs not only greatly increases the speed, but also improves the reconstruction accuracy.
Besides the problem of computation accuracy and efficiency, there is another problem that needs to be addressed. Although it has been extensively investigated in recent years, the theory of image moments mainly focuses on grayscale images. However, nowadays color images become more popular in many application fields as they provide richer information than grayscale images. Current research on color image moments is mostly based on the intensity or a single channel within the color space, while discarding the information and relationship between color components within a specific color space. Recently, quaternion-based image representation and application have become increasingly important in the field of image processing, and some of the quaternion-based methods are already applied in several domains related to image processing (e.g., quaternion wavelet transform [19], quaternion singular value decomposition [20], quaternion Fourier transform [21], quaternion polar harmonic transform [22]). Quaternion-based image processing regards a color pixel as a vector, which reserves the relationship between different channels of a color image. Based on this theory, Guo et al. [23] extended traditional Fourier–Mellin moments into a quaternion form (i.e., quaternion Fourier–Mellin moments (QOFMMs)) and successfully applied it to color image registration using the constructed geometric invariant features. Subsequently, Chen et al. [24] introduced the quaternion Zernike moments (QZMs) by using the algebra of quaternions, built a complete feature-invariant set, and achieved an outstanding result within color object recognition and color image registration. Guo et al. [25] proposed novel quaternion moment descriptors for color images in the Cartesian coordinates, which can reduce computational complexity and improve numerical stability in the field of color image processing and object recognition. Shao et al. [26] proposed quaternion Bessel–Fourier moments (QBFMs) and analyzed the importance of the phase information contained in quaternion orthogonal moments from the perspective of color image reconstruction. Chen et al. [27] summarized quaternion-type moments, including quaternion rotational moments (QROTMs), QOFMMs, QZMs, and quaternion pseudo-Zernike moments (QPZMs), and evaluated their performance in the fields of color image reconstruction, face recognition, and image registration. Additionally, they discussed the selection of quaternions in the calculation process. They also defined geometric invariant feature descriptors according to the derived rotation angle estimation algorithm and applied them in color object recognition. In recent years, some of the traditional non-orthogonal and orthogonal moments have been developed into the form of quaternion moments, respectively, such as quaternion exponent moments (QEMs) [28, 29], quaternion radial harmonic Fourier moments (QRHFMs) [30, 31], quaternion Bessel–Fourier moments (QBFMs) [32], quaternion Chebyshev–Fourier moments (QCHFMs) [2], quaternion Legendre–Fourier moments (QLFMs) [33], and quaternion polar harmonic Fourier moments (QPHFMs) [2].
Although researchers have proposed a variety of quaternion orthogonal moments, most of them have shown poor performance in image reconstruction. In this paper, accurate quaternion orthogonal moments, namely accurate quaternion radial harmonic Fourier moments (AQRHFMs), are proposed. Firstly, we proposed an accurate computational framework of RHFMs, which not only greatly increase the speed but also improve the reconstruction accuracy. Secondly, we extended the accuracy and fast RHFMs to AQRHFMs by using the algebra of quaternions, which can deal with the color images in a holistic manner. Comparison experiments are conducted on the performance in image reconstruction and color object recognition of AQRHFMs and QZMs, QPZMs, QOFMMs, QCHFMs, QRHFMs, QPHFMs and QLFMs. Experimental results show that the proposed AQRHFMs achieve the best image reconstruction performance and perform superbly in invariant object recognition in noise-free and noisy conditions.
This paper is organized as follows. Section 2 introduces the quaternion algebra and RHFMs. In Sect. 3, the definition of computational framework of AQPHFMs is discussed in detail. Section 4 presents the comparative experiments of AQPHFMs with QZMs, QPZMs, QOFMMs, QRHFMs, QCHFMs, QPHFMs, and QLFMs in terms of image reconstruction and object recognition. Section 5 concludes.
2 Preliminaries
2.1 Quaternion algebra
The quaternion is a type of hyper-complex number. It is a generalization of complex number. We know that a complex number has two components: the real part and imaginary part. However, the quaternion has four parts including one real part and three imaginary parts. A quaternion \(\mu\) can be interpreted as generalizations of complex numbers as follows:
where \(a\) is the real part of the quaternion \(\mu\); \(b{\text{i}} + c{\text{j}} + d{\text{k}}\) is the imaginary part of the quaternion \(q\); \(a\), \(b\), \(c\), and \(d\) are real numbers; and \(i\), \(j\), and \(k\) are complex operators obeying the following rules:
The conjugate and the magnitude of the quaternion \(\mu\) are \(\overline{\mu } = a - bi - cj - dk\) and \(\left| \mu \right| = \sqrt {a^{2} + b^{2} + c^{2} + d^{2} }\), respectively.
A quaternion can be considered the combination of a scalar part and a vector part: \(\mu = s(\mu ) + v(\mu )\), where \(s(\mu ) = a\) and \(v(\mu ) = b{\text{i}} + c{\text{j}} + d{\text{k}}\). A quaternion with \(s(\mu ) = 0\) can be also referred to as a pure quaternion, and a quaternion with unit magnitude is called a unit quaternion.
In [21], Wang et al. proposed to encode the three channel components of an RGB image on the three imaginary parts of a pure quaternion. In other words, a pixel at image coordinate \((m,n)\) in an RGB image can be represented as
where \(f_{R} (m,n)\), \(f_{G} (m,n)\), and \(f_{B} (m,n)\) are the red, green, and blue components of the pixel, respectively.
2.2 Radial harmonic Fourier moment
Let \(f\left( {r,\theta } \right)\) be the grayscale image in polar coordinate system, the RHFMs \(M_{p,q}\) with order \(p(p \ge 0)\) and repetition \(q(\left| q \right| \ge 0)\) over a unit disk are defined as:
Here, the “order” and “repetition” are two important parameters to calculate any orthogonal moments and they are used to decide the number of moments we can obtain. Specifically,\(H_{p,q}^{ * }\) denotes the complex conjugate of basis function \(H_{p,q} (r,\theta )\) and is obtained from the following formula:
where \(i = \sqrt { - 1}\). The radial kernel functions are defined as
The orthogonality of basis function is given as
where \(0 \le r \le 1\), \(0 \le \theta < 2\pi\), and \(\delta\) is Kronecker delta, \(2\pi\) is normalization factor. The tot al number of RHFMs for \(p = p_{{\rm max}}\) and \(q = q_{{\rm max}}\), is \(\left( {1 + p_{{\rm max}} } \right)\left( {1 + 2q_{{\rm max}} } \right)\).
The image \(M_{p,q}\) can be reconstructed approximately by using RHFMs as follows:
3 Accurate quaternion radial harmonic Fourier moments
In this section, we will introduce a new computational framework of RHFMs in detail, namely accurate quaternion radial harmonic Fourier moments (AQRHFMs). Firstly, in order to promote the speed and accuracy of conventional RHFMs, we use FFT in Cartesian coordinate system to reconstruct the RHFMs obtained in the polar coordinate system, in which the geometric error and numerical integration error can be reduced effectively. Next, we will extend the accurate RHFMs to AQRHFMs by using the algebra of quaternions, which deal with the color images in a holistic manner. Finally, we will derive and analyze the rotation and scaling invariant property of AQRHFMs.
3.1 Computation of accurate and fast RHFMs
In this subsection, we provide a precise computational framework by utilizing FFT in polar coordinates system inspired by the work [16], which reduces geometric error and numerical integration error. In addition, we will reconstruct RHFMs obtained by FFT in Cartesian coordinate system instead of polar coordinate system, in which the reconstruction complexity has been reduced by 16 times.
The RHFMs are computed in a unit circle, and we segment the radius direction \(r\left( {0 \le r \le 1} \right)\) and angular direction \(\theta \left( {0 \le \theta < 2\pi } \right)\) of the unit circle into M parts equally. Accordingly, the unit circle is segmented into \(M^{2}\) sub-regions and the initial position of each sub-region is
The polar coordinates \(\left( {r_{u} ,\theta_{v} } \right)\) can be transformed into the rectangular coordinates \(\left( {x,y} \right)\) as follows:
Then we can transform the rectangular coordinates \(\left( {x,y} \right)\) into the discrete coordinates \(\left( {i,j} \right)\) by the following formula:
where \(\left\lceil \bullet \right\rceil\) denotes the round down function. Using Eqs. (9) and (10), the polar coordinate image \(f_{T} \left( {r_{u} ,\theta_{v} } \right)\) can be obtained by
The RHFMs of \(f_{T} \left( {r_{u} ,\theta_{v} } \right)\) can be written as:
Then we can obtain the discrete representation of the above formula
with
when p is even (\(p = 2k\left( {k = 1,2,...} \right)\)), Eq. (14) can be rewritten as follows:
Let \(G_{T} \left( {r_{u} ,\theta_{v} } \right) = f_{T} \left( {r_{u} ,\theta_{v} } \right)\sqrt {\frac{{r_{u} }}{2}}\), Eq. (16) can be rewritten as follows:
where \(M_{p = 2k,q}\) includes two 2-D discrete Fourier transform parts of the function \(G_{T} \left( {r_{u} ,\theta_{v} } \right).\) Suppose F is the 2-D Fourier domain of the function \(G_{T} \left( {r_{u} ,\theta_{v} } \right)\) by moving the zero-frequency component to the center of the array. The RHFMs \(M_{p = 2k,q}\) can be obtained as follows:
The same procedure may be easily adopted to complete the relationship between F and \(M_{p,q}\):
In image reconstruction processing, the image function \(f\left( {r,\theta } \right)\) is discrete and defined in a rectangular domain with the pixel locations identified in a rectangular domain with the pixel locations identified by the row and column arrangement. Let \(\left( {j,k} \right)\) be a pixel, the index j denotes the row position and k the column, with \(j,k = 0,1, \ldots ,N - 1\), where the resolution of the image is N × N pixels. We map the pixel location \(\left( {j,k} \right)\) into the coordinates within the unit disk using the following transformation
The coordinate \(\left( {x_{j} ,y_{k} } \right)\) represents the center of the \(\left( {j,k} \right)\) pixel grid with the two opposite vertices defined by \(\left[ {x_{j} - {{\Delta x} \mathord{\left/ {\vphantom {{\Delta x} 2}} \right. \kern-\nulldelimiterspace} 2},y_{j} - {{\Delta y} \mathord{\left/ {\vphantom {{\Delta y} 2}} \right. \kern-\nulldelimiterspace} 2}} \right] \times \left[ {x_{j} + {{\Delta x} \mathord{\left/ {\vphantom {{\Delta x} 2}} \right. \kern-\nulldelimiterspace} 2},y_{j} + {{\Delta y} \mathord{\left/ {\vphantom {{\Delta y} 2}} \right. \kern-\nulldelimiterspace} 2}} \right]\), where \(\Delta x\) and \(\Delta y\) represent the horizontal and vertical separation between the centers of two pixels which are expressed as
Since the integration does not have an analytical solution for N × N image, its zeroth-order approximation, given below, is normally used
Suppose that moments of all orders \(p \le p_{{\rm max}}\) and repetition \(q \le q_{{\rm max}}\) are given, the image function is reconstructed are given as
Here, we conduct several experiments to compare the proposed computational method of RHFMs with algorithms [12, 16]. In the experiments, the standard grayscale image Lena with 128 × 128 is used as the test image. Table 1 shows the comparison about the reconstructed images (moment order \(p_{{\rm max}} = q_{{\rm max}} = 5,10,25,40,70,100\)). We use the mean square reconstruction error (MSRE) [16] to evaluate the performance of the reconstruction; a smaller MSRE indicates better reconstruction performance.
From Table 1, we know that the reconstruction performance of the proposed method is much better than other two methods [12, 16]. In addition, our method has reduced the reconstruction time significantly compared with the method in [16].
3.2 Accurate quaternion radial harmonic Fourier moments
Traditional methods for color image processing usually divide the images into 3 components and carry out a follow-up process separately for each component without taking relationships between each component into account. However, quaternion-related theory regards a color image as an integral vector, which reflects the association within components. Let us denote the red, green, blue components of a color pixel by \(f_{R} (r,\theta )\), \(f_{G} (r,\theta )\), and \(f_{B} (r,\theta )\), respectively, then the pixel can be encoded as a pure quaternion \(f(r,\theta ) = f_{R} (r,\theta )i + f_{G} (r,\theta )j + f_{B} (r,\theta )k\).
Accordingly, it is possible to define accuracy RHFMs in the quaternion field. By treating each color pixel as a whole, the resulting transforms can address the multi-dimension nature of color image. Let \(f_{T} (r,\theta )\) be a RGB color image defined in polar coordinates, we define the right side of AQRHFMS of order p with repetition q as
where \(f(r,\theta )\) is the quaternion representation of a color pixel and \(\mu\) is a pure unit quaternion. In this paper, we choose \(\mu = {{\left( {i + j + k} \right)} \mathord{\left/ {\vphantom {{\left( {i + j + k} \right)} {\sqrt 3 }}} \right. \kern-\nulldelimiterspace} {\sqrt 3 }}\) that is the gray line in the RGB space. Accordingly, the left side of AQRHFMS can be written as follows:
The \(\mu = \alpha i + \beta j + \gamma k\) is used to deduce the calculation method of AQRHFMS. This idea is based on the computation of the accurate RHFMs of the grayscale image in each channel. The detailed derivation is as follows:
with
where \(f_{R}\), \(f_{G}\), and \(f_{B}\) represent the red, green, and blue components of the color image \(f(r,\theta )\); \(M_{p,q} (f_{R} )\), \(M_{p,q} (f_{B} )\), and \(M_{p,q} \left( {f_{G} } \right)\) are the corresponding RHFMs. \({\text{Re(}}p{)}\) denotes the real part of the complex number \(p\); and \({\text{Im(}}p{)}\) is the imaginary part. It can be seen that each component of the AQRHFMs can be represented as a combination of the real and imaginary parts of the accurate RHFMs of the single-channel grayscale image.
A color image can be reconstructed based on left- and right-side AQRHFMs coefficients, which can be represented as follows:
In this paper, the AQRHFMs refer to the right-side-type AQRHFMS, which is represented by \(M_{p,q}^{R}\) and defined as Eq. (26), unless otherwise specified.
3.3 Geometric invariance of AQRHFMS
Here, we will derive and analyze the rotation and scaling invariant property of AQRHFMs.
-
(1)
Rotation invariance
Let \(\hat{f}(r,\theta ) = f(r,\theta + \alpha )\) denote the image \(f(r,\theta )\) rotated by the angle \(\alpha\). Accordingly, the right-side AQRHFMs of \(\hat{f}(r,\theta )\) are:
where \(M_{p,q}^{R}\) and \(\hat{M}_{p,q}^{R}\) are the AQRHFMs of \(f(r,\theta )\) and \(\hat{f}(r,\theta )\), respectively.
Accordingly to Eq. (30), we know that a rotation of the color image by an angle \(\alpha\) induces a phase shift \(e^{\mu q\theta }\) of the \(M_{p,q}^{R} \left( f \right)\). Taking the norm on both sides of Eq. (31), we have
Therefore, the rotation invariant can be achieved by taking the norm of ARHFMs. In other words, the AQRHFMS modulus coefficients \(\left| {M_{p,q}^{R} \left( f \right)} \right|\) are invariant with respect to image rotation.
-
(2)
Scaling invariance
Theoretically, AQRHFMS are not invariant to image scaling, but scaling invariance can be obtained by normalizing the image into a unit circle. If an image \(f(r,\theta )\) with \(N \times N\) pixels is mapped to a unit circle \((x_{j} ,y_{k} ) \in \left[ { - 1,1} \right] \times \left[ { - 1,1} \right]\) with \(x_{j} = \frac{2j - N + 1}{N},\;y_{k} = \frac{N - 1 - 2k}{N},\;(j,k = 0,1,...,N - 1)\) and a unit circle is made to cover the same contents of the image, the AQRHFMS are invariant to image scaling.
4 Experiments and analysis
4.1 Experiment on geometric invariance of AQRHFMs
-
(1)
Experiment on rotation invariance
We first evaluate the performance of the AQRHFMS invariants under rotation transform. The original color image we used is selected from the COIL-100 database of Columbia University [34]. The original and rotated images are shown in Fig. 1, where Car_R0 is the original image and from Car_R1 to Car_R9 are the rotated versions of original ones. All these images are 128 × 128 pixels. The experimental results can be found in Table 2. Each column in Table 2 is the values of same moment invariant for different images; each row is the values of different moment invariants for the same image. The bottom row is the standard deviation of each column data to indicate the stability of the moment invariants.
Rotated images for rotation invariance tests: a Car_R0: original image, b Car_R1: rotation \({3}5^{ \circ }\), c Car_R2: rotation \({60}^{ \circ }\), d Car_R3: rotation \({90}^{ \circ }\), e Car_R4: rotation \({13}5^{ \circ }\), f Car_R5: rotation \({1}60^{ \circ }\), g Car_R6: rotation \({21}0^{ \circ }\), h Car_R7: rotation \({245}^{ \circ }\), i Car_R8: rotation \({28}0^{ \circ }\), and j Car_R9: rotation \({315}^{ \circ }\)
As one can see from Table 2, the AQRHFMs invariants remain almost unchanged under different rotation changes and most of the standard deviations are less than 0.02. Therefore, the AQRHFMs invariants derived in this paper could be a useful tool in color object recognition tasks that require the rotation invariance.
-
(2)
Experiment on scaling invariance
Some experiments to evaluate the performance of the AQRHFMs invariants under scale transform are also designed. The scale images and the corresponding experimental results are shown in Fig. 2 and Table 3.
4.2 Computation time
The computation time of AQRHFMs is compared with those of QZMs [24], QPZMs [27], QOFMMs [23], QCHFMs [2], QRHFMs [30], and QPHFMs [2] in this subsection. Ten color images with 128 × 128 pixels are used in this experiment. In the experiment, programs are run on a computer with a 3.40-GHz processor and 16 GB RAM running the Microsoft Windows 10 Ultimate operating system. The experiment is conducted using MATLAB version 8.6. The average computation time of the 10 images with the number of moments from 3 to 300 is summarized in Fig. 3. It can be seen that the computation time of AQRHFMs is much less than those of QZMs and QPZMs, and is approximately equal to those of QRHFMs, and QPHFMs.
4.3 Image reconstruction
Image reconstruction performance can be used to test the image representation capability of image moments. Therefore, comparisons of image reconstruction performance between AQRHFMs and QZMs [24], QPZMs [27], QOFMMs [23], QCHFMs [2], QRHFMs [30], and QPHFMs [2] are presented in this subsection. As shown in Eq. (26), the image can be reconstructed approximately by using finite AQRHFMs. Let \(K\) be a constant. The number of moments used in image reconstruction can be limited, as shown in Table 4.
The conditions are selected, so the moments capturing the lowest-frequency information are used for image reconstruction. Moreover, the reconstruction time has obviously been reduced based on the above conditions. \(K\) is set to \(K = p_{{\rm max}}\) to ensure an ideal reconstruction performance while saving time in the reconstruction process [11]. In this paper, the reconstruction performance is evaluated by MSRE [16].
Experiment 1 Four standard color images with 128 × 128 pixels are used in this experiment, as shown in Fig. 4, referred to as “Lena,” “Barbara,” “Mandrill,” and “Peppers.” Figure 5 shows the comparison of reconstructed images for Lena, in which the maximum moment order \(p_{{\rm max}}\) is 2, 3,…, and 22, respectively. Figure 6 shows the comparisons of MSREs for 4 standard color images in Fig. 4. As can be seen from Figs. 5 and 6, the reconstruction performance of AQRHFMs is much better than those of QZMs [24], QPZMs [27], QOFMMs [23], QCHFMs [2], QRHFMs [30], and QPHFMs [2]. We can also observe that when the number of moments used in the reconstruction process increases from 0, the reconstruction performance of all 7 moments gets better. When the number of moments exceeds a certain value, the reconstruction performance of QZMs, QPZMs, QOFMMs, QCHFMs, and QRHFMs degrades, whereas the reconstruction performance of QPHFMs and our proposed AQRHFMs keeps getting better. The reason for these trends is the numerical instability problem of QZMs, QPZMs, QOFMMs, QCHFMs, and QRHFMs. Table 5 displays the reconstructed images using higher orders of AQRHFMs and QPHFMs, respectively. Columns 2, 4, and 6 of Table 5 depict the images reconstructed using QPHFMs, whereas columns 3, 5, and 7 display the images reconstructed with the proposed AQRHFMs. It is seen from Table 5 that the computation of QPHFMs results in some spurious pixel values in the neighborhood of the centre of the unit disk and also along its circumference when the number of moments exceeds a certain value, which degrades the quality of the reconstructed image. The degradation increases with the increase in the order of QPHFMs. This shows that the computation of QPHFMs is highly unstable because of the geometric error and numerical integration error. The quality of the reconstructed images of AQRHFMs shown in columns 3, 5, and 7 is far better than that of QPHFMs, which can demonstrate the superior performance of AQRHFMs in color image reconstruction.
Experiment 2 Noise may seriously affect the quality of the reconstructed image [2, 35]. To test the reconstruction performance of AQRHFMs in the presence of noise, Gaussian noise of mean 0 and variance 0.01 is added in the 4 images. The comparisons of MSREs are shown in Fig. 7. It can be seen that the trend of the MSRE in the presence of Gaussian noise is similar to Fig. 7. All our experimental results show the reconstruction performance of AQRHFMs is better than those of QZMs [24], QPZMs [27], QOFMMs [23], QCHFMs [2], QRHFMs [30], and QPHFMs [2] (i.e., the superior feature representation capability of AQRHFMs over the other 6 moments).
4.4 Color object recognition
This subsection compares AQRHFMs with QZMs [24], QPZMs [27], QOFMMs [23], QCHFMs [2], QRHFMs [30], QPHFMs [2], and QLFMs [33] in terms of color image object recognition. In the experiments, 9, 25, and 36 low-order moments are selected to carry out object recognition. The multiclass support vector machine (SVM) classifier is used to recognize the experimental images.
Experiment 1 In this experiment, 100 color images from the COIL-100 dataset [34] are used as the experimental image set. The size of the each image is 128 × 128 pixels. Some of them are shown in Fig. 8.
First, each image in the experimental image set is scaled with factors ranging from 0.5 to 2 with 0.1 increments, which makes 16 experimental images in total. Then, 8 images are randomly selected as training images, with the other 8 images as test images. Therefore, there are 800 images in the training set and another 800 images in the testing set. Then, the test images are blended with Gaussian noise of mean 0 and variance \(\sigma^{2} = 0.00,0.10,0.15,0.20,0.30\). The correct classification percentages (CCPs) [26, 36] of AQRHFMs are compared with those of QZMs [24], QPZMs [27], QOFMMs [23], QCHFMs [2], QRHFMs [30], QPHFMs [2] and QLFMs [33]. The nearest neighbor classifier based on Euclidean distance is used to measure the CCP, which is defined by
Table 6 shows the results of the classification. It can be seen from Table 6 that AQRHFMs has the best recognition accuracy, which indicates AQRHFMS has the best robustness against image noise. We can also observe that the more moments used in the recognition process, the more accurate recognition results one can expect. In addition, we can see that when the testing images are not blended with noise, the CCPs of all the moments are almost 100%. This is because all the moments satisfy scaling invariance.
Experiment 2 Face recognition is considered one of the most difficult research topics in the field of pattern recognition. In this experiment, the face images of 20 individuals with 180 × 200 pixels are used from the color face database faces 94 [37] of the University of Essex as our experimental image database. In the database, there are 20 images of each individual, and the first 10 from them are used. Then all the images are converted to the size of 180 × 180 pixels for the experiment. Figure 9 shows the face images of a single individual.
In the experiment, rotation angles of \(0^{ \circ }\), \(15^{ \circ }\), \(30^{ \circ }\), and \(45^{ \circ }\) are applied to each face image; therefore, we obtained 40 face images for each individual. Twenty face images of a single individual are randomly chosen as the training set, whereas the other 20 images are left as the testing set. Then, the test images are added with Gaussian noise of mean 0 and variance \(\sigma^{2} = 0.00,0.10,0.15,0.20,0.30\) to make 400 images in the training set and another 400 images in the testing set in total. Table 7 shows the results of the classification.
It can be seen from Table 7 that AQRHFMs have the best recognition accuracy than QZMs, QPZMs, QOFMMs, QCHFMs, QRHFMs, QPHFMs, and QLFM. The results are in good agreement with Experiment 1, which further explains that AQRHFMs have the best performance on invariant object recognition in noisy conditions. We can also see that the CCPs of all the moments are 100% when the variance of Gaussian noise is 0, which is because all the moments satisfy rotation invariance. From the above 2 experiments, we can conclude that AQRHFMs are robust to image noise attack and have superb geometric invariance, which can be used as a novel image descriptor for color image invariant recognition.
5 Conclusion
In this paper, we propose a novel computation framework of radial harmonic Fourier moments, namely accurate quaternion radial harmonic Fourier moments (AQRHFMs). Firstly, we propose an accurate computational framework of RHFMs, which not only greatly increase the speed but also improve the reconstruction accuracy. Secondly, we extend the accurate and fast RHFMs to AQRHFMs by using the algebra of quaternions, which can deal with the color images in a holistic manner. Much comparative experimental analysis on the performance of AQRHFMs and QZMs, QPZMs, QOFMMs, QCHFMs, QRHFM, QPHFMs, and QLFMs is conducted. Experimental results show that AQRHFMs performs superbly in image reconstruction and invariant object recognition in noise-free and noisy conditions.
In future work, the performance of AQRHFMs in other color image processing domains, such as color image watermarking, color image segmentation, color image retrieval, and so on, will be tested. Another interesting topic would be putting forward more effective and accurate algorithms.
References
Xiao B, Wang G (2013) Generic radial orthogonal moment invariant for invariant image recognition. J Vis Commun Image Represent 24(7):1002–1008
Wang C, Wang X, Li Y, Xia Z, Zhang C (2018) Quaternion polar harmonic Fourier moments for color images. Inf Sci 450:141–156
Khotanzad A, Hong Y (1990) Invariant image recognition by Zernike moments. IEEE Trans Pattern Anal Mach Intell 12(5):489–497
Chong C, Raveendran P, Mukundan R (2004) Translation and scale invariants of Legendre moments. Pattern Recognit 37(1):119–129
Gishkori S, Mulgrew B (2018) Pseudo-Zernike moments based sparse representations for SAR image classification. IEEE Trans Aerosp Electron Syst 55(2):1037–1044
Zhi R, Cao L, Cao G (2018) Translation and scale invariants of Krawtchouk moments. Inf Process Lett 130:30–35
Ping Z, Wu R, Sheng Y (2002) Image description with Chebyshev–Fourier moments. J Opt Soc Am A 19(9):1748–1754
Xiao B, Ma J, Wang X (2010) Image analysis by Bessel–Fourier moments. Pattern Recognit 43(8):2620–2629
Sheng YL, Shen LX (1994) Orthogonal Fourier–Mellin moments for invariant pattern recognition. J Opt Soc Am A 11(6):1748–1757
Hu H, Zhang Y, Shao C, Ju Q (2014) Orthogonal moments based on exponent functions: exponent Fourier moments. Pattern Recognit 47(8):2596–2606
Upneja R, Pawlak M, Sahan A (2018) An accurate approach for the computation of polar harmonic transforms. Optik 158:623–633
Ren H, Ping Z, Bo W, Wu W, Sheng Y (2003) Multidistortion-invariant image recognition with radial harmonic Fourier moments. J Opt Soc Am A 20(4):631–637
Wang C, Wang X, Xia Z, Zhang C (2019) Ternary radial harmonic Fourier moments based robust stereo image zero-watermarking algorithm. Inf Sci 470:109–120
Singh C, Upneja R (2012) A computational model for enhanced accuracy of radial harmonic Fourier moments. In: World congress of engineering, London, UK, pp 1189–1194
Singh C, Ranade S (2013) A high capacity image adaptive watermarking scheme with radial harmonic Fourier moments. Dig Signal Process 23(5):1470–1482
Wang C, Wang X, Xia Z (2016) Geometrically invariant image watermarking based on fast radial harmonic Fourier moments. Signal Process Image Commun 45:10–23
Deng A, Wei C, Gwo C (2016) Stable, fast computation of high-order Zernike moments using a recursive method. Pattern Recognit 56:16–25
Upneja R (2016) Accurate and fast Jacobi–Fourier moments for invariant image recognition. Optik 127(19):7925–7940
Li C, Li Y, Yuan Y, Wu X, Sang Q (2018) Quaternion wavelet transform based full reference image quality assessment for multiply distorted images. PLoS ONE 13(6):e0199430
Liu F, Ma L, Liu C, Lu Z (2018) Optimal blind watermarking for color images based on the U matrix of quaternion singular value decomposition. Multimed Tools Appl 77(18):23483–23500
Wang C, Wang X, Zhang C, Xia Z (2017) Geometric correction based color image watermarking using fuzzy least squares support vector machine and Bessel K form distribution. Signal Process 134:197–208
Xia Z, Wang X, Zhou W, Li R, Wang C, Zhang C (2019) Color medical image lossless watermarking using chaotic system and accurate quaternion polar harmonic transforms. Signal Process 157:108–118
Guo L, Zhu M (2011) Quaternion Fourier–Mellin moments for color images. Pattern Recognit 44(2):187–195
Chen B, Shu H, Zhang H, Chen G, Tounoulin C, Dillenseger JL, Luo LM (2012) Quaternion Zernike moments and their invariant for color image analysis and object recognition. Signal Process 92(2):308–318
Guo LQ, Dai M, Zhu M (2014) Quaternion moment and its invariant for color object classification. Inf Sci 273:132–143
Shao Z, Shu H, Wu J, Chen B, Coatrieux J (2014) Quaternion Bessel–Fourier moments and their invariant descriptors for object reconstruction and recognition. Pattern Recognit 47(2):603–611
Chen B, Shu H, Coatrieux G, Chen G, Sun X, Coatrieux JL (2015) Color image analysis by quaternion-type moments. J Math Imaging Vis 51(1):124–144
Wang C, Wang X, Xia Z, Zhang C, Chen X (2016) Geometrically resilient color image zero-watermarking algorithm based on quaternion exponent moments. J Vis Commun Image Represent 41:247–259
Wang X, Liu Y, Xu H, Wang P, Yang H (2018) Robust copy–move forgery detection using quaternion exponent moments. Pattern Anal Appl 21(2):451–467
Wang X, Li W, Yang H, Niu P, Li Y (2015) Invariant quaternion radial harmonic Fourier moments for color image retrieval. Opt Laser Technol 66:78–88
Xia Z, Wang X, Li X, Wang M, Zhao T (2019) Efficient copyright protection for three CT images based on quaternion polar harmonic Fourier moments. Signal Process 164:368–379
Yang T, Ma J, Miao Y, Wang X, Xiao B, He B, Meng Q (2019) Quaternion weighted spherical Bessel–Fourier moment and its invariant for color image reconstruction and object recognition. Inf Sci 505:388–405
Hosny K, Darwish M (2019) Invariant color images representation using accurate quaternion Legendre–Fourier moments. Pattern Anal Appl 22(3):1105–1122
https://www.cs.columbia.edu/CAVE/software/softlib/coil-100.php
Xiao B, Ma JF, Wang X (2010) Image analysis by Bessel–Fourier moments. Pattern Recognit 43(8):2060–2629
Xiao B, Wang G (2013) Generic radial orthogonal moment invariants for invariant image recognition. J Vis Commun Image Represent 24(7):1002–1008
Acknowledgments
This work was partially supported by the National Science Fund of China under Grant Nos. 61702262, 61861136011, and U1713208; Program for Changjiang Scholars; Natural Science Foundation of Jiangsu Province under Grant No. BK20181299; CCF-Tencent Open Fund (RAGR20180113); Young Elite Scientists Sponsorship Program by GAST (2018QNRC001); Science and Technology on Parallel and Distributed Processing Laboratory (PDL) Open Fund (WDZC20195500106); Fundamental Research Funds for the Central Universities under Grant No. 30918011322.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Liu, Y., Zhang, S., Li, G. et al. Accurate quaternion radial harmonic Fourier moments for color image reconstruction and object recognition. Pattern Anal Applic 23, 1551–1567 (2020). https://doi.org/10.1007/s10044-020-00877-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10044-020-00877-6