1 Introduction

The National Centers for Environmental Information reports the United States has experienced 69 natural disasters with losses exceeding one billion dollars between 2015 and 2019. The accumulated loss exceeds $535 billion at an average of $107.1 billion/year. The trend of disaster frequency is expected to escalate over the years due to changes in climate which will result in catastrophic losses (Lyubchich and Gel 2017). These volatile weather patterns will result in an inevitable challenge to the U.S.’s ability to sustain human and economic development (Tabuchi 2018). As a result, weather risk markets need to be capable of offsetting the financial impacts of natural disasters (Varangis et al. 2003; Dilley et al. 2005).

Unequivocally, the catastrophe losses and related risks inherent create uncertainty over the type of disaster event (Lewis and Murdock 1996; NCEI 2020a). For example, due to less coverage of insured assets and data latency in drought and flooding events, they tend to provide uncertain loss estimates compared to the losses of severe storm events in the United States (NCEI 2020a; Smith and Matthews 2015). In consequence, prioritization for mitigating the risks can be diverse and complex.

The financial losses due to natural disasters exacerbate due to changes in population and national wealth density (Van der Vink et al. 1998; Bell et al. 2018). If insurers are to retain profitability and solvency in the event of a major catastrophe that insurers must increase their prices for catastrophe insurance and reduce their exposure to risk (Roth Sr and and Kunreuther 1998). Also, reinsurers undergo severe financial stress in facilitating catastrophe insurance by offering tenable reduction for risk in large catastrophic losses (Lewis and Murdock 1996; Liang et al. 2010; Zangue and Poppo 2016). However, the substantial losses can be alleviated using protective measures such as preparedness, mitigation, and insurance (Kunreuther 1996; Ganderton et al. 2000). To better protect the clients, catastrophe insurance policies should ramp-up investments in cost-effective loss reduction mechanisms by better managing the risk.

The weather index insurance can effectively transfer spatially covariate weather risks as it pays indemnities based on realizations of a weather index that is highly correlated with actual losses (Barnett and Mahul 2007). The securitization of losses from natural disasters provides a valuable novel source of diversification for investors. Catastrophe risk bonds are a promising type of insurance-linked securities introduced to smooth transferring of catastrophic insurance risk from insurers and corporations to capital market investors by offering an alternative or complement of capital to the traditional reinsurance (Zangue and Poppo 2016). The three types of variables that pay off in insurance-linked securities (Cummins et al. 2004) are insurer-specific catastrophe losses, insurance-industry catastrophe loss indices, and parametric indices based on the physical characteristics of catastrophic events.

The first index-based catastrophe derivatives, CAT-futures, introduced by the Chicago Board of Trade using the ISO-Index was ineffective due to a lack of realistic models in the market (Christensen and Schmidli 2000). Secondly, the Property Claim Services (PCS) proposed the PCS-options based on the PCS-index and they slowed down due to market illiquidity (Biagini et al. 2008). Then, the New York Mercantile Exchange (NYMEX) designed catastrophe futures and options to enhance the transparency and liquidity of the capital markets to the insurance sector (Biagini et al. 2008). Kielholz and Durrer (1997) further explains alternative risk transfer mechanisms within the context of natural catastrophe problems in the United States.

We propose Natural Disasters Index (NDI) to address these shortcomings by creating a financial instrument for hedging the intrinsic risk induced by the property losses caused by natural disasters in the United States. The vital objective of the NDI is to forecast the severity of future systemic risk attributed to natural disasters. This provides advance warnings to the insurers and corporations allowing them to transfer insurance risk to capital market investors. Therefore, the proposed NDI is intended to make up the shortfall between the capital and insurance markets. Furthermore, the NDI could be modified to calculate the risk in other regions or countries using a data set comparable to NOAA Storm Data NCEI (2018).

We follow the methods applied in Trindade et al. (2020) on an ad hoc basis as a benchmark for NDI evaluation: (1) option pricing, (2) risk budgeting, and (3) stress testing. We provide an evaluation framework for the NDI using a discrete-time generalized autoregressive conditional heteroskedasticity model to calculate the fair values of the NDI options. Then, we simulate call and put option prices using the Monte Carlo method. We distribute the cumulative risk attributed to our equally weighted portfolio into the risk contributions of each type of natural disaster. Flood and flash flood are the main risk contributors in our portfolio according to our assessments using standard deviation and expected tail loss risk budgets. Furthermore, we evaluate the portfolio risk of the NDI to mitigate risks using monthly maximum temperature, the Palmer Drought Severity Index (PDSI), and the Global Warming Index (GWI) as stressors. We found the stress on maximum temperature significantly impacts the NDI compared to that of the PDSI at the highest stress level (1%).

The contents of the rest of this paper are as follows. We provide an exploratory data analysis in Sect. 2  and econometric analysis for NDI in Sect. 3. Section 4 presents the steps in option pricing and approximate call and put option prices for the NDI. In Sect. 5, we provide standard deviation and expected tail loss risk budgets for natural disasters in the United States. We assess the performance of the NDI via a stress testing analysis in Sect. 6. Finally, we make concluding remarks in Sect. 7.

2 Construction of the natural disasters index (NDI)

This section provides an exploratory data analysis for constructing an index on financial losses caused by natural disasters. The National Oceanic and Atmospheric Administration (NOAA) has published information on severe weather events occurring in the United States between 1950 and 2018 in their “Storm Data” database Murphy (2018). We utilize the property losses caused by the following 50 types of natural disasters from 1996-2018 to construct the index:

Avalanche, Blizzard, Coastal Flood, Cold/Wind Chill, Debris Flow, Dense Fog, Dense Smoke, Drought, Dust Devil, Dust Storm, Excessive Heat, Extreme Cold/Wind Chill, Flash Flood, Flood, Frost/Freeze, Funnel Cloud, Freezing Fog, Hail, Heat, Heavy Rain, Heavy Snow, High Surf, High Wind, Hurricane (Typhoon), Ice Storm, Lake-Effect Snow, Lakeshore Flood, Lightning, Marine Dense Fog, Marine Heavy Freezing Spray, Marine High Wind, Marine Hurricane/Typhoon, Marine Lightning, Marine Strong Wind, Marine Thunderstorm Wind, Rip Current, Seiche, Sleet, Storm Surge/Tide, Strong Wind, Thunderstorm Wind, Tornado, Tropical Depression, Tropical Storm, Tsunami, Volcanic Ash, Waterspout, Wildfire, Winter Storm, Winter Weather.

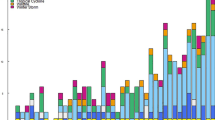
The database reports the property losses incurred by natural disasters in U.S. dollars of the given year Murphy (2018). For this study, we estimate them in U.S. dollars adjusted for inflation in 2019. Figure 1 provides examples of natural disasters between 1996 and 2018 that exemplify eccentric property losses (adjusted for inflation in 2019).

Fig. 1
figure 1

The monthly property losses (in billions adjusted for inflation in 2019) caused by (a) drought, (b) flood, (c) winter storm, (d) thunderstorm wind, (e) hail, and (f) tornado events between 1996 and 2018 generated using NOAA Storm Data NCEI (2018)

Full size image

Natural Disasters Index (NDI): We construct a reliable and dynamic aggregate index by utilizing the financial losses caused by natural disasters. To obtain an equally spaced time series, we examine the cumulative property losses for all 50 types of natural disasters in 15-day increments between 1996 and 2018. We define \(L_t\) as the total property loss at the t \(^{th}\) section 15-day period. Since there are some periods with no property losses (zero losses), we cannot employ the conventional log-returns model.

We take the first differences (lag-1 differences) of the exponents of \(L_t\), i.e., \(\Delta L_t^{\theta }\) where \(\theta = 0.1, 0.2, ..., 1\), and check stationarity of these different models using Dickey-Fuller and KPSS tests (Hamilton 2020; Kwiatkowski et al. 1992) . At the level of 5%, the tests indicate sufficient evidence to suggest that \(\Delta L_t^{\theta }\) for \(\theta = 0.1, 0.2, ..., 1\) are not unit root non-stationary. Since the high values of \(\theta\) result in “fat-tailed” or “heavy-tailed” distributions, we focus on low values of \(\theta\).

In particular, the minimum value of \(\theta\) (0.1) provides a proper Normal Inverse Gaussian (NIG) fit that has a heavy enough tail to capture the rare events using the model (which is beneficial for a GARCH-type option pricing model). Thus, we propose a Natural Disasters Index (NDI) as follows:

$$\begin{aligned} NDI_t = L_t^{0.1}-L_{t-1}^{0.1} = \Delta L_{t}^{0.1}\ , t = 1, \cdots , 552. \end{aligned}$$
(1)

The NDI illustrated in Fig. 2 shows the stationarity of the process with \(\theta = 0.1\), which resulted in a higher predictability in our future analyses in Sect. 4-6.

Fig. 2
figure 2

Our proposed Natural Disasters Index (NDI) for the United States. This NDI (1) is constructed using the property losses of natural disasters reported in NOAA Storm Data NCEI (2018) between 1996 and 2018

Full size image

For stress testing in Sect. 6, we utilize monthly maximum temperatures, the Palmer Drought Severity Index (PDSI) used in the U.S. Climate Extremes Index (NCEI 2019; Palmer 1965; Gleason et al. 2008). In addition, we use the Global Warming Index proposed by Haustein et al. (2017) that provides the combined impacts of the estimated contribution from human-induced warming and natural warming and cooling.

We define the reported highest temperature for each month in the U.S. as the monthly maximum temperature (measured in Fahrenheit) Menne et al. (2009); Vose et al. (2014). PDSI is a measurement of the severity of drought in a region for a given period Heim (2002); Alley (1984). We use the monthly PDSI in the U.S. that assigns a value in [-4,4] on a decreasing degree of dryness (i.e., the extremely dry condition and extremely wet condition provide -4 and 4, respectively) Heddinghaus and Sabol (1991). Figure 3 depicts that the first differences of the climate extreme indicators yield stationary time series.

Fig. 3
figure 3

The first differences of the climate extreme indicators, (a) Maximum Temperature (Max Temp) and (b) Palmer Drought Severity Index (PDSI), yield stationary time series, generated using NCEI (2020b) between 1996 and 2018

Full size image

3 Econometric analysis for NDI volatility

This section examines the seasonality and volatility in our NDI using AutoRegressive Moving Average (ARMA) and Generalized AutoRegressive Conditional Heteroskedasticity (GARCH) models. We assume the dynamic returns (1) follow the process:

$$\begin{aligned} R_t=\log {\frac{NDI_t}{NDI_{t-1}}}=r'_t+\uplambda _0 \sqrt{a_t}-\frac{1}{2}a_t+\sqrt{a_t} \epsilon _t, \end{aligned}$$
(2)

where \(r'_t\) and \(\epsilon _t\) are the risk-less rate of return and standardized residual during the time period t, respectively. \(\uplambda _0\) denotes the risk premium for the NDI, and \(a_t\) is the conditional variance of returns (\(R_t\)) given the information set consisting of all linear functions of the past returns available during the time period \(t-1\) (\(F_{t-1}\)), i.e., \(a_t=\text {VaR}\left( R_t \mid F_{t-1}\right)\). We examine \(a_t\) using different GARCH(m, n) models defined as follows:

$$\begin{aligned} a_t=\omega +\sum _{i=1}^{m} \alpha _{i} \ a_{t-i} +\sum _{j=1}^{n} \beta _{j} \ \epsilon _{t-j}^{2}, \end{aligned}$$
(3)

where \(\omega\) (constant), \((\alpha _i)_{i=1}^m\) and \((\beta _j)_{j=1}^n\) are non-negative parameters of the model; each of these variables is to be estimated using the data.

We find a proper GARCH model for the conditional variance of returns by comparing their performances as shown in Table 1, which reports their estimated parameters with significance and the information criteria (AIC, BICFootnote 1, ShibataFootnote 2, and Hannan-QuinnFootnote 3). According to the information criteria, GARCH(2,1) outperforms, but only \(\beta _2\) reports a statistically significant parameter. Since all the models produced results that are essentially the same, there is no benefit in selecting a model based solely on information criteria. In calibrating the parameters to option prices, the GARCH(m,n) models with \(m>1\) and \(n>1\) increase computational complexity and decrease estimation accuracy. Therefore, we choose the standard GARCH(1,1) model which provides statistically significant estimates for all model parameters. This model is expressed as:

$$\begin{aligned} a_t=\omega + \alpha \ a_{t-1} + \beta \ \epsilon _{t-1}^{2}, \end{aligned}$$
(4)

where the standardized residuals (\(\epsilon _{t}\)) are independent and identically distributed with a generalized hyperbolic distribution, \(GH\left( \uplambda ,\alpha ,\beta ,\delta ,\mu \right)\).

Table 1 Fitting GARCH models for the conditional variance of returns
Full size table

Although the seasonal GARCH, EGARCH, and APARCH models potentially outperform the standard GARCH model, they make the processes of obtaining the equivalent martingale measure and specifying the distribution of returns on risk-neutral probability space more difficult. These concepts are explained further in Sect. 4. Moreover, EGARCH and APARCH models are used for deep-out-of-the-money option prices, but we apply a discrete stochastic volatility based model for option pricing. This reasoning confirms the validity of using a GARCH(1,1) model for our study.

We test seasonality in mean and variance of monthly return volatility using the Kruskall Wallis and QS-tests included in the “seastests” package available in R software (Webel and Ollech 2018). Based on the results of these two tests, the Webel-Ollech overall seasonality test identifies annual seasonality in the mean of NDI index. However, the test does not classify seasonality in the absolute value of NDI, \(\mid \Delta L_t^{0.1}\mid\), or in the volatility of NDI.

We estimate three types of monthly volatilities for NDI: (1) historical volatility, (2) realized volatility, and (3) estimated volatility using ARMA(1,1)-GARCH(1,1) with Student’s t innovations based on historical data. We use rolling methods with a ten-year (120 months) window and each time period uses a sample of historical data for estimating the NDI volatility. According to the results of Dickey-Fuller and KPSS tests, three types of volatilities indicate unit root non-stationarity in time series. We also stabilize the variance of these three series by taking logarithmic transformation and compare the descriptive statistics of volatility and log-volatility series in Table 2. ARMA-GARCH volatility model reports comparatively high values for statistics compared to the other models (historical and realized volatility models) that present similar values.

Using the data illustrated in Fig. 4, we compare three volatility models to determine which model predicts the reported property losses more accurately. The time series behavior of the historical and realized volatility models are similar, and there is no significant difference between the two. Since the ARMA-GARCH volatility model captures huge losses in a relatively high frequency, it outperforms the other models in representing the volatility of property losses. In this section, we presented historical volatility that represents the ex-post return volatility. In Sect. 4, we will provide implied volatilities that represent ex-ante volatilities.

Table 2 Descriptive statistics for the volatility and log-volatility series
Full size table
Fig. 4
figure 4

Estimated NDI historical volatility, realized volatility, and ARMA-GARCH model volatility with reference to the total property losses

Full size image

4 Pricing NDI options

Standard insurance and reinsurance systems encounter difficulties in reimbursing the extremely high losses caused by natural disasters. Insurance companies seek more reliable approaches for hedging and transferring these types of intensive risks to capital market investors. Catastrophe risk bonds (CAT bonds) are one of the most important types of Insurance-Linked-Securities used to accomplish this. Our proposed NDI is intended to assess the degree of future systemic risk caused by natural disasters. In this section, we determine a proper model for pricing the NDI options.

Options can be used for hedging, speculating, and gauging risk. The Black–Scholes model, binomial option pricing model, trinomial tree, Monte Carlo simulation, and finite difference model are the conventional methods in option pricing. We do not implement the Black–Scholes model since we investigated the existence of heteroskedasticity in Sect. 3. The discrete stochastic volatility-based model was introduced to compute option pricesFootnote 4 and explain some well-known mispricing phenomena. In particular, Duan (1995a) proposes the application of discrete-time GARCH to price options. Considering the accuracy of pricing performance using a volatility-based modelFootnote 5, we implement the discrete-time GARCH model with NIG innovations to compute the fair values of the NDI options.

In the standard GARCH(1,1) model (4), Blaesild (1981) defines that the \(R_t\) for given \(F_{t-1}\) is distributed on real world probability space (\({\mathbb {P}})\) as follows:

$$\begin{aligned} R_t \sim NIG\left( \uplambda ,\frac{\alpha }{\sqrt{a_t}}, \frac{\beta }{\sqrt{a_t}}, \delta \sqrt{a_t}, \;r'_t+m_t+\mu \sqrt{a_t} \right) , m_t=\uplambda _0 \sqrt{a_t}-\frac{1}{2}a_t . \end{aligned}$$
(5)

The Esscher transformation given in Gerber and Shiu (1994) is the conventional method of identifying an equivalent martingale measure to obtain a consistent price for options. Since the moment generating function of the NIG distribution has exponential form, the Esscher transform takes the probability density of \(R_t\) and transforms it into the risk-neutral probability density. Using the Esscher transformation, Chorro (2012) found that \(R_t\) for given \(F_{t-1}\) is distributed on the risk-neutral probability (\({\mathbb {Q}}\)) as follows:

$$\begin{aligned} R_t \sim NIG\left( \uplambda ,\frac{\alpha }{\sqrt{a_t}},\frac{\beta }{\sqrt{a_t}}+\theta _t,\delta \sqrt{a_t},r'_t+m_t+\mu \sqrt{a_t} \right) , \end{aligned}$$
(6)

where \(\theta _t\) is the solution to \(MGF\left( 1+\theta _t \right) = MGF\left( \theta _t \right) \, e^{r'_t}\), and MGF is the conditional moment generating function of \(R_{t+1}\) given \(F_{t}\).

We generate future values of the NDI to price its call and put options using the Monte Carlo simulations (Chorro 2012) as follows:

  1. 1.

    Fitting GARCH(1,1) with NIG innovations to \(L_t^{0.1}\) and forecasting \(a_1^2\) (we set \(t=1\)).

  2. 2.

    Beginning from \(t=2\), repeat the steps (a)-(c) for \(t=3,4,...,T\), where T is time to maturity of the NDI call option.

    1. (a)

      Estimating the parameter \(\theta _t\) using \(MGF\left( 1+\theta _t \right) = MGF\left( \theta _t \right) \, e^{r'_t}\), where MGF is the conditional moment generating function of \(R_{t+1}\) given \(F_{t}\) on \({\mathbb {P}}\).

    2. (b)

      Finding an equivalent distribution function for \(\epsilon _t\) on \({\mathbb {Q}}\) and generate the value of \(\epsilon _{t+1}\) under the assumption \(\epsilon _{t} \sim NIG(\uplambda ,\alpha ,\beta +\sqrt{a_t}\theta _t,\delta ,\mu )\) on \({\mathbb {Q}}\).

    3. (c)

      Computing the values of \(R_{t+1}\) and \(a_{t+1}\) using (2) and (4).

  3. 3.

    Generating future values of \(L_t^{0.1}\) for \(t=1,....,T\) on \({\mathbb {Q}}\) where T is the time to maturity. Recursively, future values of the NDI is obtained by

    $$\begin{aligned} NDI_{t}=R_{t}^{10}+NDI_{t-1}. \end{aligned}$$
    (7)
  4. 4.

    Repeating steps 2 and 3 10,000 (N) times to simulate N paths to compute future values of the NDI.

Then, the Monte Carlo averages approximate future values of the NDI at time t for a given strike price K to price its call and put options (\({\hat{C}}\) and \({\hat{P}}\), respectively)

$$\begin{aligned}&{\hat{C}}\left( t,T,K \right) =\frac{1}{N}\,e^{-r'_t(T-t)}\sum _{i=1}^{N} \max \left( NDI^{(i)}_T-K,0 \right) \ , \end{aligned}$$
(8)
$$\begin{aligned}&{\hat{P}}\left( t,T,K \right) =\frac{1}{N}\,e^{-r'_t(T-t)}\sum _{i=1}^{N} \max \left( K-NDI^{(i)}_T, 0 \right) . \end{aligned}$$
(9)

The call option prices (\({\hat{C}}\)) help the investors to strategize buying the stocks in our NDI at a predefined price (strike price) within a specific time frame (time to maturity). In Fig. 5, we provide call option prices for the NDI based on a given strike price (K) with time to maturity (T). The NDI call option prices exponentially decrease as the strike price increases. When the strike price is up to two trillion, the call price is 15 trillion. In such cases, no insurance can afford this and also, reinsurance fails to pay this large of an amount. Therefore, if the losses are above the strike of two trillion, only the world market can absorb this.

We provide selling prices of the shares in our index in Fig. 6 by demonstrating the relationship of put option prices (\({\hat{P}}\)) to strike price (K), and time to maturity (T). As we expected, the put option price for NDI increases as the strike price increases, and there seems to be a potential linear dependence between them. The strike price, which starts at four trillion, is too high to be traded by investors on the market. Our put options seem to behave like short term insurance in which the investors will get paid only if the losses are below 17 trillion.

Implied volatility is known as an efficient forecast of future volatility over the option’s remaining lifetimeFootnote 6. In Fig. 7, we provide the implied volatility for NDI using the market price of the call option contracts to indicate the anticipation of an event in the near future. The implied volatility surface is constructed against the time to maturity (T) and moneyness (\(M=S/K\), where S and K are the stock and strike prices, respectively). The observed volatility surface has an inverted volatility smile which is usually seen in periods of high market stress. In particular, the highest implied volatilities of options are observed in the moneyness between 1.2 and 1.4. The downward sloping (volatility skew) indicates the implied volatility for upside (high strike) equity options is typically lower than the implied volatility for at-the-money equity options. Options with lower strike prices have higher implied volatilities compared to those with higher strike prices. The implied volatilities tend to converge to a constant as the time to maturity converges to 120 weeks.

Without the index being marketed by financial institutions, together with the insurance instruments on the index, such as futures and put options, it will be impossible to meet future extreme losses due to natural disasters. As in the stock market, long term investors need portfolio insurance to hedge the downturn risk (Mantilla-García 2014). With the help of the financial market at large, the government should hedge the potential financial risk caused by natural disasters. Therefore, we provide NDI option prices with volatilities for investors to strategize buying call options and selling put options based on their risk tolerance levels in this section.

Fig. 5
figure 5

The call option prices (8) for the Natural Disasters Index (NDI) at time t for a given strike price K using a GARCH(1,1) model with generalized hyperbolic innovations. The Monte Carlo simulations are generated using NOAA Storm Data NCEI (2018) between 1996 and 2018

Full size image
Fig. 6
figure 6

The put option prices (9) for the Natural Disasters Index (NDI) at time t for a given strike price K using a GARCH(1,1) model with generalized hyperbolic innovations. The Monte Carlo simulations are generated using NOAA Storm Data NCEI (2018) between 1996 and 2018

Full size image
Fig. 7
figure 7

The Natural Disasters Index (NDI) implied volatilities against time to maturity (T) and moneyness (\(M=S/K\), where S and K are the stock and strike prices, respectively) using a GARCH(1,1) model with generalized hyperbolic innovations. The Monte Carlo simulations are generated using NOAA Storm Data NCEI (2018) between 1996 and 2018

Full size image

5 Determining NDI risk budgets

Obviously, the risk created by each type of natural disaster is different. For example, floods and earthquakes cause a significantly high risk in the United States. Therefore, the typical homeowners insurance policies do not cover the damages caused by floods and earthquakes. The federal government has introduced government programs such as The Florida Hurricane Catastrophe Fund and The California Earthquake Authority to provide appropriate coverage to policyholders, individuals and companies.

Envisioning the amount of risk exposure from each type of natural disaster helps investors to determine the degree of variability in our portfolio. The risk budgets provide the risk contributions of each component in the portfolio to the aggregate portfolio risk. We provide the estimated risk allocation for each type of natural disaster to potentially help investors with their financial planning in our portfolio.

Standard deviation (Std), Value at Risk (VaR), and Expected Tail Loss (ETL), also known as Conditional Value at Risk (CVaR),Footnote 7 are conventional risk measures used in market risk assessment. As Std and ETL are coherent risk measures, we use them as the investment strategies for our portfolioFootnote 8. We assess the center risk contributions of our portfolio using Std as it measures the volatility in the market. ETL provides the chance of a loss occurring due to a rare event, i.e., tail risk contributions of the index.

ETL is a coherent risk measure used to evaluate a portfolio’s market risk, and it has properties such as convexity and monotonicity (Pflug 2000). At the level of \(q\% = (1-\alpha )\%\), ETL evaluates the portfolio’s expected return in the worst \(q\%\) of cases. ETL calculates the expected extreme losses in the tail of the return distribution, which are above the VaR cutoff point, as follows:

$$\begin{aligned} \text {ETL}\alpha (X) = \frac{1}{\alpha } \int _0^\alpha {\text {VaR}}_\gamma (X) \, d\gamma , \quad 0< \alpha < 1, \end{aligned}$$
(10)

where X is the payoff of a portfolio and \({\text {VaR}}_\gamma (X)\) is the value at risk given by

$$\begin{aligned} \text {VaR}_{\gamma }(X) = -\inf \lbrace x \in {\mathbb {R}} : F(x) \le \gamma \rbrace = F_{X}^{-1}(1-\gamma ) . \end{aligned}$$

The VaR of the portfolio at the confidence level \(\gamma\) is the minimum payoff such that the aggregate probability is not greater than \((1-\gamma )\). That is, the VaR provides the maximum possible loss after removing all worse outcomes whose cumulative probability is at most \(\gamma\) (Artzner et al. 1999).

In finance, both equally weighted and capitalization based indices are used for risk budgeting. The capitalization-based index uses the current capitalization and synthetically creates the time series of the index based on historical data. However, when the capitalization structure is changed, another model should be replaced with synthetic historical values of the index. Thus, to avoid the uncertainty of change in capitalization, we use an equally-weighted index. Doing so accounts for potential variance in the future weights of the constituencies.

For a risk measure, R(.), we define the marginal risk and risk contribution of each asset in the portfolio with a weight vector, \(\mathbf{w} =(w_1,w_2,...,w_n)\) where \(w_i=\frac{1}{n}\) (\(R(w):{\mathbb {R}}^n \rightarrow {\mathbb {R}}\)). The marginal contribution to risk (MCTR) of the ith asset to the total portfolio risk is given by

$$\begin{aligned} \text {MCTR}_i(\mathbf{w} ) = w_i \frac{\partial R(\mathbf{w} )}{\partial w_i}. \end{aligned}$$
(11)

We define the MCTR of the k \(^{th}\) subset as

$$\begin{aligned} \text {MCTR}_{M_k}(\mathbf{w} ) = \sum _{i \in M_k}^{}\text {MCTR}_i (\mathbf{w} ), \end{aligned}$$
(12)

where \(M_k\,\, \subseteq \,\left\{ 1,2,...,n \right\}\) denote s subsets of portfolio assets. The Percent Contribution to Risk (PCTR) of the i \(^{th}\) asset to the total portfolio risk is given by

$$\begin{aligned} \text {PCTR}_i(\mathbf{w} ) =\frac{\text {MCTR}_i(\mathbf{w} )}{\sum _{i=1}^{n}\text {MCTR}_i(\mathbf{w} )}. \end{aligned}$$
(13)

Since a large number of observations are involved in our analysis, we use a rolling-method for risk budgeting. We use the first 400 data (15-day loss returns) at each window as in-sample-data and the last 400 data as out-of-sample data. In Fig. 8, we provide a visual representation of ETL at the level of 95%. According to its color scale, red represents risk contributors and blue represents risk diversifiers.

Fig. 8
figure 8

The percent contribution to risk (PCTR) of the expected tail loss (ETL) risk budgets for the Natural Disasters Index (NDI) at 95% level. The legend depicts the severe weather events in ascending order of their PCTR of ETL risk budgets at 95% level. The results are generated from NOAA Storm Data NCEI (2018) between 1996 and 2018

Full size image

We provide estimated risk allocations, the Std and ETL for risk contributions, in our portfolio in Table 3. Since the table provides positive values, all types of natural disasters contribute risk to the NDI and none of them are risk diversifiers in our portfolio. We determine the main center risk contributors in our index based on the Std budgets in Table 3. Since Std measures the volatility in the market, higher the Std riskier the investment. Then, the main center risk contributors in our portfolio seem to be tornado, tropical storm, flood, ice storm, and flash flood as they demonstrate high volatility compared to the other types of disasters.

We calculate the tail risk budgets at the 95% and 99% levels using Eq (10) to find the main tail risk contributors in our portfolio. According to the estimated ETL budgets at the 95% level, ETL(95%), flash flood, wildfire, and flood provide a relatively higher tail risk than the other factors. However, hurricane, tropical storm, flood and flash flood seem to be the main tail risk contributors at the 99% level.

We take the main tail and center risk contributors into account to find the main risk contributors of our portfolio. Since flash flood and flood are both main tail and center risk contributors, they are the potential main risk contributors in our portfolio. In conclusion, identifying the main risk contributors and estimating the risk budgets will help investors to envision the amount of risk exposure when considering investing in our portfolio.

Table 3 Percent contribution to risk for standard deviation (Std) and expected tail loss (ETL) (at 95% and 99% levels) risk budgets for the Natural Disasters Index (NDI)
Full size table

6 Evaluating the impact of climate extreme indicators on the NDI performance

In this section, we evaluate how well our index would perform if an adverse weather event happened. That is, we investigate the impact of extreme weather factors on higher financial losses caused by natural disasters in the United States. Our findings will help investors to hedge strategies against possible future adverse weather events. For the climate extreme indicators, we utilize the monthly maximum temperature and the Palmer Drought Severity Index that are provided in the U.S. Climate Extremes Index proposed by NOAA and the Global Warming Index proposed by Haustein et al. (2017) (refer to Sect. 2).

In finance, stress testing is a form of scenario analysis used by regulators to investigate the robustness of a financial instrument in inevitable crashes. We implement stress testing to determine the strength of NDI and its resilience to the climate extreme indicators. This helps investors to gauge investment risk in our portfolio and also serves as a tool for hedging strategies required to mitigate potential losses caused by climate extreme indicators.

In this section, we assess the performance of NDI via stress testing using monthly maximum temperature (Max Temp), the Palmer Drought Severity Index (PDSI), and Global Warming Index (GWI) as stress factors. Instead of working with raw climate extreme factors, we use their lag-1 differences (returns) as they yield stationary time series, see Figure 3. According to the results of the Ljung-Box test, the three series of returns inherit serial correlation and dependence. To capture linear and nonlinear dependencies in returns, we put the series through the ARMA(1,1)-GARCH(1,1) filter with Student-t innovations and consider the sample innovations for our analysis.

We fit bivariate NIG models to the joint distributions of independent and identically distributed standardized innovations of each climate extreme indicator returns and NDI: Max Temp vs NDI, PDSI vs NDI, and GWI vs NDI. Then, we generate 10,000 scenarios from these bivariate NIGs to perform the scenario analysis and to compute the systemic risk measures. Figure 9 shows the fitted contour plots in each bivariate density, overlaid with the 10,000 simulated values. The empirical correlation coefficients based on the observed data suggest a weak positive relationship between the factors and the NDI. We quantify the market risk of our portfolio to assess the impact of negative events on the climate extreme indicators. In order to do that, we calculate three systemic risk measures induced from VaR for each joint NIG density.

Fig. 9
figure 9

The generated joint densities of the returns of (a) monthly maximum temperature (Max Temp) and the Natural Disasters Index (NDI), (b) the Palmer Drought Severity Index (PDSI) and the NDI, and (c) the Global Warming Index (GWI) and the NDI using the fitted bivariate NIG models of the joint distributions of independent and identically distributed standardized residuals. The figures depict the simulated values, the contour plots, and empirical correlation coefficients (R) of the joint densities

Full size image

Conditional Value at Risk (CoVaR) proposed by Adrian and Brunnermeier (2011) provides the change in the VaR of the financial system under the condition of an institution being under distress relative to its median state. As CoVaR is a coherent risk measure (Acerbi and Tasche 2002), changing VaR to CoVaR allows us to consider more severe distress events, back-test CoVaR, and improve its monotonicity concerning the dependence parameter. Girardi and Ergun (2013) improved the definition of financial distress from an institution being exactly at its VaR, \(X= \text {VaR}_{\alpha }(X)\), to being less than or equal to its VaR, \(X\le \text {VaR}_{\alpha }(X)\). We use an alternative CoVaR in terms of copulas defined in Mainik and Schaanning (2014) and denote Y as NDI and X as a climate extreme indicator. CoVaR at the level of q, \(\text {CoVaR}_q\) (or \(\xi _{q}\)), is defined as

$$\begin{aligned} \xi _q := \text {CoVaR}_q := F^{-1}_{Y|X\le F^{-1}_{X}(q)} \left( q \right) = -\text {VaR}_{q}\left( Y|X\le -\text {VaR}_{q}(X)\right) , \end{aligned}$$
(14)

where \(F_{Y}\) and \(F_{X}\) denote the cumulative distributions of Y and X, respectively, and \(F_{Y|X}\) is the cumulative conditional distribution of Y given X.

Conditional Expected Shortfall (CoES) is an extension of CoVaR which measures the tail mean beyond VaR (Mainik and Schaanning 2014). We denote CoES at level q as

$$\begin{aligned} \text {CoES}_q := \mathbb {E}\left( Y|Y\le \xi _{q},X\le -\text {VaR}_{q}(X)\right) . \end{aligned}$$
(15)

Conditional Expected Tail Loss (CoETL) is the average of the NDI losses when the NDI and the climate extreme indicators are in distress (Biglova et al. 2014). CoETL quantifies the portfolio downside risk in the presence of systemic risk. We define CoETL at level q as follows:

$$\begin{aligned} \text {CoETL}_q := \mathbb {E}\left( Y|Y\le -\text {VaR}_{q}(Y),X\le -\text {VaR}_{q}(X)\right) . \end{aligned}$$
(16)

Table 4 reports the market risk of our portfolio using the left-tail systemic risk measures on NDI based on climate extreme indicators (Max Temp, PDSI, and GWI) at different stress levels. We address how a drastic increase in the Max Temp, PDSI, and GWI impact our index. At the 10% stress level, CoVaR provides the expected return on our portfolio in the highest 10% of climate extreme indicators. Since CoVaR\(_{10\%}\)(Max Temp)=-1.78, max temperature impacts our index by -1.78 degrees at the 10% stress level. This is an enormous loss as NDI varies between -4 and 4, see Figure 2.

We compare the impacts of climate extreme indicators on our index using Table 4. At the 10% and 5% levels, the stress on maximum temperature has a greater impact on NDI compared to PDSI and GWI. However, at the highest stress level (1%), which is the worst case, PDSI shows a higher impact than maximum temperature and GWI. These findings will help investors gauge the market risk of NDI for hedging strategies to alleviate potential losses due to climate extreme indicators.

Table 4 The left-tail systemic risk measures (CoVaR, CoES, and CoETL) of the joint densities of the Natural Disasters Index (NDI) and climate extreme indicators (monthly maximum temperature, the Palmer Drought Severity Index, and the Global Warming Index) at different stress levels
Full size table

7 Discussion and conclusion

We proposed the Natural Disasters Index, NDI (1), using the United States as a model with property losses reported in NOAA Storm Data (NCEI 2018) between 1996 and 2018. In order to establish the NDI, we provided an evaluation framework using three promising approaches: (1) option pricing, (2) risk budgeting, and (3) stress testing.

We determined the fair values of the NDI options using a discrete-time GARCH model with NIG innovations and then simulated Monte Carlo averages to approximate call and put option prices (8),(9). The relationships among time to maturity, strike price, and option prices help to construct and valuate insurance-type financial instruments. Then, we disaggregated the cumulative risk attributed to natural disasters to our equally-weighted portfolio (i.e., we investigated the risk contribution of each type of natural disaster). The Std and ETL risk budgets for the NDI yield that flood and flash flood are the main risk contributors in our portfolio. Finally, we assessed the performance of the NDI via a stress testing analysis using Max Temp, PDSI, and GWI as stressors. We found the stress on Max Temp significantly impacts the NDI compared to that of the PDSI and GWI at the highest stress level (1%).

The proposed NDI is an attempt to address a financial instrument for hedging the intrinsic risk induced by the property losses caused by natural disasters in the United States. The main objective of the NDI is to forecast the degree of future systemic risk caused by natural disasters. This information could forewarn the insurers and corporations allowing them to transfer insurance risk to capital market investors. Hence the issuance of the NDI will conspicuously help to bridge the gap between the capital and insurance markets. While the NDI is specifically constructed for the United States, it could be modified to calculate the risk in other regions or countries using a data set comparable to NOAA Storm Data NCEI (2018).