Top-k overlapping densest subgraphs

Abstract

Finding dense subgraphs is an important problem in graph mining and has many practical applications. At the same time, while large real-world networks are known to have many communities that are not well-separated, the majority of the existing work focuses on the problem of finding a single densest subgraph. Hence, it is natural to consider the question of finding the top-k densest subgraphs. One major challenge in addressing this question is how to handle overlaps: eliminating overlaps completely is one option, but this may lead to extracting subgraphs not as dense as it would be possible by allowing a limited amount of overlap. Furthermore, overlaps are desirable as in most real-world graphs there are vertices that belong to more than one community, and thus, to more than one densest subgraph. In this paper we study the problem of finding top-k overlapping densest subgraphs, and we present a new approach that improves over the existing techniques, both in theory and practice. First, we reformulate the problem definition in a way that we are able to obtain an algorithm with constant-factor approximation guarantee. Our approach relies on using techniques for solving the max-sum diversification problem, which however, we need to extend in order to make them applicable to our setting. Second, we evaluate our algorithm on a collection of benchmark datasets and show that it convincingly outperforms the previous methods, both in terms of quality and efficiency.

1 Introduction

Finding dense subgraphs is a fundamental graph-mining problem, and has applications in a variety of domains, ranging from finding communities in social networks (Kumar et al. 1999; Sozio and Gionis 2010), to detecting regulatory motifs in DNA (Fratkin et al. 2006), to identifying real-time stories in news (Angel et al. 2012).

The problem of finding dense subgraphs has been studied extensively in theoretical computer science (Andersen and Chellapilla 2009; Charikar 2000; Feige et al. 2001; Khuller and Saha 2009), and recently, due to the relevance of the problem in real-world applications, it has attracted considerable attention in the data-mining community (Balalau et al. 2015; Tatti and Gionis 2015; Tsourakakis 2015; Tsourakakis et al. 2013; Sozio and Gionis 2010). In a domain where most interesting problems are $\mathbf {NP}$-hard, much of the recent work has leveraged the fact that under a specific definition of density, the average-degree density, finding the densest subgraph is a polynomially-time solvable task (Goldberg 1984). Furthermore, there is a linear-time greedy algorithm that provides a factor-2 approximation guarantee (Charikar 2000).

The exact polynomial algorithm (Goldberg 1984) and its fast approximation counterpart (Charikar 2000), apply only to the problem of finding the single densest subgraph. On the other hand, in most applications of interest we would like to find the top-k densest subgraphs in the input graph. Given an efficient algorithm for finding the single densest subgraph, there is a straightforward way to extend it in order to obtain a set of k dense subgraphs. This is a simple iterative method, in which we first find the densest subgraph, remove all vertices contained in that densest subgraph, and iterate, until k subgraphs are found or only an empty graph is left.

This natural heuristic has two drawbacks: first it produces a solution in which all discovered subgraphs are disjoint. Such disjoint subgraphs are often not desirable, as real-world networks are known to have not well-separated communities and hubs that may belong to more than one community (Leskovec et al. 2009), and hence, may participate in more than one densest subgraph. Second, when searching for the top-k densest subgraphs, we would like to maximize a global objective function, such as the sum of the densities over all k subgraphs and, as shown by Balalau et al. (2015), enforcing disjointness may lead to solutions that have very low total density, compared to solutions that allow some limited overlap among the discovered subgraphs.

From the above discussion it follows that it is beneficial to equip a top-k densest-subgraph discovery algorithm with the ability to find overlapping subgraphs. This is precisely the problem on which we focus in this paper. The challenge is to control the amount of overlap among the top-k subgraphs; otherwise one can find the densest subgraph and produce $k-1$ slight variations of it by adding or removing a very small number of vertices—so that the $k-1$ almost-copies are also very dense.

Fig. 1

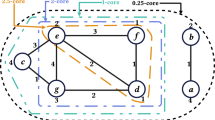
Densest overlapping subgraphs on Zachary karate club dataset (1977). $k=3,\,\beta = 2$

A simple example that demonstrates the concept of finding the top-k densest subgraphs with overlap is shown in Fig. 1. The example is the famous Zachary karate club dataset (1977), and the result is an actual execution of our algorithm, with $k=3.$ The importance of allowing overlap between dense subgraphs is immediate: subgraphs 1 and 2 overlap on vertices 33 and 34. Had those vertices been assigned only to subgraph 1, which was discovered first, subgraph 2 would fall apart.

Our paper follows up on the recent work of Balalau et al. (2015): finding top-k densest subgraphs with overlap. The main difference of the two papers is that here we use a distance function to measure overlap of subgraphs and penalize for overlap as part of our objective, while Balalau et al. are enforcing a hard constraint. Our approach allows to obtain a major improvement over the results of Balalau et al., both in theory and in practice. On the theoretical side, we provide an algorithm with worst-case approximation guarantee, while the method of Balalau et al. offers guarantees only for certain input cases. On the empirical side, our method outperforms the previous one in practically all datasets we experimented, with respect to all measures. In addition, in terms of computation time, our method is more scalable.

From the technical point of view, our approach is inspired by the results of Borodin et al. (2012) for the max-sum diversification problem. In particular, Borodin et al. designed a greedy algorithm in order to find, in a ground set U,  a set of elements S that maximizes a function of the form $f(S) + {\lambda } \sum _{\{x,y\}{\text {:}}\,x,y \in S} d \mathopen {}\left( x,\,y\right) ,$ subject to $|S|=k.$ Here f is a submodular function and d is a distance function. To apply this framework, we set S to be the set of k subgraphs we are searching for, f to capture the total density of all these subgraphs, and d to capture the distance between them—the larger the overlap the smaller the distance.

Yet, the greedy algorithm of Borodin et al. cannot be applied directly; there are a number of challenges that need to be addressed. The most important is that, for our problem, the iterative step of the greedy algorithm results in an $\mathbf {NP}$-hard problem. This is a major difficulty, as the basic scheme of the algorithm of Borodin et al. assumes that the next best item in the greedy iteration can be obtained easily and exactly. To overcome this difficulty, we design an approximation algorithm for that subproblem. Then, we show that an approximation algorithm for the greedy step yields an approximation guarantee for the overall top-k densest-subgraph problem.

We apply our algorithm on a large collection of real-world networks. Our results show that our approach exhibits an excellent trade-off between density and overlap and outperforms the previous method. We also note that density and overlap are not comparable measures, and balancing the two is achieved via the parameter $\lambda .$ As demonstrated in our experiments, executing the algorithm for a sequence of values of $\lambda$ creates a density versus overlap “profile” plot, which reveals the trade-off between the two measures, and allows the user to select meaningful values for the parameter $\lambda .$

The contributions of our work can be summarized as follows:

• We consider the problem of finding top-k overlapping densest subgraphs on a given graph. Our problem formulation relies on a new objective that provides a soft constraint to control the overlap between subgraphs.

• For the proposed objective function we present a greedy algorithm. This is the first algorithm with an approximation guarantee for the problem of finding top-k overlapping densest subgraphs.

• We evaluate the proposed algorithm against state-of-the art methods on a wide range of real-world datasets. Our study shows that our algorithm, in addition to being theoretically superior, it also outperforms its main competitors in practice, in both quality of results and efficiency.

The rest of the paper is organized as follows. We start by reviewing the related work in Sect. 2. In Sect. 3 we define our problem, and in Sect. 4 we present an overview of background techniques that our approach relies upon. Our method is presented in Sect. 5, while the experimental evaluation of our algorithm and the comparison with state-of-the-art methods is provided in Sect. 6. Finally, Sect. 7 is a short conclusion. For convenience of presentation the proofs of the main claims are given in the Appendix.

2 Related work

2.1 Dense-subgraph discovery

As already discussed, the problem of finding dense subgraphs, and its variations, have been extensively studied in the theoretical computer science and graph mining communities. The complexity of the problem depends on the exact formulation. The quintessential dense graph is the clique, but finding large cliques is a very hard problem (Håstad 1996). On the other hand, if density is defined as the average degree of the subgraph, the problem becomes polynomial. This was observed early on by Goldberg, who gave an algorithm based on a transformation to the minimum-cut problem (Goldberg 1984). For the same problem, Asahiro et al. (1996) and Charikar (2000) provided a greedy linear-time factor-2 approximation algorithm, making the problem tractable for very large datasets.

The previous algorithms do not put any constraint on the size of the densest subgraph. Requiring the subgraph to be of a certain size makes the problem $\mathbf {NP}$-hard. Feige et al. show that, for a fixed k,  the problem of asking for the dense subgraph of size exactly k can be approximated within a factor of $\mathcal {O}({\left| V\right| }^\alpha ),$ for $\alpha <\frac{1}{3}$ (Feige et al. 2001). The problems of asking for a densest subgraph of size at most k or at least k are also $\mathbf {NP}$-hard, and the latter problem can be approximated within a constant factor (Andersen and Chellapilla 2009; Khuller and Saha 2009).

Other notions of density have been considered. Tsourakakis et al. provide algorithms for the problem of finding $\alpha$-quasicliques and evidence that such subgraphs are, in practice, “more dense than the densest subgraph” (Tsourakakis et al. 2013). Recently, Tsourakakis showed that finding triangle-dense subgraphs is also a polynomial problem, and gave a faster approximation algorithm (Tsourakakis 2015) similar to Charikar’s approach (2000).

All of the above papers focus on the problem of finding a single densest subgraph. Seeking to find the top-k densest subgraphs is a much less studied problem. Tsourakakis et al. (2013) address the question, but they only considered the naïve algorithm outlined in the introduction—remove and repeat. Balalau et al. (2015) are the first to study the problem formally, and demonstrate that the naïve remove-and-repeat algorithm performs poorly. Their problem formulation is different than ours, as they impose a hard constraint on overlap. Their algorithm is also greedy, like ours, but there is no theoretical guarantee. On the other hand, our formulation allows to prove an approximation guarantee for the problem of top-k overlapping densest subgraphs. Furthermore, our experimental evaluation shows that our algorithm finds denser subgraphs for the same amount of overlap.

Finally, extracting top-k communities that can be described by conjunctions of labels was suggested by Galbrun et al. (2014). In this setup, the communities can overlap but an edge can be assigned to only one community. In addition, a community should be described with a label set. However, the algorithm can be easily modified such that it operates without labels and we use this modified algorithm as one of our baselines.

2.2 Community detection

Community detection is one of the most well-studied problems in data mining. The majority of the works deal with the problem of partitioning a graph into disjoint communities. A number of different methodologies have been applied, such as hierarchical approaches (Girvan and Newman 2002), methods based on modularity maximization (Blondel et al. 2008; Clauset et al. 2004; Girvan and Newman 2002; White and Smyth 2005), graph theory (Flake et al. 2000), random walks (Pons and Latapy 2006; van Dongen 2000; Zhou and Lipowsky 2004), label propagation (van Dongen 2000), and spectral graph partitioning (Karypis and Kumar 1998; Ng Andrew et al. 2001; Luxburg 2007). A popular suite of graph-partitioning algorithms, which is accompanied by high-quality software, includes the Metis algorithm (Karypis and Kumar 1998). The Metis algorithm is one of the baselines against which we benchmark our approach in our experimental evaluation.

A considerable amount of work has also been devoted into the problem of finding overlapping communities. Different methods have been proposed to address this problem, relying on clique percolation (Palla et al. 2005), extensions to the modularity-based approaches (Chen et al. 2014; Gregory 2007; Pinney and Westhead 2006), label propagation (Gregory 2010; Xie et al. 2011), analysis of ego-networks (Coscia et al. 2012), game theory (Chen et al. 2010), non-negative matrix factorization (Yang and Leskovec 2013) or edge clustering (Ahn et al. 2010). A comprehensive survey on the topic of overlapping community detection has been compiled by Xie et al. (2013).

Our problem formulation is different than most existing work in community detection, as we focus solely in subgraph density, while typically community-detection approaches consider a combination of high density inside the communities and small cuts across communities. In fact, there has been experimental evidence that most real-world networks do not exhibit such structure of dense and relatively isolated communities (Leskovec et al. 2009). To contrast our approach with methods for overlapping community detection, we experimentally compare our algorithm with Links, a state-of-the-art method by Ahn et al. (2010).

3 Preliminaries and problem definition

Throughout the paper we consider a graph $G = (V,\,E),$ where V is a set of vertices and E is a set of undirected edges. Given a subset of vertices $W \subseteq V,$ we write

$$\begin{aligned} E(W) = \left\{ (u,\,v) \in E \mid u,\,v \in W\right\} , \end{aligned}$$

for the edges of G that have both end-points in W,  and $G(W) = (W,\,E(W))$ for the subgraph induced by W.

As we are interested in finding dense subgraphs of G,  we need to adopt a notion of density.

Definition 1

The density of a graph $G = (V,\,E)$ is defined as $\mathrm {dens} \mathopen {}\left( G\right) = {\left| E\right| }/{\left| V\right| }.$

Note that $\mathrm {dens} \mathopen {}\left( G\right)$ is half of the average degree of G. If the graph $G=(V,\,E)$ is known from the context and we are given a subset of vertices $W \subseteq V,$ we define the density of W by $\mathrm {dens} \mathopen {}\left( W\right) = \mathrm {dens} \mathopen {}\left( G(W)\right) ,$ that is, the density of the induced subgraph G(W). Additionally, we refer to the set $X \subseteq V$ that maximizes $\mathrm {dens} \mathopen {}\left( X\right)$ as the densest subgraph of G.

Fig. 2

Toy example

Next we define the density of a collection of subsets of vertices.

Definition 2

Given a graph $G = (V,\,E)$ and a collection of subsets of vertices $\mathcal {W} = \left\{ W_1, \ldots , W_k\right\} ,\,W_i \subseteq V,$ we define the density of the collection $\mathcal {W}$ to be the sum of densities of the individual subsets, that is,

$$\begin{aligned} \mathrm {dens} \mathopen {}\left( \mathcal {W}\right) = \sum _{i = 1}^k \mathrm{dens}\left( W_i\right) . \end{aligned}$$

(1)

Example 1

Consider the graph given in Fig. 2 with three subgraphs $\mathcal {W} = \{W_1,\,W_2, W_3\}.$ The collective density of $\mathcal {W}$ is then equal

$$\begin{aligned} \mathrm {dens} \mathopen {}\left( \mathcal {W}\right) = \mathrm{dens}\left( W_1\right) + \mathrm{dens}\left( W_2\right) + \mathrm{dens}\left( W_3\right) = \frac{6}{4} + \frac{3}{3} + \frac{5}{4} = \frac{15}{4}. \end{aligned}$$

Our goal is to find a set of subgraphs $\mathcal {W}$ with high density $\mathrm {dens} \mathopen {}\left( \mathcal {W}\right) .$ At the same time we want to allow overlaps among the subgraphs of $\mathcal {W}.$ Allowing overlaps without any restriction is problematic though, as the obvious solution is to find the densest subgraph of G and repeat it k times. Therefore we need a way to control the amount of overlap among the subgraphs of $\mathcal {W}.$ To control overlaps we use a distance function defined over subsets of vertices. Let $d{\text {:}}\,2^V \times 2^V \rightarrow {\mathbb {R}}_{+}$ denote such a distance function. We are then asking to find a set of subgraphs $\mathcal {W}$ so that the overall density $\mathrm {dens} \mathopen {}\left( \mathcal {W}\right)$ is high, and the subgraphs in $\mathcal {W}$ are far apart, according to the distance function d.

More precisely, the problem definition that we work with in this paper is the following.

Problem 1

(Dense-Over-lapping-Sub-graphs) Given a graph $G = (V,\,E),$ a distance function d over subsets of vertices, a parameter $\lambda ,$ and an integer k,  find k subgraphs $\mathcal {W} = \left\{ W_1, \ldots , W_k\right\} ,\,W_i \subseteq V,$ which maximize a combined reward function

$$\begin{aligned} r \mathopen {}\left( \mathcal {W}\right) = \mathrm {dens} \mathopen {}\left( \mathcal {W}\right) + \lambda \sum _{i = 1}^k \sum _{j = i + 1}^k d\left( W_i,\,W_j\right) . \end{aligned}$$

A few remarks on our problem definition. First note that the parameter $\lambda$ is necessary as the two terms that compose the reward function, density and distance, are quantitatively and qualitatively different. Even if one normalizes them to take values in the same range, say, between 0 and 1, they would still not be directly comparable. In fact, the parameter $\lambda$ provides a weight between density and distance. A small value of $\lambda$ places the emphasis on density and gives solutions with high overlap, but as $\lambda$ increases the subgraphs of the optimal solution need to be more distant, at the expense of the density term. In our experimental evaluation we illustrate the effect of the parameter $\lambda$ by drawing a “profile” of the solution space. By displaying the evolution of the two terms of the reward function as $\lambda$ varies, such plots also allow to select meaningful values for this parameter.

Second, observe that we are not asking to assign every vertex of V in a subgraph of $\mathcal {W}.$ The fraction of vertices assigned to at least one subgraph is controlled by both parameters $\lambda$ and k. The higher the value of $\lambda ,$ the less overlap between the subgraphs, and thus, the higher the coverage. Similarly, the higher the value of k,  the more subgraphs are returned, and thus, coverage increases.

Finally, we restrict the family of functions used to define the distance between subgraphs. As is common, we work with metric and relaxed-metric functions.

Definition 3

Assume a function d mapping pairs of objects to a non-negative real number. If there is a constant $c\ge 1$ such that (i) $d \mathopen {}\left( x,\,y\right) = d \mathopen {}\left( y,\,x\right) ,$ (ii) $d \mathopen {}\left( x,\,x\right) = 0,$ and (iii)

$$\begin{aligned} d \mathopen {}\left( x,\,y\right) \le c( d \mathopen {}\left( x,\,z\right) + d \mathopen {}\left( z,\,y\right) ), \end{aligned}$$

we say that the function d is a c-relaxed metric. If (iii) holds for $c=1,$ the function d is a metric.

The distance function we use to measure distance between subgraphs in this paper is a metric. However, our approach applies more generally to any c-relaxed metric. We formulate our results in their generality, so that the dependency on the parameter c of a c-relaxed metric becomes explicit.

4 Overview of background methods

In this section we provide a brief overview of some of the fundamental concepts and algorithmic techniques that our approach relies upon.

4.1 The densest-subgraph problem

We first discuss the problem of finding the densest subgraph, according to the average-degree density function, given in Definition 1. This problem of finding the densest-subgraph can be solved in polynomial time. An elegant solution that involves a mapping to a series of minimum-cut problems was given by Goldberg (1984). However, since the fastest algorithm to solve the minimum-cut problem runs in $\mathcal {O}({\left| V\right| }{\left| E\right| })$ time, this approach is not scalable to very large graphs. On the other hand, there exists a linear-time algorithm that provides a factor-2 approximation to the densest-subgraph problem (Asahiro et al. 1996; Charikar 2000). This is a greedy algorithm, which starts with the input graph, and iteratively removes the vertex with the lowest degree, until left with an empty graph. Among all subgraphs considered during this vertex-removal process, the algorithm returns the densest. Hereinafter, we refer to this greedy algorithm as the Charikar algorithm.

4.2 Max-sum diversification

Our approach is inspired by the results of Borodin et al. (2012) for the max-sum diversification problem, which, in their general form, extend the classic Nemhauser et al. approximation results (1978) for the problem of submodular function maximization. A brief description of the problem setting and the methods of Borodin et al. follows.

Let U be a ground set, let $d{\text {:}}\,U\times U \rightarrow {\mathbb {R}}_{+}$ be a metric distance function over pairs of U,  and $f{\text {:}}\,2^U\rightarrow {\mathbb {R}}_{+}$ be a monotone submodular function over subsets of U. Recall that a set function $f{\text {:}}\,2^U\rightarrow {\mathbb {R}}$ is submodular if for all $S\subseteq T\subseteq U$ and $u\not \in T$ we have $f({T\cup \{u\}})-f({T}) \le f({S\cup \{u\}})-f({S})$ (Schrijver 2003). Also the function f is monotonically increasing if for all $S\subseteq T\subseteq U$ $f({T})\ge f({S})$ holds. For the rest of the paper, we write monotone to mean monotonically increasing.

The max-sum diversification problem is defined as follows.

Problem 2

(Max-sum diversification) Let U be a set of items, $f{\text {:}}\,2^U\rightarrow {\mathbb {R}}_{+}$ a monotone submodular function on subsets of U,  and $d{\text {:}}\,U\times U\rightarrow {\mathbb {R}}_{+}$ a distance function on pairs of U. Let k be an integer and $\lambda \ge 0.$ The goal is to find a subset $S\subseteq U$ that maximizes

$$\begin{aligned} f({S}) + {\lambda } \sum \limits _{\{x,\,\}{\text {:}}\,x,\,y \in S} d(x,\,y),\quad \mathrm{subject\,to}\quad |S|=k. \end{aligned}$$

Here, $\lambda$ is a parameter that specifies the desired trade-off between the two objectives $f(\cdot )$ and $d(\cdot ,\,\cdot ).$ Borodin et al. (2012) showed that under the conditions specified above, there is a simple linear-time factor-2 approximation greedy algorithm for the max-sum diversification problem. The greedy algorithm works as follows. For any subset $S\subseteq U$ and any element $x\not \in S$ the marginal gain is defined as

$$\begin{aligned} \phi \mathopen {}\left( x;\,S\right) = \frac{1}{2} ( f \mathopen {}\left( S\cup \{x\}\right) - f \mathopen {}\left( S\right) ) + {\lambda } \sum _{y\in S} d \mathopen {}\left( x,\,y\right) . \end{aligned}$$

(2)

The greedy starts with the empty set $S=\emptyset$ and proceeds iteratively. In each iteration it adds to S the element x which is currently not in S and maximizes the marginal gain $\phi \mathopen {}\left( x;\,S\right) .$ Note that due to the 1/2-factor in the first term, $\phi \mathopen {}\left( x;\,S\right)$ is not equal to the actual gain of the score upon adding x to S. The algorithm stops after k iterations, when the size of S reaches k. As already mentioned, this simple greedy algorithm provides a factor-2 approximation to the optimal solution of the max-sum diversification problem.

5 The proposed method

As suggested in the previous section, our method for solving Problem 1 and finding dense overlapping subgraphs relies on the techniques developed for the max-sum diversification problem. First note that, in the Dense-Overlapping-Subgraphs problem, the role of function f is taken by the density function dens. The density of a collection of subgraphs is a simple summation (Definition 2) therefore it is clearly monotone and submodular.

The other components needed for applying the method of Borodin et al. (2012) in our setting are not as simple. A number of challenges need to be addressed:

• (1) While in the max-sum diversification problem we are searching for a set of elements in a ground set U,  in the Dense-Overlapping-Subgraphs problem we are searching for a collection of subsets of vertices V. Thus, $U = \mathcal {P}({V})$ (the powerset of V) and the solution space is ${{\mathcal {P}({V})}\atopwithdelims (){k}}.$

• (2) Adapting the max-sum diversification framework discussed in the previous section requires selecting the item in U that maximizes the marginal gain $\phi$ in each iteration of the greedy algorithm. Since U is now the power-set of V,  the marginal gain computation becomes $\phi \mathopen {}\left( W,\,\mathcal {W}\right) ,$ where W is a subset of vertices, and $\mathcal {W}$ is the set of subgraphs previously selected by the greedy algorithm. Finding the subgraph W that maximizes the marginal gain now becomes a difficult computational problem. Thus, we need to extend the framework to deal with the possibility that we are only able to find a subgraph that maximizes the marginal gain approximately.

• (3) We need to specify the distance function $d{\cdot ,\,\cdot }$ that will be used to measure overlap between subsets of vertices. There are many natural choices, but not all are applicable to the general max-sum diversification framework.

Challenges (2) and (3) are intimately connected. The problem of finding the set of vertices that maximizes the marginal gain $\phi$ in each iteration of the greedy algorithm crucially depends on the distance function $d$ chosen for measuring distance between subgraphs. Part of our contribution is to show how to incorporate a distance function, which, on the one hand, is natural and intuitive, and, on the other hand, makes the marginal gain-maximization problem tractable. We present our solution in Sect. 5.2.

But before, we discuss how to extend the greedy algorithm in order to deal with approximations of the marginal gain-maximization problem and with c-relaxed metrics.

5.1 Extending the greedy algorithm

Consider the Max-Sum-Diversification problem, defined in Problem 2. To simplify notation, if X and Y are subsets of U we define

$$\begin{aligned} d \mathopen {}\left( X,\,Y\right) = \sum _{x \in X} \sum _{y \in Y} d \mathopen {}\left( x,\,y\right) \quad \text {and}\quad d \mathopen {}\left( X\right) = \frac{1}{2} \sum _{x,\,y \in X} d \mathopen {}\left( x,\,y\right) , \end{aligned}$$

so, the objective function in Problem 2 can be written as

$$\begin{aligned} r \mathopen {}\left( S\right) = f \mathopen {}\left( S\right) + \lambda d \mathopen {}\left( S\right) . \end{aligned}$$

The algorithm of Borodin et al. (2012), discussed in the previous section, is referred to as Greedy. As already mentioned, Greedy proceeds iteratively: in each iteration it needs to find the item $x^*$ of U that maximizes the marginal gain with respect to the solution set S found so far. The marginal gain is computed according to Eq. (2). The problem is formalized below.

Problem 3

(Gain) Given a ground set U,  a monotone, non-negative, and submodular function $f ,$ a c-relaxed metric $d ,$ and a set $S\subseteq U,$ find $x\in U\setminus S$ maximizing

$$\begin{aligned} \phi \mathopen {}\left( x;\,S\right) = \frac{1}{2} ( f \mathopen {}\left( S \cup \left\{ x\right\} \right) - f \mathopen {}\left( S\right) ) + {\lambda } d \mathopen {}\left( \left\{ x\right\} ,\,S\right) . \end{aligned}$$

Now consider the case where the Gain problem cannot be solved optimally, but instead an approximation algorithm is available. In particular, assume that we have access to an oracle that solves Gain with an approximation guarantee of $\alpha .$ In this case, the Greedy algorithm still provides an approximation guarantee for the Max-Sum-Diversification problem. The quality of approximation of Greedy depends on $\alpha$ as well as the c parameter of the c-relaxed metric $d .$ We prove the following proposition in Appendix.

Proposition 1

Given a non-negative, monotone and submodular function $f ,$ a c-relaxed metric $d ,$ and an oracle solving Gain with an approximation guarantee of $\alpha ,$ the Greedy algorithm yields an approximation guarantee of $\alpha$/(2c).

5.2 Greedy discovery of dense subgraphs

We now present the final ingredients of our algorithm: (i) defining a metric between subsets of vertices, and (ii) formulating the problem of maximizing marginal gain, establishing its complexity, and giving an efficient algorithm for solving it. We first define the distance measure between subgraphs.

Definition 4

Assume a set of vertices V. We define the distance between two subsets $X,\,Y \subseteq V$ as

$$\begin{aligned} D \mathopen {}\left( X,\,Y\right) = \left\{ \begin{array}{ll} 2 - \frac{{\left| X \cap Y\right| }^2}{{\left| X\right| }{\left| Y\right| }} &{} \text {if}\,X \ne Y,\\ 0 &{} \text {otherwise}. \end{array} \right. \end{aligned}$$

The distance function $D$ resembles very closely the cosine distance (1 − cosine similarity), but unlike the cosine distance, the distance function $D$ is a metric.

Proposition 2

The distance function $D$ is a metric.

Proof

Clearly, $D$ is symmetric and $D \mathopen {}\left( X,\,X\right) = 0.$ To prove the triangle inequality consider $X,\,Y,\,Z\subseteq V.$ It is easy to see that the triangle inequality holds if at least two of the three sets are identical. So, assume that $X,\, Y,$ and Z are all distinct. Note that $0 \le 1 - \frac{{\left| X \cap Y\right| }^2}{{\left| X\right| }{\left| Y\right| }} \le 1.$ This gives

$$\begin{aligned} D \mathopen {}\left( X,\,Y\right) \le 2 \le D \mathopen {}\left( X,\, Z\right) + D \mathopen {}\left( Z,\, Y\right) , \end{aligned}$$

which is the desired inequality. $\square$

Example 2

Let us consider again the graph given in Fig. 2 with $\mathcal {W} = \left\{ W_1,\,W_2,\,W_3\right\}$. We already know that $\mathrm {dens} \mathopen {}\left( \mathcal {W}\right) = 15/4.$ Let us adopt $D$ as our metric. Then we have

$$\begin{aligned} D\left( W_1,\,W_2\right) = D\left( W_2,\,W_3\right) = 2 - \frac{1}{3\times 4} = \frac{23}{12}, \end{aligned}$$

and $D \mathopen {}\left( W_1,\,W_3\right) = 2.$ We can now compute the reward of $\mathcal {W},\, r \mathopen {}\left( \mathcal {W}\right) = \frac{15}{4} + \lambda \left( 2 + 2 \times \frac{23}{12}\right) .$

Next we formulate the problem of selecting the set of vertices that maximizes the marginal gain, in the iterative step of the greedy process, given a set of subgraphs selected so far. The following problem statement specializes Problem 3 in the context of the Dense-Overlapping-Subgraphs problem. We denote the marginal gain with $\chi \mathopen {}\left( \cdot ;\,\cdot \right) ,$ instead of $\phi \mathopen {}\left( \cdot ;\,\cdot \right) ,$ to emphasize that it is a function of a vertex set given a collection of vertex sets.

Problem 4

(Dense subgraphs) Given a graph $G = (V,\,E)$ and a collection of vertex sets $\mathcal {W}=\{W_1, \ldots ,W_k\}, \,W_i\subseteq V,$ find a set of vertices $U \subseteq V$ and $U \notin \mathcal {W}$ maximizing the marginal gain

$$\begin{aligned} \chi \mathopen {}\left( U;\,\mathcal {W}\right) = \frac{1}{2} \mathrm {dens} \mathopen {}\left( U\right) + \lambda D \mathopen {}\left( \{U\},\,\mathcal {W}\right) = \frac{1}{2} \mathrm {dens} \mathopen {}\left( U\right) + \lambda \sum _{W \in \mathcal {W}} D \mathopen {}\left( U,\,W\right) . \end{aligned}$$

Example 3

Let us consider again the graph given in Fig. 2. Set $\mathcal {W}^{\prime } = \left\{ W_1,\, W_2\right\}$ and consider adding $W_3.$ In this case, the gain is equal to

$$\begin{aligned} \chi \left( W_3;\,\mathcal {W}^{\prime }\right)= & {} \frac{1}{2}\mathrm{dens}\left( W_3\right) + \lambda \left( D\left( W_3,\,W_1\right) + D\left( W_3,\,W_2\right) \right) \\= & {} \frac{1}{2}\times \frac{5}{4} + \lambda \left( 2 + \frac{23}{12}\right) . \end{aligned}$$

We should stress that $\chi \mathopen {}\left( W_3;\,\mathcal {W}^{\prime }\right)$ is not equal to the difference in rewards $r \mathopen {}\left( \mathcal {W}^{\prime } \cup \left\{ W_3\right\} \right) - r \mathopen {}\left( \mathcal {W}^{\prime }\right) .$ This is due to the 1/2-factor in the density term.

In the definition of the Dense-Subgraph problem, $\mathrm {dens}$ is the density function given in Definition 1, while $D$ is the subgraph distance function defined above. Had the term $\lambda D \mathopen {}\left( \cdot ,\,\cdot \right)$ been absent from the objective, the Dense-Subgraph problem would have been equivalent with the densest-subgraph problem, discussed in Sect. 4. In that case, the problem could be solved in polynomial time with Goldberg’s algorithm, or approximated efficiently with Charikar’s algorithm.

However, as we show next, adding the $\lambda D \mathopen {}\left( \cdot ,\,\cdot \right)$ term in the objective changes the complexity of the problem. In other words, in contrast to the densest-subgraph problem, Dense-Subgraph is not solvable in polynomial time.

Proposition 3

Dense-Subgraph is $\mathbf {NP}$-hard.

Proof

We consider the decision version of the problem. The problem is obviously in $\mathbf {NP}$. To prove the completeness, we will use Regular-Clique. An instance of Regular-Clique consists of a regular graph (all vertices have the same degree) and an integer c. We are then asked to decide whether the graph contains a clique of size at least c (Garey and Johnson 1979).

Assume that we are given a d-regular graph $G = (V,\,E)$ with $n = {\left| V\right| }$ and $m = {\left| E\right| },$ and an integer $c > 2.$ Define $\mathcal {W}$ as follows: for each $(x,\,y) \notin E,$ add a set $\left\{ x,\,y\right\}$ to $\mathcal {W}.$ Finally, set $\lambda = m.$

Let U be a subgraph and let $p = {{\left| U\right| } \atopwithdelims ()2} - {\left| E(U)\right| }$ be equal to the number of non-edges in U. A straightforward calculation shows that the gain $\chi \mathopen {}\left( U;\,\mathcal {W}\right)$ can be written as

$$\begin{aligned} \chi \mathopen {}\left( U;\,\mathcal {W}\right) = \frac{{\left| E(U)\right| }}{2{\left| U\right| }} + 2\lambda {\left| \mathcal {W}\right| } - \lambda (n - d) \frac{1}{2} - \frac{\lambda p}{{\left| U\right| }}. \end{aligned}$$

If we assume that U is a singleton set $\{u\},$ then the gain is equal to $\chi \mathopen {}\left( \{u\};\,\mathcal {W}\right) =\alpha = 2 \lambda {\left| W\right| } - \lambda (n - d)/2.$

Let U be the subgraph with the optimal gain. Assume that $p \ge 1.$ Then, since ${\left| E(U)\right| } \le m = \lambda$ the gain is at most $\alpha - m / (2{\left| U\right| }),$ which is less than the gain of a singleton. Hence, $p = 0$ and the gain is equal to $({\left| U\right| } - 1)/4 + \alpha .$ Hence, U will be the largest clique. It follows that the graph G contains a clique of size c if and only if Dense-Subgraph has a solution for which the gain is at least $(c - 1)/4 + \alpha .$ $\square$

Despite this hardness result, it is still possible to devise an approximation algorithm for the Dense-Subgraph problem. Our algorithm, named Peel, is a variant of the Charikar algorithm for the densest-subgraph problem. Peel, similar to Charikar, starts with the whole graph and proceeds iteratively, removing one vertex in each step. Peel stops when there is no vertex left, and it returns the set of vertices that maximizes the gain function, selected among all vertex sets produced during the execution of the algorithm.

Peel has two main differences when compared to Charikar. First, instead of removing the minimum-degree vertex in each iteration, Peel removes the vertex that minimizes the following adjusted degree expression

$$\begin{aligned} \deg \left( v;\,V_i\right) - 4 \lambda \sum _{W_j \ni v } \frac{{\left| V_i \cap W_j\right| }}{{\left| W_j\right| }}. \end{aligned}$$

Here $V_i$ stands for the set of vertices that constitute the candidate in the current iteration—after removing some vertices in earlier iterations. The intuition for using this adjusted degree is to lower the gain associated to vertices that belong to subgraphs selected in earlier steps of the greedy process. Indeed, we want to favor high-degree vertices but we want to penalize such vertices that are contained in previously selected subgraphs and thereby generate overlap with (i.e., reduce the distance to) the current subgraph. A further difficulty is that we do not know the current subgraph (since we are currently searching for it!) so we use as a proxy the set of vertices still contained in the candidate at that step ($V_i$). Despite making this seemingly crude approximation, as we will see shortly, the Peel algorithm provides an approximation guarantee to the Dense-Subgraph problem.

The second difference between Peel and Charikar is the following: it is possible that Peel returns a subgraph that has been selected previously. This could happen if the value of the parameter $\lambda$ is small compared to dense subgraphs that may be present in the input graph. When Peel returns a previously-selected subgraph U,  it is sufficient to modify $U{\text {:}}$ we can either add one vertex, remove one vertex, or just replace U with a trivial subgraph of size 3; among all these options we select the best solution according to our marginal gain objective $\chi .$ A detailed description of this process is given in Algorithm 3.

For the quality of approximation of Peel, which is detailed in Algorithm 2, we can show the following result, which is proved in Appendix.

Proposition 4

Assume that we are given a graph $G = (V,\,E),$ a collection of previously discovered vertex sets $\mathcal {W}$ and $\lambda > 0.$ Assume that ${\left| \mathcal {W}\right| } < {\left| V\right| }$ and G contains more than ${\left| \mathcal {W}\right| }$ wedges, i.e., connected subgraphs of size 3. Then Peel yields 2/10 approximation for Dense-Subgraph.

The approximation guarantee of 2/10 is rather pessimistic due to pathological cases, and we can obtain a better ratio if we consider these cases separately. In particular, if Peel does not call Modify, then the approximation ratio is 1/2. If $X \ne \emptyset$ during Modify, then the approximation ratio is at least $\frac{{\left| U\right| }}{2({\left| U\right| } + 1)},$ otherwise the ratio is at least 2/10.

We note that the main function of Modify is to allow us to prove a worst-case approximation guarantee; i.e., for all possible values of $\lambda .$ In practice, if Modify is called for a certain value of $\lambda ,$ the user should perceive this as a signal that $\lambda$ is too small (as overlaps are not penalized enough) and should increase it.

5.3 The DOS algorithm

Finally, we consider the specialization of the generic Greedy algorithm studied above for the problem at hand in this paper. To obtain an algorithm for the Dense-Overlapping-Subgraphs problem, we instantiate $f$ and $d$ with functions whose domains consist of collections of vertices. Specifically, we let $f = \mathrm {dens}$ and $d = D .$ The resulting overall algorithm for the Dense-Overlapping-Subgraphs problem, named DOS, is shown as Algorithm 1. By combining Propositions 1 and 4 we obtain the following result.

Theorem 1

DOS is an $\frac{1}{10}$-approximation algorithm for the Dense-Overlapping-Subgraphs problem.

5.4 Computational complexity

DOS consists of k successive runs of Peel, iteratively removing the vertex with minimum adjusted degree. To perform this operation fast, vertices are stored into separate worker queues according to the previous subgraphs they belong to. Since such vertices incur the same distance penalty, we keep the queues sorted by degree. There are at most $t = \min \{2^k,\,{\left| V\right| }\}$ such queues. In practice, the number is much smaller. To find the next vertex, we compare the top vertex of every worker queue. The search can be done in $\mathcal {O}(t)$ time. Upon deletion of a vertex, updating a single adjacent vertex in a worker queue can be done in constant time,¹ while updating the distance penalties can be done in $\mathcal {O}(k)$ time. If we are forced to call Modify, then finding the best subgraph in X and Y can be done in $\mathcal {O}({\left| E\right| } + {\left| V\right| }k)$ time. In a rare pathological case we are forced to return a wedge. We can do this by first computing k wedges before invoking DOS. If we ever need a wedge, we simply select a wedge from this list that is not yet in $\mathcal {W}.$ Consequently, we can execute DOS in $\mathcal {O}(k({\left| E\right| } + {\left| V\right| }(t + k)))$ time.

6 Experiments

In this section we report on the experimental evaluation of our proposed algorithm DOS . Our python implementation of the DOS algorithm is publicly available online.²

First, we explore the behavior of the algorithms in a controlled setting, using synthetic networks with planted ground-truth subgraphs. Then, we evaluate the algorithms on real-world networks for which the ground-truth is not accessible. In these two parts, we use different evaluation measures, as required by the distinct goals of the two scenarios.

6.1 Algorithms

In both parts, our primary baseline is the MAR algorithm recently proposed by Balalau et al. (2015). Similarly to our approach, their goal is to extract dense overlapping subgraphs while controlling the Jaccard coefficient between the discovered subgraphs.

Both methods MAR and DOS allow/require to adjust the overlap permitted between subgraphs in the solution. In MAR , this is done by fixing a strict maximum threshold for the Jaccard coefficient between two subgraphs, while in DOS , by setting the value of the parameter $\lambda ,$ which balances density and distance.

For DOS , note that the density of subgraphs vary from dataset to dataset, while the distance function $D$ is always below 2. Consequently, in practice it is easier to set the value of $\lambda$ relative to the density of the first subgraph discovered by the algorithm. Note that when extracting the first subgraph, $\lambda$ has no effect since the distance part of the score given in Problem 4 is 0. Thus, when running the algorithm we provide a value $\beta$ and we set $\lambda = \beta \mathrm {dens} \mathopen {}\left( W_1\right) .$

For MAR, we denote the Jaccard threshold by $\sigma$. Note that larger values of $\sigma$ result in increased overlap with MAR but larger values of $\beta$ reduce overlap with DOS .

6.2 Finding planted subgraphs

In the first part of our experiments, we consider synthetic networks and evaluate how well the algorithms are able to recover planted ground-truth subgraphs.

6.2.1 Datasets

Our synthetic networks are generated as follows: each network consists of a backbone of five subsets of vertices. We generate networks both with and without overlaps. In networks without overlap, the subgraphs simply consists of five disjoint subsets of 30 vertices. In configurations with overlap, the subgraphs are arranged in a circle, they are assigned 20 vertices of their own plus 10 vertices shared with the subgraph on one side and 10 shared vertices with the other side.

We consider two families of networks depending on whether connections are generated using the Erdős–Rényi model with fixed densities between 0.6 and 0.9, or using the Barabási–Albert preferential attachment model.

This way, we obtain four types of noise-free networks. We also consider noisy variants, that is, networks where noise is added on top of the backbone. Specifically, we double the number of vertices in the network by adding new vertices that do not belong to any of the subsets, and the connections are flipped with the probability of 0.01.

For each of the eight configurations, we generate ten synthetic networks, each containing five planted subgraphs.³

6.2.2 Statistics

We adopt an approach similar to Yang and Leskovec (2012) and compare the sets of subgraphs detected by the algorithms to the planted ground-truth using the following measures.

NMI::

the Normalized Mutual Information between the ground-truth and the detected subgraphs,

$F_{1}{[}t/d{]}$::

the average $F_{1}$-score of the best-matching ground-truth subgraph to each detected subgraph (“truth to detected”),

$F_{1}{[}d/t{]}$::

the average F1-score of the best-matching detected subgraph to each ground-truth subgraph (“detected to truth”),

($\Omega$)::

the Omega index, i.e., the fraction of vertex pairs that share the same number of communities in the solution and the ground-truth.

Each of these four measures takes value between 0 and 1, with values closer to 1 indicating highest similarity between the detected subgraphs and the planted ground-truth.

6.2.3 Results

The averages of these statistics over ten datasets for each configuration are shown in Table 1. We observe that the MAR algorithm performs better in the absence of overlap and noise, and is able to recover the ground truth perfectly in the case of the Erdős–Rényi graphs. This result can be explained by the fact that MAR handles overlaps with a hard constraint. However, our method is clearly superior when the backbone communities overlap, and also more resistant to noise, that is, for graphs that resemble better real-world application scenarios.

Further experiments, in a setup where the five planted subgraphs have different sizes, show that the difference between the two algorithms is less pronounced. In particular, in the absence of overlap and noise, the improved performance of DOS gets closer to the relatively stable performance of MAR , while in the presence of overlap and noise the performance of MAR is improved compared to the balanced case and gets closer to the performance of DOS , which remains relatively stable.

Table 1 Performance of DOS and MAR on synthetic data

6.3 Comparison on real-world networks

We now turn to an empirical evaluation of our proposed algorithm on real-world datasets.

6.3.1 Datasets

We use the following networks.

Co-authorship networks the first dataset is the DBLP network,⁴ where vertices represent researchers, and edges represent co-authorship relations.

From this co-authorship network we extract smaller instances. First, we consider some ego-net graphs. We start with 13 high-profile computer scientists,⁵ and consider their ego-nets of radius 2. We collectively refer to this collection of ego-nets as DBLP.E2. Second, we consider the subgraphs induced by researchers who have published in the ICDM and KDD conferences, respectively, giving rise to two networks that form the DBLP.C dataset.

The remaining collections consist of networks distributed via the Stanford network analysis project.⁶

Social circles ego-nets collected from Google+ users who have shared their circles are divided into two collections. The first one, G+.S, contains relatively small ego-nets, having fewer than 42,000 edges, while the second, G+.L, contains ego-nets with larger numbers of edges. The FB collection contains 10 ego-nets representing friend lists from Facebook.

Location-based social networks we also consider a collection of location-based networks from Brightkite and Gowalla, two websites that allow there users to share their location. We extract smaller instances by applying the following procedure: we assign each user to their most frequent location and divide the network into 8 broad geographic areas.⁷ We denote this collection of 16 networks as BKGW.

Large graphs finally, denoted by XL, we consider a number of large graphs that were used by Balalau et al. (2015): web graphs from Stanford and Google, the YouTube social network, and the internet topology graph from Skitter.

Statistics on all datasets are provided in Table 2.

6.3.2 Statistics

Again we compare our algorithm to its main competitor, the MAR algorithm. We apply both algorithms on every dataset to extract the top-k overlapping subgraphs, while varying the overlap parameters $\beta$ and $\sigma$. For each run we obtain a set of subgraphs $\mathcal {W}= \{W_1, \ldots , W_k\}.$ In some cases, MAR returns fewer than k subgraphs, therefore ${\left| \mathcal {W}{}\right| }$ can be smaller than k.

Table 2 Datasets statistics

For each solution $\mathcal {W},$ we compute its coverage, that is, the ratio of vertices that belong to at least one subgraph $C \mathopen {}\left( \mathcal {W}\right) = {\left| \cup _{i=1}^k W_i\right| }/{\left| V\right| },$ the average size of the subgraphs ${\left| W{}\right| }$ and the average vertex multiplicity over covered vertices, where the multiplicity of vertex v,  denoted as $\mu \mathopen {}\left( v\right) ,$ is the number of subgraphs it belongs to.

In addition, for each solution we compute (i) the average density $\mathrm {dens} \mathopen {}\left( W_i\right)$ over all subgraphs, (ii) the average distance $D \mathopen {}\left( W_i,\, W_j\right)$ over all pairs of subgraphs, (iii) the average Jaccard distance

$$\begin{aligned} J\left( W_{i},\,W_j\right) = 1 - \frac{{\left| W_i \cap W_j\right| }}{{\left| W_i \cup W_j\right| }}, \end{aligned}$$

over all pairs of subgraphs, and (iv) the modularity

$$\begin{aligned} Q \mathopen {}\left( \mathcal {W}\right) = \frac{1}{2{\left| E\right| }} \sum _{W \in \mathcal {W}{}} \sum _{u,\,v \in W} \left( A_{uv} - \frac{\delta (u)\delta (v)}{2{\left| E\right| }} \right) \frac{1}{\mu (u)\mu (v)}, \end{aligned}$$

where $\mu (v)$ is the number of subgraphs that vertex v belongs to, $\delta (v)$ its degree, and A the graph adjacency matrix.

Table 3 Results for DBLP.E2, $k=20$

Table 4 Results for DBLP.C, $k=20$

6.3.3 Results

Tables 3, 4, 5 and 6 provide summaries of our experimental comparison for DBLP and G+ datasets. We report the number of subgraphs (${\left| \mathcal {W}{}\right| }$), average density ($\overline{ \mathrm {dens} }$), average distance ($\overline{ D }$), average Jaccard distance ($\overline{ J }$), modularity ($Q$), coverage ($C$), average subgraph size ($\overline{{\left| W{}\right| }}$) and average vertex multiplicity ($\overline{ \mu \mathopen {}\left( v\right) }$) averaged across all networks in the collection. Results for the remaining collections are similar, and are thus omitted.

The profile of solutions obtained on five networks from different collections, for a wide range of values of $\beta$ and $\sigma$ are shown in Fig. 3. Each row corresponds to the profile of one network: the ego-net of C. Papadimitriou from DBLP.E2, the KDD network from DBLP.C, the 1183,...,6467 ego-net from G+.S, the 1684 ego-net from FB, and the Brightkite network of Latin-America from BKGW. The columns show the average distance ($\overline{ D }$), average Jaccard distance ($\overline{ J }$) and coverage ($C$) of solutions plotted against average density ($\overline{ \mathrm {dens} }$).

For reference, we added three points to the profiles, representing the solutions obtained respectively with three baseline methods which do not allow to adjust the overlap tolerance. Namely, we considered

Links::

the algorithm of Ahn et al. (2010) discovers overlapping subgraphs by performing a hierarchical clustering on the edges rather than the vertices of the input graph. We consider the top 20 densest subgraphs returned by this method.

Metis::

we apply the popular spectral graph-partitioning algorithm by Karypis and Kumar (1998) to obtain a complete partition of the graph vertices into k disjoint sets.

Dense::

this algorithm, used as a baseline by Galbrun et al. (2014), extracts dense subgraphs in the same iterative process similar to the DOS algorithm but edges are allowed to contribute to at most one subgraph and are assigned where they benefit most.

Table 5 Results for G+.S, $k=20$

Table 6 Results for G+.L, $k=20$

Fig. 3

Solution profiles for five networks. Each row corresponds to the profile of one network, as indicated on the left

At one end of the range of solutions returned by DOS lies the solution that corresponds to setting $\lambda =0,$ i.e., focusing entirely on density. This solution consists of copies of the densest subgraph. At the other end, for large values of $\lambda ,$ lies the solution that does not tolerate any overlap.

Expectedly, we observe that the density of the subgraphs returned increases as the distance decreases, that is, as more overlap is allowed, both algorithms can find denser subgraphs. However, we note that DOS exploits the overlap allowance better, returning subgraphs with greater average densities than MAR for similar values of distance $D$ and Jaccard distance. Additionally, we see that DOS tends to return larger subgraphs and to achieve better coverage scores.

Fig. 4

Running times of DOS and MAR with different values of their overlap parameters, as well as the three baselines, on networks of increasing sizes sampled from the seven datasets

6.4 Running times

Finally, we evaluate the scalability of our method.

Figure 4 shows running times for DOS and MAR , as a function of the size of the network, measured by the number of edges, for different values of their overlap parameters.

The same figure also provide running times for the baseline methods and we can observe that both MAR and DOS scale better than Links and Dense but not as well as Metis .

On average, our algorithm is faster than MAR . An added advantage is the better stability of the running time across values of the overlap parameter, with the extreme value $\sigma =0.95$ resulting in much larger running time for MAR. We should also note here that Balalau et al. (2015) offer a heuristic that is faster than MAR , but at the expense of quality.

7 Concluding remarks

We studied the problem of discovering dense and overlapping subgraphs. Our approach optimizes density as well as the diversity of the obtained collection. Our solution, inspired by the work of Borodin et al. (2012) and Charikar (2000), is an efficient greedy algorithm with an approximation guarantee of 1/10. Our method improves significantly the previous work on the problem by Balalau et al. (2015). Not only do we provide an approximation guarantee, while the baseline is a heuristic, but it also yields practical improvements, both in terms of quality and efficiency. Our experiments, especially Fig. 3, demonstrate that we obtain denser and more diverse subgraphs.

Our approach has two parameters: the number of subgraphs k and the parameter $\lambda$ controlling the relative importance of density and overlap. Since our method is greedy, the problem of selecting k is somewhat alleviated as the first k subgraphs will remain constant if we increase k. Selecting $\lambda$ is more difficult as the relation between the density and the diversity terms is not obvious. We approach this problem by computing profiles as in Fig. 3 by varying $\lambda$ and selecting values that provides a good trade-off between density and overlap.

This work opens several new directions for future work. We have shown that a subproblem, Dense-Subgraph, is $\mathbf {NP}$-hard, however, we did not establish the hardness of the main problem Dense-Overlapping-Subgraphs. We conjecture that it is also $\mathbf {NP}$-hard. Another open question is to improve the approximation guarantee, as well as to study what other types of density functions and overlap distances can be used in our framework.

Appendices

Appendix: Proof of Proposition 1

Let us first define $h(x;\,Y) = \left[ f(x \cup Y) - f(Y)\right] / 2$ and

$$\begin{aligned} g(x;\,Y) = h(x;\,Y) + d \mathopen {}\left( Y \cup x\right) - d \mathopen {}\left( Y\right) = h(x;\,Y) + d \mathopen {}\left( x,\,Y\right) . \end{aligned}$$

For proving the proposition, we will need Lemma 1.

Lemma 1

Let $d$ be a c-relaxed metric. Let X and Y be two disjoint sets. Then

$$\begin{aligned} c({\left| X\right| } - 1) d \mathopen {}\left( X,\,Y\right) \ge {\left| Y\right| } d \mathopen {}\left( X\right) . \end{aligned}$$

Proof

Let $y \in Y$ and $x,\,z \in X.$ By definition,

$$\begin{aligned} c( d \mathopen {}\left( x,\,y\right) + d \mathopen {}\left( z,\,y\right) ) \ge d \mathopen {}\left( x,\,z\right) . \end{aligned}$$

For a given $x \in X,$ there are exactly ${\left| X\right| } - 1$ pairs $(x,\,z)$ such that $x \ne z \in X.$ Consequently, summing over all $x,\,z \in X$ such that $x \ne z$ gives us

$$\begin{aligned} 2c({\left| X\right| } - 1) d \mathopen {}\left( X,\,y\right) \ge 2 d \mathopen {}\left( X\right) . \end{aligned}$$

Summing over $y \in Y$ proves the lemma. $\square$

Proof of Proposition 1

Let $G_1 \subset \cdots \subset G_k$ be the sets during Greedy. Fix $1 \le i \le k.$ Then $G_i$ is the current solution after ith iteration of Greedy.

Let O be the optimal solution. Write $A = O \cap G_i,\,C = O \setminus A,$ and $B = G_i \setminus A.$ Lemma 1 implies that

$$\begin{aligned} c({\left| A\right| } - 1) d \mathopen {}\left( A,\,C\right) \ge {\left| C\right| } d \mathopen {}\left( A\right) , \end{aligned}$$

which in turn implies

$$\begin{aligned} \begin{aligned} {\left| C\right| }i( d \mathopen {}\left( A\right) + d \mathopen {}\left( A,\,C\right) )&\le ci({\left| A\right| } - 1) d \mathopen {}\left( A,\,C\right) + {\left| C\right| }i d \mathopen {}\left( A,\,C\right) \\&= ci({\left| A\right| } - 1 + {\left| C\right| }) d \mathopen {}\left( A,\,C\right) \\&= ci(k - 1) d \mathopen {}\left( A,\,C\right) . \\ \end{aligned} \end{aligned}$$

Moreover, Lemma 1 implies that

$$\begin{aligned} \begin{aligned} c({\left| C\right| } - 1) d \mathopen {}\left( B,\,C\right)&\ge {\left| B\right| } d \mathopen {}\left( C\right) , \\ c({\left| C\right| } - 1) d \mathopen {}\left( A,\,C\right)&\ge {\left| A\right| } d \mathopen {}\left( C\right) , \\ \end{aligned} \end{aligned}$$

which, together with ${\left| C\right| } = {\left| B\right| } + k - i,$ implies

$$\begin{aligned} \begin{aligned} {\left| C\right| }i d \mathopen {}\left( C\right)&= (k - i)i d \mathopen {}\left( C\right) + {\left| B\right| }i d \mathopen {}\left( C\right) \\&= (k - i)({\left| A\right| } + {\left| B\right| }) d \mathopen {}\left( C\right) + {\left| B\right| }i d \mathopen {}\left( C\right) \\&= (k - i){\left| A\right| } d \mathopen {}\left( C\right) + {\left| B\right| }k d \mathopen {}\left( C\right) \\&\le c(k - i)({\left| C\right| } - 1) d \mathopen {}\left( A,\,C\right) + ck({\left| C\right| } - 1) d \mathopen {}\left( B,\,C\right) \\&\le c(k - i)(k - 1) d \mathopen {}\left( A,\, C\right) + ck(k - 1) d \mathopen {}\left( B,\,C\right) .\\ \end{aligned} \end{aligned}$$

Combining these two inequalities leads us to

$$\begin{aligned} \begin{aligned} {\left| C\right| }i d \mathopen {}\left( O\right)&= {\left| C\right| }i d \mathopen {}\left( A\right) + {\left| C\right| }i d \mathopen {}\left( C\right) + {\left| C\right| }i d \mathopen {}\left( A,\,C\right) \\&\le ck(k - 1)( d \mathopen {}\left( A,\,C\right) + d \mathopen {}\left( B,\, C\right) ) \\&= ck(k - 1)d\left( G_i,\,C\right) . \\ \end{aligned} \end{aligned}$$

Submodularity and monotonicity imply

$$\begin{aligned} \begin{aligned} \sum _{v \in C} g\left( v;\,G_i\right)&= \sum _{v \in C} \left[ h\left( v;\,G_i\right) + d\left( \{v\},\, G_i\right) \right] \\&= \left( \sum _{v \in C} h\left( v;\, G_i\right) \right) + d\left( C,\,G_i\right) \\&\ge \frac{1}{2}\left[ f(O) - f\left( G_i\right) \right] + \frac{i{\left| C\right| }}{ck(k - 1)} d \mathopen {}\left( O\right) \\&\ge \frac{1}{2}\left[ f(O) - f\left( G_k\right) \right] + \frac{i{\left| C\right| }}{ck(k - 1)} d \mathopen {}\left( O\right) . \end{aligned} \end{aligned}$$

Let $u_i$ be the item added at the $i + 1$th step, $G_{i + 1} = \left\{ u_i\right\} \cup G_i.$ Then, since $g(u_i;\,G_i) \ge \alpha g(v;\,G_i)$ for any $v \in C,$

$$\begin{aligned} g\left( u_i;\, G_i\right) \ge \frac{\alpha }{2k}\left[ f(O) - f\left( G_k\right) \right] + \frac{i\alpha }{ck(k - 1)} d \mathopen {}\left( O\right) . \end{aligned}$$

Summing over i gives us

$$\begin{aligned} \frac{1}{2}f\left( G_k\right) + d\left( G_k\right) = \sum _{i = 0}^{k - 1}g\left( u_i;\, G_i\right) \ge \frac{\alpha }{2}\left[ f(O) - f\left( G_k\right) \right] + \frac{\alpha }{2c} d \mathopen {}\left( O\right) . \end{aligned}$$

Since $\alpha \le 1$ and $c \ge 1,$ we have

$$\begin{aligned} r\left( G_k\right) = f\left( G_k\right) + d\left( G_k\right) \ge \frac{\alpha }{2}f(O) + \frac{\alpha }{2c} d \mathopen {}\left( O\right) \ge \frac{\alpha }{2c} r \mathopen {}\left( O\right) , \end{aligned}$$

which completes the proof. $\square$

Proof of Proposition 4

To prove the proposition we need to first show that Modify does not decrease the gain of a set significantly.

Lemma 2

Assume a graph $G = (V,\,E).$ Assume a collection of k distinct subgraphs $\mathcal {W}$ of G,  and let $U \in \mathcal {W}.$ Assume that $k < {\left| V\right| }$ and G contains more than k wedges, i.e., connected subgraphs of size 3. Let $M = \mathsf{{Modify}} (U,\, G,\, \mathcal {W},\, \lambda ).$ Then $\chi \mathopen {}\left( V;\,\mathcal {W}\right) \ge 2/5 \times ( \chi \mathopen {}\left( U,\,\mathcal {W}\right) +\lambda ).$

Proof

Write $r = {\left| U\right| }$ and $\alpha = \frac{r}{r + 1}.$ We will split the proof in two cases. Case 1 assume that X,  as given in Algorithm 3, is not empty. Select $B \in X.$ We will show that

$$\begin{aligned} \mathrm {dens} \mathopen {}\left( B\right) \ge \alpha \mathrm {dens} \mathopen {}\left( U\right) \quad \text {and}\quad D \mathopen {}\left( B,\,W\right) \ge \alpha ( D \mathopen {}\left( U,\, W\right) + I[U = W]), \end{aligned}$$

for any $W \in \mathcal {W},$ where $I[U = W] = 1$ if $U = W,$ and 0 otherwise. This automatically guarantees that

$$\begin{aligned} \chi \mathopen {}\left( B;\, \mathcal {W},\, \lambda \right) \ge \alpha ( \chi \mathopen {}\left( U;\, \mathcal {W},\, \lambda \right) + \lambda ), \end{aligned}$$

proving the result since $\alpha \ge 1/2$ and the gain of M is at least as good as the gain of B.

To prove the first inequality, note that

$$\begin{aligned} \mathrm {dens} \mathopen {}\left( B\right) = \frac{{\left| E(B)\right| }}{r + 1} \ge \frac{{\left| E(U)\right| }}{r + 1} = \alpha \frac{{\left| E(U)\right| }}{r} = \alpha \mathrm {dens} \mathopen {}\left( U\right) . \end{aligned}$$

To prove the second inequality fix $W \in \mathcal {W},$ and let $p = {\left| W\right| },\,q = {\left| W \cap U\right| }.$ Define

$$\begin{aligned} \varDelta = D \mathopen {}\left( U,\,W\right) + I[U = W] = 2 - \frac{q^2}{rp} = \frac{2rp - q^2}{rp}. \end{aligned}$$

Let v be the only vertex in $B \setminus U.$ If $v \notin W,$ then $D \mathopen {}\left( B,\,W\right) \ge \varDelta .$ Hence, we can assume that $v \in W.$ This leads to

$$\begin{aligned} \begin{aligned} D \mathopen {}\left( B,\, W\right)&= 2 - \frac{{\left| B \cap W\right| }^2}{{\left| B\right| }{\left| W\right| }} \\&= 2 - \frac{ (1 + q)^2}{(1 + r)p} = \frac{2p(1 + r) - (1 + q)^2}{(1 + r)p}. \end{aligned} \end{aligned}$$

Let us define $\beta$ as the fraction of the numerators,

$$\begin{aligned} \beta = \frac{2p(1 + r) - (1 + q)^2}{2rp - q^2}. \end{aligned}$$

We wish to show that $\beta \ge 1.$ Since $p \ge q + 1,$

$$\begin{aligned} \begin{aligned} \beta&= \frac{2p(1 + r) - (1 + q)^2}{2rp - q^2} = \frac{2rp - q^2 + 2p - 2q - 1}{2rp - q^2} \\&\ge \frac{2rp - q^2 + 2(q + 1) - 2q - 1}{2rp - q^2} = \frac{2rp - q^2 + 1}{2rp - q^2} \ge 1. \end{aligned} \end{aligned}$$

The ratio of distances is now

$$\begin{aligned} \frac{ D \mathopen {}\left( B,\,W\right) }{\varDelta } = \beta \frac{r}{r + 1} \ge \frac{r}{r + 1} = \alpha . \end{aligned}$$

This proves the first case.

Case 2 assume that $X = \emptyset .$ Then we must have $Y \ne \emptyset$ and $r \ge 2,$ as otherwise ${\left| \mathcal {W}\right| } \ge {\left| V\right| },$ which violates the assumption of the lemma.

Assume that $\mathrm {dens} \mathopen {}\left( U\right) \ge 5/3.$ Let $B \in Y.$ Removing a single item of U decreases the density by 1, at most. This gives us

$$\begin{aligned} \frac{ \mathrm {dens} \mathopen {}\left( B\right) }{ \mathrm {dens} \mathopen {}\left( U\right) } \ge \frac{ \mathrm {dens} \mathopen {}\left( U\right) - 1}{ \mathrm {dens} \mathopen {}\left( U\right) } \ge \frac{5/3 - 1}{5 / 3} = \frac{2}{5}. \end{aligned}$$

To bound the distance term, fix $W \in \mathcal {W},$ and let $p = {\left| W\right| },\,q = {\left| W \cap U\right| }.$ Let v be the only vertex in $U \setminus V.$ Define $\varDelta = D \mathopen {}\left( U,\,W\right) + I[U = W].$ If $v \in W,$ then we can easily show that $D \mathopen {}\left( V,\,W\right) \ge \varDelta .$ Hence, assume that $v \notin W.$ This implies that $q \le \min p,\,r - 1,$ or $q^2 \le p(r - 1).$ As before, we can express the distance term as

$$\begin{aligned} \varDelta = 2 - \frac{q^2}{rp} = \frac{2rp - q^2}{rp}, \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} D \mathopen {}\left( B,\, W\right)&= 2 - \frac{{\left| B \cap W\right| }^2}{{\left| B\right| }{\left| W\right| }} = 2 - \frac{ q^2}{(r - 1)p} = \frac{2p(r - 1) - q^2}{(r - 1)p}. \end{aligned} \end{aligned}$$

The ratio is then

$$\begin{aligned} \begin{aligned} \frac{ D \mathopen {}\left( B,\, W\right) }{\varDelta }&= \frac{2p(r - 1) - q^2}{2rp - q^2}\frac{r}{r - 1} \\&\ge \frac{2p(r - 1) - p(r - 1)}{2rp - p(r - 1)}\frac{r}{r - 1} = \frac{p(r - 1)}{rp + p}\frac{r}{r - 1} = \frac{r}{r + 1} \ge 1/2, \end{aligned} \end{aligned}$$

where the first inequality follows from the fact that the ratio is decreasing as function of q.

Assume that $\mathrm {dens} \mathopen {}\left( U\right) < 5/ 3.$ By assumption there is a wedge B outside $\mathcal {W}.$ Since $\mathrm {dens} \mathopen {}\left( B\right) \ge 2/3,$ we have $\mathrm {dens} \mathopen {}\left( B\right) / \mathrm {dens} \mathopen {}\left( U\right) \ge 2 / 5.$ The distance terms decrease by a factor of 1/2, since

$$\begin{aligned} D \mathopen {}\left( U,\, W\right) \le 2 = 2 \times 1 \le 2 D \mathopen {}\left( B,\, W\right) . \end{aligned}$$

Combining the inequalities proves that

$$\begin{aligned} \chi \mathopen {}\left( B;\, \mathcal {W},\, \lambda \right) \ge \frac{2}{5} \chi \mathopen {}\left( U;\, \mathcal {W},\, \lambda \right) , \end{aligned}$$

which proves the lemma. $\square$

Proof of Proposition 4

To prove the proposition, we will first form a new graph H,  and show that the density of a subgraph in H is closely related to the gain. This then allows us to prove the statement.

Let us first construct the graph $H{\text {:}}$ given a vertex v let us define

$$\begin{aligned} s(v) = {-}\sum _{v \in W_j} \frac{2\lambda }{{\left| W_j\right| }}. \end{aligned}$$

Let $H = (V,\, E^{\prime },\, c)$ be a fully connected weighted graph with self-loops where the weight of an edge $c(v,\, w)$ is

$$\begin{aligned} c(v,\, w) = I[(v,\, w) \in E] - \sum _{j \mid v,\, w \in W_j} \frac{4 \lambda }{{\left| W_j\right| }}, \end{aligned}$$

for $v \ne w,$ and $c(v,\, v) = s(v).$

Next, we connect the gain of set of vertices U (w.r.t. G) with the weighted density of U in H. Given an arbitrary set of vertices U,  we will write c(U) to mean the total weight of edges in H. Each $c(v,\, w),$ for $v \in w,$ participates in $\deg _{H}(v;\, U)$ and $\deg _{H}(w;\, U),$ and each $c(v,\, v) = s(v)$ participates (once) in $\deg _{H}(v;\, U).$ This leads to

$$\begin{aligned} 2c(U) = \sum _{v \in U} \deg _{H}(v;\, U) + s(v). \end{aligned}$$

We can express the (weighted) degree of a vertex in H as

$$\begin{aligned} \begin{aligned} \deg _{H}(v;\, U)&= s(v) + \sum _{\begin{array}{c} w \in U \\ w \ne v \end{array}} c(v,\, w) = \deg _G (v ;\, U) -\sum _{j \mid v \in W_j} \frac{2\lambda }{{\left| W_j\right| }} \\&\quad - \sum _{\begin{array}{c} w \in U \\ w \ne v \end{array}} \sum _{j \mid v,\, w \in W_j} \frac{4 \lambda }{{\left| W_j\right| }} \\&= \deg _G (v ;\, U) - \lambda \sum _{j \mid v \in W_j} \frac{4{\left| U \cap W_j\right| } - 2}{{\left| W_j\right| }}. \end{aligned} \end{aligned}$$

(3)

Write $k = {\left| \mathcal {W}\right| }.$ These equalities lead to the following identity,

$$\begin{aligned} \begin{aligned} \mathrm {dens} \mathopen {}\left( U;\,H\right) + 4\lambda k&= \frac{1}{{\left| U\right| }}c(U) + 4\lambda k \\&= 4\lambda k + \frac{1}{2{\left| U\right| }} \sum _{v \in U} \deg _{H}(v;\, U) + s(v) \\&= 4\lambda k + \mathrm {dens} \mathopen {}\left( U;\, G\right) - \frac{1}{2{\left| U\right| }} \sum _{v \in U} \lambda \sum _{j \mid v \in W_j} \frac{4{\left| U \cap W_j\right| }}{{\left| W_j\right| }} \\&= \mathrm {dens} \mathopen {}\left( U;\, G\right) - 2\lambda \sum _{j = 1}^k2 - \frac{{\left| U \cap W_j\right| }^2}{{\left| U\right| }{\left| W_j\right| }} \\&= 2 \chi \mathopen {}\left( U;\, \mathcal {W},\, \lambda \right) + \epsilon (U,\, \mathcal {W}), \\ \end{aligned} \end{aligned}$$

(4)

where $\epsilon (U,\, \mathcal {W})$ is a correction term, equal to 2$\lambda$ if $U \in \mathcal {W},$ and 0 otherwise.

Let O be the densest subgraph in H. Next we show that during the for-loop Peel finds a graph whose density close to $\mathrm {dens} \mathopen {}\left( O;\, H\right) .$ Let o be the first vertex in O deleted by Peel. We must have

$$\begin{aligned} \deg _H(o;\, O) \ge \mathrm {dens} \mathopen {}\left( O;\, H\right) , \end{aligned}$$

as otherwise we can delete o from O and obtain a better solution. Let $R = V_i$ be the graph at the moment when o is about to be removed. Let us compare $\deg _H(o;\,O)$ and $\deg _H(o;\, R).$ We can lower-bound of the second term of the right-hand side in Eq. (3) by ${-}4k\lambda - s(v).$ Since $O \subseteq R,$ this gives us

$$\begin{aligned} \begin{aligned} \deg _H(o;\, O)&\le \deg _G(o;\, O) \le \deg _G(o;\, R) \\&\le \deg _H(o;\, R) + s(o) + 4k\lambda . \end{aligned} \end{aligned}$$

To upper-bound the first two terms, note that by definition of Peel, the vertex o has the smallest $\deg _H(o;\, R) + s(o)$ among all the vertices in R. Hence,

$$\begin{aligned} \deg _H(o;\, R) + s(o) \le \sum _{v \in R} \frac{\deg _H(v;\, R) + s(v)}{{\left| R\right| }} = 2\frac{c(R)}{{\left| R\right| }} = 2 \mathrm {dens} \mathopen {}\left( R;\, H\right) . \end{aligned}$$

To complete the proof, let $O^{\prime }$ be the graph outside $\mathcal {W},$ maximizing the gain. Due to Eq. (4), we have

$$\begin{aligned} \begin{aligned} 2 \chi \mathopen {}\left( O^{\prime };\, \mathcal {W},\, \lambda \right)&= \mathrm {dens} \mathopen {}\left( O^{\prime };\, H\right) + 4k\lambda \le \mathrm {dens} \mathopen {}\left( O;\, H\right) + 4k\lambda \\&\le 2 \mathrm {dens} \mathopen {}\left( R;\, H\right) + 8k\lambda = 2( \mathrm {dens} \mathopen {}\left( R;\, H\right) + 4k\lambda ) \\&= 4 \chi \mathopen {}\left( R;\, \mathcal {W},\, \lambda \right) + 2\epsilon (R;\, \mathcal {W}). \end{aligned} \end{aligned}$$

Let S be the set returned by Peel.

If $R \notin \mathcal {W},$ then $\epsilon (R;\, \mathcal {W}) = 0.$ Moreover, R is not modified, and is one of the graphs that is tested for gain. Consequently, $\chi \mathopen {}\left( S;\, \mathcal {W}\right) \ge \chi \mathopen {}\left( R;\, \mathcal {W}\right) ,$ proving the statement.

If $R \in \mathcal {W},$ then it is modified by Modify to, say, $R^{\prime }.$ Lemma 2 implies that $5/2 \times \chi \mathopen {}\left( R^{\prime },\, \mathcal {W}\right) \ge \chi \mathopen {}\left( R;\, \mathcal {W}\right) + \epsilon (R;\, \mathcal {W}).$ Since, $\chi \mathopen {}\left( S;\, \mathcal {W}\right) \ge \chi \mathopen {}\left( R^{\prime };\, \mathcal {W}\right) ,$ this completes the proof. $\square$