Tracking control of an underwater manipulator using active disturbance rejection

Abstract

An active disturbance rejection controller for a 2-DOF underwater manipulator is proposed in this study. The manipulator system has the characteristics of non-linearity, strong coupling and uncertainties within its model. Its operation is often disturbed by unknown water currents, so the anti-disturbance control of underwater manipulators has always been a challenge. The proposed controller in this study basically does not rely on the precise mathematical model of the object, and the model even can be decoupled. This method can eliminate the influence of model errors, time-varying parameters and external interference on the control effect. First, the entire manipulator treats different joints as several subsystems. For each joint subsystem, hydrodynamic forces, coupling terms between joints and unknown environmental disturbances are regarded as total disturbances. Subsequently, an extended state observer was designed to estimate and compensate for the total interference. In order to improve the disturbance observation effect of the extended state observer, the inertia matrix of the system is used to decouple the static part. Finally, the effectiveness of the proposed method is verified by both simulation and experiments. From the comparisons, it is confirmed that the quality of our controller in the presence of a certain inertial matrix error is better than traditional PD and continuous sliding mode control in terms of accuracy, dynamic characteristics as well as robustness.

1 Introduction

In recent years, higher trajectory tracking accuracy is demanded in the field of robot and manipulator control. In many fields, such as astronomical observation [1], flight control [2], and underwater exploration [3, 4], in the presence of model uncertainties and unknown disturbances, the problem of accurate trajectory tracking has attracted the attention of researchers.

Underwater manipulators are usually working in a complex hydraulic environment. Therefore, the model of underwater manipulator is more complicated than that of common manipulators because of the unknown water flow disturbances, additional viscous resistance of fluid and additional mass forces [5].The nonlinear and uncertain system, coupled with multiple external disturbances in the underwater environment, have become principal challenges for conventional control strategies.

The control methods of the underwater manipulator system are not limited to PID control [6, 7], adaptive control [8], neural network control [9, 10] and sliding mode control [11]. For the multi-DOF underwater manipulator, a controller containing model parameter estimation and multi-layer closed-loop PID is designed [12], but nonlinear disturbances are not compensated. An adaptive control robot algorithm was proposed by Tomeiet al., which combined PD controller and dynamic compensation model [13], it enhances the nonlinear control accuracy, but requires a more accurate dynamic model of the manipulator. Neural network control [14] does not depend on the exact mathematical model, but its sample data for training is a key issue. Sliding mode control is extensively used in anti-jamming and indeterminate models. Bin Xu et al. designed an improved sliding mode controller based on fuzzy logic [15], but the output torque of the controller yet had the problem of jitter.

Since these traditional control strategies are modeled to perform in a specified and known “real” environment and cannot accommodate unavoidable disturbances, they cannot perform well enough in the presence of some modeling uncertainties. Therefore, the problem of disturbance rejection has become the main research focus in the field of underwater manipulator control. Aiming at the limitations of PID control, The Active Disturbance Rejection Controller (ADRC) [16] was provided. Based on the traditional PID control, new nonlinear dynamic structures are proposed: extended state observer (ESO),tracking differentiator (TD) [17] and nonlinear state error feedback (NLSEF) [18]. This disturbance observer method has caused great research interest, and is regarded as the inheritance and improvement of traditional PID controllers, and many comparisons have been performed to prove ADRC’s superiority [19]. The ADRC aims to not only estimate the state of the system, but also estimate most of the unknown concentrated interference [20]. On the basis of the ADRC method, the total disturbance can be considered an additional state variable in the system, estimated by a linear state observer, and finally compensated in the feedback signal. MahMoud et al. applied the ADRC to the trajectory tracking of a two-link manipulator and the simulation showed that it had better anti-jamming capability than PID[21]. Radosław used the Lyapunov analysis to prove the stability of ADRC in manipulator control and proposed model low-order estimation compensation to further improve its stability [22]. Therefore, the goal of this research is to verify actual quality of ADRC approach in controlling a complex MIMO systems without a precise model. This study takes the advantage of the ADRC to control an underwater manipulator with two rotational joints. Uncertain part of the model, the coupling term between joints and unsure environmental disturbances are considered to be the total disturbance. Therefore, the extended state observer is built to estimate them, and then feedback control law is used to actively compensate them.

The remaining parts of this paper are organized as follows: Sect. 2 presents the system overview of the underwater manipulator. Section 3 recalls basic components behind the ADRC method and focuses on the extended state observer. ADRC decoupling design of underwater manipulator is presented in Sect. 4. Then, the simulation is divided into two cases: system with inertia matrix error and system with external disturbances, which is presented in Sect. 5. Experiments are performed in Sect. 6, while the proposed method’s effectiveness is proven. Finally, Sect. 7 concludes this paper.

2 System overview

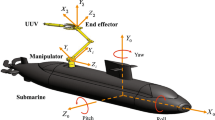
The system mainly includes a 2-DOF underwater manipulator. As shown in Fig. 1, it can be simplified as a dual-link system, whose two links can be represented by $M_1$ and $M_2$, respectively. The end of the manipulator is equipped with an end effector, which have the final effect of performing some certain underwater tasks. In this study, ADRC is used to control the manipulator to realize the tracking control of the desired trajectory in the joint space. The Cartesian coordinate system of underwater manipulator is shown in Fig. 1, which consists of the reference fixed coordinate system $O-x_0y_0z_0$, the joint coordinate system $O_i-x_iy_iz_i(i=1, 2)$ and the end-effector coordinate system $O_3-x_3y_3z_3$. Here O is the origin of the reference fixed coordinate system, and $O_1, O_2$ are the rotation centers of the robot arms $M_1, M_2$. Here $q_1$ is the angle between the $x_1$ axis and the $x_0$ axis, while $q_2$ is the angle between the $x_2$ axis and the $x_1$ axis, $l_i (i=1, 2)$ is the length of the arms. Assuming that each link of the manipulator is a homogeneous element, the center of the link and the center of gravity are coincident. And assuming that the underwater vehicle is very large relative to the underwater manipulator, so that the swing of the end effector can be ignored. Based on the Lagrangian energy equation, the dynamic model of underwater manipulator is given as follows:

$$\begin{aligned} \varvec{\tau }+{\textbf {w }}(t)=\varvec{M}\left( \varvec{q}\right) \ddot{\varvec{q}}+\varvec{C}\left( \varvec{q},\dot{\varvec{q}}\right) \dot{\varvec{q}}+\varvec{D}\left( \varvec{q},\dot{\varvec{q}}\right) \dot{\varvec{q}}+\varvec{G}\left( \varvec{q}\right) , \end{aligned}$$

(1)

where ${\textbf {M }} \left( \varvec{q}\right) \in {\Re }^{2\times 2}$ is the inertia matrix, $\varvec{C}\left( \varvec{q},\dot{\varvec{q}}\right) \in \Re ^{2\times 2}$ is the centrifugal and Coriolis vector, $\varvec{D}\left( \varvec{q},\dot{\varvec{q}}\right)$ is the hydrodynamic damping matrix formed by the terms due to fluid viscous resistance and additional mass force, and $\varvec{G}\left( \varvec{q}\right) \in \Re ^{2\times 1}$ is the gravity vector which considered the buoyant force, $\varvec{q},\ \dot{\varvec{q}}$ and $\ddot{\varvec{q}}$ are joint position, joint velocity and joint acceleration vectors, respectively. The $\varvec{\tau }\in \Re ^{2\times 1}$ is a joint input torque vector. Since this study focus on the practical performance of the underwater manipulator, $\varvec{w}(t)$ is adopted to represent the unknown disturbance including the unknown fluid disturbance and model uncertainty such as friction of the joints. and $\varvec{w}(t)$ is an unknown disturbance caused by complex fluid flow.

Fig. 1

A 2-DOF underwater manipulator model

3 ADRC method

3.1 Basic components

The active disturbance rejection controller (ADRC) depends on the role of the disturbance rejection, which is the main processor of the controller. It regards the unknown dynamics and external disturbances in the system as the total disturbance of the controlled object and takes it as the expanded state variable. The expanded state observer (ESO) estimates the total disturbance and takes the initiative compensation and cancellation. So the system with non-linearity and unknown disturbance is restored to a simple integral series type to realize active disturbance rejection. The principle block diagram of basic ADRC for a typical single-input single-output (SISO) second-order system is shown in Fig. 2. It is mainly composed of tracking differentiator (TD), extended state observer (ESO), nonlinear states error feedback control laws (NLSEF) and disturbance compensation. The TD realizes the preprocessing of the given tracking signal v to make the change process more reasonable, and obtains the transition process $v_1$ and its derivative signal $v_2$ that filter noise and retain the original signal characteristics. The idea of ESO estimates the state quantity and the total disturbance of the system in real time, and the NLSEF is a nonlinear PID algorithm to ensure that the output of the system can effectively track the given signal.

Fig. 2

The structure of a basic ADRC scheme for a second-order system

3.2 Extended state observer

The performance of ADRC mainly depends on the extended state observer (ESO). The ESO estimates the state of the object and the total perturbation acting on the object based on the output and input signals. It often aims at a second-order system with single-input and single-output, which is expressed by

$$\begin{aligned} \left\{ \begin{array}{l} \ddot{x}=f(x,\dot{x},w,t)+bu \\ y=x \end{array} \right. , \end{aligned}$$

(2)

where x is the system state variable, u is the system input, b is the input control matrix, y is the system output signal, w represents the overall external disturbances, and f is defined as the total disturbance of the system, which is a nonlinear function, which contains all internal disturbances, external disturbances and the system nonlinear terms. In order to realize the estimation and compensation of f, ADRC defines it as an extended state value $x_3$ of the system. Thereby, the above system can be formulated using the assumed phase state variables as

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x_1}=x_2 \\ \dot{x_2}=x_3+bu \\ \dot{x_3}=\dot{f} \end{array} \right. . \end{aligned}$$

(3)

Design a nonlinear extended state observer for the second-order system, one has

$$\begin{aligned} \left\{ \begin{array}{l} e=z_{1}-y \\ \dot{z}_{1}=z_{2}-\beta _{1} fal (e,\alpha _{1},\delta )\\ \dot{z}_{2}=z_{3}-\beta _{2} fal (e,\alpha _{2},\delta )+b_0u\\ \dot{z}_{3}=-\beta _{3} fal (e,\alpha _{3},\delta ) \end{array}\quad , \right. \end{aligned}$$

(4)

where $z_{1}$, $z_{2}$ and $z_{3}$ are the observed values of the state variables, where $z_3$ is the observed value of the system’s total disturbance $x_3$ (expanded state quantity), $\beta _i (i=1,2,3)$ is the observer parameter, $b_0$ is an estimation of parameter b, and $fal$ is a continuous power function with a linear segment near the origin, which is defined as

$$\begin{aligned} fal(e,\alpha ,\delta )=\left\{ \begin{array}{ll} \dfrac{e}{(\delta ^{1-\alpha })} &{} \quad \quad |e |\le \delta \vspace{1ex}\\ |e|^{\alpha } \textrm{sgn}\left( e\right) &{} \quad \quad |e|>\delta \end{array}\quad , \right. \end{aligned}$$

(5)

where $\delta$ is the length of the linear segment, $\alpha$ is an adjustable parameter to be designed. The specific values of $\alpha$ in Eq. 4 are $\alpha _1$, $\alpha _{2}$ and $\alpha _{3}$ which are usually set as 1, 0.5 and 0.25, respectively. Finally, ESO achieves a high accuracy for the estimation of the state variables of the system, i.e., Eq. 2, including the expanded state quantity of the total disturbance. In Eq. 4, the input control parameter is approximated as a constant $b_0$, then the ESO estimates the unknown part of the system input $(b-b_0)u$ as the part of total disturbance:

$$\begin{aligned} \left\{ \begin{array}{l} z_{1}\rightarrow x_1 \\ z_{2}\rightarrow x_2 \\ z_{3}\rightarrow x_{3}=f(x_1,x_2,w,t)+(b-b_0)u \end{array}. \right. \end{aligned}$$

(6)

4 ADRC decoupling design for 2-DOF underwater manipulator

In this case, the ADRC control method is used on a 2-DOF underwater manipulator, a second-order system which is described by Eq. 1. This controlled object is a Multi-Input-Multi-Output (MIMO) system, and one regards each joint of the manipulator as a Single-Input-Single-Output (SISO) system. There is a coupling between the two joints of the underwater manipulator, and the movement of one joint will affect the motion of another one, and at the same time appear strong non-linearity. This part can be regarded as internal disturbance of the system, which is part of the item f. For the 2-DOF underwater manipulator, the ADRC is designed for the two joints separately. The ADRC for the 2-DOF manipulator is decoupled in the following way shown in Fig. 3. The concepts used in the mentioned decoupling scheme are shown below as well.

Fig. 3

An ADRC decoupling scheme for the 2-DOF underwater manipulator

4.1 Tracking differentiator

For the real angle position of the i-th joint $qd_i$ and its given reference position, the transition process can be configured by TD through its tracking signal $v_{i1}$ and differential $v_{i2}$ . The linear TD is constructed as follows:

$$\begin{aligned} \left\{ \begin{array}{l} FH=-r(v_{i1}-qd_i)-2r \\ v_{i1}\,\,\, =v_{i1}+hv_{i2} \\ v_{i2}\,\,\, =v_{i2}+hFH \end{array} \right. \;, \end{aligned}$$

(7)

where $h=0.01\textrm{s}$ represents the step size of discretization, r respects the coefficient of tracking speed and FH is a linear function which is self-defined.

4.2 Extended state observer

The 2-DOF underwater manipulator’s dynamic model, i.e., Eq. 1, can be converted to the following form:

$$\begin{aligned} \begin{aligned} \ddot{\varvec{q}}=\left[ \begin{array}{cc} \dot{q}_1&\dot{q}_2 \end{array} \right] ^T&=\underbrace{\varvec{M}^{-1}\left( \varvec{w}(t)-\varvec{C}\dot{\varvec{q}}-\varvec{D}\dot{\varvec{q}}-\varvec{G}\right) }_{f(\varvec{q},\, \dot{\varvec{q}},\, \varvec{w}(t),\, t)} \\ {}&+\underbrace{\varvec{M}^{-1}}_{b}\left[ \begin{array}{cc} \tau _1&\tau _2 \end{array} \right] ^{T}, \end{aligned} \end{aligned}$$

(8)

where $\varvec{w}(t)$ is the disturbance of the flow, $f(\varvec{q},\dot{\varvec{q}},\varvec{w}(t),t)$ is the unknown part of the system, which is time-varying and include the system uncertainty, internal disturbances caused by the coupling between joints, and external fluid flow disturbance as well. If each joint of the underwater manipulator is treated as an SISO second-order independent system, $\varvec{M}^{-1}\left( \varvec{w}(t)-\varvec{C}\dot{\varvec{q}}-\varvec{D}\dot{\varvec{q}}-\varvec{G}\right)$ is the system dynamics coupling term while ${\varvec{M}^{-1}}\left[ \begin{array}{cc} \tau _1&\tau _2 \end{array} \right] ^{T}$ is the static coupling term. Defining the virtual control input $\left[ \begin{array}{cc} U_1&U_2 \end{array}\right] =\varvec{M}^{-1}\left[ \begin{array}{cc} \tau _1&\tau _2 \end{array} \right] ^T$ using inertia matrix $\textbf{M}$, the static coupling part can be decoupled, and the state space of the i-th $(i=1, 2)$ joint can be obtained

$$\begin{aligned} \left\{ \begin{array}{l} \ddot{q}_i=f(\varvec{q},\dot{\varvec{q}},w_i(t),t)+U_i \\ y_i=q_i \end{array} \right. . \end{aligned}$$

(9)

For the control object in this case, state $x_{i1}$ corresponds to the joint angle value $q_i$ of the i-th joint of the manipulator, and state $x_{i2}$ corresponds to the angle velocity value $\dot{q}_i$. The $U_i$ above is the virtual torque acting on the i-th joint, $w_i(t)$ is the disturbance from the external environment, the nonlinear function f represents the total disturbance acting on the underwater manipulator which contains the internal and external disturbance and nonlinear terms. Aiming to estimate and eliminate the influence of the total disturbance f, one defined f as a state $x_{i3}$ of ADRC system which is shown as follows:

$$\begin{aligned} x_{i3}=f(\varvec{q},\dot{\varvec{q}},w_i(t),t)\ . \end{aligned}$$

(10)

Then, the ESO is designed for each joint of the manipulator independently are as follows:

$$\begin{aligned} \left\{ \begin{array}{l} e_i=z_{i1}-q_i \\ \dot{z}_{i1}=z_{i2}-\beta _{i1} fal (e,\alpha _{i1},\delta _i)\\ \dot{z}_{i2}=z_{i3}-\beta _{i2} fal (e,\alpha _{i2},\delta _i)+U_i\\ \dot{z}_{i3}=-\beta _{i3} fal (e,\alpha _{i3},\delta _i) \end{array}\quad , \right. \end{aligned}$$

(11)

where $z_{i1}$, $z_{i2}$ and $z_{i3}$ are the estimation of i-th joint states. Using ESO to estimate the state variables of the system, including the total disturbance Eq. 6:

$$\begin{aligned} \left\{ \begin{array}{l} z_{i1}\rightarrow q_i \\ z_{i2}\rightarrow \dot{q}_i \\ z_{i3}\rightarrow x_{i3}=f(\varvec{q},\dot{\varvec{q}},w_i(t),t) \end{array}. \right. \end{aligned}$$

(12)

The estimation value of joint state $z_{i1}$, $z_{i2}$ is inputted into the state feedback control law, while $z_{i3}$ is used to compensate the control torque which are shown as follows:

$$\begin{aligned} U_i=u_i-z_{i3}\;. \end{aligned}$$

(13)

Combining Eqs.  9,  11 and  13, each joint of the manipulator is compensated by ESO and taken as a linear integral series system, both with constant input amplification factor joints of value 1. Afterwards, the virtual control torque $\varvec{U}$ which is defined by Eq. 9 can be converted to driving torque $\varvec{\tau }$ of the joints by the static decoupling law $\begin{bmatrix} \tau _1&\tau _2 \end{bmatrix}^T=\varvec{M}\begin{bmatrix} U_1&U_2 \end{bmatrix}^T$.

4.3 Nonlinear state error feedback control law

The NLSEF is a nonlinear control combination, instead of the linear combination of the traditional PID controller, which can obtain a more effective error feedback control rate. It integrates the nonlinear function $fhan (e_1,ce_2,r_1,h_1)$, which sometimes performs much better than the linear control [18]. For the i-th junction, the NLSEF is constructed by the following equations:

$$\begin{aligned} \left\{ \begin{array}{l} e_{i1}=v_{i1}-z_{i1} \\ e_{i2}=v_{i2}-z_{i2} \\ u_i=- fhan (e_{i1},ce_{i2},r_1,h_1) \end{array} \right. , \end{aligned}$$

(14)

$$\begin{aligned} \left\{ \begin{array}{l} d=r_1{h_1}^2, a_0=h_1ce_2, y=e_1+a_0\vspace{1ex}, a_1=\sqrt{d\left( d+8|y|\right) }\vspace{1ex} \\ a_2=a_0+\dfrac{\left( a_1-d\right) }{2}\textrm{sgn}\left( y\right) \vspace{1ex} \\ a=(a_0+y-a_2)\dfrac{\textrm{sgn}(y+d)-\textrm{sgn}(y-d)}{2}+a_2\vspace{1ex} \\ fhan =\\ -r_1\left[ \dfrac{a}{d}-\textrm{sgn}(a)\right] \dfrac{\textrm{sgn}(a+d)-\textrm{sgn}(a-d)}{2}-r_0\textrm{sgn}(a) \end{array} \right. . \end{aligned}$$

(15)

Here $e_{i1}$ is the joint angle position error, $e_{i2}$ is the joint angle velocity error, c is the damping coefficient, $r_1$ is the a convergence coefficient, $h_1$ is the factor of precision and $u_{i}$ is the output of the control law. And $fhan$ is an optimal control synthesis function derived from discrete optimization theory, which is defined in [18]. After the compensation of the total disturbance by ESO and the decoupling by static decoupling method, and applying the obtained control torque input to the joint subsystem, then it is concerted to

$$\begin{aligned} \begin{bmatrix} \tau _1 \\ \tau _2 \end{bmatrix} =\varvec{M}\begin{bmatrix} - fhan (e_{11},ce_{12},r_1,h_1)-z_{13} \\ - fhan (e_{21},ce_{22},r_1,h_1)-z_{23} \end{bmatrix}. \end{aligned}$$

(16)

5 Simulations

The simulation object 2-DOF underwater manipulator is shown in Fig. 1. The physical parameters, D-H parameters of the underwater manipulator are listed in Tables 1 and 2. The ADRC parameters is shown in Table 3. The aim of simulations is to verify the performance of ADRC method without the precise modeling, and simulations has two part. For the first case, simulation tests the influence level of model uncertainty on ADRC control quality. For the second case, simulation shows tracking performance of the underwater manipulator with proposed controller. The three control methods track the same desired trajectory in two cases, which the trajectory is designed as

$$\begin{aligned} \left\{ \begin{array}{l} qd_1=\dfrac{\pi }{4}+\dfrac{\pi }{4}\sin \left( 0.5t+\dfrac{\pi }{4}\right) \vspace{1ex} \\ qd_2=\dfrac{\pi }{6}\sin \left( 0.8t+\dfrac{\pi }{4}\right) \end{array}. \right. \end{aligned}$$

(17)

Table 1 Basic physical parameters

Table 2 D-H parameters

Table 3 ADRC parameters

5.1 System with inertia matrix error

In the first part, ADRC is applied for the underwater manipulator in the view of nonlinear system. The inertia matrix $\varvec{M}$ is very important to transform its static decoupling into several joint subsystems. Considering the control quality with the presence of model uncertainty. In the simulation, one adds a variation range to the inertia matrix $\varvec{M}$ in Eq. 1 as the model error, but does not impose additional external disturbances.

In the upcoming experiments, we set different inertial matrix errors in the trajectory tracking task. It is desired that the actual angular position tracking error of each joint are under different inertial matrix errors. A parameter $\rho$ is used to characterize the error between the inertial matrix $\varvec{M}_{sdl}$ during static decoupling ($\begin{bmatrix} \tau _1&\tau _2 \end{bmatrix}^T=\varvec{M}_{sdl}\begin{bmatrix} U_1&U_2 \end{bmatrix}^T$) and real inertial matrix $\varvec{M}_{rea}$ of the underwater manipulator, which is defined as

$$\begin{aligned} \varvec{M}_{sdl} = \rho \varvec{M}_{rea}. \end{aligned}$$

(18)

In the simulation, it sets $\rho =1, 0.7, \textrm{and} 1.3$, respectively, to verify the basic tracking control quality of the ADRC. The comparisons of the trajectory tracking error for the system with different inertia matrix errors are presented in Fig. 4. No significant different can be seen here, for three different values of $\rho$. The ADRC technique can realize good quality of angle tracking and angular velocity tracking. At the first 3 s of the simulation, there is a transition process that the tracking error is rapidly reduced to 0. After that, the tracking error has been kept at a small value near 0. Therefore, the ADRC can guarantee that the angle position error is at the range of $\pm 0.01\textrm{rad}$, and the angular velocity error is at the range of $\pm 0.02\mathrm {rad/s}$. However, In the case of $\rho =0$ (that means $\varvec{M}_{sdl}$=$\varvec{M}_{rea}$), the ADRC seems to be more efficient, the early transition process is shorter and the overshoot is smaller. In Fig. 4d, when $\rho =1, 0.7$ or $\rho =1.3$, respectively, a small oscillation process appeared at the 1.3 second, but it quickly adjusted and disappeared.

Fig. 4

Trajectory tracking error e for the system with different inertia matrix errors

5.2 System with external disturbances

In the second part, this study uses the original underwater manipulator as a simulation prototype ($\rho =0$). The parameters of the mathematical model are constant and remain unchanged but subject to external disturbances. Therefore, to verify control quality of ADRC, a PD controller and a (continuous sliding mode controller) CSMC were chosen to compared with ADRC with sudden external disturbances while eliminating the influence of changes in internal model parameters. Here the PD controller is chosen instead of a PID controller is because that the PD controller, with its faster response to external influences, is better suited for application in practical underwater environments.

Fig. 5

Joint angle signal tracking results for the system with external disturbances

Based on the original underwater manipulator as a simulation prototype, the entire simulation process also spends 20 s. Since the expected trajectory is often designed to be relatively smooth in practical tasks, so a sine wave trajectory is adopted as the tracking trajectory. The applied external disturbance value is 0 until $10\textrm{s}$. At the $10\textrm{s}$, external disturbances are added to the underwater manipulator, which is defined as follows:

$$\begin{aligned} \left\{ \begin{array}{l} w_1=5+15\sin \left( 0.5t-\dfrac{\pi }{4}\right) \vspace{1ex} \\ w_2=5+2\sin \left( 0.5t+\dfrac{\pi }{6}\right) \end{array}. \right. \end{aligned}$$

(19)

Figure 5 depicts the results of the signal tracking simulator. It shows that under the condition of without external disturbance in the first 10 s, and with external disturbance in the second 10 s. Compared with PD controller and CSMC, the proposed ADRC has better performance under different conditions. Fig. 6 also shows the results of the joint input torque of three tracking controllers. From the results of the chattering problem, we can know the proposed ADRC obviously has good dynamic performance.

Considering the various types of disturbances that may occur in underwater environments, including disturbances from the underwater environment and disturbances caused by the robot itself, we added noise to the applied disturbance signals (noise power of 0.5 on link 1 and noise power of 0.1 on link 2), which is shown in Fig.  7. It can be seen that ADRC can control the underwater manipulator to track the desired trajectory with minimal errors when facing with external disturbance with high uncertainty. This demonstrates the robustness of ADRC against external disturbances.

In order to simulate the performance of the proposed method in underwater tasks, a target point is predefined in the task space of the underwater manipulator to plan a trajectory using RRT for end actuator. After converting the end actuator trajectory into joint trajectory, the manipulator is tested in simulation, and the tracking performance and the input of ADRC are shown in Fig. 8a, b. It can be seen that under the control of ADRC, the underwater manipulator tracks the reference trajectory with small errors.

Fig. 6

Joint input torque results of ADRC and CSMC

Fig. 7

Tracking error of two links with disturbances with noise

Fig. 8

Tracking trajectory and control input using ADRC

6 Experiments

The proposed method of this study is applied to the actual underwater manipulator in the pool.

6.1 Experimental configuration

The trajectory tracking experimental platform consists of a round experimental pool, a Speedgoat real-time target simulator, a robotic mounting bracket, and 2-DOF underwater manipulator is shown as Fig. 9. Considering the current experimental conditions, the artificial wave is used to simulate the water flow disturbance during the operation of the actual underwater manipulator, which is shown in Fig. 10. And the influence caused by waves on the manipulator can be approximated by a sine wave [23]. The effective wave height of the artificial wave is proposed to be 0.1 m. The peak frequency does not exceed 0.5 Hz. The underwater manipulator is fixed to a aluminum alloy shelf and the center of the first joint of the underwater manipulator is flush with the water surface. The main function of Speedgoat real-time target simulator is to realize the real-time mapping conversion from the MATLAB/Simulink simulation program on the host computer to the control signal of the electronic control system of the underwater manipulator. Speedgoat real-time target machine supports a variety of protocol interfaces, including CAN, RS232, RS422, RS485, Ethernet, etc., and can be further installed with expansion boards to achieve more features.

Fig. 9

Underwater manipulator trajectory tracking experimental platform

Fig. 10

Experimental round pool. The diameter of the round pool is 5 m and the depth is 1.5 m

6.2 Experimental architecture

The Speedgoat real-time target simulator is the bridge between the PC host computer and manipulator, which specifically completes the issuance of joint motor control commands and the return of the actual motor angle sensor data. As shown in Fig. 11, the control architecture of the underwater dual-arm system experimental platform designed in this study.

The MATLAB/Simulink Real-Time simulation program is executed on a PC host computer with the core of AMD R7 5800H 4.4 GHz and the RAM of 32G, which performs fixed-step discretization processing, and realizes the connection with the Speedgoat real-time target computer through Ethernet. Then, the Speedgoat real-time target simulator translates the MATLAB program into an executable file and outputs control, which is received by the manipulator through the RS232 bus(9600 bps). To precisely response to the input torque of each joint, FHA-14C-100 and FHA-11C-100 motors with high level of torque performance are adopted for the manipulator. Therefore, the underwater manipulator links all joints into the same CAN control network. In the entire control architecture, the Speedgoat real-time target simulator and the PC host computer maintain real-time synchronization, which is determined by the underlying hardware. In the meanwhile, the control instructions of each motor of the manipulator system is also in accordance with the synchronization principle programming. Therefore, the step size of the upper and lower layers of the entire control architecture is consistent.

Fig. 11

Experimental platform control architecture diagram

6.3 Parameters setting

The whole experiment lasted 43 s, and the control frequency of the controller is 0.05 s. This control period is chosen for the aim of demonstrating the performance of the controller that is not rely on fast control period. This enables testing whether the proposed method can be applied to general underwater manipulators. In order to comparing and verifying the greater performance of the ADRC decoupling controller for the dual-joint underwater manipulator proposed, the PD feedback linearization controller and CSMC are also set, respectively. The actual ADRC parameter are also show in Table 3.

6.4 Result analysis

In the entire trajectory tracking experiment, the Speedgoat target simulator recorded each joint angular position of the underwater manipulator in real time. After the noise reduction process, the actual angle of each joint is shown in Fig. 12. At the same time, Table 4 shows the tracking error with difference controllers.

According to the analysis of Fig. 12a–f, compared with the feedback linearized PD controller and CSMC, the proposed method in this study has the best control performance. In the first 24 s, the adjustment time of the ADRC is shorter, and the tracking error is rapidly reduced. While the feedback linearized PD control and CSMC control both have a large overshoot. For the following 18 s, the feedback linearized PD control has a large oscillation especially in Fig. 12e, which is mainly caused by the overshoot of PD controller. Meanwhile, the CSMC control has a long adjustment time and has a large motion steady-state error as well as chattering phenomenon, especially in Fig. 12c, which means that the final manipulator end effector does not move precisely. Conversely, ADRC can make the end of the manipulator move into position with a small position error. This is because the feedback linearized PD is too sensitive to model parameter errors, and cannot compensate for unknown items such as hydrodynamic disturbances. The traditional PD control is unfit to the nonlinear system, making unsatisfactory control effect. Although CSMC is sensitive to disturbances and model errors, it is easy to generate high-frequency chattering on the sliding mode surface, which makes the instantaneous overshoot too large. The extended state observer in the ADRC method can compensate the internal disturbance caused by the model error and the system external disturbance caused by the external hydrodynamic term. Thereby, the better control accuracy and robustness against disturbances are realized by ADRC method.

Fig. 12

Joint angle curves of trajectory tracking motion process of underwater manipulator under different controllers

Table 4 Root mean square error of trajectory tracking of each joint based on different controllers

Comparing the root mean square error of these three controllers in Table 4, the proposed controller has the smallest comprehensive tracking control error during the entire cooperative grasping motion process of the underwater manipulator system.

7 Conclusion

The robustness and disturbance rejection of an ADRC method to the uncertainties of an underwater manipulator has been studied. The ADRC concept was implemented and simulated on the two rotational joints of the concerned manipulator. The ADRC does not require accurate data of the manipulator but require inertial matrix $\varvec{M}$ to decouple the static coupling part. For the purpose of the experiments, the control quality of ADRC in the presence of inertial matrix errors was first adjusted and verified. Then, in the case of external disturbances on the manipulator, ADRC compares the quality of trajectory tracking control with traditional PD control and CSMC. Finally, based on the underwater manipulator hardware platform, the trajectory tracking control experiment was carried out.

The ADRC defines the internal disturbance and external fluid disturbance as the total disturbance, which is estimated and compensated by ESO. From the simulation results, ADRC has good robustness of control parameter. In the presence of inertial matrix errors, it can maintain better tracking quality although it has a certain impact on the transition process in the early stage of tracking. In the comprehensive comparisons with traditional PD control and CSMC in both simulation and experiment, the results illustrate the effectiveness of the proposed design and it is demonstrated that ADRC’s control effect outperforms PD and CSMC in accuracy, dynamic characteristics and robustness.