Active Disturbance Rejection Control of Underwater Manipulator

Abstract

In this study, a method of active disturbance rejection controller (ADRC) is presented for 2-DOF underwater manipulator. The ADRC basically does not rely on the accurate mathematical model of the object and can decouple the model. This method can eliminate the influence of model errors, time-varying parameters and external interference on the control effect. Firstly, the manipulators is divided into two subsystems. For each joint subsystem, the hydrodynamic force, coupling term between joints and unknown environment disturbances are considered as the total disturbance. Subsequently, an extended state observer (ESO) is designed to estimate and compensate the total disturbance. Moreover, in order to improve the disturbance observation effect of the extended state observer, the inertia matrix of the manipulator system is used to decouple the static part. Finally, the effectiveness of ADRC is verified by simulation and it is demonstrated that ADRC’s control effect outperforms PD and CSMC in either accuracy, dynamic characteristics or robustness.

1 Introduction

Underwater manipulators are usually working in a complex hydraulic environment so it is subject to additional fluid viscous resistance, additional mass forces and some unknown water flow disturbances [1], which make the model of underwater manipulator more complicated than general manipulator. The nonlinearity and uncertainty of the system, as well as the coupling of multiple external disturbances in the underwater environment have become major challenges under conventional control strategies.

The control methods of the underwater manipulator system are not limited to PID control, adaptive control, neural network control and sliding mode control [2]. In [3], a controller including model parameter estimation and multi-layer closed loop PID is designed to control a multi-DOF underwater manipulator, but it does not compensate for nonlinear disturbances. Tomei et al. in [4] proposed an adaptive robot control algorithm combining a PD controller with a dynamic compensation model. This algorithm improves the accuracy of nonlinear control, but a more accurate dynamic model of the manipulator is required. Neural network control [5] does not rely on the precise mathematical model, however, its sample data for training is a key problem. Sliding mode control is widely used for uncertain models and anti-interference. Bin Xu et al. in [6] designed an improved sliding mode controller based on fuzzy logic, but the output torque of the controller still had chattering problem.

The Active Disturbance Rejection Controller (ADRC) [7] was proposed in response to the limitations of PID control. On the basis of traditional PID control, new nonlinear dynamic structures are proposed: tracking differentiator (TD), extended state observer (ESO) [8] and nonlinear state error feedback (NLSEF) [9]. MahMoud et al. in [10] applied the active disturbance rejection controller to the trajectory tracking of a two-link manipulator and the simulation showed that it had better anti-interference performance than PID. Radoslaw in [11] used the Lyapunov analysis to prove the stability of ADRC in manipulator control and proposed model low-order estimation compensation to further improve its stability.

This study takes the advantage of the ADRC to control a 2-DOF underwater manipulator. The coupling term between joints and unknown environment disturbances are considered as the total disturbance. The extended state observer is built to estimate them and then the feedback control law is used for active compensation. Finally, it is compared with a PD controller and a continuous sliding mode controller.

The rest of the study is organized as follows: Sect. 2 presents the system overview. Section 3 recalls basic components behind the ADRC method. ADRC decoupling design of underwater manipulator is presented in Sect. 3. Simulation and results are presented in Sect. 4 and finally, Sect. 5 concludes the study.

2 System Overview of Underwater Manipulator

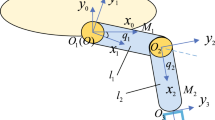
The system consists of a 2-DOF maniplator shown in Fig. 1. It can be simplified to a two-link system with $M_1, M_2$. The end of manipulator is equipped with an actuator that can perform some underwater tasks. In this study, ADRC is used to control the manipulator in order to realize the tracking control of the desired trajectory in the joint space.

The Cartesian coordinate system of underwater manipulator is shown in Fig. 1, which consists of the reference fixed coordinate system $O\textendash x_0y_0z_0$, the joint coordinate system $O_i\textendash x_iy_iz_i(i=1, 2)$ and the end actuator coordinate system $O_3\textendash x_3y_3z_3$. Here O is the origin of the reference fixed coordinate system. Assuming that each link of the manipulator is a homogeneous element, the center of the link and the center of gravity are coincident.

Based on the second type of Lagrangian energy equation, the dynamic model of underwater manipulator is given as follow,

$$\begin{aligned} \boldsymbol{\tau }+\mathbf {w}(t)=\mathbf {M}\left( \mathbf {q}\right) \ddot{\mathbf {q}}+\mathbf {C}\left( \mathbf {q},\dot{\mathbf {q}}\right) \dot{\mathbf {q}}+\mathbf {D}\left( \mathbf {q},\dot{\mathbf {q}}\right) \dot{\mathbf {q}}+\mathbf {G}\left( \mathbf {q}\right) . \end{aligned}$$

(1)

where $\mathbf {M}\left( \mathbf {q}\right) \in \mathbb {\mathfrak {R}}^{2\times 2}$ is the inertia matrix, $\mathbf {C}\left( \mathbf {q},\dot{\mathbf {q}}\right) \in \mathfrak {R}^{2\times 2}$ is the centrifugal and Coriolis vector, $\mathbf {D}\left( \mathbf {q},\dot{\mathbf {q}}\right)$ is the hydrodynamic damping matrix formed by the terms due to fluid viscous resistance and additional mass force, and $\mathbf {G}\left( \mathbf {q}\right) \in \mathfrak {R}^{2\times 1}$ is the gravity vector. $\mathbf {q},\ \dot{\mathbf {q}}$ and $\ddot{\mathbf {q}}$ are joint position, joint velocity and joint acceleration vectors, respectively. Here $\boldsymbol{\tau }\in \mathfrak {R}^{2\times 1}$ is a joint input torque vector and $\mathbf {w}(t)$ is an unknown disturbance caused by complex fluid flow.

Fig. 1.

A 2-DOF underwater maniplator model

3 ADRC Decoupling Design for Underwater Manipulator

The controlled object in this case is a 2-DOF underwater manipulator, which is a Multi Input Multi Output (MIMO) second-order system describedly Eq. (1). Each joint can be independently regarded as a Single Input Single Output (SISO) second-order system. The coupling relationship between the joints can be regarded as part of the total disturbance. Firstly, dynamic model (1) can be described as

$$\begin{aligned} \ddot{\mathbf {q}}=\left[ \begin{array}{cc} q_1&q_2 \end{array} \right] ^T =\underbrace{\mathbf {M}^{-1}\left( \mathbf {w}(t)-\mathbf {C}\dot{\mathbf {q}}-\mathbf {D}\dot{\mathbf {q}}-\mathbf {G}\right) }_{f(\mathbf {q},\dot{\mathbf {q}},\mathbf {w}(t),t)} +\underbrace{\mathbf {M}^{-1}}_{b}\left[ \begin{array}{cc} \tau _1&\tau _2 \end{array} \right] ^{T}, \end{aligned}$$

(2)

where $\mathbf {w}(t)$ is the external fluid flow disturbance, $f(\mathbf {q},\dot{\mathbf {q}},\mathbf {w}(t),t)$ is the unknown time-varying part of the system, including the system uncertainty, internal disturbances caused by the coupling between joints and external fluid flow disturbance. If each joint of the underwater manipulator is treated as an SISO second-order independent system, $\mathbf {M}^{-1}\left( \mathbf {w}(t)-\mathbf {C}\dot{\mathbf {q}}-\mathbf {D}\dot{\mathbf {q}}-\mathbf {G}\right)$ can be called dynamic coupling part of system while ${\mathbf {M}^{-1}}\left[ \begin{array}{cc} \tau _1&\tau _2 \end{array} \right] ^{T}$ can be the static coupling part of the manipulator. Using inertia matrix $\mathbf {M}$ to define the virtual control input $\left[ \begin{array}{cc} U_1&U_2 \end{array}\right] =\mathbf {M}^{-1}\left[ \begin{array}{cc} \tau _1&\tau _2 \end{array} \right] ^T$, the static coupling part can be decoupled, and the state space of the i-th $(i=1, 2)$ joint can be obtained

$$\begin{aligned} \left\{ \begin{array}{l} \ddot{q}_i=f(\mathbf {q},\dot{\mathbf {q}},w_i(t),t)+U_i \\ y_i=q_i \end{array} \right. . \end{aligned}$$

(3)

For the i-th joint, state $x_1$ is the joint angle value $q_i$ and state $x_2$ is the joint angle velocity value $\dot{q}_i$. Here $U_i$ is i-th virtual driving torque of joint i. $w_i(t)$ is the external disturbance, f is defined as the total disturbance of the system, which is a nonlinear function. It contains all internal disturbance, external disturbance and nonlinear terms. In order to estimate and compensate the f term, f is defined as an extended state $x_3$ of the system in ADRC, as

$$\begin{aligned} x_3=f(\mathbf {q},\dot{\mathbf {q}},w_i(t),t). \end{aligned}$$

(4)

Aiming at the dual-joint underwater manipulator, this study designs ADRC separately for the two joints. An ADRC decoupling scheme for the 2-DOF underwater manipulator takes the form as shown in Fig. 2, and several used concepts of ADRC decoupling scheme are shown as follows.

Fig. 2.

An ADRC decoupling scheme for the 2-DOF underwater manipulator

1) Tracking Differentiator: For a given reference i-th joint angle position signal $qd_i$, the TD generates a transient trajectory $v_{i1}$ and extracts the derivative $v_{i2}$. The linear TD is discretized which is constructed as follows,

$$\begin{aligned} \left\{ \begin{array}{l} FH=-r(v_{i1}-qd_i)-2r \\ v_{i1}=v_{i1}+hv_{i2} \\ v_{i2}=v_{i2}+hFH \end{array} \right. \;, \end{aligned}$$

(5)

where $h=0.01\mathrm {s}$ is the discretization step size, r is the tracking speed factor and FH is a self-defined linear function. 2) Extended State Observer: The ESO is used to estimate system states and the total disturbances based on the output and input signals of the object. The state space expression of each joint is shown in Eq. (3). ESO is designed independently for each joint as

$$\begin{aligned} \left\{ \begin{array}{l} e_i=z_{i1}-q_i \\ \dot{z}_{i1}=z_{i2}-\beta _{i1} fal (e,\alpha _{i1},\delta _i)\\ \dot{z}_{i2}=z_{i3}-\beta _{i2} fal (e,\alpha _{i2},\delta _i)+U_i\\ \dot{z}_{i3}=-\beta _{i3} fal (e,\alpha _{i3},\delta _i) \end{array}\quad , \right. \end{aligned}$$

(6)

where $z_{i1}$, $z_{i2}$ and $z_{i3}$ are estimated i-th joint states correspond to $q_i$, $\dot{q}_i$ and total disturbance $x_{i3}$, respectively. Here $\beta _i (i=1,2,3)$ is the observer gain coefficient and $fal$ is a continuous power function with a linear segment near the origin, which is defined as

$$\begin{aligned} fal(e,\alpha ,\delta )=\left\{ \begin{array}{ll} \dfrac{e}{(\delta ^{1-\alpha })} &{} \quad \quad \left| e\right| \le \delta \\ \left| e\right| ^{\alpha } \mathrm {sgn}\left( e\right) &{} \quad \quad \left| e\right| >\delta \end{array}\quad , \right. \end{aligned}$$

(7)

where $\delta$ is the length of the linear segment, $\alpha _i$ is an adjustable parameter and $\alpha _1$, $\alpha _{2}$ and $\alpha _{3}$ are usually set as 1, 0.5 and 0.25, respectively. ESO finally realizes the estimation of the state variables (including the total disturbance) of the system (6) . The estimation value of joint state $z_{i1}$, $z_{i2}$ is input into the state feedback control law as feedback value, while the estimated value of the total disturbance $z_{i3}$ is used to compensate the control torque as following,

$$\begin{aligned} U_i=u_i-z_{i3}\;. \end{aligned}$$

(8)

Combining Eqs. (3), (6) and (8), each joint system is compensated by ESO into a linear integral series system and the input amplification coefficients of the two joints are both 1. After that, The virtual control torque $\mathbf {U}$ defined in Eq. (3) can be restored to joint driving torque $\boldsymbol{\tau }$ of the underwater manipulator by the static decoupling law $\begin{bmatrix} \tau _1&\tau _2 \end{bmatrix}^T=\mathbf {M}\begin{bmatrix} U_1&U_2 \end{bmatrix}^T$.

3) Nonlinear State Error Feedback Control Law: The NLSEF introduces a way to integrate the nonlinear function $fhan (e_1,ce_2,r_1,h_1)$ with feedback control, which sometimes achieves dramatically better performance than linear control [9]. For i-th joint, the constructure of NLSEF is given by

$$\begin{aligned} \left\{ \begin{array}{l} e_{i1}=v_{i1}-z_{i1} \\ e_{i2}=v_{i2}-z_{i2} \\ u_i=- fhan (e_{i1},ce_{i2},r_1,h_1) \end{array} \right. , \end{aligned}$$

(9)

where $e_{i1}$ is the joint angle position error, $e_{i2}$ is the joint angle velocity error, c is the damping coefficient, $r_1$ is the control value gain, $h_1$ is the precision factor and $u_{i}$ is the control law output. The $fhan$ is fastest control synthesis function defined in [9].

After the compensation of ESO for the total disturbance and the decoupling of the static decoupling law (SDL), the final control torque input applied to the joint subsystem then becomes

$$\begin{aligned} \begin{bmatrix} \tau _1 \\ \tau _2 \end{bmatrix} =\mathbf {M}\begin{bmatrix} - fhan (e_{11},ce_{12},r_1,h_1)-z_{13} \\ - fhan (e_{21},ce_{22},r_1,h_1)-z_{23} \end{bmatrix}. \end{aligned}$$

(10)

4 Simulation and Results

In order to verify the performance of the proposed method, simulation has been established in MATLAB. The simulation object is a 2-DOFs underwater manipulator system as shown in Fig. 1. The basic physical parameters are shown in Table 1, the DH parameters are shown in Table 2 and the parameters of ADRC have been adjusted, which is shown in Table 3.

Table 1. Basic physical parameters

Table 2. D-H parameters

Table 3. ADRC parameters

According to the parameters of ADRC designed previously as in Table 3 and the basic physical parameters of the underwater manipulator as in Table 1 and in Table 2, a simulation model is established to simulate the joint trajectory tracking control compared with traditional PD and CSMC. The expected tracking trajectory is defined as

$$\begin{aligned} \left\{ \begin{array}{l} qd_1=\dfrac{\pi }{4}+\dfrac{\pi }{4}\sin \left( 0.5t+\dfrac{\pi }{4}\right) \\ qd_2=\dfrac{\pi }{6}\sin \left( 0.8t+\dfrac{\pi }{4}\right) \end{array}. \right. \end{aligned}$$

(11)

The entire simulation process spends 20 s. In order to verify the disturbance adaptability of ADRC, at the $10\,\mathrm {s}$, disturbance applied to two joints is defined as follow,

$$\begin{aligned} \left\{ \begin{array}{l} w_1=5+15\sin \left( 0.5t-\dfrac{\pi }{4}\right) \\ w_2=5+2\sin \left( 0.5t+\dfrac{\pi }{6}\right) \end{array}. \right. \end{aligned}$$

(12)

The Fig. 3 depicts the results of signal tracking simulator. The result shows that under the condition of no external disturbance in the first 10 s, both the ADRC and CSMC can achieve better tracking results, while the traditional PD controller has a certain steady-state error. When the external disturbance shown in Eq. (12) is added at 10 s, the tracking errors of the three controllers all have a certain degree of sudden change. By contrast, with the efficacy of ESO designed in ADRC, the unknown disturbance is estimated and actively compensated, so it can eliminate the sudden error faster, showing better disturbance immunity than CSMC and PD controller. At the same time, as shown in Fig. 4, the joint input torque of the decoupled ADRC controller and the CSMC controller is compared. It can be found that the joint decoupling ADRC controller in this study hardly has chattering phenomenon, and the system has good dynamic performance.

Fig. 3.

Joint angle signal tracking results and disturbance rejection

Fig. 4.

Joint input torque results of ADRC Control and CSMC Control

5 Conclusion

This study presents a decoupling ADRC technique for the 2-DOF underwater manipulator system, which is subject to complex model, nonlinearity and external disturbance. The ADRC does not require an accurate data of the manipulator and defines the internal disturbance and external fluid disturbance as the total disturbance, which is estimated and compensated by ESO. In the comprehensive comparisons with traditional PD control and continuous sliding mode control (CSMC), The results illustrate the effectiveness of the proposed design and it is demonstrated that ADRC’s control effect outperforms PD and CSMC in either accuracy, dynamic characteristics or robustness.