Adaptive non-singular fixed-time sliding mode control of moving-base underwater flexible manipulators

Abstract

This paper presents a composite controller for trajectory tracking of moving-base underwater flexible manipulators (UFM). Firstly, a dynamics model of the moving-base UFM is established, and the model is decomposed into a slow-varying subsystem and a fast-varying subsystem by using the singular perturbation method. Then, an adaptive non-singular fixed-time sliding mode controller based on a high-order sliding mode observer is proposed for the slow-varying subsystem. In this controller, the high-order sliding mode (HOSM) observers are used to estimate and compensate for lumped disturbances, and adaptive super-twisting algorithm is used to reduce sliding mode chattering, which overcomes the disadvantage that the traditional adaptive method is prone to overestimation. To further suppress the system chattering, a HOSM observer is used to obtain the flexible mode derivatives for the fast-varying subsystem to achieve the suppression of vibration modes. The main advantages of this controller are its non-singularity, fast finite-time convergence and good vibration suppression. Extensive simulation results have validated the effectiveness of the proposed control method.

1 Introduction

Underwater docking and recovery is a frontier research in ocean engineering [1]. The recovery and deployment of autonomous underwater vehicles (AUV) by large-scale underwater manipulators is an important approach for collaborative marine operations [2]. This collaborative approach can expand the functions of large submersibles, which has broad application prospects. The large submarine equipped with a manipulator to recover the AUVs is shown in Fig. 1. Due to the technical requirements of large-scale operation and small-space storage of underwater manipulators, the manipulators are usually made very slender and it is easier to produce flexible deformation and vibration under external hydrodynamic disturbance. If the flexible deformation is not taken into account, it may cause collisions between manipulators and AUVs, which will eventually lead to the failure of recovery. Therefore, it is of great significance to study the modeling and control of the underwater flexible manipulators.

Fig. 1

The AUV recovery and docking system

At present, the research of underwater manipulators mainly focuses on rigid manipulators. During the past decades, scholars have done a lot of research on the modeling of underwater manipulators. The modeling methods mainly include Lagrange method and Newton Euler method [3]. Methods to describe flexible deformation mainly include finite element method(FEM) and assumed mode method(AMM) [4]. Compared with traditional underwater manipulators, underwater flexible manipulators have dual characteristics of fluid-solid coupling and rigid-flexible coupling, and the dynamic response is more complex. Al-Khafaji et al. established the dynamic model of single-link UFM based on FEM [5]. Xue et al. further studied the fluid-solid coupling characteristics of the single-link underwater flexible manipulator by using Euler equation [6]. Shang et al. combined Morrison formula with the AMM to establish a dynamic model of a single-link UFM [7]. In the modeling of multi-link flexible manipulators, Huang et al. have taken into account the flexible deformation and hydrodynamic disturbance comprehensively and established a more accurate dynamics model of the multi-link UFM [8, 9], but the movement of the carrier was not considered. The movement of the carrier will affect both the flow field and the flexible deformation. Therefore, the influence of the carrier should be fully considered in the following research to improve the accuracy of the model.

The control methods of underwater manipulators mainly include PID control, sliding mode control, fuzzy control, adaptive control and neural network control [10, 11].

PID control is often used in the control of underwater vehicles and underwater manipulators because they are simple in design and do not depend on prior knowledge of system dynamic model. Londhe et al. proposed a nonlinear PID controller for underwater vehicle-manipulator systems(UVMS) control, which enhances the overall closed-loop stability [12]. In general, the control accuracy of PID control algorithms is not as good as that of model-based control methods [13].

Sliding mode control has the advantages of fast response, insensitivity to parameter uncertainty and external disturbances. M’Sirdi et al. applied sliding mode control method to the control of underwater manipulators, which obtained good trajectory tracking precision [14]. Esfahani et al. proposed a terminal sliding mode control method to improve the trajectory tracking accuracy under time-delay disturbance [15]. To improve the convergence speed, finite-time sliding mode control has been studied. Wang et al. proposed a non-singular terminal sliding mode controller (NTSMC) for trajectory tracking control of underwater manipulators [16, 17]. This method could enable the joint angles to converge to the desired trajectory in finite time and overcome the singularity problem. Zhou et al. further proposed an improved non-singular fast terminal sliding mode controller(NFTSMC), which can achieve higher tracking accuracy [18]. Although the sliding mode control algorithm has fast response speed and high control accuracy, it is prone to produce chattering. Therefore, how to improve convergence speed and suppress sliding mode chattering is the key point in controlling underwater manipulators.

In recent years, some novel finite-time convergence control methods have been developed to improve the convergence performance. Cheng et al. studied finite-time asynchronous output feedback control for wind turbine system [19]. He et al. researched a model predictive finite-time control strategy for discrete-time semi-Markov systems [20]. Zhang et al. proposed a finite-time sliding mode control for PDE systems to ensure finite-time convergence [21]. The sliding time of these finite-time sliding mode control methods mostly depends on the initial state and the model. To solve the problem, Zhang et al. presented a novel fixed-time sliding mode control for manipulators under lumped disturbances [22]. Li et al. proposed fixed-time integral sliding mode control for a mobile robot to achieve fast trajectory tracking [23]. Kuang et al. developed a novel stabilization controller, wherein the actual convergence time of the controller remains unaffected by the initial values of system states [24]. Liu et al. proposed an adaptive fixed-time control method, which enables the trajectory tracking errors of the manipulator system to converge within a faster fixed time with actuator saturation [25].To reduce the chattering, scholars have studied STA, an HOSM method which can effectively reduce the system chattering and does not require the derivatives of the sliding mode surface. Shtessel et al. proposed a novel adaptive-gain super-twisting sliding mode controller [26]. Borlaug et al. used the adaptive-gain super-twisting sliding mode for trajectory tracking of AUVs [27,28,29]. Zhou et al. applied STA to the design of disturbance observer for underwater manipulators [18]. Xiong et al. presented a backstepping super-twisting control method for an underwater dual-arm manipulator [30]. In summary, high-order sliding mode method can well suppress sliding mode chattering.

Underwater manipulators are subject to the disturbances of complex hydrodynamic and modeling error, intelligent control methods, such as fuzzy control, adaptive control, neural network control, and deep learning algorithms, are commonly used to deal with the disturbances. Wang et al. proposed a hybrid controller combining neural network and fuzzy algorithm for underwater manipulators, which has higher trajectory tracking accuracy and better real-time anti-disturbance capability [31]. Salloom et al. used adaptive neural network method to estimate the hydrodynamic disturbance, and used genetic algorithm to rectify the gain parameters [32]. Zhong and Yang proposed an improved adaptive fuzzy sliding mode control algorithm for underwater manipulators to reduce system chattering and improve the control accuracy [3]. Zhang et al. proposed an adaptive terminal sliding mode control method for trajectory tracking by using radial basis function neural network(RBFNN) [33]. Han et al. proposed an adaptive waveform neural network controller with force estimation for underwater manipulators under lumped disturbances [34]. Jiang et al. adopted deep learning algorithm to overcome external disturbance to ensure stable grasping performance of the manipulator in dynamic environment [35]. Zhou et al. proposed an adaptive robust controller to estimate the unknown disturbance online [36]. Furthermore, both the adaptive control method and neural network method exhibit commendable compensation capabilities for systems with motion constraints and input saturation constraints. Liu et al. proposed an adaptive controller for hypersonic flight vehicles (HFVs) with limited angle-of-attack, significantly enhancing the transient characteristics of HFVs [37]. Sun et al. presented an adaptive neural network non-singular terminal sliding mode controller for manipulators subject to input saturation [38]. From the studies mentioned above, intelligent control methods are too dependent on prior knowledge and experience because they are not based on an accurate mathematical model. In addition, these methods are computationally intensive and slow in convergence, which makes it difficult to obtain steady control performance [39, 40].

Compared with intelligent control algorithms, disturbance observers have the advantages of simple design, low computational complexity, and no reliance on prior knowledge, which are also often used to estimate and compensate for external disturbances [41, 42]. Santhakumar designed a robust controller based on a proportional differential observer for trajectory tracking control of underwater manipulators [43]. Then, Santhakumar proposed a nonlinear disturbance observer to estimate the unknown perturbation [44]. Vinoth et al. proposed a disturbance-observer-based terminal sliding mode control scheme for underwater manipulators [45]. Londhe et al. improved the overall stability of UVMS with parameter uncertainty, ocean current disturbances, and measurement noise by using a disturbance observer [46]. Han et al. proposed a sliding mode control method based on an extended-state observer to achieve asymptotic stabilization of the tracking error [47]. Although all the above studies achieved good control results, most of them simplified the hydrodynamics and did not consider the flexible deformation.

In addition to improving the anti-disturbance ability, to suppress the flexible vibration is another challenge. The manipulator with flexible deformation is a typical under-actuated system. In order to avoid the singularity of inertia matrix inversion while reducing the computational difficulty of higher-order models, the singular perturbation method is commonly used to decompose the system into a slow-varying subsystem and a fast-varying subsystem [4]. Hisseine and Lohmann proposed a dual-time-scale controller based on the singular perturbation method and verified the performance of the proposed controller by experiments [48]. Salehi and Vossoughi proposed a composite controller including a sliding mode control law and a feedback control law to suppress the vibration [49]. Chen et al. proposed a slow-varying subsystem controller with a nonlinear disturbance observer to compensate for external disturbances [50]. The above studies did not consider the disturbance of hydrodynamics. In a recent study on underwater flexible manipulators, Xue and Huang designed a feedforward control method and used discontinuous piecewise smoothing filter to reduce the vibration [6]. Shang et al. studied the coupling characteristics of a single-link underwater flexible manipulator and designed a controller with neural network compensation [7]. Huang designed an adaptive sliding mode controller for multi-link underwater flexible manipulators, which achieved higher trajectory tracking accuracy [9]. Among all the research on underwater manipulators, flexible deformation and disturbance of the moving carrier were barely considered. In addition, the control system design of flexible manipulators is based on the assumption that all states of the control system can be obtained directly. In fact, the flexible modal derivatives are difficult to be measured directly by sensors.

In order to solve the motion disturbance of the moving carrier and the indirect measurement of the flexible modal derivatives, and to improve convergence speed, anti-disturbance ability and vibration suppression performance of the controller, a dynamics model of moving-base UFM is established in this paper. This model is decomposed into a slow-varying subsystem and a fast-varying subsystem by using the singular perturbation method. An adaptive non-singular fixed-time sliding mode controller with a HOSM observer is proposed for the slow-varying subsystem. The sliding time of the controller is independent of the model and the initial state. To reduce the chattering and overestimation, the adaptive STA is introduced. To further suppress the flexible vibration, the other HOSM observer is used to obtain the flexible modal derivatives for the fast-varying subsystem.

The main contributions of this paper are as follows:

• (i) The dynamics model of the moving-base UFM is firstly established and the motion of the base and hydrodynamic disturbances are fully considered in the dynamic modeling.

• (ii) An adaptive non-singular fixed-time sliding mode controller is proposed. The sliding time of the controller is independent of the model and the initial state. The adaptive STA is introduced to reduce the chattering and overestimation.

• (iii) HOSM observers are used to compensate for lumped disturbances and to estimate flexible modal derivatives.

• (iv) The superiority of the proposed ANFSMC in terms of fast finite-time convergence and vibration suppression is verified by comparing with existing control methods [18, 22, 47] based on ADAMS and MATLAB.

This paper is organized as follows. Section 2 is the materials and methods, in which the methods for deriving dynamical equations and hydrodynamics of moving-base UFM are introduced. Section 3 is the design of controller. In this section, an adaptive non-singular fixed-time sliding mode controller with a HOSM observer is proposed. Section 4 is the stability analysis. A new Lyapunov function is designed to prove the stability of the controller. Section 5 is the simulation verification. The effectiveness of the proposed controller is analyzed and discussed. Section 6 is the summary of the whole paper.

2 Materials and methods

In this section, some notions and lemmas and the modeling methods of moving-base UFM are introduced.

2.1 Notation

For vector ${\varvec{x}}= {\left[ {{x_1},{x_2} \ldots ,{x_n}} \right] ^T}$, ${x_i} \in {R^n}$ is a real number. ${si}{{g}^\varGamma }({x_i})$ and ${si}{{g}^\varGamma }{\varvec{(x)}} \in {R^n}$ are defined as

$$\begin{aligned} {si}{{g}^\varGamma }({x_i})= & {} {\left| {{x_i}} \right| ^\varGamma } \cdot {\textrm{sgn}} ({x_i}) \end{aligned}$$

(1)

$$\begin{aligned} {si}{{g}^\varGamma }{\varvec{(x)}}= & {} \left[ {{\left| {{x_1}} \right| }^\varGamma } \cdot {\textrm{sgn}} ({x_1}),{{\left| {{x_2}} \right| }^\varGamma } \cdot {\textrm{sgn}} ({x_2}) \cdots ,\right. \nonumber \\{} & {} \left. {{\left| {{x_n}} \right| }^\varGamma } \cdot {\textrm{sgn}} ({x_n}) \right] ^T \end{aligned}$$

(2)

where ${\textrm{sgn}} ( \cdot )$ denotes the signum function and $\varGamma$ is a positive real number.

The nonlinear function $f({x_i})$ and its first derivative $h({x_i})$ are introduced in Sect. 4. The vector ${\varvec{F}}{\varvec{(x)}} \in {R^n}$ and the diagonal matrix ${\varvec{H}}{\varvec{(x)}} \in {R^{n \times n}}$ are defined as

$$\begin{aligned} {\varvec{F}}{\varvec{(x)}}= & {} {[f({x_1}),f({x_2}) \cdots ,f({x_n})]^T} \end{aligned}$$

(3)

$$\begin{aligned} {\varvec{H}}{\varvec{(x)}}= & {} diag\left\{ {{{\left[ {h({x_1}),h({x_2}) \cdots ,h({x_n})} \right] }^T}} \right\} \end{aligned}$$

(4)

where $diag\left\{ \cdot \right\}$ denotes the diagonal matrix.

The diagonal matrix ${{\varvec{D}}^\varGamma }{\varvec{(x)}} \in {R^{n \times n}}$ is defined as

$$\begin{aligned} {{\varvec{D}}^\varGamma }{\varvec{(x)}} = diag\left\{ {{{\left[ {{{\left| {{x_1}} \right| }^\varGamma },{{\left| {{x_2}} \right| }^\varGamma } \cdots ,{{\left| {{x_n}} \right| }^\varGamma }} \right] }^T}} \right\} \end{aligned}$$

(5)

2.2 Lemmas

Lemma 1

[51]

${\varvec{U}}$ and ${\varvec{V}}$ are symmetric positive definite matrices. If ${\varvec{UV}} = {\varvec{VU}}$, then, ${\varvec{UV}}$ is a symmetric positive definite matrix.

Lemma 2

[52, 53]

For the following dynamical system

$$\begin{aligned} \left\{ {\begin{array}{*{20}{c}} {{{\dot{x}}_1} = {x_2}}\\ {{{\dot{x}}_2} = {x_3}}\\ \vdots \\ {{{\dot{x}}_{n - 1}} = u + {f_1}} \end{array}} \right. \end{aligned}$$

(6)

The disturbance ${f_1}$ meets Lipschitz continuity condition, and there is a small positive constant ${\delta _0}$, so that $\left\| {{{\dot{f}}_1}} \right\| \le {\delta _0}$.

A HOSM observer takes the following form

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{{\dot{\hat{x}}_i}} = {{\hat{x}}_{i + 1}} + {\varphi _i}si{g^{\frac{{n - i}}{n}}}({{\tilde{x}}_1}), \; i = 1,2, \cdots ,n - 2;}\\ {{{\dot{\hat{x}}_{\mathrm{{n - 1}}}}} = {{\hat{x}}_n} + u + {\varphi _{n - 1}}si{g^{\frac{1}{n}}}({{\tilde{x}}_1});}\\ {{{\dot{\hat{x}}_n}} = {\varphi _n}{\textrm{sgn}} ({{\tilde{x}}_1})} \end{array}} \right. \end{aligned}$$

(7)

and the differentiation error can be expressed as

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{{\dot{\tilde{x}}_i}} = - {\varphi _i}si{g^{\frac{{n - i}}{n}}}({{\tilde{x}}_1}) + {{\tilde{x}}_{i + 1}},i = 1,2, \cdots ,n - 2;}\\ {{{\dot{\tilde{x}}_{n - 1}}} = - {\varphi _{n - 1}}si{g^{\frac{1}{n}}}({{\tilde{x}}_1}) + {{\tilde{x}}_n}}\\ {{{\dot{\tilde{x}}_n}} = - {\varphi _n}{\textrm{sgn}} ({{\tilde{x}}_1}) + {{\dot{f}}_1}} \end{array}} \right. \end{aligned}$$

(8)

where ${\varphi _i}(i = 1, \cdots ,n)$ are the gains of the observer; the observation error variable ${ {\tilde{x_i}}} = {x_i} - {\hat{x_i}}(i = 1, \cdots ,n - 1)$, and the variable ${\tilde{x}_n}={-\hat{x}_n} + {f_1}$.

The HOSM observer has finite-time stability and high observation accuracy under the bounded disturbance.

2.3 Dynamic models

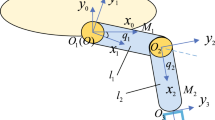
The control object in this paper is a simplified moving-base UFM system, which just considers its 2D plane motion, as shown in Fig. 2. In the moving-base UFM system, link 1 is a rigid manipulator and link 2 is a flexible manipulator. The coordinate system XOY is an inertial reference frame. ${X_0}{O_0}{Y_0}$ and ${X_1}{O_1}{Y_1}$ are local coordinate systems which were respectively fixed to the submarine and the rigid manipulator. ${X_2}{O_2}{Y_2}$ and ${X_{\tilde{2}}}{O_0}{Y_{\tilde{2}}}$ are local coordinate systems were respectively fixed to the joint and the end actuator of flexible manipulators respectively. In this section, the dynamic model of the UFM is established by combining the AMM and Lagrange equation.

Supposing that ${\varvec{{\ell _1}}}$, ${\varvec{{\ell _2}}}$, ${\varvec{{\ell _3}}}$ respectively represent the unit vectors along the axis ${X_1},{X_2},{Y_2}$, then ${\varvec{{\ell _1}}}$, ${\varvec{{\ell _2}}}$, ${\varvec{{\ell _3}}}$ can be expressed as

$$\begin{aligned} {\varvec{\ell _1}}= & {} {[\cos (\alpha - {\theta _1}),\; \sin ({\theta _1} - \alpha )]^T} \end{aligned}$$

(9)

$$\begin{aligned} {\varvec{\ell _2}}= & {} {[\cos ({\theta _1} + {\theta _2} - \alpha ),\; \sin ({\theta _1} + {\theta _2} - \alpha )]^T} \end{aligned}$$

(10)

$$\begin{aligned} {\varvec{\ell _3}}= & {} {[ - \sin ({\theta _1} + {\theta _2} - \alpha ),\; \cos ({\theta _1} + {\theta _2} - \alpha )]^T} \end{aligned}$$

(11)

The position vector of the carrier can be expressed as

$$\begin{aligned} {\varvec{o_0}}{\varvec{o_1}}= & {} {l_0}{[\sin (\alpha + \beta ),\; \cos (\alpha + \beta )]^T} \end{aligned}$$

(12)

$$\begin{aligned} {\varvec{r_0}}= & {} {[{x_0},{y_0}]^T} \end{aligned}$$

(13)

Fig. 2

The simplified coordinate frames of the moving-base UFM

To simplify the calculation, ${\varvec{{o_0}}}{\varvec{o_1}}$ is made perpendicular to the carrier while $\beta =0$. At this time, the vectors have the following geometric relationships

$$\begin{aligned} {\varvec{r_1}}= & {} {\varvec{r_0}} + {\varvec{o_0}}{\varvec{o_1}} + x{\varvec{\ell _1}} \end{aligned}$$

(14)

$$\begin{aligned} {\varvec{r_2}}= & {} {\varvec{r_0}} + {\varvec{o_0}}{\varvec{o_1}} + {l_1}{\varvec{\ell _1}} + x{\varvec{\ell _2}} + w{\varvec{\ell _3}} \end{aligned}$$

(15)

where ${l_1}$ is the length of link 1, w is flexible displacement of end-effector of flexible manipulator.

The kinetic energy and potential energy of the manipulator system are expressed as [8, 9]

$$\begin{aligned} T= & {} \frac{1}{2}{\rho _1}\int _0^{{l_1}} {{{\dot{{\varvec{r}}}_1}}^T{{\dot{{\varvec{r}}}_1}}dx + } \frac{1}{2}{\rho _2}\int _0^{{l_2}} {{{\dot{{\varvec{r}}}_2}}^T{{\dot{{\varvec{r}}}_2}}dx+ \frac{1}{2}m{\dot{{\varvec{r}}}_2}^T{\dot{{\varvec{r}}}_2}}\nonumber \\ \end{aligned}$$

(16)

$$\begin{aligned} U= & {} \int _0^{{l_2}} {\frac{1}{2}EI{w^{''2}}} dx + \int _0^{{l_1}} {{\rho _1}{\varvec{r_1}}^T{\varvec{g}}} dx \nonumber \\{} & {} + \int _0^{{l_2}} {{\rho _2}{\varvec{r_2}}^T{\varvec{g}}} dx + m{{{\varvec{r}}}_2}^T{\varvec{g}} \end{aligned}$$

(17)

where ${\varvec{g}} = {[0,g]^T}$, g is the gravitational acceleration and m is the mass of the end load.

By using the AMM, the flexible displacement can be expanded as

$$\begin{aligned} w(x,t) = \sum \limits _{i = 1}^n {{\phi _i}(x){q_i}(t)} \end{aligned}$$

(18)

A generalized coordinate ${\varvec{q_l}}$ is defined as ${\varvec{q_l}}\mathrm{{ = [}}{\varvec{\theta }} \mathrm{{,}}{\varvec{q}}\mathrm{{]}}$. By intercepting the first two modes of flexible displacement and substituting them into the Lagrange equation, the dynamic equation of underwater flexible manipulators can be deduced as follows:

$$\begin{aligned} \left( {\begin{array}{*{20}{c}} {{{\varvec{M_{\theta \theta }}}}}&{}{{{\varvec{M_{\theta q}}}}}\\ {{{\varvec{M_{q\theta }}}}}&{}{{{\varvec{M_{qq}}}}} \end{array}} \right) \left( {\begin{array}{*{20}{c}} {\ddot{{\varvec{\theta }}} }\\ {\ddot{{\varvec{q}}}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{\varvec{C_r}}}\\ {{\varvec{K_q}}{\varvec{q}} + {\varvec{C_f}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\varvec{\tau }} \\ {\varvec{0}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{\varvec{F_\theta }}}\\ {{\varvec{F_q}}} \end{array}} \right) \end{aligned}$$

(19)

where ${\varvec{\theta }} ={\left[ {\begin{array}{*{20}{c}}{{\theta _1}}&{{\theta _2}}\end{array}} \right] ^T}$; ${\varvec{q}}={\left[ {\begin{array}{*{20}{c}}{{q_1}}&{{q_2}}\end{array}} \right] ^T}$; ${\varvec{K_q}}={\left[ {\begin{array}{*{20}{c}}{{K_{q1}}}&{{K_{q2}}}\end{array}} \right] ^T}$ is the stiffness matrix; ${\varvec{C_r}}$ and ${\varvec{C_f}}$ are the nonlinear coupling terms of centrifugal forces, coriolis forces, and gravity; ${\varvec{\tau }}$ is input torque; ${\varvec{F_\theta }}$ and ${\varvec{F_q}}$ are the generalized hydrodynamic force.

The inertia matrix and stiffness matrix of the moving-base UFM are the same as those of the fixed-base UFM [8, 9]. Since the motion of the manipulator is coupled with that of the carrier, the ${\varvec{C_r}}$ and ${\varvec{C_f}}$ of moving-base UFM are more complex than those of the fixed-base UFM. The non-linear force/torque vector ${\varvec{C_r}}$ and ${\varvec{C_f}}$ are shown in Appendix.

2.4 Hydrodynamic force

The movement of the carrier will influence the flow field of the manipulator. This paper deduces the hydrodynamic force of the moving-base UFM from the previous hydrodynamic research of the fixed-base UFM [8, 9]. The angular velocity of the moving base is ${}^0{\omega _0} = \dot{\alpha }$. angular acceleration is ${}^0{\dot{\omega }_0}=\ddot{\alpha }$. The velocity and acceleration can be expressed as

$$\begin{aligned}{} & {} {}^0{\varvec{v}}{_0} = \left[ {{{\dot{x}}_0} + {l_0}\dot{\alpha }\cos \alpha ,{{\dot{y}}_0} - {l_0}\dot{\alpha }\sin \alpha } \right] ^T \nonumber \\{} & {} {}^0{\dot{{\varvec{v}}{_0}}} = \left[ {{{\ddot{x}}_0} + {l_0}\ddot{\alpha }\cos \alpha - {l_0}\alpha \dot{\alpha }\sin \alpha ,{{\ddot{y}}_0} }\right. \nonumber \\ {}{} & {} \left. - {l_0}\ddot{\alpha }\sin \alpha - {l_0}{{\dot{\alpha }}^2}\cos \alpha \right] ^T \end{aligned}$$

(20)

According to the velocity transfer formula between links, the velocity and acceleration of two manipulators in the local coordinate systems can be calculated [9]. By defining ${{\textrm{c}}_1} = \cos {\theta _1}$, ${{\textrm{c}}_2} = \cos {\theta _2}$, ${\textrm{s}}_{1} = \sin {\theta _1}$, ${\textrm{s}}_{2}= \sin {\theta _2}$, ${A_1}={\dot{x}_0} + {l_0}\dot{\alpha }\cos \alpha$, ${A_2}={\dot{y}_0} + {l_0}\dot{\alpha }\sin \alpha$, the velocity and acceleration at any position on the rigid manipulator are

$$\begin{aligned} {}^1{\varvec{v}}{(x)_1}= & {} \left[ {\begin{array}{*{20}{c}} {{\textrm{c}}_{1}}{A_1} + {{\textrm{s}} _1}{A_2}\\ { - {{\textrm{s}}_{1}}{A_1} + {{\textrm{c}}_1}{A_2} + x( - \dot{\alpha }+ {{\dot{\theta }}_1})}\\ 0\end{array}} \right] \end{aligned}$$

(21)

$$\begin{aligned} {}^1\dot{{\varvec{v}}}{(x)_1}= & {} \left[ {\begin{array}{*{20}{c}} {{{\textrm{c}}_1}{{\dot{A}}_1} + {{\textrm{s}} _1}{{\dot{A}}_2} - x{{( - \dot{\alpha }+ {{\dot{\theta }}_1})}^2}}\\ { - {{\textrm{s}} _1}{{\dot{A}}_1} + {{\textrm{c}}_1}{{\dot{A}}_2} + x( - \ddot{\alpha }+ {{\ddot{\theta }}_1})}\\ 0 \end{array}} \right] \end{aligned}$$

(22)

The velocity of the joint of the flexible manipulator is

$$\begin{aligned}{} & {} {}^2{\varvec{v_2}} \nonumber \\ {}{} & {} = \left[ {\begin{array}{*{20}{c}} {{{\textrm{c}}_1}{{\textrm{c}}_2}{A_1} + {{\textrm{s}} _1}{{\textrm{c}}_2}{A_2} - {{\textrm{s}} _1}{{\textrm{s}} _2}{A_1} + {{\textrm{c}}_1}{{\textrm{s}} _2}{A_2} + {{\textrm{s}} _2}{l_1}( - \dot{\alpha }+ {{\dot{\theta }}_1})}\\ { - {{\textrm{c}}_1}{{\textrm{s}} _2}{A_1} - {{\textrm{s}} _1}{{\textrm{s}} _2}{A_2} - {{\textrm{s}} _1}{{\textrm{c}}_2}{A_1} + {{\textrm{c}}_1}{{\textrm{c}}_2}{A_2} + {{\textrm{c}}_2}{l_1}( - \dot{\alpha }+ {{\dot{\theta }}_1})}\\ 0 \end{array}} \right] \nonumber \\ \end{aligned}$$

(23)

The velocity at any position on the flexible manipulator is

$$\begin{aligned}{} & {} {}^{\tilde{2}}{\varvec{v}}{(x)_{\tilde{2}}} \nonumber \\ {}{} & {} = \left[ {\begin{array}{*{20}{c}} {\cos {\alpha _w}{}^2{{\varvec{v}}_2}(1) + \sin {\alpha _w}{}^2{{\varvec{v}}_2}(2) - \cos {\alpha _w}w{A_3} + \sin {\alpha _w}x{A_3}}\\ { - \sin {\alpha _w}{}^2{{\varvec{v}}_2}(1) + \cos {\alpha _w}{}^2{{\varvec{v}}_2}(2) + \sin {\alpha _w}w{A_3} + \cos {\alpha _w}x{A_3}}\\ 0 \end{array}} \right] \nonumber \\ \end{aligned}$$

(24)

where ${\alpha _w}=\frac{{\partial w}}{{\partial x}}$, ${A_3}=( - \dot{\alpha }+ {\dot{\theta }_1} + {\dot{\theta }_2})$.

The acceleration of the joint of the flexible manipulator is

$$\begin{aligned} {}^2{\dot{{\varvec{v}}}_2} = \left[ {\begin{array}{*{20}{c}} {\left( \begin{array}{l} {{\textrm{c}}_1}{{\textrm{c}}_2}{{\dot{A}}_1} + {{\textrm{s}} _1}{{\textrm{c}}_2}{{\dot{A}}_2} - {{\textrm{s}} _1}{{\textrm{s}} _2}{{\dot{A}}_1} + {{\textrm{c}}_1}{{\textrm{s}} _2}{{\dot{A}}_2} \\ + {{\textrm{s}} _2}{l_1}( - \ddot{\alpha }+ {{\ddot{1} \theta }_1}) - {{\textrm{c}}_2}{l_1}{( - \dot{\alpha }+ {{\dot{\theta }}_1})^2} \end{array} \right) }\\ {\left( \begin{array}{l} - {{\textrm{c}}_1}{{\textrm{s}} _2}{A_1} - {{\textrm{s}} _1}{{\textrm{s}} _2}{A_2} - {{\textrm{s}} _1}{{\textrm{c}}_2}{A_1} + {{\textrm{c}}_1}{{\textrm{c}}_2}{A_2} \\ + {{\textrm{c}}_2}{l_1}( - \ddot{\alpha }+ {{\ddot{\theta }}_1}) + {{\textrm{s}} _2}{l_1}{( - \dot{\alpha }+ {{\dot{\theta }}_1})^2} \end{array} \right) }\\ 0 \end{array}} \right] \end{aligned}$$

(25)

The acceleration at any position on the flexible manipulator is

$$\begin{aligned} {}^{\tilde{2}}\dot{{\varvec{v}}}{(x)_{\tilde{2}}} = \left[ {\begin{array}{*{20}{c}} {\cos {\alpha _w}{}^2{{\dot{{\varvec{v}}}}_2}(1) + \sin {\alpha _w}{}^2{{\dot{{\varvec{v}}}}_2}(2)}\\ {+ \cos {\alpha _w}( - w{{\dot{A}}_3} - x{A_3}^2) + \sin {\alpha _w}x{{\dot{A}}_3}}\\ { - \sin {\alpha _w}{}^2{{\dot{{\varvec{v}}}}_2}(1) + \cos {\alpha _w}{}^2{{\dot{{\varvec{v}}}}_2}(2)}\\ {- \sin {\alpha _w}( - w{{\dot{A}}_3} - x{A_3}^2) + \cos {\alpha _w}x{{\dot{A}}_3}}\\ 0 \end{array}} \right] \nonumber \\ \end{aligned}$$

(26)

After deriving the velocity, acceleration and its normal value of the two manipulators ${}^i{\varvec{v^n}}{(x)_i}, {}^i{\dot{{\varvec{v}}}^n}{(x)_i},(i = 1,2,\tilde{2})$, the water resistance and additional mass force of each manipulator can be calculated by substituting them into Morrison formula.

The water resistance of the flexible manipulator is

$$\begin{aligned} {}^{\tilde{2}}{{\varvec{f}}_{D\tilde{2}}} = \frac{1}{2}{\rho _f}{C_D}D\int _0^{{l_2}} {{}^{\tilde{2}}{{\varvec{v}}^n}{{\left( x \right) }_{\tilde{2}}}\left\| {{}^{\tilde{2}}{{\varvec{v}}^n}{{(x)}_{\tilde{2}}}} \right\| \sqrt{1 + {{\left( {\frac{{\partial w}}{{\partial x}}} \right) }^2}} dx} \end{aligned}$$

(27)

The additional mass force of the flexible manipulator is

$$\begin{aligned} {}^{\tilde{2}}{{\varvec{f}}_{M\tilde{2}}} = {\rho _f}{C_M}{A_\mathrm{{d}}}\int _0^{{l_2}} {{}^{\tilde{2}}{{\dot{{\varvec{v}}}}^n}_{\tilde{2}}\sqrt{1 + {{\left( {\frac{{\partial w}}{{\partial x}}} \right) }^2}} dx} \end{aligned}$$

(28)

The water resistance of the rigid manipulator is

$$\begin{aligned} {}^1{{\varvec{f}}_{D1}} = \frac{1}{2}{\rho _f}{C_D}D\int _0^{{l_1}} {{}^1{{\varvec{v}}^n}{{(x)}_1}\left\| {{}^1{{\varvec{v}}^n}{{(x)}_1}} \right\| d{x_1}} \end{aligned}$$

(29)

The additional mass force of the rigid manipulator is

$$\begin{aligned} {}^1{{\varvec{f}}_{M1}} = {\rho _f}{C_M}{A_\mathrm{{d}}}\int _0^{{l_1}} {{}^1{{\dot{{\varvec{v}}}}^n}{{(x)}_1}d{x_1}} \end{aligned}$$

(30)

In addition, the buoyancy of manipulators can be expressed as

$$\begin{aligned} {{\varvec{f}}_B} = - \frac{{{\rho _f}}}{{{\rho _m}}}{\varvec{G}} \end{aligned}$$

(31)

where ${\rho _f}$ is the density of water, ${\rho _m}$ is the density of the manipulators and ${\varvec{G}}$ is gravity.

3 Controller design

In this section, the moving-base UFM system is decomposed into a slow-varying subsystem and a fast-varying subsystem. A composite controller is designed for these two subsystems.

3.1 Singular perturbation decomposition

The singular perturbation method is a method for calculating asymptotic solutions of differential equations, which has been widely used for controller design of flexible manipulators in recent years [4, 48]. The singular perturbation method takes advantage of the difference in time scale between the joint angles and the flexible modes to decompose the higher-order flexible manipulator system into a slow-varying subsystem and a fast-varying subsystem.

First, the steady-state solution of slow variables is obtained by ignoring the fast variables of the system. The specific approach is to introduce a small parameter $\varepsilon$ (${\varepsilon ^2}\mathrm{{ = 1/}}\min {({\varvec{K_q}})_{ij}}$), making ${\tilde{{\varvec{K_q}}}}={\varepsilon ^2}{\varvec{K_q}}$, ${\varepsilon ^2}{\varvec{\xi }} ={\varvec{q}}$. The slow-varying subsystem is transformed into the following form

$$\begin{aligned} \left\{ \begin{array}{l} {{\dot{{\varvec{x_1}}}}} = {\varvec{x_2}}\\ {{\dot{{\varvec{x_2}}}}} = {{\bar{{\varvec{M}}_{\theta \theta }}}}{({\varvec{x_1}})^{ - 1}}[ - {{\bar{{\varvec{C}}_r}}}({\varvec{x_1}},{\varvec{x_2}}) + \bar{{\varvec{\tau }}} + {{\bar{{\varvec{F}}_\theta }}}] \end{array} \right. \end{aligned}$$

(32)

where $\overline{( \cdot )}$ is a matrix corresponding to $( \cdot )$ when $\varepsilon = 0$; ${\varvec{x_1}} = {\left[ {\begin{array}{*{20}{c}} {{{\bar{\theta }}_1}}&{{{\bar{\theta }}_2}} \end{array}} \right] ^T}$, ${\varvec{x_2}} = {\left[ {\begin{array}{*{20}{c}} {{{\bar{\dot{\theta }_1}}}}&{{{\bar{\dot{\theta }_2}}}} \end{array}} \right] ^T}$; $\bar{{\varvec{\tau }}}$ is input torque of slow subsystem.

Then, the boundary layer correction term is calculated based on a fast variable time scale, which can be written as

$$\begin{aligned}{} & {} \bar{{\varvec{\xi }}} = - {\tilde{{\varvec{K_q}}}}^{ - 1}{\bar{{\varvec{N_{qq}}}}}^{ - 1}\left( {{{\bar{{\varvec{N}}_{q\theta }}}}{{\bar{{\varvec{C}}_r}}} + {{\bar{{\varvec{ N}}_{qq}}}}{{\bar{{\varvec{ C}}_f}}}} \right. \nonumber \\ {}{} & {} \left. - {{{\bar{{\varvec{N}}_{q\theta }}}}\bar{{\varvec{\tau }}} - {{\bar{{\varvec{N}}_{q\theta }}}}{{\bar{{\varvec{F}}_\theta }} } - {{\bar{{\varvec{ N}}_{qq}}}}{{\bar{{\varvec{F}}_q}}}} \right) \end{aligned}$$

(33)

where $\left[ {\begin{array}{*{20}{c}} {{{\varvec{N_{\theta \theta }}}}}&{}{{{\varvec{N_{\theta q}}}}}\\ {{{\varvec{N_{q\theta }}}}}&{}{{{\varvec{N_{qq}}}}} \end{array}} \right] = {\left[ {\begin{array}{*{20}{c}} {{{\varvec{M_{\theta \theta }}}}}&{}{{{\varvec{M_{\theta q}}}}}\\ {{{\varvec{M_{q\theta }}}}}&{}{{{\varvec{M_{qq}}}}} \end{array}} \right] ^{ - 1}}$.

The fast-varying state variable can be expressed as

$$\begin{aligned} {\varvec{\zeta _1}} = {\varvec{\xi }} - \bar{{\varvec{\xi }}} , {\varvec{\zeta _2}} = \varepsilon \dot{{\varvec{\xi }}} \end{aligned}$$

(34)

The fast-varying subsystem is expressed as

$$\begin{aligned} \frac{{d{\varvec{\zeta }}}}{{d{t_\varepsilon }}} = {\varvec{A_\varepsilon }}{\varvec{\zeta }} + {\varvec{B_\varepsilon }}{\varvec{\tau _f}} \end{aligned}$$

(35)

where${\varvec{\zeta }} = {(\begin{array}{*{20}{c}} {{\varvec{\zeta _1}}^T}&{{\varvec{\zeta _2}}^T} \end{array})^T}, {\varvec{A_\varepsilon }} = \left( {\begin{array}{*{20}{c}} {\varvec{0}}&{}{{\varvec{I_{2 \times 2}}}}\\ { - {{\bar{{\varvec{ N}}_{qq}}}}{{\tilde{{\varvec{K}}_q}}}}&{}{\varvec{0}} \end{array}} \right) , {\varvec{B_\varepsilon }} = \left( {\begin{array}{*{20}{c}} {\varvec{0}}\\ {{{\bar{{\varvec{N}}_{q\theta }}}}} \end{array}} \right) , {t_\varepsilon }\varepsilon = t$, ${\varvec{I_{2 \times 2}}}$ is unit matrix, ${\varvec{\tau _f}}$ is input torque of fast-varying subsystem.

3.2 Controller design of the slow-varying subsystem

The design objectives of this controller are to improve convergence speed, anti-disturbance ability and vibration suppression performance. In this section, an adaptive non-singular fixed-time sliding mode control method is proposed by combining the advantages of adaptive control methods and sliding mode control. The method introduces an adaptive super-twisting approach law, which can reduce the chattering and overestimation. A non-singular fixed-time sliding mode surface is used to overcome the drawback of slow convergence of ordinary sliding modes. Also, it does not introduce additional time-varying gain matrixes in the case of combining the terminal sliding mode method with the STA. Since the lumped disturbances from model errors, carrier motion, and hydrodynamic forces are difficult to be obtained directly in practice, high-order sliding mode observer is used to estimate and compensate for lumped disturbances.

When the model error was taken into account, eq. (32) can be rewritten as

$$\begin{aligned} {\ddot{{\varvec{x_1}}}} = {\bar{{\varvec{M_{\theta \theta }}}}}{({\varvec{x_1}})^{ - 1}}[ - {\bar{{\varvec{C_r}}}}({\varvec{x_1}},{\varvec{x_2}}) + \bar{{\varvec{\tau }}} + {\bar{{\varvec{F_\theta }}}} + {\varvec{F_L}}] \end{aligned}$$

(36)

where ${\varvec{F_L}}$ is the lumped disturbance of the slow-varying subsystem.

$$\begin{aligned} {\varvec{F_L}}= - \varDelta {\bar{{\varvec{ M_{\theta \theta }}}}}{\ddot{{\varvec{x_1}}}} + \varDelta {\bar{{\varvec{C_r}}}}({\varvec{x_1}},{\varvec{x_2}}) + \varDelta {\bar{{\varvec{F_\theta }}}} \end{aligned}$$

(37)

By defining ${\varvec{x_{1d}}}$ and ${\dot{{\varvec{ x_{1d}}}}}$ as the desired position and velocity of the joint angle, the tracking error and its derivative can be expressed as ${\varvec{e}} = {\varvec{x_1}} - {\varvec{x_{1d}}}$, $\dot{{\varvec{ e}}} = {\dot{{\varvec{x_1}}}} - {\dot{{\varvec{x_{1d}}}}}$, $\ddot{{\varvec{ e}}} = {\ddot{{\varvec{ x_1}}}} - {\ddot{{\varvec{x_{1d}}}}}$.

To design a sliding mode, a nonlinear function is defined [22, 54]

$$\begin{aligned} f({x_i}) = \left\{ {\begin{array}{*{20}{l}} {{K_a}si{g^{{\varGamma _1}}}({x_i}) + {K_b}{\sigma ^{\left| {{x_i}} \right| }} {x_i}\;,\; \left| {{x_i}} \right| < \sigma }\\ {si{g^{{\varGamma _2}}}({x_i}) \qquad \qquad ,\; \left| {{x_i}} \right| \ge \sigma } \end{array}} \right. \end{aligned}$$

(38)

where ${\varGamma _1}={\varGamma _2} + 1$, ${\varGamma _2}\mathrm{{ = 1}} - \sigma$, $\sigma \in (0,\exp ( - 1))$ is a positive constant, and

$$\begin{aligned} \left\{ {\begin{array}{*{20}{c}} {{K_a} = \frac{{ - 1 - \ln \sigma }}{{{\varGamma _2} - \lambda \ln \sigma }}}\\ {{K_b} = \frac{{{\sigma ^{2{\varGamma _2} - 2}}}}{{{\varGamma _2} - \sigma \ln \sigma }}} \end{array}} \right. \end{aligned}$$

(39)

The first-order derivative of f(x) with respect to x is expressed as

$$\begin{aligned} h({x_i}) = \left\{ {\begin{array}{*{20}{l}} {{K_a}{\varGamma _1}{{\left| {{x_i}} \right| }^{{\varGamma _1} - 1}} + {K_b}\left( {\left| {{x_i}} \right| \ln \sigma + 1} \right) {\sigma ^{\left| {{x_i}} \right| }}\;,\;\left| {{x_i}} \right| < \sigma }\\ {{\varGamma _2}{{\left| {{x_i}} \right| }^{{\varGamma _2} - 1}}({x_i})\qquad \qquad ,\; \left| {{x_i}} \right| \ge \sigma } \end{array}} \right. \end{aligned}$$

(40)

The non-singular fixed-time sliding mode term is written as

$$\begin{aligned} {\varvec{s}} = \dot{{\varvec{e}}} + {\varvec{C_1}}{\varvec{F}}({\varvec{e}}) + {\varvec{C_2}}si{g^{{\varGamma _3}}}({\varvec{e}}) \end{aligned}$$

(41)

The derivative of ${\varvec{s}}$ with respect to time is

$$\begin{aligned} \dot{{\varvec{ s }}}= \ddot{{\varvec{e}}} + {\varvec{C_1}}{\varvec{H}}({\varvec{e}})\dot{{\varvec{e}}} + {\varvec{C_2}}{{\varvec{D}}^{{\varGamma _3} - 1}}({\varvec{e}})\dot{{\varvec{e}}} \end{aligned}$$

(42)

To reduce the chattering of the system, the STA is introduced into the controller. The form of the STA is [26, 55]

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{\varvec{u}} = - {\varvec{K_1}}si{g^{1/2}}({\varvec{s}}) + {\varvec{\varpi }} }\\ {\dot{{\varvec{\varpi }}} = - \frac{1}{2}{\varvec{K_2}}{\textrm{sgn}} ({\varvec{s}})} \end{array}} \right. \end{aligned}$$

(43)

where ${\varvec{K_1}}\mathrm{{ = diag}}({K_{1i}}),{\varvec{K_2}}\mathrm{{ = diag(}}{K_{2i}})$ is gain.

The following adaptive law of the gain is adopted

$$\begin{aligned} {\dot{K}_{1i}}= & {} \left\{ {\begin{array}{*{20}{l}} {{k_1}\sqrt{\frac{{{\gamma _1}}}{2}} {\textrm{sgn}}(\left| {{s_i}} \right| - \alpha _a ), if {K_{1i}} > {K_m}}\\ {\beta _a,if {K_{1i}} \le {K_m}} \end{array}} \right. \end{aligned}$$

(44)

$$\begin{aligned} {K_{2i}}= & {} 2\kappa {K_{1i}} \end{aligned}$$

(45)

where ${k_1}$, ${\gamma _1}$, $\alpha _a$, $\beta _a$ and $\kappa$ are positive constants.

To further improve the control accuracy of the controller, the HOSM extended state observer is used to estimate and compensate for the lumped disturbance. The HOSM extended state observer takes the following form

$$\begin{aligned} \left\{ \begin{array}{*{20}{l}} \hat{\dot{{\varvec{x}}}_1} = {{\hat{{\varvec{x_2}}}}} + {\varphi _1}si{g^{2/3}}({{\tilde{{\varvec{x_1}}}}})\\ { {{\dot{\hat{{\varvec{x_2}}}}}} = {{\hat{{\varvec{x_3}}}}} + {{\bar{{\varvec{M}}_{\theta \theta }}}}{{({\varvec{x_1}})}^{ - 1}}[ - {{\bar{{\varvec{C_r}}}}}({\varvec{x_1}},{\varvec{x_2}}) + \bar{{\varvec{\tau }}} + {{\bar{{\varvec{F_\theta }}}}}]}\\ + {{\varphi _2}si{g^{1/3}}({{\tilde{{\varvec{x_1}}}}})}\\ {{{\dot{\hat{{\varvec{x_3}}}}}} = {\varphi _3}{\textrm{sgn}} ({{\tilde{{\varvec{x_1}}}}})} \end{array} \right. \end{aligned}$$

(46)

where the observer gain ${\varphi _i}(\mathrm{{i}} = 1,2,3)$ is a positive constant, ${\tilde{{\varvec{x_1}}}}={\varvec{x_1}} - {\hat{{\varvec{x_1}}}}$ and ${\tilde{{\varvec{x_2}}}}={\varvec{x_2}} - {\hat{{\varvec{x_2}}}}$. By defining observation disturbance as ${\varvec{F_o}}$, ${\varvec{F_d}} = {\bar{{\varvec{ M_{\theta \theta }}}}}{({\varvec{x_1}})^{ - 1}}{\varvec{F_L}} + {\varvec{F_o}}$, ${\tilde{{\varvec{ x_3}}}}={\varvec{F_d}} - {\hat{{\varvec{x_3}}}}$, the error model of the observer can be obtained

(47)

Assumption 1

The disturbance ${\varvec{F_d}}$ meets Lipschitz continuity condition, and $\left\| {{{\varvec{F'_d}}}} \right\|$ is bounded.

According to Assumption 1 and Lemma 2, the observation error ${\tilde{{\varvec{x_i}}}}(i = 1,2,3)$ can converge to zero in finite time, that is, ${\hat{{\varvec{ x_3}}}} = {\varvec{F_d}}$.

The joint control input based on adaptive STA and HOSM extended state observer is designed as

$$\begin{aligned} \left\{ \begin{array}{*{20}{l}} {\bar{{\varvec{\tau }}} ={{\bar{{\varvec{\tau }} }}_{eq}} + {{\bar{{\varvec{\tau }} }}_{re}}}\\ {{{\bar{{\varvec{\tau }}}}_{eq}}={{\bar{{\varvec{C_r}}}}}({\varvec{x_1}},{\varvec{x_2}}) - {{\bar{{\varvec{F_\theta }}}}} + {{\bar{{\varvec{M_{\theta \theta }}}} }}({\varvec{x_1}})({{\ddot{{\varvec{x_{1d}}}}}}} \\ {- {\varvec{C_1}}{\varvec{H}}({\varvec{e}})\dot{{\varvec{e}}} - {\varvec{C_2}}{{\varvec{D}}^{{\varGamma _3} - 1}}({\varvec{e}})\dot{{\varvec{ e}}} - {{\hat{{\varvec{x_3}}}}})}\\ {{{\bar{{\varvec{\tau }}}}_{re}} = \mathrm{{ }}{{\bar{{\varvec{M}}_{\theta \theta }}}}({{\varvec{x_1}}})\mathrm{{(}} - {\varvec{K_1}}si{g^{1/2}}({\varvec{s}}) + {\varvec{\varpi }} \mathrm{{)}}} \end{array} \right. \end{aligned}$$

(48)

3.3 Controller design of the fast-varying subsystem

The fast-varying subsystem is a fully controllable linear system, and the dynamic equation can be written as

$$\begin{aligned} \frac{{{d^2}{\varvec{\zeta _2}}}}{{d{t_\varepsilon }^{^2}}} = - {\bar{ {\varvec{N_{qq}}}}}{\tilde{{\varvec{K_q}}}}{\varvec{\zeta _2}} + {\bar{{\varvec{N_{q\theta }}}}}{{\varvec{\tau _f}}} +{\varvec{f}} \end{aligned}$$

(49)

where ${\varvec{f}}$ is the lumped disturbances of the fast-varying system.

By defining ${\varvec{e_f}}={\varvec{\zeta _1}} - {\varvec{\zeta _{1d}}}$, the sliding surface is designed as

$$\begin{aligned} {\varvec{s_f}} = \frac{{d{{\varvec{e_f}}}}}{{d{t_\varepsilon }}} + {\varvec{C_3}}{\varvec{e_f}} \end{aligned}$$

(50)

The derivative of the ${s_f}$ is

$$\begin{aligned} \frac{{d{{\varvec{s_f}}}}}{{d{t_\varepsilon }}} = \frac{{{d^2}{\varvec{e_f}}}}{{d{t_\varepsilon }^2}} + {\varvec{C_3}}\frac{{d{{\varvec{e_f}}}}}{{d{t_\varepsilon }}}= - {\bar{{\varvec{N_{qq}}}}}{\tilde{{\varvec{K_q}}}}{\varvec{\zeta _2}} + {\bar{{\varvec{N_{q\theta }}}}}{\varvec{\tau _f}} + {\varvec{C_3}}{\varvec{\zeta _2}} + {\varvec{f}} \end{aligned}$$

(51)

Since ${\varvec{\zeta _2}}$ cannot be directly obtained, it is estimated by using the other HOSM extended state observer. This observer is designed as

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {\frac{{{{\hat{{\varvec{\zeta _1}}}}}}}{{d{t_\varepsilon }}} = {{\hat{{\varvec{\zeta _2}}}}} + {\varvec{\varphi _4}}si{g^{2/3}}({{\tilde{{\varvec{\zeta _1}}}}})}\\ {\frac{{{{\hat{{\varvec{\zeta _2}}}}}}}{{d{t_\varepsilon }}} = {{\hat{{\varvec{\zeta _3}}}}} - {{\bar{{\varvec{N_{qq}}}}}}{{\tilde{{\varvec{ K_q}}}}}{{\hat{{\varvec{\zeta _2}}}}} + {{\bar{{\varvec{N_{q\theta }}}}}}{\varvec{\tau _f}} + {\varvec{\varphi _5}}si{g^{1/3}}({{\tilde{{\varvec{\zeta _1}}}}})}\\ {\frac{{{{\hat{{\varvec{\zeta _3}}}}}}}{{d{t_\varepsilon }}} = {\varvec{\varphi _6}}{\textrm{sgn}} ({{\tilde{{\varvec{\zeta _1}}}}})} \end{array}} \right. \end{aligned}$$

(52)

where the observer gain ${\varvec{\varphi _i}}(\mathrm{{i}} = 4,5,6)$ is a diagonal matrix, ${\tilde{{\varvec{\zeta _1}}}}={\varvec{\zeta _1}} - {\hat{{\varvec{\zeta _1}}}}$, ${\tilde{{\varvec{\zeta _2}}}}={\varvec{\zeta _2}} - {\hat{{\varvec{\zeta _2}}}}$. By defining observation disturbance ${\varvec{f_o}}$, ${\varvec{f_d}} = {\varvec{f}} + {\varvec{f_o}}$, ${\tilde{{\varvec{\zeta _3}}}}={\varvec{f_d}} - {\hat{{\varvec{\zeta _3}}}}$, and the error model of the observer can be obtained

(53)

Assumption 2

The disturbance ${\varvec{f_d}}$ meets Lipschitz continuity condition, and $\left\| {{\varvec{f_d}}'} \right\|$ is bounded.

According to Assumption 2 and Lemma 2, the observation error ${\tilde{{\varvec{\zeta _i}}}}(i = 1,2,3)$ can converge to zero in finite time, that is, ${\varvec{\zeta _2}}={\hat{{\varvec{\zeta _2}}}}$.

The control torque of the fast-varying subsystem is designed as

$$\begin{aligned} {\varvec{\tau _f}}={\bar{{\varvec{N_{q\theta }}}}}^{ - 1}\left( {{{\bar{{\varvec{N_{qq}}}}}}{{\tilde{{\varvec{K_q}}}}}{{\hat{{\varvec{\zeta _2}}}}} - {\varvec{C_3}}{{\hat{{\varvec{\zeta _2}}}}} - {\varvec{C_4}}{\textrm{sgn}} ({\varvec{s_f}})} \right) \end{aligned}$$

(54)

The diagram of the composite controller can be seen in Fig. 3.

Fig. 3

Diagram of composite controller

4 Stability analysis

To prove the finite-time convergence of the controller, a special Lyapunov function is chosen. The stability of slow-varying subsystem and fast-varying subsystem are discussed separately.

4.1 Stability analysis of the slow-varying subsystem

To prove finite time convergence in the approach phase, a new state variable ${\varvec{\chi }}$ is defined

$$\begin{aligned} {\varvec{\chi }}=\left[ {\begin{array}{*{20}{c}} {{{\varvec{\chi _1}}}}\\ {{{\varvec{\chi _2}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{si}{{g}^{1/2}}({\varvec{s}})}\\ {\varvec{\varpi }} \end{array}}\right] \end{aligned}$$

(55)

The time derivative of ${\varvec{\chi }}$ is

$$\begin{aligned} \dot{{\varvec{\chi }}}= & {} \left[ {\begin{array}{*{20}{c}} {{{\dot{{\varvec{\chi _1}}}}}}\\ {{{\dot{{\varvec{\chi _2}}}}}} \end{array}} \right] =\left[ {\begin{array}{*{20}{c}} {\frac{1}{2}{{\varvec{D}}^{ - 1/2}}({\varvec{s}})\dot{{\varvec{s}}}}\\ {\dot{{\varvec{\varpi }}} } \end{array}} \right] \nonumber \\= & {} \left[ {\begin{array}{*{20}{c}} {\frac{1}{2}{{\varvec{D}}^{ - 1/2}}({\varvec{s}})( - {\varvec{K_1}}si{g^{1/2}}({\varvec{s}}) +{\varvec{\varpi }} + {\varvec{E_2}})}\\ { - \frac{1}{2}{\varvec{K_2}}{\textrm{sgn}} ({\varvec{s}})} \end{array}} \right] \nonumber \\= & {} - \frac{1}{2}{\left[ {\begin{array}{*{20}{c}} {{{\varvec{D}}^{ - 1/2}}({\varvec{s}})}&{}{\varvec{0}}\\ {\varvec{0}}&{}{{{\varvec{D}}^{ - 1/2}}({\varvec{s}})} \end{array}} \right] ^{ - 1}}\nonumber \\{} & {} \left( {\left[ {\begin{array}{*{20}{c}} {{\varvec{K_1}}}&{}{ - {\varvec{I}}}\\ {{\varvec{K_2}}}&{}{\varvec{0}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{si}{{g}^{1/2}}({\varvec{s}})}\\ {\varvec{\varpi }} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {{\varvec{E_2}}}\\ {\varvec{0}} \end{array}} \right] } \right) \nonumber \\= & {} - \frac{1}{2}\left[ {\begin{array}{*{20}{c}} {{{\left( {{{\varvec{D}}^{ - 1/2}}({\varvec{s}})} \right) }^{ - 1}}}&{}{\varvec{0}}\\ {\varvec{0}}&{}{{{\left( {{{\varvec{D}}^{ - 1/2}}({\varvec{s}})} \right) }^{ - 1}}} \end{array}} \right] \nonumber \\{} & {} \left( {{\varvec{A}}{\varvec{\chi }} - \left[ {\begin{array}{*{20}{c}} {{\varvec{E_2}}}\\ {\varvec{0}} \end{array}} \right] } \right) \nonumber \\= & {} - \frac{1}{2}\left[ {\begin{array}{*{20}{c}} {{{\left( {{{\varvec{D}}^{ - 1/2}}({\varvec{s}})} \right) }^{ - 1}}}&{}{\varvec{0}}\\ {\varvec{0}}&{}{{{\left( {{{\varvec{D}}^{ - 1/2}}({\varvec{s}})} \right) }^{ - 1}}} \end{array}} \right] \tilde{{\varvec{A}}}{\varvec{\chi }}\nonumber \\= & {} - \frac{1}{2}{\varvec{\varOmega _1}}\tilde{{\varvec{A}}}{\varvec{\chi }} \end{aligned}$$

(56)

where ${\varvec{\varOmega _1}}=\left[ {\begin{array}{*{20}{c}} {{{\left( {{{\varvec{D}}^{ - 1/2}}({\varvec{s}})} \right) }^{ - 1}}}&{}{\varvec{0}}\\ {\varvec{0}}&{}{{{\left( {{{\varvec{D}}^{ - 1/2}}({\varvec{s}})} \right) }^{ - 1}}} \end{array}} \right]$, ${\varvec{A}}=\left[ {\begin{array}{*{20}{c}} {{\varvec{K_1}}}&{}{ -{\varvec{I}}}\\ {{\varvec{K_2}}}&{}{\varvec{0}} \end{array}} \right]$, $\tilde{{\varvec{A}}}=\left[ {\begin{array}{*{20}{c}} {{\varvec{K_1}} - \eta {{\varvec{I}}}}&{}{ - {\varvec{I}}}\\ {{\varvec{K_2}}}&{}{\varvec{0}} \end{array}} \right]$.

Assumption 3

Supposing that the disturbance ${\varvec{E_2}}$ is bounded, ${\varvec{E_2}}$ can be expressed as

$$\begin{aligned} {\varvec{E_2}}=\eta ({\varvec{x_1}},t){si}{{g}^{1/2}}({\varvec{s}})=\eta ({\varvec{x_1}},t){\varvec{\chi _1}} \end{aligned}$$

(57)

where $0< \eta ({\varvec{x_1}},t) < \delta$.

To prove the stability, the following Lyapunov function is taken

$$\begin{aligned} V={V_0} + \frac{1}{{2{\gamma _1}}}\sum \limits _{i = 1}^2 {{{\left( {{K_{1i}} - {K_{1i}}^\mathrm{{*}}} \right) }^2}} + \frac{1}{{2{\gamma _2}}}\sum \limits _{i = 1}^2 {{{\left( {{K_{2i}} - {K_{2i}}^\mathrm{{*}}} \right) }^2}} \end{aligned}$$

(58)

where ${\gamma _1}$, ${\gamma _2}$ are positive constants, ${V_0}={{\varvec{\chi }} ^T}{\varvec{P}}{\varvec{\chi }}$, ${\varvec{P}}$ is a positive definite matrix.

$$\begin{aligned} {\varvec{P}} = \left[ {\begin{array}{*{20}{c}} {(\mu + 4{\kappa ^2}){{\varvec{I_{2 \times 2}}}}}&{}\quad {( - 2\kappa ){{\varvec{I_{2 \times 2}}}}}\\ {( - 2\kappa ){{\varvec{I_{2 \times 2}}}}}&{}{{{\varvec{I_{2 \times 2}}}}} \end{array}} \right] , \mu> 0,\kappa > 0 \end{aligned}$$

(59)

Combining eq. (56), the time derivative of ${V_0}$ can be deduced as

$$\begin{aligned}{} & {} {{\dot{V}}_0}={{\dot{{\varvec{\chi }} }}^T}{\varvec{P}}{\varvec{\chi }} + {{\varvec{\chi }} ^T}{\varvec{P}}\dot{{\varvec{\chi }}} \nonumber \\{} & {} \quad = - \frac{1}{2}\left( {{{\varvec{\chi }} ^T}{{\left( {\tilde{{\varvec{A}}}} \right) }^T}{\varvec{\varOmega _1}}{\varvec{P}}{\varvec{\chi }} + {{\varvec{\chi }} ^T}{\varvec{P}}{\varOmega _1}\tilde{{\varvec{A}}}{\varvec{\chi }} } \right) \nonumber \\{} & {} \quad = - \frac{1}{2}{{\varvec{\chi }} ^T}\left( {{{\left( {\tilde{{\varvec{A}}}} \right) }^T}{\varvec{\varOmega _1}}{\varvec{P}} + {\varvec{P}}{\varvec{\varOmega _1}}\tilde{{\varvec{A}}}} \right) {\varvec{\chi }} \nonumber \\{} & {} \quad = - \frac{1}{{2\left\| {{\varvec{\chi _1}}} \right\| }}{{\varvec{\chi }} ^T}\left( {{{\left( {\tilde{{\varvec{A}}}} \right) }^T}{\varvec{P}} + {\varvec{P}}\tilde{{\varvec{A}}}} \right) {\varvec{\chi }} \nonumber \\{} & {} \quad - \frac{1}{2}{{\varvec{\chi }} ^T}\left( {{{\left( {\tilde{{\varvec{A}}}} \right) }^T}{\varvec{\varOmega _2}}{\varvec{P}} + {\varvec{P}}{\varvec{\varOmega _2}}\tilde{{\varvec{A}}}} \right) {\varvec{\chi }} \nonumber \\{} & {} \quad = - \frac{1}{{2\left\| {{\varvec{\chi _1}}} \right\| }}{{\varvec{\chi }} ^T}\left( {{{\left( {\tilde{{\varvec{A}}}} \right) }^T}{\varvec{P}} + {\varvec{P}}\tilde{{\varvec{A}}}} \right) {\varvec{\chi }} \nonumber \\{} & {} \quad - \frac{1}{2}{{\varvec{\chi }} ^T}\left( {{{\left( {\tilde{{\varvec{A}}}} \right) }^T}{\varvec{P}} + {\varvec{P}} \tilde{{\varvec{A}}}} \right) {\varvec{\varOmega _2}}{\varvec{\chi }} \nonumber \\{} & {} \quad = - \frac{1}{{2\left\| {{\varvec{\chi _1}}} \right\| }}\left[ {{{\varvec{\chi }} ^T}\left( {{\varvec{Q_1}} + {\varvec{Q_2}}} \right) {\varvec{\chi }} } \right] \nonumber \\{} & {} \quad - \frac{1}{2}{{\varvec{\chi }} ^T}\left( {{\varvec{Q_1}} + {\varvec{Q_2}}} \right) {\varvec{\varOmega _2}}{\varvec{\chi }} \end{aligned}$$

(60)

where

$$\begin{aligned} {\varvec{Q_1}}= & {} \left[ {\begin{array}{*{20}{c}} {2{\varvec{K_1}}(\mu + 4{\kappa ^2}) - 4{\varvec{K_2}}\kappa }&{} * \\ {( - \mu - 4{\kappa ^2}){\varvec{I_{2 \times 2}}} - {\varvec{K_1}}\kappa + {\varvec{K_2}}}&{} \quad {4\kappa {\varvec{I_{2 \times 2}}}} \end{array}} \right] \end{aligned}$$

(61)

$$\begin{aligned} {\varvec{Q_2}}= & {} - \eta \left[ {\begin{array}{*{20}{c}} {2\left( {\mu + 4{\kappa ^2}} \right) {\varvec{I_{2 \times 2}}}}&{} \quad * \\ { - 2\kappa {\varvec{I_{2 \times 2}}}}&{} \quad {\varvec{0}} \end{array}} \right] \end{aligned}$$

(62)

$$\begin{aligned} {\varvec{\varOmega _2}}= & {} \left[ \begin{array}{*{20}{c}} {{{\left( {{{\varvec{D}}^{ - 1/2}}({\varvec{s}})} \right) }^{ - 1}} - \frac{1}{{\left\| {{\varvec{\chi _1}}} \right\| }}{\varvec{I_{2 \times 2}}}}&{}{\varvec{0}}\\ {\varvec{0}}&{}{{\left( {{{\varvec{D}}^{ - 1/2}}( {\varvec{s}})} \right) }^{ - 1}} \ \frac{1}{{\left\| {{\varvec{\chi _1}}} \right\| }}{I_{2 \times 2}} \end{array} \right] \nonumber \\ \end{aligned}$$

(63)

According to Assumption 3, it can be deducted that

$$\begin{aligned} \begin{array}{l} {{\dot{V}}_0}= - \frac{1}{{2\left\| {{\varvec{\chi _1}}} \right\| }}\left[ {{{\varvec{\chi }} ^T}\left( {{\varvec{Q_1}} + {\varvec{Q_2}}} \right) {\varvec{\chi }} } \right] - \frac{1}{2}{{\varvec{\chi }} ^T}\left( {{\varvec{Q_1}} + {\varvec{Q_2}}} \right) {\varvec{\varOmega _1}}{\varvec{\chi }} \\ \le - \frac{1}{{2\left\| {{\varvec{\chi _1}}} \right\| }}{{\varvec{\chi }} ^T}{\varvec{Q}}{\varvec{\chi _1}} - \frac{1}{2}{{\varvec{\chi }} ^T}{\varvec{Q}}{\varvec{\varOmega _1}}{\varvec{\chi }} \end{array} \end{aligned}$$

(64)

where

$$\begin{aligned} {\varvec{Q}}=\left[ {\begin{array}{*{20}{c}} {2{\varvec{K_1}}(\mu + 4{\kappa ^2}) - 4{\varvec{K_2}}\kappa - 2\delta \left( {\mu + 4{\kappa ^2}} \right) {\varvec{I_{2 \times 2}}}}&{} * \\ {\left( { - \mu - 4{\kappa ^2} + 2\kappa \delta } \right) {\varvec{I_{2 \times 2}}} - 2{\varvec{K_1}}\kappa + {\varvec{K_2}}}&{}{4\kappa {\varvec{I_{2 \times 2}}}} \end{array}} \right] \end{aligned}$$

(65)

By substituting ${\varvec{K_2}} = 2\kappa {\varvec{K_1}}$ into eq. (65), it can be obtained that

$$\begin{aligned} {\varvec{Q}}=\left[ {\begin{array}{*{20}{c}} {2{\varvec{K_1}}\mu - 2\delta \left( {\mu + 4{\kappa ^2}} \right) {\varvec{I_{2 \times 2}}}}&{} * \\ {( - \mu - 4{\kappa ^2} + 2\kappa \delta ){\varvec{I_{2 \times 2}}}}&{}{4\kappa {\varvec{I_{2 \times 2}}}} \end{array}} \right] \end{aligned}$$

(66)

The matrix ${\varvec{Q}}$ will be positive definite if

$$\begin{aligned} {K_{1i}} > \frac{{{{\left( {\mu + 4{\kappa ^2} + 2\kappa \delta } \right) }^2}}}{{8\mu \kappa }},i = 1,2 \end{aligned}$$

(67)

It is easy to prove that ${\varvec{\varOmega }} ={\varvec{Q}}{\varvec{\varOmega _1}}={\varvec{\varOmega _1}}{\varvec{Q}}$, where ${\varvec{\varOmega _1}}$ is a symmetric positive definite matrix. According to Lemma 1, when ${\varvec{Q}}$ is a symmetric positive definite matrix, ${\varvec{\varOmega }}$ is also a positive definite symmetric matrix. Thus, when (67) is satisfied, it can be deducted that

$$\begin{aligned} {{\dot{V}}_0}\le & {} - \frac{1}{{2\left\| {{\varvec{\chi _1}}} \right\| }}{{\varvec{\chi }} ^T}{\varvec{Q}}{\varvec{\chi }} - \frac{1}{2}{{\varvec{\chi }} ^T}{\varvec{Q}}{\varvec{\varOmega _1}}\chi \nonumber \\\le & {} - \frac{1}{{2\left\| {{\varvec{\chi _1}}} \right\| }}{{\varvec{\chi }} ^T}{\varvec{Q}}{\varvec{\chi }} \nonumber \\\le & {} - \frac{1}{{2\left\| {{\varvec{\chi _1}}} \right\| }}{\lambda _{\min }}({\varvec{Q}}){{\varvec{\chi }} ^T}{\varvec{\chi }} \nonumber \\= & {} - \frac{1}{{2\left\| {{\varvec{\chi _1}}} \right\| }}{\lambda _{\min }}({\varvec{Q}}){\left\| {\varvec{\chi }} \right\| ^2} \end{aligned}$$

(68)

where ${\lambda _{\min }}({\varvec{Q}})$ is the minimum eigenvalue of ${\varvec{Q}}$.

Since $\left\| {\varvec{\chi }} \right\| = \left\| {{\varvec{\chi _1}}} \right\| + \left\| {{\varvec{\chi _2}}} \right\| \ge \left\| {{\varvec{\chi _1}}} \right\|$ and $\frac{{V_0^{1/2}\left( {\varvec{\chi }} \right) }}{{\lambda _{\max }^{1/2}\left( {\varvec{P}} \right) }} \le \left\| {\varvec{\chi }} \right\| \le \frac{{V_0^{1/2}\left( {\varvec{\chi }} \right) }}{{\lambda _{\min }^{1/2}\left( {\varvec{P}} \right) }}$, it can be obtained that

$$\begin{aligned} {{\dot{V}}_0}\le & {} - \frac{1}{{2\left\| {{\varvec{\chi _1}}} \right\| }}{\lambda _{\min }}({\varvec{Q}}){\left\| {\varvec{\chi }} \right\| ^2}\nonumber \\\le & {} - \frac{1}{2}\frac{{{\lambda _{\min }}({\varvec{Q}})\lambda _{\min }^{1/2}\left( {\varvec{P}} \right) }}{{{\lambda _{\max }}\left( {\varvec{P}} \right) }}V_0^{1/2}\left( {\varvec{\chi }} \right) \nonumber \\= & {} - {r_1}{V_0}^{1/2} \end{aligned}$$

(69)

where ${\lambda _{\max }}\left( {\varvec{P}} \right)$ and ${\lambda _{\min }}\left( {\varvec{P}} \right)$ is the maximum and minimum eigenvalue of ${\varvec{P}}$ respectively, ${r_1}{=}\frac{1}{2}\frac{{{\lambda _{\min }}({\varvec{Q}})\lambda _{\min }^{1/2}\left( {\varvec{P}} \right) }}{{{\lambda _{\max }}\left( {\varvec{P}} \right) }}$.

$$\begin{aligned} \dot{V}= & {} {{\dot{V}}_0} + \frac{1}{{2{\gamma _1}}}tr\left[ {{{\left( {{\varvec{K_1}} - {\varvec{K_1}}^\mathrm{{*}}} \right) }^2}} \right] + \frac{1}{{2{\gamma _2}}}tr\left[ {{{\left( {{\varvec{K_2}} - {\varvec{K_2}}^\mathrm{{*}}} \right) }^2}} \right] \nonumber \\\le & {} - {r_1}{V_0}^{1/2} + \frac{1}{{2{\gamma _1}}}tr\left[ {{{\left( {{\varvec{K_1}} - {\varvec{K_1}}^\mathrm{{*}}} \right) }^2}} \right] \nonumber \\{} & {} + \frac{1}{{2{\gamma _2}}}tr\left[ {{{\left( {{\varvec{K_2}} - {\varvec{K_2}}^\mathrm{{*}}} \right) }^2}} \right] \nonumber \\\le & {} - {r_1}{V_0}^{1/2} + \frac{1}{{{\gamma _1}}}\sum \limits _{i = 1}^2 {{{\tilde{K}}_{1i}}{{\dot{K}}_{1i}}} + \frac{1}{{{\gamma _2}}}\sum \limits _{i = 1}^2 {{{\tilde{K}}_{2i}}{{\dot{K}}_{2i}}} \nonumber \\\le & {} \left( { - {r_1}{V_0}^{1/2} - \frac{{{k_1}}}{{\sqrt{2{\gamma _1}} }}\sum \limits _{i = 1}^2 {\left| {{{\tilde{K}}_{1i}}} \right| } - \frac{{{k_2}}}{{\sqrt{2{\gamma _2}} }}\sum \limits _{i = 1}^2 {\left| {{{\tilde{K}}_{2i}}} \right| } } \right) \nonumber \\{} & {} + \frac{{{k_1}}}{{\sqrt{2{\gamma _1}} }}\sum \limits _{i = 1}^2 {\left| {{{\tilde{K}}_{1i}}} \right| } \nonumber \\{} & {} + \frac{{{k_2}}}{{\sqrt{2{\gamma _2}} }}\sum \limits _{i = 1}^2 {\left| {{{\tilde{K}}_{2i}}} \right| } + \frac{1}{{{\gamma _1}}}\sum \limits _{i = 1}^2 {{{\tilde{K}}_{1i}}{{\dot{K}}_{1i}}} \nonumber \\{} & {} +\frac{1}{{{\gamma _2}}}\sum \limits _{i = 1}^2 {{{\tilde{K}}_{2i}}{{\dot{K}}_{2i}}} \end{aligned}$$

(70)

$$\begin{aligned} {{\dot{V}}_a}= & {} - {r_1}{V_0}^{1/2} - \frac{{{k_1}}}{{\sqrt{2{\gamma _1}} }}\sum \limits _{i = 1}^2 {\left| {{{\tilde{K}}_{1i}}} \right| } - \frac{{{k_2}}}{{\sqrt{2{\gamma _2}} }}\sum \limits _{i = 1}^2 {\left| {{{\tilde{K}}_{2i}}} \right| }\nonumber \\= & {} - \left( {{r_1}{V_0}^{1/2} + \frac{{{k_1}}}{{\sqrt{2{\gamma _1}} }}\sum \limits _{i = 1}^2 {\left| {{{\tilde{K}}_{1i}}} \right| } + \frac{{{k_2}}}{{\sqrt{2{\gamma _2}} }}\sum \limits _{i = 1}^2 {\left| {{{\tilde{K}}_{2i}}} \right| } } \right) \nonumber \\\le & {} - \left( {{\left( {{r_1}{V_0}^{1/2}} \right) }^2} + {{\left( {\frac{{{k_1}}}{{\sqrt{2{\gamma _1}} }}\sum \limits _{i = 1}^2 {\left| {{{\tilde{K}}_{1i}}} \right| } } \right) }^2} \right. \nonumber \\{} & {} \left. + {{\left( {\frac{{{k_2}}}{{\sqrt{2{\gamma _2}} }}\sum \limits _{i = 1}^2 {\left| {{{\tilde{K}}_{2i}}} \right| } } \right) }^2} \right) ^{1/2} \end{aligned}$$

(71)

where ${r_2}=\min ({r_1},{k_1},{k_2})$.

The adaptive gains ${K_{1i}}$ and ${K_{2i}}$ are bounded [40], that is, ${\tilde{K}_{1i}}< 0,{\tilde{K}_{2i}} < 0$, then

$$\begin{aligned} {{\dot{V}}_b}= & {} \frac{{{k_1}}}{{\sqrt{2{\gamma _1}} }}\sum \limits _{i = 1}^2 {\left| {{{\tilde{K}}_{1i}}} \right| } + \frac{{{k_2}}}{{\sqrt{2{\gamma _2}} }}\sum \limits _{i = 1}^2 {\left| {{{\tilde{K}}_{2i}}} \right| } \nonumber \\{} & {} + \frac{1}{{{\gamma _1}}}\sum \limits _{i = 1}^2 {{{\tilde{K}}_{1i}}{{\dot{K}}_{1i}}} + \frac{1}{{{\gamma _2}}}\sum \limits _{i = 1}^2 {{{\tilde{K}}_{2i}}{{\dot{K}}_{2i}}} \nonumber \\= & {} - \sum \limits _{i = 1}^2 {\left| {{{\tilde{K}}_{1i}}} \right| \left( {\frac{1}{{{\gamma _1}}}{{\dot{K}}_{1i}} - \frac{{{k_1}}}{{\sqrt{2{\gamma _1}} }}} \right) } \nonumber \\{} & {} - \sum \limits _{i = 1}^2 {\left| {{{\tilde{K}}_{2i}}} \right| \left( {\frac{1}{{{\gamma _2}}}{{\dot{K}}_{2i}} - \frac{{{k_2}}}{{\sqrt{2{\gamma _2}} }}} \right) } \end{aligned}$$

(72)

The time derivative of V is

$$\begin{aligned} \dot{V}={\dot{V}_a} + {\dot{V}_b} \le - {r_2}{V^{1/2}} + {\dot{V}_b} \end{aligned}$$

(73)

The ${\dot{V}_b}$ is discussed in the following three situations.

Case1. when $\left| {{s_i}} \right| > \alpha _a (i = 1,2)$ and ${K_{1i}} > {K_m}$, the adaptive gain takes ${\dot{K}_{1i}}={k_1}\sqrt{\frac{{{\gamma _1}}}{2}}$ and ${\dot{K}_{2i}}=2\kappa {\dot{K}_{1i}}$. By setting $\kappa =\frac{{{k_2}}}{{2{k_1}}}\sqrt{\frac{{{\gamma _2}}}{{{\gamma _1}}}}$, then, ${\dot{V}_b}=0$ and

$$\begin{aligned} \dot{V}={\dot{V}_a} \le - {r_2}{V^{1/2}} \end{aligned}$$

(74)

The ${K_{1i}}$ will increase in accordance with ${\dot{K}_{1i}}={k_1}\sqrt{\frac{{{\gamma _1}}}{2}}$ until (67) and (74) is satisfied. The sliding surface will reach a very small range $\left| {{s_i}} \right| \le {\alpha _a}$ in finite time.

Case2. When $\left| {{s_j}} \right| < \alpha _a (j = 1 or j = 2)$, the adaptive gain takes the following form

$$\begin{aligned} {\dot{K}_{1j}} = \left\{ {\begin{array}{*{20}{c}} { - {k_1}\sqrt{\frac{{{\gamma _1}}}{2}} , if {K_{1j}} > {K_m}}\\ {\beta _a ,if {K_{1j}} \le {K_m}} \end{array}} \right. \end{aligned}$$

(75)

and

$$\begin{aligned} {\dot{V}_b} = \left\{ \begin{array}{*{20}{c}} { - \left| {{{\tilde{K}}_{1j}}} \right| \left( { - \frac{{2{k_1}}}{{\sqrt{2{\gamma _1}} }}} \right) \mathrm{{,if }}{K_{1j}} > {K_m}}\\ - \left| {{K_m} + \eta .t - {K_{1j}}^\mathrm{{*}}} \right| \left( {\frac{\beta _a }{{{\gamma _1}}} - \frac{{{k_1}}}{{\sqrt{2{\gamma _1}} }}} \right) , \qquad \qquad \\ \mathrm{{if }}{K_{1j}} \le {K_m} \end{array} \right. \end{aligned}$$

(76)

When ${K_{1j}} \le {K_m}$, ${K_{1j}}$ will increase linearly with speed $\beta _a$ until ${K_{1j}} > {K_m}$. If ${K_{1j}} > {K_m}$, it is easy to determine that ${\dot{V}_b} > 0$. According to eq. (72), the sign of Lyapunov function may change, and then $\left| {{s_j}} \right|$ may be greater than $\alpha _a$. Once $\left| {{s_j}} \right| > \alpha _a$, the condition of case1 is met, the sliding surface ${s_j}$ will reach a small range $\left| {{s_j}} \right| \le {\alpha _a}$ again in finite time. Finally, the sliding mode variable will converge in a neighborhood $\left| {{s_j}} \right| \le {\alpha _m}({\alpha _m} > \alpha _a )$ in finite time.

Case3. When $\left| {{s_i}} \right| < \alpha _a \mathrm{{(}}i = 1\mathrm{{,2}})$

$$\begin{aligned} {\dot{V}_b} = \left\{ \begin{array}{*{20}{c}} { - \sum \limits _{i = 1}^2 {\left| {{{\tilde{K}}_{1i}}} \right| \left( { - \frac{{2{k_1}}}{{\sqrt{2{\gamma _1}} }}} \right) \mathrm{{, if }}{K_{1i}} > {K_m}} }\\ - \sum \limits _{i = 1}^2 \left| {{K_m} + \eta .t - {K_{1i}}^\mathrm{{*}}} \right| \left( {\frac{\beta _a }{{{\gamma _1}}} - \frac{{{k_1}}}{{\sqrt{2{\gamma _1}} }}} \right) , \qquad \qquad \\ \mathrm{{if }}{K_{1i}} \le {K_m} \end{array} \right. \end{aligned}$$

(77)

the sliding mode variable will converge in a neighborhood $\left| {{s_j}} \right| \le {\alpha _m}({\alpha _m} > \alpha _a )$ in finite time as case2.

In sliding phase, the tracking errors converge to a small designed domain $\delta$ within a fixed-time ${T_s}$, when the nonsingular fixed-time sliding eq. (41) is adopted [22]. ${T_s} \le \frac{2}{{{c_1}(2 - {\varGamma _1})}} + \frac{2}{{{c_2}({\varGamma _3} - 1)}}$, where ${c_1}$, ${c_2}$ is respectively the minimum component of ${\varvec{C_1}}$, ${\varvec{C_2}}$.

According to the above cases, the finite time stability of the slow-varying subsystem has been proved.

4.2 Stability analysis of the fast-varying subsystem

The following Lyapunov function is chosen

$$\begin{aligned} {V_f} = \frac{1}{2}{\varvec{s_f}}^T{\varvec{s_f}} \end{aligned}$$

(78)

By combining eq. (51), the derivative of ${V_f}$ with respect to fast-varying time can be written as

$$\begin{aligned}{} & {} \frac{{d{V_f}}}{{d{t_\varepsilon }}} = {\varvec{s_f}}^T\frac{{d{\varvec{s_f}}}}{{d{t_\varepsilon }}}\nonumber \\{} & {} \quad ={\varvec{s_f}}^T( - {{\bar{{\varvec{N_{qq}}}}}}{{\tilde{{\varvec{ K_q}}}}}{\varvec{\zeta _2}} + {{\bar{{\varvec{N_{q\theta }}}}}}{\varvec{\tau _f}} + {\varvec{C_3}}{\varvec{\zeta _2}} + {\varvec{f_d}})\nonumber \\{} & {} \quad ={\varvec{s_f}}^T\left( {{\varvec{f_d}} - {\varvec{C_4}}{\textrm{sgn}} ({\varvec{s_f}})} \right) \nonumber \\{} & {} \quad \le 0 \end{aligned}$$

(79)

The stability of the fast-varying subsystem has been proved.

5 Simulation studies

In this section, to illustrate the effectiveness of the proposed controller, the simulations are conducted to show the performance improvement compared with the existing finite-time convergence controllers. The numerical simulations are carried out by combining ADAMS and MATLAB. A computer with 6 cores and 12 threads CPU is used for simulation calculation. The discrete method is used to simplify the hydrodynamic force. Specifically, each manipulator is divided into 10 units, and the water resistance and additional mass force are loaded at the midpoint of each unit. The velocity and acceleration of the midpoint of the unit are taken as the velocity and acceleration of the whole unit, as seen in Fig. 4a.

The size of the manipulators and the submarine are reduced proportionally to the actual object. The length of the manipulators are set as ${l_1} = 0.975m$, ${l_2} = 1\,m$; the distance between the manipulator base and the rotation axis of the submarine is ${l_0} = 2.0m$; the bending stiffness of the flexible manipulator is $EI = 5.3125 \times {10^4}N \cdot {m^2}$; the density of the manipulators are ${\rho _1}=13.507kg/m$, ${\rho _2}=12.363kg/m$; the hydrodynamic coefficients are ${\rho _f} = 1025.9kg/{m^3}$, ${C_D} = 1.1$, ${C_M} = 1$.

Fig. 4

a Hydrodynamic load of manipulator, b desired trajectory of end actuator

The desired trajectory of the manipulator end-effector is a circle trajectory (Fig. 4b), which is given as

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{x_d} = - \mathrm{{1}}\mathrm{{.775 + 0}}\mathrm{{.2}} \times \mathrm{{cos(}}\pi \mathrm{{ + 2}} \times \mathrm{{t)}}}\\ {{y_d} = \mathrm{{0}}\mathrm{{.6 + 0}}\mathrm{{.2}} \times \mathrm{{sin(}}\pi \mathrm{{ + 2}} \times \mathrm{{t)}}} \end{array}} \right. \end{aligned}$$

(80)

Table 1 The parameter values of the controllers

The motion parameters of the submarine are $X = - 0.1 \times t,Y = 0.01 \times t, \alpha = 0.02*t$. The lumped disturbances contain model errors and the external disturbances. The model uncertainty comes from two aspects: (a) The AMM is used to model the flexible body and the high-order mode is ignored, which produces certain modeling error compared with the flexible body established by ADAMS. (b) The geometry of physical model is irregular, and the end load is regarded as a particle, which has geometric modeling errors. The external disturbance is Y-direction disturbance of the submarine, which is set as ${Y_L}=0.02 \times \sin (t)$. In addition, we also take into account the measurement error of the joints and the maximum measurement error is 0.006rad. The initial positions of the two joints are ${\varvec{\theta _0}} = [\pi /12,\pi /12]$.

5.1 Results

Case study 1

To verify the fast finite-time stability of the ANFSMC, the simulation comparisons are performed with the NFTSMC [18] and integral fast terminal sliding mode controller(IFTSMC) [47]. In order to facilitate comparison, the same HOSM observer and adaptive super-twisting approach law are adopted.

The sliding surface of NFTSMC is given as

$$\begin{aligned} {\varvec{s}} = {\varvec{e}} + {\varvec{C_5}}si{g^{{\varGamma _4}}}({\varvec{e}}) + {\varvec{C_6}}si{g^{{\varGamma _5}}}(\dot{{\varvec{e}}}) \end{aligned}$$

(81)

where ${\varGamma _5}={p_1}/{p_2}$, ${p_1}$ and ${p_2}$ are positive odd numbers, $1< {\varGamma _5} < 2$ and ${\varGamma _4} > {\varGamma _5}$.

The derivative of sliding mode surface is

$$\begin{aligned} \dot{{\varvec{s}}}=\dot{{\varvec{e}}} + {\varGamma _4}{\varvec{C_5}}{{\varvec{D}}^{{\varGamma _4} - 1}}({\varvec{e}})\dot{{\varvec{e}}} + {\varGamma _5}{\varvec{C_6}}{{\varvec{D}}^{{\varGamma _5} - 1}}(\dot{{\varvec{e}}})\ddot{{\varvec{e}}} \end{aligned}$$

(82)

The control input is given as

$$\begin{aligned} \bar{{\varvec{\tau }}}= & {} {{\bar{{\varvec{C_r}}}}}({\varvec{x_1}},{\varvec{x_2}}) + {{\bar{{\varvec{ M_{\theta \theta }}}}}}({\varvec{x_1}})({{\ddot{{\varvec{x_{1d}}}}}} + ( - {\varvec{I_{2 \times 2}}}\nonumber \\{} & {} - {\varGamma _4}{\varvec{C_5}}{{\varvec{D}}^{{\varGamma _4} - 1}}({\varvec{e}})) \cdot {({\varGamma _5}{\varvec{C_6}})^{ - 1}}\nonumber \\{} & {} \cdot si{g^{2 - {\varGamma _5}}}(\dot{{\varvec{e}}}) - {{\hat{{\varvec{x}}_3}}}) + {{\bar{{\varvec{ M_{\theta \theta }}}}}}({\varvec{x_1}})\mathrm{{(}} - {\varvec{K_1}}si{g^{1/2}}({\varvec{s}}) \nonumber \\ {}{} & {} + {\varvec{\varpi }} \mathrm{{)}} - {{\bar{{\varvec{F_\theta }}}} } \end{aligned}$$

(83)

The sliding surface of IFTSMC is given as

$$\begin{aligned} {\varvec{s}} = {\varvec{z}} + {\varvec{C_7}}\int _0^t {si{g^{{\varGamma _6}}}({\varvec{z}})} + {\varvec{C_8}}\int _0^t {si{g^{{\varGamma _7}}}({\varvec{z}})} \end{aligned}$$

(84)

where ${\varvec{z}} = \dot{{\varvec{e}}}+ {\varvec{C_9}}{\varvec{e}}$ is an auxiliary term, ${\varGamma _6} > 1$ and $0< {\varGamma _7} < 1$ are positive constants.

The derivative of sliding mode surface is

$$\begin{aligned} \dot{{\varvec{s}}}=\dot{{\varvec{z}}} + {\varvec{C_7}}si{g^{{\varGamma _6}}}({\varvec{z}}) + {\varvec{C_8}}si{g^{{\varGamma _7}}}({\varvec{z}}) \end{aligned}$$

(85)

The control input is given as

$$\begin{aligned} \bar{{\varvec{\tau }}}= & {} {{\bar{{\varvec{C_r}}}}}({\varvec{x_1}},{\varvec{x_2}}) + {{\bar{{\varvec{ M_{\theta \theta }}}}}}({\varvec{x_1}})({{\ddot{{\varvec{x_{1d}}}}}}- {\varvec{C_9}}\dot{{\varvec{z}}} \nonumber \\{} & {} - {\varvec{C_7}}\int _0^t {si{g^{{\varGamma _6}}}({\varvec{z}})} - {\varvec{C_8}}\int _0^t {si{g^{{\varGamma _7}}}({\varvec{z}}) - {{\hat{{\varvec{x}}_3}}}} )\nonumber \\{} & {} + {{\bar{{\varvec{ M_{\theta \theta }}}}}}({\varvec{x_1}})\mathrm{{(}} - {\varvec{K_1}}si{g^{1/2}}({\varvec{s}}) + {\varvec{\varpi }} \mathrm{{)}} - {{\bar{{\varvec{F_\theta }}}}} \end{aligned}$$

(86)

The control parameters of Case study 1 should ensure that the first-order vibration modes and control torques of the flexible manipulator under three different controllers are in a relatively similar range. The control parameters of Case study 1 and Case study 2 are selected by numerous tests until an optimal performance is obtained, which is listed in Table 1.

The tracking trajectory of the three controllers are shown in Figs. 5, 6, 7, 89, where Figs. 5, 6 show the tracking trajectory of two joint angles, and Figs. 7, 8 and 9 show the tracking trajectory of the end-effector. According to Figs. 5 and 6, the trajectories of joint angles under three control strategies reach a small neighborhood, which is close to the desired value after t=0.3s. The convergence speed of the two joints under ANFSMC is faster than the other two controllers. In the initial stage, joint trajectories under ANFSMC have less chattering than the joint trajectories under NFTSMC and IFTSMC. In addition, it can be seen that the trajectory of joint 2 under NFTSMC and IFTSMC have an overshoot. After reaching steady state, the ANFSMC has a smaller tracking error than NFTSMC and IFTSMC. According to Figs. 7, 8 and 9, in the initial stage, although the NFTSMC has a faster response speed, the trajectory of the end-effector has obvious chattering in the X direction and has large overshoot in the Y direction. The chattering and overshoot under IFTSMC are smaller than those of NFTSMC. The initial convergence accuracy of IFTSMC is less than that of the other two controllers. After reaching steady state, the ANFSMC has a smaller tracking error and less chattering in the X and Y directions than NFTSMC and IFTSMC.

Fig. 5

Tracking trajectory of joint 1

Fig. 6

Tracking trajectory of joint 2

Fig. 7

X-direction tracking trajectory of end actuator

Fig. 8

Y-direction tracking trajectory of end actuator

Fig. 9

Tracking trajectory of end actuator

The tracking error of the manipulator is shown in Figs. 10, 11, 12 and 13. From Figs. 10 and 11, the NFTSMC and IFTSMC have more chattering than ANFSMC in the steady state. Although the steady error of three controllers is less than 0.005 rad, the steady error of ANFSMC is smaller than that of the other two controllers. According to Fig. 11, the maximum overshoot of NFTSMC and IFTSMC reaches 0.4 rad and 0.1 rad respectively. Figures 12 and 13 show the end position tracking error of the flexible manipulator. From Figs. 12 and 13, the ANFSMC converges faster than the other two controllers. In the first 0.1s, although the response speed of NFTSMC is the fastest, its convergence time is longer than the other two controllers due to the chattering and overshoot.

Fig. 10

Tracking error of joint 1

Fig. 11

Tracking error of joint 2

Fig. 12

X-direction tracking error of end actuator

Fig. 13

Y-direction tracking error of end actuator

Figure 14 shows the first-order mode of the flexible manipulator, which reflects the vibration of the flexible manipulator. From Fig. 14, it can be seen that the first-order vibration mode under ANFSMC and IFTSMC are close at the initial stage, and the first-order mode under IFTSMC are slightly larger than that of ANFSMC. The first-order vibration mode under IFTSMC is maximal, reaching 0.003m. After reaching steady state, the first-order mode under NFTSMC fluctuates more greatly than that of IFTSMC and ANFSMC.

Figures 15 and 16 shows the input torques of the joints. In the initial state, the input torques of NFTSMC are much greater than those of IFTSMC and ANFSMC. After reaching steady state, the input torques of the three controllers is limited to a relatively close range, and the control input torques of AFTSMC is slightly smaller than those of the other two controllers.

Fig. 14

The first-order mode of flexible manipulator

Fig. 15

Input torque of joint 1

Fig. 16

Input torque of joint 2

Fig. 17

a Estimated position of joint 1, b estimated position of joint 2, c estimated velocity of joint 1, d estimated velocity of joint 2

Fig. 18

a Estimated value of ${\zeta _{11}}$, b estimated value of ${\zeta _{12}}$, c estimated value of ${\zeta _{21}}$, d estimated value of ${\zeta _{22}}$

Figures 17 and 18 show the observed values of the HOSM observer for the slow-varying and fast-varying subsystems respectively. As can be seen from Figs. 17 and 18, both of the two extended state observers have high observation accuracy, and the estimation errors of joint variables and fast-varying state variables can converge to a smaller error range within a relatively short time.

To further compare the control performance of the three control strategies, the root mean square error (RMSE) of the tracking trajectory, and average flexible displacement (AFD) of end-effector are introduced, which are defined as:

$$\begin{aligned} {E_\varLambda }= & {} \sqrt{\frac{1}{{{N_{t1}}}}\sum \limits _{i = 1}^{{N_{t1}}} {{e_\varLambda }^2(i)} } \end{aligned}$$

(87)

$$\begin{aligned} {w_A}= & {} \sqrt{\frac{1}{{{N_{t2}}}}\sum \limits _{i = 1}^{{N_{t2}}} {{w^2}(i)} } \end{aligned}$$

(88)

where ${N_t}$ is the number of simulation steps, $\varLambda$ denotes the position of joint angle and end-effector, $\varLambda \in \left\{ {{\theta _1},{\theta _2},X,Y,\sqrt{{X^2} + {Y^2}} } \right\}$.

The steady-state error is calculated in the time interval t=[0.3,2*pi]s. The statistical values of the RMSE and the AFD under three controllers are shown in Table 2.

From Table 2, it can be seen that the steady-state tracking error and flexible vibration under the ANFSMC are less than those under the NFTSMC and IFTSMC. Compared with the NFTSMC, ANFSMC can reduce the errors of the two joints by 41.18$\%$ and 36.11$\%$ respectively, the end-effector by 34.29$\%$, and the flexible vibration by 61.79$\%$. Compared with the IFTSMC, ANFSMC can reduce the errors of the two joints by 48.72$\%$ and 17.86$\%$ respectively, the end-effector by 41.03$\%$, and the flexible vibration by 22.89$\%$.

Case study 2

To verify the vibration suppression effect of the ANFSMC, the simulation comparisons are performed with the NFSMC. The ANFSMC and NFSMC adopt the same equivalent control law ${\bar{\tau }_{eq}}$ and the control parameters are listed in Table 1.

The control law of NFSMC [22] is given as

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {\bar{{\varvec{\tau }}} = {{\bar{{\varvec{\tau }}} }_{eq}} + {{\varvec{\tau }}_0}}\\ {{{\varvec{\tau }} _0} = - {{\varvec{C}}_{10}}si{g^{{\varGamma _8}}}(s) - {{\varvec{C}}_{11}}si{g^{{\varGamma _9}}}(s)} \end{array}} \right. \end{aligned}$$

(89)

where ${{\varvec{C}}_{10}}$ and ${{\varvec{C}}_{11}}$ are constant matrix.

Figures 19 and 20 show the trajectory tracking results of the manipulator under ANFSMC and NFSMC. According to Figs. 19 and 20, compared with NFSMC, ANFSMC has smaller overshoot, faster convergence speed and higher control accuracy. Figure 21 shows the first-order mode of the flexible manipulator. Figures 22 and 23 shows the control torques of the two joints. According to Figs. 22 and 23, the first-order mode and control input torques of the transient and steady-state under ANFSMC are much smaller than those under NFSMC.

From Table 2, it can be seen that the steady-state tracking error and flexible vibration under the NFSMC are much larger than those under the ANFSMC. Compared with the NFSMC, ANFSMC can reduce the errors of the two joints by 44.44$\%$ and 8$\%$ respectively, the end-effector by 45.88$\%$, and the flexible vibration by 57.34$\%$.

Figures 24 and 25 show the nephogram of the flexible manipulator at t=0.1s and t=2.4s respectively. It can be seen from the figures that the strain value of the flexible manipulator under ANFSMC is much smaller than that under NFSMC, which further confirms the good vibration suppression effect of ANFSMC.

Table 2 The tracking errors and flexible displacement comparison

Fig. 19

Tracking trajectory of joint 1

Fig. 20

Tracking trajectory of joint 2

Fig. 21

The first-order mode of flexible manipulator

Fig. 22

Input torque of joint 1

Fig. 23

Input torque of joint 2

5.2 Discussion

The simulation of Case study 1 has verified the effectiveness of the proposed extended state observers, which can accurately identify the lumped disturbance and derivatives of flexible modes. The trajectory tracking results show that the proposed ANFSMC has a faster convergence speed than NFTSMC and IFTSMC, because the sliding time of the ANFSMC is independent of the initial states and models, which can be calculated in advance. Furthermore, some parameters of the NFTSMC and IFTSMC needs to satisfy the conditions of odd integers, therefore, the ANFSMC has more freedom in parameter selection, which makes it easier to obtain parameters with fast convergence performance. Compared with IFTSMC, joint 1 under NFTSMC converges faster, while joint 2 under NFTSMC converges slower. This is because the convergence speed of IFTSMC and NFTSMC is related to the initial state. NFTSMC has a faster response in the initial stage, and joint 1 can quickly converge to the desired trajectory. Joint 2 is the joint of the flexible manipulator. Under the large input torque, the flexible manipulator will produce significant deformation, thus delaying the convergence of joint 2. Compared with the other two controllers, the ANFSMC has less vibration and tracking error, which is due to the chosen continuous nonlinear function. The application of this function makes the input torque smoother, which effectively reduces sliding mode chattering and overshoot, and suppresses flexible vibration caused by high-frequency excitation forces.

Simulation in Case study 2 shows that ANFSMC can significantly suppress the chattering and flexible vibration, and has better control accuracy than NFSMC. This is because adaptive STA hides the discontinuous switching term in the differential part of the control input to reduce chattering, and retains the dynamic characteristics of the first-order sliding modes. The application of the adaptive law can enhance the convergence speed of the STA and ensure the smoothness of the control without knowing the upper bound of the lumped disturbance in advance.

Fig. 24

a The strain of flexible manipulator under NFSMC at t = 0.1s, b the strain of flexible manipulator under ANFSMC at t = 0.1s

Fig. 25

a The strain of flexible manipulator under NFSMC at t = 2.4 s, b the strain of flexible manipulator under ANFSMC at t = 2.4s

The proposed control method combines the advantages of fast convergence of fixed time SMC and small chattering of adaptive STA, and used a high-order sliding mode state observer to compensate lumped disturbance, which effectively improve the control accuracy and suppression of vibration.

6 Conclusion and future work

In this paper, the dynamic equation of moving-based UFM is established for the first time. Based on the dynamic equation, the trajectory tracking control and vibration suppression of moving-base UFM are studied, and an ANFSMC is proposed. Two HOSM observers are used to estimate the lumped disturbance of the slow-varying subsystem and the first two mode derivatives of the fast-varying subsystem respectively. This control method combines the advantages of fixed -time sliding mode controller and STA. The simulation results indicate that, ANFSMC can converge to the stable state faster than NFTSMC and IFTSMC. In addition, ANFSMC can reduce excessive compensation through adaptive gain adjustment, and at the same time, STA can effectively avoid the oscillation caused by unsaturated function, so as to improve the trajectory tracking performance of moving-base UFM, which is of great significance for the underwater collaborative application of large submersible vehicles and AUVs. Although this paper presents the derivation of the hydrodynamic and dynamic model for a moving-base underwater flexible manipulator, its high computational complexity limits practical applications of multi-link underwater flexible manipulators. Future research may focus on developing simplified computational methods for the dynamic model. Furthermore, this paper only addresses hydrodynamic forces and control algorithms in two-dimensional motion; however, investigating the more complex dynamic model and coupling response of flexible manipulators in three-dimensional motion is essential for future studies.

Appendix

$$\begin{aligned} {M_{11}}= & {} {\rho _1}\int _0^{{l_1}} {{x_1}^2} d{x_1} + {\rho _2}\int _0^{{l_2}} {\left( {{l_1}^2 + {x_2}^2} \right) } d{x_2} \nonumber \\{} & {} + {\rho _2}\sum \limits _{i = 1}^2 {\int _0^{{l_2}} {{\phi _i}^2} } {q_i}^2d{x_2}\nonumber \\{} & {} + 2{\rho _2}\int _0^{{l_2}} {{l_1}{x_2}\cos {\theta _2}} d{x_2} - 2{\rho _2}\nonumber \\ {}{} & {} \sum \limits _{i = 1}^2 {\int _0^{{l_2}} {{l_1}{\phi _i}} } {q_i}\sin {\theta _2}d{x_2} \nonumber \\{} & {} +\left( {l_1}^2 + {l_2}^2 + 2{l_1}{l_2}\cos {\theta _2} + \sum \limits _{i = 1}^2 {{\phi _i}^2({l_2})} {q_i}^2 \right. \nonumber \\{} & {} \left. - 2{l_1}\sin {\theta _2}\sum \limits _{i = 1}^2 {{\phi _i}} ({l_2}){q_i} \right) m \end{aligned}$$

(A1)

$$\begin{aligned} {M_{12}}= & {} {\rho _2}\int _0^{{l_2}} {{x_2}^2d{x_2} + } {\rho _2}\sum \limits _{i = 1}^2 {\int _0^{{l_2}} {{\phi _i}^2} } {q_i}^2d{x_2}\nonumber \\{} & {} + {\rho _2}\int _0^{{l_2}} {{l_1}{x_2}\cos {\theta _2}d{x_2}} \nonumber \\{} & {} - {\rho _2}\sum \limits _{i = 1}^2 {\int _0^{{l_2}} {{l_1}{\phi _i}{q_i}\sin {\theta _2}d{x_2}} } + \left( {l_2}^2 + {l_1}{l_2}\cos {\theta _2} \right. \nonumber \\{} & {} \left. + \sum \limits _{i = 1}^2 {{\phi _i}^2} ({l_2}){q_i}^2 { - {l_1}\sin {\theta _2}\sum \limits _{i = 1}^2 {{\phi _i}({l_2})} {q_i}} \right) m \end{aligned}$$

(A2)

$$\begin{aligned} {M_{13}}= & {} {\rho _2}\int _0^{{l_2}} {{l_1}{\phi _1}\cos {\theta _2}d{x_2} + {\rho _2}\int _0^{{l_2}} {{x_2}{\phi _1}d{x_2}} } \nonumber \\{} & {} +\left( {{l_1}{\phi _1}({l_2})\cos {\theta _2} + {l_2}{\phi _1}({l_2})} \right) m \end{aligned}$$

(A3)

$$\begin{aligned} {M_{14}}= & {} {\rho _2}\int _0^{{l_2}} {{l_1}{\phi _2}\cos {\theta _2}d{x_2} + {\rho _2}\int _0^{{l_2}} {{x_2}{\phi _2}d{x_2}} }\nonumber \\{} & {} +\left( {{l_1}{\phi _2}({l_2})\cos {\theta _2} + {l_2}{\phi _2}({l_2})} \right) m \end{aligned}$$

(A4)

$$\begin{aligned} {M_{22}}= & {} {\rho _2}\int _0^{{l_2}} {{x_2}^2d{x_2} + {\rho _2}\sum \limits _{\mathrm{{i = }}1}^2 {\int _0^{{l_2}} {{\phi _\mathrm{{i}}}^2{q_\mathrm{{i}}}^2d{x_2}} } } \nonumber \\{} & {} + \left( {{l_2}^2 + \sum \limits _{i = 1}^2 {{\phi _i}^2({l_2}){q_i}^2} } \right) m \end{aligned}$$

(A5)

$$\begin{aligned} {M_{23}}= & {} {\rho _2}\int _0^{{l_2}} {{x_2}{\phi _1}} d{x_2} + {l_2}{\phi _1}({l_2})m \end{aligned}$$

(A6)

$$\begin{aligned} {M_{24}}= & {} {\rho _2}{\int _0^{{l_2}} {{x_2}\phi } _2}d{x_2} + {l_2}{\phi _2}({l_2})m \end{aligned}$$

(A7)

$$\begin{aligned} {M_{33}}= & {} {\rho _2}\int _0^{{l_2}} {{\phi _1}^2d{x_2}} + {\phi _1}^2({l_2})m \end{aligned}$$

(A8)

$$\begin{aligned} {M_{34}}= & {} 0 \end{aligned}$$

(A9)

$$\begin{aligned} {M_{44}}= & {} {\rho _2}\int _0^{{l_2}} {{\phi _2}^2} d{x_2} + {\phi _2}^2({l_2})m \end{aligned}$$

(A10)

$$\begin{aligned} {K_{q1}}= & {} EI\int _0^{{l_2}} {{{\left( {{{\phi ''}_1}} \right) }^2}} d{x_2} \end{aligned}$$

(A11)

$$\begin{aligned} {K_{q2}}= & {} EI\int _0^{{l_2}} {{{\left( {{{\phi ''}_2}} \right) }^2}} d{x_2} \end{aligned}$$

(A12)

$$\begin{aligned} {C_{r1}}= & {} \frac{1}{2}{\rho _1}\Bigg \{ - {l_1}^2\left( {{\ddot{x}}_0}\sin \left( {{\theta _1} - \alpha } \right) - {{\ddot{y}}_0}\cos \left( {{\theta _1} - \alpha } \right) \right. \\{} & {} \left. + {l_0}\dot{\alpha }\cos {\theta _1}\right) - \frac{{2{l_1}^3}}{3}\ddot{\alpha }\\{} & {} - {l_0}{l_1}^2\ddot{\alpha }\sin {\theta _1} - {l_0}{l_1}^2\dot{\alpha }{{\dot{\theta }}_1}\cos {\theta _1}\Bigg \} \\{} & {} +\frac{1}{2}\Bigg \{ - 2\left( {{\rho _2}{l_2} + m} \right) {l_1}^2\ddot{\alpha }- 2\left( {\frac{1}{3}{\rho _2}{l_2} + m} \right) {l_2}^2\ddot{\alpha }\\{} & {} - 2\sum \limits _{i = 1}^2 {\left( {{\rho _2}\int _0^{{l_2}} {{\phi _i}^2dx} + {\phi _i}^2({l_2})m} \right) {q_i}^2} \ddot{\alpha }\\{} & {} +4\sum \limits _{i = 1}^2 {\left( {{\rho _2}\int _0^{{l_2}} {{\phi _i}^2dx + {\phi _i}^2({l_2})m} } \right) } \\{} & {} {q_i}{{\dot{q}}_i}\left( {{{\dot{\theta }}_1} + {{\dot{\theta }}_2} - \dot{\alpha }} \right) - 4\left( {\frac{1}{2}{\rho _2}{l_2} + m} \right) {l_1}{l_2}\ddot{\alpha }\cos {\theta _2}\\{} & {} - 2\left( {\frac{1}{2}{\rho _2}{l_2} + m} \right) {l_1}{l_2}\\{} & {} \left( {2{{\dot{\theta }}_1} + {{\dot{\theta }}_2} - 2\dot{\alpha }} \right) {{\dot{\theta }}_2}\sin {\theta _2} \\{} & {} - 2\left( {{\rho _2}{l_2} + m} \right) {l_1}\left( {{{\ddot{x}}_0}\sin \left( {{\theta _1} - \alpha } \right) - {{\ddot{y}}_0}\cos \left( {{\theta _1} - \alpha } \right) } \right) \\{} & {} + 2\left( {\frac{1}{2}{\rho _2}{l_2} + m} \right) {l_2}\left( - {{\ddot{x}}_0}\sin ({\theta _1} + {\theta _2} - \alpha ) \right. \\{} & {} \left. + {{\ddot{y}}_0}\cos ({\theta _1} + {\theta _2} - \alpha )\right) \\{} & {} - 2\left( {{\rho _2}{l_2} + m} \right) {l_0}{l_1}\ddot{\alpha }\sin {\theta _1} - 2\left( {\frac{1}{2}{\rho _2}{l_2} + m} \right) \\ {}{} & {} {l_0}{l_2}\ddot{\alpha }\sin \left( {{\theta _1} + {\theta _2}} \right) \\{} & {} - 2{l_1}\sum \limits _{i = 1}^2 {\left( {\int _0^{{l_2}} {{\phi _i}dx{\rho _2} + {\phi _i}({l_2})m} } \right) } {{\dot{q}}_i}{{\dot{\theta }}_2}\sin {\theta _2} \\{} & {} - 2{l_0}\sum \limits _{i = 1}^2 {\left( {\int _0^{{l_2}} {{\phi _i}dx{\rho _2} + {\phi _i}({l_2})m} } \right) } \end{aligned}$$

$$\begin{aligned}{} & {} {q_i}\ddot{\alpha }\cos \left( {{\theta _1} + {\theta _2}} \right) - 2\left( {{\rho _2}{l_2} + m} \right) {l_0}{l_1}{{\dot{\alpha }}^2}\cos {\theta _1} \nonumber \\{} & {} + 2\sum \limits _{i = 1}^2 {\left( {\int _0^{{l_2}} {{\phi _i}dx{\rho _2} + {\phi _i}({l_2})m} } \right) } {q_i}\nonumber \\{} & {} \left( { - {{\ddot{x}}_0}\cos \left( {{\theta _1} + {\theta _2} - \alpha } \right) - {{\ddot{y}}_0}\sin \left( {{\theta _1} + {\theta _2} - \alpha } \right) } \right) \nonumber \\{} & {} + 2{l_1}\sum \limits _{i = 1}^2 {\left( {\int _0^{{l_2}} {{\phi _i}dx{\rho _2} + {\phi _i}({l_2})m} } \right) } \nonumber \\{} & {} \left( {{\dot{q}}_i}\sin {\theta _2}\left( {2\dot{\alpha }- 2{{\dot{\theta }}_1} - {{\dot{\theta }}_2}} \right) + {q_i}{{\dot{\theta }}_2}\right. \nonumber \\{} & {} \left. \cos {\theta _2}\left( {2\dot{\alpha }- 2{{\dot{\theta }}_1} - {{\dot{\theta }}_2}} \right) + 2{q_i}\sin {\theta _2}\ddot{\alpha }\right) \nonumber \\{} & {} - 2\left( {\frac{1}{2}{\rho _2}{l_2} + m} \right) {l_0}{l_2}^2{{\dot{\alpha }}^2}\cos \left( {{\theta _1} + {\theta _2}} \right) \nonumber \\{} & {} + 2{{\dot{\alpha }}^2}{l_0}\sum \limits _{i = 1}^2 {\left( {\int _0^{{l_2}} {{\phi _i}dx{\rho _2} + {\phi _i}({l_2})m} } \right) } \nonumber \\{} & {} {q_i}\sin \left( {{\theta _1} + {\theta _2}} \right) \Bigg \} - \Bigg \{ \frac{1}{2}{\rho _1}g{l_1}^2\cos \left( {{\theta _1} - \alpha } \right) \nonumber \\{} & {} + \left( {{\rho _2}{l_2} + m} \right) {l_1}g\cos \left( {{\theta _1} - \alpha } \right) \nonumber \\{} & {} + \left( {\frac{1}{2}{\rho _2}{l_2} + m} \right) g{l_2}\cos \left( {{\theta _1} + {\theta _2} - \alpha } \right) \nonumber \\{} & {} - g\sin \left( {{\theta _1} + {\theta _2} - \alpha } \right) \nonumber \\{} & {} \sum \limits _{i = 1}^2 {\left( {\int _0^{{l_2}} {{\phi _i}dx{\rho _2} + {\phi _i}({l_2})m} } \right) {q_i}} \Bigg \} \end{aligned}$$

(A13)

$$\begin{aligned} {C_{r2}}= & {} \frac{1}{2}\Bigg \{ - 2\left( {\frac{1}{3}{\rho _2}{l_2} + m} \right) {l_2}^2\ddot{\alpha }\nonumber \\{} & {} - 2\sum \limits _{i = 1}^2 {\left( {{\rho _2}\int _0^{{l_2}} {{\phi _i}^2dx + {\phi _i}^2({l_2})m} } \right) } {q_i}^2\ddot{\alpha }\nonumber \\{} & {} +4\sum \limits _{i = 1}^2 {\left( {{\rho _2}\int _0^{{l_2}} {{\phi _i}^2dx + {\phi _i}^2({l_2})m} } \right) }\nonumber \\{} & {} {q_i}{{\dot{q}}_i}\left( {{{\dot{\theta }}_1} + {{\dot{\theta }}_2} - \dot{\alpha }} \right) - 2\left( {\frac{1}{2}{\rho _2}{l_2} + m} \right) \nonumber \\{} & {} {l_1}{l_2}\ddot{\alpha }\cos {\theta _2} - 2\left( {\frac{1}{2}{\rho _2}{l_2} + m} \right) {l_0}{l_2}\ddot{\alpha }\sin \left( {{\theta _1}+ {\theta _2}} \right) \nonumber \\{} & {} + 2\left( {\frac{1}{2}{\rho _2}{l_2} + m} \right) {l_2}\left( - {{\ddot{x}}_0}\sin \left( {{\theta _1} + {\theta _2} - \alpha } \right) \right. \nonumber \\{} & {} \left. + {{\ddot{y}}_0}\cos \left( {{\theta _1} + {\theta _2} - \alpha } \right) \right) \nonumber \\{} & {} - 2\sum \limits _{i = 1}^2 {\left( {{\rho _2}\int _0^{{l_2}} {{\phi _i}dx + {\phi _i}({l_2})m} } \right) }\nonumber \\{} & {} {q_i}\left( {{{\ddot{x}}_0}\cos \left( {{\theta _1} + {\theta _2} - \alpha } \right) } \right. \nonumber \\{} & {} \left. {+ {{\ddot{y}}_0}\sin \left( {{\theta _1} + {\theta _2}- \alpha } \right) } \right) \nonumber \\{} & {} - 2{l_0}\sum \limits _{i = 1}^2 {\left( {{\rho _2}\int _0^{{l_2}} {{\phi _i}dx + {\phi _i}({l_2})m} } \right) } \nonumber \\{} & {} {q_i}\ddot{\alpha }\cos \left( {{\theta _1} + {\theta _2}} \right) \nonumber \\ {}{} & {} + 2{l_1}\sum \limits _{i = 1}^2 {\left( {{\rho _2}\int _0^{{l_2}} {{\phi _i}dx + {\phi _i}({l_2})m} } \right) } {q_i}\sin {\theta _2}\ddot{\alpha }\nonumber \\{} & {} + 2\left( {\frac{1}{2}{\rho _2}{l_2} + m} \right) {l_1}{l_2}{\left( {\dot{\alpha }- {{\dot{\theta }}_1}} \right) ^2}\sin {\theta _2}\nonumber \\ {}{} & {} - 2\left( {\frac{1}{2}{\rho _2}{l_2} + m} \right) \nonumber \\{} & {} {{\dot{\alpha }}^2}{l_0}{l_2}\cos \left( {{\theta _1} + {\theta _2}} \right) + 2{{\dot{\alpha }}^2}{l_0}\nonumber \\ {}{} & {} \sum \limits _{i = 1}^2 {\left( {{\rho _2}\int _0^{{l_2}} {{\phi _i}dx + {\phi _i}({l_2})m} } \right) } \nonumber \\{} & {} {q_i}\sin \left( {{\theta _1} + {\theta _2}} \right) + 2{l_1}{\left( {\dot{\alpha }- {{\dot{\theta }}_1}} \right) ^2}\nonumber \\ {}{} & {} \sum \limits _{i = 1}^2 {\left( {{\rho _2}\int _0^{{l_2}} {{\phi _i}dx + {\phi _i}({l_2})m} } \right) } \nonumber \\{} & {} {q_i}\cos {\theta _2}\Bigg \} - \Bigg \{\left( {\frac{1}{2}{\rho _2}{l_2} + m} \right) g{l_2}\cos \left( {{\theta _1} + {\theta _2} - \alpha } \right) \nonumber \\{} & {} - g\sin \left( {{\theta _1} + {\theta _2} - \alpha } \right) \nonumber \\ {}{} & {} \sum \limits _{i = 1}^2 {\left( {{\rho _2}\int _0^{{l_2}} {{\phi _i}dx + {\phi _i}({l_2})m} } \right) {q_i}} \Bigg \} \end{aligned}$$

(A14)

$$\begin{aligned} {C_{f1}}= & {} \frac{1}{2}\mathrm{{\Bigg \{ }}2\left( {{\rho _2}\int _0^{{l_2}} {{\phi _1}dx} + {\phi _1}({l_2})m} \right) \nonumber \\ {}{} & {} \left( { - {{\ddot{x}}_0}\sin \left( {{\theta _1} + {\theta _2} - \alpha } \right) } \right. \nonumber \\{} & {} \left. +{{{\ddot{y}}_0}\cos \left( {{\theta _1} + {\theta _2} - \alpha } \right) } \right) \nonumber \\{} & {} - 2\ddot{\alpha }{l_0}\left( {{\rho _2}\int _0^{{l_2}} {{\phi _1}dx} + {\phi _1}({l_2})m} \right) \sin \left( {{\theta _1} + {\theta _2}} \right) \nonumber \\{} & {} - 2{l_1}\left( {{\rho _2}\int _0^{{l_2}} {{\phi _1}dx} + {\phi _1}({l_2})m} \right) \ddot{\alpha }\cos {\theta _2}\nonumber \\{} & {} - 2\ddot{\alpha }\left( {{\rho _2}\int _0^{{l_2}} {x{\phi _1}dx + {l_2}{\phi _1}({l_2})m} } \right) \nonumber \\{} & {} - 2\left( {{\rho _2}\int _0^{{l_2}} {{\phi _1}^2dx} + {\phi _1}^2({l_2})m} \right) {q_1}{\left( {{{\dot{\theta }}_1} + {{\dot{\theta }}_2} - \dot{\alpha }} \right) ^2}\nonumber \\{} & {} - 2{{\dot{\alpha }}^2}{l_0}\left( {{\rho _2}\int _0^{{l_2}} {{\phi _1}dx} + {\phi _1}({l_2})m} \right) \cos \left( {{\theta _1} + {\theta _2}} \right) \nonumber \\{} & {} + 2{l_1}{\left( {\dot{\alpha }- {{\dot{\theta }}_1}} \right) ^2}\left( {{\rho _2}\int _0^{{l_2}} {{\phi _1}dx} + {\phi _1}({l_2})m} \right) \sin {\theta _2}\nonumber \\{} & {} - 2g\cos \left( {{\theta _1} + {\theta _2} - \alpha } \right) \left( {{\rho _2}\int _0^{{l_2}} {{\phi _1}dx + {\phi _1}({l_2})m} } \right) \Bigg \}\nonumber \\ \end{aligned}$$

(A15)

$$\begin{aligned} {C_{f2}}= & {} \frac{1}{2}\mathrm{{\Bigg \{ }}2\left( {{\rho _2}\int _0^{{l_2}} {{\phi _2}dx} + {\phi _2}({l_2})m} \right) \left( { - {{\ddot{x}}_0}\sin \left( {{\theta _1} + {\theta _2} - \alpha } \right) } \right. \nonumber \\{} & {} +\left. {{{\ddot{y}}_0}\cos \left( {{\theta _1} + {\theta _2} - \alpha } \right) } \right) \nonumber \\{} & {} - 2\ddot{\alpha }{l_0}\left( {{\rho _2}\int _0^{{l_2}} {{\phi _2}dx} + {\phi _2}({l_2})m} \right) \sin \left( {{\theta _1} + {\theta _2}} \right) \nonumber \\{} & {} - 2{l_1}\left( {{\rho _2}\int _0^{{l_2}} {{\phi _2}dx} + {\phi _2}({l_2})m} \right) \ddot{\alpha }\cos {\theta _2}\nonumber \\{} & {} - 2\ddot{\alpha }\left( {{\rho _2}\int _0^{{l_2}} {x{\phi _2}dx + {l_2}{\phi _2}({l_2})m} } \right) \nonumber \\{} & {} - 2\left( {{\rho _2}\int _0^{{l_2}} {{\phi _2}^2dx} + {\phi _2}^2({l_2})m} \right) \nonumber \\{} & {} {q_1}{\left( {{{\dot{\theta }}_1} + {{\dot{\theta }}_2} - \dot{\alpha }} \right) ^2} - 2{{\dot{\alpha }}^2}{l_0}\left( {{\rho _2}\int _0^{{l_2}} {{\phi _2}dx} + {\phi _2}({l_2})m} \right) \nonumber \\ {}{} & {} \cos \left( {{\theta _1} + {\theta _2}} \right) \nonumber \\{} & {} + 2{l_1}{\left( {\dot{\alpha }- {{\dot{\theta }}_1}} \right) ^2}\left( {{\rho _2}\int _0^{{l_2}} {{\phi _2}dx} + {\phi _2}({l_2})m} \right) \sin {\theta _2}\nonumber \\{} & {} - 2g\cos \left( {{\theta _1} + {\theta _2} - \alpha } \right) \left( {{\rho _2}\int _0^{{l_2}} {{\phi _2}dx + {\phi _2}({l_2})m} } \right) \Bigg \}\nonumber \\ \end{aligned}$$

(A16)