1 Introduction

Capsizing is a dangerous phenomenon, capable of causing considerable loss of life. Therefore, capsize should be absolutely avoided. Unlike conventional strip theory of ship motions, which is linear, the equation of ship roll motion is highly nonlinear due to the restoring curve, culminating in a complete loss of restoring force at the angle of vanishing stability (a softening-spring effect). Whereas the governing equations of electrical engineering and similar fields are typified by a hardening restoring component, ship roll motion is dominated by softening characteristics.

In a pioneering study, Nayfeh et al. treated the capsizing problem as a nonlinear dynamical system. In 1986, they showed the existence of chaos in beam-sea roll motions [1,2,3]. Using the equation of motion with a quadratic restoring term, Thompson uncovered the fractal structure in the safe basin boundary of capsizing [4,5,6]. At that time, Virgin newly reported the bifurcation conditions and chaos in this ship motion [7,8,9]. Following these successes, Kan and Taguchi considered the fractal metamorphoses of the equation of ship roll motion. Following Melnikov’s method, they showed that a heteroclinic bifurcation threshold appears in this system [10, 11]. Later contributions were made by Falzarano et al. [12], Spyrou et al. [13], Wu and McCue [14] and Maki et al. [15, 16]. With the exception of Thompson, all of these researchers applied the softening Duffing equation because of its similarity to the equation of ship roll motion in beam seas. The divergence in the solutions of the softening Duffing equation can be regarded as the capsizing phenomenon in the ship motion. Although the actual shape of the GZ (restoring arm) slightly differs from the cubic polynomial in the softening Duffing system, this relatively simple system has provided much fruitful and practical knowledge on nonlinear ship motion and the capsizing phenomenon. Therefore, the present research considers the stability of periodic solutions in the unbiased softening Duffing equation.

Numerical methods have substantially progressed over the past several decades. However, in preliminary design or for regulatory purposes, analytical results remain important to this day, as evidenced by the wide application of theoretical methods and approaches in the first and second phases of next-generation intact stability criteria. Therefore, approximation methods such as the perturbation technique, harmonic balance method, and averaging method will be important in future analyses.

As stated above, the softening Duffing equation has been extensively applied to ship roll, and various bifurcation conditions, namely, saddle-node bifurcation [17], flip bifurcation [9, 18] and heteroclinic bifurcation [10], e.g., [15], have been revealed. The present research explains the derivations of the saddle-node and flip bifurcations, and characterizes the flip bifurcation in greater detail than previously. Based on the obtained knowledge, we finally review the capsizing conditions.

2 Saddle-node (fold) and period-doubling bifurcations

The simplified beam-sea roll equation in regular beam seas is represented by

$$\left( {{I_{xx}}+{J_{xx}}} \right)\ddot {\Phi }+R \cdot \dot {\Phi }+W \cdot {\text{GM}} \cdot \Phi \left[ {1 - {{\left( {\Phi /{\Phi _{\text{V}}}} \right)}^2}} \right]={M_0}+M\cos \left( {\omega t+\delta } \right),$$
(1)

where \(\Phi\) is the instantaneous roll angle of the ship. Of course, \(\Phi\) is a function of time t. Ixx and Jxx are the moment of inertia and the added moment of inertia in the roll, respectively, R is the roll-damping coefficient, W is the ship mass, and GM is the metacentric height. \({\Phi _{\text{V}}}\) is the vanishing angle of the roll restoring moment, and M0 and M denote the amplitudes of the wind-induced and wave-induced roll moments, respectively. ω is the wave frequency and δ is the phase of the wave-induced moment. In this equation, over dot denotes the differentiation with respect to time t.

In this equation, the restoring curve is represented as Duffing-type cubic polynomial. The GZ-curve of many vessels is characterized by linear or lightly stiffening features for normally expected roll angles. In case extreme roll motion leads to capsizing occurs, the restoring moment tends to decrease with increase of heel angle due to deck submergence and/or bottom emergence. This can be approximated by a softening spring so that this paper used the GZ-curve having Duffing-type softening spring nature.

Dividing both sides of Eq. 1 by the moment of inertia, the equation of motion becomes:

$$\ddot {\phi }+\kappa \dot {\phi }+{c_1}\phi - {c_3}{\phi ^3}={B_0}+B\cos \left( {\omega t+\delta } \right),$$
(2)

where the coefficients are given by

$$\left\{ \begin{gathered} \phi \equiv \Phi /{\Phi _{\,{\text{V}}}} \hfill \\ \kappa \equiv \frac{R}{{{I_{xx}}+{J_{xx}}}},\,{c_1} \equiv \frac{{W \cdot {\text{GM}}}}{{{I_{xx}}+{J_{xx}}}},\,{c_3} \equiv \frac{{W \cdot {\text{GM}}}}{{\left( {{I_{xx}}+{J_{xx}}} \right)\Phi _{{\text{V}}}^{2}}} \hfill \\ {B_0} \equiv \frac{{{M_0}}}{{{I_{xx}}+{J_{xx}}}},\,B \equiv \frac{M}{{{I_{xx}}+{J_{xx}}}}. \hfill \\ \end{gathered} \right.$$
(3)

Now, when \({B_0}=0\) and \(\delta =0\), Eq. 2 reduces to

$$\ddot {\phi }+\kappa \dot {\phi }+{c_1}\phi - {c_3}{\phi ^3}=B\cos \omega t.$$
(4)

This is a symmetric equation with respect to the roll angle ϕ. Now we apply the harmonic balance method [17]. In the beginning, its first order solution is assumed as

$$\phi =A\cos (\omega t+\varepsilon ).$$
(5)

One may naturally assume a symmetric solution, as elaborated later. Substituting the above solution into the equation of motion and comparing the coefficients of \(\cos \omega t\) and \(\sin \omega t\), we obtain

$$\left\{ \begin{gathered} \left[ {A({c_1} - {\omega ^2}) - \frac{3}{4}{A^3}{c_3}} \right]\sin \varepsilon +\kappa \omega A\cos \varepsilon =B \\ \left[ {A({c_1} - {\omega ^2}) - \frac{3}{4}{A^3}{c_3}} \right]\cos \varepsilon - \kappa \omega A\sin \varepsilon =0. \\ \end{gathered} \right.$$
(6)

From these two conditions, the amplitude of the periodic solution is found as

$${B^2}={A^2}\left\{ {{{\left[ {\left( {{c_1} - {\omega ^2}} \right) - \frac{3}{4}{A^2}{c_3}} \right]}^2}+{\kappa ^2}{\omega ^2}} \right\}.$$
(7)

This is well known result. The stability of the periodic solutions is determined as described in Hayashi [17]. Introducing the nondimensional time \(\tau =\omega t\), the governing equation becomes:

$$\ddot {\phi }+\beta \dot {\phi }+{\alpha _1}\phi +{\alpha _3}{\phi ^3}={B_1}\cos \tau ,$$
(8)

where the coefficients are redefined as

$$\beta =\frac{\kappa }{\omega },\,{\alpha _1}=\frac{{{c_1}}}{{{\omega ^2}}},\,{\alpha _3}= - \frac{{{c_3}}}{{{\omega ^2}}},\,{B_1}=\frac{B}{{{\omega ^2}}}.$$
(9)

In Eq. 8, over dot denotes the differentiation with respect to nondimensional time τ. The periodic solution \({\varphi _0}(\tau )\), already assumed as Eq. 5, satisfies the following equation.

$${\ddot {\phi }_0}+\beta {\dot {\phi }_0}+{\alpha _1}{\phi _0}+{\alpha _3}\phi _{0}^{3}={B_1}\cos \tau .$$
(10)

Now, assume a small perturbation in the periodic motion \(\xi (\tau )\). Substituting \(\phi (\tau )={\phi _0}(\tau )+\xi (\tau )\) into Eq. 8 yields

$$\ddot {\xi }+\beta \dot {\xi }+({\alpha _1}+3{\alpha _3}\phi _{0}^{2})\quad \xi =0.$$
(11)

To eliminate the damping term, we introduce the following transformation:

$$\xi (\tau )=\exp \left[ { - \frac{1}{2}\beta \tau } \right]\eta (\tau ),$$
(12)

from which we get

$$\ddot {\eta }+\left( {{\alpha _1} - \frac{1}{4}{\beta ^2}+3{\alpha _3}\varphi _{0}^{2}} \right)\quad \eta =0.$$
(13)

The steady-state periodic oscillation is given by:

$${\varphi _0}(\tau )=A\cos (\tau - \varepsilon ^{\prime}).$$
(14)

Substituting Eq. 14 into Eq. 13 gives

$$\ddot {\eta }+({\theta _0}+2{\theta _1}\cos 2(\tau - \varepsilon ^{\prime}))\quad \eta =0.$$
(15)

In the above Mathieu’s equation, the coefficients \({\theta _0}\) and \({\theta _1}\) are defined as follows:

$$\left\{ \begin{aligned} & {\theta _0}={\alpha _1} - \frac{1}{4}{\beta ^2}+\frac{3}{2}{\alpha _3}{A^2} \\ & 2{\theta _1}=\frac{3}{2}{\alpha _3}{A^2}. \\ \end{aligned} \right.$$
(16)

If the following equation describing the first instability region in Mathieu’s equation is satisfied, the solution is stable (as shown in Eq. 4.6 in Hayashi [17]).

$${\left( {{\theta _0} - 1} \right)^2}+2\left( {{\theta _0}+1} \right){\beta ^2}+{\beta ^4}>\theta _{1}^{2}.$$
(17)

Substituting \({\theta _0}\) and \({\theta _1}\) into the above inequality condition and setting \({c_1}=1\) and \({c_3}=1\), the critical condition takes the following simple form:

$${C^2}+\,\frac{3}{2}C{A^2}+{\kappa ^2}{\omega ^2}=0,$$
(18)

with

$$C \equiv {\omega ^2} - 1+\frac{3}{4}{A^2}.$$
(19)

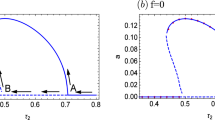
We focus on the saddle-node bifurcation (fold bifurcation). As the amplitude of the external forcing is increased, this system realizes multiple solutions (see Fig. 1). The left and right panels of Fig. 1 are the numerical and analytical solutions, respectively, with \({c_1}=1\), \({c_3}=1\), \({B_0}=0.0\) and \(\kappa =0.04455\). The numerical solutions were obtained by Kawakami’s method [19,20,21]. In this methodology, with the use of Newton method, not only the trajectory in the time domain, but also characteristic multipliers obtained from the Poincaré map is simultaneously calculated. In the left panel of this figure, the amplitude is defined as the absolute value of the maximum value of φ in the periodic solution. Furthermore, if Eq. 18 is satisfied, the periodic solution becomes unstable (hatched region in the right panel). The theoretical results (right panel) are unstable only when the saddle-node bifurcation appears. Note that the capability of other bifurcations is not considered in the theoretical analysis.

Fig. 1
figure 1

Response amplitude of the primary motion with \({c_1}=1\), \({c_3}=1\), \(\kappa =0.04455\) and \({B_0}=0.0\) (left: numerical solution, right: analytical solution). Solid and dashed lines delineate the stable and unstable regions, respectively

Full size image

When a saddle-node bifurcation occurs, the following “vertical tangent” condition is satisfied:

$$\frac{{{\text{d}}B}}{{{\text{d}}A}}=0.$$
(20)

To obtain \({\text{d}}B/{\text{d}}A\), we differentiate both sides of Eq. 7 with respect to the amplitude \(A\) as follows:

$$2B\frac{{{\text{d}}B}}{{{\text{d}}A}}=2A\left\{ {{{\left[ {(1 - {\omega ^2}) - \frac{3}{4}{A^2}} \right]}^2}+{\kappa ^2}{\omega ^2}} \right\} - 3{A^3}\left[ {(1 - {\omega ^2}) - \frac{3}{4}{A^2}} \right].$$
(21)

Applying Eq. 19, we have:

$$\frac{{{\text{d}}B}}{{{\text{d}}A}}=\frac{A}{B}\left[ {{C^2}+\frac{3}{2}C{A^2}+{\kappa ^2}{\omega ^2}} \right].$$
(22)

Finally, the following equation is obtained:

$${C^2}+\frac{3}{2}C{A^2}+{\kappa ^2}{\omega ^2}=0,$$
(23)

which is equivalent to Eq. 18. Notably, the conditions of the saddle-node bifurcation and stable periodic solutions are identical. This finding is reasonable because a saddle-node bifurcation destabilizes the tracing solution. Figure 2 shows a representative saddle-node bifurcation occurring in this system at a specific forcing frequency. Stable and unstable fixed points are generated around B = 0.02, and disappear around B = 0.035.

Fig. 2
figure 2

Saddle node bifurcation with \({c_1}=1\), \({c_3}=1\), \(\kappa =0.04455\), \({B_0}=0.0\) and \(\omega =0.905\). The analytical fold bifurcation points are \(B=0.01968\) and \(B=0.03615\). Black and gray regions indicate that under the initial conditions, the solution converges to a periodic attractor (fixed point, represented by the white points)

Full size image

The flip bifurcation condition was identified by Holmes and Rand [18] and Virgin [9]. In their formulations, a negative stiffness condition in a Mathieu-type equation was imposed on Eq. 15. Under this condition, \({\theta _0}<0\) in Eq. 15, and we have:

$${\alpha _1} - \frac{1}{4}{\beta ^2}+\frac{3}{2}{\alpha _3}{A^2}<0 \Rightarrow {A^2}>- \frac{{2{\alpha _1}}}{{3{\alpha _3}}}\left( {1 - \frac{{{\beta ^2}}}{{4{\alpha _3}}}} \right).$$
(24)

In terms of Eq. 9, this becomes:

$$A>\sqrt {\frac{{2{c_1}}}{{3{c_3}}}\left( {1+\frac{{{\kappa ^2}}}{{4{c_3}}}} \right)} .$$
(25)

In the equation of ship roll motion, κ is generally small, so the above inequality reduces to

$$A>\sqrt {\frac{{2{c_1}}}{{3{c_3}}}} ,$$
(26)

which is unstable condition for the flip bifurcation. In the hardening-type Duffing equation, the above condition cannot be satisfied because \({c_3}<0\). Combining the condition

$$A=\sqrt {\frac{{2{c_1}}}{{3{c_3}}}} .$$
(27)

with Eq. 7, we obtain

$${B^2}=\frac{{2{c_1}}}{{3{c_3}}}\left[ {{{\left( {{\omega ^2} - \frac{{{c_1}}}{2}} \right)}^2}+{\kappa ^2}{\omega ^2}} \right].$$
(28)

Under the condition in which the motion amplitude exceeds the stability vanishing angle \(\varphi ={( - {\alpha _1}/{\alpha _3})^{1/2}}\), we obtain another condition:

$$A=\sqrt {\frac{{{c_1}}}{{{c_3}}}} .$$
(29)

Equation 29 resembles the conservative results given by Eq. 27.

3 Symmetry breaking and pitchfork bifurcation

In the numerical results of Fig. 1, the large-amplitude periodic motion at B = 0.05 becomes unstable around ω = 0.6. The bifurcation in the vicinity of this point is shown in Fig. 3. In this bifurcation diagram, a flip-type bifurcation appears around \(\omega =0.58\). This is a pitchfork rather than a period-doubling bifurcation because the solution does not change the period of the motion. Furthermore, this point marks the onset of asymmetry in the previously symmetric solution. This transition from symmetry to asymmetry is sometimes called symmetry breaking. Kan and Taguchi’s [11] description unfortunately omitted the upper branch in the right panel of Fig. 3, although the pitchfork bifurcation and symmetry breaking had been already reported by Nayfeh, e.g., [1]. The three periodic solutions, with asymmetry in the phase plane at the two larger amplitudes, are shown in Fig. 4. Figure 5 shows the initial condition set which converges to three different periodic solutions. The red and blue colors correspond to the simultaneous upper and lower branches, respectively, and the gray region corresponds to the primary solution.

Fig. 3
figure 3

Numerically obtained bifurcation diagram with \({c_1}=1\), \({c_3}=1\), \(\kappa =0.04455\), \(B=0.05\) and \({B_0}=0.0\). The light panel is the magnified plot of the left panel

Full size image
Fig. 4
figure 4

Phase portrait of the numerically obtained asymmetric motion with \({c_1}=1\), \({c_3}=1\), \(\kappa =0.04455\), \(B=0.05\), \({B_0}=0.0\) and \(\omega =0.579\) (line: lower branch, dotted line: upper branch, bold line: another branch with small amplitude)

Full size image
Fig. 5
figure 5

Convergence of an initial condition set to three different solutions in a safe basin with \({c_1}=1\), \({c_3}=1\), \(\kappa =0.04455\), \(B=0.05\), \({B_0}=0.0\) and \(\omega =0.579\)

Full size image

To investigate this phenomenon in detail, we numerically calculated the characteristic exponents μ by Kawakami’s method [19,20,21]. The result is shown in Fig. 6. When the pitchfork bifurcation (symmetry breaking) occurs at ω = 0.5800, the characteristic exponent crosses 1 (on the unit circle) as shown in the left panel of Fig. 6. Clearly, this bifurcation is not a period-doubling bifurcation. On the other hand, at ω = 0.5720, the bifurcation takes the same shape (Fig. 3) but one of the characteristic exponents crosses − 1 on the unit circle (right panel of Fig. 6), clearly indicating a period-doubling bifurcation.

Fig. 6
figure 6

Characteristic exponents with \({c_1}=1\), \({c_3}=1\), \(\kappa =0.04455\), \(B=0.05\) and \({B_0}=0.0\) (left: around \(\omega =0.580\), right: around \(\omega =0.572\)). Solid and dashed lines denote the different characteristic exponents in each panel

Full size image

4 Condition of pitchfork bifurcation

As evidenced in Fig. 3, the symmetry breaks just prior to the period-doubling bifurcation point, and an asymmetrical solution appears. To obtain this asymmetrical solution from the symmetric equation, we applied the harmonic balance method. In the previous consideration, we assume the symmetry solution. However, to find the asymmetry solution, the constant bias term should be taken into account. Using the same equation of motion, namely,

$$\ddot {\phi }+\kappa \dot {\phi }+{c_1}\phi - {c_3}{\phi ^3}=B\cos \omega t,$$
(30)

we add a constant (a “bias” term C0) to the assumed solution form:

$$\phi ={C_0}+A\cos \left( {\omega t+\varepsilon } \right).$$
(31)

In Eq. 30, over dot denotes the differentiation with respect to time t. Substituting this solution into Eq. 30, we obtain the following conditions:

$$\left\{ \begin{aligned} & {C_0}\left( {{c_1} - \frac{3}{2}{c_3}{A^2} - C_{0}^{2}{c_3}} \right)=0 \\ & A\left[ {({c_1} - {\omega ^2}) - \frac{3}{4}{A^2}{c_3} - 3C_{0}^{2}{c_3}} \right]\sin \varepsilon - \kappa \omega A\cos \varepsilon =B \\ & A\left[ {({c_1} - {\omega ^2}) - \frac{3}{4}{A^2}{c_3} - 3C_{0}^{2}{c_3}} \right]\cos \varepsilon +\kappa \omega A\sin \varepsilon =0. \\ \end{aligned} \right.$$
(32)

If A satisfies

$$A=\sqrt {\frac{{2{c_1}}}{{3{c_3}}}} .$$
(33)

in the first expression of Eq. 32, then

$${C_0}=0.$$
(34)

Note that Eq. 33 is almost recognizable as the flip bifurcation [condition 25]. The small difference between Eqs. 33 and 25 derives from the treatment of κ. In Eq. 26, we ignored the squared damping term κ in Eq. 25 because the damping component is negligibly small in the ship roll equation. In this sense, the pitchfork condition is almost identical to Eq. 26. Of course, amplitude of external wave moment at pitchfork bifurcation is obtained as:

$${B^2}=\frac{{2{c_1}}}{{3{c_3}}}\left[ {{{\left( {{\omega ^2} - \frac{{{c_1}}}{2}} \right)}^2}+{\kappa ^2}{\omega ^2}} \right].$$
(35)

This is also identical to Eq. 28. On the other hand, combining the second and third equations in Eq. 32, the amplitude of the motion is obtained from:

$${B^2}={A^2}\left\{ {{{\left[ {({c_1} - {\omega ^2}) - \frac{3}{4}{c_3}({A^2}+4C_{0}^{2})} \right]}^2}+{\kappa ^2}{\omega ^2}} \right\}.$$
(36)

Furthermore, when C0 is non-zero, C0 value is obtained from the first equation in Eq. 32 as:

$${C_0}= \pm \sqrt {\frac{{{c_1}}}{{{c_3}}} - \frac{3}{2}{A^2}} .$$
(37)

This result confirms two candidates for C0: a positive or negative side shift with the same absolute value of the angle. Therefore, the motion amplitudes A calculated from Eq. 36 are also identical. Consequently, as observed in Fig. 4, the phase trajectories develop a line symmetry in the phase plane. In Eq. 37, important condition is:

$$A<\sqrt {\frac{{2{c_1}}}{{3{c_3}}}} .$$
(38)

On the other hand, let us consider the stability for the obtained solution:

$$\ddot {\eta }+\left( {{c_1} - \frac{1}{4}{\beta ^2} - 3{c_3}\phi _{0}^{2}} \right)\eta =0.$$
(39)

Now, periodic solution is:

$${\phi _0}={C_0}+A\cos \left( {\omega t+\varepsilon } \right).$$
(40)

The equation with respect to \(\eta\) is finally obtained as follows;

$$\ddot {\eta }+\left[ {{\theta _0}+2{\theta _1}\cos \left( {\tau - \varepsilon } \right)+2{\theta _2}\cos 2\left( {\tau - \varepsilon } \right)} \right]\eta =0.$$
(41)

where

$$\tau \equiv \omega t.$$
(42)

In the above Hill’s equation, the coefficients \({\theta _0}\) and \({\theta _1}\) mean as follows;

$$\left\{ \begin{gathered} {\theta _0}={c_1} - \frac{1}{4}{\beta ^2} - 3{c_3}\left( {C_{0}^{2}+\frac{1}{2}{A^2}} \right) \hfill \\ 2{\theta _1}= - 6{c_3}A{C_0} \hfill \\ 2{\theta _2}= - \frac{3}{2}{c_3}{A^2}. \hfill \\ \end{gathered} \right.$$
(43)

From the negative stiffness condition in Hill’s equation, we have:

$$A>\sqrt {\frac{{2{c_1}}}{{3{c_3}}}\left( {1+\frac{{{\kappa ^2}}}{{8{c_1}}}} \right)} .$$
(44)

\({c_1}\) and \({c_3}\) are always positive. Equations 38 and 44 conflict. Therefore, the assumed from Eq. 31 becomes unstable.

To analyze the stability further, we apply the averaging technique. At first, we transform Eq. 1 as:

$$\left\{ \begin{aligned} & \dot {\phi }=p \\ & \dot {p}= - {\omega ^2}\phi - \kappa p+({\omega ^2} - {c_1})\phi +{c_3}{\phi ^3}+B\cos \omega t. \\ \end{aligned} \right.$$
(45)

Assume the solution as:

$$\left\{ \begin{gathered} \phi ={C_0}+A\cos \left( {\omega t+\psi } \right) \hfill \\ \dot {\phi }= - A\omega \sin \left( {\omega t+\psi } \right). \hfill \\ \end{gathered} \right.$$
(46)

Newly introduced A and ψ are slowly varying function with respect to time t. By substituting Eq. 46 and averaging in one roll period, the differential Eqs. 45 for the averaged system were finally obtained:

$$\left\{ \begin{aligned} & \dot {A}= - \frac{\kappa }{2}A - \frac{B}{{2\omega }}\sin \psi \\ & \dot {\psi }=\frac{{{c_1}}}{{2\omega }} - \frac{{3{c_3}}}{{8\omega }}{A^2} - \frac{{3C_{0}^{2}{c_3}}}{{2\omega }} - \frac{\omega }{2} - \frac{B}{{2\omega }}\frac{1}{A}\cos \psi . \\ \end{aligned} \right.$$
(47)

The stationary solution can be obtained from the condition:

$$\left\{ \begin{gathered} \dot {A}=0 \\ \dot {\psi }=0. \\ \end{gathered} \right.$$
(48)

And its solution becomes:

$${B^2}={A^2}\left\{ {{{\left[ {({c_1} - {\omega ^2}) - \frac{3}{4}{c_3}({A^2}+4C_{0}^{2})} \right]}^2}+{\kappa ^2}{\omega ^2}} \right\}.$$
(49)

This is identical to Eq. 36. Here, Jacobi matrix is as follows:

$${\mathbf{J}}=\left[ {\begin{array}{*{20}{c}} { - \frac{\kappa }{2}}&{ - \frac{B}{{2\omega }}\cos \psi } \\ {\frac{{15{c_3}}}{{4\omega }}A+\frac{B}{{2\omega }}\frac{1}{{{A^2}}}\cos \psi }&{\frac{B}{{2\omega }}\frac{1}{A}\sin \psi } \end{array}} \right].$$
(50)

Note that, before making Jacobi matrix, C0 is replaced by A. In this process, the results of harmonic balance method, namely Eq. 37, is utilized. From the Jacobi matrix, the eigenvalues can be calculated. Then, we can detect the stability of the solution. As a result, we finally noticed that main branches shown as \(A \pm {C_0}\), which are obtained from the solution (Eqs. 36 or 49), is unstable as shown in Fig. 7. After pitchfork bifurcation, stable branches are normally generated. However, in this case, the generated branches are unstable. It could be considered as the limitation of the first order approximation, and it is our one of future researches.

Fig. 7
figure 7

Analytically obtained bifurcation diagram with \({c_1}=1\), \({c_3}=1\), \(\kappa =0.04455\), \({B_0}=0.0\) and \(\omega =1.0\) (solid line: stable solution, dashed line: unstable solution)

Full size image

5 Bifurcation and capsizing boundary

This section presents the numerical results. Figure 8 is a higher-resolution reproduction of Fig. 12 in Kan and Taguchi [10] with all initial conditions set to zero. The used values of the coefficients are \({c_1}=1\), \({c_3}=1\), \(\kappa =0.04455\) and \({B_0}=0.0\), and the time step of Runge–Kutta method is set to be T/200 (T is defined as 2π/ω). These values are identical with those used in Kan and Taguchi [10]. On the other hand, Fig. 12 in Kan and Taguchi [10] consists of 1.35 million points, whereas Fig. 8 does of 4 million points. Within the white regions of this figure, the set of forcing parameters will lead to capsizing. On the other hand, within the black region, the combination of forcing parameters will guarantee no capsizing (typically some kind of stable oscillation). This figure clearly shows the fractal structure explained by Kan and Taguchi [10], which is also observed in a semi-submersible model [22]. Moreover, as pointed out by Kan and Taguchi [10], the structure strongly depends on the initial conditions, so the shape of Fig. 8 will change under another set of initial conditions. The topological structure of this phenomenon has been recently investigated by Miino et al. [23].

Fig. 8
figure 8

Bifurcation and capsizing boundary with \({c_1}=1\), \({c_3}=1\), \(\kappa =0.04455\) and \({B_0}=0.0\) (this figure duplicates Fig. 12 in the literature [10], but at high resolution)

Full size image

Figure 9 compares the numerically obtained stability thresholds of the periodic solutions (numerical results of capsizing) and the analytically obtained thresholds. The numerical capsizing threshold traces a periodic solution with increasing amplitude of the external force B until the capsize event. The threshold defines the amplitude leading to capsizing. In the region of the co-existing periodic and saddle-node bifurcation line, another periodic solution exists. Therefore, the thresholds are meaningful above ω = 1.0. The contours of the safe basin boundary are also drawn in Fig. 8. As pointed out by Kan and Taguchi [10], the saddle-node bifurcation line in the small-ω region reasonably agrees with the safe basin contours. Further, as also pointed by them [10], in the higher frequency region (around ω = 1.0), the pitchfork bifurcation point almost coincides with the numerically obtained capsizing region. It also gives moderately conservative results, whereas the estimates of the other bifurcation line are either too conservative or non-conservative. Therefore, including the pitchfork bifurcation in the capsizing assessment is apparently suitable for practical cases.

Fig. 9
figure 9

Bifurcation and capsizing boundary with \({c_1}=1\), \({c_3}=1\), \(\kappa =0.04455\) and \({B_0}=0.0\)

Full size image

6 Concluding remarks

This research investigated the roles of fold and flip bifurcations in a softening-spring oscillator model of ship roll motion, and presented different derivations of the bifurcations. The symmetry breaking noted in Kan and Taguchi [11] was found to be identical to the pitchfork bifurcation noted in Nayfeh, e.g. [1]. The pitchfork bifurcation condition was then derived by the harmonic balance method. This derivation confirmed that the pitchfork bifurcation condition is identical to the flip bifurcation condition derived by Holms and Rand [18], and by Virgin [9]. On the other hand, after pitchfork bifurcation, the generated branches are unstable in the first order analytical methods. It could be considered as the limitation of the first order approximation, and it could be our future research topics. Furthermore, future research will consider the period-doubling bifurcation occurring after the pitchfork bifurcation, and a more realistic hull form for practical applications.