Melnikov integral formula for beam sea roll motion utilizing a non-Hamiltonian exact heteroclinic orbit: analytic extension and numerical validation

Abstract

In the research field of nonlinear dynamical system theory, it is well known that a homoclinic/heteroclinic point leads to unpredictable motions, such as chaos. Melnikov’s method enables us to judge whether the system has a homoclinic/heteroclinic orbit. Therefore, in order to assess a vessel's safety with respect to capsizing, Melnikov’s method has been applied for investigations of the chaos that appears in beam sea rolling. This is because chaos is closely related to capsizing incidents. In a previous paper (Maki et al. in J Mar Sci Technol 15:102–106, 2010), a formula to predict the capsizing boundary by applying Melnikov’s method to analytically obtain the non-Hamiltonian heteroclinic orbit was proposed. However, in that paper, only limited numerical investigation was carried out. Therefore, further comparative research between the analytical and numerical results is conducted, with the result being that the formula is validated.

1 Introduction

Currently, investigations into chaos in cases of nonlinear vessel rolling in beam seas have been extensively investigated [2–11], with Melnikov’s method being effectively applied [12]. Melnikov’s method enables us to detect the onset of the heteroclinic point, which assures the existence of the horseshoe map via the Smale–Birkhoff theorem [13]. For instance, Kan and Taguchi [5] implied that the threshold of fractal metamorphoses in the control plane obtained from the Melnikov analysis of the non-biased roll equation could be applicable for a vessel’s stability criterion. On the other hand, Spyrou et al. [11] investigated the biased roll equation with an appropriate variable transformation and performed the Melnikov analysis using an analytically obtained homoclinic orbit. A nonlinear system, however, is not necessarily solvable, so in general it is difficult to analytically obtain the separatrix closed loop. Consequently, Wu and McCue [14] applied the extended Melnikov’s method [15] for a numerically obtained heteroclinic orbit based upon Endo and Chua’s work [16].

In order to apply Melnikov’s method, it is required to obtain the separatrix closed loop for the autonomous part of the full system. Thanks to recent advances in nonlinear science, several solitary solutions have already been found via methods using nonlinear equations [17]. Maki et al. [1] pointed out that the escape equation used by Kan and Taguchi [6] is identical with FHN (FitzHugh–Nagumo), with the exception of some of the coefficients. They investigated analytically the heteroclinic orbit in the time domain by using the solution technique that is originally used for analysing nonlinear waves, and then extended Melnikov’s method proposed by Salam [15] was applied. The paper [1], however, mainly addresses the analytical formulation, and limited numerical results were presented. The objective of this paper is to numerically validate the proposed formula, and carry out additional analysis of the escape equation. This paper is structured as follows: firstly, following the brief explanation of the formulation for the biased roll equation, the analytical results of the heteroclinic orbit are validated by using numerical bifurcation analysis. Then the results of the Melnikov integral are shown, and the obtained threshold of fractal metamorphoses that appear in the control plane is compared with numerical simulation result.

2 Non-Hamiltonian heteroclinic obit

In order to apply Melnikov’s method introduced by Salam [15], it is necessary to obtain the non-Hamiltonian heteroclinic orbit. Although it is difficult to find the exact solution of a nonlinear equation, the solutions of the equation could be found by employing a solution technique used in nonlinear waves. Maki et al. [1] applied this technique for the escape equation, and then provided the heteroclinic orbit and its condition. In this paper, the same methodology is used, but the treatment of the bias term that appears in the equation is slightly different from that presented in the previous paper [1]. Thus, it is shown that the following brief reformulation is suitable for the numerical validation.

Consider the following biased roll equation with linear damping and nonlinear cubic term in the restoring force:

$$ I\frac{{{\text{d}}^{2} \varPhi }}{{{\text{d}}t^{2} }} + N\frac{{{\text{d}}\varPhi }}{{{\text{d}}t}} + W \cdot {\text{GM}} \cdot \varPhi \left( {1 - \varPhi /\varPhi_{\text{V}} } \right)\left( {1 + a \cdot \varPhi /\varPhi_{\text{V}} } \right) = M_{\text{r}} \cos \left( {\omega t + \delta } \right). $$

(1)

where a is the coefficient representing the bias of roll equation, GM is the metacentric height, I is the moment of inertia in roll, M _r is the amplitude of the 1st-order wave-induced roll moment, N is the damping coefficient in roll, t is time, W is the ship mass, Φ is the roll angle and Φ _V is the angle of vanishing stability. The appropriate non-dimensionalization for Eq. 1 yields:

$$ \ddot{\phi } + \beta \dot{\phi } + \mu \cdot \phi \left( {1 - \phi } \right)\left( {1 + a \cdot \phi } \right) = \gamma \cos \left( {\omega t + \delta } \right), $$

(2)

where:

$$ \left\{ \begin{gathered} \phi \equiv \varPhi /\varPhi_{\text{V}} \hfill \\ \beta \equiv N/I,\,\,\mu \equiv W \cdot {\text{GM}}/I,\,\,\gamma \equiv M_{\text{r}} /I\varPhi_{\text{V}} \hfill \\ \end{gathered} \right.. $$

(3)

In order to obtain the heteroclinic orbit of the homogeneous part of Eq. 2, an addition of the parameter for both sides of the equation are as follows:

$$ \ddot{\phi } + \beta \dot{\phi } + \mu \cdot \phi \left( {1 - \phi } \right)\left( {1 + a \cdot \phi } \right) + \sigma = \sigma + \gamma \cos \left( {\omega t + \delta } \right), $$

(4)

Here σ can be calculated by using the procedure described in the previous paper [1], and the results are shown as follows:

$$ \tilde{\mu }\left( {\frac{1}{2} - \tilde{a}} \right) \pm \tilde{\beta }\sqrt {\frac{{\tilde{\mu }}}{2}} = 0, $$

(5)

where

$$ \left\{ \begin{gathered} \tilde{a} \equiv \left( {\phi_{{{\kern 1pt} 2}} - \phi_{{{\kern 1pt} 1}} } \right)/\left( {\phi_{{{\kern 1pt} 3}} - \phi_{{{\kern 1pt} 1}} } \right) \hfill \\ \tilde{\beta } \equiv \beta ,\,\,\tilde{\mu } \equiv a\mu \left( {\phi_{{{\kern 1pt} 3}} - \phi_{{{\kern 1pt} 1}} } \right)^{2} \hfill \\ \end{gathered} \right., $$

(6)

and ϕ ₁, ϕ ₂, ϕ ₃ are the solutions of the following equation.

$$ \mu \cdot \phi \left( {1 - \phi } \right)\left( {1 + a \cdot \phi } \right) + \sigma = 0. $$

(7)

This is a third-order polynomial with respect to ϕ and can be factorised using Cardano’s method. In Eq. 5, a positive or a negative sign corresponds to the trajectory on the upper and/or lower phase plane, respectively. When the condition of Eq. 5 is satisfied, a heteroclinic orbit is realized, and it can be represented in the time domain as:

$$ \phi_{{{\kern 1pt} 0}} \left( t \right) = \phi_{{{\kern 1pt} 1}} + \frac{{\phi_{{{\kern 1pt} 3}} - \phi_{{{\kern 1pt} 1}} }}{{1 + e^{{ \pm \sqrt {0.5\tilde{\mu }} t}} }}. $$

(8)

Additionally, this is achieved by using the quadratic function in the phase plane, thus

$$ \dot{\phi }_{{{\kern 1pt} 0}} \left( t \right) = \mp \sqrt {\frac{{\tilde{\mu }}}{2}} \frac{{\left( {\phi_{{{\kern 1pt} 0}} \left( t \right) - \phi_{{{\kern 1pt} 1}} } \right)\left( {\phi_{{{\kern 1pt} 0}} \left( t \right) - \phi_{{{\kern 1pt} 3}} } \right)}}{{\phi_{{{\kern 1pt} 3}} - \phi_{{{\kern 1pt} 1}} }}. $$

(9)

Note the double sign in the same order with Eq. 5 in Eqs. 8 and 9. It is now possible to compare the results using the proposed method and numerical bifurcation analysis. In this paper, the numerical bifurcation analysis proposed by Kawakami et al. [18] is employed for finding the critical parameter σ. Using this method, all the conditions necessary for realizing the heteroclinic bifurcation, i.e., the equilibrium of saddle points, their eigenvalues, their eigenvectors, and the connection of both trajectories at the intermediate point, are simultaneously solved with Newton’s method. Using Kawakami’s method, an allowable numerical displacement vector norm of 1.0⁻⁶ error is applied when using the Newton method. To further retain the numerical accuracy, a 5th-order Runge–Kutta integral scheme is also applied.

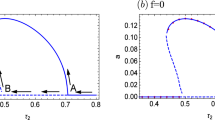
Figure 1 presents the comparison of the critical value σ for the non-biased escape equation, i.e., when a = 1, obtained by using these two methods, whereas Fig. 2 presents the case in which the bias a = 0.9. Since only a small discrepancy can be observed in these figures, the proposed analytical method is considered to be satisfactory. Figures 3 and 4 illustrate the heteroclinic orbits in phase plane spanned by ϕ and $\dot{\phi }$ obtained using these two methods. Note that the analytically obtained heteroclinic orbit is a quadratic function (Eq. 9). It can also be observed that the two orbits are completely identical. Although the uniqueness of a heteroclinic orbit for this system cannot be proved, mutual agreement indicates Eq. 8 is locally consistent and represents the heteroclinic orbit of Eq. 2. Since this solution for obtaining the heteroclinic bifurcation point is quite simple and robust, it can be used easily to calculate the parameter set required, thus realizing the heteroclinic bifurcation as shown in Fig. 5.

Fig. 1

Comparison of parameter σ obtained by using analytical method and numerical method with a of 1.0

Fig. 2

Comparison of parameter σ obtained by using analytical method and numerical method with a of 0.9

Fig. 3

Comparison of phase trajectories obtained by using analytical method and numerical method with a of 1.0 and β of 0.1

Fig. 4

Comparison of phase trajectories obtained by using analytical method and numerical method with a of 0.9 and β of 0.1

Fig. 5

Parameter set of the heteroclinic bifurcation points

3 Critical forcing

If an heteroclinic orbit is obtained, Melnikov’s method is analytically applicable. Next, the biased case is examined. Wu and McCue [14] used

$$ \ddot{\phi } + \beta \dot{\phi } + \mu \left( {\phi - \phi^{3} } \right) = \left( {1 - a} \right)\left( {\phi^{2} - \phi^{3} } \right) + \gamma \cos \left( {\omega t + \delta } \right) $$

(10)

based upon the assumption of small 1 - a, as an alternative to directly manipulating Eq. 4, and then Melnikov integral

$$ M\left( {t_{0} } \right) = \int\limits_{ - \infty }^{\infty } {\dot{\phi }_{{{\kern 1pt} 0}} \left( t \right)\left[ {\gamma \cos \omega \left( {t + t_{0} } \right) + \sigma + \left( {1 - a} \right)\left( {\phi_{0}^{2} \left( t \right) - \phi_{0}^{3} \left( t \right)} \right)} \right]e^{{\tilde{\beta }t}} {\text{d}}t} $$

(11)

is carried out for the heteroclinic orbit of the left-hand side of Eq. 10. Note that the left-hand side of Eq. 10 is the non-biased roll equation. By using the analytically obtained heteroclinic orbit (Eq. 9), the critical forcing is obtained as follows:

$$ \gamma = \frac{{\left( {1 - a} \right)\left( {A_{{{\kern 1pt} 0}} I_{0} + A_{{{\kern 1pt} 1}} I_{1} + A_{{{\kern 1pt} 2}} I_{2} + A_{{{\kern 1pt} 3}} I_{3} } \right) + \sigma I_{0} }}{{\sqrt {I_{r}^{2} + I_{i}^{2} } }}. $$

(12)

In this equation, the values I _r , I _i , I ₀, I ₁, I ₂, I ₃ can be calculated analytically as follows:

$$ \begin{gathered} I_{r} \equiv \text{Re} \left[ {\frac{1}{4}\int\limits_{ - \infty }^{\infty } {\frac{{\exp \left( {\tilde{\beta }t + i\omega t} \right)}}{{\cosh^{2} \left( {\tilde{c}t/2} \right)}}{\text{d}}t} } \right] = \text{Re} \left[ {\frac{{\pi \left( {\tilde{\beta } + i\omega } \right){ \csc }\left[ {\pi \left( {\tilde{\beta } + i\omega } \right)/\tilde{c}} \right]}}{{\tilde{c}^{2} }}} \right]\text{sgn} \tilde{c} \\ = - \frac{{2\pi \left[ {\tilde{\beta }\cosh \left( {\omega \pi /\tilde{c}} \right)\sin \left( {\tilde{\beta }\pi /\tilde{c}} \right) + \omega \cos \left( {\tilde{\beta }\pi /\tilde{c}} \right)\sinh \left( {\omega \pi /\tilde{c}} \right)} \right]}}{{\tilde{c}^{2} \left[ {\cos \left( {2\tilde{\beta }\pi /\tilde{c}} \right) - \cosh \left( {2\omega \pi /\tilde{c}} \right)} \right]}}\text{sgn} \tilde{c} \\ \end{gathered} $$

(13)

$$ \begin{gathered} I_{i} \equiv \text{Im} \left[ {\frac{1}{4}\int\limits_{ - \infty }^{\infty } {\frac{{\exp \left( {\tilde{\beta }t + i\omega t} \right)}}{{\cosh^{2} \left( {\tilde{c}t/2} \right)}}{\text{d}}t} } \right] = \text{Im} \left[ {\frac{{\pi \left( {\tilde{\beta } + i\omega } \right){ \csc }\left[ {\pi \left( {\tilde{\beta } + i\omega } \right)/\tilde{c}} \right]}}{{\tilde{c}^{2} }}} \right]\text{sgn} \tilde{c} \\ = \frac{{2\pi \left[ { - \omega \cosh \left( {\omega \pi /\tilde{c}} \right)\sin \left( {\tilde{\beta }\pi /\tilde{c}} \right) + \tilde{\beta }\cos \left( {\tilde{\beta }\pi /\tilde{c}} \right)\sinh \left( {\omega \pi /\tilde{c}} \right)} \right]}}{{\tilde{c}^{2} \left[ {\cos \left( {2\tilde{\beta }\pi /\tilde{c}} \right) - \cosh \left( {2\omega \pi /\tilde{c}} \right)} \right]}}\text{sgn} \tilde{c} \\ \end{gathered} $$

(14)

$$ I_{0} \equiv \int\limits_{ - \infty }^{\infty } {\frac{{\exp \left( {\tilde{\beta }t + \tilde{c}t} \right)}}{{\left( {1 + \exp \left( {\tilde{c}t} \right)} \right)^{2} }}{\text{d}}t} = \frac{{\tilde{\beta }\pi }}{{\tilde{c}^{2} \sin \left( {\tilde{\beta }\pi /\tilde{c}} \right)}}\text{sgn} \tilde{c} $$

(15)

$$ I_{1} \equiv \int\limits_{ - \infty }^{\infty } {\frac{{\exp \left( {\tilde{\beta }t + 2\tilde{c}t} \right)}}{{\left( {1 + \exp \left( {\tilde{c}t} \right)} \right)^{3} }}{\text{d}}t} = \frac{{\tilde{\beta }\left( {\tilde{\beta } + \tilde{c}} \right)\pi }}{{2!\tilde{c}^{3} \sin \left( {\tilde{\beta }\pi /\tilde{c}} \right)}}\text{sgn} \tilde{c} $$

(16)

$$ I_{2} \equiv \int\limits_{ - \infty }^{\infty } {\frac{{\exp \left( {\tilde{\beta }t + 3\tilde{c}t} \right)}}{{\left( {1 + \exp \left( {\tilde{c}t} \right)} \right)^{4} }}{\text{d}}t} = \frac{{\tilde{\beta }\left( {\tilde{\beta } + \tilde{c}} \right)\left( {\tilde{\beta } + 2\tilde{c}} \right)\pi }}{{3!\tilde{c}^{4} \sin \left( {\tilde{\beta }\pi /\tilde{c}} \right)}}\text{sgn} \tilde{c} $$

(17)

$$ I_{3} \equiv \int\limits_{ - \infty }^{\infty } {\frac{{\exp \left( {\tilde{\beta }t + 4\tilde{c}t} \right)}}{{\left( {1 + \exp \left( {\tilde{c}t} \right)} \right)^{5} }}{\text{d}}t} = \frac{{\tilde{\beta }\left( {\tilde{\beta } + \tilde{c}} \right)\left( {\tilde{\beta } + 2\tilde{c}} \right)\left( {\tilde{\beta } + 3\tilde{c}} \right)\pi }}{{4!\tilde{c}^{5} \sin \left( {\tilde{\beta }\pi /\tilde{c}} \right)}}\text{sgn} \tilde{c} $$

(18)

$$ A_{{{\kern 1pt} 0}} = \phi_{1}^{2} \left( {1 - \phi_{1} } \right) $$

(19)

$$ A_{{{\kern 1pt} 1}} = \phi_{2} \left( {\phi_{3} - \phi_{1} } \right)\left( {2 - 3\phi_{2} } \right) $$

(20)

$$ A_{{{\kern 1pt} 2}} = \left( {\phi_{3} - \phi_{1} } \right)^{2} \left( {1 - 3\phi_{1} } \right) $$

(21)

$$ A_{{{\kern 1pt} 3}} = - \left( {\phi_{3} - \phi_{1} } \right)^{3} $$

(22)

where

$$ \tilde{c} \equiv \pm \sqrt {\tilde{\mu }/2} . $$

(23)

In following figures, the results based on Eq. 12 are plotted as ‘Formula of a non-biased heteroclinic orbit’.

On the other hand, the Melnikov integral can be carried out without transposing the part of the restoring term to the right side, since the non-biased roll equation is solved analytically, as shown in the previous section. In this case, the critical forcing can be obtained as:

$$ \gamma = \frac{{\sigma I_{0} }}{{\sqrt {I_{r}^{2} + I_{i}^{2} } }}. $$

(24)

The terms I ₀, I _r and I _i , are the same as those shown in Eqs. 13–15. Note, for the calculation of I ₀, I _r and I _i , an heteroclinic orbit with respect to the biased-roll equation should be employed. In the following figures, the results based on Eq. 24 are plotted as ‘Proposed formula’.

Figure 6 shows the final results of the critical forcing γ for the non-biased case. In this figure, the results are obtained by using the formula [14] given by:

$$ \gamma = \left[ {\frac{2\beta }{3} - \frac{{\sqrt 2 \left( {1 - a} \right)}}{3}} \right]\frac{{\sinh \left( {\pi \omega /\sqrt 2 } \right)}}{\pi \omega }, $$

(25)

Fig. 6

Comparison of critical forcing for non-biased roll, i.e., a of 1.0 and β of 0.1

These are plotted as ‘Formula from Hamiltonian heteroclinic orbit’ for comparative purposes. Note that Eq. 25, with a of 1.0, is identical with the formula obtained by Kan and Taguchi [6]. From Fig. 6, it can be seen that there is only a minor discrepancy between the two. Figure 7 indicates comparative results of the critical forcing obtained by using several methods, and it shows that the results of critical forcing do not wholly depend upon an assumed heteroclinic orbit. The reason is considered as follows. In this study, the extended Melnikov method introduced by Salam [15] is employed. The significant difference between the original method and the extended method is whether or not the damping term of a heteroclinic orbit is taken into account. However, it is well known that roll dumping is generally small, and that the contribution of its difference also becomes small. The proposed calculation technique is relatively complicated compared to that proposed by Kan and Taguchi [6] and the method proposed by Spyrou et al. [11], and these methods are considerably validated by numerical simulation. Therefore, these two methods are more practical and are thus recommended.

Fig. 7

Comparison of critical forcing with a of 0.975 and β of 0.1

Finally, we confirm whether the obtained critical forcing actually represents the bound of chaos or fractals. Since the obtained values using the proposed method are: γ of 0.06344, a of 0.975, β of 0.1 and ω of 0.8, a numerical calculation is carried out for γ of 0.07. It is necessary to magnify the figure significantly in order to clearly observed fractal metamorphoses of basin boundary at γ close to 0.06344. However, this magnification makes the figure difficult to understand, since the drawn area is exceedingly limited. Therefore, a value slightly above the critical forcing, that is γ of 0.07, is chosen for numerical calculation. Figure 8 shows the onset of a safe basin erosion near this value. The black shaded part of the plot represents the non-capsizing region while white non-shaded part is a capsize region. From this figure it can be concluded that the critical forcing obtained by using Melnikov’s integral formula can approximately demonstrate the onset of chaos and fractals.

Fig. 8

An example of fractal metamorphoses of basin boundary with a of 0.975, β of 0.1, ω of 0.8 and γ of 0.07, which is slightly above the critical forcing

Although this analysis is carried out for the escape equation having only linear damping terms, the same procedure is of course applicable for equations having higher-order damping terms. As an example, in Appendix 1, the method employing the equation having linear and quadratic damping terms is described, and an extended analysis for a 1 DoF roll equation having 4th-order polynomial restoring term and a quadratic polynomial damping term is described in Appendix 2. Furthermore, it is worth noting that saddle-node bifurcation appears in the escape equation and the relation to the Melnikov analysis is demonstrated based on Yagasaki’s [19] work in a previous paper [20].

4 Concluding remarks

The main conclusions to be drawn from this work can be summarized as follows:

• 1. The proposed equation representing the heteroclinic orbit from previous work is verified by numerical results.

• 2. By using an analytically obtained heteroclinic orbit, the Melnikov integral can be analytically evaluated. As a result, it is concluded that, for the equation with a small damping term, such as the escape equation, whether or not the damping term is taken into account the calculation of the separatrix does not strongly influence the final result.

Appendices

Appendix 1

In this paper, the damping term in the state equation is assumed as linear, but the critical forcing should be formulated for a general case. Therefore, the formulation is shown for the case of linear, quadratic and cubic dumpling:

$$ \ddot{\varphi } + \beta \dot{\varphi } + \beta_{2} \dot{\varphi }^{2} \text{sgn} \dot{\varphi } + \beta_{3} \dot{\varphi }^{3} + \varphi \left( {1 - \varphi } \right)\left( {\varphi - \tilde{a}} \right) = \sigma + F\sin \omega t. $$

(26)

Manipulation of this equation easily leads to following expression:

$$ \frac{\text{d}}{{{\text{d}}t}}\left( \begin{gathered} \varphi \hfill \\ {\dot{\varphi }} \hfill \\ \end{gathered} \right) = \left( \begin{gathered} {\dot{\varphi }} \\ - \beta \dot{\varphi } - \varphi \left( {1 - \varphi } \right)\left( {\varphi - \tilde{a}} \right) \\ \end{gathered} \right) + \left( \begin{gathered} 0 \\ - \beta_{2} \dot{\varphi }^{2} \text{sgn} \dot{\varphi } - \beta_{3} \dot{\varphi }^{3} + \sigma + F\sin \omega t \\ \end{gathered} \right) \equiv {\mathbf{F}}\left( {\mathbf{x}} \right) + {\mathbf{G}}\left( t \right). $$

(27)

Then the Melnikov integral becomes:

$$ \begin{gathered} M\left( {t_{0} } \right) = \int\limits_{ - \infty }^{\infty } {{\mathbf{F}}\left( {\varphi^{0} \left( t \right)} \right) \wedge {\mathbf{G}}\left( {t + t_{0} } \right) \cdot \exp \left( { - \int\limits_{0}^{t} {{\text{tr}}D{\mathbf{F}}\left( {\mathbf{x}} \right){\text{d}}s} } \right){\text{d}}t} \\ = - \text{sgn} \tilde{c}\int\limits_{ - \infty }^{\infty } {\beta_{2} \tilde{c}^{3} \left( {\varphi^{0} \left( t \right)} \right)^{3} \left( {1 - \varphi^{0} \left( t \right)} \right)^{3} \cdot \exp \left( {\int\limits_{0}^{t} {\beta {\text{d}}s} } \right){\text{d}}t} \\ - \int\limits_{ - \infty }^{\infty } {\beta_{3} \tilde{c}^{4} \left( {\varphi^{0} \left( t \right)} \right)^{4} \left( {1 - \varphi^{0} \left( t \right)} \right)^{4} \cdot \exp \left( {\int\limits_{0}^{t} {\beta {\text{d}}s} } \right){\text{d}}t} \\ + \int\limits_{ - \infty }^{\infty } {F\sin \omega \left( {t + t_{0} } \right)\tilde{c}\varphi^{0} \left( t \right)\left( {1 - \varphi^{0} \left( t \right)} \right) \cdot \exp \left( {\int\limits_{0}^{t} {\beta {\text{d}}s} } \right){\text{d}}t} \\ + \int\limits_{ - \infty }^{\infty } {\sigma \tilde{c}\varphi^{0} \left( t \right)\left( {1 - \varphi^{0} \left( t \right)} \right) \cdot \exp \left( {\int\limits_{0}^{t} {\beta {\text{d}}s} } \right){\text{d}}t} \\ = F\tilde{c}\sqrt {I_{r}^{2} + I_{i}^{2} } \sin \left( {\omega t_{0} + \tan^{ - 1} \left( {I_{i} /I_{r} } \right)} \right) + \sigma \tilde{c}I\left( 0 \right) - \beta_{2} \tilde{c}^{3} K_{2} \text{sgn} \tilde{c} - \beta_{3} \tilde{c}^{4} K_{3} . \\ \end{gathered} $$

(28)

Here I, K ₂ and K ₃ are defined as follows:

$$ I\left( \omega \right) \equiv \int\limits_{ - \infty }^{\infty } {\varphi^{0} \left( t \right)\left( {1 - \varphi^{0} \left( t \right)} \right)e^{{\tilde{\beta }t}} e^{i\omega t} {\text{d}}t} , $$

(29)

$$ K_{2} \equiv \int\limits_{ - \infty }^{\infty } {\left( {\varphi^{0} \left( t \right)} \right)^{3} \left( {1 - \varphi^{0} \left( t \right)} \right)^{3} \cdot \exp \left( {\int\limits_{0}^{t} {\tilde{\beta }{\text{d}}s} } \right){\text{d}}t} , $$

(30)

$$ K_{3} \equiv \int\limits_{ - \infty }^{\infty } {\left( {\varphi^{0} \left( t \right)} \right)^{4} \left( {1 - \varphi^{0} \left( t \right)} \right)^{4} \cdot \exp \left( {\int\limits_{0}^{t} {\tilde{\beta }{\text{d}}s} } \right){\text{d}}t} , $$

(31)

where we put I _r = Re[I] and I _i = Im[I]. K ₂ and K ₃ can be calculated via Cauchy’s integral theorem as follows:

$$ K_{2} \equiv \frac{{\pi \beta \left( {\beta^{2} - 4\tilde{c}^{2} } \right)\left( {\beta^{2} - \tilde{c}^{2} } \right)}}{{5!\tilde{c}^{6} \sin \left( {\pi \beta /\tilde{c}} \right)}}\text{sgn} \tilde{c} $$

(32)

$$ K_{3} \equiv \frac{{ - \pi \beta \left( {\beta^{2} - 9\tilde{c}^{2} } \right)\left( {\beta^{2} - 4\tilde{c}^{2} } \right)\left( {\beta^{2} - \tilde{c}^{2} } \right)}}{{7!\tilde{c}^{8} \sin \left( {\pi \beta /\tilde{c}} \right)}}\text{sgn} \tilde{c}. $$

(33)

Note that a singular point of the Eq. 30, i.e., $t = \pi i\left( {2n + 1} \right)/\tilde{c}$, is a pole of order 6. Here n denotes the arbitrary integer. Therefore, the following condition must be held.

$$ \frac{{\sigma I\left( 0 \right) - \beta_{2} \tilde{c}^{2} K_{2} {\text sgn} \tilde{c} - \beta_{3} \tilde{c}^{3} K_{3} }}{{\sqrt {I_{r}^{2} + I_{i}^{2} } }} < F $$

(34)

Appendix 2

In the main section, the 1 DoF roll equation with cubic, quadratic and linear restoring term is carried out. In this appendix, the study for the 1 DoF roll equation is shown, with a 4th-order polynomial restoring term and a quadratic polynomial damping term.

$$ {\ddot{x}} + \tilde{\beta }_{1} \dot{x} + \tilde{\beta }_{2} \dot{x}^{2} + \tilde{\gamma }x\left( {1 - x} \right)\left( {x - k} \right)\left( {x - s_{1} } \right) = 0. $$

(35)

The reason why these terms are represented by a higher-order polynomial is to fit their original curves. Taking the following as a solution in the time domain:

$$ x = a_{0} /\left( {e^{{ - c_{0} t}} + b_{0} } \right), $$

(36)

and substituting Eq. 36 into 35, yields:

$$ \begin{gathered} a_{0} \left( { - \tilde{\gamma }a_{0}^{3} + \tilde{\gamma }a_{0}^{2} b_{0} + \tilde{\gamma }ka_{0}^{2} b_{0} + \tilde{\gamma }s_{1} a_{0}^{2} b_{0} - \tilde{\gamma }ka_{0} b_{0}^{2} - \tilde{\gamma }s_{1} a_{0} b_{0}^{2} - \tilde{\gamma }ks_{1} a_{0} b_{0}^{2} + \tilde{\gamma }ks_{1} b_{0}^{3} } \right) \hfill \\ + a_{0} e^{{ - c_{0} t}} \left( {\tilde{\gamma }a_{0}^{2} + \tilde{\gamma }ka_{0}^{2} + \tilde{\gamma }s_{1} a_{0}^{2} - 2\tilde{\gamma }ka_{0} b_{0} - 2\tilde{\gamma }s_{1} a_{0} b_{0} - 2\tilde{\gamma }ks_{1} a_{0} b_{0} + 3\tilde{\gamma }ks_{1} a_{0} b_{0} + 3\tilde{\gamma }ks_{1} b_{0}^{2} + \tilde{\beta }_{1} b_{0}^{2} c_{0} - b_{0}^{2} c_{0}^{2} } \right) \hfill \\ + a_{0} e^{{ - 2c_{0} t}} \left( { - \tilde{\gamma }ka_{0} - \tilde{\gamma }s_{1} a_{0} - \tilde{\gamma }ks_{1} a_{0} + 3\tilde{\gamma }ks_{1} a_{0} b_{0} + 2\tilde{\beta }_{1} b_{0} c_{0} + \tilde{\beta }_{2} a_{0} c_{0}^{2} } \right) \hfill \\ + a_{0} e^{{ - 3c_{0} t}} \left( {\tilde{\gamma }ks_{1} + \tilde{\beta }_{1} c_{0} + c_{0}^{2} } \right) = 0. \hfill \\ \end{gathered} $$

(37)

Comparing both sides of the equation when considering:

$$ a_{0} = b_{0} = 1, $$

(38)

we can obtain the following equations:

$$ \left\{ \begin{gathered} \tilde{\gamma } - \tilde{\gamma }k - \tilde{\gamma }s_{1} + \tilde{\gamma }ks_{1} + \tilde{\beta }_{1} c_{0} - c_{0}^{2} = 0 \hfill \\ - \tilde{\gamma }k - \tilde{\gamma }s_{1} + 2\tilde{\gamma }ks_{1} + 2\tilde{\beta }_{1} c_{0} + \tilde{\beta }_{2} c_{0}^{2} = 0 \hfill \\ \tilde{\gamma }ks_{1} + \tilde{\beta }_{1} c_{0} + c_{0}^{2} = 0. \hfill \\ \end{gathered} \right. $$

(39a,b,c)

Solving Eq. 39c with respect to $\tilde{\beta }_{1}$ yields:

$$ \tilde{\beta }_{1} = \frac{{ - \tilde{\gamma }ks_{1} - c_{0}^{2} }}{{c_{0} }}. $$

(40)

Substituting the above in to Eq. 39a and 39b, we can obtain:

$$ \left\{ \begin{gathered} \tilde{\gamma } - \tilde{\gamma }k - \tilde{\gamma }s_{1} - 2c_{0}^{2} = 0 \hfill \\ - \tilde{\gamma }k - \tilde{\gamma }s_{1} + \tilde{\beta }_{2} c_{0}^{2} - 2c_{0}^{2} = 0 \hfill \\ \end{gathered} \right.. $$

(41a,b)

Eqiation 41b can be rewritten as:

$$ c_{0}^{2} = \frac{{\tilde{\gamma }k + \tilde{\gamma }s_{1} }}{{ - 2 + \tilde{\beta }_{2} }}, $$

(42)

so that, substituting the above expression into Eq. 41a, the following relationship is obtained:

$$ - \frac{{\tilde{\gamma }\left[ {2 + \tilde{\beta }_{2} \left( { - 1 + k + s_{1} } \right)} \right]}}{{ - 2 + \tilde{\beta }_{2} }} = 0. $$

(43)

Solving the above equation with respect to $\tilde{\beta }_{2}$ and assuming $\tilde{\beta }_{2} \ne - 2$, we can obtain

$$ \tilde{\beta }_{2} = - \frac{2}{{ - 1 + k + s_{1} }}. $$

(44)

If this relationship is satisfied, the solution with regard to polynomial approximated equation is determined as follows:

$$ x = 1/\left\{ {1 + \exp \left[ { - \frac{{\sqrt { - \tilde{\gamma }\left( { - 1 + k + s_{1} } \right)} }}{\sqrt 2 }t} \right]} \right\}. $$

(45)

Here c ₀ is assumed as a positive value as:

$$ c_{0} = \sqrt {\frac{{ - \tilde{\gamma }\left( { - 1 + k + s_{1} } \right)}}{2}} , $$

(46)

so that, substitution of above equation into Eq. 40 yields:

$$ \tilde{\beta }_{1} = \frac{{\tilde{\gamma }\left( { - 1 + k + s_{1} - 2ks_{1} } \right)}}{{\sqrt { - 2\tilde{\gamma }\left( { - 1 + k + s_{1} } \right)} }}. $$

(47)

This is the condition of heteroclinic bifurcation. Obviously, the condition $\tilde{\gamma } < 0\,\,{\text{and}}\,\,s_{1} > 0$, or, $\tilde{\gamma } > 0\,\,{\text{and}}\,\,s_{1} < 0$ is required. Here we briefly consider the heteroclinic orbit. Eliminating the time t from Eq. 45 yields the trajectory in the phase plane consists of x and $\dot{x}$ as quadratic equations. However, if we substitute the trajectory having a quadratic form into Eq. 35, this equation is not satisfied. This is because the Eq. 47 is only defined between the two saddle points. Note that Eqs. 44 and 47 should be simultaneously satisfied, and it implies that the solution surface is formed in a 4-dimensional parameter plane consisting of $\tilde{\beta }_{1} ,\,\tilde{\beta }_{2} ,\,k,\,s_{1} k$. Note, therefore, that the obtained heteroclinic trajectory cannot represent the all the trajectories of Eq. 35.

Using the quadratic form of the trajectory in the time domain, chaos that appears in Eq. 35 can be studied. Considering the following relationships:

$$ {\mathbf{F}}\left( {q^{0} \left( t \right)} \right) \wedge {\mathbf{G}}\left( {t + t_{0} } \right) = \dot{\varphi }\left( {b_{0} + b\sin \omega t} \right) $$

(48)

$$ D{\mathbf{F}}\left( {\mathbf{x}} \right) = \left( {\begin{array}{*{20}c} 0 & 1 \\ {\tilde{\gamma }\left[ {4x^{3} - 3\left( {k + s_{1} + 1} \right)x^{2} + 2\left( {ks_{1} + k + s_{1} } \right)x - ks_{1} } \right]} & { - \tilde{\beta }_{1} - 2\tilde{\beta }_{2} \dot{x}} \\ \end{array} } \right) $$

(49)

$$ {\text{tr}}D{\mathbf{F}}\left( {\mathbf{x}} \right) = - \tilde{\beta }_{1} - 2\tilde{\beta }_{2} \dot{x} $$

(50)

then the Melnikov integral becomes:

$$ \begin{gathered} M(t_{0} ) = \int\limits_{{\text{ - }\infty }}^{\infty } {{\mathbf{F }}\text{(}\varphi^{0} \text{(t))} \wedge {\mathbf{G}}\text{(}t\text{ + }t_{0} \text{)} \times \text{exp( - }\int\limits_{0}^{t} {{\text{tr}}D} {\mathbf{F}}\text{(}{\mathbf{x}}\text{)d}s\text{)d}t} \hfill \\ = \int\limits_{{\text{ - }\infty }}^{\infty } {b\sin \omega (t\text{ + }t_{0} )\tilde{c}} \varphi^{0} (t)(1\text{ - }\varphi^{0} (t)) \times \exp (\int\limits_{0}^{t} {(\tilde{\beta }_{1} \text{ - }2\tilde{\beta }_{2} \dot{x}){\text{d}}s} ){\text{dt}} \hfill \\ { + }\int\limits_{{\text{ - }\infty }}^{\infty } {b_{0} } \tilde{c}\varphi^{0} (t)(1\text{ - }\varphi^{0} (t)) \times \exp (\int\limits_{0}^{t} {(\tilde{\beta }_{1} \text{ - }2\tilde{\beta }_{2} \dot{x}){\text{d}}s} ){\text{dt}} \hfill \\ = b\tilde{c}(I_{i}^{{\prime }} \cos \omega t_{0} + I_{r}^{{\prime }} \sin \omega t_{0} ) + b_{0} \tilde{c}I^{{\prime }} (0) \hfill \\ = b\tilde{c}\sqrt {I_{r}^{{{\prime 2}}} + I_{i}^{{{\prime 2}}} } \sin (\omega t_{0} + \tan^{{\text{ - }1}} ({{I_{i}^{{\prime }} } \mathord{\left/ {\vphantom {{I_{i}^{{\prime }} } {I_{r}^{{\prime }} }}} \right. \kern-0pt} {I_{r}^{{\prime }} }})) + b\tilde{c}I^{{\prime }} (0) \hfill \\ \end{gathered} $$

(51)

where I(ω) is defined with the following Fourier transformation:

$$ I\left( \omega \right) \equiv \int\limits_{ - \infty }^{\infty } {\varphi^{0} \left( t \right)\left( {1 - \varphi^{0} \left( t \right)} \right)e^{{\tilde{\beta }_{1} t - 2\tilde{\beta }_{2} \varphi^{0} \left( t \right)}} e^{i\omega t} {\text{d}}t} . $$

(52)

This equation has a form shown as follows:

$$ I\left( \omega \right) = \frac{1}{4}\int\limits_{ - \infty }^{\infty } {\frac{{\exp \left( {\tilde{\beta }_{1} t - \frac{{2\tilde{\beta }_{2} }}{{1 + \exp \left( { - \tilde{c}t} \right)}} + i\omega t} \right)}}{{\cosh^{2} \left( {\tilde{c}t/2} \right)}}{\text{d}}t} = \frac{1}{4}\int\limits_{ - \infty }^{\infty } {\frac{{\exp \left( {\tilde{\beta }_{1} t - \tilde{\beta }_{2} - \tilde{\beta }_{2} \tanh \left( {\tilde{c}t/2} \right) + i\omega t} \right)}}{{\cosh^{2} \left( {\tilde{c}t/2} \right)}}{\text{d}}t} , $$

(53)

However, further analytical manipulation is considered to be difficult.