1 Introduction

Ships navigating rough seas experience several types of wave-induced excitations, which can lead to dynamic instabilities and high-amplitude rolling. The roll motion of a ship is less damped than the pitch and yaw motions [1]; in extreme cases, roll excitation can result in capsizing. Furthermore, rolling can cause seasickness, impede crew performance, and damage equipment on naval vessels. It is critical to study and understand the dynamics, stability, and control of ship roll motion to mitigate these adverse effects.

Fig. 1
figure 1

A ship equipped with an actively controlled anti-roll tank. The pump (“P”) pumps air between tanks to displace water (block arrows) and generate corrective torques (curved arrows)

Full size image

Instabilities in a ship’s roll motion can be induced by two mechanisms: direct excitation and parametric excitation. Direct excitation occurs when waves collide with the port side or starboard side of a ship and can be caused by both beam waves (waves that are approximately perpendicular to the ship’s heading direction) and oblique waves. If the frequency of such waves coincides with the ship’s roll natural frequency, direct resonance will occur, leading to high-amplitude rolling. To minimize direct excitation in a beam sea, ships are typically navigated perpendicular to waves, thereby resulting in a head sea or following sea. However, this strategy leads to excitation of the ship’s pitch motion, which may induce parametric excitation.

Parametric excitation of the roll motion can arise from the inherent coupling between a ship’s pitch and roll dynamics, from the shape of the hull, due to the ratio of the pitch and roll frequencies, and when the ship encounters a head sea or following sea whose wavelength is similar to the length of the ship [2]. Direct excitation of the pitch motion is caused by head and following waves (waves that are directed toward the bow and stern of the ship, respectively) as well as oblique waves. If the frequency of the pitch motion becomes twice the natural frequency of the roll motion, the ship experiences parametric resonance and, consequently, indirect roll excitation.

The frequency of roll excitation can be adjusted by altering the speed and heading of the ship. However, the speed and amplitude of the ocean waves cannot be controlled, and there are limitations to the rate and range of adjustments that can be made to ship speed. A more reliable strategy is to use active control methods such as bilge keels, fins, rudders, gyroscopic stabilizers, and U-tube anti-roll tanks (ARTs) [3]. ARTs have two key advantages over other control strategies. First, ARTs are not affected by the ship’s forward speed, making them appropriate for use even when the vessel is moored, such as during loading and unloading operations. Second, the performance of an ART is independent of the natural frequency of either the ship or the tank.

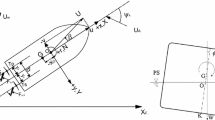
Anti-roll tanks can be either passive or actively controlled. A passive ART functions like a tuned mass–damper system. In contrast, an actively controlled ART pumps air between tanks on the port side and starboard side of the ship to displace water, moving it from one tank to the other, thereby generating torques that counteract the roll motion (Fig. 1). In general, time delays occur in this correction-torque control system due to the time required to displace water from one ART tank to the other, the inertia of large impeller blades and linkages in the pump, and the measurement and processing time of the roll-sensing unit. The transfer of fluid between tanks affects the restoring arm of the vessel through weight redistribution as well as the roll damping due to friction losses from fluid flow. As a result, ARTs can be modeled as proportional–derivative (PD) feedback control systems with time delay. Although an ART’s hydraulics exhibit nonlinear behavior, an actively controlled ART can be operated using a simple linear proportional or PD controller [4, 5].

Here, we outline the existing literature in the area of ship dynamics. We first discuss general studies carried out in this field, then restrict our attention to studies that consider active control for ship stabilization with specific focus on studies exploring ARTs. In the mid-1980 s, Nayfeh and Khdeir [6, 7] performed pioneering work in which they modeled a rolling ship as a single-degree-of-freedom nonlinear dynamical system, demonstrating the existence of chaos when the ship was subjected to beam waves. Spyrou and Thompson [8, 9], Ibrahim and Grace [10], and Neves [11] have published comprehensive reviews of the literature on ship motion dynamics.

Strategies to control the rolling of ships have been explored for many years. In 1935, Minorsky [4] analyzed the active control of ship rolling, including nonlinear damping and linear restoring moments. Minorsky proposed a control law based on the rate of rolling and its effect on roll damping, noting the importance of delay but ignoring higher-order terms in the delayed control function. In recent years, numerous studies have assessed the effects of passive and active ARTs on a ship’s roll motion [12, 13] and the coupled roll, pitch, and heave motions [14, 15]. In 2001, Abdel Gawad et al. [16] studied the application of a single passive U-tube ART to control the roll motion of a ship. This work includes a comprehensive review of the literature on the development of ARTs. In 2009, Marzouk and Nayfeh [5] investigated an active U-tube ART controlled by a PD control law. They concluded that, compared to a passive ART, an active ART is superior in terms of roll reduction, size, weight, and responsiveness to parametric rolling. Moaleji and Greig [17] proposed an active U-tube ART that employs an adaptive inverse model as its controller.

The effect of feedback delays has been well documented and is an active topic of investigation [18]. Spyrou studied the effect of heading and yaw rate feedback delays on the performance of a course-keeping controller [19]. However, there is limited work on the effect of delays in control systems employing active U-tube ARTs to stabilize ship roll dynamics. Shaik et al. [20] analyzed the roll dynamics of a ship controlled by an active U-tube ART with delayed feedback. A detailed parametric study was performed and the controller parameters that provide maximum damping were determined. Two key findings were reported. First, derivative feedback is detrimental to the stability of ship roll motion. Hence, a proportional-feedback control law was studied, and it was shown to be capable of preventing a ship from capsizing when using the optimal gain and time delay. Second, they demonstrated the existence of Hopf bifurcation boundaries and double Hopf bifurcation points in the parameter space of time delay and proportional-control gain.

Hopf bifurcation points in ship roll models correspond to large-amplitude roll motion, which can exceed capsizing roll angles in some cases. Thus, it is crucial to understand the behavior of the system at the Hopf bifurcation points. Although Shaik et al. [20] studied single Hopf bifurcation points in detail, the system response near double Hopf bifurcation points was not explored. In the present study, we extend this work and perform a detailed double Hopf bifurcation analysis.

Double Hopf bifurcations have been investigated in the nonlinear dynamics literature in various mathematical models, using many techniques. In models comprising nonlinear ordinary differential equations (ODEs), the method of multiple scales (MMS) was employed by Yu [21]. In models governed by partial differential equations (PDEs), the MMS method has been employed [22, 23] as well as center manifold reductions and normal form theory [24, 25]. These methods have also been used successfully for systems of delay differential equations (DDEs), with appropriate modifications. On this topic, we refer the reader to studies that have used center manifold reductions [26,27,28,29], normal form theory (bypassing the center manifold reductions) [30,31,32,33], and the MMS method (bypassing the center manifold reductions and normal forms) [20, 34,35,36].

Our formulation can be briefly summarized as follows. First, we model a low-freeboard ship undergoing rolling motion as a single-degree-of-freedom system. The system model includes nonlinear damping and restoring functions and an actively controlled ART with delayed feedback. The ART is modeled using two parameters: control function gain and time delay. After defining the system equations, we perform a stability analysis to demonstrate the existence of double Hopf bifurcation points. Finally, we investigate the system’s response near the first double Hopf bifurcation point using slow-flow equations, which are obtained via the MMS method.

The remainder of the paper is organized as follows. In Sects. 2, 3, and 4, we demonstrate the existence of the first double Hopf bifurcation point using three techniques. In Sect. 2, we perform a linear stability analysis and demonstrate existence graphically. In Sects. 3 and 4, we demonstrate existence analytically and through calculation of eigenvalues, respectively. In Sect. 5, the slow-flow equations are obtained using the MMS method at the first double Hopf bifurcation point; phase portraits and a fixed-point analysis are presented. In Sect. 6, the qualitative behavior of the phase portraits is validated numerically. Finally, conclusions are presented in Sect. 7.

2 Linear stability analysis

We consider the single-degree-of-freedom system used by Shaik et al. [20] to model the rolling of a ship in a calm sea. The governing equation for the roll angle \(\phi (t)\) is

$$\begin{aligned}&\ddot{\phi }(t) + \omega _0^2 \phi (t) + 2 \hat{\mu }_1 \dot{\phi }(t) + \hat{\mu }_3 \dot{\phi }^3(t) + \hat{\alpha }_3 \phi ^3(t)\nonumber \\&\quad + \hat{\alpha }_5 \phi ^5(t) + k_p \phi (t-\tau ) = 0, \end{aligned}$$
(1)

where \(\omega _0\) is the roll natural frequency, \(\hat{\mu }_1\) and \(\hat{\mu }_3\) are the linear and cubic damping coefficients, \(\hat{\alpha }_3\) and \(\hat{\alpha }_5\) are coefficients of the restoring function, and \(k_p \phi (t-\tau )\) is the delayed proportional control function representing the effect of an anti-roll tank. In Eq. (1), the restoring moment is represented by an odd polynomial in \(\phi \) as \(K(\phi ) = \omega _0^2 \phi + \hat{\alpha }_3 \phi ^3 + \hat{\alpha }_5 \phi ^5\), with coefficients obtained from experimental data. In general, the damping moment may be represented as \(D(\dot{\phi }) = 2 \hat{\mu }_1 \dot{\phi } + \hat{\mu }_3 \left| \dot{\phi } \right| \dot{\phi }\), comprising a linear term in \(\dot{\phi }\) due to viscous damping and a quadratic term due to frictional resistance and eddies around bilge keels and sharp bilge corners [37]. However, Dalzell [37] determined that the mixed linear-plus-quadratic roll damping model can be reasonably approximated by a mixed linear-plus-cubic model, namely \(D(\dot{\phi }) = 2 \hat{\mu }_1 \dot{\phi } + \hat{\mu }_3 \dot{\phi }^3\), which we have used in Eq. (1).

To investigate the linear stability of the system around the trivial fixed point \(\phi = 0\), hereafter denoted \(\bar{\phi }\), we substitute \(\phi (t) = r(t) + \bar{\phi }\) into Eq. (1) to obtain

$$\begin{aligned}&\ddot{r}(t) + \omega _0^2 r(t) + 2\hat{\mu }_1 \dot{r}(t) + \hat{\mu }_3 \dot{r}^3(t) + \hat{\alpha }_3 r^3(t)\nonumber \\&\quad + \hat{\alpha }_5 r^5(t) + k_p r(t-\tau ) = 0. \end{aligned}$$
(2)

Retaining only the linear terms in r(t) in Eq. (2), we obtain

$$\begin{aligned} \ddot{r}(t) + \omega _0^2 r(t) + 2 \hat{\mu }_1 \dot{r}(t) + k_p r(t-\tau ) = 0. \end{aligned}$$
(3)

Substituting \(r(t) = \beta e^{\lambda t}\) into Eq. (3) produces the following characteristic equation:

$$\begin{aligned} D \left( \lambda , k_p, \tau \right) = \lambda ^2 + 2 \hat{\mu }_1 \lambda + \omega _0^2 + k_p e^{-\lambda \tau } = 0, \end{aligned}$$
(4)

where \(\lambda \), \(\beta \in \mathbb {C}\). Equation (4) is a transcendental equation and possesses infinitely many roots, known as characteristic exponents. To obtain the Hopf bifurcation boundary, we substitute \(\lambda = j \omega _{cr}\) into Eq. (4):

$$\begin{aligned} D \left( \omega _{cr}, k_p, \tau \right) =&-\omega _{cr}^2 + 2j \hat{\mu }_1 \omega _{cr} + \omega _0^2\nonumber \\&+ k_p e^{-j \omega _{cr} \tau } = 0. \end{aligned}$$
(5)

(Note that, if \(j \omega _{cr}\) is a root of the characteristic equation, then so is its complex conjugate \(-j \omega _{cr}\).) Using Euler’s formula \(e^{-j \omega _{cr} \tau } = \cos \left( \omega _{cr} \tau \right) - j \sin \left( \omega _{cr} \tau \right) \), we separate \(D \left( \omega _{cr}, k_p, \tau \right) \) into its real and imaginary parts to obtain the following real-valued equations:

$$\begin{aligned} R \left( \omega _{cr}, k_p, \tau \right)&= k_p \cos \left( \omega _{cr} \tau \right) - \omega _{cr}^2 + \omega _0^2\nonumber \\&= 0, \end{aligned}$$
(6a)
$$\begin{aligned} C \left( \omega _{cr}, k_p, \tau \right)&= 2 \hat{\mu }_1 \omega _{cr} - k_p \sin \left( \omega _{cr} \tau \right) = 0. \end{aligned}$$
(6b)

We solve Eqs. (6a) and (6b) to obtain the following linear stability boundary in the space of \(k_p\) and \(\tau \):

$$\begin{aligned} k_p =&\ \sqrt{4 \hat{\mu }_1^2 \omega _{cr}^2 + \left( \omega _{cr}^2 - \omega _0^2 \right) ^2}, \end{aligned}$$
(7a)
$$\begin{aligned} \tau =&\ \frac{2}{\omega _{cr}} \left[ n \pi + \arctan \left( \frac{k_p - \omega _{cr}^2 + \omega _0^2}{2 \hat{\mu }_1 \omega _{cr}} \right) \right] ,\nonumber \\&\ n = 0, 1, 2, \ldots \ . \end{aligned}$$
(7b)

Equations (7a) and (7b) represent a family of curves called the stability lobes, where n is the lobe number.

For the numerical analysis that follows, we use the parameter values used in the low-freeboard model of Wright and Marshfield [38]. The values of the system parameters related to the damping and restoring functions are given in Table 1. The critical roll angle \(\phi _{cr}\) given in Table 1 is defined as the roll angle associated with the maximum restoring moment \(K(\phi )\) before capsizing. The critical roll angle can be obtained by plotting \(K(\phi )\) vs. \(\phi \), as shown in Fig. 2 for the parameters given in Table 1. (This curve is also known as the GZ curve.)

Table 1 Parameters used in numerical analysis of low-freeboard model (obtained from Shaik et al. [20])
Full size table
Fig. 2
figure 2

The restoring function \(K(\phi )\) vs. roll angle \(\phi \) for the low-freeboard model. \(K(\phi )\) reaches a maximum at the critical roll angle \(\phi _{cr}\)

Full size image

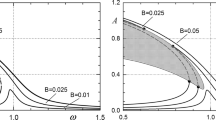
The stability boundaries of the system for lobes \(n=0\) and \(n=1\) are shown in Fig. 3. Similar lobes can be evaluated for \(n \ge 2\); however, the present analysis concerns the first double Hopf bifurcation point, which occurs at the intersection of the lobes corresponding to \(n=0\) and \(n=1\). Hence, we focus on only these two lobes. (Note that, to plot the stability boundary, we vary the independent parameter \(\omega _{cr}\) between a very small positive number and a very large number.) Hereafter, we refer to the values of the delay and the proportional gain at the first double Hopf bifurcation point as the “critical parameters” for brevity, and denote them as \(\tau _{cr}\) and \(k_{cr}\), respectively. From Fig. 3, their values are

$$\begin{aligned} \left( \tau _{cr}, k_{cr} \right) = \left( 0.9475, 17.0998\right) , \end{aligned}$$
(8)

and the corresponding frequencies are

$$\begin{aligned} \omega _1 = 3.2811 \quad \text {and} \quad \omega _2 = 6.7023, \end{aligned}$$
(9)

for lobes \(n=0\) and \(n=1\), respectively.

Fig. 3
figure 3

Linear stability chart near the double Hopf bifurcation point in the parameter space of \(\left( \tau , k_p \right) \). The critical parameters are \(\left( \tau _{cr}, k_{cr} \right) = \left( 0.9475, 17.0998\right) \). The shaded region indicates stable zero equilibrium

Full size image

3 Analytical demonstration of existence of double Hopf bifurcation

In this section, we demonstrate the existence of the double Hopf bifurcation point analytically by computing the crossing velocities of the eigenvalues of Eq. (3) at the critical parameters. As mentioned earlier, at the stability boundary, the eigenvalues \(\lambda \) cross the imaginary axis of the complex plane. Mathematically, this means \(\displaystyle {\Re \left( \frac{\partial \lambda }{\partial k_p} \right) \ne 0}\) and \(\displaystyle {\Re \left( \frac{\partial \lambda }{\partial \tau } \right) \ne 0}\), where \(\Re (\cdot )\) is the real part of a complex number [39, 40]. We obtain the partial derivatives \(\partial \lambda / \partial k_p\) and \(\partial \lambda / \partial \tau \) from implicit differentiation of Eq. (4):

$$\begin{aligned} \frac{\partial \lambda }{\partial k_p}&= -\frac{\partial D}{\partial k_p} \left( \frac{\partial D}{\partial \lambda } \right) ^{-1} = \frac{-e^{-\lambda \tau }}{2 \lambda + 2 \hat{\mu }_1 - \tau k_p e^{-\lambda \tau }}, \end{aligned}$$
(10a)
$$\begin{aligned} \frac{\partial \lambda }{\partial \tau }&= -\frac{\partial D}{\partial \tau } \left( \frac{\partial D}{\partial \lambda } \right) ^{-1} = \frac{k_p \lambda e^{-\lambda \tau }}{2 \lambda + 2 \hat{\mu }_1 - \tau k_p e^{-\lambda \tau }}. \end{aligned}$$
(10b)

Substituting \(\lambda = j \omega _i\) and \(e^{-j \omega _i \tau } = \cos \left( \omega _i \tau \right) - j \sin \left( \omega _i \tau \right) \) into Eqs. (10a) and (10b), we obtain the following expressions for the real parts of the slopes:

$$\begin{aligned} \gamma _{1i} =&\ \Re \left. \left( \frac{\partial \lambda }{\partial k_p}\right) \right| _{\lambda = j \omega _i}\nonumber \\ =&\ \Big [ \tau \left( \omega _0^2 - \omega _i^2 \right) ^2 + 4 \tau \hat{\mu }_1^2 + 2 \hat{\mu }_1 \left( \omega _0^2 + \omega _i^2 \right) \Big ] \Big /\nonumber \\&\ \Big [ k_p \tau ^2 \left( \left( \omega _0^2 - \omega _i^2 \right) ^2 + 4 \hat{\mu }_1^2 \right) + 4 k_p \hat{\mu }_1 \tau \big ( \omega _0^2\nonumber \\&\ + \omega _i^2 \big ) + 4 k_p \left( \hat{\mu }_1^2 + \omega _i^2 \right) \Big ], \end{aligned}$$
(11a)
$$\begin{aligned} \gamma _{2i} =&\ \Re \left. \left( \frac{\partial \lambda }{\partial \tau }\right) \right| _{\lambda = j \omega _i} = \Big [ 2 \omega _i^2 \left( \omega _i^2 - \omega _0^2 + 2 \hat{\mu }_1^2 \right) \Big ] \Big /\nonumber \\&\ \Big [ \tau ^2 \left( \omega _0^2 - \omega _i^2 \right) ^2 + 4 \tau ^2 \hat{\mu }_1^2 + 4 \hat{\mu }_1 \tau \left( \omega _0^2 + \omega _i^2 \right) \nonumber \\&\ + 4 \left( \hat{\mu }_1^2 + \omega _i^2 \right) \Big ], \end{aligned}$$
(11b)

where the index \(i \in \left\{ 1, 2 \right\} \) corresponds to the critical frequencies \(\omega _1\) and \(\omega _2\) at the double Hopf bifurcation point. We define a square matrix

$$\begin{aligned} {\varvec{\Lambda }} = \begin{bmatrix} \gamma _{11} &{} \gamma _{12}\\ \gamma _{21} &{} \gamma _{22} \end{bmatrix}, \end{aligned}$$
(12)

whose determinant must be nonzero for the existence of a double Hopf bifurcation at the critical point [41]. Using the parameters \(k_p = 17.0998\), \(\tau = 0.9475\), \(\omega _1 = 3.2811\), and \(\omega _2 = 6.7023\), \({\varvec{\Lambda }}\) at the critical point is evaluated as follows:

$$\begin{aligned} {\varvec{\Lambda }} = \begin{bmatrix} 0.0521 &{} 0.0363\\ -1.1557 &{} 3.2934 \end{bmatrix}, \end{aligned}$$
(13)

and \(\det ({\varvec{\Lambda }}) = 0.2135\), proving the existence of the double Hopf bifurcation point.

4 Demonstration of existence of double Hopf bifurcation via eigenvalue computation

In this section, we demonstrate the occurrence of a double Hopf bifurcation point through direct computation. Specifically, we show that two pairs of purely imaginary complex-conjugate eigenvalues exist at the double Hopf bifurcation point and that the eigenvalues cross the imaginary axis upon perturbing \(k_p\) and \(\tau \) around that point. Because Eq. (4) is transcendental, we use a combination of spectral Tau [42] and Newton–Raphson methods to compute its roots.

To use the spectral Tau method, we first write Eq. (3) as a pair of first-order differential equations in state variables \({\varvec{r}}(t) = \left[ r(t), \dot{r}(t) \right] ^{{\text {T}}}\):

$$\begin{aligned} \dot{{\varvec{r}}}(t)&= {\varvec{B}}_1 {\varvec{r}}(t) + {\varvec{B}}_2 {\varvec{r}}(t-\tau ), \end{aligned}$$
(14a)
$$\begin{aligned} {\varvec{r}}(t)&= {\varvec{\gamma }}(t), \quad t \in [-\tau , 0), \end{aligned}$$
(14b)

where \(\displaystyle {{\varvec{B}}_1 = \begin{bmatrix} 0 &{} 1\\ -\omega _0^2 &{} -2\hat{\mu }_1 \end{bmatrix}}\), \(\displaystyle {{\varvec{B}}_2 = \begin{bmatrix} 0 &{} 0\\ -k_p &{} 0 \end{bmatrix}}\), and \({\varvec{\gamma }}(t)\) is the history function. We then introduce a time shift in \({\varvec{r}}(t)\):

$$\begin{aligned} {\varvec{r}}(t+s) = {\varvec{y}}(s,t), \quad s \in [-\tau , 0). \end{aligned}$$
(15)

Due to this transformation, the initial-value problem expressed by Eq. (14) is transformed into the following boundary-value problem:

$$\begin{aligned}&\frac{\partial {\varvec{y}}(s,t)}{\partial t} = \frac{\partial {\varvec{y}}(s,t)}{\partial s}, \end{aligned}$$
(16a)
$$\begin{aligned}&\left. \frac{\partial {\varvec{y}}(s,t)}{\partial t}\right| _{s=0} = {\varvec{B}}_1 {\varvec{y}}(0, t) + {\varvec{B}}_2 {\varvec{y}}(-\tau , t), \end{aligned}$$
(16b)
$$\begin{aligned}&{\varvec{y}}(s, 0) = {\varvec{\gamma }}(s), \qquad s \in [-\tau , 0). \end{aligned}$$
(16c)

We assume a solution for Eq. (16a) of the following form:

$$\begin{aligned} y_i(s,t) = \sum _{j=1}^{\infty } \Psi _{j}(s) z_{ij}(t), \quad i = 1, 2, \end{aligned}$$
(17)

where \(\Psi _j(s)\) are appropriate basis functions (see Appendix A) and \(z_{ij}(t)\) are time-dependent coordinates. We retain N terms in the expansion:

$$\begin{aligned} y_i(s,t) = {\varvec{\Psi }}^{{\text {T}}}(s) {\varvec{z}}_i(t), \end{aligned}$$
(18)

where \({\varvec{\Psi }}\) and \({\varvec{z}}_i\) are column vectors of dimension N. Accordingly, \({\varvec{y}}(s,t)\) can be written as

$$\begin{aligned} {\varvec{y}}(s,t) = {\varvec{\Theta }}^{{\text {T}}}(s) {\varvec{\eta }}(t), \end{aligned}$$
(19)

where \({\varvec{\Theta }} = {\text {diag}} \left( {\varvec{\Psi }}(s), {\varvec{\Psi }}(s) \right) \in \mathbb {R}^{2N \times 2}\) and \({\varvec{\eta }} = \left[ {\varvec{z}}_1(t), {\varvec{z}}_2(t) \right] ^{{\text {T}}} \in \mathbb {R}^{2N \times 1}\). We substitute Eq. (19) into Eq. (16a) to obtain

$$\begin{aligned} {\varvec{\Theta }}^{{\text {T}}}(s) \dot{{\varvec{\eta }}}(t) = \left( {\varvec{\Theta }}^{\prime }(s) \right) ^{{\text {T}}} {\varvec{\eta }}(t), \end{aligned}$$
(20)

where \(\dot{{\varvec{\eta }}}(t) = \displaystyle {\frac{d {\varvec{\eta }}(t)}{dt}}\) and \({\varvec{\Theta }}^{\prime }(s) = \displaystyle {\frac{d {\varvec{\Theta }}(s)}{ds}}\). We pre-multiply both sides of Eq. (20) by \({\varvec{\Theta }}(s)\) and integrate over the domain \(s \in \left[ -\tau , 0 \right) \) to obtain the following set of ODEs:

$$\begin{aligned} {\varvec{W}} \dot{{\varvec{\eta }}}(t) = {\varvec{Q}} {\varvec{\eta }}(t), \end{aligned}$$
(21)

where \({\varvec{W}} = {\text {diag}} \left( {\varvec{W}}^{(1)}, {\varvec{W}}^{(2)} \right) \), \({\varvec{Q}} = {\text {diag}} \left( {\varvec{Q}}^{(1)}, {\varvec{Q}}^{(2)} \right) \), and

$$\begin{aligned} {\varvec{W}}^{(i)}&= \int _{-\tau }^0 \Psi (s) \Psi (s)^{{\text {T}}} ds, \end{aligned}$$
(22a)
$$\begin{aligned} {\varvec{Q}}^{(i)}&= \int _{-\tau }^0 \Psi (s) \left( \Psi ^{\prime }(s) \right) ^{{\text {T}}} ds, \quad i = 1, 2. \end{aligned}$$
(22b)

The boundary conditions are obtained by substituting Eq. (19) into Eq. (16b):

$$\begin{aligned} {\varvec{\Theta }}^{{\text {T}}}(0) \dot{{\varvec{\eta }}}(t) = {\varvec{B}}_1 {\varvec{\Theta }}^{{\text {T}}}(0) {\varvec{\eta }}(t) + {\varvec{B}}_2 {\varvec{\Theta }}^{{\text {T}}}(-\tau ) {\varvec{\eta }}(t). \end{aligned}$$
(23)

Equations (21) and (23) comprise a system of \(2N+2\) linear scalar equations in 2N variables—an over-determined system. We remove the Nth and 2Nth equations from Eq. (21) and replace them with Eq. (23). The resulting set of equations can be written as

$$\begin{aligned} {\varvec{M}} \dot{{\varvec{\eta }}}(t) = {\varvec{K}} {{\varvec{\eta }}}(t). \end{aligned}$$
(24)

Finally, we re-write Eq. (24) as

$$\begin{aligned} \dot{{\varvec{\eta }}}(t) = {\varvec{G}} {{\varvec{\eta }}}(t), \end{aligned}$$
(25)

where \({\varvec{G}} = {\varvec{M}}^{-1} {\varvec{K}}\). Equation (25) is a system of linear first-order differential equations; hence, the rightmost eigenvalues of \({\varvec{G}}\) determine the stability of the zero equilibrium.

Figure 4 illustrates the evolution of the real part of the rightmost eigenvalues of \({\varvec{G}}\) as \(k_p\) varies with \(\tau = \tau _{cr}\) fixed, and as \(\tau \) varies with \(k_p = k_{cr}\) fixed. We note two observations in Fig. 4a, for both \(n=0\) and \(n=1\): (1) at the critical point \(\left( \tau , k_p \right) = \left( 0.9475, 17.0998 \right) \), the real part of \(\lambda \) is zero; and (2) as \(k_p\) varies with \(\tau \) held fixed, the real part of \(\lambda \) changes sign. Analogous observations are noted in Fig. 4b. We conclude that the critical point discussed above is a double Hopf bifurcation point.

Fig. 4
figure 4

Evolution of the real part of the rightmost characteristic roots near the critical point a with \(k_p\) where \(\tau = \tau _{cr}\) is fixed, and b with \(\tau \) where \(k_p = k_{cr}\) is fixed, for \(N=20\)

Full size image

To verify the correctness of our approach, we compute the slopes of the curves plotted in Fig. 4 and arrange them in the following matrix:

$$\begin{aligned} {\varvec{\Lambda }}_1 = \begin{bmatrix} 0.0524 &{} 0.0365\\ -1.1535 &{} 3.2872 \end{bmatrix}. \end{aligned}$$
(26)

We see that \({\varvec{\Lambda }}_1 \approx {\varvec{\Lambda }}\) (Eq. (13)), confirming agreement with our previous analysis.

5 Slow-flow equations at the double Hopf bifurcation point

Slow-flow equations are used to approximate systems of ordinary or delay differential equations governing mechanical systems. In general, slow-flow equations are first-order ODEs, thus determining fixed points and performing stability analyses are simplified. In this section, we derive slow-flow equations for Eq. (2) at the double Hopf bifurcation point. Usually, slow-flow equations at a Hopf bifurcation point are obtained using the method of center manifold reduction [43, 44] or the method of multiple scales (MMS) [35, 36]. For the analysis that follows, we use MMS.

We begin by scaling the time in Eq. (2) as \(\bar{t} = \left( 1 + \epsilon \Delta \right) t\) to introduce a perturbation in the delay parameter \(\tau \) near the critical point [36], whereupon we obtain the following:

$$\begin{aligned}&\ddot{r}(\bar{t}) + \frac{\omega _0^2}{ \left( 1 + \epsilon \Delta \right) ^2} r(\bar{t}) + \frac{2 \hat{\mu }_1}{1 + \epsilon \Delta } \dot{r}(\bar{t})\nonumber \\&\quad + \left( 1 + \epsilon \Delta \right) \hat{\mu }_3 \dot{r}^3(\bar{t}) + \frac{1}{\left( 1 + \epsilon \Delta \right) ^2}\nonumber \\&\quad \left( \hat{\alpha }_3 r^3(\bar{t}) + \hat{\alpha }_5 r^5(\bar{t}) + k_pr(\bar{t} - \bar{\tau }) \right) = 0, \end{aligned}$$
(27)

where derivatives are taken with respect to \(\bar{t}\). A delay of \(\tau _{cr}\) in the \(\bar{t}\) time scale corresponds to a delay of \(\displaystyle {\frac{\tau _{cr}}{1 + \epsilon \Delta }}\) in the original time t. Hence, as \(\epsilon \Delta \) increases, the delay in the original time scale decreases. For notational convenience, we drop the bars over t and \(\tau \), and use \(\epsilon \) as a book-keeping parameter. Substituting \(k_p = k_{cr} + \epsilon \delta \), \(\hat{\mu }_3 = \epsilon \mu _3\), \(\hat{\alpha }_3 = \epsilon \alpha _3\), \(\hat{\alpha }_5 = \epsilon \alpha _5\), \(\left( 1 + \epsilon \Delta \right) ^{-1} = 1 - \epsilon \Delta + \mathcal {O} \left( (\epsilon \Delta )^2 \right) \), and \(\left( 1 + \epsilon \Delta \right) ^{-2} = 1 - 2 \epsilon \Delta + \mathcal {O} \left( (\epsilon \Delta )^2 \right) \) into Eq. (27), we obtain the following:

$$\begin{aligned}&\ddot{r}(t) + \omega _0^2 r(t) + 2 \hat{\mu }_1 \dot{r}(t) + k_{cr} r(t-\tau _{cr})\nonumber \\&\quad + \epsilon \big [ \mu _3 \dot{r}^3(t) + \alpha _3 r^3(t) + \alpha _5 r^5(t) + \delta r(t-\tau _{cr})\nonumber \\&\quad - 2 \omega _0^2 \Delta r(t) - 2 \hat{\mu }_1 \Delta \dot{r}(t) - 2 \Delta k_{cr} r(t-\tau _{cr}) \big ]\nonumber \\&\quad + \mathcal {O} \left( \epsilon ^2 \right) = 0. \end{aligned}$$
(28)

For \(\epsilon =0\), Eq. (28) becomes a linear DDE with damping; hence, Eq. (28) represents the perturbation of Eq. (27).

We assume

$$\begin{aligned} r(t) = r_0(T_0,T_1) + \epsilon r_1(T_0,T_1), \end{aligned}$$
(29)

where \(T_0=t\) and \(T_1=\epsilon t\). Substituting Eq. (29) into Eq. (28) and equating the coefficients of the first two powers of \(\epsilon \) to zero, we obtain the following:

$$\begin{aligned}&\mathcal {O} \left( \epsilon ^0 \right) :\nonumber \\&D_0^2 r_0(T_0,T_1) + 2 \hat{\mu }_1 D_0 r_0(T_0,T_1) + \omega _0^2 r_0(T_0,T_1)\nonumber \\&\quad + k_{cr} r_0(T_0-\tau _{cr},T_1) = 0, \end{aligned}$$
(30a)
$$\begin{aligned}&\mathcal {O} \left( \epsilon ^1 \right) :\nonumber \\&D_0^2 r_1(T_0,T_1) + 2 \hat{\mu }_1 D_0 r_1(T_0,T_1) + \omega _0^2 r_1(T_0,T_1)\nonumber \\&\quad + k_{cr} r_1(T_0-\tau _{cr},T_1) + 2 D_{0,1}^2 r_0(T_0,T_1)\nonumber \\&\quad - 2 \omega _0^2 \Delta r_0(T_0,T_1) - 2 \hat{\mu }_1 \Delta D_0 r_0(T_0,T_1)\nonumber \\&\quad - 2 \Delta k_{cr} r_0(T_0-\tau _{cr},T_1) + 2 \hat{\mu }_1 D_1 r_0(T_0,T_1)\nonumber \\&\quad + \mu _3 \left( D_0 r_0(T_0,T_1) \right) ^3 {+} \alpha _3 r_0^3(T_0,T_1) {+} \alpha _5 r_0^5(T_0,T_1)\nonumber \\&\quad + \delta r_0(T_0-\tau _{cr},T_1) - \Delta D_0 r_0(T_0-\tau _{cr},T_1)\nonumber \\&\quad - k_{cr} \tau _{cr} D_1 r_0(T_0-\tau _{cr},T_1) = 0, \end{aligned}$$
(30b)

where \(\displaystyle {D_i = \frac{\partial }{\partial T_i}}\) and \(\displaystyle {D_{i,j} = \frac{\partial ^2}{\partial T_i \partial T_j}}\). Because we are considering a double Hopf bifurcation, we assume a solution to Eq. (30a) of the form

$$\begin{aligned}&r_0(t) = A_1(T_1) \sin (\omega _1 T_0) + A_2(T_1) \cos (\omega _1 T_0)\nonumber \\&\quad + A_3(T_1) \sin (\omega _2 T_0) + A_4(T_1) \cos (\omega _2 T_0). \end{aligned}$$
(31)

Substituting Eq. (31) into Eq. (30b) yields

$$\begin{aligned}&D_0^2 r_1(T_0,T_1) + 2 \hat{\mu }_1 D_0 r_1(T_0,T_1) + \omega _0^2 r_1(T_0,T_1)\nonumber \\&\quad + k_{cr} r_1(T_0-\tau _{cr},T_1) + P_1 \cos (\omega _1 T_0) + P_2 \sin (\omega _1 T_0)\nonumber \\&\quad + P_3 \cos (\omega _2 T_0) + P_4 \sin (\omega _2 T_0) + P_5 \cos (3 \omega _1 T_0)\nonumber \\&\quad + P_6 \sin (3 \omega _1 T_0) + P_7 \cos (3 \omega _2 T_0) + P_8 \sin (3 \omega _2 T_0)\nonumber \\&\quad + P_9 \cos (5 \omega _1 T_0) + P_{10} \sin (5 \omega _1 T_0) + P_{11} \cos (5 \omega _2 T_0)\nonumber \\&\quad + P_{12} \sin (5 \omega _2 T_0) + P_{13} \cos \left( (\omega _1 - 2 \omega _2) T_0 \right) \nonumber \\&\quad + P_{14} \sin \left( (\omega _1 - 2 \omega _2) T_0 \right) + P_{15} \cos \left( (2 \omega _1 - \omega _2) T_0 \right) \nonumber \\&\quad + P_{16} \sin \left( (2 \omega _1 - \omega _2) T_0 \right) + P_{17} \cos \left( (\omega _1 + 2 \omega _2) T_0 \right) \nonumber \\&\quad + P_{18} \sin \left( (\omega _1 + 2 \omega _2) T_0 \right) + P_{19} \cos \left( (2 \omega _1 + \omega _2) T_0 \right) \nonumber \\&\quad + P_{20} \sin \left( (2 \omega _1 + \omega _2) T_0 \right) + P_{21} \cos \left( (4 \omega _1 + \omega _2) T_0 \right) \nonumber \\&\quad + P_{22} \sin \left( (4 \omega _1 + \omega _2) T_0 \right) + P_{23} \cos \left( (\omega _1 + 4 \omega _2) T_0 \right) \nonumber \\&\quad + P_{24} \sin \left( (\omega _1 + 4 \omega _2) T_0 \right) + P_{25} \cos \left( (2 \omega _1 + 3 \omega _2) T_0 \right) \nonumber \\&\quad + P_{26} \sin \left( (2 \omega _1 + 3 \omega _2) T_0 \right) + P_{27} \cos \left( (3 \omega _1 + 2 \omega _2) T_0 \right) \nonumber \\&\quad + P_{28} \sin \left( (3 \omega _1 + 2 \omega _2) T_0 \right) + P_{29} \cos \left( (3 \omega _1 - 2 \omega _2) T_0 \right) \nonumber \\&\quad + P_{30} \sin \left( (3 \omega _1 - 2 \omega _2) T_0 \right) + P_{31} \cos \left( (2 \omega _1 - 3 \omega _2) T_0 \right) \nonumber \\&\quad + P_{32} \sin \left( (2 \omega _1 - 3 \omega _2) T_0 \right) + P_{33} \cos \left( (4 \omega _1 - \omega _2) T_0 \right) \nonumber \\&\quad + P_{34} \sin \left( (4 \omega _1 - \omega _2) T_0 \right) + P_{35} \cos \left( (\omega _1 - 4 \omega _2) T_0 \right) \nonumber \\&\quad + P_{36} \sin \left( (\omega _1 - 4 \omega _2) T_0 \right) = 0. \end{aligned}$$
(32)

The coefficients \(P_1\), \(P_2\), \(P_3\), and \(P_4\) in Eq. (32) correspond to secular terms and therefore, can be equated to zero, yielding \(\displaystyle {\frac{d A_i(T_1)}{d T_1}}\) for \(i \in \left\{ 1, 2, 3, 4 \right\} \). Moreover, for each of the cases \(\omega _1 = 3 \omega _2\), \(\omega _2 = 3 \omega _1\), \(\omega _1 = 5 \omega _2\), and \(\omega _2 = 5 \omega _1\), additional secular terms arise, and must duly considered. For instance, when \(\omega _1 = 3 \omega _2\), the coefficients \(P_{13}\) and \(P_{14}\) are added to \(P_3\) and \(P_4\), respectively. However, for the current analysis, \(\omega _2 = 2.0427 \omega _1\) (see Eq. (9)), hence additional secular terms do not arise in our case. The coefficients \(P_i\) have lengthy expressions; thus, we list only the pertinent coefficients \(P_1\), \(P_2\), \(P_3\), and \(P_4\) in Appendix B.

We equate the coefficients \(P_1\), \(P_2\), \(P_3\), and \(P_4\) to zero and solve the resulting equations to obtain the derivatives \(\displaystyle {\frac{d A_i(T_1)}{d T_1}}\) for \(i \in \left\{ 1, 2, 3, 4 \right\} \). These derivatives are then used to calculate

$$\begin{aligned} \frac{d A_i}{d T_0} = \epsilon \frac{d A_i}{d T_1} + \mathcal {O} \left( \epsilon ^2 \right) , \quad i \in \left\{ 1, 2, 3, 4 \right\} . \end{aligned}$$
(33)

Next, we introduce polar coordinates and represent \(A_i\) as follows:

$$\begin{aligned} A_1(T_0)&= R_1(T_0) \cos \left( \phi _1(T_0) \right) , \end{aligned}$$
(34a)
$$\begin{aligned} A_2(T_0)&= R_1(T_0) \sin \left( \phi _1(T_0) \right) , \end{aligned}$$
(34b)
$$\begin{aligned} A_3(T_0)&= R_2(T_0) \cos \left( \phi _2(T_0) \right) , \end{aligned}$$
(34c)
$$\begin{aligned} A_4(T_0)&= R_2(T_0) \sin \left( \phi _2(T_0) \right) . \end{aligned}$$
(34d)

Substituting Eqs. (34) into Eq. (31), we obtain

$$\begin{aligned}&r_0(T_0) = R_1(T_0) \sin \left( \omega _1 T_0 + \phi _1(T_0) \right) \nonumber \\&\quad + R_2(T_0) \sin \left( \omega _2 T_0 + \phi _2(T_0) \right) . \end{aligned}$$
(35)

Equations (34) are then substituted into Eqs. (33), and the resulting equations are solved for \(\displaystyle {\frac{d R_1}{d T_0}}\), \(\displaystyle {\frac{d R_2}{d T_0}}\), \(\displaystyle {\frac{d \phi _1}{d T_0}}\), and \(\displaystyle {\frac{d \phi _2}{d T_0}}\) to obtain the following slow-flow equations:

$$\begin{aligned} \frac{d R_1}{d T_0} =&\ \frac{R_1}{H_1} \big ( N_{11} R_1^4 + N_{12} R_2^4 + N_{13} R_1^2 R_2^2\nonumber \\&+ N_{14} R_1^2 + N_{15} R_2^2 + N_{16}(\epsilon \Delta ) + N_{17}(\epsilon \delta ) \big ), \end{aligned}$$
(36a)
$$\begin{aligned} \frac{d R_2}{d T_0} =&\ \frac{R_2}{H_2} \big ( N_{21} R_1^4 + N_{22} R_2^4 + N_{23} R_1^2 R_2^2\nonumber \\&+ N_{24} R_1^2 + N_{25} R_2^2 + N_{26}(\epsilon \Delta ) + N_{27}(\epsilon \delta ) \big ), \end{aligned}$$
(36b)
$$\begin{aligned} \frac{d \phi _1}{d T_0} =&\ \frac{1}{H_1} \big ( N_{31} R_1^4 + N_{32} R_2^4 + N_{33} R_1^2 R_2^2\nonumber \\&+ N_{34} R_1^2 + N_{35} R_2^2 + N_{36}(\epsilon \Delta ) + N_{37}(\epsilon \delta ) \big ), \end{aligned}$$
(36c)
$$\begin{aligned} \frac{d \phi _2}{d T_0} =&\ \frac{1}{H_2} \big ( N_{41} R_1^4 + N_{42} R_2^4 + N_{43} R_1^2 R_2^2\nonumber \\&+ N_{44} R_1^2 + N_{45} R_2^2 + N_{46}(\epsilon \Delta ) + N_{47}(\epsilon \delta ) \big ). \end{aligned}$$
(36d)

The expressions for the coefficients in Eqs. (36) are provided in Appendix C. We observe that the amplitude equations (Eqs. (36a) and (36b)) and the phase equations (Eqs. (36c) and (36d)) are decoupled. Accordingly, the fixed points can be found using only the amplitude equations.

For simplicity, we first consider \(\hat{\alpha }_5 = 0\), in which case the quintic amplitude equations (Eqs. (36a) and (36b)) reduce to cubic equations. It will be shown later that the nature of the fixed points thus obtained do not change even when \(\hat{\alpha }_5\) is nonzero (though additional fixed points appear).

5.1 Slow-flow equations without quintic nonlinearity (\(\hat{\alpha }_5 = 0\))

Setting \(\hat{\alpha }_5 = 0\) in Eqs. (36a) and (36b) yields

$$\begin{aligned} \frac{d R_1}{dt} =&\ R_1 \big ( 1.7539 R_1^2 + 3.1029 R_2^2 + 1.0952(\epsilon \Delta )\nonumber \\&+ 0.0521(\epsilon \delta ) \big ), \end{aligned}$$
(37a)
$$\begin{aligned} \frac{d R_2}{dt} =&\ R_2 \big ( -2.7897 R_1^2 - 1.9717 R_2^2 - 3.1200(\epsilon \Delta )\nonumber \\&+ 0.0363(\epsilon \delta ) \big ). \end{aligned}$$
(37b)

The fixed points of Eqs. (37) can be grouped into the following four categories:

  1. 1.

    Zero equilibrium solution:

    $$\begin{aligned} R_1^* = 0, \qquad R_2^* = 0. \end{aligned}$$
    (38)
  2. 2.

    Hopf bifurcation solution with frequency \(\omega _1\):

    $$\begin{aligned} R_1^*&= \pm \sqrt{-0.6244(\epsilon \Delta ) - 0.0297(\epsilon \delta )}, \end{aligned}$$
    (39a)
    $$\begin{aligned} R_2^*&= 0. \end{aligned}$$
    (39b)

    \(R_1^*\) must be a real number, hence

    $$\begin{aligned} \epsilon \delta \le -21.0022(\epsilon \Delta ). \end{aligned}$$
    (40)
  3. 3.

    Hopf bifurcation solution with frequency \(\omega _2\):

    $$\begin{aligned} R_1^*&= 0, \end{aligned}$$
    (41a)
    $$\begin{aligned} R_2^*&= \pm \sqrt{-1.5824(\epsilon \Delta ) + 0.0184(\epsilon \delta )}. \end{aligned}$$
    (41b)

    Because \(R_2^*\) is real, we have the following inequality:

    $$\begin{aligned} \epsilon \delta \ge 85.8457(\epsilon \Delta ). \end{aligned}$$
    (42)
  4. 4.

    Quasi-periodic solution with both frequencies \(\omega _1\) and \(\omega _2\):

    $$\begin{aligned} R_1^*&= \pm \sqrt{-1.4470(\epsilon \Delta ) + 0.0415(\epsilon \delta )}, \end{aligned}$$
    (43a)
    $$\begin{aligned} R_2^*&= \pm \sqrt{0.4649(\epsilon \Delta ) - 0.0402(\epsilon \delta )}. \end{aligned}$$
    (43b)

    Because \(R_1^*\) and \(R_2^*\) are real, we have

    $$\begin{aligned} \epsilon \delta \ge 34.8890(\epsilon \Delta ), \end{aligned}$$
    (44a)
    $$\begin{aligned} \epsilon \delta \le 11.5517(\epsilon \Delta ). \end{aligned}$$
    (44b)

Lines 1, 2, 3, and 4 in Fig. 5 are obtained using the inequality conditions of Eqs. (40), (42), (44a), and (44b), respectively. These four lines divide the parameter space of \(\epsilon \Delta \) and \(\epsilon \delta \) into six exclusive regions, which we denote as I-a, II, III, IV, I-b, and V. Regions I-a and I-b satisfy Eqs. (40) and (42). Region II satisfies Eq. (42). Region IV satisfies Eq. (40). Region V satisfies Eqs. (40), (42), and (44). The remaining area is Region III. Note that \(\epsilon \Delta \) and \(\epsilon \delta \) denote small perturbations in the delay and proportional gain parameters, respectively; hence, the origin in Fig. 5 corresponds to \(\left( \tau _{cr}, k_{cr} \right) \).

Fig. 5
figure 5

Boundaries delineating six topologically distinct stability structures in \(\epsilon \Delta \) and \(\epsilon \delta \) parameter space. Note that \(\epsilon \Delta \) and \(\epsilon \delta \) denote small perturbations in \(\tau _{cr}\) and \(k_{cr}\); hence, the origin corresponds to \(\left( \tau _{cr}, k_{cr} \right) \)

Full size image
Table 2 Fixed points (\(R_1^*\) and \(R_2^*\)) and the eigenvalues of the corresponding Jacobian matrices (\(\xi _1\) and \(\xi _2\)) in each region (I-a to V) without quintic nonlinearity. The labels \(\Gamma _0^0\), \(\Gamma _0^{R_1}\), \(\Gamma _{R_2}^0\), and \(\Gamma _{R_2}^{R_1}\) represent, respectively, the zero equilibrium, a Hopf bifurcation limit cycle with frequency \(\omega _1\), a Hopf bifurcation limit cycle with frequency \(\omega _2\), and a quasi-periodic solution
Full size table

For the purpose of demonstration, we choose a representative \(\left( \epsilon \Delta , \epsilon \delta \right) \) point in each region and find the fixed points \(R_1^*\) and \(R_2^*\) corresponding to it. To comment on the nature of these fixed points, we evaluate the eigenvalues \(\xi _1\) and \(\xi _2\) of the Jacobian matrix at these points. (This is done by taking the partial derivatives of the right-hand sides of Eqs. (37a) and (37b) with respect to \(R_1\) and \(R_2\).) This analysis is presented in Table 2. We use the variables \(\Gamma _0^0\), \(\Gamma _0^{R_1}\), \(\Gamma _{R_2}^0\), and \(\Gamma _{R_2}^{R_1}\) to represent, respectively, the zero equilibrium, a Hopf bifurcation limit cycle with frequency \(\omega _1\), a Hopf bifurcation limit cycle with frequency \(\omega _2\), and a quasi-periodic solution. We observe from Table 2 that, depending on the value of \(\left( \epsilon \Delta , \epsilon \delta \right) \), we obtain saddle points, stable nodes, unstable nodes, and unstable foci. We also see that Regions I-a and I-b have fixed points of the same type: \(\Gamma _0^0\), \(\Gamma _0^{R_1}\), and \(\Gamma _{R_2}^0\); however, they exhibit topologically different phase portraits. Finally, we note that Region V has unstable foci.

Although we have presented the results for stability analysis in Table 2 for only one representative point in each region, we have verified numerically that the nature of stability remains the same in a given region. For instance, we will obtain unstable foci for all parameter values belonging to Region V.

We now comment on the implications of the above analysis on a ship’s roll stability for the chosen values of \(\left( \epsilon \Delta , \epsilon \delta \right) \). Recall that fixed points of the slow-flow amplitude equations (Eqs. (37a) and (37b)) correspond to the magnitude of the roll angle. Accordingly, the zero-amplitude fixed point (\(\Gamma _0^0\)) corresponds to the zero equilibrium of the ship, whereas nonzero fixed points (\(\Gamma _0^{R_1}\), \(\Gamma _{R_2}^0\), and \(\Gamma _{R_2}^{R_1}\)) correspond to an oscillating ship. Stable nodes are found only in Regions IV (a stable zero equilibrium) and I-b (a stable limit cycle with frequency \(\omega _2\)). Because the zero equilibrium is stable in Region IV, delayed proportional control can be employed in its vicinity to maintain stability. In Region I-b, the amplitude of the stable limit cycle is 0.0813 rad, which is well below the capsizing roll angle of 0.48 rad [20], indicating the suitability of employing delayed proportional control in this region as well.

In Fig. 6, we plot the phase portraits corresponding to Eqs. (37a) and (37b) for the six regions discussed above. The phase portraits are obtained by solving Eqs. (37a) and (37b) using the ode45 ODE solver in Matlab®. Note that the nature of each fixed point shown in Fig. 6 is indicated in the last column of Table 2.

Fig. 6
figure 6

Phase portraits in the six regions without the quintic nonlinearity (i.e., \(\hat{\alpha }_5 = 0\)) for the chosen values of \(\left( \epsilon \Delta , \epsilon \delta \right) \): a Region I-a, b Region II, c Region III, d Region IV, e Region I-b, and f Region V. In each phase portrait, the horizontal axis represents \(R_1\), the vertical axis represents \(R_2\), and the origin represents the zero equilibrium. Stable nodes are shown as green circles, saddle nodes as blue upward-pointing triangles, and unstable nodes and unstable foci as red downward-pointing triangles. Shaded regions indicate basins of attraction for stable fixed points

Full size image

5.2 Slow-flow equations with quintic nonlinearity

As mentioned in Sect. 5.1, setting \(\hat{\alpha }_5 = 0\) in Eqs. (36) simplifies the task of finding fixed points. Using the insight from Sect. 5.1, we now investigate the more general case where \(\hat{\alpha }_5 \ne 0\). For this case, the slow-flow equations are

$$\begin{aligned} \dot{R}_1 =&\ R_1 \big ( -0.5669 R_1^4 - 1.7008 R_2^4 - 3.4015 R_1^2 R_2^2\nonumber \\&+ 1.7539 R_1^2 + 3.1029 R_2^2 + 1.0952(\epsilon \Delta )\nonumber \\&+ 0.0521(\epsilon \delta ) \big ), \end{aligned}$$
(45a)
$$\begin{aligned} \dot{R}_2 =&\ R_2 \big ( 1.1350 R_1^4 + 0.3783 R_2^4 + 2.2700 R_1^2 R_2^2\nonumber \\&- 2.7897 R_1^2 - 1.9717 R_2^2 - 3.1200(\epsilon \Delta )\nonumber \\&+ 0.0363(\epsilon \delta ) \big ), \end{aligned}$$
(45b)
$$\begin{aligned} \dot{\phi }_1 =&\ 0.2457 R_1^4 + 0.7371 R_2^4 + 1.4743 R_1^2 R_2^2\nonumber \\&- 0.9350 R_1^2 - 2.8040 R_2^2 - 0.5088(\epsilon \Delta )\nonumber \\&- 0.0206(\epsilon \delta ), \end{aligned}$$
(45c)
$$\begin{aligned} \dot{\phi }_2 =&\ 1.0285 R_1^4 + 0.3428 R_2^4 + 2.0570 R_1^2 R_2^2\nonumber \\&- 1.7971 R_1^2 - 0.2600 R_2^2 - 2.7552(\epsilon \Delta )\nonumber \\&+ 0.0287(\epsilon \delta ). \end{aligned}$$
(45d)

The right-hand sides in the amplitude equations (Eqs. (45a) and (45b)) are fifth-order polynomials; thus, we will obtain more fixed points than in Sect. 5.1. Numerical calculations reveal that the fifth-order terms have small numerical values; hence, we obtain fixed points that are numerically close to those obtained when \(\hat{\alpha }_5 = 0\). Below, we will show that the stability nature of these fixed points remains the same. We focus our analysis on the new fixed points that appear when \(\hat{\alpha }_5 \ne 0\).

Table 3 Fixed points (\(R_1^*\) and \(R_2^*\)) and the eigenvalues of the corresponding Jacobian matrices (\(\xi _1\) and \(\xi _2\)) in Region I-a with quintic nonlinearity. The labels \(\Gamma _0^0\), \(\Gamma _0^{R_1}\) (or \(\widehat{\Gamma }_0^{R_1}\)), \(\Gamma _{R_2}^0\) (or \(\widehat{\Gamma }_{R_2}^0\)), and \(\Gamma _{R_2}^{R_1}\) (or \(\widehat{\Gamma }_{R_2}^{R_1}\)) represent, respectively, the zero equilibrium, a Hopf bifurcation limit cycle with frequency \(\omega _1\), a Hopf bifurcation limit cycle with frequency \(\omega _2\), and a quasi-periodic solution
Full size table

In each region, fixed points numerically close to those listed in Table 2 were obtained and the stability nature of each of these points was the same as before. We also obtained exactly three additional fixed points in each region (\(\widehat{\Gamma }_0^{R_1}\), \(\widehat{\Gamma }_{R_2}^0\), and \(\widehat{\Gamma }_{R_2}^{R_1}\)) having the same stability nature in each region. We use Region I-a to demonstrate our results. All the fixed points obtained in this region and the eigenvalues of the corresponding Jacobian matrices are listed in Table 3. The first three fixed points (\(\Gamma _0^0\), \(\Gamma _0^{R_1}\), and \(\Gamma _{R_2}^0\)) are numerically close to those listed in Table 2 for Region I-a and have the same stability nature. The last three fixed points (\(\widehat{\Gamma }_0^{R_1}\), \(\widehat{\Gamma }_{R_2}^0\), and \(\widehat{\Gamma }_{R_2}^{R_1}\)) are the additional fixed points found when \(\hat{\alpha }_5 \ne 0\).

Analysis of these results produces the following observations. In Region IV, there exist fixed points corresponding to a stable zero equilibrium and large-amplitude stable limit cycles. In Region I-b, fixed points corresponding to both small-amplitude and large-amplitude stable limit cycles exist. In all other regions, fixed points with only large-amplitude stable limit cycles exist. These phenomena are clearly illustrated in Fig. 7, which shows the phase portraits corresponding to each region. Because the trajectories are densely clustered near the origin, a magnified view near the origin is also shown for each phase portrait.

Fig. 7
figure 7

Phase portraits in the six regions with the quintic nonlinearity (i.e., \(\hat{\alpha }_5 \ne 0\)) for the chosen values of \(\left( \epsilon \Delta , \epsilon \delta \right) \): a Region I-a, b Region II, c Region III, d Region IV, e Region I-b, and f Region V. In each phase portrait, the horizontal axis represents \(R_1\), the vertical axis represents \(R_2\), and the origin represents the zero equilibrium. Stable nodes and stable foci are shown as green circles, saddle nodes as blue upward-pointing triangles, and unstable nodes and unstable foci as red downward-pointing triangles. Diamond and square markers are initial points for the direct numerical computations presented in Sect. 6. A magnified view near the origin of each phase portrait is indicated with a blue rectangle. Shaded regions indicate basins of attraction for stable fixed points

Full size image

The existence of fixed points of different stability nature gives rise to interesting characteristics of ship rolling dynamics. For example, in Region IV (Fig. 7d), if the amplitude of the initial disturbance corresponds to the shaded region, then the ship stabilizes at the zero equilibrium; otherwise, it stabilizes at the large-amplitude limit cycle corresponding to \(\widehat{\Gamma }_{R_2}^{R_1}\). Similarly, in Region I-b (Fig. 7e), if the amplitude of the initial disturbance corresponds to the shaded region, then the ship stabilizes at the small-amplitude limit cycle corresponding to \(\Gamma _{R_2}^0\) near the origin; otherwise, it stabilizes at the large-amplitude limit cycle corresponding to \(\widehat{\Gamma }_{R_2}^{R_1}\). However, we have noted in an additional analysis (not presented here) that the amplitudes of the large-amplitude limit cycles corresponding to \(\widehat{\Gamma }_{R_2}^{R_1}\) are greater than the critical roll angle in all regions. For example, the amplitude of the large-amplitude limit cycle corresponding to \(\widehat{\Gamma }_{R_2}^{R_1}\) in Region I-a (see Table 3) is 1.5415 rad, which is greater than the critical roll angle of 0.48 rad. Practically, this means that the ship will capsize in all regions at the large-amplitude limit cycles corresponding to \(\widehat{\Gamma }_{R_2}^{R_1}\).

6 Numerical validation of observations in Sect. 5

In Sect. 5, we used the MMS method to analyze the behavior of the system near the double Hopf bifurcation point. We observed that the \(\left( \epsilon \Delta , \epsilon \delta \right) \) parametric space comprised six distinct regions of different dynamical behavior. However, MMS is an approximate numerical method; hence, it is imperative to validate the observations that were made in Sect. 5. To this end, we use direct numerical computation of the solutions of the governing differential equation (Eq. (27)). If the MMS analysis is correct, then the numerical simulations of the system should converge to the stable zero equilibrium or a stable limit cycle, as the case may be, as predicted by the MMS analysis.

The numerical simulations are performed using the dde23 DDE solver in Matlab®. The history functions r(s) and \(\dot{r}(s)\) for \(s \in \left[ -\tau , 0 \right) \) used for the computations are motivated from Eq. (35) and are taken to be

$$\begin{aligned} r(s)&= R_1 \sin \left( \omega _1 s \right) + R_2 \sin \left( \omega _2 s \right) , \end{aligned}$$
(46a)
$$\begin{aligned} \dot{r}(s)&= R_1 \omega _1 \cos \left( \omega _1 s \right) + R_2 \omega _2 \cos \left( \omega _2 s \right) , \end{aligned}$$
(46b)

where \(R_1\) and \(R_2\) are constants that determine the initial point in the phase portrait. We study the effect of different initial conditions on subsequent system dynamics by choosing several values of \(R_1\) and \(R_2\) in Eqs. (46). In Table 4, we list the values of \(R_1\) and \(R_2\) chosen in each region.

Table 4 Initial points used in each region for numerical computation of solutions of Eq. (27) in terms of \(R_1\) and \(R_2\)
Full size table

We now present the results of the direct numerical simulations, beginning with Region I-a. We choose \(R_1\) and \(R_2\) such that the initial points in the phase portrait are \(Q^{Ia}_1\) (indicated with a red diamond in Fig. 7a) and \(Q^{Ia}_2\) (indicated with a red square). It can be seen that \(Q^{Ia}_1\) is near the fixed point \(\Gamma _{R_2}^0\), which is a saddle node, suggesting that the trajectory of the system will migrate to the large-amplitude stable limit cycle corresponding to \(\widehat{\Gamma }_{R_2}^{R_1}\). The corresponding time evolution of the system is shown in Fig. 8a. The system reaches a limit cycle in approximately 50 s. In contrast, \(Q^{Ia}_2\) is located between the unstable zero equilibrium and the unstable limit cycle corresponding to \(\Gamma _0^{R_1}\) (red square in Fig. 7a). The trajectory in the phase portrait first approaches the origin, but is repelled toward the unstable limit cycle corresponding to \(\Gamma _{R_2}^0\); it is then further deflected and, subsequently, asymptotically approaches the large-amplitude stable limit cycle corresponding to \(\widehat{\Gamma }_{R_2}^{R_1}\). This slow approach to the limit cycle in phase space is evident in Fig. 8b, which shows the time evolution of the system. In this case, the limit cycle is reached in approximately 200 s. Note, however, that the amplitudes of these stable limit cycles exceed the critical roll angle of 0.48 rad. Thus, practically, the ship would capsize.

Fig. 8
figure 8

Time response of Eq. (27) for Region I-a with initial conditions at a \(Q^{Ia}_1\), i.e., \((R_1, R_2) = (0.01, 0.21)\) and b \(Q^{Ia}_2\), i.e., \((R_1, R_2) = (0.08, 0)\)

Full size image

Similar analyses are performed for the other regions; we summarize the results here for completeness. Figure 9 shows the time response of the system in Region II with initial conditions \(Q^{II}_1\) (indicated with a red diamond in Fig. 7b) and \(Q^{II}_2\) (indicated with a red square). The system reaches the large-amplitude stable limit cycle corresponding to \(\widehat{\Gamma }_{R_2}^{R_1}\) in both cases. It takes longer for the system to reach the limit cycle in the case of \(Q^{II}_2\) because of the presence of an unstable limit cycle corresponding to \(\Gamma _{R_2}^0\).

Fig. 9
figure 9

Time response of Eq. (27) for Region II with initial conditions at a \(Q^{II}_1\), i.e., \((R_1, R_2) = (0.015, 0.18)\) and b \(Q^{II}_2\), i.e., \((R_1, R_2) = (0.02, 0)\)

Full size image

Figure 10 shows the time response of the system in Region III with initial conditions \(Q^{III}_1\) (indicated with a red diamond in Fig. 7c) and \(Q^{III}_2\) (indicated with a red square). The system reaches the large-amplitude stable limit cycle corresponding to \(\widehat{\Gamma }_{R_2}^{R_1}\) in both cases. Figure 11 shows the time response of the system in Region IV with initial conditions \(Q^{IV}_1\) (indicated with a red diamond in Fig. 7d) and \(Q^{IV}_2\) (indicated with a red square). The system reaches the stable zero equilibrium for \(Q^{IV}_1\) and the large-amplitude stable limit cycle corresponding to \(\widehat{\Gamma }_{R_2}^{R_1}\) for \(Q^{IV}_2\).

Fig. 10
figure 10

Time response of Eq. (27) for Region III with initial conditions at a \(Q^{III}_1\), i.e., \((R_1, R_2) = (0, 0.08)\) and b \(Q^{III}_2\), i.e., \((R_1, R_2) = (0.02, 0)\)

Full size image
Fig. 11
figure 11

Time response of Eq. (27) for Region IV with initial conditions at a \(Q^{IV}_1\), i.e., \((R_1, R_2) = (0.1, 0.02)\) and (b) \(Q^{IV}_2\), i.e., \((R_1, R_2) = (0.115, 0.02)\)

Full size image

Figure 12 shows the time response of the system in Region I-b with initial conditions \(Q^{Ib}_1\) (indicated with a red diamond in Fig. 7e) and \(Q^{Ib}_2\) (indicated with a red square). The system reaches the small-amplitude stable limit cycle corresponding to \(\Gamma _{R_2}^0\) for \(Q^{Ib}_1\) and the large-amplitude stable limit cycle corresponding to \(\widehat{\Gamma }_{R_2}^{R_1}\) for \(Q^{Ib}_2\). Finally, in Fig. 13, we show the time response of the system in Region V with initial conditions \(Q^{V}_1\) (indicated with a red diamond in Fig. 7f) and \(Q^{V}_2\) (indicated with a red square). The system reaches the large-amplitude stable limit cycle corresponding to \(\widehat{\Gamma }_{R_2}^{R_1}\) in both cases. It takes longer for the system to reach the limit cycle in the case of \(Q^{V}_2\) because of the presence of the unstable zero equilibrium and the unstable small-amplitude limit cycle corresponding to \(\Gamma _{R_2}^{R_1}\).

Fig. 12
figure 12

Time response of Eq. (27) for Region I-b with initial conditions at a \(Q^{Ib}_1\), i.e., \((R_1, R_2) = (0.13, 0.02)\) and b \(Q^{Ib}_2\), i.e., \((R_1, R_2) = (0.16, 0.02)\)

Full size image
Fig. 13
figure 13

Time response of Eq. (27) for Region V with initial conditions at a \(Q^{V}_1\), i.e., \((R_1, R_2) = (0.01, 0.2)\) and b \(Q^{V}_2\), i.e., \((R_1, R_2) = (0.16, 0)\)

Full size image

7 Conclusions

In this paper, we considered the roll motion of a low-freeboard ship, controlled actively with a U-tube ART with delayed feedback. The rolling dynamics of the ship were modeled as a single-degree-of-freedom system with cubic and quintic nonlinearities. Building upon previous work in which a detailed stability analysis was performed for states near single Hopf bifurcation points, we focused this work on the first double Hopf bifurcation point. We first identified and proved the existence of the first double Hopf bifurcation point using three techniques: graphically, analytically, and through calculation of eigenvalues. We then obtained the slow-flow equations using the MMS method, bypassing the center manifold reductions and normal forms. The slow-flow equations revealed the existence of six distinct regions in the parameter space, which we labeled Regions I-a, II, III, IV, I-b, and V. These regions are characterized by the nature of their fixed points and the corresponding phase portraits.

A detailed study of the fixed points in each region of the parameter space yielded interesting observations with regard to the stability of a low-freeboard ship. All six regions contain a stable large-amplitude limit cycle (\(\widehat{\Gamma }_{R_2}^{R_1}\)) with amplitude greater than the critical roll angle of a low-freeboard model. As a result, large disturbances will cause the ship to capsize as it evolves toward the large-amplitude limit cycle. In Regions I-a, II, III, and V, even a small disturbance could result in the capsizing of the ship due to its tendency to reach a large-amplitude limit cycle (\(\widehat{\Gamma }_{R_2}^{R_1}\)). In Region IV, the system has a stable zero equilibrium (\(\Gamma _0^0\)), so a small disturbance will subside and the ship will return to the zero equilibrium. On the other hand, in Region I-b, the system has a limit cycle (\(\Gamma _{R_2}^0\)) whose amplitude is less than the critical roll angle, indicating that a small disturbance will cause the ship to perform small roll oscillations without capsizing.

Based on this analysis, it can be concluded that the optimal operating region for a delayed-feedback controller is Region IV, followed by Region I-b as the second-best option. In the worst case, Regions V and I-a would provide a substantial amount of time prior to capsizing, allowing for necessary measures to be taken to protect the crew and cargo. These qualitative observations, made from slow-flow equations, were validated through numerical simulation of the original DDE system. Future work includes experimental validation of these results and applying similar analyses to different ship models.