Nonlinear planar vibrations of a cable with a linear damper

Abstract

This paper minutely studies the effects of the damper on nonlinear behaviors of a cable–damper system. By modeling the damper as a combination of a viscous damper and a linear spring, the primary resonance and subharmonic resonance (1/2 order and 1/3 order) of the cable are explored. The equation of motion of the cable is treated by using Galerkin’s method, and the ordinary differential equation (ODE) is obtained subsequently. To solve the ODE, the method of multiple timescales is applied, and the modulation equations corresponding to different types of resonance are derived. Then, the frequency–/force–response curves are acquired by utilizing Newton–Raphson method and pseudo-arclength algorithm, so as to explore the vibration suppression effect from a nonlinear point of view. Meanwhile, the time histories, phase portraits and Poincaré sections are also provided to discuss the influences of the damping and spring stiffness on the nonlinear characteristics of the cable. The results show that the damper has a significant effect on nonlinear resonances of the cable, and the increase in damping (spring stiffness) makes the dual characteristic gradually convert to the softening (hardening) characteristic.

1 Introduction

As a tension-only member, cables are widely used in cable-stayed bridges [1] or suspension bridges [2, 3], power transmission conductors, and offshore marine systems. Due to the low damping and lightweight, cables are susceptible to the surrounding environments, and large amplitude vibrations of the cable may occur in some extreme situations [4]. Therefore, the dynamic problems of the cable have received a considerable number of attentions in the past few decades [5,6,7,8,9] and are summarized in Ref. [10]. As a result of large vibration of the cable, the system performance may degrade. Accordingly, the suppression of the cable vibration becomes a hot topic recently.

To suppress the vibration of the cable, a damper is usually equipped with the cable. Based on this fact, a cable–damper model has been studied in lots of literature. Krenk [11] solved the vibration problem of a taut cable attached with a viscous damper. By utilizing complex modes, a considerably simple transcendental equation is derived. He pointed out that the complex eigenfrequency and modal damping ratio can be obtained by an explicit asymptotic expression. Tabatabai and Mehrabi [12] calculated the first mode frequency and damping ratio of a cable with a viscous damper by considering the sag and bending stiffness of the cable. The results showed that the effect of the cable sag on the damping ratios is small, while the bending stiffness of the cable has a significant influence. Meanwhile, a practical experiment is also performed to demonstrate the results. In the final, a formula is presented for designing the location and size of the damper to suppress the vibration of the cable. Main and Jones [13] confirmed the availability of the linear dampers for suppressing cable vibrations from an experimental point of view by comparing the response with and without a damper. They also predicted the potential benefits of nonlinear damping in suppressing cable vibrations. Shortly after that, Main and Jones [14] studied the in-plane complex eigenvalue problem for a cable with a linear damper using an analytical formulation without approximation. In another paper [15], they attacked the damping ratios of a cable with a nonlinear damper by utilizing approximate formulation. The results showed that the nonlinear dampers may offer potential advantages compared with the linear dampers. Krenk and Nielsen [16] applied the complex eigenvalue analysis to shallow cables, and the corresponding complex solutions were obtained.

In addition to the studies above, many researches on the models evolving from a cable–damper system are also documented. Caracoglia and Jones [17] considered a cable attached with two dampers, and complex eigenvalue analysis was carried out systematically. They found that placing the dampers at each end of the cable is an ideal arrangement, because the damping ratio became larger. Chen et al. [18] discussed the case that the cable was equipped with both lateral and rotational dampers. Inspired by cross-ties and dampers, Zhou et al. [19] studied a taut cable with a damper and a spring. By applying the transfer matrix method, the modal damping ratio and complex frequency were obtained. Meanwhile, the influence of the stiffness and location of the spring on the damping and frequency were also explored. Huang and Jones [20] discussed the influence of damper support on a cable–damper system by taking the damper support into account. In the study, the damper support was modeled as a linear elastic spring, and the results showed that the linear elastic support may deteriorate the performance of the damper. Additionally, to better suppress cable vibrations, active/semi-active [21,22,23,24] vibration control of the cable has been extensively studied in the past three decades, which can provide large equivalent damping to the cable.

Nevertheless, the above researches are mainly devoted to complex eigenvalue problem/modal damping ratio of the cable–damper system. Quite few studies focus on nonlinear behaviors of the cable–damper system. It is worth mentioning that Chen and Sun [25] studied the effect of the nonlinear damping on cable vibration by examining two cases of damping coefficients. But the vibration equation of the cable is linear. Yu and Xu [26, 27] explored the nonlinear behaviors of a cable with oil dampers by using harmonic balance method. However, they didn’t consider the spring stiffness of the damper, and only primary resonance was explored. Despite an amount of investigations of the cable–damper model, large vibrations of the cable are still reported from time to time. For example, Sutong Bridge (Jiangsu, China) was subjected to large vibrations caused by Typhoon Rumbia on August 17, 2018, which caused the dampers to detach from the cables. Why is the installation of the damper still not effective in vibration suppression? One may wonder if the damper still works effectively when a particular nonlinear resonance occurs. Actually, in practical engineering, the damper is installed at one end of the cable and interacts with the structure, which will cause an effect on the damping and frequency of the cable and may further influence nonlinear behaviors of the system. Hence, special attention should be paid to nonlinear phenomena of the cable–damper model [28].

In this work, our motivation is to explore and to discuss the vibration suppression effect of the damper from a nonlinear perspective, especially, considering the common resonance types in nonlinear dynamics of the cable. In addition, the damper model takes the spring stiffness into account. More importantly, this paper reveals some new phenomena that have not been reported in previous studies. For example, when the damping and spring stiffness of the damper decrease to a certain value, the response curve can exhibit both softening and hardening characteristics. Following Rega [29], three different cases, i.e., the primary resonance and subharmonic resonance (1/2 order and 1/3 order), are discussed by using the method of multiple timescales. The equilibrium solutions of the modulation equations are sought by the Newton–Raphson method and continued by pseudo-arclength algorithm. Based on the frequency–/force–response curves, the influence of the damping and spring stiffness of the damper on the nonlinear behaviors of the cable–damper system is studied. Meanwhile, the time histories, phase portraits, and Poincaré sections are also given to reveal different nonlinear behaviors of the cable with various damping and spring stiffnesses of the damper.

The remainder of the paper is organized as follows. First, the cable–damper model and governing equations of the system are presented. In Sect. 3, the perturbation analysis is performed. Section 4 is devoted to numerical results and discussion. Finally, summary and conclusions are provided.

2 Cable–damper model and governing equation

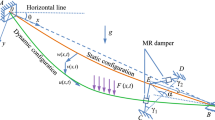
Figure 1 depicts the problem under consideration. In the Figure, the cable is subjected to a harmonic loading $F_{1}^{ * } (x^{ * } )\cos \Omega^{ * } t$. The length of the cable is $l_{c}$. $l_{1}^{ * }$($l_{2}^{ * }$) denotes the distance between the damper and upper (lower) end of the cable. The damper is modeled as a combination of a viscous damping and a linear spring. The corresponding damping coefficient and spring stiffness are $C_{d}^{ * }$ and $K_{d}^{ * }$, respectively. $\theta$ is the angle between the cable and the horizontal line. Meanwhile, the Cartesian coordinates x^*oy^* are established to describe the motion of the cable. For the sake of derivation, the following assumptions are made:

• (a) The axial vibration, torsional and shear rigidities of the cable are negligible [30];

• (b) The static equilibrium configuration for the inclined cable is described by the parabola [16].

Fig. 1

A cable–damper model with linear damping and spring

According to the extended Hamilton’s principle, the integral–differential equation governing the transverse vibration of the cable can be obtained as [30]

$$\rho_{c} A_{c} \ddot{v}_{c}^{*} + \mu_{c}^{*} \dot{v}_{c}^{*} - \left[ {H_{c} v^{\prime \prime *}_{c} + E_{c} A_{c} \left( {v^{\prime \prime *}_{c} + y^{\prime \prime *}_{c} } \right)e_{c}^{*} (t)} \right] = p^{*} (x,t)$$

(1)

where $\rho_{c}$, $A_{c}$, $\mu_{c}^{ * }$, $H_{c}$, $E_{c}$, and $v_{c}^{ * }$ are mass per unit volume, cross-sectional area, damping coefficient, initial force, Young’s modulus, and planar transverse displacement of the cable. The dot and prime denote the differentiations with respect to time t and coordinate x^*, respectively. $p^{ * } (x,t)$ is the total load acting on the cable, which includes two parts, namely, the external harmonic force and the action applied to the cable by the damper. The expression of $p^{ * } (x,t)$ is

$$p^{ * } (x,t) = - f^{ * } (t)\delta (x^{ * } - l_{1}^{ * } ) + F_{1}^{ * } (x^{ * } )\cos \Omega^{ * } t$$

(2)

where $\delta ()$ denotes the Kronecker delta function. $f^{ * } (t)$ is the force applied by the damper to the cable and is given by

$$f^{ * } (t) = K_{d}^{ * } v_{c}^{ * } (l_{1}^{ * } ,t) + C_{d}^{ * } \dot{v}_{c}^{ * } (l_{1}^{ * } ,t).$$

(3)

In Eq. (1), $e_{c}^{ * } (t)$ denotes the uniform dynamic elongation and can be written as

$$e_{c}^{ * } (t) = \frac{1}{{l_{c} }}\int\limits_{0}^{{l_{c} }} {\left( {y_{c}^{\prime * } v_{c}^{\prime * } + \frac{1}{2}v_{c}^{\prime 2 * } } \right)dx^{ * } }$$

(4)

where $y_{c}^{ * }$ is the static equilibrium configuration of the cable. According to assumption (b), $y_{c}^{ * }$ has the following expression:

$$y_{c}^{ * } (x^{ * } ) = 4d_{c}^{ * } \left[ {\frac{{x^{ * } }}{{l_{c} }} - \left( {\frac{{x^{ * } }}{{l_{c} }}} \right)^{2} } \right]$$

(5)

where $d_{c}^{ * }$ is the cable sag and is determined by $d_{c}^{ * } { = }\rho_{c} A_{c} \varsigma l_{c}^{2} \cos \theta /(8H_{c} )$ ($\varsigma$ is the gravity acceleration).

To render the equations non-dimensional, the following non-dimensional variables and parameters are defined:

$$\begin{aligned} x & = \frac{{x^{ * } }}{{l_{c} }},\;\tau = \omega _{0} t,\;d_{c} = \frac{{d_{c}^{ * } }}{{l_{c} }},\;l_{1} = \frac{{l_{1}^{ * } }}{{l_{c} }},\;l_{2} = \frac{{l_{2}^{ * } }}{{l_{c} }},\;y_{c} = \frac{{y_{c}^{ * } }}{{l_{c} }},\;v_{c} = \frac{{v_{c}^{ * } }}{{l_{c} }},\\ \mu _{c} & = \frac{{\mu _{c}^{ * } }}{{\rho _{c} A_{c} \omega _{0} }},\;\lambda _{c} = \frac{{E_{c} A_{c} }}{{H_{c} }},\;\beta _{c}^{2} = \frac{{\rho _{c} A_{c} \omega _{0}^{2} l_{c}^{2} }}{{H_{c} }},\;\omega _{0} = 1.0\;{\text{rad}} \cdot s^{{ - 1}} ,\\ \Omega & = \frac{{\Omega^{ * } }}{{\omega _{0} }},\;F_{1} (x) = \frac{{F_{1}^{ * } (x^{ * } )}}{{\rho _{c} A_{c} \omega _{0}^{2} l_{c} }},\;f(t) = \frac{{f^{ * } (t)}}{{\rho _{c} A_{c} \omega _{0}^{2} l_{c} }},\;K_{d} = \frac{{K_{d}^{ * } }}{{\rho _{c} A_{c} \omega _{0}^{2} }},\;C_{d} = \frac{{C_{d}^{ * } }}{{\rho _{c} A_{c} \omega _{0} }}.\end{aligned}$$

In this way, Eqs. (1), (4), and (5) can be rewritten as

$$\ddot{v}_{c} + \mu_{c} \dot{v}_{c} - \frac{1}{{\beta_{c}^{2} }}\left[ {v^{\prime\prime}_{c} + \lambda_{c} \left( {v^{\prime\prime}_{c} + y^{\prime\prime}_{c} } \right)e_{c} (\tau )} \right] = - [K_{d} v_{c} (l_{1} ,\tau ) + C_{d} \dot{v}_{c} (l_{1} ,\tau )]\delta (x - l_{1} ) + F_{1} (x)\cos \Omega \tau,$$

(6)

$$e_{c} (\tau ) = \int\limits_{0}^{1} {\left( {y^{\prime }_{c} v^{\prime }_{c} + \frac{1}{2}v_{c}^{\prime 2} } \right){\text{d}}x},$$

(7)

$$y_{c} (x) = 4d_{c} x\left( {1 - x} \right).$$

(8)

A discrete model of the continuum system is obtained by assuming the planar transverse displacements of the cable to be of the following form:

$$v_{c} (x,\tau ) = \phi_{c} (x)q_{c} (\tau )$$

(9)

where $q_{c} (\tau )$ is an unknown time function, and $\phi_{c} (x)$ is the shape function of the cable. In practical situations, the damper attachment point is very close to the lower end of the cable (2–4% of the cable span), and the effect of the damper on the shape function of the cable is quite small [11, 31]. Hence, the sine function $\phi_{c} (x) = \sin (\pi x)$ is a simple and convenient choice of shape function for a rather taut cable, which is used in many previous studies [32,33,34].

Substituting Eq. (9) into Eq. (6) and applying Galerkin’s method, the following ODE can be derived:

$$\ddot{q}_{c} + b_{11} q_{c} + b_{12} \dot{q}_{c} + b_{13} q_{c}^{2} + b_{14} q_{c}^{3} - b_{15} \cos (\Omega \tau ) = 0$$

(10)

where b_1j(j =  1, 2…5) are Galerkin integral coefficients and are reported in the Appendix A. It can be seen from Appendix A that the damping coefficient and spring stiffness of the damper directly influence the values of b₁₁ and b₁₂, thus influencing the nonlinear characteristics of the cable. In the following, three different forms of resonance are examined to explore such an effect of the damper on nonlinear behaviors of the cable, namely primary resonance, 1/2-order subharmonic resonance, and 1/3-order subharmonic resonance.

3 Perturbation analysis

3.1 Primary resonance

Following the multiple timescale method, a small bookkeeping parameter ε is used. Meanwhile, new independent time variables $T_{n} = \varepsilon^{n} \tau (n = 0,1,2...)$ are introduced. To analyze the primary resonance, we need to reorder the damping, the nonlinearity and the excitation terms so that they can appear at the same time in the perturbation scheme, i.e.,

$$b_{12}\, { = }\,\varepsilon^{2} \tilde{b}_{12} ,b_{{1{3}}} \,{ = }\,\varepsilon \tilde{b}_{13} ,b_{14} \,{ = }\,\varepsilon^{2} \tilde{b}_{14} ,b_{15} \,{ = }\,\varepsilon^{2} \tilde{b}_{15} .$$

(11)

Accordingly, Eq. (10) is rewritten as

$$\ddot{q}_{c} + \omega_{c}^{2} q_{c} + \varepsilon^{2} b_{12} \dot{q}_{c} + \varepsilon b_{13} q_{c}^{2} + \varepsilon^{2} b_{14} q_{c}^{3} - \varepsilon^{2} b_{15} \cos (\Omega \tau ) = 0$$

(12)

where the wavy symbols have been removed for brevity and $\omega_{c}^{2} = b_{11}$. Sometimes expanding the solution to order $\varepsilon^{2}$ may cause qualitative errors (see Fig. 2c). To overcome this problem, the solution is expanded to the fourth order, namely

$$q_{c} = \sum\limits_{i = 1}^{5} {\varepsilon^{i - 1} q_{ci} (T_{0} ,T_{2} ,T_{4} )} + O(\varepsilon^{5} ).$$

(13)

Fig. 2

The frequency–response curves of the cable with different excitation amplitudes by expanding the solution to the second order; a F = 0.005, b F = 0.01 and c F = 0.02

Here, it should be noted that q_c is found to be independent of T₁ and T₃ by eliminating the secular terms in the equations of order $\varepsilon^{1}$ and $\varepsilon^{3}$. Therefore, T₁ and T₃ are dropped in Eq. (13). Substituting Eq. (13) into Eq. (12) and equating terms of like order in ε yields

Order $\varepsilon^{0}$,

$$(D_{0}^{2} + \omega_{c}^{2} )q_{c1} = 0,$$

(14)

Order $\varepsilon^{1}$,

$$(D_{0}^{2} + \omega_{c}^{2} )q_{c2} = - b_{13} q_{c1}^{2},$$

(15)

Order $\varepsilon^{2}$,

$$(D_{0}^{2} + \omega_{c}^{2} )q_{c3} = b_{15} \cos (\Omega T_{0} ) - b_{14} q_{c1}^{3} - 2b_{13} q_{c1} q_{c2} - b_{12} D_{0}^{1} q_{c1} - 2D_{0}^{1} D_{2}^{1} q_{c1},$$

(16)

Order $\varepsilon^{3}$,

$$(D_{0}^{2} + \omega_{c}^{2} )q_{c4} = - 3b_{14} q_{c1}^{2} q_{c2} - b_{13} q_{c2}^{2} - 2b_{13} q_{c1} q_{c3} - b_{12} D_{0}^{1} q_{c2} - 2q_{c2} D_{0}^{1} D_{2}^{1} q_{c2},$$

(17)

Order $\varepsilon^{4}$,

$$\begin{gathered} (D_{0}^{2} + \omega_{c}^{2} )q_{c5} = - 3b_{14} q_{c1} q_{c2}^{2} - 3b_{14} q_{c1}^{2} q_{c3} - 2b_{13} q_{c2} q_{c3} - 2b_{13} q_{c1} q_{c4} - b_{12} D_{2}^{1} q_{c1} \hfill \\ - D_{2}^{2} q_{c1} - b_{12} D_{0}^{1} q_{c3} - 2D_{0}^{1} D_{4}^{1} q_{c1} - 2D_{0}^{1} D_{2}^{1} q_{c3} \hfill \\ \end{gathered}$$

(18)

where $D_{n}^{m}$ is defined as $D_{n}^{m} = \partial^{m} /\partial T_{n}$.

The solutions of problems (14) and (15) are

$$q_{c1} = A_{1} (T_{2} ,T_{4} )\;\exp ({\text{i}}\omega_{c} T_{0} ) + cc,$$

(19)

$$q_{c2} = \frac{{b_{13} A_{1}^{2} \exp \;(2{\text{i}}T_{0} \omega_{c} )}}{{3\omega_{c}^{2} }} - \frac{{b_{13} A_{1} B_{1} }}{{\omega_{c}^{2} }} + cc$$

(20)

where B₁ is the complex conjugate of A₁. This part studies primary resonance of the cable with a damper, and the nearness of the resonance is described by introducing an external detuning parameter σ, i.e.,

$$\Omega = \omega_{c} + \varepsilon^{2} \sigma .$$

(21)

Hence, substituting Eqs. (19) and (20) into Eq. (16) yields

$$\begin{aligned} (D_{0}^{2} + \omega _{c}^{2} )q_{{c3}} = & \frac{1}{2}b_{{15}} \exp ({\text{i}}T_{0} \Omega ) - {\text{i}}b_{{12}} \omega _{c} \exp ({\text{i}}T_{0} \omega _{c} )A_{1} + \exp ({\text{i}}T_{0} \omega _{c} )\Gamma _{{11}} A_{1}^{2} B_{1} \\ &\quad - 2{\text{i}}\omega _{c} \exp ({\text{i}}T_{0} \omega _{c} )D_{2}^{1} A_{1} - \underbrace {{\exp (3{\text{i}}T_{0} \omega _{c} )\Gamma _{{12}} A_{1}^{3} }}_{{NST_{1} }} + cc \\ \end{aligned}$$

(22)

where $\Gamma_{11}$ and $\Gamma_{12}$ are reported in Appendix B and NST denotes non-secular terms. After eliminating the secular terms in Eq. (22), the solutions for q_c3 and q_c4 are as follows:

$$q_{c3} = \frac{{\Gamma_{12} A_{1}^{3} \exp (3{\text{i}}T_{0} \omega_{c} )}}{{8\omega_{c}^{2} }} + cc,$$

(23)

$$\begin{aligned} q_{c4} =\, & \frac{{2b_{13} b_{15} A_{1} \exp (\Omega + \omega_{c} )}}{{9\omega_{c}^{4} }} - \frac{{2{\text{i}}b_{12} b_{13} A_{1}^{2} \exp (2{\text{i}}T_{0} \omega_{c} )}}{{9\omega_{c}^{3} }} + \frac{{b_{13}^{3} A_{1}^{4} \exp (4{\text{i}}T_{0} \omega_{c} )}}{{54\omega_{c}^{6} }} \\& + \frac{{b_{13} b_{14} A_{1}^{4} \exp (4{\text{i}}T_{0} \omega_{c} )}}{{12\omega_{c}^{4} }} + \frac{{59b_{13}^{3} A_{1}^{3} B_{1} \exp (2{\text{i}}T_{0} \omega_{c} )}}{{54\omega_{c}^{6} }} - \frac{{31b_{13} b_{14} A_{1}^{3} B_{1} \exp (2{\text{i}}T_{0} \omega_{c} )}}{{12\omega_{c}^{4} }} \\& - \frac{{19b_{13}^{3} A_{1}^{2} B_{1}^{2} }}{{9\omega_{c}^{6} }} + \frac{{5b_{13} b_{14} A_{1}^{2} B_{1}^{2} }}{{\omega_{c}^{4} }} + cc. \\ \end{aligned}$$

(24)

Substituting Eqs. (19), (20), (23), and (24) into Eq. (18) may yield

$$\begin{aligned} (D_{0}^{2} + \omega_{c}^{2} )q_{c5} =\, & {\text{i}}\overline{\Gamma }_{11} \exp ({\text{i}}T_{0} \Omega ) + \overline{\Gamma }_{12} \exp ({\text{i}}T_{0} \Omega ) + \frac{{b_{12}^{2} }}{4}\exp ({\text{i}}T_{0} \omega_{c} )A_{1} + \exp ({\text{i}}T_{0} (2\omega_{c} - \Omega ))\overline{\Gamma }_{13} A_{1}^{2} \\& + \exp ({\text{i}}T_{0} \Omega )\overline{\Gamma }_{14} A_{1} B_{1} + {\text{i}}\exp ({\text{i}}T_{0} \omega_{c} )\overline{\Gamma }_{15} A_{1}^{2} B_{1} + \exp ({\text{i}}T_{0} \omega_{c} )\overline{\Gamma }_{16} A_{1}^{3} B_{1}^{2} \\& - 2{\text{i}}\omega_{c} \exp ({\text{i}}T_{0} \omega_{c} )D_{4}^{1} A_{1} + NST_{2} + cc \\ \end{aligned}$$

(25)

where $\overline{\Gamma }_{11}$–$\overline{\Gamma }_{16}$ are reported in Appendix B. Introducing the polar form

$$A_{1} (T_{2} ,T_{4} ) = \frac{1}{2}a(T_{2} ,T_{4} )\exp ({\text{i}}\Phi (T_{2} ,T_{4} )),$$

(26)

Eq. (26) is substituted into the secular terms in Eqs. (22) and (25). Then, eliminating the secular terms and separating the real and imaginary parts, respectively, the following autonomous modulation equations can be derived:

$$D_{2}^{1} a = - \frac{{b_{12} a}}{2} + \frac{{b_{15} \sin \alpha }}{{2\omega_{c} }},$$

(27)

$$aD_{2}^{1} \alpha = a\sigma + \frac{{\Gamma_{11} a^{3} }}{{8\omega_{c} }} + \frac{{b_{15} \cos \alpha }}{{2\omega_{c} }},$$

(28)

$$D_{4}^{1} a = - \frac{{\overline{\Gamma }_{15} a^{3} }}{{8\omega_{c} }} + \frac{{\overline{\Gamma }_{11} \cos \alpha }}{{\omega_{c} }} + \frac{{\overline{\Gamma }_{12} \sin \alpha }}{{\omega_{c} }} - \frac{{\overline{\Gamma }_{13} a^{2} \sin \alpha }}{{4\omega_{c} }} + \frac{{\overline{\Gamma }_{14} a^{2} \sin \alpha }}{{4\omega_{c} }},$$

(29)

$$aD_{4}^{1} \alpha = \frac{{ab_{12}^{2} }}{{8\omega_{c} }} + \frac{{\overline{\Gamma }_{16} a^{5} }}{{32\omega_{c} }} + \frac{{\overline{\Gamma }_{12} \cos \alpha }}{{\omega_{c} }} + \frac{{\overline{\Gamma }_{13} a^{2} \cos \alpha }}{{4\omega_{c} }} + \frac{{\overline{\Gamma }_{14} a^{2} \cos \alpha }}{{4\omega_{c} }} - \frac{{\overline{\Gamma }_{11} \sin \alpha }}{{\omega_{c} }}$$

(30)

where $\alpha = T_{2} \sigma - \Phi$. Using the method of reconstitution [8, 29], the total modulation equations are determined by eliminating the amplitude and phase with respect to the actual non-dimensional timescale $\tau$, namely

$$\dot{a} = \frac{\partial a}{{\partial T_{2} }}\frac{{{\text{d}}T_{2} }}{{{\text{d}}\tau }} + \frac{\partial a}{{\partial T_{4} }}\frac{{{\text{d}}T_{4} }}{{{\text{d}}\tau }} = \varepsilon^{2} D_{2}^{1} a + \varepsilon^{4} D_{4}^{1} a, \quad a\dot{\alpha } = \varepsilon^{2} aD_{2}^{1} \alpha + \varepsilon^{4} aD_{4}^{1} \alpha$$

(31)

where ε is set equal to unity [35]. Letting $\dot{a} = \dot{\alpha } = 0$, the steady-state solutions of the system can be obtained by using the Newton–Raphson method. Starting with the above results, the response curves are extended by the pseudo-arclength algorithm [36]. The stability of the equilibrium solutions can be examined by evaluating whether the real part of each eigenvalue of the linearized system is negative or not [37]. Simultaneously, to compare the accuracy between the higher-order and lower-order expansions, a second-order approximation is also reported in Appendix C.

It is worth pointing out that in deriving Eq. (25) from Eq. (18), the derivative terms $D_{2}^{1} ( \cdot )$ and $D_{2}^{2} ( \cdot )$ in Eq. (18) are carefully accounted for by employing the solvability condition of Eq. (22), rather than simply neglecting them. This is closely related to the complete/incomplete issue of the reconstitution method, fully discussed in Ref. [38].

3.2 1/2-order subharmonic resonance

This part discusses the 1/2-order subharmonic resonance of the cable with a damper. To this end, we need to reorder the excitation and damping so that the excitation appears at the same time as the free oscillation part of the solution and the damping appear first in the same perturbation equation as the quadratic nonlinearity. Following Rega [8, 29], Eq. (10) is rewritten as

$$\ddot{q}_{c} + \omega_{c}^{2} q_{c} + \varepsilon b_{12} \dot{q}_{c} + \varepsilon b_{13} q_{c}^{2} + \varepsilon^{2} b_{14} q_{c}^{3} - b_{15} \cos (\Omega \tau ) = 0.$$

(32)

To seek a second-order approximation, the solution of $q_{c}$ is uniformly expanded in power series of ε, namely

$$q_{c} = \sum\limits_{i = 1}^{3} {\varepsilon^{i - 1} q_{ci} (T_{0} ,T_{1} ,T_{2} )} + O(\varepsilon^{3} ).$$

(33)

Different from Eq. (C.1), q_c is also function of T₁. Substituting Eq. (33) into Eq. (32) and equating terms of like order in ε yields:

Order $\varepsilon^{0}$,

$$(D_{0}^{2} + \omega_{c}^{2} )q_{c1} = b_{15} \cos (\Omega T_{0} ),$$

(34)

Order $\varepsilon^{1}$,

$$(D_{0}^{2} + \omega_{c}^{2} )q_{c2} = - (b_{13} q_{c1}^{2} + b_{12} D_{0}^{1} q_{c1} + 2D_{0}^{1} D_{1}^{1} q_{c1} ),$$

(35)

Order $\varepsilon^{2}$,

$$(D_{0}^{2} + \omega_{c}^{2} )q_{c3} = - (b_{14} q_{c1}^{3} + 2b_{13} q_{c1} q_{c2} + b_{12} D_{1}^{1} q_{c1} + D_{1}^{2} q_{c1} + b_{12} D_{0}^{1} q_{c2} + 2D_{0}^{1} D_{2}^{1} q_{c1} + 2D_{0}^{1} D_{1}^{1} q_{c2} ).$$

(36)

The solution of problem (34) is

$$q_{c1} = A_{1} (T_{1} ,T_{2} )\exp ({\text{i}}\omega_{c} T_{0} ) + \Lambda \exp ({\text{i}}\Omega T_{0} ) + cc$$

(37)

where $\Lambda = \frac{{b_{15} }}{{2(\omega_{c}^{2} - \Omega^{2} )}}$. Substituting Eq. (37) into Eq. (35) leads to

$$\begin{aligned} (D_{0}^{2} + \omega_{c}^{2} )q_{c2} = & - b_{13} \Lambda^{2} - b_{13} \Lambda^{2} \exp (2{\text{i}}T_{0} \Omega ) - {\text{i}}b_{12} \Lambda \Omega \exp ({\text{i}}T_{0} \Omega ) - 2b_{13} \Lambda \exp ({\text{i}}T_{0} (\Omega + \omega_{c} ))A_{1} \\& - b_{13} \exp (2{\text{i}}T_{0} \omega_{c} )A_{1}^{2} - b_{13} A_{1} B_{1} \\& \underbrace {{ - {\text{i}}b_{12} \omega_{c} \exp ({\text{i}}T_{0} \omega_{c} )A_{1} - 2b_{13} \Lambda \exp ({\text{i}}T_{0} (\Omega - \omega_{c} ))B_{1} - 2{\text{i}}\omega_{c} \exp ({\text{i}}T_{0} \omega_{c} )D_{1}^{1} A_{1} }}_{\text{secular terms}} + cc. \\ \end{aligned}$$

(38)

The nearness of the resonance is described by introducing an external detuning parameter σ, i.e.,

$$\Omega = 2\omega_{c} + \varepsilon \sigma .$$

(39)

Substituting Eq. (39) into Eq. (38) and eliminating the secular terms in Eq. (38), the first-order solvability condition can be derived as follows:

$${\text{i}}b_{12} \omega_{c} A_{1} + 2b_{13} \Lambda \exp ({\text{i}}T_{1} \sigma )B_{1} + 2{\text{i}}\omega_{c} D_{1}^{1} A_{1} = 0.$$

(40)

After eliminating the secular terms in Eq. (38), the solution for q_c2 is obtained,

$$\begin{aligned} q_{c2} = & - \frac{{b_{13} \Lambda^{2} }}{{\omega_{c}^{2} }} + \frac{{{\text{i}}b_{12} \Lambda \Omega \exp ({\text{i}}T_{0} \Omega )}}{{\Omega^{2} - \omega_{c}^{2} }} + \frac{{b_{13} \Lambda^{2} \exp (2{\text{i}}T_{0} \Omega )}}{{4\Omega^{2} - \omega_{c}^{2} }} + \frac{{2b_{13} \Lambda \exp ({\text{i}}T_{0} (\Omega + \omega_{c} ))A_{1} }}{{\Omega (\Omega + 2\omega_{c} )}} \\& + \frac{{b_{13} \exp (2{\text{i}}T_{0} \omega_{c} )A_{1}^{2} }}{{3\omega_{c}^{2} }} - \frac{{b_{13} A_{1} B_{1} }}{{\omega_{c}^{2} }} + cc. \\ \end{aligned}$$

(41)

Substituting Eqs. (37) and (41) into Eq. (36) and considering $D_{1}^{1} A_{1}$ and $D_{1}^{2} A_{1}$ via Eq. (40), the second-order solvability condition can be derived by eliminating the secular terms, i.e.,

$$\begin{gathered} \exp ({\text{i}}T_{0} \omega _{c} )\Gamma _{{21}} A_{1} + \exp ({\text{i}}T_{0} (\Omega - \omega _{c} ))\Gamma _{{22}} B_{1} + {\text{i}}\exp ({\text{i}}T_{0} (\Omega - \omega _{c} ))\Gamma _{{23}} B_{1} + \hfill \\ \exp ({\text{i}}T_{0} \omega _{c} )\Gamma _{{24}} A_{1}^{2} B_{1} - 2{\text{i}}\omega _{c} \exp ({\text{i}}T_{0} \omega _{c} )D_{2}^{1} A_{1} = 0 \hfill \\ \end{gathered}$$

(42)

where $\Gamma_{21}$–$\Gamma_{24}$ are reported in Appendix B. The following the polar form is introduced:

$$A_{1} (T_{1} ,T_{2} ) = \frac{1}{2}a(T_{1} ,T_{2} )\exp ({\text{i}}\Phi (T_{1} ,T_{2} )).$$

(43)

Substituting Eq. (43) into Eqs. (40) and (42) and separating the real and imaginary parts, respectively, the following autonomous modulation equations can be derived:

$$D_{1}^{1} a = - \frac{{b_{12} a}}{2} - \frac{{b_{13} \Lambda a\sin \alpha }}{{\omega_{c} }},$$

(44)

$$aD_{1}^{1} \alpha = a\sigma - \frac{{2b_{13} \Lambda a\cos \alpha }}{{\omega_{c} }},$$

(45)

$$D_{2}^{1} a = \frac{{\Gamma_{23} a\cos \alpha }}{{2\omega_{c} }} + \frac{{\Gamma_{22} a\sin \alpha }}{{2\omega_{c} }},$$

(46)

$$aD_{2}^{1} \alpha = \frac{{\Gamma_{21} a}}{{\omega_{c} }} + \frac{{\Gamma_{24} a^{3} }}{{4\omega_{c} }} + \frac{{\Gamma_{22} a\cos \alpha }}{{\omega_{c} }} - \frac{{\Gamma_{23} a\sin \alpha }}{{\omega_{c} }}$$

(47)

where $\alpha = T_{1} \sigma - 2\Phi$. Equations (44)–(47) are combined together according to the method of reconstitution, namely

$$\dot{a} = \varepsilon D_{1}^{1} a + \varepsilon^{2} D_{2}^{1} a \quad a\dot{\alpha } = \varepsilon aD_{1}^{1} \alpha + \varepsilon^{2} aD_{2}^{1} \alpha .$$

(48)

In this way, we can obtain

$$\dot{a} = - \frac{{b_{12} a}}{2} + \frac{{\Gamma_{23} a\cos \alpha }}{{2\omega_{c} }} + \frac{{\Gamma_{22} a - 2b_{13} \Lambda a}}{{2\omega_{c} }}\sin \alpha,$$

(49)

$$a\dot{\alpha } = a\sigma + \frac{{\Gamma_{21} a}}{{\omega_{c} }} + \frac{{\Gamma_{24} a^{3} }}{{4\omega_{c} }} - \frac{{\Gamma_{23} a\sin \alpha }}{{\omega_{c} }} + \frac{{\Gamma_{22} a - 2b_{13} \Lambda a}}{{\omega_{c} }}\cos \alpha .$$

(50)

Letting $\dot{a} = \dot{\alpha } = 0$, the steady-state solutions of the system can be obtained. It can be seen from Eqs. (49) and (50) that there is a trivial solution a = 0. Nevertheless, the non-trivial solutions, which will be discussed in detail in Sect. 4, correspond to

$$b_{12}^{2} + \left(\sigma + \frac{{\Gamma_{21} }}{{\omega_{c} }} + \frac{{\Gamma_{24} a^{2} }}{{4\omega_{c} }}\right)^{2} = \frac{{\Gamma_{23}^{2} + (\Gamma_{22} - 2b_{13} \Lambda )^{2} }}{{\omega_{c}^{2} }}.$$

(51)

3.3 1/3-order subharmonic resonance

To examine the 1/3-order subharmonic resonance, a new ordering is adopted so that the damping appears first in the same perturbation equation as the cubic nonlinearity [8, 29], namely

$$\ddot{q}_{c} + \omega_{c}^{2} q_{c} + \varepsilon^{2} b_{12} \dot{q}_{c} + \varepsilon b_{13} q_{c}^{2} + \varepsilon^{2} b_{14} q_{c}^{3} - b_{15} \cos (\Omega \tau ) = 0.$$

(52)

Similar to the case of primary resonance, q_c is independent of T₁. The nearness of the resonance is described by

$$\Omega = 3\omega_{c} + \varepsilon^{2} \sigma .$$

(53)

Substituting Eq. (C.1) into Eq. (52) and following the same steps as in the primary resonance, the following autonomous modulation equations can be derived:

$$D_{2}^{1} a = \frac{{\Gamma_{31} a^{2} \sin \alpha }}{{4\omega_{c} }} + \frac{{\Gamma_{32} a}}{{2\omega_{c} }},$$

(54)

$$aD_{2}^{1} \alpha = a\sigma + \frac{{3\Gamma_{33} a}}{{2\omega_{c} }} + \frac{{3\Gamma_{34} a^{3} }}{{8\omega_{c} }} + \frac{{3\Gamma_{31} a^{2} \cos \alpha }}{{4\omega_{c} }}$$

(55)

where $\Gamma_{31}$–$\Gamma_{34}$ are reported in Appendix B and $\alpha = T_{2} \sigma - 3\Phi$. Similar to the 1/2-order subharmonic resonance, there is a trivial solution a = 0 by letting $D_{2}^{1} a = D_{2}^{1} \alpha = 0$. The non-trivial solutions, which will be discussed in detail in Sect. 4, correspond to

$$\frac{{\Gamma_{32}^{2} }}{{4\omega_{c}^{2} }} + \left( {\frac{\sigma }{3} + \frac{{\Gamma_{33} }}{{2\omega_{c} }} + \frac{{\Gamma_{34} a^{2} }}{{8\omega_{c} }}} \right)^{2} = \frac{{\Gamma_{31}^{2} a^{2} }}{{16\omega_{c}^{2} }}.$$

(56)

4 Numerical results and discussion

Based on the obtained theoretical solutions in the last Section, the effect of the damper on the nonlinear behaviors of the cable is studied in this part. A cable–damper model shown in Fig. 1 is considered here. The damper is located at a distance of 2% of cable length from the lower end of the cable. The spring stiffness is K_d = 100, and the damping coefficient is C_d = 20. The parameters of the cable are selected as follows: the total length l_c is 200 m; cross-sectional area is 1.11 × 10⁻³ m²; Young’s modulus is 210 Gpa; mass per unit length is 48.62 kg/m; damping coefficient $\mu_{c}$ is 0.03; the initial force is 4.64 × 10⁵ N; the mechanical parameter $\lambda_{c} = E_{c} A_{c} {/}H_{c}$ is approximately 500 [8, 29]; the ratio of rise to span is 1/45; the angle between the cable and horizontal line is 30°. In the following analysis, SN, HB, and PF denote saddle-node bifurcations, Hopf bifurcations, and pitch-fork bifurcations, respectively. Stable solutions are depicted by solid lines, while unstable solutions are described by dashed lines.

4.1 Primary resonance

Figure 2 shows the frequency–response curves of the cable subjected to different excitation amplitudes when the solution is expanded to the second order. In order to verify the correctness of the results obtained by the method of multiple timescales, the Runge–Kutta method is also applied by integrating directly Eq. (10). In Fig. 2a, the agreement between the numerical and perturbation solutions is very satisfactory. However, the agreement between the two methods is not so good for the region with higher amplitudes when F = 0.01. As illustrated in Fig. 2b, the numerical results lose stability earlier than the perturbation solutions when the detuning parameter (i.e., σ) decreases from a relatively large value. Moreover, in Fig. 2c, the numerical results indicate that the solutions obtained by the Runge–Kutta method are more complicated. In other words, the perturbation solutions bend to the left all the time, while the numerical solutions bend to the right when σ is up to about − 0.4. Similar phenomena are also reported in Refs. [29, 39]. It seems that the second-order approximation is not so correct. Actually, it is a good choice to perform a higher-order analysis [29, 39] in this case, as we can obtain better accuracy when expanding to higher orders.

Therefore, Fig. 3 gives the frequency–response curves of the cable when the solution is expanded to the fourth order. As shown in the Figure, the numerical and perturbation solutions agree well with each other. Comparing Fig. 3 with Fig. 2, it can be found that when the excitation amplitudes are relatively small (i.e., F = 0.005), there is almost no difference between the second-order and fourth-order approximations. However, the second-order and fourth-order approximations differ greatly if F is increased to 0.01 and 0.02. Obviously, fourth-order solutions are more accurate. It is worth pointing out that the asymptotic results should be carefully verified by numerical results, which can also be produced either by the finite difference method or direct simulation of the multi-mode Galerkin truncated model [40, 41]. We choose the latter by the following references [40, 41]. The results of one-mode and five-mode discretization for the continuous system are given in Fig. 4. It can be seen that they show good agreement.

Fig. 3

The frequency–response curves of the cable with different excitation amplitudes by expanding the solution to the fourth order; a F = 0.005, b F = 0.01 and c F = 0.02

Fig. 4

Comparison between the numerical integrations; a F = 0.005 and σ = 0.6, b F = 0.01 and σ = 0.55, and c F = 0.02 and σ = –0.05

In Fig. 3a, b, a softening characteristic can be observed in the Figure because the response curves bend to the left. Due to the multivaluedness of the response curve, a jumping phenomenon triggered by SN can be detected. When the excitation is relatively small, i.e., F = 0.005 (see Fig. 3a), there are only stable solutions in the response curve, and the softening characteristic is relatively weaker. When the excitation amplitude is larger, i.e., F = 0.01 (see Fig. 3b), the stable solution will lose its stability via saddle-node bifurcation. If we go on increasing the excitation amplitude to 0.02 (see Fig. 3c), more SNs appear, and the double-jumping phenomenon [42] is observed. It can be concluded that the increase in the excitation amplitude will lead to the appearance of unstable solutions. Comparing Figs. 3a–c, it can be found that with the increase in excitation amplitude the response amplitudes increase obviously, and the distance between two branches of the solutions expands. More interestingly, the cable exhibits dual characteristic in Fig. 3c, namely, softening characteristic at low response and hardening characteristic at large response, which is similar to the results in reference [43]. In the following analyses, the results are based on the fourth-order approximation, since it is more accurate.

From Appendix A, we can find that the linear damping and spring stiffness affect the values of the coefficients b₁₁ and b₁₂ and further affect the nonlinear behaviors of the cable. Therefore, the cable–damper model may exhibit different nonlinear behaviors compared with a pure cable. To explore the differences between the two cases, the comparison between the frequency–response curves of the cable with (without) linear damper is carried out. In particular, letting K_d = C_d = 0 in b₁₁ and b₁₂ and substituting the results into the modulation equations, the frequency–response curves corresponding to the pure cable can be obtained, as shown in Fig. 5. It can be seen in Fig. 5a that when the excitation amplitude is small, the response amplitude of the cable with a damper is smaller than that of the pure cable. For the cable with a damper, the dual characteristic and SNs disappear. The above phenomena indicate that the linear damper has a good suppression on the vibration of the cable, and the damper improves the dynamic properties of the cable to some extent. When the excitation amplitude is larger (see Fig. 5b), the suppression on the left branch of the solutions is generally good, while it is a little worse for the right branch.

Fig. 5

Comparison between the frequency–response curves of the cable with/without damper; a F = 0.005 and b F = 0.02

To explore the effect of the damper on the nonlinear behaviors of the cable, different damping and spring stiffnesses are selected, and the corresponding frequency–response curves are given in Fig. 6. Obviously, the effect of the damping and spring stiffness on the large response region is more pronounced than those on the small response region. An interesting phenomenon is that the cable exhibits dual characteristic when C_d = 10, which implies that if the damping of the damper decreases to a certain value, softening and hardening characteristics will coexist in the response curve. Observing Fig. 6a, it can be found that the response amplitudes decrease with the increase in damping, and the damper has a good effect on the vibration suppression of the cable. As the damping increases, the horizontal distance between two branches of the same response curves is smaller, and the softening characteristic becomes weaker. This indicates that the increase in damping will lead to the reduction of the resonance region. If the damping is larger, say C_d = 30 and 40, the SNs disappear, and there are no unstable solutions.

Fig. 6

The frequency–response curves of the cable with different damping and spring stiffness of the damper when F = 0.01; a different damping, and b different spring stiffness

Similar phenomena can also be observed in Fig. 6b. For instance, the peaks of the curves decrease with the increase in spring stiffness. The range of unstable solutions is narrowed, and the horizontal distance between two branches of the same response curves becomes smaller. Moreover, a larger stiffness will lead to a weaker softening characteristic and the disappearance of the SNs. Nevertheless, an increase in stiffness does not always lead to smaller response amplitude as an increase in damping does. Observing the large response region in Fig. 6b, the response amplitudes will increase with the increase in spring stiffness, which is different from that in Fig. 6a. Recall that the dual characteristic vanishes with the increase in damping. Actually, similar phenomenon can also be observed in the variation of the spring stiffness if the excitation amplitude is increased to 0.02. Figure 7 shows the frequency–response curves with different spring stiffnesses when F = 0.02. It can be seen that the response curves gradually exhibit a single hardening characteristic with the increase in spring stiffness. However, unlike Fig. 6a, what disappears is the softening characteristic in Fig. 7.

Fig. 7

The frequency–response curves of the cable with different spring stiffnesses of the damper when F = 0.02

On the other hand, letting b₁₃ and b₁₄ in Eq. (10) be equal to zero, we can obtain the linear case of the system as shown in Fig. 8. It can be seen that adding a damper provides an effective suppression on the vibration of the cable. There are no bends in the response curves, and the whole curves are symmetrical about σ = 0.

Fig. 8

Linear case: comparison between the frequency–response curves of the cable with/without damper when F = 0.005

By integrating directly Eq. (10), numerical results of the system can be easily obtained. Figures 9, 10, and 11 show the time histories, phase portraits, and Poincaré sections of the cable with/without damper when F = 0.005. For the sake of convenience, only the cases when σ = − 0.3, 0, and 0.3 are given. As illustrated in these Figures, there is only one closed circle in phase portraits, and one clustered point can be observed in Poincaré sections, which represents period-1 motion. Although the response amplitudes with a damper are very close to those without damper (see the time histories in Figs. 9, 10, and 11), they can be recognized by phase portraits and Poincaré sections. As shown in Figs. 9, 10, and 11, a quantitative difference between the two cases (with and without damper) can be evidently observed in the shape of phase portraits and Poincaré sections. This means that the damper has a significant influence on the nonlinear characteristics of the cable. Actually, Poincaré section is a fundamental way to assist us grasping nonlinear behaviors of the system, which is very helpful [44]. Observing Figs. 9b, c, we can find that there are large discrepancies between not only response amplitudes but also phase portraits and Poincaré sections. This indicates that the stable steady solutions belonging to distinct branches exhibit different nonlinear behaviors even though other conditions, such as the excitation amplitude and detuning parameter, are the same, which should attract our attention in practical engineering.

Fig. 9

Time histories, phase portraits, and Poincaré sections of the cable when σ = –0.3 and F = 0.005

Fig. 10

Time histories, phase portraits, and Poincaré sections of the cable when σ = 0 and F = 0.005

Fig. 11

Time histories, phase portraits, and Poincaré sections of the cable when σ = 0.3 and F = 0.005

4.2 1/2-order subharmonic resonance

This part examines the nonlinear behaviors of the cable when 1/2-order subharmonic resonance occurs. It should be pointed out that only the non-trivial solutions are discussed in the following Figures. Figure 12 presents the frequency–response curve of the cable. It is found that the response curve is symmetric about the σ-axis, so only the nonnegative values are drawn in the Figure. The numerical results are also obtained by using the Runge–Kutta method to compare with the perturbation solutions, and a good agreement between the two methods can be observed. It can be seen in Fig. 12 that when the excitation frequency decreases from a relatively large value, the solutions are trivial and stable at the beginning until PF is reached. Obviously, PF is a supercritical pitch-fork bifurcation. If we go on decreasing the excitation frequency, PF will give rise to two branches, one of which is stable, while another one is non-trivial and unstable. The stable one increases with the further decrease in excitation frequency. The above phenomena are similar to those obtained by Rega [29].

Fig. 12

The frequency–response curve of the cable with excitation amplitude F = 0.08

Figure 13 illustrates the frequency–response curves of the cable when there is (no) damper. It can be seen that the adding of the damper makes PF moving to the left. This means that the unstable solutions of the cable with damper appear later than those of the pure cable when the excitation frequency decreases from a relatively large value. Moreover, the suppression of the damper on the small amplitude vibration is satisfactory, but on the large amplitude vibration is not so ideal. This is similar to the results in Fig. 5b.

Fig. 13

Comparison between the frequency–response curves of the cable with/without damper when F = 0.08

Figure 14 presents the frequency–response curve of the cable with different damping and stiffness. It can be seen in Fig. 14a that the response amplitudes become smaller with the increase in damping of the damper. Additionally, the location of PF moves gradually to the left. As far as the location of PF is concerned, increasing the spring stiffness has the same effect as increasing the damping. As illustrated in Fig. 14b, the location of PF is also closer to the origin with the increase in spring stiffness. An interesting phenomenon can be seen in Fig. 14b that the intersection points of three curves are very close to each other, as shown by points A, B, and C in the enlarged part. It seems that there is a ‘fixed point,’ at which the response curves with different stiffnesses intersect. Due to the existence of the intersection points, the response amplitudes do not decrease but increase with the increase in spring stiffness in the large response region, which is different from Fig. 14a. A similar phenomenon can also be seen in Fig. 6b.

Fig. 14

The frequency–response curves of the cable with different damping and spring stiffnesses of the damper when F = 0.08; a different damping, and b different spring stiffnesses

Figure 15 shows the time histories and phase portraits of the cable with different damping when σ = − 0.2 and F = 0.08. A single circle is also observed in the phase portraits for specific damping. It can be seen from time histories that the difference between the response amplitudes with different dampings is small. Nevertheless, they can be recognized by detecting the shape of phase portraits, since the discrepancies between the phase portraits are apparent, as shown in Fig. 15. If we increase σ to 0.2, the damping will have a large influence not only on the phase portraits but also on the time histories, and the corresponding results are given in Fig. 16. As illustrated in the Figure, the response amplitudes are 0.01264 (C_d = 10), 0.01155 (C_d = 20) and 0.00918 (C_d = 30), respectively. It can be obtained that the response amplitude is decreased by 8.6% when C_d = 20 and 27.4% when C_d = 30 with respect to that when C_d = 10. Recall that the response amplitudes with various damping in Fig. 15 are almost indistinguishable; we can learn that the damping has a more remarkable influence on the small amplitude vibration of the cable, which is different from Fig. 6a. Comparing Figs. 15 and 16 with Figs. 9, 10, and 11, it can be found that the shapes of the phase portraits are different. To explore the reason, Fig. 17 presents the power spectr corresponding to Figs. 15 and 16, respectively. For the sake of simplicity, only the case of C_d = 20 is given. The power spectr, obtained by using fast Fourier transform (FFT) show that the vibration response contains two frequency components, namely, 0.38 Hz (or 0.41 Hz) and 0.76 Hz (or 0.82 Hz). Notice that the natural frequency of the cable is ω_c = 0.40 Hz at this time. Hence, in addition to the response corresponding to the fundamental frequency of the cable itself (0.38 (or 0.41) $\approx$ ω_c), the response of forced harmonic (0.76 (or 0.82) $\approx$ Ω) is also excited. Moreover, the frequency of the cable occupies the dominant one in the response, which is consistent with the results obtained by Rega [29].

Fig. 15

Time histories and phase portraits of the cable with different damping when σ = − 0.2 and F = 0.08

Fig. 16

Time histories and phase portraits of the cable with different damping when σ = 0.2 and F = 0.08

Fig. 17

Power spectr of the cable when Cd = 20, Kd = 100 and F = 0.08; a σ = − 0.2, b σ = 0.2

4.3 1/3-order subharmonic resonance

This part examines the nonlinear behaviors of the cable when 1/3-order subharmonic resonance occurs. It should be pointed out that only the non-trivial solutions are drawn in the following Figures. To explore the effect of the damper on 1/3-order subharmonic resonance of the cable, the comparison between the frequency–response curves of the cable with/without damper is executed, as illustrated in Fig. 18. It can be seen that the damper makes the whole curve moving to the upper left, and when σ belongs to [− 0.32, 0.06], there are no solutions for the cable with damper compared with a pure cable. In other words, the resonance region becomes smaller, thus controlling the vibration of the cable.

Fig. 18

Comparison between the frequency–response curves of the cable with/without damper when F = 0.24

Figure 19 gives the frequency–/force–response curves of the cable with different damping. Obviously, the difference between the response amplitudes is small for the large response region. As can be seen in Fig. 19a, the response curves are relatively simple, and there is only one branch for a specific damping. With the increase in damping, the stable solutions of the response are reduced, and the locations of SNs move gradually to the upper left. Moreover, the distance between stable and unstable solutions becomes smaller, and it looks like the response curves have been compressed. As the excitation frequency is increased from a relatively small value, the response amplitudes decrease correspondingly until SNs are reached. Nevertheless, different phenomena are observed in Fig. 19b. By way of example, the locations of SNs move gradually to the upper right with the increase in damping, and the stable solutions become larger with the increase in excitation amplitude.

Fig. 19

The response curves of the cable with different damping; a frequency–response curves with F = 0.24, and b force–response curves with σ = − 0.2

Figure 20 gives the frequency–/force–response curves of the cable with different spring stiffnesses under 1/3-order subharmonic resonance. Different from Fig. 19, the difference between the response amplitudes is larger for the large response region. By and large, the response amplitudes increase with the increase in spring stiffness, which is different from Figs. 6b and 14b. An interesting phenomenon can be seen in Fig. 20a that the system has solutions only when σ is smaller than a certain threshold. This can be used to control the cable’s vibration related to 1/3-order subharmonic resonance in practical engineering. Similarly, Fig. 20b shows that there are solutions only when the excitation amplitude is larger than a certain threshold, which means that 1/3-order subharmonic resonance may not be excited unless the excitation is large enough. The above phenomena can also be observed in Fig. 19.

Fig. 20

The response curves of the cable with different spring stiffnesses; a frequency–response curves with F = 0.24 and b force–response curves with σ = − 0.2

5 Conclusions and prospects

In order to study the effect of the damping and spring stiffness on the nonlinear behaviors of the cable–damper system, the primary and subharmonic resonances of the cable are explored. In the cable–damper model, the damper is modeled as a combination of a linear damper and a spring. The ODE is obtained by discretizing the equation of motion of the cable and solved by applying the method of multiple timescales. Based on different resonance forms of the cable, the modulation equations are derived, and the corresponding equilibrium solutions are sought by pseudo-arclength algorithm. Then the frequency–/force– response curves are drawn. Meanwhile, the time histories, phase portraits, and Poincaré sections are also presented to investigate the effect of the damper on nonlinear resonances of the cable. Finally, the following conclusions and prospects are given.

• (i) By and large, the response of the cable decreases with the increase in damping of the damper. For the subharmonic resonance, the suppression of the damper on the small amplitude vibration is generally good, while that on the large amplitude vibration is not so satisfactory. There are significant differences between the phase portraits of the cable when there is (no) a damper, which indicates that the damper has a remarkable influence on the nonlinear behaviors of the cable.

• (ii) For the primary resonance, the influences of the damping and spring stiffness on the large response of the cable are larger than those on the small response. The increase in damping and spring stiffness results in the weakening of the softening characteristic. When the excitation amplitude is relatively large, softening and hardening characteristics appear simultaneously in the response curve. However, the increase in damping (spring stiffness) makes the dual characteristic transition to the softening (hardening) characteristic. The suppression effect of the damper varies with different excitation amplitudes.

• (iii) For the 1/2-order subharmonic resonance, the influences of the damping and spring stiffness on the small response of the cable are larger than those on the large response. A quantitative difference can be observed in the phase portraits with various damping. Two frequency components can be found in the spectr, in which the fundamental frequency of the cable is a higher one.

• (iv) For the 1/3-order subharmonic resonance, the response amplitudes increase with the increase in spring stiffness. There are solutions only when excitation frequency (or amplitude) belongs to a certain range. The increase in damping and spring stiffness makes the resonance region becoming smaller.

In general, the large vibration of the cable may be excited by a parametric excitation. Hence, a cable–damper model subjected to the motion of the support is expected to be studied. Other types of the dampers will be in the focus of our future work. Furthermore, experimental analyses on the model will also be performed in the future, so as to reveal the role of the damper from an experimental point of view.

Appendices

Appendix A

The expressions of the Galerkin integral coefficients in Eq. (10) are given as follows:

$b_{11} = \omega_{c}^{2} = \frac{1}{{\int_{0}^{1} {\phi_{c}^{2} (x)} {\text{d}}x}}\left[K_{d} \phi_{c}^{2} (l_{1} ) - \frac{{\lambda_{c} \int_{0}^{1} {y^{\prime}_{c} (x)\phi^{\prime}_{c} (x)dx} \int_{0}^{1} {y^{\prime\prime}_{c} (x)\phi_{c} (x)dx} }}{{\beta_{c}^{2} }} - \int_{0}^{1} {\frac{{\phi_{c} (x)\phi^{\prime\prime}_{c} (x)}}{{\beta_{c}^{2} }}} {\text{d}}x\right]$;

$b_{12} = \frac{1}{{\int_{0}^{1} {\phi_{c}^{2} (x)} {\text{d}}x}}\left[\mu_{c} \int_{0}^{1} {\phi_{c}^{2} (x)} {\text{d}}x + C_{d} \phi_{c}^{2} (l_{1} )\right]$;

$b_{13} = \frac{1}{{\int_{0}^{1} {\phi_{c}^{2} (x)} {\text{d}}x}}\left[ - \frac{{\lambda_{c} \int_{0}^{1} {\phi^{\prime}_{c} (x)\phi^{\prime}_{c} (x){\text{d}}x} \int_{0}^{1} {y^{\prime\prime}_{c} (x)\phi_{c} (x){\text{d}}x} }}{{2\beta_{c}^{2} }} - \frac{{\lambda_{c} \int_{0}^{1} {y^{\prime}_{c} (x)\phi^{\prime}_{c} (x){\text{d}}x} \int_{0}^{1} {\phi^{\prime\prime}_{c} (x)\phi_{c} (x){\text{d}}x} }}{{\beta_{c}^{2} }}\right]$;

$b_{14} = - \frac{1}{{\int_{0}^{1} {\phi_{c}^{2} (x)} {\text{d}}x}}\frac{{\lambda_{c} \int_{0}^{1} {\phi^{\prime}_{c} (x)\phi^{\prime}_{c} (x){\text{d}}x} \int_{0}^{1} {\phi^{\prime\prime}_{c} (x)\phi_{c} (x){\text{d}}x} }}{{2\beta_{c}^{2} }}$; $F = \frac{{\int_{0}^{1} {F_{1} (x)\phi_{c} (x){\text{d}}x} }}{{\int_{0}^{1} {\phi_{c} (x){\text{d}}x} }}$; $b_{15} = \frac{{F\int_{0}^{1} {\phi_{c} (x){\text{d}}x} }}{{\int_{0}^{1} {\phi_{c}^{2} (x)} {\text{d}}x}}$.

Appendix B

The expressions of the coefficients in Eqs. (22), (25), (42), (54), and (55) are given as follows:

$\Gamma_{11} = \left( - 3b_{14} + \frac{{10b_{13}^{2} }}{{3\omega_{c}^{2} }}\right)$; $\Gamma_{12} = \left(b_{14} + \frac{{2b_{13}^{2} }}{{3\omega_{c}^{2} }}\right)$; $\overline{\Gamma }_{11} = \frac{{b_{12} b_{15} }}{{8\omega_{c} }}$; $\overline{\Gamma }_{12} = - \frac{{b_{15} \sigma }}{{4\omega_{c} }}$; $\overline{\Gamma }_{13} = - \frac{{5b_{13}^{2} b_{15} }}{{12\omega_{c}^{4} }} + \frac{{3b_{14} b_{15} }}{{8\omega_{c}^{2} }}$; $\overline{\Gamma }_{14} = \frac{{7b_{13}^{2} b_{15} }}{{18\omega_{c}^{4} }} - \frac{{3b_{14} b_{15} }}{{4\omega_{c}^{2} }}$; $\overline{\Gamma }_{15} = - \frac{{11b_{12} b_{13}^{2} }}{{9\omega_{c}^{3} }} + \frac{{3b_{12} b_{14} }}{{2\omega_{c} }}$; $\overline{\Gamma }_{16} = \frac{{485b_{13}^{4} }}{{54\omega_{c}^{6} }} - \frac{{173b_{13}^{2} b_{14} }}{{6\omega_{c}^{4} }} + \frac{{15b_{14}^{2} }}{{8\omega_{c}^{2} }}$;

$\Gamma_{21} = \frac{{b_{12}^{2} }}{4} - 6b_{14} \Lambda^{2} + \frac{{3b_{13}^{2} \Lambda^{2} }}{{\omega_{c}^{2} }} - \frac{{4b_{13}^{2} \Lambda^{2} }}{{\Omega (\Omega + 2\omega_{c} )}}$; $\Gamma_{22} = \frac{{b_{13} \Lambda \sigma }}{{\omega_{c} }}$; $\Gamma_{23} = - \frac{{2b_{12} b_{13} \Lambda \Omega }}{{\Omega^{2} - \omega_{c}^{2} }}$; $\Gamma_{24} = - 3b_{14} + \frac{{10b_{13}^{2} }}{{3\omega_{c}^{2} }}$.

$\Gamma_{31} = - 3b_{14} \Lambda - \frac{{4b_{13}^{2} \Lambda }}{{\Omega (\Omega - 2\omega_{c} )}} - \frac{{2b_{13}^{2} \Lambda }}{{3\omega_{c}^{2} }}$; $\Gamma_{32} = - b_{12} \omega_{c}$; $\Gamma_{33} = - 6b_{14} \Lambda^{2} - \frac{{4b_{13}^{2} \Lambda^{2} }}{{\Omega (\Omega - 2\omega_{c} )}} + \frac{{4b_{13}^{2} \Lambda^{2} }}{{\omega_{c}^{2} }} - \frac{{4b_{13}^{2} \Lambda^{2} }}{{\Omega (\Omega + 2\omega_{c} )}}$; $\Gamma_{34} = - 3b_{14} + \frac{{10b_{13}^{2} }}{{3\omega_{c}^{2} }}$.

Appendix C

To seek a second-order approximation, the solution of q_c is uniformly expanded in power series of ε, namely

$$q_{c} = \sum\limits_{i = 1}^{3} {\varepsilon^{i - 1} q_{ci} (T_{0} ,T_{2} )} + O(\varepsilon^{3} ).$$

(C.1)

Here, it should be noted that q_c is found to be independent of T₁ by eliminating the secular terms in the equation of order $\varepsilon^{1}$. Therefore, T₁ is dropped in Eq. (C.1). Following similar treatment to that of higher-order expansion, the following autonomous modulation equations can be derived:

$$D_{2}^{1} a = - \frac{{b_{12} a}}{2} + \frac{{b_{15} \sin \alpha }}{{2\omega_{c} }},$$

(C.2)

$$aD_{2}^{1} \alpha = a\sigma + \frac{{\Gamma_{11} a^{3} }}{{8\omega_{c} }} + \frac{{b_{15} \cos \alpha }}{{2\omega_{c} }}.$$

(C.3)

Letting $D_{2}^{1} a = D_{2}^{1} \alpha = 0$ and eliminating $\alpha$, Eqs. (C.2) and (C.3) can be simplified as

$$\frac{{b_{12}^{2} a^{2} }}{4} + \left(a\sigma + \frac{{\Gamma_{11} a^{3} }}{{8\omega_{c} }}\right)^{2} = \frac{{b_{15}^{2} }}{{4\omega_{c}^{2} }}.$$

(C.4)

The stable solutions of the system can be obtained according to Eq. (C.4).