1 Introduction

Cable-stayed bridges have gained rapid progress in the last few decades because of their aesthetic appeal, economic grounds and ease of erection [1,2,3,4]. Due to their large flexibility, relatively small mass and very low damping, cables are prone to vibrating under ambient excitations [5], which will result in rich and interesting nonlinear behaviors. Therefore, the dynamics of cable-stayed bridges have been a hot research area and attracted many researchers’ attentions. The research on the dynamics of cable-stayed bridges began with those of a single cable or beam. Irvine [6, 7] developed cable’s linear dynamic model. Luongo [8] investigated elastic cable’s nonlinear oscillation. Thereafter, many scholars have made indispensable contributions to cable dynamics. Main et al. [9] investigated the free vibration of a taut cable by adding a nonlinear damper near the end. They pointed out that the nonlinear damper may offer potential advantages compared with traditional linear damper. Rega and his co-workers [10,11,12,13,14] systematically investigated the dynamics and modal interactions of cables by the means of multi-dimensional Galerkin discretization and a second-order multiple scales approach. Wang and Zhao [15] explored the chaotic dynamics of a suspended cable subjected to a harmonic excitation, and the effects of excitation amplitudes and sag-to-span ratios on the nonlinear dynamics of the suspended cable were carried out. Kang et al. [16] studied the linear and nonlinear dynamics of a suspended cable by taking into bending stiffness account. The three-to-one internal resonance between the first- and third-order in-plane symmetric modes is analyzed.

However, a single cable could not help us to understand the dynamic interactions among cables and the other structural components such as the beams and towers. Thus, the hybrid structures such as cable-stayed beam and cable-arch are given more attention recently by many researchers. Lenci and Ruzziconi [17] discussed the nonlinear dynamics of a planar cable-stayed beam. They said that even though the considered model was simple, it could reveal the complex dynamics of the cable-supported beam. Nevertheless, more complicated models were expected if one wanted to enrich the observed phenomena. Huang et al. [18] studied the 1:2 internal resonance of suspended-cable-stayed beam by considering the curvature and deformation of cables. They pointed out that a mono-modal motion, bi-modal motion, quasi-periodic motion or a chaos would occur under the principle and the 1:2 internal resonances. Gattulli and Lepidi [19] proposed an analytical model, namely, cable-beam model, to study the nonlinear interactions between a beam and a cable, and investigated the internal resonant mechanisms of 1:2 global–local resonance and 2:1 global–local resonance. Wang et al. [20] solved the in-plane and out-of-plane eigenvalue problems of cable-stayed beam and investigated mainly the 2:1 internal resonance of the system. Recently, Kang and Cong et al. [21, 22] established a novel nonlinear dynamic double-cable-stayed shallow-arch model by considering the initial configuration of the beam. They investigated the in-plane 1:1:1 and 1:2:2 internal resonances among three first modes of two cables and the shallow arch under external harmonic excitation.

Above cable-beam and cable-arch models are still relatively simple, which can give only rough information on the mechanical behaviors of cable-stayed bridges. In order to further understand the overall dynamic properties of the cable-stayed bridge, Cao et al. [23] proposed a novel model consisting of a simply supported four-cable-stayed deck beam and two rigid towers. Then, Song et al. [24] studied the dynamic response of a cable-stayed bridge subjected to a moving vehicle load based on the model in Ref. [23]. Except for theoretically modeling, the researches on cable-stayed bridges are mainly carried out by experiments [25,26,27]. Experimental analysis plays a fundamental role in the detection of new dynamic phenomena and their mechanism associated with the actual nonlinearities existing in a given system [28]. Wilson et al. [29] conducted full-scale ambient vibration tests to measure the dynamic response of a 542-m (center span of 274 m) cable-stayed bridge. Ren et al. [30] measured the field ambient vibration of the bridge deck and all stay cables about Qingzhou cable-stayed bridge in Fuzhou, China. The experimental modal analysis was conducted and many significant modes below 1.0 Hz of the bridge were identified. Macdonald et al. [31] performed dynamic monitoring during the construction of the Second Severn Crossing cable-stayed bridge. The natural frequencies of bridge were identified based on ambient vibration measurement, and the mode shapes were matched with those obtained by a finite element model. Sun et al. [32] designed the scale model of a cable-stayed bridge based on the similarity theory and conducted the nonlinear dynamic experiment to investigate the modal interaction process.

The previous investigations are considerably enlightening and there are many other rich and interesting phenomena to be explored in the nonlinear dynamics of cable-stayed bridge. This paper aims to reveal the mechanisms and phenomena of nonlinear coupled vibration more generally and comprehensively, which is an extension of our previous work [32]. As mentioned above, most of the nonlinear phenomena in cable-stayed bridge are studied theoretically (and experimentally [28, 33]) aiming to a single member or a hybrid structure due to the difficulty of global modeling. However, the frequency spectrum of cable-stayed bridge is very dense, and there may be many other rich nonlinear phenomena and their mechanism need to be observed and revealed, especially for modal interaction (internal resonance) among different modes in cables and beam. This paper is expected to explore the nonlinear interactions among different modes in cables and beam and verify qualitatively the existing theoretical results from an experimental point of view. The related experimental results in this paper can provide a practical guidance for theoretical researches and vibration control of cable-stayed bridges. To this end, the model of the Xiangshangang Bridge with a scale of 1:250 was established based on the similarity principle. And the dynamic parameters, such as frequencies and mode shapes, are measured by free vibration test again in order to study dynamic behaviors of the physical model more accurately. In order to compare with the experimental data, two finite element (FE) models are developed, i.e., one-element cable system (OECS) and multi-element cable system (MECS). Moreover, a vertical harmonic excitation is applied at 10 cm left from the middle of the beam and some interesting phenomena are observed.

This paper is organized as follows. In Sect. 2, a brief introduction about the model and experimental apparatus is presented. In Sect. 3, the modal analysis is performed. Section 4 is devoted to test free vibration of cables. After free vibration analysis, the nonlinear resonance of the cable-stayed bridge under the external excitation is studied in Sect. 5. Some conclusions are given in Sect. 6.

2 The model and instruments

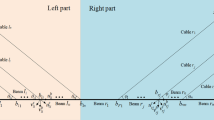
Xiangshangang Bridge, the prototype of the experimental model, is located at Ningbo, China. It is a three-span steel cable-stayed bridge with semi-floating system. By taking all the conditions (such as the size of the lab) into account, the scaled factor is chosen to be 1:250. Then, the main dimensions of the model are as follows: the total length is 5500 mm, the span layout is 1375 + 2750 + 1375 mm, the height is 1040 mm, the upper part of the tower is 680 mm and the lower part is 360 mm. Figure 1 shows the model and the numbers of cables.

Fig. 1
figure 1

The elevation and the physical map of the model

Full size image

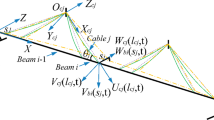
The model’s details are shown in Fig. 2a–d. In this model, the bridge deck is made of an aluminum alloy with a rectangular section of 100 mm\(\times \)5 mm. Every two 160 mm\(\times \)80 mm\(\times \)5 mm steel plates form one group to simulate the quality of the bridge deck, and the spacing between the adjacent groups is 120 mm. The tower consists of two rectangular aluminum alloy boxes, which are laterally installed on both sides of the bridge deck. The size of the box is 38 mm\(\times \)25 mm\(\times \)0.8 mm. A connecting plate is arranged on the tower through a nut. Then, a crossbeam made of 20 mm\(\times \)20 mm square steel is arranged on the plate to anchor cables. The cables are chosen to be stainless steel wire, with iron cylinders (\(\Phi \)10 mm\(\times \)16 mm) as lumped mass. The interval spacing of cables on the bridge deck is 120 mm and on the tower is 30 mm. As for the arrangement of cables’ boundary conditions, one end of each cable is threaded into a perforated screw which is then screwed into the crossbeam. The other end is fixed on the bridge deck by two steel plates. It should be noted that the center of the steel plates should coincide with the center of the bridge deck where cables are anchored on. Since the bridge is a semi-floating system, only horizontal and vertical constraints are set at the connection of the tower and beam. Smooth stainless cylinders are mounted on the top of side piers to release the longitudinal freedom of the beam, and the bolts are used to connect the beam to the ground to prevent from capsizing. In addition, the tower is fixed on the ground through a 500 mm\(\times \)500 mm\(\times \)10 mm steel plate. The other parameters and details of the prototype bridge and the model can be seen in Ref. [32].

Fig. 2
figure 2

The experimental model and main equipment

Full size image

In this paper, the experiment was carried out with video measuring instrument—Imetrum, instead of the traditional acceleration sensor. The main equipment is shown in Fig. 2e and f. Imetrum is a dynamic real-time measure system based on video image adopting noncontact measuring method with no influence on the mechanical properties and behaviors of the model. Its basic principle is optical imaging. By means of a high-speed camera, the data of the vibrating object are imported into the computer for analysis. Compared with the sensors, Imetrum has the following advantages:

  1. (i)

    Simple. What we should do is just to point the camera at the model, calibrate the coordinate system, select the measurement point, and the software is simple to operate, the instrument is easy to move and the measurement point is flexible to choose;

  2. (ii)

    Efficient. Imetrum can record the vibration information of arbitrary position;

  3. (iii)

    High pixel. The lenses are of good pixel, precision and resolution.

3 Modal analysis

In this paper, the modal parameters such as frequencies and mode shapes are evaluated and compared with those obtained by two FE models (OECS and MECS) as shown in Fig. 3 to obtain more accurate modal parameters. In the two FE models, the tower and the beam are modeled with BEAM188, the cables are modeled with LINK10 and the tower–beam connection is modeled with COMBIN14. Each cable is divided into one element in OECS model and eight elements in MECS model.

Fig. 3
figure 3

The finite element model of the experimental model

Full size image
Fig. 4
figure 4

Time history and power spectrum of the beam

Full size image
Fig. 5
figure 5

Mode shapes of the beam after filtering

Full size image
Fig. 6
figure 6

Time history, power spectrum and mode shape of the cable A1

Full size image

Firstly, the free vibration analysis of the beam is conducted. We selected 24 measurement points in total with spacing of 24 cm and the vibration data is collected by Imetrum. In order to investigate the possible nonlinear behaviors between the low-order modes of the beam and cables, FFT is applied to the collected data. Figure 4 shows time history response at 1/4 span of the beam. As can be seen from the figure, the vibration response of the beam contains two frequency components, 3.81 Hz and 4.78 Hz, where 3.81 Hz is the dominant one. Furthermore, we can get vibration components corresponding to 3.81 Hz and 4.78 Hz, respectively, after filtering. By extracting the displacements of all measurement points at a certain time (e.g., 25 s), we can get the mode shapes corresponding to 3.81 Hz and 4.78 Hz as shown in Fig. 5, which agree with the result obtained in Ref. [34]. This confirms that the experimental setup and model are credible and the model can reveal the general dynamic properties of a semi-floating cable-stayed bridge.

The first-order frequency is measured based on the free vibration analysis of each cable. Then, the initial cable force and Ernst elastic modulus can be computed. Take the cable A1 as an example. A small perturbation is applied to the mid-span of the cable A1, and the time history is recorded as shown in Fig. 6. It can be seen that its frequency is 5.86 Hz. Due to the randomness of the vibration, we cannot determine whether 5.86 Hz is the first-order frequency or not. Therefore, we have drawn the mode shape (see Fig. 6) corresponding to 5.86 Hz. There is no doubt that the mode shape indicates that 5.86 Hz is just the first-order frequency of the cable A1, which is a coincidence with our previous work [32]. Similarly, the fundamental frequencies of other cables are measured, and the corresponding cable force and Ernst elastic modulus are obtained as shown in Table 1.

Table 1 The parameters of all cables
Full size table

Figures 7 and 8 show the first five mode shapes of OECS and MECS models. Comparing the mode shapes, we can find that they are similar. Table 2 shows the first five frequencies obtained by FE models and experimental test. It should be noted that the out-of-plane frequencies are not measured and denoted by ‘–’. It can be seen from Table 2 that the difference between the frequencies of the same modes obtained by the OECS model and the MECS model is small. Furthermore, it is found that the frequencies of MECS model are slightly lower than those obtained by OECS model. The reason may be that the sags of cables are considered in MECS model, which makes the equivalent Young’s modulus less than that in OECS model, resulting in the reduction of the overall stiffness. The consistency between the frequencies of the experiment and two FE models makes a sound foundation for further research.

Fig. 7
figure 7

The first five mode shapes of OECS model

Full size image
Fig. 8
figure 8

The first five mode shapes of MECS model

Full size image

4 Free vibrations of cables

In previous theoretical and experimental studies, there is no work which concerns the interaction of cables in cable-stayed bridge. In order to explore the dynamic interaction among cables, free vibrations of cables are studied. During the experiment, it is found that when the cable A5 is given a slight disturbance, the cable A6 vibrates simultaneously. Thus, we apply an initial disturbance to cable A5 and record the in-plane lateral displacements of cables A5 and A6 as shown in Fig. 9. The results of FFT show that there exist two vibration frequencies for cables A5 and A6, namely, 9.22 Hz and 9.34 Hz. 9.22 Hz is close to the fundamental frequency of cable A5 presented in Table 1, and 9.34 Hz is near the fundamental frequency of cable A6 (9.96 Hz in Table 1). In return, an initial disturbance is applied to cable A6 and the in-plane lateral displacements of cables A5 and A6 are plotted in Fig. 10, from which the analogous rules can be observed.

Table 2 The comparison of the first five frequencies
Full size table

It can be concluded from Figs. 9 and 10 that when one cable is perturbed, the other cables with close frequency will also vibrate simultaneously, which is due to the fact that the 1:1 resonance among cables occurs. As shown in Fig. 11, the vibrations of A5 and A6 are synchronous, namely, the two responses reach peaks simultaneously. During vibration, cables will interact with each other and ‘infiltrate into’ each other’s vibrations, which indicate the cable–cable coupling vibrations that occur and cause multiple frequencies to exist in FFT results. Owing to the closeness of the frequencies, the beating vibration occurs. Comparing Fig. 9 with Fig. 10, it is found that the beating vibration occurring between A5 and A6 is sensitive to initial disturbance. The beating vibration shown in Fig. 10 is much clearer than that in Fig. 9, which further confirms the previous conclusion. The similar phenomena tend to occur among cables (A7 and B7) with close frequencies, where they are located in a symmetric position of the system.

Fig. 9
figure 9

Free vibration time history of cables A5 and A6 when the cable A5 is perturbed

Full size image
Fig. 10
figure 10

Free vibration time history of cables A5 and A6 when the cable A6 is perturbed

Full size image
Fig. 11
figure 11

Free vibration time history of cables A5 and A6 when the cable A6 is perturbed

Full size image
Fig. 12
figure 12

Free vibration time history of cables A1 and B1 when the cable A1 is perturbed

Full size image

Figure 12 shows the time history of cables A1 and B1 which are located in symmetric position of the system. As expected, the beating vibration also occurs, because the fundamental frequencies of A1 and B1 are close. Unlike Fig. 11, vibrations of A1 and B1 are interlaced, which means that one of the responses reaches peak and simultaneously the other is almost zero and vice versa. This indicates that there exists an energy exchange between A1 and B1, which confirms the possibility of energy exchange from the experimental point of view. The dense spectrum is one of the most obvious characteristics of the cable-stayed bridge, which will lead to the analogous phenomenon occur between/among the other components, such as what is shown in Fig. 13.

Fig. 13
figure 13

Free vibration time history of cables A1 and C1 when the cable C1 is perturbed

Full size image

In order to verify the experimental results, the experimental data of a cable of the model bridge is compared with test data obtained by on-site measurement of a real cable of Sutong Bridge as shown in Fig. 14. Although the acceleration and deflection responses are plotted, respectively, in Fig. 14, they can reveal the same dynamic behavior of a structure except for response amplitude. It can be found that the free vibration response obtained by on-site measurement coincide qualitatively with that obtained by experiments in this paper. Additionally, the similar phenomena can also be seen in the literatures [35,36,37]. This indicates that the results in this paper are credible, which makes a sound foundation for further study. It is worth mentioning that Caetano et al. [34] deeply discussed the possibility of occurrence of different internal resonance conditions (1:1, 1:2 and 2:1) between local and global modes based on on-site measurements and finite element modeling aiming to the International Guadiana Bridge. Many nonlinear phenomena, such as internal resonance and beating vibration of cable deck, are observed. However, they did not concern the interactions among cables. It can be expected that there exists energy transfer through internal resonance among different cables, which is demonstrated by the experimental data in this paper. Therefore, the internal resonance should be taken into account the vibration control of cables.

Fig. 14
figure 14

Measured time histories

Full size image

5 Forced vibration test

The complex environmental load, such as winds, traffic and earthquakes, commonly leads to large vibration of cables in the cable-stayed bridge [38]. However, there is almost no work that investigates and tests the superharmonic, primary and subharmonic resonances of a real bridge. In order to further study the nonlinear behavior of the cable-stayed bridge, a vertical harmonic excitation with a single frequency and certain amplitude is applied at the location which is 10 cm left from the middle of the beam of the model bridge. Figure 15 shows the positions of excitation and measurement points.

Fig. 15
figure 15

Layout of excitation and measurement points

Full size image

5.1 The parametric vibrations of cables

Figure 16 shows the response of cables and the beam when the excitation amplitude is 0.14 mm with different frequencies. In Fig. 16a–f, the excitation frequency is 4.8 Hz and the others are different. It is observed that the response amplitude of the beam is up to 0.62 mm as shown in Fig. 16b, which is more than 4 times of the excitation amplitude. That is, the large vibration of the beam is induced. Recall that the frequency of the excitation is 4.8 Hz, which is approximately equal to the first-order antisymmetric vertical bending frequency (4.78 Hz); therefore, the primary resonance of the beam occurs. Figure 16c shows the response of the cable A1. It can be observed that the cable’s response amplitude is 6.15 mm, which is up to 12 times of its diameter and more than 40 times of the excitation amplitude. However, the cable’s vibration frequency is 4.8 Hz, which is not its natural frequency but the excitation frequency. This indicates that large amplitude vibration of cable A1 is induced by the parametric excitation. Figure 16d–f plots the responses of cables A2, B1 and B2, respectively. As can be seen from these figures, the response frequencies of these cables are all 4.8 Hz, but their amplitudes are different, namely, 4.52 mm, 4.29 mm and 3.63 mm, which indicates that the same large amplitude vibrations occur due to parametric excitation. In the following, the different excitation frequencies are considered and investigated. The excitation frequencies, 4.7 Hz and 4.9 Hz, are applied and the responses of the same cable A1 are presented in Fig. 16g and h. From the two figures, we can see that both of the response frequencies are excitation frequencies and their response amplitudes are 4.69 mm and 5.24 mm, respectively. Although the response amplitudes are slightly reduced compared with those shown in Fig. 16c, the large amplitude parametric vibrations of cable A1 are also observed. Therefore, it can be concluded that when the excitation frequency is close to the frequency of global mode of cable-stayed bridge, the primary resonance of the beam and the parametric vibrations of the long cables can be triggered simultaneously, which can lead to the large vibrations of cables and further verifies the previous theoretical results on the parametric vibration of cables [27]. The more attention should be paid to the parametric vibration in the cable-stayed bridge.

Fig. 16
figure 16

The responses of cables and the beam under single frequency excitation

Full size image

5.2 Harmonic resonance of cables

Figure 17a and b illustrates the response of measured point at the mid-span of the cable A5 and the joint point between the cable A5 and the beam, respectively, with excitation frequency of 4.6 Hz. The large vibration of cable A5 is observed from Fig. 17a, and its steady-state response amplitude is up to 1.63 mm, which is quite large and more than 10 times of the excitation amplitude. The power spectrum shows that there exist two frequencies and 9.19 Hz is the dominant one. Actually, 9.19 Hz is exactly twice of the excitation frequency (4.6 Hz) and also very close to the fundamental frequency (9.24 Hz) of the cable A5. However, the response frequency of the joint point between the cable A5 and the beam is 4.59 Hz as shown in Fig. 17b, which is almost the excitation frequency. This indicates that the large amplitude vibration of the cable A5 is not caused by the parametric vibration, but by the superharmonic resonance of the cable A5 due to the fact that the ratio of the excitation frequency to its fundamental frequency is 1:2. Hence, the superharmonic resonances of cables can occur when the ratio of the excitation frequency to the fundamental frequency of the cable is 1:2.

Figure 17c shows the response of the cable A1 at its mid-span with excitation frequency of 11.7 Hz. As can be seen in the figure, the large amplitude of the cable A1 occurs and its response amplitude is up to 1.3 mm, which is nearly 10 times of the excitation amplitude. From the power spectrum, it is seen that there exist two frequencies namely, 11.7  Hz and 5.85 Hz, and the latter is the dominant one. The slight response of cable with 11.7 Hz reflects the slight effect of the bridge deck as a forced excitation on the cable. The large vibration with frequency of 5.85 Hz implies that the subharmonic resonance of the cable A1 occurs due to the parametric excitation, because the ratio of the excitation frequency (11.7 Hz) to the fundamental frequency (5.86 Hz) of the cable A1 is close to 2:1. Figure 17d shows the response of the joint point between the cable A1 and the beam with response frequency of 11.7 Hz and 5.85 Hz, and the former is the dominant one. The response of the joint point with frequency of 11.7 Hz is induced by forced excitation and the slight response with frequency of 5.85 Hz is induced by cable vibration. Therefore, it can be concluded that the subharmonic resonances of cables can be triggered by motion of the beam and the slight influence of cable motion on the beam vibration can also occur due to the interaction between them, which brings about the large amplitude vibration of the cable in the cable-stayed bridge.

Fig. 17
figure 17

The responses of cables and the beam with single frequency excitation

Full size image

5.3 Multiple internal resonance and primary resonance of cables

Figure 18 presents the response of cables and the beam when the excitation frequency and amplitude are 5.4 Hz and 0.14 mm, respectively. Figure 18a plots the response of the beam at the excitation position. It can be seen that there exist only two frequencies, 5.41 Hz and 10.82 Hz. Figure 18b and d shows the responses of the mid-span of cables C1 and D1. It shows that the response amplitudes come up to 1.84 mm and 2.47 mm, nearly 15 times and 18 times of the excitation amplitude, respectively. The power spectrums present that motion of cables consists of three components with different frequencies, namely, 5.41 Hz, 10.82 Hz and 16.22 Hz. It is obvious that the response component with frequency of 5.41 Hz dominates mainly the motion of cables. Figure 18c and e presents the response at the joint points between the cable C1(D1) and the beam. Similarly, 5.4 Hz is the dominant frequency of the responses. There exists simultaneously a response component with frequency of 10.8 Hz in Fig. 18c. As shown in Table 1, the fundamental frequencies of cables C1 and D1 are 5.42 Hz and 5.45 Hz, respectively; hence, when excitation frequencies are close to the fundamental frequencies of cables, their primary resonances are triggered. Additionally, the 10.82 Hz and 16.22 Hz are identified from the responses of cables, which are the frequencies of higher modes of cables, namely, the second and third modes. That means the 1:2 and 1:3 internal resonances between the local modes of cables occur simultaneously. On the other hand, the frequencies of higher modes of cables are also identified in the response of the beam, such as 10.8 Hz, which reveals that cables’ motion can excite the vibration of the beam due to the variation in cable forces. As seen in Fig. 18c and e, the influence of cables’ motion on the vibration of beam is smaller than that of the beam on cables due to the obvious difference between their masses.

Meanwhile, the drift phenomena of responses of cables are observed because their equilibrium positions appear to drift, which indicates that the response components are not simply linear superposition but nonlinear coupling.

Fig. 18
figure 18

The responses of the cables C1 and D1 with excitation frequency of 5.4 Hz

Full size image
Fig. 19
figure 19

The responses of cables C2 and D2 with excitation frequency of 5.4 Hz

Full size image
Fig. 20
figure 20

The vibration time histories corresponding to 5.4  Hz, 10.8 Hz and 16.2 Hz after filtering

Full size image

5.4 Cable–cable coupling vibration

Figure 19a and b shows the responses of the mid-span of the cable C2 and the joint point between the cable C2 and the beam. Figure 19c and d shows the responses of the mid-span of the cable D2 and the joint point between the cable D2 and the beam. It is observed from Fig. 19a that the response amplitude of the cable C2 is up to 1.48 mm, which is more than 10 times of the excitation amplitude. That means the large vibration of the cable C2 is observed. Furthermore, it is noted that there exist three frequencies, namely, 5.41 Hz, 10.82 Hz and 16.22 Hz in the response of the cable C2. The response amplitude of the joint point between its lower end and the beam is 0.32 mm and the corresponding response frequency is 5.4 Hz as shown in Fig. 19b. Similar phenomena to Fig. 19a and b can also be observed in Fig. 19c and d. Comparing with Fig. 18, we can find that the analysis results, such as responses and frequencies, are analogous to those shown in Fig. 19. However, the fundamental frequencies of the cables C2 and D2 are 6.12 Hz and 6.28 Hz, respectively, which are obviously different from the excitation frequency (5.4 Hz). That is, the phenomenon may be induced by other mechanisms, which is different from that obtained in the last section.

In order to explore the reason, the responses of cables in Figs. 18 and 19 are filtered, and the time histories corresponding to 5.41 Hz, 10.82 Hz and 16.22 Hz are shown in Fig. 20. According to the filtered time histories, it can be seen that the corresponding time histories of cables C1, C2, D1 and D2 are similar to one another, that is, the variation trend is almost identical despite there exists a difference in response amplitudes. The other cables, such as A2 and B2, have the fundamental frequency of 6.09 Hz, and their positions in the cable-stayed bridge are analogous to C2 and D2, but the similar behaviors are not excited and observed. This indicates that the responses of C2 and D2 may be affected and caused by the coupling vibrations between adjacent cables, which can be confirmed by the free vibration as illustrated in Sect. 4.

6 Conclusions

In this paper, a detailed scaled model of cable-stayed bridge is established and the modal analysis is carried out based on the experimental and FE models. The results show that they are in good agreement. The beating phenomena in in-plane free vibrations of cables are observed. Then, the experimental model is excited by a single frequency excitation, and the rich nonlinear resonance phenomena are observed, including energy transfer, the parametric vibration, the primary resonance, the harmonic resonance, the 1:2 and 1:3 internal resonance and the coupling resonance. By previous studies of the linear modes and mechanism of nonlinear resonance, some interesting conclusions are drawn as follows:

  1. (1)

    Compared with the OECS model, the modal analysis results of the MECS model are closer to the experimental results, which show that the modal analysis results of the MECS model are more reliable, and that the influence of cables on the vibration of the whole bridge is important.

  2. (2)

    When one cable is given a slight disturbance, the other cables with the close frequency can also be excited to vibrate due to the 1:1 resonance among cables and the beating vibration can be observed in the time histories of cables. The vibration processes may be synchronous or interlaced with each other with energy transfer occurring.

  3. (3)

    When the excitation frequency is close to one of the global frequencies of the bridge, the primary resonance may be triggered and the parametric vibrations of the long cables can be excited, which leads to the large vibration of cables.

  4. (4)

    When the ratio of the excitation frequency to the fundamental frequency of the cable is 1:2 or 2:1, the superharmonic or subharmonic resonance of cables can be excited, which inevitably leads to the large vibration of the corresponding cable.

  5. (5)

    When the excitation frequency is close to the fundamental frequency of the cable, the primary resonance of the cable can also be triggered by parametric excitation namely motion of the beam, and then the multiple internal resonances of 1:2 and 1:3 may be induced separately or simultaneously. At the same time, the primary resonance of the cable may give rise to the coupling vibration between the adjacent cables.

The nonlinear vibration of the cable-stayed bridge can lead to the large vibrations of some cables. Hence, it should be paid more attention to the corresponding theoretical and experimental studies and to the corresponding control method.