1 Introduction

The stability of structural plates is one of the most important design criteria in mechanics, civil, aerospace and marine engineering. During their lifetime, various loads are applied on them to perform in-plane stresses on their edges. In addition to shear stress, the edges may experience compressive or tensile (biaxial) stresses and due to the geometrical and material properties of the plate, inelastic buckling may occur. An analytical procedure may be quite complicated for the solution of the inelastic buckling equation of the plate with diverse boundary conditions and under multiaxial loadings. Thus, an explicit solution should be preferably developed using the theories of plasticity to predict the inelastic buckling load of plates.

In the 1940s, two main plasticity models were applied to describe the inelastic buckling of plates. Ilyushin [1], Stowell [2] and Bijlaard [3] used the deformation (total) theory of plasticity, while Handelman and Prager [4] used the incremental (flow) theory of plasticity. In the deformation theory of plasticity, the total strain is related to the total stress by the secant modulus without any consideration of stress history and then, the surveyed path to get a particular point on the stress–strain curve is not important. As only the secant modulus appears in the stress–strain relations, the hardening is isotropic in this theory. Nevertheless, in the incremental theory of plasticity, the stress at any point and time is a function of the current strain as well as the history of strain. In other words, increments in strain are related to increments of stress by the tangent modulus, leading to a complicated nonlinear stress–strain relation. Applying the variational approach on the stress–strain relations, only the tangent modulus appears in the incremental theory, while both the secant and tangent modulus appear in the deformation theory. Generally, the not very complicated deformation theory relations are comparable with very complicated incremental theory relations for inelastic stress analysis. Although the incremental theory is more general than the deformation theory, the latter can be successfully applied to proportional loading problems in which the components of the stress tensor increase in a constant ratio to each other [5, 6]. In addition, the deformation theory is an acceptable approach for the bifurcation check in the buckling of plates and provides good agreement with measured buckling loads for bars, plates and shells, while the incremental theory predicts much higher than the measured buckling loads [7]. This discrepancy, which is called ‘plastic buckling paradox’ [7], has not been solved generally until recently [8]. One of the oldest problems which directly refers to this ‘paradox’ and reported in the literature is the inelastic stability of cruciform columns [7,8,9,10,11]. Recently, Guarracino and Simonelli [12] showed that the torsional buckling of a cruciform column in the inelastic range is not actually the ‘plastic buckling paradox’ if effects of the imperfections are accurately computed up to the limit load. Their analytical procedure represented very good agreement between flow and deformation theories for this problem. The ‘plastic buckling paradox’ was also tried to solve for circular cylindrical shells under both axial and non-proportional loading [13, 14]. The results of finite element analysis were compared with those of experimental studies and it was shown that the adaptation of flow theory of plasticity with the experimental findings depends on the assumption of initial imperfections and buckling shapes.

Shamass [15] reviewed in detail many aspects which affect on the ‘plastic buckling paradox’. In this review, the considered aspects are the effective shear modulus, initial imperfections, different material constitutive models, transverse shear deformation, deformations in the pre-bifurcation state, actual boundary conditions, sensitivity of the predictions by different plasticity theories and effects of the kinematic constraints used in analytical treatments. It is concluded that the incremental theory does not have any limitation and a number of combined approximations affect the results predicted by the incremental theory.

Generally, the variations of strains and stresses during buckling are used to develop the inelastic buckling equation of plates. In the initial studies of deformation theory of plasticity, the material was supposed to be incompressible in the nonlinear (elastoplastic) region of the stress–strain curve and then, the Poisson’s ratio was always ½ for isotropic materials. As a result, the variation was only being applied on the strains and the secant modulus in the stress–strain relations (Hooke’s law) as seen in the approaches of Ilyushin [1] and Stowell [2]. Pifko and Isakson [16], Bradford and Azhari [17], Ibearugbulem et al. [18, 19], Onwuka et al. [20] and Eziefula et al. [21] applied Stowell’s procedure in their studies. However, in several investigations [22,23,24,25,26,27,28,29,30,31,32,33,34,35], Bijlaard’s formulation [3] was applied in which the Poisson’s ratio appears in the elastic value during inelastic buckling. Gerard and Wildhorn [36] showed that for a nonlinear stress–strain curve such as the Ramberg–Osgood representation [37], the Poisson’s ratio changes from the elastic value to the incompressible value of ½ as the stress is increased above the yield stress,

$$ \nu = \frac{1}{2} - \frac{E_{{\rm sec}}}{E}\left( {\frac{1}{2} - \nu_{{\text{e}}} } \right), $$
(1)

where \(E\) is the Young’s modulus (or the slope of the stress–stain curve at zero stress), \({E}_{{\rm sec}}\) is the secant modulus and \({\nu }_{{\rm e}}\) is the elastic Poisson’s ratio. Using Eq. (1), the variable Poisson’s ratio is considered in the elastoplastic region of the stress–strain curve as well as the other parameters [38,39,40,41,42,43]. Jones [6] successfully applied variation to the Poisson’s ratio and developed the inelastic buckling equation of a plate subjected to biaxial loads, although the obtained equation was only solved for uniaxial loading.

The elastic/inelastic buckling of plates is analytically formulated with a fourth-order linear partial differential equation. In recent decades, several numerical and semi-analytical methods have been proposed to solve this equation with different boundary conditions and mostly uniaxial loading. The most important of these methods are finite element (FE) [16, 44, 45], finite difference [42], finite strip [31], spline finite strip [24], isoparametric spline finite strip [29, 46], complex finite strip [17, 26, 47], finite layer (FL) [48], differential quadrature (DQ) [30, 43], generalized differential quadrature (GDQ) [33,34,35], element-free Galerkin (EFG) [32], funicular polygon (FP) [23], p-Ritz [49, 50], Rayleigh–Ritz [51,52,53], and the virtual work principle [18,19,20,21]. Integral transforms have already been used for solving complex boundary value problems in elastic bending, buckling and vibration of beams. Fourier series were differentiated as many as four times to solve the corresponding ordinary differential equations. In 1944, Green [54] extended the double Fourier series for solving elastic problems of isotropic rectangular plates in which partial differential equations appear. Later, this method was used for the buckling of simply supported orthotropic and isotropic skew plates, subjected to in-plane compressive and shear edge loads [55]. Afterward, double finite integral transform and the corresponding inverstion were analytically used to solve the bending equation of rectangular thin/thick plates with different boundary conditions [56,57,58,59,60]. As the double finite integral transform has some restrictions for complex boundary conditions, it may be modified to the generalized integral transform technique (GITT) which is mathematically more general and also faster convergence. This technique was previously applied in the automatic and accuracy-controlled solution of nonlinear diffusion and convection–diffusion problems as well as the solution of Navier–Stokes equations [61]. In the GITT, an appropriate auxiliary eigenvalue problem is solved to find the kernel of the integral transform. Then, applying the integral transformation to an ordinary/a partial differential equation, it is transformed into infinite algebraic/ordinary differential equations and then, they are truncated at finite terms to allow the computational solution. Alternatively, the double integral transformation can be directly applied to a PDE for obtaining the infinite algebraic equations. For bending, buckling and vibration problems of rectangular plates, kernels of the double integral transform are similar to the vibrating functions of two beams which have the same material properties and boundary conditions of plates in two orthogonal directions. If the original PDE is linear, then the linear algebraic equations are naturally obtained, so that they can be analytically solved for the bending problem and on the other hand, lead to an algebraic eigenvalue problem for buckling/vibration of a plate. Thus, the buckling load/natural frequency is obtained for each mode as well as the corresponding mode shape. An et al. [62] used the GITT as single integral transform, so that the original PDE is transformed into a set of coupled ordinary differential equations. Ullah et al. [63] employed the GITT and solved an eigenvalue problem to obtain the elastic buckling coefficient of uniaxial loaded fully clamped plates (CCCC), plates with three clamped and one edge simply supported (CCCS), and plates with two adjacent edges clamped and the other edges simply supported (CCSS). The GITT has been also applied for the bending solution of orthotropic rectangular thin foundation plates [64] as well as free vibration of orthotropic rectangular plates with free edges [65].

In this study, using the deformation theory of plasticity [6] and applying variations to all mechanical components of an isotropic perfect rectangular plate, the complete equation of inelastic buckling of plates under combined biaxial and shear stresses is developed. The parameters of the Ramberg–Osgood representation are used to find the secant and tangent moduli in the nonlinear region of the stress–strain curve. Then, using the generalized integral transform technique (GITT) [62,63,64,65], the inelastic buckling equation is solved for simply supported (SSSS) and fully clamped (CCCC) plates and the effect of variation of Poisson’s ratio on the inelastic buckling load is compared with those of previous studies. The rectangular plate may be subjected to compressive–compressive–shear (CCS), compressive–tensile–shear (CTS), tensile–compressive–shear (TCS) or tensile–tensile–shear (TTS) loads. A geometrical solution and an algorithm are presented to find the inelastic buckling coefficient of a plate based on the aspect ratio, thickness ratio, load ratios, secant to Young’s modules ratio, elastic Poisson’s ratio and Ramberg–Osgood parameters. Using the obtained results and linear regression technique (linear least squares), a semi-analytical procedure is also suggested to calculate the lowest inelastic buckling coefficient. In this procedure, a qth-order equation must be solved using a trial and error method in which q is the shape parameter of the Ramberg–Osgood representation. The procedure is applicable to practical purposes and can be easily programmed in usual scientific calculators.

2 Analytical approach

2.1 Inelastic buckling equation of a plate

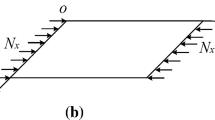
Consider a rectangular plate with dimensions of a × b × t subjected to CCS, CTS, TCS or TTS loads as shown in the Cartesian coordinate system of Fig. 1. In this figure, \(N_{x} = t\sigma_{x}\), \(N_{y} = t\sigma_{y}\) and \(N_{xy} = t\tau\) are the applied loads per unit length on the plate edges in the x-, y- and xy-directions, respectively. Also, \(\sigma_{x}\), \(\sigma_{y}\) and \(\tau\) are the applied stresses in the x-, y- and xy-directions, respectively.

Fig. 1
figure 1

A rectangular plate subjected to a CCS, b CTS, c TCS and d TTS loads

Full size image

In the deformation theory of plasticity, using general nonlinear material properties (\(E_{{\rm sec}}\) and ν), the two-dimensional stress–strain relations are established as shown in Eq. (2). In these relations, \(\varepsilon_{x}\), \(\varepsilon_{y}\) and \(\gamma\) are the strains in the x-, y- and xy-directions, respectively, and ν is obtained from Eq. (1):

$$ \left[ {\begin{array}{l} {\sigma_{x} } \\ {\sigma_{y} } \\ \tau \\ \end{array} } \right] = \frac{E_{{\rm sec}}}{{1 - \nu^{2} }}\left[ {\begin{array}{lll} 1 &\quad \nu &\quad 0 \\ \nu &\quad 1 &\quad 0 \\ 0 &\quad 0 &\quad {\frac{1 - \nu }{2}} \\ \end{array} } \right]\left[ {\begin{array}{l} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ \gamma \\ \end{array} } \right]. $$
(2)

After applying the variations to all components of Eq. (2),

$$ \left[ {\begin{array}{l} {\delta \sigma_{x} } \\ {\delta \sigma_{y} } \\ {\delta \tau } \\ \end{array} } \right] = \frac{E_{{\rm sec}}}{1 - \nu^{2}}\left[ {\begin{array}{lll} {D_{11} } &\quad {D_{12} } &\quad {D_{13} } \\ {D_{12} } &\quad {D_{22} } &\quad {D_{23} } \\ {D_{13} } &\quad {D_{23} } &\quad {D_{33} } \\ \end{array} } \right]\left[ {\begin{array}{l} {\delta \varepsilon_{0x} + z\delta k_{x} } \\ {\delta \varepsilon_{y0} + z\delta k_{y} } \\ {\delta \gamma_{0} + z\delta k_{xy} } \\ \end{array} } \right], $$
(3)

where \(\delta \varepsilon_{0x} { }\), \(\delta \varepsilon_{y0}\) and \(\delta \gamma_{0}\) are the variations of the middle surface strains in the x-, y- and xy-directions, respectively, \(\delta \kappa_{x} = - \frac{\partial^{2} \delta w}{\partial x^{2}}\), \(\delta \kappa_{y} = - \frac{\partial^{2} \delta w}{\partial y^{2}}\) are the variations of the curvatures in the x- and y-directions, respectively, \(\delta \kappa_{xy} = - 2\frac{\partial^{2} \delta w}{\partial x\partial y}\) is the variation of twist, and z is the distance from the middle surface of the plate as shown in Fig. 1. In addition,

$$ D_{11} = 1 - \frac{\overline{K}}{4\left( {1 - \nu^{2} } \right)}\left[ {\left( {2 - \nu } \right)\sigma_{x} - \left( {1 - 2\nu } \right)\sigma_{y} } \right]^{2}, $$
(4)
$$ D_{12} = \nu - \frac{\overline{K}}{4\left( {1 - \nu^{2} } \right)}\left[ {\left( {2 - \nu } \right)\sigma_{x} - \left( {1 - 2\nu } \right)\sigma_{y} } \right]\left[ {\left( {2 - \nu } \right)\sigma_{y} - \left( {1 - 2\nu } \right)\sigma_{x} } \right], $$
$$ D_{13} = - \frac{3\overline{K}\tau}{4\left( {1 + \nu } \right)}\left[ {\left( {2 - \nu } \right)\sigma_{x} - \left( {1 - 2\nu } \right)\sigma_{y} } \right], $$
$$ D_{22} = 1 - \frac{\overline{K}}{4\left( {1 - \nu^{2} } \right)}\left[ {\left( {2 - \nu } \right)\sigma_{y} - \left( {1 - 2\nu } \right)\sigma_{x} } \right]^{2}, $$
$$ D_{23} = - \frac{3\overline{K}\tau}{4\left( {1 + \nu } \right)}\left[ {\left( {2 - \nu } \right)\sigma_{y} - \left( {1 - 2\nu } \right)\sigma_{x} } \right], $$
$$ D_{33} = \frac{1 - \nu }{2}\left[ {1 - \frac{9\overline{K}\tau^{2}}{2\left( {1 + \nu } \right)}} \right]. $$

In Eq. (4), \(\overline{K} = \frac{1}{\sigma_{i}^{2} \overline{H}}\left( {1 - \frac{E_{{\rm tan}}}{E_{{\rm sec}}}} \right),\) where \(\sigma_{i} = \sqrt {\sigma_{x}^{2} - \sigma_{x} \sigma_{y} + \sigma_{y}^{2} + 3\tau^{2} }\) is the stress intensity based on von Mises criteria and \(E_{{\rm tan}}\) is the tangent modulus. Also,

$$ \overline{H} = 1 - \frac{1 - 2{\nu_e} }{{2\left( {1 - \nu^{2} } \right)}}\frac{E_{{\rm sec}}}{E}\left( {1 - \frac{E_{{\rm tan}}}{E_{{\rm sec}}}} \right)\left[ {2\nu - \frac{\left( {1 + 2\nu } \right)\left( {\sigma_{x}^{2} + \sigma_{y}^{2} } \right) - 2\left( {2 + \nu } \right)\sigma_{x} \sigma_{y} + 6\left( {1 + \nu } \right)\tau^{2}}{2\sigma_{i}^{2} }} \right]. $$
(5)

Substituting Eq. (3) into Eq. (6), the moment–curvature relations can be determined:

$$ \left[ {\begin{array}{l} {\delta M_{x} } \\ {\delta M_{y} } \\ {\delta M_{xy} } \\ \end{array} } \right] = \mathop \int \limits_{{ - \frac{t}{2}}}^{\frac{t}{2}} \left[ {\begin{array}{l} {\delta \sigma_{x} } \\ {\delta \sigma_{y} } \\ {\delta \tau } \\ \end{array} } \right]z{\text{d}}z, $$
(6)
$$ \left[ {\begin{array}{l} {\delta M_{x} } \\ {\delta M_{y} } \\ {\delta M_{xy} } \\ \end{array} } \right] = \frac{E_{{\rm sec}} t^{3} }{12\left( {1 - \nu^{2} } \right)}\left[ {\begin{array}{lll} {D_{11} } & {D_{12} } & {D_{13} } \\ {D_{12} } & {D_{22} } & {D_{23} } \\ {D_{13} } & {D_{23} } & {D_{33} } \\ \end{array} } \right]\left[ {\begin{array}{l} {\delta k_{x} } \\ {\delta k_{y} } \\ {\delta k_{xy} } \\ \end{array} } \right]. $$
(7)

Then, substituting Eq. (7) into the equilibrium equation,

$$ \frac{\partial^{2} \left( {\delta M_{x} } \right)}{\partial x^{2}} + \frac{\partial^{2} \left( {\delta M_{xy} } \right)}{\partial x\partial y} + \frac{\partial^{2} \left( {\delta M_{y} } \right)}{\partial y^{2}} = N_{x} \frac{\partial^{2} \left( {\delta w} \right)}{\partial x^{2}} + 2N_{xy} \frac{\partial^{2} \left( {\delta w} \right)}{\partial x\partial y} + N_{y} \frac{\partial^{2} \left( {\delta w} \right)}{\partial y^{2} }, $$

the inelastic buckling equation of the plate is obtained:

$$ \begin{aligned} & D_{11} \frac{\partial^{4} \left( {\delta w} \right)}{\partial x^{4}} + 4D_{13} \frac{\partial^{4} \left( {\delta w} \right)}{\partial x^{3} \partial y} + 2\left( {D_{12} + 2D_{33} } \right)\frac{\partial^{4} \left( {\delta w} \right)}{\partial x^{2} \partial y^{2}} + 4D_{23} \frac{\partial^{4} \left( {\delta w} \right)}{\partial x\partial y^{3}} \hfill \\ &\quad + D_{22} \frac{\partial^{4} \left( {\delta w} \right)}{\partial y^{4}} + \frac{12\left( {1 - \nu^{2} } \right)}{E_{sec} t^{3}}\left[ {N_{x} \frac{\partial^{2} \left( {\delta w} \right)}{\partial x^{2} } + 2N_{xy} \frac{\partial^{2} \left( {\delta w} \right)}{\partial x\partial y} + N_{y} \frac{\partial^{2} \left( {\delta w} \right)}{\partial y^{2}}} \right] = 0. \hfill \\ \end{aligned} $$
(8)

2.2 Generalized integral transform technique (GITT)

When the GITT is used for a two-dimensional boundary value problem, two appropriate auxiliary ODEs must be solved. Here, they are the vibrating beam equations (Eq. (9)) which satisfy the corresponding boundary conditions (Eqs. (10, 11)) and orthogonality (Eqs. (12, 13)) in the x- and y-directions:

$$ \left\{ {\begin{array}{l} {\frac{{\text{d}}^{4} X_{m} \left( x \right)}{{\text{d}}x^{4}} = \alpha_{m}^{4} X_{m} \left( x \right)} \\ {\frac{{\text{d}}^{4} Y_{n} \left( y \right)}{{\text{d}}y^{4}} = \beta_{n}^{4} Y_{n} \left( y \right)} \\ \end{array} } \right. $$
(9)
$$ \left. {\begin{array}{l} {x = 0,\,\,\,a \to \left\{ {\begin{array}{l} {X_{m} \left( x \right) = 0} \\ {\frac{{\text{d}}^{2} X_{m} \left( x \right)}{{\text{d}}x^{2}} = 0} \\ \end{array} } \right.} \\ {y = 0,\,\,\,b \to \left\{ {\begin{array}{l} {Y_{n} \left( y \right) = 0} \\ {\frac{{\text{d}}^{2} Y_{n} \left( y \right)}{{\text{d}}y^{2}} = 0} \\ \end{array} } \right.} \\ \end{array} } \right\};\,\,\,{\rm SS} $$
(10)
$$ \left. {\begin{array}{l} {x = 0,\,\,a \to \left\{ {\begin{array}{l} {X_{m} \left( x \right) = 0} \\ {\frac{{\text{d}}X_{m} \left( x \right)}{{\text{d}}x} = 0} \\ \end{array} } \right.} \\ {y = 0,\,\,b \to \left\{ {\begin{array}{l} {Y_{n} \left( y \right) = 0} \\ {\frac{{\text{d}}Y_{n} \left( y \right)}{{\text{d}}y} = 0} \\ \end{array} } \right.} \\ \end{array} } \right\};\,\,\,{\rm CC} $$
(11)
$$ \left. {\begin{array}{l} {\mathop \int \limits_{0}^{a} X_{m} \left( x \right)X_{r} \left( x \right){\text{d}}x = \left\{ {\begin{array}{l} {\frac{a}{2} ;\,\,\, m = r} \\ {0 ; \,\,\,m \ne r} \\ \end{array} } \right.} \\ {\mathop \int \limits_{0}^{b} Y_{n} \left( y \right)Y_{s} \left( y \right){\text{d}}y = \left\{ {\begin{array}{l} {\frac{b}{2} ;\,\,\, n = s} \\ {0 ;\,\,\,n \ne s} \\ \end{array} } \right.} \\ \end{array} } \right\};\,\,\,{\rm SS} $$
(12)
$$ \left. {\begin{array}{l} {\mathop \int \limits_{0}^{a} X_{m} \left( x \right)X_{r} \left( x \right){\text{d}}x = \left\{ {\begin{array}{l} {a ;\,\,\, m = r} \\ {0 ;\,\,\, m \ne r} \\ \end{array} } \right.} \\ {\mathop \int \limits_{0}^{b} Y_{n} \left( y \right)Y_{s} \left( y \right){\text{d}}y = \left\{ {\begin{array}{l} {b ;\,\,\, n = s} \\ {0 ; \,\,\,n \ne s} \\ \end{array} } \right.} \\ \end{array} } \right\};{\rm CC} $$
(13)

where SS and CC are used for simply supported and clamped beams, respectively, and m, n, r and s are positive integers. Equations (9) are readily solved for the different boundary conditions (Eqs. (10, 11)) to yield the related eigenfunctions which are shown in Eqs. (14) and (15) for SS and CC beams, respectively:

$$ \left\{ {\begin{array}{l} {X_{m} \left( x \right) = \sin \alpha_{m} x} \\ {Y_{n} \left( y \right) = \sin \beta_{n} y} \\ \end{array} } \right. $$
(14)
$$ \left\{ {\begin{array}{l} {X_{m} \left( x \right) = \cosh \alpha_{m} x - \cos \alpha_{m} x - c_{m} \left( {\sinh \alpha_{m} x - \sin \alpha_{m} x} \right)} \\ {Y_{n} \left( y \right) = \cosh \beta_{n} y - \cos \beta_{n} y - c_{n} \left( {\sinh \beta_{n} y - \sin \beta_{n} y} \right)} \\ \end{array} } \right. $$
(15)

where

$$ \left\{ {\begin{array}{l} {c_{m} = \frac{\cosh \alpha_{m} a - \cos \alpha_{m} a}{\sinh \alpha_{m} a - \sin \alpha_{m} a}} \\ {c_{n} = \frac{\cosh \beta_{n} b - \cos \beta_{n} b}{\sinh \beta_{n} b - \sin \beta_{n} b}} \\ \end{array} } \right. $$
(16)

In Eqs. (14) and (15), \(\alpha_{m}\) and \(\beta_{n}\) are the roots of transcendental beam frequency equations:

$$ \left\{ {\begin{array}{l} {\sin \alpha_{m} a \cdot \sinh \alpha_{m} a = 0 \Rightarrow \alpha_{m} a = m\pi } \\ {\sin \beta_{n} b \cdot \sinh \beta_{n} b = 0 \Rightarrow \beta_{n} b = n\pi } \\ \end{array} } \right\};\,\,\,{\rm SSSS} $$
(17)
$$ \left\{ {\begin{array}{l} {\cosh \alpha_{m} a \cdot \cos \alpha_{m} a = 1 \Rightarrow \alpha_{m} a \cong \left[ {\left( {2m + 1} \right)\frac{\pi }{2} + 2\left( { - 1} \right)^{m + 1} {\text{e}}^{{ - \left( {2m + 1} \right)\frac{\pi }{2}}} } \right]} \\ {\cosh \beta_{n} b \cdot \cos \beta_{n} b = 1 \Rightarrow \beta_{n} b \cong \left[ {\left( {2n + 1} \right)\frac{\pi }{2} + 2\left( { - 1} \right)^{n + 1} {\text{e}}^{{ - \left( {2n + 1} \right)\frac{\pi }{2}}} } \right]} \\ \end{array} } \right\};\,\,\,{\rm CCCC} $$
(18)

Using the obtained eigenfunctions in Eqs. (14, 15), the two-dimensional generalized finite integral transform and the corresponding inversion are defined as:

$$ \delta w_{mn} = \mathop \int \limits_{0}^{a} \mathop \int \limits_{0}^{b} \delta w\left( {x,y} \right)X_{m} \left( x \right)Y_{n} \left( y \right){\text{d}}xdy, $$
(19)
$$ \delta w\left( {x,y} \right) = \frac{1}{{\mu \phi b^{2} }}\mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } \delta w_{mn} X_{m} \left( x \right)Y_{n} \left( y \right), $$
(20)

where

$$ \mu = \frac{1}{{\phi b^{2} }}\mathop \int \limits_{0}^{a} X_{m}^{2} \left( x \right){\text{d}}x \cdot \mathop \int \limits_{0}^{b} Y_{n}^{2} \left( y \right){\text{d}}y = \left\{ {\begin{array}{ll} \frac{1}{4} & \quad {{\rm SSSS}} \\ 1 & \quad {{\rm CCCC}} \\ \end{array} } \right. $$
(21)

and \(\phi = \frac{a}{b} \) is the plate aspect ratio.

2.3 Analytical procedure for inelastic buckling

The GITT should be applied to all terms of Eq. (8). Using integration by parts in the successive steps, the fourth- and second-order partial derivatives in Eq. (8) are reduced and finally, \(\delta w\left( {x,y} \right)\) is transformed to \(\delta w_{mn}\) based on Eq. (19). In Eqs. (22)–(29), these transformations are shown with the dimensionless coefficients.

$$ b^{4} \mathop \int \limits_{0}^{a} \mathop \int \limits_{0}^{b} \frac{\partial^{4} \left( {\delta w} \right)}{\partial x^{4}}X_{m} \left( x \right)Y_{n} \left( y \right){\text{d}}xdy = \left( {\frac{\alpha_{m} a}{\phi }} \right)^{4} \delta w_{mn}, $$
(22)
$$ b^{4} \mathop \int \limits_{0}^{a} \mathop \int \limits_{0}^{b} \frac{\partial^{4} \left( {\delta w} \right)}{\partial x^{3} \partial y}X_{m} \left( x \right)Y_{n} \left( y \right){\text{d}}xdy = \frac{1}{{\mu \phi^{3} }}\mathop \sum \limits_{r = 1}^{\infty } \mathop \sum \limits_{s = 1}^{\infty } \delta w_{rs} \left[ {\left( {B_{mr} a^{2} } \right) + \left( {J_{mr} a^{2} } \right)} \right]L_{ns}, $$
(23)
$$ b^{4} \mathop \int \limits_{0}^{a} \mathop \int \limits_{0}^{b} \frac{\partial^{4} \left( {\delta w} \right)}{\partial x^{2} \partial y^{2}}X_{m} \left( x \right)Y_{n} \left( y \right){\text{d}}xdy = \frac{1}{{\mu \phi^{2} }}\mathop \sum \limits_{r = 1}^{\infty } \mathop \sum \limits_{s = 1}^{\infty } \delta w_{rs} \left( {I_{mr} a} \right)\left( {P_{ns} b} \right), $$
(24)
$$ b^{4} \mathop \int \limits_{0}^{a} \mathop \int \limits_{0}^{b} \frac{\partial^{4} \left( {\delta w} \right)}{\partial x\partial y^{3}}X_{m} \left( x \right)Y_{n} \left( y \right){\text{d}}xdy = \frac{1}{\mu \phi }\mathop \sum \limits_{r = 1}^{\infty } \mathop \sum \limits_{s = 1}^{\infty } \delta w_{rs} \left[ {\left( {F_{ns} b^{2} } \right) + \left( {Q_{ns} b^{2} } \right)} \right]H_{mr}, $$
(25)
$$ b^{4} \mathop \int \limits_{0}^{a} \mathop \int \limits_{0}^{b} \frac{\partial^{4} \left( {\delta w} \right)}{\partial y^{4}}X_{m} \left( x \right)Y_{n} \left( y \right){\text{d}}xdy = \left( {\beta_{n} b} \right)^{4} \delta w_{mn}, $$
(26)
$$ b^{2} \mathop \int \limits_{0}^{a} \mathop \int \limits_{0}^{b} \frac{\partial^{2} \left( {\delta w} \right)}{\partial x^{2}}X_{m} \left( x \right)Y_{n} \left( y \right){\text{d}}xdy = \frac{1}{{\mu \phi^{2} }}\mathop \sum \limits_{r = 1}^{\infty } \mathop \sum \limits_{s = 1}^{\infty } \delta w_{rs} \left( {I_{mr} a} \right)\left( {\frac{K_{ns}}{b}} \right), $$
(27)
$$ b^{2} \mathop \int \limits_{0}^{a} \mathop \int \limits_{0}^{b} \frac{\partial^{2} \left( {\delta w} \right)}{\partial x\partial y}X_{m} \left( x \right)Y_{n} \left( y \right){\text{d}}xdy = \frac{1}{\mu \phi }\mathop \sum \limits_{r = 1}^{\infty } \mathop \sum \limits_{s = 1}^{\infty } \delta w_{rs} H_{mr} L_{ns}, $$
(28)
$$ b^{2} \mathop \int \limits_{0}^{a} \mathop \int \limits_{0}^{b} \frac{\partial^{2} \left( {\delta w} \right)}{\partial y^{2}}X_{m} \left( x \right)Y_{n} \left( y \right){\text{d}}xdy = \frac{1}{\mu }\mathop \sum \limits_{r = 1}^{\infty } \mathop \sum \limits_{s = 1}^{\infty } \delta w_{rs} \left( {\frac{G_{mr}}{a}} \right)\left( {P_{ns} b} \right), $$
(29)

with

$$ a^{2} B_{mr} = a^{2} \left( {\left. {\frac{{\text{d}}X_{r}}{\text{d}x}} \right|_{x = a} \cdot \left. {\frac{\text{d}X_{m}}{\text{d}x}} \right|_{x = a} - \left. {\frac{\text{d}X_{r}}{\text{d}x}} \right|_{x = 0} \cdot \left. {\frac{\text{d}X_{m}}{\text{d}x}} \right|_{x = 0} } \right) = \left\{ {\begin{array}{ll} { - \left[ {1 - \left( { - 1} \right)^{m + r} } \right]mr\pi^{2} ;} \hfill & {{\rm SS}} \hfill \\ {0;} \hfill & {{\rm CC}} \hfill \\ \end{array} } \right. $$
(30)
$$ \frac{G_{mr}}{a} = \frac{1}{a}\mathop \int \limits_{0}^{a} X_{r} \left( x \right)X_{m} \left( x \right){\text{d}}x = \left\{ {\begin{array}{ll} {\left\{ {\begin{array}{l} {\frac{1}{2} ; m = r} \\ {0 ; m \ne r} \\ \end{array} } \right\};} \hfill & {{\rm SS}} \hfill \\ {\left\{ {\begin{array}{ll} {1 ; m = r} \\ {0 ; m \ne r} \\ \end{array} } \right\};} \hfill & {{\rm CC}} \hfill \\ \end{array} } \right. $$
(31)
$$ H_{mr} = \mathop \int \limits_{0}^{a} X_{r} \left( x \right)\frac{\text{d}X_{m} \left( x \right)}{\text{d}x}{\text{d}}x = \left\{ {\begin{array}{ll} {\left\{ {\begin{array}{l} {\frac{2mr}{{r^{2} - m^{2} }} ;\quad m \pm r = odd} \\ {0 ;\quad m \pm r = even} \\ \end{array} } \right\};} \hfill & {{\rm SS}} \hfill \\ {\left\{ {\begin{array}{l} {0 ;\quad m = r} \\ {\frac{4\left( {\alpha_{m} a} \right)^{2} \left( {\alpha_{r} a} \right)^{2}}{\left( {\alpha_{r} a} \right)^{4} - \left( {\alpha_{m} a} \right)^{4}}\left[ {1 - \left( { - 1} \right)^{m + r} } \right] ;\quad m \ne r} \\ \end{array} } \right\};} \hfill & {{\rm CC}} \hfill \\ \end{array} } \right. $$
(32)
$$ aI_{mr} = a\mathop \int \limits_{0}^{a} X_{r} \left( x \right)\frac{\text{d}^{2} X_{m} \left( x \right)}{\text{d}x^{2} }{\text{d}}x = \left\{ {\begin{array}{ll} {\left\{ {\begin{array}{l} { - \frac{m^{2} \pi^{2}}{2} ;\quad m = r} \\ {0 ;\quad m \ne r} \\ \end{array} } \right\};} \hfill & {\rm SS} \hfill \\ {\left\{ {\begin{array}{l} {c_{m} \left( {\alpha_{m} a} \right)\left[ {2 - c_{m} \left( {\alpha_{m} a} \right)} \right] ;\quad m = r} \\ {\frac{4\left( {\alpha_{m} a} \right)^{2} \left( {\alpha_{r} a} \right)^{2}}{\left( {\alpha_{m} a} \right)^{4} - \left( {\alpha_{r} a} \right)^{4}}\left[ {c_{m} \left( {\alpha_{m} a} \right) - c_{r} \left( {\alpha_{r} a} \right)} \right]\left[ {1 + \left( { - 1} \right)^{m + r} } \right] ;\quad m \ne r} \\ \end{array} } \right\};} \hfill & {{\rm CC}} \hfill \\ \end{array} } \right. $$
(33)
$$ \begin{aligned} a^{2} J_{mr} & = a^{2} \mathop \int \limits_{0}^{a} X_{r} \left( x \right)\frac{\text{d}^{3} X_{m} \left( x \right)}{\text{d}x^{3}}{\text{d}}x \\ & = \left\{ {\begin{array}{ll} {\left\{ {\begin{array}{l} {\frac{2m^{3} r\pi^{2}}{m^{2} - r^{2}} ;\quad m \pm r = odd} \\ {0 ;\quad m \pm r = even} \\ \end{array} } \right\};} \hfill & {\rm SS} \hfill \\ {\left\{ {\begin{array}{l} {0 ;\quad m = r} \\ {\frac{4\left( {\alpha_{m} a} \right)^{3} \left( {\alpha_{r} a} \right)^{3}}{\left( {\alpha_{m} a} \right)^{4} - \left( {\alpha_{r} a} \right)^{4}}c_{m} c_{r} \left[ {1 - \left( { - 1} \right)^{m + r} } \right] ;\quad m \ne r} \\ \end{array} } \right\};} \hfill & {{\rm CC}} \hfill \\ \end{array} } \right. \\ \end{aligned} $$
(34)
$$ b^{2} F_{ns} = b^{2} \left( {\left. {\frac{\text{d}Y_{s}}{\text{d}y}} \right|_{y = b} \cdot \left. {\frac{\text{d}Y_{n}}{\text{d}y}} \right|_{y = b} - \left. {\frac{\text{d}Y_{s}}{\text{d}y}} \right|_{y = 0} \cdot \left. {\frac{\text{d}Y_{n}}{\text{d}y}} \right|_{y = 0} } \right) = \left\{ {\begin{array}{ll} { - \left[ {1 - \left( { - 1} \right)^{n + s} } \right]ns\pi^{2} ; } \hfill & {\rm SS} \hfill \\ {0;} \hfill & {{\rm CC}} \hfill \\ \end{array} } \right. $$
(35)
$$ \frac{{K_{ns} }}{b} = \frac{1}{b}\mathop \int \limits_{0}^{b} Y_{s} \left( y \right)Y_{n} \left( y \right){\text{d}}y = \left\{ {\begin{array}{ll} {\left\{ {\begin{array}{l} {\frac{1}{2} ;\quad n = s} \\ {0 ;\quad n \ne s} \\ \end{array} } \right\};} \hfill & {\rm SS} \hfill \\ {\left\{ {\begin{array}{l} {1 ;\quad n = s} \\ {0 ;\quad n \ne s} \\ \end{array} } \right\};} \hfill & {{\rm CC}} \hfill \\ \end{array} } \right. $$
(36)
$$ L_{ns} = \mathop \int \limits_{0}^{b} Y_{s} \left( y \right)\frac{\text{d}Y_{n} \left( y \right)}{\text{d}x}{\text{d}}y = \left\{ {\begin{array}{ll} {\left\{ {\begin{array}{l} {\frac{2ns}{{s^{2} - n^{2} }} ;\quad n \pm s = odd} \\ {0 ;\quad n \pm s = even} \\ \end{array} } \right\};} \hfill & {\rm SS} \hfill \\ {\left\{ {\begin{array}{l} {0 ;\quad n = s} \\ {\frac{{4\left( {\beta_{n} b} \right)^{2} \left( {\beta_{s} b} \right)^{2} }}{{\left( {\beta_{s} b} \right)^{4} - \left( {\beta_{n} b} \right)^{4} }}\left[ {1 - \left( { - 1} \right)^{n + s} } \right] ;\quad n \ne s} \\ \end{array} } \right\};} \hfill & {{\rm CC}} \hfill \\ \end{array} } \right. $$
(37)
$$ \begin{aligned} bP_{ns} & = b\mathop \int \limits_{0}^{b} Y_{s} \left( y \right)\frac{\text{d}^{2} Y_{n} \left( y \right)}{\text{d}y^{2}}{\text{d}}y \\ & = \left\{ {\begin{array}{ll} {\left\{ {\begin{array}{ll} { - \frac{{n^{2} \pi^{2} }}{2} ;} \hfill & {n = s} \hfill \\ {0;} \hfill & {n \ne s} \hfill \\ \end{array} } \right\};} \hfill & {\rm SS} \hfill \\ {\left\{ {\begin{array}{ll} {c_{n} \left( {\beta_{n} b} \right)\left[ {2 - c_{n} \left( {\beta_{n} b} \right)} \right] ;} \hfill & {n = s} \hfill \\ {\frac{{4\left( {\beta_{n} b} \right)^{2} \left( {\beta_{s} b} \right)^{2} }}{{\left( {\beta_{n} b} \right)^{4} - \left( {\beta_{s} b} \right)^{4} }}\left[ {c_{n} \left( {\beta_{n} b} \right) - c_{s} \left( {\beta_{s} b} \right)} \right]\left[ {1 + \left( { - 1} \right)^{n + s} } \right] ;} \hfill & {n \ne s} \hfill \\ \end{array} } \right\};} \hfill & {{\rm CC}} \hfill \\ \end{array} } \right. \\ \end{aligned} $$
(38)
$$ b^{2} Q_{ns} = b^{2} \mathop \int \limits_{0}^{b} Y_{s} \left( y \right)\frac{\text{d}^{3} Y_{n} \left( y \right)}{\text{d}y^{3}}{\text{d}}y = \left\{ {\begin{array}{ll} {\left\{ {\begin{array}{ll} {\frac{{2n^{3} s\pi^{2} }}{{n^{2} - s^{2} }}; } \hfill & {n \pm s = {\text{odd}}} \hfill \\ {0;} \hfill & {n \pm s = {\text{even}}} \hfill \\ \end{array} } \right\};} \hfill & {\rm SS} \hfill \\ {\left\{ {\begin{array}{ll} {0;} \hfill & {n = s} \hfill \\ {\frac{{4\left( {\beta_{n} b} \right)^{3} \left( {\beta_{s} b} \right)^{3} }}{{\left( {\beta_{n} b} \right)^{4} - \left( {\beta_{s} b} \right)^{4} }}c_{n} c_{s} \left[ {1 - \left( { - 1} \right)^{n + s} } \right]; } \hfill & {n \ne s} \hfill \\ \end{array} } \right\};} \hfill & {{\rm CC}} \hfill \\ \end{array} } \right. $$
(39)

Applying the GITT into Eq. (8) and using Eqs. (22)–(29), the characteristic equation in dimensionless form is obtained:

$$ \begin{aligned} & \left[ {\left( {\frac{{\alpha_{m} a}}{\phi }} \right)^{4} D_{11} + \left( {\beta_{n} b} \right)^{4} D_{22} } \right]\delta w_{mn} \\ & \quad + \frac{1}{\mu \phi }\mathop \sum \limits_{r = 1}^{\infty } \mathop \sum \limits_{s = 1}^{\infty } \delta w_{rs} \left\{ {\frac{4}{{\phi^{2} }}D_{13} \left[ {\left( {a^{2} B_{mr} } \right) + \left( {a^{2} J_{mr} } \right)} \right]L_{ns} } \right. \\ & \quad + \frac{2}{\phi }\left( {D_{12} + 2D_{33} } \right)\left( {aI_{mr} } \right)\left( {bP_{ns} } \right) + 4D_{23} \left[ {\left( {b^{2} F_{ns} } \right) + \left( {b^{2} Q_{ns} } \right)} \right]H_{mr} \\ & \quad \left. + \frac{{E\left( {1 - \nu^{2} } \right)}}{{E_{{\rm sec}} \left( {1 - \nu_{\rm e}^{2} } \right)}}k_{s} \pi^{2} \left[ {\frac{{\psi_{x} }}{\phi }\left( {aI_{mr} } \right)\left( {\frac{{K_{ns} }}{b}} \right) + 2H_{mr} L_{ns} + \phi \psi_{y} \left( {\frac{{G_{mr} }}{a}} \right)\left( {bP_{ns} } \right)} \right] \right\} = 0, \\ \end{aligned} $$
(40)

where \(\psi_{x} = \frac{{N_{x} }}{{N_{xy} }}\) and \(\psi_{y} = \frac{{N_{y} }}{{N_{xy} }}\) are the load ratios supposing that \(N_{xy} \ne 0\) and \(k_{s} = \frac{{12\left( {1 - \nu_{\rm e}^{2} } \right)}}{{\pi^{2} }}\left( \frac{b}{t} \right)^{2} \frac{{N_{xy} }}{Et}\) is the inelastic buckling coefficient.

Equation (40) establishes an infinite system of linear equations. For a practical calculation, the positive integers m, n, r and s must be limited to an upper value, h. Thus, Eq. (40) can be shown with a finite number of linear equations in matrix form:

$$\left[\begin{array}{l}{M}_{11}^{11}\\ \vdots \\ {M}_{1h}^{11}\\ \vdots \\ {M}_{h1}^{11}\\ \vdots \\ {M}_{hh}^{11}\end{array}\begin{array}{l} \dots \\ \ddots \\ \dots \\ \ddots \\ \dots \\ \ddots \\ \dots \end{array}\begin{array}{l}{M}_{11}^{1h}\\ \vdots \\ {M}_{1h}^{1h}\\ \vdots \\ {M}_{h1}^{1h}\\ \vdots \\ {M}_{hh}^{1h}\end{array}\begin{array}{l} \dots \\ \ddots \\ \dots \\ \ddots \\ \dots \\ \ddots \\ \dots \end{array}\begin{array}{l} {M}_{11}^{h1} \\ \vdots \\ {M}_{1h}^{h1}\\ \vdots \\ {M}_{h1}^{h1}\\ \vdots \\ {M}_{hh}^{h1}\end{array}\begin{array}{l}\dots \\ \ddots \\ \dots \\ \ddots \\ \dots \\ \ddots \\ \dots \end{array}\begin{array}{l}{ M}_{11}^{hh}\\ \vdots \\ {M}_{1h}^{hh}\\ \vdots \\ {M}_{h1}^{hh}\\ \vdots \\ {M}_{hh}^{hh}\end{array}\right]\left[\begin{array}{l}{\delta w}_{11}\\ \vdots \\ {\delta w}_{1h}\\ \vdots \\ {\delta w}_{h1}\\ \vdots \\ {\delta w}_{hh}\end{array}\right]=\left[\begin{array}{l}0\\ \vdots \\ 0\\ \vdots \\ 0\\ \vdots \\ 0\end{array}\right],$$
(41)

where

$$ M_{mn}^{rs} = \left\{ {\begin{array}{ll} {\left( {\frac{{\alpha_{m} a}}{\phi }} \right)^{4} D_{11} + \left( {\beta_{n} b} \right)^{4} D_{22} + T_{mn}^{rs} ;} \hfill & {m = r\,{\text{ and}}\, n = s} \hfill \\ {T_{mn}^{rs} ;} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right. $$
(42)

and

$$ \begin{aligned} T_{mn}^{rs} & = \frac{1}{\mu \phi }\left\{ {\frac{4}{{\phi^{2} }}D_{13} \left[ {\left( {a^{2} B_{mr} } \right) + \left( {a^{2} J_{mr} } \right)} \right]L_{ns} + \frac{2}{\phi }\left( {D_{12} + 2D_{33} } \right)\left( {aI_{mr} } \right)\left( {bP_{ns} } \right)} \right. \\ & \quad + 4D_{23} \left[ {\left( {b^{2} F_{ns} } \right) + \left( {b^{2} Q_{ns} } \right)} \right]H_{mr} \\ & \quad \left. { + \frac{{E\left( {1 - \nu^{2} } \right)}}{{E_{sec} \left( {1 - \nu_{\rm e}^{2} } \right)}}k_{s} \pi^{2} \left[ {\frac{{\psi_{x} }}{\phi }\left( {aI_{mr} } \right)\left( {\frac{{K_{ns} }}{b}} \right) + 2H_{mr} L_{ns} + \phi \psi_{y} \left( {\frac{{G_{mr} }}{a}} \right)\left( {bP_{ns} } \right)} \right]} \right\}. \\ \end{aligned} $$
(43)

Supposing \(\psi_{x}\), \(\psi_{y}\), \(\nu_{\rm e}\), \(\frac{{E_{{\rm sec}} }}{E}\), \(\frac{{E_{{\rm tan}} }}{{E_{{\rm sec}} }}\), \(k_{s}\), \(\phi\) and h in Eq. (41), the eigenvalues of the coefficient matrix can be calculated for SSSS or CCCC plates. If the smallest eigenvalue is zero, the supposed \(k_{s}\) will be the lowest inelastic critical coefficient \(\left( {k_{s,cr}^{\left( 1 \right)} = k_{s} } \right)\). Likewise, if the second, third, …. or ith eigenvalue is zero, the inelastic critical coefficient is obtained for the corresponding mode. Using the general software Python [66] and selecting a few series terms (h) for the arrays of the coefficient matrix in Eq. (41), the inelastic critical coefficient \(\left( {k_{s,cr} } \right)\) can be obtained accurately enough for the different buckling modes. However, the secant and tangent moduli relation obviously affects the inelastic buckling coefficient. For a Ramberg–Osgood stress–strain model, the secant and tangent moduli are defined as [37]:

$$ E_{{\rm sec}} = \frac{E}{{1 + \frac{3}{7}\left( {\frac{{\sigma_{i} }}{{\sigma_{.7E} }}} \right)^{q - 1} }}, $$
(44)
$$ E_{{\rm tan}} = \frac{E}{{1 + \frac{3q}{7}\left( {\frac{{\sigma_{i} }}{{\sigma_{.7E} }}} \right)^{q - 1} }}, $$
(45)

where \({\sigma }_{.7E}\) is the stress at which the line with slope \(0.7E\) intersects the stress–strain curve and q is a shape parameter which describes the curvature of the stress–strain curve. Considering two dimensionless parameters, \(\xi = \frac{{E_{{\rm sec}} }}{E} \le 1\) and \(\eta = \frac{{E_{{\rm tan}} }}{{E_{{\rm sec}} }} \le 1\), Eqs. (44) and (45) may be combined into

$$ \eta = \frac{1}{{q\left( {1 - \xi } \right) + \xi }} $$
(46)

so that all terms of the arrays of the coefficient matrix (Eq. 42) can be expressed by \(\phi ,{\psi }_{x}, {\psi }_{y},\xi ,q,{\nu }_{\rm e}\) and \({k}_{s}\). Then using an implicit function, \({k}_{s}\) can be briefly described as:

$$ k_{s} = f\left( {\phi ,\psi_{x} , \psi_{y} ,\xi ,q,\nu_{\rm e} } \right). $$
(47)

On the other hand, using Eq. (44), \(k_{s}\) can be expressed with an explicit function:

$$ k_{s} = g\left( {\lambda ,\frac{E}{{\sigma_{.7E} }},\psi_{x} , \psi_{y} ,\xi ,q,\nu_{\rm e} } \right) = \frac{{12\left( {1 - \nu_{\rm e}^{2} } \right)\lambda^{2} }}{{\pi^{2} }} \cdot \frac{{\sigma_{.7E} }}{E} \cdot \frac{{\left[ {\frac{7}{3}\left( {\frac{1}{\xi } - 1} \right)} \right]^{{\frac{1}{q - 1}}} }}{{\left( {\psi_{x}^{2} - \psi_{x} \psi_{y} + \psi_{y}^{2} + 3} \right)^{\frac{1}{2}} }}, $$
(48)

where \(\lambda = \frac{b}{t}\) is the plate thickness ratio.

In Eqs. (47) and (48), \(\xi \) is a mutual variable in both \(f\) and \(g\) as well as \({\psi }_{x}, {\psi }_{y}, {\nu }_{\rm e}\) and q. As \(\xi \) is a continuous variable \(\left(0\le \xi \le 1\right)\), both \(f\) and \(g\) can be plotted in the \({k}_{s}-\xi \) plane. The intersection of the two plotted curves gives the inelastic buckling coefficient as well as the corresponding secant modulus. The described geometrical solution may be summarized by an algorithm as shown in Fig. 2. In this algorithm, an initial value of \(\xi \) is assumed (\({\xi }_{ini}\) in Fig. 2). In the next steps, \(\xi \) is increased by \(\delta \xi \) unless \(\xi >1\). Here, \({\xi }_{ini}=\delta \xi =0.025\). In addition, defining a dimensionless parameter, \(\Omega ={\left({\psi }_{x}^{2}-{\psi }_{x}{\psi }_{y}+{\psi }_{y}^{2}+3\right)}^{\frac{1}{2}}\), Eqs. (4) and (5) are briefly rewritten and finally, the coefficients matrix in Eq. (41) is re-established. At the end of the procedure, the \({k}_{s}-\xi \) curve will be found for the corresponding buckling mode based on the known parameters: \(\phi ,{\psi }_{x}, {\psi }_{y},{\nu }_{\rm e}\) and \(q\). In this study, the lowest buckling coefficient is calculated. The procedure can be repeated using the new parameters to find new curves.

Fig. 2
figure 2

An algorithm to plot the \({k}_{s}-\xi \) curve of the plate

Full size image

3 Results and discussion

In this study, the Ramberg–Osgood representation is used for the nonlinear mechanical properties of the material, although this approach can also be developed for the other known models of nonlinear behavior.

3.1 Validation, effects of variation of Poisson’s ratio and number of series terms

In order to verify the analytical approach, four studies are considered. The first one is an experimental study for plastic buckling of simply supported uniaxial compressed plates [67]. In the second study [45], the solution of the ‘plastic buckling paradox’ was sought in the mode of testing which had previously been done in Ref. [67]. The authors applied the incremental theory of plate buckling and involved the boundary stresses introduced by the friction between the plate and the testing machine heads. For the pre-buckling stress analysis, an incremental finite element procedure was performed using ANSYS, so that the load was subdivided into a sequence of small increments. The material properties and dimensions of the plates were the same or similar to those in Ref. [67] as shown in Tables 1 and 2, respectively. The plate was divided into 80 rectangular elements and the boundary conditions were zero force on the two longitudinal edges and zero displacement on the lower edge in both directions. On the upper edge, uniform and zero displacements were applied in the longitudinal and transverse directions, respectively. In the buckling analysis stage, the finite element procedure for plastic plate buckling described in Ref. [16] was generalized to the case of nonuniform pre-buckling stress state. In the third and fourth studies [16, 23], the finite element and funicular polygon methods are employed for plastic buckling of simply supported and fully clamped plates under uniaxial, biaxial or shear loads.

Table 1 Boundary and loading conditions and mechanical properties in the considered studies (1 ksi = 6.895 MPa)
Full size table
Table 2 Comparison of critical uniaxial stresses for SSSS plates
Full size table
Table 3 Comparison of critical shear stresses for CCCC square plates \(\left({k}_{s}^{e}=14.6\right)\)
Full size table

The suggested algorithm (Fig. 2) can be changed for the uniaxial and biaxial loadings and \({N}_{xy}=0\). In these cases, new load ratios are defined as \({\stackrel{-}{\psi }}_{y}=\frac{{N}_{y}}{{N}_{x}}\) and \({\stackrel{-}{\psi }}_{xy}=\frac{{N}_{xy}}{{N}_{x}}\). The arrays of the stiffness matrix (4) and the characteristic equation (40) should be rewritten by the new load ratios. As a result, \({k}_{x}\) will be obtained instead of \({k}_{s}\), and then \({\sigma }_{x,cr}=\frac{{k}_{x}{\pi }^{2}E}{12\left(1-{\nu }_{\rm e}^{2}\right)}{\left(\frac{t}{b}\right)}^{2}\). Table 1 shows the boundary and load conditions and Ramberg–Osgood parameters in the experimental and numerical studies. In this section, the dimensions of parameters are represented by imperial units to match the results found from the literature.

In Tables 2 and 3, the results of the analytical approach (h = 20) are compared with those of the experimental study [67], numerical analysis (ANSYS and FEM) [45] and funicular polygon method [23]. The results show excellent agreement for both uniaxially loaded simply supported and shear loaded fully clamped plates. The maximum differences are less than 4%, 2.6% and 2% for the experimental, FE (ANSYS) and funicular polygon methods, respectively.

In the fourth study [16], a finite element technique is used in conjunction with the Stowell’s theory [2]. Thus, incompressible material is considered (the Poisson’s ratio is 0.5) during inelastic buckling. Here, the analytical approach is applied for two states: initially, the incompressible material is used \(\left(\nu =0.5\right)\) to compare the analytical and numerical methods, and then, it is repeated using variable Poisson’s ratio (Eq. (1)) to compare the results of the two situations. In Tables 4 and 5, the results are shown for the simply supported plates with aspect ratios 1 and 1.5, respectively, which are under uniaxial and biaxial loads. Table 6 shows the results for the fully clamped and simply supported square plates under uniaxial and pure shear loads, respectively. In Tables 4 and 5, there is no difference between the analytical and numerical methods when the incompressible material is supposed, likewise in Table 6, a negligible difference (< 0.5%) is seen.

Table 4 Comparison of critical stresses for SSSS square plates (a = b = 20 in.)
Full size table
Table 5 Comparison of critical stresses for SSSS plates with a = 30 in. and b = 20 in.
Full size table
Table 6 Comparison of critical stresses for square plates (a = b = 20 in.) with different boundary and loading conditions
Full size table

In the last row of each section of Tables 4, 5 and 6, results of the second state are compared. These comparisons show that due to the variation of the Poisson’s ratio, in both uniaxial and shear loadings, the inelastic buckling loads decrease. As expected, increasing λ makes a more slender plate and less plasticity occurs prior to buckling. In Figs. 3, 4 and 5, the differences are obviously shown for the different aspect ratios, thickness ratios, boundary and loading conditions. As seen in these figures, increasing the thickness ratio in all cases, the difference increases up to 18.8%. This upper bound only depends on the elastic Poisson’s ratio and can be analytically expressed as \(\frac{1-4{\nu }_{\rm e}^{2}}{3}\). In addition, increasing the plate aspect ratio, the slope of the difference curve increases and reaches a constant value for \(\phi \ge 1\), \(\phi \ge 4\) and \(\phi \ge 5\) as seen in Figs. 3, 4 and 5, respectively.

Fig. 3
figure 3

Difference of \({\sigma }_{x,cr}\left(\nu =0.5\right)\) and \({\sigma }_{x,cr}\left(\nu <0.5\right)\) for a SSSS square plate under uniaxial load

Full size image
Fig. 4
figure 4

Difference of \({\tau }_{cr}\left(\nu =0.5\right)\) and \({\tau }_{cr}\left(\nu <0.5\right)\) for a SSSS square plate under pure shear load

Full size image
Fig. 5
figure 5

Difference of \({\sigma }_{x,cr}\left(\nu =0.5\right)\) and \({\sigma }_{x,cr}\left(\nu <0.5\right)\) for a CCCC square plate under uniaxial stress

Full size image

The number of series terms (h) directly affects the accuracy of the GITT. Table 7 shows a sensitivity analysis of the inelastic buckling coefficient \(\left({k}_{s}\right)\) with \({\nu }_{\rm e}=0.33\), \(\frac{E}{{\sigma }_{0.7E}}=100\) and q = 10. Considering this table, it can be concluded that for small thickness ratios, \({k}_{s}\) converges with 10–15 terms very well for all aspect ratios, boundary conditions and loading combinations. For larger thickness ratios, 20 terms are usually necessary for the convergence, although in TTS loading more terms may be used for more accuracy. However, 20 terms are used for the considered cases in this study.

Table 7 Convergence of \({k}_{s}\) with different geometrical, boundary and loading conditions
Full size table

3.2 Estimation of the inelastic buckling coefficient

In the proposed geometrical solution, the curves of \({k}_{s}=f\left(\xi ,\phi ,{\psi }_{x}, {\psi }_{y},q,{\nu }_{\rm e}\right)\) and \({k}_{s}=g\left(\xi ,{\psi }_{x}, {\psi }_{y},q,{\nu }_{\rm e},\lambda ,\frac{E}{{\sigma }_{.7E}}\right)\) are intersected in the \({k}_{s}-\xi \) plane to find \({k}_{s}\) as well as the corresponding \(\xi \). Figures 6 and 7 show some interaction curves in which \(f\) and \(g\) are plotted with solid and dashed curves, respectively. In each figure, \(\frac{E}{{\sigma }_{.7E}},{\psi }_{x}, {\psi }_{y},q\) and \({\nu }_{\rm e}\) are constants and \(\phi \) and \(\lambda \) are variables to provide the interaction curves. In addition, the intersections of \(\phi =1\) curves and some \(\lambda \) curves are highlighted which correspond to the shown results in Table 3 and the second section of Table 6, respectively. The comparisons show the adequate accuracy of the geometrical solution.

Fig. 6
figure 6

Interaction curves for fully clamped plates with \({\psi }_{x}=0\) and \({\psi }_{y}=0\)

Full size image
Fig. 7
figure 7

Interaction curves for simply supported plates with \({\psi }_{x}=0\) and \({\psi }_{y}=0\)

Full size image

In addition to the geometrical solution, a semi-analytical approach may be supposed to simplify the calculation of the inelastic buckling coefficient. The depicted figures in Appendix 1 show that the variation of \(f\) with constant values of \({\nu }_{\rm e}\), \({\psi }_{x}\), \({\psi }_{y}\), \(\phi \) and \(q\) may be estimated by linear or bilinear curves in the \({k}_{s}-\xi \) plane. Equation (49) shows the general form of bilinear (or linear, if \(C=0\) and \({S}_{1}={S}_{2}\)) description of \({k}_{s}\). If the correlation coefficient of the linear approximation \(R<0.999\), then the bilinear curve is considered for the estimation.

$${k}_{s}=\left\{\begin{array}{l}{S}_{1}\xi ; \quad \xi \le \stackrel{-}{\xi },\\ {S}_{2}\xi +C ; \quad \xi >\stackrel{-}{\xi },\end{array}\right.$$
(49)

where \(\stackrel{-}{\xi }=\frac{C}{{S}_{1}-{S}_{2}}\). The depicted figures in Appendix 2 show that \({S}_{1}\), \({S}_{2}\) and \(C\) with a constant value of \({\nu }_{\rm e}\), \({\psi }_{x}\), \({\psi }_{y}\), \(\phi \) may be estimated by linear curves in the \({S}_{1}-\mathrm{ln}q\), \({S}_{2}-\mathrm{ln}q\) and \(C-\mathrm{ln}q\) planes, respectively. Thus,

$$\left[\begin{array}{l}{S}_{1}\\ {S}_{2}\\ C\end{array}\right]=\left[\begin{array}{l}{s}_{11}\\ {s}_{21}\\ {c}_{1}\end{array}\begin{array}{l}{s}_{12}\\ {s}_{22}\\ {c}_{2}\end{array}\right]\left[\begin{array}{l}\mathrm{ln}q\\ 1\end{array}\right],$$
(50)

where \({s}_{11}\), \({s}_{12}\), \({s}_{21}\), \({s}_{22}\), \({c}_{1}\) and \({c}_{2}\) are numerically presented in Tables 8 and 9 for SSSS and CCCC plates, respectively. The method of linear least squares (LLS) is applied in two stages on the results with \(\phi =1, 1.5, 2, 4\), \({\psi }_{x}\), \({\psi }_{y}=-1, -0.5, 0, 0.5, 1\), \(q=2, 3, 5, 10, 15, 20\) and \({\nu }_{\rm e}=0.33\) to find \({S}_{1}\), \({S}_{2}\) and \(C\) as well as \({s}_{ij} \left(i,j=1, 2\right)\) and \({c}_{i} \left(i=1, 2\right)\). If \({\psi }_{x}={\psi }_{y}=-1\), then no shear buckling occurs in the plate, and this case is naturally eliminated. In Tables 8 and 9, \(\stackrel{-}{q}\) is the smallest integer of \(q\), so that \(R<0.999\). Therefore, if \(q<\stackrel{-}{q}\) (i.e., \(R\ge 0.999\)), then the linear approximation must be considered and vice versa.

Substituting Eq. (49) into Eq. (48), qth-order equations will be obtained (Eq. (51)) which can be solved by a trial and error method and usual scientific calculators. It can be shown that each of them always has a positive root which is the acceptable \({k}_{s},\)

$$ \left\{ {\begin{array}{ll} {k_{s}^{q} + A^{q - 1} k_{s} - A^{q - 1} S_{1} = 0 ;} \hfill & {A \le \overline{A}}, \hfill \\ {k_{s}^{q} - Ck_{s}^{q - 1} + A^{q - 1} k_{s} - A^{q - 1} \left( {S_{2} + C} \right) = 0 ;} \hfill & {A > \overline{A}}, \hfill \\ \end{array} } \right. $$
(51)

where

$$A=\frac{12\left(1-{\nu }_{\rm e}^{2}\right){\lambda }^{2}}{{\pi }^{2}\Omega }\bullet \frac{{\sigma }_{.7E}}{E}{\left(\frac{7}{3}\right)}^{\frac{1}{q-1}}$$
(52)

and

$$\stackrel{-}{A}={S}_{1}{\left(\frac{{\stackrel{-}{\xi }}^{q}}{1-\stackrel{-}{\xi }}\right)}^{\frac{1}{q-1}}.$$
(53)

The semi-analytical approach can be summarized by a step-by-step procedure as follows:

  1. 1.

    Select \({s}_{ij} \left(i,j=1, 2\right)\), \({c}_{i} \left(i=1, 2\right)\) and \(\stackrel{-}{q}\) from Tables 8 and 9 according to the boundary conditions and \({\nu }_{\rm e}\), \({\psi }_{x}\), \({\psi }_{y}\) and \(\phi \). In this study, the fundamental parameters \(\left({s}_{ij} \& {c}_{i}\right)\) are obtained for SSSS and CCCC plates with \({\nu }_{\rm e}=0.33\), \(\phi =1, 1.5, 2 \& 4\) and \({\psi }_{x},{\psi }_{y}=-1, -0.5, 0, 0.5 \& 1\) except \({\psi }_{x}={\psi }_{y}=-1\). It is evident that the fundamental parameters can also be found for the other states.

  2. 2.

    If \(q<\stackrel{-}{q}\), then

    1. 2.1

      using the first equation of Eqs. (50), \({S}_{1}\) is calculated.

    2. 2.2

      using Eq. (52), \(A\) is calculated by the known parameters: \(\frac{E}{{\sigma }_{.7E}}\), \(\Omega \), \(\lambda \), \({\nu }_{\rm e}\) and \(q\).

    3. 2.3

      using the first equation of Eqs. (51), \({k}_{s}\) is calculated by trial and error.

  3. 3.

    If \(q\ge \stackrel{-}{q}\), then

    1. 3.1

      \(S_{1}\), \(S_{2}\) and \(C\) are calculated using Eq. (50) and then \(\stackrel{-}{\xi }=\frac{C}{{S}_{1}-{S}_{2}}\).

    2. 3.2

      Using Eqs. (52) and (53), \(A\) and \(\stackrel{-}{A}\) are calculated, respectively, by the known parameters: \(\frac{E}{{\sigma }_{.7E}}\), \(\Omega \), \(\lambda \), \({\nu }_{\rm e}\) and \(q\).

    3. 3.3

      If \(A\le \stackrel{-}{A}\), then the first equation of Eqs. (51) is solved and \({k}_{s}\) is calculated by trial and errors.

    4. 3.4

      If \(A>\stackrel{-}{A}\), then the second equation of Eqs. (51) is solved and \({k}_{s}\) is calculated by trial and error.

Table 8 Fundamental parameters for SSSS plates with \({\nu }_{\rm e}=0.33\)
Full size table
Table 9 Fundamental parameters for CCCC plates with \({\nu }_{\rm e}=0.33\)
Full size table

Note that if \(q=2\) or \(q=3\), Eq. (51) has explicit solutions.

The shown examples in Table 3 and the second section of Table 6 are resolved using the suggested step-by-step procedure. Table 10 shows the obtained results for which the differences are less than 3%. In this table, for CCCC and SSSS plates, \(\xi >0.8\) and \(\xi >0.6\) are shown in Figs. 6 and 7, respectively. The semi-analytical method is also applied for SSSS and CCCC plates with four aspect ratios and load ratios (TTS, CTS, TCS and CCS) as shown in Tables 11 and 12, respectively. In these examples, the required Ramberg–Osgood parameters are \(q=10\) and \(\frac{E}{{\sigma }_{.7E}}=100\). For each aspect ratio in SSSS and CCCC plates, a maximum of four thickness ratios \(\left({\lambda }_{i},i=1, 2, 3, 4\right)\) are selected provided that \({\lambda }_{i}=5\left(j+1\right); j=1, 2, 3,\dots \) and:

  • \({\lambda }_{1}\) is the last \(\lambda \) where \({\xi }_{1}\le 0.2\), otherwise is the first \(\lambda \) where \(0.2\le {\xi }_{1}\le 0.3\).

  • \({\lambda }_{2}\) is the first \(\lambda \) where \(0.3\le {\xi }_{2}\le 0.5\).

  • \({\lambda }_{3}\) is the first \(\lambda \) where \(0.6\le {\xi }_{3}\le 0.8\).

  • \({\lambda }_{4}\) is the first \(\lambda \) where \(0.9\le {\xi }_{4}\le 1\).

Table 10 Estimation of \({k}_{s}\) for the shown examples in Table 3 and the second section of Table 6 (\(\phi =1\) and \({\psi }_{x}={\psi }_{y}=0\))
Full size table
Table 11 Estimation of \({k}_{s}\) for SSSS plates with \(q=10\) and \(\frac{E}{{\sigma }_{.7E}}=100\)
Full size table
Table 12 Estimation of \({k}_{s}\) for CCCC plates with \(q=10\) and \(\frac{E}{{\sigma }_{.7E}}=100\)
Full size table

Tables 11 and 12 show that the difference between two methods are less than 12% for all examples. For each loading state, the maximum difference (M.D.) appears as follows:

  • TTS loading: 10% < M.D. < 12% where \(0.1\le \xi \le 0.2\) for all plates.

  • CTS loading: 5% < M.D. < 7% where \(0.1\le \xi \le 0.2\) for SSSS plates and 5% < M.D. < 8% where \(0.1\le \xi \le 0.2\) for CCCC plates.

  • TCS loading: 7% < M.D. < 11% where \(0.1\le \xi \le 0.3\) for SSSS plates and 8% < M.D. < 10% where \(0.1\le \xi \le 0.2\) for CCCC plates.

  • CCS loading: 2% < M.D. < 10% where \(0.4\le \xi \le 0.7\) for SSSS plates and 8% < M.D. < 10% where \(0.2\le \xi \le 0.3\) for CCCC plates.

In addition, the results show that increasing the thickness ratio in each aspect ratio, the differences are usually decreased. As a result, the semi-analytical method has better accuracy for \(\lambda >70\) in TTS loading and \(\lambda >20\) in CTS, TCS and CCS loadings. Of course, if \(\frac{E}{{\sigma }_{.7E}}\), \(q\), \({\psi }_{x}\) and \({\psi }_{y}\) are changed, the differences may vary slowly.

4 Conclusion

An analytical approach is presented to obtain the inelastic buckling coefficient of simply supported and fully clamped rectangular plates subjected to combined biaxial (both compressive and tensile) and shear loads. The deformation theory of plasticity, variations to all mechanical properties of plate, the generalized integral transform technique (GITT) and eigenvalue solution are applied in the different sequences to obtain the inelastic buckling coefficient of plate. The Ramberg–Osgood parameters are used to describe the nonlinear stress–strain behavior of material, although the solution can be generalized for the other nonlinear behaviors. Then, applying the method of linear least squares (LLS) on the obtained results, a semi-analytical solution is also proposed. An approximate polynomial equation is obtained and solved by trial and error method to simplify the calculation of the inelastic buckling coefficient. The proposed semi-analytical solution is simple and applicable for the practical purposes. The calculated results show that good accuracy may be obtained for all loading cases, so that the maximum difference (< 12%) is seen in tensile–tensile–shear loading state; nevertheless, increasing thickness ratio of plate, the accuracy increases.