New analytic buckling solutions of moderately thick clamped rectangular plates by a straightforward finite integral transform method

Abstract

A first endeavor is made in this paper to explore new analytic buckling solutions of moderately thick rectangular plates by a straightforward double finite integral transform method, with focus on typical non-Lévy-type fully clamped plates that are not easy to solve in a rigorous way by the other analytic methods. Solving the governing higher-order partial differential equations with prescribed boundary conditions is elegantly reduced to processing four sets of simultaneous linear equations, the existence of nonzero solutions of which determines the buckling loads and associated mode shapes. Both numerical and graphical results confirm the validity and accuracy of the developed method and solutions by favorable comparison with the literature and finite element analysis. The succinct but effective technique presented in this study can provide an easy-to-implement theoretical tool to seek more analytic solutions of complex boundary value problems.

1 Introduction

The buckling analysis of moderately thick plates is an important research topic owing to its broad applications in numerous engineering fields such as civil, mechanical, marine and aerospace engineering. Representative practical examples include rigid pavements, aircraft wings, wallboards of the launch vehicles, etc., where the load carrying plate structures must endure enough compressive forces such that buckling of the structures, which may cause premature failure, is avoided. Obviously, predicting the buckling loads of such structures is indispensable for both the structural design and safety evaluation. To conduct the buckling analysis of plates, a series of theories have been developed, among which the classical plate theory (CPT) [1] is the simplest one that is usually used for thin plates by ignoring through-thickness shear effect. However, for moderately thick plates, the CPT underestimates deflections and overestimates buckling loads and natural frequencies. In order to overcome the limitations of the CPT, Reissner [2] and Mindlin [3] proposed the most commonly used shear deformation plate theories, both of which take the effect of transverse shear deformation into account. With the shear deformation theories, many studies have been reported to investigate the bending, vibration and buckling behavior of thick plates with different combinations of boundary constraints, loading conditions and material properties [4,5,6,7].

Some recent publications are reviewed here to reveal recent progresses in the field. Ghannadpour et al. [8] used an exact finite strip for the buckling and post-buckling analysis of thick plates; the strip was assumed to be simply supported at the loaded ends. Jafari and Azhari [9] presented a simple hp-cloud meshless method for the stability analysis of thick plates with various shapes. Civalek [10] applied an effective discrete singular convolution method for the three-dimensional static, buckling and vibration analyses of thick rectangular plates with clamped and simply supported boundary conditions. Bui et al. [11] proposed an elegant robust meshfree moving Kriging interpolation method incorporating the shear-locking elimination technique for buckling analysis of thick plates. Bodaghi and Saidi [12] formulated a successful accurate thermal buckling analysis of Lévy-type thick functionally graded rectangular plates by decoupling the stability equations into two independent ones. Nazarimofrad et al. [13] successfully analyzed the buckling of a Lévy-type rotationally restrained orthotropic rectangular thick plate resting on a Pasternak elastic foundation by the Rayleigh–Ritz method. Yiotis and Katsikadelis [14] developed a straightforward meshless analog equation method for buckling analysis of thick plates resting on Pasternak-type elastic foundation. Recently, Li et al. [15,16,17] developed a novel symplectic superposition method for bending, buckling and free vibration of rectangular plates under different boundary conditions, which was a combination of the superposition method and symplectic elasticity approach developed by Yao et al. [18], Lim et al. [19], Lim [20] and Lim and Xu [21].

While many important achievements have been made, the research on plate buckling problems is still prosperous. One of the major concerns is on seeking new succinct but effective analytic techniques to solve some difficult plate buckling problems. In this context, a straightforward finite integral transform method has been developed in recent years by Li et al. [22], Tian et al. [23], and Zhang et al. [24] for bending of clamped thin plates and free thick plates as well as vibration of rotationally restrained thin plates. The method has also been adopted by Nwoji et al. [25] and Mama et al. [26] for bending and buckling of simply supported thin plates. The main advantage of the method is that it offers a simple general approach to handling a class of complex boundary value problems (BVPs) of higher-order partial differential equations (PDEs) represented by the plate problems, which provides an easy-to-implement tool for exploring more analytic solutions. However, there have been no reports on the use of the finite integral transform method for buckling analysis of thick plates, as far as the authors know.

This study presents a first endeavor to extend the double finite integral transform method to analytically solving the buckling problems of rectangular Mindlin plates, with focus on typical non-Lévy-type fully clamped plates that are not easy to solve in a rigorous way by the other analytic methods. Via the integral transform, solving the PDEs governing the bucking of a thick plate reduces to solving a system of linear algebraic equations. The analytic buckling load solutions are then readily determined by the existence of nonzero solutions of the system of equations. The analytic mode shape solutions can be further obtained. The numerical examples for the plates with different thickness-to-width and length-to-width ratios subjected to both uniaxial and biaxial compressive loads are given as the benchmark results, whose validity is well confirmed by satisfactory agreement with available solutions as well as the refined finite element analysis (FEA). Good convergence of the present solutions is also shown by the numerical results obtained by taking different numbers of series terms.

2 Governing equations and finite integral transform solutions for the buckling of Mindlin plates

2.1 Governing equations

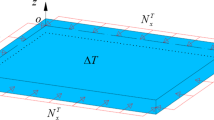
Figure 1 illustrates a moderately thick rectangular plate in the xoy coordinate system, with a and b being the length and width of the plate in the x and y directions, and h the plate thickness in the z direction. According to Mindlin’s first-order shear deformation theory, the governing buckling equations of the plate can be expressed as [27]

$$\begin{aligned}&\frac{\partial ^{2}W}{\partial x^{2}}+\frac{\partial ^{2}W}{\partial y^{2}}-\frac{\partial \varphi _x }{\partial x}-\frac{\partial \varphi _y }{\partial y}+\frac{N_x }{C}\frac{\partial ^{2}W}{\partial x^{2}}+\frac{N_y }{C}\frac{\partial ^{2}W}{\partial y^{2}}=0 \nonumber \\&\frac{\partial ^{2}\varphi _x }{\partial x^{2}}+\frac{1-\mu }{2}\frac{\partial ^{2}\varphi _x }{\partial y^{2}}+\frac{1+\mu }{2}\frac{\partial ^{2}\varphi _y }{\partial x\partial y}+\frac{C}{D}\left( {\frac{\partial W}{\partial x}-\varphi _x } \right) =0 \nonumber \\&\frac{\partial ^{2}\varphi _y }{\partial y^{2}}+\frac{1-\mu }{2}\frac{\partial ^{2}\varphi _y }{\partial x^{2}}+\frac{1+\mu }{2}\frac{\partial ^{2}\varphi _x }{\partial x\partial y}+\frac{C}{D}\left( \frac{\partial W}{\partial y}-\varphi _y \right) =0 \end{aligned}$$

(1)

where W is the transverse deflection of the plate, $\varphi _x$ and $\varphi _y$ are the rotations of the normal to the mid-surface about the y and x coordinates, $N_x$ and $N_y$ are the in-plane edge loads per unit length along the x and y coordinates; $C=sGh$ is the shear stiffness, with s being the shear correction factor (= 5/6 in this study), G the shear modulus satisfying $G=E/{\left[ {2\left( {1+\mu } \right) } \right] }$ in which E is the Young’s modulus and $\mu$ the Poisson’s ratio; $D={Eh^{3}}/{\left[ {12\left( {1-\mu ^{2}} \right) } \right] }$ is the flexural stiffness.

Fig. 1

Schematic illustrations of a a clamped Mindlin Plate, b the plate under uniaxial in-plane compression in the x direction, and c the plate under biaxial compression in both the x and y directions

For a fully clamped plate under consideration, all the displacements are restricted at each edge. Therefore, the following boundary conditions hold: $W |_{x=0,a} =0$, ${\varphi _x }|_{x=0,a} =0$, ${\varphi _y } |_{x=0,a} =0$, and $W |_{y=0,b} =0$, ${\varphi _x } |_{y=0,b} =0$, ${\varphi _y } |_{y=0,b} =0$.

2.2 Finite integral transform

In order to solve Eq. (1), the double finite integral transforms are defined in “Appendix A” for W, $\varphi _x$ and $\varphi _y$. The inversion gives

$$\begin{aligned} W\left( {x,y} \right)= & {} \frac{4}{ab}\sum _{m=1}^\infty {\sum _{n=1}^\infty {W^{\hbox {ss}}} } \sin \left( {\alpha _m x} \right) \sin \left( {\beta _n y} \right) \nonumber \\ \varphi _x \left( {x,y} \right)= & {} \frac{2}{ab}\sum _{m=0}^\infty { \sum _{n=1}^\infty {\varepsilon _m \varphi _x^{\mathrm{cs}} } } \cos \left( {\alpha _m x} \right) \sin \left( {\beta _n y} \right) \nonumber \\ \varphi _y \left( {x,y} \right)= & {} \frac{2}{ab}\sum _{m=1}^\infty {\sum _{n=0}^\infty {\varepsilon _m \varphi _y^{\mathrm{sc}} } } \sin \left( {\alpha _m x} \right) \cos \left( {\beta _n y} \right) \end{aligned}$$

(2)

where $\alpha _m ={m\pi }/a$, $\beta _n ={n\pi }/b$, and $\varepsilon _m \left( {\varepsilon _n } \right) =\left\{ {\begin{array}{l} 1\hbox { for }\;m\left( n \right) =0 \\ 2\hbox { for }\;m\left( n \right) =1,\;2,\ldots \\ \end{array}} \right.$; the superscripts “SS”, “CS” and “SC” represent the double sine, cosine-sine and sine-cosine integral transforms with respect to variables x and y.

Applying the integral transforms to each term of Eq. (1), the following relationships are derived in sequence:

$$\begin{aligned} \mathop \int \limits _0^a {\mathop \int \limits _0^b {\frac{\partial ^{2}W}{\partial x^{2}}} } \sin \left( {\alpha _m x} \right) \sin \left( {\beta _n y} \right) \hbox {d}x\hbox {d}y= & {} -\alpha _m^2 W^{\hbox {ss}}-\alpha _m \mathop \int \limits _0^b {\left[ {\left( {-1} \right) ^{m}\left. W \right| _{x=a} -\left. W \right| _{x=0} } \right] } \sin \left( {\beta _n y} \right) \hbox {d}y \nonumber \\ \mathop \int \limits _0^a {\mathop \int \limits _0^b {\frac{\partial ^{2}W}{\partial y^{2}}} } \sin \left( {\alpha _m x} \right) \sin \left( {\beta _n y} \right) \hbox {d}x\hbox {d}y= & {} -\beta _n^2 W^{\hbox {ss}}-\beta _n \mathop \int \limits _0^a {\left[ {\left( {-1} \right) ^{n}\left. W \right| _{y=b} -\left. W \right| _{y=0} } \right] } \sin \left( {\alpha _m x} \right) \hbox {d}x \nonumber \\ \mathop \int \limits _0^a {\mathop \int \limits _0^b {\frac{\partial \varphi _x }{\partial x}} } \sin \left( {\alpha _m x} \right) \sin \left( {\beta _n y} \right) \hbox {d}x\hbox {d}y= & {} -\alpha _m \varphi _x^{\hbox {cs}} \nonumber \\ \mathop \int \limits _0^a {\mathop \int \limits _0^b {\frac{\partial \varphi _y }{\partial y}} } \sin \left( {\alpha _m x} \right) \sin \left( {\beta _n y} \right) \hbox {d}x\hbox {d}y= & {} -\beta _n \varphi _y^{\hbox {sc}} \nonumber \\ \mathop \int \limits _0^a {\mathop \int \limits _0^b {\frac{\partial ^{2}\varphi _x }{\partial x^{2}}} } \cos \left( {\alpha _m x} \right) \sin \left( {\beta _n y} \right) \hbox {d}x\hbox {d}y= & {} -\alpha _m^2 \varphi _x^{\hbox {cs}} +\mathop \int \limits _0^b {\left[ {\left( {-1} \right) ^{m}\left. {\frac{\partial \varphi _x }{\partial x}} \right| _{x=a} -\left. {\frac{\partial \varphi _x }{\partial x}} \right| _{x=0} } \right] } \sin \left( {\beta _n y} \right) \hbox {d}y \nonumber \\ \mathop \int \limits _0^a {\mathop \int \limits _0^b {\frac{\partial ^{2}\varphi _x }{\partial y^{2}}} } \cos \left( {\alpha _m x} \right) \sin \left( {\beta _n y} \right) \hbox {d}x\hbox {d}y= & {} -\beta _n^2 \varphi _x^{\hbox {cs}} -\beta _n \mathop \int \limits _0^a {\left[ {\left( {-1} \right) ^{n}\left. {\varphi _x } \right| _{y=b} -\left. {\varphi _x } \right| _{y=0} } \right] } \cos \left( {\alpha _m x} \right) \hbox {d}x \nonumber \\ \mathop \int \limits _0^a {\mathop \int \limits _0^b {\frac{\partial ^{2}\varphi _y }{\partial x\partial y}} } \cos \left( {\alpha _m x} \right) \sin \left( {\beta _n y} \right) \hbox {d}x\hbox {d}y= & {} -\alpha _m \beta _n \varphi _y^{\hbox {sc}} -\beta _n \mathop \int \limits _0^b {\left[ {\left( {-1} \right) ^{m}\left. {\varphi _y } \right| _{x=a} -\left. {\varphi _y } \right| _{x=0} } \right] } \cos \left( {\beta _n y} \right) \hbox {d}y \nonumber \\ \mathop \int \limits _0^a {\mathop \int \limits _0^b {\frac{\partial W}{\partial x}} } \cos \left( {\alpha _m x} \right) \sin \left( {\beta _n y} \right) \hbox {d}x\hbox {d}y= & {} \alpha _m W^{\hbox {ss}}+\mathop \int \limits _0^b {\left[ {\left( {-1} \right) ^{m}\left. W \right| _{x=a} -\left. W \right| _{x=0} } \right] } \sin \left( {\beta _n y} \right) \hbox {d}y \nonumber \\ \mathop \int \limits _0^a {\mathop \int \limits _0^b {\frac{\partial ^{2}\varphi _y }{\partial y^{2}}} } \sin \left( {\alpha _m x} \right) \cos \left( {\beta _n y} \right) \hbox {d}x\hbox {d}y= & {} -\beta _n^2 \varphi _y^{\hbox {sc}} +\mathop \int \limits _0^a {\left[ {\left( {-1} \right) ^{n}\left. {\frac{\partial \varphi _y }{\partial y}} \right| _{y=b} -\left. {\frac{\partial \varphi _y }{\partial y}} \right| _{y=0} } \right] } \sin \left( {\alpha _m x} \right) \hbox {d}x \nonumber \\ \mathop \int \limits _0^a {\mathop \int \limits _0^b {\frac{\partial ^{2}\varphi _y }{\partial x^{2}}} } \sin \left( {\alpha _m x} \right) \cos \left( {\beta _n y} \right) \hbox {d}x\hbox {d}y= & {} -\alpha _m^2 \varphi _y^{\hbox {sc}} -\alpha _m \mathop \int \limits _0^b {\left[ {\left( {-1} \right) ^{m}\left. {\varphi _y } \right| _{x=a} -\left. {\varphi _y } \right| _{x=0} } \right] } \cos \left( {\beta _n y} \right) \hbox {d}y \nonumber \\ \mathop \int \limits _0^a {\mathop \int \limits _0^b {\frac{\partial ^{2}\varphi _x }{\partial x\partial y}} } \sin \left( {\alpha _m x} \right) \cos \left( {\beta _n y} \right) \hbox {d}x\hbox {d}y= & {} -\alpha _m \beta _n \varphi _x^{\hbox {cs}} -\alpha _m \mathop \int \limits _0^a {\left[ {\left( {-1} \right) ^{n}\left. {\varphi _x } \right| _{y=b} -\left. {\varphi _x } \right| _{y=0} } \right] } \cos \left( {\alpha _m x} \right) \hbox {d}x \nonumber \\ \mathop \int \limits _0^a {\mathop \int \limits _0^b {\frac{\partial W}{\partial y}} } \sin \left( {\alpha _m x} \right) \cos \left( {\beta _n y} \right) \hbox {d}x\hbox {d}y= & {} \beta _n W^{\hbox {ss}}+\mathop \int \limits _0^a {\left[ {\left( {-1} \right) ^{n}\left. W \right| _{y=b} -\left. W \right| _{y=0} } \right] } \sin \left( {\alpha _m x} \right) \hbox {d}x \end{aligned}$$

(3)

Using Eq. (3), the integral transform of Eq. (1) yields

$$\begin{aligned}&\alpha _m^2 W^{\hbox {ss}}+\beta _n^2 W^{\hbox {ss}}-\alpha _m \varphi _x^{\hbox {cs}} -\beta _n \varphi _y^{\hbox {sc}} \nonumber \\&\quad +\,\alpha _m \mathop \int \limits _0^b {\left[ {\left( {-1} \right) ^{m}\left. W \right| _{x=a} -\left. W \right| _{x=0} } \right] } \sin \left( {\beta _n y} \right) \hbox {d}y \nonumber \\&\quad +\,\beta _n \mathop \int \limits _0^a {\left[ {\left( {-1} \right) ^{n}\left. W \right| _{y=b} -\left. W \right| _{y=0} } \right] } \sin \left( {\alpha _m x} \right) \hbox {d}x \nonumber \\&\quad +\,\frac{N_x }{C}\left\{ {\alpha _m^2 W^{\hbox {ss}}+\alpha _m \mathop \int \limits _0^b {\left[ {\left( {-1} \right) ^{m}\left. W \right| _{x=a} -\left. W \right| _{x=0} } \right] } \sin \left( {\beta _n y} \right) \hbox {d}y} \right\} \nonumber \\&\quad +\,\frac{N_y }{C}\left\{ {\beta _n^2 W^{\hbox {ss}}+\beta _n \mathop \int \limits _0^a {\left[ {\left( {-1} \right) ^{n}\left. W \right| _{y=b} -\left. W \right| _{y=0} } \right] } \sin \left( {\alpha _m x} \right) \hbox {d}x} \right\} =0 \end{aligned}$$

(4)

$$\begin{aligned}&\alpha _m^2 \varphi _x^{\hbox {cs}} -\mathop \int \limits _0^b {\left[ {\left( {-1} \right) ^{m}\left. {\frac{\partial \varphi _x }{\partial x}} \right| _{x=a} -\left. {\frac{\partial \varphi _x }{\partial x}} \right| _{x=0} } \right] } \sin \left( {\beta _n y} \right) \hbox {d}y \nonumber \\&\quad +\,\frac{1-\mu }{2}\left\{ {\beta _n^2 \varphi _x^{\hbox {cs}} +\beta _n \mathop \int \limits _0^a {\left[ {\left( {-1} \right) ^{n}\left. {\varphi _x } \right| _{y=b} -\left. {\varphi _x } \right| _{y=0} } \right] } \cos \left( {\alpha _m x} \right) \hbox {d}x} \right\} \nonumber \\&\quad +\,\frac{1+\mu }{2}\left\{ {\alpha _m \beta _n \varphi _y^{\hbox {sc}} +\beta _n \mathop \int \limits _0^b {\left[ {\left( {-1} \right) ^{m}\left. {\varphi _y } \right| _{x=a} -\left. {\varphi _y } \right| _{x=0} } \right] } \cos \left( {\beta _n y} \right) \hbox {d}y} \right\} \nonumber \\&\quad +\,\frac{C}{D}\left\{ {\varphi _x -\alpha _m W^{\hbox {ss}}-\mathop \int \limits _0^b {\left[ {\left( {-1} \right) ^{m}\left. W \right| _{x=a} -\left. W \right| _{x=0} } \right] } \sin \left( {\beta _n y} \right) \hbox {d}y} \right\} =0 \end{aligned}$$

(5)

$$\begin{aligned}&\beta _n^2 \varphi _y^{\hbox {sc}} -\mathop \int \limits _0^a {\left[ {\left( {-1} \right) ^{n}\left. {\frac{\partial \varphi _y }{\partial y}} \right| _{y=b} -\left. {\frac{\partial \varphi _y }{\partial y}} \right| _{y=0} } \right] } \sin \left( {\alpha _m x} \right) \hbox {d}x \nonumber \\&\quad +\,\frac{1-\mu }{2}\left\{ {\alpha _m^2 \varphi _y^{\hbox {sc}} +\alpha _m \mathop \int \limits _0^b {\left[ {\left( {-1} \right) ^{m}\left. {\varphi _y } \right| _{x=a} -\left. {\varphi _y } \right| _{x=0} } \right] } \cos \left( {\beta _n y} \right) \hbox {d}y} \right\} \nonumber \\&\quad +\,\frac{1+\mu }{2}\left\{ {\alpha _m \beta _n \varphi _x^{\hbox {cs}} +\alpha _m \mathop \int \limits _0^a {\left[ {\left( {-1} \right) ^{n}\left. {\varphi _x } \right| _{y=b} -\left. {\varphi _x } \right| _{y=0} } \right] } \cos \left( {\alpha _m x} \right) \hbox {d}x} \right\} \nonumber \\&\quad +\,\frac{C}{D}\left\{ {\varphi _y -\beta _n W^{\hbox {ss}}-\mathop \int \limits _0^a {\left[ {\left( {-1} \right) ^{n}\left. W \right| _{y=b} -\left. W \right| _{y=0} } \right] } \sin \left( {\alpha _m x} \right) \hbox {d}x} \right\} =0 \end{aligned}$$

(6)

By applying the boundary conditions $\left. W \right| _{x=0,a} =0$, $\left. W \right| _{y=0,b} =0$, $\left. {\varphi _y } \right| _{x=0,a} =0$ and $\left. {\varphi _x } \right| _{y=0,b} =0$, Eqs. (4)–(6) give

$$\begin{aligned}&\alpha _m \varphi _x^{\mathrm{cs}} +\beta _n \varphi _y^{\mathrm{sc}} -\left( {\alpha _m^2 +\beta _n^2 +\frac{N_x }{C}\alpha _m^2 +\frac{N_y }{C}\beta _n^2 } \right) W^{\mathrm{ss}}=0 \end{aligned}$$

(7)

$$\begin{aligned}&\frac{C}{D}\alpha _m W^{\hbox {ss}}-\left( {\alpha _m^2 +\frac{1-\mu }{2}\beta _n^2 +\frac{C}{D}} \right) \varphi _x^{\hbox {cs}} -\frac{1+\mu }{2}\alpha _m \beta _n \varphi _y^{\hbox {sc}} =\left( {-1} \right) ^{m+1}K_n +L_n \end{aligned}$$

(8)

$$\begin{aligned}&\frac{C}{D}\beta _n W^{\hbox {ss}}-\frac{1+\mu }{2}\alpha _m \beta _n \varphi _x^{\hbox {cs}} -\left( {\beta _n^2 +\frac{1-\mu }{2}\alpha _m^2 +\frac{C}{D}} \right) \varphi _y^{\hbox {sc}} =\left( {-1} \right) ^{n+1}I_m +J_m \end{aligned}$$

(9)

where

$$\begin{aligned} I_m= & {} \int _0^a {\left. {\frac{\partial \varphi _y }{\partial y}} \right| _{y=b} } \sin \left( {\alpha _m x} \right) \hbox {d}x \nonumber \\ J_m= & {} \int _0^a {\left. {\frac{\partial \varphi _y }{\partial y}} \right| _{y=0} } \sin \left( {\alpha _m x} \right) \hbox {d}x \nonumber \\ K_n= & {} \int _0^b {\left. {\frac{\partial \varphi _x }{\partial x}} \right| _{x=a} } \sin \left( {\beta _n y} \right) \hbox {d}y \nonumber \\ L_n= & {} \int _0^b {\left. {\frac{\partial \varphi _x }{\partial x}} \right| _{x=0} } \sin \left( {\beta _n y} \right) \hbox {d}y \end{aligned}$$

(10)

Assume $N_x =s_1 N$ and $N_y =s_2 N$, where $s_1$ and $s_2$are the scaling parameters for the in-plane loads N in the x and y directions, respectively. From Eqs. (7)–(9), the following matrix form is obtained for the expression of $W^{\mathrm{ss}}$, $\varphi _x^{\mathrm{cs}}$and $\varphi _y^{\mathrm{sc}}$:

$$\begin{aligned} \left\{ {\begin{array}{l} W^{\mathrm{ss}} \\ \varphi _x^{\mathrm{cs}} \\ \varphi _y^{\mathrm{sc}} \\ \end{array}} \right\} =\mathbf{T}_{3\times 3} \left\{ {\begin{array}{l} 0 \\ \left( {-1} \right) ^{m+1}K_n +L_n \\ \left( {-1} \right) ^{n+1}I_m +J_m \\ \end{array}} \right\} \end{aligned}$$

(11)

where $\mathbf{T}_{3\times 3}$ is the coefficient matrix, the elements of which, $T_{ij}$ (i, $j = 1, 2, 3$), are shown in “Appendix B”.

2.3 Analytic buckling solutions

The remaining boundary conditions that have not been satisfied include $\left. {\varphi _x } \right| _{x=0,a} =0$ and $\left. {\varphi _y } \right| _{y=0,b} =0$, which require, according to Eq. (2),

$$\begin{aligned} \begin{array}{l} \mathop \sum \limits _{n=1}^\infty {\left[ {\frac{2}{ab}\sum \limits _{m=0}^\infty {\left. {\varepsilon _m \varphi _x^{\hbox {cs}} \cos \left( {\alpha _m x} \right) } \right| _{x=0,a} } } \right] } \sin \left( {\beta _n y} \right) =0 \\ \\ \mathop \sum \limits _{m=1}^\infty {\left[ {\frac{2}{ab}\sum \limits _{n=0}^\infty {\left. {\varepsilon _n \varphi _y^{\hbox {sc}} \cos \left( {\beta _n y} \right) } \right| _{y=0,b} } } \right] } \sin \left( {\alpha _m x} \right) =0 \\ \end{array} \end{aligned}$$

(12)

Substitute Eq. (11) into Eq. (12), in view of the orthogonality of the sine series, we finally obtain

$$\begin{aligned}&2\sum _{m=1} {\left( {-1} \right) ^{n}T_{23} I_m } -2\sum _{m=1} {T_{23} J_m } \nonumber \\&\quad +\left[ {T_{22} \left( {m=0} \right) +2\sum _{m=1} {\left( {-1} \right) ^{m}T_{22} } } \right] K_n -\left[ {T_{22} \left( {m=0} \right) +2\sum _{m=1} {T_{22} } } \right] L_n =0 \end{aligned}$$

(13)

and

$$\begin{aligned}&2\sum _{m=1} {\left( {-1} \right) ^{m+n}T_{23} I_m } -2\sum _{m=1} {\left( {-1} \right) ^{m}T_{23} J_m } \nonumber \\&\quad +\left[ {T_{22} \left( {m=0} \right) +2\sum _{m=1} {T_{22} } } \right] K_n -\left[ {T_{22} \left( {m=0} \right) +2\sum _{m=1} {\left( {-1} \right) ^{m}T_{22} } } \right] L_n =0 \end{aligned}$$

(14)

for $n=1,2,3,\ldots$, and

$$\begin{aligned}&\left[ {T_{33} \left( {n=0} \right) +2\sum _{n=1} {\left( {-1} \right) ^{n}T_{33} } } \right] I_m -\left[ {T_{33} \left( {n=0} \right) +2\sum _{n=1} {T_{33} } } \right] J_m \nonumber \\&\quad +\,2\sum _{n=1} {\left( {-1} \right) ^{m}T_{23} K_n -2\sum _{n=1} {T_{23} } } L_n =0 \end{aligned}$$

(15)

and

$$\begin{aligned}&\left[ {T_{33} \left( {n=0} \right) +2\sum _{n=1} {T_{33} } } \right] I_m -\left[ {T_{33} \left( {n=0} \right) +2\sum _{n=1} {\left( {-1} \right) ^{n}T_{33} } } \right] J_m \nonumber \\&\quad +\,2\sum _{n=1} {\left( {-1} \right) ^{m+n}T_{23} K_n -2\sum _{n=1} {\left( {-1} \right) ^{n}T_{23} } } L_n =0 \end{aligned}$$

(16)

for $m=1,2,3,\ldots$.

Table 1 Buckling factors, ${Nb^{2}}/{\left( {D\pi ^{2}} \right) }$, for CCCC Mindlin plates subjected to uniaxial compression $\left( {S_1 =-1,S_2 =0} \right)$

Equations (13)–(16) are four sets of simultaneous linear equations with respect to the constants $I_m$, $J_m$, $K_n$ and $L_n$ ($m,n=1,2,3,\ldots )$. A finite number of equations are treated in practice with the same number of constants. For example, Eqs. (13) and (14) are taken for $n=1,2,3,\ldots ,N$, and Eqs. (15) and (16) are taken for $m=1,2,3,\ldots ,M$, where M and N represent any positive integers; meanwhile, instead of $\infty$, M and N are taken in Eqs. (13)–(16) as the upper limits of summations with respect to $I_m$ and $J_m$, and $K_n$ and $L_n$, respectively. Accordingly, $2M+2N$ equations are formed with respect to $I_m$, $J_m$, $K_n$ and $L_n$ ($m=1,2,3,\ldots ,M$; $n=1,2,3,\ldots ,N)$. The existence of nonzero solutions requires that the determinant of the coefficient matrix of the above sets of equations be zero; this leads to the equation of buckling loads, substituting one of the roots (i.e., a buckling load solution) back to the sets of equations yields nonzero solutions for the constants. By substituting the above constant solutions into Eq. (11), then into Eq. (2), we finally get the analytic mode shape solutions of the plate corresponding to the buckling load.

3 Numerical and graphical results

Table 1 presents the non-dimensional finite integral transform solutions for the buckling loads, denoted by ${Nb^{2}}/{\left( {D\pi ^{2}} \right) }$, of fully clamped thick plates with different geometric parameters subjected to uniaxial compression ($S_1 =-1$ and $S_2 =0)$. The results are listed for the aspect ratios being 0.5, 1, 1.5, 2 and 2.5 under the thickness-to-width ratios 0.05, 0.1, 0.15 and 0.2, respectively. The present results for the first six buckling modes are compared with the FEA by the commercial software ABAQUS [28] (with S4R shell element adopted) as well as numerical solutions from the literature [29, 30] that only provide the lowest buckling loads. Good agreement is observed with those for comparison, especially with the refined FEA. The quantitative results show that increasing the thickness-to-width ratio decreases the buckling load and vice versa, which indicates that shear deformation plays an important role as a plate gets thicker. It is also found that the buckling load decreases as the aspect ratio increases. The buckling mode shapes for uniaxially compressed square plates with two different thickness-to-width ratios are plotted in Fig. 2, with good agreement observed with the FEA results.

Fig. 2

First six buckling mode shapes of CCCC square plates subjected to uniaxial compression $\left( {S_1 =-1,S_2 =0} \right)$, with h/b= 0.05 and 0.2

Table 2 Buckling factors for CCCC Mindlin plates subjected to biaxial compression $\left( {S_1 =-1,S_2 =-1.5} \right)$

Table 2 shows the buckling loads of fully clamped thick plates subjected to biaxial compression ($S_1 =-1$ and $S_2 =-1.5)$. The solutions are presented in the same way as those in Table 1. The results are partly compared with the numerical solutions available from the literature [10, 29] and are all compared with the FEA. Again, good agreement is realized, which confirms the validity and accuracy of the present solutions. The buckling mode shapes for biaxially compressed square plates with two different thickness-to-width ratios are plotted in Fig. 3, where satisfactory agreement with the FEA is achieved.

Fig. 3

First six buckling mode shapes of CCCC square plates subjected to biaxial compression $\left( {S_1 =-1,S_2 =-1.5} \right)$, with h/b= 0.05 and 0.2

Table 3 Convergence study for buckling factors of CCCC Mindlin plates subjected to uniaxial compression

Table 4 Convergence study for buckling factors of CCCC Mindlin plates subjected to biaxial compression.

Tables 3 and 4 show the convergence study of the solutions for plates under both uniaxial and biaxial compressions by taking extreme thickness-to-width ratios (0.05 and 0.2) and length-to-width ratios (0.5 and 2.5) as per Tables 1 and 2, with the convergent results marked in bold. The accuracy of five significant figures is attained by taking 100 series terms at most (e.g., $M =N = 100$) in our solution, which can be easily conducted on an ordinary personal computer. Accordingly, $M =N = 100$ has been adopted throughout this study.

4 Conclusions

The double finite integral transform method is extended to the buckling problems of rectangular thick plates. The solution procedure is conducted in a concise but rigorous way, which starts from the governing high-order PDEs. By satisfying some boundary conditions, the relationship is found between the displacements in the transform domain and the constants that are determined by the equations yielded by the remaining boundary conditions. The inversion of the integral transforms gives the analytic buckling solutions of the plates. Comprehensive buckling loads and mode shapes are obtained for fully clamped thick plates with different geometric parameters subjected to both uniaxial and biaxial compressions, which are well validated by the available studies and refined FEA. Besides helping one to pursue more analytic solutions of the plate and shell problems, the present method is also expected to serve as a benchmark approach for examining the accuracy of other numerical methods.

Appendices

Appendix A: Definition of double finite integral transforms

The following double finite integral transforms are used for W, $\varphi _x$ and $\varphi _y$:

$$\begin{aligned} W^{\mathrm{ss}}= & {} \mathop \int \limits _0^a {\mathop \int \limits _0^b {W\left( {x,y} \right) \sin (\alpha _m x)\sin (\beta _n y)\hbox {d}x\hbox {d}y} } \\ \varphi _x^{\mathrm{cs}}= & {} \mathop \int \limits _0^a {\mathop \int \limits _0^b {\varphi _x \left( {x,y} \right) } } \cos (\alpha _m x)\sin (\beta _n y)\hbox {d}x\hbox {d}y \\ \varphi _y^{\mathrm{sc}}= & {} \mathop \int \limits _0^a {\mathop \int \limits _0^b {\varphi _y \left( {x,y} \right) } } \sin (\alpha _m x)\cos (\beta _n y)\hbox {d}x\hbox {d}y \\ \end{aligned}$$

where the superscripts “SS”, “CS” and “SC” represent the double sine, cosine-sine and sine-cosine integral transforms with respect to variables x and y.

Appendix B: Matrix elements in Eq. (12)

$$\begin{aligned} T_{11}= & {} \frac{C\left[ {C+D\left( {\alpha _m^2 +\beta _n^2 } \right) } \right] }{\left[ {C+D\left( {\alpha _m^2 +\beta _n^2 } \right) } \right] \left[ {\alpha _m^2 \left( {C+N_x } \right) +\beta _n^2 \left( {C+N_y } \right) } \right] -C^{2}\left( {\alpha _m^2 +\beta _n^2 } \right) },\\ T_{12}= & {} -\frac{CD\alpha _m }{CN_x \alpha _m^2 +D\alpha _m^4 \left( {C+N_x } \right) +\beta _n^2 \left[ {CN_y +D\alpha _m^2 \left( {2C+N_x +N_y } \right) } \right] +D\beta _n^4 \left( {C+N_y } \right) },\\ T_{13}= & {} -\frac{CD\beta _n }{CN_x \alpha _m^2 +D\alpha _m^4 \left( {C+N_x } \right) +\beta _n^2 \left[ {CN_y +D\left( {2C+N_x +N_y } \right) \alpha _m^2 } \right] +D\beta _n^4 \left( {C+N_y } \right) },\\ T_{21}= & {} -\frac{C}{D}T_{12} ,\\ T_{22}= & {} -\frac{D\left\{ {\begin{array}{l} \alpha _m^2 \left( {C+N_x } \right) \left[ {2C+D\alpha _m^2 \left( {1-\mu } \right) } \right] \\ +\beta _n^2 \left\{ {2CN_y +D\alpha _m^2 \left[ {C\left( {3-\mu } \right) +2N_x +N_y \left( {1-\mu } \right) } \right] } \right\} +2D\beta _n^4 \left( {C+N_y } \right) \\ \end{array}} \right\} }{\left[ {2C+D\left( {1-\mu } \right) \left( {\alpha _m^2 +\beta _n^2 } \right) } \right] \left\{ {\begin{array}{l} CN_x \alpha _m^2 +D\alpha _m^4 \left( {C+N_x } \right) \\ +\beta _n^2 \left[ {CN_y +D\alpha _m^2 \left( {2C+N_x +N_y } \right) } \right] +D\beta _n^4 \left( {C+N_y } \right) \\ \end{array}} \right\} },\\ T_{23}= & {} -\frac{D\alpha _m \beta _n \left\{ {2C^{2}-D\left( {1+\mu } \right) \left[ {\alpha _m^2 \left( {C+N_x } \right) +\beta _n^2 \left( {C+N_y } \right) } \right] } \right\} }{\left[ {2C+D\left( {1-\mu } \right) \left( {\alpha _m^2 +\beta _n^2 } \right) } \right] \left\{ {\begin{array}{l} CN_x \alpha _m^2 +D\alpha _m^4 \left( {C+N_x } \right) \\ +\beta _n^2 \left[ {CN_y +D\alpha _m^2 \left( {2C+N_x +N_y } \right) } \right] +D\beta _n^4 \left( {C+N_y } \right) \\ \end{array}} \right\} },\\ T_{31}= & {} -\frac{C}{D}T_{13} ,\\ T_{32}= & {} -T_{23} ,\\ T_{33}= & {} -\frac{D\left\{ {\begin{array}{l} 2CN_x \alpha _m^2 +2D\alpha _m^4 \left( {C+N_x } \right) \\ +\beta _n^2 \left\{ {2C\left( {C+N_y } \right) +D\alpha _m^2 \left[ {C\left( {3-\mu } \right) +N_x \left( {1-\mu } \right) +2N_y } \right] } \right\} +D\beta _n^4 \left( {1-\mu } \right) \left( {C+N_y } \right) \\ \end{array}} \right\} }{\left[ {2C+D\left( {1-\mu } \right) \left( {\alpha _m^2 +\beta _n^2 } \right) } \right] \left\{ {\begin{array}{l} CN_x \alpha _m^2 +D\alpha _m^4 \left( {C+N_x } \right) \\ +\beta _n^2 \left[ {CN_y +D\alpha _m^2 \left( {2C+N_x +N_y } \right) } \right] +D\beta _n^4 \left( {C+N_y } \right) \\ \end{array}} \right\} }. \end{aligned}$$