1 Introduction

The exceptional potential of the carbon nanotubes to improve the mechanical, electrical and thermal properties of the polymeric material has attracted the attention of many investigators, and it is considered as one of the most promising reinforcement materials for composites with enormous application span.

Two types of epoxy resins and low weight fraction of randomly oriented CNTs have been used by Fidelus et al. (Fidelus et al. 2005) to study the thermo-mechanical properties of the nano-composites. Hu et al. (Hu et al. 2005) investigated the macroscopic elastic properties of the FG-CNTRC beam under different loading conditions. Vodenitcharova and Zhang (Vodenitcharova and Zhang 2006) studied the deformation of a FG-CNTRC beam through the Airy stress-function method and presented the relation between the thickness size of matrix and bending angles.

Mokashi et al. (Mokashi et al. 2007) used molecular mechanics simulations to investigate the mechanical properties of polyethylene and carbon nanotube (CNT). Han and Elliott (Han and Elliott 2007) presented classical molecular dynamics (MD) simulations of the elastic properties of polymer/CNT composites constructed by embedding a single-walled (10, 10) CNT into amorphous polymer matrices, while the molecular dynamics were used by Zhu et al. (Zhu et al. 2007) to study the stress–strain relation for single-walled carbon nanotube-reinforced Epon 862 composites. Ke et al. (Ke et al. 2010) investigated the nonlinear free vibration of composite beams based on Timoshenko beam theory, which were reinforced by carbon nanotubes, with three various end supports. Yas and Heshmati (Yas and Heshmati 2012) used the numerical finite element method to study the vibrations of FG-CNTRC beams subjected to moving load according to Timoshenko and Euler–Bernoulli beam theories. Wattanasakulpong and Ungbhakorn (Wattanasakulpong and Ungbhakorn 2013) considered the bending, buckling and vibration behaviors of single-walled carbon nanotube-reinforced composite (SW-CNTRC) beams. Eltaher et al. (Eltaher et al. 2014) investigated the static and buckling behaviors of functionally graded Timoshenko nano beams. Nonlinear forced vibration analysis of FG-CNTRC beams based on Timoshenko beam theory has been studied by Ansari et al. (Ansari et al. 2014). Liew et al. (Liew et al. 2015) reviewed mechanical analysis of functionally graded carbon nanotube-reinforced composites. These studies demonstrated that adding a small amount of CNTs to polymeric composite will increase the mechanical, electrical and thermal properties. Wu et al. (Wu et al. 2016) studied the nonlinear vibration of functionally graded carbon nanotube-reinforced composite beams with geometric imperfections. The weak interfacial bonding between CNTs and matrix was resolved by Shen (Shen 2009); he suggested the concept of functionally graded distribution be used for CNTs to improve the interfacial bonding between matrix and reinforcement and studied the nonlinear bending behavior of FG-CNTRC plates in thermal environment.

Vibration of the beam structures is a serious problem, and the mitigation and control of the amplitude of these vibrations have attracted the interest of researchers. Choi et al. (Choi et al. 2007) mentioned the importance of rotating structures and used a negative velocity feedback control algorithm to control the vibration of pre-twisted rotating composite beam. Considering lateral strains, Mahieddine and Ouali (Mahieddine and Ouali 2008) investigated the behavior of the finite element model of a beam with piezoelectric sensors and actuators. Viscosity and Kelvin–Voigt (strain rate) damping and active controller have been used by Kayacik et al. (Kayacik et al. 2008) to converge the amplitude vibrations of a cantilever beam to zero, while the piezoelectric layers were bonded to both sides of the beam as sensors and actuators. The behavior of a FGM beam containing two piezoelectric layers has been studied by Gharib et al. (Gharib et al. 2008), in which the power law distribution was employed for volume fraction of the FGM layer. Alhazza et al. (Alhazza et al. 2009) considered a reduced-order model consisting of the first n vibration modes and used the first two vibration modes to verify the nonlinear equations of motion; they considered the effects of the location and size of the piezoelectric patches on the stability of a flexible cantilever beam. Using piezoelectric actuator, Trindade (Trindade 2011) presented an analysis of three active–passive damping design configurations applied to a cantilever beam. An active vibration control of an Euler–Bernoulli beam with piezoelectric actuators bonded to the top and bottom surfaces of it was considered by Kucuk et al. (Kucuk et al. 2011). Fazelzadeh and Kazemi-Lari (Fazelzadeh and Kazemi-Lari 2013) investigated the effects of a lumped mass located in an arbitrary position on the stability of the column resting on an elastic foundation which was subjected to a partially distributed follower force. Fallah and Ebrahimnejad (Fallah and Ebrahimnejad 2013) studied the performance of piezoelectric actuators for active control of building structures. Based on finite volume (FV) formulation, they continued their studies on active vibration control of the smart beams with piezoelectric sensors and actuators (Fallah and Ebrahimnejad 2014). Li et al. (Li and Lyu 2014) attached the piezoelectric layers as a sensor and actuator to both sides of a lattice sandwich beam to control the vibration of it. Khorshidi et al. (Khorshidi et al. 2015) used piezoelectric layers on both sides of a circular plate as a sensor to study the active vibration control of this plate. The vibration analysis and control of the functionally graded carbon nanotube-reinforced composite beams using piezoelectric layers have been studied by some researchers. Rafiee et al. (2013) studied the effects of temperature changes in vibration of FG-CNTRC beams with surface-bonded piezoelectric layers. They continued their studies on the nonlinear bifurcation buckling of single-walled carbon nanotube-reinforced composite piezoelectric beams subjected to a thermal loading (2013). Alibeigloo (2014) used the elasticity theory to consider the free vibration of FG-CNTRC cylindrical panel which was embedded in piezoelectric layers. Rafiee et al. (2014) investigated the effects of combined thermal and electrical loading on nonlinear dynamic stability of piezoelectric FG-CNTRC plates, based on first-order shear deformation theory. The nonlinear free vibrations of CNTs-/fiber-/polymer-laminated composite plates with piezoelectric actuators attached on both sides of it were studied by Rafiee et al. (2014). Wu and Chang (Wu and Chang 2014) analyzed the stability of the CNTRC plates whose surface-bonded piezoelectric layers were subjected to bi-axial compression. Based on elasticity theory, Alibeigloo (2014) studied the static behavior of a FG-CNTRC plate embedded in piezoelectric sensor and actuator layers and subjected to thermal loads. Selim et al. (Selim et al. 2017) applied an active control to suppress the vibration of CNT-reinforced composite plates with piezoelectric layers based on Reddy’s higher-order shear deformation theory. Based on a higher-order shear deformation theory, Song et al. (Song et al. 2016) studied active vibration control of CNT-reinforced functionally graded plates.

In this study, to suppress the vibrations of the functionally graded carbon nanotube-reinforced composite beams, an active controller will be designed which benefits the piezoelectric layers as sensors and actuators. The FG-CNTRC beam is fixed from one end and subjected to a follower force, which can cause dynamical system instability, from the other end. Considering Euler–Bernoulli beam theory, the governing equations of motion of the CNTRC beam are derived by employing the Lagrange–Rayleigh–Ritz technique. An inverse dynamics controller is designed to adjust the voltages of piezoelectric actuators according to the feedback of piezoelectric sensors to control the vibration of the system. Finally, the effects of the system parameters such as the carbon nanotube volume fractions, distribution patterns of CNTs, the magnitude of the follower force, and the length of the piezoelectric layers on the stability of the FG-CNTRC beam structure and controller efficiency are investigated.

By a thorough look at the literature, it can be observed that only a few researchers have studied an active control to suppress the vibrations of a CNTRC beam. Therefore, it is understood that the study of the suppression of the flutter vibration of a CNTRC beam under follower force is important and requires attention. In spite of the researches in the area of the CNTRC beam, there has been no attempt to tackle the problem described in the present paper. Applying an active control to suppress the flutter vibration of a CNTRC beam under follower force, using piezoelectric sensors/actuators, and analyzing the stability of the beam in different conditions is the main contribution of the present paper.

2 Properties of FG-CNTRC Materials

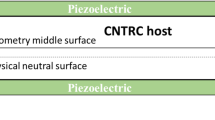
In this study, a cantilever beam made from a mixture of single-walled carbon nanotube and an isotropic polymer matrix is considered. The FG-CNTRC beam with length, L, has been fixed from one end and subjected to a follower force from the free end. The piezoelectric actuators/sensors are attached to both sides of the beam, as shown in Fig. 1. Four patterns of carbon nanotubes distribution over the thickness direction of the beam are considered to reinforce the beam structure (see Fig. 2). According to the rule of mixture, the effective material properties of the CNTRC beams are presented as follows:

$$\begin{aligned} E_{11} = \eta_{1} V_{\text{cnt}} E_{11}^{\text{cnt}} + V_{\text{m}} E^{m} \hfill \\ \frac{{\eta_{2}}}{{E_{22}}} = \frac{{V_{\text{cnt}}}}{{E_{22}^{\text{cnt}}}} + \frac{{V_{\text{m}}}}{{E^{m}}} \hfill \\ \frac{{\eta_{3}}}{{G_{12}}} = \frac{{V_{\text{cnt}}}}{{G_{12}^{\text{cnt}}}} + \frac{{V_{\text{m}}}}{{G^{m}}} \hfill \\ \end{aligned}$$
(1)

where the variable E and G refer to the Young’s and shear modulus, respectively. The CNT efficiency parameters \(\eta_{j} \left({j = 1, {\kern 1pt} 2} \right)\) are estimated by matching the Young’s moduli \(E_{11}^{\text{cnt}}\) and \(E_{22}^{\text{cnt}}\) of CNTRCs obtained by Han and Elliott (Han and Elliott 2007) using molecular dynamics. These parameters are illustrated in Table 1. The efficiency parameters change with CNT volume fractions. Herein, V is the volume fraction and the subs and superscripts, cnt, and m refer to the carbon nanotube and isotropic matrix, respectively. The volume fractions of the carbon nanotube, \(V_{\text{cnt}}\), and matrix, \(V_{\text{m}}\), are related as:

Fig. 1
figure 1

CNTRC beam with attached piezoelectric layers

Full size image
Fig. 2
figure 2

Cross sections of different distribution patterns of SW-CNTs. a UD pattern, b\(\varLambda\) pattern, c X pattern, d O pattern

Full size image
Table 1 Comparison of Young’s modulus of PMMA/CNT composite reinforced by (10, 10) SWCNT at the temperature T0 = 300°K (Ke et al. 2010)
Full size table
$$V_{\text{cnt}} + V_{\text{m}} = 1$$
(2)

The volume fraction of the carbon nanotube, \(V_{\text{cnt}}\), is assumed to vary linearly along the thickness of the beam and is calculated by these mathematical functions (Ke et al. 2010):

$$\begin{aligned} UD - {\text{Beam}}: V_{\text{cnt}} &= V_{\text{cnt}}^{*} \hfill \\ \varLambda - {\text{Beam}}: V_{\text{cnt}} &= \left({1 - \frac{2z}{h}} \right)V_{\text{cnt}}^{*} \hfill \\ X - {\text{Beam}}: V_{\text{cnt}} &= 4 \frac{\left| z \right|}{h}V_{\text{cnt}}^{*} \hfill \\ O - {\text{Beam}}: V_{\text{cnt}} &= 2\left({1 - 2\frac{\left| z \right|}{h}} \right)V_{\text{cnt}}^{*} \hfill \\ \end{aligned}$$
(3)

The O, X, \(\varLambda\), and UD are the patterns of the distributed carbon nanotube reinforcement on the isotropic matrix; the four different distribution patterns of SW-CNTs are presented in Fig. 2.

$$V_{\text{cnt}}^{*} = \frac{{\forall_{\text{cnt}}}}{{\forall_{\text{cnt}} + \left({\rho^{\text{cnt}}/\rho^{m}} \right) - \left({\rho^{\text{cnt}}/\rho^{m}} \right)\forall_{\text{cnt}}}}$$
(4)

where \(\forall_{\text{cnt}}\) is the mass fraction of carbon nanotube. \(\rho_{\text{cnt}}\), and \(\rho_{\text{m}}\) are the densities of the carbon nanotube and the matrix, respectively.

Similarly, Poisson’s ratio, ν, and mass density, ρ, can be calculated as follows.

$$\begin{aligned} \nu = V_{\text{cnt}} \nu^{\text{{\rm cnt}}} + V_{\text{m}} \nu^{m} \hfill \\ \rho = V_{\text{cnt}} \rho^{{\rm cnt}} + V_{\text{m}} \rho^{m} \hfill \\ \end{aligned}$$
(5)

where \(\nu^{\text{cnt}}\) and \(\nu^{\text{m}}\) are Poisson’s ratios of the carbon nanotube and the matrix, respectively.

3 Governing Equations of the System

The width, thickness, and length of the FG-CNTRC beam are b, h and L, respectively. The piezoelectric sensors/actuators are attached on the top and bottom surfaces of the beam and have the thickness \(h_{\text{p}}\), length \(L_{\text{p}}\), width \(b_{\text{p}}\), density \(\rho_{\text{p}}\), Young’s modulus \(E_{\text{p}}\), and equivalent piezoelectric coefficient, \(e_{31}\).

In non-symmetry distributions of the CNTs, the neutral axis of the beam is not located on its axis of symmetry; the definition of \(\bar{z}\) is the distance between the neutral axis and axis of symmetry of the FG-CNTRC beam which is calculated as:

$$\bar{z} = \left({\mathop \int \limits_{{- \frac{h}{2}}}^{{\frac{h}{2}}} E_{22} \left(z \right)z {\text{d}}z} \right)/\left({\mathop \int \limits_{{- \frac{h}{2}}}^{{\frac{h}{2}}} E_{22} \left(z \right) {\text{d}}z} \right)$$
(6)

\(\xi = z - \bar{z}\) is a new coordinate system. In this coordinate system, \(\xi = 0\) is the natural axis of the FG-CNTRC beam. In the symmetrical patterns of the CNTs distribution along the thickness direction \(\bar{z} = 0\), so \(\xi = z = 0\) is the natural axis of the beam in these distribution patterns.

To formulate the dynamical equations, the Euler assumption is adopted; thus, the shear deformation and rotary inertia effect in the structure are omitted, and the displacement field of the FG-CNTRC beam is written as follows (Wang and Quek 2002):

$$\bar{U}\left({x,z,t} \right) = u\left({x,t} \right) = - \xi \frac{{\partial w\left({x,t} \right)}}{\partial x}, \bar{W}\left({x,z,t} \right) = w\left({x,t} \right)$$
(7)

where \(w\left({x,t} \right)\) is the transverse displacement of the FG-CNTRC beam in ξ direction, and \(u\left({x,t} \right)\) is the longitudinal x-direction.

The linear strain–displacement and stress–displacement relationships of the beam can be written as

$$\begin{aligned} \varepsilon_{x} &= \frac{\partial u}{\partial x} = - \xi \frac{{\partial^{2} w\left({x,t} \right)}}{{\partial x^{2}}} \hfill \\ \sigma_{x} &= Q_{11} \left(\xi \right).\varepsilon_{x} = - Q_{11} \left(\xi \right)\xi \frac{{\partial^{2} w\left({x,t} \right)}}{{\partial x^{2}}} \hfill \\ \end{aligned}$$
(8)

where

$$Q_{11} \left(\xi \right) = \frac{{E_{11}^{cnt} \left(\xi \right)}}{{1 - \nu^{2} \left(\xi \right)}}$$
(9)

The kinetic energy and potential energy of the system are calculated as

$$\begin{aligned} T = T_{\text{b}} + T_{\text{p}} \hfill \\ V = V_{\text{b}} + V_{\text{p}} \hfill \\ \end{aligned}$$
(10)

where T and V are the kinetic energy and potential energy of the system, respectively. The subscripts b and p stand for beam and piezoelectric layers, respectively. The kinetic and potential energies of the beam and piezoelectric layers are calculated as follow:

$$\begin{aligned} T = T_{\text{b}} + T_{\text{p}} \hfill \\ V = V_{\text{b}} + V_{\text{p}} \hfill \\ \end{aligned}$$
(11)

where b is the width of the beam,\(Y\) is the number of piezoelectric layers, \(\rho_{{p_{n}}}\) is the density of the \(n\) th piezoelectric layer, \(x_{{1_{n}}}\) and \(x_{{2_{n}}}\) are the two end positions of the \(n\) th piezoelectric layer, and \(H\left(x \right)\) is the Heaviside function.

$$\begin{aligned} V_{b} &= \frac{1}{2}\int\limits_{v} {\sigma_{x}^{T} \cdot \varepsilon_{x} {\text{dv}}} + \frac{1}{2}\mathop \int \limits_{0}^{L} P\left({\frac{{\partial w\left({x,t} \right)}}{\partial x}} \right)^{2} {\text{d}}x \\ & = \frac{1}{2}\mathop \int \limits_{0}^{L} \mathop \int \limits_{{- \frac{h}{2} - \bar{z}}}^{{\frac{h}{2} - \bar{z}}} b Q_{11} \left(\xi \right) \cdot \left({- \xi \frac{{\partial^{2} w\left({x,t} \right)}}{{\partial x^{2}}}} \right)^{2} {\text{dv}} + \frac{1}{2}\mathop \int \limits_{0}^{L} P\left({\frac{{\partial w\left({x,t} \right)}}{\partial x}} \right)^{2} {\text{d}}x \\ V_{p} &= \frac{1}{2}\mathop \sum \limits_{n = 1}^{Y} \int\limits_{{PZT_{n}}} {E_{{p_{n}}} \xi^{2} \left({\frac{{\partial^{2} w\left({x,t} \right)}}{{\partial x^{2}}}} \right)^{2} {\text{dv}}} + \mathop \sum \limits_{n = 1}^{Y} \int\limits_{{PZT_{n}}} {\xi e_{31} E_{{z_{n}}} \frac{{\partial^{2} w\left({x,t} \right)}}{{\partial x^{2}}} {\text{dv}}} + \frac{1}{2}\mathop \sum \limits_{n = 1}^{Y} \int\limits_{{PZT_{n}}} {E_{{z_{n}}} d_{n} {\text{dv}}} \\ \end{aligned}$$
(12)

where \(P\) is the follower force and \(d_{n}\) is the electric displacement of the \(n\) th piezoelectric patch. \(E_{\text{z}}\) is the electric field of the piezoelectric layer.

According to Lagrange’s method, the governing equation of motion is written as

$$\begin{aligned} &\varPi = T - V \hfill \\ &\frac{\text{d}}{{{\text{d}}t}}\left({\frac{\partial \varPi}{{\partial \dot{\varvec{q}}}}} \right) - \frac{\partial \varPi}{{\partial \varvec{q}}} = Q \hfill \\ \end{aligned}$$
(13)

where \(\varPi\) is the Lagrangian parameter,\(\varvec{q}\) is the vector of generalized coordinate, and \(Q\) is the generalized force. The non-conservative work which is related to the follower force is

$$W = P\frac{{\partial w\left({L,t} \right)}}{\partial x} w\left({L,t} \right)$$
(14)

4 Rayleigh–Ritz Methods

Because of the convolution of the governing equations, an approximate solution method is used to investigate the solutions. For this purpose, a series of trial shape functions,\(\varphi_{i}\), is defined instead of the displacement \(w\), which should satisfy the geometrical boundary conditions, multiplied by time-dependent generalized coordinates, \(q_{i}\).

To which, the displacement \(w\) is:

$$w\left({x,t} \right) = \sum \emptyset_{i} q_{i} = {\varvec{\Phi}}^{T} \varvec{q}$$
(15)

where \({\varvec{\Phi}}\), and \(\varvec{q}\) are the vectors of assumed mode shapes and generalized coordinates, respectively.

By substituting Eqs. (15) into (11)–(14) and utilizing the Rayleigh–Ritz procedure on the governing equations, Eq. (16) is obtained:

$$\begin{aligned} &\left[{\mathbf{M}} \right]\varvec{\ddot{q}} + \left[{\mathbf{K}} \right]\varvec{q} = - K_{{p_{{{\text{elastelect}}_{\text{a}}}}}} \varvec{v}_{\text{a}} \hfill \\ &\varvec{v}_{\text{s}} = K_{{p_{\text{elect}}}}^{- 1} K_{{p_{{{\text{elastelect}}_{\text{s}}}}}}^{T} \varvec{q} \hfill \\ \end{aligned}$$
(16)

Herein \(\left[{\mathbf{M}} \right] = {\mathbf{M}}_{\text{b}} + {\mathbf{M}}_{\text{p}}\), and \(\left[{\mathbf{K}} \right] = {\mathbf{K}}_{\text{b}} + {\mathbf{K}}_{\text{p}} + {\mathbf{K}}_{\text{w}}\) are the mass and stiffness matrices, respectively. The voltages of the piezoelectric actuators and sensors are \(\varvec{v}_{\text{a}}\), and \(\varvec{v}_{\text{s}}\), respectively. The terms of the mass matrix are

$$\begin{aligned} {\mathbf{M}}_{\text{b}} = \mathop \int \limits_{0}^{L} \mathop \int \limits_{{- \frac{h}{2} - \bar{z}}}^{{\frac{h}{2} - \bar{z}}} b \rho \left(\xi \right)\left[{\xi^{2} \mathop \sum \limits_{i = 1}^{N} \mathop \sum \limits_{j = 1}^{N} \frac{{\partial \emptyset_{i} \left(x \right)}}{\partial x}\frac{{\partial \emptyset_{j} \left(x \right)}}{\partial x} + \mathop \sum \limits_{i = 1}^{N} \mathop \sum \limits_{j = 1}^{N} \emptyset_{i} \left(x \right) \emptyset_{j} \left(x \right)} \right]{\text{d}}\xi {\text{d}}x \hfill \\ {\mathbf{M}}_{\text{p}} = \mathop \sum \limits_{n = 1}^{Y} \mathop \int \limits_{{x_{{1_{n}}}}}^{{x_{{2_{n}}}}} \rho_{{p_{n}}} b_{{p_{n}}} h_{{p_{n}}} \mathop \sum \limits_{i = 1}^{N} \mathop \sum \limits_{j = 1}^{N} \emptyset_{i} \left(x \right) \emptyset_{j} \left(x \right){\text{d}}x \hfill \\ \end{aligned}$$
(17)

and the terms of the stiffness matrix are

$$\begin{aligned} K_{b} = \mathop \int \limits_{0}^{L} P\mathop \sum \limits_{i = 1}^{N} \sum\limits_{j = 1}^{N} {\frac{{\partial \emptyset_{i} \left(x \right)}}{\partial x}\frac{{\partial \emptyset_{j} \left(x \right)}}{\partial x}{\rm d}x} + \mathop \int \limits_{0}^{L} \int\limits_{{- \frac{h}{2} - \bar{z}}}^{{\frac{h}{2} - \bar{z}}} {b\xi^{2} Q_{11} \left(\xi \right)\left[{\mathop \sum \limits_{i = 1}^{N} \mathop \sum \limits_{j = 1}^{N} \frac{{\partial^{2} \emptyset_{i} \left(x \right)}}{{\partial x^{2}}}\frac{{\partial^{2} \emptyset_{j} \left(x \right)}}{{\partial x^{2}}}} \right]{\rm d}\xi {\rm d}x} \hfill \\ K_{p} = \mathop \sum \limits_{n = 1}^{Y} \iiint_{{PZT_{n}}} {E_{{p_{n}}} \xi^{2} \mathop \sum \limits_{i = 1}^{N} \sum\limits_{j = 1}^{N} {\frac{{\partial^{2} \emptyset_{i} \left(x \right)}}{{\partial x^{2}}}\frac{{\partial^{2} \emptyset_{j} \left(x \right)}}{{\partial x^{2}}}{\rm d}v}} \hfill \\ K_{w} = - P\mathop \sum \limits_{i = 1}^{N} \sum\limits_{j = 1}^{N} {\emptyset_{i} \left(x \right)\left. {\frac{{\partial \emptyset_{j} \left(x \right)}}{\partial x}} \right|_{x = L}} \hfill \\ \end{aligned}$$
(18)

herein N is the number of the mode shapes. \(K_{{P_{{{\text{elatelect}}_{\text{a}}}}}}\) and \(K_{{P_{{{\text{elatelect}}_{\text{s}}}}}}\) are the matrices which contain the elastic–electric effects of the piezoelectric actuators and sensors, respectively. These matrices are determined as follows (Azadi et al. 2014):

$$K_{{P_{{{\text{elatelect}}_{\text{a}}}}}} \quad {\text{or}}\quad K_{{P_{{{\text{elatelect}}_{\text{s}}}}}} = \left[{K_{{{\text{pee}}_{1}}} K_{{{\text{pee}}_{2}}} \ldots K_{{{\text{pee}}_{n }}}} \right]$$
(19)

The columns of the elastic–electric matrix are determined as

$$K_{{pee_{n}}} = \frac{{e_{{31_{n}}}}}{{h_{{p_{n}}}}}\mathop \int \limits_{{PZT_{n}}}^{} \xi \frac{{\partial^{2} \varPhi}}{{\partial x^{2}}} d{\text{v}}$$
(20)

The piezoelectric diagonal capacitance matrix, KPelect, is

$$K_{{p_{\text{elect}}}} = \mathop \sum \limits_{n = 1}^{Y} \int\limits_{{PZT_{n}}} {\varepsilon_{{p_{n}}} p_{n} p_{n}^{T} {\text{dv}}}$$
(21)

where \(p_{n}\) is a \(Y \times 1\) zero vector whereby only its nth row is equal to \(1/h_{{p_{n}}}\). \(\varepsilon_{p}\) is given in Table 2.

Table 2 Material properties and constants (Gharib et al. 2008)
Full size table

5 Controller Design

An Inverse dynamics control scheme is used to suppress the flutter vibration of the CNTRC beam. Using this control scheme, the actuator voltages are designed as

$$u_{0} = - K_{D} K_{{p_{{{\text{elastelect}}_{\text{s}}}}}}^{+ T} K_{{p_{\text{elect}}}} \dot{v}_{\text{s}} - K_{P} K_{{p_{{{\text{elastelect}}_{\text{s}}}}}}^{+ T} K_{{p_{\text{elect}}}} v_{\text{s}}$$
(22)

where the superscript (+) denotes the pseudoinverse matrix. u0 is an auxiliary control input and is designed as follows:

$$u_{0} = - K_{D} K_{{p_{{{\text{elastelect}}_{\text{s}}}}}}^{+ T} K_{{p_{\text{elect}}}} \dot{v}_{\text{s}} - K_{P} K_{{p_{{{\text{elastelect}}_{\text{s}}}}}}^{+ T} K_{{p_{\text{elect}}}} v_{\text{s}}$$
(23)

By substituting Eqs. (23) into (22), the actuator voltages are derived.

$$\begin{aligned} \varvec{v}_{\text{a}} &= K_{{p_{{{\text{elastelect}}_{\text{a}}}}}}^{+} \left[{\mathbf{M}} \right]K_{D} K_{{p_{{{\text{elastelect}}_{\text{s}}}}}}^{+ T} K_{{p_{\text{elect}}}} \dot{v}_{\text{s}} + K_{{p_{{{\text{elastelect}}_{\text{a}}}}}}^{+} \left[{\mathbf{M}} \right]K_{P} K_{{p_{{{\text{elastelect}}_{\text{s}}}}}}^{+ T} K_{{p_{\text{elect}}}} v_{\text{s}} \hfill \\ &\quad-\, K_{{p_{{{\text{elastelect}}_{\text{a}}}}}}^{+} \left[{\mathbf{K}} \right]K_{{p_{{{\text{elastelect}}_{\text{s}}}}}}^{+ T} K_{{p_{\text{elect}}}} v_{\text{s}} \hfill \\ \end{aligned}$$
(24)

Substituting Eq. (24) into Eq. (16), the following equation for generalized coordinates is obtained.

$$\ddot{\varvec{q}} + K_{D} \dot{\varvec{q}} + K_{P} \varvec{q} = 0$$
(25)

Considering the matrices KD and KP as the positive definite diagonal matrices, Eq. (25) is discretized to the N exponentially stable equations. So, for any initial conditions the magnitude of generalized coordinates will asymptotically converge to zero; therefore, by considering Eq. (15), the vibrations of the CNTRC beam will asymptotically converge to zero, too.

6 Numerical Results and Discussion

Because of intricate boundary conditions which are involved in the governing equations, it is difficult to generate appropriate functions which can satisfy all of the geometric and natural boundary conditions. Based on the above description, the following family of shape functions to approximate \(w\) which should satisfy the geometrical boundary condition is defined as (Fazelzadeh et al. 2010)

$$\emptyset_{i} = \frac{{\left({\frac{x}{L}} \right)^{1 + i} \left\{{6 + i^{2} \left({1 - \frac{x}{L}} \right)^{2} + i\left[{5 - 6\frac{x}{L} + \left({\frac{x}{L}} \right)^{2}} \right]} \right\}}}{{i\left({1 + i} \right)\left({2 + i} \right)\left({3 + i} \right)}}$$

Note that the response of the system should be independent of the number of bending modes. So, to simulate the system, six bending modes are considered.

The effective material properties of CNTRC beams are determined. Poly methyl methacrylate (PMMA) is considered as the matrix. For numerical evaluations, the material properties of matrix at room temperature (300 K) are assumed to take the following values (Shen 2009):

$$E^{m} = 2.5\,{\text{GPa}}., \nu^{m} = 0.34, \rho^{m} = 1150\,\,{{\text{Kg}} \mathord{\left/{\vphantom {{\text{Kg}} {{\text{m}}^{ 3}}}} \right. \kern-0pt} {{\text{m}}^{ 3}}}$$

Also, considering (10, 10) SW-CNTs for reinforcement, their material properties at room temperature associated with the effective wall thickness (\(h_{\text{CNT}} = 0.067\) nm) are taken to be as follows (Shen 2009):

$$E_{11}^{\text{CNT}} = 5.6466 \text{TPa}, E_{22}^{\text{CNT}} = 7.0800 \text{TPa}, G_{12}^{\text{CNT}} = 1.9445 \text{TPa}, \nu_{12}^{\text{CNT}} = 0.175 \text{TPa}, \rho^{\text{CNT}} = 1400 {\text{Kg}}/{\text{m}}^{ 3}$$

The material properties of piezoelectric layers are shown in Table 2. Two dimensionless parameters which are used in simulation process are:

$$\bar{P} = \frac{P}{{P_{\text{cr}}}}, \quad \bar{\omega} = \rho_{m} bh\frac{{\omega^{2} L^{4}}}{{E_{m} I_{m}}}$$

where \(P_{\text{cr}} = \pi^{2} E_{\text{m}} I_{\text{m}}/L^{2}\) is the critical buckling load of an isotropic PMMA beam. \(\omega\) is the natural frequency of the system, and \(I_{\text{m}}\) is the mass moment of inertia of the PMMA beam. In the simulation results, length to the thickness ratio \({L \mathord{\left/{\vphantom {L h}} \right. \kern-0pt} h} = 20\) has been considered.

The variation of the first two dimensionless frequencies of the CNTRC beam with zero volume fraction versus dimensionless follower force has been compared with the results reported by Fazelzadeh et al. (Fazelzadeh et al. 2010) and is shown in Fig. 3.

Fig. 3
figure 3

Validation of the first two natural frequencies of the beam

Full size image

The load at which the first two frequencies are equal gives the flutter capacity. The first two frequencies of the beam, for four patterns of CNTs distribution with different volume fraction, without any piezoelectric layer, are shown in Figs. 4, 5, 6, and 7. As can be seen, follower force in horizontal axis is plotted against dimensionless frequency in vertical axis; the effects of the CNTs volume fractions and distribution patterns on the stiffness and flutter capacity of the CNTRC beam have been clarified; as expected, by increasing the quantity of the CNT’s volume fraction, the flutter capacity of the beam will rise; for example, in Fig. 4, the dimensionless flutter capacity for 28% of CNTs is almost 2750, a bit more than two times the level of this parameter for 12%. Surprisingly the dimensionless flutter capacity for X form of CNT’s distribution with 17% CNTs is threefold of this item for O distribution pattern at the same volume fraction of 17%, because the X distribution pattern has a higher moment of inertia compared with the other patterns; so, the flutter capacity of this distribution pattern is more than other patterns at the same volume fraction of the CNTs. After that, UD, \(\varLambda\), and O distribution patterns of CNTs have the more capacities, respectively. Nonzero initial conditions, \((\left. q \right|_{t = 0} = [\begin{array}{*{20}l} {0.1} \hfill & 0 \hfill & {0.1} \hfill & 0 \hfill & {0.2} \hfill & {0.1} \hfill \\ \end{array}]^{T})\), have been considered to analyze the ability and performance of the controller. The controller gains for all cases are KP = diag(4, 1.2 × 106, 2, 0.24, 0.64, 0.72) × 103 and KD = 5I6 × 6.

Fig. 4
figure 4

Dimensionless frequency versus dimensionless follower force for X distribution pattern of CNTs

Full size image
Fig. 5
figure 5

Dimensionless frequency versus dimensionless follower force for UD distribution pattern of CNTs

Full size image
Fig. 6
figure 6

Dimensionless frequency versus dimensionless follower force for \(\varLambda\) distribution pattern of CNTs

Full size image
Fig. 7
figure 7

Dimensionless frequency versus dimensionless follower force for \(O\) distribution pattern of CNTs

Full size image

The tip vibration of the CNTRC beam for four different distribution patterns has been illustrated in Fig. 8. Herein, for four cases, the CNTs volume fraction, and the dimensionless follower force are considered as 17% and 500, respectively. The effects of applying controller and the distribution patterns of the CNTs on the tip vibration of the beam are shown in this figure. To control the vibrations of the CNTRC beam, six pairs of piezoelectric layers with length ratio lp/L = 0.15 have been used. The dimensionless amplitudes of the open loop vibrations vary approximately from 0.046 to 0.028, while the O distribution pattern of the CNTs has the largest and the X distribution has the shortest one. The effectiveness of the controller is depicted in this figure, clearly.

Fig. 8
figure 8

Tip vibration response of the CNTRC beam when CNTs volume fraction is 17%, and the magnitude of the dimensionless follower force is 500. a O distribution pattern, b\(\varLambda\) distribution pattern, c UD distribution pattern, d X distribution pattern

Full size image

To show the applicability of the controller to strongly flutter problem, the critical follower force has been applied to the system and the response of the system has been compared with other conditions. The response of the tip vibration of the CNTRC beam for two different conditions of the \(\varLambda\) distribution pattern is clarified in Fig. 9; the first part of this figure shows the response of the system when the magnitude of the dimensionless follower force is less than critical ones, \(\bar{P} = 500\), and the CNTs volume fraction is equal to 12%; the second part of Fig. 9 indicates the high performance of the controller system, where the magnitude of the dimensionless follower force has been adjusted near the critical zone of flutter, while the amplitude of the tip vibration of the beam in the critical condition rocketed approximately two times; these vibrations have been suppressed rapidly by utilizing the piezoelectric actuators, which illustrates the applicability of the controller.

Fig. 9
figure 9

Tip vibration of the CNTRC beam for the \(\varLambda\) distribution pattern with \(V_{cnt}\) = 12%, a\(\bar{P}\), b\(\bar{P}\)

Full size image

The positive correlation between the volume fraction of CNTs and the flutter capacity of the composite beam is shown in Fig. 10, where the distribution pattern is considered the same as the condition of Fig. 9, and the volume fraction of CNTs grew to 28%; as can be seen, increasing the volume fraction of the CNTs significantly reduced the amplitude of the vibrations to half.

Fig. 10
figure 10

Tip vibration of the CNTRC beam for the \(\varLambda\) distribution pattern with \(V_{cnt}\) = 28% and \(\bar{P}\)

Full size image

The effect of the piezoelectric size is shown in Fig. 11; clearly, six pairs of piezoelectric layers were used to control the vibration of the X distribution pattern of the CNTRC beam; the length ratio of the piezoelectric layers has been considered as 8, 10, and 15%. The fluctuations declined substantially by increasing the length of piezoelectric layers; these trends are indicative of a relationship between the size of the piezoelectric layers and improving the performance of the controller. It is noteworthy to mention that the magnitude of the controller gains can improve the performance of the controller, so for studying the effect of piezoelectric size, the controller gains are considered to be constant for all cases which were examined in this part of the results. Generally, the performance and the applicability of the controller have been illustrated during this section.

Fig. 11
figure 11

Tip vibration of the X distribution pattern of the CNTRC beam with different piezoelectric actuator length ratios. a\(V_{cnt}\) = 12% and \(\bar{P}\), b) \(V_{cnt}\) = 12% and \(\bar{P}\), c) \(V_{cnt}\) = 28% and \(\bar{P}\), d) \(V_{cnt}\) = 28% and \(\bar{P}\)

Full size image

7 Conclusion

In this study, a CNTRC beam subjected to a follower force was considered. Based on the Euler–Bernoulli beam theory and Lagrange–Rayleigh–Ritz technique, the governing equations of the CNTRC beam were obtained. An inverse dynamics controller was applied to the system to damp the flutter vibration of it. Several piezoelectric layers which were attached to both side of the beam were considered as sensors and actuators. The system was simulated, and the effects of the system parameters, such as the CNTs volume fractions, distribution patterns of CNTs, the magnitude of the follower force, and the length of the piezoelectric layers on the stability of the FG-CNTRC beam structure, were studied. Also, the performance and applicability of the controller were proved during this simulation.