1 Introduction

Rockburst is a sudden geological disaster induced by the rapid release of accumulated elastic strain energy, and it leads to brittle failure such as rock throwing, ejection, and spalling in mines, tunnels and other geotechnical engineering (Askaripour et al. 2022; Zhao and Chen 2020). The U.S. witnessed a total of 172 rockburst cases in the period 1936–1993 (Mark 2016), and countries such as Canada, India, Sweden, and China have also undergone rockburst for many times (Leveille et al. 2017; Sepehri et al. 2020; Simser 2019; Sun et al. 2021), yet this is not an exhaustive list. As the depth of mining and the locations of excavation activities pose greater challenges (Xu et al. 2022), more cases of rockburst have occurred. For the purpose of predicting intensity grades of rockburst accurately and finding targeted preventive measures, scholars worldwide proposed a large number of methods, including empirical criteria(Gong et al. 2020, 2019; Xue et al. 2020a), numerical simulation (Lu et al. 2021; Yang et al. 2022; Yu et al. 2023), and on-site monitoring (Hu et al. 2023a; Xue et al. 2021; Zhang et al. 2018). The empirical criteria method is an empirical method in which the parameters can be obtained through experiments, but it fails to be transferred effectively between different engineering scenarios. The results generated by the numerical simulation method always deviate from actual on-site situations, being far from satisfactory. Although relevant parameters can be obtained in real time by means of on-site monitoring, it is still difficult to determine the rockburst threshold. Machine learning (ML), as a branch of artificial intelligence, can better explore the nonlinear relationships between various indices and samples (Kadkhodaei and Ghasemi 2022a; Shukla et al. 2021), and its prediction will become increasingly accurate over time. Therefore, studying the prediction of rockburst intensity grades based on ML is of great significance (Sun et al. 2021).

Research on ML-based rockburst intensity grade prediction mainly focuses on the rockburst data structure and the algorithms for rockburst intensity grade prediction. In terms of data structure, the dataset may encounter data anomalies or data imbalance (Fig. 1). Considering this problem, scholars proposed various methods to eliminate outliers (Hu et al. 2023b; Li et al. 2018; Zeng et al. 2022). Tan et al. (2021) and Asniar et al. (2022) detected and eliminated data outliers with the aid of the local outlier factor (LOF). Nnamoko and Korkontzelos (2020) and Xue et al. (2020b) identified outliers through interquartile range (IQR). It is generally believed that oversampling is one of the most effective methods to resolve data imbalance (Yi et al. 2022; Zhang et al. 2022a, 2022b). Wang et al. (2023) adopted the random oversampling method, but this method tends to cause overfitting. Li et al. (2023) and Feng et al. (2021) addressed data imbalance by the synthetic minority oversampling technique (SMOTE). On the other hand, in terms of algorithms, single models were applied predict rockburst intensity grade prediction first (Fig. 1). Kadkhodaei et al. (2022b) using stochastic modeling based on Monte Carlo (MC) simulation predict rockburst potential, the results reveal that stochastic modeling can effectively predict rockburst potential. Ullah et al. (2022) predicted rockburst intensity grades with extreme gradient boosting (XGBoost). Yang et al. (2021) established a prediction model based on the self-organizing feature map (SOFM) neural network. However, since many network parameters in the model need to be set from experience, its performance remains to be improved. Lin et al. (2018) established a cloud model evaluation system based on common influencing factors of rockburst. Ghasemi et al. (2020) for the first time applied C5.0 decision tree algorithm to rockburst prediction; this model can show the relationship between the input and output. Subsequently, it is proved that combination algorithms perform better in prediction than single algorithms, and the optimal parameters of the models can be determined by optimization algorithms. Li et al. (2017) and Xue et al. (2020b) used GA algorithm and PSO algorithm to determine the hyper-parameters in extreme learning machine (ELM) respectively. Ji et al. (2020) determined hyper-parameters in support vector machine (SVM) through genetic algorithm (GA) and built a GA-SVM rockburst prediction model. Liu and Hu (2019) used PSO algorithm to optimize back propagation neural network (BP), probabilistic neural network (PNN), and support vector machine (SVM); the results show that the prediction performance of PSO–PNN model is the best. In recent years, ensemble algorithms have found wide application in predicting rockburst intensity grades. Ensemble algorithms mainly comprise Bagging, Boosting, and Stacking (Fig. 1). Taking six classifiers as individual learners, Liang et al. (2021) created ensemble classifiers with different weightings based on different weighting rules. Voting, an ensemble learning model that follows the majority rule, can integrate performances of individual classifiers better than other ensemble algorithms. Li et al. (2022a) and Tan et al. (2022) built various models of Voting, Bagging, and AdaBoost, and the comparison reveals that Voting-Soft performs the best. However, all the Voting models calculate the voting weights of classifiers according to accuracy, recall, and F1-score, and thus have limitations to some extent. Some scholars determined the weights of classifiers in Voting-Soft by means of optimization algorithms. Zhang et al. (2020) optimized the Voting-Soft model with the beetle antennae search (BAS) algorithm which has a low convergence rate and takes a long time to train the model.

Fig. 1
figure 1

ML methods for classification and prediction of rockburst intensity grades

Full size image

Though ensemble algorithms, especially Voting, are usually superior to single algorithms with respect to prediction, the determination of the type and number of individual learners in Voting is unfounded, and the determination of voting weights of individual learners has a significant impact on model performance. Moreover, the datasets used to train models are likely to be beset by data imbalance or data anomalies. SMOTE can make data structures balanced, but it fails to eliminate class differences between data of different types. Therefore, the following work was done in this study to address problems in existing researches: (1) The method for rockburst data preprocessing was improved. Outliers were eliminated by means of density-based spatial clustering of applications with noise (DBSCAN), and CURE-MeanradiusSMOTE was proposed to obtain a balanced data structure. (2) The AOA-Voting-Soft model was established to predict the rockburst intensity grades. (3) The best classifier combination in Voting was determined by the game theory and method of exhaustion. (4) The weights of individual learners in Voting were determined through arithmetic optimization algorithm (AOA) and fivefold cross-validation (CV).

In this study, a data preprocessing method and an ensemble algorithm prediction model were proposed and applied to rockburst intensity grade prediction. The manuscript is organized as follows. First, rockburst data were preprocessed. Next, the AOA-Voting-Soft ensemble learning model was established. Furthermore, the effect of data preprocessing was verified, and the predictive performance of the proposed model was compared with those of single models and other ensemble models. Finally, the model was applied to rockburst intensity grade prediction of projects like the Dochu La Tunnel, and its generalization ability was verified.

2 Dataset Preparation

2.1 Data Collection

All data in this paper are from worldwide rockburst cases that have been extensively cited and employed. The dataset consists of data of 319 rockburst cases, of which 213 rockburst cases are from Zhou et al. (2016), 21 from Wang et al. (2013), 19 from Zhou et al. (2013), 46 from Dong et al. (2013), and 20 from Xue et al. (2019). These data involve different underground projects such as mines, traffic tunnels, diversion tunnels, and underground chambers. Their diversity ensures that the established ML model has excellent generalization ability.

The occurrence of rockburst is influenced by many factors. When evaluating the intensity grade of rockburst, different scholars choose different parameters as evaluation indicators of criterion for rockburst. Currently, the mainstream input parameters of criteria for rockburst are the maximum tangential stress of the surrounding rock (\(\sigma_{\theta }\)), the uniaxial compressive strength of the rock (\(\sigma_{{\text{c}}}\)), the uniaxial tensile strength of the rock (\(\sigma_{{\text{t}}}\)), the rock brittleness coefficient (\(\sigma_{{\text{c}}} /\sigma_{{\text{t}}}\)), the rock stress coefficient (\(\sigma_{\theta } /\sigma_{{\text{c}}}\)), and the elastic strain energy index (\(W_{{{\text{et}}}}\)). Specifically, wet \(\sigma_{\theta }\) can reflect the strata stress characteristics of rockburst. \(\sigma_{{\text{t}}}\) and \(\sigma_{{\text{c}}}\) can effectively characterize the lithologic conditions of the surrounding rock in practical engineering. \({{\sigma_{{\text{c}}} } \mathord{\left/ {\vphantom {{\sigma_{{\text{c}}} } {\sigma_{{\text{t}}} }}} \right. \kern-0pt} {\sigma_{{\text{t}}} }}\) considers the influences of joints and the block size of the rock mass. \(\sigma_{\theta } /\sigma_{{\text{c}}}\), one of the commonly used rockburst evaluation indicators, represents the stress concentration of the surrounding rock after excavation. Rockburst is also related to the energy stored in the rock mass. \(W_{{{\text{et}}}}\) reflects the ability of rock to store elastic energy. The above six indicators reflect the characteristics of rockburst from different aspects (Xu et al. 2022) and are generally acknowledged by scholars worldwide to be closely related to rockburst (Li et al. 2023; Xu et al. 2022; Zhou et al. 2016).

The output indices of the dataset are the rockburst intensity grade. In this study, the database was classified into four grades (Zhou et al. 2012) according to the general standard for rockburst intensity classification, namely, Grades 0, 1, 2, and 3, which represent cases of none rockburst, weak rockburst, moderate rockburst, and strong rockburst, respectively (Table 1).

Table 1 Standard for rockburst intensity classification
Full size table

2.2 Data Analysis

The data in the database built in this study are fairly unbalanced, with data of Grade 0 accounting for 18.2% (58 cases), Grade 1 for 27.6% (88 cases), Grade 2 for 36.1% (115 cases), and Grade 3 for 18.2% (58 cases). The data sizes of none rockburst and strong rockburst are the smallest, and that of moderate rockburst is the largest. The ratio of data sizes of Grades 0–3 is 1:1.5:1.9:1.

The data distribution characteristics and ranges of the four grades are exhibited by the maximum, minimum, mean, and variable coefficient, and descriptive statistics are presented in Table 2. \(\sigma_{\theta }\) characterizes the in situ stress in the rockburst sector, and it is affected by geometry of the opening. The larger the value of \(\sigma_{\theta }\), the higher the risk and intensity grade of the rockburst. The data of \(\sigma_{\theta }\) in Table 2 increase as the intensity grade rises. For instance, the mean value of \(\sigma_{\theta }\) increases from 25.8 MPa to 115.8 MPa, by 348.4%. \(\sigma_{{\text{c}}}\) is a base rock mechanics index that shows the hardness of rock. The higher \(\sigma_{{\text{c}}}\) is, the greater the elastic strain energy is, and the higher the risk and intensity grade of rockburst are. Likewise, the data of \(\sigma_{{\text{c}}}\) in Table 2 increase as the intensity grade rises. For example, the mean value of \(\sigma_{{\text{c}}}\) increases from 107.9 to 135.7 MPa, an increase of 25.8%. The initiation and propagation of cracks during rockburst are closely related to the uniaxial tensile strength of rock mass \(\sigma_{{\text{t}}}\). The data in Table 2 indicate that \(\sigma_{{\text{t}}}\) increases with the increase of rockburst intensity grade. It is worth noting that since brittle crack failure occurs in rock mass during rockburst, the brittle coefficient \(\sigma_{{\text{c}}} /\sigma_{{\text{t}}}\) can be deemed a characteristic index of rockburst intensity. In addition, Tang and Wang (2002) proposed a new empirical criterion based on \(\sigma_{{\text{c}}} /\sigma_{{\text{t}}}\). The values of \(\sigma_{{\text{c}}} /\sigma_{{\text{t}}}\) in Table 2 are barely correlated with the rockburst intensity grade, and the data are highly discrete, which may result from the large number of outliers in the database. The gob-side rock mass with a larger stress coefficient \(\sigma_{\theta } /\sigma_{{\text{c}}}\) has poorer stability of equilibrium and thereby is more prone to rockburst. Russenes (1974) proposed a rockburst criterion based on \(\sigma_{\theta } /\sigma_{{\text{c}}}\).This can be verified by the positive correlation between \(\sigma_{\theta } /\sigma_{{\text{c}}}\) and the rockburst intensity grade (Table 2). \(W_{{{\text{et}}}}\) represents the ratio of the accumulated energy from elastic deformation of the surrounding rock to the released energy from its plastic deformation. Kidybinski (1981) proposed a classic rockburst classification criterion by testing the energy storage characteristics of rocks. Clearly, if more energy is accumulated while less energy is released, the risk and intensity grade of rockburst would be higher. The mean value of \(W_{{{\text{et}}}}\) in Table 2 rises from 2.9 of Grade 0 to 8.8 of Grade 3, by 206.2%. Moreover, some of the data in Table 2 have a large coefficient of variation. For example, the coefficient of variation of \(\sigma_{\theta } /\sigma_{{\text{c}}}\) in data of Grade 0 is 0.8, and that of \(\sigma_{\theta } /\sigma_{{\text{c}}}\) in data of Grade 3 is 1. This demonstrates outliers in the database affect the predictive performance of the ML model.

Pairs plots of the database built in this study are depicted in Fig. 2, where different colors of scattered points denote data of different rockburst grades. Kernel density maps of variables are on the diagonal lines of pairs plots, and the scatter diagrams of correlation between the two variables are in the non-diagonal areas. Besides, the Pearson correlation coefficient of the two variables is presented. Discrete points can be observed in all these correlation scatter diagrams. Meanwhile, data points of different rockburst grades overlap each other significantly in correlation scatter diagrams, which influences the predictive performance of ML models. In Kernel density maps in Fig. 2, data of \(\sigma_{\theta }\) are concentrated in the range of 30–70 MPa (accounting for 66.7% of the total data), \(\sigma_{{\text{c}}}\) in 90–130 MPa (48.6%), \(\sigma_{{\text{t}}}\) in 3–7 MPa (55.2%), and \(W_{{{\text{et}}}}\) in 3–7 MPa (80.3%). The maximum Pearson correlation coefficient is 0.49, which means variables are mutually independent .

Fig. 2
figure 2

Matrix scatter plot

Full size image
Table 2 Statistical parameters of different rockburst grades
Full size table

2.3 Data Preprocessing

2.3.1 Eliminating Outliers by DBSCAN

According to the analysis in Sect. 2.2, outlier points in the original data have a considerable impact on the predictive performance of the ML model. Therefore, abnormal data in the dataset were detected and eliminated by means of DBSCAN. DBSCAN, one of the density-based clustering algorithms, is used to determine the clusters of any shape that may exist in a given dataset (Ester et al. 1996). As this algorithm does not require human efforts to determine the number of clusters in advance, it can tackle with errors resulting from unreasonable setting of the cluster number.

DBSCAN only requires two parameters to create a new cluster, namely the radius of the cluster (eps) and the minimum number of points (MinPts) within a circle of radius eps (Hao et al. 2015). And it classifies all points into three types: core points, border points, and noise points. In Fig. 3a, A is the core point because the number of points within its cluster radius eps is more than or equal to MinPts; B is the border point because it is not a core point but it is within the cluster of a core point; a point that belongs to neither the type of Point A nor the type of Point B is a noise point, e.g., Point C in Fig. 3a.

Fig. 3
figure 3

DBSCAN. a DBSCAN clustering; b K-distance graph

Full size image

DBSCAN is quite sensitive to the eps value. Specifically, an excessively small eps value may lead to an expanded range of noise points, whereas an excessively large eps value may result in a poor detection effect of outliers. The K-distance graph technique is used to determine the eps (Starczewski et al. 2020). As illustrated in Fig. 3b, with the number of nearest neighbors of each point in the rockburst database \(K\) regarded as the abscissa, K-distance was calculated and taken as the ordinate. Subsequently, \(k_{{{\text{dist}}}}\) graph was plotted in ascending order, and the ordinate of its maximum curvature point is the best eps. The value of MinPts was determined based on Eq. (1) (Arafa et al. 2022).

$${\text{MinPts}} = \ln N,$$
(1)

where \(N\) is the number of samples in the rockburst database.

The results indicate that the values of MinPts and eps are 6 and 1.014, respectively. Moreover, two samples of moderate rockburst and fifteen samples of strong rockburst are removed from the original database by means of DBSCAN.

2.3.2 Eliminating Dataset Imbalance Through Cure-MeanradiusSMOTE

According to the analysis in Sect. 2.2, the initial rockburst dataset is imbalanced. Consequently, ML models may mistake minority-class samples as majority-class ones, thereby weakening the predictive performance of ML models. Hence, the rockburst database needs to be oversampled. It is noteworthy that oversampling should be performed on rockburst datasets where the outliers have been omitted so as to prevent the generation of new outliers during the oversampling process. The CURE-MeanradiusSMOTE method proposed in this study is based on Kmeans-SMOTE, a common oversampling method.

CURE-MeanradiusSMOTE includes three stages, i.e., clustering, filtering, and oversampling. In the clustering stage, clustering is conducted on rockburst data by the clustering using representatives (CURE) algorithm. In the oversampling stage, the radius and geometric center are considered when new data are generated. Compared with the Kmeans-SMOTE, the proposed algorithm is more efficient for datasets of any shape, and can generate new data that are more likely to be distributed around the average radius of minority-class samples. In this way, it enhances ML models’ ability to recognize decision boundaries.

The CURE-MeanradiusSMOTE schematic is shown in Fig. 4CURE-MeanradiusSMOTE schematic is shown, the specific procedure of CURE-MeanradiusSMOTE is introduced as follows:

  1. 1.

    Clustering is conducted on rockburst data by the CURE algorithm, and clusters with a high proportion of minority-class samples are retained. The center of these clusters is calculated and denoted by \(x_{{\text{c}}}\).

  2. 2.

    The weights of rockburst characteristic indices are calculated by principal component analysis.

  3. 3.

    The weighted Euclidean distances between points in retained clusters in Step 1 and the cluster center are calculated, and then their average is calculated and represented by \(d_{m}\).

  4. 4.

    \(k\) minority-class samples are randomly selected from clusters retained in Step 1, and then \(k\) vectors \(v_{i}\) from the sample center to samples are calculated. Resultant vector \(\sum\limits_{i = 0}^{k} {v_{i} }\) of \(k\) vectors is calculated.

  5. 5.

    The distance between the new sample and the cluster center \(x_{{\text{c}}}\) is determined based on the average distance \(d_{m}\) and the parameter \(\theta\). The new sample is created according to Eq. (2):

    $$\begin{array}{*{20}c} {x_{new} = x_{c} + r * \sum\limits_{i = 0}^{k} {\nu_{i} } } & r \\ \end{array} \sim (\frac{{d_{m} }}{\theta },d_{m} ).$$
    (2)
  6. 6.

    Steps 3–5 are repeated until the number of majority-class and minority-class samples becomes balanced.


After data were made balanced, 55 data of none rockburst, 26 data of weak rockburst, and 71 data of strong rockburst were generated. The new rockburst database has a total of 452 rockburst data, the ratio of data of Grades 0–3 being 1:1:1:1 .

Fig. 4
figure 4

Schematic diagram of CURE-MeanradiusSMOTE

Full size image

3 ML Modeling

3.1 Fundamental Theory of AOA and Voting

3.1.1 Voting-Soft Algorithm

Ensemble learning, also known as a multi-classifier system or committee-based learning, is an algorithm that creates and combines multiple learners to complete learning tasks (Wang et al. 2020). Voting is a kind of ensemble learning that consists of multiple heterologous individual classifiers (Rojarath and Songpan 2021). The schematic diagram of Voting is depicted in Fig. 5. Voting is carried out in two ways: Voting-Hard and Voting-Soft. For Voting-Hard, the final result is determined in line with the majority rule. As presented in Fig. 5, three out of five classifiers choose Type B, so the prediction result is B. For Voting-Soft, the average of probability that all model prediction samples are of a certain type is regarded as the standard, and then the type with the highest probability is the final prediction result. As can be seen from Fig. 5, since the average of probability that five classifiers choose Type A is 0.6 and that for Type B is 0.3, the prediction result is A. It should be noted that the voting weights of C1–C5 in Fig. 5 are all set to 1. Unlike Voting-Hard, Voting-Soft requires each individual learner to calculate the probability of each type. It can give higher weights to individual learners with excellent predictive performance, so it typically outperforms Voting-Hard in terms of prediction.

Fig. 5
figure 5

Schematic diagram of Voting

Full size image

3.1.2 AOA

AOA is a population-based metaheuristic algorithm proposed by Abualigah et al. in (2021). The inspiration for AOA comes from the application of arithmetic operators (addition, subtraction, multiplication, and division) in solving arithmetic problems. The algorithm can deal with optimization without calculating derivatives. It is simple, and boasts few control parameters and excellent output performance. AOA consists of three stages, i.e., initialization, exploration, and exploitation, and its schematic diagram is shown in Fig. 6.

Fig. 6
figure 6

Flowchart of AOA

Full size image

Step 1 Initialization. Optimization strategies are selected with the aid of math optimizer accelerated (MOA).

AOA performs global search when r1 is greater than MOA, while it conducts local search when r1 is smaller than MOA. MOA is calculated based on Eq. (3):

$${\text{MOA}}\left( {C_{{{\text{Iter}}}} } \right) = {\text{Min}} + C_{{{\text{Iter}}}} \times \left( {\frac{{{\text{Max}} - {\text{Min}}}}{{M_{{{\text{Iter}}}} }}} \right),$$
(3)

where \({\text{MOA}}(C_{{{\text{Iter}}}} )\) is the function value at the tth iteration; \(C_{{{\text{Iter}}}}\) is the present iteration whose value lies between 1 and \(M_{{{\text{Iter}}}}\); \({\text{Max}}\) and \({\text{Min}}\) are the maximum and minimum values of the acceleration function, respectively.

Step 2 Exploration.

AOA carries out diversified global search by means of multiplication or division in the exploration stage. It performs division when \(r_{2}\) is smaller than 0.5, while it conducts multiplication when \(r_{2}\) is greater than or equal to 0.5. \(r_{2}\) is a random number, and \(r_{2}\) \(\in\) [0,1]. The location update strategy is:

$$x_{i,j} (C_{Iter} + 1) = \left\{ {\begin{array}{*{20}l} {{\text{best}}(x_{j} ) \div (E + \varepsilon ) \times \left[ {\left( {{\text{UB}}_{j} - {\text{LB}}_{j} } \right) \times \mu + {\text{LB}}_{j} } \right]} \hfill & {r_{2} < 0.5} \hfill \\ {{\text{best}}(x_{j} ) \times {\text{MOP}} \times \left[ {\left( {{\text{UB}}_{j} - {\text{LB}}_{j} } \right) \times \mu + {\text{LB}}_{j} } \right]} \hfill & {{\text{otherwise}},} \hfill \\ \end{array} } \right.$$
(4)

where \(x_{i,j} (C_{{{\text{Iter}}}} + 1)\) is the ith solution in the next iteration; \(x_{i,j} (C_{{{\text{Iter}}}} )\) is the jth position of the ith solution in the present iteration; \({\text{best}}(x_{j} )\) is the jth position of the best solution obtained so far; \(\varepsilon\) is a decimal number; \({\text{UB}}_{j}\) and \({\text{LB}}_{j}\) are the upper and lower limits of the jth position, respectively; \(\mu\) is the control parameter that adjusts the searching process. Multi-objective optimization problem (MOP), which is the coefficient of mathematical optimization rate, is calculated according to Eq. (5):

$${\text{MOP}}(C_{{{\text{Iter}}}} ) = 1 - \frac{{C_{{{\text{Iter}}}}^{1/a} }}{{M_{{{\text{Iter}}}}^{1/a} }},$$
(5)

where \({\text{MOP}}(C_{{{\text{Iter}}}} )\) is the function value at the tth iteration; \(M_{{{\text{Iter}}}}\) is the maximum number of iterations; \(a\) is the sensitive parameter, which defines the development accuracy of iteration.

Step 3 Exploitation.

AOA searches for the optimal solution in many dense regions in the exploration stage through the strategy of search by subtraction or addition. r3 is a random number, and \(r_{3}\) ∈ [0,1]. When r3 is smaller than 0.5, the strategy of search by subtraction is taken; when \(r_{3}\) is greater than 0.5, the strategy of search by addition is adopted. The location update strategy is:

$$x_{i,j} (C_{{{\text{Iter}}}} + 1) = \left\{ {\begin{array}{*{20}c} {{\text{best}}(x_{j} ) - {\text{MOP}} \times \left[ {\left( {{\text{UB}}_{j} - {\text{LB}}_{j} } \right) \times \mu + {\text{LB}}_{j} } \right]} & {r_{3} < 0.5} \\ {{\text{best}}(x_{j} ) + {\text{MOP}} \times \left[ {\left( {{\text{UB}}_{j} - {\text{LB}}_{j} } \right) \times \mu + {\text{LB}}_{j} } \right]} & {{\text{otherwise}}.} \\ \end{array} } \right.$$
(6)

3.2 CV

CV is a common method for evaluating the generalization ability of ML models. In CV, the dataset is divided many times, and several models need to be trained. K-fold CV is the most common CV method (Wong and Yeh 2020). In this study, k was set to 5 according to previous studies (Motsinger and Ritchie 2006). In addition, the training set was randomly and evenly divided into five subsets, of which four were used for training models and determining their hyper-parameters, and one was for verifying these models’ generalization ability. The above process was repeated five times to obtain five different hyper-parameters, whose average was considered the final hyper-parameter (Fig. 7).

Fig. 7
figure 7

Fivefold CV

Full size image

3.3 Modeling and Hyper-parameter Tuning

3.3.1 Game Theory-Based Model Combination

According to Sect. 3.1.1, though Voting-Soft has some advantages over Voting-Hard, it requires each individual learner to have remarkable predictive performance and obtain diversified predictive results, which is extremely difficult to achieve. Hence, individual learners in Voting-Soft are required to take into consideration both accuracy and diversity. The accuracy of models shows their predictive performance, and their diversity can be seen from the correlation between their predictive results. In this study, the conflict between diversity and accuracy of models was mitigated by using the combination weighting method of game theory (Feng et al. 2019). Besides, the best classifier combination in Voting-Soft was determined through the exhaustive search method. The flow chart is shown in Fig. 8, the steps of calculation are as follows:

  1. 1.

    Prediction is performed by N ML models to obtain their prediction results and accuracy.

  2. 2.

    The diversity and accuracy weights of each individual learner are calculated.


    First, the Kendall correlation coefficients (Kendall) of prediction results of N models are calculated. The sum of correlation coefficients between an individual learner and others is averaged to obtain the correlation between this individual learner and others. The smaller the correlation is, the greater the difference between this individual learner and others. The diversity weight of the model is calculated through Eqs. (7) and (8):

    $$\lambda_{i}^{ * } = \frac{{{{\sum\limits_{i = 1}^{n - 1} {b_{i} } } \mathord{\left/ {\vphantom {{\sum\limits_{i = 1}^{n - 1} {b_{i} } } {n - 1}}} \right. \kern-0pt} {n - 1}}}}{{\sum\limits_{i = 1}^{n} {({{\sum\limits_{i = 1}^{n - 1} {b_{i} } } \mathord{\left/ {\vphantom {{\sum\limits_{i = 1}^{n - 1} {b_{i} } } {n - 1}}} \right. \kern-0pt} {n - 1}})} }},$$
    (7)
    $$\lambda_{i} = \frac{{1/\lambda_{i}^{ * } }}{{\sum\limits_{i = 1}^{n} {1/\lambda_{i}^{ * } } }},$$
    (8)

    where \(b\) is the correlation between a model and others; \(n\) is the number of models;\(\lambda_{i}^{*}\) is the diversity coefficient of the model; \(\lambda_{i}\) is the diversity weight of the model (Fig. 8).

    Fig. 8
    figure 8

    Schematic diagram of weight calculation by the game theory

    Full size image

    The greater the accuracy of a model is, the better its performance is. The accuracy weight of a model is calculated by Eq. (9):

    $$w_{i} = {{a_{i} } \mathord{\left/ {\vphantom {{a_{i} } {\sum\limits_{i = 1}^{n} {a_{i} } }}} \right. \kern-0pt} {\sum\limits_{i = 1}^{n} {a_{i} } }},$$
    (9)

    where \(a\) is the accuracy of the model; and \(w_{i}\) is the accuracy weight of the model.

  3. 3.

    The comprehensive weight of each individual learner is calculated by the combination weighting method of game theory according to Eq. (10):

    $$\left( {\begin{array}{*{20}c} {\lambda_{1} \lambda_{1}^{T} } & {\lambda_{1} a^{T} } \\ {a\lambda_{1}^{T} } & {aa^{T} } \\ \end{array} } \right)\left[ {\begin{array}{*{20}c} {b_{1} } \\ {b_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\lambda_{1} \lambda_{1}^{T} } \\ {aa^{T} } \\ \end{array} } \right],$$
    (10)
    $$W = b_{1}^{ * } \lambda_{1}^{T} + b_{2}^{ * } \lambda_{2}^{T} ,$$
    (11)

    where \(\lambda\) is the diversity weight matrix; \(a\) is the accuracy weight matrix; \(b_{1}\) and \(b_{2}\) are the linear combination coefficients to be solved; and \(W\) is the combination weight matrix. \(b_{1}^{ * }\) and \(b_{2}^{ * }\) are calculated through Eqs. (12) and (13):

    $$b_{1}^{ * } = \frac{{b_{1} }}{{b_{1} + b_{2} }},$$
    (12)
    $$b_{2}^{ * } = \frac{{b_{2} }}{{b_{1} + b_{2} }}.$$
    (13)
  4. 4.

    N models are placed into Voting for training and prediction, and models with small weights are eliminated in sequence to select the optimal model combination for rockburst intensity grade prediction in Voting.

3.3.2 Modeling

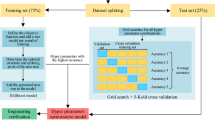
The dataset, consisting of 419 data, is split into the training and test sets. ML models are trained on the training set, and their generalization ability is tested on the test set. Because the type, number, voting weight, and predictive capability of individual learners in Voting-Soft models influence their predictive performance, in this study, the optimal combination of individual learners was determined based on the game theory, and the hyper-parameter and voting weight of each individual learner were determined by means of AOA and fivefold CV. Furthermore, the maximum number of iterations was set to 100, with ten individuals in each iteration. The sensitive parameter was 5, and the control parameter was 0.499. All parameters of AOA were determined through experimental testing. The modeling process is displayed in Fig. 9, and its steps are as follows:

  1. 1.

    Data are collected and analyzed.

  2. 2.

    Outliers are detected and eliminated by DBSCAN, and the data structure is made balanced by MeanRadius-SMOTE.

  3. 3.

    The preprocessed rockburst database is split into the training and test sets at a ratio of 7:3.

  4. 4.

    Hyper-parameters of base classifiers are determined by means of AOA and fivefold CV.

  5. 5.

    The combination weight of each individual learner is calculated through the combination weighting method of game theory.

  6. 6.

    The Voting-Soft model is built, and voting weights of base classifiers in Voting-Soft are determined through AOA and fivefold CV.

  7. 7.

    Individual learners with low weights are removed in sequence.

  8. 8.

    Whether the termination condition is met is determined. If it is, the Voting-Soft-AOA model is established based on the optimal combination of individual learners and voting weight; otherwise, Step 6 is performed.

  9. 9.

    The generalization ability is tested, and importance analysis is conducted on characteristic variables.

Fig. 9
figure 9

Flowchart of modeling

Full size image

3.4 Model Evaluation

Accuracy and recall, which are common indicators to evaluate predictive ability of classification models, are calculated with the confusion matrix (Fig. 10). The confusion matrix is widely adopted for evaluating the predictive accuracy of classification models in binary classification. In the confusion matrix for multi-class classification, each class is deemed positive in turn, and others negative. In this way, multi-class classification is converted into binary classification (Trajdos and Kurzynski 2018). The schematic diagram is exhibited in Fig. 10.

Fig. 10
figure 10

Schematic diagram of confusion matrix

Full size image

In addition to the above metrics, the receiver operating characteristic (ROC) and a larger area under the curve (AUC) evaluation metrics were applied in this study. False-positive rate and true-positive rate at different thresholds need to be calculated to draw a ROC curve whose abscissa and ordinate are the false-positive rate and the true-positive rate, respectively. AUC usually means higher classification accuracy. ROC and AUC can demonstrate the false-positive rate and the true-positive rate comprehensively. It is noteworthy that AUC and ROC can only be used for binary classification. Curves of each class are plotted for rockburst intensity grade prediction by binary decomposition. Four ROC curves were drawn, and four AUC values were calculated. Subsequently, these four ROC curves were averaged to obtain the curve of multi-class classification, and the four AUC values were also averaged to obtain the value of multi-class classification. Generally, a higher AUC value is indicative of better predictive performance of a model (Chen et al. 2022).

4 Results and Discussion

4.1 Verification of Data Preprocessing Effect

Voting in this study contains seven heterogenous individual classifiers, including three ensemble learning algorithms (XGBoost, GBDT, and RF), one neural network algorithm (MLP), and three single classical ML algorithms (KNN, SVM, and Bayesian). For the purpose of verifying the effect of the data preprocessing method (DBSCAN and Cure-MeanradiusSMOTE) used in this study, the prediction effects of these seven individual learners in the original rockburst database and the preprocessed rockburst database were compared by regarding model accuracy as the evaluation indicator. As presented in Table 3, the prediction accuracy of GBDT in the original rockburst data is 0.677. After being processed by SMOTE (Chawla et al. 2002; Fernandez et al. 2018), Kmeans-SMOTE (Douzas et al. 2018)and the data preprocessing method presented in this study, the model’s prediction accuracy is raised by 5.8%, 7.5%, and 11.7%, respectively. Obviously, the algorithm accuracy of seven individual learners is improved to varying degrees after data are preprocessed by the method presented in this study.

Table 3 Prediction accuracy of individual learners with different data preprocessing methods
Full size table

For the purpose of better demonstrating the preprocessing effect of rockburst data, dimensionality reduction and visualization were conducted on rockburst data by t-distributed stochastic neighbor embedding (TSNE). TSNE is a visualization tool that can maintain data separability of low-dimensional spaces in high-dimensional ones (Zhu et al. 2019). The distribution of the rockburst dataset before and after preprocessing is depicted in Fig. 11. It can be found from Fig. 11 that many outliers exist in the original rockburst data, and data of all intensity grades are mixed together. SMOTE creates new classes in the area of majority-class samples, and the new samples generated may be outliers. Samples created by KMeans-SMOTE seriously overlap, which may lead to overfitting. As presented in Fig. 11d, new samples generated by the method in this study are distributed uniformly in the space of minority class, and rockburst data of an intensity grade cluster together without outliers.

Fig. 11
figure 11

3D spatial distribution map of rockburst data. a Original data; b Data preprocessed by SMOTE; c Data preprocessed by KMeans-SMOTE; d Data processed by the method presented in this study

Full size image

4.2 Hyper-parameter Tuning for Base Classifiers

Hyper-parameters of seven individual learners in Voting were optimized by means of AOA and fivefold CV. Bayesian does not need optimization owing to its particularity. Accuracy was set as the objective function of AOA to find optimal hyper-parameters for other individual classifiers. Hyper-parameters and optimal values of classifiers are displayed in Table 4.

Table 4 Hyper-parameters of individual learners
Full size table

Figure 12 shows the iteration process in which AOA finds the maximum accuracy. Due to randomness of initial points in AOA, objective functions of different models have different values in the initial state. For instance, in SVM, the accuracy of objective functions increases gradually as the iteration is performed, which means AOA is effective in tuning SVM architecture. The highest accuracy is 0.62 at the 1st iteration, while it increases to 0.79 at the 50th iteration. At this time, the penalty coefficient is 1.012567, and the Kernel function is the radial basis function (RBF).

Fig. 12
figure 12

Hyper-parameter tuning for individual learners

Full size image

4.3 Optimal Combination of Base Classifiers

To calculate the combination weight of each individual classifier, the diversity weight, accuracy weight, and combination weight of each individual classifier were calculated with the method introduced in Sect. 3.3.1 based on the prediction results of optimized individual classifiers. The calculation results in Table 5 indicate that Bayesian has the lowest combination weight, 0.136, while GBDT has the highest combination weight, 0.150.

Table 5 Comprehensive weights of individual learners
Full size table

Voting-Soft-AOA models were built based on seven classifiers, and then those with low weights were eliminated sequentially by the exhaustive search method. According to the results in Fig. 13, the Voting-Soft-AOA model built with seven base classifiers has the best performance, with an overall accuracy of 0.875. As the number of base classifiers reduces, the performance of Voting-Soft-AOA models becomes progressively worse. The Voting-Soft-AOA model built with three base classifiers has the lowest overall accuracy, 0.80147. Hence, the Voting-Soft-AOA model build with seven base classifiers was ultimately chosen in this study.

Fig. 13
figure 13

Accuracy of Voting-Soft-AOA models with different classifier combinations in the test set

Full size image

4.4 Voting Weight Tuning for Base Classifiers

Figure 14 displays the iterative process in which AOA finds the maximum accuracy. It can be seen from Fig. 14 that the accuracy increases gradually as AOA iterates, which means AOA is effective in optimizing weights of base classifiers. The first iteration witnesses the lowest accuracy of 0.8459, and it rises to 0.875 in the 27th iteration. Hyper-parameters of Voting-Soft are listed in Table 6.

Fig. 14
figure 14

Schematic diagram of Voting-Soft-AOA iteration

Full size image
Table 6 Voting weights of base classifiers
Full size table

4.5 Prediction Performance

4.5.1 Performance Comparison Between Ensemble and Individual Classifiers

Table 7 reveals F1-score, recall, and accuracy of the ensemble classifier (Voting-Soft-AOA), and individual classifiers at three rockburst intensity grades (grades 0–3). In prediction of none rockburst, Voting-Soft-AOA has the highest F1-score, recall, and accuracy of 0.96, 0.91, and 1, respectively. In prediction of weak rockburst, Voting-Soft-AOA has the highest F1-score, recall, and accuracy of 0.79, 0.88, and 0.72, respectively. In prediction of moderate rockburst, GBDT and XGBoost have the highest recall of 0.75, while Voting-Soft-AOA has the highest F1-score and accuracy of 0.77 and 0.82, respectively. In prediction of strong rockburst, XGBoost has the highest accuracy of 0.87, while Voting-Soft-AOA has the highest F1-score and recall of 0.91 and 0.86, respectively. Overall, Voting-Soft-AOA shows the best predictive performance at all the three rockburst intensity grades.

Table 7 Performance comparison of Voting-Soft-AOA and other ML models
Full size table

Figure 15 exhibits the overall accuracy of seven individual classifiers and Voting-Soft-AOA. Among the seven individual classifiers, GBDT has the highest accuracy of 83.1%, followed by XGBoost, SVM, MLP, KNN, RF, and Bayesian in turn. The Voting-Soft-AOA model has the highest overall accuracy of 87.5%, 4.4% higher than that of the ensemble learning algorithm GBDT. It suggests that Voting-Soft-AOA is superior in rockburst intensity grade prediction.

Fig. 15
figure 15

Accuracy of Voting-Soft-AOA and other ML models

Full size image

Figure 16 presents ROC curves and AUC values of seven individual classifiers and Voting-Soft-AOA. ROC curves of all the prediction models are on the upper left. In general, the ROC curve of Voting-Soft-AOA is the closest to the upper left corner, which proves the best predictive performance of Voting-Soft-AOA. Among the seven individual learners, GBDT has the highest AUC value of 0.948, while KNN has the lowest AUC value of 0.891. Voting-Soft-AOA has the highest AUC value of 0.952, 0.004 higher than that of GBDT. The results demonstrate that Voting-Soft-AOA achieves the best performance in predicting rockburst intensity grades.

Fig. 16
figure 16

ROC curves and AUC values of seven individual classifiers and Voting-Soft-AOA on the test set

Full size image

4.5.2 Performance Comparison Between Voting-Soft-AOA and Other Ensemble Algorithms

To compare the predictive performance of Voting-Soft-AOA with other ensemble algorithms, Voting-Hard, Voting-Soft, Stacking, Bagging SVM (BagSVM), and Bagging KNN (BagKNN) were selected as comparative models. Figure 17 displays the overall accuracy of different ensemble algorithms on the test set. Voting-Soft-AOA has the highest overall accuracy, followed by Stacking, and BagKNN performs the worst. In addition, Voting-Soft performs better than Voting-Hard, which demonstrates that giving different weights to different individual learners can improve the predictive performance of Voting. After hyper-parameter tuning for Voting-Soft with the aid of AOA, the accuracy of Voting-Soft model is 0.875, better than that of other ensemble learning models.

Fig. 17
figure 17

Accuracy of different ensemble algorithms on the test set

Full size image

In the hope of further testing the predictive performance of different ensemble algorithms, F1-score was regarded as an evaluation index here. The F1-score values of different ensemble algorithms on the test set are illustrated in Fig. 18. Voting-Soft-AOA is superior to other ensemble models, while BagKNN is inferior to other ensemble models in terms of predictive capability at all the rockburst intensity grades.

Fig. 18
figure 18

F1-scores of different ensemble algorithms on the test set

Full size image

4.6 Variable Importance

To calculate the relative importance of rockburst characteristic variables, Voting-Soft-AOA was taken as the objective function, and sensitivity analysis was performed on characteristic variables by the random balance design Fourier amplitude sensitivity test (RBD-FAST). RBD-FAST is a method that achieves the latest development in FAST by RBD, so as to reduce computational costs (Mara 2009). All parameters are set to the same frequency, and they are randomly recombined after sampling. Then, Fourier decomposition is performed with fast Fourier transform (FFT) on the model output based on the order of the previous recombination to obtain the first-order sensitivity analysis results of parameters (Gao et al. 2020).

In RBD-FAST, changes in the results are decomposed into:

$$S_{i} = {\raise0.7ex\hbox{${V_{{x_{i} }} }$} \!\mathord{\left/ {\vphantom {{V_{{x_{i} }} } {V(Y)}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${V(Y)}$}},$$
(14)

where \(V_{{x_{i} }}\) is the variance-based first-order influence of input factor \(x_{i}\); and \(V(Y)\) is the total variance output by Voting-Soft-AOA.

The relative importance of each input variable was calculated (Fig. 19). It can be seen from Fig. 19 that \(W_{{{\text{et}}}}\) is the most important input variable with a relative importance score of 0.45, followed by \(\sigma_{\theta }\) (0.31), \({{\sigma_{\theta } } \mathord{\left/ {\vphantom {{\sigma_{\theta } } {\sigma_{{\text{c}}} }}} \right. \kern-0pt} {\sigma_{{\text{c}}} }}\) (0.15), \(\sigma_{t}\) (0.04), \({{\sigma_{{\text{c}}} } \mathord{\left/ {\vphantom {{\sigma_{{\text{c}}} } {\sigma_{{\text{t}}} }}} \right. \kern-0pt} {\sigma_{{\text{t}}} }}\) (0.03), and \(\sigma_{{\text{c}}}\) (0.02) in turn.

Fig. 19
figure 19

Relative importance of characteristic variables

Full size image

The calculation results show that \(W_{{{\text{et}}}}\) is the most important factor affecting the intensity grade of rockburst. As one of the most commonly used evaluation indicators for the intensity grade of rockburst, \(W_{{{\text{et}}}}\) is often used in research on rockburst empirical criteria. The larger its value is, the more energy is released during rockburst. Thus, it can effectively reflect the occurrence and intensity of rockburst. In addition, the calculation results in this study are consistent with the research results of many scholars (Sun et al. 2021; Xue et al. 2022; Zhang et al. 2020). It is noteworthy that although the calculation results show that \(\sigma_{{\text{c}}}\) has the lowest relative importance, it does not mean that \(\sigma_{{\text{c}}}\) is unimportant, because the results were observed by comparing all the influencing factors together. Meanwhile, the calculation results in this study are also different from those of some other scholars (Guo et al. 2022; Li et al. 2022b), mainly for the following reasons: (1) Different datasets can result in different degrees of variation, extremum values, input parameters, and rockburst grades of each variable, all of which can lead to different final calculation results. Besides, different data preprocessing methods may also yield different calculation results. (2) Different prediction models may lead to different nonlinear relationships between input and output variables, thereby producing different calculation results. Therefore, in future work, the authors will collect more samples, construct larger databases, and establish models with stronger generalization ability to make the calculation results more accurate.

A larger \(W_{{{\text{et}}}}\) means that more energy is stored in the surrounding rock, and thus the risk of rockburst is higher. Scholars have put forward various measures (He et al. 2020; Zhang et al. 2023, 2019; Zhao et al. 2016) to reduce the impact of \(W_{{{\text{et}}}}\) on rockburst intensity grades: (1) Roof pressure relief technology. It destroys those rock strata with large energy storage ahead of time by virtue of technologies including blasting, hydraulic fracturing, and surface fracturing, thus making rock strata less intact and releasing the stored energy. In this way, the value of \(W_{{{\text{et}}}}\) can be decreased to make engineering less prone to rockburst. (2) Floor pressure relief technology. It damages floor structures, and thus releases stored elastic energy in a timely manner by methods including deep hole floor-break blasting and floor grooving.

5 Case Application

For the purpose of testing the predictive performance of Voting-Soft-AOA in practical engineering, on-site data were collected from five different tunnels and mining projects, and six parameters obtained on-site were taken as input into this model to predict the on-site rockburst intensity grade. Besides, the prediction results were compared with those of the empirical prediction method based on the Russenes criterion (Russenes 1974). The prediction results revealed in Table 8 show that predictions of Voting-Soft-AOA are in line with actual situations of all these projects. Meanwhile, the overall prediction accuracy of Voting-Soft-AOA is superior to that of the Russell criterion. This proves that the model has great generalization ability and thereby can be applied in practical engineering. Moreover, these new rockburst data can enrich the rockburst database to improve the predictive ability of models.

Table 8 Engineering application of the proposed Voting-Soft-AOA model
Full size table

6 Conclusions

A Voting-Soft-AOA ML model for rockburst data preprocessing and rockburst intensity grade prediction was proposed in this study. Besides, multiple data preprocessing methods were compared to verify the superiority of DBSCAN and Meancure-SMOTE in data prediction, as well as the accuracy of Voting-Soft-AOA in rockburst intensity grade prediction. Conclusions are summarized as follows:

  1. 1.

    The data were preprocessed by eliminating Outliers in the rockburst database through DBSCAN and then making the dataset balanced through Meancure-SMOTE. The predictive abilities of seven prediction models on different datasets were compared, and the distribution of these datasets in three-dimensional space was observed. It is drawn from the results that methods proposed in this study show better predictive performance than Kmeans-SMOTE, and SMOTE.

  2. 2.

    Hyper-parameters and voting weights for base classifiers in Voting were determined by means of AOA and fivefold CV. In addition, the optimal combination of base classifiers in Voting-Soft-AOA was determined by the combination weighting method of game theory and the exhaustive search method.

  3. 3.

    Voting-Soft-AOA outperforms individual learners and other ensemble models in terms of prediction at all the four rockburst intensity grade and overall prediction.

  4. 4.

    Sensitivity study was conducted on input variables with RBD-FAST, and the results suggest that \(W_{{{\text{et}}}}\) is the most important input variable, with a relative importance score of 44.94%. Hence, emphasis should be placed on \(W_{{{\text{et}}}}\) in practical underground engineering to prevent rockburst.

  5. 5.

    The application of Voting-Soft-AOA to practical engineering proves that it can provide reference for rockburst warning in actual underground engineering.