A Unified Constitutive Model for Rock Based on Newly Modified GZZ Criterion

Abstract

This paper proposes a unified constitutive model for rock based on the newly modified generalized Zhang-Zhu (GZZ) criterion. The constitutive model adopts a non-associated plastic flow rule and a continuous potential function that takes the three effective principal stresses into account. To reflect strain-softening, strain-hardening, and elastic-perfectly plastic behavior of rock in a unified way, a general expression is proposed to model the post-failure behavior of rock using the deviatoric plastic shear strain as the fundamental variable. The proposed constitutive model has been successfully implemented in a 3D finite-difference code and validated using it to simulate the true triaxial test of two types of rocks and comparing the simulation results with the experimental data. Finally, a 3D numerical model based on the proposed constitutive model is constructed to simulate a highway rock tunnel during construction. The results show that the predicted displacements of the rock tunnel are in good agreement with the field measurements.

1 Introduction

Modeling rock behavior is one of the most important problems in rock mechanics and rock engineering (Zhang 2016). Much work has been carried out during the past decades regarding the constitutive model for rock. Singh (1973) proposed a constitutive model for jointed rock mass based on the assumption that discontinuities can be seen as staggered joints and the intact rock between the joints deforms elastically. Following the same idea, other empirical equations or flow rule functions on the joints were proposed to model the jointed rock mass (Gens et al. 1990; Cai and Horii 1992; Sitharam et al. 2001; Zandarin et al. 2013). However, those constitutive models apply to the joints rather than the whole rock mass, and the assumed elastic behavior for the intact rock between joints can result in the overestimation of rock stability.

To take the rock mass as a whole, it is of great importance to consider the strength of rock mass under a true triaxial stress condition rather than the failure stress in only one specific direction. The Hoek–Brown strength criterion (Hoek and Brown 1980, 1988; Hoek et al. 2002) is one of the most popular empirical failure criteria in rock mechanics due to its accuracy and wide applicability to different types of rock masses. However, the effective intermediate principal stress, ${\sigma }_{2}^{{\prime}}$, is ignored in the Hoek–Brown criterion, which may cause inaccurate predictions under true triaxial stress states in practical applications. To overcome this limitation, many researchers have proposed 3D versions of the Hoek–Brown criterion by considering the effect of ${\sigma }_{2}^{{\prime}}$ (Pan and Hudson 1988; Priest 2005, 2012; Zhang and Zhu 2007; Jiang et al. 2011; Zhang et al. 2013; Wu et al. 2018). Among those 3D criteria, the generalized Zhang-Zhu (GZZ) criterion (Zhang and Zhu 2007; Zhang 2008) can reduce to the 2D Hoek–Brown criterion and has a simple and explicit form. To solve the non-smoothness and non-convexity problems of the GZZ criterion, Zhang et al. (2013) successfully extended the GZZ criterion to a version with a smooth and convex surface. However, the modified GZZ criterion is not in a simple, explicit form and a numerical iterative procedure is required for determining the aspect ratio, a parameter used by Zhang et al. (2013) to define the shape of the criterion in $\pi$-plane. To tackle the non-smoothness and non-convexity problems more simply, a newly modified GZZ criterion with an explicit formulation expressed by the three stress invariants was proposed by Chen et al. (2019). In this paper, the newly modified GZZ criterion is adopted as the yield function for developing the unified constitutive model for rock.

The current commercial finite element (FE) and finite difference (FD) codes mainly use constitutive models based on the 2D Hoek–Brown criterion for rock. Although the strain hardening/softening behavior of soil, metal, and concrete can be properly considered, these codes usually only provide simple elastic-perfectly plastic constitutive models for rock masses (Itasca 2017; Brinkgreve et al. 2013; ABAQUS 2015; LSTC 2017). Therefore, this paper proposes a unified constitutive model based on the newly modified GZZ criterion, which considers not only the 3D strength but also the strain-softening, strain-hardening and elastic-perfectly plastic behavior of rock in a general way. The proposed constitutive model has been implemented in an FD code, FLAC3D, and validated by applying it to simulate the true triaxial test of two types of rocks and comparing the simulation results with the experimental data. Finally, the constitutive model is utilized to analyze a highway rock tunnel during construction to check its applicability to practical engineering problems.

2 Newly Modified GZZ Criterion

To provide the background information for developing the new constitutive model, this section briefly describes and discusses the Hoek–Brown criterion and the newly modified GZZ criterion.

The original Hoek–Brown criterion is given as (Hoek and Brown 1980):

$$\begin{array}{c}{\sigma }_{1}^{{\prime}}={\sigma }_{3}^{{\prime}}+{\sigma }_{c}{\left({m}_{i}\frac{{\sigma }_{3}^{{\prime}}}{{\sigma }_{c}}+1\right)}^{0.5},\end{array}$$

(1)

where ${\sigma }_{1}^{{\prime}}$ and ${\sigma }_{3}^{{\prime}}$ are the maximum and minimum effective principal stresses, respectively; ${\sigma }_{c}$ denotes the unconfined compressive strength (UCS) of the intact rock; and ${m}_{i}$ is a material constant for the intact rock.

For jointed rock masses, the generalized Hoek–Brown criterion, which takes both the fracture and rock mass conditions into account, is expressed as (Hoek et al. 1992):

$$\begin{array}{c}{\sigma }_{1}^{{\prime}}={\sigma }_{3}^{{\prime}}+{\sigma }_{c}{\left({m}_{b}\frac{{\sigma }_{3}^{{\prime}}}{{\sigma }_{c}}+s\right)}^{a},\end{array}$$

(2)

where ${m}_{b}$ denotes a material constant for rock masses; and a and s are two constants reflecting the characteristics of the rock masses. The three parameters can be determined by the empirical relations (Hoek et al. 2002):

$$\begin{array}{c}{m}_{b}={m}_{i}\cdot {\text{exp}}\left(\frac{\mathrm{GSI}-100}{28-14D}\right),\end{array}$$

(3a)

$$\begin{array}{c}s={\text{exp}}\left(\frac{\mathrm{GSI}-100}{9-3D}\right),\end{array}$$

(3b)

$$\begin{array}{c}a=\frac{1}{2}+\frac{1}{6}\left[\mathrm{exp}\left(-\frac{\mathrm{GSI}}{15}\right)-\mathrm{exp}\left(-\frac{20}{3}\right)\right],\end{array}$$

(3c)

where GSI is the geological strength index (GSI) (Hoek et al. 2002); and D is the disturbance factor representing the level of blast damage and stress relaxation to the rock mass.

Considering that the intermediate principal stress can have a significant effect on the strength of rock (Mogi 1971; Pan and Hudson 1988), Zhang and Zhu (2007) proposed a 3D version of the Hoek–Brown criterion with a = 0.5. Later on, Zhang (2008) extended it to a generalized form for all a values:

$$\begin{array}{c}\frac{1}{{\sigma }_{c}^{(1/a-1)}}{\left(\frac{3}{\sqrt{2}}{\tau }_{\mathrm{oct}}\right)}^{1/a}+\frac{{m}_{b}}{2}\left(\frac{3}{\sqrt{2}}{\tau }_{\mathrm{oct}}\right)-{m}_{b}{\sigma }_{m,2}^{{\prime}}=s{\sigma }_{c},\end{array}$$

(4)

where ${\tau }_{\mathrm{oct}}$ is the octahedral shear stress and ${\sigma }_{m,2}^{{\prime}}$ denotes the effective mean stress, which are determined by:

$$\begin{array}{c}{\tau }_{\mathrm{oct}}=\frac{1}{3}\sqrt{{\left({\sigma }_{1}^{{\prime}}-{\sigma }_{2}^{{\prime}}\right)}^{2}+{\left({\sigma }_{2}^{{\prime}}-{\sigma }_{3}^{{\prime}}\right)}^{2}+{\left({\sigma }_{3}^{{\prime}}-{\sigma }_{1}^{{\prime}}\right)}^{2}},\end{array}$$

(5a)

$$\begin{array}{c}{\sigma }_{m,2}^{{\prime}}=\frac{{\sigma }_{1}^{{\prime}}+{\sigma }_{3}^{{\prime}}}{2},\end{array}$$

(5b)

where ${\sigma }_{2}^{{\prime}}$ is the intermediate effective principal stress. The generalized 3D criterion (Eq. 4) has been named the generalized Zhang-Zhu criterion (Priest 2012) and, to be simple, is called the GZZ criterion in this paper.

The GZZ criterion uses the same parameters as the Hoek–Brown criterion and can reduce to the Hoek–Brown criterion under both triaxial compression (TC) and triaxial extension (TE) conditions, but it is neither smooth at the TC or TE state nor convex at the TE state. Therefore, Zhang et al. (2013) adopted three smooth and convex Lode dependences to replace the original Lode dependence of the GZZ criterion to address the non-smoothness and non-convexity problems. The modified GZZ criterion is given as:

$$\begin{array}{c}\sqrt{{J}_{2}}=L{\left({\theta }_{\sigma }\right)}_{X-D}\sqrt{{J}_{2,\mathrm{max}}};\;\; X=E,H \, {\text{and}} \, S,\end{array}$$

(6)

where J₂ is the second deviatoric stress invariant defined by:

$$\begin{array}{c}{J}_{2}=\frac{1}{6}\left[{\left({\sigma }_{1}^{{\prime}}-{\sigma }_{2}^{{\prime}}\right)}^{2}+{\left({\sigma }_{2}^{{\prime}}-{\sigma }_{3}^{{\prime}}\right)}^{2}+{\left({\sigma }_{3}^{{\prime}}-{\sigma }_{1}^{{\prime}}\right)}^{2}\right]=\frac{3}{2}{\tau }_{\mathrm{oct}}^{2}.\end{array}$$

(7a)

The subscripts E, H and S stand for the dependencies using elliptical approximation, hyperbolic expression and spatial mobilized plane, respectively, which are expressed by:

$$\begin{array}{c}L{\left({\theta }_{\sigma }\right)}_{E-D}=\frac{2(1-{\delta }^{2})\cos(\frac{\pi }{6}-{\theta }_{\sigma })+(2\delta -1)\sqrt{4(1-{\delta }^{2}){\cos}^{2}(\frac{\pi }{6}-{\theta }_{\sigma })+\delta (5\delta -4)}}{4(1-{\delta }^{2}){\cos}^{2}(\frac{\pi }{6}-{\theta }_{\sigma })+(2\delta -1{)}^{2}},\end{array}$$

(7b)

$$\begin{array}{c}L{\left({\theta }_{\sigma }\right)}_{H-D}=\frac{2\delta (1-{\delta }^{2})\cos(\frac{\pi }{6}+{\theta }_{\sigma })+\delta (\delta -2)\sqrt{4({\delta }^{2}-1){\cos}^{2}(\frac{\pi }{6}+{\theta }_{\sigma })+(5-4\delta )}}{4(1-{\delta }^{2}){\cos}^{2}(\frac{\pi }{6}+{\theta }_{\sigma })-(\delta -2{)}^{2}},\end{array}$$

(7c)

$$\begin{array}{c}L{\left({\theta }_{\sigma }\right)}_{S-D}=\frac{\sqrt{3}\delta }{2\sqrt{{\delta }^{2}-\delta +1}}\frac{1}{\mathrm{cos}\psi };\psi =\left\{\begin{array}{c}\frac{1}{6}\mathrm{arccos}\left[-1+\frac{27{\delta }^{2}(1-\delta {)}^{2}}{2({\delta }^{2}-\delta +1{)}^{3}}{\sin}^{2}(3{\theta }_{\sigma })\right], \, {\text{for}} \, {\theta }_{\sigma }\ge 0\\ \frac{\pi }{3}-\frac{1}{6}\mathrm{arccos}\left[-1+\frac{27{\delta }^{2}(1-\delta {)}^{2}}{2({\delta }^{2}-\delta +1{)}^{3}}{\sin}^{2}(3{\theta }_{\sigma })\right], \, {\text{for}} \, {\theta }_{\sigma }<0\end{array}\right.,\end{array}$$

(7d)

$$\begin{array}{c}\delta =\sqrt{\frac{{J}_{2,\mathrm{min}}}{{J}_{2,\mathrm{max}}}}=\sqrt{\frac{{J}_{2}\left(-\frac{\pi }{6}\right)}{{J}_{2}\left(\frac{\pi }{6}\right)}},\end{array}$$

(7e)

$$\begin{array}{c}{\theta }_{\sigma }=\frac{1}{3}{\sin}^{-1}\left(\frac{3\sqrt{3}{J}_{3}}{2{J}_{2}^{3/2}}\right),\end{array}$$

(7f)

$$\begin{array}{c}{J}_{3}=\left({\sigma }_{1}^{{\prime}}-{p}^{{\prime}}\right)\left({\sigma }_{2}^{{\prime}}-{p}^{{\prime}}\right)\left({\sigma }_{3}^{{\prime}}-{p}^{{\prime}}\right),\end{array}$$

(7g)

$$\begin{array}{c}{p}^{{\prime}}=\frac{{\sigma }_{1}^{{\prime}}+{\sigma }_{2}^{{\prime}}+{\sigma }_{3}^{{\prime}}}{3},\end{array}$$

(7h)

For a given rock, ${J}_{2,\mathrm{max}}$ and ${J}_{2,\mathrm{min}}$, in the same $\uppi$ plane, can be determined from an explicit expression if a = 0.5, but an iterative algorithm is needed when $a\ne 0.5$. This can result in difficulty in implementing the criterion in FE or FD codes.

To address the non-smoothness and non-convexity problems in a simpler way and with an explicit function, Chen et al. (2019) further modified the GZZ criterion as below:

$$\begin{array}{c}\frac{1}{{\sigma }_{c}^{\left(1/a-1\right)}}{\left(\frac{3}{\sqrt{2}}{\tau }_{\mathrm{oct}}\right)}^{1/a}+\frac{{m}_{b}}{2}\left(\frac{3}{\sqrt{2}}{\tau }_{\mathrm{oct}}\right)-\frac{{m}_{b}}{2}\sqrt{\frac{18{I}_{1}^{*3}{\tau }_{\mathrm{oct}}^{2}-81{I}_{1}^{*}{\tau }_{\mathrm{oct}}^{4}-54{I}_{3}^{*}{\tau }_{\mathrm{oct}}^{2}}{4{I}_{1}^{*3}-18{{I}_{1}^{*}\tau }_{\mathrm{oct}}^{2}-108{I}_{3}^{*}}}=0,\end{array}$$

(8)

where

$$\begin{array}{c}{I}_{1}^{*}=3{p}^{*}{=\sigma }_{1}^{*}+{\sigma }_{2}^{*}+{\sigma }_{3}^{*}={I}_{1}+3\frac{{\sigma }_{c}}{{m}_{b}}s,\end{array}$$

(9a)

$$\begin{array}{c}{I}_{3}^{*}={\sigma }_{1}^{*}{\sigma }_{2}^{*}{\sigma }_{3}^{*}=\left({\sigma }_{1}^{{\prime}}+\frac{{\sigma }_{c}}{{m}_{b}}s\right)\left({\sigma }_{2}^{{\prime}}+\frac{{\sigma }_{c}}{{m}_{b}}s\right)\left({\sigma }_{3}^{{\prime}}+\frac{{\sigma }_{c}}{{m}_{b}}s\right).\end{array}$$

(9b)

The newly modified GZZ criterion (Chen et al. 2019) can be seen as a 3D version of the Hoek–Brown criterion using the same parameters. Furthermore, the explicit expression with a smooth and convex shape in the $\pi$-plane makes it easier to be implemented into FE and FD codes than both the Hoek–Brown criterion (Hoek et al. 2002) and the modified GZZ criterion (Zhu et al. 2017). Therefore, the newly modified GZZ criterion by Chen et al. (2019) is adopted as the yield function for the proposed constitutive model.

3 Constitutive Model Based on the Newly Modified GZZ Criterion

3.1 Fundamentals of Plasticity and Return Mapping

In the theory of plasticity, the total strain increment can be decomposed into an elastic part and a plastic part (Owen and Hinton 1980):

$$\begin{array}{c}d\varepsilon =d{\varepsilon }^{e}+d{\varepsilon }^{p},\end{array}$$

(10a)

$$\begin{array}{c}\varepsilon =\left[{\varepsilon }_{x},{\varepsilon }_{y},{\varepsilon }_{z},{2\varepsilon }_{xy},2{\varepsilon }_{xz},2{\varepsilon }_{yz}\right],\end{array}$$

(10b)

where $d\varepsilon$ is the total strain increment; $d{\varepsilon }^{e}$ is the elastic strain increment, and $d{\varepsilon }^{p}$ is the plastic strain increment. $d{\varepsilon }^{p}$ does not occur when the stress state is within the yield surface f, while both $d{\varepsilon }^{e}$ and $d{\varepsilon }^{p}$ happen after yielding.

According to Hooke’s law, the stress increment caused by the elastic strain increment can be defined as:

$$\begin{array}{c}d\sigma =Dd{\varepsilon }^{e}=D\left(d\varepsilon -d{\varepsilon }^{p}\right),\end{array}$$

(11a)

$$\begin{array}{c}\sigma =\left[{\sigma }_{x}^{{\prime}},{\sigma }_{y}^{{\prime}},{\sigma }_{z}^{{\prime}},{\tau }_{xy},{\tau }_{xz},{\tau }_{yz}\right],\end{array}$$

(11b)

where $D$ is the elastic constitutive matrix with respect to Young’s modulus E and Poisson’s ratio $\nu$ as follows:

$$\begin{array}{c}D=\left[\begin{array}{cc}\begin{array}{ccc}{a}_{1}& {a}_{2}& {a}_{2}\\ {a}_{2}& {a}_{1}& {a}_{2}\\ {a}_{2}& {a}_{2}& {a}_{1}\end{array}& \begin{array}{ccc}& & \\ & & \\ & & \end{array}\\ \begin{array}{ccc}& & \\ & & \\ & & \end{array}& \begin{array}{ccc}G& & \\ & G& \\ & & G\end{array}\end{array}\right],\end{array}$$

(12a)

$$\begin{array}{c}{a}_{1}=K+\frac{4}{3}G,\end{array}$$

(12b)

$$\begin{array}{c}{a}_{2}=K-\frac{2}{3}G,\end{array}$$

(12c)

$$\begin{array}{c}K=\frac{E}{3\left(1-2\nu \right)},\end{array}$$

(12d)

$$\begin{array}{c}G=\frac{E}{2\left(1+\nu \right)}.\end{array}$$

(12e)

Equation (11a) can also be written as:

$$\begin{array}{c}d\sigma =Dd{\varepsilon }^{e}=D\left(d\varepsilon -d{\varepsilon }^{p}\right)=d{\sigma }^{e}-d{\sigma }^{p},\end{array}$$

(13)

which indicates that the stress increment can also be decomposed to an elastic part, $d{\sigma }^{e}$, and a plastic part, $d{\sigma }^{p}$.

As shown in Fig. 1, when the stress state (point A) is within but close to the yield curve (f = 0), a small strain increment may result in the initial trial stress state (point B) falling outside the yield surface (i.e., f (${\sigma }_{B}$) > 0). For the estimation of the initial trial stress state, it is assumed that no plastic strain occurs and thus ${\sigma }_{B}$ can be calculated using incremental elasticity as:

Fig. 1

(After Clausen and Damkilde 2008)

Schematic diagram of return mapping method.

$$\begin{array}{c}{\sigma }_{B}={\sigma }_{A}+Dd\varepsilon .\end{array}$$

(14)

Then a so-called plastic corrector stress increment, $\Delta {\sigma }^{p}$, is needed to drag the stress state (point B) back to the yield surface (point C), which can be described as:

$$\begin{array}{c}{\sigma }_{C}={\sigma }_{B}-\Delta {\sigma }^{p}={\sigma }_{B}-Dd{\varepsilon }^{p}={\sigma }_{A}+D\left(d\varepsilon -d{\varepsilon }^{p}\right).\end{array}$$

(15)

Equations (14) and (15) are the so-called return mapping method (Clausen and Damkilde 2008). According to the flow rule, the plastic strain increment can be expressed as:

$$\begin{array}{c}d{\varepsilon }^{p}=d\lambda \frac{\partial g}{\partial \sigma },\end{array}$$

(16)

where $d\lambda$ denotes the plastic multiplier and $g$ is the potential function. When $g=f$, the flow rule is associated and if $g\ne f$, it is non-associated.

Hence, the aforementioned plastic corrector stress increment can be formulated as

$$\begin{array}{c}\Delta {\sigma }^{p}={\int }_{\lambda }^{\lambda +\Delta \lambda }D\frac{\partial g}{\partial \sigma }d\lambda =\Delta \lambda D{\left.\frac{\partial g}{\partial \sigma }\right|}_{D},\end{array}$$

(17)

where $\Delta \lambda$ is the incremental form of $d\lambda$ and ${\left.\frac{\partial g}{\partial \sigma }\right|}_{D}$ means the value of $\frac{\partial g}{\partial \sigma }$ at point D which should be between points B and C. For convenience and simplification consideration, point D can be taken as point B or C if the strain increment is infinitesimal. It should be noted that the derivation of $g$ at B or C yields the same value for a liner potential function, but substituting ${\left.\frac{\partial g}{\partial \sigma }\right|}_{B}$ for ${\left.\frac{\partial g}{\partial \sigma }\right|}_{D}$ in a non-linear potential function, such as the Hoek–Brown criterion, can cause a radical return (Krieg and Krieg 1977).

Since point C is located on the yield surface f,

$$\begin{array}{c}f\left({\sigma }_{C}\right)=0.\end{array}$$

(18)

By solving Eq. (18), the value of the plastic multiplier can be determined; then by substituting $\Delta \lambda$ back into Eqs. (15) and (17), the final stress state at point C can be determined.

3.2 Constitutive Model Based on Newly Modified GZZ Criterion

Following the classical plasticity theory, the isotropic elastic behavior of the proposed constitutive model obeys Hooke’s law expressed by Eqs. (12a–e) and (13). Since the yield function, Eq. (8), contains a square root term, a negative value of the expression inside can lead to non-convergence of the constitutive model during return mapping. To solve the possible non-convergence problem and increase the speed of convergence, Eq. (8) is rewritten as:

$$\begin{array}{c}f=\left[{\left(\frac{q}{{\sigma }_{c}}\right)}^{2/a-2}+{m}_{b}{\left(\frac{q}{{\sigma }_{c}}\right)}^{1/a-1}\right]\left({I}_{1}^{*}{I}_{2}^{*}-9{I}_{3}^{*}\right)-2{{m}_{b}^{2}I}_{3}^{*}=0,\end{array}$$

(19)

where

$$\begin{array}{c}q=\sqrt{{I}_{1}^{*2}-3{I}_{2}^{*}},\end{array}$$

(20a)

$$\begin{array}{c}{I}_{2}^{*}={\sigma }_{1}^{*}{\sigma }_{2}^{*}{+{\sigma }_{2}^{*}\sigma }_{3}^{*}+{{\sigma }_{3}^{*}\sigma }_{1}^{*}.\end{array}$$

(20b)

Similarly, the potential function of the proposed constitutive model is defined as follows:

$$\begin{array}{c}g=\left[{\left(\frac{q}{{\sigma }_{c}}\right)}^{2/a-2}+{m}_{d}{\left(\frac{q}{{\sigma }_{c}}\right)}^{1/a-1}\right]\left({I}_{1}^{*}{I}_{2}^{*}-9{I}_{3}^{*}\right)-2{{m}_{d}^{2}I}_{3}^{*}=0,\end{array}$$

(21)

where ${m}_{d}$ is a material constant of rock. When ${m}_{d}$ is equal to ${m}_{b}$, the flow rule is associated; otherwise, the flow rule is non-associated.

To implement the return mapping algorithm, an expression for the plastic multiplier $\Delta \lambda$ needs to be derived. As shown in Eq. (11b), there are six basic stress components involved in the updating of the stress state, which makes it complicated for derivation. FLAC3D determines the effective principal stresses through the getEigenInfo() function by solving the following equations:

$$\begin{array}{c}{\sigma }_{1}^{{\prime}}+{\sigma }_{2}^{{\prime}}+{\sigma }_{3}^{{\prime}}={I}_{1}={\sigma }_{x}^{{\prime}}+{\sigma }_{y}^{{\prime}}+{\sigma }_{z}^{{\prime}},\end{array}$$

(22a)

$$\begin{array}{c}{\sigma }_{1}^{{\prime}}{\sigma }_{2}^{{\prime}}+{\sigma }_{2}^{{\prime}}{\sigma }_{3}^{{\prime}}+{\sigma }_{3}^{{\prime}}{\sigma }_{1}^{{\prime}}={I}_{2}={\sigma }_{x}^{{\prime}}{\sigma }_{y}^{{\prime}}+{\sigma }_{y}^{{\prime}}{\sigma }_{z}^{{\prime}}+{\sigma }_{z}^{{\prime}}{\sigma }_{x}^{{\prime}}-{\tau }_{xy}^{2}-{\tau }_{yz}^{2}-{\tau }_{xz}^{2},\end{array}$$

(22b)

$$\begin{array}{c}{\sigma }_{1}^{{\prime}}{\sigma }_{2}^{{\prime}}{\sigma }_{3}^{{\prime}}={I}_{3}={\sigma }_{x}^{{\prime}}{\sigma }_{y}^{{\prime}}{\sigma }_{z}^{{\prime}}+2{\tau }_{xy}{\tau }_{xz}{\tau }_{yz}-{\tau }_{xy}^{2}{\sigma }_{z}^{{\prime}}-{\tau }_{yz}^{2}{\sigma }_{x}^{{\prime}}-{\tau }_{xz}^{2}{\sigma }_{y}^{{\prime}}.\end{array}$$

(22c)

The stress state of point B will first be expressed as a principal stress tensor and then returned to point C via the return mapping algorithm. Finally, the principal stresses of point C will be converted back to the corresponding six stress components using the resolve() function. Therefore, the derivations below will use only the three principal stresses.

According to the flow rule and Eq. (15),

$$\begin{array}{c}d{\sigma }_{1}^{*p}=d{\sigma }_{1}^{p}=d\lambda \left[{a}_{1}\frac{\partial g}{\partial {\sigma }_{1}}+{a}_{2}\frac{\partial g}{\partial {\sigma }_{2}}+{a}_{2}\frac{\partial g}{\partial {\sigma }_{3}}\right],\end{array}$$

(23a)

$$\begin{array}{c}d{\sigma }_{2}^{*p}=d{\sigma }_{2}^{p}=d\lambda \left[{a}_{2}\frac{\partial g}{\partial {\sigma }_{1}}+{a}_{1}\frac{\partial g}{\partial {\sigma }_{2}}+{a}_{2}\frac{\partial g}{\partial {\sigma }_{3}}\right],\end{array}$$

(23b)

$$\begin{array}{c}d{\sigma }_{3}^{*p}=d{\sigma }_{3}^{p}=d\lambda \left[{a}_{2}\frac{\partial g}{\partial {\sigma }_{1}}+{a}_{2}\frac{\partial g}{\partial {\sigma }_{2}}+{a}_{1}\frac{\partial g}{\partial {\sigma }_{3}}\right],\end{array}$$

(23c)

where

$$\begin{array}{c}\frac{\partial g}{\partial {\sigma }_{i}}=\frac{3}{2}\frac{\partial g}{\partial q}\frac{{\sigma }_{i}-p}{q}+\frac{\partial g}{\partial {I}_{1}^{*}}+\frac{\partial g}{\partial {I}_{2}^{*}}\left({I}_{1}^{*}{-\sigma }_{i}^{*}\right)+\frac{\partial g}{\partial {I}_{3}^{*}}\frac{{I}_{3}^{*}}{{\sigma }_{i}^{*}};i=\mathrm{1,2},3,\end{array}$$

(24a)

$$\begin{array}{c}\frac{\partial g}{\partial q}=\frac{1}{q}\left[2{\frac{1-a}{a}\left(\frac{q}{{\sigma }_{c}}\right)}^{2/a-2}+{m}_{b}\frac{1-a}{a}{\left(\frac{q}{{\sigma }_{c}}\right)}^{1/a-1}\right]\left({I}_{1}^{*}{I}_{2}^{*}-9{I}_{3}^{*}\right),\end{array}$$

(24b)

$$\begin{array}{c}\frac{\partial g}{\partial {I}_{1}^{*}}=\left[{\left(\frac{q}{{\sigma }_{c}}\right)}^{2/a-2}+{m}_{d}{\left(\frac{q}{{\sigma }_{c}}\right)}^{1/a-1}\right]{I}_{2}^{*},\end{array}$$

(24c)

$$\begin{array}{c}\frac{\partial g}{\partial {I}_{2}^{*}}=\left[{\left(\frac{q}{{\sigma }_{c}}\right)}^{2/a-2}+{m}_{d}{\left(\frac{q}{{\sigma }_{c}}\right)}^{1/a-1}\right]{I}_{1}^{*},\end{array}$$

(24d)

$$\begin{array}{c}\frac{\partial g}{\partial {I}_{3}^{*}}=-9\left[{\left(\frac{q}{{\sigma }_{c}}\right)}^{2/a-2}+{m}_{d}{\left(\frac{q}{{\sigma }_{c}}\right)}^{1/a-1}\right]-2{m}_{d}^{2}.\end{array}$$

(24e)

Substitution of Eqs. (23a–c) into Eq. (17) yields,

$$\begin{array}{c}{\sigma }_{1C}^{*}={\sigma }_{1B}^{*}-\Delta {\sigma }_{1}^{{\prime}}={\sigma }_{1B}^{*}-\Delta \lambda \left[{a}_{1}{\left.\frac{\partial g}{\partial {\sigma }_{1}^{{\prime}}}\right|}_{D}+{a}_{2}{\left.\frac{\partial g}{\partial {\sigma }_{2}^{{\prime}}}\right|}_{D}+{a}_{2}{\left.\frac{\partial g}{\partial {\sigma }_{3}^{{\prime}}}\right|}_{D}\right],\end{array}$$

(25a)

$$\begin{array}{c}{\sigma }_{2C}^{*}={\sigma }_{2B}^{*}-\Delta {\sigma }_{2}^{{\prime}}={\sigma }_{2B}^{*}-\Delta \lambda \left[{a}_{2}{\left.\frac{\partial g}{\partial {\sigma }_{1}^{{\prime}}}\right|}_{D}+{a}_{1}{\left.\frac{\partial g}{\partial {\sigma }_{2}^{{\prime}}}\right|}_{D}+{a}_{2}{\left.\frac{\partial g}{\partial {\sigma }_{3}^{{\prime}}}\right|}_{D}\right],\end{array}$$

(25b)

$$\begin{array}{c}{\sigma }_{3C}^{*}={\sigma }_{3B}^{*}-\Delta {\sigma }_{3}^{{\prime}}={\sigma }_{3B}^{*}-\Delta \lambda \left[{a}_{2}{\left.\frac{\partial g}{\partial {\sigma }_{1}^{{\prime}}}\right|}_{D}+{a}_{2}{\left.\frac{\partial g}{\partial {\sigma }_{2}^{{\prime}}}\right|}_{D}+{a}_{1}{\left.\frac{\partial g}{\partial {\sigma }_{3}^{{\prime}}}\right|}_{D}\right].\end{array}$$

(25c)

Since point C should be located on the yield surface, Eqs. (25a–c) can be placed in Eq. (19) and the resulted equation can then be solved to determine the multiplier, $\Delta \lambda$. For an infinitesimal stress increment,

$$\begin{array}{c}f\left({\sigma }_{C}\right)-f\left({\sigma }_{B}\right)=\Delta f=-{\left.\frac{\partial f}{\partial {\sigma }_{1}^{{\prime}}}\right|}_{B}\Delta {\sigma }_{1}^{{\prime}}-{\left.\frac{\partial f}{\partial {\sigma }_{2}^{{\prime}}}\right|}_{B}\Delta {\sigma }_{2}^{{\prime}}-{\left.\frac{\partial f}{\partial {\sigma }_{3}^{{\prime}}}\right|}_{B}\Delta {\sigma }_{3}^{{\prime}}.\end{array}$$

(26)

Substitution of Eqs. (25a–c) into Eq. (26) yields,

$$\begin{array}{c}\Delta \lambda =\frac{f\left({\sigma }_{B}\right)}{{a}_{2}\left({\left.\frac{\partial g}{\partial {\sigma }_{1}^{{\prime}}}\right|}_{D}+{\left.\frac{\partial g}{\partial {\sigma }_{2}^{{\prime}}}\right|}_{D}+{\left.\frac{\partial g}{\partial {\sigma }_{3}^{{\prime}}}\right|}_{D}\right)\left({\left.\frac{\partial f}{\partial {\sigma }_{1}^{{\prime}}}\right|}_{B}+{\left.\frac{\partial f}{\partial {\sigma }_{2}^{{\prime}}}\right|}_{B}+{\left.\frac{\partial f}{\partial {\sigma }_{3}^{{\prime}}}\right|}_{B}\right)+G\left({\left.\frac{\partial f}{\partial {\sigma }_{1}^{{\prime}}}\right|}_{B}{\left.\frac{\partial g}{\partial {\sigma }_{1}^{{\prime}}}\right|}_{D}+{\left.\frac{\partial f}{\partial {\sigma }_{2}^{{\prime}}}\right|}_{B}{\left.\frac{\partial g}{\partial {\sigma }_{2}^{{\prime}}}\right|}_{D}+{\left.\frac{\partial f}{\partial {\sigma }_{3}^{{\prime}}}\right|}_{B}{\left.\frac{\partial g}{\partial {\sigma }_{3}^{{\prime}}}\right|}_{D}\right)}.\end{array}$$

(27)

Since Eq. (27) is derived under the condition of an infinitesimal stress increment, too large an error may be induced if the stress increment is not small enough. Therefore, the following iterative algorithm is proposed for determining $\Delta \lambda$:

• (1) Calculate an initial value of plastic multiplier $\Delta \lambda$, denoted as ${\left(\Delta \lambda \right)}_{1}$, from Eq. (27) and set $j=1$;

• (2) Calculate the updated stress state at point C:

  $$\begin{array}{c}{\sigma }_{C}={\sigma }_{B}-{\left(\Delta \lambda \right)}_{j}D{\left.\frac{\partial g}{\partial \sigma }\right|}_{B};\;\;j=\mathrm{1,2},3,\dots \end{array}$$

  (28)

• (3) Calculate the new plastic multiplier $\Delta \lambda$ using Newton’s method, denoted as ${\left(\Delta \lambda \right)}_{j+1}$:

  $$\begin{array}{c}{\left(\Delta \lambda \right)}_{j+1}={\left(\Delta \lambda \right)}_{j}-\frac{f\left[{\left(\Delta \lambda \right)}_{j}\right]}{{f}^{{\prime}}\left[{\left(\Delta \lambda \right)}_{j}\right]};\;\;j=\mathrm{1,2},3,\dots \end{array}$$

  (29)

  where

  $$\begin{array}{c}f\left[{\left(\Delta \lambda \right)}_{j}\right]=\left[{\left(\frac{{\left({q}_{C}\right)}_{j}}{{\sigma }_{c}}\right)}^{2/a-2}+{m}_{b}{\left(\frac{{\left({q}_{C}\right)}_{j}}{{\sigma }_{c}}\right)}^{1/a-1}\right]\left({\left({I}_{1C}^{*}\right)}_{j}{\left({I}_{2C}^{*}\right)}_{j}-9{\left({I}_{3C}^{*}\right)}_{j}\right)-2{m}_{b}^{2}{\left({I}_{3C}^{*}\right)}_{j},\end{array}$$

  (30a)
  $$\begin{array}{c}{f}^{{\prime}}\left[{\left(\Delta \lambda \right)}_{j}\right]=G{\left.\frac{\partial f}{\partial {\sigma }_{i}^{{\prime}}}\right|}_{C}{\left.\frac{\partial g}{\partial {\sigma }_{i}^{{\prime}}}\right|}_{B}+{a}_{2}\left({\left.\frac{\partial f}{\partial {\sigma }_{1}^{{\prime}}}\right|}_{C}+{\left.\frac{\partial f}{\partial {\sigma }_{2}^{{\prime}}}\right|}_{C}+{\left.\frac{\partial f}{\partial {\sigma }_{3}^{{\prime}}}\right|}_{C}\right)\left({\left.\frac{\partial g}{\partial {\sigma }_{1}^{{\prime}}}\right|}_{B}+{\left.\frac{\partial g}{\partial {\sigma }_{2}^{{\prime}}}\right|}_{B}+{\left.\frac{\partial g}{\partial {\sigma }_{3}^{{\prime}}}\right|}_{B}\right),\end{array}$$

  (30b)

  and update $j$: $j=j+1$;

• (4) Check the yield function f as follows:

  $$\begin{array}{c}\left|\frac{f\left[{\left(\Delta \lambda \right)}_{j}\right]}{{\sigma }_{c}^{3}}\right|\le \epsilon ,\end{array}$$

  (31)

  where $\epsilon$ is a prescribed convergence limit, i.e., 0.0001. If Eq. (31) is not satisfied, steps (2)–(4) are repeated. After Eq. (31) is satisfied, $\Delta \lambda ={\left(\Delta \lambda \right)}_{j}$ and the stress state is then calculated with Eq. (28).

3.3 General Strain-Softening and Strain-Hardening Rule

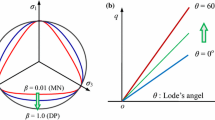
The post-failure of rock can be classified into three types: strain-softening, perfectly plastic and strain-hardening as shown in Fig. 2, with the corresponding parameters defined below and listed in Table 1. To characterize the three types of post-failures in a unified way, the deviatoric shear plastic strain ${\varepsilon }_{q}^{p}$ is selected as the fundamental variable and a general exponential function as shown in Fig. 3a is used to describe the evolution of the parameters in the yield function f. In the figure, x can be ${m}_{b}$, s or ${m}_{d}$. For example, for ${m}_{b}$ and s, we have

$$\begin{array}{c}{m}_{b}={m}_{\mathrm{br}}+\left({m}_{\mathrm{bi}}-{m}_{\mathrm{br}}\right){e}^{-3\frac{{\varepsilon }_{q}^{p}}{{\varepsilon }_{f}}},\end{array}$$

(32a)

$$\begin{array}{c}s={s}_{r}+\left({s}_{i}-{s}_{r}\right){e}^{-3\frac{{\varepsilon }_{q}^{p}}{{\varepsilon }_{f}}},\end{array}$$

(32b)

where the subscript i and r denote the initial value and residual value of rock parameters ${m}_{b}$ and s; ${\varepsilon }_{f}$ is the plastic deviatoric strain at which the yield function would almost evolve to the corresponding residual state f; and ${\varepsilon }_{q}^{p}$ is the plastic deviatoric shear strain defined by:

Fig. 2

Three types of post-failures of rock (the related parameters are listed in Table 1)

Table 1 Material parameters for strain-hardening, elastic-perfectly-plastic and strain softening models shown in Fig. 1

Fig. 3

a Relation between rock parameter and plastic deviatoric shear strain; and Evolution of yield function in ${p}^{*}$–$q$–${\varepsilon }_{q}^{p}$ space for: b strain-softening; c perfectly-plastic; and d strain-hardening

$$\begin{array}{c}{\varepsilon }_{q}^{p}=\int d{\varepsilon }_{q}^{p},\end{array}$$

(33a)

$$\begin{array}{c}d{\varepsilon }_{q}^{p}=\sqrt{\frac{{\left(d{\varepsilon }_{1}^{p}-d{\varepsilon }_{2}^{p}\right)}^{2}+{\left(d{\varepsilon }_{2}^{p}-d{\varepsilon }_{3}^{p}\right)}^{2}+{\left(d{\varepsilon }_{3}^{p}-d{\varepsilon }_{1}^{p}\right)}^{2}}{2}},\end{array}$$

(33b)

The potential function, $g$, shares the same parameters $a$ and $s$ as the yield function, $f$. In this case, if ${m}_{d}={m}_{b}$, the constitutive model is associated. Otherwise, the constitutive model is non-associated. Similar to ${m}_{b}$, the evolution of ${m}_{d}$ is defined by:

$$\begin{array}{c}{m}_{d}={m}_{\mathrm{dr}}+\left({m}_{\mathrm{di}}-{m}_{\mathrm{dr}}\right){e}^{-3\frac{{\varepsilon }_{q}^{p}}{{\varepsilon }_{g}}}\end{array}$$

(34)

where ${\varepsilon }_{g}$ is the plastic deviatoric strain at which the potential function would almost evolve to its residual state.

Taking advantage of the general strain softening/hardening rule, the yield curve of the proposed constitutive model evolves with the increase of the plastic deviatoric shear strain in the p*–q–${\varepsilon }_{q}^{p}$ space as shown in Fig. 3. When the stress state is within the yield surface, no plastic strain occurs and the yield function f₀, the red curve in Fig. 3b–d, is defined by the initial values of the rock material parameters. When the accumulated plastic deviatoric shear strain, ${\varepsilon }_{q}^{p}$, reaches a value, say ${\varepsilon }_{1}$ in Fig. 3a, the rock material parameters change as shown in Fig. 3a and the yield surface evolves to f_1s, f_1p or f_1h, the magenta curve in Fig. 3b–d depending on the type of post-failure. Finally, as ${\varepsilon }_{q}^{p}$ almost approaches ${\varepsilon }_{f}$, the yield surface (blue curves in Fig. 3b–d in p*–q–${\varepsilon }_{q}^{p}$ space would tend to the corresponding residual one.

In summary, the proposed unified constitutive model contains the following parameters:

• Young’s modulus E and Poisson’s ratio $\nu$.

• Unconfined compressive strength ${\sigma }_{c}$.

• Parameters for the initial yield function: ${m}_{\mathrm{bi}}$, ${s}_{i}$, $a$.

• Parameter for the initial potential function: ${m}_{\mathrm{di}}$, ${s}_{i}$, $a$.

• Parameters for the residual yield function: ${m}_{\mathrm{br}}$, ${s}_{r}$, $a$.

• Parameters for the residual potential function: ${m}_{\mathrm{dr}}$, ${s}_{r}$, $a$.

• Parameters for controlling the rate of softening/hardening: ${\varepsilon }_{f}$, ${\varepsilon }_{g}$.

The determination of these parameters is discussed in the next section.

3.4 Determination of Model Parameters

For the application of the proposed constitutive model, the 12 parameters involved in it should be determined. The following describes the recommended procedure for determining the parameters of the proposed model for intact rock and rock mass, respectively.

3.4.1 Intact Rock

For intact rock, uniaxial (at least one) and triaxial (at least three) compression tests can be conducted for determining the parameters as follows:

• (1) E, $\nu$ and ${\sigma }_{c}$ can be determined from the test results by following the standard procedure (Hudson and Harrison 1997).

• (2) ${m}_{\mathrm{bi}}$, ${s}_{i}$, $a$ are determined by fitting the peak strength data of the uniaxial and triaxial compression tests with the Hoek–Brown criterion with ${s}_{i}=1$ and $a=0.5$.

• (3) ${m}_{\mathrm{br}}$ and ${s}_{r}$ are determined by fitting the residual strength data of the uniaxial and triaxial compression tests with the Hoek–Brown criterion with $a=0.5$.

• (4) ${m}_{\mathrm{di}}$ and ${m}_{\mathrm{dr}}$ are determined based on the ratio of axial strain rate to lateral strain rate when the plastic strain takes place and when the stresses approach the final state from the triaxial compression tests, respectively.

• (5) ${\varepsilon }_{f}$ is the plastic deviatoric shear strain at which ${m}_{b}$ and $s$ approach ${m}_{\mathrm{br}}$ and ${s}_{r}$. Similarly, ${\varepsilon }_{g}$ is the plastic deviatoric shear strain at which ${m}_{d}$ approaches ${m}_{\mathrm{dr}}$. Both can be determined from the stress–strain relation of the triaxial compression tests.

3.4.2 Rock Mass

In terms of rock mass, it is difficult and even impossible to perform the required large-scale tests for determining the various parameters. In this case, the empirical methods based on the GSI system and typical data ranges can be used.

• (1) E, $\nu$, ${\sigma }_{c}$, ${m}_{\mathrm{bi}}$, and ${s}_{i}$, $a$ can be determined using the method based on GSI from Hoek and Brown (2018). The deformation modulus of can be estimated by (Hoek and Diederichs 2006):

$$\begin{array}{c}{E}_{\mathrm{rm}}={10}^{5}\frac{1-D/2}{1+\mathrm{exp}\left[\left(75+25D-\mathrm{GSI}\right)/11\right]}\quad \left(\mathrm{MPa}\right),\end{array}$$

(35a)

or

$$\begin{array}{c}{E}_{\mathrm{rm}}={E}_{i}\left\{0.02+\frac{1-D/2}{1+\mathrm{exp}\left[\left(60+15D-\mathrm{GSI}\right)/11\right]}\right\}\quad \left(\mathrm{MPa}\right),\end{array}$$

(35b)

in which, the initial GSI of the rock mass is determined by field observations and the disturbed factor D is estimated based on blast damage and stress relaxation; and E_i is the Young’s modulus of the intact rock. The Poisson’s ratio $\nu$ can be determined following Gercek (2007) and Zhang (2016). The unconfined compressive strength ${\sigma }_{c}$ of the intact rock can be obtained from the uniaxial compression test in the lab. And ${m}_{\mathrm{bi}}$, ${s}_{i}$, and $a$ can be determined from Eqs. (3a–c) with known GSI and D.

• (2) The residual strength parameters of the rock mass, ${m}_{\mathrm{br}}$ and ${s}_{r}$, can also be determined from Eqs. (3a–c), but the residual GSI, ${\mathrm{GSI}}_{r}$, of the rock mass should be used. The ${\mathrm{GSI}}_{r}$ can be estimated following Cai et al. (2007). For example, the following simple equation from Cai et al. (2007) can be used:

  $$\begin{array}{c}{\mathrm{GSI}}_{r} = {\text{GSI}}\times \mathrm{exp}\left(-0.0134\mathrm{GSI}\right),\end{array}$$

  (36)

  in which, GSI is the initial GSI.

• (3) As for ${m}_{\mathrm{di}}$ and ${m}_{\mathrm{dr}}$, a value within the range of 0.4–1.0 ${m}_{\mathrm{bi}}$ can be selected for ${m}_{\mathrm{di}}$, and a typical estimation of ${m}_{\mathrm{dr}}$ can be ${m}_{\mathrm{dr}}={m}_{\mathrm{br}}$.

• (4) A typical value of ${\varepsilon }_{f}$ and ${\varepsilon }_{g}$ should be in the range of 1–10% (Farmer 1983; Walton et al. 2014, 2017; Zhao and Cai 2010).

Some of the above recommendations for determining the model parameters, such as the range of ${\varepsilon }_{f}$ and ${\varepsilon }_{g}$, are based on limited data. As more data are available, the range can be narrowed for specific rocks and the accuracy can be improved.

4 Validation of Proposed Constitutive Model

To validate the proposed constitutive model, it is implemented in finite-difference code FLAC3D and applied to simulate the true triaxial test of two types of rocks: Mizuho trachyte and Beishan granite.

4.1 Mizuho Trachyte

The true triaxial test results of Mizuho trachyte (Mogi 1971), the $\left({\sigma }_{1}^{{\prime}}-{\sigma }_{3}^{{\prime}}\right)$ versus ${\varepsilon }_{1}$ and ${\varepsilon }_{3}$ versus ${\varepsilon }_{1}$ curves under different stress states are shown in Figs. 4 and 5, respectively. Based on the experimental $\left({\sigma }_{1}^{{\prime}}-{\sigma }_{3}^{{\prime}}\right)$ versus ${\varepsilon }_{1}$ relation, the rock can be considered to follow the elastic-perfectly plastic constitutive model. In this case, the parameters of the constitutive model for simulating the true triaxial test of Mizuho trachyte are determined and summarized in Table 2.

Fig. 4

Comparison of $\left({\sigma }_{1}^{{\prime}}-{\sigma }_{3}^{{\prime}}\right)$ versus ${\varepsilon }_{1}$ of Mizuho trachyte from simulations and experiments

Fig. 5

Comparison of ${\varepsilon }_{1}$ versus ${\varepsilon }_{3}$ of Mizuho trachyte from simulations and experiments

Table 2 Material parameters for Mizuho trachyte

The $\left({\sigma }_{1}^{{{\prime}}}-{\sigma }_{3}^{{{\prime}}}\right)$ versus ${\varepsilon }_{1}$ relations from the simulation under different intermediate stresses are also shown in Fig. 4. The good agreement of the simulation results with the experimental data indicates that the elastic-perfectly plastic constitutive model can capture the stress–strain relation of Mizuho trachyte well. For further comparison, Fig. 5 shows the ${\varepsilon }_{3}$ versus ${\varepsilon }_{1}$ relations at different intermediate effective stresses from both experiments and simulations. The ${\varepsilon }_{3}$ versus ${\varepsilon }_{1}$ relations from the simulation are also in quite good agreement with those from the experiments.

4.2 Beishan Granite

For rock, strain-softening is a very common post-failure mode under true triaxial stress states. In this regard, the true triaxial test results of Beishan granite which shows strain-softening (Zhang et al. 2019) are selected for verification of the proposed constitutive model. Table 3 summarizes the rock parameters for the Beishan granite used for the numerical simulation.

Table 3 Material parameters for Beishan granite

Figure 6 shows the stress–strain curves from the true triaxial tests (Zhang et al. 2019) and those from the numerical simulations at different values of ${\sigma }_{3}^{{\prime}}.$ As can be seen, the Beishan granite exhibits strong brittle-ductile characteristics. ${\varepsilon }_{2}$ changes much less than ${\varepsilon }_{1}$ and ${\varepsilon }_{3}$ after the peak shear stress (during fracturing) because the failure (fracture) surfaces are parallel to the direction of ${\sigma }_{2}^{{\prime}}$ (Zhang et al. 2019). It can also be seen that the simulation results are in good agreement with those from the experiments. The predictions from elastic-perfectly plastic models such as Zhu et al. (2017) are not included for comparison because the predicted ${\sigma }_{1}^{{\prime}}$ would not change after failure and apparently cannot represent the strain-softening behavior of the rock. This is one of the major advantages of the proposed constitutive model over other perfectly plastic models.

Fig. 6

Comparison of effective major principal stress versus strains of Beishan granite from simulations and experiments

5 Application of Proposed Constitutive Model

To further verify the applicability of the proposed constitutive model in practical engineering, it is used to analyze a highway rock tunnel during construction in Guizhou province, China. The tunnel is 8 km long and was constructed by the so-called top-heading-and-bench method. Two linings, one layer of plain concrete and one layer of reinforced concrete, were used to support the tunnel. To simplify the analysis, only a 50 m long section of the tunnel at a buried depth of around 140 m is considered. Considering the symmetry and to eliminate the effect of boundaries, a numerical model of 75 m × 140 m × 75 m as shown in Fig. 7 is constructed. The bottom boundary and the four side boundaries are constrained in the normal direction, and an equivalent normal uniform loading of 1.54 MPa based on rock mass unit weight and buried depth is applied at the top boundary to simulate the overburden. The in situ horizontal stress is assumed to be equal to the in situ vertical stress in the analysis. 110 steps of construction processes, including the up and down bench cut, the first lining installation, the second lining installation and backfilling, are considered in the analysis. The length of each bench and the first lining is 2 m, while one section of the second lining and backfill is 10 m long. The material properties of the two linings and the backfill are summarized in Table 4.

Fig. 7

Numerical model of tunnel

Table 4 Material parameters for initial lining, second lining, and backfill

The in-situ rock is sandstone and the unconfined compressive strength, ${\sigma }_{c}$, of the intact rock is 13.2 MPa. According to Zhu et al. (2017), the material parameter ${m}_{i}$ can be estimated as 17. Using the modified geological strength index (GSI) system (Sonmez and Ulusay 1999) and following Zhu et al. (2017), the GSI of the rock mass is 47. The tunnel was excavated by the blast drilling method, which could cause some disturbance to the surrounding rock. Therefore, a disturbance factor D of 0.3 is assumed for the disturbed zone. According to Hoek (2012), the disturbed zone of a 10 m diameter tunnel could extend as much as 3 m into the rock. Since the simulated tunnel is 30 m and 22 m in the horizontal and vertical directions, the disturbed zone is assumed to extend 9 m and 6 m from the tunnel into the rock along the horizontal and vertical directions, respectively (Fig. 7). Beyond the disturbed zone, the disturbance factor is assigned as 0. With the obtained ${m}_{i}$, GSI and D, the other parameters of the proposed constitutive model can be determined by Eqs. (3a–c). To be simple, ${m}_{d}$ is selected to be equal to ${m}_{b}$. Since no information is available about the residual strength or strain-softening properties of the rock, the elastic-perfectly plastic model is used. The Young’s modulus, ${E}_{\mathrm{rm}}$, of both the disturbed and undisturbed zones are determined by (Hoek and Diederichs 2006). All the parameters for the rock mass are summarized in Table 5.

Table 5 Material parameters for rock mass around the tunnel

Figure 8 shows the displacement contour after excavation. For the roof and floor zones, the excavation would affect the rock mass within about one diameter from the tunnel, while in the horizontal direction, the excavation has much less influence on the surrounding rock mass. The maximum displacement occurs in the first section of the cut because this part was excavated first and affected by the whole excavation process.

Fig. 8

Displacement contour of rock around tunnel after excavation

Figure 9 shows the roof settlement and horizontal convergence deformation from the numerical analysis. For comparison, the field measurements and the numerical results based on the original Hoek–Brown constitutive model and the modified GZZ constitutive model from Zhu et al. (2017) are also shown in the figure. As can be seen, the roof settlement and the horizontal convergence deformation from the analysis based on the original Hoek–Brown constitutive model are both significantly larger than those from the field measurements. The roof settlement and the horizontal convergence deformation from the analyses based on the modified GZZ constitutive model and the proposed constitutive model, however, are in good agreement with those from the field measurements. The slight difference between the results from the analysis based on the modified GZZ constitutive model and those based on the proposed constitutive model could be due to the difference in the total number of elements used in the analyses, the different potential functions adopted, and the absence of undisturbed zone in the simulation of Zhu et al. (2017).

Fig. 9

Comparison of a tunnel roof displacement and b tunnel horizontal convergence deformation from field measurements and simulations

To explore the influence of strain-softening, a numerical simulation is performed using the strain-softening model within the disturbed zone. The residual GSI of the rock mass within the disturbed zone is estimated from Eq. (36) as 25 and ${m}_{\mathrm{br}}$ and ${s}_{r}$ can be further determined from Eqs. (3a–c) as 0.728 and 0.0001. As for the rest parameters, ${m}_{\mathrm{di}}={m}_{\mathrm{bi}}$, ${m}_{\mathrm{dr}}={m}_{\mathrm{br}}$ and ${\varepsilon }_{f}={\varepsilon }_{g}=5\mathrm{ \%}$ following the recommendations in Sect. 3.3. The simulation results are also shown in Fig. 9. It can be seen that the accuracy of the predictions is slightly improved when the strain-softening is considered.

6 Conclusions

The major conclusions can be summarized below:

• 1. The unified constitutive model adopts a continuous potential function that takes the three effective principal stresses into account and a non-associated plastic flow rule. The three types of post-failure modes, strain-softening, strain-hardening and elastic-perfectly plastic, are described in a unified way using a general exponential expression.

• 2. The proposed constitutive model is implemented in a finite-difference code FLAC3D and used to simulate the true triaxial test of two types of rocks. The results indicate that the proposed constitutive model can effectively capture the stress–strain behavior of the rock in different directions.

• 3. The proposed constitutive model is successfully used to analyze a highway rock tunnel during construction. The predicted tunnel roof displacement and horizontal convergence deformation are in good agreement with the field measurements, indicating the applicability of the proposed constitutive model to practical engineering problems.