3D Finite Element Application of Elastoplastic Constitutive Model for Intact Rock

Abstract

A 3D finite element user-defined material (UMAT) is developed to describe the elasto-plastic behaviour of the intact rocks. The model comprises the pre-peak elastic and post-peak strain-softening behaviour. In order to capture the plastic deformation and dilation of rocks, the non-associated flow rule is assumed in the formulation. Based on the further development platform provided by ABAQUS the FORTRAN subroutine is developed. The stress-strain relationships obtained by ABAQUS are compared with triaxial test data. The numerical predictions show good agreement with the observed behaviour in experiments, which verified the UMAT and proved the applicability of elasto-plastic model to rocks. The three dimensional application of developed UMAT in ABAQUS provides the commercial FEM code a new optional constitutive law for the elastoplastic problems in rock mechanics.

1 Introduction

With the current advancements in technology, the demand of deep underground structures (such as tunnels) in complex geomechanical environments is increased, which has led rock engineering to practice more efficient and advanced constitutive material models in numerical simulation to capture the realistic response of the geological material. The development of a constitutive model which is more efficient in capturing the pre-peak and post-peak response of rocks is a difficult task. In rocks, the nonlinear behaviour is caused by the initiation and propagation of cracks, which leads to an increase in the volume of the rocks under plastic deformation, termed as dilation.

The Mohr-Coulomb is the most well-known constitutive model in geomechanics. The failure criterion of the Mohr-Coulomb is linear envelope intersecting the Mohr’s circle representing the minimum and maximum stresses at the failure of rocks (Jaeger et al. 2009). The criterion states that failure occurs if the magnitude of the shear stress on a particular plane reaches a critical threshold, which is dependent on the friction resistance and cohesion of the rocks grains.

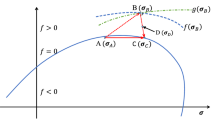
Pourhosseini and Shabanimashcool (2014) proposed a constitutive model for intact rocks that is capable of capturing the strain-softening and dilation behaviour of the rocks. This model is based on the Mohr-Coulomb failure criteria, with a gradual decrease in cohesion strength of the rock material and mobilisation of the dilation ($\psi$) whereas the friction angle $(\phi )$ remains constant. The plastic deformation is calculated using the non-associative flow rule. Figure 1 shows a typical stress-strain response of a rock material subjected to compressive loads (Brace 1964; Alejano and Alonso 2005; Zhao and Cai 2010; Wang et al. 2011).

Fig. 1.

Typical stress-strain behaviour of an intact rock sample in the triaxial test (modified after, Jaeger et al. 2007).

ABAQUS is a powerful finite element analysis software package used for various engineering simulation problems, which is capable of solving relatively simple linear analysis problems as well as complex nonlinear problems. The ABAQUS provided a platform to develop the user-defined material (UMAT), which can be added to the ABAQUS library and can be further used in the simulation. The UMAT update the stresses and solution-dependent state variable and provide the Jacobian matrix ($\partial \sigma /\partial \varepsilon$) of the material for the constitutive model. In this study, based on the platform provided by the ABAQUS, the elasto-plastic constitutive model proposed by Pourhosseini and Shabanimashcool (2014) for intact rocks is implemented in the FEM, and three axial stress tests are simulated, and results are compared with the observed experimental data.

2 Framework of Elasto-Plastic Model

Pourhosseini and Shabanimashcool (2014) developed a constitutive model for intact rocks which can capture the strain-softening behaviour with a non-associative flow rule. The yield function f is based on the Mohr-Coulomb, which is defined as:

$$f={\sigma }_{1}-\frac{2c\left(\eta \right)\mathit{cos}\phi }{1-\mathit{sin}\phi }-{\sigma }_{3}\frac{1+\mathit{sin}\phi }{1-\mathit{sin}\phi }$$

(1)

where, c is cohesion which function of softening parameter $(\eta$); ϕ friction angle; ${\sigma }_{1}$ and ${\sigma }_{3}$ are principal stresses. Softening parameter (η) is equal to zero in the elastic region and η > 0 from the peak strength to the residual strength, which can be defined as:

$$\eta ={\varepsilon }_{1}^{p}-{\varepsilon }_{3}^{p}$$

(2)

$$\dot{\eta }=\frac{\partial \eta }{\partial t}$$

(3)

where, t is time; ${\varepsilon }_{1}$ and ${\varepsilon }_{3}$ principal strains.

The plastic strain increment is obtained from the plastic potential function ($g=f(\sigma ,\eta )$:

$${\dot{\varepsilon }}_{ij}=\lambda \frac{\partial g}{\partial {\sigma }_{ij}}$$

(4)

where, $\lambda$ is plastic multiplier.

In a non-associative flow rule, the yielding function (f) is different from the potential function (g). Various researchers (Drucker 1959; Barton and Bandis 1982; Vermeer and De Borst 1984) suggested that the potential function should be the function of the dilation angle. Therefore, the potential function (g) can be written as:

$$g={\sigma }_{1}-{\sigma }_{3}\ tan[\psi \left(\eta ,{\sigma }_{3}\right)]$$

(5)

where, $\psi$ is dilation angle which is the function of $\eta \mathrm{and}{ \sigma }_{3}$. The $\psi$ is maximum at the peak strength of the rocks and reduces with the increase in plastic deformation of the rock and confining stress.

The plastic multiplier ($\lambda )$ can be estimated as:

$$\lambda =\frac{1}{h}\frac{\partial f}{\partial \sigma }\dot{\sigma }$$

(6)

where,

$$h=-\sqrt{[1/3(1+\mathit{sin}\,\phi \, \mathit{sin}\,\psi ]}\frac{\partial f}{\partial \eta }$$

(7)

Pourhosseini and Shabanimashcool (2014) has found that the cohesion and dilation angle of rocks decrease with an increase in plastic parameter and proposed the following equations to calculate the cohesion (c) and dilation angle ($\psi )$ corresponding to the plastic parameter ($\eta$) during strain-softening.

$$c={c}_{p}{\left(1-\frac{\mathrm{tanh}\left(100\eta \right)}{\mathrm{tanh}\left(10\right)}+0.001\right)}^{n}$$

(8)

where, ${c}_{p}$ is cohesion at the peak strength of the rock where $\eta =0$, and n is fitting parameter that vary depending on the type of rock.

Similarly, dilation angle ($\psi )$ can be calculated as:

$$\psi ={\psi }_{p} {\left(1-\frac{\mathrm{tanh}\left(100\eta \right)}{\mathrm{tanh}\left(10\right)}+0.001\right)}^{m}$$

(9)

where, m is model parameter; ${\psi }_{p}$ is maximum value of dilation angle can be calculated as:

$${\psi }_{p}=A\mathrm{ln}\left(\frac{\phi {\sigma }_{c} }{{\sigma }_{3}+0.1}\right)-B$$

(10)

where, ${\sigma }_{c}$ is uniaxial compressive strength of rock; A and B are model parameters depends on the rock type.

3 Implementation in Finite Element Method

The total strain increment $(d{\varepsilon }_{ij})$ is the sum of elastic strain increment ($d{{\varepsilon }_{ij}}^{e}$) and plastic strain ($d{{\varepsilon }_{ij}}^{p}$) can be expressed as:

$$d{\varepsilon }_{ij}=d{\varepsilon }_{ij}^{e}+d{\varepsilon }_{ij}^{p}$$

(11)

in the elastic region, the stress increment is defined using the Hook’s law as:

$$d{\sigma }_{ij}= {C}_{ij}^{e}d{\varepsilon }_{ij}^{e}$$

(12)

using the non-associated flow rule, the strain increment can be written as:

$$d{\varepsilon }_{ij}^{p}=\lambda \frac{\partial g}{\partial {\sigma }_{ij}}$$

(13)

the elasto-plastic stress-strain relationship can be expressed as:

$$d{\sigma }_{ij}= {C}_{ij}^{ep}d{\varepsilon }_{ij}$$

(14)

where, ${C}_{ij}^{ep}$ is the constitutive matrix of the material in the inelastic range and can be expressed in terms of the yielding function (f) and potential function (g) as:

$$C_{ij}^{ep} = C_{ij}^{e} - C_{ij}^{p} ;\,\,\,\,\,\,\,C_{ij}^{p} = \frac{1}{H}C_{ij}^{e} \frac{\partial g}{{\partial \sigma_{ij} }}\left( {\frac{\partial f}{{\partial \sigma_{ij} }}} \right)C_{ij}^{e}$$

(15)

where, $H$ is defined as:

$$H=B+{\left(\frac{\partial f}{\partial {\sigma }_{ij}}\right)}^{T}{C}_{ij}^{e}\frac{\partial g}{\partial {\sigma }_{ij}}$$

(16)

and B is:

$$B=-\frac{\partial f}{\partial \eta }\frac{d\eta }{d\lambda }$$

(17)

using the above elasto-plastic constitutive matrix model, corresponding to the stress-strain in the element, the stiffness of the element is updated. Based on the new stress in the element, check for $f,$ if $f>0$, the element is loading elasto-plastically and if $f\le 0$ the element is under elastic loading.

4 Comparison of FEM with Test Data

In the present study, the validation of the UMAT is performed by simulating the three axial loading test on a cylindrical sample with a diameter of 7 cm and height of 14 cm. the mechanical properties of the sample is presented in Table 1. The geometry and boundary conditions of the model are shown in Fig. 2. Two different rock characteristics (mudstone and sandstone) are considered for the simulations.

The vertical and horizontal displacement at the bottom of the cylinder is fixed, and fixed downward direction velocity is applied at the upper boundary of the model. The applied loading is in compressive manner throughout the simulation. Confining stress is applied at the cylindrical surface of the specimen. The simulation is performed for two different confining stress (0 and 4 MPa). For simulation, the model is discretised into 73,730 elements (approx. size of 5.5 mm).

Table 1. Mechanical properties of the model used in the numerical simulation. (after Pourhosseini and Shabanimashcool 2014).

Fig. 2.

(a) Boundary conditions and geometry of rock sample (b) FEM model of the rock sample

Figure 3 (a, b) shows the stress-strain behaviour of the mudstone rock sample for different confining stresses. It is observed that for no confining stress, there is good agreement between the UMAT and with those provided by experimental test data (Pourhosseini and Shabanimashcool 2014). However, when confining stress is increased to 4 MPa, the residual strength of the rock model is higher in experimental data as compared to numerical simulation. This could be due to assumptions made in the model, such as homogenous isotropic mechanical properties are considered, whereas the real rock samples have anisotropic mechanical properties. Similarly, Fig. 4 (a, b) presents the stress-strain behaviour of the sandstone rock sample under different confining stresses (0 and 4 MPa). It could be seen that the experimental and numerical simulated results are in good agreement. However, peak axial stress in the numerical results are found to be higher compared to experimental results in both confining stresses. It is also observed that for sandstone rock sample, the UMAT is overestimating the residual strength.

Fig. 3.

Comparison of results obtained for Mudstone rock sample from test data (obtained from Pourhosseini and Shabanimashcool 2014) and FEM user-defined material (UMAT) for (a) ${\sigma }_{3}=0$ (b) ${\sigma }_{3}=4$ MPa.

Fig. 4.

Comparison of results obtained for Sandstone rock sample from test data (obtained from Pourhosseini and Shabanimashcool 2014) and FEM user-defined material (UMAT) for (a) ${\sigma }_{3}=0$ (b) ${\sigma }_{3}=4$ MPa.

Figure 5 shows the volumetric strain of both rock samples (mudstone and sandstone) for 0 and 4 MPa confining stresses. Both the rock samples show a similar trend of dilation behaviour. Compared to mudstone (Fig. 5a), sandstone (Fig. 5b) depicts more dilation, especially at high confining stress. The dilation rate of sandstone is also higher as compared to mudstone. However, the behaviour of both rock samples is sensitive to confining stress.

Fig. 5.

Volumetric strain curve (a) mudstone rock (b) sandstone rock, calculated using UMAT.

From the above discussion, it can be concluded that developed UMAT can capture the strain-softening behaviour of the rocks. However, the numerical simulation does not show good agreement with high confining stress in the case of mudstone. In contrast, for the sandstone with the increase in confining stress, correlation improves. Hence, developed UMAT can be used for geotechnics problems.

5 Conclusions

In the present study, a three-dimension UMAT is developed for the ABAQUS FEM package for elasto-plastic behaviour of intact rock. The constitutive model is based on the Mohr-Coulomb failure criterion considering the non-associative flow rule. This constitutive model utilise the shrinking of the failure criteria by progress of plastic deformation. Three axial stress simulation is performed for two different rock samples (mudstone and sandstone) UMAT, which is written in FORTRAN programming language. The applicability of the UMAT is verified with experimental triaxial test data. The results show good agreement with predicted and experimental data, which confirm the validity of UMAT for mechanical elastio-plastic with strain-softening behaviour intact rocks. Therefore, the UMAT could be further used for various geomechanical engineering problems.