1 Introduction

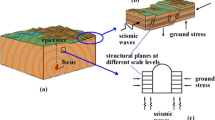
Deep underground mining or rock excavation disturbs the equilibrium of the in situ rock mass, frequently causing the rock mass near the excavation boundary into a stress state of high tangential stress and low radial confinement due to stress concentration and relaxation (Diederichs 2007; Kaiser et al. 2001). Consequently, the near-boundary rock mass is in the most critical state and may be prone to brittle failure (Fig. 1), such as spalling/slabbing, floor heave, buckling, and rockbursts (Cai and Kaiser 2014, 2018; Diederichs 2007; Du et al. 2016; Gong et al. 2012; Hu et al. 2020; Zhang et al. 2012; Zhao et al. 2014; Li et al. 2019, 2020). Among these failure modes, rockbursts in general are the most destructive (Cai and Kaiser 2014; Feng et al. 2018; Zhang et al. 2012). The term rockburst refers to ‘damage to an excavation that occurs in a sudden and violent manner and is associated with a seismic event’ (Cai and Kaiser 2018). There are three types of rockbursts, i.e., strainbursts, fault-slip bursts and pillar bursts, among which the strainburst is the most common one (Cai and Kaiser 2018; Hu et al. 2018; Ortlepp and Stacey 1994). This study is devoted to strainbursts. A strainburst often occurs in deep massive hard rocks, and is either induced by gradual static stress variation or coupled static stress and dynamic disturbances. A dynamic disturbance can both trigger a strainburst whether substantial dynamic stress increment or significant energy transfer is caused or not (Cai 2013; Cai and Kaiser 2018; Du et al. 2016; He et al. 2012; Hu et al. 2018; Su et al. 2017a, b). In a broad sense, there are two scenarios of deep rocks subjected to coupled static and dynamic loading (Li et al. 2017, 2008b), that is by a ‘critical static stress + slight disturbance’ or an ‘elastic static stress + impact disturbance’. The former represents a triggered strainburst, and the latter is a dynamically loaded strainburst associated with rock failures induced by high strain rate dynamic loads, such as from blasting. The frequently encountered ‘slight disturbance’ causing a strainburst stems from seismic events or analogous stress waves, such as the attenuated stress wave caused by remote blasting (Hu et al. 2018; Su et al. 2017a, b), the remote seismic event caused by fault-slip (Cai and Kaiser 2018), rockbursts in nearby excavations, and the ground vibration caused by huge vehicles (Fig. 2). Figure 2 illustrates the mechanical conditions of seismically-induced strainburst considering that a strainburst is a structural failure of the near-boundary rockmass (Hu et al. 2018, 2020; Su et al. 2017c, d). The frequency of the seismic disturbance causing triggered or dynamically loaded strainbursts is frequently low in the range of several to tens of Hertz (Hz) (Hu et al. 2018; Su et al. 2017a). Its amplitude is related to the magnitude of the triggering seismic event and the rock mass properties. For example, the dynamic stress increment \(\Delta \sigma_{\max }^{{\text{d}}}\) caused by a shear stress wave can be calculated by (Cai and Kaiser 2018):

$$\Delta \sigma_{\max }^{{\text{d}}} = \pm 4\rho c_{s} PGV_{s}$$
(1)
Fig. 1
figure 1

Typical failure modes of hard rock near deep excavation: a spalling/slabbing (Gong et al. 2012), b floor heave (Cai and Kaiser 2018), c buckling, and d rockburst (Zhang et al. 2012)

Full size image
Fig. 2
figure 2

Illustration of the mechanical conditions of the seismically-induced strainburst (modified after Hu et al. (2018))

Full size image

where \(\rho\) is the rock mass density, \(c_{s}\) is the velocity of shear stress wave, and \(PGV_{s}\) is the peak ground velocity. Therefore, the stress environment of the ‘high static stress + low-frequency seismic disturbance’ is common for rock masses in deep underground engineering circumstances (Cai and Kaiser 2018; Du et al. 2016; Hu et al. 2018; Su et al. 2017a, b).

Recently, several investigations have been conducted through experimental (Du et al. 2016; He et al. 2015; Hu et al. 2018; Jiang et al. 2020; Li et al. 2008a, b, 2017, ; Su et al. 2017a, b), numerical (Hu et al. 2018; Li and Weng 2016; Zhu et al. 2010), and theoretical approaches (He et al. 2017; Li et al. 2015; Zuo et al. 2005) on the rock failures under coupled static and dynamic loading conditions. Generally, rock failures under ‘elastic static stress + impact disturbance’ attract extensive attention mainly through experimental and numerical studies (Hu et al. 2018; Su et al. 2017b). However, few quantitative studies have been reported on rock failures under ‘high static stress + low-frequency seismic disturbance’, which are crucial for revealing the failure mechanism of the dynamically-induced strainburst. In situ micro-seismic (MS) monitoring and observations (Cai and Kaiser 2018; Feng et al. 2018; He et al. 2017; Zhang et al. 2012) showed that the occurrence of the dynamically-induced strainburst involves initiation, propagation, and coalescence of microcracks, which is a process of damage accumulation and energy re-balance, and closely associated with energy store, dissipation and release (Hu et al. 2018; Su et al. 2017a, b). Therefore, further studies are urgent to quantify the damage and energy evolution of the dynamically-induced strainburst, particularly the dynamic disturbance in promoting damage and energy release. This favors in-depth understanding towards the failure mechanism and optimized support design to prevent and mitigate the dynamically-induced strainburst.

Based on the experimental results of the strainbursts induced by low-frequency cyclic disturbance under true triaxial conditions, termed the cyclic disturbance-induced strainburst (Su et al. 2017b), the damage evolution and energy balance of this type of strainburst are quantitatively assessed. In this paper, we first briefly introduce the experimental study on the cyclic disturbance-induced strainburst. Then, a damage variable definition method for the cyclic disturbance-induced strainburst and the damage evolution characteristics of this type of strainburst under different test conditions are discussed. Subsequently, the energy balance under different test conditions and the mechanism of the cyclic disturbance-induced strainburst are presented.

2 Experimental Study

2.1 Overview of the Experimental Approach and Equipment

In a series of the studies of the authors and their colleagues (Hu et al. 2018; Su et al. 2017a, b), a seismically-induced strainburst is simulated by ‘high static stress + low-frequency cyclic disturbance’ under true triaxial conditions using hard brittle white–gray granodiorite samples with the size of 100 mm (x direction) × 100 mm (y direction) × 200 mm (z direction). The applied cyclic disturbance is a half-sinusoidal cyclic load with the frequencies up to 10 Hz, with variable amplitude as required in the range of 0 to 5000 kN. According to Eq. (1), assuming that \(c_{s}\) = 3000 m/s, \(\rho\) = 2600 kg/m3, with \(PGV_{s}\) = 0.3–1 m/s (moderate rockburst condition) (Cai and Kaiser 2018), the caused dynamic stress increment \(\Delta \sigma_{\max }^{{\text{d}}}\) ranges from 10 to 30 MPa. Therefore, the amplitude of the cyclic disturbance is set between 10 and 40 MPa in the experiment. An improved high-pressure servo-controlled true triaxial rockburst testing system was employed to conduct the strainburst tests. The improved experimental system not only includes the basic functions of a conventional true triaxial test machine, but also can simulate the seismic wave disturbance in mining or excavation by applying low-frequency disturbance loads with multiple waveforms in three perpendicular directions. The stiffness of the loading frame is 9 GN/m in vertical direction and 4 GN/m in horizontal direction, which is lower than the unloading stiffness of the tested granodiorite rock samples, and therefore imposes energy from the test frame into the failure process. More details on the experimental methods and equipment can be found in Hu et al. (2018) and Su et al. (2017b, c, d).

2.2 Stress–Strain Relationship of the Cyclic Disturbance-Induced Strainburst

In this study, eight typical cyclic disturbance-induced strainburst tests under four groups of conditions (i.e., different stress in the z direction \(\sigma_{z}\), y direction stress \(\sigma_{y}\), disturbance amplitude \(\Delta \sigma\), and disturbance frequency \(f\), respectively) are selected from the database of the strainburst experiments (Su et al. 2017b). The damage evolution and energy balance of the cyclic disturbance-induced strainburst are investigated based on the complete stress–strain curves (Fig. 3). Since the stress and strain in the z direction are considerably higher than those in x and y directions and, thus, dictate the strainburst occurrence, the rock response in the z direction is analyzed.

Fig. 3
figure 3

Typical z direction stress–strain curves of cyclic disturbance-induced strainburst under (the curves without post-peak segment represent that strainburst did not occur under these test conditions): a different z direction stress \(\sigma_{z}\), b different y direction stress \(\sigma_{y}\), c different disturbance amplitude \(\Delta \sigma\), and d different disturbance frequency \(f\) (Su et al. 2017b)

Full size image

3 Rock Damage and Energy Evolution During Cyclic Disturbance-Induced Strainbursts

Damage and energy are two salient indicators of the cyclic disturbance-induced strainbursts. Damage is the degradation of the rock due to cracking and fracturing. When the rock loses its bearing capacity, e.g. a strainburst occurs, its damage reaches the maximum value. Therefore, to study rock damage, we should pay attention to the pre-peak response, particularly the damage characteristics in the process of cyclic disturbance which plays a critical role in damage promotion. From a viewpoint of energy, the prominent feature that distinguishes a strainburst from the conventional brittle rock failure is the release of the kinetic energy of rock fragments in the post-peak stage. Therefore, the entire process of the cyclic disturbance-induced strainburst should be considered to disclose its energy evolution. The energy balance precedes a burst, especially during the disturbance, which includes the energy criterion and failure mechanism of how the cyclic disturbance induces a strainburst. The energy balance in the post-peak stage reflects the mechanism of the kinetic energy release, which is related to the rockburst intensity. Based on the above statements and experimental observations, the damage and energy evolution in each stage of the cyclic disturbance-induced strainburst are illustrated in Fig. 4.

Fig. 4
figure 4

Illustration of damage and energy during the development of the cyclic disturbance-induced strainburst

Full size image

3.1 Damage Evolution

3.1.1 Definition of the Damage Variable

Rock damage during cyclic disturbance-induced strainbursts has rarely been studied and few damage analysis methods are available. To study the damage of brittle rocks, it is key to choose an appropriate definition of the damage variable. Various definitions of damage for rocks under different loading conditions have been proposed (Ge et al. 2003; Su et al. 2017a, b; Xiao et al. 2010; Zuo et al. 2005). Among these definitions, the residual strain method has been proven to be most suitable for rocks under the cyclic loading because of its explicit physical meaning, quantifying degradation, and considering the initial fatigue damage (Xiao et al. 2010). The damage variable defined by the residual strain method (D) is a function of the residual strain after n cycles (\(\varepsilon_{r}^{n}\)) and the ultimate residual strain upon rock failure (\(\varepsilon_{r}^{N}\)) (Xiao et al. 2010):

$$D = \frac{{\varepsilon_{r}^{n} }}{{\varepsilon_{r}^{N} }}$$
(2)

Considering the similarity between the cyclic disturbance-induced strainburst and the rock failure under the cyclic loading, we improved the residual strain method to define the damage variable of the cyclic disturbance-induced strainburst. Based on Eq. (2), the damage variable for the cyclic disturbance-induced strainburst (Dc) is defined as:

$$\left\{ \begin{gathered} D_{C} = \frac{{{\kern 1pt} {\kern 1pt} \varepsilon_{r}^{n} }}{{{\kern 1pt} \varepsilon_{r}^{N} }} = \frac{{\varepsilon^{n} - \sigma_{\min } /E^{\prime}_{1} }}{{\varepsilon^{N} - \sigma_{f} /E^{\prime}_{2} }} \hfill \\ \sigma_{f} = \sigma_{\min } + p*\Delta \sigma \hfill \\ p = p\left( {\Delta \sigma ,f} \right) \hfill \\ \end{gathered} \right.$$
(3)

where \({\kern 1pt} {\kern 1pt} \varepsilon_{r}^{n}\) and \(\varepsilon^{n}\) are the residual strain and total strain after n cycles (point A in Fig. 5), respectively;\(\varepsilon_{r}^{N}\) and \(\varepsilon^{N}\) are the residual strain and total strain when a strainburst occurs (point B in Fig. 5), respectively;\(\sigma_{\min }\),\(\sigma_{f}\),\(\Delta \sigma\), and \(f\) are the lower limit stress of cyclic disturbance, stress at failure (point B in Fig. 5), amplitude of cyclic disturbance, and frequency of cyclic disturbance, respectively;\(E^{\prime}_{1}\) and \(E^{\prime}_{2}\) are the unloading stiffnesses at points A and B, respectively; \(p\) is a parameter relating to the disturbance amplitude \(\Delta \sigma\) and frequency \(f\).

Fig. 5
figure 5

Interpretation of the parameters in damage variable definition of the cyclic disturbance-induced strainburst

Full size image

Prior to the cyclic disturbance, cracks have been considerably developed in the rock due to the high static loading. Because the amplitude of cyclic disturbance is low and the number of cycles the rock underwent is insufficiently large, the rock state is constantly adjusted and the cracks are compressed during the disturbance. The unloading stiffness at the end of each cycle (i.e.,\(E^{\prime}_{1}\)) increases marginally (Fig. 5), but the accumulated irreversible deformation increases significantly. Thus, we have \(\sigma_{\min } < \sigma_{f} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} E^{\prime}_{1} < E^{\prime}_{2}\) in Eq. (3). For simplicity, we approximately take \({\kern 1pt} {\kern 1pt} E^{\prime}_{1} = E^{\prime}_{2} = {\kern 1pt} {\kern 1pt} E\), where E is the rock elastic modulus. Consequently, Eq. (3) is updated as:

$$D_{{\text{C}}} = \frac{{{\kern 1pt} {\kern 1pt} \varepsilon_{r}^{n} }}{{{\kern 1pt} \varepsilon_{r}^{N} }} \approx \frac{{\varepsilon^{n} - \sigma_{\min } /E}}{{\varepsilon^{N} - \sigma_{f} /E}}.$$
(4)

The parameters in the right-hand side of Eq. (4) are all physical parameters, which are experimentally measured (Table 1). Therefore, rock damage of the cyclic disturbance-induced strainburst can be calculated according to Eq. (4).

Table 1 Experimental results of the parameters for damage analysis
Full size table

3.1.2 Physical Meaning of the Damage Variable and Sensitivity Analysis of Influencing Factors

According to Eq. (3), the damage variable \(D_{C}\) comprehensively considers the deformation characteristics (\(\varepsilon_{r}^{n}\) and \(\varepsilon_{r}^{N}\)), the coupled static and dynamic loading (\(\sigma_{\min }\),\(\Delta \sigma\), and \(f\)), and the rock deformability (E). The influences of each factor on the damage of the cyclic disturbance-induced strainburst are examined according to Eq. (3) or its simplified form, Eq. (4).

  1. 1.

    Influence of disturbance amplitude on damage.

    The relationships between the disturbance amplitude \(\Delta \sigma\) and the other parameters in Eq. (3) are as the following:\(\varepsilon^{n} \sim \varepsilon^{n} \left( {{\Delta }\sigma } \right)\) is an increasing function (Fig. 3c);\(\sigma_{\min }\),\(E_{1}^{^{\prime}}\) and \(E_{2}^{^{\prime}}\) are constants independent of \(\Delta \sigma\); the statistical analysis of the experimental data shows that the strain \(\varepsilon^{N}\) at the failure point is approximately constant under experimental conditions of each group of the cyclic disturbance-induced strainburst tests (Table 1) (Ge et al. 2003; Su et al. 2017b). Thus, \(\varepsilon^{N}\) can also be considered as irrelevant to \(\Delta \sigma\), and \(p\) is a parameter positively correlated with \(\Delta \sigma\). Thus, Eq. (3) can be rewritten as a function of \(\Delta \sigma\):

    $$D_{C} = \frac{{\varepsilon^{n} \left( {\Delta \sigma } \right) - a}}{b - c \times \Delta \sigma },$$
    (5)

    where \(a\),\(b\),and \(c\) are positive constants independent of \(\Delta \sigma\). Therefore, \(D_{C} \sim D_{C} \left( {{\Delta }\sigma } \right)\) is an increasing function, i.e., the greater is the amplitude \(\Delta \sigma\), the greater is the damage and the higher the probability to induce a strainburst.

  2. 2.

    Influence of static stress \(\sigma_{\min }\) on damage.

    The static stress \(\sigma_{\min }\) induces rock damage preceding the dynamic disturbance (Su et al. 2017a, b; Xiao et al. 2010). Since the dynamic disturbance has not yet been applied, the damage variable should be calculated according to the initial definition (Eq. 2) of the residual strain method:

    $$D_{0} = \frac{{\varepsilon_{r}^{0} }}{{\varepsilon_{r}^{N} }},$$
    (6)

    where \(D_{0}\) and \(\varepsilon_{r}^{0}\) are the initial damage and residual strain caused by the static stress \(\sigma_{\min }\). Because \(\varepsilon_{{\text{r}}}^{N}\) is nearly constant, Eq. (6) clearly shows that a greater \(\sigma_{\min }\) leads to a larger \(\varepsilon_{r}^{0}\) and \(D_{0}\). The initial damage of the cyclic disturbance-induced strainburst will affect the damage evolution, which is described in Sect. 3.1.3.

  3. 3.

    Influence of elastic modulus on damage.

    To investigate the influence of the elastic modulus (E) on damage, Eq. (4) is further simplified to:

    $$D_{{\text{C}}} = \frac{{{\kern 1pt} {\kern 1pt} \varepsilon_{r}^{n} }}{{{\kern 1pt} \varepsilon_{r}^{N} }} \approx \frac{{\varepsilon^{n} - \sigma_{\min } /E}}{{\varepsilon^{N} - \sigma_{f} /E}} \approx \frac{{\varepsilon^{n} - \sigma_{\min } /E}}{{\varepsilon^{N} - \sigma_{\min } /E}}.$$
    (7)

Subsequently, the derivative of \(D_{{\text{C}}}\) with respect to \(E\) is:

$$\frac{{dD_{C} }}{dE} = - \frac{{\left( {\varepsilon^{N} - \varepsilon^{n} } \right)\sigma_{\min } }}{{E^{2} \left( {\varepsilon^{N} - \sigma_{\min } /E} \right)^{2} }} < 0.$$
(8)

Therefore, \(D_{C} \sim D_{C} \left( E \right)\) is a decreasing function, i.e., a larger \(E\) yields a smaller \(D_{C}\). This means that the harder and more brittle the rock is, the lower are the damage degree and energy consumption during the cyclic disturbance. Consequently, once a strainburst is induced, the released kinetic energy and the rockburst intensity will be higher. Equation (8) can, therefore, reflect the influence of lithology on the intensity of the cyclic disturbance-induced strainburst.

3.1.3 Damage Evolution

The parameters in Eq. (4) determined through experiments are listed in Table 1. With the parameters and the measured stress–strain curves, the damage evolution of the cyclic disturbance-induced strainburst under different experimental conditions is subsequently studied (Fig. 6).

Fig. 6
figure 6

Damage evolution characteristics of the cyclic disturbance-induced strainburst (the rock sample No. and the test conditions are presented in Table 1): a different \(\sigma_{z}\), b different \(\sigma_{y}\), c different \(\Delta \sigma\), and d different \(f\)

Full size image

Figure 6a shows that the damage evolution curve is an inverted S-shape with three stages, i.e., the initial rapid growth stage, the constant speed growth stage after certain cycles of cyclic disturbance, and the accelerated growth stage approaching a strainburst. This damage evolution resembles that of rocks under the cyclic loading (Ge et al. 2003; Xiao et al. 2010). According to Fig. 6b, the initial damage of the sample with a lower radial stress \(\sigma_{y}\) is larger than that of the sample with a larger \(\sigma_{y}\). The damage evolution curve of the sample with a lower \(\sigma_{y}\) is not a typical inverted S-shape, whereas the curve with a larger \(\sigma_{y}\) is. This difference is attributed to the following reasons. The lower \(\sigma_{y}\) the sample subjected to, the weaker the constraint on the sample, and the lower the sample strength. Therefore, when the axial stress \(\sigma_{x}\) and the tangential stress \(\sigma_{z}\) are loaded to the same state, the sample with a lower \(\sigma_{y}\) is relatively higher loaded with respect to its strength, i.e., the static loading causes a higher initial damage. Consequently, when subjected to a cyclic disturbance, the sample damage with a lower \(\sigma_{y}\) develops faster. According to Fig. 6c, although the static stress state is the same, the initial damages of the two samples with different disturbance amplitudes are slightly different, which is possibly caused by rock heterogeneity. In addition, the damage evolution curves of the two samples possess different forms. The sample with a lower \(\Delta \sigma\) exhibits a typical inverted S-shape, whereas the constant speed growth stage of the damage curve of the sample with a larger \(\Delta \sigma\) is not obvious. This is primarily because the larger the \(\Delta \sigma\), the more noticeable its effect on the activation and aggravation of rock damage. According to Fig. 6d, the damage evolution curves of each sample with different disturbance frequencies exhibit a typical inverted S-shape, and the initial damages of each sample are close.

The three-stage trend is caused by the cyclic disturbance. The cyclic disturbance first activates cracks initiated by the high static stress (initial stage), and then it drives cracks to propagate steadily (constant speed stage). When the cracks accumulate to a critical extent, crack propagation accelerates rapidly and eventually induces a strainburst. The above-described damage evolution is similar to the inverse logistic function, which is used to represent the developing trends of natural and societal dynamical systems (Jin et al. 2014) (Fig. 7). The logistic function has the following form (Jin et al. 2014; Verhulst 1838):

$$y = \frac{L}{{1 + e^{{ - k\left( {x - x_{0} } \right)}} }},$$
(9)
Fig. 7
figure 7

The logistic function and its inverse form

Full size image

where \(L\) is the maximum y-value,\(x_{0}\) is the x-value of the curve’s midpoint, and \(k\) is the growth rate of the curve. The inverse function of Eq. (9) is:

$$y = x_{0} - \frac{1}{k}\ln \left( {\frac{L}{x} - 1} \right).$$
(10)

Figure 7 illustrates the logistic function and the inverse logistic function with parameters of \(L\) = 1, \(x_{0}\) = 0.5, and \(k\) = 10 in range of [0,1]. The comparison of Figs. 6, 7 indicates that the damage evolution of the cyclic disturbance-induce strainburst exhibits a similar inverted S-shape as the inverse logistic function. Taking the relative cycle \(n/N\) as independent variable, the inverse logistic function is used to model the damage evolution. The damage evolution model therefore has the following general form:

$$y = \alpha - \beta \ln \left( {\frac{1}{n/N} - \gamma } \right),$$
(11)

where the parameters \(\alpha\),\(\beta\) and \(\gamma\) control the shape of the curve. The damage evolution model can be determined, provided that the parameters in Eq. (11) are experimentally acquired. In this paper, a MATLAB program was coded to fit the damage evolution model with the experimental data based on the least square theory (Fig. 8). The parameters of the fitting curves in Fig. 8 are listed in Table 2.

Fig. 8
figure 8

Damage evolution of the cyclic disturbance-induced strainburst simulated by the inverse logistic function (the rock sample No. and the test conditions are presented in Table 1 and the parameters of the fitting curves are listed in Table 2): a different \(\sigma_{{\text{z}}}\), b different \(\sigma_{{\text{y}}}\), c different \(\Delta \sigma\), and d different \(f\)

Full size image
Table 2 Parameters of the fitting curves of damage evolution in Fig. 8
Full size table

According to Fig. 8, the model expressed by Eq. (11) can well describe the damage evolution of the cyclic disturbance-induced strainburst.\(\alpha\),\(\beta\) and \(\gamma\), respectively, control the damage accumulation rates in the initial stage, the constant speed stage, and the acceleration stage (Figs. 7, 8). From a mechanical perspective,\(\alpha\), \(\beta\) and \(\gamma\) are affected by the coupled static and disturbance loading conditions and rock properties of the cyclic disturbance-induced strainburst.

3.2 Energy Balance and Failure Mechanism

3.2.1 Energy Balance

As a special manifestation of the unstable failure of rocks, energy analysis on the cyclic disturbance-induced strainburst must focus on the post-peak response. The post-peak energy of rock is mutually affected by the loading system stiffness and the shape of post-peak stress–strain curve (Cook 1965; Tarasov and Stacey 2017; Xu and Cai 2017). When the loading system stiffness is lower than the unloading stiffness of rock in the post-peak stage, violent rock failure (e.g., strainbursting) occurs. In this study, two basic assumptions are made for the energy analysis of the cyclic disturbance-induced strainburst based on the experimental results in Su et al. (2017b):

  1. 1.

    The loading system stiffness is lower than the unloading stiffness of the experimented granodiorite rock samples, i.e., the loading system is relatively soft.

  2. 2.

    The typical post-peak stress–strain curve of cyclic disturbance-induced strainburst is a class-I curve.

The energy evolution during the unstable failure of a rock under the static loading is first analyzed (Fig. 9). In this paper, the term ‘energy’ refers to energy density with the unit of J/m3, and only the energy terms in the z direction are considered because they are substantially higher than those in x and y directions. Figure 9a shows the pre-peak energy terms. When the rock is loaded, it stores elastic strain energy \(U_{{\text{E}}} \left( \varepsilon \right)\) and dissipates energy \(U_{{\text{P}}} \left( \varepsilon \right)\). Figure 9b shows the full-process energy analysis (Tarasov and Stacey 2017), where the pre-peak energy balance of the rock is exhibited prior to point A. The rock absorbs an external input energy \(U_{{{\text{pre}}}}\)(area of graph OAB), stores elastic strain energy \(U_{{\text{E}}}\)(area of triangle ABC), and dissipates energy \(U_{{\text{p}}}^{1}\)(area of graph OAC). After point A is the post-peak energy balance, including absorption of external input energy, energy dissipation, and kinetic energy release. Among them, the external input energy consists of two parts, including the work \(U_{{\text{F}}}\) done by the external load (contact force between the machine and the rock sample) (area of graph ABFD), and the elastic deformation energy \(U_{{\text{M}}}\) released by the machine (experimental system) (area of graph ADG). In the post-peak stage, owing to plastic deformation, cracking, damage, etc., the rock dissipates energy \(U_{{\text{p}}}^{2}\)(area of graph ADEC). Because the sample maintains a certain residual strength, some residual elastic strain energy \(U_{{\text{E}}}^{{\text{r}}}\)(area of graph DEF) is retained in the sample. According to Fig. 9b, it is interesting that the post-peak dissipated energy \(U_{{\text{p}}}^{2}\) can be larger than the pre-peak stored elastic strain energy \(U_{{\text{E}}}\). The elastic energy stored in the pre-peak stage does not satisfy the need for energy dissipation in the post-peak stage. Thus, it is less likely to be the energy source of the kinetic energy of the ejected rock fragments. In fact, the elastic deformation energy \(U_{{\text{M}}}\) released by the experimental system is the surplus energy for the rock sample. A part of this energy (UM) will eventually be converted into the kinetic energy \(U_{{\text{K}}}\) of the ejected rock fragments (Tarasov and Stacey 2017). Note that a small portion of \(U_{{\text{M}}}\) will be converted into the energy for the loading system oscillation.

Fig. 9
figure 9

Energy evolution during unstable failure process of rock: a pre-peak, and b full-process (Tarasov and Stacey 2017)

Full size image

In the overall failure process of the unstable failure of the rock (Fig. 9), the total input external energy \(U_{{\text{T}}}\)(area of graph OAGF) is converted into three parts, namely the dissipated energy (pre-peak dissipated energy \(U_{{\text{p}}}^{1}\) and post-peak dissipated energy \(U_{{\text{p}}}^{2}\)), residual elastic strain energy \(U_{{\text{E}}}^{{\text{r}}}\), and kinetic energy \(U_{{\text{K}}}\) of the ejected rock fragments. The above analysis not only determines the energy source of the kinetic energy, but also verifies the applicability of the rigidity theory in which a strainburst is caused by the soft loading of the rock.

Based on the energy analysis in Fig. 9, we calculate corresponding graphical areas of the experimental stress–strain curves, to study the energy balance of the cyclic disturbance-induced strainburst (Fig. 10). For simplicity, it is assumed that the kinetic energy is released linearly in the post-peak stage (Fig. 10c). The energy balances of cyclic disturbance-induced strainburst under different experimental conditions are presented in Fig. 11.

Fig. 10
figure 10

Illustration of energy balance of the cyclic disturbance-induced strainburst and calculation method of each energy term: a static loading stage, b cyclic disturbance stage, and c post-peak stage

Full size image
Fig. 11
figure 11figure 11

Energy balance of the cyclic disturbance-induced strainburst calculated from experimental data (the rock sample No. and the test conditions are presented in Table 1): a DZ-1, b DZ-2, c DY-1, d DY-2, e DA-2, f DF-1, g DF-2, and h DF-4

Full size image

Figure 11 shows the energy balance evolution of absorbing input total energy, storing elastic energy, dissipating energy and releasing kinetic energy during the whole development of the cyclic disturbance-induced strainburst. In the static loading stage, the energy input to the rock gradually increases. Most of the energy is stored in the rock in the form of elastic energy and only a small amount of the energy is dissipated. During the cyclic disturbance, the elastic energy stored in rock remains nearly unchanged. The dissipated energy increases approximately proportional to the input total energy, indicating that energy dissipation is predominant in this stage. In the post-peak stage, as the rock continues to absorb external energy, the stored elastic energy gradually decreases, the dissipated energy increases rapidly, and the surplus energy of the rock-machine system is released rapidly in the form of the kinetic energy of the injected rock fragments.

3.2.2 Energy-Based Failure Mechanism

Figures 11, 12 demonstrate the energy-based failure mechanism of the cyclic disturbance-induced strainburst. When studying the energy-based failure mechanism of the cyclic disturbance-induced strainburst, the following two significant issues are to be addressed. First, the energy criterion, i.e., when a strainburst will be induced. Second, the intensity, that is, how severe a cyclic disturbance-induced strainburst can be, which is measured by the released kinetic energy of the injected rock fragments.

Fig. 12
figure 12

Illustration of the energy-based failure mechanism of the cyclic disturbance-induced strainburst

Full size image

Energy drives the deformation and failure of rock with external and internal mechanisms. The external mechanism is the continuous input of the external energy. The internal mechanism is the decrease of the strength and the ultimate energy storage capacity of the rock (Du et al. 2016; Su et al. 2017b). A rock will be damaged when the driving force caused by the external energy is greater than its resistance. Therefore, the energy criterion for the cyclic disturbance-induced strainburst is:

$$\left\{ \begin{gathered} U_{{{\text{SD}}}} = U_{{\text{S}}} + U_{{\text{D}}} > U_{{\text{C}}} \hfill \\ U_{{\text{C}}} \propto - D \hfill \\ \end{gathered} \right.,$$
(12)

where \(U_{{{\text{SD}}}}\) is the total input energy by static loading (i.e.,\(U_{{\text{S}}}\)) and cyclic disturbance (i.e.,\(U_{{\text{D}}}\)); \(U_{{\text{C}}}\) is the ultimate energy storage capacity, which is negative with the damage \(D\). In the development of the cyclic disturbance-induced strainburst, the static load and cyclic disturbance provide input energy to the rock. Meanwhile, the cyclic disturbance continuously exacerbates the rock damage and weakens the ultimate energy storage capacity of the rock. When Eq. (12) is satisfied (e.g. at time \(T_{{\text{c}}}\) in Fig. 12), a strainburst will occur.

\(U_{{{\text{SD}}}}\) in Eq. (12) can be calculated from experimental data (Figs. 10, 11). If \(U_{{\text{C}}}\) in Eq. (12) is to be determined experimentally, the strainburst criterion expressed by Eq. (12) can be determined. Generally, \(U_{{\text{C}}}\) is related to the rock properties, rock stress state, and damage state:

$$U_{{\text{C}}} = f\left( {E,R_{{\text{c}}} ;\sigma_{1} ,\sigma_{2} ,\sigma_{3} ;D} \right),$$
(13)

where \(R_{{\text{c}}}\) is the uniaxial compressive strength of the rock. If Eq. (13) can be determined, the energy criterion for the cyclic disturbance-induced strainburst (Eq. 12) will provide a new energy index, which can be embedded into numerical models to assess the strainburst potential (Jiang et al. 2010; Li and Weng 2016).

For the rockburst intensity, the released kinetic energy is (Fig. 12):

$$\left\{ \begin{gathered} U_{{\text{K}}} = U_{{{\text{SD}}}} + U_{{{\text{PS}}}} - U_{{\text{p}}} - U_{{\text{E}}}^{{\text{r}}} \hfill \\ U_{{{\text{PS}}}} = U_{{\text{F}}} + U_{{\text{M}}} \hfill \\ U_{{\text{p}}} = U_{{\text{p}}}^{1} + U_{{\text{p}}}^{2} \hfill \\ s.t.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} U_{{{\text{SD}}}} = U_{{\text{S}}} + U_{{\text{D}}} > U_{{\text{C}}} \hfill \\ \end{gathered} \right.,$$
(14)

where \(U_{{{\text{PS}}}}\) is the input external energy in the post-peak stage and the meaning of other energy items can be found in Sect. 3.2.1. The measurement and calculation for the energy parameters in Eq. (14) can be found in Tarasov and Stacey (2017).

In summary, the failure mechanism of the cyclic disturbance-induced strainburst can be described as the ‘rock degradation through energy dissipation’ of the cyclic disturbance. That is, when a cyclic disturbance of low frequency and amplitude is applied to the highly stressed rock, nearly all the input energy is gradually dissipated. This energy dissipation degrades the bearing capacity or strength of the rock (Eq. 12). Once the stress reaches the strength and the sample is strained in the post-peak stage, the surplus energy is released as the kinetic energy according to Eq. (14), thereby resulting in a strainburst.

4 Discussion

The residual strain method used to define the damage variable for rocks under the cyclic loading is improved to quantify the damage evolution and the influences of various factors on the rock damage of the cyclic disturbance-induced strainburst. The residual strain method is used mainly because that the deformation and failure of rock during the cyclic disturbance-induced strainburst exhibit remarkable fatigue damage characteristics resembling those of rocks under the cyclic loading (Su et al. 2017b). This method is improved to suit the cyclic disturbance-induced strainburst due to differences between a cyclic disturbance and a cyclic load. The amplitude of a cyclic load is normally high, up to 70% of the UCS of rock and then unloaded to an extremely small value approximating zero (Ge et al. 2003; Xiao et al. 2010). Based on the improved residual strain method, the damage evolution of the cyclic disturbance-induced strainburst under different conditions was calculated. It is found that the damage evolution of the cyclic disturbance-induced strainburst is typically inverted S-shaped, which can be well represented by the inverse logistic function. The three parameters in the inverse logistic model (Eq. 11) which shape the damage evolution curve are affected by the coupled static and dynamic loading conditions and rock properties.

The remarkable feature of the cyclic disturbance-induced strainburst is that most of the energy input to the rock by the cyclic disturbance is dissipated. An energy criterion for the cyclic disturbance-induced strainburst is established (Eq. 12), where the cyclic disturbance gradually decreases the ultimate energy storage capacity of the rock by dissipating energy. When this capacity is lower than the external input energy, the strain energy stored in the rock and the experimental system is released instantaneously to generate a strainburst. The energy release reflected in the cyclic disturbance-induced rock ejection was discussed, and the energy failure mechanism of the cyclic disturbance-induced strainburst is described as ‘rock degradation through energy dissipation’ of the cyclic disturbance.

The ultimate aim of rockburst study for the researchers and practitioners is to effectively and practically predict, mitigate and control a rockburst. Rockburst prediction requires adequate rockburst criteria, among which the energy-based ones that rarely reflect the impact of the loading system stiffness are frequently used in numerical models (Jiang et al. 2010; Li and Weng 2016; Xu et al. 2017; Zhou et al. 2018). However, relevant investigations for the cyclic disturbance-induced strainburst have been rarely reported. For this purpose, a new energy index for the cyclic disturbance-induced strainburst is proposed by combining its energy criterion (Eq. 12) and the kinetic energy release mechanism (Eq. 14). The kinetic energy release mechanism (Eq. 14) not only determines the energy source of the kinetic energy, but also verifies the validity of the rigidity theory of the strainburst (Cook 1965; Hauquin et al. 2018; Manouchehrian and Cai 2016).

Damage and energy are two critical aspects to investigate the cyclic disturbance-induced strainburst. In the present study, we investigated the damage evolution and energy balance of the cyclic disturbance-induced strainburst separately. Further efforts are required to quantify the relationship between damage and energy evolution of rock during the cyclic disturbance-induced strainburst.

5 Conclusion

We studied the damage evolution and energy balance of the cyclic disturbance-induced strainburst that is frequently encountered in deep underground engineering under the condition of a relatively soft loading system. The findings facilitate the establishment of a damage model of hard rocks subjected to ‘high static stress + low-frequency seismic disturbance’ and deepen the fundamental understanding of a strainburst. The main conclusions are as follows:

  1. 1.

    The seismic disturbance can be simulated by a low-frequency cyclic disturbance in the laboratory. The cyclic disturbance has significant effects on activating and accelerating damage of the rock, and degrading the rock by dissipating energy.

  2. 2.

    The proposed damage variable improved from the residual strain method can reflect the damage evolution of the cyclic disturbance-induced strainburst, and it can be used to quantify the effects of various factors on the damage evolution.

  3. 3.

    The damage evolution curve of the cyclic disturbance-induced strainburst is typically inverted S-shaped with three stages, i.e., initial stage, constant speed stage, and acceleration stage.

  4. 4.

    During the energy balance of the cyclic disturbance-induced strainburst, most of the energy input by the cyclic disturbance is dissipated, and the energy mechanism of this type of strainburst is explained as the ‘rock degradation through energy dissipation’ due to the cyclic disturbance.