Weak disturbance-triggered seismic events: an experimental and numerical investigation

Abstract

Geological masses can be regarded as rock blocks of different scale of structural planes with the ability to store various forms of energy. Propagation of stress waves generated by weak external disturbances in rock blocks may trigger the release of internal potential energies and slip movements along these structural planes, resulting in seismic events, such as residual deformations, fault-slip rock bursts, ground motions, etc. First, based on a simplified rock block system, a novel experimental system, and a numerical model, we investigated weak disturbance-triggered seismic events. We then conducted a theoretical analysis in which we quantitatively characterized the critical energy conditions of seismic events. The experimental and numerical results showed that the tensile stages of the stress waves generated by the disturbance loading reduced the normal stress on the interface of adjacent blocks, leading to an ultra-low friction phenomenon. This phenomenon resulted in the slip movements of the work block. The residual displacements and the critical energy conditions significantly depended on the initial stress states. As the initial shearing force ratio β increased, greater residual displacements were observed and lower disturbance energy was required to trigger a seismic event. When β was close to 1, even an extremely weak disturbance was able to trigger large residual displacements or sustainable slip failures. A dimensionless parameter k was introduced to characterize the critical energy conditions of the seismic events. The critical condition for initiating a slip was that k should exceed a critical value, while the critical conditions for a slip failure were that k should reach a larger critical value and the work block should be in a subcritical stress state. It can be concluded that disturbances, initial shear forces, and friction-weakening mechanisms are the most important factors, with the initial shear forces providing the potential energies, which are locked by the static friction force (the shear strength). The disturbances reduce the shear strength and weaken the restrictions. The friction-weakening mechanisms determine energy conversion coefficient efficiency.

Introduction

The triggering mechanisms of seismic events are a significant research topics in geological engineering and seismology. Typical seismic events include a wide range of irreversible displacements along fault zones, ground motions, and rock bursts in deep rock masses. Many seismic events have resulted in extensive loss of life and catastrophic damage to infrastructure and property.

Prior studies have shown that most seismic events are usually triggered by external disturbances, such as construction blasting, tunnel excavating, and underground nuclear testing. Glasstone and Dolan (1977) monitored and recorded thousands of weak aftershocks on the surface in the six weeks following the BENHAM underground nuclear explosion test. Kocharyan and Spivak (2001) reported that a 230-T BB blast at a depth of 252 m triggered an earthquake with a magnitude of approximately 5. The seismic energy of the earthquake was 10¹² J, while the explosive energy was only 10⁸ ~ 10⁹ J. Hill et al. (1993) reported the California Randes earthquake with a magnitude of 7.3 triggered multiple earthquakes over dozens of hours at distances of up to 1250 km from its epicenter. Other large earthquakes, such as the 1999 magnitude 7.1 Hector Mine (Gomberg et al. 2001) and the 2002 magnitude 7.9 Denali (Gomberg et al. 2004) earthquakes, have also been observed to induce dynamic triggering at remote distances. In addition to triggered earthquakes, rock bursts, which can be regarded as engineering earthquakes, have also been observed to be triggered by external disturbances. Tan (1988) found that blasting triggered 89 (78%) of 114 coal bursts at depths of 700 ~ 900 m in the Mentougou mine and more than 50% of the coal bursts at a depth of 700 m in the Longfeng mine.

These investigations indicate that seismic events may occur at a distance far from the dynamic disturbance and that the disturbance energy is always much lower than the energy released by the triggered seismic events. Wang et al. (2005, 2016) provide a preliminary explanation for these phenomena using theory analysis. They report that rock masses have the abilities to store energy and that rock masses are in a subcritical equilibrium state under high ground stress. Under these conditions, a small disturbance can break the balance and release the stored energy, resulting in seismic events. This explanation is based on theoretical analysis only, and the physical mechanisms of seismic events remain unclear to date. Kocharyan et al. (2008) found that crustal earthquakes are more likely to be a slipping motion over the existing fracture surface than the propagation of a new fracture in a brittle material. Their findings are based on seismic events simulated in laboratory experiments; however, while the experimental results provide a first insight into seismic events, the critical conditions were not well discussed. Ma et al. (2009) analytically investigated the ultra-low friction phenomenon in blocky rock systems but did not consider the seismic events induced by the ultra-low friction phenomenon.

There is still a lack of information on the physical mechanisms and critical conditions of seismic events. In the present study, we investigated weak disturbance-triggered seismic events using both an experimental and a numerical approach. First, we simplified geological masses to a rock block system in order to easily describe seismic events such as irreversible deformations and slip-type rock bursts. Then, based on this simplified mechanical model, we designed a novel experimental system and a numerical model in which we carried out a series of slip experiments using granite blocks and numerical simulations to investigate the physical mechanism of disturbance-triggered seismic events. The relationships among the disturbance energies, the initial stress states, and the released energies were studied. Based on energy analysis we then quantitatively characterized the critical energy conditions of the seismic events.

Simplified mechanical model

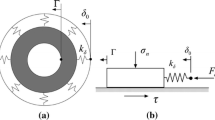
In the long-term natural environment, geological masses comprise various structural planes. Generally, these structural planes are tectonic cracks of different scales or crushing zones with filling layers. The stabilities of the geological masses are mainly determined by friction forces and the properties of the structural planes, as structural planes usually have considerably lower effective strength and deformation characteristics. Therefore, when carrying out stability analysis of geological masses, it is necessary to take into account the slip movement of the structural planes.

Figure 1 shows the slip movements of two different scales of structural planes. After the earthquake occurs, an abrupt slip along the rupture surface may occur with the effect of seismic waves (see Fig. 1b). The slip of faults in rock masses may lead to residual deformations or slip-type rock bursts (see Fig. 1c), which can be understood as smaller seismic events. All of these seismic events may result in dangerous geologic hazards.

Fig. 1

Seismic events at different scales triggered by an earthquake

Previous studies have shown that the structural hierarchy of rock masses involves a very wide range of scales, from a microscopic to a macroscopic scale (Sadovskiy 1979; Kurlenya et al. 1993; Qi et al. 2005). Rock masses can therefore be regarded as rock blocks with different scales of structural planes. To describe seismic events along the structural planes, it is possible to simplify the rock masses to a rock block system, as shown in Fig. 2. The vertical shock loading represents the external disturbances. The propagation of the stress waves in the vertical direction may cause horizontal sliding movements, which is considered to be the true seismic event. The horizontal static force T in Fig. 2 represents the initial ground stress. Based on this simplified mechanical model, we designed a novel experimental system and a numerical model, which will be discussed in the following sections.

Fig. 2

Simplified mechanical model for seismic events. T Horizontal static force, F friction force between blocks, N normal force on the structural plane

Experimental tests

Experimental system

Based on the simplified mechanical model shown in Fig. 2, we designed a novel experimental system, as shown in Fig. 3. The vertical disturbance loading is provided by the vertical electric vibration exciter (see Fig. 3a). The electric vibration exciter impacts the rock block system via a flexible stinger and a force sensor. The stinger transmits the excitation signals to the rock block system in the vertical direction, reducing secondary forms of excitation due to possible misalignments (Varoto and de Oliveira 2002). The disturbance forces applied to the rock block system are measured by the force sensor attached to the exciter and recorded by a computer. The maximum excitation force can reach 1000 N, and the disturbance time can be precisely controlled over a wide range of time, namely 0 ~ 200 ms. Compared to previous studies (Kocharyan et al. 2005) that used drop-weight apparatuses, the electrodynamic vibration exciter can control the disturbance process with greater precision, which is convenient for quantitative analysis. The horizontal static loading is provided by a wire–wheel–weight plate system (see Fig. 3a, c). The magnitude of the horizontal pulling force is regulated by changing the number of weights. The height of the weight plate is set to a safe range to avoid large displacements of the work block, which may lead to a collapse of the rock block system.

Fig. 3

Photograph and structural diagram of rock blocks, a Photograph of the experimental system, b schematic diagram of vertical vibration experiment, c schematic diagram of horizontal slip experiment

Schematic diagrams of a vertical vibration experiment and horizontal slip experiment are shown in Fig. 3b and c, respectively. The displacements of the rock blocks are recorded by fiber-optic displacement sensors with a measurement sensitivity of 1.1 μm/mV, a range of 20 mm, and a frequency response of 20 kHz. The use of non-contact measurement methods can reduce the effects of measuring instruments on the experimental model and generally does not require numerous stringent requirements for the experimental conditions. In Fig. 3b, the rock blocks are slightly staggered relative to each other to allow the placement of the displacement sensors to investigate the vertical vibrations. These displacement sensors in Fig. 3b are fixed on a metal frame. As shown in Fig. 3c, for the horizontal slip experiment we remove the stringer and force sensor in the horizontal vibration exciter and fix a displacement sensor on it instead. In our investigation of the horizontal slip movements of the work block, the placement of several baffles restricts the horizontal movements of other blocks.

With the experimental system shown in Fig. 3, the disturbance loading can be accurately controlled to allow a quantitative study. The disturbance loading is applied in the orthogonal direction to the slip movements, which is to illustrate that the disturbance loading may not be the energy source of the seismic events. In addition, it is easy to consider the effect of the initial stress states by regulating the number of weights.

Experimental specimens

The experimental specimens are granite blocks (dimensions 160 × 125 × 125 mm) that have been cut from an intact rock. To reflect the roughness, the surfaces of the granite blocks are not especially polished. The mass of a single block is 6.8 kg, and the density is calculated to be 2720 kg/m³. As shown in Fig. 4, the rock block system comprises five granite blocks that are vertically stacked. In the horizontal slip movement study, block 3 is considered to be the work block, and the horizontal movements of the other blocks are restricted using baffles.

Fig. 4

Photograph of granite blocks

Experimental procedures

First, the maximum static friction force, namely the shear strength, was measured. The experimental model and instruments were arranged as shown in Fig. 3c. Under the condition of no vertical disturbance loading, we gradually increased the weights until block 3 started to slip. To eradicate any discrepancies, the process was repeated three times. The shear strength obtained was F_p = 170 N. The static friction coefficient μ_s can then be calculated as follows:

$$ {\mu}_{\mathrm{s}}=\frac{F_{\mathrm{p}}}{N}=\frac{F_{\mathrm{p}}}{5 mg}=0.5 $$

(1)

where N is the normal force, m is the rock mass, and g is the gravity acceleration.

To represent the initial stress state of the work block, an initial shear force ratio β is defined as follows:

$$ \beta =\frac{T}{F_{\mathrm{p}}} $$

(2)

where T is the horizontal static force. In the initial state, the horizontal static force of the work block should satisfy T < F_p(i.e., β < 1) to ensure an initial equilibrium state with no vertical disturbance loading. When β is close to 1, the rock system is near a critical state, referred to as the subcritical state.

Then, to investigate the vertical vibrations of the rock blocks, we conducted impact experiments with no horizontal pulling force. The experimental model and instruments were arranged as shown in Fig. 3b. The force sensor in the vertical electric exciter recorded the time-history curve of the vertical disturbance force, as shown in Fig. 5. The maximum disturbance force in Fig. 5 was approximately 75 N and the duration was approximately 7 ms. Based on an integral calculation the impulse can be obtained as ${I}_{\mathrm{m}}={\int}_0^{\infty }p(t)\mathrm{d}t=0.16\ \mathrm{N}\cdot \mathrm{s}$. Assuming that the initial velocity of block 1 is zero and the impact time is quite short, the relationship between the disturbance energy W and the impulse I_m can be expressed as follows:

$$ W=\frac{1}{2m}{\left|{\int}_0^{\infty }p(t)\mathrm{d}t\right|}^2=\frac{{I_{\mathrm{m}}}^2}{2m} $$

(3)

where p(t) is the disturbance force, as shown in Fig. 5.

Fig. 5

Time-history curve of the vertical disturbance force

Finally, a series of slip experiments of various horizontal pulling forces and vertical dynamic disturbances were performed to investigate the seismic events of the work block. The experimental model and instruments were arranged as shown in Fig. 3c. The same horizontal pulling force was maintained while the maximum disturbance force was increased gradually until a slip failure of the work block was observed. A fiber-optic displacement sensor recorded the horizontal displacements of the work block during the entire slip process.

Experimental results

Vertical vibrations

The vertical displacement of rock blocks under the vertical disturbance loading of W = 165.94 mJ is shown in Fig. 6. The positive values in Fig. 6 represent the compression direction, while the negative values represent the tensile direction. As shown in Fig. 6, when the vertical disturbance loading was applied, the rock blocks first generated compression displacements, which then became tensile displacements. When the vertical disturbance force ceased, the displacement oscillation continued, and displacements of the adjacent blocks may be generated in opposite directions. As shown in Fig. 7, the maximum relative displacements increased with increases in disturbance energy. The normal forces on the interfaces are affected by the maximum relative displacements. The relative tensile displacements of the adjacent blocks will reduce the normal forces, resulting in a significant decrease in the maximum static friction force, which is known as an ultra-low friction phenomenon (Kurlenya et al. 1999, 1997; Ma et al. 2009). The main reason for this phenomenon is the relative displacements of the adjacent blocks. In addition, with the increase of disturbance energies, the phenomenon can be more significant, which facilitates the slipping of the work block along the interfaces.

Fig. 6

Vertical displacements of blocks with a disturbance energy of W = 165.94 mJ

Fig. 7

Maximum relative displacement between adjacent blocks

Horizontal slip movements

When conditions with a horizontal pulling force applied on the work block are considered, slip movements may be observed due to the ultra-low friction phenomenon. Figure 8 shows the horizontal displacements of the work block with various initial shear force ratios β and vertical disturbance energies W. If W was large enough, the work block began to move. A larger W was required to create a slip movement of a block with a small β (see Fig. 8a, b). When the vertical vibrations finally ceased, the slip movement may stop due to the friction force. In this case, residual displacements could be observed. Figure 9 shows the relation between the residual displacements and W. The residual displacements seemed to increase with increasing W, and the increase was especially noticeable when β was large. When β was close to 1, the residual displacements were very sensitive to W, and even a slight disturbance could cause significant residual displacements.

Fig. 8

Horizontal displacements of the work block

Fig. 9

Relationship between residual displacement and disturbance energy

When β was close to 1 and W was sufficiently large, the slip movements of the work block could not stop and the horizontal displacements continuously increased until the weight plate dropped to the ground (see Figs. 8f, 9g, h). The sustained slip failure of the work block represented seismic events with a large energy release, such as a slip-type rock burst in the rock mass around an underground tunnels (see Fig. 1c). The critical energy decreased as β became closer to 1. When β = 0.94 (see Fig. 8h), a considerable slight disturbance with energy could trigger a slip failure of the work block.

From Fig. 8, it can be concluded that there were three final states of the work block: (1) if both β and W were sufficiently low, the work block remained stationary, and no obvious horizontal displacement was observed; (2) as β and W increased, the work block began to slip and finally stopped; in this case, residual displacement was observed; (3) if β was close to 1 and W was sufficiently large, the slip movement of the work block did not stop, and a slip failure was observed. Figure 10 shows the critical energy conditions for these three cases, which corresponded to the elastic deformation zone, residual displacement zone, and slip failure zone, respectively. Kurlenya et al. (1996a, b) used a dimensionless parameter k to estimate the critical energy conditions for the quasi-resonance operating mode of a block system. k was expressed as follows:

$$ k=\frac{W}{{mc_{\mathrm{p}}}^2} $$

(4)

Fig. 10

The critical energy conditions with various initial shear force ratios. k Dimensionless parameter (Kurlenya et al. 1996a, b), β initial stress state

Referring to Kurlenya et al. (1996a, b)‘s studies, we introduced the same dimensionless parameter k to characterize the critical energy conditions. As shown in Fig. 10, the critical energy conditions strongly depended on β, namely, the initial stress state. When β was low, the disturbance could only trigger residual displacement, and slip failure never occurred. The dimensionless parameter k significantly decreased with increasing β. In the subcritical state (β → 1), slip failure can easily occur. The relation between k and β will be discussed in more detail in the following sections.

Based on the results of the experimental tests, we suggest that the disturbance loading may lead to the ultra-low friction phenomenon, which enables the block to slip easier along the interfaces. We investigated the slip movements of the work block with various initial shear force ratios β and vertical disturbance energies W. However, the physical mechanism of the slip movements remained unclear. This led us to conduct a numerical modeling study to determine how the residual displacements are generated and how the slip failures occur.

Numerical modeling

Equilibrium equations

The numerical modeling methods referred to by Ma et al. (2009) in their analytical study were not well discussed in terms of the effect of initial stress states and the critical conditions. In our numerical modeling study, we simplified the rock block system into a multiple-degree-of-freedom mass–spring–dashpot system, as shown in Fig. 11. Taking the static equilibrium position as the initial position, the equilibrium equation of the mass–spring–dashpot system can be expressed as follows:

$$ M\left(\ddot{y}(t)-g\right)+C\dot{y}(t)+ Ky(t)={P}_{\mathrm{v}}(t) $$

(5)

where M is the mass matrix, C is the damping matrix, K is the stiffness matrix, y(t) is the vertical displacement vector, and P_v(t) is the vertical loading vector expressed as P_v(t) = [p(t), 0, 0, 0, 0,]^T.

Fig. 11

Simplified rock block system. a Numerical model in the vertical direction, b numerical model in the horizontal direction. m_i Mass, c_i Viscous damping coefficient, k_i stiffness. The subscripts correspond to the block number

The equilibrium equation of the work block can be expressed as follows:

$$ m\ddot{x}(t)=T-\mu \left[{N}_2(t)+{N}_3(t)\right] $$

(6)

where x(t) is the horizontal displacement vector, N_i(t) = k_iy_i(t) is the normal force, and μ is the friction coefficient, which depends on the relative velocity or displacement (Olsson et al. 1998).

Dynamic friction-weakening mechanisms

If the work block keeps sliding, the friction coefficient μ will gradually decrease from the static friction coefficient μ_s to the dynamic friction coefficient μ_d. The dynamic friction-weakening mechanisms are quite complicated, and in the present study, a simplification was made to facilitate the numerical calculation.

The experimental results of Rabinowicz (1951) suggest that the friction force should be described as a function of displacement and not of velocity. The proposed relationship between friction force and displacement is shown in Fig. 12. The peak friction force F_p typically occurs at a considerable small displacement x_p from the starting point. In the post-peak state, the friction force decreases gradually, and the decrease gradually slows down. Thus, we simplified the curve into three segments (see the red lines in Fig. 12). The dynamic friction-weakening mechanism shown in Fig. 12 can be described as follows:

$$ \mu =\Big\{{\displaystyle \begin{array}{cc}{\mu}_{\mathrm{s}}& x\le {x}_{\mathrm{p}}\\ {}{u}_{\mathrm{s}}+\frac{u_{\mathrm{d}}-{u}_{\mathrm{s}}}{x_{\mathrm{d}}-{x}_{\mathrm{p}}}\left(x-{x}_{\mathrm{p}}\right)& {x}_{\mathrm{p}}<x\le {x}_{\mathrm{d}}\\ {}{\mu}_{\mathrm{d}}& x>{x}_{\mathrm{d}}\end{array}}\operatorname{} $$

(7)

Fig. 12

The relation between friction force and displacement. F_p Peak friction force, x_p displacement from the starting point,F_d final dynamic friction force,x_d displacement for final dynamic friction force

Calculation procedure

From the aforementioned equations, the procedure for making a calculation was as follows:

• 1. Set up the disturbance force p(t). p(t) can be obtained from the time-history curve recorded by the vertical force sensor, as shown in Fig. 5. Or, p(t) can be simply represented as a half-sine curve (Ma et al. 2009).

• 2. Calculate the vertical displacements y(t) of all the rock blocks from Eq. (5). We used the MATLAB® (MathWorks Inc., Natick, MA, USA) ‘ode45’ function to solve Eq. (5).

• 3. Calculate the horizontal displacement x(t) of the work block from Eq. (6) using an iterative calculation. In every calculation step, we used Eq. (7) to update the friction coefficient μ. The horizontal velocity $\dot{x}(t)$ and acceleration $\ddot{x}(t)$ were also obtained.

Numerical calculation results

Calculation parameters and fitting results

From the experimental results, the static friction coefficient μ_s and the mass of each rock block in Fig. 11 m_i = 6.8 kg/m³ to represent that mass of every block is set to be 6.8 kg/m³. Similarly, we use k_i and c_i can be obtained as μ_s = 0.5, and m_i = 6.8 kg/m³. To fit the experimental results, we used trial and error methods to obtain the other parameters, such as μ_d = 0.43, k_i = 3 × 10⁷ N ⋅ m^‐1, c_i = 1.45 × 10⁴ N ⋅ s ⋅ m^‐1, x_p = 10 μm, and x_d = 800 μm. The disturbance force p(t) can be obtained from the time-history curve recorded by the vertical force sensor. The fitting results with fixed horizontal force T = 150 N(β = 0.88) are shown in Fig. 13, which shows that the numerical model can describe well the slip movements triggered by disturbance loading. Both the experimental results (see Fig. 8) and the numerical results (see Fig. 13) show three seismic events of different levels. The physical mechanisms of these seismic events will be discussed in the following section.

Fig. 13

Comparison of numerical results (dashed lines) and experimental results (solid lines), with a fixed horizontal force T = 150 N and various disturbance energies

Physical mechanisms of seismic events

As previously discussed, the vertical disturbance loading can reduce the friction force, which makes it easier for the work block to slip. Figure 14 shows the time-history curve of a horizontal force with a disturbance energy of 60 mJ. It can be seen that under vertical disturbance loading, the friction force converts into oscillation changes and can reach the quite low value of F_{pd, min} = 46.35 N. Obviously, F_{pd, min} can be lower as disturbance energy W increases. As seen in Fig. 14, T₁, T₂, and T₃ are the horizontal pulling forces for three different conditions:

• 1. T < F_{pd, min}(see T₁ in Fig. 14). T cannot exceed the shear strength at all times. In this case, no horizontal movement can be observed, and the rock block system is always stable, which corresponds to Zone I in Fig. 10.

• 2. F_{pd, min} ≤  T < F_d(see T₂ in Fig. 14). Time-curves of the displacement, the velocity, and the acceleration of the work block are shown in Fig. 15. The tensile stages of the vertical relative displacements can reduce the normal stress on the interface of the adjacent blocks, which leads to a reduction in the maximum static friction force (the shear strength). Once the friction force F_pd decreases to a value of less than T, the work block starts to slip horizontally. The horizontal velocity has an initial increase under the shear force deviator T − F_pd during the tensile stages. However, if the vertical disturbance loading stops, the work block will slow down under the shear force deviator F_d − T and finally stop. In this case, residual displacements can be observed, which correspond to Zone II in Fig. 10.

• 3. F_d ≤  T ≤  F_p(see T₃ in Fig. 14). This case is more complicated. Figure 16 shows the time-curves of the vertical relative displacement, the horizontal displacement, and the velocity and acceleration of the work block considering two different situations. The friction force gradually decreases as the displacement increases during the post-peak stage (see Fig. 12). If the vertical disturbance loading stops, the final friction force is still higher than T. In this case, the work block will stop and cannot start to slip again. Residual displacements can be observed (see solid lines in Fig. 16), which correspond to the zone below Zone III in Fig. 10. Another situation is that the final friction force is lower than T when the vertical disturbance loading ends. In this case, the work block continues to accelerate and finally causes slip failure (see dashed lines in Fig. 16), which corresponds to Zone III in Fig. 10.

Fig. 14

Time-history curve of horizontal force with the disturbance energy of 60 mJ. T₁, T₂, T₃ Horizontal pulling forces for three different conditions, F_pd maximum static friction force with disturbance loading, F_p maximum static friction force with no disturbance loading, F_d dynamic friction force when disturbance loading ceases, F_{pd, min} minimum of F_pd

Fig. 15

Time-curves of the displacement (a), the velocity (b) and the acceleration (c) of the work block with T = 100 N and W = 60 mJ

Fig. 16

Time-curves of the vertical relative displacement (a), the horizontal displacement (b), the velocity (c), and the acceleration (d) of the work block with T = 150 N

Based on these results we concluded that if the vertical disturbance energy is sufficiently large to reduce the shear strength to less than the initial shear force, the work block starts to slip along the contact surface. To observe a slip failure, the initial shear force should be larger than the dynamic friction force and, at the same time, the vertical disturbance energy should be large enough to generate a displacement that makes the final friction force less than the initial shear force. In the following section, we report on the theoretical formulations we developed to quantitatively characterize these conditions.

Theoretical analysis

Critical energy conditions for starting to slip

The friction force F can be considered as two parts: the friction due to the block gravities, denoted as F_N, and the friction due to the disturbance loading, denoted as F_ND. When T > F, the work block starts to slip. The critical conditions can be expressed as follows:

$$ T=F={F}_{\mathrm{N}}+{F}_{\mathrm{N}\mathrm{D}}={F}_{\mathrm{p}}-{\mu}_{\mathrm{s}}{k}_i{A}_{\mathrm{y}} $$

(8)

where A_y is the maximum vertical relative displacement. In the critical condition, we have F_N = F_p. In the simplified rock block system shown in Fig. 11, the disturbance energy W is directly proportional to the square of the maximum relative displacement A_y, with the relationship of

$$ W={k}_y{A_{\mathrm{y}}}^2 $$

(9)

where k_y is an equivalent spring coefficient.

From Eqs. (4), (8), and (9), the dimensionless parameter k for the initiation of slip can be expressed as follows:

$$ k=\frac{W}{{mc_{\mathrm{p}}}^2}=\frac{W{\chi}^2}{VG}=\frac{k_y{k}_1{\gamma_{\mathrm{p}}}^2{\chi}^2}{{\left({\mu}_{\mathrm{s}}{k}_i\right)}^2}{\left(1-\beta \right)}^2 $$

(10)

where χ is the wave velocity ratio, χ = c_s/c_p, c_s is S-wave velocity, c_p is P-wave velocity, V is the block volume, G is the shear modulus, k₁ is the elastic coefficients during the pre-peak phase of Fig. 12, and γ_p is the yield shear strain γ_p = x_p/H.

Critical energy conditions for slip failure

As previously discussed, slip failure can only occur in the subcritical state of F_d ≤ T ≤ F_p, namely, β_d ≤ β ≤ 1, where the dynamic shear force ratio β_d can be expressed as β_d = μ_s/μ_d. Based on the simplified curve of F_N as shown in Fig. 12, the horizontal force–displacement curves of the work block with β_d ≤ β ≤ 1 are shown in  Fig. 17. The critical condition for slip failure is that when the vertical disturbance ends, the final friction force should be equal to the shear force, namely, T = F_N (see point C in Fig. 17). Therefore, in the critical condition, the work done by F_ND can be expressed as follows:

$$ {W}_{\mathrm{d}}={\int}_{x_0}^{x_{\mathrm{c}}}\left({F}_{\mathrm{N}}-T\right) dx $$

(11)

Fig. 17

Horizontal force–displacement curves of the work block with β_d ≤ β ≤ 1. β_d Dynamic shear force ratio

Notice that Eq. (11) represents the area of the triangle ABC. Thus, we have

$$ {W}_{\mathrm{d}}=\frac{1}{2}\left(\frac{1}{k_1}+\frac{1}{k_2}\right){\left({F}_{\mathrm{p}}-T\right)}^2 $$

(12)

where k₁ and k₂ are the elastic coefficients of the elastic deformation phase and post-peak phase, respectively.

In Fig. 17, point B represents the critical condition for initiation of slip. Similarly, the work done by F_ND to trigger the initial slip can be obtained as follows:

$$ {W_{\mathrm{d}}}^{\hbox{'}}=\frac{1}{2}\frac{1}{k_1}{\left({F}_{\mathrm{p}}-T\right)}^2 $$

(13)

Considering the critical condition for initiation of slip (point B in Fig. 17), from Eqs. (8), (9), and (13), it can be determined that both W and W_d^' are directly proportional to the square of the amplitude of the relative vertical displacement A_y. Thus, the relationship between W and W_d^' is linear and can be expressed as follows:

$$ W=\eta {W_{\mathrm{d}}}^{\hbox{'}} $$

(14)

where η is a dimensionless coefficient expressed as follows:

$$ \eta =\frac{2{k}_{\mathrm{y}}{k}_1}{{\left({\mu}_{\mathrm{s}}{k}_{\mathrm{i}}\right)}^2} $$

(15)

From Eqs. (4), (12), (13), (14) and (15), the dimensionless parameter k for initiation of slip can be obtained as follows:

$$ k=\frac{W}{{mc_{\mathrm{p}}}^2}=\left(1+\frac{k_1}{k_2}\right)\frac{k_{\mathrm{y}}{k}_1{\gamma_{\mathrm{p}}}^2{\chi}^2}{{\left({\mu}_{\mathrm{s}}{k}_{\mathrm{i}}\right)}^2}{\left(1-\beta \right)}^2 $$

(16)

Note that Eqs. (10) and (16) have similar forms. The dimensionless parameter k seems to be proportional to (1 − β)². In the present study, Eqs. (10) and (16) are obtained from the simplified force–displacement curves shown in Fig. 12. The real force–displacement curves should be nonlinear, and the friction force can be affected by the relative velocity and other parameters. Considering the complexity of real seismic events, we can use a more general expression to describe the relationship between the disturbance energies and the initial shear force ratios, which can be written as follows:

$$ k=\lambda {\left(1-\beta \right)}^{\alpha } $$

(17)

where λ and α are fitting parameters.

For the experimental results, we have

$$ {\displaystyle \begin{array}{l}{k}_{\mathrm{rd}}=1.85{\left(1-\beta \right)}^{7.6}\times {10}^{\hbox{-} 9}\\ {}{k}_{\mathrm{sf}}=790.70{\left(1-\beta \right)}^{3.04}\times {10}^{\hbox{-} 9}\end{array}} $$

(18)

where k_rd represents the critical energy condition for initiation of slip, namely, for residual displacements, and k_sf represents the critical energy condition for slip failures.

A comparison of the fitting curves is shown in Fig. 10, and it can be seen that Eq. (18) can characterize well the critical energy conditions of seismic events. In Fig. 10, it should be noted that β ≥ β_d is a supplementary boundary for Zone III. This means that to trigger a slip failure, both the conditions of β ≥  β_d and k ≥  k_sf should be satisfied at the same time.

Discussion

In the experimental system (see Fig. 3) and the numerical model (see Fig. 11) described here, the disturbance loading is applied in the orthogonal direction to the shear force. This design is to illustrate that the disturbance energies are not the energy sources of the slip movements; rather, the real energy sources are the stored potential energies due to the existence of shear force T. These potential energies are locked by the friction forces F before the disturbance loading is applied. The effect of the disturbance is to reduce F and weaken the restrictions, which is known as an ultra-low friction phenomenon (Kurlenya et al. 1999, 1997; Ma et al. 2009). Once the condition of T > F is fulfilled, the stored potential energies will be converted into the kinetic energies of the work block. Because the disturbance energies may not be the energy sources of the seismic events, the seismic events can occur at a distance far from the dynamic disturbances. In addition, if the critical energy conditions for slip failures are fulfilled, the slip movements of the work block will be sustainable due to the shear force deviator T − F_d. As a result, the released kinetic energies can be larger than the disturbance energies if the slip movements continue.

Once the work block starts to move, the potential energies will be converted into kinetic energies. The energy conversion coefficient efficiency depends on the dynamic friction-weakening mechanism. The expressions of the dimensionless parameters [see Eq. (16)] show this dependency relationship. If the friction coefficient decreases slowly during the post-peak stage—namely, k₂ is relative low—there should be larger disturbance energies to trigger the slip failure.

Note that the pore pressure-triggered seismic events can also be explained partly from the results of the present study. Natural faults in deep rock masses are subjected to fluid-filled conditions, and recent investigations (Hill et al. 1993; Bao and Eaton 2016) show that the change in pore pressures can trigger seismic events. Both pore pressure-triggered and disturbance-triggered seismic events have similar physical mechanisms. The increase in pore pressure may significantly reduce the effective normal stresses and lead to a reduction in the friction force, which in turn allows the rock blocks to slip easier on structural planes in the subcritical state.

The results presented here can provide a better understanding of weak disturbance-triggered seismic events and provide helpful data for carrying out stability analyses of underground engineering. As the critical conditions strongly depend on the initial shear force, especially in the subcritical state, an efficient approach to prevent the seismic event is to reduce the initial shear force and release the stored potential energies. Equations (10) and (16) show that the critical energies also depend on the strength and deformation characteristics of the structural planes (e.g., the yield shear strain γ_p, the ratio of the elastic coefficients of the pre-peak and post-peak phases k₁/k₂, and the friction coefficient μ_s). Thus, reinforcements of the structural planes can also effectively prevent the seismic events triggered by weak disturbances. In addition, the dependency relationships indicated by Eqs. (10) and (16) can help to determine the optimally oriented structural planes, along which the seismic events are most likely to occur after weak disturbances.

Conclusion

Geological masses can be regarded as rock blocks with different scales of structural planes. Seismic events associated with deformations over these structural planes, such as large-scale irreversible displacements, fault-slip rock bursts, and ground motions, can easily occur following external weak disturbances. In the present study, weak disturbance-triggered seismic events are studied in both an experimental and a numerical investigation. A series of slip experiments using granite blocks and numerical simulations were carried out to investigate the physical mechanism of disturbance-triggered seismic events. Then, based on the energy analysis, we quantitatively characterized the critical energy conditions of the seismic events. The main conclusions of our studies are:

• 1. The physical cause of the slip movements triggered by the dynamic disturbance loading is the reduction in the compressive stress on the contact surface caused by the tensile stages of the stress waves, which leads to a decrease in the maximum static friction force, namely, the shear strength. If the shear strength is reduced to less than the horizontal pulling force, namely, shear force T, the work block starts to slip along the contact surface, leading to irreversible slip movements (or residual displacements). When the disturbance loading finally ends, if the final friction force F_d is less than the shear force T, the slip movements will continue, leading to a slip failure of the block system. Slip failure can only occur in the subcritical state (β ≥ β_d).

• 2. Residual displacements and the critical energy conditions significantly depend on the initial stress states. As the initial shearing force ratio β increases, larger residual displacements can be observed with the same disturbances and fewer disturbance energies are required to trigger a seismic event. When β is close to 1, even an extremely weak disturbance can trigger large residual displacements or sustainable slip failures.

• 3. A dimensionless parameter k is introduced to characterize the critical energy conditions of the seismic events. The condition for triggering residual displacements is that the disturbance energies should be sufficiently large to make the dimensionless energy parameter k exceed a critical value given by Eq. (10). The slip failures should satisfy two conditions: (1) during the initial stage, the rock blocks should be in the subcritical state of β ≥  β_d; (2) the dimensionless energy parameter k should exceed a critical value given by Eq. (16).

• 4. Weak disturbance-triggered seismic events can be regarded as processes which convert the stored potential energies of the work block to kinetic energies. Based on experimental and numerical investigations, it can be concluded that disturbances, initial shear forces, and friction-weakening mechanisms are the most important factors. The initial shear forces provide the potential energies locked by the static friction force (the shear strength). These disturbances reduce the shear strength and weaken the restrictions. The friction-weakening mechanisms determine energy conversion coefficient efficiency.