Influence of Loading System Stiffness on Post-peak Stress–Strain Curve of Stable Rock Failures

Abstract

It is well known from laboratory testing that the rock failure process becomes unstable in a soft test machine due to excessive energy released from the machine. Great efforts had been devoted to increasing the loading system stiffness (LSS) of laboratory test machines to ensure that the post-peak stress–strain curve of rock can be obtained for underground rock engineering design. A comprehensive literature review on the development of stiff test machines reveals that because of the differences in the manufacturing arrangement of the test machines, LSS values of the test machines used for rock property testing are always finite and vary in a large range, and the influence of LSS on stable rock failure is less understood. A FEM-based numerical experiment is carried out to study the influence of LSS on the stress–strain curves of stable rock failure in uniaxial compression, with a focus on the post-peak deformation stage. Three test machine loadings including idealized rigid loading, platen loading, and frame–platen loading with finite LSS are considered, and the simulation results are analyzed and compared. The modeling results obtained from the simulations indicate that even if the LSS value is large enough to inhibit unstable rock failure, as long as LSS is finite, it has an influence on the post-peak stress–strain curve of rock. It is revealed that because the input energy supplied by the external energy source to drive the stable rock failure process is affected by the finite LSS of a test machine, the post-peak descending slopes of the stress–strain curves are all steeper than the post-peak descending slope obtained under an ideal loading condition of infinite LSS. An insight from this numerical experiment is that it might be more feasible to develop laboratory test machines with variable LSS that can match the local mine stiffness in the field for rock property testing.

1 Introduction

Understanding rock deformation behaviors under compression is critical for studying the stability of structures built in or on rock. Knowing the compressive strength of rock is important in rock mechanical property testing, and test machines with high loading capacities were developed to measure rock strength (Cook and Hojem 1966; Bieniawski 1966; Wawersik 1968; Stavrogin and Tarasov 2001; Mogi 2007). Moreover, the importance of obtaining not only the peak strength but also the complete stress–strain curve of rock by laboratory testing has been recognized, because the post-peak behavior of rock affects the extent of excavation-damaged zones (Bieniawski 1967b; Alonso et al. 2003; Cai et al. 2007) and the likelihood of violent pillar failures (Morsy and Peng 2002). Accordingly, the requirement for increasing the loading system stiffness (LSS) of the test machines to control rock failure process was specified by some researchers (Cook 1965; Salamon 1970).

Although a detailed testing method for determining uniaxial compressive strength (UCS) and deformability of rock has been suggested by the International Society for Rock Mechanics (ISRM) (Fairhurst and Hudson 1999), there is no standard regarding the LSS of test machines. As a result, LSS in rock laboratory testing varies among different test machines. On the other hand, it is observed that the post-peak stress–strain curve of rock is loading condition dependent (Wawersik and Fairhurst 1970; Peng 1973; Xu and Cai 2015). It is thus hypothesized in this study that LSS can affect the post-peak stress–strain curve of rock, even if LSS is sufficiently high to inhibit unstable rock failure.

In this paper, the development of stiff test machines and the stable rock failure criterion along with the influence of LSS on the post-peak behavior of rock are reviewed first. Next, the advantage of using a finite element method (FEM) numerical tool to model the structural response of a rock specimen–test machine system in rock laboratory testing is discussed. Subsequently, a comprehensive numerical experiment is carried out to study the influence of LSS on the stable rock failure in uniaxial compression tests. Inspired by the laboratory test results of Bieniawski et al. (1969), who used a test machine that could vary its LSS, the goal of this study is to numerically confirm that LSS can influence the post-peak stress–strain curve of stable rock failure.

2 Review of Loading System Stiffness (LSS)

Loading system stiffness (LSS) in rock laboratory property testing is reviewed first before a comprehensive numerical experiment is carried out. In this way, the readers can deepen the understanding why it is important to increase LSS and how the LSS values of test machines differ with each other. This will lead to the research question of this study, i.e., whether the post-peak stress–strain curves obtained from property testing are affected by LSS.

2.1 Development of Stiff Test Machines

2.1.1 Traditional Stiff Test Machines

According to the review on rock testing by Ulusay (2012), mechanical property testing of materials using simple test machines was first reported in the sixteenth century. According to Ulusay (2012), Hooke published his experimental results in 1678 and found that the relation between the applied load and the elastic deformation of an elastic material is linear. According to Hudson et al. (1972), in about 1770, Émiland-Marie Gauthey built a lever system and carried out the first rock property test and measured the compressive strength of cubic rock specimens. Having developed a large horizontal hydraulic test machine, David Kirkaldy opened the first commercial testing laboratory in London in 1865 (Smith 1980).

From the 1930s to the 1950s, studies on the rock failure process began. Pioneering works were conducted by Griggs (1936), Kiendl and Maldari (1938), and Handin (1953), and this greatly promoted the development of rock laboratory test machines using stiff components. Before 1966, observations of the load–deformation curves of rock were limited in the pre-peak deformation stage because the rock failure process was violent immediately after the ultimate load-carrying capacity of rock had been reached, largely due to the low LSS of test machines relative to the post-peak stiffness of rock as we know it today.

Cook (1965) explained the possibility of obtaining information on the post-peak behavior of rock by increasing LSS. The first sets of complete load–deformation relations of rock were obtained by Cook and Hojem (1966) and Bieniawski (1966) with the aid of stiff test machines. Since then, these precursors, along with other researchers (Wawersik and Fairhurst 1970; Cook and Hojem 1971; Stavrogin and Tarasov 2001), had devoted great efforts to increasing LSS of test machines. A test machine normally consists of a steel frame that accommodates the rock specimen inside, end loading platens contacting the specimen to distribute load, and a hydraulic ram to deform the specimen (Fig. 1). According to Hudson et al. (1972) and Stavrogin and Tarasov (2001), one technique to stiffen a test machine is to add stiff components (e.g., steel bars) in parallel with the rock specimen; another technique is to add a fluid ram with a large cross-sectional area and a small height. These types of test machines mentioned above belong to the traditional stiff test machine.

Fig. 1

Schematic of a traditional stiff test machine for determining stress–strain curves of rock, modified from Cook (1965)

2.1.2 Other Types of Stiff Test Machines

On the basis of traditional stiff test machines, other types of stiff test machines were developed, with a focus on increasing LSS by alleviating the reduction of LSS due to the fluid ram. For instance, Cook and Hojem (1966) and Wawersik (1968) employed a thermal circuit in their loading frames as the means of contracting the frames to apply load to deform rock specimens. An advantage of employing the thermal contraction method is that the reduction of LSS due to the fluid ram is avoided, but a disadvantage is that the loading rate is hard to be controlled in the post-peak deformation stage.

Bieniawski et al. (1969) designed a novel test machine where the fluid ram was separated from the rock specimen–steel frame system so that the compressibility of the fluid (e.g., oil) did not affect LSS. Figure 2 illustrates the design principle for the test machine described in Bieniawski et al. (1969), and in the subsequent discussions, we call it Bieniawski-type test machine. The rock specimen tested by the Bieniawski-type test machine was arranged in parallel with steel bars of a large cross-sectional area so that the applied load to deform the rock was shared with steel bars only. According to Bieniawski (1967a) and Bieniawski et al. (1969), LSS of the Bieniawski-type test machine could be varied from 103 to 1803 MN/m. Although the original descriptions regarding the design principle for varying LSS were given elsewhere, based on Bieniawski (1967a) and Bieniawski et al. (1969), it is reasonable to reckon that by adjusting the number of steel bars in parallel with the rock specimen, it is possible to vary the LSS of the Bieniawski-type test machine. However, one disadvantage of the Bieniawski-type test machine was that the effective loading capacity of the machine was reduced due to the low compressibility of the steel bars and the deformation range of rock specimens was also small (Hudson et al. 1972).

Fig. 2

Schematic of the Bieniawski-type test machine, after Bieniawski et al. (1969)

The failure process must be controlled to obtain the complete load–deformation curve of rock. It was realized that in some cases, the failure process of brittle rocks (refer to Fig. 4) could not be controlled even when a very stiff test machine was used (Wawersik and Fairhurst 1970). Consequently, closed-loop, servo-controlled test machines were developed in the 1970s. The ground-breaking work of Fairhurst and his colleagues on rock laboratory testing (Hudson et al. 1971, 1972) paved the way for recognizing two advantages of using a servo-controlled test machine to obtain the complete load–deformation curve of rock (Fig. 3). Firstly, the response time of the traducer in a servo-controlled test machine is shorter than that in the rock failure process; as a result, instability of the rock failure process can be detected in advance. Secondly, a servo-controlled pump can be activated by the onset of instability to reduce the fluid pressure rapidly and thereby increase the effective unloading stiffness of the test machine (Rummel and Fairhurst 1970).

Fig. 3

Schematic of a closed-loop, servo-controlled test machine, modified from Hudson et al. (1972)

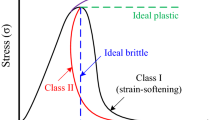
If the failure process is potentially unstable due to the release of energy stored in the specimen itself, using the lateral or radial displacement instead of the axial displacement as the control variable, a servo-controlled test machine allows any extra energy to be extracted from the test machine rather than to release to the specimen (Wawersik and Fairhurst 1970; Okubo and Nishimatsu 1985; He et al. 1990; Labuz and Biolzi 2007). This often leads to a Class II-type load–deformation (or stress–strain) relation (purple line in Fig. 4). Class II failure type shows that the strength decreases with the decrease of axial strain in the post-peak deformation stage, as opposed to Class I failure type (red lines in Fig. 4), which primarily shows a strain-softening behavior (Martin and Chandler 1994; Lockner 1995; Vardoulakis et al. 1998). With the advancement of closed-loop, servo-controlled test machines, more sophisticated rock behaviors can be observed and studied under various loading conditions (Gettu et al. 1996; Paterson and Wong 2005; Mogi 2007; He et al. 2010; Zhao et al. 2013).

Fig. 4

Simplified post-peak deformation behaviors of rock (color figure online)

Stavrogin and Tarasov (2001) developed an “intrinsically” stiff test machine which had a stiffness of up to 2 × 10⁴ MN/m. Similar to the test machine developed by Bieniawski et al. (1969), the fluid ram in Stavrogin and Tarasov’s machine was intentionally separated from the rock specimen and the steel frame. Moreover, two design strategies were adopted in this machine to achieve high LSS. First and foremost, the alignment of the fluid pumping system and the fluid ram was perpendicular to the compression direction of the specimen (Fig. 5). The horizontal movement of the ram was translated into a vertical movement by the wedge system underneath the specimen. As soon as the applied vertical load reached the load-carrying capacity of the rock, the screw would prevent the wedge from moving, thereby preventing energy releasing from the pressurized fluid and fluid ram, and violent failure of the rock could be prevented. The second strategy involves minimizing the number of the loading components as well as the longitudinal height of these components subjected to compression (refer to discussion in Sect. 2.2.1). They believed that their test machine was stiff enough to minimize the release of extra-large energy stored in the machine during the unloading process; hence, very brittle rocks could deform in a stable fashion at the post-peak deformation stage, even without the utilization of a servo-controlled test machine. It should be pointed out that although this test machine is stiff, this does not make it drastically different from other traditional stiff test machines (Fig. 1) because of its finite LSS.

Fig. 5

Simplified schematic of an “intrinsically” stiff test machine, modified from Stavrogin and Tarasov (2001)

2.2 Influence of LSS on Post-peak Behavior of Rock

2.2.1 Stable Rock Failure Criterion for Laboratory Testing

LSS of a test machine is largely governed by the deformation characteristics of the loading frame, loading platens, hydraulic fluid and rams. The stiffness of an elastic structure is defined as the force per unit deformation required to deform the structure in a particular direction. Therefore, the unit of stiffness is N/m for load–deformation relation; for stress–strain relation, the unit of stiffness is N/m² or Pa. For a column-shaped elastic structure under axial loading (Baumgart 2000, Chen and Han 2007), its longitudinal stiffness (k) is determined by the cross-sectional area (A), Young’s modulus (E), and height (H) as:

$$k = \frac{AE}{H}$$

(1)

Hudson et al. (1972) provided Eq. (2) to calculate the composite stiffness of a test machine:

$$\text{LSS} = \left[ {\sum\limits_{i = 1}^{N} {\frac{1}{{k_{i} }}} } \right]^{ - 1}$$

(2)

where k _i is the stiffness of each loading component. The existence of any elastic loading component in a test machine reduces its composite LSS, which makes the composite LSS always lower than the stiffness of any single loading component. Thus, to increase the composite LSS, it is important to decrease the number of loading components and to increase their stiffness.

The loading frame has a large contribution to the composite stiffness of a test machine, and its stiffness is often quoted in manufacturer’s specifications (e.g., MTS 2013). The loading frame generally consists of a set of parallel steel columns, and its stiffness can be calculated using Eq. (1). However, the deformation of the loading platen is complicated by the combination of bending and indentation effects (Bobet 2001). Furthermore, affected by the compressibility of fluid, the dilation of containing vessels and pipes, the incompatible deformation of seal, and the deflection of ram (Bieniawski et al. 1969; Snowdon et al. 1983; Zipf Jr 1992), the stiffness of the hydraulic fluid in compression is even more complex. Because of the complex boundary condition and the interaction between different loading components of a test machine, Hudson et al. (1972) suggested the use of numerical modeling to evaluate the influence of LSS on rock deformation behaviors.

LSS is important in rock property testing because it determines whether a rock failure process in laboratory testing is stable or not. Salamon (1970) summarized some laboratory compression test results and reasoned that unstable rock failure does not occur if the test machine is unable to introduce further deformation without the supplement of additional external energy once the ultimate load-carrying capacity of rock has been reached. The stable rock failure criterion is formulated as (Salamon 1970):

$$\text{LSS}{ > }\lambda$$

(3)

where λ is the post-peak stiffness of a rock specimen Fig. 4 and it is proportional to the steepest descending slope in the load–deformation curve of the rock specimen. The slopes of post-peak load–deformation curves are assumed negative in this study. For simplicity, only the absolute values of the post-peak stiffness are compared.

2.2.2 Influence of LSS on Stable Rock Failures

The stable rock failure criterion states that unstable rock failure occurs when the LSS value is less than λ. However, laboratory evidences regarding the influence of LSS on the post-peak behavior of rock are rare when the LSS value is sufficiently high to ensure a stable rock failure process occurs during the post-peak deformation stage. According to Hudson et al. (1972), Späth (1935) provided a conceptual model (Fig. 6) to explain the difference between the ideal and the apparent material behaviors due to the difference in LSS. Only a very stiff machine can produce a material behavior that is close to the ideal one. Hudson et al. (1972) reviewed that the first laboratory study concerning the effect of LSS on the material property was conducted by Whitney (1943). Whitney measured LSS of four test machines, and a difference between the descending slope in the stress–strain curve of concrete cylinders and the unloading slope of scaled LSS in different test machines was noted. However, the descending slope of the stress–strain curve was just virtually extrapolated from the point of peak strength, and the method used to measure LSS was somewhat ambiguous and questionable. An extensive round robin test project aiming at studying the factors that influence the strain-softening behavior of concrete was carried out by the International Union of Laboratories and Experts in Construction Materials, Systems and Structures (Van Mier et al. 1997). LSS was first considered as one of the inspecting parameters. However, only a limited number of results were collected, and it was impossible to make a reasonable comparison based on these results.

Fig. 6

Conceptual illustration of the deviation between a ideal material behavior and b material behaviors obtained under different LSS values, modified from Hudson et al. (1972) who reproduced after Späth (1935)

To verify the assumption that different descending slopes of stress–strain curves may be obtained by different stiffness of test machine, quartzite specimens were tested by Bieniawski et al. (1969) using the Bieniawski-type test machine (Sect. 2.1.2) in uniaxial compression. The Bieniawski-type test machine had three measured LSS values—103, 1029, and 1803 MN/m. The test results confirmed that “depending upon the stiffness of the loading system different negative slopes of the stress–strain curve are obtained resulting in different levels of stress and strain at rupture” (Bieniawski 1967a). It is worth noting that the post-peak failure behaviors of the rocks (including some brittle rocks like norite) obtained by the Bieniawski-type test machine all showed strain-softening behaviors (Bieniawski 1966, 1967b; Bieniawski et al. 1969), which is different from the post-peak positive descending slopes of brittle rocks (e.g., brittle failure illustrated in Fig. 4) obtained by other types of test machines (Wawersik and Fairhurst 1970; Tarasov and Potvin 2013). This is an indirect evidence that shows that the post-peak failure characteristics of rock can be affected by different test machines.

It is preferable to carry out laboratory tests on specimens with the same rock property to study the influence of LSS on the rock deformation behaviors. However, it is impossible to have rock specimens with exactly the same mechanical property, even if the sampling is carefully conducted (Zhao et al. 2015). The behaviors of rock show variability due to rock heterogeneity, and this is especially the case in the post-peak deformation stage, where localized failure normally takes place (Rudnicki and Rice 1975; Bobet and Einstein 1998). Therefore, laboratory study on how LSS affects the post-peak behavior of rock is extremely difficult. On the other hand, laboratory evidence showing the influence of LSS on the response of elastic–plastic materials with relatively homogeneous properties can help us to gain insights into this problem (Schulson 1999). Sinha and Frederking (1979) carried out a series of strength tests on ice, and it was found that test machines of varying LSS values (i.e., Instron Model TTDM-L, Instron Model 112, and MTS Model 90) had a large influence on the stress–strain curves of ice. The ice specimens were made with care and could be considered as identical. Rist et al. (1991) further argued that different strain rates associated with different LSS values could be responsible for the difference in the strain-softening behaviors of ice observed in the triaxial compression tests.

We have stated that rock specimens with the same property are difficult to be prepared in rock laboratory tests. In addition, LSS of a test machine is difficult to be varied in a large range to study the influence of LSS on the post-peak behaviors of rock. Hence, numerical experiment seems to be the best approach (Cai 2008; Dai et al. 2015; Xu and Cai 2017) for studying this problem. Kias and Ozbay (2013) used a hybrid numerical method to study the influence of LSS on unstable pillar failures. Two codes, FLAC2D used for modeling elastic platens and PFC2D used for modeling coal, were coupled. It was found that the parameters of the test machine could change the pillar failure mode drastically. Similarly, Hemami and Fakhimi (2014) used a hybrid FEM-DEM numerical model to study the rock specimen–test machine interaction. Their research focus was placed on the difference between a stiff test machine and a soft test machine. They noticed that a soft test machine underestimated the slope of the post-peak stress–strain curve. It is seen that most previous simulations were conducted using models with a loading platen atop of the specimen that represented the test machine. The test machines in these models were simplified without considering the compounded influences of other loading components such as loading frame and ram, which are important in defining LSS (Sect. 2.1.1).

3 Numerical Models and Modeling Parameters

Section 2 reveals that different manufacturing arrangements lead to different LSS values of test machines. So far, the research on the influence of LSS on the post-peak behavior of rock is limited. This is partially due to the fact that there is no agreeable method to measure LSS in laboratory tests (Van Mier et al. 1997), and it is impractical to vary LSS in a large range to test rock specimens with “identical” rock properties. On the other hand, it is possible to carry out such an investigation using the numerical experiment approach because the mechanical parameters of a test machine and a rock specimen can be readily varied in the modeling. Previous numerical modeling focused on the influence of LSS on the unstable failure of rock or pillars. In this numerical experiment, the influence of LSS on the stress–strain curves of stable rock failure is investigated numerically. In addition, the loading frame and the loading ram of test machines will be considered in the numerical modeling.

3.1 Simulation Statement

A numerical experiment using the FEM tool ABAQUS^2D (ABAQUS 2010) is performed to study the influence of LSS on the post-peak deformation behavior of rock, with a focus on the post-peak stress–strain curve of stable rock failure. ABAQUS^2D is a powerful tool in solving highly nonlinear structure system problems under transient loads by employing the explicit algorithm. It is also robust to solve problems involving complex boundary conditions with efficient contact convergence and oscillation control. These two merits are significant for the simulation objective, i.e., modeling the interaction between a rock specimen and the test machine in compression tests. Note that because a continuum numerical tool is used in this study, it is not possible to capture explicitly the crack initiation and propagation processes that lead to discontinuous failure of rock. In Sect. 3.2, it will be demonstrated how the simulation of post-peak failure (i.e., strain-softening) is performed.

Uniaxial compression test is widely used in rock property testing and the numerical simulation is restricted to this type of compression test in this study. In addition, because we focus on LSS in the direction normal to the specimen–platen contact surfaces, shear constraint along the surfaces is excluded using frictionless contact behavior (i.e., coefficient of friction µ = 0). Note that the post-peak slope of the rock specimen in uniaxial compression is assumed negative (Class I), and LSS is greater than the absolute value of the post-peak stiffness of the rock specimen (λ). Thus, rock failure is stable and will follow the characteristics of Class I-type failure (Wawersik and Fairhurst 1970; Salamon 1970). In such a case, the servo-controlled test machine will act like a traditional stiff test machine. Therefore, the elastic response of a traditional stiff test machine (Fig. 1) and its influence on the post-peak stress–strain relation of a rock specimen are investigated in the numerical modeling.

In this study, it is hypothesized that LSS plays a role in defining the post-peak behavior of rock even the rock fails in a stable fashion. The research approach is as follows: Firstly, a displacement-controlled loading is applied directly onto a rock specimen’s ends, and the behavior obtained in this way is termed as the base case, as opposed to the rock behavior obtained by a test machine with a finite LSS. Next, the rock deformation behaviors in different test machines are modeled, and the influence of LSS on the post-peak stress–strain curve of the same rock specimen is investigated by comparing the result of the base case with the ones obtained with different LSS values. Aside from the loading platen, the loading frame and the ram are simulated eventually in the model to characterize the stiffness of a traditional stiff test machine realistically (Fig. 1).

3.2 Ideal Loading Condition

The result of the base case under uniaxial compression is obtained first before carrying out a parametric study. This section presents the assumptions used to define the rock properties for the base case. According to the ISRM suggested method for determining UCS (Fairhurst and Hudson 1999), a rectangular specimen with a height of 100 mm and a width of 50 mm is used for the simulation. The pre-peak behavior of the rock in compression is simplified as linear elastic. A standard Mohr–Coulomb failure criterion with a tension cutoff is employed to determine the ultimate strength, and a strain-softening model is used to define the post-peak deformation behavior. The strain-softening behavior is defined by degrading the cohesion yield stress as a function of plastic strain. The mechanical and strain-softening parameters of the rock are presented in Tables 1 and 2, respectively.

Table 1 Mechanical parameters used in simulation

Table 2 Strain-softening parameters of the rock used in simulation

Figure 7 presents the complete stress–strain curve of the rock in uniaxial compression obtained by direct axial displacement loading. The steepest descending slope of the stress–strain curve is indicated by a red line, which tells that the post-peak stiffness of the rock in the stress–strain curve (E _p) is about 47 GPa, or λ = 24 GN/m if the load–deformation relation is used [according to Eq. (1)]. The stress–strain curve is obtained by applying a constant displacement at a rate of 0.016 m/s¹ symmetrically onto the specimen’s top and bottom ends (Fig. 8). This loading method implies that LSS in the loading direction of the specimen is infinite and it is called the ideal loading condition. We consider the rock behavior obtained under the ideal loading condition as the base case because the rock is free from the influence of LSS. Hence, once the geometry and the applied loading velocity of the rock specimen are determined, the result of the base case, which will be compared with other results under different LSS values, is indicated by the curve shown in Fig. 7.

Fig. 7

Stress–strain curve of a rock specimen under the ideal loading condition in uniaxial compression (color figure online)

Fig. 8

Rock specimen under uniaxial compression applied by the ideal loading condition: a schematic of the loading condition, and b FEM model

3.3 Numerical Models of Test Machines

Different models of test machines, from the simplified to more complex test machines consisting of some essential loading components, are introduced in this section. LSS is the control variable that is varied in the study. The range of LSS spans from relatively soft to extremely stiff. In addition to the ideal loading condition, rigid loading, finite LSS of platen loading, and finite LSS of frame–platen loading are considered. In the more complex test machine models, the actual geometrical relation between the test machine and the rock specimen is considered in a qualitative manner because precise modeling of all the components in a test machine is beyond the intended scope of this study.

3.3.1 Rigid Loading Condition

The simplest loading condition uses a rigid body to represent the test machine. A rigid body is an idealization of a solid body with infinite stiffness, and the deformation in the rigid body is zero. Hence, if a constant displacement rate is applied to a rigid body, it will move at the same rate and in the same direction as the applied load. The numerical model of a rock specimen in uniaxial compression, applied by two rigid platens, is shown in Fig. 9. This loading condition is termed as the rigid loading condition. Because the influence of LSS is eliminated, rock behaviors obtained under the rigid loading condition are expected to be close to that of the base case. In other words, it is reasonable to state that if LSS approaches infinity, the rock behavior should approach that of the base case.

Fig. 9

Rock specimen under uniaxial compression applied by the rigid loading condition: a schematic of the loading condition, and b FEM model

3.3.2 Platen Loading Condition

The numerical model of a rock specimen under uniaxial compression applied by two identical loading platens is shown in Fig. 10. This loading condition is termed as the platen loading condition. A constant displacement rate, which is the same as that under the ideal loading condition, is applied to the specimen through the loading platens. In this case, the composite stiffness of the test machine is manifested by the two loading platens, the stiffness of which can be calculated using Eq. (1). The Young’s moduli of the loading platens are varied to study the influence of LSS on the post-peak behavior of rock.

Fig. 10

Rock specimen under uniaxial compression applied by the platen loading condition: a schematic of the loading condition, and b FEM model

3.3.3 Frame–Platen Loading Condition

In this section, a simplified frame–platen loading test machine is simulated. Two loading platens of the same geometry are in contact with the specimen and a loading frame encapsulating the specimen–platen complex is modeled (Fig. 11). The Young’s moduli of the loading frame and the platens are the same. Inspired by the thermal loading mechanism by Cook and Hojem (1966) and Wawersik (1968), the loading platen underneath the specimen is defined with an orthotropic thermal property, i.e., thermal expansion occurs only in the vertical direction and the thermal expansion in the horizontal direction is zero. This is an attempt to simulate the loading ram in a stiff test machine, and in this fashion, the loading frame that encapsulates the specimen–platen–ram complex similar to that shown in Fig. 1 can be included in the numerical model.

Fig. 11

Rock specimen under uniaxial compression applied by the frame–platen loading condition: a schematic of the loading condition, and b FEM model

The platen at the bottom consisting of an idealized material is called the thermal loading platen, and the test machine is called the frame–platen loading test machine. When a constant heat flux is provided to the thermal loading platen, the platen will expand lineally in the vertical direction to contract the rock specimen in a way quite similar to that a fluid ram does.² In reality, the fluid in a fluid ram can reduce LSS. If such a frame–platen loading test machine is not considered, high LSS values cannot be achieved in the numerical model. Consequently, three essential loading components of a test machine (Sect. 2.1.1)—loading platen, loading frame, and loading ram—are conceptually imbedded in the numerical model (Fig. 11), and this is termed as the frame–platen loading condition.

The heat flux applied to the thermal loading platen is calibrated so that the specimen under the frame–platen loading condition is subjected to an applied loading displacement rate the same as that in other loading conditions. Figure 12 shows the comparison of the displacement–time relation of the specimen calibrated under the frame–platen loading condition with that under the ideal loading condition. The displacement under the frame–platen loading condition is recorded at the top end of the thermal loading platen, and the whole body of which is continuously exposed to a constant heat flux. Table 3 presents the thermal parameters for the thermal loading platen used in the numerical simulation.

Fig. 12

Displacement–time relations of rock specimens under two loading conditions

Table 3 Thermal parameters for the thermal loading platen used in the numerical simulation

The Young’s moduli of the loading frame and the platens are varied to change LSS. To compare the rock behaviors between the frame–platen loading test machine and the platen loading test machine, the Young’s moduli of the frame–platen loading test machine need to be adjusted in order to equalize the stiffness of the frame–platen loading test machine and that of the platen loading test machine. According to the definition of stiffness (Sect. 2.2.1), Fig. 13 illustrates how the composite stiffness of a frame–platen loading test machine (LSS_F) is calibrated in the numerical modeling. If a pair of concentrated reaction load (F) is applied to the top and bottom loading platens through two rigid platens, the relative displacement (δ ₁ + δ ₂) of the rigid platens will cause an elastic response of the test machine. Then, the load–deformation relation tells LSS_F. Similarly, the stiffness of the platen loading test machine (LSS_P) can be calibrated in this fashion. Figure 14 presents the calibrated load–displacement relations of the two test machines, along with the theoretical LSS_P value (LSS_theory) of 2577 GN/m calculated using Eq. (1). Based on the slopes of the fitting lines for the load–displacement relations (Fakhimi et al. 2016), LSS_F and LSS_P are obtained as 2579 and 2575 GN/m, respectively. In this way, the Young’s moduli of the frame–platen loading test machine can be adjusted to yield LSS the same as the LSS of platen loading test machine.

Fig. 13

Calibration of the stiffness of the frame–platen loading test machine in numerical modeling

Fig. 14

Load–displacement relations of two test machines (LSS_theory = 2577 GN/m as an illustration)

4 Modeling Results and Discussion

4.1 Rigid Loading Results

Figure 15 shows the stress–strain curve of the rock under the rigid loading condition, along with that under the ideal loading condition. It is seen that the two curves are very close to each other. The modeling results show that the influence of LSS on the post-peak stress–strain curve of rock can be eliminated by assigning a rigid property to the test machine. Thus, when LSS is finite, the post-peak stress–strain curve of rock should approach that of the base case if LSS becomes very stiff.

Fig. 15

Stress–strain curves of the rock under ideal and rigid loading conditions

4.2 Platen Loading Results

Figure 16 presents the stress–strain curves of the rock under the platen loading condition with different LSS values and that under the ideal loading condition. It is seen that different LSS values result in different post-peak stress–strain curves of the rock, even though the peak strengths are the same. With the increase of LSS, the post-peak stress–strain curve of the rock first becomes steeper (colored solid curves) than that of the base case (bold black curve), and becomes the steepest at LSS = 825 GN/m (pink dash curve). As LSS further increases, the post-peak stress–strain curve gradually approaches (green and blue dash curves) that of the base case.

Fig. 16

Post-peak stress–strain curves of the rock under the ideal loading condition and the platen loading condition with different LSS values; the complete stress–strain curves are shown in the inset (color figure online)

When LSS = 19 GN/m < λ (24 GN/m), unstable rock failure is observed. The slope in the post-peak stress–strain curve of the unstable rock failure (gray solid curve) is flatter than that under the ideal loading condition, indicating that excessive energy is released from the test machine to the rock specimen. The modeling result of the unstable rock failure agrees well with laboratory and field observations (Shepherd et al. 1981; Milev et al. 2001; Blake and Hedley 2003; Zhang et al. 2012; Dai et al. 2016).

When LSS = 24 GN/m = λ, which is the minimal or the critical LSS loading condition to ensure that stable rock failure occurs, the post-peak stress–strain curve (red solid curve) is close to the base case under the ideal loading condition. There are no solid laboratory observations on the rock deformation behavior under the loading condition of LSS = λ, but the modeling result with LSS = λ of this study agrees with the results by other researchers using DEM numerical models (Kias and Ozbay 2013; Hemami and Fakhimi 2014) and more recently using a 3D FEM numerical model (Manouchehrian and Cai 2015).

The above modeling results show that LSS influences the post-peak stress–strain curve of rock even though the rock failure process is stable. According to the loading system reaction intensity (LSRI, defined as the ratio of the maximum velocity of the loading platen at the rock specimen–loading platen contact to the applied loading velocity at the other end of the platen) proposed by Manouchehrian and Cai (2015) to identify stable and unstable rock failures, there is a sudden reaction movement of the loading platen toward the failing rock if the rock failure is unstable. In contrast, the reaction of the loading platen during a stable rock failure is not easily noticeable. Manouchehrian and Cai (2015) pointed out that LSRI is normally smaller than 2.0 when stable rock failures occur. Table 4 presents the relation between LSRI and LSS under the platen loading condition. The calculated LSRI values confirm that the rock failures are stable when LSS > λ. Referring to the stress–strain curves of stable rock failures in Fig. 16, it is seen that as LSS increases, the post-peak stress–strain curves gradually depart from that of the base case and reach the steepest descending slope when LSS = 825 GN/m. Then, as LSS increases, the post-peak stress–strain curves become less steep and approach the base case when LSS is very stiff.

Table 4 Relation between LSRI and LSS under the platen loading condition

It is observed that for the stable rock failures in the numerical modeling, the stress distributions in the rock specimen are not the same for different LSS values. Figures 17 and 18 present maximum principal stress σ ₁ and minimal principal stress σ ₃ distributions, respectively, in the rock specimen at the post-peak deformation stage at ε = 0.4% under the platen loading condition for LSS ≥ λ, along with those under the ideal loading condition. When LSS is critical or very stiff, the platen loading condition will result in similar stress distributions in the rock specimen as that under the ideal loading condition. Hence, the post-peak stress–strain curve obtained under either the critical LSS or very stiff LSS loading condition is very close to that under the ideal loading condition.

Fig. 17

σ ₁ distributions in the rock specimen at ε = 0.4% at the post-peak deformation stage under the platen loading condition for LSS ≥ λ and the ideal loading condition (compressive stress is taken as negative in ABAQUS)

Fig. 18

σ ₃ distributions in the rock specimen at ε = 0.4% at the post-peak deformation stage under the platen loading condition for LSS ≥ λ and the ideal loading condition

It is important to investigate the energy consumed in the rock specimen because both the stress–strain curves and the stress distributions in the rock specimen are macro-behaviors of the rock specimen in response to the input energy (E _in) supplied by an external energy source (independent of the rock specimen–test machine system) to the rock specimen–test machine system. Figure 19 illustrates the energy consumed in a rock specimen (E _r) and the energy stored in a test machine (E _t), where the test machine is idealized and represented by a spring and E _in from an external energy source is provided to the rock specimen–test machine system to deform the rock. As the load increases to the peak load of the rock specimen, both the energy stored in the test machine and the energy consumed in the rock specimen increase, and the energy conservation equation of the system at the peak load is:

$$E_{\text{in}} = E_{\text{t}} + E_{\text{r}}$$

(4)

Fig. 19

Illustration of energy consumed in a rock specimen and energy stored in a test machine with the supply of external input energy

At the post-peak deformation stage, Eq. (4) still holds true for the system and asterisk (*) is used to differentiate the energy items at the post-peak deformation stage from those at the peak load. The energy conservation equation of the system at the post-peak deformation stage is:

$$E_{\text{in}}^ * = E_{\text{t}}^ * + E_{\text{r}}^ *$$

(5)

Part of the energy stored in the test machine (ΔE _t) is released to the rock specimen due to the unloading of the test machine (E _t > E ^*_t ); thus, E _r < E ^*_r and ΔE _t = E _t − E ^*_t . Meanwhile, as discussed in Sect. 2.2.1, additional input energy (ΔE _in) is required when the rock failure is stable (E _in < E ^*_in ), because ΔE _t alone is not sufficient to drive the deformation of the rock during the post-peak deformation stage (ΔE _in = E ^*_in  − E _in). Therefore, Eq. (5) for the system in the unloading of the test machine while ΔE _in is introduced into the system can be expressed in an incremental form as:

$$E_{\text{in}} + \Delta E_{\text{in}} = (E_{\text{t}} - \Delta E_{\text{t}} ) + (E_{\text{r}} + \Delta E_{\text{t}} + \Delta E_{\text{in}} )$$

(6)

Accordingly, compared Eq. (6) with Eq. (5), the energy consumed in the rock specimen in the post-peak deformation stage (ΔE _r = E ^*_r  − E _r) is composed of two energy items:

$$\Delta E_{\text{r}} = \Delta E_{\text{t}} + \Delta E_{\text{in}}$$

(7)

Based on traditional viewpoints regarding ΔE _r during the unloading of a test machine (Bieniawski et al. 1969; Salamon 1970; Hudson et al. 1972; Hudson and Harrison 2000), Fig. 20 illustrates conceptually the relation between ΔE _r and LSS for stable rock failure, where the rock behavior under the ideal loading condition (i.e., the base case) is simplified by red lines. LSS = ∞ and LSS = λ are two special loading conditions of stable rock failure. In the subsequent discussion, the energy provided to the rock under the ideal loading condition (LSS = ∞) to obtain the post-peak load–deformation curve is denoted as ΔE ^B_r , as opposed to ΔE _r which is under the loading condition with a finite LSS. Because a test machine of LSS = ∞ cannot store and release any energy (red dash line), ΔE ^B_r has to be provided wholly by ΔE _in from the external energy source. On the other hand, no additional input energy ΔE _in is required for a test machine of LSS = λ to obtain the post-peak load–deformation curve of the base case (black dash line), because the energy released from the test machine is just the right amount needed to drive rock failure (ΔE _t = ΔE _r = ΔE ^B_r ). When LSS of a test machine is finite and greater than λ (blue dash line), in addition to ΔE _t released from the test machine, additional input energy ΔE _in from the external energy source is required to drive rock failure.

Fig. 20

Conceptual illustration of the relation between the energy consumed in a rock specimen and LSS during stable rock failure (color figure online)

The relation between ΔE _r under a finite LSS > λ and ΔE ^B_r under LSS = ∞ is important for verifying the hypothesis of this study—the post-peak stress–strain (or load–displacement) curve of stable rock failures varies with LSS. Obviously, ΔE _r cannot be greater than ΔE ^B_r ; otherwise, the rock is not capable of absorbing extra energy and unstable rock failure will occur. If LSS has no influence on the post-peak stress–strain curve, then the stable rock behavior obtained under various finite LSS > λ and that under the ideal loading condition are the same. In such a case, ΔE _r should be constant and equal to ΔE ^B_r . Thus, a specific amount of ΔE _in has to be varied each time when ΔE _t is varied (variation of LSS) so that the summation of ΔE _in and ΔE _t is constant and equal to ΔE ^B_r (e.g., green and pink filled areas illustrated in Fig. 20).

The modeling results demonstrate that different ΔE _r consumed in the post-peak deformation stage result in different post-peak stress–strain curves. Hence, the post-peak stress–strain curve is affected by LSS. Figure 21 compares the variation of ΔE _r and ΔE ^B_r (black curve) values with strain starting at the peak load in the rock under the platen loading condition for LSS ≥ λ. ΔE _r is obtained by subtracting the accumulative energy provided to the rock at the post-peak deformation stage (E ^*_r ) by that at the peak load (E _r). ΔE _r approaches ΔE ^B_r only if the rock is loaded under a very stiff loading condition (2577 GN/m). The ΔE _r values under the critical LSS condition (24 GN/m) are close to the ΔE ^B_r values, but are not as close to that under the very stiff LSS condition. As a result, the post-peak stress–strain curves under a finite LSS ≥ λ are always stiffer than that under the ideal loading condition. Referring to Eq. (7), ΔE _r is comprised of ΔE _t and ΔE _in. To understand how the post-peak stress–strain curve is varied with the increase of LSS, the variation of ΔE _t and ΔE _in with increasing LSS is examined separately.

Fig. 21

Variation of ΔE _r and ΔE ^B_r (LSS = ∞) with strain under the platen loading condition for LSS ≥ λ

Figure 22 shows the comparison of the variation of ΔE _t and ΔE ^B_r values with strain starting at the peak load in the rock under the platen loading condition for LSS ≥ λ. ΔE _t is obtained by subtracting the elastic energy stored in the test machine at the peak load (E _t) by that at the post-peak deformation stage (E ^*_t ).

Fig. 22

Variation of ΔE _t and ΔE ^B_r (LSS = ∞) with strain under the platen loading condition for LSS ≥ λ

ΔE _t decreases with the increase of LSS because the stiffer a test machine is, the lower the storing and releasing energy capacity of the test machine is. In particular, within the range of LSS ≥ λ, ΔE _t is the highest when the LSS value is equal to the critical value λ. In this case, the test machine can release the most energy needed to the rock so that the post-peak stress–strain is close to that of the base case. Note that for the case of critical LSS loading condition, ΔE _t < ΔE ^B_r , which is different from the illustration shown in Fig. 20, where ΔE _t = ΔE ^B_r . This is because that the post-peak load–deformation curve of the rock shown in Fig. 20 has been idealized as a straight line, which is rarely the case for rocks. In the numerical modeling, the post-peak load–deformation (or stress–strain) curve is nonlinear. λ is the stiffness at the point where the descending load–deformation curve is the steepest. Therefore, the ΔE _t value under the critical LSS condition is lower than ΔE ^B_r , and additional input energy ΔE _in is needed to drive rock failure (to increase ΔE _r).

Figure 23 shows the comparison of the variation of ΔE _in and ΔE ^B_r values with strain starting at the peak load in the rock under the platen loading condition for LSS ≥ λ. ΔE _in is obtained by subtracting the accumulative external energy input to the rock specimen–test machine system at the post-peak deformation stage (E ^*_in ) by that at the peak load (E _in).

Fig. 23

Variation of ΔE _in and ΔE ^B_r (LSS = ∞) with strain under the platen loading condition for LSS ≥ λ (color figure online)

ΔE _in increases with the increase of LSS, except for the cases for LSS = 289 and 825 GN/m. If LSS is very stiff, ΔE _in can match ΔE ^B_r well, while ΔE _t is very small. Therefore, it is inferred that the ΔE _in provided to the rock for driving rock failure from an external energy source is somewhat influenced by the test machine so that ΔE _r is always lower than ΔE ^B_r . Only if the test machine is perfectly stiff, i.e., the test machine is a rigid body, the influence of the test machine on the rock to absorb the right amount of ΔE _in = ΔE ^B_r can be eliminated and the post-peak stress–strain curve in this case is the same as that in the base case. This has been demonstrated by using the numerical model of rigid loading test machine (refer to Fig. 9) to obtain the post-peak stress–strain curve (Fig. 15).

The modeling results presented in Figs. 21 and 22 are summarized in Fig. 24, which shows the evolution of ΔE _t, ΔE _in, ΔE _r, and ΔE ^B_r in the rock with the increase of LSS at the post-peak deformation stage. The abscissa is natural logarithm of LSS. Note that ΔE _r = ΔE _t + ΔE _in and ΔE ^B_r shown in Fig. 24 determine the relation between the post-peak stress–strain curve obtained under a finite LSS ≥ λ and that under the ideal loading condition. Therefore, it is understood that as LSS increases, ΔE _t decreases and ΔE _in increases simultaneously at different rates and their summation is not a constant. That is why as LSS increases the slopes of the post-peak stress–strain curves first become steeper, then become flatter, and finally approach that of base case obtained under the ideal loading condition.

Fig. 24

Evolution of energy in the rock with the increase of LSS at the post-peak deformation stage (ε = 0.5% as an illustration, trend is the same for other strain levels)

This numerical experiment focuses on studying stable rock failure under different LSS loading conditions. Based on the modeling results from this study, Fig. 25 illustrates conceptually that for stable rock failure to occur under a finite LSS loading condition (e.g., rock laboratory testing using a stiff test machine), ΔE _r consisting of ΔE _t and ΔE _in (area under the blue solid line) is always smaller than ΔE ^B_r consisting of ΔE _in solely (area under the red descending line). The modeling results suggest that ΔE _in is affected by the test machine with a finite LSS; ΔE _in and ΔE _t are varied with LSS. Consequently, the slope of the post-peak stress–strain curve of a rock under a finite LSS > λ loading condition is always steeper than the one under the ideal loading condition (LSS = ∞). Therefore, it is concluded that the post-peak stress–strain curve of stable rock failure is influenced by test machines with various LSS values.

Fig. 25

Comparison of the load–deformation curve of the rock under the ideal loading condition with that under the loading condition of a finite LSS > λ (color figure online)

This conclusion drawn by the numerical modeling is partially supported by the incomplete laboratory test results on nearly identical material specimens, which show that different stress–strain curves of concrete (Hudson et al. 1972 based on Whitney 1943) and ice (Sinha and Frederking 1979) were obtained by different test machines. Most importantly, the modeling results confirmed the laboratory results conducted by Bieniawski et al. (1969), whose work revealed that the descending slopes of the post-peak stress–strain curves of rock were dependent on LSS.

4.3 Frame–Platen Loading Results

The influence of LSS on stable failure of rock under the frame–platen loading condition is investigated, and the results are presented in this section. The LSRI values shown in Table 5 confirm that for a LSS value the same as that under the platen loading condition, rock failure is stable under the frame–platen loading condition. Figure 26 shows the comparison of the stress–strain curves under the frame–platen loading condition with different LSS values with that under the ideal loading condition (bold black curve). As LSS increases, the slope of the post-peak stress–strain curve of the rock increases gradually and then reaches the steepest at LSS = 289 GN/m (colored solid curves). With further increase of LSS, the slope of the post-peak stress–strain curve decreases and eventually approaches that of post-peak stress–strain curve for the base case as LSS becomes very large (colored dash curves).

Table 5 Relation between LSRI and LSS under the frame–platen loading condition

Fig. 26

Stress–strain curves of the rock under the ideal loading condition and the frame–platen loading condition with different LSS values; the complete stress–strain curves are shown in the inset (color figure online)

Figure 27 shows the comparison of the stress–strain curves of the rock under the frame-platen and platen loading conditions with different LSS values. It is seen that unless LSS is very stiff or equal to λ, which are the LSS loading conditions that lead the post-peak behavior of the rock close to that of the base case, the post-peak stress–strain curves of the rock under these two loading conditions are different even though their LSS values are the same. It seems that the platen loading condition leads to a steeper descending slope of the stress–strain curves than that under the frame–platen loading condition (e.g., LSS = 825 GN/m).

Fig. 27

Comparison of stress–strain curves of the rock under the platen (subscript “P”) and frame–platen loading (subscript “F”) conditions with different LSS values; the complete stress–strain curves are shown in the inset

Figure 28 presents σ ₁ distributions of the two test machines at the post-peak deformation stage at a strain of ε = 0.4%. It is seen from the σ ₁ distributions that tensile stresses (white contoured areas) dominate in the frame–platen loading test machine because the loading frame is in tension to balance the load applied to the specimen; however, compressive stresses dominate in the platen loading test machine. It is reckoned that these two test machines with different loading conditions can affect the ΔE _in values provided to drive the rock failure process and hence the post-peak stress–strain curves of the rock. The ΔE _in values in the two test machines are plotted and presented in Fig. 29 as a function of strain. The additional input energy provided to the rock ΔE _in in the frame–platen loading test machine is indeed different from that in the platen loading test machine. As a result, the ΔE _r values between the frame–platen loading and platen loading test machines are different and this is reflected in the difference in the post-peak stress–strain curves (Fig. 27). This indicates that the post-peak stress–strain curves of a rock obtained from a laboratory test is affected not only by LSS but also by the loading method.

Fig. 28

σ ₁ distributions of the two test machines (for LSS = 825 GN/m) at the post-peak deformation stage (ε = 0.4%)

Fig. 29

Variation of ΔE _in and ΔE ^B_r (LSS = ∞) with strain in the rock by the two test machines at the post-peak deformation stage for LSS = 825 GN/m (subscripts “P” and “F” indicate platen and frame–platen loading conditions, respectively)

4.4 Final Remarks

The numerical modeling in this study was conducted using 2D models. One concern that may arise is that 2D models sometimes overlook the 3D nature of the physical problem. While 3D modeling results were missing in previous sections, this study indeed began with 3D modeling of uniaxial compression test. 3D modeling results show that by increasing LSS of 3D loading platens (50 mm in square and 25 mm in height), the post-peak stress–strain curve of the rock specimen (44 mm in square and 100 mm in height) experiences the same trend as that of the 2D models of the platen and frame–platen loading test machines presented in Figs. 16 and 26, respectively.

As highlighted in this study, modeling a frame–platen loading test machine that can more realistically (compared with platen loading test machine) reflect the mechanical property of test machines is the research objective. Apparently, due to the complexity of the frame–platen loading test machine model used in the simulation, it is difficult to carry out a 3D modeling of such a frame–platen loading test machine model. Hence, to keep the consistency of the numerical models, only 2D modeling results are presented. It is a common practice to carry out 2D modeling of uniaxial compression test (Tang et al. 2000; Potyondy and Cundall 2004; Kias and Ozbay 2013; Hemami and Fakhimi 2014) to study the deformation behaviors of rock. Useful insight can be obtained from such modeling work.

Regarding the trend of the influence of LSS on the post-peak stress–strain curves presented in Figs. 16 and 26, one may wonder what the trend would be with further increase of LSS from 2577 GN/m. A follow-up simulation using both the platen loading and frame–platen loading test machine models with a higher LSS of 4000 GN/m is presented in Fig. 30. It demonstrates that the stress–strain curves of the rock under the platen and frame–platen loading conditions with a very stiff LSS value are close to that under the ideal loading condition.

Fig. 30

Stress–strain curves of the rock under the platen and frame–platen loading conditions with LSS = 4000 GN/m and 825 GN/m

If LSS of a test machine is very high, ΔE _t is minimal compared with ΔE _in (refer to Fig. 24). In such a case, the ΔE _r that determines the post-peak stress–strain curve is mostly coming from ΔE _in, a loading condition quite similar to the ideal loading condition (refer to the blue dash curve and black solid curve in Fig. 23). It is easy to imagine that if a test machine becomes very stiff, it will act like a rigid body and compress the rock specimen the same way as the rigid loading test machine does (Sect. 3.3.1). As a result, the post-peak stress–strain curve obtained by a very stiff test machine or rigid loading test machine will be very close to that under the ideal loading condition (Fig. 15).

5 Conclusions

Great efforts had been made to develop stiff test machines to capture post-peak stress–strain curves of rock for engineering design; however, the influence of the loading system stiffness (LSS) on the post-peak behavior of rock is less understood. This is in part due to the difficulty in varying LSS to conduct tests using rock specimens with nearly identical material properties. Numerical experiment provides a solution to address this problem.

In the numerical experiment, the post-peak stress–strain curves of rock specimens with the same material property under uniaxial compression were examined using test machines with different LSS values. The modeling results indicate that the post-peak stress–strain curve of stable rock failure depends on LSS. The slope of the post-peak stress–strain curves under finite LSS are all steeper than the slope for LSS = ∞. In other words, the post-peak behaviors obtained by test machines with finite LSS are more brittle than the one obtained by an extremely rigid test machine. We find that this difference is attributed to the energy supplied by the external energy source to drive the rock failure process in the post-peak deformation stage. When LSS is finite, the amount of energy released from the test machine (ΔE _t), combined with that supplied from the external energy source (ΔE _in), determines the post-peak stress–strain curve of the rock. In this case, both ΔE _in and ΔE _t are influenced by LSS.

One important insight gained from the numerical experiment is that perhaps there is no need to develop extremely stiff test machines for rock property testing. This is because that the modeling results suggest that even if a test machine is stiff enough to ensure stable rock failure, as long as its LSS is neither extremely rigid nor equal to the post-peak stiffness of the rock specimen, the post-peak stress–strain curve is always LSS dependent and different from that of the base case. However, obtaining an unbiased post-peak stress–strain curve that can characterize the intrinsic mechanical behavior of rock was the motivation of developing stiff test machines in the 1960s in the first place (Sect. 2.1).

On the other hand, test machines that can vary LSS are useful. This study makes a contribution to suggesting an alternative approach to develop test machines with probably less manufacturing costs but can obtain more meaningful testing results. The post-peak stress–strain curve is important in underground rock engineering design, but it is neither necessary nor practical to obtain such a curve for rock under the ideal loading condition because the ideal loading condition does not exist in an underground rock engineering setting. Instead, it might be useful to investigate the local mine stiffness (LMS) and to study its influence on the post-peak deformation behavior of rock or pillar. Once the LMS surrounding a rock of interests (e.g., pillar) is quantified, test machines with variable LSS values that can accommodate the measured LMS can be used for rock property testing. The test machine developed by Bieniawski et al. (1969) can vary its LSS. Manufacturing and control techniques have been advanced since then, and it is possible to develop a test machine that can vary its LSS in a more controllable fashion. In this way, the post-peak deformation behavior of rock obtained by such a test machine with LSS matching LMS would be more meaningful for rock engineering design.

The modeling results show that the trend of the post-peak stress–strain curves of the rock obtained by the frame–platen loading test machine is consistent with that by the platen loading test machine. However, the post-peak stress–strain curves are different between these two models of test machines. This indicates that the loading method can supply different amounts of energy to the rock at the post-peak deformation stage. Future study will consider the influence of a frame–platen loading test machine on unstable rock failure, a process that is strongly related to the energy stored in the test machine. In addition, LMS is important for determining whether pillar burst will occur or not. Hence, future study will investigate pillar stability under different LMS values.