1 Introduction

The mechanical behaviors of structures and materials at nano or microscale are different from their behaviors at macroscale due to the influence of size effects and surfaces stress which are not present at larger scales. Therefore, a thorough understanding of the dynamical and mechanical behaviors of nano-sized structures is of importance in the analysis and design of nano or micro structures such as micro- and nano-electromechanical systems (MEMS and NEMS).

The accurate mathematical modeling of the torsional dynamic and static behavior of nano/micro bars seems to be crucial to study the different mechanical behaviors of these type of structures. Since the classical elasticity theories are proved to fail at micro and nanoscale, some molecular/atomic dynamic simulations and new higher order elasticity theories are necessary. During past years, some higher order elasticity theories such as the strain gradient, nonlocal, couple stress, modified couple stress theories have been developed, introduced, and employed to study the nano and micro-scaled materials. These higher order elasticity theories such as micro-polar elasticity theory (Eringen and Suhubi 1964; Chen et al. 2004; Ramezani et al. 2009), strain gradient elastic theory (Yayli 2011), couple stress approach (Toupin 1962), the modified couple stress theory (Ma et al. 2008; Park and Gao 2006) and nonlocal elasticity theory (Eringen 1983; Eringen and Edelen 1972; Yang et al. 2010), have been receiving much attention in studying nano/micro structures. In these higher order elasticity theories, some length scale parameters are considered in addition to the Poisson ratio and elastic modulus, which enable these higher order elasticity theories to capture the small size effect.

Potential applications of carbon nanotube have been made to many different areas on account of its specially properties (Bachtold et al. 2001; Kim and Lieber 1999), such as field-effect transistor, graphene transistors, chemical sensors, solar cells, logic circuits with filed-effect transistor, gas detection, diagnosis devices, transparent and conductive films, ultracapacitors and ultrastrength composite materials. Since classical elasticity theories cannot predict the characteristic behaviors of the carbon nanotubes, some higher order elasticity theories have been proposed managing to predict mechanical properties of carbon nanotubes in recent years (Wang et al. 2008; Schadler et al. 1998; Ru 2001; Wagner et al. 1998; Qian et al. 2000; Danesh et al. 2012; Bower et al. 1999; Chang 2012; Simsek 2012; Akgoz and Civalek 2014; Murmu et al. 2014; Huang 2012). Buckling, bending and vibration of nonhomogeneous nanotubes have been studied by Pradhan and Phadikar (2009) using differential quadrature method. Wave propagation in carbon nanotubes has been investigated by Lu et al. (2007) and Wang (2005). Torsional buckling analysis of carbon nanotubes has been examined by Khademolhosseini et al. (2010). Reddy and Pang (2008) have presented different beam theories (Euler–Bernoulli–Timoshenko) using the nonlocal elasticity theory proposed by Eringen and Edelen (1972). Several researchers (Murmu et al. 2011; Lim et al. 2012; Kiani 2013; Li 2014) have studied torsional vibration of single walled carbon nanotubes based on the nonlocal theory. Free longitudinal vibrations of carbon nanotubes has been explored by Aydogdu (2009). Aydogdu and Elishakoff (2014) have investigated the vibration of nanorods restrained by a linear spring in-span. Roostai and Haghpanahi (2014), Loya et al. (2014) have studied the vibration behavior of cracked nanorods using nonlocal elasticity theory. A compact analytical method for vibration analysis of single-walled carbon nanotubes and beams with deformable boundary conditions has been proposed by Yayli (2016; 2017).

The nano/micro hollow/solid bars subjected to torsional displacements and torsional moments are widely used in various kinds of nano/micro electro mechanical systems (NEMS/MEMS) such as micro-gyroscopes. In this paper, an attempt is made to propose a new analytic approach for free torsional vibration analysis of a carbon nanotube with torsional springs at both ends. The governing differential equations of motion and boundary conditions are deduced by considering the small scale effects and the torsional springs due to the end restraints, but the warping effect of the cross-section is neglected because the cross-section is assumed to be circular. Present analytical model bridges the gap between classical and the deformable boundary conditions, which is of great significance for the application of the modified couple stress theory to micro and nanostructures. Some numerical examples for rigid and deformable boundary conditions are given to valid the proposed method in this study and investigate the effects of several parameters, such as the spring coefficients, length and small scale parameter on the torsional dynamic responses of the carbon nanotube.

2 Modified couple stress theory

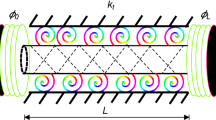
Classical elasticity theory is not capable of capturing the size dependency of materials; consequently, many higher order elasticity theories are introduced to improve the results obtained for micro or nano sized structures. These higher order theories, mainly, try to improve the method by introducing small scale parameters to capture the so-called size effects (Guo et al. 2016; Delfani 2017; Swadener et al. 2002; Lam et al. 2003; Liebold and Mller 2016; Lei et al. 2016). In order to derive the equation of motion for torsional vibration of carbon nanotube in term of angular rotation based on the modified couple stress theory, Hamiltons’ principle will be employed. The use of modified couple stress theory with torsional vibration developed by Lam et al. (2003) will be briefly reviewed first. Consider a straight uniform carbon nanotube with length L and a circular cross section as shown in Fig. 1. According to the size dependent modified couple stress theory, isotropic linear elastic strain energy U can be written as follows (Gheshlaghi and Hasheminejad 2010):

$$\begin{aligned} U=\frac{1}{2}\int _V(\sigma \epsilon +m\chi )dV, \end{aligned}$$
(1)

where \(\sigma \) is the stress, \(\epsilon \) is strain and m is the deviatoric part of the couple stress. \(\chi \) denotes the curvature,

$$\begin{aligned} \sigma =\lambda tr(\epsilon ) I +2\mu \epsilon , \end{aligned}$$
(2)
$$\begin{aligned} \epsilon =\frac{1}{2}\left[ \nabla v+(\nabla v)^T\right] , \end{aligned}$$
(3)
$$\begin{aligned} m=2l^2\mu \chi , \end{aligned}$$
(4)
$$\begin{aligned} \chi =\frac{1}{2}\left[ \nabla \theta +(\nabla \theta )^T\right] , \end{aligned}$$
(5)

where \(\lambda \) and \(\mu \) are the Lame’s constants, \({ tr}(\epsilon )\) denotes the sum of diagonal elements of the strain tensor. I denotes the third order identity matrix. l is a material scale parameter and v is the displacement vector. \(\theta \) is the rotation vector as follows:

$$\begin{aligned} \theta =\frac{1}{2}{} { curl}(v). \end{aligned}$$
(6)

The displacement components of the carbon nanotube can be written as:

$$\begin{aligned} v_x(x,t)=0, \end{aligned}$$
(7)
$$\begin{aligned} v_y(x,t)=-z\phi (x,t), \end{aligned}$$
(8)
$$\begin{aligned} v_z(x,t)=y\phi (x,t), \end{aligned}$$
(9)

in which \(v_x\), \(v_y\) and \(v_z\) are the x, y and z components of the displacement vector. \(\phi (x,t)\) is angular rotation about the center of twist. Following equations can be derived from Eqs. (3), (7), (8) and (9)

$$\begin{aligned} \epsilon _{xy}=-\frac{z}{2}\frac{\partial \phi (x,t)}{\partial x}, \end{aligned}$$
(10)
$$\begin{aligned} \epsilon _{xz}=-\frac{y}{2}\frac{\partial \phi (x,t)}{\partial x}, \end{aligned}$$
(11)
$$\begin{aligned} \epsilon _{xx}=\epsilon _{yy}=\epsilon _{zz}=\epsilon _{yz}=0, \end{aligned}$$
(12)

Similarly, following equations are obtained from Eqs. (6), (7), (8) and (9)

$$\begin{aligned} \theta _x=\phi (x,t), \end{aligned}$$
(13)
$$\begin{aligned} \theta _y=-\frac{y}{2}\frac{\partial \phi (x,t)}{\partial x}, \end{aligned}$$
(14)
$$\begin{aligned} \theta _z=-\frac{z}{2}\frac{\partial \phi (x,t)}{\partial x}, \end{aligned}$$
(15)

By using Eqs. (2), (10), (11) and (12), the stress tensor can be calculated as follows (Gheshlaghi and Hasheminejad 2010):

$$\begin{aligned} \sigma =\mu \left[ \begin{array}{lll} 0 &{}\quad -z\frac{\partial \phi (x,t)}{\partial x} &{}\quad y\frac{\partial \phi (x,t)}{\partial x} \\ -z\frac{\partial \phi (x,t)}{\partial x} &{}\quad 0 &{}\quad 0 \\ y\frac{\partial \phi (x,t)}{\partial x} &{}\quad 0 &{}\quad 0 \\ \end{array} \right] , \end{aligned}$$
(16)

In a similar way by using Eqs. (5), (13), (14) and (15), deviatoric part of couple stress tensor read as (Gheshlaghi and Hasheminejad 2010):

$$\begin{aligned} m=\mu l^2 \left[ \begin{array}{lll} 2 \frac{\partial \phi (x,t)}{\partial x} &{}\quad -\,\frac{y}{2}\frac{\partial ^2 \phi (x,t)}{\partial x^2} &{}\quad -\,\frac{z}{2}\frac{\partial ^2 \phi (x,t)}{\partial x^2} \\ -\,\frac{y}{2}\frac{\partial ^2 \phi (x,t)}{\partial x^2} &{}\quad -\,\frac{\partial \phi (x,t)}{\partial x} &{}\quad 0 \\ -\,\frac{z}{2}\frac{\partial ^2 \phi (x,t)}{\partial x^2} &{}\quad 0 &{}\quad -\,\frac{\partial \phi (x,t)}{\partial x} \\ \end{array} \right] . \end{aligned}$$
(17)

Generally, Hamilton’s principle could be written as

$$\begin{aligned} \int _{t_1}^{t_2}\left\{ U-T-W\right\} dt=0, \end{aligned}$$
(18)

where U, T, W denote strain, kinetic energies and work done by external force, respectively.

$$\begin{aligned} U=\frac{1}{2}\int _{V}\left\{ \mu (y^2+z^2+3l^2)\left( \frac{\partial \phi (x,t)}{\partial x}\right) ^2+\frac{1}{4}\mu l^2(y^2+z^2)\left( \frac{\partial ^2 \phi (x,t)}{\partial x^2}\right) ^2\right\} dV, \end{aligned}$$
(19)

above equation can be written by using \(I_p=\int _{A}(y^2+z^2)dA\),

$$\begin{aligned} U=\frac{1}{2}\int _{0}^L\left\{ \mu \left( \frac{\partial \phi (x,t)}{\partial x}\right) ^2 (I_p +3l^2A)+\frac{1}{4}\mu l^2\left( \frac{\partial ^2 \phi (x,t)}{\partial x^2}\right) ^2 I_p \right\} dx. \end{aligned}$$
(20)

The kinetic energy of carbon nanotube can be written as:

$$\begin{aligned} T=\frac{1}{2}\int _{0}^L \left\{ \rho I_p\left( \frac{\partial ^2 \phi (x,t)}{\partial x^2}\right) ^2 \right\} dx \end{aligned}$$
(21)

and the work done by the twisting moment (\(m_t\)) can be expressed as:

$$\begin{aligned} W=\int _{0}^L m_t \phi (x,t) dx. \end{aligned}$$
(22)

Substituting the work done by the twisting moment (22), the kinetic energy of carbon nanotube (21) and the strain energy (20) into the Hamiltons principle (18) and using integrations by parts, the equation of motion considering the effects of small scale will be derived. Taking the first variation of total potential energy (\(\delta \int _{t_1}^{t_2}\{U-T-W\}dt\)):

$$\begin{aligned}&\delta \int _{t_1}^{t_2}\int _{0}^{L}{\left[ \frac{1}{4}\frac{\partial ^2}{\partial x^2}\left[ \mu l^2 I_p\left( \frac{\partial ^2 \phi (x,t)}{\partial x^2}\right) \right] \right. } \\ \nonumber&-{\frac{\partial }{\partial x}\left[ \mu (I_p+3l^2A)\frac{\partial \phi (x,t)}{\partial x}\right] +\frac{\partial }{\partial t}\left[ \rho I_p\left( \frac{\partial \phi (x,t)}{\partial t}\right) \right] -m_t \Bigg ]\delta \phi }dxdt \\ \nonumber&+ \int _{t_1}^{t_2} \left[ (\mu I_p+3l^2A)\left( \frac{\partial \phi (x,t)}{\partial x}\right) -\frac{1}{4}\frac{\partial }{\partial x}\left[ l^2I_p\mu \left( \frac{\partial ^2 \phi (x,t)}{\partial x^2}\right) \right] \delta \phi \right] \\ \nonumber&+\frac{1}{4}l^2I_p\mu \left( \frac{\partial ^2 \phi (x,t)}{\partial x^2}\right) \delta \left( \frac{\partial \phi }{\partial x}\right) ^{L_1}_0 dt \\ \nonumber&+ \int _{t_1}^{t_2}\left\{ \rho I_p(\frac{\partial \phi (x,t)}{\partial t}\delta \phi )\right\} ^{t_1}_{t_2} dx. \end{aligned}$$
(23)

Governing equation (Euler Lagrange equation) read as

$$\begin{aligned} \Gamma _1\frac{\partial ^4 \phi (x,t)}{\partial x^4}-\Gamma _2\frac{\partial ^2 \phi (x,t)}{\partial x^2}+\Gamma _3\frac{\partial ^2 \phi (x,t)}{\partial t^2}=m_t, \end{aligned}$$
(24)

where,

$$\begin{aligned} \Gamma _1=\frac{l^2 \mu I_p}{4}, \end{aligned}$$
(25)
$$\begin{aligned} \Gamma _2=\mu I_p+3 \mu l^2 A, \end{aligned}$$
(26)
$$\begin{aligned} \Gamma _3=\rho I_p. \end{aligned}$$
(27)

The initial conditions can be obtained from Eq. (23);

$$\begin{aligned} \left( \frac{\partial \phi (x,t_2)}{\partial t}\right) \delta \phi (x,t_2)-\left( \frac{\partial \phi (x,t_1)}{\partial t}\right) \delta \phi (x,t_1)=0, \end{aligned}$$
(28)
$$\begin{aligned} \Gamma _2\left( \frac{\partial \phi (x,t)}{\partial x}\right) -\Gamma _1\left( \frac{\partial ^3 \phi (x,t)}{\partial x^3}\right) =0\quad \hbox {or}\quad \phi =0, \end{aligned}$$
(29)
$$\begin{aligned} \frac{\partial ^2 \phi (x,t)}{\partial x^2}=0\quad \hbox {or}\quad \frac{\partial \phi (x,t)}{\partial x}. \end{aligned}$$
(30)

Note that Eq. (24) represents the equation of motion torsional vibrating carbon nanotube related to angular rotation based on the modified couple stress theory (Gheshlaghi and Hasheminejad 2010). Provided that the cross-section of the carbon nanotube is circular, the above equation of motion is independent of the geometry of the section.

3 Method of solution

In this section, the carbon nanotube with elastic torsional restraints (see Fig. 1) for a torsional vibration is examined based on modified couple stress theory. The idea of the present model is to obtain a coefficient matrix for eigen-value analysis involving the torsional spring coefficients.

Fig. 1
figure 1

A single walled carbon nanotube with torsional springs at both ends

Full size image

3.1 Modal displacement function

In order to obtain the explicit expressions of the Fourier sine series, the unknown constants (Fourier coefficients) need to be determined with the equation of motion. In this study, Fourier sine series is utilized to calculate the torsional vibration frequencies. With the aid of method separation of variables, \(\phi (x,t)\) can be rewritten as the following form:

$$\begin{aligned} \phi (x, t)=\psi (x)e^{i\omega t}, \end{aligned}$$
(31)

where \(\psi (x)\) is the angular rotation function and \(\omega \) is the natural frequency. By substituting the above equation into equation Eq. (24) yields

$$\begin{aligned} \Gamma _1\frac{d^4 \psi (x)}{d x^4}-\Gamma _2\frac{d^2 \psi (x)}{dx^2}-\Gamma _3 \omega ^2\psi (x) =m_t, \end{aligned}$$
(32)

Adequate knowledge of the torsional vibration of such carbon nanotubes with deformable boundary conditions is necessary to properly design certain nanostructures, particularly when those structures are subjected to dynamic loads caused by an blast waves and other sources. The angular rotation about the center of twist \(\psi (x)\) is described here as follows:

$$\begin{aligned} \psi (x)=\left[ \begin{array}{ll} \psi _0 &{}\quad x=0\\ \psi _{L} &{} \quad x=L\\ \sum \nolimits _{n=1}^\infty C_n\sin (\alpha _n x)&{} \quad 0<x<L \end{array}\right] , \end{aligned}$$
(33)

where

$$\begin{aligned} \alpha _n =\frac{n\pi x}{L}. \end{aligned}$$
(34)

3.2 Stokes’ transformation

Although torsional vibration analysis of carbon nanotube is a widely studied topic, there are only few works that exist in the literature pertaining to the torsional vibration analysis of single walled carbon nanotubes with torsional restraints. In this study, in order to assess the effects of torsional spring coefficients, Stokes’ transformation is applied to the governing equation and boundary conditions. The Fourier coefficients (\(C_n\)) in Eq. (33) may be expressed as

$$\begin{aligned} C_n=\frac{2}{L}\int _0^{L} \psi (x)\sin (\alpha _n x)dx. \end{aligned}$$
(35)

First derivative of Eq. (33) can be computed as follows:

$$\begin{aligned} \psi '(x)=\sum \limits _{n=1}^\infty \alpha _n C_n\cos (\alpha _n x). \end{aligned}$$
(36)

Equation (36) may be written by a cosine series as follows:

$$\begin{aligned} \psi '(x)=\frac{f_0}{L}+ \sum \limits _{n=1}^\infty f_n\cos (\alpha _n x). \end{aligned}$$
(37)

The explicit expressions of two Fourier constants are given as follows

$$\begin{aligned} f_0=\frac{2}{L}\int _0^{L} \psi '(x) dx = \frac{2}{L}\left[ \psi (L)-\psi (0)\right] , \end{aligned}$$
(38)
$$\begin{aligned} f_n=\frac{2}{L}\int _0^{L} \psi '(x)\cos (\alpha _n x)dx \quad (n=1,2\ldots ), \end{aligned}$$
(39)

the \(f_n\) coefficient is obtained by integrating by parts of using Eq. (39)

$$\begin{aligned} f_n&=\frac{2}{L}\left[ \psi (x)\cos (\alpha _n x)\right] _{0}^{L}\\ \nonumber&\quad +\frac{2}{L}\left[ \alpha _n \int _0^{L} \psi (x)\sin (\alpha _n x)dx\right] , \end{aligned}$$
(40)
$$\begin{aligned} f_n=\frac{2}{L}\left[ (-1)^n \psi (L)-\psi (0)\right] + \alpha _n C_n. \end{aligned}$$
(41)

The present analytical solution method (Stokes’ transformation and Fourier series) will be helpful when dealing with carbon nanotubes with torsional elastic boundary conditions. The first-fourth derivatives of \(\psi (x)\) can be obtained as:

$$\begin{aligned} \frac{d \psi (x)}{d x} =\frac{\psi _{L}-\psi _0}{L} + \sum \limits _{n=1}^\infty \cos \left( \alpha _n x \right) \left( \frac{2 \left( (-1)^n \psi _{L}-\psi _0\right) }{L}+\alpha _n C_n\right) , \end{aligned}$$
(42)
$$\begin{aligned} \frac{d^2 \psi (x)}{d x^2} = -\sum \limits _{n=1}^\infty \alpha _n \sin \left( \alpha _n x\right) \left( \frac{2 \left( (-1)^n \psi _{L}-\psi _0\right) }{L}+\alpha _n C_n\right) . \end{aligned}$$
(43)
$$\begin{aligned} \frac{d^3 \psi (x)}{d x^3}&=\frac{\psi _L''-\psi _0''}{L} \\ \nonumber&\quad +\sum \limits _{n=1}^\infty \cos (\alpha _n x ) \left( \frac{2 ((-1)^n \psi _L''-\psi _0'')}{L}\right. \\ \nonumber&\quad \left. -\alpha _n^2 \left( \frac{2 ((-1)^n \psi _L-\psi _0)}{L}+\alpha _n C_n\right) \right) , \end{aligned}$$
(44)
$$\begin{aligned} \frac{d^4 \psi (x)}{d x^4}&=-\sum \limits _{n=1}^\infty \alpha _n \sin (\alpha _n x) \left( \frac{2 ((-1)^n \psi _L''-\psi _0'')}{L}\right. \\ \nonumber&\quad \left. -\alpha _n^2 \left( \frac{2 ((-1)^n \psi _L-\psi _0)}{L}+\alpha _n C_n\right) \right) . \end{aligned}$$
(45)

Fourier coefficients which simultaneously satisfy the governing equation need to be determined. Therefore, substituting Eqs. (33), (43) and (45) into Eqs. (32), the Fourier coefficients \(C_n\) and the angular rotation about the center of twist could be written in terms of \(\psi _0\), \(\psi _L\), \(\psi _0''\) and \(\psi _L''\)as follows:

$$\begin{aligned} C_n&= \frac{2 \pi n \left( \Gamma _2 L^2 \left( (-1)^{n+1} \psi _L+\psi _0\right) \right) }{\Gamma _3 L^4 \left( -\omega ^2\right) +\pi ^2 \Gamma _2 L^2 n^2+\pi ^4 \Gamma _1 n^4} \\ \nonumber&\quad + \frac{2 \pi n \left( \Gamma _1 \left( \pi ^2 n^2 \left( (-1)^{n+1} \psi _L+\psi _0\right) -L^2 \left( (-1)^{n+1} \psi _L''+\psi _0''\right) \right) \right) }{\Gamma _3 L^4 \left( -\omega ^2\right) +\pi ^2 \Gamma _2 L^2 n^2+\pi ^4 \Gamma _1 n^4}, \end{aligned}$$
(46)
$$\begin{aligned} \psi (x)&= \sum \limits _{n=1}^\infty \frac{2 \pi n \left( \Gamma _2 L^2 \left( (-1)^{n+1} \psi _L+\psi _0\right) \right) }{\Gamma _3 L^4 \left( -\omega ^2\right) +\pi ^2 \Gamma _2 L^2 n^2+\pi ^4 \Gamma _1 n^4} \\ \nonumber&\quad + \frac{2 \pi n \left( \Gamma _1 \left( \pi ^2 n^2 \left( (-1)^{n+1} \psi _L+\psi _0\right) -L^2 \left( (-1)^{n+1} \psi _L''+\psi _0''\right) \right) \right) }{\Gamma _3 L^4 \left( -\omega ^2\right) +\pi ^2 \Gamma _2 L^2 n^2+\pi ^4 \Gamma _1 n^4}\times \sin (\alpha _n x). \end{aligned}$$
(47)

Fourier coefficients are derived for modified couple stress theory here, which can be reduced to those for the classical elasticity theory. In fact, the Fourier coefficients of classical elasticity theory can be derived with \(l= 0\) .

3.3 Boundary conditions

In this work, a carbon nanotube with torsional springs attached to ends is considered (see Fig 1). In order to achieve a general solution to this problem, we have to use following force boundary conditions.

$$\begin{aligned} \Gamma _2\frac{d \psi }{dx}-\Gamma _1\frac{d^3 \psi }{\partial x^3}|_{x=0}=S_0 \psi _0, \end{aligned}$$
(48)
$$\begin{aligned} \Gamma _2\frac{d \psi }{dx}-\Gamma _1\frac{d^3 \psi }{\partial x^3}|_{x=L}=S_L \psi _L, \end{aligned}$$
(49)
$$\begin{aligned} \psi _0''|_{x=0}=0, \end{aligned}$$
(50)
$$\begin{aligned} \psi _L''|_{x=L}=0. \end{aligned}$$
(51)

where \(S_0\) and \(S_L\) are the torsional stiffnesses of the springs at the ends of the carbon nanotube. The substitution of Eqs. (42), (44) and (46) into Eqs. (48)–(51) leads to the two simultaneous homogeneous equations

$$\begin{aligned}&\left( -\frac{\Gamma _2}{L}-S_0+\sum \limits _{n=1}^\infty \frac{2 \Gamma _3 L \omega ^2 \left( \Gamma _2 L^2+\pi ^2 \Gamma _1 n^2\right) }{\Gamma _3 L^4 \left( -\omega ^2\right) +\pi ^2 \Gamma _2 L^2 n^2+\pi ^4 \Gamma _1 n^4} \right) \psi _0 \\\nonumber&\quad + \left( \frac{\Gamma _2}{L}+\sum \limits _{n=1}^\infty \frac{2 \Gamma _3 L (-1)^{n+1} \omega ^2 \left( \Gamma _2 L^2+\pi ^2 \Gamma _1 n^2\right) }{\Gamma _3 L^4 \left( -\omega ^2\right) +\pi ^2 \Gamma _2 L^2 n^2+\pi ^4 \Gamma _1 n^4}\right) \psi _L \end{aligned}$$
(52a)
$$\begin{aligned}&\left( \frac{\Gamma _2}{L}+\sum \limits _{n=1}^\infty \frac{2 \Gamma _3 L (-1)^{n+1} \omega ^2 \left( \Gamma _2 L^2+\pi ^2 \Gamma _1 n^2\right) }{\Gamma _3 L^4 \left( -\omega ^2\right) +\pi ^2 \Gamma _2 L^2 n^2+\pi ^4 \Gamma _1 n^4}\right) \psi _0 \\\nonumber&\quad + \left( -\frac{\Gamma _2}{L}-S_L+\sum \limits _{n=1}^\infty \frac{2 \Gamma _3 L \omega ^2 \left( \Gamma _2 L^2+\pi ^2 \Gamma _1 n^2\right) }{\Gamma _3 L^4 \left( -\omega ^2\right) +\pi ^2 \Gamma _2 L^2 n^2+\pi ^4 \Gamma _1 n^4} \right) \psi _L \end{aligned}$$
(52b)

An eigenvalue problem involving the torsional spring constants can be constructed according to above equations:

$$\begin{aligned} \left[ \begin{array}{ll} \Psi _{11} &{}\quad \Psi _{12} \\ \Psi _{21} &{} \quad \Psi _{22} \\ \end{array} \right] \left[ \begin{array}{l} \psi _{0} \\ \psi _{L} \end{array} \right] =0. \end{aligned}$$
(53)

In this work, angular rotation about the center of twist is sought as the superposition of a Fourier series and Stokes’ transformation that is used to take care of the torsional restraints. The classical rigid boundary conditions can be given by setting the values of torsional stiffness parameters. For example, the free-free boundary conditions at \(x = 0\) and \(x = L\) are achieved by letting \(S_0= 0\) and \(S_L= 0\). The fixed-fixed boundary conditions at \(x = 0\) and \(x = L\) can be obtained with \(S_0= \infty \) and \(S_L= \infty \). And the fixed-free boundary conditions at \(x = 0\) and \(x = L\) can be computed with \(S_0= \infty \) and \(S_L= 0\). The torsional vibration frequencies can be obtained by requiring the determinant of the coefficient matrix to zero;

$$\begin{aligned} \left| \Psi _{ij}\right| =0 ~~ ~~~ (i,j=1,2,3,4), \end{aligned}$$
(54)

where

$$\begin{aligned} \Psi _{11}=-\frac{\Gamma _2}{L}-S_0+\sum \limits _{n=1}^\infty \frac{2 \Gamma _3 L \omega ^2 \left( \Gamma _2 L^2+\pi ^2 \Gamma _1 n^2\right) }{\Gamma _3 L^4 \left( -\omega ^2\right) +\pi ^2 \Gamma _2 L^2 n^2+\pi ^4 \Gamma _1 n^4} , \end{aligned}$$
(55)
$$\begin{aligned} \Psi _{12}=\frac{\Gamma _2}{L}+\sum \limits _{n=1}^\infty \frac{2 \Gamma _3 L (-1)^{n+1} \omega ^2 \left( \Gamma _2 L^2+\pi ^2 \Gamma _1 n^2\right) }{\Gamma _3 L^4 \left( -\omega ^2\right) +\pi ^2 \Gamma _2 L^2 n^2+\pi ^4 \Gamma _1 n^4}, \end{aligned}$$
(56)
$$\begin{aligned} \Psi _{21}=\frac{\Gamma _2}{L}+\sum \limits _{n=1}^\infty \frac{2 \Gamma _3 L (-1)^{n+1} \omega ^2 \left( \Gamma _2 L^2+\pi ^2 \Gamma _1 n^2\right) }{\Gamma _3 L^4 \left( -\omega ^2\right) +\pi ^2 \Gamma _2 L^2 n^2+\pi ^4 \Gamma _1 n^4}, \end{aligned}$$
(57)
$$\begin{aligned} \Psi _{22}=-\frac{\Gamma _2}{L}-S_L+\sum \limits _{n=1}^\infty \frac{2 \Gamma _3 L \omega ^2 \left( \Gamma _2 L^2+\pi ^2 \Gamma _1 n^2\right) }{\Gamma _3 L^4 \left( -\omega ^2\right) +\pi ^2 \Gamma _2 L^2 n^2+\pi ^4 \Gamma _1 n^4} , \end{aligned}$$
(58)

Before closing this section, it should be mentioned that the theoretical model given in this subsection accounts for both rigid and restrained boundary conditions. Therefore, this model can be utilized to analyze the free torsional vibration of carbon nanotubes for various boundary conditions. It is remarkable that if the length scale coefficient is neglected, namely \(l = 0\), then a coefficient matrix for circular bars based on classical elasticity theory is deduced.

4 Applications and verifications

On the basis of the theoretical formulation and solution procedure presented in the previous section, a computer code has been written and representative eigen value examples have been solved to demonstrate the efficiency of the developed method. Free torsional frequencies of the carbon nanotube can be achieved by solving Eq. (54). Firstly, accuracy and the validity of the present method is checked. Then, the effects of small scale parameter and torsional springs on the free torsional vibration characteristics of the carbon nanotube are investigated.

4.1 Comparison with existing results

The validity and accuracy of the present analytical solution method is examined by comparing their results with examples chosen from the literature (Tabassian 2013; Gorman 1975). Theoretically, there are infinite terms in Eq. (54). However, in the practical applications the infinite series should be truncated and only finite terms are taken into consideration. To validate the analytical method employed in this study, free torsional frequencies are compared predicted by the current method for modified couple stress theory with those predicted by prismatic bar theory. The free torsional frequencies according to the classical elasticity theory can be calculated from following formulation for fixed-fixed boundary conditions (Gorman 1975):

$$\begin{aligned} \varpi _k=\frac{\pi n}{L} \sqrt{\frac{G}{\rho }}, \end{aligned}$$
(59)

where \(\varpi _k\) are the torsional frequencies in classical elasticity theory. In order to compare the results available in the literature material properties are taken as \(G = 79.3\) GPa and \(\rho = 7800\, \mathrm{kg/m}^3\). Geometrical properties are assumed as: inner radius \(R_1 = 0.0\) nm and outer radius is \(R_2 = 50.0\) mm. and the length is \(L = 1000\) mm (Tabassian 2013). The length scale parameter \(l^2\) is assumed to be zero. Area and polar moment of inertia of the cross section could be written as.

$$\begin{aligned} A=\pi (R_2^2-R_1^2) \quad J_p=\frac{\pi }{2}(R_2^4-R_1^4) , \end{aligned}$$
(60)

Clamped-clamped boundary conditions are special case of a bar with torsional springs of infinite stiffness. In this work, to demonstrate the solution of clamped-clamped boundary conditions, torsional spring coefficients are assumed as \(S_0 = 10 \times 10^{10}\) N/mm and \(S_L = 10 \times 10^{10}\) N/mm. For validation purpose torsional vibration frequencies obtained by using different truncated number of terms are compared with those predicted by prismatic bar theory (\(\varpi =\frac{\pi n}{L} \sqrt{\frac{G}{\rho }}\)). The results computed by using exact formulation given in Eq. (59) are also mentioned in the last row of Table 1 to be compared with results obtained by the Fourier sine series with Stokes’ transformation. As tabulated in Table 1 by choosing \(n=\) 10–200 terms infinite series, the first five non-dimensional free torsional frequencies of the present problem with high order of accuracy are achieved.

Table 1 Five non-dimensional torsional frequencies of the fixed-fixed boundary conditions
Full size table

4.2 Effects of the small scale parameter

The free torsional frequencies in classical continuum theory can be obtained from equation (59). Similarly, the free torsional frequencies in modified couple stress theory may be calculated from the following equation (Gheshlaghi and Hasheminejad 2010):

$$\begin{aligned} \hat{\omega _k}=\frac{\pi n}{L} \sqrt{n^2\frac{\mu l^2 \pi ^2}{4 \rho L^2}+\frac{3 A \mu l^2}{\rho I_p} + \frac{\mu }{\rho } }, \end{aligned}$$
(61)

Herein, the normalized free torsional vibration frequencies are defined as the form of \(\Omega _k = \omega _k/\varpi _k\), (\(k =1,2,3,4,\ldots \)). The index k indicates the mode number. The parameter \(\Omega _k\) is used to give a better illustration of the small scale effects in torsional vibration response of single walled carbon nanotubes. It can be observe from Eq. (54) that small scale effects are neglected (\(l =0\)), we get the similar results whether using traditional equation given in (59) or Eq. (54). For higher values of torsional spring parameters, similarly, small scale effects are not neglected (\(l\ne 0\)), we get the similar results whether using traditional equation given in (61) or Eq. (54). For numerical illustration, the material and geometric properties of nanotube utilized in this paper are: Young’s modulus \(E=0.72\) TPa, Poisson ratio \(\nu = 0.25\), density \( = 2.3\) \(\mathrm{g}/\mathrm{cm}^{3}\) (Wang 2005), diameter \(d=5\) nm, the length L = 10 nm. and the thickness of the carbon nanotube \(t=0.34\) nm (Wang 2005). It should be pointed out that small scale parameter l must be smaller than 2 nm for carbon nanotubes (Wang and Wang 2007). Consequently, the small scale parameter l is selected in the range 0–2 nm (Lim et al. 2015).

Table 2 Seven non-dimensional torsional frequencies \(\Omega _k \) of for different small scale parameter with \(S_0=5\) nN/nm \(S_L=5\) nN/nm
Full size table

It can be seen in Tables 2 and 3 that the first seven normalized torsional frequencies with various length scale parameter (l) are tabulated for different spring parameters. It is investigated that the normalized frequencies increase with increasing length scale parameter, that is the small scale effect strengthens the torsional rigidity. Small scale parameter has also greater influence on higher order modes than that on lower-modes. As tabulated in Tables 2 and 3, torsional spring coefficients at the ends has obvious effects on dynamic treatment of carbon nanotubes.

Table 3 Seven non-dimensional torsional frequencies \(\Omega _k \) of for different small scale parameter with \(S_0=1\) nN/nm \(S_L=1\) nN/nm
Full size table

In Figs. 2, 3, 4, 5, comparisons of the first seven normalized frequencies based on present analytical method with those of classical theories are revealed. It can be concluded that the normalized frequencies predicted by modified couple stress theory exhibit larger than those of classical elasticity theory, showing “small size effect”. It is remarkable that the difference of normalized frequencies between modified couple stress theory and the classical elasticity theory decreases with spring coefficient decreased.

Fig. 2
figure 2

The effect of small scale parameter (l) on the first seven normalized frequencies with different symmetrical spring parameters

Full size image

Figure 2 shows the variation of the first seven dimensionless frequencies (\(\Omega _k\)) versus the small scale parameter (l) for various values of the torsional spring parameters. The mathematical results in each figure are calculated for a given symmetrical torsional spring coefficients (\(S_0=S_L=100\), 5, 1 nN/nm). As can be observed, with increasing length scale parameter (l) the normalized frequencies increase for all values of the mode number and the spring parameters. In addition, for a given torsional spring coefficients, the effect of the length scale parameter in increasing the normalized frequencies for the higher vibration modes is larger than those of the lower ones.

Fig. 3
figure 3

The effect of normalized length (L / l) on the first seven normalized frequencies with different symmetrical spring parameters

Full size image

Figure 3 shows the variation of normalized frequencies with normalized length change for frequencies computed from classical elasticity theory and the modified couple stress theory: as the increase in length of carbon nanotube decreases the normalized frequencies. As found earlier the modified couple stress theory-frequencies are always larger than the classical elasticity theory-frequencies.

Fig. 4
figure 4

The effect of mode number on the first seven normalized frequencies with different symmetrical spring parameters

Full size image

One of the chief contributions of present study is the derivation of a coefficient matrix including the both small scale and torsional spring parameter for calculating the torsional vibration frequencies. In Fig. 4, it is again noted that the small scale effects increases with increasing mode number, or stronger small scale effects result in higher order vibration modes. It is also observed from the Fig. 4, the torsional frequencies of the modified couple stress theory are larger than those of classical elasticity theory.

4.3 Effects of the torsional spring coefficients

By employing modified couple stress theory with the material properties of nanotube: Young’s modulus \(E=0.72\) TPa, Poisson ratio \(\nu = 0.25\), density \(= 2.3\) \(\mathrm{g}/\mathrm{cm}^{3}\) (Wang 2005), diameter \(d=5\) nm, the length L = 10 nm. and the thickness of the carbon nanotube \(t=0.34\) nm (Wang 2005). The first three normalized frequencies are calculated and the solutions are shown in Fig. 5, where both the modified couple stress theory and classical elastic theory solutions are calculated for different spring coefficients and plotted for direct comparison. It could be seen that with increasing symmetrical spring coefficients (\(S_0=S_L\)) the first normalized frequency increases for all values of the spring parameters. It is interesting the note that higher order modes are sensitive to the torsional spring coefficient variations, while the first mode of the torsional vibration depend essentially on increasing values of spring coefficient.

Fig. 5
figure 5

The effect of symmetrical spring coefficient on the first three normalized frequencies with different small scale parameter

Full size image

5 Conclusions

Torsional vibrations of single walled carbon nanotubes with torsional springs have been studied using the Fourier sine series. This new analytical method is virtually different from all previous methods where, instead of rigid boundary conditions (fixed-free), restrained boundary conditions with the higher-order boundary conditions are used by considering the torsional spring coefficients. Such theoretical analysis has not been reported in previous studies. Angular rotation about the center of twist is sought as the superposition of a Fourier sine series and Stokes’ transformation that is used to take care of the elastic torsional restraints. Analytical results are calculated with deformable boundary conditions of the carbon nanotubes. The validity of the solutions is discussed in numerical ways. The theoretical analysis in this study show that the free torsional frequency results from the present method are very close to those calculated from references. It is remarkable that the procedure proposed in this study gives more flexibility in boundary conditions.

Rigid (idealized) boundary conditions (fixed-fixed, fixed-free) are nothing but special cases of elastic deformable boundary conditions. For instance, a fixed bar is a special case of a bar with torsional springs of infinite stiffness. The main objective of this paper is to propose a general analytical method for the free torsional vibration of carbon nanotubes with general elastic boundary conditions. Although these theoretical analysis have been confined to single walled carbon nanotubes with circular cross-sections for simplicity, they can be extended to double walled carbon nanotubes.