1 Introduction

Carbon nanotube (CNT) represent one of the most promising material extensively used in various nanoelectromechanical systems (NEMS) based applications. This is mainly due to its distinguished mechanical properties such its remarkably high Young’s modulus, high aspect ratio, and low material density. Therefore, an extensive experimental and numerical research wave in the nanoscale level has been conducted aiming to investigate CNT-based nanostructure structural and dynamical behaviors.

Nevertheless, conducting an experimental investigation to examine the mechanical behaviors of the CNT is somehow difficult, expensive and requires fancy equipment an experimental set-ups. Therefore, and in order to overcome the above mentioned difficulty, people developed some methodical theoretical modes, through utilizing continuum theory to investigate the mechanical behaviors of the CNT-based nanostructure. Many groups (Wang et al. 2008; Lee and Chang 2009; Ouakad and Younis 2010, 2011a, b; Ouakad 2010; Ansari et al. 2011; Kang et al. 2015; Wang and Hu 2016) had reported on using the classical continuum mechanics to simulate the structural response of CNT based NEMS devices. Later, some researchers carried out few modifications to the classical continuum mechanics for the sake of demonstrating the small scale effect in such tiny structures. To cite few of these attempts: the nonlocal Eringen (Ansari and Ramezannezhad 2011; Wang and Wang 2016; Sudak 2003; Zhang et al. 2005; Wang and Varadan 2006; Lu et al. 2007; Kumar et al. 2008; Reddy and Pang 2008; Hu et al. 2008; Benzair et al. 2008; Murmu and Pradhan 2009, 2010; Ansari and Sahmani 2012; Arash and Wang 2012; Seyyed Fakhrabadi et al. 2014, 2015; Ansari et al. 2017; Shaat and Abdelkefi 2017) and the strain gradient (SGT) (Mindlin 1965; Akgöz and Civalek 2012; Fakhrabadi et al. 2013, 2014; Xu and Deng 2015; Pradiptya and Ouakad 2016) theories were among the most used non-classical models capable of apprehending the small size effects in micro, nano and even sub-nano scale structures. These effects were reported to be indispensable to accurately model the nonlinear structural behaviors of microstructure as well (Arash and Wang 2012; Yang et al. 2002; Lam et al. 2003). For example, in the strain gradient theory, and instead of using one length scale dependent parameter, the model uses three different and dependent size scale parameters in order to capture the micro/nano structure 3D size dependent effects. These three higher-order strain gradient parameters are associated with the dilatation, the deviatoric stretch, and the rotation gradients and therefore allowing to model any 3D size dependent effect in sub-micro scale (Lam et al. 2003). In addition, surface effect has been reported as an important factor in the small scale modeling under certain circumstance. Wang and Wang (2014, 2015) and Wang et al. (2015) reported that the surface effect is significantly change the pull-in instability and free vibration behaviors for the cantilever switch modeling with large gap-length ratio and short length of fixed electrode. Wang et al. (2015, 2017a, b) also stressed that the surface effect is significant for beam with the square profile and becoming more indispensable for thinner plate while imposed a large amplitude of vibration scenario.

Another fundamental effect that had been reported to be imperative in the CNT-based NEMS modeling is the thermal effect. Ansari et al. (2011) studied CNT-based nanobeam with several boundary conditions. The limitation of this study is the absent of any external or even actuating load which is mostly used in almost all CNT-based NEMS devices. Another work qualitatively similar to the work of Ansari et al. (2011) was reported by Kang et al. (2015). In this work, the group solved nonlinear classical continuum beam equations to model the nonlinear structural behavior of CNT nanobeam under the effect of a simple harmonic thermal load. Another group (Lee and Chang 2009) proposed an analytic solution to predict the critical buckling temperature of single-walled carbon nanotube (SWCNT). They reported that SWCNT may buckle for very minor temperature load. This buckling instability may lead the CNT into deflected state which maybe behave like a curved/slacked CNT.

To the best of the authors knowledge, and after a thorough survey of the literature, it is concluded that a very limited number of investigations considered the nonlinear structural problem of CNT based nanobeams, using the strain gradient elasticity theory Along with the thermal effect are both taken into consideration. Furthermore, there is some deficiency in the current literature on investigating the effect of higher order strain gradient parameters on the possibility of structural instabilities. To fill this gap in the literature, the present study propose to investigate the thermal effect on the free and forced vibration of a doubly-clamped single-walled carbon nanotube and while assuming a non-classical nanobeam continuum model. In this regards, a higher-order strain gradient deformation model is taken into account in the framework of the Euler–Bernoulli nonlinear beam theory. The numerical approaches and methodologies to predict the natural frequency dispersion of the SWCNT when subjected by AC and DC load under certain thermal excitations will be thoroughly presented. In the presence of a temperature variation, we will also discuss the possibility of the fundamental CNT modal frequencies veering and crossing which usually occur on an initially deflected/curved fixed–fixed structure due to a thermal load. The effect of size scale dependent effect on the resonant frequency of SWCNT will also be presented.

The contribution of the paper is as follows. First, based on few of our previous works (Pradiptya and Ouakad 2016, 2017), a reduced order model (ROM) using the Galerkin’s decomposition procedure is adopted to solve the above nonlinear problem. Second, the nonlinear free-vibration problem of doubly clamped CNT under parallel plate electrostatic actuation is solved using a reduced-order model Jacobian matrix process. Then, the effect of a temperature variation to possibility initiate modes veering and modes crossing of the CNT when operated in the post buckling temperature regime will be carried out. Finally, the nonlinear response of the doubly-clamped CNT when driven by DC superimposed by AC load is examined using one mode in the ROM procedure.

This paper is arranged as follows. Following this introduction, a nonlinear partial differential Euler–Bernoulli beam equation employing a modified strain gradient theory while taking into consideration the von Karman nonlinear strain deformations, the nonlinear electric parallel-plates actuating force, and the thermal effect is presented in Sect. 2. Then, a Galerkin based reduced-order discretization technique to convert the nonlinear partial differential equation into ordinary differential equations is described in Sect. 3. Section 4 summarizes the outcomes of the size scale dependent parameters effect on the critical buckling temperature of the investigated CNT based nano-resonator. In Sect. 5, the free vibration analysis is conducted by considering two thermal conditions: a low temperature regime and then a high temperature situation. An analytical/numerical technique called the Jacobian-Galerkin method to predict the fundamental frequencies of the CNT-based nano-resonator is also presented in Sect. 5. The forced vibration analysis under low gate voltage regimes to investigate the effect of geometrical size of the resonator while assuming higher-order strain gradient deformation is carried out in Sect. 6. Finally, the main contributions and conclusions of this study are summarized in Sect. 7.

2 Problem formulation

In this section, the problem formulation of the static and dynamic behaviors of a doubly-clamped CNT-based resonator under both electric actuation and thermal loading is presented. Accordingly, we consider a straight CNT-based nano-resonator operating in a thermally fluctuating environment. We adopt the same non-classical nonlinear continuum beam model, incorporating the nonlinear von-Karman strain demonstrating the mid-plane stretching effect, the size scale dependent effect through the strain gradient theory, a nonlinear actuating parallel-plates electrostatic actuating force, and a temperature effect as presented in one of our previous work (Pradiptya and Ouakad 2016, 2017). It is worth mentioning here that, for simplicity, both the van der Waals and Casimir effects were not considered in this current investigation. This is mainly because we have assumed gap sizes between the CNT and its lower actuating electrode larger enough to make their effect somehow negligible. In reality these effects are only significant when the gap width is too small in ten range of only few nanometers (Dequesnes et al. 2002; Marc et al. 2002).

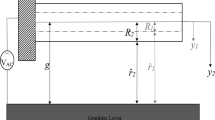
The CNT-based nano-resonator is modeled in the framework of a nonlinear Euler–Bernoulli beam theory, with a radius r, a shell thickness h, an effective length L, a mass density ρ, a Young’s modulus E, a cross-sectional area A, and a cross-sectional moment of inertia I. The schematic is presented in Fig. 1. We should note here that the slack effect in this current model is also neglected as we only considered the case of straight SWCNT-based nano-resonators. Consequently, the equation of motion along with its respective boundary conditions governing the transverse displacement of the straight CNT-based nanoresonator, while considering both the size dependent parameters as well as the thermal effects are given by (Pradiptya and Ouakad 2016):

$$\rho A\frac{{\partial^{2} w}}{{\partial t^{2} }} + \tilde{C}_{v} \frac{\partial w}{\partial t} - Q\frac{{\partial^{6} w}}{{\partial x^{6} }} + P\frac{{\partial^{4} w}}{{\partial x^{4} }} + \left( {EA\alpha_{T} \Delta T - \frac{EA}{2L}\int\limits_{0}^{L} {\left( {\frac{\partial w}{\partial x}} \right)^{2} dx} } \right)\frac{{\partial^{2} w}}{{\partial x^{2} }} = F_{e} (x,t),$$
(1)
$$w(0,t) = w(L,t) = 0,\quad \left. {\frac{\partial w}{\partial x}} \right|_{x = 0} = \left. {\frac{\partial w}{\partial x}} \right|_{x = L} = 0,\quad \left. {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right|_{x = 0} = \left. {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right|_{x = L} = 0,$$
(2)

where the constants P and Q are defined as \(P = \left( {EI_{y} + GA\left( {2l_{0}^{2} + \frac{8}{15}l_{1}^{2} + l_{2}^{2} } \right)} \right)\) and \(Q = GI_{y} \left( {2l_{0}^{2} + \frac{4}{5}l_{1}^{2} } \right)\). The size scale parameters noted above as l 0, l 1, and l 2 are the dilatation, the deviatoric stretch, and the rotation gradients, respectively (Pradiptya and Ouakad 2016, 2017; Lam et al. 2003)

Fig. 1
figure 1

Schematic of a doubly-clamped CNT-based nano-resonator under parallel plate electrostatic actuation arrangement

Full size image

Note that in Eq. (2), the first four boundary conditions are the classical one. w and \(\partial w/\partial x\) represent the deflection and slope boundary conditions for both end-clamped configuration, respectively. The last two boundary conditions which are appeared to be second derivative of the deflection represent the bending moment term obtained from the equation of motion derivation using Hamilton’s principle. The detail of this derivation can be found in Pradiptya and Ouakad (2017). This is also consistent with few other published works in which they all assumed that the non-classical moment equation can be written as combination of the second and fourth derivative of the beam transverse deflection (Yang et al. 2002; Pradiptya and Ouakad 2017; Kong et al. 2009; Belardinelli et al. 2014; Ghayesh 2014).

The electrostatic force function for a CNT-based nanoresonator under a parallel-plates electric field assumption can be written as (Ouakad and Younis 2010, 2011a, b; Ouakad 2010):

$$F_{e} (x,t) = \frac{{\pi \varepsilon_{0} (V_{DC} + V_{AC} \cos (\varOmega t))^{2} }}{{\sqrt {(d - w)(d - w + 2r)} (\cosh^{ - 1} \left( {1 + (d - w)/r} \right))^{2} }},$$
(3)

For convenience and in order to avoid some numerical problems that may occur when computing small numbers mainly in the nano-scale, the below nondimensional variables will be used to acquire normalized equations of motion:

$$\hat{w} = \frac{w}{d};\quad b = \frac{{b_{0} }}{d};\quad \hat{w}_{0} = \frac{{w_{0} }}{d};\quad \hat{x} = \frac{x}{L};\quad \hat{t} = \frac{t}{T};\quad T = \sqrt {\frac{{\rho AL^{4} }}{P}} ;\quad \hat{r} = \frac{r}{d},$$
(4)

Substituting the above expressions into Eqs. (1)–(3), then dropping the hat, we are therefore left with the following normalized equation of motion and its respective boundary conditions:

$$\beta_{0} w^{vi} + w^{iv} + \ddot{w} + C_{v} \dot{w} = \left[ { - \beta_{2} \alpha_{T} \Delta T_{high/low} + \beta_{1} \left( {\int\limits_{0}^{1} {(w^{\prime})^{2} dx} } \right)} \right](w^{\prime\prime}) + \beta_{3} F_{e} (x,t),$$
(5)
$$w(0) = 0,\quad w(1) = 0,\quad \frac{\partial w(0)}{\partial x} = 0,\quad \frac{\partial w(1)}{\partial x} = 0,\quad \frac{{\partial^{2} w(0)}}{{\partial x^{2} }} = 0,\quad \frac{{\partial^{2} w(1)}}{{\partial x^{2} }} = 0,$$
(6)

where:

$$F_{e} = \frac{{(V_{DC} + V_{AC} \cos (\varOmega t))^{2} }}{{\sqrt {(1 - w)(1 - w + 2r)} \left( {\cos^{ - 1} \left( {1 + \frac{1 - w}{r}} \right)} \right)^{2} }},$$
(7)

and:

$$\begin{aligned} & \beta_{0} = - \frac{Q}{{PL^{2} }},\quad \beta_{1} = \frac{{EAd^{2} }}{2P},\quad \beta_{2} = \frac{{EAL^{2} }}{P}, \\ & C_{v} = \frac{{\tilde{C}_{v} L^{2} }}{{\sqrt {\rho AP} }},\quad \varOmega = \tilde{\varOmega }\sqrt {(\rho AL^{4} )/P} ,\quad \beta_{3} = \frac{{\pi \varepsilon_{0} L^{4} }}{{Pd^{2} }}, \\ \end{aligned}$$
(8)

3 Galerkin’s modal decomposition technique

In this work, the Galerkin’s modal decomposition procedure is used to discretize the above nonlinear partial differential equation (PDE), Eq. (5), into finite number of ordinary differential equations (ODEs) which are easier to be numerically solved. This model decomposition procedure is first assuming the solution of the PDE as two separated independent functions, i.e. one space and one time varying functions. Next, assuming that the solution of Eq. (5) can be approximated as modal coordinates and modes shape representing the transverse deflection of the CNT-based nanoresonator, we can approximate the solution of the PDE as follow:

$$w(x,t) = \sum\limits_{i = 1}^{n} {q_{i} (t)\phi_{i} (x)} ,$$
(9)

where, \(q_{i \le i \le n} (t)\) are the modal coordinates, and \(\phi_{i \le i \le n} (x)\) are the admissible modes shape function of the doubly-clamped CNT. The modes shape functions should satisfy the nonclassical boundary conditions, Eq. (8), and therefore the classical modes shape functions are no longer valid to be considered in these type of ROM calculations. Hence, we decided to develop a model to acquire the nonclassical modes shape functions that satisfy all the classical and the non-classical boundary conditions (Pradiptya and Ouakad 2016, 2017). Henceforth, the nonclassical mode shape function can be expressed as Pradiptya and Ouakad (2016, 2017):

$$\phi (x) = C_{1} \cosh (\lambda_{1} x) + C_{2} \sinh (\lambda_{1} x) + C_{3} \cos (\lambda_{3} x) + C_{4} \sinh (\lambda_{3} x) + C_{5} \frac{{e^{{ - \lambda_{2} x}} }}{{\lambda_{2}^{2} }} + C_{6} \frac{{e^{{ - \lambda_{2} x - \lambda_{2} }} }}{{\lambda_{2}^{2} }},$$
(10)

where C i− and \(\lambda_{i}\) are the constant coefficients and roots of the characteristic equation of the characteristic nonlinear frequency equation obtained through considering the linearized undamped eigenvalue problem of Eq. (5). We should note here that all the mode shape parameters will depend on the geometrical dimensions of the CNT and its assumed size scale dependent parameters.

Next, by substituting Eq. (9) into Eq. (5), then multiplying the whole equation with the mode-shape function \(\phi_{1 \le i \le n} (x)\), then integrating numerically from 0 to 1, we get the ROM governing the dynamic behavior of the CNT-based nano-resonator in term of its modal coordinates functions \(q_{1 \le i \le n} (t)\). The numerical solutions representing the dynamic behavior of the nano-resonator can be obtained using long time integration while assuming a Runge–Kutta method. To designate the obtained ROM coupled ODE nonlinear equations, the following is the equation describing the ODE when assuming only one modal coordinate, \(q_{i = 1} (t)\) in the Galerkin decomposition procedure:

$$\ddot{q}_{1} (t) + C_{v} \dot{q}_{1} (t) + (\beta_{0} \varGamma_{1} + \varGamma_{2} )q_{1} (t) = \beta_{1} \varPi_{1} \varPi_{2} (q_{1} (t))^{3} + \beta_{3} \int\limits_{0}^{1} {(F_{e} (x,t)\phi_{1} )dx} ,$$
(11)

where,

$$\begin{aligned} \varGamma_{1} & = \int\limits_{0}^{1} {(\phi_{1}^{vi} (x)\phi_{1} (x))dx} ,\quad \varGamma_{2} = \int\limits_{0}^{1} {(\phi_{1}^{iv} (x)\phi_{1} (x))dx} , \\ \varPi_{1} & = \int\limits_{0}^{1} {(\phi^{\prime}_{1} (x))^{2} dx} ,\quad \varPi_{2} = \int\limits_{0}^{1} {\phi^{\prime\prime}_{1} (x)\phi_{1} (x)dx} , \\ \end{aligned}$$
(12)

and,

$$F_{e} = \frac{{(V_{DC} + V_{AC} \cos (\varOmega t))^{2} }}{{\sqrt {(1 - q_{1} (t)\phi_{1} (x))(1 - q_{1} (t)\phi_{1} (x) + 2r)} \left( {\cos^{ - 1} \left( {1 + \frac{{1 - q_{1} (t)\phi_{1} (x)}}{r}} \right)} \right)^{2} }}.$$
(13)

We propose next to validate the constructed reduced-order model with results available in Fakhrabadi et al. (2014). Figure 2 shows the comparison while assuming strain gradient theory with the length scales are all equal to 0.2 nm. The results show an acceptable agreement with Fakhrabadi et al. (2014).

Fig. 2
figure 2

ROM validation with literature (Fakhrabadi et al. 2014) assuming SGT

Full size image

4 Buckling analysis under thermal load

This section is organized mainly to investigate the critical (threshold) temperature value that would trigger a thermal expansion sufficient for the buckling initiation of the clamped–clamped CNT based nano-resonator. We calculate this onset value thermal expansion of the CNT by neglecting all the time dependent functions as well as the electrostatic force in the nonlinear beam equation of motion, Eq. (12), while conserving the mid-plane stretching term and the temperature changing \(\Delta T_{high/low}\). To this end, the time-dependent modal coordinate functions \(q_{1 \le i \le n} (t)\) are all replaced by time-independent coefficients \(a_{1 \le i \le n}\). Consequently, we are left with the following nonlinear algebraic equations all function of the constant parameters \(a_{1 \le i \le n}\), and governing the CNT static deflection under the effect of any thermal load \(\Delta T\):

$$\begin{aligned} \sum\limits_{i = 1}^{n} {\beta_{0} a_{i} \int\limits_{0}^{1} {\phi_{i}^{VI} (x)\phi_{j} (x)dx} } + \sum\limits_{i = 1}^{n} {a_{i} \int\limits_{0}^{1} {\phi_{i}^{IV} (x)\phi_{j} (x)dx} - \beta_{3} \int\limits_{0}^{1} {F_{e} (x)\phi_{j} dx} } \hfill \\ + \int\limits_{0}^{1} {\left\{ {\left[ {\beta_{2} \alpha_{T} \Delta T - \beta_{1} \left( {\int\limits_{0}^{1} {\left( {\sum\limits_{i = 1}^{n} {a_{i} \phi_{i}^{\prime } (x)} } \right)^{2} dx} } \right)} \right]\left( {\sum\limits_{i = 1}^{n} {a_{i} \phi^{\prime\prime}_{i} (x)} } \right)\phi_{j} (x)} \right\}dx = 0,\quad j = 1,2,3, \ldots ,n.} \hfill \\ \end{aligned}$$
(14)

As a numerical case, we consider a CNT with tube shell thickness h = 0.34 nm, length L = 3000 nm, and Young’s modulus of 1.2 GPa. Table 1 summarize several CNT parameters which are considered toward this study. Figure 3 displays the CNT static deflection versus an assumed temperature changing \(\Delta T_{high/low}\) using one mode shape in the ROM process for case 3 of Table 1. In the same figure, we assume all size scale dependent parameters equal to \(l_{0} = l_{1} = l_{2} = l = 1\) nm.

Table 1 The CNT parameters for dynamic analysis
Full size table
Fig. 3
figure 3

Variation of CNT static deflection with the thermal load and while assuming a SGT with \(l = 1\) nm for the case study number 3 of Table 1

Full size image

The figure shows that for this case study, a critical buckling thermal threshold is occurring at around \(\Delta T\) ≈ 9.4 K. Increasing the temperature changing value \(\Delta T_{high/low}\) above this critical thermal threshold will initiate a post-buckling state. The same figure is demonstrating that the CNT exhibits in a nonlinear manner the post-buckling regime when the change of the temperature is furtherly increased.

To compliment the above numerical results, we propose next to compute the CNT critical buckling temperatures while considering different SGT parameters, Fig. 4. Additionally and in the same figure, the SGT results will be compared with those obtained while assuming classical continuum theory. The classical results show that the critical buckling while considering one mode in the calculation is very small. This finding is in agreement with what was previously reported in Lee and Chang (2009). In fact, they have investigated in their work the critical buckling temperatures of single wall carbon nanotube (SWCNT) using the classical continuum theory, and they have concluded that these critical temperatures are relatively small values for the fundamental mode (the first mode of vibration).

Fig. 4
figure 4

Variation of the CNT static deflection with an assumed high temperature regimes while varying the strain gradient parameters as follows: l = 0 nm (the classical continuum theory case); l = 1.0 nm; l = 1.25 nm and l = 1.5 nm for the case number 3 of Table 1

Full size image

Figure 4 shows that taking into account the nonlinear geometric terms due to the assumed thermal load along with the mid-plane stretching are affecting significantly the computation of the critical thermal buckling thresholds. Similarly, it is clearly shown that increasing the SGT parameters, i.e. decreasing the CNT radius to the size scale dependent parameters ratio, tends to increase the critical buckling temperature thresholds, as compared to the classical continuum theory. This is mainly due to the stiffening effect of the CNT-based nanobeam in the presence of higher-order strain gradient deformations. That to say that the strain gradient effects are considerably related to the stiffness of any considered nanostructure (Lam et al. 2003).

5 Free vibration analysis

In this section, we propose to examine the thermal effects on the natural frequencies dispersion of the doubly-clamped carbon nanotube when varying its actuating DC load. To this end, we consider a linear eigenvalue problem through linearizing all nonlinear terms in the CNT equation of motion, i.e.: the geometric stretching nonlinearity, the actuating electric force, the size-dependent terms, and the thermal load. We then plan to use a combined method called Jacobian-Galerkin matrix method to calculate all the eigenvalues of the eigenvalue problem, i.e. the CNT natural frequencies of the CNT-based nanoresonator. All the computed results will be then compared with those while assuming the CNT operating with a room temperature condition.

5.1 The Jacobian-Galerkin procedure

We start here by deriving the linearized eigenvalue problem (LEVP) to investigate the thermal effects on the natural frequencies of CNT-based nanobeam. Through assuming the Galerkin decomposition, the normalized equation of motion with its respective boundary conditions of the doubly clamped straight CNT, Eqs. (5)–(8), can be re-written as:

$$\begin{aligned} &\frac{\partial }{\partial t}\left( {\frac{\partial }{\partial t}\sum\nolimits_{i = 1}^{n} {q_{i} (t)\phi_{i} (x)} } \right) = - \beta_{0} \frac{{\partial^{6} }}{{\partial x^{6} }}\left[ {\sum\nolimits_{i = 1}^{n} {q_{i} (t)\phi_{i} (x)} } \right] - \frac{{\partial^{4} }}{{\partial x^{4} }}\left[ {\sum\nolimits_{i = 1}^{n} {q_{i} (t)\phi_{i} (x)} } \right] + \\ &\, + \beta_{3} \frac{{\left( {V_{DC} } \right)^{2} }}{{\sqrt {\left( {1 - \sum\nolimits_{i = 1}^{n} {q_{i} (t)\phi_{i} (x)} } \right)\left( {1 - \sum\nolimits_{i = 1}^{n} {q_{i} (t)\phi_{i} (x)} + 2r} \right)} \left( {\cos^{ - 1} \left( {1 + \frac{{1 - \sum\nolimits_{i = 1}^{n} {q_{i} (t)\phi_{i} (x)} }}{r}} \right)} \right)^{2} }} \\& \, + \left[ { - \beta_{2} \alpha_{T} \Delta T + \beta_{1} \int\nolimits_{0}^{1} {\left( {\frac{\partial }{\partial x}\left[ {\sum\limits_{i = 1}^{n} {u_{i} (t)\phi_{i} (x)} } \right]} \right)^{2} dx} } \right]\frac{{\partial^{2} }}{{\partial x^{2} }}\left[ {\sum\limits_{i = 1}^{n} {u_{i} (t)\phi_{i} (x)} } \right]. \\ \end{aligned}$$
(15)

The above Eq. (15) can be re-written in the following state-space representation form:

$$\dot{\varUpsilon } = K(\varUpsilon ),$$
(16)

where,

$$\varUpsilon = [\begin{array}{*{20}c} {x_{1} } & {x_{2} } & \cdots & {x_{n} } \\ \end{array} ]^{T} = [\begin{array}{*{20}c} {q_{1} } & {\dot{q}_{1} } & {q_{2} } & {\dot{q}_{2} } & \cdots & {q_{n} } & {\dot{q}_{n} } \\ \end{array} ]^{T} ,$$
(17)

Here, the vector \(\varUpsilon\) represents the modal coordinate vector. The vector \(K(\varUpsilon )\) symbolizes the right-hand side vector comprising all the stiffness coefficients as well as the nonlinear terms that are in Eq. (15). One can note here that vector \(K(\varUpsilon )\) is a nonlinear function in the term modal coordinates \(q_{1 \le i \le n} (t)\). Next, by splitting \(\varUpsilon\) into a static part denoted by \(\varUpsilon_{static}\), representing the equilibrium position due to the DC actuation, and a dynamic part denoted by \(\varUpsilon_{dynamic} (t)\) representing the perturbed oscillations around the equilibrium position, the vector \(\varUpsilon\) can be re-written as:

$$\varUpsilon = \varUpsilon_{static} + \varUpsilon_{dynamic} (t),$$
(18)

Then, substituting Eq. (18) into Eq. (17), using a Taylor series expansion for small variation of \(\varUpsilon_{dynamic} (t)\), neglecting the higher-order terms (\({\text{h}} . {\text{o}} . {\text{t}}\)), and knowing that \(K(\varUpsilon_{static} ) = 0,\) we are left with the below Taylor’s series simplified expression:

$$\dot{\varUpsilon }_{dynamic} \approx {\mathbf{J}}(\varUpsilon_{static} )\varUpsilon_{dynamic} + \underbrace {{{\text{h}} . {\text{o}} . {\text{t}}}}_{ \to 0} ,$$
(19)

where \({\mathbf{J}}(\varUpsilon_{static} )\) is the Jacobian matrix estimated at the CNT perturbed points (Ouakad and Younis 2011a; Nayfeh and Balachandran 1995). If one considers n-modes shape in the Galerkin decomposition ROM process, the Jacobian matrix will be an n × n matrix and can then be written as follows:

$${\mathbf{J}}(x_{1} ,x_{2} , \cdots ,x_{n} ) = \left[ {\begin{array}{*{20}c} {\frac{{\partial f_{1} (x_{1} ,x_{2} , \cdots ,x_{n} )}}{{\partial x_{1} }}} & \cdots & {\frac{{\partial f_{1} (x_{1} ,x_{2} , \cdots ,x_{n} )}}{{\partial x_{n} }}} \\ \vdots & \ddots & \vdots \\ {\frac{{\partial f_{n} (x_{1} ,x_{2} , \cdots ,x_{n} )}}{{\partial x_{1} }}} & \cdots & {\frac{{\partial f_{n} (x_{1} ,x_{2} , \cdots ,x_{n} )}}{{\partial x_{n} }}} \\ \end{array} } \right],$$
(20)

where f n are the state space form of the EOM, correspondingly for all the assumed nth mode-shapes. Then, to estimate the natural frequencies of the CNT for any presumed DC electrostatic voltage, one should substitute the fixed stable static solution \(\varUpsilon_{static}\) into the matrix J and then calculate its corresponding eigenvalues, using the below equation:

$$\left| {{\mathbf{J}}(\varUpsilon_{static} ) - \lambda I} \right| = 0,$$
(21)

where I is the identity matrix. Finally, the natural frequencies of the system can be obtained by taking the square roots of the Jacobian matrix eigenvalues.

5.2 Thermal effect

In order to examine the thermal effect on the natural frequencies dispersion of the doubly clamped straight carbon nanotube, we adopted the following steps: we first examine the variation of the CNT fundamental natural frequency with the DC voltage and for various thermal loads (low and high regimes). Next, we propose to study the effect of the thermal load on the natural frequencies with zero gate voltage in order to predict any possibilities of modes crossing and modes veering in the case of higher temperature regimes. In the last part of this sub-section, the dispersion curves for the straight CNT first five natural frequencies are computed through varying the DC actuating amplitude in the low gate voltage regime. It is worth noting here that we propose to analyze all of the above case studies while assuming the strain gradient theory where all size scale dependent parameters are equal to \(l_{0} = l_{1} = l_{2} = l = 1\) nm. In addition, the geometric mid-plane stretching nonlinearity, post-buckling deflection, the actuating force nonlinearity, and the temperature changing are all taken into account in the below simulations.

In the below simulations, we first consider the linearized EVP with only considering one mode in the ROM and with including the thermal term. We examine the both cases of low and high temperature regimes then we display both outcomes using two separates figures: Fig. 5a, b respectively. In these figures, we display the variation of the first fundamental natural frequency of the CNT with the DC load and while assuming a gap width of d = 300 nm for the CNT of case 3 in Table 1.

Fig. 5
figure 5

Variation of the first (fundamental) natural frequency of the CNT for the case number 3 of Table 1 while assuming a low temperature regime, and b high temperature regime

Full size image

For the fundamental frequency dispersion in the low temperature regime, Fig. 5a, the results indicate a significant deviation especially around the low gate voltage domain. This is attributed to the dominance of the mid-plane stretching stiffening effect mainly governed by the low temperature regime in the low DC gate voltage regime. In fact, one can realize that considering low actuating voltage regime (DC voltage below 3 V), a low temperature tends to increase the natural frequency of the CNT. However this phenomenon is in contrast changing when the DC load increases beyond 3 V until reaching the pull-in instability, where the frequency drops to zero. This can be attributed to the decrease of the effective CNT length due to a tensile like thermal load. Therefore, the effective mid-plane stretching effect, which principally stiffen the CNT, is then decreased by a tensile load in this low thermal regime. In addition, we can understand from the same plot that for high gate DC voltages, the fundamental frequency values are slightly lower as compared to the room temperature case where \(\Delta T \approx 0\). This is mainly due to the dominance of the electrostatic force nonlinearity, at high DC load amplitudes, which is essentially of quadratic (softening) type.

Next, Fig. 5b depicts the same dispersion of the CNT first natural frequency with the DC load but while assuming high temperature regime. The obtained results are significantly different as compared to the low temperature results of Fig. 4a. We can visibly comprehend that, in this case, the fundamental frequency increases with the increase of temperature changing. This is recognized as the post buckling structural behavior which contributes more than the temperature changing effect which tends to increase the frequency of the CNT for all assumed values of the DC actuating load. As was previously discussed in Sect. 4, doubly-clamped CNT subjected to high thermal loading tends to expand the length of the CNT. This expansion contributes mostly to curve the straight CNT due to the both clamping boundary conditions right after exhibiting the critical buckling temperature instability. This structural behavior tends to let the cubic geometric nonlinearity to be more dominant, therefore increasing the natural frequency of the CNT based nanobeam. It also can be inferred from Fig. 5b that the natural frequencies of CNT when assuming high temperature changing drop earlier to zero (near pull-in) than the case of the room temperature where \(\Delta T \approx 0\).

Afterward, we propose to assess the high temperature changing effect of the doubly clamped CNT-based nanobeam while assuming zero gate voltage. We assume here zero actuation load in order to investigate the CNT mid-plane stretching effect which will be here mainly ruled by any assumed thermal load. As was formerly argued in Sect. 4, doubly clamped CNT based nanobeam behaves like slacked CNT when operated above a critical buckling temperature threshold. To this end, we propose to investigate any possibility of crossing and veering between the first few lower CNT natural frequencies. First, to more understand the above pronounced results of Fig. 5b, we consider the first five modes of vibration in the linearized eigenvalue problem while varying the higher temperature regime from 0 to 500 K and while assuming the SGT size scale dependent parameters all equal to l = 1 nm. The results are displayed in Fig. 6. It can be observed from the figure that the first natural frequency is increasing nonlinearly with the thermal effect to finally saturate for \(\Delta T \succ 50\) K. It also can be observed that the third and fifth frequencies are also sensitive to the temperature variations. They both increase nonlinearly as we increase the temperature variations. The second and fourth frequencies are completely unaffected by the temperature changes, as indicated with the first and second straight dashed lines.

Fig. 6
figure 6

Variation of the first five normalized in-plane natural frequencies of the CNT of case number 3 of Table 1 with the higher temperature changes, for zero DC load, and while assuming a SGT parameters of \(l_{0} = l_{1} = l_{2} = l = 1\) nm

Full size image

Two mode crossings are observed here (labeled by red arrows in Fig. 6): the first is occurring for a temperature changes around 25 K between the first mode and the second one, the second is happening at around 100 K temperature changes involving the third mode and the fourth mode. Hence, the results of Fig. 6 show that when the temperature variations is varied from zero to a value greater that 100 K, two modes crossing will possibly occur. These results also indicate that the mid-plane stretching effect due to the buckling deflection is more prevailing in the post-buckling regime.

Subsequently, to more clarify the above discussed mode veering and mode crossing issues when assuming high temperature changes with zero gate voltage, we propose next to investigate these mode interactions options with including the DC electrostatic actuating load. To this end, we consider three different temperature cases: \(\Delta T_{high} = 0\) K (room temperature condition), \(\Delta T_{high} = 200\) K and \(\Delta T_{high} = 400\) K, Fig. 7a, b, c, respectively. Figure 7a shows the variation of normalized first five natural frequencies with the applied DC voltage for the room temperature condition. We can observe from the figure that for the case of straight CNT in a room temperature condition, the frequencies dispersion is showing not a single potential of modes crossing or modes veering. These results are in perfect agreement with the outcomes of Ouakad and Younis (2011a) which reported on the straight CNTs natural frequencies dispersion without considering any thermal effect.

Fig. 7
figure 7

Variation of the first five normalized in-plane natural frequencies of the straight CNT of case number 3 of Table 1 with the DC load, while assuming a SGT parameters of \(l = 1\) nm, and for a \(\Delta T_{high} = 0\) K (room temperature condition), b \(\Delta T_{high} = 200\) K, and c \(\Delta T_{high} = 400\) K

Full size image

Increasing further the thermal amplitude to higher values as compared to the room temperature situation, Fig. 7b, c display the straight CNT normalized first five in-plane natural frequencies dispersion with the applied DC load and for two different temperature values of \(\Delta T_{high} = 200\) K and \(\Delta T_{high} = 400\) K, respectively. We can initially observe from Fig. 7b, that assuming temperature ΔT high = 200 K, one modes veering (indicated in the figure by a red dashed square) and two modes crossing (designated by two red arrows) were introduced at low gate voltages, i.e. 0 V < V DC < 10 V. A veering between the first mode and the third one is occurring around a gate voltage of 2.5 V, however this was not predicted in the case of room temperature condition, Fig. 7a. In addition, when we increased the temperature to \(\Delta T_{high} = 400\) K, Fig. 7c, we observed that the extra thermal load resulted into an extra thermal expansion and therefore an addition deflection in new post-buckling state of the CNT. We can also see that the additional thermal loads resulted into altering the modes veering and modes crossing locations.

It is clearly shown in Fig. 7c that the first-third modes veering location is shifted to a higher gate voltage around 4 V, as compared to 2.5 V in the case of \(\Delta T_{high} = 200\) K. The modes crossing positions are also moved to higher gate voltages as we increased of the higher temperature regime. Moreover, one can observe that the third and fifth natural frequencies are slightly decreasing in low gate voltage regime to then increase with the increase of the DC load. This indicate that the CNT is of softening effect governed by its initial post-buckling deflection state in the low gate voltage regime, to the become less dominant as compared to geometric cubic nonlinearity with tends to stiffen the nano-structure when increasing the gate voltage amplitude.

Lastly, we consider next studying the low temperature changing effect with assuming two different cases, \(\Delta T_{low} = - 200\) K, Fig. 8a, and \(\Delta T_{low} = - 400\) K, Fig. 8b, for the sake of verifying the integrity of the static buckling analysis of Sect. 4, where we indicated that the CNT length reduction effect is dominant in the low gate voltage regime. We can clearly see from both figures the dominance of the stiffening effect (increase of all natural frequencies) in the CNT structural behavior for all considered DC amplitudes and in the low temperature conditions. It can similarly be observed that there are no possibilities of modes veering and modes crossing occurrences. This is mainly attributed to the reason that assuming low thermal loads would always result into straight CNT based nanobeam configuration. In addition, the natural frequencies dispersion in this case of CNT operating under very low ambient temperature values indicate exactly the same trend as for the case of straight CNT with ambient temperature condition. The straight CNT with low thermal values will remain straight due to the reduction in its effective length. Indeed, decreasing the temperature will increase the natural frequency in the low gate voltage, therefore the hardening mid-plane stretching effect convert to be more dominant than the softening electrostatic actuation term in these loading conditions.

Fig. 8
figure 8

Variation of the first five normalized in-plane natural frequencies of the straight CNT of case number 1 of Table 1 with the DC load, while assuming a SGT parameters of \(l = 1\) nm, and for a \(\Delta T_{low} = - 200\) K, and b \(\Delta T_{low} = - 400\) K

Full size image

6 Forced vibration analysis

In this section, we plan to investigate the dynamic response of the doubly clamped straight CNT-based nano-resonator under DC static and AC harmonic loads. A one mode in the ROM, Eq. (11), is used in this regards to investigate the CNT dynamic response near its fundamental mode. The one mode nonlinear differential equation of motion, Eq. (11) is to be numerically integrated in the time domain. Through using a long time integration technique, we consider small gate voltages to investigate the dynamic responses of the CNT in order to ensure converged results without much hysteretic behavior. The effects of the size scale dependent parameters will be then presented and discussed.

6.1 The size scale dependent parameter effects

Next, we use the Galerkin based reduced-order model coupled differential equations developed in Sect. 3 and integrate them with time using a fourth Runge–Kutta method to get the dynamic response of the straight CNT under static DC and harmonic AC harmonic load. Figure 9 shows the dynamic response of case number 1 of Table 1 subjected to a static 2 V DC load superimposed to a dynamic 2 V AC harmonic load with forcing frequency near the CNT-based nanobeam fundamental frequency (\(\varOmega\) ≈ 22). In the same figure, we are assuming a nanoresonator quality factor of Q NR  = 100, and zero initial conditions for the modal coordinates. The damping coefficient in these simulations is related to the quality factor Q NR as follows:

$$\tilde{C} = \rho A\omega_{n} /Q_{NR} ,\quad C = \tilde{C}\frac{{L^{4} }}{EIT},\quad \varOmega = \frac{{\tilde{\varOmega }}}{{\omega_{n} }}.$$
(22)
Fig. 9
figure 9

Time history curve of the CNT of case number 1 of Table 1 at Ω ≈ 22 and for \(l = 1\) nm, V DC  = V AC  = 2 V, and a quality factor of Q NR  = 100

Full size image

One can observe that the CNT time history dynamic response at its mid-point is reaching the steady-state response for values of normalized time greater than 50.

Then, we develop an algorithm to compute the frequency response curves displaying the CNT based nanobeam converged dynamical solutions while varying the AC harmonic input excitation frequency denoted by \(\varOmega\). The values of the normalizing frequency \(\omega_{n}\) are obtained from the results of the linear eigenvalue problem which mainly depend on the value of static DC load. Figure 10 shows the variation of the CNT of case 1 of Table 1 mid-point maximum dynamic values for various AC load frequency ranging from 20 to 30, and for various size scale dependent parameters. The figure demonstrates that in all cases, the CNT dynamic response exhibit a hardening behavior where the resonant frequency is greater that the natural frequency of the excited structure. Moreover, as the strain gradient parameters tend to increase, the resonance frequency of the CNT increase as well. In fact, these results infer a consistent consequence of the previously discussed conclusion of the linearized eigenvalue problem that the strain gradient theory is by all means altering the rigidity of the CNT-based nanobeam by making it stiffer.

Fig. 10
figure 10

Frequency-response curve of the CNT of case number 1 of Table 1 for various strain gradient parameters values, V DC  = V AC  = 2 V, and a quality factor of Q NR  = 100

Full size image

As previously identified from the linearized eigenvalue problem simulations, the strain gradient effect is more prominent for CNT with smaller radii, consequently we propose next to simulate the CNT dynamic responses of the case 2 and 3 of Table 1, Figs. 11 and 12 respectively. Both figures are illustrating similar frequency response curves shapes all demonstrating hardening behaviors with increasing resonance frequencies. Indeed, through comparing all reproduced frequency response curves, Figs. 10, 11 and 12, we can deduce that the discrepancies between the results when assuming classical continuum mechanics as compared to those obtained using the strain gradient theory are becoming higher when the CNT radius is decreased. Moreover, the resonance frequency shift is more significant as the CNT radii are reduced to smaller values. It can be concluded that the strain gradient effect is definitely more evident when the geometrical dimensions of the CNT are closer to the strain gradient parameters. These results again show the capability of the strain gradient theory to capture the size scale dependent effect especially while considering very small CNT structural geometry. Finally, it can be comprehended from Fig. 12 that the strain gradient effects are not altering only the location of the resonant frequency, but also change the CNT dynamic response through reducing its maximum dynamic oscillation, therefore stiffening its overall structural behavior. This significant outcome may explain one of the causes behind the discrepancies reported in the literature when comparing the results of classical continuum mechanics to experimental data for CNTs driven harmonically at resonance near their fundamental modes.

Fig. 11
figure 11

Frequency-response curve of the CNT of case number 2 of Table 1 for various strain gradient parameters values, V DC  = V AC  = 0.25 V, and a quality factor of Q NR  = 100

Full size image
Fig. 12
figure 12

Frequency-response curve of the CNT of case 3 of Table 1 for various strain gradient parameters values, V DC  = 10 mV, V AC  = 2 mV, and a quality factor of Q NR  = 100

Full size image

7 Conclusions

In this paper, a doubly-clamped CNT-based nano-resonator model when assuming higher-order strain gradient deformation theory is formulated to investigate the temperature changes and size dependent effects on the CNT nonlinear structural and dynamical behavior. The adopted model is taken into account three size scale dependent parameters as well as the temperature gradient term emerging into a nonlinear partial differential equation governing the dynamical behavior of the nano-resonator. The Galerkin based reduced-order model (ROM) along with Jacobian approaches were both employed to analyze the free vibration problem. Computed natural frequency dispersion curves showed that for cases assuming higher temperature regime are significantly affecting the existence of modes veering and modes crossing. On the other hand, when assuming cases with low temperature regime, the CNT frequency dispersions curved were not showing any single possibility of modes veering and modes crossing. The model also confirmed the stiffening effect behavior while operating the resonator in a low temperature conditions. Succeeding the free-vibration analysis, a forced vibration analysis under low gate actuation was conducted to investigate the size scale dependent effect to the dynamical behavior of the CNT based nano-resonator. Three different CNT geometrical parameters were assumed in order to study the size scale effect. Results showed that the discrepancies between the CNT dynamic responses obtained when using the classical continuum mechanics and those when assuming the strain gradient model are becoming more significant while assuming smaller CNT geometries. The obtained results allow better understanding of the nonlinear behavior of CNT based nanoresonators and can guide NEMS engineers accordingly in the design consideration stages.