1 Introduction

The analysis regarding heat transfer phenomena towards stretched surface captured the attention of numerous investigators and scientists owing to its extensive demands in industrial and engineering processes. These applications includes wire drawing, crystal growing, brisk spray cooling, liquid films in condensation process, broadsheet manufacture, cooling of metallic sheet, construction of sticky tape, continuous modeling of metals, portrayal of plastic films, ice cooler in air-conditioning frameworks, glass blowing, etc. The quality of end product in industry highly depends upon both the stretching and cooling rate. Flow induced by stretching of sheet is initially explored by Crane [1]. Afterwards several attempts have been made on stretched flows and heat transported characteristics. Cortell [2] explored the aspects of viscous dissipation and thermal radiation over a stretched flow. Ibrahim et al. [3] studied MHD stretched flow of nanofluid. An exponentially stretched 3D flow with radiation aspects is examined by Mustafa et al. [4]. Electrical MHD nanoliquid flow with slip effects on a stretching sheet is documented by Hsiao [5]. The simultaneous aspect of melting heat transfer and thermal radiation in stagnation point flow of nanofluid past a stretching cylinder is tackled by Hayat et al. [6]. Non-linear radiative MHD flow of Casson fluid subject to Cattaneo–Chirstov theory is discussed by Ramandevi et al. [7]. Stretched flow of Powell–Eyring nanoliquid with heat and mass flux conditions is addressed by Hayat et al. [8]. On the other side, the convective heat transport has also generated substantial attraction because of its excessive importance in the industrial and environmental technologies comprising gas turbines, nuclear plants, energy storage, rocket propulsion, photovoltaic panels and geothermal reservoirs. Referring to several engineering and industrial processes, the convective conditions are more practical including transpiration cooling, material drying, etc. Due to all these practical demands numerous researchers have inspected and reported convective surface condition via various aspects (see refs. [9,10,11,12,13,14,15]).

The analysis of dynamics of allosterically conducting liquid, i.e. magnetohydrodynamics is standout amongst the most noteworthy region of research since different engineering issues rely on it. Its importance is widely expressed in various aspects like metallurgy and metal working, pumps, droplet filter pumps, boundary layer control, bearings and MHD generators, in nuclear reactors, plasma investigation and geothermal energy extraction and polymer industry, in astrophysics and geophysics. Due to its wide applications many scientists carried out MHD flows in various physical phenomenons. Ellahi et al. [16] presented numerical study for MHD flow and heat transfer with nonlinear slip. Sheikholeslami et al. [17] reported the consequences of MHD flow of Cu–water nanofluid. Zhang et al. [18] examined chemical reaction in magnetohydrodynamic nanofluids flow with variable surface heat flux in porous media. MHD Oldroyed-B nanofluid flow over a radiative surface was explored by Shehzad et al. [19]. Hayat et al. [20] inspected flow of Sisko nanoliquid with magnetic aspects. Recently Hayat et al. [21] investigated MHD flow of Powell–Eyring nanoliquid with variable thickness. Some other studies about MHD flow can be seen via refs. [22,23,24,25,26,27,28,29].

Researchers and engineers are still interested to inspect the fluid flow when chemical reaction is present. Some general applications of chemical reactions including the formation and dispersion of fog, hydrometallurgical industry, ceramics and polymer production, energy supply in a wet cooling tower, water and air pollutions, damage of crops due to freezing, atmospheric flows, electric power generation and forbears insulation. No doubt reactions are of two types namely heterogeneous and homogeneous. Homogeneous reaction is occurring in the fluid while heterogeneous reaction is carried out on some catalyst surface. The influence of homogeneous–heterogeneous reactions in the stagnation-point layer fluid was reported by Chaudhary and Marken [30]. He intended various diffusivities of the reactants and autocatalyst. Bachok et al. [31] explored the homogeneous–heterogeneous effect in stagnation-point stretched flow. Rashidi et al. [32] reported the effect of mixed convection and chemical reactions through horizontal surface. The stretched flow of Maxwell fluid with homogeneous–heterogeneous reactions is examined by Hayat et al. [33]. Khan and Pop [34] put forward such effects on the flow of viscoelastic liquid over a stretching sheet. Hayat et al. [35] investigated the consequences of homogeneous–heterogeneous reactions in Jeffrey fluid.

Very less data are accessible in the literature about the fluid model suggested by Sisko [36]. Some significant attempts about Sisko can be consulted in the Refs. [37,38,39,40,41]. It should be pointed out that earlier investigators have not focused on homogeneous and heterogeneous reactions in flow of Sisko fluid. Thus our basic theme of present attempt is to fill such gaps. Especially the novelty of the current article is through the following aspects. Firstly to consider Sisko fluid model with effects of magnetohydrodynamic. Secondly to utilize convective heat transfer in the flow by stretched surface. Thirdly to carry out analysis in the presence of homogeneous and heterogeneous reactions. Fourth to develop numerical solutions via ND solve Shooting technique. The impact of distinct embedded variables on velocity, temperature and concentration are made and scrutinize graphically. Surface drag coefficients and mass transfer rate at the surface are also studied numerically. Further comparative study is provided which confirms the surety of our present attempt.

2 Formulation

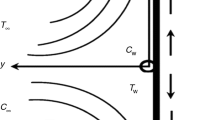
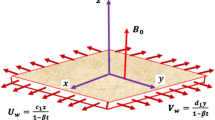
Here we intend to inspect steady 3D incompressible flow of Sisko fluid. Stretched surface at z = 0 is responsible for the fluid flow. The surface stretching velocities along x- and y- directions are denoted by U w  = cx and V w  = dy, respectively (where c and d are positive dimensional constants). Magnetic field of strength B0 is utilized (see Fig. 1). Consequences of induced magnetic and electric fields are neglected. Heat transport characteristics incorporate the convective condition. Let T∞ be ambient fluid temperature and Tf  the hot liquid temperature which heated the bottom surface via convection. We assume a simple model of heterogeneous–homogeneous reaction:

$$A_{1} + 2A_{2} \to 3A_{2} ,{\text{ rate}} = k_{c} a_{1} b_{1}^{2},$$
(1)

where the catalyst surface heterogeneous reaction is

$$A_{1} \to A_{2} ,{\text{ rate}} = k_{s} a_{1} .$$
(2)

Here the chemical species A1 and A2 have concentrations a1 and b1 respectively, while k c and k s are rate constants. Also both these reactions are isothermal. The resulting expressions after utilizing the boundary layer concept are:

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} = 0,$$
(3)
$$\rho \left( {u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} + w\frac{\partial u}{\partial z}} \right) = a\frac{{\partial^{2} u}}{{\partial z^{2} }} - b\frac{\partial }{\partial z}\left( { - \frac{\partial u}{\partial z}} \right)^{n} - \sigma B_{0}^{2} u,$$
(4)
$$\rho \left( {u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} + w\frac{\partial v}{\partial z}} \right) = a\frac{{\partial^{2} v}}{{\partial z^{2} }} + b\frac{\partial }{\partial z}\left( { - \frac{\partial u}{\partial z}} \right)^{n - 1} \frac{\partial v}{\partial z} - \sigma B_{0}^{2} v,$$
(5)
$$u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} +w\frac{\partial T}{\partial z}= \alpha_{m} \frac{{\partial^{2} T}}{{\partial y^{2} }},$$
(6)
$$u\frac{{\partial a_{1} }}{\partial x} + v\frac{{\partial a_{1} }}{\partial y} + w\frac{{\partial a_{1} }}{\partial z} = D_{A} \frac{{\partial^{2} a_{1} }}{{\partial z^{2} }} - k_{c} a_{1} b_{1}^{2} ,$$
(7)
$$u\frac{{\partial b_{1} }}{\partial x} + v\frac{{\partial b_{1} }}{\partial y} + w\frac{{\partial b_{1} }}{\partial z} = D_{B} \frac{{\partial^{2} b_{1} }}{{\partial z^{2} }} + k_{c} a_{1} b_{1}^{2} .$$
(8)
Fig. 1
figure 1

Flow configuration

Full size image

The relevant conditions are

$$\left. {\begin{array}{ll} {u = U_{w} = cx, \, v = V_{w} = dy, \, w = 0, \, - k\tfrac{\partial T}{\partial z} = h_{f} (T_{f} - T),} \\ {D_{A} \tfrac{{\partial a_{1} }}{\partial z} = k_{s} a_{1} , \, D_{B} \tfrac{{\partial b_{1} }}{\partial z} = - k_{s} a_{1} {\text{ at }}z = 0,} \\ \end{array} } \right\}$$
(9)
$$u \to 0, \, v \to 0, \, T \to T_{\infty } , \, a_{1} \to a_{0} \, b_{1} \to 0{\text{ when }}z \to \infty .$$
(10)

Here the respective components of velocity in the (x, y, z) directions are designated by (u, v, w), ρ the density of liquid, D A and D B the respective diffusion species coefficients of A1 and A2 and a0 the positive dimensionless constant, T the surface fluid temperature and \(\alpha_{m} = \tfrac{k}{{\rho c_{p} }}\) the thermal diffusivity. Here a and b denote the material parameters of Sisko materials and n > 0 characterizes the non-Newtonian features of fluid. Further note that for n = 1, a = 0 and b = μ or a = μ and b = 0 the fluid is viscous. For n > 1 the behavior is dilatant (shear thickening) and 0 < n < 1 the situation corresponds to pseudoplastic (shear-thinning). Make use of the following transformations [33, 41]:

$$\left. {\begin{array}{ll} {u = cxf^{\prime}(\xi ), \, v = dg^{\prime}(\xi ), \, w = - c\left( {\tfrac{{c^{n - 2} }}{\rho /b}} \right)^{1/(n + 1)} \left( {\tfrac{2n}{n + 1}f + \tfrac{1 - n}{n + 1}\xi f^{\prime} + g} \right)x^{{\tfrac{n - 1}{n + 1}}} ,} \\ {\theta (\xi ) = \tfrac{{T - T_{\infty } }}{{T_{f} - T_{\infty } }}, \, a_{1} = a_{0} \phi (\xi ), \, b_{1} = a_{0} h(\xi ), \, \xi = z\left( {\tfrac{{c^{2 - n} }}{\rho /b}} \right)^{1/n + 1} x^{{\tfrac{1 - n}{1 + n}}} .} \\ \end{array} } \right\}$$
(11)

Expression (3) is trivially verified and Eqs. (4)–(10) lead to:

$$\beta f^{\prime\prime\prime} +n ( - f^{\prime\prime})^{n - 1} f^{\prime\prime\prime} + \left( {\frac{2n}{n + 1}} \right)ff^{\prime\prime} - (f^{\prime})^{2} + gf^{\prime\prime} - M^{2} f^{\prime} = 0,$$
(12)
$$\beta g^{\prime\prime\prime} + ( - f^{\prime\prime})^{n - 1} g^{\prime\prime\prime} - (n - 1)g^{\prime\prime}f^{\prime\prime\prime}\left( { - f^{\prime\prime}} \right)^{n - 2} + \left( {\frac{2n}{n + 1}} \right)fg^{\prime\prime} - (g^{\prime})^{2} + gg^{\prime\prime} - M^{2} g^{\prime} = 0,$$
(13)
$$\theta^{\prime\prime} + \mathop {\Pr }\limits \left( {\frac{2n}{n + 1}} \right)\theta^{\prime}f+Prg\theta^{\prime} = 0,$$
(14)
$$\frac{1}{Sc}\phi^{\prime\prime} + \left( {\frac{2n}{n + 1}} \right)f\phi^{\prime} + g\phi^{\prime} - k_{1} \phi h^{2} = 0,$$
(15)
$$\frac{{\delta_{1} }}{Sc}h^{\prime\prime} + \left( {\frac{2n}{n + 1}} \right)fh^{\prime} + gh^{\prime} + k_{1} \phi h^{2} = 0,$$
(16)
$$\left. {\begin{array}{ll} {f = 0, \, g = 0, \, f^{\prime} = 1, \, g^{\prime} = \alpha , \, \theta^{\prime} = - \gamma (1 - \theta ), \, \phi^{\prime} = k_{2} \phi , \, \delta_{1} h^{\prime} = - k_{2} \phi {\text{ at }}\xi = 0,} \\ {f^{\prime} \to 0, \, g^{\prime} \to 0, \, \theta \to 0, \, \phi \to 1, \, h \to 0{\text{ when }}\xi \to \infty .} \\ \end{array} } \right\}.$$
(17)

Here β signifies the Sisko fluid material parameter, Re a and Re b show the local Reynolds numbers, M indicates the magnetic parameter, α designates the ratio parameter, k1 signifies the measure of strength of homogeneous reaction, Pr denotes Prandtl number, k2 shows measure of strength of heterogeneous reaction, Sc designates Schmidt number, δ1 represents the diffusion coefficient ratio, γ the Biot number due to temperature and prime indicates derivative via ξ. These dimensionless quantities are expressed as follows:

$$\left. {\begin{array}{c} {\beta = \tfrac{{Re_{b}^{{\tfrac{2}{n + 1}}} }}{{Re_{a} }},\, \, Re_{a} = \tfrac{{\rho xU_{w} }}{a},\, \, Re_{b} = \tfrac{{\rho x^{n} U_{w}^{2 - n} }}{b},\, \, M^2 = \tfrac{{\sigma B_{0}^{2} }}{\rho c},\, \, \alpha = \tfrac{d}{c},} \\ {k_{1} = \tfrac{{k_{c} a_{0}^{2} }}{c},\,k_{2} = \tfrac{{k_{s}cx }}{{D_{A}z }}Re_{b}^{\tfrac{ - 1}{(n + 1)}} ,\, \, \gamma = \tfrac{{h_{f} }}{k}xRe_{b}^{{\tfrac{ - 1}{(n + 1)}}} ,} \\ {\Pr = \tfrac{{Re_{a} Re_{b}^{{\tfrac{ - 2}{n + 1}}} }}{ak/c},\, \, Sc = \frac{D_{A}}{U_{w}x}Re_{b}^{{\tfrac{ 2}{n + 1}}} ,\, \, \delta_{1} = \tfrac{{D_{B} }}{{D_{A} }}.} \\ \end{array} } \right\}\,$$
(18)

Note that for α = 1 and α = 0, the axisymmetric and two-dimensional flows are, respectively, reduced. The similarity solutions are possible only in the case n = 1 (for viscous fluid). In this situation, the parameters β = 0 and γ do not depend upon x, i.e. γ is constant. With these view points, our intention now is to develop local similar solutions since the parameters in present analysis depends on an independent variable x (for details one can see the studies [42,43,44]). Comparable size is presumed for the coefficients of diffusion of chemical species A1 and A2. This fact provides us to establish further supposition that the diffusion coefficients D A and D B are same, i.e. δ1 = 1 and thus [45,46,47] 

$$\phi (\xi ) + h(\xi ) = 1.\,$$

Equations (15) and (16) yield

$$\frac{1}{Sc}\phi^{\prime\prime} + \left( {\frac{2n}{n + 1}} \right)\,f\phi^{\prime} + g\phi^{\prime} - k_{1} \phi (1 - \phi )^{2} = 0,\,$$
(19)

with the relevant conditions

$$\phi^{\prime}(0) = k_{2} \phi (0), \, \phi (\infty ) \to 1.$$
(20)

Surface drag coefficients along x- and y-directions are

$$\left. {\begin{array}{ll} {Re_{b}^{{\tfrac{1}{(n + 1)}}} C_{fx} = \beta f^{\prime\prime}(0) + (f^{\prime\prime}(0))^{n} ,} \\ {Re_{b}^{{\tfrac{1}{(n + 1)}}} C_{fy} = \tfrac{{V_{w} }}{{U_{w} }}(\beta g^{\prime\prime}(0)f(0) + ( - f^{\prime\prime}(0))^{n - 1} g^{\prime\prime}(0)).} \\ \end{array} } \right\}$$
(21)

Expressions for local Nusselt number can be written as:

$$Re_{b}^{ - 1/(n + 1)} Nu_{x} = - \theta^{\prime}(0),$$
(22)

where \(Re_{a} = \tfrac{{\rho_{f} xU_{w} }}{a}\) and \(Re_{b} = \tfrac{{\rho_{f} x^{n} U_{w}^{2 - n} }}{b}\) elucidate the local Reynolds numbers.

3 Method for solution

The considered problem is modeled through boundary layer assumptions. To compute the numerical solutions of Eqs. (12)–(14) and (20) with imposed boundary conditions stated in Eqs. (17) and (21), we utilized the ND solve Shooting technique via Mathematica. We also numerically executed the characteristics of surface drag coefficients and local Nusselt number for various emerging variables.

4 Result and discussion

Feature of numerous pertinent variables like magnetic parameter (M), Prandtl number (Pr), Biot number due to temperature (γ), ratio parameter (α), strength of homogeneous variable (k1), Schmidt number (Sc), power law index (n) and strength of heterogeneous variable (k2) on temperature θ(ξ) and concentration ϕ(ξ) are declared graphically in this portion. For such analysis Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 and 13 have been interpreted. Temperature profile against magnetic parameter M is demonstrated in Fig. 2. Here temperature field θ(ξ) is upgraded for higher M. This rise in temperature is due to heat generated by resistive force caused by magnetic field. Figure 3 is displayed to confess the significance of α on temperature θ(ξ). It is observed that liquid temperature decays with an increment in ratio parameter. Variation of Biot number γ on temperature distribution is depicted in Fig. 4. It is revealed that an enhancement in γ increases the temperature field. When γ is enhanced the convection resistance of side hot plate decreases and ultimately it rises θ(ξ). Feature of Pr on temperature field is presented in Fig. 5. Here we found that fluid temperature decreases with the increase in Pr. Since thermal diffusivity decreases for higher Pr so temperature diminishes. Characteristics of material parameter β on θ(ξ) is shown in Fig. 6. It is found that temperature profile diminishes via β. Also it is interesting to mention that (β = 0 and n = 1) correspond to Newtonian fluid while (β = 0 and n ≠ 1) shows the power-law fluid situation. In physical sense Sisko material parameter is ratio of higher shear rate viscosity to consistency index. Enhancement in Sisko fluid parameter corresponds to low consistency index (viscosity of fluid) at high shear rate and thus temperature is decreased. An increment in n decays the temperature field θ(ξ) (see Fig. 7). Higher viscosity is associated with larger values of n which implies that temperature field is reduced. Further it is concluded that influence of β on θ(ξ) dominates for shear thinning when compared with other value of n. Impact of Sc on concentration profile is declared in Fig. 8. As Sc is equal to viscous diffusion divided by molecular diffusion rate, an increment in Sc diminishes the molecular diffusion rate and consequently there is an increase in fluid concentration. The effect of homogeneous reaction parameter k1 on concentration field ϕ(ξ) is drawn in Fig. 9. In fact more reactants are consumed when k1 is enhanced. This leads to decrease in the concentration distribution ϕ(ξ). Similar phenomenon is observed for k2 (see Fig. 10). Figure 11 illustrates variation of β on concentration distribution. Here higher concentration profile is associated with varying β. In fact increment in Sisko material parameter leads to higher ratio of higher shear rate viscosity. It raises the concentration and its corresponding boundary layer thickness. The impact of α on concentration field is portrayed in Fig. 12. It is depicted that ϕ(ξ) has increasing behavior via α. Figure 13 elucidates feature of n on ϕ(ξ). Clearly ϕ(ξ) is increasing function of n. When we increase the values of n, fluid viscosity increases which consequently raise the concentration layer thickness. The numerical data of surface drag coefficients associated with various sundry variables M, n, α, and β (when Sc = 1.0, k1 = 0.5 = k2 and Pr = 4.0) are declared in Table 1. It is reported that surface drag coefficients in both x- and y-directions are enhanced via M, n, α and β. Comparison of some numerical values of skin frictions in present analysis with that of Hayat et al. [35] are captured via Table 2. All the outcomes are found in good agreement. Table 3 is constructed to analyze the variation of surface heat transfer rate (Re −1/(n+1) b Nu x ) for numerous values of involved variables M, γ, α, β, Sc and Pr when n = 1.0 and k1 = 0.5 = k2. It is inspected that rising values of γ, α, β and Pr result local Nusselt number enhancement. However, reverse behavior is analyzed for larger M.

Fig. 2
figure 2

Variation of θ(ξ) via M

Full size image
Fig. 3
figure 3

Variation of θ(ξ) via α

Full size image
Fig. 4
figure 4

Variation of θ(ξ) via γ

Full size image
Fig. 5
figure 5

Variation of θ(ξ) via Pr

Full size image
Fig. 6
figure 6

Variation of θ(ξ) via β

Full size image
Fig. 7
figure 7

Variation of θ(ξ) via n

Full size image
Fig. 8
figure 8

Variation of ϕ(ξ) via Sc

Full size image
Fig. 9
figure 9

Variation  of ϕ(ξ) via k1

Full size image
Fig. 10
figure 10

Variation of ϕ(ξ) via k2

Full size image
Fig. 11
figure 11

Variation of ϕ(ξ) via β

Full size image
Fig. 12
figure 12

Variation of ϕ(ξ) via α

Full size image
Fig. 13
figure 13

Variation of ϕ(ξ) via n

Full size image
Table 1 Numerical data of surface drag coefficients via various pertinent variables
Full size table
Table 2 Comparison of skin friction coefficients for different values of α when A = 0.0 = M and n = 1.0
Full size table
Table 3 Numerical data of local Nusselt number − θ′(0) via M, γ, α, β, Pr and Sc when keeping k1, k2 and n fixed
Full size table

5 Concluding remarks

Particular points of present study are:

  • An increment in M demonstrates decay in fluid temperature.

  • Temperature θ(ξ) is enhanced via γ and α.

  • Homogeneous and heterogeneous reactions have similar effect on concentration field.

  • Increasing values of n show opposite behavior for the temperature and concentration fields.

  • Surface drag coefficients is enhanced via M and α.

  • Magnitude of surface heat transfer rate is more for larger values of α, β, γ and Pr.