1 Introduction

Microlectromechanical systems (MEMS) devices have been investigated thoroughly in the literature for their potential to build more effective and robust sensors and actuators (Burg et al. 2006; Kim et al. 2005; Hsu et al. 2001; Nathanson and Wickstrom 1965; Nathanson et al. 1967). Examples of these include mass, acceleration, and temperature sensors (Burg et al. 2006; Kim et al. 2005; Hsu et al. 2001). MEMS devices have several advantages that are related to their manufacturing technology allowing them to be compatible with the complementary metal oxide semiconductor (CMOS) processes. This resulted into lower cost, low power consumption, and an increased reliability and manufacturability. Papers dating back to the 60s by Nathanson et al. (1967) and Nathanson and Wickstrom (1965) have described the utilization of microbeams as MEMS resonators.

Bistable MEMS devices, such as initially curved microbeams, have been under increasing interest in the research community in recent years. Curved beams refer here to beams that are fabricated intentionally to be curved (arches) or made curved by buckling straight beams through compressive axial loads (buckled beams). Many groups (Saif 2000; Masters and Howell 2003; Receveur et al. 2005; Charlot et al. 2008; Sulfridge et al. 2004; Vangbo 1998; Qui et al. 2004; Han et al. 2002; Seunghoon and Dooyoung 2008; Ko et al. 2006; Michael and Kwok 2006; Qui et al. 2005; Casals-Terré and Shkel 2005; Zhang et al. 2007; Krylov et al. 2008; Das and Batra 2009) studied the bi-stability behavior of initially curved microbeams, which were found to be suitable for applications such as micro-shutter positioning, micro-valves, and electrical micro-relays. These beams have been proposed also as switches and actuators based on their snap-through motion. Most of the MEMS literature has been focused on utilizing snap-through as a static phenomenon due to the actuation of static forces. Those forces can be mechanical (Qui et al. 2004), magnetic (Han et al. 2002; Seunghoon and Dooyoung 2008; Ko et al. 2006), thermal (Michael and Kwok 2006; Qui et al. 2005), and electrostatic (Casals-Terré and Shkel 2005; Zhang et al. 2007; Krylov et al. 2008; Das and Batra 2009).

When actuating a curved microbeam by parallel-plates electrostatic technique, the stability behavior of the arch becomes more interesting. Studies of electrostatically-actuated curved microbeams have shown that they may exhibit snap-through buckling or pull-in instability as well as bistable behavior depending on the interaction between mechanical and electrostatic nonlinearities (Casals-Terré and Shkel 2005; Zhang et al. 2007; Krylov et al. 2008; Das and Batra 2009). Casals-Terré and Shkel (2005) studied theoretically and experimentally the possibility of triggering the snap-through motion of a bi-stable electrically-actuated beam driven dynamically by means of mechanical resonance. Zhang et al. (2007) and Krylov et al. (2008) conducted theoretical and experimental investigations of initially curved clamped–clamped microbeams actuated by DC loads. Their simulations were based on the Galerkin method and they have shown good agreement among their theoretical and experimental results. Das and Batra (2009) conducted a transient analysis of curved microbeams using coupled finite-element and boundary-element methods. They have shown the softening effect of the MEMS arch may be dominant before it experiences its snap-through motion.

To solve the nonlinear differential equation governing the structural behavior of MEMS arches, various methods can be assumed such as Finite-Element Method (Hung and Senturia 1999), Finite-Difference Method (Najar et al. 2006), Shooting Method (Abdel-Rahman et al. 2002; Ouakad and Younis 2009), Differential-Quadrature Method (Najar et al. 2006)…, etc., which are considered to be computationally expensive and in some cases unstable since some rely on initial guesses. Another powerful technique is the so-called Galerkin expansion discretization which is mainly used to derive Reduced-Order Models (ROM) from distributed (continuous) systems. This method is a well-used technique in the literature of MEMS devices (Younis 2011). The main problem with this approach is that the distributed electrostatic force comes in an integral form in the resulting ROM equations, and consequently this collocated arrangement (integral with a nonlinear denominator function of the ROM components) is not easy to deal analytically due to nonlinearities arising from its denominator. As an attempt to overcome this challenge, some groups (Zand and Ahmadian 2009; Chao et al. 2008) used Taylor-series expansion procedure, which brings the nonlinearity to the numerator of the electrostatic force and hence simplifies the calculation of nonlinear ROM integrals. However, due to neglected higher-order terms in the Taylor-series expansion, accuracy of this method is still questionable as the system approaches some of its structural instability such as pull-in (Younis et al. 2003). Therefore, without retaining sufficient number of terms in the Taylor-series expansion, this approach may give erroneous results.

The other suggested method for dealing with the nonlinear Galerkin integrals is to multiply the whole equation of motion by the nonlinear denominator of the electrostatic force before performing Galerkin’s expansion technique (Younis et al. 2003). This approach prevented initiation of the complicated nonlinear integrals and therefore made the process of reduced-order modeling simple. Nevertheless, this method resulted in non-diagonal mass and stiffness matrices in the discretized ROM equations, and hence increased exponentially the computational costs (Younis 2011). In some of our previous work (Ouakad and Younis 2014; Ouakad 2013, 2014), we proposed an alternative approach to deal with the complicated integral terms due to the nonlinear forces. We suggested evaluating the spatial integrals containing the mode shapes numerically simultaneously while solving the modal-amplitude equations with respect to time in the Galerkin Expansion. Efficiency of this approach for higher mode shapes was investigated and results showed excellent agreement with other numerical methods.

Electric fringing-fields have been previously modeled and many groups (Zand and Ahmadian 2009; Chao et al. 2008; Batra et al. 2006a, b, 2008; Ramezani et al. 2007) have demonstrated that this component is an important and effective nonlinearity in investigating electrostatically-actuated MEMS devices. Two models for the electric fringing-fields effects, namely the Palmer’s and the Mejis-Fokkema models have been suggested and investigated in these works: Das and Batra (Batra et al. 2008) have considered this effect in their numerical investigations of bistable arch-shaped MEMS, Krylov et al. (2011) considered this effect as a driving actuation for a specific initially curved microbeam. In one of our previous numerical investigation of MEMS arches (Ouakad and Younis 2010), we assumed the Mejis-Fokkema model to account for the electric fringing-fields effects but we are not able to prove the significance of these effects on the structural behavior of MEMS arches. Hence, more detailed analysis seems to be essential.

The above few cited investigations reported the derivation of the governing equations of motion of MEMS arches, and then presented some diagrams to investigate their structural behavior while looking at the effects of their various geometrical properties. In this paper, effect of the electric fringing-fields on the structural behavior of a clamped–clamped initially curved shallow microbeam is investigated. Contributions of this work are the following: First, a nonlinear structural model for a MEMS arch while including the electric fringing-fields effects is derived. Second, a Galerkin based numerical scheme is implemented to handle the derived highly nonlinear beam model in order to calculate numerically the variation of the MEMS arch deflection and its fundamental natural frequency with the applied electric force. Third, simulations results demonstrating the influence of considering the effect of the electric fringing-fields are discussed.

In the coming sections, the governing equations of the proposed actuator are first presented. Then, description of the reduced-order model is presented. The static and eigenvalue problem of the electrostatic actuator under a DC load and with considering the electric fringing-fields effect are solved and discussed. Finally, the main results of this theoretical investigation are summarized in the conclusion section.

2 Problem formulation

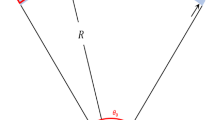
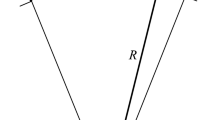
In this section, we present and describe the problem governing the in-plane structural behavior of an electrostatically actuated shallow arch. Hereafter, (ˆ) denotes dimensional quantities. We consider a flexible doubly-clamped prismatic microbeam, Fig. 1a, initial shape \(\hat{w}_{0} (\hat{x}) = b_{o} [1 - cos(2\pi \hat{x})]/2\), where \(b_{o}\) is the initial rise, actuated by an electrode underneath it with a gap width \(\hat{d}\) through a DC electrostatic load, Fig. 1b. Its length is \(\hat{L}\), cross-section area is \(\hat{A} = \hat{b}\hat{h}\), second moment area is \(\hat{I} = I_{{\hat{y}\hat{y}}} = {{\hat{b}\hat{h}^{3} }/{12}}\), where \(\hat{b}\) and \(\hat{h}\) are the width and the thickness of the beam, respectively. The beam is assumed to be made of homogeneous isotopic elastic material with mass density \(\hat{\rho }\), Young’s modulus \(\hat{E}\) and Poisson’s ratio \(\hat{\nu }\). Since the width of microbeam is somehow assumed to be larger than its thickness, we assume an effective modulus of elasticity \(\hat{E^{\prime}} = \hat{E}/2(1 - \hat{\nu }^{2} )\).

Fig. 1
figure 1

a 3D schematic and, b in-plane view of the electrostatically-actuated clamped-clamped MEMS arch

Full size image

In this investigation, we assume a shallow arch, in which \(\hat{w}^{\prime}_{0} < < 1\), where the “\('\)” denotes the derivative with respect to x. Hence, when actuated by electrostatic forces, the parallel-plates assumption can be considered valid. In another word, the axial component of the electrostatic force, due to the upper deformed electrode (the arch), is assumed negligible. This assumption however may not be valid for deep arches. The shallow arched microbeam is free to deflect in the \((\hat{x},\hat{z})\) plane, while its clamped ends are constrained in both lateral \(\hat{z}\) and axial \(\hat{x}\) directions by unmovable anchors. The beam is actuated by an electrostatic force assumed to have only a \(\hat{z}\)-component by a grounded electrode located underneath the beam and with an initial gap distance d in the \(\hat{z}\) direction, Fig. 1b. Therefore, assuming an Euler–Bernoulli beam model, the nonlinear equation of motion governing the transverse deflection \(\hat{w}\left( {\hat{x},\hat{t}} \right)\) of the arch of width \(\hat{b}\), thickness \(\hat{h}\), and length \(\hat{L}\) is expressed as (Nayfeh 2000)

$$\hat{E}^{'} \hat{I}\frac{{\partial^{4} \hat{w}}}{{\partial \hat{x}^{4} }} + \hat{\rho }\hat{A}\frac{{\partial^{2} \hat{w}}}{{\partial \hat{t}^{2} }} + \tilde{c}\frac{{\partial \hat{w}}}{{\partial \hat{t}}} = \hat{F}_{elect} \left( {\hat{w},V_{DC} } \right) + \frac{{\hat{E}^{'} \hat{A}}}{{2\hat{L}}}\left[ {\frac{{\partial^{2} \hat{w}}}{{\partial \hat{x}^{2} }} - \frac{{\partial^{2} \hat{w}_{0} }}{{\partial \hat{x}^{2} }}} \right]\left[ {\int\limits_{0}^{{\hat{L}}} {\left( {\frac{{\partial \hat{w}}}{{\partial \hat{x}}}} \right)^{2} - 2\left( {\frac{{\partial \hat{w}}}{{\partial \hat{x}}}\frac{{\partial \hat{w}_{0} }}{{\partial \hat{x}}}} \right)d\hat{x}} } \right],$$
(1)

where the function \(\hat{F}_{elect} \left( {\hat{w},V_{DC} } \right)\) represents the distributed electrostatic force per unit length arising between the two parallel electrodes, the curved microbeam and its lower stationary actuating electrode, respectively. Neglecting the electric fringing-fields effect, the electrostatic force per unit length of the beam can be approximated as (Batra et al. 2006a, b)

$$\hat{F}_{elect\_PP} \left( {\hat{w},V_{DC} } \right) = \frac{{\varepsilon_{0} \hat{b}V_{DC}^{2} }}{{2\left( {\hat{W}(\hat{x},\hat{t})} \right)^{2} }},$$
(2)

where \(\hat{W}(\hat{x},\hat{t}) = \hat{d} - \hat{w}_{0} (\hat{x}) - \hat{w}(\hat{x},\hat{t})\), and where \(\varepsilon_{0} = 8.854 \times 10^{ - 12} {\text{ F}} . {\text{m}}^{ - 1} ,\) is the permittivity of free space and \(V_{\text{DC}}\) is the DC voltage applied between the moving arched electrode and the stationary electrode which are initially separated by a gap distance of \(\hat{d} - \hat{w}_{0} (\hat{x})\). Note that the subscript “\(elect\_PP\)” in Eq. (2) denotes the parallel-plates electric force without considering the fringing-fields effects.

To complement the electric fringing-fields effects, a correction is to be suggested to the electrostatic equation, Eq. (2). Two famous models for this correction are extensively used in the literature: the Palmer and the Mejis-Fokkema models. These models adjust the electrostatic force for a clamped–clamped microbeam, respectively, as follows (Batra et al. 2006a):

$$\hat{F}_{elect\_P} \left( {\hat{w},V_{DC} } \right) = \frac{{\varepsilon_{0} \hat{b}V_{DC}^{2} }}{{2\left( {\hat{W}(\hat{x},\hat{t})} \right)^{2} }}\left( {1 + 0.65\frac{{\hat{W}(\hat{x},\hat{t})}}{{\hat{b}}}} \right),$$
(3)
$$\hat{F}_{elect\_MF} \left( {\hat{w},V_{DC} } \right) = \frac{{\varepsilon_{0} \hat{b}V_{DC}^{2} }}{{2\left( {\hat{W}(\hat{x},\hat{t})} \right)^{2} }}\times\left( {1 + 0.265\left( {\frac{{\hat{W}(\hat{x},\hat{t})}}{{\hat{b}}}} \right)^{{\frac{3}{4}}} + 0.53\frac{{\hat{h}}}{{\hat{b}}}\left( {\frac{{\hat{W}(\hat{x},\hat{t})}}{{\hat{b}}}} \right)^{{\frac{1}{2}}} } \right),$$
(4)

The subscripts “\(elect\_P\)” and “\(elect\_MF\)” in Eqs. (3) and (4) denote the modified electrostatic force while considering the fringing-fields effects through the Palmer model and the Mejis-Fokkema model, respectively.The boundary conditions of the MEMS arch are

$$\hat{w}\left( {0,\hat{t}} \right) = 0, \, \frac{{\partial \hat{w}}}{{\partial \hat{x}}}\left( {0,\hat{t}} \right) = 0, \, \hat{w}\left( {L,\hat{t}} \right) = 0, \, \frac{{\partial \hat{w}}}{{\partial \hat{x}}}\left( {L,\hat{t}} \right) = 0$$
(5)

For convenience, we introduce the following nondimensional variables:

$$w = \frac{{\hat{w}}}{{\hat{d}}} , { }w_{0} = \frac{{\hat{w}_{0} }}{{\hat{d}}} , { }x = \frac{{\hat{x}}}{{\hat{L}}} , { }t = \frac{{\hat{t}}}{{\hat{T}}},$$
(6)

where \(\hat{T}\) is a time constant defined by \(\hat{T} = \sqrt {{{\hat{\rho }\hat{A}\hat{L}^{4} } \mathord{\left/ {\vphantom {{\hat{\rho }\hat{A}\hat{L}^{4} } {\hat{E}^{\prime}\hat{I}}}} \right. \kern-0pt} {\hat{E}^{\prime}\hat{I}}}}\).

By substituting Eq. (6) into Eqs. (1)–(5), the normalized equation of motion and associated boundary conditions for the considered clamped–clamped arch are written as

$$\frac{{\partial^{4} w}}{{\partial x^{4} }} + \frac{{\partial^{2} w}}{{\partial t^{2} }} + c\frac{\partial w}{\partial t} = F_{elec} + \alpha_{s} \left[ {\frac{{\partial^{2} w}}{{\partial x^{2} }} - \frac{{d^{2} w_{0} }}{{dx^{2} }}} \right]\times\left[ {\int\limits_{0}^{1} {\left\{ {\left( {\frac{\partial w}{\partial t}} \right)^{2} - 2\left( {\frac{\partial w}{\partial t}\frac{{dw_{0} }}{dx}} \right)dx} \right\}} } \right],$$
(7)
$$w\left( {0,t} \right) = 0, \, \frac{\partial w}{\partial x}\left( {0,t} \right) = 0, \, w\left( {1,t} \right) = 0, \, \frac{\partial w}{\partial x}\left( {1,t} \right) = 0,$$
(8)

where

$$\begin{aligned} w_{0} (x) = \frac{{b_{o} }}{2d}[1 - \cos (2\pi x)], \, \\ F_{elect\_PP} \left( {w,V_{DC} } \right) = \frac{{\alpha_{e} V_{DC}^{2} }}{{\left( {W(x,t)} \right)^{2} }} \\ F_{elect\_P} \left( {w,V_{DC} } \right) = \frac{{\alpha_{e} V_{DC}^{2} }}{{\left( {W(x,t)} \right)^{2} }}\left( {1 + 0.65\frac{W(x,t)}{b}} \right), \\ F_{elect\_MF} \left( {w,V_{DC} } \right) = \frac{{\alpha_{e} V_{DC}^{2} }}{{\left( {W(x,t)} \right)^{2} }}\left( {1 + 0.265\left( {\frac{W(x,t)}{b}} \right)^{{\frac{3}{4}}} + 0.53h\left( {\frac{W(x,t)}{b}} \right)^{{\frac{1}{2}}} } \right), \\ \end{aligned}$$
(9)

and where

$$\alpha_{s} = \frac{{\hat{A}\hat{d}^{2} }}{{2\hat{I}}} = 6\left( {\frac{{\hat{d}}}{{\hat{h}}}} \right)^{2} , \, \alpha_{e} = \frac{{\varepsilon_{0} \hat{b}\hat{L}^{4} }}{{2\hat{E^{\prime}}\hat{I}\hat{d}^{3} }}, \, h = \frac{{\hat{h}}}{{\hat{b}}}, \, b = \frac{{\hat{b}}}{{\hat{d}}},$$
(10)

The solution of the above nonlinear equations, Eqs. (7)–(10) cannot be calculated analytically in a closed form, but will be approximated numerically in the next section.

3 Numerical model

To solve the obtained normalized equations governing the in-plane deflection of the curved microbeam, Eqs. (7)–(8) along with the respective electrostatic actuating function given by Eq. (9), the equations are discretized using the Galerkin expansion technique to yield a ROM (Ouakad and Younis 2014; Ouakad 2013). Hence, the deflection of the actuator is assumed as

$$w\left( {x,t} \right) = \sum\limits_{i = 1}^{n} {u_{i} \left( t \right)\phi_{i} \left( x \right)} ,$$
(11)

where the special functions \(\phi_{i} \left( x \right)\) are assumed to be the linear normalized un-damped mode-shapes of a fixed–fixed microbeam and the time varying functions \(u_{i} \left( t \right)\) are its normalized modal amplitude coordinates.

To get the ROM, we substitute Eq. (11) into Eqs. (7)–(9) and Eq. (8), multiply by \(\phi_{i} \left( x \right)\), use the orthogonality conditions of the normalized un-damped mode-shapes, and then integrate the resultant equations from 0 to 1. The outcome is a set of differential equations function of the modal amplitudes \(u_{i} \left( t \right)\).

It is worth to mention here that, in the process of getting the ROM equations, the mode-shape functions \(\phi_{i} \left( x \right)\) will remain embedded inside the denominator of the electrostatic force approximated expression, Eq. (9), in the ROM (Ouakad 2014). To deal with the complicated resulting integral terms due to that nonlinear electric force, we simultaneously evaluate the spatial integrals containing the space-dependent mode-shape functions \(\phi_{i} \left( x \right)\) numerically while integrating the differential equations with respect to the time-dependent modal amplitude functions \(u_{i} \left( t \right)\).

Since we are considering here to solve for the static behavior of the arched microbeam under the fringing-fields electrostatic force, we calculate its deflection by setting all time-dependent terms in the ROM differential equations equal to zero. Then the modal amplitudes \(u_{i} \left( t \right)\) are replaced by unknown constant quantities a i . This results in a system of nonlinear algebraic equations in terms of those coefficients. The system is then solved numerically using the Newton–Raphson method.

4 The eigenvalue problem

To investigate the eigenvalue problem of the MEMS arch, we propose to calculate the variation of its natural frequencies under the effect of the applied DC voltage. To this end, we consider the ROM modal amplitudes discretized equations, which can be written in a state-space form as:

$$\dot{U} = R\left( U \right),$$
(12)

where

$$U = \left[ {u_{1} ,u_{2} ,\ldots ,u_{n} } \right]^{T} ,$$
(13)

is the arch normalized modal coordinates vector and \(R\left( U \right)\) is a right-hand side vector representing its stiffness coefficients. Note that the vector \(R\left( U \right)\) is a nonlinear function of the modal amplitudes functions \(u_{i} \left( t \right)\). We considered in this particular problem the symmetric and anti-symmetric mode-shapes in the ROM to get all the possible natural frequencies of the actuator. Next, we split \(U\) into a static part \(u_{s}\), representing the equilibrium position due to the DC actuation, and a dynamic part \(\eta \left( t \right)\) representing the dynamic perturbation around the equilibrium position, that is:

$$U = u_{s} + \eta \left( t \right),$$
(14)

Then, substituting Eq. (14) into Eq. (12), using a Taylor-series expansion assuming small perturbation \(\eta \left( t \right)\), then eliminating the higher-order components, and using the fact that \(R\left( {u_{s} } \right) = 0\), we get the following equation:

$$\dot{\eta }\left( t \right) = J\left( {u_{s} } \right)\eta \left( t \right),$$
(15)

where \(J\left( {u_{s} } \right)\) represents the Jacobian matrix of the curved microbeam evaluated at its equilibrium points (Nayfeh and Balachandran 1995).

To get the natural frequencies of the MEMS arch at a given DC voltage, we substitute the static solution \(u_{s}\) into the matrix J and then find its corresponding eigenvalues which are calculated by solving numerically the below characteristic equation for the eigenvalue \(\lambda\), that is:

$$det\left( {J\left( {w_{s} } \right) - \lambda I} \right) = 0,$$
(16)

where I represents the identity matrix and “det” refers to the determinant operator. Then each eigenvalue represents a particular natural frequency of the arched microbeam.

5 The static response

As a case study, we consider the fabricated clamped–clamped shallow arch made of silicon of Krylov et al. (2008) of \(\hat{L}\) = 1000 µm, \(\hat{h}\) = 2.4 µm, \(\hat{b}\) = 30 µm, \(\hat{d}\) = 10.1 µm, and initial rise b o  = 3.5 µm. First, we examine the static bifurcation diagram of the shallow arch. Figure 2 shows the maximum static deflection (the mid-deflection) of the shallow arch when using one up to ten mode shapes in Eq. (11) while varying the DC load. As shown in the figure, for relatively small DC load, only one stable fixed point exists. This stable branch ends with a point for which a small increase in the applied DC voltage results in an instability; simply called the snap-through instability, and after which another stable fixed point is born if the applied DC load is increased further. We can also see that there is an interval of DC loads representing the possibility of having two co-existing stable solutions. This interval is called the bi-stability band (also called snap-through band). The stable branch that initiates after this band ends with another structural instability: the so-called pull-in instability where the arched moving electrode touches its lower stationary actuating electrode.

Fig. 2
figure 2

Comparison between the variation of the static deflection of the shallow arch with the DC voltage with and without including the effect of the electric fringing-fields of the electrostatic force, and with experimental data of Krylov et al. (2008)

Full size image

In the same figure we demonstrate the difference in the static response of the MEMS arch with and without considering the electric fringing-fields effect. It is noted from the displayed results that assuming either models (the Palmer and the Mejis-Fokkema models) the values of voltages at which the shallow arch is undergoing snap-through and pull-in are different from the parallel-plates model only. We can clearly see that the shallow arch undergoes a snap-through motion near V DC  = 90 V and then a pull-in instability near V DC  = 113 V, while neglecting the fringing-fields effects. Whereas, these values were around 80–83 and 102–105 V, respectively, when we considered the effect of the electric fringing-fields.

In the same figure, we validate the results using the ten modes of the ROM for the clamped–clamped arch by comparing them with the experimental data of Krylov et al. (2008). In order to compare all the assumed models results obtained numerically assuming the ROM with the experimental data available in the literature for the snap-through buckling instability. As a comparison criterion, we use the static deflection value of each assume model for several DC voltages of the actuating distributed force and compare them with the measured experimental value reported in Krylov et al. (2008). The comparison is illustrated in Table 1. It is clear that the experimental data and the ROM results are in good agreement while considering the electric fringing-fields effects in the ROM equations.

Table 1 Relative error (%) at different DC voltages between the ROM with and without including the effect of the electric fringing-fields of the electrostatic force in comparison with experimental data of Krylov et al. (2008)
Full size table

In Fig. 3, the effect of the initial rise on the static deflection of the arch is presented while considering only the electric parallel-plates model. For the cases of b o  = 2.5 µm and b o  = 3.5 µm, the arch undergoes a snap-through first and then it pulls-in while increasing the applied DC load. However, for the case of b o  = 4.5 µm the arch undergoes immediate pull-in without snap-through. The figure shows that the snap-through voltage increases and the pull-in voltage decreases when increasing the initial rise value of the shallow arch. This indicates that the stiffness of the shallow arch increases before snap-through and then decreases in the buckled position with the increase of its initial rise parameter b o .

Fig. 3
figure 3

Variation of the static deflection of the shallow arch with the DC voltage for various values of initial rise b o and with considering the electric parallel-plates model

Full size image

Figure 4a, b show the effect on the static deflection of the arch for two different values of initial rise while neglecting and then considering the effect of the electric fringing-fields. We assumed for both figures the Mejis-Fokkema model. Comparing the two models confirms that electric fringing-fields effect is mainly substantial to be included in any analysis of the structural behavior of MEMS arches. We calculated a maximum of 12 % relative error in the prediction of static deflection of the MEMS arch when neglecting this effect. Also we found a relative error of almost 22–25 % in predicting the snap-through as well as the pull-in voltages, respectively.

Fig. 4
figure 4

a, b Variation of the static deflection of the shallow arch with the DC voltage for two values of initial rise b o with and without considering the electric fringing-fields effect. c The finite-elements method model in ANSYS®

Full size image

In order to validate the obtained ROM based results, comparison with the finite-elements (FE) software ANSYS are also shown. The ANSYS model shown in Fig. 4c consists of a coupled electrostatic-structural element (TRANS126 elements) to model the electrostatic coupling between the curved microbeam (moving electrode) and a grounded gate (the lower stationary electrode). The assumed element is a two-node element which has one structural degree of freedom and an electrical potential between the nodes. One end of each element is held fixed, while the other is coupled to a structural node in the upper electrode. A voltage difference is applied across the TRANS126 element, which creates an attractive force that is resisted by the stiffness of the moving electrode. The comparison shows excellent agreement among the ROM nonlinear beam model and the nonlinear finite-element model.

6 The fundamental frequency under dc load

Next, we show the effect of the initial rise on the fundamental natural frequency of the MEMS arch with (when considering the Mejis-Fokkema model) and without (while assuming the Parallel-Plates model) considering the electric fringing-fields effect, Fig. 5a, b. For the first case of b o  = 3.5 µm, the natural frequency drops to zero when the DC load is close to the snap-through instability value, Fig. 5a. Beyond this critical value, the curves in Fig. 5a show an increase of the natural frequency followed by a sudden drop to zero when the DC voltage reached the pull-in voltage. For the second case where b o  = 4 µm, Fig. 5b, the arch undergoes immediate pull-in without snapping-through if the DC load is increased continuously. In this case, the softening effect of the electrostatic force is always dominant. As seen in the same figures, including the electric fringing-fields effect caused a significant change in the values of the calculated fundamental natural frequency for both cases.

Fig. 5
figure 5

Variation of the fundamental natural frequency with the DC voltage of the shallow arch for various values of initial rise b o with and without considering the electric fringing-fields effect

Full size image

7 Conclusions

In this paper, an investigation into the nonlinear structural behavior of an electrically actuated clamped–clamped shallow MEMS arch under distributed DC electrostatic actuation was presented. An Euler–Bernoulli continuous beam model was adopted while considering the nonlinear electric fringing-fields effects. Two models of the electric fringing-field effects (the Palmer’s model and the Mejis-Fokkema model) were adopted in this regards. The derived nonlinear differential equation was discretized using a ROM obtained through a Galerkin expansion technique and then solved numerically assuming Newton–Raphson method. First, the numerical static deflection results of a MEMS arch were compared with and without considering the two fringing-fields effect models. The comparison to previously reported experimental data showed excellent agreement when compared to the models where the fringing-fields effects were included. Then, calculation of the normalized fundamental natural frequency of the MEMS arch with and without considering these effects confirmed the significant change in this fundamental frequency. Further, the results discussed in this paper showed that neglecting electric fringing-fields effects caused significant errors in modeling the resultant electrostatic actuating force and consequently in estimating accurately the structural parameters of the MEMS arch such as: its static deflection (6–10 % error), its snap-through and pull-in voltages (12–25 % error), and its fundamental natural frequency. Therefore, the electric fringing-fields effects should not be neglected in modeling the structural behavior of MEMS arches if accurate estimations of all its structural parameters are needed.