1 Introduction

Currently, rotating electrical machines generate almost all of the world’s electricity. It is estimated that rotating machines (motors) consume approximately 70 % of all electrical power (Salon 1990). Given the fact that most of the moving parts of equipment are driven by different types of electrical motors, such motors are prevalent in our life. However, electric generators or motors also generate heat, vibration, and acoustic noise while converting either electrical power to mechanical power (motors) or vice versa (generators). Our working environment has become difficult to escape from noise as the degree of office automation increased since more and more automation equipment are utilized in office. Moreover, greater numbers of motors are employed in automation to realize multiple functions to attract customers. As a result, motors which can run more quietly are much more sought after than ever. One of the main causes of acoustic noise from motors is the resonance between the electromagnetic forces e.g., unbalanced magnetic pulls (UMPs) and the stator and the frame of the motor. Therefore, the accurate determination of the natural frequencies of stator at the design stage to reduce resonance noise becomes very important (Watanabe et al. 1983). Researchers have studied motor natural frequencies, vibration and acoustic signals in recent years (Watanabe et al. 1983; Silva 2005; Ishibashi et al. 2003; Bouzek 2011). In this paper, the mathematical model for the stator structure analysis of a PM Synchronous motor’s stator structure is introduced and has been validated using a 12 slots and 5 pole-pairs PM surface mounting Synchronous motor named as M 1 . The dynamic responses of M 1 with excitation force are studied through numerical and experimental approaches to further validate the analytical model.

2 Approach

2.1 Analytical model

2.1.1 Teeth of stator core

Each tooth of the stator coil can be modeled as a cantilever beam as shown in Fig. 1. The dominant vibration of a cantilever beam is its bending mode. The natural frequencies of a cantilever beam can be calculated (Watanabe et al. 1983) as follow.

$$\omega_{i} = \lambda_{i}^{2} \sqrt {\frac{EI}{\rho A}} ,\,i = 1, 2, 3\ldots , n$$
(1)

where λ i can be obtained by solving:

$$\cos (\lambda l)\cosh (\lambda l) = - 1,$$
(2)

where l is the length of the stator tooth.

There are infinite numbers of pertaining to Eq. (2), the first three solutions are:

$$\lambda _{1} l\; = \;1.875104;\;\lambda _{2} l\; = \;4.694091;\;\lambda _{3} l\; = \;7.854757$$

The approximate solutions for i > 3 can be expressed as:

$$\lambda_{i} l = \left( { 2i - 1} \right)\pi / 2.$$
(3)
Fig. 1
figure 1

Analytical model of teeth

Full size image

2.1.2 Main body of stator core

The stator core of the motor can be modeled as a ring type element. The mode shape can be seen in Fig. 2.

Fig. 2
figure 2

First three vibration mode (2, 3, 4) shapes of ring type element

Full size image

If the ratio between the length of stator and its diameter, l/Dc is less than or equal to unity, the stator can be considered as a hollow cylinder, and the natural frequencies can be calculated by the following equation (Silva 2005; Ishibash et al. 2003):

$$f_{n} = \frac{2}{{\pi D_{c} }}\frac{{n(n^{2} - 1)}}{{\sqrt {n^{2} + 1} }}\sqrt {\frac{{E_{c} I_{c} }}{{\rho_{c} L_{c} h_{c} }}},$$
(4)

where I c is the moment of inertia of the stator core, E c is the modulus of elasticity, and h c is the length of the stator core. If the ratio of l/D c is larger than unity, the stator can be considered as a cylindrical shell, and the natural frequencies can be calculated by:

$$f_{i} = \frac{{\varOmega_{i} }}{{\pi D_{c} }}\sqrt {\frac{{E_{c} }}{{\rho_{c} (1 - \mu_{c}^{2} )}}} ,i = 1, 2, 3\ldots , n,$$
(5)

where μ c is the Poisson coefficient of the stator coil, and Ω i can be calculated:

$$\varOmega_{i} = \left\{ {\begin{array}{*{20}l} 1 \hfill \\ {\frac{1}{2}\sqrt {(1 + i^{2} + k^{2} i^{4} ) + \sqrt {(1 + i^{2} + k^{2} i^{4} )^{2} - 4k^{2} i^{6} } } } \hfill \\ \end{array} } \right.,\begin{array}{*{20}c} {i = 0} \\ {i > 0} \\ \end{array}$$
(6)

where k is a non-dimensional coefficient and has:

$$k = \frac{{h_{c}^{2} }}{{D_{c}^{2} }}$$
(7)

If the stator teeth, the stator core, and the motor case, in which the stator is tightly inserted, are considered as a single component, the natural frequency of stator given by Eq. (5) should be modified as:

$$f_{i} = \frac{1}{2\pi }\sqrt {\frac{{K_{i}^{c} + K_{i}^{case} }}{{M_{c} + M_{teeth} + M_{case} }}},$$
(8)

where

$$K_{i}^{c} = \frac{{4\varOmega_{i}^{2} }}{{D_{c} }}\frac{{\pi L_{c} h_{c} E_{c} }}{{1 - \mu_{c}^{2} }},$$
(9)
$$K_{i}^{case} = \frac{{4\varOmega_{i}^{2} }}{{D_{case} }}\frac{{\pi L_{case} h_{case} E_{case} }}{{1 - \mu_{case}^{2} }},$$
(10)

and

$$M_{c} = \pi \rho_{c} D_{c} L{}_{c}h_{c},$$
(11)
$$M_{case} = \pi \rho_{case} D_{case} L{}_{case}h_{case},$$
(12)
$$M_{teeth} = N_{t} L_{t} W_{t} L_{c} \rho_{c},$$
(13)

where N t is the number of teeth in the stator core, L t is the tooth length, and W t is the width of the teeth in Eq. (13).

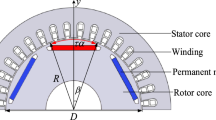
The stator system consists of the motor case, stator core, and winding. The materials of the motor case, stator core, winding are aluminum, silicon steel, copper respectively. The geometry of the stator is shown in Fig. 3 and the detailed dimensions of each component of the stator are shown in Table 1.

The motor case is made of aluminum, which has light weight, excellent machinability, and high thermal conductivity; the stator core is made of silicon steel, it has high magnetic permeability and can have high corrosion resistance after surface treatment;The motor winding is made of copper; which has very high thermal and electrical conductivity. It can have high corrosion resistance after surface treatment. The material properties of aluminum, silicon steel and copper are shown in Tables 2, 3 and 4 respectively. Based on the motor dimensions in Table 1 and the material properties of Silicon steel in Table 3, the natural frequency of the stator core teeth in the first three modes can then be obtained as:

$$\begin{aligned} f_{teeth} &= \frac{1}{2\pi }\omega_{i} = \frac{1}{2\pi }\lambda_{i}^{2} \sqrt {\frac{EI}{\rho A}} = \frac{1}{2\pi }\lambda_{i}^{2} \sqrt {\frac{{E_{Silicon\_steel} I_{teeth} }}{{\rho_{Silicon\_steel} A_{teeth} }}} \\ &= 0.5638\lambda_{i}^{2} \\ &= \left\{ {\begin{array}{*{20}l} {11.727kHz} \hfill & {i = 1} \hfill \\ {73.47kHz} \hfill & {i = 2} \hfill \\ {205.8kHz} \hfill & {i = 3} \hfill \\ \end{array} } \right. \\ \end{aligned}$$
(14)

In order to obtain the natural frequencies of the stator core’s main body, the moment of inertia of the stator has to be calculated first, and it is:

$$\begin{aligned} I_{stator\_core} = \frac{\pi }{32}\rho_{stator\_core} L_{stator\_core} [(D_{stator\_core\_outer} )^{4} - (D_{stator\_core\_inner} )^{4} ] \\ = 7.06 \times 10^{ - 7} (m^{4} ) \\ \end{aligned}$$
(15)

Then, the ratio between the length of the stator core and its diameter is calculated as following;

$$L_{stator\_core} /[(D_{stator\_core\_outer} + (D_{stator\_core\_inner} )/2] = 15/71 \le 1$$
(16)

Because the ratio between the length of the stator core and its diameter is less than unity, the stator should be considered a hollow cylinder, and its equivalent stiffness can be calculated by:

$$\begin{aligned} K_{stator\_core\_eq\_n} &= [\frac{4}{{D_{c} }}\frac{{n(n^{2} - 1)}}{{\sqrt {n^{2} + 1} }}]^{2} \frac{{E_{stator\_core} I_{stator\_core} }}{{\rho_{c} L_{c} h_{c} }}M_{stator\_core\_eq} \\& = [\frac{4}{{D_{c} }}\frac{{n(n^{2} - 1)}}{{\sqrt {n^{2} + 1} }}]^{2} \frac{{E_{stator\_core} I_{stator\_core} }}{{\rho_{c} L_{c} h_{c} }}\rho_{c} L_{c} h_{c} D_{c} \\& = 79.55\frac{{n^{2} (n^{2} - 1)^{2} }}{{n^{2} + 1}}10^{5} \\ \end{aligned}$$
(17)

Using the same approach, the equivalent stiffness of the motor case can be obtained by:

$$\begin{aligned} K_{case\_eq\_n}& = 32\frac{{n^{2} (n^{2} - 1)^{2} }}{{n^{2} + 1}}\frac{{E_{case} I_{case} }}{{D_{case} + D_{case} }} \\& = 60.8\frac{{n^{2} (n^{2} - 1)^{2} }}{{n^{2} + 1}}10^{5} \\ \end{aligned}$$
(18)

Normally, the stator core is tight-fitted to the motor case. The equivalent stiffness of the whole stator can be assumed to be the parallel connection between the stator core and motor case. The equivalent stiffness of the stator can be calculated by:

$$\begin{aligned} K_{whole\_stator\_eq\_n} &= K_{stator\_core\_eq\_n} + K_{case\_eq\_n} \\& = 140.35\frac{{n^{2} (n^{2} - 1)^{2} }}{{n^{2} + 1}}10^{5} \\ \end{aligned}$$
(19)

After the equivalent mass and stiffness of the whole stator are obtained, the natural frequencies of it can be obtained, and expressed as:

$$\begin{aligned} f_{stator\_n} &= \frac{1}{2\pi }\sqrt {\frac{{K_{whole\_stator\_eq\_n} }}{{M_{whole\_stator} }}} \\& = \frac{1}{2\pi }\sqrt {32\frac{{n^{2} (n^{2} - 1)^{2} }}{{n^{2} + 1}}} \times \sqrt {\frac{{K_{stator\_core\_eq\_n} + K_{case\_eq\_n} }}{{M_{whole\_stator} }}} \\ &= \begin{array}{*{20}c} {993.89\frac{{n(n^{2} - 1)}}{{\sqrt {n^{2} + 1} }}} & {(n = 2,3,4 \ldots )} \\ \end{array} \\ \end{aligned}$$
(20)

So, the frequencies for the first four modes can be obtained as:

$$f_{stator\_n} = \left\{ {\begin{array}{*{20}l} {2,666Hz} \hfill & {n = 2} \hfill \\ {7,543Hz} \hfill & {n = 3} \hfill \\ {14,463Hz} \hfill & {n = 4} \hfill \\ { \ldots Hz} \hfill & {n = \ldots } \hfill \\ \end{array} } \right.$$
(21)
Fig. 3
figure 3

Simulation model of M 1

Full size image
Table 1 PM synchronous motor specifications
Full size table
Table 2 Material properties of Aluminum (Polmear 1985)
Full size table
Table 3 Material properties of Silicon steel (Selection Election of Electrical Steels 2007)
Full size table
Table 4 Material properties of copper (http://en.wikipedia.org/wiki/Copper)
Full size table

2.2 Simulation model

2.2.1 Model analysis

Vibration numerical model is built in ANSYS® and the first mode natural frequency of the teeth is shown in Fig. 4. The first three modes natural frequencies of stator core in M1 are shown in Figs. 5, 6 and 7 respectively.

Fig. 4
figure 4

The first mode of stator teeth of M 1

Full size image
Fig. 5
figure 5

Modal analyses results of M 1 (second mode)

Full size image
Fig. 6
figure 6

Modal analyses results of M 1 (third mode)

Full size image
Fig. 7
figure 7

Modal analyses results of M 1 (fourth mode)

Full size image

From Fig. 4, it can be inspected that the lowest natural frequency of the stator teeth is the first bending mode, which is 12,080 Hz. This is in the high-frequency range compared to the mechanical excitation frequency of 50 Hz if the motor’s rotating speed is 3000 RPM. Due to the large difference between the excitation and natural frequency, the induced response amplitude will be small and can be considered negligible. The second and higher modes of the stator teeth, their frequencies are at least 2 times higher than the fundamental frequency of the teeth, and the vibration amplitudes are much lower than that of the fundamental frequency of the teeth. Hence, vibration of motor caused by teeth resonance can be ignored.

Figures 5, 6 and 7 illustrate that the second, third and fourth modes natural frequencies of the stator core are 2642.3, 7343.8, and 11,106 Hz respectively. These frequencies should decrease if there is any crack on the motor case or on the motor stator. This is however beyond the scope of this paper and may be considered in-depth for future studies.

2.2.2 Transient analysis

In order to simulate the vibration response of the PM motor M 1 due to dominant excitation frequencies of dynamic unbalanced magnetic pull (DUMP) in radial direction, a transient analysis is employed. The different grades of DUMP of M1 are calculated by using ANSOFT® and the results in space and frequency domain are shown in Figs. 8 and 9 respectively. The results of transient response of M 1 in time and frequency domain are shown in Figs. 10 and 11 when M 1 has different grades of DUMP faults.

Fig. 8
figure 8

DUMP of M 1 in space domain with different radial eccentricity

Full size image
Fig. 9
figure 9

DUMP of M 1 in frequency domain with different radial eccentricity

Full size image
Fig. 10
figure 10

Dynamic responses of DUMP in the time domain with different radial eccentricity

Full size image
Fig. 11
figure 11

Dynamic responses of DUMP in the frequency domain with different radial eccentricity

Full size image

3 Experimental validation

Figure 12 demonstrates an experimental platform for measuring the vibration induced by DUMP faults on the anti-vibration table. A modified permanent magnet synchronous motor (PMSM) is mounted on a testing bench with four EBGONG40250 vibration isolator pad. The PMSM is controlled using a BLHD50K motor driver. Two Polytec OFV-5000 Laser Doppler vibrometers (LDVs) are employed to measure the velocity power spectrum of the points on the out surface of the PM Synchronous Motor.

Fig. 12
figure 12

An experimental platform for measuring the vibration induced by DUMP faults

Full size image

The experimental results with different grades of dynamic eccentricity faults are shown in Table 5. It can be observed that the two columns of field data (at 50 Hz and 550 Hz in y and z) increase obviously with increasing dynamic eccentricity grades in the y and z directions.

Table 5 Experimental results induced by DUMP with different grades of DE faults
Full size table

4 Results and discussion

The modal analysis results of the stator obtained through the analytical model and the numerical model are compared in Table 6.

Table 6 Modal analysis results in two models
Full size table

The differences of these four modes frequencies of stator are less than 5 %, implying that the analytical model is correct and it can be used as a first prediction of the natural frequency of the stator.

Table 7 compares the experiment and simulation results at 3000 Hz in the x direction. It can be observed that the experimental results with different eccentricity grades are well matched with the simulation results of the same grades faults.

Table 7 Comparison between the experimental and simulation results with 4 faulty grades of DE faults at 3000 Hz
Full size table

The differences of vibration level with four faulty grades motor between simulation and experimental results are also less than 5 %, implying that the numerical model is correctly modeled and it can be utilized to verify the results obtained through analytical approach.

5 Conclusions

The stator teeth and stator core are modeled, respectively, as a cantilever beam and a hollow cylinder. Parametric studies on the dynamic structure of the whole stator system have been conducted to predict the natural frequencies and the numerical calculations have been carried out to validate the correctness and effectiveness of the proposed mathematical models. All these analytical models are validated with experimental results, and the correctness and effectiveness of the models are thus confirmed.