Keywords

1 Introduction

Permanent magnet synchronous machines (PMSM) had been widely used in industry as the driving element because of their good performance in power density and efficiency [1]. Recently, the vibration-noise indicator has become one of the key indicators to measure motor performance. The vibration and noise of the PM motor are investigated in many researchers [2,3,4,5]. The results show the low-order radial force can cause a significant vibration, and the order numbers of radial force are related to the pole and slot number of the motor.

The real slotted structure of the stator always be treated as the perfect ring in the analytical method to measure the vibration, and the high-order radial forces are always ignored when the vibration is calculated [6,7,8].The study of high-order radial force on PM motor vibration is studied in [9, 10], and the breathing zeroth mode shape vibration in the PM machine is analyzed in [11, 12].

However, the study of the high-order radial force on motor vibration is not further explored and analyzed, and this paper focuses on the detailed motor vibration analysis excited by high-order radial force. This research will provide the idea for the accurate vibration prediction and vibration reduction of the slotted PM motor.

2 Teeth Chopping Effect

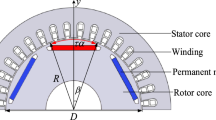
To explore the effect of high-order force on electromagnetic vibration in slotted PM motors, the teeth chopping effect [10] is introduced to describe the principle of the low-mode radial vibration excited by high-order radial force, as shown in Fig. 1, and it indicates the slot-number order force near the air-gap can induce a zeroth-mode vibration.

Fig. 1.
figure 1

Teeth chopping effect

Full size image

3 Analysis of Exciting Force

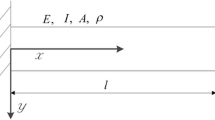
The distributed radial force in the air-gap generated by PM magnetic field on no-load can be expressed by

$$ f_{r,PM} (\theta ,t) = \frac{{B_{PM}^{2} (\theta ,t)}}{{2\mu_{0} }} \approx f_{r,PM1} (\theta ,t) + f_{r,PM2} (\theta ,t) $$
(1)

where

$$ \begin{aligned} f_{{r,PM1}} (\theta ,t) & = \frac{1}{{\mu _{0} }}B_{{PM1}} (\theta ,t) \cdot B_{{PM2}} (\theta ,t){\kern 1pt} {\kern 1pt} = \frac{{\Lambda _{0} }}{{4\mu _{0} }}\sum\limits_{{n_{1} }} {\sum\limits_{{n_{2} }} {\sum\limits_{k} {F_{{n_{1} }} } } } F_{{n_{2} }} \Lambda _{k} \cdot \cos \{ (n_{1} \pm n_{2} )p\omega t \\ & \; - [(n_{1} \pm n_{2} )p \pm kZ]\theta {\kern 1pt} \} \\ \end{aligned} $$
(2)
$$ f_{r,PM2} (\theta ,t) = \frac{1}{{2\mu_{0} }}B_{PM1}^{2} (\theta ,t){ \,= \,}\frac{1}{{4\mu_{0} }}\varLambda_{0}^{2} \sum\limits_{{n_{1} }} {\sum\limits_{{n_{2} }} {F_{{n_{1} }} } } F_{{n_{2} }} \cdot \cos [(n_{1} \pm n_{2} )p\omega t - (n_{1} \pm n_{2} )p\theta ] $$
(3)

Suppose \((n_{1} \pm n_{2} )p{ \,= \,}kZ\), and k = 1, k is preceded by a minus sign, it can be deduced as:

$$ f_{r,PM1} (\theta ,t)\left| {_{r = 0} } \right. = \frac{1}{{\mu_{0} }}B_{PM1} (\theta ,t) \cdot B_{PM2} (\theta ,t) = \frac{{\varLambda_{0} }}{{4\mu_{0} }}\varLambda_{1} \cdot \sum\limits_{{n_{1} }} {\sum\limits_{{n_{2} }} {F_{{n_{1} }} F_{{n_{2} }} \cos \{ (n_{1} \pm n_{2} )p\omega t\} } } $$
(4)

This is the zeroth-order force density. When k = 1, and the positive sign is taken in front of k, the second slot-order force density at first slot frequency can be deduced:

$$ f_{r,PM1} (\theta ,t)\left| {_{r \,=\, 2Z} } \right. = {\kern 1pt} \frac{{\varLambda_{0} }}{{4\mu_{0} }}\varLambda_{2} \sum\limits_{{n_{1} }} {\sum\limits_{{n_{2} }} {F_{{n_{1} }} F_{{n_{2} }} \cdot \cos \{ {\kern 1pt} (n_{1} \pm n_{2} )p\omega t + 2Z\theta \} } } $$
(5)

In fact, when k = 3, the second slot number order force density at slot frequency will also exist. When k = 2, the third slot-order force density will be deduced.

$$ f_{r,PM1} (\theta ,t)\left| {_{r \,=\, 3Z} } \right. = \frac{{\varLambda_{0} }}{{4\mu_{0} }}\varLambda_{3} \sum\limits_{{n_{1} }} {\sum\limits_{{n_{2} }} {F_{{n_{1} }} F_{{n_{2} }} \cdot \cos \{ {\kern 1pt} (n_{1} \pm n_{2} )p\omega t + 3Z\theta \} } } $$
(6)

where, the values of \(\Lambda_{1}\), \(\Lambda_{2}\) and \(\Lambda_{3}\) are related to the Carter factor.

Equation (3) shows that if \((n_{1} \pm n_{2} )p{ \,= \,}Z\), the slot number order force density at slot frequency dominates. The concentrated force obtained from Eq. (3) on i-th tooth is:

$$ F_{r2,i} (t) = \frac{{R_{si} L\Lambda_{0}^{2} }}{{2\mu_{0} }}\sum\limits_{{n_{1} }} {\sum\limits_{{n_{2} }} {F_{{n_{1} }} F_{{n_{2} }} \frac{{\sin [(n_{1} \pm n_{2} )p\theta_{b} /2]}}{{(n_{1} \pm n_{2} )p}}\cos [(n_{1} \pm n_{2} )p\omega t - (n_{1} \pm n_{2} )p\frac{2\pi }{Z}i]} } $$
(7)

The concentrated force obtained from Eq. (4) on the i-th tooth is:

$$ F_{r1,i} (t) = \frac{{R_{si} L\theta_{b} \Lambda_{0} }}{{4\mu_{0} }}\Lambda_{1} \sum\limits_{{n_{1} }} {\sum\limits_{{n_{2} }} {F_{n1} F_{n2} \cos [(n_{1} \pm n_{2} )p\omega t]} } $$
(8)

The concentrated force obtained from Eq. (5) on the i-th tooth is:

$$ \begin{aligned} F_{{r1,i}} (t)\left| {_{{r = 2Z}} } \right. & = \frac{{R_{{si}} L\Lambda _{0} }}{{2\mu _{0} }}\sum\limits_{{n_{1} }} {\sum\limits_{{n_{2} }} {F_{{n_{1} }} F_{{n_{2} }} \frac{{\sin [Z\theta _{b} ]}}{{2Z}}(\Lambda _{1} + \Lambda _{3} )\cos [(n_{1} \pm n_{2} )p\omega t} } \\ & - 2(n_{1} \pm n_{2} )p\frac{{2\pi }}{Z}i] \\ \end{aligned} $$
(9)

The concentrated force obtained from Eq. (6) on the i-th tooth is:

$$ \begin{aligned} F_{{r1,i}} (t)\left| {_{{r = 3Z}} } \right. & = \frac{{R_{{si}} L\Lambda _{0} }}{{2\mu _{0} }}\sum\limits_{{n_{1} }} {\sum\limits_{{n_{2} }} {F_{{n_{1} }} F_{{n_{2} }} \frac{{\sin [3Z\theta _{b} /2]}}{{3Z}}(\Lambda _{1} + \Lambda _{3} )\cos [(n_{1} \pm n_{2} )p\omega t} } \\ & - 3(n_{1} \pm n_{2} )p\frac{{2\pi }}{Z}i] \\ \end{aligned} $$
(10)

As can be seen from the Eq. (7), (8), (9) and (10), the \(F_{r2,i}\), \(F_{r1,i}\), \(F_{r1,i} \left| {_{r \,=\, 2Z} } \right.\) and \(F_{r1,i} \left| {_{r\, =\, 3Z} } \right.\) can contribute to the 0-mode deformation and vibration. So, the 0-order force acting on the motor should be the resultant force of the Eq. (7), (8), (9) and (10). Therefore, the total slot-order frequency zero-order forces can be shown as:

$$ F_{T,i} = F_{r2,i} + F_{r1,i} + F_{r1,i} \left| {_{r \,=\, 2Z} } \right. + F_{r1,i} \left| {_{r \,=\, 3Z} } \right. $$
(11)

As shown in (11), the total force consists of four items in turn: the force excited by the first slot-order force density, the force caused by zero-order force density, the force excited by the second slot-order force density and the force excited by the third slot-order force density. Furthermore, the values of these force densities are affected by the Carter factor. To explain it, three examples of different motors are analysed.

4 Simulation Results

4.1 6p/36s IPMSM (Type I)

The FEM model is built by Ansys Maxwell, as shown in Fig. 2. The specific parameters can be seen in [10].

Fig. 2.
figure 2

FEM model

Full size image
Fig. 3.
figure 3

The integral line

Full size image

As shown in Fig. 3, the radial force density is calculated by using Maxwell stress tensor method near the stator inner air-gap,and then the resultant forces of the tooth are calculated by integrating the force density. Considering the periodicity, twelve of the 36 resultant forces are shown in Fig. 4.

Fig. 4.
figure 4

The resultant forces of 12 tooth

Full size image
Fig. 5.
figure 5

The spatial order of force at slot frequency

Full size image
Fig. 6.
figure 6

Force in the air/iron interface

Full size image
Fig. 7.
figure 7

Force density distribution at slot frequency

Full size image

Thereafter, the temporal and spatial harmonics of the resultant forces are obtained using 2D FFT with the 36 resultant force waveforms. Figure 5 presents the spatial order of force at the slot frequency. As can be shown that the main spatial force harmonic is the zero-order force, and the value is 0.81 N.

Fig. 8.
figure 8

FFT of force density at slot frequency

Full size image
Fig. 9.
figure 9

Enlarged partial view of FFT

Full size image
Fig. 10.
figure 10

The 36-order (temporal order) force harmonics

Full size image

On the other hand, the spatial force harmonics of the resultant force on tooth can also be calculated using the formula. Firstly, the force density on the stator inner bore is obtained, its spatial distribution at one time step is shown in Fig. 6. Then, the temporal and spatial harmonics of the force density are calculated using 2D FFT. The 36-order force harmonics (which is related to the stator slot number) are shown in Fig. 6. Figure 7 presents the distributed slot-frequency radial force. Figure 8 is the FFT results of slot-frequency force, and Fig. 9 is the enlarged view of Fig. 8. The 36-(slot number) order force density harmonics are seen in Fig. 10.

In Fig. 10, the amplitude of the zero-order spatial force density is 847 N/m2. According to the (9), we can get that Fr1,i = 0.28. The maximum spatial force density harmonic is the 36-order force density harmonics, and its amplitude is 13930 N/m2. Similarly, the zero-order force integrated from the first slot-order force density is Fr2,i  = 1.11. Then, the value of zero-order force caused by second-order force density is Fr1,i|r = 72 =  0.252, and the value of zero-order force caused by third-order force density is Fr1,i|r = 108 = 0.18. Special attention needs to be paid to the phase between different spatial orders, as can be shown from Fig. 9. Therefore, the total slot-order frequency zero-order force is equal to.

$$ {{\text{F}}_{{\text{T}}} = - {\text{F}}_{{r1,i}} - {\text{F}}_{{r2,i}} + \left. {{\text{F}}_{{r1,i}} } \right|_{{r = 72}} + \left. {{\text{F}}_{{r1,i}} } \right|_{{r = 108}} = - 0.28 - 1.11 + 0.252 + 0.18 = - 0.96\text{N}} $$

and the magnitude is close to the resultant force 0.81 in Fig. 5.

4.2 6p/36s SPMSM (Type II)

The FEM model is built by Ansys Maxwell, as shown in Fig. 11. The specific parameters can be seen in [10].

Fig. 11.
figure 11

FEM model

Full size image
Fig. 12.
figure 12

FEM model

Full size image

4.3 6p/36s SPMSM with Narrow Slot Width (Type III)

Table 1. Simulation Results of three motors
Full size table

This FEM model of 6p/36s SPMSM only changes the slot width based on the Example 2, as shown in Fig. 12. Table 1 shows the slot-order frequency zero-order forces calculated by two methods under three motors. Comparing the total force by Method 1 and Method 2, the results are close.

5 Experiments

Fig. 13.
figure 13

Vibration test rig

Full size image
Fig. 14.
figure 14

Tested vibration acceleration when the motor runs at 900 r/min

Full size image

Figure 13 is the motor vibration test platform, and it includes the 6-pole/36-slot PM motor, SCM205 data acquisition, Inverter, Scope, Load and Laptop. Figure 14 presents the tested vibration acceleration when the motor runs at 1200 r/min with no-load. It can be seen that the peak frequency harmonics of the measured vibrations are the integer multiples of the product of the motor poles and rotor rotation frequency (f = n/60). The vibration mode shape shows a breathing shape at the frequency 720 Hz, which is the same as the analytical result.

6 Conclusion

In this paper, it can be conclude that: 1) The high-order air-gap radial force can induce the low-mode radial vibration; in the integer-slot PM motor, the high-order slot-number force is the dominant force to excite the vibration with 0th-mode, and the slot-order frequency zero-order forces obtained from the slot-number radial force occupy a large proportion; 2) If the proportion of zero-order force \(F_{r1,i}\) obtained by the zero-order radial force is relatively small, the resultant force is basically equal to the force calculated by the slot-order air-gap radial force, and its contribution is independent of the load; the values of different spatial order harmonics of radial force are related to Carter coefficient; 3) In the design process of low vibration motor, the shape of the PM and stator tooth can be optimized.