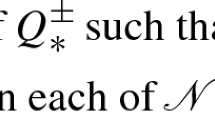Torus-like solutions for the Landau-de Gennes model. Part III: torus vs split minimizers

Abstract

We study the behaviour of global minimizers of a continuum Landau–de Gennes energy functional for nematic liquid crystals, in three-dimensional axially symmetric domains diffeomorphic to a ball (a nematic droplet) and in a restricted class of $\mathbb {S}^1$-equivariant configurations. It is known from our previous paper (Dipasquale et al. in J Funct Anal 286:110314, 2024) that, assuming smooth and uniaxial (e.g. homeotropic) boundary conditions and a physically relevant norm constraint in the interior (Lyuksyutov constraint), minimizing configurations are either of torus or of split type. Here, starting from a nematic droplet with the homeotropic boundary condition, we show how singular (split) solutions or smooth (torus) solutions (or even both) for the Euler–Lagrange equations do appear as energy minimizers by suitably deforming either the domain or the boundary data. As a consequence, we derive symmetry breaking results for the minimization among all competitors.

1 Introduction

The present article is the third of a series in a project on the analysis of the Landau–de Gennes (LdG) model for nematic liquid crystal. Relying on our previous results [11, 12] (see [36] for a short overview), we pursue our investigations on the qualitative properties of minimizers of the Landau–de Gennes functional restricted to a class of axially symmetric configurations with pointwise unit norm (the Lyuksyutov constraint). We refer to [11, 12] and the references therein for an extensive discussion on this model and its physical background. For the sake of concision, we shall simply recall the main elements and basic features of the model.

As customary in LdG Q-tensor theory (see, e.g., [34, 41]), we consider $\mathscr {M}_{3\times 3}(\mathbb {R})$ the vector space made of $3\times 3$-matrices with real entries and its 5-dimensional subspace of admissible matrices

Here $Q^\textsf{t}$ denotes the transpose of Q, $\textrm{tr}(Q)$ the trace of Q. The space ${\mathcal {S}}_0$ is endowed with the usual (Frobenius) inner product. As in [11, 12], the indicator function of physical interest is provided by the signed biaxiality parameter

(1.1)

For a matrix Q satisfying $|Q|=1$, the extremal values ${\widetilde{\beta }}(Q)=\pm 1$ occur iff the minimal/maximal eigenvalue of Q is double which corresponds to the purely positive/negative uniaxial phase in the language of liquid crystals. In turn, the case $-1< {\widetilde{\beta }}(Q)<1$ corresponds to the biaxial phase, and it is maximal for ${\widetilde{\beta }}(Q)=0$ (i.e., maximal gap between the distinct eigenvalues).

Following [11, 12], (rescaled) liquid crystal configurations occupying a given bounded domain $\Omega \subseteq \mathbb {R}^3$ (with $C^{1}$-smooth boundary at least) are described through Sobolev maps $Q \in W^{1,2}(\Omega ; {\mathbb S}^4)$. The choice of the target ${\mathbb S}^4 \subseteq {\mathcal {S}}_0$, the unit sphere of ${\mathcal {S}}_0$, encodes the Lyuksyutov constraint typical of soft biaxial nematics [32] (see also [35]). As first suggested in [11], the qualitative properties of a smooth (or merely Sobolev) configuration $Q:\Omega \rightarrow {\mathbb S}^4$ can be described by means of the signed biaxiality function $\widetilde{\beta }\circ Q$, through the biaxiality regions, i.e.,

(1.2)

and the corresponding biaxial surfaces $\big \{ \beta = t \big \}:=\big \{ x \in \overline{\Omega }: {\widetilde{\beta }} \circ Q(x) = t \big \}$. Among these sets, a crucial role is played by $\big \{ \beta =-1\big \}$, which should correspond to the experimentally observed disclination lines, where eigenvalues exchange occurs (see, e.g., [27, 28]).

After rescaling and under the Lyuksyutov constraint, the reduced LdG energy functional obtained in [11] takes the form

(1.3)

for a material-dependent constant $\lambda >0$. It reduces to the Dirichlet integral ${\mathcal {E}}_0$ for maps into ${\mathbb S}^4$ when $\lambda =0$. The parameter $\lambda ^{-1/2}$ is known as the biaxial coherence length. The functional ${\mathcal {E}}_\lambda$ formally corresponds to a LdG energy with quartic potential in the 1-constant approximation for the elastic energy and in the regime of zero uniaxial correlation length reflecting the norm constraint (see the discussion in [11, Section 1]). The reduced potential $W:{\mathcal {S}}_0\rightarrow \mathbb {R}$, when restricted to unit norm matrices, is given by

(1.4)

Hence W is nonnegative on $\mathbb {S}^4$. Its set of minima is called the vacuum manifold ${\mathcal {Q}}_\textrm{min}:=\{W=0\}\cap \mathbb {S}^4$, and $\nabla _{\textrm{tan}} W (Q)=0$ for any $Q \in {\mathcal {Q}}_{\textrm{min}}$. The minimum of W is achieved when the signed biaxiality is maximal, so that $W(Q)=0$ iff $Q \in {\mathcal {Q}}_{\textrm{min}}={\mathbb R}P^2 \subseteq {\mathbb S}^4$, where we regard the projective plane ${\mathbb R}P^2 \subseteq {\mathbb S}^4$ embedded as the set of positive uniaxial matrices

(1.5)

Since ${\mathcal {Q}}_{\textrm{min}}=\mathbb {R}P^2$, it has nontrivial topology, and both homotopy groups $\pi _2({\mathcal {Q}}_\textrm{min})=\mathbb {Z}$ and $\pi _1({\mathcal {Q}}_{\textrm{min}})=\mathbb {Z}_2$ play a role in the presence of defects, especially in the restricted class of axisymmetric configurations. A critical point $Q_\lambda \in W^{1,2}(\Omega ;\mathbb {S}^4)$ of ${\mathcal {E}}_\lambda$ among $\mathbb {S}^4$-valued maps satisfies in the weak sense the Euler–Lagrange equations

(1.6)

where the tangential gradient of W at $Q\in \mathbb {S}^4 \subseteq {\mathcal {S}}_0$ is given by

The left-hand side in (1.6) is the tension field of the $\mathbb {S}^4$-valued map $Q_\lambda$ as in the theory of harmonic maps, see e.g. [30].

Symmetry ansätze have been considered in several recent articles dedicated to Landau–de Gennes models in dimension two or three, see e.g. [1, 2, 4, 22,23,24, 40, 42]. In the present paper, we consider the LdG functional ${\mathcal {E}}_\lambda$ restricted to a class of $\mathbb {S}^1$-equivariant configurations, continuing the analysis initiated in [12]. As reviewed in Sect. 2, we identify the group $\mathbb {S}^1$ with the subgroup of ${{\,\textrm{SO}\,}}(3)$ made of rotations around the vertical axis of $\mathbb {R}^3$, and we consider the induced action on ${\mathcal {S}}_0$ given by ${\mathcal {S}}_0 \ni A \mapsto R A R^\textsf{t}\in {\mathcal {S}}_0$. Assuming that the open set $\Omega \subseteq \mathbb {R}^3$ is bounded, smooth, and $\mathbb {S}^1$-invariant, i.e., $R \cdot \Omega =\Omega$ for any $R \in \mathbb {S}^1$, we restrict ourselves to maps $Q :\Omega \rightarrow {\mathcal {S}}_0$ which are $\mathbb {S}^1$-equivariant, i.e.,

(1.7)

with the obvious analogue definition for maps defined on the boundary. Following our notations from [11, 12], given an $\mathbb {S}^1$-equivariant Dirichlet boundary data $Q_\textrm{b}:\partial \Omega \rightarrow \mathbb {S}^4$, we set

and

(1.8)

We are then interested in minimizers $Q_\lambda$ of ${\mathcal {E}}_\lambda$ over the restricted class ${\mathcal {A}}^{\textrm{sym}}_{Q_{\textrm{b}}}(\Omega )$. As already discussed in [12, Theorem 1.1] (and reviewed in the next sections), if $\partial \Omega$ and $Q_{\textrm{b}}$ are smooth enough, then minimizers always exist and they are smooth up to a singular set, denoted by $\textrm{sing}(Q_\lambda )$, made of (at most) finitely many interior point singularities located on the symmetry axis. When present, these singular points are due either to a topological obstruction related to the equivariance constraint or to an energy efficiency mechanism.

The main purpose of this article is to shed some light on the delicate interplay between the geometry of the boundary and the properties of the Dirichlet boundary condition in determining the qualitative properties of the corresponding minimizers. As initiated in [12], we investigate nonexistence vs existence of singularities for maps minimizing ${\mathcal {E}}_\lambda$ over the symmetric class ${\mathcal {A}}^{\textrm{sym}}_{Q_\textrm{b}}(\Omega )$ for a boundary data $Q_{\textrm{b}}$ exploiting the topology of the vacuum manifold ${\mathcal {Q}}_{\textrm{min}}={\mathbb R}P^2$. The topology of minimizers will be either of what we called torus type, or split type in [12]. Here, a torus type minimizer $Q_\lambda$ refers to a smooth minimizer (i.e., $\textrm{sing}(Q_\lambda )=\emptyset$), while a split type minimizer $Q_\lambda$ is a singular minimizer (i.e., $\textrm{sing}(Q_\lambda )\not =\emptyset$). This terminology, adopted in [12, Section 7], has been chosen according to our qualitative description of the biaxiality regions and surfaces, i.e., the sublevel and level sets of the composite function $\widetilde{\beta }\circ Q_\lambda$, see [12, Theorems 1.4 & 1.5]. In few words, the torus type refers to the fact that a biaxial surface of $Q_\lambda$ must have a connected component of genus one enclosing at least a circle of negative uniaxiality, i.e., a (invariant) disclination ring. In turn, the split type indicates that singularities come in pairs with a biaxiality assuming the value $-1$ in between (i.e., there are disclination segments on the vertical axis), and biaxial surfaces contain spheres with poles at the singular points. For the sake of concision, we refer to [12] for a more detailed description and the precise results.

For simplicity, we restrict ourselves to axisymmetric cylinder-type domains diffeomorphic to a ball (see Definition 2.3), or to the model case of a nematic droplet, i.e., the unit ball $\Omega =B_1 \subseteq {\mathbb R}^3$. Concerning the boundary data, a natural choice is to take it smooth (at least of class $C^1$) and valued in the vacuum manifold, i.e., $Q_{\textrm{b}}\in C^1(\partial \Omega ; \mathbb {R}P^2)$. Since $\partial \Omega \simeq {\mathbb S}^2$, every such map can be written in the form

$$\begin{aligned} Q_{\textrm{b}}(x)=\sqrt{\frac{3}{2}} \left( v(x) \otimes v(x) -\frac{1}{3} \textrm{Id}\right) \qquad \hbox {for all } x\in \partial \Omega \,, \quad v\in C^1(\partial \Omega ;\mathbb {S}^2) \,. \end{aligned}$$

(1.9)

Since $\Omega$ is axisymmetric, such map $Q_{\textrm{b}}$ is $\mathbb {S}^1$-equivariant if and only if its lift v is itself $\mathbb {S}^1$-equivariant (with respect to the obvious action of $\mathbb {S}^1$ on $\mathbb {S}^2\subseteq \mathbb {R}^3$ by rotation). Then, the topological nontriviality of $Q_{\textrm{b}}$ introduced in [12] and required here amounts to the assumption that the topological degree $\deg \, v \in {\mathbb Z}$ of the lift is odd (this assumption only depends on $Q_{\textrm{b}}$ and not on a particular choice of the lift v). For instance, if $\partial \Omega$ is of class $C^2$ and v in (1.9) is the outer unit normal field on $\partial \Omega$ (i.e., $v(x)=\overset{\rightarrow }{n}(x)$), then we obtain the so-called homeotropic boundary condition (see (2.4)) which is ${\mathbb S}^1$-equivariant and its lift v satisfies $\deg \, v= 1$, i.e., it satisfies our topological requirement. A main example entering in our discussion below is the case a nematic droplet $\Omega =B_1$ with homeotropic boundary data. Then $\overset{\rightarrow }{n}(x)=\frac{x}{|x|}$ and $Q_\textrm{b}(x)=H(x)$ where H is the unit-norm hedgehog

$$\begin{aligned} H(x)=\sqrt{\frac{3}{2}} \left( \frac{x}{|x|}\otimes \frac{x}{|x|} -\frac{1}{3} \textrm{Id}\right) \qquad \hbox {for all } x\in \partial B_1 \,, \end{aligned}$$

(1.10)

which is actually equivariant in the sense of (1.7) with respect to the full orthogonal group ${{\,\textrm{O}\,}}(3)$.

Besides $\mathbb {R}P^2$-valued maps, we shall also consider more general $\mathbb {S}^4$-valued boundary data. According to [11, 12], we shall always assume that $\Omega$ and $Q_{\textrm{b}}$ are smooth enough, axisymmetric, and satisfying the conditions:

($HP_1$):

${\bar{\beta }}:=\min _{x \in \partial \Omega } {\widetilde{\beta }}\circ Q_{\textrm{b}}(x)>-1$;

($HP_2$):

$\Omega$ is diffeomorphic (equivariantly and up to the boundary) to a ball;

($HP_3$):

$\deg (v, \partial \Omega )$ is odd;

where $(HP_3)$ has to be understood in the following way. In view of ($HP_1$), the maximal eigenvalue $\lambda _{\textrm{max}}(x)$ of $Q_{\textrm{b}}(x)$ is simple and the function $\lambda _\textrm{max}:\partial \Omega \rightarrow \mathbb {R}$ is smooth, hence there is a well defined and smooth eigenspace map $V_{\textrm{max}}: \partial \Omega \rightarrow \mathbb {R}P^2$ (which inherits equivariance). Since $\partial \Omega \simeq {\mathbb S}^2$ by ($HP_2$), the mapping $V_{\textrm{max}}$ has a (nonunique) smooth lifting $v: \partial \Omega \rightarrow \mathbb {S}^2$, which is required to satisfy ($HP_3$). In the case $\Omega =B_1$, besides the radial hedgehog H, the main examples of boundary data satisfying our general assumptions are the $\mathbb {S}^1$-equivariant harmonic spheres $\mathbf {\omega }_{\mu _1,\mu _2}: {\mathbb S}^2 \rightarrow {\mathbb S}^4$, for positive parameters $\mu _1$ and $\mu _2$ (see the full classification [12, Proposition 3.8 and proof of Theorem 1.3]).

In [12, Theorem 1.4 & 1.5], we have shown that under assumptions ($HP_1$)-($HP_3$), minimizers of ${\mathcal {E}}_\lambda$ over the class ${\mathcal {A}}^{\textrm{sym}}_{Q_{\textrm{b}}}(\Omega )$ must be either of torus type (when smooth) or of split type (when singular), in agreement with some physical expectations based on numerical simulations (e.g., [10, 14, 21, 27, 28]). To complement this result, [12, Theorem 1.2 & 1.3] provide in the case $\Omega =B_1$ two explicit continuous deformations¹$\Gamma :[0,1]\rightarrow C^{2,\alpha }_\textrm{sym}(\partial B_1;\mathbb {S}^4)$ of the hedgehog map H along which ($HP_1$)-($HP_3$) are preserved and such that minimizers corresponding to the final map $Q_{\textrm{b}}=\Gamma (1)$ are either all of torus type or all of split type respectively (see also Remark 3.16). Our first main result actually shows that both type of minimizers coexist for the same boundary data when suitably chosen at some intermediate stage of one of these deformations.

Theorem 1.1

Let $\alpha \in (0,1)$, $\lambda \geqslant 0$, and $\Gamma :[0,1]\rightarrow C^{2,\alpha }_{\textrm{sym}}(\partial B_1;\mathbb {S}^4)$ a continuous curve along which ($HP_1$)-($HP_3$) are satisfied. Assume that for $Q_{\textrm{b}}=\Gamma (0)$ and $Q_{\textrm{b}}=\Gamma (1)$, the minimizers of ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}^{\textrm{sym}}_{Q_{\textrm{b}}}(B_1)$ are all of torus type and all of split type, respectively. Then there exist $0<t_1\leqslant t_2<1$ such that

• (i) for every $0\leqslant t<t_1$ and $Q_{\textrm{b}}=\Gamma (t)$, any minimizer of ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}^{\textrm{sym}}_{Q_{\textrm{b}}}(B_1)$ is smooth and thus of torus type;

• (ii) for every $t_2<t\leqslant 1$ and $Q_{\textrm{b}}=\Gamma (t)$, any minimizer of ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}^{\textrm{sym}}_{Q_{\textrm{b}}}(B_1)$ is singular and thus of split type;

• (iii) for $t\in \{t_1,t_2\}$ and $Q_{\textrm{b}}=\Gamma (t)$, there exist a smooth and a singular minimizer of ${\mathcal {E}}_\lambda$ over the class ${\mathcal {A}}^{\textrm{sym}}_{Q_{\textrm{b}}}(B_1)$, hence of torus and split type respectively.

As a consequence, there exists $Q_{\textrm{b}} \in C^{2,\alpha }_{\textrm{sym}}(\partial B_1;\mathbb {S}^4)$ satisfying ($HP_1$)–($HP_3$) which yields coexistence of torus and split minimizers of ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}_{Q_\textrm{b}}^{\textrm{sym}}(B_1)$.

The proof of Theorem 1.1, in Sect. 3, essentially relies on the interior and boundary regularity theory developed in [11, 12] and suitably presented in Sect. 3.1. Along with further refinements, it follows that both smoothness and presence of singularities persist under strong $W^{1,2}$-convergence as the pair $(Q_{\textrm{b}}, \lambda )$ varies in the space of data $C^{2,\alpha }_{\textrm{sym}}(\partial \Omega ;{\mathbb S}^4)\times [0,\infty )$, in analogy with [3, 18] in the case of minimizing harmonic maps into $\mathbb {S}^2$. Using these properties together with unique continuation arguments, we prove in Theorem 3.14 a decomposition of the space of data into two open sets, for which all the minimizers are of the same type (smooth or singular), and their common boundary, where coexistence occurs. Then Theorem 1.1 follows as a direct consequence (see Corollary 3.15) as the two open sets are not empty by [12, Theorem 1.2 & 1.3] and there exists an explicit continuous path connecting them (as already mentioned). It is a natural open question to understand if for such explicit path deforming the data used in [12, Theorem 1.2] into the one used in [12, Theorem 1.3] and passing through the hedgehog H, the coexistence parameters given in Theorem 1.1 are precisely those of the hedgehog, i.e., if $Q_{\textrm{b}}=H$ yields coexistence of torus and split minimizers in the class ${\mathcal {A}}_{H}^{\textrm{sym}}(B_1)$.

Our coexistence property is somehow related to a similar result established in the recent article [42], although the methods employed are completely different. As already commented in more details in [12, Section 7], the analysis in [42] is performed to the case $\Omega =B_1$ with boundary condition given by the unit norm hedgehog H, and the minimization is restricted to the strictly smaller class of ${{\,\textrm{O}\,}}(2)\times \mathbb {Z}_2$-equivariant configurations (the extra ${\mathbb Z}_2$-symmetry corresponding to the reflection across the horizontal plane). In this restricted class, the author performs a clever further constrained minimization which yields coexistence of minimizers of “torus” and “split” type, although these notions are in a sense weaker than ours in [12]. However, their energy minimality in the full symmetric class ${\mathcal {A}}_{H}^\textrm{sym}(B_1)$ remains unclear.

The second part of the article is dedicated to minimizers of ${\mathcal {E}}_\lambda$ over the equivariant class (1.8) with homeotropic boundary conditions on axisymmetric domains $\Omega \subseteq {\mathbb R}^3$ diffeomorphic to the unit ball. Here the goal is to show that the presence of smooth or singular minimizers and even their coexistence depends in a subtle way on the shape of $\Omega$. To capture the essence of these phenomena, we restrict ourselves to an explicit family of axisymmetric cylinder-type domains denoted by ${\mathfrak {C}}^h_{\ell ,\rho }$ and obtained as a regularization (near the angles) of vertical cylinders of height 2h and radius $\ell$, the parameter $\rho$ being the smoothing parameter (see Definition 2.3). The boundary condition $Q_{\textrm{b}}$ is the homeotropic boundary data given by (1.9) with $v=\overrightarrow{n}$ the outer unit normal field. Under these choices of $\Omega$ and $Q_{\textrm{b}}$, assumptions ($HP_1$)–($HP_3$) above are satisfied and the results in [12] apply. Exploiting these facts, we discuss here the nature of minimizers, i.e., smooth or singular, and thus their type, torus or split, as the characteristic lengths h and $\ell$ vary. Borrowing a terminology from physics (see, e.g., [6], for the case of Bose-Einstein condensates in trapping potentials), we are interested in two opposite regimes, namely: (i) the case $h \gg \ell$ of long and thin cylinders, (the “cigar shape”), and its opposite, i.e., (ii) the case $h \ll \ell$ of flat and very large cylinders (the “pancake shape”). Both cases are somehow natural, as they are a mathematical idealization of the case in which the liquid crystals occupy a long pipe or it is arranged as a thin film respectively.

We shall see in Theorem 1.3 below that, in the asymptotic regime $h\gg \ell$, a 2D-reduction phenomenon occurs and the 3D-minimizers in ${\mathfrak {C}}^h_{\ell ,\rho }$ tend to minimize the 2D-energy on most of the horizontal cross-sections of the domain. To present and describe this dimension reduction, it is useful to anticipate and analyse the effective 2D-variational problem which involves maps defined on a generic horizontal cross-section ${\mathbb D}_\ell$ of the smoothed cylinder ${\mathfrak {C}}^h_{\ell ,\rho }$. This 2D-minimization problem is of independent interest and resembles the one considered in [22] without the norm constraint.

For simplicity, we rescale the disc ${\mathbb D}_\ell$ of radius $\ell$ to the unit disc ${\mathbb D}$ and, to distinguish the 2D from the 3D case, we shall use the notation $E_\lambda$ (instead of ${\mathcal {E}}_\lambda$) to refer to the LdG energy in two dimensions. In other words, we consider for each $\lambda \geqslant 0$ the 2D-LdG energy

$$\begin{aligned} E_\lambda (Q):= \int _{\mathbb {D}} \frac{1}{2}\left| \nabla Q \right| ^2 + \lambda W(Q) \,dx, \end{aligned}$$

(1.11)

defined for configurations in the class $W^{1,2}(\mathbb {D}; \mathbb {S}^4)$. Note that in the case $\lambda =0$, the energy $E_0$ still reduces to the Dirichlet integral.

In the 2D-problem, we are interested in minimizers of $E_\lambda$ over the $\mathbb {S}^1$-equivariant class

$$\begin{aligned} {\mathcal {A}}^{\textrm{sym}}_{\overline{H}}(\mathbb {D}):= \big \{ Q \in W^{1,2}_{\textrm{sym}}(\mathbb {D};\mathbb {S}^4): Q = \overline{H} \text { on } \partial \mathbb {D}\big \} \,, \end{aligned}$$

(1.12)

where ${\overline{H}}:\mathbb {R}^2{\setminus }\{0\}\rightarrow \mathbb {R}P^2 \subseteq \mathbb {S}^4$ is the radial anchoring map (or constant norm hedgehog), i.e.,

$$\begin{aligned} {\overline{H}}(x):=\sqrt{\frac{3}{2}}\left( \frac{1}{|x|^2} \begin{pmatrix} x_1 \\ x_2\\ 0 \end{pmatrix} \otimes \begin{pmatrix} x_1 \\ x_2\\ 0 \end{pmatrix} -\frac{1}{3}\textrm{Id}\right) . \end{aligned}$$

(1.13)

The restriction of $\overline{H}$ to $\partial {\mathbb D}_\ell$ corresponds precisely to the homeotropic boundary condition at the boundary of the cross-section $\partial {\mathbb D}_\ell \subseteq \partial {\mathfrak {C}}^h_{\ell ,\rho }$ where the outer normal is horizontal. We observe that maps belonging to ${\mathcal {A}}^\textrm{sym}_{\overline{H}}(\mathbb {D})$ are continuous in $\overline{{\mathbb D}}$ (see Sect. 2), hence there is a natural decomposition ${\mathcal {A}}_{\overline{H}}^{\textrm{sym}}(\mathbb {D}) = {\mathcal {A}}_{\textrm{N}} \cup {\mathcal {A}}_{\textrm{S}}$ (with disjoint union) according to the respective value at the origin $Q(0)=\pm \textbf{e}_0$, where $\textbf{e}_0$ is the matrix given by (2.8). Indeed, $\pm \textbf{e}_0$ are the only unit norm matrices invariant under the action of $\mathbb {S}^1$ on $\mathbb {S}^4$, so that equivariance, norm constraint, and continuity imply this decomposition.

Our second main result discusses the nature of 2D-minimizers as the parameter $\lambda \geqslant 0$ varies, that is the belonging to the class ${\mathcal {A}}_{\textrm{N}}$ or to the class ${\mathcal {A}}_{\textrm{S}}$. Note that fixing the cross-section of the sample and varying the biaxial coherence length $\lambda ^{-1/2}$ is mathematically equivalent, by rescaling, to fixing the material-dependent length $\lambda ^{-1/2}$ and varying the width of the sample, which is physically more realistic.

Theorem 1.2

There exist $0<\lambda _0<\lambda _*<\lambda ^*< +\infty$ such that the following statements hold.

• (i) The maps ${\overline{Q}}\simeq {\bar{u}}$ with $\bar{u}(z)=g_{\overline{H}}(\pm z)$ explicitly given by (4.34), are (positively) uniaxial, they are minimizers of $E_\lambda$ over ${\mathcal {A}}_{\textrm{N}}$, and local minimizers of $E_\lambda$ over ${\mathcal {A}}^{\textrm{sym}}_{\overline{H}}(\mathbb {D})$ for every $\lambda \geqslant 0$. In addition, these maps are the unique absolute minimizers for $\lambda \in ( \lambda _*,\infty )$.

• (ii) If $\lambda \in [0,\lambda ^*)$ then there exist minimizers $Q_\lambda$ of $E_\lambda$ over ${\mathcal {A}}_{\textrm{S}}$. Moreover, these are local minimizers of $E_\lambda$ over ${\mathcal {A}}^\textrm{sym}_{\overline{H}}(\mathbb {D})$, and they satisfy $\widetilde{\beta }\circ Q_\lambda ({\overline{\mathbb {D}}})=[-1,1]$. In addition, if $\lambda \in [0, \lambda _*)$, then minimizers over ${\mathcal {A}}_{\textrm{S}}$ are the the only minimizers of $E_\lambda$ over ${\mathcal {A}}^\textrm{sym}_{\overline{H}}(\mathbb {D})$, and uniqueness holds for $\lambda <\lambda _0$. If $\lambda >\lambda ^*$, then there is no minimizer of $E_\lambda$ over ${\mathcal {A}}_{\textrm{S}}$.

• (iii) If $\lambda =\lambda _*$, then the maps ${\overline{Q}}$ in (i) and $Q_\lambda$ in (ii) are both minimizers of $E_\lambda$ over ${\mathcal {A}}^{\textrm{sym}}_{\overline{H}}(\mathbb {D})$.

The previous theorem provides a purely energetic explanation of the biaxial escape phenomenon in 2D-biaxial nematics, at least under norm and axial symmetry constraints. The escape mechanism here is explained in a completely different way compared to [9], where complete biaxial escape in 2D is inferred in the low-temperature limit. In our case, the boundary data (1.13) is trivial in $\pi _1({\mathbb R}P^2)$, while in [9] its nontriviality implies that almost uniaxial extensions cannot exist, even without the norm constraint. Indeed, according to claim (i), if $\lambda$ is very large (equivalently, when the size of the sample is large compared to the characteristic length $\lambda ^{-1/2}$), then energy minimizers are purely positively uniaxial (and even explicit, due to the norm constraint), because of the strong penalization of the biaxial phase induced by the potential W. On the other hand, claim (ii) shows that reducing $\lambda$ to smaller values (equivalently, reducing the size the sample compared to $\lambda ^{-1/2}$) makes uniaxiality non necessarily favorable. Indeed, for $\lambda$ below the coexistence threshold $\lambda _*$, the biaxiality parameter of minimizers attains its full range $[-1,1]$, and complete biaxial escape occurs.

The proof of Theorem 1.2 is presented in Sect. 4. As commented in more details there, the cornerstone is Theorem 4.4 which gives an energy gap phenomenon between the infimum of Dirichlet integral $E_0$ over the class ${\mathcal {A}}_{\textrm{N}}$ and the class ${\mathcal {A}}_{\textrm{S}}$ together with a complete classification of the corresponding optimal maps following the lines of [12]. The main difficulties come from the conformal invariance of the Dirichlet integral in 2D and the associated concentration/compactness alternative with possible bubbling-off of harmonic spheres along minimizing sequences (see the proof of Proposition 4.15) as the pointwise constraints $Q(0)=\pm \textbf{e}_0$ are not weakly closed. This intermediate step and Theorem 1.2 can be seen as analogues of the construction of small and large solutions for $\mathbb {S}^2$-valued harmonic maps in two dimensions, see [8, 26]. Borrowing the terminology from the $\mathbb {S}^2$-valued case, the large solutions $\overline{Q}$ in (i) escape from the (small) spherical cap of ${\mathbb S}^4$ centered at $-\textbf{e}_0$ containing the image of the boundary datum $\overline{H}$, as opposed to smalls solutions $Q_\lambda$ in (ii) (at least for $\lambda$ small enough) for which the escape phenomenon does not happen. In the critical case $\lambda =\lambda ^*$, bubbling-off of harmonic spheres cannot be excluded by a direct energetic comparison, and existence or not of minimizers over the class ${\mathcal {A}}_{\textrm{S}}$ remains to be established. Similarly, a detailed analysis of $Q_\lambda$ minimizer over ${\mathcal {A}}_{\textrm{S}}$ as $\lambda$ increases to $\lambda ^*$ has still to be performed. In particular, it would interesting to determine whether or not the branch $\{Q_\lambda \}$ can be continued beyond $\lambda ^*$ as a branch of critical points. Since these issues do not affect our main line of investigation, we do not pursue the analysis further, and we leave those as open questions.

In Sect. 5, we take advantage of the previous 2D result to describe the asymptotic behaviour of minimizers in the 3D cylindrical domains ${\mathfrak {C}}^h_{\ell ,\rho }$ with homeotropic boundary condition in the regime $h\gg \ell$. Our third main result below shows that, for such long “cigar shaped” domains, any minimizing configuration must be singular, hence of split type in the sense of [12].

Theorem 1.3

Let $\lambda \geqslant 0$ be a fixed number and $\lambda _0$, $\lambda _*$ the values provided by Theorem 1.2. Given $0<2\rho <\ell$ and a sequence $h_n\rightarrow +\infty$ satisfying $h_n>\ell$, set $\Omega _n:={\mathfrak {C}}^{h_n}_{\ell ,\rho }$ and let $Q_{\textrm{b}}^{(n)}$ be the homeotropic boundary data on $\partial \Omega _n$. If, for each n, $Q^{(n)}$ is a minimizer of ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}^{\textrm{sym}}_{Q_\textrm{b}^{(n)}}(\Omega _n)$, then the following statements hold for n large enough.

• (i) (Split Structure) If $\ell <\sqrt{\lambda _*/\lambda }$, then ${{\,\mathrm{\textrm{sing}}\,}}{(Q^{(n)})} \ne \emptyset$. As a consequence, $Q^{(n)}$ is of split type and $\beta _n:={\widetilde{\beta }}\circ Q^{(n)}$ satisfies $\beta _n(\overline{\Omega _n})=[-1,1]$.

• (ii) (2D-reduction) If $\ell <\sqrt{\lambda _0/\lambda }$ and ${\widehat{Q}}_\ell$ denotes the unique minimizer of $E_\lambda (\,\cdot ; {\mathbb D}_\ell )$ over ${\mathcal {A}}^{\textrm{sym}}_{\overline{H}}({\mathbb D}_\ell )$, then $Q^{(n)}\rightarrow {\widehat{Q}}_{\ell }$ strongly in $W^{1,2}_\textrm{loc}({\mathfrak {C}}^\infty _\ell )$ and in fact, locally smoothly in $\overline{{\mathfrak {C}}^\infty _\ell }$ as $n\rightarrow +\infty$.

• (iii) (Singularities Ejection) If $\ell <\sqrt{\lambda _0/\lambda }$, then ${{\,\mathrm{\textrm{sing}}\,}}{(Q^{(n)})} \cap \{x_3\geqslant 0\}$ and ${{\,\mathrm{\textrm{sing}}\,}}{(Q^{(n)})} \cap \{x_3< 0\}$ are both nonempty, each one of them contains an odd number of points, ${{\,\mathrm{\textrm{sing}}\,}}{(Q^{(n)})}\subseteq \{x_3\text {-axis}\}\cap \{h_n-\alpha \leqslant |x_3|\leqslant h_n-\frac{1}{\alpha } \}$ for some constant $\alpha \geqslant 1$ independent of n, and $Q^{(n)} = -\textbf{e}_0$ on $\{x_3\text{-axis }\}\cap \{|x_3|< h_n-\alpha \}$. In addition, $\textrm{Card}\big ({{\,\mathrm{\textrm{sing}}\,}}{(Q^{(n)})}\big )$ remains bounded as $n\rightarrow \infty$.

This theorem shows that singularities occur purely for reasons of energy efficiency, in analogy with the case of minimizing harmonic maps into $\mathbb {S}^2$ first described in [17]. Claim (ii) in the theorem above states that minimizers tend to become two-dimensional (i.e., independent of $x_3$) on each fixed bounded portion of the (smoothed) cylinder as the height goes to infinity. For sufficiently thin cylinders (below the critical threshold $\sqrt{\lambda _0/\lambda }$), 2D minimizers on the cross sections assume the value $-\textbf{e}_0$ at the origin by Theorem 1.2, so that negative uniaxiality must occur on the symmetry axis for 3D minimizers. This property, in combination with the boundary data, forces the presence of point singularities, and thus the split structure. Finally, according to (iii), singularities have to escape to infinity along the symmetry axis in a certain quantitative way, whereas full regularity on each fixed bounded portion of the cylinders is inherited from the limiting map. From the presence of singularities, we derive in Corollary 5.13 the instability of minimizers over ${\mathcal {A}}^{\textrm{sym}}_{Q_{\textrm{b}}^{(n)}}(\Omega _n)$ in the full class ${\mathcal {A}}_{Q_{\textrm{b}}^{(n)}}(\Omega _n)$. As a consequence, minimizers of ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}_{Q_\textrm{b}^{(n)}}(\Omega _n)$ are not symmetric and non uniqueness holds, in analogy with our previous result [12, Corollary 7.15]. Such symmetry breaking phenomena were already proved in [3] and [16] for minimizing harmonic maps into $\mathbb {S}^2$ (i.e., for the Frank-Oseen model). Hence, our result is a natural counterpart for the Landau–de Gennes model, in agreement with the numerical simulations in [10].

The proof of Theorem 1.3 relies on various energy identities leading to uniform a priori bounds and compactness properties. But the heart of the matter is a 2D-rigidity result for local minimizers in infinite cylinders, see Proposition 5.10. Relying on the 2D-uniqueness property in Theorem 1.2, we obtain $x_3$-independence by constructing comparison maps with optimal energy growth, and to this purpose it is crucial to assume that the cylinders are sufficiently thin. Our analysis also shows that the number of singularities is bounded and that, near each tip of the cylinder, there must be an odd number of them. It remains an open question whether or not there is exactly one singular point near each tip for h large enough.

The next result describes the asymptotic behaviour of minimizers over the equivariant class in the opposite regime $h \ll \ell$. It shows that for such “pancake shaped” domains the minimizing configurations must be smooth, hence of torus type in the sense of [12].

Theorem 1.4

Let $\lambda \geqslant 0$ be a fixed number. Given $0<2\rho <h$ and an increasing sequence $\ell _n\rightarrow +\infty$ satisfying $\ell _n>\sqrt{2}h$, set $\Omega _n:={\mathfrak {C}}^h_{\ell _n,\rho }$ and let $Q_{\textrm{b}}^{(n)}$ be the homeotropic boundary data on $\partial \Omega _n$. If, for each n, $Q^{(n)}$ is a minimizer of ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}^{\textrm{sym}}_{Q_\textrm{b}^{(n)}}(\Omega _n)$, then the following statements hold for n large enough.

• (i) (Torus Structure) We have ${{\,\mathrm{\textrm{sing}}\,}}{(Q^{(n)})} = \emptyset$. As a consequence, $Q^{(n)}$ is of torus type, $\beta _n:={\widetilde{\beta }}\circ Q^{(n)}$ satisfies $\beta _n(\overline{\Omega _n})=[-1,1]$, and the level set $\{\beta _n = -1\}$ contains an invariant horizontal circle mutually linked to the vertical axis.

• (ii) (Asymptotic Behaviour) $Q^{(n)}\rightarrow \textbf{e}_0$ strongly in $W^{1,2}_{\textrm{loc}}({\mathfrak {C}}^h_\infty )$ and in fact, locally smoothly in $\overline{{\mathfrak {C}}^h_\infty }$ as $n\rightarrow +\infty$.

• (iii) (Biaxiality Ejection) For any $t \in [-1,1)$, there exist $n_t \in \mathbb {N}$ and a value $d_t > 0$ independent of n such that $\{\beta _n \leqslant t \} \cap {\mathfrak {C}}_{\ell _n-d_t}^h=\emptyset$ for any $n \geqslant n_t$.

According to claim (ii), minimizers approach the constant map $\textbf{e}_0$ on each fixed bounded portion of the cylinder as the width increases to infinity. Indeed, the influence of the nonconstant part of the boundary data, which is present only on the curved part of $\partial \Omega _n$, fades as this curved part is sent to infinity when $\ell _n\rightarrow +\infty$. Then, full regularity near the symmetry axis (and hence everywhere) is inherited from the limiting map, whence the torus type structure. Furthermore, the local smooth convergence to a constant uniaxial map pushes the biaxial sets to infinity, in such a way that they remain at finite distance from the lateral boundary.

The proof of Theorem 1.4 also relies on monotonicity formulae, local energy bounds and compactness arguments. The first key estimate is a linear law for the growth of the total energy with respect to $\ell$ obtained through comparison maps. Refining it into a sublinear estimate slightly in the interior (see Lemma 6.6) leads to the constancy of the limiting map and to a uniform bound for the distance of the biaxial sets from the lateral boundary.

In our last main result, we discuss how the nature of minimizers of ${\mathcal {E}}_\lambda$ over the symmetric class changes under deformations of the domain, in analogy with and complementing Theorem 1.1 when varying the boundary data. Theorem 1.5 below refines the conclusions in Theorems 1.3 and 1.4, and it shows how the transition from the “cigar shape” to the “pancake shape” naturally leads to coexistence of torus and split minimizers under homeotropic boundary data for domains of suitable limiting size. More precisely, starting from a cigar shape domain provided by Theorem 1.3 where any minimizer is of split type, and then enlarging it sufficiently we arrive at a pancake shape where any minimizer is of torus type by Theorem 1.4. Then Theorem 1.5 shows that split and torus minimizers must coexist in some domains of intermediate size.The proof is similar in spirit to the one for Theorem 1.1 and it is still based on persistence of smoothness and persistence of singularities.

Theorem 1.5

Let $\lambda \geqslant 0$ and $h,\ell _0,\rho >0$ be fixed numbers such that $2\rho <\ell _0/6$ and $\ell _0<3\,h$. For $\ell \geqslant \ell _0$, set $\Omega _\ell :={\mathfrak {C}}^h_{\ell ,\rho }$ and let $Q^{(\ell )}_\textrm{b}$ be the homeotropic boundary data on $\partial \Omega _\ell$. Assume that every minimizer of ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}^{\textrm{sym}}_{Q_{\textrm{b}}^{(\ell _0)}}(\Omega _{\ell _0})$ is of split type (i.e., it has a non empty singular set). Then there exist numbers $\ell _2\geqslant \ell _1>\ell _0$ such that

• (i) for every $\ell _0\leqslant \ell <\ell _1$, every minimizer of ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}^{\textrm{sym}}_{Q_{\textrm{b}}^{(\ell )}}(\Omega _{\ell })$ is of split type (i.e., singular);

• (ii) for every $\ell >\ell _2$, every minimizer of ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}^{\textrm{sym}}_{Q_{\textrm{b}}^{(\ell )}}(\Omega _{\ell })$ is of torus type (i.e., smooth);

• (iii) for $\ell \in \{\ell _1,\ell _2\}$, ${\mathcal {E}}_\lambda$ admits both a split and a torus minimizer over ${\mathcal {A}}^{\textrm{sym}}_{Q_{\textrm{b}}^{(\ell )}}(\Omega _{\ell })$.

In the previous statement, we emphasize that the existence of $\ell _0$ is not conditional thanks to Theorem 1.3 and a simple rescaling of variables. Indeed, fixing a height $h>0$, setting $\rho =\ell {{\bar{\rho }}}$ with ${{\bar{\rho }}}>0$ small enough, and rescaling variables with respect to the width $\ell >0$, one obtains ${\mathcal {E}}_\lambda (\cdot ,{\mathfrak {C}}^h_{\ell ,\rho })=\ell \, {\mathcal {E}}_{\ell ^2\lambda }(\cdot ,{\mathfrak {C}}^{h/\ell }_{1,\bar{\rho }})$. Then, applying (i) in Theorem 1.3 to ${\mathcal {E}}_{\ell ^2\lambda }(\cdot ,{\mathfrak {C}}^{h/\ell }_{1,\bar{\rho }})$ as $\ell \rightarrow 0$ shows that for $\ell >0$ sufficiently small, any minimizer of ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}^\textrm{sym}_{Q_{\textrm{b}}^{(\ell )}}(\Omega _{\ell })$ must be singular. Concerning the values $\ell _1$ and $\ell _2$, we actually expect that $\ell _1=\ell _2$, i.e., only one critical size of the domain provides the coexistence property, but it seems to be a quite difficult problem. Existence of a singular minimizer in the symmetric class at the intermediate sizes $\ell =\ell _1$ and $\ell =\ell _2$ indicates once again that a symmetry breaking occurs for global minimizers of ${\mathcal {E}}_\lambda$ over the global class ${\mathcal {A}}_{Q_{\textrm{b}}^{(\ell )}}(\Omega _{\ell })$. We shall prove in Corollary 6.12 that symmetry breaking still occurs in a neighborhood of $\ell =\ell _1$ and $\ell =\ell _2$, even for $\ell >\ell _2$ when all minimizers in the symmetric class are smooth. This fact enlightens the difficulty of proving or disproving axial symmetry of minimizers over the full class. For instance, it would be already very interesting to determine whether or not minimizers of ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}_{Q_\textrm{b}^{(\ell )}}(\Omega _{\ell })$ are actually $\mathbb {S}^1$-equivariant for $\ell \gg \ell _2$ large enough.

To conclude, we would like to mention that all the results presented here should have an analogue when the Lyuksyutov constraint is replaced by the Lyuksyutov (asymptotic) regime as in [11, Section 4], and isotropic points playing the role of singular points. This will be the object of future investigations.

2 Axisymmetric domains, symmetric criticality, and Euler–Lagrange equations

2.1 Axially symmetric domains

In this preliminary subsection, we define the relevant class of cylindrical domains of interest in the present paper. For geometric and topological properties of arbitrary axisymmetric domains $\Omega \subseteq \mathbb {R}^3$, we refer to [12, Section 2].

First, we recall that the unit circle $\mathbb {S}^1$ is identified with the subgroup of ${{\,\textrm{SO}\,}}(3)$ made of all rotations around the vertical $x_3$-axis (see (2.1)), so that a matrix $R\in \mathscr {M}_{3\times 3}(\mathbb {R})$ represents a rotation of angle $\theta$ around the vertical axis iff it writes

$$\begin{aligned} R=\begin{pmatrix} {\widetilde{R}} &{} 0 \\ 0 &{} 1 \end{pmatrix} \quad \text {with}\quad {\widetilde{R}}:= \begin{pmatrix} \cos \theta &{} -\sin \theta \\ \sin \theta &{} \cos \theta \end{pmatrix}. \end{aligned}$$

(2.1)

Axisymmetry is defined accordingly.

Definition 2.1

A set $\Omega \subseteq \mathbb {R}^3$ is said to be axisymmetric (or $\mathbb {S}^1$-invariant, or rotationally symmetric) if it is invariant under the action of $\mathbb {S}^1$, i.e., $R\cdot \Omega =\Omega$ for every $R\in \mathbb {S}^1$. Equivalently, $\Omega$ is axisymmetric if

$$\begin{aligned} \Omega =\bigcup _{R\in \mathbb {S}^1}R\cdot {\mathcal {D}}_\Omega \quad \text {where}\quad {\mathcal {D}}_\Omega :=\Omega \cap \{x_2=0\}. \end{aligned}$$

For such domains, it is also useful to consider the (relatively) open subsets

$$\begin{aligned} {\mathcal {D}}^+_\Omega :={\mathcal {D}}_\Omega \cap \{x_1>0\} \text { and } {\mathcal {D}}^-_\Omega :={\mathcal {D}}_\Omega \cap \{x_1<0\} \end{aligned}$$

(2.2)

of the vertical plane $\{x_2=0\}$, so that $R_\pi {\mathcal {D}}^{\pm }_\Omega ={\mathcal {D}}^{\mp }_\Omega$. Indeed, if $I=\Omega \cap \{ x_3\hbox {-axis}\}$ then the following obvious identities hold:

$$\begin{aligned} \Omega \setminus I=\mathbb {S}^1 \cdot {\mathcal {D}}^+_\Omega \,, \qquad \partial \Omega \cup I= \mathbb {S}^1 \cdot \partial {\mathcal {D}}^+_\Omega \,, \qquad \overline{\Omega } =\mathbb {S}^1 \cdot \overline{{\mathcal {D}}^+_\Omega } \,, \end{aligned}$$

(2.3)

with $\partial {\mathcal {D}}^+_\Omega \subseteq \overline{{\mathcal {D}}^+_\Omega } \subseteq \{ x_2=0\}$. Note that if $\Omega \subseteq \mathbb {R}^3$ is a bounded and smooth open set then ${\mathcal {D}}_\Omega$ (or ${\mathcal {D}}^\pm _\Omega$) is a bounded and smooth (resp. piecewise smooth and Lipschitz) relatively open subset of the plane $\{x_2=0\}$.

Remark 2.2

(homeotropic boundary data) We observe that if $\Omega$ is axisymmetric and $C^3$-smooth (resp. $C^{k,\alpha }$-smooth with $k\geqslant 3$), then the same property holds for the function given by the signed distance to the boundary. Hence its gradient is an $\mathbb {S}^1$-equivariant map, and in particular the outer normal field $\overrightarrow{n}(x)$ along $\partial \Omega$ is $C^2$-smooth (resp. $C^{k-1,\alpha }$-smooth) and equivariant. As a consequence, the corresponding homeotropic boundary data given by

$$\begin{aligned} Q_{\textrm{b}}(x):= \left( \overrightarrow{n}(x) \otimes \overrightarrow{n}(x) - \frac{1}{3}\textrm{Id} \right) \end{aligned}$$

(2.4)

is $C^2$-smooth (resp. $C^{k-1,\alpha }$-smooth) and equivariant.

We shall be mainly concerned with axisymmetric domains $\Omega \subseteq \mathbb {R}^3$ which are homeomorphic to a cylinder. To define properly those domains, let us first set some useful notations.

Notation (rectangles & cylinders). Let $h,\ell \in (0,\infty ]$ and $y\in \mathbb {R}^3$.

• (i) The rectangle ${\mathfrak {R}}_\ell ^h$ centered at the origin and the rectangle ${\mathfrak {R}}_\ell ^h(y)$ centered at $y \in \{x_2=0\}$ are the sets

  $$\begin{aligned} {\mathfrak {R}}_\ell ^h:=(-\ell ,\ell )\times \{0\} \times (-h,h) \quad \text {and}\quad {\mathfrak {R}}_\ell ^h (y):=y+ {\mathfrak {R}}_\ell ^h . \end{aligned}$$

  (2.5)

• (ii) The cylinder ${\mathfrak {C}}_\ell ^h$ centered at the origin and the cylinder ${\mathfrak {C}}_\ell ^h(y)$ centered at $y\in \mathbb {R}^3$ are the sets

  $$\begin{aligned} {\mathfrak {C}}_\ell ^h:= \big \{ x_1^2+x_2^2<\ell ^2\big \} \times \{ |x_3|<h \}\,, \qquad {\mathfrak {C}}_\ell ^h (y):=y+ {\mathfrak {C}}_\ell ^h . \end{aligned}$$

  (2.6)

We shall refer to h as the height and $\ell$ as the thickness (or radius) of a cylinder.

In order to apply our boundary regularity theory in [12] for energy minimizers under $\mathbb {S}^1$-symmetry constraint, we need to consider some regularized version of the cylinders in (2.6). To define those, we first recall that for $p\in (1,\infty )$, a p-disc centered at $y=(y_1,0,y_3)$ and radius $\rho >0$ included in the vertical plane $\{x_2 = 0\}$ is a set of the form

$$\begin{aligned} D^{(p)}_\rho (y):= \big \{ x=(x_1,0,x_3) \in \mathbb {R}^3: \left( \left| x_1-y_1 \right| ^p + \left| x_3-y_3 \right| ^p \right) ^{1/p} < \rho \big \}. \end{aligned}$$

We shall use p-discs with $p=4$ to obtain inner $C^3$-regularizations of rectangles and cylinders. The scale of regularization $\rho >0$ will usually be a fixed number to be explicitly specified in terms of h and $\ell$ in the calculations.

Definition 2.3

(smoothed rectangles & cylinders) Let $h,\ell >0$ and $0<2\rho < \min \{h,\ell \}$.

• (i) For vertical rectangles ${\mathfrak {R}}_\ell ^h$ (resp. ${\mathfrak {R}}_\ell ^h(y)$) as in (2.5), the corresponding smoothed $\rho$-rectangle ${\mathfrak {R}}_{\ell ,\rho }^h$ (resp. ${\mathfrak {R}}_{\ell ,\rho }^h(y)$) is the union of all 4-discs $D_\rho ^{(4)}(z)$, $z=(z_1,z_3) \in \{x_2=0\}$, contained in ${\mathfrak {R}}_\ell ^h$ (resp. ${\mathfrak {R}}_\ell ^h(y)$).

• (ii) For vertical cylinders ${\mathfrak {C}}_\ell ^h$ and ${\mathfrak {C}}_\ell ^h(y)$ as in (2.6), the corresponding smoothed $\rho$-cylinder ${\mathfrak {C}}^{h}_{\ell ,\rho }$ and ${\mathfrak {C}}^{h}_{\ell ,\rho }(y)$, $y\in \mathbb {R}^3$, are defined as

  $$\begin{aligned} {\mathfrak {C}}^h_{\ell ,\rho }:= \bigcup _{R \in \mathbb {S}^1} R \cdot {\mathfrak {R}}^h_{\ell ,\rho }\,, \qquad {\mathfrak {C}}^{h}_{\ell ,\rho }(y):=y+ {\mathfrak {C}}^{h}_{\ell ,\rho } \,. \end{aligned}$$

The radius $\rho$ is called smoothing scale of ${\mathfrak {R}}^h_\ell$ and ${\mathfrak {C}}^h_\ell$. When it is not relevant, we shall simply speak of smoothed rectangles and smoothed cylinders.

In view of the previous definition, ${\mathfrak {C}}^{h}_{\ell ,\rho }$ is axially symmetric and the same holds for ${\mathfrak {C}}^{h}_{\ell ,\rho }(y)$ if and only if y belongs to the vertical axis, i.e., $y=(0,0,y_3)$, $y_3\in \mathbb {R}$. Moreover, ${\mathfrak {C}}^{h}_{\ell ,\rho }(y) \cap \{x_2=0\}={\mathfrak {R}}^h_{\ell ,\rho }(y)$ whenever $y \in \{x_2=0\}$.

Remark 2.4

The boundary of a smooth rectangle is of class $C^{3,1}$ by our choice of $D^{(p)}_\rho (y)$ with $p=4$ (more generally, it is of class $C^{p -1,1}$ for each integer $p\geqslant 2$). The radius $\rho >0$ of the approximating discs gives the size of the region near the angles on which smoothing takes place. In addition, it is straightforward to check that ${\mathfrak {R}}^h_{\ell ,\rho } \uparrow {\mathfrak {R}}^h_\ell$ and ${\mathfrak {C}}^h_{\ell ,\rho } \uparrow {\mathfrak {C}}^h_\ell$ (and similarly for their translated counterparts) in the Hausdorff distance as $\rho \downarrow 0$ as a consequence of the elementary inclusions (recall that $0<2\rho <\min \{h,\ell \}$)

$$\begin{aligned} {\mathfrak {R}}^h_{\ell -\rho } \cup {\mathfrak {R}}^{h-\rho }_\ell \subseteq {\mathfrak {R}}^h_{\ell ,\rho } \subseteq {\mathfrak {R}}^h_\ell \,, \qquad {\mathfrak {C}}^h_{\ell -\rho } \cup {\mathfrak {C}}^{h-\rho }_\ell \subseteq {\mathfrak {C}}^h_{\ell ,\rho } \subseteq {\mathfrak {C}}^h_\ell \,, \end{aligned}$$

(2.7)

and the obvious analogues for their translated counterparts.

2.2 Decomposition of ${\mathcal {S}}_0$ into invariant subspaces

In order to give an efficient description of $\mathbb {S}^1$-equivariant configurations, we will use the following decomposition results from [12, Section 2] for the space ${\mathcal {S}}_0$ of admissible tensors.

Lemma 2.5

([12, Lemmas 2.1 & 2.2, and Remark 2.3]) There is a distinguished orthonormal basis $\big \{\textbf{e}_0, \textbf{e}^{(1)}_1, \textbf{e}^{(1)}_2, \textbf{e}^{(2)}_1, \textbf{e}^{(2)}_2\big \}$ of ${\mathcal {S}}_0$ given by

$$\begin{aligned}{} & {} \textbf{e}_0:= \frac{1}{\sqrt{6}}\begin{pmatrix} -1 &{} 0 &{} 0 \\ 0 &{} -1 &{} 0 \\ 0 &{} 0 &{} 2 \end{pmatrix},\;\textbf{e}^{(1)}_1:= \frac{1}{\sqrt{2}}\begin{pmatrix} 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} 0 \\ 1 &{} 0 &{} 0 \end{pmatrix}, \;\textbf{e}^{(1)}_2:= \frac{1}{\sqrt{2}}\begin{pmatrix} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 \\ 0 &{} 1 &{} 0 \end{pmatrix},\nonumber \\{} & {} \textbf{e}^{(2)}_1:= \frac{1}{\sqrt{2}}\begin{pmatrix} 1 &{} 0 &{} 0 \\ 0 &{} -1 &{} 0 \\ 0 &{} 0 &{} 0 \end{pmatrix}, \; \textbf{e}^{(2)}_2: = \frac{1}{\sqrt{2}}\begin{pmatrix} 0 &{} 1 &{} 0 \\ 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \end{pmatrix},\qquad \qquad \qquad \qquad \end{aligned}$$

(2.8)

such that the subspaces

$$\begin{aligned} L_0:= {\mathbb R}\textbf{e}_0,\quad L_1:= {\mathbb R} \textbf{e}^{(1)}_1\oplus {\mathbb R} \textbf{e}^{(1)}_2,\quad L_2:= {\mathbb R} \textbf{e}^{(2)}_1\oplus {\mathbb R} \textbf{e}^{(2)}_2, \end{aligned}$$

are invariant under the induced action of ${\mathbb S}^1$ on ${\mathcal {S}}_0$, namely, ${\mathcal {S}}_0 \ni A \mapsto RAR^{\textrm{t}} \in {\mathcal {S}}_0$, and

$$\begin{aligned} {\mathcal {S}}_0 =L_0 \oplus L_1 \oplus L_2 \simeq \mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C}. \end{aligned}$$

(2.9)

Moreover, the ${\mathbb S}^1$-action on ${\mathcal {S}}_0$ corresponds to an $\mathbb {S}^1$-action on each $L_k$ by rotations of degree k, in the sense that the induced $\mathbb {S}^1$-action on $\mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C}$ is given by

$$\begin{aligned} R_\alpha \cdot (t, \zeta _1, \zeta _2) = (t, e^{i\alpha } \zeta _1, e^{2i\alpha }\zeta _2) \quad \forall R_\alpha \in \mathbb {S}^1. \end{aligned}$$

(2.10)

As a straightforward consequence of the decomposition (2.9) in the orthonormal basis (2.8), we derive the following explicit formulas for a tensor Q and its determinant.

Lemma 2.6

Elements $Q \in {\mathcal {S}}_0$ are in one-to-one (linear) correspondence with elements $u=(u_0,u_1,u_2) \in \mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C}$. This correspondence, denoted as $Q\simeq u$, is given by

$$\begin{aligned} Q= \frac{1}{\sqrt{2}} \left( \begin{array}{ccc} -\frac{u_0}{\sqrt{3}}+ \textrm{Re} (u_2) &{} \textrm{Im} (u_2) &{} \textrm{Re} (u_1) \\ \textrm{Im} (u_2) &{} -\frac{u_0}{\sqrt{3}}-\textrm{Re} (u_2) &{} \textrm{Im}(u_1) \\ \textrm{Re} (u_1) &{} \textrm{Im} (u_1) &{} \frac{2 u_0}{\sqrt{3}} \end{array} \right) \,. \end{aligned}$$

(2.11)

In addition, it is isometric, i.e., $|Q|^2=\textrm{Tr}(Q^2) =|u|^2= u_0^2 + \left| u_1 \right| ^2 + \left| u_2 \right| ^2$, and

$$\begin{aligned} \textrm{det} \,Q= \frac{1}{2\sqrt{2}}\left[ \frac{2u_0}{\sqrt{3}} \left( \frac{u_0^2}{3}+\frac{1}{2}|u_1|^2-|u_2|^2\right) +\textrm{Re} (u_1^2 \overline{u_2})\right] \,. \end{aligned}$$

(2.12)

The previous lemmas yield in the obvious way a (linear, isometric) correspondence between Q-tensor fields on $\Omega$ and maps from $\Omega$ into $\mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C}$. The following corollary is a direct consequence of (2.8), (2.9), and (2.11). The proof is elementary and left to the reader.

Corollary 2.7

Let $\Omega$ be an open subset of $\mathbb {R}^d$. Elements $Q \in W^{1,2}(\Omega ;{\mathcal {S}}_0)$ are in one-to-one (linear) correspondence with elements $u=(u_0,u_1,u_2) \in W^{1,2}(\Omega ; \mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C})$. This correspondence, still denoted as $Q\simeq u$, is given by relation (2.11) holding a.e. in $\Omega$. In addition, if $Q\simeq u$, then $|Q|^2=|u|^2$ and $\left| \nabla Q \right| ^2 = \left| \nabla u \right| ^2$ a.e. in $\Omega$. In particular, $Q \in W^{1,2}(\Omega ;\mathbb {S}^4)$ if and only if $u \in W^{1,2}(\Omega ; {\mathbb S}^4)$.

2.3 $\mathbb {S}^1$-equivariant Q-tensor fields

We now specialize our previous discussion to $\mathbb {S}^1$-equivariant Q-tensor fields on rotationally invariant bounded open sets. It is natural to describe such sets and Q-tensor fields in terms of cylindrical coordinates $(r,x_3,\phi )$ (which of course reduce to polar coordinates $(r,\phi )$ in the case of horizontal discs). This description yields the following refinement of the decomposition in Corollary 2.7.

Lemma 2.8

Let $\Omega \subseteq \mathbb {R}^3$ be a bounded and axisymmetric open set and ${\mathcal {D}}_\Omega ^+$ its vertical section given by (2.2). If $Q \in W^{1,2}_\textrm{sym}(\Omega ;{\mathcal {S}}_0)$ and $Q\simeq u = (u_0,u_1,u_2) \in W^{1,2}(\Omega ;\mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C})$ is the corresponding map in the sense of Corollary 2.7, then u is $\mathbb {S}^1$-equivariant with respect to the action (2.10) on $\mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C}$. As a consequence, for each $k \in \{0,1,2\}$, $u_k$ can be decomposed as

$$\begin{aligned} u_k(x) = f_k(r,x_3) e^{i k \phi }, \end{aligned}$$

for functions $f_k \in W^{1,2}({\mathcal {D}}_\Omega ^+,rdrdx_3)$ which are $\mathbb {C}$-valued for $k=1,2$, and $\mathbb {R}$-valued for $k=0$. Thus,

$$\begin{aligned} \left| \nabla Q \right| ^2 = \left| \nabla f_0 \right| ^2 + \left| \nabla f_1 \right| ^2 + \left| \nabla f_2 \right| ^2 + \frac{\left| f_1 \right| ^2 + 4\left| f_2 \right| ^2}{r^2}\quad \hbox { a.e. in}\ \Omega , \end{aligned}$$

(2.13)

where $\left| \nabla f_k \right| ^2:= \left| \partial _r f_k \right| ^2 + \left| \partial _{x_3} f_k \right| ^2$. In particular, $\left| \nabla Q \right| ^2$ does not depend on $\phi$, and

$$\begin{aligned} {\mathcal {E}}_0(Q) =\pi \int _{{\mathcal {D}}_\Omega ^+} \left( \left| \nabla f_0 \right| ^2 + \left| \nabla f_1 \right| ^2 + \left| \nabla f_2 \right| ^2 + \frac{\left| f_1 \right| ^2 + 4\left| f_2 \right| ^2}{r^2}\right) \,r\,drdx_3<\infty . \nonumber \\ \end{aligned}$$

(2.14)

Proof

In view of (2.10), the $\mathbb {S}^1$-equivariance of Q translates into the identities

$$\begin{aligned} u_0(R_\alpha x) = u_0(x) ,\quad u_1(R_\alpha x) = e^{i\alpha } u_1(x) , \quad u_2(R_\alpha x) = e^{2i\alpha } u_2(x), \end{aligned}$$

which hold for every $R_\alpha \in \mathbb {S}^1$ and a.e. $x \in \Omega$. In terms of cylindrical coordinates, those identities imply

$$\begin{aligned} u_0(x) = f_0(r,x_3) ,\quad u_1(x) = f_1(r,x_3) e^{i\phi } ,\quad u_2(x) = f_2(r,x_3) e^{2i\phi }, \end{aligned}$$

(2.15)

a.e. in $\Omega$. Hence $f_k \in W^{1,2}({\mathcal {D}}_\Omega ^+,rdrdx_3)$ since $u_k \in W^{1,2}(\Omega )$ for each $k \in \{0,1,2\}$.

Moreover, Corollary 2.7 yields

$$\begin{aligned} \left| \nabla Q \right| ^2 = \sum _{k=0}^2 \left| \nabla u_k \right| ^2 = \sum _{k=0}^2 \left| \nabla f_k \right| ^2 + \frac{k^2 \left| f_k \right| ^2}{r^2}\quad \text {a.e. in } \Omega , \end{aligned}$$

which proves (2.13). Finally, since the right hand side above only depends on $(r,x_3)$, applying Fubini’s theorem leads to

$$\begin{aligned} \int _{\Omega } \left| \nabla u_k \right| ^2 \,dx = 2\pi \int _{{\mathcal {D}}_\Omega ^+} \left| \nabla f_k \right| ^2 + \frac{k^2 \left| f_k \right| ^2}{r^2} \,r\,dr dx_3< +\infty . \end{aligned}$$

Then (2.14) follows summing this equality over $k=0,1,2$. $\square$

Remark 2.9

It is straightforward to check that the previous lemma also holds in two dimensions, i.e., if $\Omega ={\mathbb D}_\rho \subseteq \mathbb {R}^2$ is a disc of radius $\rho >0$ centered at the origin. In this case, if $Q \in W^{1,2}_{\textrm{sym}}({\mathbb D}_\rho ;{\mathcal {S}}_0)$ and $Q\simeq u = (u_0,u_1,u_2)$, then

$$\begin{aligned} u_k(x)=f_k(r)e^{ik\phi } \end{aligned}$$

(2.16)

where $(r,\phi )$ are the polar coordinates, and each $f_k$ belongs to $W^{1,2}((0,\rho ), rdr)$. In addition, (2.13) and (2.14) still holds under the forms

$$\begin{aligned} \left| \nabla Q \right| ^2=|\nabla u|^2= \left| f^\prime _0 \right| ^2 + \left| f^\prime _1 \right| ^2 + \left| f^\prime _2 \right| ^2 + \frac{\left| f_1 \right| ^2 + 4\left| f_2 \right| ^2}{r^2}\quad \hbox { a.e. in}\ \mathbb {D}_\rho , \end{aligned}$$

(2.17)

and

$$\begin{aligned} \frac{1}{2}\int _{\mathbb {D}_\rho }|\nabla Q|^2\,dx=\pi \int _0^\rho \left( \left| f^\prime _0 \right| ^2 + \left| f^\prime _1 \right| ^2 + \left| f^\prime _2 \right| ^2 + \frac{\left| f_1 \right| ^2 + 4\left| f_2 \right| ^2}{r^2}\right) \,r\,dr<\infty , \nonumber \\ \end{aligned}$$

(2.18)

respectively.

The next result describes a fine property of the space $W^{1,2}_{\textrm{sym}}({\mathbb D}_\rho ;\mathbb {S}^4)$ in the 2D-case $D_\rho \subseteq \mathbb {R}^2$. Symmetry and norm constraints yield the inclusion $W^{1,2}_{\textrm{sym}}({\mathbb D}_\rho ;\mathbb {S}^4) \subseteq C^0(\overline{{\mathbb D}_\rho };{\mathbb S}^4)$, a property which will be of crucial importance for the 2D-minimization problems discussed in Sect. 4. Up to a rescaling, we may assume without loss of generality in the following statement that $\rho = 1$.

Lemma 2.10

Let ${\mathbb D} \subseteq \mathbb {R}^2$ be the unit disc. If $Q \in W^{1,2}_\textrm{sym}(\mathbb {D};\mathbb {S}^4)$, then

• (i) $Q \in C^0(\overline{\mathbb {D}}; {\mathbb S}^4)$ and either $Q(0) = \textbf{e}_0$ or $Q(0) = -\textbf{e}_0$.

Moreover, for $\{Q_n\} \subseteq W^{1,2}_{\textrm{sym}}(\mathbb {D};\mathbb {S}^4)$ and $Q_* \in W^{1,2}(\mathbb {D};{\mathcal {S}}_0)$, the following statements hold.

• (ii) If $Q_n \rightharpoonup Q_*$ weakly in $W^{1,2}(\mathbb {D})$, then $Q _*\in W^{1,2}_{\textrm{sym}}(\mathbb {D};\mathbb {S}^4)$ and $Q_n \rightarrow Q_*$ in $C^0_{\textrm{loc}}(\overline{\mathbb {D}} {\setminus } \{0\})$. In particular, $Q_* \vert _{\partial \mathbb {D}}\rightarrow Q_n \vert _{\partial \mathbb {D}}$ uniformly on $\partial \mathbb {D}$.

• (iii) If $Q_n \rightarrow Q_*$ strongly in $W^{1,2}(\mathbb {D})$ then $Q _*\in W^{1,2}_{\textrm{sym}}(\mathbb {D};\mathbb {S}^4)$, $Q_*(0)\equiv Q_n(0)$ for n large enough, and $Q_n \rightarrow Q_*$ uniformly on $\overline{\mathbb {D}}$.

Claims (i), (ii), and (iii) still hold replacing Q, $Q_n$, and $Q_*$ with the corresponding maps with values into “the unit sphere” of $\mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C}$.

Proof

(i) According to Corollary 2.7, we write $Q\simeq u=(u_0,u_1, u_2)$ with $u_k \in W^{1,2}({\mathbb D})$, $k=0,1,2$. By Remark 2.9 above, each function $f_k$ in (2.16) belongs to $W^{1,2}((0,1),rdr)$. Then the 1D-Sobolev embedding implies that $f_k \in C^{0,\frac{1}{2}}_\textrm{loc}((0,1])$, and in turn $Q \in C^{0,\frac{1}{2}}_\textrm{loc}(\overline{\mathbb {D}} {\setminus } \{0\}) \subseteq C^0(\overline{\mathbb {D}} {\setminus } \{0\})$ by $\mathbb {S}^1$-equivariance. Then it only remains to prove continuity at the origin. To this purpose, we fix $0< \rho '<\rho <1$. Combining Young’s inequality with (2.18) and Remark 2.9, we compute

$$\begin{aligned} \left| \left| f_1(\rho ) \right| ^2-\left| f_1(\rho ') \right| ^2 \right| +&\left| \left| f_2(\rho ) \right| ^2-\left| f_2(\rho ') \right| ^2 \right| =\left| \int _{\rho '}^\rho \partial _r \left| f_1 \right| ^2 dr \right| + \left| \int _{\rho '}^\rho \partial _r \left| f_2 \right| ^2 dr \right| \nonumber \\&\leqslant \int _{\rho '}^\rho \left( \left| f^\prime _1 \right| ^2 + \frac{\left| f_1 \right| ^2}{r^2} \right) \,r\,dr + \int _{\rho '}^\rho \left( \left| f^\prime _2 \right| ^2 + \frac{\left| f_2 \right| ^2}{r^2} \right) \,r\,dr\nonumber \\&\leqslant \int _{\rho '}^\rho \left( \left| f^\prime _0 \right| ^2 + \left| f^\prime _1 \right| ^2 + \left| f^\prime _2 \right| ^2 + \frac{\left| f_1 \right| ^2+4\left| f_2 \right| ^2}{r^2} \right) \,r\,dr\nonumber \\&\leqslant \frac{1}{2\pi }\int _{\mathbb {D}_\rho }|\nabla Q|^2\,dx\, . \end{aligned}$$

(2.19)

Since Q belongs to $W^{1,2}(\mathbb {D})$, we have $\int _{\mathbb {D}_\rho }|\nabla Q|^2\,dx \rightarrow 0$ as $\rho \rightarrow 0$. Hence both $\ell _1:=\lim _{r \rightarrow 0} |f_1(r)|$ and $\ell _2:=\lim _{r \rightarrow 0} |f_2(r)|$ exist. On the other hand, it follows from (2.18) that $\ell _1=\ell _2=0$. Thus, both $f_1$ and $f_2$ extend by continuity to elements of $C^0([0,1];\mathbb {C})$ with $f_1(0)=f_2(0)=0$. In turn, (2.16) yields $u_k \in C^0(\overline{{\mathbb D}};\mathbb {C})$ with $u_k(0)=0$ for $k=1,2$.

Finally, combining Corollary 2.7 with (2.16) leads to $|Q(re^{i \phi })|^2=|f_0(r)|^2+|f_1(r)|^2+|f_2(r)|^2\equiv 1$. Since $f_1(0)=f_2(0)=0$, we have $|f_0(r)|\rightarrow 1$ as $r \rightarrow 0$. Moreover, either $f_0(r) \rightarrow 1$ or $f_0(r) \rightarrow -1$ as $r \rightarrow 0$. Indeed, if the limit does not exist, then $\liminf _{r \rightarrow 0}f_0(r)=-1<1=\limsup _{r \rightarrow 0} f_0(r)$. By continuity, it would imply the existence of $r_n \downarrow 0$ such that $f_0(r_n)\equiv 0$, and leading to the identity $1 \equiv |f_0(r_n)|^2+|f_1(r_n)|^2+|f_2(r_n)|^2\rightarrow 0$ as $n \rightarrow \infty$, a contradiction. Thus, $f_0$ extends by continuity to a function in $C^0([0,1];\mathbb {R})$ with $f_0(0)=\pm 1$, and in turn $u \in C^0(\overline{{\mathbb D}};{\mathbb S}^4)$ with $u(0)=(\pm 1,0,0)$. As a consequence, $Q \simeq u$ is continuous on $\overline{{\mathbb D}}$, and $Q(0)=\pm \textbf{e}_0$ which proves (i).

(ii) In view of (i) all the maps involved are continuous. Moreover, $\mathbb {S}^1$-equivariance allows us to use the continuous embedding $W^{1,2}((0,1),rdr) \hookrightarrow C^{0,\frac{1}{2}}_\textrm{loc}((0,1])$ and the compact embedding $C^{0,\frac{1}{2}}_\textrm{loc}((0,1]) \hookrightarrow C^0_{\textrm{loc}}((0,1])$ to deduce that $Q_n \rightarrow Q_*$ locally uniformly on $\overline{\mathbb {D}} {\setminus } \{0\}$. As the convergence is also pointwise on $\overline{\mathbb {D}} {\setminus } \{0\}$, both equivariance and norm constraints persist, and we have $Q_* \in W^{1,2}_{\textrm{sym}}(\mathbb {D};\mathbb {S}^4)\cap C^0(\overline{\mathbb {D}})$. Moreover $Q_n|_{\partial D} \rightarrow Q_*|_{\partial D}$ uniformly on $\partial \mathbb {D}$.

(iii) Assume now $Q_n \rightarrow Q_*$ strongly in $W^{1,2}(\mathbb {D})$. By (ii), it only remains to prove uniform convergence in a (small) disc centered at the origin. To achieve this, it suffices to show that $Q_n(0)\equiv Q_*(0)$ for n large enough and that the sequence $\{Q_n\}$ is equicontinuous at the origin. To check these properties, we first notice that (2.19) holds for each $Q_n$. By (i), we can choose $\rho ^\prime =0$ and any fixed $\rho \in (0,1)$ to obtain from (2.19),

$$\begin{aligned} \left| f^{(n)}_1(\rho ) \right| ^2+ \left| f^{(n)}_2(\rho ) \right| ^2\leqslant \frac{1}{2\pi }\int _{{\mathbb D}_\rho }|\nabla Q_n|^2\,dx \,. \end{aligned}$$

(2.20)

Letting $n \rightarrow \infty$ above, the same inequality holds for the components $f^*_k$, $k=1,2$, of $Q_*$.

By the Vitali–Hahn–Saks theorem (see e.g. [5, Theorem 1.30]), the strong $W^{1,2}$-convergence of the sequence $\{Q_n\}$ implies that $\{ \left| \nabla Q_n \right| ^2 \}$ is equiintegrable. Combining this fact with (2.20), it follows that $\{f^{(n)}_1\}$ and $\{f^{(n)}_2\}$ are equicontinuous at the origin. Moreover, there exists ${\bar{\rho }}>0$ such that

$$\begin{aligned} \int _{\mathbb {D}_{{{\bar{\rho }}}}}|\nabla Q_n|^2\,dx + \int _{\mathbb {D}_{{{\bar{\rho }}}}}|\nabla Q_*|^2\,dx\leqslant \frac{3\pi }{2} \quad \text {for { n} large enough}. \end{aligned}$$

Hence $\big |f_1^{(n)}\big |^2+ \big |f^{(n)}_2\big |^2\leqslant \frac{3}{4}$ in $[0,{{\bar{\rho }}}]$ for n large enough, which in turn implies that $\big |f_0^{(n)}\big |\geqslant \frac{1}{2}$ in $[0,{{\bar{\rho }}}]$ for n large enough. By continuity, it follows that each $f_0^{(n)}$ has constant sign in $[0,{{\bar{\rho }}}]$ for n large enough. The same property holds for $f^*_0$, and the sign of $f_0^{(n)}$ must be the same of $f_0^*$ for n large enough because of the pointwise convergence in ${\mathbb D}_{{\bar{\rho }}}\setminus \{0\}$. This proves that $Q_n(0)\equiv Q_*(0)$ for n large enough.

Finally, combining the pointwise inequalities on $f_0^{(n)}$, the norm constraint, and (2.20), we have for every $0<\rho \leqslant {\bar{\rho }}$,

$$\begin{aligned} \left| f^{(n)}_0(\rho )-f^{(n)}_0(0) \right| =\frac{ 1- \left| f^{(n)}_0(\rho ) \right| ^2}{ \left| f^{(n)}_0(\rho )+f^{(n)}_0(0) \right| } \leqslant \left| f^{(n)}_1(\rho ) \right| ^2+ \left| f^{(n)}_2(\rho ) \right| ^2\leqslant \frac{1}{2\pi } \int _{\mathbb {D}_\rho } |\nabla Q_n|^2\,dx \,.\end{aligned}$$

Hence the sequence $\{f_0^{(n)}\}$ is also equicontinuous at the origin by the Vitali–Hahn–Saks theorem. Going back to (2.16), we deduce that the maps $\{u^{(n)}\}$ are equicontinuous at the origin, and thus the same holds for $\{Q_n\}$ which completes the proof of the uniform convergence.

The final claim concerning the corresponding maps into $\mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C}$ follows taking scalar products with the orthonormal basis in (2.8). $\square$

With Lemma 2.10 in hands, we can easily prove that $W^{1,2}$-tensor fields on a 3D-axisymmetric domain $\Omega$ have a well-defined trace on the vertical axis.

Corollary 2.11

Let $\Omega \subseteq \mathbb {R}^3$ be a bounded and axisymmetric open set with Lipschitz boundary, and set $I:=\Omega \cap \{x_3\hbox {-axis}\}$. There is a (strongly) continuous trace operator $\textrm{Tr}: W^{1,2}_{\textrm{sym}}(\Omega ;\mathbb {S}^4) \rightarrow L^1(I;\{ \pm \textbf{e}_0\})$ satisfying $\textrm{Tr}\,Q=Q_{\vert _I}$ whenever $Q \in W^{1,2}_{\textrm{sym}}(\Omega ;\mathbb {S}^4)\cap C^0(\overline{\Omega })$.

Proof

We first notice that for $\ell >0$ small enough and $h>0$ large enough, the set $\overline{\Omega \cap {\mathfrak {C}}_\ell ^h}$ is (equivariantly) biLipschitz homeomorphic to a finite union of disjoint ${\mathbb S}^1$-invariant closed cylinders, the homeomorphism being the identity on the vertical axis. Hence, up to a change of variables, it is enough to construct the trace operator when the domain is an arbitrary cylinder to have a well defined induced operator $\textrm{Tr}: W^{1,2}_{\textrm{sym}}(\Omega \cap {\mathfrak {C}}_\ell ^h;\mathbb {S}^4) \rightarrow L^1(I;\{ \pm \textbf{e}_0\})$. In turn, the conclusion follows by composition with the continuous restriction operator $W^{1,2}(\Omega ) \rightarrow W^{1,2}(\Omega \cap {\mathfrak {C}}_\ell ^h)$.

Assuming now that $\Omega ={\mathfrak {C}}_\ell ^h={\mathbb D}_\ell \times (-h,h)={\mathbb D}_\ell \times I$, then we have

$$\begin{aligned} W^{1,2}_{\textrm{sym}}({\mathfrak {C}}_\ell ^h;{\mathbb S}^4)\subseteq L^2\big (I; W^{1,2}_{\textrm{sym}}({\mathbb D}_\ell ;{\mathbb S}^4)\big ) \subseteq L^1\big (I; W^{1,2}_{\textrm{sym}}({\mathbb D}_\ell ;{\mathbb S}^4)\big ) \end{aligned}$$

with continuous inclusions. In view of Lemma 2.10 the mapping $W^{1,2}_{\textrm{sym}}({\mathbb D}_\ell ;{\mathbb S}^4) \ni Q \mapsto Q(0) \in \{ \pm \textbf{e}_0\}$ is well defined and (strongly) continuous. Hence, by composition of this map with the inclusion maps above, we have a well defined and (strongly) continuous map $\textrm{Tr}: W^{1,2}_{\textrm{sym}}({\mathfrak {C}}_\ell ^h;\mathbb {S}^4) \rightarrow L^1(I;\{ \pm \textbf{e}_0\})$ with all the desired properties. $\square$

2.4 Existence of minimizers and Euler–Lagrange equations

We recall from [12] the following results about “symmetric criticality” and existence of minimizers over the class ${\mathcal {A}}_{Q_{\textrm{b}}}^{\textrm{sym}}(\Omega )$. Even if the results were stated in case of 3D domain, their proofs hold with obvious modifications in the planar case, i.e., when $\Omega$ is disc a centered at the origin.

Proposition 2.12

([12, Proposition 6.1 and 6.2]) Let $\Omega \subseteq \mathbb {R}^3$ be a bounded and axisymmetric open set.

• (i) If $Q_\lambda \in W^{1,2}_{\textrm{sym}}(\Omega ;\mathbb {S}^4)$ is a critical point of ${\mathcal {E}}_\lambda$ over $W^{1,2}_{\textrm{sym}}(\Omega ;\mathbb {S}^4)$, then $Q_\lambda$ is a critical point of ${\mathcal {E}}_\lambda$ among all maps $W^{1,2}(\Omega ;\mathbb {S}^4)$.

• (ii) If $\partial \Omega$ is Lipschitz regular and $Q_{\textrm{b}} \in {{\,\mathrm{\textrm{Lip}}\,}}(\partial \Omega ;\mathbb {S}^4)$ is $\mathbb {S}^1$-equivariant, then ${\mathcal {A}}_{Q_{\textrm{b}}}^{\textrm{sym}}(\Omega )$ is not empty and there exists at least one minimizer of ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}_{Q_{\textrm{b}}}^{\textrm{sym}}(\Omega )$.

In other words, critical points of ${\mathcal {E}}_\lambda$ among equivariant compactly supported perturbations preserving the $\mathbb {S}^4$-constraint are critical points with respect to every compactly supported perturbation still preserving the $\mathbb {S}^4$-constraint (i.e., even with respect to those which are not equivariant). In other words, they are weak solutions to (1.6).

Remark 2.13

For a map $Q\in W^{1,2}_{\textrm{sym}}(\Omega ;{\mathbb S}^4)$, the energy functional (1.3) can be rewritten in terms the correspondence $Q\simeq u=(f_0, f_1 e^{i \phi },f_2 e^{i2\phi })$ in Lemma 2.8. By (2.12), we have

$$\begin{aligned} {\widetilde{\beta }}(f):={\widetilde{\beta }}(Q) = 3 \sqrt{6} \det Q = f_0\left( f_0^2 +\frac{3}{2}\left| f_1 \right| ^2 - 3 \left| f_2 \right| ^2 \right) + \frac{3\sqrt{3}}{2}\textrm{Re}(f_1^2 \overline{f_2}),\nonumber \\ \end{aligned}$$

(2.21)

where $f:=(f_0,f_1,f_2)$. Combining identity (1.4) with (2.14) yields

$$\begin{aligned} {\mathcal {E}}_\lambda (Q)=\pi \int _{{\mathcal {D}}^+_\Omega }\left( \left| \nabla f \right| ^2+ \frac{\left| f_1 \right| ^2 + 4\left| f_2 \right| ^2}{r^2} +2\lambda \frac{1-{\tilde{\beta }}(f)}{3\sqrt{6}} \right) \, rdrdx_3 \,. \end{aligned}$$

(2.22)

If Q is a critical point of ${\mathcal {E}}_\lambda$ among equivariant compactly supported perturbations (preserving the $\mathbb {S}^4$-constraint), then Q weakly solves (1.6) from the proposition above. To rephrase the equations in terms of f, we may project (1.6) onto the orthonormal frame (2.8) or, equivalently, take variations in the energy functional (2.22). The criticality condition (1.6) then translates into the following nonlinear system for $f=(f_0,f_1,f_2)\in W^{1,2}({\mathcal {D}}^+_\Omega ;{\mathbb S}^4,rdrdx_3)$, namely,

$$\begin{aligned} \left\{ \begin{aligned} \partial ^2_{r} f_0 + \frac{1}{r} \partial _r f_0 + \partial ^2_{x_3} f_0&= - \left| \nabla Q \right| ^2 f_0 + \frac{\lambda }{\sqrt{6}} \left( \left| f_2 \right| ^2-f_0^2 - \frac{1}{2}\left| f_1 \right| ^2 + {\widetilde{\beta }}(f) f_0 \right) ,\\ \partial ^2_{r} f_1 + \frac{1}{r} \partial _r f_1 + \partial ^2_{x_3} f_1&= - \left| \nabla Q \right| ^2 f_1 - \frac{1}{r^2} f_1 + \frac{\lambda }{\sqrt{6}} \left( - \sqrt{3}f_2 \overline{f_1}-f_0 f_1+{\widetilde{\beta }}(f) f_1 \right) ,\\ \partial ^2_{r} f_2 + \frac{1}{r} \partial _r f_2 + \partial ^2_{x_3} f_2&= - \left| \nabla Q \right| ^2 f_2 - \frac{4}{r^2}f_2 + \frac{\lambda }{\sqrt{6}} \left( -\frac{\sqrt{3}}{2} f_1^2 + 2f_0 f_2+ {\widetilde{\beta }}(f) f_2 \right) , \end{aligned} \right. \nonumber \\ \end{aligned}$$

(2.23)

with ${\widetilde{\beta }}(f)$ as in (2.21) and $|\nabla Q|^2$ as in (2.13), both depending only on $f=(f_0,f_1,f_2)$.

Remark 2.14

(2D-case) In Sect. 4 (mostly), we shall consider the two dimensional case $\Omega ={\mathbb D}_\rho \subseteq \mathbb {R}^2$. To differentiate the 2D from the 3D case, we shall use the notation $E_\lambda (Q,\mathbb {D}_\rho )$ (instead of ${\mathcal {E}}_\lambda$) for the 2D-energy of a configuration $Q\in W^{1,2}_\textrm{sym}(\mathbb {D}_\rho ;\mathbb {S}^4)$. In view of Remark 2.9, and as in (2.22), the energy of $Q\simeq u=(f_0, f_1 e^{i \phi },f_2 e^{i2\phi })$ can be written in terms of f, leading to

$$\begin{aligned} E_\lambda (Q,\mathbb {D}_\rho )=\pi \int _0^\rho \left( \left| f^\prime \right| ^2+ \frac{\left| f_1 \right| ^2 + 4\left| f_2 \right| ^2}{r^2} +2\lambda \frac{1-{\tilde{\beta }}(f)}{3\sqrt{6}} \right) \, rdr. \end{aligned}$$

Then the criticality condition (in terms of f) for the functional $E_\lambda$ is almost identical to (2.23). It is obtained from it simply neglecting in each equation the terms $\partial ^2_{x_3}$ and $\partial _{x_3}$ in the left hand side and the right hand side respectively.

3 Coexistence of smooth and singular minimizers

3.1 Regularity theory

The purpose of this subsection is to gather (and slightly refine) the main regularity results and tools obtained in [11, 12] to have them at disposal in the most convenient form when they will be repeatedly used in the next subsections. To this end, let us recall the usual definition of singular set for a map Q defined on an open set $\Omega$. It is then defined as

$$\begin{aligned} \textrm{sing}(Q):=\Omega \setminus \big \{x\in \Omega : \hbox {} Q \hbox { is continuous in a neighborhood of} x\big \}. \end{aligned}$$

The following interior regularity theorem, even if not explicitly stated in [12], is a direct consequence of the discussion in [12, Section 6]. In particular, formula (3.2) below is a combination of the strong $W^{1,2}$-convergence of the rescaled maps $Q_\lambda ^{{\bar{x}},\rho }$ together with the explicit form (3.1) of all possible blow-up limits at a singular point. In our statement below, we require Lipschitz regularity of the boundary only to ensure that the $W^{1,2}$-trace operator on $\partial \Omega$ is well defined.

Theorem 3.1

([12], interior regularity) Let $\Omega \subseteq \mathbb {R}^3$ be a bounded and axisymmetric open set with Lipschitz boundary, and $Q_\lambda \in W^{1,2}_\textrm{sym}(\Omega ;\mathbb {S}^4)$ minimizing ${\mathcal {E}}_\lambda$ among all $Q \in W^{1,2}_{\textrm{sym}}(\Omega ;\mathbb {S}^4)$ satisfying $Q=Q_\lambda$ on $\partial \Omega$. Then $Q_\lambda \in C^\omega (\Omega {\setminus } \textrm{sing}(Q_\lambda ))$ and $\textrm{sing}(Q_\lambda )\subseteq \{x_3\text {-axis}\}\cap \Omega$ is locally finite in $\Omega$. In addition, for every ${\bar{x}}\in \textrm{sing}(Q_\lambda )$, there exist a rotation $R_\alpha \in \mathbb {S}^1$ and $Q_*\in \{\pm Q^{(\alpha )}\}$ such that

• (i) $Q_\lambda ^{{\bar{x}},\rho }\rightarrow Q_*$ strongly in $W^{1,2}_{\textrm{loc}}(\mathbb {R}^3)$ as $\rho \rightarrow 0$;

• (ii) $\Vert Q_\lambda ^{{\bar{x}},\rho }- Q_*\Vert _{C^2({\overline{B}}_2{\setminus } B_1)}=O(\rho ^\nu )$ as $\rho \rightarrow 0$ for some $\nu >0$;

where $Q_\lambda ^{{\bar{x}},\rho }(x):=Q_\lambda ({\bar{x}}+\rho x)$ and

$$\begin{aligned} Q^{(\alpha )}(x):=R_\alpha \cdot \frac{1}{\sqrt{6}}\frac{1}{|x|} \left( \begin{array}{ccc} -x_3 &{} 0 &{} \sqrt{3} x_1\\ 0 &{} -x_3 &{} \sqrt{3}x_2 \\ \sqrt{3} x_1 &{} \sqrt{3} x_2 &{} 2 x_3 \end{array}\right) . \end{aligned}$$

(3.1)

In particular,

$$\begin{aligned} \lim _{\rho \rightarrow 0}\frac{1}{\rho }\int _{B_\rho ({\bar{x}})} \frac{1}{2} |\nabla Q_\lambda |^2\,dx= \lim _{\rho \rightarrow 0}\frac{1}{\rho }{\mathcal {E}}_\lambda \big (Q_\lambda ,B_\rho (\bar{x})\big )=4\pi \quad \text {for every }{\bar{x}}\in \textrm{sing}(Q_\lambda ).\nonumber \\ \end{aligned}$$

(3.2)

Regularity at the boundary holds whenever the boundary of $\Omega$ and the boundary data are smooth enough. In this case, the singular set is made of finitely many points inside the domain $\Omega$.

Theorem 3.2

([12], regularity up to the boundary) Let $\Omega \subseteq \mathbb {R}^3$ be a bounded and axisymmetric open set with boundary of class $C^3$, and let $Q_{\textrm{b}}\in C^{1,1}(\partial \Omega ;\mathbb {S}^4)$ be an $\mathbb {S}^1$-equivariant map. If $Q_\lambda$ is a minimizer of ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}^{\textrm{sym}}_{Q_\textrm{b}}(\Omega )$, then $Q_\lambda \in C^\omega (\Omega {\setminus }\textrm{sing}(Q_\lambda ))\cap C^{1,\alpha }({\overline{\Omega }}{\setminus }\textrm{sing}(Q_\lambda ))$ for every $\alpha \in (0,1)$ and $\textrm{sing}(Q_\lambda )$ is a finite subset of $\Omega \cap \{x_3\text {-axis}\}$. Moreover,

• (i) if $Q_{\textrm{b}}\in C^{2,\alpha }(\partial \Omega )$, then $Q_\lambda \in C^{2,\alpha }({\overline{\Omega }}{\setminus }\textrm{sing}(Q_\lambda ))$;

• (ii) if $\partial \Omega$ is of class $C^{k,\alpha }$ and $Q_{\textrm{b}}\in C^{k,\alpha }(\partial \Omega )$ with $k\geqslant 3$, then $Q_\lambda \in C^{k,\alpha }({\overline{\Omega }}{\setminus }\textrm{sing}(Q_\lambda ))$;

• (iii) if $\partial \Omega$ is analytic and $Q_{\textrm{b}}\in C^\omega (\partial \Omega )$, then $Q_\lambda \in C^{\omega }({\overline{\Omega }}{\setminus }\textrm{sing}(Q_\lambda ))$.

Those two theorems rest on analytical tools that we shall repeatedly use. The first one is a monotonicity formula for the energy on balls, and we have to distinguish between balls inside the domain and balls centered at the boundary. Our statement below about the interior monotonicity formula is slightly different from the one in [12, Proposition 6.6] (in the sense that we do not impose here a smooth boundary data), but a quick inspection of the proof (which is based on [11, Proposition 2.4]) reveals that smoothness at the boundary is only used to establish the boundary monotonicity formula. Concerning the boundary case, the formula in [12, Proposition 6.6] involve constants depending only on $\lambda$, the domain $\Omega$, and the boundary data. We provide in Proposition 3.4 below a statement with a control on those constant which is transparent from the proof of [12, Proposition 6.6].

Proposition 3.3

([11, 12], interior monotonicity formula) Let $\Omega \subseteq \mathbb {R}^3$ be a bounded and axisymmetric open set with Lipschitz boundary, and $Q_\lambda \in W^{1,2}_\textrm{sym}(\Omega ;\mathbb {S}^4)$ minimizing ${\mathcal {E}}_\lambda$ among all $Q \in W^{1,2}_{\textrm{sym}}(\Omega ;\mathbb {S}^4)$ satisfying $Q=Q_\lambda$ on $\partial \Omega$. Then,

$$\begin{aligned}{} & {} \frac{1}{\rho }{\mathcal {E}}_\lambda \big (Q_\lambda ,B_\rho ({\bar{x}})\big ) - \frac{1}{\sigma }{\mathcal {E}}_\lambda \big (Q_\lambda ,B_\sigma ({\bar{x}})\big ) \\{} & {} \quad = \int _{B_\rho ({\bar{x}})\setminus B_\sigma ({\bar{x}})}\frac{1}{|x-\bar{x}|}\bigg |\frac{\partial Q_\lambda }{\partial |x-{\bar{x}}|}\bigg |^2\,dx +2\lambda \int _\sigma ^\rho \bigg (\frac{1}{t^2}\int _{B_t(\bar{x})}W(Q_\lambda )\,dx\bigg )\,dt \end{aligned}$$

for every ${\bar{x}}\in \Omega$ and $0<\sigma<\rho <\textrm{dist}(\bar{x},\partial \Omega )$.

Proposition 3.4

([11, 12], boundary monotonicity formula) Let $\Lambda ,L>0$ and $\Omega \subseteq \mathbb {R}^3$ a bounded and axisymmetric open set with boundary of class $C^3$. Let $Q_\textrm{b}\in C^{1,1}(\partial \Omega ;\mathbb {S}^4)$ be an $\mathbb {S}^1$-equivariant map satisfying $\Vert Q_\textrm{b}\Vert _{C^1(\partial \Omega )}\leqslant L$. If $\lambda \in [0,\Lambda ]$ and $Q_\lambda$ is a minimizer of ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}^{\textrm{sym}}_{Q_{\textrm{b}}}(\Omega )$, then

$$\begin{aligned}{} & {} \frac{1}{\rho }{\mathcal {E}}_\lambda \big (Q_\lambda ,B_\rho ({\bar{x}})\cap \Omega \big ) - \frac{1}{\sigma }{\mathcal {E}}_\lambda \big (Q_\lambda ,B_\sigma ({\bar{x}})\cap \Omega \big )\geqslant -K_*(\rho -\sigma ) \\{} & {} \quad + \int _{\big (B_\rho ({\bar{x}})\setminus B_\sigma (\bar{x})\big )\cap \Omega }\frac{1}{|x-{\bar{x}}|}\bigg |\frac{\partial Q_\lambda }{\partial |x-{\bar{x}}|}\bigg |^2\,dx +2\lambda \int _\sigma ^\rho \bigg (\frac{1}{t^2}\int _{B_t(\bar{x})\cap \Omega }W(Q_\lambda )\,dx\bigg )\,dt \end{aligned}$$

for every ${\bar{x}}\in \partial \Omega$ and every $0<\sigma<\rho <\textbf{r}_*$, where the radius $\textbf{r}_*>0$ only depends on $\Omega$, and $K_*>0$ is a constant depending only on $\Lambda$, L, and $\Omega$.

The second main ingredient we need to emphasize is an epsilon-regularity result, consequence of a more general regularity theorem in [11, Theorem 2.12 & Proposition 2.18]. Here again, we have to distinguish the interior and the boundary case, and our statements below provide a better control on the involved constants inherited from their proofs (see [12, Section 6] and [11, Section 2]).

Proposition 3.5

([11, 12], interior $\varvec{\varepsilon }$-regularity) Let $\Lambda >0$ and $\Omega \subseteq \mathbb {R}^3$ be a bounded and axisymmetric open set with Lipschitz boundary. Let $\lambda \in [0,\Lambda ]$ and $Q_\lambda \in W^{1,2}_\textrm{sym}(\Omega ;\mathbb {S}^4)$ minimizing ${\mathcal {E}}_\lambda$ among all $Q \in W^{1,2}_{\textrm{sym}}(\Omega ;\mathbb {S}^4)$ satisfying $Q=Q_\lambda$ on $\partial \Omega$. There exist a universal constant $\varvec{\varepsilon }_{\textrm{in}}>0$ such that for every ball $B_r(x_0)\subseteq \Omega$ with r small enough (depending only on $\Lambda$), the condition

$$\begin{aligned} \frac{1}{r}\int _{B_r(x_0)}|\nabla Q_\lambda |^2\,dx\leqslant \frac{\varvec{\varepsilon }_{\textrm{in}}}{4} \end{aligned}$$

implies $Q_\lambda \in C^\omega (B_{r/8}(x_0))$, and $\Vert \nabla ^k Q_\lambda \Vert _{L^\infty (B_{r/16}(x_0))}\leqslant C_k r^{-k}$ for each $k\in \mathbb {N}$ and a constant $C_k$ depending only on k.

Sketch of the proof

We consider the universal constant $\varvec{\varepsilon }_\textrm{in}>0$ provided by [11, Corollary 2.19]. By Proposition 3.3, $Q_\lambda$ satisfies the interior monotonicity formula which allows us to argue as in [11, proof of Lemma 2.6] and obtain

$$\begin{aligned}{} & {} \sup _{B_\rho ({\bar{x}})\subseteq B_{r/2}(x_0)} \frac{1}{\rho }\int _{B_\rho ({\bar{x}})} \frac{1}{2} |\nabla Q_\lambda |^2\,dx\leqslant \sup _{B_\rho ({\bar{x}})\subseteq B_{r/2}(x_0)} \frac{1}{\rho } {\mathcal {E}}_\lambda \big (Q_\lambda ,B_\rho ({\bar{x}})\big )\\{} & {} \quad \leqslant \frac{2}{r}{\mathcal {E}}_\lambda \big (Q_\lambda ,B_r(x_0)\big )\leqslant \frac{1}{r} \int _{B_r(x_0)}|\nabla Q_\lambda |^2\,dx+ \frac{\varvec{\varepsilon }_{\textrm{in}}}{4}\leqslant \frac{\varvec{\varepsilon }_{\textrm{in}}}{2} \end{aligned}$$

for r small enough (depending only on $\Lambda$). By Proposition 2.12, $Q_\lambda$ is a weak solution of (1.6) in $\Omega$. Hence [11, Corollary 2.19] applies, and we conclude that $Q_\lambda \in C^\omega (B_{r/8}(x_0))$ with the announced estimates. $\square$

Compared to [11, 12], we provide below a localized version (in terms of the data) of the boundary epsilon-regularity. This statement will be of first importance when varying the domain $\Omega$. The arguments remain essentially the same so that we only sketch the main changes. The first version we state here holds under uniform smallness of the scaled Dirichlet integral.

Proposition 3.6

([11, 12], boundary $\varvec{\varepsilon }$-regularity 1) Let $\Lambda ,L>0$ and $\Omega \subseteq \mathbb {R}^3$ a bounded and axisymmetric open set with boundary of class $C^3$. Let $Q_\textrm{b}\in C^{1,1}(\partial \Omega ;\mathbb {S}^4)$ be an $\mathbb {S}^1$-equivariant map. Let $\lambda \in [0,\Lambda ]$ and $Q_\lambda$ be a minimizer of ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}^{\textrm{sym}}_{Q_{\textrm{b}}}(\Omega )$. Let $x_*\in \partial \Omega$ and $r_*>0$ be such that $\Vert Q_\textrm{b}\Vert _{C^{1,1}(\partial \Omega \cap B_{r_*}(x_*))}\leqslant L$. There exist $\bar{\varvec{\varepsilon }}_{\textrm{bd}}>0$ and $\bar{\varvec{\kappa }}\in (0,1)$ depending only on $\partial \Omega \cap B_{r_*}(x_*)$ such that for every $x_0\in \partial \Omega \cap B_{r_*/4}(x_*)$ and every radius $r\in (0,r_*/4)$ small enough (depending only on $\partial \Omega \cap B_{r_*}(x_*)$, $\Lambda$, and L), the condition

$$\begin{aligned} \sup _{B_\rho ({\bar{x}})\subseteq B_{r}(x_0)} \frac{1}{\rho } \int _{B_\rho ({\bar{x}})\cap \Omega }|\nabla Q_\lambda |^2\,dx\leqslant \bar{\varvec{\varepsilon }}_{\textrm{bd}} \end{aligned}$$

implies $Q_\lambda \in C^{\omega }(B_{\bar{\varvec{\kappa }}r}(x_0)\cap \Omega )\cap C^{1,\alpha }(B_{\bar{\varvec{\kappa }}r}(x_0)\cap {\overline{\Omega }})$ for every $\alpha \in (0,1)$ with the estimate $\Vert \nabla Q_\lambda \Vert _{L^\infty (B_{\bar{\varvec{\kappa }}r}(x_0)\cap \Omega )}\leqslant C r^{-1}$ and a constant $C>0$ depending only on $\partial \Omega \cap B_{r_*}(x_*)$ and L. In addition, if $\partial \Omega \cap B_{r_*}(x_*)$ is of class $C^{k,\alpha }$ (of class $C^3$ for $k=2$) and $Q_{\textrm{b}}\in C^{k,\alpha }(\partial \Omega \cap B_{r_*}(x_*))$ with $k\geqslant 2$, then $Q_\lambda \in C^{k,\alpha }(B_{\bar{\varvec{\kappa }}r/2}(x_0)\cap {\overline{\Omega }})$ and $\Vert Q_\lambda \Vert _{C^{k,\alpha }(B_{\bar{\varvec{\kappa }}r/2}(x_0)\cap {\overline{\Omega }})}\leqslant C_{k,\alpha ,r}$ for a constant $C_{k,\alpha , r}>0$ depending only on r, $\partial \Omega \cap B_{r_*}(x_*)$, and $\Vert Q_{\textrm{b}}\Vert _{ C^{k,\alpha }(\partial \Omega \cap B_{r_*}(x_*))}$.

Sketch of the proof

Since $\partial \Omega$ is of class $C^3$, we can find $\delta >0$ such that the nearest point projection $\varvec{\pi }_\Omega$ on $\partial \Omega$ is well defined and of class $C^2$ in the $2\delta$-tubular neighborhood of $\partial \Omega \cap B_{r_*/2}(x_*)$. Then we argue as in [11, Section 2.2], and we consider the reflection of $Q_\lambda$ across $\partial \Omega$ given by [11, (2.22)] and denoted by ${{\widehat{Q}}}_\lambda$. Then we choose $r\in (0,\delta /2)$ small enough in such a way that $\varvec{\pi }_\Omega (B_r(y))\subseteq \partial \Omega \cap B_{2r}(y)$ and $\varvec{\sigma }_\Omega (B_r(y))\subseteq B_{2r}(y)$ for every $y\in \partial \Omega \cap B_{r_*/2}(x_*)$, where $\varvec{\sigma }_\Omega :=2\varvec{\pi }_\Omega -\textrm{id}$ is the geodesic reflection across $\partial \Omega$.

Arguing as in the proof of [11, Lemma 2.10], there exists a constant $\varvec{\kappa }\in (0,1)$ depending only on $\partial \Omega \cap B_{r_*}(x_*)$ such that

$$\begin{aligned} \sup _{B_\sigma (z)\subseteq B_{\varvec{\kappa }r}(x_0)} \frac{1}{\sigma } \int _{B_\sigma (z)}|\nabla {{\widehat{Q}}}_\lambda |^2\,dx\leqslant \sup _{B_\rho ({\bar{x}})\subseteq B_{r}(x_0)} \frac{C_1}{\rho } \int _{B_\rho ({\bar{x}})\cap \Omega }|\nabla Q_\lambda |^2\,dx + C_2 r \leqslant C_1 \bar{\varvec{\varepsilon }}_{\textrm{bd}} +C_2 r, \end{aligned}$$

for a constant $C_1>0$ depending only on $\partial \Omega \cap B_{r_*}(x_*)$, and a constant $C_2>0$ depending only on $\partial \Omega \cap B_{r_*}(x_*)$ and L. Then we choose $\bar{\varvec{\varepsilon }}_{\textrm{bd}}$ and r in such a way that $C_1 \bar{\varvec{\varepsilon }}_{\textrm{bd}} +C_2 r\leqslant \varvec{\varepsilon }_{\textrm{bd}}$, where $\varvec{\varepsilon }_{\textrm{bd}}>0$ is the constant provided by [11, Corollary 2.17] (note that $\varvec{\varepsilon }_{\textrm{bd}}$ only depends on $\partial \Omega \cap B_{r_*}(x_*)$). By Proposition 2.12, $Q_\lambda$ is a weak solution of (1.6) in $\Omega$. By our choice of $\varvec{\varepsilon }_{\textrm{bd}}>0$, the proofs of [11, Corollary 2.17 and Corollary 2.20] apply and lead to the main conclusions with $\bar{\varvec{\kappa }}:=\varvec{\kappa }/4$. Once the gradient estimate is obtained, higher order estimates follow from standard elliptic theory (see e.g. [15]). $\square$

Combining Proposition 3.6 with the boundary monotonicity formula in Proposition 3.4, we recover the following (more usual) epsilon-regularity at the boundary, which holds under smallness of the Dirichlet integral in a neighborhood of a single point.

Corollary 3.7

([11, 12], boundary $\varvec{\varepsilon }$-regularity 2) Let $\Lambda ,L>0$ and $\Omega \subseteq \mathbb {R}^3$ a bounded and axisymmetric open set with boundary of class $C^3$. Let $Q_\textrm{b}\in C^{1,1}(\partial \Omega ;\mathbb {S}^4)$ be an $\mathbb {S}^1$-equivariant map such that $\Vert Q_\textrm{b}\Vert _{C^{1,1}(\partial \Omega )}\leqslant L$. Let $\lambda \in [0,\Lambda ]$ and $Q_\lambda$ a minimizer of ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}^{\textrm{sym}}_{Q_{\textrm{b}}}(\Omega )$. There exist $\bar{\varvec{\varepsilon }}^\prime _{\textrm{bd}}>0$ and $\bar{\varvec{\kappa }}^\prime \in (0,1)$ depending only on $\Omega$ such that for every $x_0\in \partial \Omega$ and every radius $r>0$ small enough (depending only on $\Omega$, $\Lambda$, and L), the condition

$$\begin{aligned} \frac{1}{r} \int _{B_r(x_0)\cap \Omega }|\nabla Q_\lambda |^2\,dx\leqslant \bar{\varvec{\varepsilon }}^\prime _{\textrm{bd}} \end{aligned}$$

implies $Q_\lambda \in C^{\omega }(B_{\bar{\varvec{\kappa }}^\prime r}(x_0)\cap \Omega )\cap C^{1,\alpha }(B_{\bar{\varvec{\kappa }}^\prime r}(x_0)\cap {\overline{\Omega }})$ for every $\alpha \in (0,1)$ with the estimate $\Vert \nabla Q_\lambda \Vert _{L^\infty (B_{\bar{\varvec{\kappa }}^\prime r}(x_0)\cap \Omega )}\leqslant C r^{-1}$ and a constant $C>0$ depending only on $\Omega$ and L. In addition, if $\partial \Omega$ is of class $C^{k,\alpha }$ (of class $C^3$ for $k=2$) and $Q_{\textrm{b}}\in C^{k,\alpha }(\partial \Omega )$ with $k\geqslant 2$, then $Q_\lambda \in C^{k,\alpha }(B_{\bar{\varvec{\kappa }}^\prime r/2}(x_0)\cap {\overline{\Omega }})$ and $\Vert Q_\lambda \Vert _{C^{k,\alpha }(B_{\bar{\varvec{\kappa }}^\prime r/2}(x_0)\cap {\overline{\Omega }})}\leqslant C_{k,\alpha }$ for a constant $C_{k,\alpha }>0$ depending only on $\Omega$, and $\Vert Q_{\textrm{b}}\Vert _{ C^{k,\alpha }(\partial \Omega )}$.

Proof

Using the boundary monotonicity formula in Proposition 3.4, we can argue as [11, Proof of Lemma 2.6, Step 2] to show that

$$\begin{aligned} \sup _{B_\rho ({\bar{x}})\subseteq B_{r/6}(x_0)}\frac{1}{\rho }{\mathcal {E}}_\lambda (Q_\lambda ,B_\rho ({\bar{x}})\cap \Omega )\leqslant \frac{4}{r}{\mathcal {E}}_\lambda (Q_\lambda ,B_r(x_0)\cap \Omega )+C_1 r, \end{aligned}$$

for a constant $C_1>0$ depending only on $\Lambda$, L, and $\Omega$. Hence,

$$\begin{aligned} \sup _{B_\rho ({\bar{x}})\subseteq B_{r/6}(x_0)} \frac{1}{\rho } \int _{B_\rho ({\bar{x}})\cap \Omega }|\nabla Q_\lambda |^2\,dx\leqslant \frac{4}{r} \int _{B_r(x_0)\cap \Omega }|\nabla Q_\lambda |^2\,dx +C_2 r, \end{aligned}$$

for $r>0$ small and a further constant $C_2>0$ depending only on $\Lambda$, L, and $\Omega$.

Next we set $r_*:=4$, and we consider a finite covering of $\partial \Omega$ by balls $B_1(x_*^k)$, $k=1,\ldots , K$. We denoted by $\bar{\varvec{\varepsilon }}^k_{\textrm{bd}}$ and $\bar{\varvec{\kappa }}_k$ the constants provided by Proposition 3.6 with $x_*=x_*^k$. Choosing $\bar{\varvec{\varepsilon }}^\prime _{\textrm{bd}}:= \frac{1}{8}\min _k\bar{\varvec{\varepsilon }}^k_{\textrm{bd}}$, $\bar{\varvec{\kappa }}^\prime :=\frac{1}{6}\min _k\bar{\varvec{\kappa }}_k$, and then $r>0$ small enough such that $C_2r\leqslant \bar{\varvec{\varepsilon }}^\prime _{\textrm{bd}}$ (depending only on $\Omega$, $\Lambda$, and L), we obtain that $Q_\lambda$ satisfies

$$\begin{aligned} \sup _{B_\rho ({\bar{x}})\subseteq B_{r/6}(x_0)} \frac{1}{\rho } \int _{B_\rho ({\bar{x}})\cap \Omega }|\nabla Q_\lambda |^2\,dx\leqslant \bar{\varvec{\varepsilon }}^k_{\textrm{bd}}, \end{aligned}$$

for an index k such that $x_0\in \partial \Omega \cap B_1(x_*^k)$. Then the conclusion follows from Proposition 3.6. $\square$

Remark 3.8

(Locally flat geometry) In the following sections, we shall consider the situation where, for some $x_*\in \{x_3\text {-axis}\}$ and $r_*>0$, $\Omega \cap B_{2r_*}(x_*)=x_*+\{\pm x_3>0\}\cap B_{2r_*}(0)$ and $Q_{\textrm{b}}=\textbf{e}_0$ on $\partial \Omega \cap B_{2r_*}(x_*)=x_*+\{x_3=0\}\cap B_{2r_*}(0)$. According to [11, Remark 2.5] (see the proof of [12, Proposition 6.6]), if $Q_\lambda$ is as in Proposition 3.6, then

$$\begin{aligned}{} & {} \frac{1}{\rho }{\mathcal {E}}_\lambda \big (Q_\lambda ,B_\rho ({\bar{x}})\cap \Omega \big ) - \frac{1}{\sigma }{\mathcal {E}}_\lambda \big (Q_\lambda ,B_\sigma ({\bar{x}})\cap \Omega \big ) \nonumber \\{} & {} \quad = \int _{\big (B_\rho ({\bar{x}})\setminus B_\sigma (\bar{x})\big )\cap \Omega }\frac{1}{|x-{\bar{x}}|}\bigg |\frac{\partial Q_\lambda }{\partial |x-{\bar{x}}|}\bigg |^2\,dx +2\lambda \int _\sigma ^\rho \bigg (\frac{1}{t^2}\int _{B_t(\bar{x})\cap \Omega }W(Q_\lambda )\,dx\bigg )\,dt \nonumber \\ \end{aligned}$$

(3.3)

for every ${\bar{x}}\in \partial \Omega \cap B_{2r_*}(x_*)$ and $0<\rho<\sigma <2r_*-|x_*-{\bar{x}}|$. As in [11, Remark 2.7], it implies that

$$\begin{aligned} \sup _{B_\rho ({\bar{x}})\subseteq B_{r/6}(x_0)}\frac{1}{\rho }{\mathcal {E}}_\lambda (Q_\lambda ,B_\rho ({\bar{x}})\cap \Omega )\leqslant \frac{4}{r}{\mathcal {E}}_\lambda (Q_\lambda ,B_r(x_0)\cap \Omega ) \end{aligned}$$

for every $x_0\in \partial \Omega \cap B_{r_*}(x_*)$ and $0<r<r_*$. Repeating the proof of Corollary 3.7, we can apply Proposition 3.6 to obtain the existence of universal constants $\varvec{\varepsilon }^\sharp _{\textrm{bd}}>0$ and $\varvec{\kappa }^\sharp \in (0,1)$, such that for every $x_0\in \partial \Omega \cap B_{r_*/4}(x_*)$ and $r\in (0,r_*/4)$ small enough (depending only on $\Lambda$), the condition

$$\begin{aligned} \frac{1}{r}\int _{B_r(x_0)\cap \Omega }|\nabla Q_\lambda |^2\,dx\leqslant \varvec{\varepsilon }^\sharp _{\textrm{bd}} \end{aligned}$$

implies the same conclusions as in Proposition 3.6 in $B_{\varvec{\kappa }^\sharp r}(x_0)\cap \Omega$.

3.2 Persistence of smoothness

We now apply the regularity theory of the previous subsection to show that absence of singularities in energy minimizing configurations (within the equivariant class) is a strongly $W^{1,2}$-open/closed property.

Lemma 3.9

Let $(Q_*,\lambda _*)$ and a sequence $\{(Q_n,\lambda _n)\}$ in $W^{1,2}_{\textrm{sym}}(B_r;\mathbb {S}^4)\times [0,\infty )$ be such that $Q_n\rightarrow Q_*$ strongly in $W^{1,2}(B_r)$ and $\lambda _n\rightarrow \lambda _*$ as $n\rightarrow \infty$. Assume that $Q_*$ is minimizing ${\mathcal {E}}_{\lambda _*}$ among all $Q \in W^{1,2}_\textrm{sym}(B_r;\mathbb {S}^4)$ satisfying $Q=Q_*$ on $\partial B_r$, and that $Q_n$ is minimizing ${\mathcal {E}}_{\lambda _n}$ among all $Q \in W^{1,2}_{\textrm{sym}}(B_r;\mathbb {S}^4)$ satisfying $Q=Q_n$ on $\partial B_r$.

• (i) If $\textrm{sing}(Q_*)\cap B_r=\emptyset$, then for every $0<\rho <r$, there exists an integer $n_\rho$ such that $\textrm{sing}(Q_n) \cap B_\rho =\emptyset$ whenever $n\geqslant n_\rho$.

• (ii) If $\textrm{sing}(Q_n)\cap B_r=\emptyset$ for every n, then $\textrm{sing}(Q_*)\cap B_r=\emptyset$.

Proof

We start proving claim (i). Fix a radius $0<\rho <r$, and assume by contradiction that there exists a (not relabeled) subsequence such that $\textrm{sing}(Q_n) \cap B_\rho \not =\emptyset$ for every n. Then we choose for each n a point $x_n\in \textrm{sing}(Q_n) \cap B_\rho$. Extracting a further subsequence if necessary, we may assume that $x_n\rightarrow x_*\in {\overline{B}}_\rho$. On the other hand, since $Q_*$ is smooth in $B_r$, we can find a small enough radius $0<\sigma <r-\rho$ such that

$$\begin{aligned} \frac{1}{\sigma }\int _{B_\sigma (x_*)} |\nabla Q_*|^2\,dx\leqslant \frac{\varvec{\varepsilon }_{\textrm{in}}}{8}, \end{aligned}$$

where the universal constant $\varvec{\varepsilon }_{\textrm{in}}>0$ is given by Proposition 3.5. From the strong convergence of $Q_n$ toward $Q_*$, we deduce that

$$\begin{aligned} \frac{1}{\sigma }\int _{B_\sigma (x_*)} |\nabla Q_n|^2\,dx\leqslant \frac{\varvec{\varepsilon }_{\textrm{in}}}{4} \end{aligned}$$

for n large enough. By Proposition 3.5, it implies that $Q_n$ is smooth in $B_{\sigma /8}(x_*)$. Since $x_n\rightarrow x_*$, we have $x_n\in B_{\sigma /8}(x_*)$ for n large enough, contradicting the fact that $Q_n$ is singular at $x_n$.

We now prove claim (ii). To this purpose, it is enough to show that $\textrm{sing}(Q_*)\cap B_\rho =\emptyset$ for every $0<\rho <r$. Hence we fix an arbitrary radius $0<\rho <r$, and we assume by contradiction that $\textrm{sing}(Q_*)\cap B_\rho \not =\emptyset$. By Theorem 3.1, $\textrm{sing}(Q_*)\cap \overline{B}_\rho \subseteq \{x_3\text{-axis }\}$ is finite, and setting $I_\rho :=B_\rho \cap \{x_3\text{-axis }\}$, the trace of $Q_*$ on $I_\rho$ (see Corollary 2.11) is a non trivial piecewise constant function with values in $\{\pm \textbf{e}_0\}$ (since we are assuming that $\textrm{sing}(Q_*)\cap B_\rho \not =\emptyset$). On the other hand, $Q_n$ is smooth in ${\overline{B}}_\rho$, so that either $Q_n\equiv \textbf{e}_0$ or $Q_n\equiv -\textbf{e}_0$ on $I_\rho$. Extracting a subsequence if necessary, we may assume for instance that ${Q_n}_{|I_\rho }\equiv \textbf{e}_0$ for every n. By the strong $W^{1,2}$-convergence of $Q_n$ and the continuity of the trace operator established in Corollary 2.11, we infer that ${Q_n}_{|I_\rho }\rightarrow {Q_*}_{|I_\rho }$ in $L^1(I_\rho )$ as $n\rightarrow \infty$. Hence ${Q_*}_{|I_\rho }\equiv \textbf{e}_0$ contradicting its non triviality. $\square$

Corollary 3.10

Let $\Omega \subseteq \mathbb {R}^3$ be a bounded and axisymmetric open set with boundary of class $C^3$. Let $(Q^*_{\textrm{b}},\lambda _*)$ and a sequence $\{(Q^{(n)}_{\textrm{b}},\lambda _n)\}$ in $C^2_\textrm{sym}(\partial \Omega ;\mathbb {S}^4)\times [0,\infty )$ be such that $Q^{(n)}_{\textrm{b}}\rightarrow Q^*_{\textrm{b}}$ in $C^2(\partial \Omega )$, and $\lambda _n\rightarrow \lambda _*$ as $n\rightarrow \infty$. For each $n\in \mathbb {N}$, let $Q_n$ be a minimizer of ${\mathcal {E}}_{\lambda _n}$ over ${\mathcal {A}}^{\textrm{sym}}_{Q^{(n)}_{\textrm{b}}}(\Omega )$, $Q_*$ a minimizer of ${\mathcal {E}}_{\lambda _*}$ over ${\mathcal {A}}^\textrm{sym}_{Q^*_{\textrm{b}}}(\Omega )$, and assume that $Q_n\rightarrow Q_*$ strongly in $W^{1,2}(\Omega )$.

• (i) If $\textrm{sing}(Q_*)=\emptyset$, then there exists an integer $n_*$ such that $\textrm{sing}(Q_n)=\emptyset$ whenever $n\geqslant n_*$.

• (ii) If $\textrm{sing}(Q_n)=\emptyset$ for every n, then $\textrm{sing}(Q_*)=\emptyset$.

Proof

We start proving claim (i). To prove it, it is enough to show that there exists $\delta >0$ independent of n such that the $C^1$-norms of $Q_n$ are uniformly bounded in a $\delta$-neighborhood of $\partial \Omega$ (recall that $\textrm{sing}(Q_n)$ coincides with the discontinuity points of $Q_n$). Indeed, in this case we have $\textrm{sing}(Q_n)\subseteq \Omega \cap \{\textrm{dist}(\cdot ,\partial \Omega )\geqslant \delta \}$ for every n. Recalling that $\textrm{sing}(Q_n)\subseteq \{x_3\text {-axis}\}$ by Theorem 3.1, we choose a finite covering of $\Omega \cap \{\textrm{dist}(\cdot ,\partial \Omega )\geqslant \delta \}\cap \{x_3\text {-axis}\}$ by open balls $B_{\delta /2}(x_1),\ldots ,B_{\delta /2}(x_K)$. We apply Lemma 3.9 in each $B_{\delta }(x_j)$ to find an integer $n_*$ such that $\textrm{sing}(Q_n)\cap B_{\delta /2}(x_j)=\emptyset$ for each j and every $n\geqslant n_*$. Hence $\textrm{sing}(Q_n)=\emptyset$ for every $n\geqslant n_*$.

To show that the $C^1$-norm of $Q_n$ remains bounded in a $\delta$-neighborhood of $\partial \Omega$, we shall make use of the regularity estimates from Sect. 3.1. By Theorem 3.2, $Q_*$ is of class $C^{1,\alpha }$ for every $\alpha \in (0,1)$ in a neighborhood of $\partial \Omega$. Hence, for a radius $\eta >0$ to be chosen small enough, we have

$$\begin{aligned} \frac{1}{\eta } \int _{B_{\eta }(y)\cap \Omega }|\nabla Q_*|^2\,dx \leqslant \frac{\bar{\varvec{\varepsilon }}^\prime _{\textrm{bd}}}{2}\quad \hbox { for every}\ y\in \partial \Omega , \end{aligned}$$

where the constant $\bar{\varvec{\varepsilon }}^\prime _\textrm{bd}>0$ (depending only on $\Omega$) is provided by Corollary 3.7. Next we set $\Lambda :=\sup _n\lambda _n<\infty$, and $L:=\sup _n\Vert Q^{(n)}_{\textrm{b}}\Vert _{C^{1,1}(\partial \Omega )}<\infty$. We now choose $\eta >0$ small enough (depending only on $\Lambda$, L, and $\Omega$) such that the conclusion of Corollary 3.7 holds. We also set $r_*:=\bar{\varvec{\kappa }}^\prime \eta$ with constant $\bar{\varvec{\kappa }}^\prime \in (0,1)$ still given by Corollary 3.7 (depending only on $\Omega$), and we consider a finite covering $B_{r_*}(y_1),\ldots , B_{r_*}(y_J)$ of $\partial \Omega$ with $y_j\in \partial \Omega$. Since $Q_n\rightarrow Q_*$ strongly in $W^{1,2}(\Omega )$, we can find an integer $n_*$ such that

$$\begin{aligned} \frac{1}{\eta } \int _{ B_{\eta }(y_j)\cap \Omega }|\nabla Q_n|^2\,dx\leqslant \bar{\varvec{\varepsilon }}^\prime _{\textrm{bd}}\quad \hbox {for each}\,\, j=1,\ldots ,J\,\, \hbox {and every}\,\, n\geqslant n_*. \end{aligned}$$

Applying Corollary 3.7, we infer that $Q_n\in C^{1,\alpha }(B_{r_*}(y_j)\cap \Omega )$ for every $\alpha \in (0,1)$ and each j with the estimate $\Vert \nabla Q_n\Vert _{L^\infty (B_{r_*}(y_j)\cap \Omega )}\leqslant C r_*^{-1}$ and a constant C independent of n. Since the balls $B_{r_*}(y_1),\ldots , B_{r_*}(y_J)$ cover $\partial \Omega$, the $C^1$-norm of $Q_n$ remains bounded in a $\delta$-neighborhood of $\partial \Omega$ for some $\delta \in (0,r_*)$.

We now prove claim (ii). Assume by contradiction that $\textrm{sing}(Q_*)\not =\emptyset$, i.e., $Q_*$ has at least one singular point $x_*\in \Omega$, which must belong to the $\{x_3\text {-axis}\}$ by Theorem 3.1. Choose a radius $r>0$ such that $B_r(x_*)\subseteq \Omega$. Since $Q_n\rightarrow Q_*$ strongly in $W^{1,2}(\Omega )$, we can apply Lemma 3.9 in the ball $B_r(x_*)$ to infer that $Q_*$ is smooth in $B_r(x_*)$, a contradiction. $\square$

3.3 Persistence of singularities

By analogy with the previous subsection, we now study the behavior of the singular set along strongly $W^{1,2}$-convergent sequences of minimizers, proving that singular points converge to singular points. The following result is the counterpart in the present context of [3, Theorem 1.8] (see also [18]).

Proposition 3.11

Let $(Q_*,\lambda _*)$ and a sequence $\{(Q_n,\lambda _n)\}$ in $W^{1,2}_{\textrm{sym}}(B_r;\mathbb {S}^4)\times [0,\infty )$ be such that $Q_n\rightarrow Q_*$ strongly in $W^{1,2}(B_r)$ and $\lambda _n\rightarrow \lambda _*$ as $n\rightarrow \infty$. Assume that $Q_*$ is minimizing ${\mathcal {E}}_{\lambda _*}$ among all $Q \in W^{1,2}_\textrm{sym}(B_r;\mathbb {S}^4)$ satisfying $Q=Q_*$ on $\partial B_r$, and that $Q_n$ is minimizing ${\mathcal {E}}_{\lambda _n}$ among all $Q \in W^{1,2}_{\textrm{sym}}(B_r;\mathbb {S}^4)$ satisfying $Q=Q_n$ on $\partial B_r$. Then, for every radius $\rho \in (0,r)$ such that $\textrm{sing}(Q_*)\cap \partial B_\rho =\emptyset$ and $\textrm{sing}(Q_*)\cap B_\rho =\{a_1^*,\ldots , a_K^*\}$, there exists an integer $n_\rho$ such that for every $n\geqslant n_\rho$, $\textrm{sing}(Q_n)\cap \partial B_\rho =\emptyset$ and $\textrm{sing}(Q_n)\cap B_\rho =\{a_1^n,\ldots , a_K^n\}$ for some distinct points $a_1^n, \ldots ,a_K^n\in B_\rho$ satisfying $|a_j^n-a_j^*|\rightarrow 0$ as $n\rightarrow \infty$ for $j = 1, \dots , K$.

Proof

By Theorem 3.1, $\textrm{sing}(Q_*)$ and $\textrm{sing}(Q_n)$ are made of locally finitely many points in $B_r\cap \{x_3\text {-axis}\}$. If $\textrm{sing}(Q_*)\cap \partial B_\rho =\emptyset$, then $Q_*$ is smooth in a neighborhood of $\partial B_\rho$. Applying Lemma 3.9 at the north and south pole of $\partial B_\rho$, we infer that there exists an integer ${\bar{n}}_\rho$ such that $Q_n$ is smooth in a uniform neighborhood of $\partial B_\rho$ for every $n\geqslant {\bar{n}}_\rho$. Then we set $\Sigma ^\rho _*:=\textrm{sing}(Q_*)\cap B_\rho$ and $\Sigma ^\rho _n:=\textrm{sing}(Q_n)\cap B_\rho$. We claim that $\Sigma ^\rho _n\rightarrow \Sigma ^\rho _*$ in the Hausdorff distance. To prove this claim, let us first consider $a_*\in \Sigma ^\rho _*$, and prove that there exists $a_n\in \Sigma ^\rho _n$ such that $a_n\rightarrow a_*$. By contradiction, assume that $\Sigma ^\rho _n$ remains at a positive distance from $a_*$ for n large. Then we can find $\eta >0$ such that $B_\eta (a_*)\cap \Sigma ^\rho _n=\emptyset$ for n large enough. Applying Lemma 3.9 in $B_\eta (a_*)$, we deduce that $B_\eta (a_*)\cap \Sigma ^\rho _*=\emptyset$, a contradiction. The other way around, let $a_n\in \Sigma ^\rho _n$ be a sequence converging to some point $a_*$. Since $\Sigma ^\rho _n$ remains at a positive distance from $\partial B_\rho$, we have $a_*\in B_\rho$, and let us show that $a_*\in \Sigma ^\rho _*$. Again by contradiction, assume that $a_*\not \in \Sigma ^\rho _*$. Then we can find $\eta >0$ such that $B_{2\eta }(a_*)\cap \Sigma ^\rho _*=\emptyset$. Applying Lemma 3.9 in $B_{2\eta }(a_*)$, we infer that $B_{\eta }(a_*)\cap \Sigma ^\rho _n=\emptyset$ for n large enough, which contradicts the fact that $a_n\rightarrow a_*$. Hence $\Sigma ^\rho _n\rightarrow \Sigma ^\rho _*$ in the Hausdorff distance.

To complete the proof of Proposition 3.11, we shall make use of the following key lemma, giving a lower bound on the mutual distance between singularities for minimizers, in the spirit of [3, Theorem 2.1] for minimizing harmonic maps into $\mathbb {S}^2$.

Lemma 3.12

Let $M,\Lambda >0$ and $\lambda \in [0,\Lambda ]$. Assume that $Q_\lambda \in W^{1,2}_{\textrm{sym}}(B_1;\mathbb {S}^4)$ is minimizing ${\mathcal {E}}_\lambda (\cdot ,B_1)$ among all maps $Q\in W^{1,2}_\textrm{sym}(B_1;\mathbb {S}^4)$ satisfying $Q=Q_\lambda$ on $\partial B_1$, and that ${\mathcal {E}}_\lambda (Q_\lambda ,B_1)\leqslant M$. Then there exists a constant $\kappa =\kappa (M,\Lambda )>0$ depending only on M and $\Lambda$ such that

$$\begin{aligned} |a-b|\geqslant \kappa \quad \hbox { for every}\ a,b\in \textrm{sing}(Q_\lambda )\cap {\overline{B}}_{1/2}, a\not =b. \end{aligned}$$

Proof

We argue by contradiction assuming that there exists a sequence $\{Q_n\}$ in $W^{1,2}_{\textrm{sym}}(B_1;\mathbb {S}^4)$ and $\lambda _n\in [0,\Lambda ]$ such that $Q_n$ is minimizing ${\mathcal {E}}_{\lambda _n}(\cdot ,B_1)$ among all maps $Q\in W^{1,2}_{\textrm{sym}}(B_1;\mathbb {S}^4)$ satisfying $Q=Q_n$ on $\partial B_1$, and ${\mathcal {E}}_{\lambda _n}(Q_{n},B_1)\leqslant M$, and such that there exists two distinct points $a_n,b_n\in \textrm{sing}(Q_\lambda )\cap {\overline{B}}_{1/2}$ satisfying $r_n:=|a_n-b_n|\rightarrow 0$ as $n\rightarrow \infty$. Extracting a subsequence if necessary, we may assume that $\lambda _n\rightarrow \lambda _*\in [0,\Lambda ]$, $\lim _{n\rightarrow \infty } a_n=\lim _{n\rightarrow \infty } b_n= c_*\in {\overline{B}}_{1/2}$. By the compactness theorem in [12, Theorem 5.1], we can find a (not relabeled) subsequence such that $Q_n\rightarrow Q_*$ strongly in $W^{1,2}_{\textrm{loc}}(B_1)$ for a map $Q_*\in W^{1,2}_{\textrm{sym}}(B_1;\mathbb {S}^4)$ which is minimizing ${\mathcal {E}}_{\lambda _*}(\cdot ,B_1)$ among all maps $Q\in W^{1,2}_{\textrm{sym}}(B_1;\mathbb {S}^4)$ satisfying $Q=Q_*$ on $\partial B_1$. Arguing as in the proof of Proposition 3.11, we infer that $c_*\in \textrm{sing}(Q_*)$. Setting $c_n:=(a_n+b_n)/2$, we have $c_n\rightarrow c_*$, and we define for $x\in B_2$ and n large enough,

$$\begin{aligned} {\bar{Q}}_n(x):=Q_n(c_n+r_n x). \end{aligned}$$

Since $a_n,b_n\in \{x_3\text {-axis}\}$, we have $c_n\in \{x_3\text {-axis}\}$, and thus ${\bar{Q}}_n\in W^{1,2}_\textrm{sym}(B_2;\mathbb {S}^4)$. From the minimality of $Q_n$ and a change of variables, we infer that ${\bar{Q}}_n$ minimizes ${\mathcal {E}}_{r_n^2\lambda _n}(\cdot ,B_2)$ among all maps $Q\in W^{1,2}_{\textrm{sym}}(B_2;\mathbb {S}^4)$ such that $Q={\bar{Q}}_n$ on $\partial B_2$. Extracting a subsequence if necessary, we may assume that $p_1:=(a_n-c_n)/r_n=(0,0,1/2)$ and $p_2:=(b_n-c_n)/r_n=(0,0,-1/2)$. Then, by construction, $p_1,p_2\in \textrm{sing}({\bar{Q}}_n)$.

By the interior monotonicity formula in Proposition 3.3, we have for every $x_0\in B_2$, every $t\in (0,\textrm{dist}(x_0,\partial B_2)]$ and $r \in (0,1)$,

$$\begin{aligned} \frac{1}{t}{\mathcal {E}}_{r^2_n\lambda _n}\big ({\bar{Q}}_n,B_t(x_0)\big )&= \frac{1}{r_n t}{\mathcal {E}}_{\lambda _n}\big (Q_n,B_{r_nt}(c_n+r_n x_0))\big )\nonumber \\&\leqslant \frac{1}{r-|c_n+r_nx_0-c_*|}{\mathcal {E}}_{\lambda _n}\big (Q_n,B_{r-|c_n+r_n x_0-c_*|}(c_n+r_n x_0)\big )\nonumber \\&\leqslant \frac{1}{r-|c_n+r_nx_0-c_*|}{\mathcal {E}}_{\lambda _n}\big (Q_n,B_{r+|c_n+r_n x_0-c_*|}(c_*)\big ) \end{aligned}$$

(3.4)

whenever n is large enough. Since $Q_n\rightarrow Q_*$ strongly in $W^{1,2}_{\textrm{loc}}(B_1)$ and $\lambda _n\rightarrow \lambda _*$, we have

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{1}{r-|c_n+r_nx_0-c_*|}{\mathcal {E}}_{\lambda _n}\big (Q_n,B_{r+|c_n+r_n x_0-c_*|}(c_*)\big )=\frac{1}{r}{\mathcal {E}}_{\lambda _*}\big (Q_*,B_{r}(c_*)\big ). \end{aligned}$$

(3.5)

In view of (3.4)–(3.5) with $x_0=0$ and $t=2$, we first deduce that $\sup _n{\mathcal {E}}_{r_n^2\lambda _n}(\bar{Q}_n,B_2) <\infty$. By the compactness result in [12, Theorem 5.1], we can find a (not relabeled) subsequence such that ${\bar{Q}}_n\rightarrow {\bar{Q}}_*$ strongly in $W^{1,2}_{\textrm{loc}}(B_2)$ for a map ${\bar{Q}}_*\in W^{1,2}_{\textrm{sym}}(B_2;\mathbb {S}^4)$ which is minimizing ${\mathcal {E}}_{0}(\cdot ,B_2)$ among all maps $Q\in W^{1,2}_{\textrm{sym}}(B_2;\mathbb {S}^4)$ satisfying $Q={\bar{Q}}_*$ on $\partial B_2$.

Letting $n\rightarrow \infty$ in (3.4), we infer from (3.5) that for every $x_0\in B_2$, every $t\in (0,\textrm{dist}(x_0,\partial B_2))$, and $r \in (0,1/2)$ small enough,

$$\begin{aligned} \frac{1}{t}{\mathcal {E}}_{0}\big ({\bar{Q}}_*,B_t(x_0)\big )\leqslant \frac{1}{r}{\mathcal {E}}_{\lambda _*}\big (Q_*,B_{r}(c_*)\big ). \end{aligned}$$

(3.6)

On the other hand, since $c_*\in \textrm{sing}(Q_*)$, Theorem 3.1 tells us that

$$\begin{aligned} \lim _{r\rightarrow 0}\frac{1}{r}\int _{B_r(c_*)} \frac{1}{2} |\nabla Q_*|^2\,dx= 4\pi . \end{aligned}$$

Letting now $r\rightarrow 0$ in (3.6) yields

$$\begin{aligned} \frac{1}{t}{\mathcal {E}}_{0}\big ({\bar{Q}}_*,B_t(x_0)\big )\leqslant 4\pi \quad \text {for every }x_0\in B_2\text { and }t\in (0,\textrm{dist}(x_0,\partial B_2)). \end{aligned}$$

(3.7)

On the other hand, $p_1$ and $p_2$ are singular points of ${\bar{Q}}_n$ for each n, and thus $p_1,p_2\in \textrm{sing}({\bar{Q}}_*)$ by Lemma 3.9. As a consequence, Theorem 3.1 and the interior monotonicity formula in Proposition 3.3 imply that for $j=1,2$,

$$\begin{aligned} \frac{1}{t}{\mathcal {E}}_{0}\big ({\bar{Q}}_*,B_t(p_j)\big )\geqslant 4\pi \quad \forall t\in (0,1). \end{aligned}$$

(3.8)

Setting $y_t:=(0,0,t-1/2)$ for $t\in (0,1)$, since $B_t(p_1) \cup B_{1-t}(p_2) \subseteq B_1(y_t)$, we gather (3.7) and (3.8) to derive

$$\begin{aligned}{} & {} 4\pi \geqslant {\mathcal {E}}_{0}\big ({\bar{Q}}_*,B_1(y_t)\big ) \\{} & {} \quad \geqslant {\mathcal {E}}_{0}\big ({\bar{Q}}_*,B_t(p_1)\big )+ {\mathcal {E}}_{0}\big ({\bar{Q}}_*,B_{1-t}(p_2)\big )\geqslant 4\pi t+ 4\pi (1-t)=4\pi \quad \forall t\in (0,1). \end{aligned}$$

Therefore $|\nabla {\bar{Q}}_*|^2\equiv 0$ a.e. in $B_1(y_t)\setminus \big (B_t(p_1)\cup B_{1-t}(p_2)\big )$ for every $t\in (0,1)$. Since

$$\begin{aligned} B_1\cap \bigcup _{0<t<1}\Big ( B_1(y_t)\setminus \big (B_t(p_1)\cup B_{1-t}(p_2)\big )\Big )= B_1\setminus [p_1,p_2] , \end{aligned}$$

we conclude that $|\nabla {\bar{Q}}_*|^2\equiv 0$ a.e. in $B_1$. Thus ${\bar{Q}}_*$ is constant in $B_1$, which contradicts the fact that ${\bar{Q}}_*$ is singular at $p_1,p_2\in B_1$. $\square$

Proof of Proposition  3.11Completed. To complete the proof, it remains to show that there exists an integer $n_\rho \geqslant {\bar{n}}_\rho$ such that $\textrm{Card}\,\Sigma ^\rho _n=\textrm{Card}\,\Sigma ^\rho _*$ for $n\geqslant n_\rho$. Once again we argue by contradiction assuming that for some (not relabeled) subsequence, we have $\textrm{Card}\,\Sigma ^\rho _n \not =\textrm{Card}\,\Sigma ^\rho _*$. In view of the previous discussion, $\textrm{Card}\,\Sigma ^\rho _n >\textrm{Card}\,\Sigma ^\rho _*$ for n large enough. As a consequence, there exist at least two points $a_n,b_n\in \Sigma ^\rho _n$ such that $a_n\not =b_n$ and $\lim _n a_n= \lim _n b_n= c_*$ for a point $c_*\in \Sigma ^\rho _*$. In particular, $|a_n-b_n|\rightarrow 0$. Then we choose a radius $\eta >0$ such that $B_\eta (c_*)\subseteq B_r$. For n large enough, we have $a_n,b_n\in B_{\eta /2}(c_*)$. Rescaling variables, we can apply Lemma 3.12 in $B_\eta (c_*)$ to deduce that $|a_n-b_n|\geqslant \kappa \eta$ for some constant $\kappa >0$ depending only on $\sup _n\frac{1}{\eta }{\mathcal {E}}_{\lambda _n}\big (Q_n,B_\eta (c_*)\big )<\infty$ and $\sup _n \eta ^2\lambda _n<\infty$, which contradicts the fact that $|a_n-b_n|\rightarrow 0$. $\square$

The following result is the global counterpart of Proposition 3.11.

Corollary 3.13

Let $\Omega \subseteq \mathbb {R}^3$ be a bounded and axisymmetric open set with boundary of class $C^3$. Let $(Q^*_{\textrm{b}},\lambda _*)$ and a sequence $\{(Q^{(n)}_{\textrm{b}},\lambda _n)\}$ in $C^2_\textrm{sym}(\partial \Omega ;\mathbb {S}^4)\times [0,\infty )$ be such that $Q^{(n)}_{\textrm{b}}\rightarrow Q^*_{\textrm{b}}$ in $C^2(\partial \Omega )$, and $\lambda _n\rightarrow \lambda _*$ as $n\rightarrow \infty$. For each $n\in \mathbb {N}$, let $Q_n$ be a minimizer of ${\mathcal {E}}_{\lambda _n}$ over ${\mathcal {A}}^{\textrm{sym}}_{Q^{(n)}_{\textrm{b}}}(\Omega )$, $Q_*$ a minimizer of ${\mathcal {E}}_{\lambda _*}$ in ${\mathcal {A}}^{\textrm{sym}}_{Q^*_\textrm{b}}(\Omega )$, and assume that $Q_n\rightarrow Q_*$ strongly in $W^{1,2}(\Omega )$. If $\textrm{sing}(Q_*)=\{a^*_1,\ldots ,a_K^*\}$, then there exists an integer $n_*$ such that for every $n\geqslant n_*$, $\textrm{sing}(Q_n)=\{a^n_1,\ldots ,a_K^n\}$ for some distinct points $a_1^n,\ldots ,a_K^n$ satisfying $|a_j^n-a_j^*|\rightarrow 0$ as $n\rightarrow \infty$.

Proof

By Theorem 3.2, $Q_*$ is smooth in $\Omega {\setminus }\textrm{sing}(Q_*)$ and $\textrm{sing}(Q_*)$ is a finite subset of $\Omega \cap \{x_3\text {-axis}\}$, i.e., $\textrm{sing}(Q_*)=\{a^*_1,\ldots ,a_K^*\}\subseteq \Omega \cap \{x_3\text {-axis}\}$. Let us fix $\delta >0$ such that $B_{3\delta }(a_i^*)\cap B_{3\delta }(a_j^*)=\emptyset$ if $i\not =j$, and $\textrm{dist}(a^*_j,\partial \Omega )\geqslant 3\delta$. We set $K_\delta :=\{x\in \Omega : \textrm{dist}(x,\partial \Omega )\geqslant \delta \}{\setminus }\cup _jB_{\delta }(a^*_j)$, and we claim that $Q_n \rightarrow Q_*$ in $C^2(K_\delta )$. Indeed, by smoothness of $Q_*$ away from $\textrm{sing}(Q_*)$, we can find a radius $r\in (0,\delta /2)$ such that

$$\begin{aligned} \frac{1}{r}\int _{B_r(x_0)}|\nabla Q_*|^2\,dx\leqslant \frac{\varvec{\varepsilon }_{\textrm{in}}}{8} \quad \hbox { for every}\ x_0\in K_\delta , \end{aligned}$$

where the universal constant $\varvec{\varepsilon }_{\textrm{in}}>0$ is provided by Proposition 3.5. Choosing r smaller if necessary (depending only on $\Lambda :=\sup _n\lambda _n<\infty$), we may assume that the conclusion of Proposition 3.5 holds for every $\lambda _n$. Then we consider a finite covering $B_{r/16}(y_1),\ldots , B_{r/16}(y_J)$ of $K_\delta$. Since $Q_n\rightarrow Q_*$ strongly in $W^{1,2}(\Omega )$, we have for n large enough,

$$\begin{aligned} \frac{1}{r}\int _{B_r(y_j)}|\nabla Q_n|^2\,dx\leqslant \frac{\varvec{\varepsilon }_{\textrm{in}}}{4} \quad \hbox { for every}\ j=1,\ldots ,J. \end{aligned}$$

By Proposition 3.5, for n large enough, $Q_n$ is smooth in each $B_{r/16}(y_j)$ and $\Vert Q_n\Vert _{C^3(B_{r/16}(y_j))}\leqslant C_r$ for some constant $C_r>0$. Therefore $Q_n$ remains bounded in $C^3(K_\delta )$ for n large enough. From the $W^{1,2}$-convergence of $Q_n$ towards $Q_*$ and the Arzelà-Ascoli Theorem, we deduce that $Q_n\rightarrow Q_*$ in $C^2(K_\delta )$.

Now we set $\Omega _\delta :=\Omega \setminus \cup _jB_{2\delta }(a^*_j)$ which is a bounded and axisymmetric open set with boundary of class $C^3$. By our discussion above and the assumption on $Q^{(n)}_{\textrm{b}}$, the restriction of $Q_n$ to $\partial \Omega _\delta$ converges in the $C^2$-topology to the restriction of $Q_*$ to $\partial \Omega _\delta$. Applying Corollary 3.10 in $\Omega _\delta$, we infer that $\textrm{sing}(Q_n)\cap \Omega _\delta =\emptyset$ for n large enough. Then we can apply Proposition 3.11 in each ball $B_{3\delta }(a^*_j)$ with $\rho =2\delta$. It shows that for n large enough, $\textrm{sing}(Q_n)\cap \overline{B}_{2\delta }(a^*_j)=\{a^n_j\}$ for some point $a^n_j\rightarrow a^*_j$ as $n\rightarrow \infty$. $\square$

3.4 Coexistence results in a ball

In this subsection, we take advantage of the results above to study the space $(\text {boundary condition})\times (\lambda \text {-parameter})$. We are interested in the nature of the sets of data leading to smooth or/and singular solutions. To motivate this question, we recall the results in [12] showing the existence for $\lambda \geqslant 0$ arbitrary of boundary conditions $Q^{\textrm{smooth}}_{\textrm{b}}$ and $Q^\textrm{sing}_{\textrm{b}}$ in $C^\infty _{\textrm{sym}}(\partial B_1;\mathbb {S}^4)$ such that any minimizer of ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}^\textrm{sym}_{Q^{\textrm{smooth}}_{\textrm{b}}}(B_1)$, resp. over ${\mathcal {A}}^\textrm{sym}_{Q^{\textrm{sing}}_{\textrm{b}}}(B_1)$, is smooth, resp. singular. To apply the results of the previous subsection, the topology for the space of boundary conditions we shall working with is the $C^{2,\alpha }$-topology for some $\alpha \in (0,1)$.

Given $\alpha \in (0,1)$, we consider the sets

$$\begin{aligned}{} & {} BD^{\textrm{smooth}}_\alpha :=\Bigg \{(Q_{\textrm{b}},\lambda ) \in C_{\textrm{sym}}^{2,\alpha }(\partial B_1;\mathbb {S}^4)\times [0,\infty ): \textrm{sing}(Q_\lambda )=\emptyset \text { for every }Q_\lambda \in \mathop \textrm{argmin}_{{\mathcal {A}}^{\textrm{sym}}_{Q_{\textrm{b}}}(B_1)}{\mathcal {E}}_\lambda \Bigg \} , \\{} & {} BD^{\textrm{sing}}_\alpha :=\Bigg \{(Q_{\textrm{b}},\lambda ) \in C_{\textrm{sym}}^{2,\alpha }(\partial B_1;\mathbb {S}^4)\times [0,\infty ): \textrm{sing}(Q_\lambda )\not =\emptyset \text { for every }Q_\lambda \in \mathop \textrm{argmin}_{{\mathcal {A}}^{\textrm{sym}}_{Q_{\textrm{b}}}(B_1)}{\mathcal {E}}_\lambda \Bigg \} , \end{aligned}$$

and

$$\begin{aligned} BD^{\textrm{coexist}}_\alpha :=\Big (C_{\textrm{sym}}^{2,\alpha }(\partial B_1;\mathbb {S}^4)\times [0,\infty )\Big )\setminus \Big (BD^{\textrm{smooth}}_\alpha \cup BD^{\textrm{sing}}_\alpha \Big ). \end{aligned}$$

As already mentioned, $BD^{\textrm{smooth}}_\alpha \not =\emptyset$ and $BD^{\textrm{sing}}_\alpha \not =\emptyset$ by [12, Theorem 1.2 & Theorem 1.3], and more precisely,

$$\begin{aligned} BD^{\textrm{smooth}}_\alpha \cap \big (C_{\textrm{sym}}^{2,\alpha }(\partial B_1;\mathbb {S}^4)\times \{\lambda \}\big )\ne \emptyset \hbox { and } BD^{\textrm{sing}}_\alpha \cap \big (C_{\textrm{sym}}^{2,\alpha }(\partial B_1;\mathbb {S}^4)\times \{\lambda \}\big )\ne \emptyset \text { for every}\ \lambda \geqslant 0. \end{aligned}$$

The main result of this subsection is the following theorem whose proof is postponed to the end of the subsection.

Theorem 3.14

Let $\alpha \in (0,1)$. The (disjoint) sets $BD^{\textrm{smooth}}_\alpha$ and $BD^{\textrm{sing}}_\alpha$ are open in $C^{2,\alpha }_\textrm{sym}(\partial B_1;\mathbb {S}^4)\times [0,\infty )$, and $BD^\textrm{coexist}_\alpha$ coincides with their common boundary, i.e.,

$$\begin{aligned} \partial BD^{\textrm{smooth}}_\alpha = BD^{\textrm{coexist}}_\alpha =\partial BD^{\textrm{sing}}_\alpha . \end{aligned}$$

As a direct consequence of Theorem 3.14, we obtain the following corollary proving immediately claims (i), (ii), and (iii) of Theorem 1.1. With the aid of Remark 3.16 below, also the last claim of Theorem 1.1, and hence its full proof, follows at once from the corollary.

Corollary 3.15

Let $\alpha \in (0,1)$, $\lambda >0$, and $\Gamma :[0,1]\rightarrow C^{2,\alpha }_{\textrm{sym}}(\partial B_1;\mathbb {S}^4)$ a continuous curve such that $(\Gamma (0),\lambda )\in BD^{\textrm{sing}}_\alpha$ and $(\Gamma (1),\lambda )\in BD^{\textrm{smooth}}_\alpha$. There exist $0<t_1\leqslant t_2<1$ such that

• (i) $(\Gamma (t),\lambda )\in BD^{\textrm{sing}}_\alpha$ for every $0\leqslant t<t_1$;

• (ii) $(\Gamma (t),\lambda )\in BD^{\textrm{smooth}}_\alpha$ for every $t_2<t\leqslant 1$;

• (iii) $(\Gamma (t_1),\lambda ), (\Gamma (t_2),\lambda )\in BD^{\textrm{coexist}}_\alpha$.

Proof

Consider the continuous curve ${\widehat{\Gamma }}:[0,1]\rightarrow C^{2,\alpha }_{\textrm{sym}}(\partial B_1;\mathbb {S}^4)\times [0,\infty )$ given by ${\widehat{\Gamma }}(t):=(\Gamma (t),\lambda )$. Then $\widehat{\Gamma }(0)\in BD^{\textrm{sing}}_\alpha$ and ${\widehat{\Gamma }}(1)\in BD^{\textrm{smooth}}_\alpha$. Consider

$$\begin{aligned} t_1:=\sup \big \{t\in [0,1]: {\widehat{\Gamma }}(s)\in BD^{\textrm{sing}}_\alpha \hbox { for every}\ 0\leqslant s\leqslant t\}. \end{aligned}$$

By Theorem 3.14 and the continuity of ${\widehat{\Gamma }}$, we have $t_1\in (0,1)$ and ${\widehat{\Gamma }}(t_1)\in \partial BD^{\textrm{sing}}_\alpha = BD^{\textrm{coexist}}_\alpha$, so that (i) holds.

Then we consider

$$\begin{aligned} t_2:=\inf \big \{t\in [0,1]: {\widehat{\Gamma }}(s)\in BD^{\textrm{smooth}}_\alpha \hbox { for every}\ t\leqslant s\leqslant 1\}. \end{aligned}$$

Clearly $t_1\leqslant t_2$, and as above, Theorem 3.14 and the continuity of ${\widehat{\Gamma }}$ imply $t_2<1$ and $\widehat{\Gamma }(t_2)\in \partial BD^{\textrm{smooth}}_\alpha = BD^\textrm{coexist}_\alpha$ proving (ii), and completing the proof. $\square$

Remark 3.16

As already alluded in the Introduction, there exists at least one curve $\Gamma$ with the properties required by Corollary 3.15. This is obtained by concatenating the curves built in (the proofs of) [12, Theorem 1.2 and Theorem 1.3]. Thus, the corollary shows in particular that $BD^{\textrm{coexist}}_{\alpha }$ is not empty, clearly implying the last claim of Theorem 1.1, and concluding its proof.

The proof of Theorem 3.14 rests on our regularity results together with the unique continuation property for real analytic maps. This tool leads to the following uniqueness statement.

Lemma 3.17

Let $Q_\lambda \in W^{1,2}_{\textrm{sym}}(B_1;\mathbb {S}^4)$ be a minimizer of ${\mathcal {E}}_\lambda (\cdot ,B_1)$ among all $Q\in W^{1,2}_{\textrm{sym}}(B_1;\mathbb {S}^4)$ satisfying $Q=Q_\lambda$ on $\partial B_1$. For every radius $\rho \in (0,1)$ such that $\textrm{sing}(Q_\lambda )\cap \partial B_\rho =\emptyset$, the restriction of $Q_\lambda$ to $B_\rho$ is the unique minimizer of ${\mathcal {E}}_\lambda$ over the class ${\mathcal {A}}^\textrm{sym}_{Q_{\lambda }}(B_\rho )$.

Proof

By Theorem 3.1 and since $\textrm{sing}(Q_\lambda )\cap \partial B_\rho =\emptyset$, $Q_\lambda$ is (real) analytic in a neighborhood of $\partial B_\rho$. We fix a further radius $\rho ^\prime \in (\rho ,1)$ such that $Q_\lambda$ is analytic in the open annulus $A:=B_{\rho ^\prime }{\setminus } \overline{B}_\rho$. Now, let $Q_\rho$ be a minimizer of ${\mathcal {E}}_\lambda$ over the class ${\mathcal {A}}^{\textrm{sym}}_{Q_{\lambda }}(B_\rho )$. We consider the comparison map

$$\begin{aligned} {\bar{Q}}_\lambda (x):={\left\{ \begin{array}{ll} Q_\rho (x) &{} \hbox { if}\ x\in B_\rho \\ Q_\lambda (x) &{} \hbox { if}\ x\in B_1\setminus B_\rho , \end{array}\right. } \end{aligned}$$

which belongs to $W^{1,2}_{\textrm{sym}}(B_1;\mathbb {S}^4)$ and agrees with $Q_\lambda$ on $\partial B_1$. Hence,

$$\begin{aligned}{} & {} {\mathcal {E}}_\lambda (Q_\rho ,B_\rho )+{\mathcal {E}}_\lambda (Q_\lambda ,B_1\setminus B_\rho ) \leqslant {\mathcal {E}}_\lambda (Q_\lambda ,B_\rho )+{\mathcal {E}}_\lambda (Q_\lambda ,B_1\setminus B_\rho )\\{} & {} \quad ={\mathcal {E}}_\lambda (Q_\lambda ,B_1) \leqslant {\mathcal {E}}_\lambda (\bar{Q}_\lambda ,B_1)= {\mathcal {E}}_\lambda (Q_\rho ,B_\rho )+{\mathcal {E}}_\lambda (Q_\lambda ,B_1\setminus B_\rho ). \end{aligned}$$

Thus ${\mathcal {E}}_\lambda (Q_\lambda ,B_1)= {\mathcal {E}}_\lambda (\bar{Q}_\lambda ,B_1)$ which in turn implies that ${\bar{Q}}_\lambda$ minimizes ${\mathcal {E}}_\lambda (\cdot ,B_1)$ among all $Q\in W^{1,2}_{\textrm{sym}}(B_1;\mathbb {S}^4)$ satisfying $Q=Q_\lambda$ on $\partial B_1$. Once again, by Theorem 3.1, $\bar{Q}_\lambda$ is real analytic in $B_1{\setminus } \textrm{sing}(\bar{Q}_\lambda )$ with $\textrm{sing}({\bar{Q}}_\lambda )$ a locally finite subset in $B_1$. As a consequence, the map $\bar{Q}_\lambda -Q_\lambda$ is analytic in the open set $B_1 \setminus \Sigma$ containing A, where $\Sigma = \textrm{sing}(Q_\lambda )\cup \textrm{sing}({\bar{Q}}_\lambda )$ is a locally finite set in $B_1$, and ${\bar{Q}}_\lambda -Q_\lambda \equiv 0$ in A. Thus, by unique continuation for real analytic maps, ${\bar{Q}}_\lambda =Q_\lambda$ in $B_1 {\setminus } \Sigma$, which shows that $Q_\rho =Q_\lambda$ in $B_\rho$. $\square$

In order to apply the results of the previous subsections, we establish now the following strong $W^{1,2}$-compactness property of minimizers.

Lemma 3.18

Let $\alpha \in (0,1)$ and $\{(Q^{(n)}_{\textrm{b}},\lambda _n)\}$ be a converging sequence in $C^{2,\alpha }_{\textrm{sym}}(\partial B_1;\mathbb {S}^4)\times [0,\infty )$, and denote by $(Q^*_\textrm{b},\lambda _*)$ its limit. Every sequence $\{Q_n\}$ such that $Q_n$ minimizes ${\mathcal {E}}_{\lambda _n}$ over ${\mathcal {A}}^\textrm{sym}_{Q^{(n)}_{\textrm{b}}}(B_1)$ admits a subsequence strongly converging in $W^{1,2}(B_1)$ to some $Q_*$ minimizing ${\mathcal {E}}_{\lambda _*}$ over ${\mathcal {A}}^{\textrm{sym}}_{Q^*_\textrm{b}}(B_1)$.

Proof

We consider the comparison map ${\bar{Q}}_n$ defined by $\bar{Q}_n(x):=Q^{(n)}_{\textrm{b}}(x/|x|)$. A direct computation shows that $\sup _n{\mathcal {E}}_{\lambda _n}({\bar{Q}}_n,B_1)<\infty$ since $Q^{(n)}_{\textrm{b}}$ is bounded in the $C^{2,\alpha }$-topology. By minimality of $Q_n$, we have ${\mathcal {E}}_{\lambda _n}(Q_n,B_1)\leqslant {\mathcal {E}}_{\lambda _n}({\bar{Q}}_n,B_1)\leqslant C$ for a constant C independent of n. Applying [12, Theorem 5.1], we deduce that for a (not relabeled) subsequence, $Q_n\rightharpoonup Q_*$ weakly in $W^{1,2}(B_1)$ and $Q_n\rightarrow Q_*$ strongly in $W^{1,2}_\textrm{loc}(B_1)$ for some $Q_*$ minimizing ${\mathcal {E}}_{\lambda _*}$ over ${\mathcal {A}}^{\textrm{sym}}_{Q^*_{\textrm{b}}}(B_1)$. Hence it remains to prove that $Q_n\rightarrow Q_*$ strongly in $W^{1,2}(B_1)$.

First we notice that $Q_n\rightarrow Q_*$ strongly in $L^4(B_1)$ by the compact Sobolev embedding $W^{1,2}(B_1)\hookrightarrow L^4(B_1)$. Therefore,

$$\begin{aligned} \lambda _n\int _\Omega W(Q_n)\,dx\rightarrow \lambda _* \int _\Omega W(Q_*)\,dx. \end{aligned}$$

(3.9)

Now we fix an arbitrary small $\delta \in (0,1)$, and we define for $x\in B_1$,

$$\begin{aligned} {\widetilde{Q}}_n(x):={\left\{ \begin{array}{ll} \displaystyle Q_*\bigg (\frac{x}{1-\delta }\bigg ) &{} \hbox { if}\ x\in B_{1-\delta },\\ \displaystyle \bigg (1-\frac{1-|x|}{\delta }\bigg )Q_\textrm{b}^n\bigg (\frac{x}{|x|}\bigg ) + \frac{1-|x|}{\delta }Q_\textrm{b}^*\bigg (\frac{x}{|x|}\bigg ) &{} \text {if }x\in B_1\setminus B_{1-\delta }. \end{array}\right. } \end{aligned}$$

Then ${\widetilde{Q}}_n\in W^{1,2}_{\textrm{sym}}(B_1;{\mathcal {S}}_0)$ satisfies ${\widetilde{Q}}_n=Q_{\textrm{b}}^{(n)}$ on $\partial B_1$. Since $Q_{\textrm{b}}^{(n)}\rightarrow Q_{\textrm{b}}^*$ in $C^{2,\alpha }(\partial B_1)$, ${\widetilde{Q}}_n$ converges to the mapping $x\mapsto Q_\textrm{b}^*(x/|x|)$ in $C^{2,\alpha }({\overline{B}}_1{\setminus } B_{1-\delta })$. In particular, $|{\widetilde{Q}}_n|\geqslant 1/2$ for n large enough which allows us to define

$$\begin{aligned} {{\widehat{Q}}}_n:= \frac{{\widetilde{Q}}_n}{|{\widetilde{Q}}_n|} \in {\mathcal {A}}^{\textrm{sym}}_{Q^n_{\textrm{b}}}(B_1). \end{aligned}$$

By minimality of $Q_n$, we have ${\mathcal {E}}_{\lambda _n}(Q_n,B_1)\leqslant {\mathcal {E}}_{\lambda _n}({{\widehat{Q}}}_n,B_1)$. Since ${{\widehat{Q}}}_n$ also converges to $x\mapsto Q_{\textrm{b}}^*(x/|x|)$ in $C^{2,\alpha }({\overline{B}}_1\setminus B_{1-\delta })$, we have

$$\begin{aligned}{} & {} \limsup _{n\rightarrow \infty } {\mathcal {E}}_{\lambda _n}(Q_n,B_1)\leqslant \lim _{n\rightarrow \infty } {\mathcal {E}}_{\lambda _n}({{\widehat{Q}}}_n,B_{1-\delta })+ \lim _{n\rightarrow \infty } {\mathcal {E}}_{\lambda _n}({{\widehat{Q}}}_n,B_1\setminus B_{1-\delta }) \\{} & {} \quad = (1-\delta ){\mathcal {E}}_{(1-\delta )^2\lambda _*}(Q_*,B_{1}) + {\mathcal {E}}_{\lambda ^*}\big ( Q^*_{\textrm{b}}(x/\left| x \right| ), B_1 \setminus B_{1-\delta }\big ), \end{aligned}$$

Now letting $\delta \rightarrow 0$, we deduce that

$$\begin{aligned} \limsup _{n\rightarrow \infty } {\mathcal {E}}_{\lambda _n}(Q_n,B_1)\leqslant {\mathcal {E}}_{\lambda _*}(Q_*,B_{1}) . \end{aligned}$$

In view of (3.9), we thus have $\limsup _{n}\int _{B_1}|\nabla Q_n|^2\,dx\leqslant \int _{B_1}|\nabla Q_*|^2\,dx$. On the other hand, $\liminf _n\int _{B_1}|\nabla Q_n|^2\,dx\geqslant \int _{B_1}|\nabla Q_*|^2\,dx$ by lower semicontinuity of the Dirichlet energy. Hence $\lim _n\int _{B_1}|\nabla Q_n|^2\,dx= \int _{B_1}|\nabla Q_*|^2\,dx$, and the conclusion classically follows. $\square$

Proof

Step 1. We first prove that $BD^{\textrm{smooth}}_\alpha$ is open. Let $\{(Q^{(n)}_{\textrm{b}},\lambda _n)\}$ be a sequence in $C^{2,\alpha }(\partial B_1;\mathbb {S}^4)\times [0,\infty )$ such that $\lambda _n\rightarrow \lambda _*$ and $Q^{(n)}_{\textrm{b}}\rightarrow Q^*_{\textrm{b}}$ in $C^{2,\alpha }(\partial B_1)$ for some $(Q^*_{\textrm{b}},\lambda _*)\in BD^{\textrm{smooth}}_\alpha$. We aim to prove that $(Q^{(n)}_\textrm{b},\lambda _n)\in BD^{\textrm{smooth}}_\alpha$ for n large enough. By contradiction, assume that $(Q^{(n)}_{\textrm{b}},\lambda _n)\not \in BD^{\textrm{smooth}}_\alpha$ for some (not relabeled) subsequence. Then, for each n we can find a minimizer $Q_n$ of ${\mathcal {E}}_{\lambda _n}$ over ${\mathcal {A}}^{\textrm{sym}}_{Q^{(n)}_\textrm{b}}(B_1)$ such that $\textrm{sing}(Q_n)\not =\emptyset$. By Lemma 3.18, we can extract a further subsequence such that $Q_n\rightarrow Q_*$ strongly in $W^{1,2}(B_1)$ for some map $Q_*$ minimizing ${\mathcal {E}}_{\lambda _*}$ over ${\mathcal {A}}^\textrm{sym}_{Q^*_{\textrm{b}}}(B_1)$. Since $(Q^*_{\textrm{b}},\lambda _*)\in BD^\textrm{smooth}_\alpha$, we have $\textrm{sing}(Q_*)=\emptyset$, and we infer from Corollary 3.10 that $\textrm{sing}(Q_n)=\emptyset$ for n large enough, a contradiction.

Step 2. We now prove that $BD^{\textrm{sing}}_\alpha$ is open following the same argument as above. Assume that $\{(Q^{(n)}_{\textrm{b}},\lambda _n)\}$ is a sequence in $C^{2,\alpha }(\partial B_1;\mathbb {S}^4)\times [0,\infty )$ converging to some $(Q^*_{\textrm{b}},\lambda _*)\in BD^\textrm{sing}_\alpha$. Assume also by contradiction that $(Q^{(n)}_\textrm{b},\lambda _n)\not \in BD^{\textrm{sing}}_\alpha$. Then we can find minimizers $Q_n$ of ${\mathcal {E}}_{\lambda _n}$ over ${\mathcal {A}}^\textrm{sym}_{Q^{(n)}_{\textrm{b}}}(B_1)$ such that $\textrm{sing}(Q_n)=\emptyset$. Then $Q_n\rightarrow Q_*$ strongly in $W^{1,2}(B_1)$ for some $Q_*$ minimizing ${\mathcal {E}}_{\lambda _*}$ over ${\mathcal {A}}^\textrm{sym}_{Q^*_{\textrm{b}}}(B_1)$ (up to a subsequence). Since $(Q^*_\textrm{b},\lambda _*)\in BD^{\textrm{sing}}_\alpha$, we have $\textrm{sing}(Q_*)\not =\emptyset$ which is in contradiction with $\textrm{sing}(Q_n)=\emptyset$ and Corollary 3.10.

Step 3. To conclude the proof, it remains to prove that $BD^{\textrm{coexist}}_\alpha$ is the common boundary of $BD^\textrm{smooth}_\alpha$ and $BD^{\textrm{sing}}_\alpha$. Let $(Q^*_\textrm{b},\lambda _*)\in BD^{\textrm{coexist}}_\alpha$, and $Q^{\textrm{t}}_*$ and $Q^{\textrm{s}}_*$ be two minimizers of ${\mathcal {E}}_{\lambda _*}$ over ${\mathcal {A}}^{\textrm{sym}}_{Q^*_{\textrm{b}}}(B_1)$ such that $\textrm{sing}(Q^{\textrm{t}}_*)=\emptyset$ and $\textrm{sing}(Q^\textrm{s}_*)\not =\emptyset$. By Theorem 3.2, we have $Q^\textrm{t}_*\in C^{2,\alpha }({\overline{B}}_1)$ and we can find a radius $\rho _*\in (0,1)$ such that $Q^{\textrm{s}}_*\in C^{2,\alpha }(\overline{B}_1{\setminus } B_{\rho _*})$ (i.e., $\textrm{sing}(Q^{\textrm{s}}_*)\subseteq {\overline{B}}_{\rho _*}$). We fix an arbitrary sequence $\{\rho _n\} \subseteq (\rho _*,1)$ such that $\rho _n\rightarrow 1$ as $n\rightarrow \infty$, and we set for $x\in \partial B_1$,

$$\begin{aligned} Q^{\textrm{t},n}_{\textrm{b}}(x):= Q^{\textrm{t}}_*(\rho _n x)\quad \text {and}\quad Q^{\textrm{s},n}_{\textrm{b}}(x):= Q^{\textrm{s}}_*(\rho _n x). \end{aligned}$$

Then $(Q^{\textrm{t},n}_{\textrm{b}},\rho _n^2\lambda _*)\rightarrow (Q^*_\textrm{b},\lambda _*)$ and $(Q^{\textrm{s},n}_{\textrm{b}},\rho _n^2\lambda _*)\rightarrow (Q^*_{\textrm{b}},\lambda _*)$ in $C^{2,\alpha }(\partial B_1)\times [0,\infty )$. On the other hand, rescaling variables we infer from Lemma 3.17 that the maps $Q^\textrm{t}_n:x\mapsto Q^{\textrm{t}}_*(\rho _n x)$ and $Q^{\textrm{s}}_n:x\mapsto Q^{\textrm{s}}_*(\rho _n x)$ are the unique minimizers of ${\mathcal {E}}_{\rho _n^2\lambda _*}$ over ${\mathcal {A}}^\textrm{sym}_{Q^{\textrm{t},n}_{\textrm{b}}}(B_1)$ and ${\mathcal {A}}^\textrm{sym}_{Q^{\textrm{s},n}_{\textrm{b}}}(B_1)$ respectively. Since $\textrm{sing}(Q^{\textrm{t}}_n)=\emptyset$ and $\textrm{sing}(Q^{\textrm{s}}_n)\not =\emptyset$, it shows that $(Q^{\textrm{t},n}_\textrm{b},\rho _n^2\lambda _*)\in BD^{\textrm{smooth}}_\alpha$ and $(Q^{\textrm{s},n}_{\textrm{b}},\rho _n^2\lambda _*)\in BD^{\textrm{sing}}_\alpha$ for n large enough. Hence $(Q^*_{\textrm{b}},\lambda _*)\in \partial BD^\textrm{smooth}_\alpha \cap \partial BD^{\textrm{sing}}_\alpha$, thus $BD^\textrm{coexist}_\alpha \subseteq \partial BD^{\textrm{smooth}}_\alpha \cap \partial BD_\alpha ^{\textrm{sing}}$. Now, to reach the claimed conclusion, it is enough to prove that $BD^{\textrm{coexists}}_\alpha \supseteq \partial BD^{\textrm{smooth}}_\alpha \cup \partial BD^\textrm{sing}$. Indeed, this and the previous inclusion together imply as announced $BD^{\textrm{coexists}}_\alpha = \partial BD^\textrm{smooth}_\alpha = \partial BD^{\textrm{smooth}}_\alpha$. To this end, notice that $C^{2,\alpha }(\partial B_1;\mathbb {S}^4) \times [0,\infty )$ is the union of the disjoint sets $BD_\alpha ^{\textrm{smooth}}$, $BD_\alpha ^{\textrm{sing}}$, and $BD^{\textrm{coexist}}_\alpha$. Since the first two sets are open, $BD_\alpha ^{\textrm{smooth}} \cup BD^\textrm{coexist}_\alpha$ and $BD_\alpha ^{\textrm{sing}} \cup BD^\textrm{coexist}_\alpha$ are closed, hence they must contain the closures of $BD_\alpha ^{\textrm{smooth}}$ and $BD_\alpha ^{\textrm{sing}}$, respectively. In turn, this means that $BD_\alpha ^{\textrm{coexist}}$ contains both $\partial BD_\alpha ^{\textrm{smooth}}$ and $\partial BD_\alpha ^\textrm{sing}$ (indeed, $BD_\alpha ^{\textrm{smooth}}$ and $BD_\alpha ^{\textrm{sing}}$, being open, are disjoint from their boundaries). Therefore, $\partial BD_\alpha ^{\textrm{smooth}} \cup \partial BD_\alpha ^{\textrm{sing}} \subseteq BD_\alpha ^{\textrm{coexist}}$, and the conclusion follows. $\square$

4 Landau–de Gennes minimizers in 2D

In this section, we examine a two dimensional minimization problem whose importance (beyond its own interest) will be revealed mostly in Sect. 5. We consider the minimization of the LdG energy among equivariant unit norm configurations defined on a two dimensional disc $\mathbb {D}_\rho := \left\{ z \in \mathbb {C}: \left| z \right| < \rho \right\}$. We will always assume $\rho =1$ (discarding the subscript for simplicity) which can always be achieved by rescaling the domain. In view of Lemma 2.6 and Corollary 2.7, admissible configurations can be described as maps in the space $W_{\textrm{sym}}^{1,2}({\mathbb D};{\mathbb S}^4)$ with the two equivalent forms: either in terms of tensors $Q \in {\mathbb S}^4 \subseteq {\mathcal {S}}_0$, or in terms of $u \in {\mathbb S}^4 \subseteq \mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C}$. However, we shall mostly rely on the $\mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C}$-description as it is more suited for our purposes.

We consider, for fixed $\lambda \geqslant 0$, the 2D-LdG energy $E_\lambda$ as in (1.11) and we aim to minimize it over the $\mathbb {S}^1$-equivariant class ${\mathcal {A}}^\textrm{sym}_{\overline{H}}(\mathbb {D})$ defined in (1.12), where ${\overline{H}}:\partial \mathbb {D}\rightarrow \mathbb {R}P^2 \subseteq \mathbb {S}^4$ denotes the radial anchoring map defined in (1.13). According to the correspondence in Corollary 2.7, we have ${\overline{H}}\simeq g_{\overline{H}}$ where $g_{\overline{H}}:\partial \mathbb {D}\rightarrow \mathbb {S}^4\subseteq \mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C}$ is given by

$$\begin{aligned} g_{\overline{H}}(z):=\left( -\frac{1}{2},0,\frac{\sqrt{3}}{2}z^2\right) . \end{aligned}$$

(4.1)

Here and in the sequel, we make use of the complex variable $z:=x_1+ix_2$, identifying in this way $\mathbb {R}^2$ with the complex plane $\mathbb {C}$.

As we announced in Theorem 1.2 and proved in the present section, the uniaxial or biaxial character of any minimizer of $E_\lambda$ over ${\mathcal {A}}^{\textrm{sym}}_{\overline{H}}(\mathbb {D})$ depends on $\lambda$ in a crucial way. More precisely, a sharp transition in the qualitative properties of minimizers occurs through a biaxial escape mechanism, as the strength parameter $\lambda$ of the confining potential W in (1.11) decreases.

Note that, by Lemma 2.10, we have ${\mathcal {A}}_{\overline{H}}^{\textrm{sym}}(\mathbb {D}) = {\mathcal {A}}_{\textrm{N}} \cup {\mathcal {A}}_{\textrm{S}}$ with disjoint union, and

$$\begin{aligned} {\mathcal {A}}_{\textrm{N}}:= \big \{ Q \in {\mathcal {A}}^\textrm{sym}_{\overline{H}}(\mathbb {D}): Q(0) = \textbf{e}_0\big \}\simeq \big \{ u \in \widetilde{{\mathcal {A}}}^{\textrm{sym}}_{ g_{\overline{H}}}(\mathbb {D}): u(0) = (1,0,0) \big \}=: \widetilde{{\mathcal {A}}}_{\textrm{N}}, \end{aligned}$$

(4.2)

and

$$\begin{aligned} {\mathcal {A}}_{\textrm{S}}\!:=\! \big \{ Q \in {\mathcal {A}}^{\textrm{sym}}_{ \overline{H}}(\mathbb {D}): Q(0)\!=\! -\textbf{e}_0\big \} \!\simeq \! \big \{ u \in \widetilde{{\mathcal {A}}}^{\textrm{sym}}_{ g_{\overline{H}}}(\mathbb {D}): u(0) \!=\! (-1,0,0) \big \}\!=:\! \widetilde{{\mathcal {A}}}_{\textrm{S}}\,. \end{aligned}$$

(4.3)

We aim to describe precisely to which of these two components the minimizers of $E_\lambda$ over ${\mathcal {A}}^\textrm{sym}_{\overline{H}}(\mathbb {D})$ belong to as the parameter $\lambda$ varies. To tackle this question, we rely in an essential way on a gap phenomenon for the Dirichlet energy $E_0$ over the two components of the class ${\mathcal {A}}_{\overline{H}}^{\textrm{sym}}(\mathbb {D}) = {\mathcal {A}}_{\textrm{N}} \cup {\mathcal {A}}_{\textrm{S}}$ which is of independent interest. This is the object of the next two subsections. By studying the minimization problem of $E_0$ in each class ${\mathcal {A}}_{\textrm{N}}$ or ${\mathcal {A}}_{\textrm{S}}$, we shall prove that the corresponding infima are different. Describing the set of minimizers for both the infima, we shall also make the energy gap fully explicit.

4.1 Large equivariant harmonic maps in 2D

In this subsection, we classify all critical points of the Dirichlet energy $E_0$ in the class ${\mathcal {A}}_{\overline{H}}^\textrm{sym}(\mathbb {D})$ satisfying $Q(0)= \textbf{e}_0$. According to Proposition  2.12, those are critical points of $E_0$ over $W^{1,2}(\mathbb {D};\mathbb {S}^4)$, and thus equivariant (weakly) harmonic maps from $\mathbb {D}$ into $\mathbb {S}^4$ satisfying $Q=\overline{H}$ on $\partial \mathbb {D}$. In terms of the isometric correspondence $Q\simeq u$ from Corollary 2.7, we are interested in equivariant (weakly) harmonic maps u into $\mathbb {S}^4\subseteq \mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C}$ satisfying $u=\ g_{\overline{H}}$ on $\partial \mathbb {D}$ and $u(0)=(1,0,0)$. As recalled in the Introduction, these harmonic maps are usually referred to in the literature as the large solutions of the harmonic map system, see [8]. They escape from the (small) spherical cap containing the image of the boundary data $g_{\overline{H}}$ given in (4.1), as opposed to the small solution discussed in Proposition 4.6, for which the escape phenomenon does not hold.

Recall that $u \in W^{1,2}(\mathbb {D};\mathbb {S}^4)$ is a weakly harmonic map in $\mathbb {D}$ if u is a critical point of the Dirichlet energy

$$\begin{aligned} \widetilde{E}_0(u):= \int _{\mathbb {D}} \frac{1}{2}\left| \nabla u \right| ^2\,dx \end{aligned}$$

(4.4)

with respect to compactly supported perturbations preserving the $\mathbb {S}^4$-constraint. If, in addition, $u=g_{\overline{H}}$ on $\partial \mathbb {D}$ in the sense of traces, then u is a distributional solution of the following boundary value problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta u + \left| \nabla u \right| ^2 u=0 &{} \text{ in } \mathbb {D},\\ u = g_{\overline{H}} &{} \text{ on } \partial \mathbb {D}. \end{array}\right. } \end{aligned}$$

(4.5)

By Hélein’s theorem [19] and the general analyticity results for elliptic systems from [33, Chapter 6], such a map u is real analytic in the interior. Under the Dirichlet boundary condition $g_{\overline{H}}$, the map u is actually real analytic up to the boundary by [33, 37]. Hence it is harmonic in $\overline{\mathbb {D}}$ in the classical sense. According to (2.16), an equivariant harmonic map u has the form

$$\begin{aligned} u(re^{i\phi })=(f_0(r),f_1(r) e^{i \phi },f_2(r) e^{i2\phi }), \end{aligned}$$

(4.6)

and the Euler–Lagrange equation in (4.5) rewrites into a system of ODEs for $r \in (0,1]$ (see Remark 2.14),

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle f^{\prime \prime }_0+\frac{1}{r} f^\prime _0 = -\left| \nabla u \right| ^2 f_0 ,\\ \displaystyle f^{\prime \prime }_1+\frac{1}{r} f^\prime _1 = -\left| \nabla u \right| ^2 f_1 -\frac{1}{r^2}f_1 ,\\ \displaystyle f^{\prime \prime }_2+\frac{1}{r} f^\prime _2 = -\left| \nabla u \right| ^2 f_2 -\frac{4}{r^2}f_2 . \end{array}\right. } \end{aligned}$$

(4.7)

Here $f(r):=(f_0(r),f_1(r),f_2(r)) \in \mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C}$, and by (2.17),

$$\begin{aligned} \left| \nabla u \right| ^2=\left| \partial _r u \right| ^2+\frac{1}{r^2}\left| \partial _\phi u \right| ^2=\left| f^\prime \right| ^2+\frac{1}{r^2}\left( \left| f_1 \right| ^2 +4\left| f_2 \right| ^2 \right) \,. \end{aligned}$$

(4.8)

In order to describe the equivariant solutions to (4.5) satisfying the condition $u(0)=(1,0,0)$, we shall combine (4.7) with the classification of equivariant harmonic spheres from [12]. Following [12], it is convenient to use complex differentiation through the usual Wirtinger’s operators

$$\begin{aligned}\partial _z=\frac{1}{2} \left( \frac{\partial }{\partial x_1} -i \frac{\partial }{\partial x_2}\right) \,, \quad \partial _{\bar{z}}=\frac{1}{2} \left( \frac{\partial }{\partial x_1} +i \frac{\partial }{\partial x_2}\right) \,. \end{aligned}$$

Since $\left| \nabla u \right| ^2=2 \left| \partial _z u \right| ^2+2 \left| \partial _{\bar{z}} u \right| ^2$ and $\Delta u=4 \partial _{\bar{z}z}u$, the harmonic map equation (4.5) rewrites as

$$\begin{aligned} \partial _{\bar{z}z}u +\frac{1}{2} \big ( \left| \partial _z u \right| ^2+ \left| \partial _{\bar{z}} u \right| ^2\big ) u=0. \end{aligned}$$

Let us now recall the classical notions of conformality and isotropy.

Definition 4.1

A smooth map $u:\Omega \rightarrow {\mathbb S}^4 \subseteq \mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C}$ defined on an open set $\Omega \subseteq {\mathbb C}$ is said to be

• (i) conformal if

  $$\begin{aligned} \partial _z u \cdot \partial _z u:= \sum _{j=0}^4 (\partial _z u_j)^2= \frac{1}{4} \left| \partial _{x_1} u \right| ^2- \frac{1}{4} \left| \partial _{x_2} u \right| ^2- \frac{i}{2}\partial _{x_1}u \cdot \partial _{x_2}u \equiv 0 , \end{aligned}$$

  (4.9)

  where “$\,\cdot \,$” denotes the Euclidean scalar product in $\mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C}\simeq \mathbb {R}^5$ extended by bilinearity to $\mathbb {C}^5$;

• (ii) isotropic if

  $$\begin{aligned} \partial ^2_{z} u \cdot \partial ^2_{z} u:= \sum _{j=0}^4 (\partial ^2_{z} u_j)^2\equiv 0 \,, \end{aligned}$$

  (4.10)

  where $\partial ^2_{z} = \frac{1}{4} (\partial ^2_{x_1} -\partial ^2_{x_2}) -\frac{i}{2} \partial _{x_1x_2}$.

Here we shall not need the full definition of total isotropy from [20, Chapter 6], which is satisfied by the harmonic spheres discussed in [12, Section 3]. Actually, under (4.9)–(4.10), it will be automatically satisfied for the equivariant solutions to (4.5), as we are going to show in the following lemma. This extension result is the starting point of the classification of all large equivariant solutions to (4.5).

Lemma 4.2

If $u \in W^{1,2}_{\textrm{sym}}(\mathbb {D}; \mathbb {S}^4)$ is a weak solution of (4.5), then u is real analytic and conformal in $\overline{{\mathbb D}}$. Moreover, u uniquely extends to a map $U \in C^\omega (\mathbb {C};{\mathbb S}^4)$ which is equivariant, harmonic, conformal, and isotropic in the whole $\mathbb {C}$.

Proof

The map u being a weak solution to (4.5), it is real analytic up to the boundary, as we already remarked. Being equivariant, it is of the form (4.6), where the map $f=(f_0, f_1,f_2)$ satisfies $|f|\equiv 1$ and solves system (4.7) for $r \in (0,1]$.

Since u belongs to $W^{1,2}(\mathbb {D})$, we infer from (4.8) that

$$\begin{aligned} \int _0^1 \big (r^2 \left| f^\prime \right| ^2+\left| f_1 \right| ^2+4\left| f_2 \right| ^2\big ) \frac{dr}{r} <\infty . \end{aligned}$$

Hence $r_j^2 \left| f^\prime (r_j) \right| ^2+\left| f_1(r_j) \right| ^2+4\left| f_2(r_j) \right| ^2 \rightarrow 0$ for some sequence $r_j \downarrow 0$. Since $|f|^2\equiv 1$, we have $f^\prime \cdot f\equiv 0$. Hence, taking the scalar product of (4.7) with $r^2 f^\prime$ and integrating between $r_j$ and r leads to

$$\begin{aligned}{} & {} r^2 \left| \partial _r f (r) \right| ^2-\left| f_1(r) \right| ^2-4\left| f_2(r) \right| ^2 \\{} & {} \quad = r_j^2 \left| \partial _r f (r_j) \right| ^2-\left| f_1(r_j) \right| ^2-4\left| f_2(r_j) \right| ^2 \rightarrow 0 \hbox { as}\ j\rightarrow \infty . \end{aligned}$$

Thus $\left| \partial _r u \right| ^2- \frac{1}{r^2} \left| \partial _\phi u \right| ^2 =\left| \partial _r f (r) \right| ^2-\frac{1}{r^2}\big (\left| f_1(r) \right| ^2+4\left| f_2(r) \right| ^2\big )\equiv 0$. On the other hand, it follows from (4.6) that $\partial _r u \cdot \frac{1}{r} \partial _\phi u \equiv 0$. Therefore u is conformal in the sense of Definition 4.1 since such property is independent of the chosen orthonormal frame.

Now we solve the Cauchy problem for (4.7) with Cauchy data $(f(1), f^\prime (1))$ to extend f to its maximal interval of existence $(0,r_{\max }) \supseteq (0,1]$. We denote by $\widetilde{f}$ the maximal solution. Then ${\widetilde{f}}$ is real analytic, and therefore it satisfies

$$\begin{aligned} |\widetilde{f}(r)|^2 =1 \quad \text {and}\quad | \widetilde{f}^\prime |^2=\frac{1}{r^2} \big ( |\widetilde{f}_1|^2+4|\widetilde{f}_2|^2\big ) \quad \text {for every } r\in (0, r_{\max }), \end{aligned}$$

(4.11)

since these identities hold for every $r \in (0,1]$. As a consequence of the uniform a priori bounds induced by (4.11), it follows that $r_{\max }=+\infty$, i.e., $\widetilde{f}$ solves (4.7) for $r \in (0,\infty )$.

Setting

$$\begin{aligned} U(re^{i\phi }):=\big (\widetilde{f}_0(r),\widetilde{f}_1(r) e^{i \phi },\widetilde{f}_2(r) e^{i2\phi }\big ), \end{aligned}$$

it follows by construction that U is an equivariant real analytic harmonic map from $\mathbb {C}$ into ${\mathbb S}^4$, extending u to the whole plane. Repeating the argument above on $\widetilde{f}$ with $r \in (0,\infty )$, we infer that U is conformal in $\mathbb {C}$. To complete the proof, it thus remains to show that U is isotropic, i.e., it satisfies (4.10). To this purpose, we adapt to the equivariant setting the strategy in [20, Proposition 6.1]. First, we notice that

$$\begin{aligned}{} & {} \partial _z U\cdot U= \frac{1}{2} \partial _z |U|^2 \equiv 0 \,, \\{} & {} \partial ^2_{z} U\cdot U= \partial _z (\partial _z U\cdot U ) - \partial _z U \cdot \partial _z U \equiv 0 \,, \end{aligned}$$

and

$$\begin{aligned} \partial ^2_{z} U\cdot \partial _z U= \frac{1}{2} \partial _z (\partial _z U\cdot \partial _z U) \equiv 0 \,, \end{aligned}$$

since $|U|^2=1$ and U is conformal. Then we consider $g:=\partial ^2_{z}U \cdot \partial ^2_{z}U$ which is a complex-valued smooth function. Since U is a harmonic map, we have

$$\begin{aligned} \begin{aligned} \partial _{\bar{z}} g&=\partial _{\bar{z}} (\partial ^2_{z}U \cdot \partial ^2_{z}U )= \partial ^2_{z} U \cdot \partial _z ( 2\partial _{\bar{z}z}U )=-\partial ^2_{z} U \cdot \partial _z \left( \big (\left| \partial _z U \right| ^2+ \left| \partial _{\bar{z}} U \right| ^2\big ) U \right) \\&= -\big (\partial ^2_{z} U \cdot U\big ) \partial _z \big ( \left| \partial _z U \right| ^2+ \left| \partial _{\bar{z}} U \right| ^2 \big ) -\big (\partial ^2_{z} U \cdot \partial _z U\big ) \big ( \left| \partial _z U \right| ^2+ \left| \partial _{\bar{z}} U \right| ^2 \big ) \equiv 0 \,, \end{aligned} \end{aligned}$$

and thus g is an entire holomorphic function. On the other hand, w.r.to the ${\mathbb S}^1$-action on $\mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C}$ given in (2.10), the map U satisfies the equivariance property $R \cdot U (z)=U ( R z)$ for all $R=e^{i \theta } \in {\mathbb S}^1$ and for all $z \in \mathbb {C}$. Long but elementary calculations now give

$$\begin{aligned} \begin{aligned} \partial ^2_{z} U (z) \cdot \partial ^2_{z} U(z)&= \partial ^2_{z} \big (R \cdot U (z)\big ) \cdot \partial ^2_{z} \big (R \cdot U (z)\big )\\&= \partial ^2_{z} \big (U (Rz)\big ) \cdot \partial ^2_{z} \big ( U (Rz)\big )=R^4\big ( \partial ^2_{z} U (Rz) \cdot \partial ^2_{z} U (Rz) \big ) . \end{aligned} \end{aligned}$$

Hence $g(e^{i\theta }z)\equiv e^{-4i \theta } g(z)$. Since g is holomorphic, from the identity principle on the domain ${\mathbb C}{\setminus } \{0\}$, we infer that $g(z)\equiv c/z^4$ for some $c \in {\mathbb C}$. Since g is smooth at the origin, we conclude that $c=0$, and thus $g \equiv 0$. Therefore (4.10) holds, and the proof is complete. $\square$

We now are ready to classify all large solutions to (4.5), i.e., solutions in the class $\widetilde{{\mathcal {A}}}_{\textrm{N}}$. The proof of this classification parallels the one for harmonic mappings $\omega$ from $\mathbb {C}\cup \{ \infty \}\simeq \mathbb {S}^2$ into $\mathbb {S}^4$ satisfying $\omega (0)=\textbf{e}_0$ (which is a combination of [12, Proposition 3.6, Proposition 3.8, Remark 3.11 and Theorem 3.19]). It shows that large solutions are precisely the restriction to the unit disc of those entire harmonic maps satisfying the boundary condition and the constraint at the origin.

Proposition 4.3

If $u \in W^{1,2}_{\textrm{sym}}(\mathbb {D}; \mathbb {S}^4)$ is a weak solution to (4.5) satisfying $u(0)=\textbf{e}_0$, then there exists $\mu _1 \in \mathbb {C}$ such that

$$\begin{aligned}{} & {} u(z) = \frac{1}{D(z)} \left( 1 - \left| \mu _1 \right| ^2 \left| z \right| ^2- 3 \left| z \right| ^4 +\frac{\left| \mu _1 \right| ^2}{3}\left| z \right| ^6, \right. \nonumber \\{} & {} \left. 2 \mu _1 z \left( 1 - \left| z \right| ^4 \right) , 2 \sqrt{3} z^2 \left( 1 + \frac{\left| \mu _1 \right| ^2}{3} \left| z \right| ^2 \right) \right) , \end{aligned}$$

(4.12)

with

$$\begin{aligned} D(z):= 1 + \left| \mu _1 \right| ^2 \left| z \right| ^2+ 3 \left| z \right| ^4 +\frac{\left| \mu _1 \right| ^2}{3}\left| z \right| ^6 . \end{aligned}$$

(4.13)

In particular,

$$\begin{aligned} {\widetilde{E}}_0(u):=\int _{\mathbb {D}}\frac{1}{2}|\nabla u|^2\,dx=6\pi . \end{aligned}$$

Proof

In view of Lemma 4.2, u extends to a harmonic map $U \in C^\omega (\mathbb {C};{\mathbb S}^4)$ which equivariant, conformal and isotropic in the whole $\mathbb {C}$. By equivariance, it writes $U(re^{i\phi })=(f_0(r),f_1(r) e^{i \phi },f_2(r) e^{i2\phi })$.

Step 1. We assume in this step that U is not linearly full, and we aim to show that (4.12)–(4.13) hold with $\mu _1=0$. First we notice that, in this case, $f_1\equiv 0$ by [12, Remark 2.4] and the boundary condition $U=g_{\overline{H}}$ on $\partial \mathbb {D}$. Hence U takes values in the unit 2-sphere of $\mathbb {R}\oplus \{0\}\oplus \mathbb {C}$, that we denote by $\mathbb {S}^2_2$. Setting $\varvec{\sigma }_2: \mathbb {S}^2_2 \rightarrow \mathbb {C}\cup \{\infty \}$ to be the stereographic projection from its south pole $(-1,0,0)$, we consider

$$\begin{aligned}\eta (re^{i\phi }):={\varvec{\sigma }}_2\circ U(re^{i\phi })= \frac{{f}_2(r)}{1+{f}_0(r)}e^{i2\phi } \,.\end{aligned}$$

Since $U(0)=(1,0,0)$, we have $U(z)\not =(-1,0,0)$ for all $z \in \mathbb {C}$ by [12, Remark 3.4]. Therefore $\eta :\mathbb {C}\rightarrow \mathbb {C}$ is well defined, real analytic, and conformal since U and $\varvec{\sigma }_2$ are. Then, $\eta$ being conformal, it is either holomorphic or anti-holomorphic. Anti-holomorphicity is easily excluded. Indeed, it would give $\eta (z)=c/\bar{z}^2$ by the identity principle on $\mathbb {C}\setminus \{0\}$ for a suitable $c \in \mathbb {C}$ (since the two functions coincide on $\{|z|=1\}$ by equivariance). But $\eta$ is smooth near the origin, so that $c=0$. In turn $\eta \equiv 0$ which is clearly impossible because $U(z)\ne (1,0,0)$ for $|z|=1$. Then, $\eta$ being holomorphic on $\mathbb {C}$, we have $\eta (z)=c z^2$ for a suitable $c \in \mathbb {C}{\setminus } \{0\}$, again by the identity principle and equivariance. Therefore,

$$\begin{aligned} U(z)=\varvec{\sigma }_2^{-1} \circ \eta (z)=\left( \frac{1-|c|^2|z|^4}{1+|c|^2|z|^4},0,\frac{2cz^2}{1+|c|^2|z|^4}\right) . \end{aligned}$$

Since $U(z)=g_{\overline{H}}(z)$ for $|z|=1$, we obtain $c=\sqrt{3}$ which shows that (4.12)–(4.13) hold with $\mu _1=0$. As a consequence, we have $f_2(r)=\frac{2\sqrt{3}r^2}{1+3r^4}$, and by conformality and equivariance of u,

$$\begin{aligned}{} & {} {\widetilde{E}}_0(u)= \int _{{\mathbb D}} \frac{1}{2} |\nabla u|^2 dx \\{} & {} \quad = \int _{{\mathbb D}} \frac{1}{r^2} |\partial _\phi u|^2 dx=2\pi \int _0^1 \frac{4|f_2(r)|^2}{r^2} r dr =2\pi \int _0^1 \frac{48 r^3 }{(1+3r^4)^2} dr=6 \pi \,. \end{aligned}$$

Step 2. We now assume U is linearly full, and we claim that (4.12)–(4.13) hold for some $\mu _1\in \mathbb {C}\setminus \{0\}$. Following [12, Section 3.3], we set $\varvec{\sigma }_4: \mathbb {S}^4 \rightarrow \mathbb {C}\cup \{\infty \}$ to be the stereographic projection from the south pole $(-1,0,0)$, and we consider

$$\begin{aligned} \big (\xi (re^{i\phi }),\eta (re^{i\phi })\big ):={\varvec{\sigma }}_4\circ U(re^{i\phi })= \left( \frac{{f}_1(r)}{1+{f}_0(r)}e^{i\phi },\frac{{f}_2(r)}{1+{f}_0(r)}e^{i2\phi }\right) \,. \end{aligned}$$

Once again, since $U(0)=(1,0,0)$, we have $U(z)\not =(-1,0,0)$ for all $z \in \mathbb {C}$ by [12, Remark 3.4]. Hence $(\xi ,\eta ):\mathbb {C}\rightarrow \mathbb {C}^2$ is well defined and real analytic. Notice that the conclusions of [12, Lemma 3.12] still hold in the present case (although we don’t know yet that U extends to a harmonic sphere $U:\mathbb {C}\cup \{\infty \}\simeq {\mathbb S}^2 \rightarrow {\mathbb S}^4$) because U is conformal and isotropic on the whole $\mathbb {C}$ by Lemma 4.2.

Now we can transpose word-by-word the argument in the proof of [12, Theorem 3.19] to show that U extends to a finite energy harmonic sphere $U \in C^\omega ({\mathbb S}^2;{\mathbb S}^4)$ (indeed, the positive lift $\widetilde{U}^+: \mathbb {C}\rightarrow \mathbb {C}P^3$ defined there extends holomorphically to the whole $\mathbb {C}P^1\simeq {\mathbb S}^2\simeq \mathbb {C}\cup \{\infty \}$ and $U=\varvec{\tau } \circ \widetilde{U}^+$ on ${\mathbb S}^2$, where $\varvec{\tau }:\mathbb {C}P^3 \rightarrow {\mathbb S}^4$ is the twistor fibration). As a consequence (compare with [12, Proposition 3.8]), there exist $\mu _1, \mu _2 \in \mathbb {C}\setminus \{0\}$ such that

$$\begin{aligned}{} & {} U(z) = \frac{1}{D(z)} \left( 1 - \left| \mu _1 \right| ^2 \left| z \right| ^2- \left| \mu _2 \right| ^2 \left| z \right| ^4 +\frac{\left| \mu _1 \right| ^2\left| \mu _2 \right| ^2}{9}\left| z \right| ^6, \right. \nonumber \\{} & {} \left. 2 \mu _1 z \left( 1 - \frac{\left| \mu _2 \right| ^2}{3}\left| z \right| ^4 \right) , 2 \mu _2 z^2 \left( 1 + \frac{\left| \mu _1 \right| ^2}{3} \left| z \right| ^2 \right) \right) , \end{aligned}$$

(4.14)

with

$$\begin{aligned} D(z):= 1 + \left| \mu _1 \right| ^2 \left| z \right| ^2+ \left| \mu _2 \right| ^2 \left| z \right| ^4 +\frac{\left| \mu _1 \right| ^2\left| \mu _2 \right| ^2}{9}\left| z \right| ^6 . \end{aligned}$$

(4.15)

The constraint $U=(U_0,U_1,U_2)\equiv g_{\overline{H}}$ on $\partial {\mathbb D}$ first implies $U_1\equiv 0$ on $\partial {\mathbb D}$, which in turn yields $|\mu _2|=\sqrt{3}$. Then $U(z)=\left( -\frac{1}{2}, 0, \frac{\mu _2}{2} z^2\right) =g_{\overline{H}}(z)$ for every $z\in \partial \mathbb {D}$, whence $\mu _2=\sqrt{3}$. Thus, (4.14)–(4.15) hold.

To complete the proof, it remains to show that $\widetilde{E}_0(u)=6\pi$ for all $\mu _1 \in \mathbb {C}$ in (4.12)–(4.13). In view of (4.8)–(4.11), the energy ${\widetilde{E}}_0(u)$ just depends on $|\mu _1|$. It is continuous with respect to $\mu _1$, and ${\widetilde{E}}_0(u)=6\pi$ for $\mu _1=0$ as already computed in the previous step. Then it is enough to check that ${\widetilde{E}}_0(u)$ is independent of $|\mu _1|$ by showing that it has zero derivative for $|\mu _1|$ positive. To see this, we first notice that $\langle u, \partial _{|\mu _1|} u \rangle \equiv 0$ since $|u|^2=1$, and $\partial _{|\mu _1|} u= 0$ on $\partial {\mathbb D}$ since $u=g_{\overline{H}}$ on $\partial \mathbb {D}$. Differentiating under integral sign, integrating by parts and using (4.5), we obtain

$$\begin{aligned} \begin{aligned} \partial _{|\mu _1|} {\widetilde{E}}_0(u)&= \int _{\mathbb {D}} \partial _ {\left| \mu _1 \right| }\Big ( \frac{1}{2} \left| \nabla u \right| ^2\Big ) \,dx = \int _{\mathbb {D}} \nabla u \cdot \nabla \big (\partial _{|\mu _1|} u\big ) \,dx \\&= - \int _{\mathbb {D}} \Delta u \cdot \partial _{|\mu _1|} u\,dx = \int _{\mathbb {D}} \left| \nabla u \right| ^2 u\cdot \partial _{|\mu _1|} u \,dx =0 . \end{aligned} \end{aligned}$$

which concludes the proof. $\square$

4.2 Energy gap for the Dirichlet integral of maps into $\mathbb {S}^4$

In this subsection, we compute explicitly the minimum values and describe the minimizers of the minimization problems

$$\begin{aligned} \min _{u \in \widetilde{{\mathcal {A}}}_{\textrm{N}}} {\widetilde{E}}_0(u), \end{aligned}$$

(4.16)

and

$$\begin{aligned} \min _{u \in \widetilde{{\mathcal {A}}}_{\textrm{S}}} {\widetilde{E}}_0(u) \,, \end{aligned}$$

(4.17)

where $\widetilde{E}_0$ is given in (4.4), thus making explicit a corresponding gap phenomenon. The following theorem is the main result of the subsection, and it is a direct consequence of Propositions 4.6 and 4.7 below.

Theorem 4.4

The following gap holds for the Dirichlet energy (4.4):

$$\begin{aligned} 2\pi =\min _{u \in \widetilde{{\mathcal {A}}}_{\textrm{S}}} \widetilde{E}_0(u) < \min _{u \in \widetilde{{\mathcal {A}}}_{\textrm{N}}} \widetilde{E}_0(u)=6\pi . \end{aligned}$$

(4.18)

In addition, the minimum value of $\widetilde{E}_0$ over $\widetilde{{\mathcal {A}}}_{\textrm{S}}$ is uniquely achieved by

$$\begin{aligned} u_{\textrm{S}}(z):= \left( \frac{\left| z \right| ^4-3}{\left| z \right| ^4+3}, \, \, 0, \, \, \frac{2 \sqrt{3} z^2}{{\left| z \right| ^4+3}} \right) , \end{aligned}$$

(4.19)

while the minimum value of $\widetilde{E}_0$ over $\widetilde{{\mathcal {A}}}_{\textrm{N}}$ is attained at $u\in \widetilde{{\mathcal {A}}}_{\textrm{N}}$ iff u is of the form (4.12)–(4.13).

Remark 4.5

(“Bubbling-off” of harmonic spheres) The resolution of (4.16)–(4.17) suffers two main difficulties: (i) the conformal invariance of the functional ${\widetilde{E}}_0$ and the induced lack of compactness of energy-bounded sequences; (ii) the fact that the classes $\widetilde{{\mathcal {A}}}_{\textrm{N}}$ and $\widetilde{{\mathcal {A}}}_\textrm{S}$ are not closed under weak $W^{1,2}$-convergence. To illustrate these facts, let us consider for $\mu _1 \in \mathbb {C}$, the mapping $u_{\mu _1} \in \widetilde{{\mathcal {A}}}_{\textrm{N}}$ given by Proposition 4.3 and satisfying $\widetilde{E}_0(u_{\mu _1})= 6 \pi$. As $|\mu _1|\rightarrow \infty$, we have $u_{\mu _1} \rightharpoonup u_{\textrm{S}} \in \widetilde{{\mathcal {A}}}_{\textrm{S}}$ weakly in $W^{1,2}(\mathbb {D})$, where $u_{\textrm{S}}$ is given by (4.19). Note that $u_{\textrm{S}}$ solves (4.5) and satisfies ${\widetilde{E}}_0(u_\textrm{S})=2\pi$. As the convergence is smooth away from the origin, $\frac{1}{2} \left| \nabla u_{\mu _1} \right| ^2 dx \rightharpoonup \frac{1}{2} \left| \nabla u_{\textrm{S}} \right| ^2 dx +4\pi \delta _0$ as measures on $\overline{{\mathbb D}}$. Finally, if $\mu _1/|\mu _1| \rightarrow e^{i \theta }$ as $|\mu _1| \rightarrow \infty$, then $u_{\mu _1}(z/\mu _1) \rightarrow {\tilde{u}}(z)$ strongly in $W_{\textrm{loc}}^{1,2}(\mathbb {C};{\mathbb S}^4)$, where

$$\begin{aligned} {\tilde{u}}(z):= \left( \frac{1 - \left| z \right| ^2}{1+\left| z \right| ^2}, \frac{ 2 e^{i\theta } z}{1+\left| z \right| ^2}, 0 \right) \end{aligned}$$

(4.20)

is a finite energy harmonic 2-sphere (a “bubble”), ${\tilde{u}}: \mathbb {C}\cup \{\infty \} \simeq {\mathbb S}^2 \rightarrow {\mathbb S}^4$ with $\widetilde{E}_0({\tilde{u}};\mathbb {C})=4\pi$.

To discuss the minimization problem (4.17), we rely on existing results in the literature [25, 39], and we actually prove that the minimality of $u_{\textrm{S}}$ holds even among non symmetric competitors.

Proposition 4.6

The map $u_{\textrm{S}}$ given by (4.19) is the unique minimizer of $\widetilde{E}_0$ in $W^{1,2}_{g_{\overline{H}}}({\mathbb D}; {\mathbb {S}}^4)$. As a consequence, $\min _{u \in \widetilde{{\mathcal {A}}}_{\textrm{S}}} \widetilde{E}_0(u)=2\pi$ and $u_{\textrm{S}}$ is the unique minimizer of $\widetilde{E}_0$ over $\widetilde{{\mathcal {A}}}_{\textrm{S}}$.

Proof

We shall use the real coordinates $u=(u_0, \dots , u_4)\in {\mathbb R}^5 \simeq \mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C}$, and we shall denote by ${\mathbb S}^4_\pm =\{ u \in {\mathbb S}^4: u_0 \gtrless 0 \}$ the upper/lower open half spheres.

First, we observe that $u_{\textrm{S}}({\overline{\mathbb {D}}})\subseteq \mathbb {S}^4_-$. Since $u_{\textrm{S}}$ is a smooth harmonic map (see Remark 4.5), we deduce from [39, Lemma 2.1] that $u_{\textrm{S}}$ minimizes $\widetilde{E}_0$ over the whole $W^{1,2}_{g_{\overline{H}}}({\mathbb D}; {\mathbb {S}}^4)$. Now we claim that $u_{\textrm{S}}$ is actually the unique minimizer over $W^{1,2}_{g_{\overline{H}}}({\mathbb D}; {\mathbb {S}}^4)$. Since $\mathbb {S}^4_-$ is geodesically convex, the uniqueness result from [25] tells us that $u_{\textrm{S}}$ is the unique (smooth) solution to (4.5) whose range is strictly included in $\mathbb {S}^4_-$. Now, if $u\in W^{1,2}_{g_{\overline{H}}}({\mathbb D};{\mathbb S}^4)$ is any minimizer of $\widetilde{E}_0$, then u is a harmonic map smooth up to the boundary. Hence it suffices to show that $u(\overline{\mathbb {D}})\subseteq \mathbb {S}^4_-$ to conclude that $u=u_{\textrm{S}}$. Assume by contradiction that $u(z)=(u_0(z), u_1(z),\ldots , u_4(z))$ satisfies $u_0(z_*)=0$ for some $z_*\in {\mathbb D}$. Then the competitor ${\tilde{u}}(z):=(-|u_0(z)|, u_1(z), \ldots , u_4(z))$ belongs to $W^{1,2}_{g_{\overline{H}}}(\mathbb {D};\mathbb {S}^4)$, and $\widetilde{E}_0({{\tilde{u}}})\leqslant \widetilde{E}_0(u)$. Thus, ${\tilde{u}}$ is also a minimizer, whence a harmonic map in $\mathbb {D}$ smooth up to the boundary. Then the function $v(z):=|u_0(z)|$ is a smooth solution in $\mathbb {D}$ to $-\Delta v =|\nabla u|^2 v \geqslant 0$, with $v(z) = \frac{1}{2}$ on $\partial \mathbb {D}$. By the maximum principle, we have $v\geqslant \frac{1}{2}$ in $\mathbb {D}$, in contradiction with the assumption $v(z_*) = 0$. Therefore $u(\overline{\mathbb {D}})\subseteq \mathbb {S}^4_-$, leading to $u=u_{\textrm{S}}$. Finally, since $u_{\textrm{S}}\in \widetilde{{\mathcal {A}}}_{\textrm{S}}$, it obviously follows that $u_{\textrm{S}}$ is the unique minimizer of $\widetilde{E}_0$ over $\widetilde{{\mathcal {A}}}_{\textrm{S}}$, and a direct computation yields $\widetilde{E}_0(u_{\textrm{S}})=2\pi$ (see the the proof of Proposition 4.3). $\square$

Concerning (4.16), we have the following result.

Proposition 4.7

It holds

$$\begin{aligned} \min _{u \in \widetilde{{\mathcal {A}}}_{\textrm{N}}} \widetilde{E}_0(u) = 6\pi , \end{aligned}$$

(4.21)

and the minimum is attained at a map u if and only if u is of the form (4.12)–(4.13).

The proof of Proposition 4.7 is postponed to the end of this subsection. In contrast with the proof of Proposition 4.6, we now have to overcome the possible lack of compactness of minimizing sequences and concentration of energy. To this purpose, we shall construct suitable minimizing sequences considering a regularization of problem (4.16). This regularization is based on the following subclasses of $\widetilde{{\mathcal {A}}}_{\textrm{N}}$,

$$\begin{aligned} \widetilde{{\mathcal {A}}}_{\textrm{N}}^\rho :=\big \{ u \in \widetilde{{\mathcal {A}}}_{\textrm{N}}: u= (1,0,0) \text{ a.e. } \text{ on } \mathbb {D}_\rho \big \} \text { with } 0<\rho<1 \,, \quad \widetilde{{\mathcal {A}}}^0_{\textrm{N}}:=\bigcup _{0<\rho <1} \widetilde{{\mathcal {A}}}_{\textrm{N}}^\rho \,. \end{aligned}$$

(4.22)

As opposed to $\widetilde{{\mathcal {A}}}_{\textrm{N}}$, the subsets $\widetilde{{\mathcal {A}}}_{\textrm{N}}^\rho$ are closed under weak $W^{1,2}$-convergence. The following lemma relates those different classes and their corresponding minimization problems.

Lemma 4.8

The following properties hold.

• (i) $\widetilde{{\mathcal {A}}}_{\textrm{N}}^0$ is a strongly dense subset of $\widetilde{{\mathcal {A}}}_{\textrm{N}}$ in $W^{1,2}(\mathbb {D})$.

• (ii) $\displaystyle {\inf _{u \in \widetilde{{\mathcal {A}}}_{\textrm{N}}} \widetilde{E}_0(u) = \inf _{u \in \widetilde{{\mathcal {A}}}_{\textrm{N}}^0} \widetilde{E}_0(u)=\lim _{\rho \rightarrow 0} \inf _{u \in \widetilde{{\mathcal {A}}}_{\textrm{N}}^\rho } \widetilde{E}_0(u)}$ .

• (iii) For each integer $n \geqslant 1$, the minimization problem

  $$\begin{aligned} \min _{u\in \widetilde{{\mathcal {A}}}_{\textrm{N}}^{\frac{1}{n}}} \widetilde{E}_0(u) \end{aligned}$$

  (4.23)

  admits a solution. In addition, for any solution $u_n\in \widetilde{{\mathcal {A}}}_{\textrm{N}}^{\frac{1}{n}}$, we have

  $$\begin{aligned} \displaystyle \lim _{n\rightarrow \infty }\widetilde{E}_0(u_n)=\inf _{u \in \widetilde{{\mathcal {A}}}_{\textrm{N}}} \widetilde{E}_0(u) . \end{aligned}$$

  (4.24)

Proof

We start proving claim (i). Let us fix $u \in \widetilde{{\mathcal {A}}}_{\textrm{N}}$ arbitrary. We aim to construct $u_\rho \in \widetilde{{\mathcal {A}}}_{\textrm{N}}^\rho$ such that $u_\rho \rightarrow u$ strongly in $W^{1,2}(\mathbb {D})$ as $\rho \rightarrow 0$. Writing $u(re^{i\phi })=(f_0(r),f_1(r) e^{i\phi },f_2(r)e^{i2\phi })$, we first set

$$\begin{aligned} {\tilde{u}}_\rho (re^{i\phi }):= {\left\{ \begin{array}{ll} \textbf{e}_0&{} \hbox { if}\ r \in [0, \rho ] \,, \\ \displaystyle \textbf{e}_0+\frac{r-\rho }{\sqrt{\rho }-\rho } \big (u(\sqrt{\rho }e^{i\phi })-\textbf{e}_0\big ) &{} \hbox { if}\ r \in [\rho , \sqrt{\rho }] \,, \\ u(re^{i\phi }) &{} \hbox { if}\ r \in [\sqrt{\rho }, 1] \,. \end{array}\right. } \end{aligned}$$

Then ${\tilde{u}}_\rho \in W^{1,2}_{\textrm{sym}}({\mathbb D}; \mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C})\cap C^0({\overline{\mathbb {D}}})$ and ${\tilde{u}}_\rho =g_{\overline{H}}$ on $\partial \mathbb {D}$. Moreover, ${\tilde{u}}_\rho \rightarrow u$ uniformly in $\overline{{\mathbb D}}$, which implies that $|{\tilde{u}}_\rho | \rightarrow 1$ uniformly in $\overline{{\mathbb D}}$ as $\rho \rightarrow 0$. For $\rho >0$ small enough, we thus have $|{\tilde{u}}_\rho |\geqslant 1/2$ in $\overline{\mathbb {D}}$, and we can define

$$\begin{aligned} u_\rho (z):= \frac{{\tilde{u}}_\rho (z)}{|{\tilde{u}}_\rho (z)|}. \end{aligned}$$

By construction, we have $u_\rho \in \widetilde{{\mathcal {A}}}_\textrm{N}^\rho$, and $u_\rho \rightarrow u$ uniformly in $\overline{{\mathbb D}}$ as $\rho \rightarrow 0$. In addition,

$$\begin{aligned} \widetilde{E}_0(u_\rho ) = \widetilde{E}_0\big (u_\rho ; {\mathbb D}_{\sqrt{\rho }}\setminus \mathbb {D}_\rho \big )+\widetilde{E}_0(u;{\mathbb D} \setminus {\mathbb D}_{\sqrt{\rho }}) , \end{aligned}$$

and

$$\begin{aligned}{} & {} \widetilde{E}_0\big (u_\rho ; {\mathbb D}_{\sqrt{\rho }}\setminus \mathbb {D}_\rho \big )\leqslant C \widetilde{E}_0\big ({\tilde{u}}_\rho ; {\mathbb D}_{\sqrt{\rho }}\setminus \mathbb {D}_\rho \big ) \\{} & {} \quad \leqslant C\big (|1-f_0(\sqrt{\rho })|^2+|f_1(\sqrt{\rho })|^2+|f_2(\sqrt{\rho })|^2\big ) \mathop {\longrightarrow }\limits _{\rho \rightarrow 0} 0. \end{aligned}$$

Hence $\widetilde{E}_0(u_\rho ) \rightarrow \widetilde{E}_0(u)$ as $\rho \rightarrow 0$, which implies that $u_\rho \rightarrow u$ strongly in $W^{1,2}(\mathbb {D})$.

Concerning (ii), the first equality is an obvious consequence of (i) since $\widetilde{E}_0$ is (strongly) $W^{1,2}$-continuous. Then we observe that $\rho \mapsto \inf _{ \widetilde{{\mathcal {A}}}_\textrm{N}^\rho } \widetilde{E}_0$ is non decreasing. Therefore,

$$\begin{aligned} \inf _{\widetilde{{\mathcal {A}}}_{\textrm{N}}^0} \widetilde{E}_0=\inf _{0<\rho <1} \inf _{\widetilde{{\mathcal {A}}}_{\textrm{N}}^\rho } \widetilde{E}_0= \lim _{\rho \rightarrow 0}\inf _{\widetilde{{\mathcal {A}}}_{\textrm{N}}^\rho } \widetilde{E}_0. \end{aligned}$$

To prove claim (iii), we recall that $\widetilde{{\mathcal {A}}}_\textrm{N}^{\frac{1}{n}}$ is weakly $W^{1,2}$-closed. Hence existence of solutions to (4.23) follows from the direct method of calculus of variations. Finally, (4.24) is a consequence of (ii) together with the monotonicity of $\rho \mapsto \inf _{ \widetilde{{\mathcal {A}}}_{\textrm{N}}^\rho } \widetilde{E}_0$. $\square$

By the previous lemma, a sequence $\{u_n\}$ of solutions to (4.23) provides a minimizing sequence for (4.16). In the next result, we provide the key step for the asymptotic analysis of such a sequence.

Lemma 4.9

Let $\{ u_n\} \subseteq \widetilde{{\mathcal {A}}}_{\textrm{N}}^0$ be such that $u_n$ solves (4.23) for every $n\geqslant 1$. Assume that, for some (not relabelled) subsequence, $u_n \rightharpoonup u_*$ weakly in $W^{1,2}({\mathbb D})$. Then $u_* \in \widetilde{{\mathcal {A}}}^{\textrm{sym}}_{ g_{\overline{H}}}(\mathbb {D})$ and $u_*$ is a smooth harmonic map in $\overline{\mathbb {D}}$. Moreover, if $u_* \in \widetilde{{\mathcal {A}}}_{\textrm{S}}$, then there exists a further (not relabelled) subsequence and $r_n\rightarrow 0^+$ such that ${\tilde{u}}_n(z):=u_n(r_n z)$ satisfies ${\tilde{u}}_n \rightharpoonup {\tilde{u}}$ weakly in $W^{1,2}_{\textrm{loc}} (\mathbb {C})$ for some equivariant nonconstant finite energy smooth harmonic map ${\tilde{u}}:\mathbb {C}\rightarrow {\mathbb S}^4$.

Proof

Using maps of the form (4.12)–(4.13) as competitors, we infer from Lemma 4.8 that

$$\begin{aligned} \lim _{n \rightarrow \infty } \widetilde{E}_0(u_n)=\inf _{u\in \widetilde{{\mathcal {A}}}_{\textrm{N}}} \widetilde{E}_0(u)\leqslant 6\pi . \end{aligned}$$

(4.25)

The class $\widetilde{{\mathcal {A}}}^{\textrm{sym}}_{ g_{\overline{H}}}(\mathbb {D})$ being weakly $W^{1,2}$-closed, we have $u_*\in \widetilde{{\mathcal {A}}}^{\textrm{sym}}_{ g_{\overline{H}}}(\mathbb {D})$. By minimality, each $u_n$ is a harmonic map in $\mathbb {D}\setminus \overline{\mathbb {D}}_{1/n}$. Since $u_n\rightharpoonup u_*$ weakly in $W^{1,2}(\mathbb {D})$, it classically follows that $u_*$ is a (weakly) harmonic map in $\mathbb {D}\setminus \{0\}$, see e.g. [13, Theorem 1, p. 50]. Moreover, since $u_*$ belongs to $W^{1,2}(\mathbb {D})$ and the set $\{0\}$ has zero capacity, $u_*$ is actually a weakly harmonic map in the whole disc $\mathbb {D}$, and thus a smooth harmonic map in $\overline{\mathbb {D}}$ by regularity theory.

We now assume that $u_* \in \widetilde{{\mathcal {A}}}_{\textrm{S}}$. Recalling Lemma 2.10, we write

$$\begin{aligned} u_n(re^{i\phi })=:\big (f^{(n)}_0(r), f^{(n)}_1(r) e^{i\phi }, f^{(n)}_2(r) e^{i 2\phi } \big )\,\,\text { and }\,\, u_*(re^{i\phi })=:(f^*_0(r), f^*_1(r) e^{i \phi }, f^*_2(r) e^{i2\phi }) \,, \end{aligned}$$

so that

$$\begin{aligned} \big (f^{(n)}_0(0), f^{(n)}_1(0), f^{(n)}_2(0)\big )=(1,0,0) \quad \text { and } \quad \big (f^*_0(0), f^*_1(0), f^*_2(0)\big )=(-1,0,0) \,. \end{aligned}$$

The functions $f^{(n)}_0$ and $f^*_0$ are continuous in [0, 1] and taking values in $[-1,1]$ by the $\mathbb {S}^4$-constraint. In addition, we have $f^*_0(r) \in (-1,1)$ for every $r \in (0,1]$. Indeed, assume by contradiction that $f^*_0(t)=\pm 1$ for some $t\in (0,1)$. Then, $u_*=(\pm 1,0,0)$ on $\partial \mathbb {D}_t$ which implies that $u_*=(\pm 1,0,0)$ in $\mathbb {D}_t$ by Lemaire’s constancy theorem [29]. Then $u_* \equiv (\pm 1,0,0)$ in ${\mathbb D}$ by unique continuation, in contradiction with the boundary condition.

By Lemma 2.10, $u_n \rightarrow u_*$ locally uniformly in $\overline{{\mathbb D}} \setminus \{0\}$, and thus $f^{(n)}_0 \rightarrow f^*_0$ locally uniformly in (0, 1]. Since $f^*_0(0)=-1$, we have

$$\begin{aligned} \lim _{n\rightarrow \infty }\, \min _{[0,1]} f^{(n)}_0=-1. \end{aligned}$$

(4.26)

Recalling that $f_0^{(n)}(1)=-\frac{1}{2}$ and $f_0^{(n)}(0)=1$, each function $f_0^{(n)}$ must vanish on the interval [0, 1]. We can thus define

$$\begin{aligned} r_n:=\min \big \{r\in [0,1]: f_0^{(n)}(r)=0\big \}\in (0,1), \end{aligned}$$

and

$$\begin{aligned} r^{\textrm{min}}_n:=\min \Big \{r\in [0,1]: f_0^{(n)}(r)= \min _{[0,1]} f^{(n)}_0\Big \}\in (0,1). \end{aligned}$$

Since $u_n \in \widetilde{{\mathcal {A}}}_{\textrm{N}}^{\frac{1}{n}}$ and $f_0^*(r)>-1$ for every $r>0$, we infer from (4.26) that

$$\begin{aligned} \frac{1}{n}< r_n < r_n^{\textrm{min}}\mathop {\longrightarrow }\limits _{n\rightarrow \infty }0, \end{aligned}$$

whence $r_n\rightarrow 0$. Combining Cauchy-Schwarz inequality and (4.8) leads to

$$\begin{aligned} 1=|f_0^{(n)}(r_n)-f_0^{(n)}(1/n)| \leqslant \int _{1/n}^{r_n} \sqrt{r}|\partial _r f_0^{(n)}(r)| \frac{dr}{\sqrt{r}} \leqslant \sqrt{\pi ^{-1} \widetilde{E}_0(u_n)} \sqrt{ \log \left( n r_n\right) }\,.\end{aligned}$$

From the energy bound in (4.25), we conclude that

$$\begin{aligned} r_*:=\limsup _{n\rightarrow \infty } \frac{1}{n r_n} <1. \end{aligned}$$

Now we set

$$\begin{aligned} {\tilde{u}}_n(z):=u_n(r_n z), \end{aligned}$$

so that ${\tilde{u}}_n \in W^{1,2}_{\textrm{sym}}({\mathbb D}_{1/r_n};{\mathbb S}^4)$, ${\tilde{u}}_n = (1,0,0)$ in $\mathbb {D}_{1/nr_n}$, and ${\tilde{u}}_n$ is a harmonic map in the annulus

$$\begin{aligned} \Omega _n:=\big \{ 1/{nr_n}<|z|< 1/r_n\big \}. \end{aligned}$$

Setting ${\tilde{u}}_n(re^{i\phi })=:({\tilde{f}}^{(n)}_0(r), {\tilde{f}}^{(n)}_1(r) e^{i\phi }, {\tilde{f}}^{(n)}_2(r) e^{i 2\phi } )$, we also have ${\tilde{f}}^{(n)}_0(1)=0$ by construction.

In view of (4.25), we have for every $r>0$,

$$\begin{aligned} \limsup _{n\rightarrow \infty } \widetilde{E}_0({\tilde{u}}_n,{\mathbb D}_r)\leqslant \limsup _{n\rightarrow \infty } \widetilde{E}_0({\tilde{u}}_n,{\mathbb D}_{1/r_n}) =\limsup _{n\rightarrow \infty } \widetilde{E}_0(u_n,{\mathbb D})\leqslant 6\pi . \end{aligned}$$

Therefore we can extract a (not relabelled) subsequence such that ${\tilde{u}}_n \rightharpoonup {\tilde{u}}$ in $W^{1,2}_{\textrm{loc}}(\mathbb {C})$ for some equivariant map ${\tilde{u}} \in W^{1,2}_{\textrm{loc}}(\mathbb {C};{\mathbb S}^4)$ satisfying $\widetilde{E}_0({\tilde{u}};\mathbb {C}) \leqslant 6 \pi$ by lower semicontinuity of the Dirichlet energy. By Lemma 2.10 again, ${\tilde{u}}_n \rightarrow {\tilde{u}}$ locally uniformly in $\mathbb {C}\setminus \{0\}$, so that ${\tilde{f}}^{(n)}_0 \rightarrow {\tilde{f}}_0$ locally uniformly in $(0,\infty )$ where $\tilde{u}(re^{i\phi })=:( {\tilde{f}}_0(r), {\tilde{f}}_1(r)e^{i\phi }, {\tilde{f}}_2(r)e^{2i\phi })$. Then $\tilde{f}_0(1)=\lim _n{\tilde{f}}^{(n)}_0(1)=0$, and $|{{\tilde{f}}}_0(0)|=1$ by equivariance. In particular, ${{\tilde{u}}}$ is nonconstant.

Extracting a further subsequence if necessary, we have $1/nr_n\rightarrow r_*$, so that

$$\begin{aligned} \Omega _ n \rightarrow \Omega _*:=\{ |z|> r_*\}. \end{aligned}$$

Arguing as above, we infer that ${\tilde{u}}$ is a weakly harmonic map in $\Omega _*$, and hence a classical (smooth) harmonic map in $\Omega _*$. Next, we claim that $r_*=0$. Indeed, assume by contradiction that $0<r_*<1$. Then ${\tilde{u}}= (1,0,0)$ in $\mathbb {D}_{r_*}$ since ${\tilde{u}}_n \rightarrow {\tilde{u}}$ locally uniformly on $\mathbb {C}{\setminus }\{0\}$. For $z \in \overline{ {\mathbb D}}_{1/r_*}{\setminus } \{0\}$, we now consider the inverted map $v(z):= {\tilde{u}}(1/\bar{z})$. By conformal invariance of $\widetilde{E}_0$, we have $\widetilde{E}_0(v,{\mathbb D}_{1/r_*})=\widetilde{E}_0({\tilde{u}}, \Omega _*) \leqslant 6\pi$, and v is a weakly harmonic map in ${\mathbb D}_{1/r_*}{\setminus }\{0\}$ satisfying $v = (1,0,0)$ on $\partial {\mathbb D}_{1/r_*}$. Again, since $\{0\}$ has a vanishing capacity, v is actually a weakly harmonic map in the whole disc ${\mathbb D}_{1/r_*}$, and thus a smooth harmonic map in $\overline{{\mathbb D}}_{1/r_*}$. Since $v = (1,0,0)$ on $\partial {\mathbb D}_{1/r_*}$, Lemaire’s theorem [29] tells us that $v\equiv (1,0,0)$ in ${\mathbb D}_{1/r_*}$. Hence, ${{\tilde{u}}}\equiv (1,0,0)$ in $\Omega _*$, in contradiction with the fact that ${{\tilde{f}}}_0(1)=0$.

Since $r_*=0$, ${{\tilde{u}}}$ is weakly harmonic in $\mathbb {C}\setminus \{0\}$, and thus weakly harmonic in the whole $\mathbb {C}$ as argued above. Hence ${{\tilde{u}}}$ is a smooth, nonconstant, equivariant harmonic map satisfying $\widetilde{E}_0({\tilde{u}};\mathbb {C}) \leqslant 6 \pi$. $\square$

Proof of Proposition 4.7

Using maps of the form (4.12)–(4.13) as competitors, we obtain

$$\begin{aligned} \inf _{u \in \widetilde{{\mathcal {A}}}_{\textrm{N}}} \widetilde{E}_0(u)\leqslant 6 \pi . \end{aligned}$$

(4.27)

We are going to show that equality actually holds, so that any map of the form (4.12)–(4.13) is a minimizer. Moreover, since any minimizer is a solution of (4.5), it must be of the form (4.12)–(4.13) by Proposition 4.3, so that no other minimizers exist.

Let us now consider a sequence $\{ u_n\} \subseteq \widetilde{{\mathcal {A}}}_{\textrm{N}}^0$ such that $u_n$ solves (4.23) for every $n\geqslant 1$. In view of Lemma 4.8, $\{ u_n\}$ is a minimizing sequence for (4.16). To show that equality holds in (4.27), it thus suffices to prove that $\lim _{n} \widetilde{E}_0(u_n)=6\pi$. By construction, $\{u_n\}$ is bounded in $W^{1,2}(\mathbb {D})$, so that we can find a (not relabelled) subsequence such that $u_n\rightharpoonup u_*$ weakly in $W^{1,2}(\mathbb {D})$. By Lemma 4.9, $u_* \in \widetilde{{\mathcal {A}}}_{\overline{H}}^{\textrm{sym}}$ is a smooth harmonic map in $\mathbb {D}$.

We now distinguish between two scenarios.

Case I. Compact case: $u_* \in \widetilde{{\mathcal {A}}}_{\textrm{N}}$. Under this assumption, we have $\widetilde{E}_0(u_*)=6\pi$ by Proposition 4.3. In addition, by weak lower semicontinuity of the Dirichlet energy,

$$\begin{aligned} 6\pi =\widetilde{E}_0(u_*) \leqslant \lim _{n\rightarrow \infty } \widetilde{E}_0(u_n)= \inf _{ \widetilde{{\mathcal {A}}}_{\textrm{N}}} \widetilde{E}_0\leqslant 6\pi , \end{aligned}$$

which proves (4.21).

Case II. Noncompact case: $u_* \in \widetilde{{\mathcal {A}}}_{\textrm{S}}$. Under this assumption, we have $\widetilde{E}_0(u_*)\geqslant 2\pi$ by Proposition 4.6. In view of Lemma 4.9, there exists a (not relabelled) subsequence and $r_n\rightarrow 0$ such that the rescaled sequence ${\tilde{u}}_n(z):=u_n(r_n z)$ converges weakly in $W^{1,2}_{\textrm{loc}}(\mathbb {C})$ to an entire nonconstant equivariant smooth harmonic map ${{\tilde{u}}}$ of finite Dirichlet energy. Being of finite energy, ${{\tilde{u}}}$ extends to $\mathbb {C}\cup \{\infty \} \simeq {\mathbb S}^2$ to an equivariant weakly harmonic map, and thus a smooth equivariant harmonic 2-sphere into $\mathbb {S}^4$. By the classification result in [12, Section 3], we thus have $\widetilde{E}_0({\tilde{u}},\mathbb {C})\geqslant 4\pi$.

Setting $r_n'=\sqrt{r_n}\rightarrow 0$ and using the weak lower semicontinuity of the Dirichlet energy, we infer that

$$\begin{aligned} \begin{aligned} 6\pi&\geqslant \inf _{\widetilde{{\mathcal {A}}}_{\textrm{N}}} \widetilde{E}_0=\lim _{n\rightarrow \infty } \widetilde{E}_0(u_n)\geqslant \liminf _{n\rightarrow \infty } \widetilde{E}_0(u_n; {\mathbb D}_{r_n'})+\liminf _{n \rightarrow \infty }\widetilde{E}_0(u_n; {\mathbb D} \setminus \overline{{\mathbb D}}_{r_n'})\\&\geqslant \liminf _{n\rightarrow \infty } \widetilde{E}_0({\tilde{u}}_n; {\mathbb D}_{r_n'/r_n})+ \widetilde{E}_0(u_*) \geqslant \widetilde{E}_0({\tilde{u}};\mathbb {C})+\widetilde{E}_0(u_*) \geqslant 6\pi \,, \end{aligned} \end{aligned}$$

which again proves (4.21). $\square$

4.3 Uniaxiality vs Biaxiality in the 2D-LdG minimization

In the light of the previous section, we now discuss for $\lambda > 0$ the variational problems

$$\begin{aligned} \min _{Q \in {\mathcal {A}}_{\textrm{N}}} E_\lambda (Q), \end{aligned}$$

(4.28)

and

$$\begin{aligned} \min _{Q \in {\mathcal {A}}_{\textrm{S}}} E_\lambda (Q) , \end{aligned}$$

(4.29)

where $E_\lambda$ is the 2D-LdG energy in (1.11), and ${\mathcal {A}}_{\textrm{N}}$, ${\mathcal {A}}_{\textrm{S}}$ are the classes defined in (4.2)–(4.3).

Once again we rely in an essential way on the (isometric) identification ${\mathcal {S}}_0 \simeq \mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C}$ and the induced correspondence $Q\simeq u$ between Q-tensor maps and $\mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C}$-valued maps from Corollary 2.7. Recalling that $\textrm{tr}(Q^3)= 3 \det Q$ for every $Q\in {\mathcal {S}}_0$, we infer from (2.12) that

$$\begin{aligned} W(Q)=\frac{1}{3\sqrt{6}}\bigg (1 - u_0\big (u_0^2+\frac{3}{2}|u_1|^2-3|u_2|^2\big )-\frac{3\sqrt{3}}{2}\textrm{Re} \big (u_1^2 \overline{u_2}\big )\bigg )=:\widetilde{W}(u)\quad \hbox { for}\ Q\simeq u.\nonumber \\ \end{aligned}$$

(4.30)

Setting, for $u\in W^{1,2}(\mathbb {D};\mathbb {S}^4)$,

$$\begin{aligned} {\widetilde{E}}_\lambda (u):= \int _{\mathbb {D}} \frac{1}{2} |\nabla u|^2 + \lambda {\widetilde{W}}(u) \,dx, \end{aligned}$$

we obtain

$$\begin{aligned} E_\lambda (Q)={\widetilde{E}}_\lambda (u) \quad \hbox { for}\ Q\simeq u. \end{aligned}$$

If $Q\simeq u\in W^{1,2}_{\textrm{sym}}(\mathbb {D};\mathbb {S}^4)$ and $u(re^{i\phi })=(f_0(r),f_1(r)e^{i\phi },f_2(r)e^{i2\phi })$, then

$$\begin{aligned} E_\lambda (Q)={\widetilde{E}}_\lambda (u) = \pi \int _0^1\left( \left| f^\prime \right| ^2+ \frac{\left| f_1 \right| ^2 + 4\left| f_2 \right| ^2}{r^2} +2\lambda \frac{1-{\widetilde{\beta }}(f)}{3\sqrt{6}} \right) \, rdr \,, \end{aligned}$$

(4.31)

with $f:=(f_0,f_1,f_2)$ and ${\widetilde{\beta }}(f)$ given in (2.21). Equivariant critical points $Q\simeq u$ of the energy functional $E_\lambda$ satisfy the following system of ODEs

$$\begin{aligned} \left\{ \begin{aligned} f^{\prime \prime }_0 + \frac{1}{r} f^\prime _0&= - |\nabla u|^2 f_0 + \frac{\lambda }{\sqrt{6}} \left( \left| f_2 \right| ^2-f_0^2 - \frac{1}{2}\left| f_1 \right| ^2 + {\widetilde{\beta }}(f) f_0 \right) ,\\ f^{\prime \prime }_1 + \frac{1}{r} f^\prime _1&= - |\nabla u|^2 f_1 - \frac{1}{r^2} f_1 + \frac{\lambda }{\sqrt{6}} \left( - \sqrt{3}f_2 \overline{f_1}-f_0 f_1+{\widetilde{\beta }}(f) f_1 \right) ,\\ f^{\prime \prime }_2 + \frac{1}{r} f^\prime _2&= - |\nabla u|^2 f_2 - \frac{4}{r^2}f_2 + \frac{\lambda }{\sqrt{6}} \left( -\frac{\sqrt{3}}{2} f_1^2 + 2f_0 f_2+ {\widetilde{\beta }}(f) f_2 \right) , \end{aligned} \right. \end{aligned}$$

(4.32)

with $|\nabla u|^2$ as in (4.8) depending also on f only.

In the sequel, our goal is to establish existence/nonexistence of solutions to (4.28)–(4.29) starting from the gap phenomenon in Theorem 4.4. In turn, we shall derive qualitative properties of minimizers of $E_\lambda$ in ${\mathcal {A}}_{\overline{H}}^{\textrm{sym}}(\mathbb {D})={\mathcal {A}}_{\textrm{S}} \cup {\mathcal {A}}_{\textrm{N}}$. The main result, Theorem 1.2, is postponed to the end of the subsection. It reveals the nature of minimizers of $E_\lambda$ in ${\mathcal {A}}_{\overline{H}}^{\textrm{sym}}(\mathbb {D})$ as $\lambda$ varies. In particular, we shall see that biaxial escape occurs for reasons of energy efficiency.

We start with the following proposition providing the complete description of solutions to (4.28).

Proposition 4.10

For all $\lambda > 0$,

$$\begin{aligned} \min _{Q \in {\mathcal {A}}_{\textrm{N}}} E_\lambda (Q) = 6\pi , \end{aligned}$$

(4.33)

and the minimum is attained at $Q\simeq u$ if and only if $u(z)=g_{\overline{H}}(\pm z)$ with $g_{\overline{H}}$ given by (4.34) below.

The proof is essentially based on the following preliminary lemma of independent interest.

Lemma 4.11

Let $Q \in {\mathcal {A}}_{\textrm{N}}$ with $Q\simeq u$ of the form (4.12)–(4.13). Then Q is positively uniaxial if and only if $\mu _1=\pm \sqrt{3}$, that is $u(z)=g_{\overline{H}}(\pm z)$ where

$$\begin{aligned} g_{\overline{H}}(z):= \frac{1}{(1+|z|^2)^2} \left( 1 - 4 \left| z \right| ^2 +\left| z \right| ^4, 2 \sqrt{3} z \big ( 1 - \left| z \right| ^2 \big ), 2 \sqrt{3} z^2 \right) \end{aligned}$$

(4.34)

extends (4.1) to $\mathbb {D}$. Moreover, if H denotes the unit norm nematic hedgehog in (1.10), then we have $g_{\overline{H}} \simeq (H\circ \varvec{\sigma }_2^{-1})$ where $\varvec{\sigma }_2:\mathbb {S}^2\setminus \{(0,0,-1)\}\rightarrow \mathbb {C}$ is the stereographic projection from the south pole of $\mathbb {S}^2$.

Proof

Let us fix $Q\in \mathbb {S}^4$ with $Q\simeq u=(u_0,u_1,u_2)$. For a given $\theta \in \mathbb {R}$, we set $\widetilde{Q}\simeq \widetilde{u}:=(u_0, \pm |u_1|e^{i\theta }, |u_2|e^{i2\theta })$. From (4.30), we derive that $W(Q) \geqslant W(\widetilde{Q})$ with equality if and only if $u_1^2 \overline{u_2}\geqslant 0$. Hence equality holds if and only if $\textrm{Re}(u_1^2 \overline{u_2})=|u_1|^2 |u_2|$ and $Q=\widetilde{Q}$ for some $\theta \in \mathbb {R}$. As a consequence, $W(Q)=0$ if and only if

$$\begin{aligned} 0&=1 - u_0\big (u_0^2+\frac{3}{2}|u_1|^2-3|u_2|^2\big )-\frac{3\sqrt{3}}{2}|u_1|^2|u_2|\\&= 1-u_0\bigg (\frac{3}{2}-\frac{1}{2}u_0^2-\frac{9}{2}|u_2|^2\bigg )-\frac{3\sqrt{3}}{2}\big (1-u_0^2-|u_2|^2\big )|u_2|\\&=\frac{3}{2}\big (u_0+\sqrt{3}|u_2|-1\big )\big (u_0+\sqrt{3}|u_2|+2\big )\,, \end{aligned}$$

where we have used that $|u|^2=u_0^2+|u_1|^2+|u_2|^2=1$. Hence, $W(Q)=0$ if and only if either $u_0+\sqrt{3}|u_2|=1$, or $u_0+\sqrt{3}|u_2|=-2$.

Let us now consider $Q \in {\mathcal {A}}_{\textrm{N}}$ with $Q\simeq u$ a map of the form (4.12)–(4.13), and $Q\simeq u$. If $W(Q)=0$ in $\mathbb {D}$, then $u_1^2 \overline{u_2}\geqslant 0$ in $\mathbb {D}$ which implies that $\mu _1\in \mathbb {R}$. Since $u_0+\sqrt{3}|u_2|=1$ on $\partial \mathbb {D}$, we infer that $u_0+\sqrt{3}|u_2|=1$ in $\mathbb {D}$ by continuity. Inserting (4.12)–(4.13) in this equation leads to $\mu _1=\pm \sqrt{3}$. The other way around, if $\mu _1=\pm \sqrt{3}$, it is now easily seen that $W(Q)=0$ in $\mathbb {D}$. $\square$

Proof of Proposition 4.10

Using $H\circ \varvec{\sigma }_2^{-1}\simeq g_{{\overline{H}}}$ as a competitor, we infer from Proposition 4.7 and Lemma 4.11 that for any $Q\in {\mathcal {A}}_{\textrm{N}}$ with $Q\simeq u$,

$$\begin{aligned} E_\lambda (H\circ \varvec{\sigma }_2^{-1})=E_0(H\circ \varvec{\sigma }_2^{-1})=\widetilde{E}_0(g_{\overline{H}}) =6\pi \leqslant {\widetilde{E}}_0(u) \leqslant {\widetilde{E}}_\lambda (u)= E_\lambda (Q) \,. \end{aligned}$$

(4.35)

Hence (4.33) holds and $\overline{H}$ is a minimizer. On the other hand, if $Q\in {\mathcal {A}}_{\textrm{N}}$ is a minimizer, then $E_\lambda (Q)=6\pi$ and all inequalities in (4.35) are equalities. Hence $W(Q)\equiv 0$ and $\widetilde{E}_0(u)=6\pi$. Finally, combining again Proposition 4.7 with Lemma 4.11, we deduce that $u(z)=g_{\overline{H}}(\pm z)$. $\square$

Remark 4.12

In the previous proof, the characterization of uniaxial minimizers can be derived in a different way. Indeed, if a minimizer Q is (positively) uniaxial, then it must be a minimizer over the restricted class of maps ${\widetilde{Q}}\in W^{1,2}_{\textrm{sym}}({\mathbb D};\mathbb {R}P^2)$ with trace ${\widetilde{Q}}=\overline{H}$ on $\partial {\mathbb D}$. Combining with the fact that the mapping $\Pi :{\mathbb S}^2 \rightarrow \mathbb {R}P^2$,

$$\begin{aligned} \mathbb {R}\oplus \mathbb {C}\supseteq {\mathbb S}^2 \ni v \rightarrow \Pi (v)=\sqrt{\frac{3}{2}}\left( v \otimes v-\frac{1}{3} \textrm{Id}\right) \in \mathbb {R}P^2 \subseteq {\mathbb S}^4 \,, \end{aligned}$$

is an isometric two-fold cover with the result in [7], one can lift any such $\widetilde{Q}$ to a map $\widetilde{v} \in W^{1,2}_{\textrm{sym}}({\mathbb D};{\mathbb S}^2)$ with trace $\widetilde{v}(z)=(0, z)$ on $\partial {\mathbb D}$ (equivariance of the lift being a consequence of its uniqueness when a lift at the boundary is chosen). Then we have $E_0(\widetilde{Q})=\frac{3}{2}\int _{\mathbb {D}}|\nabla \widetilde{v}|^2\,dx$. Thus, minimizing maps are of the form $Q=\Pi \circ v$ with $v(z)=\frac{1}{1+|z|^2}\left( \pm (1- |z|^2), 2z \right)$, the unique minimizing harmonic maps in the class $W^{1,2}_{\textrm{sym}}({\mathbb D};{\mathbb S}^2)$ with trace (0, z) on $\partial \mathbb {D}$ (compare [22, Section 3.1, equations (3.5)–(3.6)]).

We now address problem (4.29), and we begin with the dependence on $\lambda$ of the associated value. Existence of solutions will be the object of Proposition 4.15.

Proposition 4.13

Setting

$$\begin{aligned} {\mathfrak {e}}^*_\lambda := \inf _{Q \in {\mathcal {A}}_{\textrm{S}}} E_\lambda (Q) \,, \end{aligned}$$

(4.36)

then $2\pi \leqslant {\mathfrak {e}}^*_\lambda \leqslant 10 \pi$ for every $\lambda \geqslant 0$, and the function $\lambda \mapsto {\mathfrak {e}}^*_\lambda$ is continuous and nondecreasing. In addition, there exists $\lambda ^* \in \left[ \frac{48 \sqrt{2}}{2\pi -3\sqrt{3}}, 5^2 \cdot 3^6 \cdot \frac{\sqrt{6}}{4} \pi ^2\right]$ such that $\lambda \mapsto {\mathfrak {e}}^*_\lambda$ is strictly increasing in $[0,\lambda ^*]$, ${\mathfrak {e}}^*_0=2\pi$, and ${\mathfrak {e}}^*_\lambda = 10 \pi$ for $\lambda \geqslant \lambda ^*$.

To prove the proposition, we shall need the following technical lemma.

Lemma 4.14

(Bubble insertion) For each $\rho \in (0,1)$ there exists $v_\rho \in \widetilde{{\mathcal {A}}}_{\textrm{S}}$ such that $v_\rho \equiv (1,0,0)$ for $|z|\geqslant \rho$, and satisfying $\widetilde{E}_0(v_\rho ) \rightarrow 4\pi$ as $\rho \rightarrow 0$. As a consequence, for each $u \in \widetilde{{\mathcal {A}}}_{\textrm{N}}$, there exists $\{ w_\rho \} \subseteq \widetilde{{\mathcal {A}}}_{\textrm{S}}$ such that $w_\rho \rightharpoonup u$ weakly in $W^{1,2}({\mathbb D})$, $w_\rho \rightarrow u$ strongly in $W^{1,2}_{\textrm{loc}}(\overline{{\mathbb D}} {\setminus } \{0\})$, and $\widetilde{E}_0(w_\rho ) \rightarrow \widetilde{E}_0(u)+4\pi$ as $\rho \rightarrow 0$.

Proof

Define

$$\begin{aligned} {\widehat{v}}(z):=\frac{1}{|z|^2+1}\big (|z|^2-1, 2z,0 \big ), \end{aligned}$$

so that ${\widehat{v}} \in W^{1,2}_{\textrm{loc}}(\mathbb {C};{\mathbb S}^4)$, $\widehat{v}$ is $\mathbb {S}^1$-equivariant, ${\widehat{v}}(0)=(-1,0,0)$, and $\widetilde{E}_0({\widehat{v}},\mathbb {C})=4 \pi$. We rescale the map ${{\widehat{v}}}$ setting, for $\rho \in (0,1)$, ${\widehat{v}}_\rho (z):={\widehat{v}}(z/\rho ^3)$. Then,

$$\begin{aligned} \max _{|z|=\rho ^2}|{\widehat{v}}_\rho (z)+{\widehat{v}}(0)|\mathop {\longrightarrow }\limits _{\rho \rightarrow 0}0 \quad \text {and}\quad \widetilde{E}_0({\widehat{v}}_\rho ,{\mathbb D}_{\rho ^2})\mathop {\longrightarrow }\limits _{ \rho \rightarrow 0} 4 \pi . \end{aligned}$$

Next we consider the linear interpolation between ${\widehat{v}}_\rho$ and $-{\widehat{v}}(0)$,

$$\begin{aligned} \widetilde{v}_\rho (re^{i\phi }):= {\left\{ \begin{array}{ll} {\widehat{v}}_\rho (re^{i\phi }) &{} \text {if }|z| \leqslant \rho ^2 \,, \\ \displaystyle {\widehat{v}}_\rho (\rho ^2 e^{i\phi }) -\frac{|z|-\rho ^2}{\rho -\rho ^2} \big ({\widehat{v}}(0)+{\widehat{v}}_\rho (\rho ^2 e^{i \phi })\big ) &{} \text {if }|z| \in [\rho ^2, \rho ] \,, \\ -{\widehat{v}}(0) &{} \text {if }|z| \in [\rho , 1] \,. \end{array}\right. } \end{aligned}$$

Since $\max _{|z|=\rho ^2}|{\widehat{v}}_\rho (z)+{\widehat{v}}(0)|\rightarrow 0$, we have $|{\widehat{v}}_\rho (z)|\geqslant 1/2$ on $\partial \mathbb {D}_{\rho ^2}$ for $\rho$ small enough. It allows us to define

$$\begin{aligned} v_\rho :=\frac{{{\widehat{v}}}_\rho }{|{{\widehat{v}}}_\rho |}\in \widetilde{{\mathcal {A}}}_{\textrm{S}} , \end{aligned}$$

which satisfies $v_\rho (z)=(1,0,0)$ for $|z|\geqslant \rho$. Arguing in Lemma 4.8, we obtain $\widetilde{E}_0(v_\rho ; {\mathbb D}_\rho {\setminus } {\mathbb D}_{\rho ^2}) \rightarrow 0$, and consequently

$$\begin{aligned} \lim _{\rho \rightarrow 0}\widetilde{E}_0(v_\rho )= \lim _{\rho \rightarrow 0}\widetilde{E}_0(v_\rho ;{\mathbb D}_\rho ) =\lim _{\rho \rightarrow 0} \widetilde{E}_0({\widehat{v}}_\rho ;{\mathbb D}_{\rho ^2}) =4 \pi , \end{aligned}$$

proving the first claim.

To prove the second claim, we fix $u \in \widetilde{{\mathcal {A}}}_{\textrm{N}}$ and we apply Lemma 4.8 (i) to obtain $u_\rho \in \widetilde{{\mathcal {A}}}_{\textrm{N}}^\rho$ (see (4.22)) such that $u_\rho \rightarrow u$ strongly in $W^{1,2}({\mathbb D})$ as $\rho \rightarrow 0$. Then $\widetilde{E}_0(u_\rho )=\widetilde{E}_0(u_\rho ;{\mathbb D} {\setminus } {\mathbb D}_{\rho })\rightarrow \widetilde{E}_0(u)$. Finally, we set

$$\begin{aligned} w_\rho (z):= {\left\{ \begin{array}{ll} v_\rho (z) &{} \text {if } |z| \leqslant \rho \,, \\ u_\rho (z) &{} \text {if } |z| \in [\rho , 1] \,, \end{array}\right. } \end{aligned}$$

and it is straightforward to check that $w_\rho \in \widetilde{{\mathcal {A}}}_{\textrm{S}}$ has all the announced properties. $\square$

Proof of Proposition 4.13

First, we observe that for each $Q \in {\mathcal {A}}_{\textrm{S}}$, the function $\lambda \mapsto E_\lambda (Q) \in \mathbb {R}$ is affine and nondecreasing. Hence $\lambda \mapsto {\mathfrak {e}}^*_\lambda$ is nondecreasing and concave, therefore continuous in $(0,\infty )$. In view of Proposition 4.6, we have ${\mathfrak {e}}^*_0=2\pi =E_0(Q_{\textrm{S}})$ with $Q_{\textrm{S}}\simeq u_\textrm{S}$ given by (4.19). Consequently,

$$\begin{aligned} 2\pi \leqslant {\mathfrak {e}}_\lambda ^* \leqslant E_\lambda (Q_{\textrm{S}})=\widetilde{E}_\lambda (u_{\textrm{S}}) \mathop {\longrightarrow }\limits _{\lambda \rightarrow 0} \widetilde{E}_0(u_{\textrm{S}})=2\pi , \end{aligned}$$

so that continuity also holds at 0.

Next we consider $H\circ \varvec{\sigma }_2^{-1}$ with $H\circ \varvec{\sigma }_2^{-1}\simeq g_{\overline{H}}$ as in (4.34), and $w_\rho \in \widetilde{{\mathcal {A}}}_{\textrm{S}}$ obtained by applying Lemma 4.14 to $g_{\overline{H}}$. Then, $\int _{{\mathbb \mathbb {D}}} \widetilde{W}(w_\rho ) \,dx \rightarrow \int _{{\mathbb \mathbb {D}}} \widetilde{W}(g_{\overline{H}})\, dx=0$. If $Q_\rho \simeq w_\rho$, it follows from Proposition 4.10 and Lemma 4.14 that

$$\begin{aligned} {\mathfrak {e}}^*_\lambda \leqslant E_\lambda (Q_\rho )=\widetilde{E}_0(w_\rho )+\lambda \int _{{\mathbb \mathbb {D}}} \widetilde{W}(w_\rho ) \,dx\mathop {\longrightarrow }\limits _{\rho \rightarrow 0} \widetilde{E}_0(g_{\overline{H}})+4\pi =10\pi \,.\end{aligned}$$

By monotonicity we deduce that $2\pi = {\mathfrak {e}}^*_0 \leqslant {\mathfrak {e}}_\lambda ^* \leqslant 10\pi$ for every $\lambda \geqslant 0$.

An elementary calculation yields

$$\begin{aligned} \int _{{\mathbb D}} \widetilde{W}(u_\textrm{S})\,dx{} & {} = \frac{18}{\sqrt{6}}\int _{{\mathbb D}}\frac{(|z|^4-1)^2}{(|z|^4+3)^3}\,dz=3\sqrt{6}\pi \int _0^1 \frac{(t^2-1)^2}{(t^2+3)^3}\,dt\nonumber \\{} & {} =-\frac{\sqrt{6}}{4}\pi +\frac{\sqrt{2}}{6} \pi ^2 \,. \end{aligned}$$

(4.37)

As a consequence, if ${\mathfrak {e}}^*_\lambda =10\pi$ for some $\lambda >0$, then

$$\begin{aligned} 10 \pi ={\mathfrak {e}}^*_\lambda \leqslant E_\lambda (Q_{\textrm{S}})=\widetilde{E}_\lambda (u_{\textrm{S}})=2\pi +\lambda \left( -\frac{\sqrt{6}}{4}\pi +\frac{\sqrt{2}}{6} \pi ^2 \right) \,, \end{aligned}$$

which implies that $\lambda \geqslant \frac{48 \sqrt{2}}{2\pi -3\sqrt{3}}$.

To complete the proof, we are going to show that if $\lambda >5^2 \cdot 3^6\cdot \frac{\sqrt{6}}{4} \pi ^2$, then $E_\lambda (Q)>10\pi$ for every $Q\in {\mathcal {A}}_{\textrm{S}}$. As a consequence ${\mathfrak {e}}^*_\lambda =10 \pi$ for $\lambda > 5^2 \cdot 3^6 \cdot \frac{\sqrt{6}}{4} \pi ^2$, so that the conclusion follows by setting $\lambda ^*:=\min \{\lambda \,: \, {\mathfrak {e}}^*_\lambda =10 \pi \}$ and noticing that $\lambda \mapsto {\mathfrak {e}}^*_\lambda$ is strictly increasing on $[0,\lambda ^*]$ by concavity. To derive the previous claim, we fix $Q\in {\mathcal {A}}_{\textrm{S}}$ and we observe that $\textrm{B}:={\widetilde{\beta }}(Q)=\sqrt{6} \textrm{tr} (Q^3)$ belongs to $W^{1,2}({\mathbb D}) \cap C(\overline{{\mathbb D}})$ with

$$\begin{aligned}|\nabla \textrm{B}| \leqslant 3 \sqrt{6} \big ( \textrm{tr} (Q^4)\big )^{1/2} |\nabla Q|= 3\sqrt{3} |\nabla Q| \,, \end{aligned}$$

where we used that $\textrm{tr} (Q^4)=\frac{1}{2}$ for $Q\in {\mathbb S}^4 \subseteq {\mathcal {S}}_0$. From this last inequality and Young’s inequality, we deduce that

$$\begin{aligned}E_\lambda (Q) \geqslant \int _{\mathbb D} \frac{1}{2\cdot 3^3} |\nabla \textrm{B}|^2+ \frac{\lambda }{3\sqrt{6}} \left( 1-\textrm{B}\right) \, dx \geqslant \frac{\sqrt{\lambda }}{9}\cdot \frac{1}{(24)^{1/4}} \int _{{\mathbb D}}\sqrt{1-\textrm{B}}|\nabla \textrm{B}| \,dx \,.\end{aligned}$$

Since $Q\in {\mathcal {A}}_{\textrm{S}}$, we have $\textrm{B}(\overline{{\mathbb D}})=[-1,1]$, so that the coarea formula yields

$$\begin{aligned}E_\lambda (Q) \geqslant \frac{\sqrt{\lambda }}{9}\cdot \frac{1}{(24)^{1/4}} \int _{{\mathbb D}}\sqrt{1-\textrm{B}}\,|\nabla \textrm{B}| \,dx= \frac{\sqrt{\lambda }}{9}\cdot \frac{1}{(24)^{1/4}} \int _{-1}^1\sqrt{1-t}\, dt=\frac{4}{3^3}\cdot \frac{\sqrt{\lambda }}{6^{1/4}} \,, \end{aligned}$$

and the conclusion follows. $\square$

We are now ready to discuss existence of solutions for variational problem (4.29) with $\lambda \geqslant 0$. The proof the proposition below is postponed as it requires two auxiliary results.

Proposition 4.15

Let $\lambda ^*>0$ be the constant defined in Proposition 4.13. The following holds.

• (i) If $0 \leqslant \lambda <\lambda ^*$, then ${\mathfrak {e}}^*_\lambda <10 \pi$ and there exists $Q_\lambda \in {\mathcal {A}}_{\textrm{S}}$ solving (4.29). In addition, $\beta _\lambda :={\widetilde{\beta }} \circ Q_\lambda$ satisfies $\beta _\lambda (\overline{{\mathbb D}})=[-1,1]$.

• (ii) If $\lambda >\lambda ^*$, then ${\mathfrak {e}}^*_\lambda =10 \pi$ and (4.29) has no solution.

To solve problem (4.29), we proceed as for (4.16) constructing an enhanced minimizing sequence for which the eventual lack of compactness is easy to describe. It rests on the following subclasses defined for $\rho \in (0,1)$ by

$$\begin{aligned} \widetilde{{\mathcal {A}}}_{\textrm{S}}^\rho :=\big \{ u \in \widetilde{{\mathcal {A}}}_{\textrm{S}}: u= (-1,0,0) \text{ a.e. } \text{ in } {\mathbb D}_\rho \big \} \,, \qquad \widetilde{{\mathcal {A}}}^0_\textrm{S}:=\bigcup _{0<\rho <1} \widetilde{{\mathcal {A}}}_{\textrm{S}}^\rho \,. \end{aligned}$$

(4.38)

Note that, as for the class $\widetilde{{\mathcal {A}}}^\rho _{\textrm{N}}$ in (4.22), the subsets $\widetilde{{\mathcal {A}}}_\textrm{S}^\rho$ are weakly $W^{1,2}$-closed for any $\rho \in (0,1)$. The following lemma is the analogue of Lemma 4.8 for $\widetilde{E}_\lambda$ restricted to $\widetilde{{\mathcal {A}}}_\textrm{S}$, instead of $\widetilde{E}_0$ restricted to $\widetilde{{\mathcal {A}}}_{\textrm{N}}$. The proof being completely similar, it is left to the reader.

Lemma 4.16

The following properties hold.

• (i) $\widetilde{{\mathcal {A}}}_{\textrm{S}}^0$ is a strongly dense subset of $\widetilde{{\mathcal {A}}}_{\textrm{S}}$ in $W^{1,2}(\mathbb {D})$.

• (ii) $\displaystyle {\inf _{u \in \widetilde{{\mathcal {A}}}_{\textrm{S}}} \widetilde{E}_\lambda (u) = \inf _{u \in \widetilde{{\mathcal {A}}}_{\textrm{S}}^0} \widetilde{E}_\lambda (u)=\lim _{\rho \rightarrow 0} \inf _{u \in \widetilde{{\mathcal {A}}}_{\textrm{S}}^\rho } \widetilde{E}_\lambda (u)}$ .

• (iii) For each integer $n \geqslant 1$, the minimization problem

  $$\begin{aligned} \min _{u\in \widetilde{{\mathcal {A}}}_{\textrm{S}}^{\frac{1}{n}}} \widetilde{E}_\lambda (u) \end{aligned}$$

  (4.39)

  admits a solution. In addition, for any solution $u_n\in \widetilde{{\mathcal {A}}}_{\textrm{S}}^{\frac{1}{n}}$, we have

  $$\begin{aligned} \displaystyle \lim _{n\rightarrow \infty }\widetilde{E}_\lambda (u_n)=\inf _{u \in \widetilde{{\mathcal {A}}}_{\textrm{S}}} \widetilde{E}_\lambda (u) ={\mathfrak {e}}^*_\lambda . \end{aligned}$$

  (4.40)

In the vein of Lemma 4.9, we now aim to describe the lack of compactness of the minimizing sequence $\{u_n\}$ constructed in Lemma 4.16. The proof has some similarities with the one of Lemma 4.9, and we concentrate on the main differences.

Lemma 4.17

Let $\{ u_n\} \subseteq \widetilde{{\mathcal {A}}}_{\textrm{S}}^0$ be such that $u_n$ solves (4.39) for every $n\geqslant 1$. Assume that for some (not relabelled) subsequence, $u_n \rightharpoonup u_*$ weakly in $W^{1,2}({\mathbb D})$. Then $u_* \in \widetilde{{\mathcal {A}}}^{\textrm{sym}}_{ g_{\overline{H}}}(\mathbb {D})$ and $u_*$ is a critical point of $\widetilde{E}_\lambda$. Moreover, if $u_* \in \widetilde{{\mathcal {A}}}_{\textrm{N}}$, then there exist a further (not relabelled) subsequence and $r_n\rightarrow 0^+$ such that ${\tilde{u}}_n(z):=u_n(r_n z)$ satisfies ${\tilde{u}}_n \rightharpoonup {\tilde{u}}$ weakly in $W^{1,2}_{\textrm{loc}} (\mathbb {C})$ for some equivariant nonconstant finite energy smooth harmonic map ${\tilde{u}}:\mathbb {C}\rightarrow {\mathbb S}^4$.

Proof

In view of Proposition 4.13 and Lemma 4.16 we have

$$\begin{aligned} \lim _{n \rightarrow \infty } \widetilde{E}_\lambda (u_n)=\inf _{u\in \widetilde{{\mathcal {A}}}_{\textrm{S}}} \widetilde{E}_\lambda (u)=\inf _{Q\in {{\mathcal {A}}}_{\textrm{S}}} {E}_\lambda (Q) ={\mathfrak {e}}^*_\lambda \leqslant 10\pi \,, \end{aligned}$$

(4.41)

which is the key a priori bound to obtain compactness properties.

By equivariance, $u_n$ and $u_*$ write

$$\begin{aligned} u_n(re^{i\phi })=\big (f^{(n)}_0(r), f^{(n)}_1(r) e^{i\phi }, f^{(n)}_2(r) e^{i 2\phi } \big ) \,, \quad u_*(re^{i\phi })=\big (f^*_0(r), f^*_1(r) e^{i \phi }, f^*_2(r) e^{i2\phi }\big ) \,, \end{aligned}$$

where $f^{(n)}:=(f^{(n)}_0, f^{(n)}_1, f^{(n)}_2)$ and $f^{*}:=(f^{*}_0, f^{*}_1, f^{*}_2)$ are continuous on [0, 1] by Lemma 2.10.

By minimality of $u_n$, each $f^{(n)}$ solves (4.32) in the interval (1/n, 1). As a consequence, $f^*$ solves (4.32) in (0, 1). Indeed, (4.41) implies a $W^{2,1}_\textrm{loc}((0,1])$-bound on the sequence $\{f^{(n)}\}$, hence a $W^{1,\infty }_{\textrm{loc}}((0,1])$-bound by Sobolev embedding. Back to the ODE (4.32), it yields a $C^2_{\textrm{loc}}((0,1])$ bound on $\{f^{(n)}\}$. This is then enough to pass to the limit $n\rightarrow \infty$ in (4.32) for $r \in (0,1)$. Thus, since $f^*$ solves (4.32) in (0, 1), $Q_*\simeq u_*$ is a weak solution to (1.6) in ${\mathbb D} {\setminus } \{0\}$. However, $Q_*$ being of finite energy and $\{0\}$ of zero capacity, $Q_*$ weakly solves (1.6) in the whole ${\mathbb D}$, i.e., $Q_*$ is a critical point of $E_\lambda$ or equivalently, $u_*$ is a critical point of $\widetilde{E}_\lambda$.

We claim that $f^*_0(r)<1$ for every $r \in (0,1]$. To prove this claim, we argue as in the proof of Lemma 4.2. Since $\widetilde{E}_0(u_*)<\infty$, we infer from (4.31) that there exists a sequence $r_k \downarrow 0$ satisfying $r_k^2 \left| (f^*)^\prime (r_k) \right| ^2+\left| f^*_1(r_k) \right| ^2+4\left| f^*_2(r_k) \right| ^2 \rightarrow 0$ as $k \rightarrow \infty$. Then we multiply (4.32) by $r^2(f^*)^\prime$ and integrate between $r_k$ and a fixed $r\in (0,1)$. Using $(f^*)^\prime \cdot f^* = 0$ and letting $k\rightarrow \infty$, we obtain

$$\begin{aligned} r^2 \left| (f^*)^\prime (r) \right| ^2=\left| f^*_1(r) \right| ^2+4\left| f^*_2(r) \right| ^2+\frac{2\lambda }{3\sqrt{6}}\big (1-{\widetilde{\beta }}(f^*(r))\big )r^2 \,. \end{aligned}$$

Now assume by contradiction that $f^*_0(\bar{r})=1$ for some $\bar{r}\in (0,1)$. Then $f^*(\bar{r})=(1,0,0)$ because $|f^*(\bar{r})|=1$, and the previous identity yields $(f^*)^\prime (\bar{r})=0$. By uniqueness of the Cauchy problem for (4.32), it follows that $f^*(r)= f^*(\bar{r})=(1,0,0)$ for every $r \in (0,1]$. However, since $u_* =g_{\overline{H}}$ on $\partial \mathbb {D}$, we have $f^*(1)=(-1/2,0,\sqrt{3}/2)$, a contradiction.

Let us now assume that $u_*\in \widetilde{{\mathcal {A}}}_{\textrm{N}}$. Since $u_n\in \widetilde{{\mathcal {A}}}_{\textrm{S}}$, we have

$$\begin{aligned} (f^{(n)}_0(0), f^{(n)}_1(0), f^{(n)}_2(0))=(-1,0,0)\, \text { and } \,(f^*_0(0), f^*_1(0), f^*_2(0))=(1,0,0) \,. \end{aligned}$$

Arguing as in the proof of Lemma 4.9, $f^{(n)}_0 \rightarrow f^*_0$ locally uniformly in (0, 1], and

$$\begin{aligned} \lim _{n\rightarrow \infty }\max _{[0,1]} f^{(n)}_0 =1 \,. \end{aligned}$$

Since $f^{(n)}_0(0)=-1$, each $f_0^{(n)}$ must vanish on [0, 1] by continuity, at least for n large enough. This allows us to define

$$\begin{aligned} r_n:= \min \big \{ r\in [0,1]: f^{(n)}_0(r)=0\big \}\in (0,1), \end{aligned}$$

and

$$\begin{aligned} r_n^{\max }:= \min \big \{ r\in [0,1]:f^{(n)}_0(r) = \max _{[ 0,1]} f^{(n)}_0 \big \}\in (0,1) \,. \end{aligned}$$

As in the proof of Lemma 4.9, we have $1/n<r_n<r_n^{\max } \rightarrow 0$ as $n \rightarrow \infty$, and

$$\begin{aligned} r_*:=\limsup _{n\rightarrow \infty } \frac{1}{nr_n} <1. \end{aligned}$$

Now we set ${\tilde{u}}_n(z):=u_n(r_n z)$, so that ${\tilde{u}}_n \in W^{1,2}_{\textrm{sym}}({\mathbb D}_{1/r_n};{\mathbb S}^4)$, ${\tilde{u}}_n(z) = -\textbf{e}_0$ for $|z| \leqslant \frac{1}{nr_n}$, and ${{\tilde{u}}}_n$ is a critical point of $\widetilde{E}_{\lambda r_n^2}$ in the domain $\Omega _n:=\left\{ \frac{1}{nr_n}<|z|< 1/r_n\right\}$. In addition, setting ${\tilde{u}}_n(re^{i\phi })=:({\tilde{f}}^{(n)}_0(r), {\tilde{f}}^{(n)}_1(r) e^{i\phi }, {\tilde{f}}^{(n)}_2(r) e^{i 2\phi } )$, ${\tilde{f}}^{(n)}_0$ satisfies ${\tilde{f}}^{(n)}_0(1)=0$ by our choice of $r_n$.

By (4.41), we have $\widetilde{E}_{\lambda r_n^2}({{\tilde{u}}}_n,\mathbb {D}_{1/r_n})= \widetilde{E}_\lambda (u_n)\leqslant 10\pi$. Hence, we can find a (not relabelled) subsequence such that ${\tilde{u}}_n \rightharpoonup {\tilde{u}}$ weakly in $W^{1,2}_\textrm{loc}(\mathbb {C})$ for a limiting equivariant map ${\tilde{u}}\in W^{1,2}_\textrm{loc}(\mathbb {C};{\mathbb S}^4)$ satisfying $\widetilde{E}_0({\tilde{u}};\mathbb {C}) \leqslant 10 \pi$. Since $\Omega _ n \rightarrow \Omega _*:=\{ |z|> r_*\}$, we obtain that ${\tilde{u}}$ is a weakly harmonic map in $\Omega _*$. Indeed, $\tilde{f}_n:=({\tilde{f}}^{(n)}_0, {\tilde{f}}^{(n)}_1, {\tilde{f}}^{(n)}_2)$ satisfies (4.32) with $\lambda r_n^2$ in place of $\lambda$. Using the energy bound and the ODE as above, we derive that ${\tilde{f}}^{(n)}$ is bounded in $C^2_{\textrm{loc}}((r_*,\infty ))$. Arguing again as above and since $\lambda r_n^2\rightarrow 0$, it implies that ${{\tilde{u}}}$ is a critical point of $\widetilde{E}_0$ in $\Omega _*$, i.e., ${\tilde{u}}$ is a weakly harmonic map in $\Omega _*$. The rest of the proof now follows exactly as in the proof of Lemma 4.9: ${\tilde{u}}$ is nonconstant by the normalization ${\tilde{f}}_0(1)=0$, $r_*=0$ by Lemaire’s theorem, and ${\tilde{u}}$ extends to a finite energy harmonic map in the whole $\mathbb {C}$. $\square$

Proof of Proposition 4.15

We start proving (i), arguing as in the proof of Proposition 4.7. We thus assume that $\lambda <\lambda ^*$. We consider $\{ u_n\} \subseteq \widetilde{{\mathcal {A}}}_{\textrm{S}}^0$ be such that $u_n$ solves (4.39) for every $n\geqslant 1$. From Proposition 4.13 and Lemma 4.16, we infer that $\widetilde{E}_\lambda (u_n)\rightarrow {\mathfrak {e}}^*_\lambda <10\pi$ as $n\rightarrow \infty$. The sequence $\{u_n\} \subseteq \widetilde{{\mathcal {A}}}_{\textrm{S}}$ being bounded, we can find a (not relabelled) subsequence such that $u_n \rightharpoonup u_*$ weakly in $W^{1,2}(\mathbb {D})$. By Lemma 4.17, $u_* \in \widetilde{{\mathcal {A}}}_{g_{{\overline{H}}}}^{\textrm{sym}}(\mathbb {D})$ and $u_*$ is a critical point of $\widetilde{E}_\lambda$.

Now we claim that $u_* \in \widetilde{{\mathcal {A}}}_{\textrm{S}}$. Assuming this claim holds, we have ${\mathfrak {e}}^*_\lambda \leqslant \widetilde{E}_\lambda (u_*) \leqslant \widetilde{E}_\lambda (u_n)$ and $\liminf _n \widetilde{E}_\lambda (u_n)={\mathfrak {e}}^*_\lambda$ by weak lower semicontinuity. Hence equality holds, and since $u_*\in \widetilde{{\mathcal {A}}}_{\textrm{S}}$, we conclude that $Q_*\simeq u_*$ is a minimizer for (4.29). In addition, $\widetilde{\beta }\circ Q_*(0)=-1$ and $\widetilde{\beta }\circ Q_* \equiv 1$ on $\partial \mathbb {D}$, so that $\widetilde{\beta }\circ Q_*({\overline{\mathbb {D}}})=[-1,1]$ by continuity (and Lemma 2.10).

To show that $u_* \in \widetilde{{\mathcal {A}}}_{\textrm{S}}$, we argue by contradiction assuming that $u_* \in \widetilde{{\mathcal {A}}}_\textrm{N}$. According to Lemma 4.17, there exist a further (not relabelled) subsequence and $r_n\rightarrow 0^+$ such that ${\tilde{u}}_n(z):=u_n(r_n z)$ satisfies ${{\tilde{u}}}_n\rightharpoonup {{\tilde{u}}}$ weakly in $W^{1,2}_{\textrm{loc}} (\mathbb {C})$ for some equivariant nonconstant finite energy smooth harmonic map ${\tilde{u}}$. Setting $r_n'=\sqrt{r_n}$ and rescaling variables, we derive by weak lower semicontinuity that

$$\begin{aligned} 10\pi{} & {} > {\mathfrak {e}}^*_\lambda =\lim _{n\rightarrow \infty } \widetilde{E}_\lambda (u_n)\geqslant \liminf _{n\rightarrow \infty } \widetilde{E}_\lambda (u_n; {\mathbb D}_{r_n'})+\liminf _{n \rightarrow \infty }\widetilde{E}_\lambda (u_n; {\mathbb D} \setminus \overline{{\mathbb D}_{r_n'}}) \nonumber \\{} & {} \geqslant \liminf _{n\rightarrow \infty } \widetilde{E}_0({\tilde{u}}_n; {\mathbb D}_{r_n'/r_n})+ \widetilde{E}_\lambda (u_*) \geqslant E_0({\tilde{u}};\mathbb {C})+\widetilde{E}_\lambda (u_*) \geqslant 10 \pi \,, \end{aligned}$$

(4.42)

a contradiction. The last inequality above combines the inequality $\widetilde{E}_\lambda (u_*)\geqslant 6\pi$ from Proposition 4.10, with $E_0({\tilde{u}};\mathbb {C})\geqslant 4\pi$ from the classification result in [12, Section 3] (${\tilde{u}}$ being of finite energy, it extends to $\mathbb {C}\cup \{\infty \} \simeq {\mathbb S}^2$ as a nonconstant equivariant harmonic 2-sphere into $\mathbb {S}^4$). Hence, $u_* \in \widetilde{{\mathcal {A}}}_{\textrm{S}}$ as claimed.

To prove (ii), we first observe that Proposition 4.13 yields ${\mathfrak {e}}^*_\lambda =10\pi$ for $\lambda >\lambda _*$. Next we argue by contradiction assuming that a minimizer $Q_\lambda \in {\mathcal {A}}_{\textrm{S}}$ for (4.29) exists for some $\lambda >\lambda ^*$. Since $W(Q_\lambda (0))=W(-\textbf{e}_0)>0$, we have $\int _{{\mathbb D}}W(Q_\lambda )\,dx>0$. Therefore,

$$\begin{aligned} 10 \pi = {\mathfrak {e}}^*_{\lambda '} \leqslant E_{\lambda '}(Q_\lambda )<E_{\lambda '}(Q_\lambda )+(\lambda -\lambda ')\int _{{\mathbb D}}W(Q_\lambda )\,dx=E_\lambda (Q_\lambda )={\mathfrak {e}}^*_\lambda =10\pi \end{aligned}$$

for every $\lambda ^*<\lambda '<\lambda$, which gives the contradiction. $\square$

Remark 4.18

It is an open problem whether the solution $Q_\lambda \simeq u_\lambda$ of (4.29) is unique or not for each $\lambda \in (0,\lambda ^*)$. If $u_\lambda (re^{i\phi })=(f_0^\lambda (r), f^\lambda _1(r)e^{i\phi },f_2^\lambda (r)e^{i2\phi })$, then choosing as competitors $(f_0^\lambda (r),\pm |f^\lambda _1(r)| e^{i\phi },|f_2^\lambda (r)|e^{i2\phi })$ implies that $f_2^\lambda (r)\geqslant 0$ (since it is positive at the boundary), and $f_1^\lambda$ is real with constant sign. As a consequence, either $f_1^\lambda \equiv 0$ and in turn $u_\lambda$ is unique at least for $\lambda$ small (see Theorem A.3, Lemma A.1 and Lemma 2.10), or $f_1^\lambda \not \equiv 0$ and both $\pm f_1^\lambda$ give rise to minimizers.

Remark 4.19

The previous proof obviously breaks down in the limiting case $\lambda =\lambda ^*$. In this case, it is unknown if a minimizer of (4.29) exists, or if the minimizing sequence $\{u_n\}$ exhibits concentration of energy and bubbling-off of a harmonic sphere at the origin according to Lemma 4.17.

We are finally in the position to discuss the global minimization of the energy $E_\lambda$ in the class (1.12). To this purpose, we define for $\lambda \geqslant 0$,

$$\begin{aligned} {\mathfrak {e}}_\lambda :=\inf _{Q \in {\mathcal {A}}^{\textrm{sym}}_{\overline{H}}(\mathbb {D})} E_\lambda (Q) , \end{aligned}$$

(4.43)

and we recall that the constant $\lambda ^*>0$ is defined in Proposition 4.13, and ${\mathfrak {e}}^*_\lambda$ is given by (4.36).

Proposition 4.20

For every $\lambda \geqslant 0$, we have ${\mathfrak {e}}_\lambda =\min \{6\pi , {\mathfrak {e}}^*_\lambda \}$ with ${\mathfrak {e}}^*_\lambda$ given by (4.36), so that $\lambda \mapsto {\mathfrak {e}}_\lambda$ is nondecreasing, continuous, and concave. Moreover, there exists $\lambda _* \in \left[ \frac{24 \sqrt{2}}{2\pi -3\sqrt{3}}, 3^8 \cdot \frac{\sqrt{6}}{4} \pi ^2\right]$ with $\lambda _*<\lambda ^*$, such that $\lambda \mapsto {\mathfrak {e}}_\lambda$ is strictly increasing in $[0,\lambda _*]$, and ${\mathfrak {e}}_{\lambda }=6\pi$ for $\lambda \geqslant \lambda _*$.

Proof

Recalling that ${\mathcal {A}}^\textrm{sym}_{\overline{H}}(\mathbb {D})={\mathcal {A}}_{\textrm{S}} \cup {\mathcal {A}}_\textrm{N}$, combining Proposition 4.7, Proposition 4.10, and Proposition 4.13, we infer that ${\mathfrak {e}}_\lambda =\min \{6\pi , {\mathfrak {e}}^*_\lambda \}$ for every $\lambda \geqslant 0$. It is therefore continuous, concave, and nondecreasing. Choosing $\lambda _*$ to be the unique solution to ${\mathfrak {e}}^*_\lambda =6\pi$, the rest of claim follows from Proposition 4.13. By obvious modifications of the proof of Proposition 4.13, we obtain the announced lower and upper bounds on $\lambda _*$. $\square$

We are finally ready to prove the main result concerning 2D-minimization, i.e., to give the full proof of Theorem 1.2.

Proof of Theorem 1.2

To prove (i) we argue as follows. According to Proposition 4.7 and Proposition 4.10, the maps ${\overline{Q}}$ are uniaxial and minimizing $E_\lambda$ over ${\mathcal {A}}_{\textrm{N}}$ for every $\lambda \geqslant 0$ with $E_\lambda ({\overline{Q}})=6\pi$. As a consequence, these maps are local minimizers of $E_\lambda$ in ${\mathcal {A}}^{\textrm{sym}}_{\overline{H}}(\mathbb {D})$ because in the decomposition ${\mathcal {A}}^\textrm{sym}_{\overline{H}}(\mathbb {D})={\mathcal {A}}_{\textrm{S}} \cup {\mathcal {A}}_\textrm{N}$ into open and closed sets (see Lemma 2.10). Finally, combining Propositions 4.13 and 4.20 we have ${\mathfrak {e}}^*_\lambda >6\pi$ and ${\mathfrak {e}}_\lambda =6\pi$ for $\lambda >\lambda _*$, hence these maps are the absolute minimizers of $E_\lambda$ because of Proposition 4.10.

In a similar way, concerning (ii), existence of a minimizer (hence, of a local minimizer) $Q_\lambda$ in the class ${\mathcal {A}}_{\textrm{S}}$ follows from Proposition 4.15. Moreover, we have ${\mathfrak {e}}_\lambda ={\mathfrak {e}}^*_\lambda <6\pi$ for $\lambda <\lambda _*$, and therefore $Q_\lambda$ is a minimizer over ${\mathcal {A}}^{\textrm{sym}}_{\overline{H}}(\mathbb {D})$. Uniqueness for $\lambda <\lambda _0$ and $\lambda _0>0$ small enough is proved in Theorem A.3 in the Appendix.

Finally, concerning (iii) we have $E_{\lambda _*}(u_{\lambda _*})={\mathfrak {e}}^*_{\lambda _*}=6\pi ={\mathfrak {e}}_{\lambda _*}=E_{\lambda _*}(\bar{u})$ for $\lambda =\lambda _*$. Hence ${\overline{Q}}$ and $Q_{\lambda _*}$ are both global minimizers over the class ${\mathcal {A}}^\textrm{sym}_{\overline{H}}(\mathbb {D})$. $\square$

Remark 4.21

According to Theorem 1.2, a sharp transition occurs in the qualitative properties of energy minimizers of $E_\lambda$ over ${\mathcal {A}}^\textrm{sym}_{\overline{H}}(\mathbb {D})$ for $\lambda$ close to the critical value $\lambda _*$. At $\lambda =\lambda _*$, coexistence of uniaxial and biaxial minimizers occurs. For $\lambda >\lambda _*$, the influence of the potential energy is so strong that it forces the uniaxial character of energy minimizers (and the explicit form (4.34)), although a biaxial locally minimizing configuration exists. For $\lambda <\lambda _*$, uniaxiality is no longer energetically convenient as the effect of the potential energy gets weaker, and minimizers are biaxial configurations satisfying $Q_\lambda (0)=-\textbf{e}_0$ and ${\widetilde{\beta }} \circ Q_\lambda (\overline{{\mathbb D}})=[-1,1]$. In this latter case, we see that although the boundary condition is topologically trivial in $\pi _1(\mathbb {R}P^2)$ and two uniaxial local minimizers exist, biaxial escape occurs for energy minimizers. This phenomenon of purely energetic nature is of definite interest, also in comparison with [9] where the biaxial escape mechanism is essentially deduced from topological nontriviality of the boundary data.

5 Split minimizers in long cylinders

In this section, we return to the analysis of the LdG energy ${\mathcal {E}}_\lambda$ in three space dimension. We shall discuss qualitative properties of minimizers of ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}_{Q_{\textrm{b}}}^{\textrm{sym}}(\Omega )$ for specific choices of axisymetric domains $\Omega \subseteq \mathbb {R}^3$ and boundary data $Q_\textrm{b}$. Namely, we consider throughout this section the homeotropic boundary data on $\partial \Omega$ as defined in (2.4) for a domain $\Omega$ of “cigar shape”, i.e., $\Omega ={\mathfrak {C}}^h_{\ell ,\rho }$ is the smoothed cylinder from Definition 2.3 in a regime where the height h is large and the width $\ell$ is small.

By means of an asymptotic analysis, our aim is to show that in the regime of parameters for which the cylinders ${\mathfrak {C}}^h_{\ell ,\rho }$ are very long and very thin (namely, $\ell \sqrt{\lambda } \ll 1$ and $h \gg \ell$), minimizers must be singular for reasons of energy efficiency. In addition, we shall see that an energy gap occurs between minimizers and any smooth configuration. This singular behavior might be surprising since the homeotropic boundary condition admits smooth $\mathbb {S}^1$-equivariant extensions, and smoothness of minimizers can’t be ruled out by some topological obstruction. This phenomenon is clearly reminiscent of the energy gap for harmonic maps into ${\mathbb S}^2$ first observed in [17]. By the presence of singularities, minimizers in this parameter regime are thus of split type in the sense of [12, Section 7], and their regular biaxial sets $\{\beta =t\}$, $t \in (-1,1)$, contain topological spheres according to [12, Theorem 1.5].

5.1 Global energy identities for minimizers

We start with the following general lemma based on the partial regularity result from Theorems 3.1 & 3.2. It provides a key integral identity to derive monotonicity inequalities and rigidity results in the present and next section.

Lemma 5.1

Let $\Omega \subseteq \mathbb {R}^3$ be a bounded and axisymmetric open set with boundary of class $C^3$, and let $Q_\textrm{b}\in C^{1,1}(\partial \Omega ;\mathbb {S}^4)$ be an $\mathbb {S}^1$-equivariant map. Let Q be a minimizer of ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}^{\textrm{sym}}_{Q_\textrm{b}}(\Omega )$, and $\Omega '\subseteq \mathbb {R}^3$ a bounded axisymmetric open set with boundary of class $C^1$ such that $\partial \Omega$ and $\partial \Omega '$ meet transversally and $\partial \Omega ' \cap \textrm{sing}(Q)=\emptyset$. For every vector field $V \in C^1(\mathbb {R}^3;\mathbb {R}^3)$, the following identity holds,

$$\begin{aligned}{} & {} \int _{\Omega \cap \Omega '} \Big [ \Big ( \frac{1}{2} \left| \nabla Q \right| ^2+\lambda W(Q)\Big ) {{\,\mathrm{\textrm{div}}\,}}{V} -\sum _{i,j} (\partial _i Q:\partial _j Q) \partial _j V_i\Big ] \, dx\nonumber \\{} & {} \quad =\int _{\partial (\Omega \cap \Omega ')} \Big [ \Big ( \frac{1}{2} \left| \nabla Q \right| ^2+\lambda W(Q)\Big )V \cdot \overrightarrow{n} - \Big (\frac{\partial Q}{\partial V}:\frac{\partial Q}{\partial \overrightarrow{n}} \Big )\Big ]\, d{\mathcal {H}}^2 \,, \end{aligned}$$

(5.1)

where $\overrightarrow{n}$ denotes the (${\mathcal {H}}^2$-a.e. defined) outer unit normal along $\partial (\Omega \cap \Omega ')$.

Proof

We shall derive (5.1) through the Pohozaev multiplier argument, i.e., multiplying equation (1.6) by $V\cdot \nabla Q$ and integrating by parts the result. However, since $\textrm{sing}(Q)$ might not be empty, we shall first integrate on a punctured domain, removing finitely many balls centered at singular points, and then let the radius of this balls go to zero.

Recalling that $Q\in C^\infty (\Omega \setminus \textrm{sing}(Q))$, the constraint $|Q|^2=1$ implies that $Q:(V\cdot \nabla Q)= 0$ in ${\overline{\Omega }}\setminus \textrm{sing}(Q)$. Hence, taking the scalar product of (1.6) with $V\cdot \nabla Q$ in $\Omega \setminus \textrm{sing}(Q)$ yields

$$\begin{aligned} \Delta Q: (V \cdot \nabla Q)=\lambda \nabla _{\textrm{tan}}W(Q):(V\cdot \nabla Q ) \,. \end{aligned}$$

(5.2)

Direct computations lead to

$$\begin{aligned}{} & {} {{\,\mathrm{\textrm{div}}\,}}\Big (\frac{1}{2} \left| \nabla Q \right| ^2 V \Big )= \frac{1}{2} \left| \nabla Q \right| ^2{{\,\mathrm{\textrm{div}}\,}}V+\sum _{i,j} (\partial _{ij} Q:\partial _j Q)V_i \nonumber \\{} & {} \quad =\frac{1}{2} \left| \nabla Q \right| ^2{{\,\mathrm{\textrm{div}}\,}}V - \sum _{i,j}(\partial _i Q:\partial _j Q)\partial _j V_i +\textrm{div}\big ( (V\cdot \nabla Q): \nabla Q \big ) \nonumber \\{} & {} \quad -\Delta Q:(V\cdot \nabla Q)\,, \end{aligned}$$

(5.3)

and

$$\begin{aligned} {{\,\mathrm{\textrm{div}}\,}}\big ( W(Q) V\big )=W(Q){{\,\mathrm{\textrm{div}}\,}}V + \nabla _{\textrm{tan}}W(Q):(V \cdot \nabla Q)\,. \end{aligned}$$

(5.4)

Combining (5.2)–(5.3)–(5.4), we obtain the following equality in $\Omega \setminus \textrm{sing}(Q)$,

$$\begin{aligned}{} & {} \Big ( \frac{1}{2} \left| \nabla Q \right| ^2+\lambda W(Q)\Big ) {{\,\mathrm{\textrm{div}}\,}}{V} -\sum _{i,j}\partial _j V_i \partial _i Q:\partial _j Q \nonumber \\{} & {} \quad = {{\,\mathrm{\textrm{div}}\,}}\Big [ \Big ( \frac{1}{2} \left| \nabla Q \right| ^2+\lambda W(Q)\Big )V -\frac{\partial Q}{\partial V}:\nabla Q\Big ] \,. \end{aligned}$$

(5.5)

If $\textrm{sing}(Q)=\emptyset$, then (5.1) follows as in the general case, integrating by parts the right hand side of (5.5) over $\Omega \cap \Omega '$. So we may assume that $\textrm{sing}(Q) \ne \emptyset$. Since $\textrm{sing}(Q) \cap \partial \Omega '=\emptyset$, we can find $\sigma _0>0$ small enough that the balls $\displaystyle {\{B_{2\sigma _0}(p)\}_{p \in \textrm{sing}(Q)}}$ are disjoint and $B_{2\sigma _0}(p) \subseteq \Omega \cap \Omega '$ for each $p\in \textrm{sing}(Q)\cap \Omega '$. For $0<\sigma \leqslant \sigma _0$, we consider punctured domain

$$\begin{aligned} \Omega _\sigma :=(\Omega \cap \Omega ') \setminus \cup _{p \in \textrm{sing}(Q) \cap \Omega '} \overline{B_{\sigma }(p)} \end{aligned}$$

which is obviously a piecewise smooth domain with $\partial \Omega _\sigma = \partial (\Omega \cap \Omega ') \cup \left( \cup _{p \in \textrm{sing}(Q) \cap \Omega '} \partial B_{\sigma }(p) \right)$.

By Theorem 3.2, we have $Q\in C^1(\overline{\Omega } {\setminus } \cup _{p \in \textrm{sing}(Q)}B_\sigma (p))$ and $Q\in C^\omega (\cup _{p \in \textrm{sing}(Q)} \partial B_{\sigma }(p))$. Hence $\Delta Q\in L^\infty (\Omega {\setminus } \cup _{p \in \textrm{sing}(Q)}B_\sigma (p))$ by equation (1.6). Since $\partial \Omega$ is of class $C^3$ and $Q_{\textrm{b}} \in C^{1,1}(\partial \Omega ) \subseteq W^{3/2,2}(\partial \Omega )$, it follows from standard elliptic theory that $Q \in W^{2,2}(\Omega {\setminus } \cup _{p \in \textrm{sing}(Q)} \overline{B_\sigma (p)})$ (see e.g. [15, Theorem 8.12]). As a consequence, the vector field

$$\begin{aligned}\Phi :=\Big ( \frac{1}{2} \left| \nabla Q \right| ^2+\lambda W(Q)\Big ) V -\frac{\partial Q}{\partial V}:\nabla Q\end{aligned}$$

satisfies $\Phi \in W^{1,2}(\Omega _\sigma ;\mathbb {R}^3) \cap C(\overline{\Omega _\sigma };\mathbb {R}^3)$ for every $0<\sigma <\sigma _0$. By the divergence theorem (on a Lipschitz regular domain), we have

$$\begin{aligned} \int _{\Omega _\sigma } {{\,\mathrm{\textrm{div}}\,}}{\Phi }\, dx=\int _{\partial (\Omega \cap \Omega ')}\Phi \cdot \overrightarrow{n} \, d{\mathcal {H}}^2-\sum _{p \in \textrm{sing}(Q) \cap \Omega '}\int _{\partial B_\sigma (p)}\Phi \cdot \overrightarrow{n} \, d{\mathcal {H}}^2 , \end{aligned}$$

(5.6)

while (5.5) yields

$$\begin{aligned} \int _{\Omega \cap \Omega '} \Big [\Big ( \frac{1}{2} \left| \nabla Q \right| ^2+\lambda W(Q)\Big ) {{\,\mathrm{\textrm{div}}\,}}{V} -\sum _{i,j}\partial _j V_i \partial _i Q:\partial _j Q \Big ]\, dx= \lim _{\sigma \rightarrow 0} \int _{\Omega _\sigma } {{\,\mathrm{\textrm{div}}\,}}{\Phi }\, dx. \end{aligned}$$

Hence (5.1) follows once we prove that

$$\begin{aligned} \lim _{\sigma \rightarrow 0} \int _{\partial B_\sigma (p)} \Big [ \Big ( \frac{1}{2} \left| \nabla Q \right| ^2+\lambda W(Q)\Big )V \cdot \overrightarrow{n} - \frac{\partial Q}{\partial V}:\frac{\partial Q}{\partial \overrightarrow{n}} \Big ]\, d{\mathcal {H}}^2=0 \qquad \forall p\in \textrm{sing}(Q) \,.\nonumber \\ \end{aligned}$$

(5.7)

Let us now fix an arbitrary point $p\in \textrm{sing}(Q)$, that we may assume without loss of generality to be the origin, i.e., $p=0$. By Theorem 3.1, there exists a 0-homogeneous harmonic map $Q_*$ which is smooth away from the origin, and an exponent $\nu >0$ such that $\Vert Q_\rho -Q_*\Vert _{C^2(\overline{B_2}{\setminus } B_1)}=O(\rho ^\nu )$ as $\rho \rightarrow 0$ with $Q_\rho (x):=Q(\rho x)$. In addition, the explicit expression in (3.1) yields $|\nabla Q_*(x)|^2=2|x|^{-2}$ for $x\ne 0$. As a a consequence, we easily infer the following expansions as $x \rightarrow 0$,

$$\begin{aligned} \left| \frac{\partial Q}{\partial \overrightarrow{n}} \right| =o\left( |x|^{-1}\right) \,, \quad \left| \frac{\partial Q}{\partial V} \right| =O \left( |x|^{-1}\right) \,, \quad \left| \nabla Q \right| ^2=2|x|^{-2} \big (1+o(1)\big ) \,, \;{ \text {and }}\; W(Q)=O(1) \,. \end{aligned}$$

In particular, $|V-V(0)|\left| \nabla Q \right| ^2=o \left( |x|^{-2}\right)$ by continuity of V. Since ${\mathcal {H}}^{2}(\partial B_\sigma )=O(\sigma ^2)$, the previous expansions yield

$$\begin{aligned}{} & {} \lim _{\sigma \rightarrow 0} \int _{\partial B_\sigma } \Big [\Big ( \frac{1}{2} \left| \nabla Q \right| ^2+\lambda W(Q)\Big )V \cdot \overrightarrow{n} - \frac{\partial Q}{\partial V}:\frac{\partial Q}{\partial \overrightarrow{n}} \Big ]\, d{\mathcal {H}}^2\nonumber \\{} & {} \quad = \lim _{\sigma \rightarrow 0} \int _{\partial B_\sigma } \left( \frac{1}{2} \left| \nabla Q \right| ^2+\lambda W(Q)\right) V \cdot \overrightarrow{n} \, d{\mathcal {H}}^2= \lim _{\sigma \rightarrow 0} \int _{\partial B_\sigma } \frac{1}{2} \left| \nabla Q \right| ^2 V \cdot \overrightarrow{n}\, d{\mathcal {H}}^2\nonumber \\{} & {} \quad = \lim _{\sigma \rightarrow 0} \int _{\partial B_\sigma } \frac{1}{2} \left| \nabla Q \right| ^2 V(0) \cdot \overrightarrow{n} \, d{\mathcal {H}}^2= \lim _{\sigma \rightarrow 0} \frac{1}{\sigma ^2}\int _{\partial B_\sigma } V(0)\cdot \overrightarrow{n} \, d{\mathcal {H}}^2=0 \,, \end{aligned}$$

(5.8)

and the last equality holds since $\int _{\partial B_\sigma }\overrightarrow{n}\,d{\mathcal {H}}^2=0$ for every $\sigma >0$. $\square$

With suitable choices of the vector field V in the previous lemma, we obtain the following key identities in smoothed cylinders.

Corollary 5.2

Let ${\mathfrak {C}}^h_{\ell ,\rho }$ be a smoothed cylinder and $Q_{\textrm{b}}$ its homeotropic boundary data given by (2.4). If Q is minimizing ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}_{Q_{\textrm{b}}}^\textrm{sym}{({\mathfrak {C}}^h_{\ell ,\rho })}$, then the following identities hold.

• (i) (radial energy identity) For every $\ell \leqslant r_1<r_2 \leqslant h-\rho$, we have

  $$\begin{aligned}{} & {} \frac{1}{r_1}{\mathcal {E}}_\lambda (Q, {\mathfrak {C}}^h_{\ell ,\rho } \cap B_{r_1}) + \int _{{\mathfrak {C}}^h_{\ell ,\rho } \cap (B_{r_2} \setminus B_{r_1}) } \frac{1}{\left| x \right| }\left| \frac{\partial Q}{\partial \left| x \right| } \right| ^2 \,dx + \int _{r_1}^{r_2} \frac{1}{r^2} \int _{{\mathfrak {C}}^h_{\ell ,\rho } \cap B_r} 2\lambda W(Q) \,\textrm{d}x \,dr \nonumber \\{} & {} \quad = \frac{1}{r_2}{\mathcal {E}}_\lambda (Q, {\mathfrak {C}}^h_{\ell ,\rho } \cap B_{r_2}) +\ell \int _{r_1}^{r_2} \frac{1}{r^2} \int _{\partial {\mathfrak {C}}^h_{\ell ,\rho } \cap B_r} \Big [ \frac{1}{2} \left| \nabla _{\textrm{tan}} Q_{\textrm{b}} \right| ^2+\lambda W(Q_{\textrm{b}}) -\frac{1}{2} \left| \frac{\partial Q}{\partial \overrightarrow{n}} \right| ^2 \Big ]\, d{\mathcal {H}}^2\, d r. \nonumber \\ \end{aligned}$$

  (5.9)

• (ii) (horizontal energy identity) For any $0\leqslant s \leqslant h-\rho$ such that $(0,0,\pm s)\not \in \textrm{sing}(Q)$ we have

  $$\begin{aligned}{} & {} \ell \int _{\partial {\mathfrak {C}}^s_{\ell } \cap \{|x_3|<s \}}\Big [ \frac{1}{2} \left| \nabla _{\textrm{tan}} Q_{\textrm{b}} \right| ^2+\lambda W(Q_{\textrm{b}}) -\frac{1}{2} \left| \frac{\partial Q}{\partial \overrightarrow{n}} \right| ^2 \Big ]\, d{\mathcal {H}}^2 \nonumber \\{} & {} \quad = \int _{{\mathfrak {C}}^s_{\ell }} \Big [ \left| \frac{\partial Q}{\partial x_3} \right| ^2 +2 \lambda W(Q) \Big ]\, dx+ \int _{\partial {\mathfrak {C}}^s_{\ell }\cap \{|x_3|=s\}} (x'\cdot \nabla _{x'} Q): \frac{\partial Q}{\partial \overrightarrow{n}} \, d{\mathcal {H}}^2 \,, \end{aligned}$$

  (5.10)

  where $x=:(x^\prime ,x_3)\in \mathbb {R}^2\times \mathbb {R}$.

• (iii) (vertical energy identity) For every $t_1,t_2 \in [-h+\rho ,h-\rho ]$ such that $(0,0,t_i)\not \in \textrm{sing}(Q)$ for $i=1,2$, we have

  $$\begin{aligned}{} & {} E_\lambda \big (Q(\, \cdot \,, t_1),{\mathbb D}_\ell \big )-\frac{1}{2} \int _{{\mathfrak {C}}^h_{\ell ,\rho }\cap \{x_3=t_1\}} \left| \frac{\partial Q}{\partial x_3} \right| ^2 \, d{\mathcal {H}}^2 \nonumber \\{} & {} \quad =E_\lambda \big (Q(\, \cdot \,,t_2),{\mathbb D}_\ell \big ) -\frac{1}{2} \int _{{\mathfrak {C}}^h_{\ell ,\rho }\cap \{x_3=t_2\}} \left| \frac{\partial Q}{\partial x_3} \right| ^2 \, d{\mathcal {H}}^2 \,, \end{aligned}$$

  (5.11)

  where $E_\lambda$ is the 2D-LdG energy in (1.11).

Proof

Proof of (i). For all $r \in (\ell , h-\rho ]$ except finitely many if $\textrm{sing}(Q)\not =\emptyset$, $\Omega ={\mathfrak {C}}^h_{\ell ,\rho }$ and $\Omega ' = B_r$ satisfy the assumptions of Lemma 5.1 that we use with $V(x)=x$. Then $V=r\overrightarrow{n}$ on ${\mathfrak {C}}^h_{\ell ,\rho } \cap \partial B_r$, and $V\cdot \overrightarrow{n}=\ell$ on $\partial {\mathfrak {C}}^h_{\ell ,\rho } \cap B_r$. Noticing that

$$\begin{aligned} \frac{\partial Q}{\partial V}:\frac{\partial Q}{\partial \overrightarrow{n}}= \ell \left| \frac{\partial Q}{\partial \overrightarrow{n}} \right| ^2\quad \text {on }\partial {\mathfrak {C}}^h_{\ell ,\rho } \cap B_r, \end{aligned}$$

because $\displaystyle \frac{\partial Q}{\partial x_3} =0$ on $\partial {\mathfrak {C}}^h_{\ell ,\rho } \cap B_r$, we infer from identity (5.1),

$$\begin{aligned}{} & {} \int _{{\mathfrak {C}}^h_{\ell ,\rho } \cap B_r} \Big [ \Big ( \frac{1}{2} \left| \nabla Q \right| ^2+\lambda W(Q)\Big ) +2 \lambda W(Q) \Big ]\, dx= \ell \int _{\partial {\mathfrak {C}}^h_{\ell ,\rho } \cap B_r} \Big [ \frac{1}{2} \left| \nabla Q \right| ^2+\lambda W(Q) -\left| \frac{\partial Q}{\partial \overrightarrow{n}} \right| ^2 \Big ]\, d{\mathcal {H}}^2 \\{} & {} \quad + r\int _{{\mathfrak {C}}^h_{\ell ,\rho } \cap \partial B_r} \Big [ \frac{1}{2} \left| \nabla Q \right| ^2+\lambda W(Q) -\left| \frac{\partial Q}{\partial \overrightarrow{n}} \right| ^2 \Big ] \, d{\mathcal {H}}^2 \,, \end{aligned}$$

which rewrites as

$$\begin{aligned}{} & {} \frac{1}{r} \int _{{\mathfrak {C}}^h_{\ell ,\rho } \cap \partial B_r} \left| \frac{\partial Q}{\partial \overrightarrow{n}} \right| ^2 \, d{\mathcal {H}}^2 + \frac{1}{r^2} \int _{{\mathfrak {C}}^h_{\ell ,\rho } \cap B_r} 2\lambda W(Q) \, dx =\frac{d}{dr} \left\{ \frac{1}{r} \int _{{\mathfrak {C}}^h_{l,\rho } \cap B_r} \frac{1}{2} \left| \nabla Q \right| ^2+\lambda W(Q) \, dx \right\} \nonumber \\{} & {} \quad + \frac{\ell }{r^2} \int _{\partial {\mathfrak {C}}^h_{\ell ,\rho } \cap B_r} \Big [ \frac{1}{2} \left| \nabla _{\textrm{tan}} Q_{\textrm{b}} \right| ^2+\lambda W(Q_{\textrm{b}}) -\frac{1}{2} \left| \frac{\partial Q}{\partial \overrightarrow{n}} \right| ^2 \Big ]\, d{\mathcal {H}}^2 \,\,. \end{aligned}$$

(5.12)

Integrating (5.12) between $r_1$ and $r_2$ the conclusion follows.

Proof of (ii). We apply Lemma 5.1 with $\Omega ={\mathfrak {C}}^h_{\ell ,\rho }$ and $\Omega '={\mathfrak {C}}^s_{2\ell ,\rho }$ for $s<h-\rho$, so that $\Omega \cap \Omega ^\prime ={\mathfrak {C}}^s_{\ell }$. Choosing $V(x)=(x',0)$, we notice that $V\cdot \overrightarrow{n}=0$ on $\partial {\mathfrak {C}}^s_{\ell }\cap \{|x_3|=s\}$, and $V\cdot \overrightarrow{n}=\ell$ on $\partial {\mathfrak {C}}^s_{\ell } \cap \{|x_3|<s\}$. Using that $\frac{\partial Q}{\partial V}:\frac{\partial Q}{\partial \overrightarrow{n}}= \ell \left| \frac{\partial Q}{\partial \overrightarrow{n}} \right| ^2$ on $\partial {\mathfrak {C}}^s_{\ell } \cap \{|x_3|<s\}$, we arrive at (5.10) directly from identity (5.1).

Proof of (iii). We assume that $t_1<t_2$ and we apply Lemma 5.1 with the domains $\Omega ={\mathfrak {C}}^h_{\ell ,\rho }$ and $\Omega '={\mathfrak {C}}^{(t_2-t_1)/2}_{2\ell -\rho }(0,0,(t_1+t_2)/2)$, so that $\Omega \cap \Omega ^\prime ={\mathfrak {C}}^{h}_{\ell ,\rho }\cap \{t_1<x_3<t_2\}$. We choose the constant vector field $V(x)=(0,0,1)$ which satisfies $V= \overrightarrow{n}$ on ${\mathfrak {C}}^h_{\ell ,\rho } \cap \{x_3=t_2\}$, $V=- \overrightarrow{n}$ on ${\mathfrak {C}}^h_{\ell ,\rho } \cap \{x_3=t_1\}$, and $V\cdot \overrightarrow{n}=0$ on $\partial {\mathfrak {C}}^h_{\ell ,\rho } \cap \{t_1<x_3<t_2\}$. Using that $\partial _3 Q_{\textrm{b}} \equiv 0$ on $\partial {\mathfrak {C}}^h_{\ell ,\rho } \cap \{t_1<x_3<t_2\}$, we derive (5.11) once again directly from (5.1). $\square$

Remark 5.3

It is straightforward to check that identity (5.9) still holds for a ball $B_r(p)$ instead of $B_r$, whenever $p=(0,0,z) \in \Omega$, $|z|<h-\rho$, and $\ell \leqslant r_1 <r_2 \leqslant h-\rho -|z|$.

5.2 A priori bounds and local compactness

In this subsection, we derive the necessary local boundedness and compactness properties needed in the asymptotic analysis of minimizers for cylinders of divergent height.

The following result is the fundamental tool to obtain local uniform energy bounds for energy minimizing configurations.

Proposition 5.4

Let ${\mathfrak {C}}^h_{\ell ,\rho }$ be a smoothed cylinder with $h-\rho >\sqrt{2}\ell$, and $Q_{\textrm{b}}$ its homeotropic boundary data given by (2.4). If Q is minimizing ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}_{Q_\textrm{b}}^{\textrm{sym}}({\mathfrak {C}}^h_{\ell ,\rho })$, then

$$\begin{aligned}{} & {} \Big (1-\sqrt{2}\ell \Big ( \frac{1}{r_1}-\frac{1}{r_2} \Big ) \Big ) \frac{1}{r_1}{\mathcal {E}}_\lambda \big (Q,{\mathfrak {C}}^h_{\ell ,\rho } \cap B_{r_1}\big ) + \int _{{\mathfrak {C}}^h_{\ell ,\rho } \cap (B_{r_2} \setminus B_{r_1}) } \frac{1}{\left| x \right| }\left| \frac{\partial Q}{\partial \left| x \right| } \right| ^2 \,\textrm{d}x \nonumber \\{} & {} \quad \leqslant \frac{1}{r_2}{\mathcal {E}}_\lambda \big (Q, {\mathfrak {C}}^h_{\ell ,\rho } \cap B_{r_2}\big ) +\frac{3}{r_1} \int _{ {\mathfrak {C}}^h_{\ell ,\rho } \cap B_{r_2}} \left| \frac{\partial Q}{\partial x_3} \right| ^2\textrm{d}x \end{aligned}$$

(5.13)

for every $\sqrt{2}\ell \leqslant r_1 < r_2 \leqslant h-\rho$.

Proof

For $\sqrt{2}\ell \leqslant r_1 <r \leqslant r_2 \leqslant h-\rho$, we set

$$\begin{aligned} s_1:=\sqrt{r_1^2-\ell ^2}\in (\ell ,h-\rho ),\;s:=\sqrt{r^2-\ell ^2}\in (\ell ,h-\rho ),\;s_2:=\sqrt{r_2^2-\ell ^2}\in (\ell ,h-\rho ), \end{aligned}$$

and we assume that $(0,0,\pm s) \not \in \textrm{sing}(Q)$. By (5.10) and Young’s inequality, we estimate

$$\begin{aligned}{} & {} - \int _{{\mathfrak {C}}^s_{\ell }} 2\lambda W(Q) \,\textrm{d}x +\ell \int _{\partial {\mathfrak {C}}^s_{\ell } \cap \{|x_3|<s\}} \Big [ \frac{1}{2} \left| \nabla _{\textrm{tan}} Q_{\textrm{b}} \right| ^2+\lambda W(Q_{\textrm{b}}) -\frac{1}{2} \left| \frac{\partial Q}{\partial \overrightarrow{n}} \right| ^2 \Big ]\, d{\mathcal {H}}^2\nonumber \\{} & {} \quad =\int _{{\mathfrak {C}}^s_{\ell }} \left| \frac{\partial Q}{\partial x_3} \right| ^2 \, dx+ \int _{\partial {\mathfrak {C}}^s_{\ell } \cap \{x_3=s\}} (x'\cdot \nabla _{x'} Q): \frac{\partial Q}{\partial \overrightarrow{n}} \, d{\mathcal {H}}^2 \nonumber \\{} & {} \quad \leqslant \int _{{\mathfrak {C}}^s_{\ell }} \left| \frac{\partial Q}{\partial x_3} \right| ^2 \, dx+\ell \int _{\partial {\mathfrak {C}}^s_{\ell } \cap \{|x_3|=s\}} \frac{1}{2} \left| \nabla _{x'} Q \right| ^2 \, d{\mathcal {H}}^2+\frac{\ell }{2} \int _{\partial {\mathfrak {C}}^s_{\ell } \cap \{|x_3|=s\}} \left| \frac{\partial Q}{\partial x_3} \right| ^2 \, d{\mathcal {H}}^2. \nonumber \\ \end{aligned}$$

(5.14)

Averaging (5.11) over $t_2\in [-s_1, s_1]$, we derive that for any $t\in [-h+\rho ,h-\rho ]$ such that $(0,0,t)\not \in \mathrm{sing(Q)}$,

$$\begin{aligned}{} & {} E_\lambda \big (Q(\, \cdot \,, t),{\mathbb D}_\ell \big )\leqslant \frac{1}{2} \int _{{\mathfrak {C}}^h_{\ell ,\rho }\cap \{x_3=t\}} \left| \frac{\partial Q}{\partial x_3} \right| ^2 \, d{\mathcal {H}}^2 + \frac{1}{2s_1} {\mathcal {E}}_\lambda (Q;{\mathfrak {C}}^{s_1}_{\ell }) \nonumber \\{} & {} \quad \leqslant \frac{1}{2} \int _{{\mathfrak {C}}^h_{\ell ,\rho }\cap \{x_3=t\}} \left| \frac{\partial Q}{\partial x_3} \right| ^2 \, d{\mathcal {H}}^2 + \frac{1}{\sqrt{2} r_1} {\mathcal {E}}_\lambda \big (Q,{\mathfrak {C}}^h_{\ell ,\rho } \cap B_{r_1}\big )\,, \end{aligned}$$

(5.15)

using ${\mathfrak {C}}^{s_1}_{\ell } \subseteq {\mathfrak {C}}^h_{\ell ,\rho }\cap B_{r_1}$ in the last inequality. Summing now (5.15) over $t\in \{\pm s\}$ yields

$$\begin{aligned}{} & {} \ell \int _{{\mathfrak {C}}^h_{\ell ,\rho } \cap \{ |x_3|=s\}} \frac{1}{2} \left| \nabla _{x'} Q \right| ^2 \, d{\mathcal {H}}^2\leqslant \ell \Big ( E_\lambda \big (Q(\, \cdot \,, s\big ),{\mathbb D}_\ell ) + E_\lambda \big (Q(\, \cdot \,, -s),{\mathbb D}_\ell \big ) \Big ) \nonumber \\{} & {} \quad \leqslant \frac{\ell }{2} \int _{{\mathfrak {C}}^h_{\ell ,\rho }\cap \{|x_3|=s\}} \left| \frac{\partial Q}{\partial x_3} \right| ^2 \, d{\mathcal {H}}^2 + \frac{\sqrt{2}\ell }{r_1} {\mathcal {E}}_\lambda \big (Q, {\mathfrak {C}}^h_{\ell ,\rho } \cap B_{r_1}\big ) \,. \end{aligned}$$

(5.16)

Noticing that ${\mathfrak {C}}^h_{\ell ,\rho }\cap \{|x_3|=s\}=\partial {\mathfrak {C}}^s_{\ell }\cap \{|x_3|=s\}$, we combine (5.14) with (5.16) to obtain

$$\begin{aligned}{} & {} - \int _{{\mathfrak {C}}^s_{\ell }} 2\lambda W(Q) \,\textrm{d}x +\ell \int _{\partial {\mathfrak {C}}^s_{\ell } \cap \{|x_3|<s\}} \Big [ \frac{1}{2} \left| \nabla _{\textrm{tan}} Q_\textrm{b} \right| ^2+\lambda W(Q_{\textrm{b}}) -\frac{1}{2} \left| \frac{\partial Q}{\partial \overrightarrow{n}} \right| ^2 \Big ]\, d{\mathcal {H}}^2 \nonumber \\{} & {} \quad \leqslant \int _{{\mathfrak {C}}^s_{\ell }} \left| \frac{\partial Q}{\partial x_3} \right| ^2 \, dx+\ell \int _{\partial {\mathfrak {C}}^s_{\ell } \cap \{|x_3|=s\}} \left| \frac{\partial Q}{\partial x_3} \right| ^2 \, d{\mathcal {H}}^2 +\frac{\sqrt{2}\ell }{r_1} {\mathcal {E}}_\lambda (Q, {\mathfrak {C}}^h_{{{\ell }},\rho } \cap B_{r_1}) \,. \end{aligned}$$

(5.17)

Next we observe that $\partial {\mathfrak {C}}^s_{\ell } \cap \{|x_3|<s\} =\partial {\mathfrak {C}}^h_{\ell ,\rho } \cap B_r$ and ${\mathfrak {C}}^s_{\ell } \subseteq {\mathfrak {C}}^h_{\ell ,\rho } \cap B_r$. Then, multiplying (5.17) by $1/r^2$, integrating between $r_1$ and $r_2$, and then adding the resulting inequality to (5.9) (term-by-term), we obtain

$$\begin{aligned}{} & {} \left( 1- \sqrt{2}\ell \left( \frac{1}{r_1}-\frac{1}{r_2} \right) \right) \frac{1}{r_1}{\mathcal {E}}_\lambda (Q, {\mathfrak {C}}^h_{\ell ,\rho } \cap B_{r_1}) + \int _{{\mathfrak {C}}^h_{\ell ,\rho } \cap (B_{r_2} \setminus B_{r_1}) } \frac{1}{\left| x \right| }\left| \frac{\partial Q}{\partial \left| x \right| } \right| ^2 \,dx\nonumber \\{} & {} \quad \leqslant \frac{1}{r_2}{\mathcal {E}}_\lambda (Q, {\mathfrak {C}}^h_{\ell ,\rho } \cap B_{r_2}) +\int _{r_1}^{r_2} \frac{1}{r^2} \Bigg ( \int _{{\mathfrak {C}}^{s(r)}_{\ell }} \left| \frac{\partial Q}{\partial x_3} \right| ^2 \, dx +\ell \int _{\partial {\mathfrak {C}}^{s(r)}_{\ell } \cap \{|x_3|=s(r)\}} \left| \frac{\partial Q}{\partial x_3} \right| ^2 \, d{\mathcal {H}}^2 \Bigg ) \, dr, \nonumber \\ \end{aligned}$$

(5.18)

where we write $s(r):=\sqrt{r^2-\ell ^2}$. Since ${\mathfrak {C}}^{s(r)}_{\ell }\subseteq {\mathfrak {C}}^{h}_{\ell ,\rho }\cap B_{r_2}$ for every $r\in (r_1,r_2)$, we obtain by a change of variable,

$$\begin{aligned}&\int _{r_1}^{r_2} \frac{1}{r^2} \Big ( \int _{{\mathfrak {C}}^{s(r)}_{\ell }} \left| \frac{\partial Q}{\partial x_3} \right| ^2 \, dx+\ell \int _{\partial {\mathfrak {C}}^{s(r)}_{\ell } \cap \{|x_3|=s(r)\}} \left| \frac{\partial Q}{\partial x_3} \right| ^2 \, d{\mathcal {H}}^2 \Big ) \, dr \nonumber \\&\quad \leqslant \Big (\frac{1}{r_1}-\frac{1}{r_2}\Big ) \int _{ {\mathfrak {C}}^h_{\ell ,\rho } \cap B_{r_2}} \left| \frac{\partial Q}{\partial x_3} \right| ^2\,dx + \ell \int _{s_1}^{s_2} \frac{s}{(s^2+\ell ^2)^{3/2}} \Big (\int _{\partial {\mathfrak {C}}^{s}_{\ell } \cap \{|x_3|=s\}} \left| \frac{\partial Q}{\partial x_3} \right| ^2 \, d{\mathcal {H}}^2 \Big ) \, ds \nonumber \\&\quad \leqslant \Big (\frac{1}{r_1}-\frac{1}{r_2}\Big ) \int _{ {\mathfrak {C}}^h_{\ell ,\rho } \cap B_{r_2}} \left| \frac{\partial Q}{\partial x_3} \right| ^2\,dx +\frac{\ell }{s_1^2}\int _{{\mathfrak {C}}^{s_2}_{\ell } \setminus {\mathfrak {C}}^{s_1}_{\ell } } \left| \frac{\partial Q}{\partial x_3} \right| ^2 \, dx \nonumber \\&\quad \leqslant \frac{3}{r_1} \int _{ {\mathfrak {C}}^h_{\ell ,\rho } \cap B_{r_2}} \left| \frac{\partial Q}{\partial x_3} \right| ^2\,dx \,. \end{aligned}$$

(5.19)

Combining (5.19) with (5.18), the conclusion follows. $\square$

Combining Proposition 5.4 with a comparison argument, we now derive a fundamental energy estimate for minimizers in terms of the height h of a “cigar shaped” smoothed cylinder.

Corollary 5.5

Let ${\mathfrak {C}}^h_{\ell ,\rho }$ be a smoothed cylinder with $h-\rho >2\sqrt{2}\ell$, and $Q_{\textrm{b}}$ its homeotropic boundary data given by (2.4). If Q is minimizing ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}_{Q_\textrm{b}}^{\textrm{sym}}({\mathfrak {C}}^h_{\ell ,\rho })$, then

$$\begin{aligned} {\mathcal {E}}_\lambda (Q,{\mathfrak {C}}^h_{\ell ,\rho })\leqslant 2h {\mathfrak {e}}_{\lambda \ell ^2} +C_1, \end{aligned}$$

where ${\mathfrak {e}}_{\lambda \ell ^2}$ is defined by (4.43), and $C_1=C_1(\ell ,\rho ,\lambda )$ is a constant independent of h. In addition,

$$\begin{aligned} \frac{1}{r} {\mathcal {E}}_\lambda \big (Q,{\mathfrak {C}}^h_{\ell ,\rho }\cap B_r\big )+\int _{{\mathfrak {C}}^h_{\ell ,\rho } \cap B_r} \left| \frac{\partial Q}{\partial x_3} \right| ^2 \, dx\leqslant C_2\quad \forall r\in (2\sqrt{2}\ell , h-\rho )\,, \end{aligned}$$

(5.20)

for a constant $C_2=C_2(\ell ,\rho ,\lambda )$ also independent of h. Moreover, the dependence of $C_1$ and $C_2$ on $\lambda \geqslant 0$ is locally uniform.

Proof

We define $\Omega _h^\pm :=({\mathfrak {C}}^h_{\ell ,\rho } {\setminus }{\mathfrak {C}}^{h-\rho }_\ell ) \cap \{\pm x_3> 0\}$, so that ${\mathfrak {C}}^h_{\ell ,\rho }={\mathfrak {C}}^{h-\rho }_\ell \cup \Omega _h^+\cup \Omega _h^-$, and

$$\begin{aligned} \partial \Omega _h^\pm =\big (\mathbb {D}_\ell \times \{\pm x_3=h-\rho \}\big )\cup \big (\partial {\mathfrak {C}}^{h}_{\ell ,\rho }\cap \{\pm x_3\geqslant h-\rho \} \big ). \end{aligned}$$

Setting ${\widetilde{\lambda }}:=\lambda \ell ^2$, we fix $Q_{{\widetilde{\lambda }}} \in {\mathcal {A}}^\textrm{sym}_{\overline{H}}({\mathbb D})$ such that $E_{{\widetilde{\lambda }}}(Q_{{\widetilde{\lambda }}})={\mathfrak {e}}_{{\widetilde{\lambda }}}$. Since $Q_{{\widetilde{\lambda }}}$ is minimizing $E_{\widetilde{\lambda }}$ over ${\mathcal {A}}^\textrm{sym}_{\overline{H}}({\mathbb D})$, $Q_{{\widetilde{\lambda }}}$ is smooth up to $\partial \mathbb {D}$ (see Sect. 4). Rescaling variables, we have $E_{\lambda }(\widetilde{Q}_\lambda ;{\mathbb D}_\ell )={\mathfrak {e}}_{\lambda \ell ^2}$ for ${\widetilde{Q}}_\lambda ( \, \cdot \,):=Q_{{\widetilde{\lambda }}}(\cdot / \ell \,)$. We define a Lipschitz map $\widetilde{Q}^h$ on $\partial \Omega _h^\pm$ setting $\widetilde{Q}^h(x):=Q_{\textrm{b}}(x)$ if $x\in \partial {\mathfrak {C}}^{h}_{\ell ,\rho }\cap \{\pm x_3\geqslant h-\rho \}$, and $\widetilde{Q}^h(x):={\widetilde{Q}}_\lambda (x^\prime )$ if $x=(x^\prime ,x_3)\in \mathbb {D}_\ell \times \{\pm x_3=h-\rho \}$. Considering the points $p^\pm :=(0,0,\pm (h-\rho /2)) \in \Omega ^\pm _h$, we extend $\widetilde{Q}^h$ to the interior of $\Omega ^\pm _h$ by 0-homogeneity from the point $p^\pm$. Then we finally extend $\widetilde{Q}^h$ to ${\mathfrak {C}}^{h}_{\ell ,\rho }$ setting $\widetilde{Q}^h(x)={\widetilde{Q}}_\lambda (x^\prime )$ if $x=(x^\prime ,x_3)\in {\mathfrak {C}}^{h-\rho }_{\ell }$. By construction, we have $\widetilde{Q}^h \in {\mathcal {A}}^{\textrm{sym}}_{Q_\textrm{b}}({\mathfrak {C}}^{h}_{\ell ,\rho }) \cap {{\,\mathrm{\textrm{Lip}}\,}}_\textrm{loc}(\overline{{\mathfrak {C}}^{h}_{\ell ,\rho }}{\setminus } \{p^\pm \})$,

$$\begin{aligned} {\mathcal {E}}_\lambda (\widetilde{Q}^h,{\mathfrak {C}}^{h-\rho }_\ell )=2(h-\rho ) E_\lambda ({\widetilde{Q}}_\lambda ,{\mathbb D}_\ell )=2(h-\rho ) {\mathfrak {e}}_{\lambda \ell ^2}, \end{aligned}$$

and

$$\begin{aligned} {\mathcal {E}}_\lambda (\widetilde{Q}^h,\Omega ^\pm _h)\leqslant C( \Vert \nabla _{\textrm{tan}} \widetilde{Q}^h\Vert ^2_{L^2(\partial \Omega _h^\pm )} +\lambda )\leqslant C_1, \end{aligned}$$

(5.21)

for a constant $C_1=C_1(\ell ,\rho ,\lambda )$ independent of h and continuous w.r.to $\lambda$. If Q is minimizing ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}_{Q_{\textrm{b}}}^\textrm{sym}({\mathfrak {C}}^h_{\ell ,\rho })$, then

$$\begin{aligned} {\mathcal {E}}_\lambda (Q) \leqslant {\mathcal {E}}_\lambda (\widetilde{Q}^h)= {\mathcal {E}}_\lambda (\widetilde{Q}^h,{\mathfrak {C}}^{h-\rho }_\ell )+ {\mathcal {E}}_\lambda (\widetilde{Q}^h,\Omega ^+_h)+ {\mathcal {E}}_\lambda (\widetilde{Q}^h,\Omega ^-_h) \leqslant 2(h-\rho ) {\mathfrak {e}}_{\lambda \ell ^2} +2C_1. \nonumber \\ \end{aligned}$$

(5.22)

On the other hand, by definition of ${\mathfrak {e}}_{\lambda \ell ^2}$, we have

$$\begin{aligned}{} & {} {\mathcal {E}}_\lambda (Q)\geqslant \int _{-h+\rho }^{h-\rho } E_\lambda \big ({Q}(\, \cdot , x_3),{\mathbb D}_\ell \big ) \, {d}x_3+ \int _{{\mathfrak {C}}^{h-\rho }_\ell } \frac{1}{2}\left| \frac{\partial Q}{\partial x_3} \right| ^2 \, { d}x\nonumber \\{} & {} \quad \geqslant 2(h-\rho ) {\mathfrak {e}}_{\lambda \ell ^2} +\int _{{\mathfrak {C}}^{h-\rho }_\ell } \frac{1}{2}\left| \frac{\partial Q}{\partial x_3} \right| ^2 \, { d}x \,. \end{aligned}$$

(5.23)

Since ${\mathfrak {C}}^h_{\ell ,\rho } \cap B_r\subseteq {\mathfrak {C}}^{h-\rho }_\ell$, combining (5.22) and (5.23) leads to $\int _{{\mathfrak {C}}^{h}_{\ell ,\rho }\cap B_r} |\frac{\partial Q}{\partial x_3}|^2 \, { d}x\leqslant 4C_1$ for every $r\leqslant h-\rho$. In view of this estimate and (5.22), we can apply Proposition 5.4 with $r_2=h-\rho$ and $r_1=r \geqslant 2\sqrt{2}\ell$ to obtain

$$\begin{aligned} \frac{1}{2r}{\mathcal {E}}_\lambda \big (Q,{\mathfrak {C}}^h_{\ell ,\rho } \cap B_{r}\big ) \leqslant \frac{1}{h-\rho } {\mathcal {E}}_\lambda (Q)+\frac{3}{r} \int _{{\mathfrak {C}}^{h}_{\ell ,\rho }\cap B_{h-\rho }} \left| \frac{\partial Q}{\partial x_3} \right| ^2 \, { d}x\leqslant 2 {\mathfrak {e}}_{\lambda \ell ^2} +\frac{8C_1}{\ell },\nonumber \\ \end{aligned}$$

(5.24)

which proves (5.20) once we choose $C_2 = 2 {\mathfrak {e}}_{\lambda \ell ^2} + \frac{8C_1}{\ell }$. Since $C_2$ is continuous in its arguments, hence locally bounded w.r.to $\lambda$, the proof is complete. $\square$

Combining identity (5.11) with Corollary 5.5, we obtain an energy bound as in (5.20) for arbitrary balls centered on the vertical axis.

Corollary 5.6

Let ${\mathfrak {C}}^h_{\ell ,\rho }$ be a smoothed cylinder with $h-\rho >2\sqrt{2}\ell$, and $Q_{\textrm{b}}$ its homeotropic boundary data given by (2.4). If Q is minimizing ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}_{Q_{\textrm{b}}}^\textrm{sym}({\mathfrak {C}}^h_{\ell ,\rho })$, then there exists a constant $C_3=C_3(\ell ,\rho ,\lambda )$ independent of h such that

$$\begin{aligned} \frac{1}{r}{\mathcal {E}}_\lambda \big (Q,{\mathfrak {C}}^h_{\ell ,\rho }\cap B_r(p)\big )\leqslant C_3 \end{aligned}$$

for every $p=(0,0,z)\in {\mathfrak {C}}^h_{\ell ,\rho }\cap \{x_3\text {-axis}\}$ and $2\sqrt{2}\ell< r < h-\rho -|z|-\ell$.

Proof

Integrating (5.11) with respect to $t_1\in [z-r,z+r]$ and dividing the result by 2r, we obtain

$$\begin{aligned}{} & {} \frac{1}{2r}{\mathcal {E}}_\lambda \big (Q,{\mathfrak {C}}^r_{\ell }(p)\big ) -\frac{1}{4r}\int _{{\mathfrak {C}}^r_{\ell }(p)} \left| \frac{\partial Q}{\partial x_3} \right| ^2 \, dx\nonumber \\{} & {} \quad =E_\lambda \big (Q(\, \cdot \,,t_2),{\mathbb D}_\ell \big ) -\frac{1}{2} \int _{{\mathfrak {C}}^h_{\ell ,\rho }\cap \{x_3=t_2\}} \left| \frac{\partial Q}{\partial x_3} \right| ^2 \, d{\mathcal {H}}^2 \end{aligned}$$

(5.25)

for every $t_2\in [-h+\rho ,h-\rho ]$ such that $t_2\not \in \textrm{sing}(Q)$. Then, integrating (5.25) with respect to $t_2\in [-r,r]$, we derive that

$$\begin{aligned}{} & {} {\mathcal {E}}_\lambda \big (Q,{\mathfrak {C}}^h_{\ell ,\rho }\cap B_r(p)\big )\leqslant {\mathcal {E}}_\lambda \big (Q,{\mathfrak {C}}^r_{\ell }(p)\big ) \leqslant {\mathcal {E}}_\lambda \big (Q,{\mathfrak {C}}^r_{\ell }\big )+\frac{1}{2}\int _{{\mathfrak {C}}^r_{\ell }(p)} \left| \frac{\partial Q}{\partial x_3} \right| ^2 \, dx\nonumber \\{} & {} \quad \leqslant {\mathcal {E}}_\lambda \big (Q,{\mathfrak {C}}^h_{\ell ,\rho }\cap B_{r+\ell }\big )+\frac{1}{2}\int _{{\mathfrak {C}}^h_{\ell ,\rho }\cap B_{r+|z|+\ell }} \left| \frac{\partial Q}{\partial x_3} \right| ^2 \, dx, \end{aligned}$$

(5.26)

since ${\mathfrak {C}}^h_{\ell ,\rho }\cap B_r(p)\subseteq {\mathfrak {C}}^r_{\ell }(p)$, ${\mathfrak {C}}^r_{\ell }\subseteq {\mathfrak {C}}^h_{\ell ,\rho }\cap B_{r+\ell }$, and ${\mathfrak {C}}^r_{\ell }(p)\subseteq {\mathfrak {C}}^h_{\ell ,\rho }\cap B_{r+|z|+\ell }$. The conclusion now follows from Corollary 5.5 with $C_3=2C_2(1+1/\ell )$ and $C_2$ given by (5.20). $\square$

Using suitable competitors, we can now deduce from the previous corollary that the energy of minimizers remains bounded also near the top and bottom parts of the cylinder.

Corollary 5.7

Let ${\mathfrak {C}}^h_{\ell ,\rho }$ be a smoothed cylinder with $h-2\rho >4\ell$, and $Q_{\textrm{b}}$ its homeotropic boundary data given by (2.4). If Q is minimizing ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}_{Q_{\textrm{b}}}^\textrm{sym}({\mathfrak {C}}^h_{\ell ,\rho })$, then there exists a constant $C_4=C_4(\ell ,\rho ,\lambda )$ independent of h such that ${\mathcal {E}}_\lambda \big (Q,{\mathfrak {C}}^h_{\ell ,\rho }{\setminus }{\mathfrak {C}}^{h-\rho }_\ell \big )\leqslant C_4$.

Proof

Applying Corollary 5.6 with $r=3\ell$ and $p^\pm :=(0,0,\pm t)$ and $t:=h-2\rho -4\ell$, we infer that ${\mathcal {E}}_\lambda \big (Q,{\mathfrak {C}}^\ell _{\ell }(p^\pm )\big )\leqslant C_3$ since ${\mathfrak {C}}^\ell _{\ell }(p^\pm )\subseteq {\mathfrak {C}}^h_{\ell ,\rho }\cap B_r(p^\pm )$ with $C_3=C_3(\ell ,\rho ,\lambda )$. By Fubini’s theorem, we can find a level ${\bar{t}}\in (h-2\rho -4\ell , h-2\rho -3\ell )$ such that $E_\lambda \big (Q(\cdot ,\pm {\bar{t}}), {\mathbb D}_\ell \big )\leqslant C_3/\ell$. We shall now construct a competitor following an argument from the proof of Corollary 5.5. First, we consider the domains $\Omega ^\pm _h:=({\mathfrak {C}}^h_{\ell ,\rho }{\setminus } {\mathfrak {C}}^{{\bar{t}}}_{\ell })\cap \{\pm x_3>0\}$. We define a map ${\widetilde{Q}}$ on $\partial \Omega ^\pm _h$ by setting $\widetilde{Q}=Q$ on $\partial \Omega ^\pm _h\cap \{\pm x_3={\bar{t}}\,\}$, and ${\widetilde{Q}}=Q_{\textrm{b}}$ on $\partial \Omega ^\pm _h\cap \{\pm x_3>\bar{t}\,\}$. Then we extend ${\widetilde{Q}}$ to the interior of $\Omega ^\pm _h$ by 0-homogeneity from the point $q^\pm :=(0,0,\pm (h-\rho -2\ell ))$. As in the proof of Corollary 5.5 (see (5.21)), we have ${\mathcal {E}}_\lambda ({\widetilde{Q}},\Omega ^\pm _h)\leqslant C$ for some constant C independent of h, thanks to our choice of ${\bar{t}}$. Now we extend ${\widetilde{Q}}$ to ${\mathfrak {C}}^h_{\ell ,\rho }$ setting ${\widetilde{Q}}=Q$ in ${\mathfrak {C}}^h_{\ell ,\rho }{\setminus } \Omega ^\pm _h$. In this this way, ${\widetilde{Q}}\in {\mathcal {A}}_{Q_{\textrm{b}}}^{\textrm{sym}}({\mathfrak {C}}^h_{\ell ,\rho })$ is a competitor to test the minimality of Q which leads to ${\mathcal {E}}_\lambda (Q,\Omega ^+_h\cup \Omega ^-_h)\leqslant {\mathcal {E}}_\lambda ({\widetilde{Q}},\Omega ^+_h\cup \Omega ^-_h)\leqslant 2C$. Since ${\mathfrak {C}}^h_{\ell ,\rho }{\setminus }{\mathfrak {C}}^{h-\rho }_{\ell }\subseteq \Omega ^+_h\cup \Omega ^-_h$, the conclusion follows. $\square$

The next result will be useful to turn the local boundedness in Corollaries 5.5 & 5.6 into a local compactness property up to “the lateral boundary”. The arguments here are suitable modifications of [12, Theorem 5.1 and 5.2], taking advantage of the translation invariance of the Dirichlet boundary data. Before stating the result, let us define precisely the notion of local minimality we shall use in the sequel.

Definition 5.8

Let ${\mathfrak {C}}^h_\ell$ be a cylinder with $\ell <\infty$. We call lateral boundary of the cylinder ${\mathfrak {C}}^h_\ell$, the set

$$\begin{aligned} \partial ^{\textrm{lat}} {\mathfrak {C}}^h_\ell :=\partial {\mathfrak {C}}^h_\ell \cap \{|x_3|<h\}=\partial \mathbb {D}_\ell \times (-h,h). \end{aligned}$$

(5.27)

An equivariant map $Q\in W^{1,2}_{\textrm{loc}}({\mathfrak {C}}^h_\ell ;{\mathbb S}^4)$ is said to be an equivariant local minimizer of ${\mathcal {E}}_{\lambda }$ in ${\mathfrak {C}}^h_\ell$ up to the lateral boundary if for every $\eta \in (0,h)$, $Q\in W^{1,2}_\textrm{sym}({\mathfrak {C}}^\eta _\ell ;{\mathbb S}^4)$ and ${\mathcal {E}}_{\lambda }(Q,{\mathfrak {C}}^\eta _\ell )\leqslant {\mathcal {E}}_{\lambda }({\widetilde{Q}},{\mathfrak {C}}^\eta _\ell )$ for every $\widetilde{Q}\in W^{1,2}_\textrm{sym}({\mathfrak {C}}^\eta _\ell ;{\mathbb S}^4)$ satisfying $\widetilde{Q}=Q$ on $\partial {\mathfrak {C}}^\eta _\ell$.

Lemma 5.9

Let ${\mathfrak {C}}^h_\ell$ be a bounded cylinder and $Q_{\textrm{b}}$ its homeotropic boundary data given by (2.4). Let $\lambda _j\rightarrow \lambda$ and $\{Q_j\} \subseteq W^{1,2}_{\textrm{sym}}({\mathfrak {C}}^h_\ell ;{\mathbb S}^4)$ a sequence such that each $Q_j$ is an equivariant local minimizer of ${\mathcal {E}}_{\lambda _j}$ in ${\mathfrak {C}}^h_\ell$ up to the lateral boundary and $Q_j=Q_{\textrm{b}}$ on $\partial ^{\textrm{lat}} {\mathfrak {C}}^h_\ell$. If $\sup _j {\mathcal {E}}_{\lambda _j}(Q_j,{\mathfrak {C}}^h_\ell )<\infty$, then there exists a (not relabeled) subsequence such that $Q_j \rightarrow Q_*$ strongly in $W^{1,2}( {\mathfrak {C}}^\eta _\ell )$ for every $\eta \in (0,h)$, where $Q_* \in W^{1,2}_\textrm{sym}({\mathfrak {C}}^h_\ell ;{\mathbb S}^4)$ is an equivariant local minimizer of ${\mathcal {E}}_\lambda$ up to the lateral boundary satisfying $Q_*=Q_{\textrm{b}}$ on $\partial ^{\textrm{lat}} {\mathfrak {C}}^h_\ell$.

Proof

By the uniform energy bound, the sequence $\{Q_j\}$ is bounded in $W^{1,2}({\mathfrak {C}}^h_\ell )$. Hence, we can find a (not relabeled) subsequence such that $Q_j \rightharpoonup Q_{*}$ weakly in $W^{1,2}({\mathfrak {C}}^h_\ell )$, strongly in $L^2({\mathfrak {C}}^h_\ell )$, and also a.e. in ${\mathfrak {C}}^h_\ell$, for some $Q_* \in W^{1,2}_{\textrm{sym}}({\mathfrak {C}}^h_\ell ;{\mathbb S}^4)$. By $W^{1,2}$-weak continuity and locality of the trace operator, $Q_*=Q_{\textrm{b}}$ on $\partial ^{\textrm{lat}} {\mathfrak {C}}^h_\ell$. In addition, [12, Theorem 5.1] implies that $Q_j \rightarrow Q_{*}$ strongly in $W^{1,2}_{\textrm{loc}}(B_r(p))$ for every $p\in {\mathfrak {C}}^h_\ell \cap \{x_3\text {-axis}\}$ and $r > 0$ such that $B_r(p)\subseteq {\mathfrak {C}}^h_\ell$. As a consequence, given an arbitrary $\delta >0$ with $2\delta <\min \{h,\ell \}$, we have $Q_j \rightarrow Q_{*}$ strongly in $W^{1,2}$ in the set ${\mathbb D}_{\delta /2}\times \{h-\delta<|x_3|<h-\delta /2\}$. By a standard application of Fubini’s theorem and Fatou’s lemma, extracting a further subsequence if necessary, we can find $\eta \in (h-\delta , h-\delta /2)$ such that the restrictions ${\widehat{Q}}^\pm _j$ and ${\widehat{Q}}^\pm _*$ of $Q_j$ and $Q_*$ to ${\mathfrak {C}}^h_\ell \cap \{x_3=\pm \eta \}$ satisfy ${\widehat{Q}}^\pm _j \rightharpoonup {\widehat{Q}}_*^\pm$ weakly in $W^{1,2}({\mathbb D}_\ell )$ and strongly in $W^{1,2}({\mathbb D}_{\delta /3})$. By Lemma 2.10, we conclude that ${\widehat{Q}}^\pm _j, {\widehat{Q}}_*^\pm \in C^0(\overline{{\mathbb D}}_\ell )$ and ${\widehat{Q}}^\pm _j \rightarrow {\widehat{Q}}_*^\pm$ uniformly in $\overline{{\mathbb D}}_\ell$.

Let us now fix an arbitrary $\widetilde{Q}\in W^{1,2}_\textrm{sym}({\mathfrak {C}}^{h-\delta }_\ell ;{\mathbb S}^4)$ satisfying $\widetilde{Q}=Q_*$ on $\partial {\mathfrak {C}}^{h-\delta }_\ell$. We extend $\widetilde{Q}$ to ${\mathfrak {C}}^{\eta }_\ell$ setting $\widetilde{Q}=Q_*$ in ${\mathfrak {C}}^{\eta }_\ell {\setminus } {\mathfrak {C}}^{h-\delta }_\ell$, and we set $\sigma _j:=\Vert {\widehat{Q}}^+_j-{\widehat{Q}}_*^+\Vert _\infty + \Vert {\widehat{Q}}^-_j-{\widehat{Q}}_*^-\Vert _\infty +2^{-j} \rightarrow 0$ as $j \rightarrow \infty$. For j large enough we have $\sigma _j<1$, and we define $v_j \in W^{1,2}_{\textrm{sym}}({\mathfrak {C}}^\eta _\ell ;{\mathcal {S}}_0)$ as

$$\begin{aligned} v_j(x^\prime ,x_3):= {\left\{ \begin{array}{ll} \displaystyle \frac{x_3- (1-\sigma _j )\eta }{\sigma _j \eta }\big ({\widehat{Q}}^+_j(x^\prime ) -{\widehat{Q}}^+_*(x^\prime )\big )+{\widehat{Q}}^+_*(x^\prime ) &{} \text {if } (1-\sigma _j)\eta \leqslant x_3 \leqslant \eta \,, \\ \widetilde{Q}\big (x^\prime , x_3/(1-\sigma _j)\big ) &{} \text {if } |x_3|< (1-\sigma _j)\eta , \\ \displaystyle \frac{-x_3+ (\sigma _j-1 )\eta }{\sigma _j \eta }\big ({\widehat{Q}}^-_j(x^\prime ) -{\widehat{Q}}^-_*(x^\prime )\big )+{\widehat{Q}}^-_*(x^\prime ) &{} \text {if } -\eta \leqslant x_3 \leqslant -(1-\sigma _j)\eta \,. \end{array}\right. } \end{aligned}$$

(5.28)

Since the restriction of $Q_{\textrm{b}}$ to $\partial ^{\textrm{lat}} {\mathfrak {C}}^h_\ell$ is independent of $x_3$, we have $v_j=Q_\textrm{b}$ on $\partial ^{\textrm{lat}} {\mathfrak {C}}^\eta _\ell$. Hence $v_j=Q_j$ on $\partial {\mathfrak {C}}^\eta _\ell$. A simple calculation yields

$$\begin{aligned} \int _{{\mathfrak {C}}^{(1-\sigma _j)\eta }_\ell } |\nabla v_j|^2 \, dx \leqslant \frac{1}{1-\sigma _j} \int _{{\mathfrak {C}}^\eta _\ell } |\nabla \widetilde{Q}|^2 \, dx \end{aligned}$$

(5.29)

and

$$\begin{aligned}{} & {} \int _{{\mathfrak {C}}^\eta _\ell \setminus {\mathfrak {C}}^{(1-\sigma _j)\eta }_\ell } |\nabla v_j|^2 \, dx\leqslant C \sigma _j \int _{{\mathbb D}_\ell } |\nabla {\widehat{Q}}^+_j|^2+|\nabla {\widehat{Q}}^-_j|^2+ |\nabla {\widehat{Q}}^+_*|^2+|\nabla {\widehat{Q}}^-_*|^2 \, dx^\prime \nonumber \\{} & {} \quad +\frac{C}{ \sigma _j}\big (\Vert {\widehat{Q}}^+_j-{\widehat{Q}}_*^+\Vert ^2_\infty + \Vert {\widehat{Q}}^-_j-{\widehat{Q}}_*^-\Vert ^2_\infty \big ) \leqslant C\sigma _j, \end{aligned}$$

(5.30)

for some constant $C=C(\delta ,\eta )$ independent j. By construction, we have $|v_j|=1$ in ${\mathfrak {C}}^{(1-\sigma _j)\eta }_\ell$, and $0\leqslant 1-|v_j|\leqslant \sigma _j$ in ${\mathfrak {C}}^{\eta }_\ell {\setminus } {\mathfrak {C}}^{(1-\sigma _j)\eta }_\ell$. Therefore, $|v_j|\geqslant 1/2$ for j large enough, and we can define the competitor

$$\begin{aligned} \widetilde{Q}_j:=\frac{v_j}{|v_j|}\in W^{1,2}_{\textrm{sym}}({\mathfrak {C}}^{\eta }_\ell ;{\mathbb S}^4) \end{aligned}$$

which satisfies $\widetilde{Q}_j= Q_j$ on $\partial {\mathfrak {C}}^{\eta }_\ell$. Since ${\widetilde{Q}}_j=v_j$ in ${\mathfrak {C}}^{(1-\sigma _j)\eta }_\ell$ and $|v_j|\geqslant 1/2$, we infer from (5.29) and (5.30) that

$$\begin{aligned} \int _{{\mathfrak {C}}^\eta _\ell } |\nabla \widetilde{Q}_j|^2 \, dx \leqslant \frac{1}{1-\sigma _j} \int _{{\mathfrak {C}}^\eta _\ell } |\nabla \widetilde{Q}|^2 \, dx+ C \sigma _j \,.\nonumber \\ \end{aligned}$$

(5.31)

On the other hand, $Q_j \rightarrow Q_*$ and $\widetilde{Q}_j \rightarrow \widetilde{Q}$ a.e. in ${\mathfrak {C}}^\eta _\ell$. Then,

$$\begin{aligned}{} & {} \lim _{j\rightarrow \infty } \lambda _j\int _{{\mathfrak {C}}^\eta _\ell } W( Q_j)\,dx= \lambda \int _{{\mathfrak {C}}^\eta _\ell } W( Q_*)\,dx\quad \text {and}\quad \lim _{j\rightarrow \infty } \lambda _j\int _{{\mathfrak {C}}^\eta _\ell } W({\widetilde{Q}}_j)\,dx\nonumber \\{} & {} \quad = \lambda \int _{{\mathfrak {C}}^\eta _\ell } W({\widetilde{Q}})\,dx \end{aligned}$$

(5.32)

by dominated convergence. By minimality of $Q_j$, (5.31)–(5.32), and weak lower semicontinuity of the Dirichlet integral, we finally deduce that

$$\begin{aligned}{} & {} {\mathcal {E}}_\lambda (Q_*,{\mathfrak {C}}^\eta _\ell ) \leqslant \liminf _{j \rightarrow \infty } {\mathcal {E}}_{\lambda _j}(Q_j,{\mathfrak {C}}^\eta _\ell ) \leqslant \limsup _{j \rightarrow \infty } {\mathcal {E}}_{\lambda _j}(Q_j, {\mathfrak {C}}^\eta _\ell ) \leqslant \limsup _{j \rightarrow \infty } {\mathcal {E}}_{\lambda _j}(\widetilde{Q}_j,{\mathfrak {C}}^\eta _\ell )\nonumber \\{} & {} \quad ={\mathcal {E}}_\lambda (\widetilde{Q},{\mathfrak {C}}^\eta _\ell ) \,. \end{aligned}$$

(5.33)

Since ${\widetilde{Q}}=Q_*$ in ${\mathfrak {C}}^{\eta }_\ell {\setminus } {\mathfrak {C}}^{h-\delta }_\ell$, it follows that ${\mathcal {E}}_\lambda (Q_*,{\mathfrak {C}}^{h-\delta }_\ell ) \leqslant {\mathcal {E}}_\lambda (\widetilde{Q},{\mathfrak {C}}^{h-\delta }_\ell )$ proving the minimality of $Q_*$ in ${\mathfrak {C}}^{h-\delta }_\ell$. Moreover, choosing ${\widetilde{Q}}=Q_*$ leads to $\lim _j{\mathcal {E}}_{\lambda _j}(Q_j,{\mathfrak {C}}^\eta _\ell )= {\mathcal {E}}_\lambda (Q_*,{\mathfrak {C}}^\eta _\ell )$ which, in view of (5.32), implies that $Q_j\rightarrow Q_*$ strongly in $W^{1,2}({\mathfrak {C}}^\eta _\ell )$ (and thus strongly in $W^{1,2}({\mathfrak {C}}^{h-\delta }_\ell )$). The conclusion now follows from the arbitrariness of $\delta$. $\square$

5.3 Rigidity in infinite cylinders and proof of Theorem 1.3

The following rigidity result will be the key ingredient to deduce qualitative properties for minimizers of ${\mathcal {E}}_\lambda$ on expanding cylinders ${\mathfrak {C}}^h_{\ell ,\rho }$ as $h \rightarrow +\infty$. To this purpose, we will heavily use results from Sect. 4, to which the reader is referred also for some of the notation employed here. We only recall from Theorem 1.2 that in the case $\lambda \ell ^2<\lambda _0$, the functional $E_{\lambda }$ admits a unique minimizer ${{\widehat{Q}}}_\ell$ over ${\mathcal {A}}^\textrm{sym}_{\overline{H}}({\mathbb D}_\ell )$, and it satisfies $\widehat{Q}_\ell (0)=-\textbf{e}_0$.

Proposition 5.10

Let $\ell >0$ be such that $\lambda \ell ^2<\lambda _0$ with $\lambda _0$ the constant given by Theorem 1.2. Assume that $Q \in W^{1,2}_\textrm{loc}({\mathfrak {C}}^\infty _\ell ;{\mathbb S}^4)$ is an equivariant local minimizer of ${\mathcal {E}}_\lambda$ in ${\mathfrak {C}}^\infty _\ell$ up to the lateral boundary satisfying $Q=Q_{\textrm{b}}$ on $\partial ^\textrm{lat}{\mathfrak {C}}^\infty _\ell$, where $Q_{\textrm{b}}$ denotes the homeotropic boundary data given by (2.4). If ${\mathcal {E}}_\lambda (Q,{\mathfrak {C}}_\ell ^h)=O(h)$ as $h \rightarrow \infty$, then $Q(x)\equiv {{\widehat{Q}}}_\ell (x^\prime )$ where ${{\widehat{Q}}}_\ell$ denotes the unique minimizer of the 2D-functional $E_{\lambda }$ over ${\mathcal {A}}^{\textrm{sym}}_{\overline{H}}({\mathbb D}_\ell )$. In particular, Q is smooth, independent of $x_3$, and $Q= -\textbf{e}_0$ on the $x_3$-axis.

Proof

We first notice that

$$\begin{aligned} \int _{2^n}^{2^{n+1}} \bigg (E_\lambda \big (Q(\, \cdot , t),{\mathbb D}_\ell \big )+E_\lambda (Q(\, \cdot , -t),{\mathbb D}_\ell \big )\bigg )\,dt\leqslant {\mathcal {E}}_\lambda \big (Q,{\mathfrak {C}}^{2^{n+1}}_\ell \big )\leqslant C 2^n\qquad \forall n\in \mathbb {N}. \end{aligned}$$

Hence, for each integer n, there exists $h_n\in (2^n,2^{n+1})$ such that $Q(\cdot ,\pm h_n)\in W^{1,2}({\mathbb D}_\ell )$ with $E_\lambda \big (Q(\, \cdot , \pm h_n),{\mathbb D}_\ell \big )=O(1)$ as $n\rightarrow \infty$.

We claim that

$$\begin{aligned} {\mathcal {E}}_\lambda (Q,{\mathfrak {C}}^{h_n}_\ell )=2h_n {\mathfrak {e}}_{\lambda \ell ^2}+O(1)\quad \hbox { as}\ n\rightarrow \infty . \end{aligned}$$

(5.34)

We argue as in Corollary 5.5 to construct competitors, and we set $\Omega _n^\pm :=({\mathfrak {C}}^{h_n}_\ell {\setminus } \overline{{\mathfrak {C}}^{h_n-1}_\ell } ) \cap \{\pm x_3> 0\}$. We define a map $\widetilde{Q}_n$ in ${\mathfrak {C}}^{h_n}_\ell \cap \{|x_3|\leqslant h_n-1\}$ setting $\widetilde{Q}_n(x):={{\widehat{Q}}}_\ell (x^\prime )$. For $x\in \partial \Omega _n^\pm \cap \{|x_3|>h_n-1\}$, we set $\widetilde{Q}_n(x):=Q(x)$ and we then extend $\widetilde{Q}_n$ inside $\Omega _n^\pm$ by 0-homogeneity from the point $p_n^\pm =(0,0,\pm (h_n-1/2))$. As in the proof of Corollary  5.5 (see (5.21)), our choice of $h_n$ ensures that ${\mathcal {E}}_\lambda (\widetilde{Q}_n,\Omega _n^\pm )=O(1)$ as $n\rightarrow \infty$. Since ${\mathcal {E}}_\lambda (\widetilde{Q}_n,{\mathfrak {C}}^{h_n-1}_\ell )=2(h_n-1) {\mathfrak {e}}_{\lambda \ell ^2}$, the claim follows.

In view of (5.34), we now have

$$\begin{aligned}{} & {} 2h_n {\mathfrak {e}}_{\lambda \ell ^2}+\int _{-h_n}^{h_n} \Big (E_\lambda \big (Q(\, \cdot ,x_3),{\mathbb D}_\ell \big )-{\mathfrak {e}}_{\lambda \ell ^2}\Big )\, dx_3 +\int _{{\mathfrak {C}}^{h_n}_\ell }\frac{1}{2} \left| \frac{\partial Q}{\partial x_3} \right| ^2\,dx_3\nonumber \\{} & {} \quad \leqslant {\mathcal {E}}_\lambda (Q,{\mathfrak {C}}^{h_n}_\ell )=2h_n {\mathfrak {e}}_{\lambda \ell ^2}+O(1)\,. \end{aligned}$$

(5.35)

Recalling that $E_\lambda \big (Q(\, \cdot \,,x_3),{\mathbb D}_\ell \big )-{\mathfrak {e}}_{\lambda \ell ^2}\geqslant 0$, letting $n\rightarrow \infty$ in (5.35) yields

$$\begin{aligned} \int _{-\infty }^{\infty } \Big (E_\lambda (Q\big (\, \cdot ,x_3),{\mathbb D}_\ell \big )-{\mathfrak {e}}_{\lambda \ell ^2}\Big ) \, dx_3 +\int _{{\mathfrak {C}}^{\infty }_\ell }\frac{1}{2} \left| \frac{\partial Q}{\partial x_3} \right| ^2\, dx_3 <\infty \,.\end{aligned}$$

As a consequence, there exists ${\tilde{h}}_n \nearrow +\infty$ such that $E_\lambda \big (Q(\, \cdot \,,\pm {\tilde{h}}_n),{\mathbb D}_\ell \big ) \rightarrow {\mathfrak {e}}_{\lambda \ell ^2}$ as $n \rightarrow \infty$. Since $\lambda \ell ^2 <\lambda _0$, it follows from Theorem 1.2 that $Q(\, \cdot \,,\pm {\tilde{h}}_n) \rightarrow {\widehat{Q}}_\ell$ strongly in $W^{1,2}({\mathbb D}_\ell )$. Indeed, by weak lower semicontinuity of $E_\lambda$, any weak limit is a minimizer of $E_\lambda$ over ${\mathcal {A}}_{\overline{H}}^{\textrm{sym}}({\mathbb D}_\ell )$ so that convergence is in fact $W^{1,2}$-strong. Convergence of the full sequence follows from the uniqueness of the limit. In addition, Theorem 1.2 also ensures that the smooth map ${{\widehat{Q}}}_\ell$ satisfies ${{\widehat{Q}}}_\ell (0)=-\textbf{e}_0$. Applying Lemma 2.10, we also infer that $Q(\, \cdot \,,\pm {\tilde{h}}_n) \rightarrow {\widehat{Q}}_\ell$ uniformly on $\overline{{\mathbb D}}_\ell$.

Finally, we construct a further competitor ${{\widehat{Q}}}_n$ testing the minimality of Q following the construction in the proof of Lemma 5.9. We first define a sequence a map $v_n$ as in (5.28) with ${{\tilde{h}}}_n$ in place of $\eta$, ${\widetilde{Q}}$ and ${{\widehat{Q}}}_*^\pm$ replaced by $\widehat{Q}_\ell$, and $Q(\cdot ,\pm {{\tilde{h}}}_n)$ instead of $\widehat{Q}_j^\pm$. Then $|v_n|\geqslant 1/2$ for n large enough which allows us to define ${{\widehat{Q}}}_n:=v_n/|v_n|$. Then ${{\widehat{Q}}}_n\in W_\textrm{sym}^{1,2}({\mathfrak {C}}^{{\tilde{h}}_n}_\ell ;{\mathbb S}^4)$ satisfies ${{\widehat{Q}}}_n=Q$ on $\partial {\mathfrak {C}}^{{\tilde{h}}_n}_\ell$. As in the proof of of Lemma 5.9, the minimality of Q implies that ${\mathcal {E}}_\lambda (Q,{\mathfrak {C}}^{{\tilde{h}}_n}_\ell )\leqslant {\mathcal {E}}_\lambda ({{\widehat{Q}}}_n,{\mathfrak {C}}^{{\tilde{h}}_n}_\ell )= 2{\tilde{h}}_n {\mathfrak {e}}_{\lambda \ell ^2}+o(1)$ as $n\rightarrow \infty$. Combining this upper bound with the lower bound (5.35) with ${{\tilde{h}}}_n$ instead of $h_n$, and letting $n\rightarrow \infty$ we conclude that $\frac{\partial Q}{\partial x_3}\equiv 0$ in ${\mathfrak {C}}^\infty _\ell$ and $E_\lambda (Q(\, \cdot \,,x_3),{\mathbb D}_\ell )\equiv {\mathfrak {e}}_{\lambda \ell ^2}$. By uniqueness of ${{\widehat{Q}}}_\ell$, the conclusion follows. $\square$

Remark 5.11

It is not known whether Proposition 5.10 still holds for $\lambda \ell ^2\geqslant \lambda _0$, or if there exists a map $Q \in W^{1,2}_\textrm{loc}({\mathfrak {C}}^\infty _\ell ;{\mathbb S}^4)$ which is an equivariant local minimizer of ${\mathcal {E}}_\lambda$ up to the lateral boundary connecting two different minimizers ${\widehat{Q}}^\pm _\ell$ of $E_\lambda$ over ${\mathcal {A}}^{\textrm{sym}}_{\overline{H}}({\mathbb D}_\ell )$ as $x_3 \rightarrow \pm \infty$. One may expect that such local minimizer do exist for $\lambda \ell ^2>\lambda _*$ with ${\widehat{Q}}_\ell ^\pm (x^\prime )=g_{\overline{H}}(\pm x^\prime /\ell )$ and $g_{\overline{H}}$ defined through (4.34). We have not pursued these issues, and these questions remain open.

We are now in position to prove the main result of this section, that is Theorem 1.3.

Proof of Theorem 1.3

To prove claim (i), we argue by contradiction assuming that $Q^{(n)}$ is smooth for some subsequence. Notice that $I_n:=\overline{\Omega }_n\cap \{ x_3\hbox {-axis}\}$ is a closed interval and that $Q_{\textrm{b}}^{(n)}(x)=\textbf{e}_0$ for each $x\in \partial \Omega _n\cap \{ x_3\hbox {-axis}\}=\partial I_n$. Hence $Q^{(n)}\equiv \textbf{e}_0$ on $I_n$ by continuity, which implies that $Q^{(n)}(\, \cdot \, /\ell ,x_3) \in {\mathcal {A}}_{\textrm{N}}$ whenever $|x_3|<h-\rho$. Combining Proposition 4.10 with Theorem 1.2 yields

$$\begin{aligned} {\mathcal {E}}_\lambda (Q^{(n)},\Omega _n)\!\geqslant \!\! \int _{-h_n+\rho }^{h_n-\rho }\! E_\lambda \big (Q^{(n)}(\, \cdot \,,x_3),{\mathbb D}_\ell \big ) \, dx_3 \!\geqslant \!6\pi \cdot 2(h_n-\rho )=2(h_n-\rho ) {\mathfrak {e}}_{\lambda _*} \,.\qquad \end{aligned}$$

(5.36)

On the other hand, ${\mathcal {E}}_\lambda (Q^{(n)},\Omega _n) \leqslant 2h_n {\mathfrak {e}}_{\lambda \ell ^2}+O(1)$ as $n\rightarrow \infty$ by Corollary 5.5. Since $\lambda \ell ^2<\lambda _*$, we have ${\mathfrak {e}}_{\lambda \ell ^2}<{\mathfrak {e}}_{\lambda _*}$ by Proposition 4.20. Hence this upper bound contradicts (5.36) for n large enough.

Therefore ${{\,\mathrm{\textrm{sing}}\,}}(Q^{(n)})\ne \emptyset$ for n large enough. According to [12, Theorem 1.1], we then have $\beta _n (\overline{\Omega _n})=[-1,1]$ since this property holds for the tangent map at any singular point (see also [12, Remark 7.18]). Finally, since $\Omega _n$ is connected, simply connected, with boundary of class $C^3$, and $Q^{(n)}_\textrm{b}$ is the homeotropic boundary data, assumptions ($HP_1$)–($HP_3$) in [11, 12] are satisfied and each $Q^{(n)}$ is a split minimizer in the sense of [12, Definition 7.11].

We now prove claim (ii). According to Corollary 5.5, $Q^{(n)}$ satisfies the uniform bound (5.20) whenever $h_n -\rho>r>2\sqrt{2}\ell$. On the other hand, for each $\eta >0$ such that ${\mathfrak {C}}^\eta _\ell \subseteq {\mathfrak {C}}^{h_n}_{\ell ,\rho }\cap B_r$, $Q^{(n)}$ is obviously an equivariant local minimizer of ${\mathcal {E}}_{\lambda _j}$ in ${\mathfrak {C}}^\eta _\ell$ up to the lateral boundary, so that Lemma 5.9 applies. By a standard diagonal argument, we infer the existence of a (not relabeled) subsequence such that $Q^{(n)}\rightarrow Q^*$ strongly in $W^{1,2}({\mathfrak {C}}^\eta _\ell )$ for every $\eta >0$ as $n \rightarrow \infty$, where $Q^*\in W^{1,2}_\textrm{loc}({\mathfrak {C}}^\infty _\ell ;\mathbb {S}^4)$ an equivariant local minimizer of ${\mathcal {E}}_{\lambda }$ in ${\mathfrak {C}}^\infty _\ell$ up to the lateral boundary agreeing with the homeotropic boundary data (2.4) on $\partial {\mathfrak {C}}^\infty _\ell$. Then, letting $n\rightarrow \infty$ in (5.20), we deduce that ${\mathcal {E}}_\lambda (Q^*,{\mathfrak {C}}^h_\ell )=O(h)$ as $h \rightarrow \infty$. Applying Proposition 5.10, it follows that $Q^*={\widehat{Q}}_\ell$. By uniqueness of the limit, the full sequence actually converges to ${\widehat{Q}}_\ell$ as claimed.

To prove the locally smooth convergence, we rely on the regularity results in Sect. 3.1. We fix an arbitrary $\eta >0$, and we aim to prove that $Q^{(n)}$ is bounded in $C^k(\overline{{\mathfrak {C}}^\eta _\ell })$ for every $k\in \mathbb {N}$, which is clearly enough for our purposes. Let us first fix an arbitrary point $x^*\in \mathbb {D}_\ell \times [-\eta ,\eta ]$. By smoothness of ${\widehat{Q}}_\ell$, we can find $\delta >0$ small enough such that $B_\delta (x^*)\subseteq {\mathfrak {C}}^\infty _\ell$ and $\frac{1}{\delta } {\mathcal {E}}_\lambda \big ({{\widehat{Q}}}_\ell , B_\delta (x^*)\big )\leqslant \varvec{\varepsilon }_{\textrm{in}}/16$, where $\varvec{\varepsilon }_{\textrm{in}}>0$ denotes the universal constant from Proposition 3.5. By the strong $W^{1,2}$-convergence of $Q^{(n)}$, we have $\frac{1}{\delta } {\mathcal {E}}_\lambda \big (Q^{(n)}, B_\delta (x^*)\big )\leqslant \varvec{\varepsilon }_{\textrm{in}}/8$ for n large enough. By Proposition 3.5, it implies that $Q^{(n)}$ is bounded in $C^k(B_{\delta /16}(x^*))$ for every $k\in \mathbb {N}$. Next we fix $x^*\in \partial {\mathbb D}_\ell \times [-\eta ,\eta ]$ and a radius $r_*\in (0,\ell )$. By $\mathbb {S}^1$-equviariance, without loss of generality we can assume that $x^*=(x^*_1,0,x^*_3)\in \{x_2=0\}$. For n large enough, we have $\Omega _n\cap B_{r_*}(x^*)={\mathfrak {C}}^\infty _\ell \cap B_{r_*}(x^*)$ and $\partial \Omega _n\cap B_{r_*}(x^*)=\partial {\mathfrak {C}}^\infty _\ell \cap B_{r_*}(x^*)$, so that $\partial \Omega _n\cap B_{r_*}(x^*)$ and the restriction of $Q_\textrm{b}^{(n)}$ to $\partial \Omega _n\cap B_{r_*}(x^*)$ are independent of n. Accordingly, the constants $\bar{\varvec{\varepsilon }}_\textrm{bd}>0$ and $\bar{\varvec{\kappa }}>0$ from Proposition 3.6 only depends on $\ell$. Arguing as in the proof of [12, Proposition 6.9], the equivariance of $Q^{(n)}$ implies that for $r\in (0,r_*/4)$ and every ball $B_\rho (\bar{x})\subseteq B_r(x^*)$,

$$\begin{aligned} \frac{1}{\rho }\int _{B_\rho ({\bar{x}})\cap {\mathfrak {C}}^\infty _\ell }|\nabla Q^{(n)}|^2\,dx \leqslant \frac{C_*}{\ell } \int _{{\mathcal {D}}_r(x^*)} |\nabla Q^{(n)}|^2\,d{\mathcal {H}}^2, \end{aligned}$$

where $C_*>0$ is a universal constant and ${\mathcal {D}}_r(x^*):={\mathfrak {C}}^\infty _\ell \cap B_{r}(x^*)\cap \{x_2=0\}$. By the strong $W^{1,2}$-convergence of $Q^{(n)}$ and equivariance, the restriction of $|\nabla Q^{(n)}|^2$ to the slice ${\mathcal {D}}_{r_*}(x^*)$ is strongly converging in $L^1({\mathcal {D}}_{r_*}(x^*))$. By the Vitali–Hahn–Sacks Theorem (see e.g. [5, Theorem 1.30]), we can find $r\in (0,r_*/4)$ such that $\int _{{\mathcal {D}}_r(x^*)} |\nabla Q^{(n)}|^2\,d{\mathcal {H}}^2\leqslant \ell \bar{\varvec{\varepsilon }}_{\textrm{bd}}/C_*$ for n large enough. Hence,

$$\begin{aligned} \sup _{B_\rho ({\bar{x}})\subseteq B_r(x^*)}\frac{1}{\rho }\int _{B_\rho ({\bar{x}})\cap {\mathfrak {C}}^\infty _\ell }|\nabla Q^{(n)}|^2\,dx \leqslant \bar{\varvec{\varepsilon }}_{\textrm{bd}}, \end{aligned}$$

and we infer from Proposition  3.6 that $Q^{(n)}$ is bounded in $C^k(B_{\bar{\varvec{\kappa }} r/2}(x^*)\cap \overline{{\mathfrak {C}}^\infty _\ell })$ for every $k\in \mathbb {N}$. In view of the arbtrariness of $x^*$ (either in the interior or at the boundary), by a standard covering argument we finally conclude that $Q^{(n)}$ is bounded in $C^k(\overline{{\mathfrak {C}}^\eta _\ell })$ for every $k\in \mathbb {N}$.

It remains to prove claim (iii). Writing $\Sigma _n:={{\,\mathrm{\textrm{sing}}\,}}(Q^{(n)})$ to ease the notation, we first observe that the convergence of $Q^{(n)}$ towards ${{\widehat{Q}}}_\ell$ established in claim (ii) implies that $\Sigma _n\cap \{|x_3|<1\}=\emptyset$ and $Q^{(n)}=-\textbf{e}_0$ on $\{x_3\text {-axis}\}\cap \{|x_3|<1\}$ for n large enough. Since $Q^{(n)}(q^\pm _n)=\textbf{e}_0$ at $q^\pm _n:=(0,0,\pm h_n)$ and $Q^{(n)}(x)\in \{\textbf{e}_0,-\textbf{e}_0\}$ for every $x\in (\Omega _n\cap \{x_3\text {-axis}\}){\setminus } \Sigma _n$, we deduce that both sets $\Sigma _n^+:=\Sigma _n\cap \{x_3\geqslant 0\}$ and $\Sigma _n^-:=\Sigma _n\cap \{x_3< 0\}$ are nonempty (recall that $\Sigma _n$ is a finite subset of $\Omega \cap \{x_3\text {-axis}\}$). In view of Theorem 3.1, the restriction of $Q^{(n)}$ to $(\Omega _n\cap \{x_3\text {-axis})\setminus \Sigma _n$ is constant on each connected component and jumps from $\textbf{e}_0$ to $-\textbf{e}_0$ at each point of $\Sigma _n$. It easily implies that both $\Sigma _n^+$ and $\Sigma _n^-$ contain an odd number of points.

Let us now set $t^{\textrm{min}}_n:=\min \big \{|p|: p\in {{\,\mathrm{\textrm{sing}}\,}}(Q^{(n)})\big \}\in (0,h_n)$. We claim that $h_n-t_n\leqslant \alpha$ for some constant $\alpha > 0$. To prove this claim, we argue by contradiction assuming that for some (not relabeled) subsequence, we have $h_n-t^{\textrm{min}}_n\rightarrow + \infty$. Next we consider a point $p^{\textrm{min}}_n\in {{\,\mathrm{\textrm{sing}}\,}}(Q^{(n)})$ such that $|p^{\textrm{min}}_n|=t^\textrm{min}_n$. Notice that claim (ii) implies that $|p^{\textrm{min}}_n|=t^\textrm{min}_n\rightarrow \infty$, so that the translated domain $\widetilde{\Omega }_n:=\Omega _n-p^{\textrm{min}}_n$ satisfies $\widetilde{\Omega }_n\rightarrow {\mathfrak {C}}^\infty _\ell$ as $n\rightarrow \infty$. By Corollary 5.6, for every $r>2\sqrt{2}\ell$ we have ${\mathcal {E}}_\lambda \big (Q^{(n)},\Omega _n\cap B_r(p^\textrm{min}_n)\big )\leqslant Cr$ for n large enough (so that $r<h_n-\rho -|p^{\textrm{min}}_n|-\ell$), where the constant C is independent of n. Considering the translated map $\widetilde{Q}^{(n)}(x):=Q^{(n)}(x+p^{\textrm{min}}_n)$, we then have ${\mathcal {E}}_\lambda \big ({\widetilde{Q}}^{(n)},\widetilde{\Omega }_n\cap B_r\big )\leqslant Cr$. Arguing as in the proof of claim (ii), we infer from Lemma 5.9 and Proposition 5.10 that ${\widetilde{Q}}^{(n)}\rightarrow \widehat{Q}_\ell$ strongly in $W^{1,2}({\mathfrak {C}}^\eta _\ell )$ for every $\eta >0$. In particular, ${\widetilde{Q}}^{(n)}\rightarrow {{\widehat{Q}}}_\ell$ strongly in $W^{1,2}(B_{\ell })$. Since ${{\widehat{Q}}}_\ell$ is smooth, we deduce from Lemma 3.9 (applied in the ball $B_\ell$) that $\textrm{sing}({\widetilde{Q}}^{(n)})\cap B_{\ell /2}=\emptyset$ for n large enough, contradicting the fact that $0\in \textrm{sing}({\widetilde{Q}}^{(n)})$. Hence $h_n-t^\textrm{min}_n$ remains bounded from above.

Next we consider $t_n^{\textrm{max}}:=\max \big \{|p|: p\in {{\,\mathrm{\textrm{sing}}\,}}(Q^{(n)})\big \}\in (0,h_n)$, and we claim that $t_n^\textrm{max}\leqslant h_n-\delta$ for some $\delta >0$ independent of n. Without loss of generality, we can assume $t_n^{\textrm{max}}$ is achieved at a singular point $p_n^{\textrm{max}}$ belonging to $\{x_3< 0\}$ (the other case being analoguous). To prove the claim, we argue by contradiction assuming that $\tau ^2_n:=h_n-t_n^{\textrm{max}}\rightarrow 0$ as $n\rightarrow \infty$ for some (not relabeled) subsequence. We observe that $\Omega _n\cap B_\rho (q^-_n)=q^-_n+B^+_\rho$ with $B^+_\rho :=B_\rho \cap \{x_3>0\}$, and $Q^{(n)}=\textbf{e}_0$ on $\partial \Omega _n\cap B_\rho (q^-_n)=q^-_n+B_\rho \cap \{x_3=0\}$. According to Remark 3.8, we have $\frac{1}{\tau _n}{\mathcal {E}}_\lambda \big (Q^{(n)},\Omega _n\cap B_{\tau _n}(q^-_n)\big )\leqslant \frac{8}{\rho }{\mathcal {E}}_\lambda (Q^{(n)},\Omega _n\cap B_\rho (q^-_n))$. Since $\Omega _n\cap B_\rho (q^-_n)\subseteq \Omega _n{\setminus }{\mathfrak {C}}^{h-\rho }_\ell$, Corollary 5.7 tells us that ${\mathcal {E}}_\lambda (Q^{(n)},\Omega _n\cap B_\rho (q^-_n))=O(1)$ as $n\rightarrow \infty$. Therefore, ${\mathcal {E}}_\lambda \big (Q^{(n)},\Omega _n\cap B_{\tau _n}(q^-_n)\big )= O(\tau _n)$ as $n\rightarrow \infty$. Then we consider the translated and rescaled map $\widehat{Q}^{(n)}(x):=Q^{(n)}(\tau _nx+q^-_n)$ which satisfies $\widehat{Q}^{(n)}=\textbf{e}_0$ on $B_\rho \cap \{x_3=0\}$. Since $\Omega _n\cap B_\rho (q^-_n)\subseteq \Omega _n{\setminus }{\mathfrak {C}}^{h-\rho }_\ell$, we deduce from Corollary 5.7 that ${\mathcal {E}}_{\lambda \tau _n^2}({{\widehat{Q}}}^{(n)},B^+_{1})= \frac{1}{\tau _n}{\mathcal {E}}_\lambda (Q^{(n)},\Omega _n\cap B_\rho (q^-_n))\leqslant C$ for a constant C independent of n. According to [12, Theorem 5.5], there exists a (not relabeled) subsequence and ${{\widehat{Q}}}^*\in W^{1,2}_\textrm{sym}(B_1^+;{\mathbb S}^4)$ such that ${{\widehat{Q}}}^{(n)}\rightarrow {{\widehat{Q}}}^*$ strongly in $W^{1,2}(B_r^+)$ for every $r\in (0,1)$. By continuity of the trace operator, we have ${{\widehat{Q}}}^*=\textbf{e}_0$ on $B_1\cap \{x_3=0\}$. Rescaling variables, we realize that $\widehat{Q}^{(n)}$ is a weak solution of (1.6) in $B_1^+$ with $\lambda \tau _n^2\rightarrow 0$ in place of $\lambda$. From the locally strong $W^{1,2}$-convergence of ${{\widehat{Q}}}^{(n)}$, we deduce that ${{\widehat{Q}}}^*$ is a weakly harmonic map into ${\mathbb S}^4$ in $B_1^+$. Now we observe that (after rescaling variables), ${{\widehat{Q}}}^{(n)}$ satisfies the interior monotonicity formula from Proposition 3.3 in $B_1^+$ with $\lambda \tau _n^2\rightarrow 0$ in place of $\lambda$. Once again, by the established locally strong $W^{1,2}$-convergence, we infer that ${{\widehat{Q}}}^*$ satisfies the same interior monotonicity formula with $\lambda =0$. In view of Remark 3.8 (applied to $Q^{(n)}$), the same argument shows that ${{\widehat{Q}}}^*$ satisfies the boundary monotonicity formula (3.3) with $\lambda =0$ for balls centered on $B_1\cap \{x_3=0\}$. This is then enough to apply the boundary regularity theory from [38] (see also [11, Section 2]) and conclude that ${{\widehat{Q}}}^*$ is smooth in a neighborhood of $B_1\cap \{x_3=0\}$. In particular, we can find a radius $\eta \in (0,1)$ such that $\frac{1}{\eta }{\mathcal {E}}_0({{\widehat{Q}}}^*, B_\eta ^+)\leqslant \varvec{\varepsilon }^\sharp _{\textrm{bd}}/4$, where $\varvec{\varepsilon }^\sharp _{\textrm{bd}}>0$ is the universal constant provided by Remark 3.8. By strong $W^{1,2}$-convergence, we then have $\frac{1}{\eta }{\mathcal {E}}_0({{\widehat{Q}}}^{(n)}, B_\eta ^+)\leqslant \varvec{\varepsilon }^\sharp _{\textrm{bd}}/2$ for n large enough. According to Remark 3.8, it implies that $\widehat{Q}^{(n)}$ is smooth in $B_{\varvec{\kappa }^\sharp \eta }\cap \{x_3\geqslant 0\}$ for n large enough where $\varvec{\kappa }^\sharp >0$ is a further universal constant. On the other hand, by construction ${{\widehat{Q}}}^{(n)}$ is singular at ${\bar{p}}_n:=(p_n^{\textrm{max}}-q_n^-)/\tau _n=(0,0,\tau _n)\rightarrow 0$ as $n\rightarrow \infty$, a contradiction. This proves the upper bound $t_n^{\textrm{max}}\leqslant h_n-\delta$ for a constant $\delta >0$ that we can choose to be equal to $1/\alpha$, taking the constant $\alpha$ larger if necessary.

It finally remains to prove that $\textrm{Card}\,\Sigma _n=O(1)$ as $n\rightarrow \infty$. By inequality in (5.26) (applied with $r=(\rho +\alpha +1)/2$ and $z=h_n-r$), we have ${\mathcal {E}}_\lambda \big (Q^{(n)}, {\mathfrak {C}}^{h_n-\rho }_\ell \cap \{|x_3|>h_n-\rho -\alpha -1\}\big )=O(1)$, which in view of Corollary 5.7 yields ${\mathcal {E}}_\lambda \big (Q^{(n)}, \Omega _n\cap \{|x_3|>h_n-\rho -\alpha -1\}\big )=O(1)$ as $n\rightarrow \infty$. Hence, there exists a constant $M>0$ independent of n such that ${\mathcal {E}}_\lambda \big (Q^{(n)}, B_{1/\alpha }(x)\big )\leqslant M$ for every $x\in \{x_3\text {-axis}\}\cap \{h_n-\alpha \leqslant |x_3|\leqslant h_n-\frac{1}{\alpha }\}$. In turn, applying Lemma 3.12 in such a ball $B_{1/\alpha }(x)$ shows that there exists a constant $\textbf{c}=\textbf{c}(M,\lambda ,\alpha )>0$ (independent of n and x) such that $|p-p^\prime |\geqslant \textbf{c}$ for every $p,p^\prime \in \Sigma _n\cap B_{1/(2\alpha )}(x)$ with $p\ne p^\prime$. Since $\Sigma _n\subseteq \{x_3\text {-axis}\}\cap \{h_n-\alpha \leqslant |x_3|\leqslant h_n-\frac{1}{\alpha }\}$, we conclude that $\textrm{Card}\,\Sigma _n\lesssim \alpha /\textbf{c}$. Since this holds for every n large enough, the proof is complete. $\square$

5.4 Instability and symmetry breaking in long cylinders

To conclude this section, we discuss two important consequences of Theorem 1.3. We first present a general result about the instability of singular configurations minimizing ${\mathcal {E}}_\lambda$ among $\mathbb {S}^1$-equivariant maps. This instability is essentially issued from the instability of singular tangent maps for the Dirichlet energy (see [30]).

Proposition 5.12

Let $\Omega \subseteq \mathbb {R}^3$ be a bounded and axisymmetric open set with boundary of class $C^3$, and let $Q_{\textrm{b}} \in C^{1,1}(\partial \Omega ;\mathbb {S}^4)$ be an $\mathbb {S}^1$-equivariant map. If $Q_\lambda$ is a minimizer of ${\mathcal {E}}_\lambda$ in the class ${\mathcal {A}}^{\textrm{sym}}_{Q_{\textrm{b}}}(\Omega )$ such that ${{\,\mathrm{\textrm{sing}}\,}}(Q_\lambda )\not =\emptyset$, then $Q_\lambda$ is an unstable critical point of ${\mathcal {E}}_\lambda$ in the class ${\mathcal {A}}_{Q_{\textrm{b}}}(\Omega )$. More precisely, for every radial function $\eta \in C^\infty _c(B_1 \setminus \{0\})$ satisfying $\int _{B_1} |\nabla \eta |^2- \frac{2}{|x|^2} \eta ^2 \, dx<0$ and every $p \in \textrm{sing}(Q_\lambda )$, there exists a small $r>0$ such that for every $\bar{v}\in {\mathbb S}^4 \cap L_2$, $Q_\lambda$ is unstable along the variations $\Phi ^{p,r}(x):=\frac{1}{\sqrt{r}}\eta \left( \frac{x-p}{r} \right) \bar{v}$, i.e., ${\mathcal {E}}_\lambda ''(\Phi ^{p,r};Q_\lambda )<0$.

Proof

According to Theorem 3.1, if $p\in {{\,\mathrm{\textrm{sing}}\,}}(Q_\lambda )$, then there exist a degree-zero and equivariant homogeneous harmonic map $Q_* \in C^\infty (\mathbb {R}^3{\setminus }\{ 0\};{\mathbb S}^4)$ and $\nu >0$ such that $Q_*$ is taking values in $L_0 \oplus L_1$, and

$$\begin{aligned} \Vert Q_\lambda ^{p,r}-Q_*\Vert _{C^2(\overline{B_2}\setminus B_1)}=O(r^\nu )\quad \hbox { as}\ r\rightarrow 0, \end{aligned}$$

(5.37)

where $Q_\lambda ^{p,r}(x):=Q_\lambda (p+r x)$. By formula (3.1), we have $|\nabla Q_*|^2=\frac{2}{|x|^2}$. In turn, (5.37) implies that $|\nabla Q_\lambda ^{p,r}|^2 \rightarrow \frac{2}{|x|^2}$ locally uniformly in $\mathbb {R}^3 {\setminus } \{0\}$.

Recall that the second variation of the energy at a general map $\Phi \in C^\infty _c( \Omega ; {\mathcal {S}}_0)$ is defined as

$$\begin{aligned} {\mathcal {E}}^{''}_\lambda (\Phi ;Q_\lambda ):=\left[ \frac{d^2}{dt^2} {\mathcal {E}}_\lambda \left( \frac{Q_\lambda +t\Phi }{|Q_\lambda +t\Phi |} \right) \right] _{t=0} \,. \end{aligned}$$

Using (1.6), one may proceed as for second variation formula for harmonic maps (see e.g. [31, Chapter 1] or [11, Section 4.3]), to obtain

$$\begin{aligned} {\mathcal {E}}^{''}_\lambda (\Phi ;Q_\lambda )=\int _{\Omega } |\nabla \Phi _T|^2- |\nabla Q_\lambda |^2 |\Phi _T|^2 +\lambda (D^2 W (Q_\lambda ) \Phi _T ):\Phi _T \, dx \,, \end{aligned}$$

(5.38)

where $\Phi _T:=\Phi - (Q_\lambda :\Phi )Q_\lambda$ denotes the tangential component of $\Phi$ along $Q_\lambda$. Choosing $r>0$ small enough in such a way that $B_r(p)\subseteq \Omega$ and $B_r(p)\cap \textrm{sing}(Q_\lambda )=\{p\}$, we have $\Phi ^{p,r} \in C^\infty _c( \Omega ; L_2)$, and rescaling/translating $B_r(p)$ to the unit ball $B_1(0)$ yields

$$\begin{aligned} {\mathcal {E}}^{''}_\lambda (\Phi ^{p,r};Q_\lambda )= \int _{B_1} |\nabla \Phi ^{0,1}_T|^2- |\nabla Q^{p,r}_\lambda |^2 |\Phi ^{0,1}_T|^2+\lambda r^2 (D^2 W (Q^{p,r}_\lambda ) \Phi ^{0,1}_T):\Phi ^{0,1}_T \, dx \end{aligned}$$

Since $\Phi ^{0,1}=\eta {\bar{v}}$ and $Q_*$ is taking values in $L_0\oplus L_1=L_2^\perp$, we infer that $\Phi ^{0,1}: Q_\lambda ^{p,r} \rightarrow \Phi ^{0,1}: Q_*=0$ in $C^1_\textrm{loc}(B_1{\setminus }\{0\})$ as $r\rightarrow 0$. Hence $\Phi ^{0,1}_T\rightarrow \Phi ^{0,1}=\eta {\bar{v}}$ in $C^1_{\textrm{loc}}(B_1{\setminus }\{0\})$. Since $D^2W(Q_\lambda ^{p,r}) \rightarrow D^2W (Q_*)$ in $C^0_\textrm{loc}(B_1{\setminus }\{0\})$ and $\eta$ is compactly supported in $B_1\setminus \{0\}$, we have

$$\begin{aligned} \lim _{r \rightarrow 0} {\mathcal {E}}^{''}_\lambda (\Phi ^{p,r};Q_\lambda )= \int _{B_1} |\nabla \left( \bar{v}\eta \right) |^2- \left| \nabla Q_* \right| ^2 \left| \bar{v}\eta \right| ^2 \, dy ={\mathcal {E}}_0''(\eta {\bar{v}};Q_*) = \int _{B_1} |\nabla \eta |^2- \frac{2}{|x|^2} \eta ^2 \, dx \,, \end{aligned}$$

where we used the fact that $|{\bar{v}}|=1$ in the last equality. By the sharp Hardy inequality in $\mathbb {R}^3$ and the last equality above, there exist radial functions $\eta \in C^\infty _c (B_1 {\setminus }\{0\})$ such that ${\mathcal {E}}_0''(\eta \bar{v};Q_*)<0$ (see e.g. [11, proof of Proposition 4.7]). Then, for any such function, the conclusion follows for r small enough. $\square$

Combining Theorem 1.3 with Proposition 5.12 and the full regularity of global minimizers (without symmetry constraint) from [11, Theorem 1.1], we readily obtain the following consequences for minimizers of ${\mathcal {E}}_\lambda$ in sufficiently long cylinders.

Corollary 5.13

Assume that $\lambda \ell ^2 <\lambda _0$. Let $\Omega _n:={\mathfrak {C}}^{h_n}_{\ell ,\rho }$ for varying $h_n>\ell$, $h_n \nearrow +\infty$ as in Theorem 1.3, and $Q_{\textrm{b}}^{(n)}:=Q_\textrm{b}^{h_n}$ the homeotropic boundary data given by (2.4). If $Q^{(n)}_{\textrm{sym}}$ and ${Q}_{\textrm{glob}}^{(n)}$ are minimizers of ${\mathcal {E}}_\lambda$ in the respective classes ${\mathcal {A}}^{\textrm{sym}}_{Q_\textrm{b}^{(n)}}(\Omega _n)$ and ${\mathcal {A}}_{Q_{\textrm{b}}^{(n)}}(\Omega _n)$, then the following properties hold for n large enough:

• (i) ${{\,\mathrm{\textrm{sing}}\,}}(Q_{\textrm{sym}}^{(n)})\ne \emptyset$ and $Q_{\textrm{sym}}^{(n)}$ is an unstable critical point of ${\mathcal {E}}_\lambda$ (under some symmetry breaking perturbations);

• (ii) ${{\,\mathrm{\textrm{sing}}\,}}(Q_{\textrm{glob}}^{(n)})= \emptyset$ and ${Q}_{\textrm{glob}}^{(n)}$ is not $\mathbb {S}^1$-equivariant. In particular, the orbit under the ${\mathbb S}^1$-action $\{R \cdot Q_{\textrm{glob}}^{(n)} (R^\textsf{t}\cdot )\}_{R\in {\mathbb S}^1}$ provides infinitely many ${\mathcal {E}}_\lambda$-minimizers in the class ${\mathcal {A}}_{Q_{\textrm{b}}^{(n)}}(\Omega _n)$, and nonuniqueness holds.

6 Torus minimizers in large cylinders

We consider in this section the homeotropic boundary condition for large (smoothed) cylinders, the geometry opposite to the one in the previous section. We shall prove that for sufficiently large cylinders, any equivariant minimizers is smooth and thus of torus type, as claimed in Theorem 1.4. This result is the counterpart of the main result of the previous section in case of long (smoothed) cylinders but the conclusions are in the opposite direction. In the spirit of Sect. 3, we shall exploit these two extreme cases to show that smooth and singular minimizers actually coexist for intermediate cylinders, i.e., Theorem 1.5, and deduce that symmetry breaking occurs when minimization is performed without the symmetry constraint (see Corollary 6.12).

The analysis in case of large cylinders resembles the one in Sect. 5. It essentially relies on a monotonicity formula, the construction of suitable competitors, local compactness of minimizers, and regularity theory. In the last subsections, we obtain the coexistence result of Theorem 1.5 applying the persistence of smoothness and the persistence of singularities for minimizers developed in Sect. 3, and symmetry breaking follows by continuity w.r.t. the thickness of the infimum values of the energy functional.

6.1 A priori energy bounds and local compactness

In this subsection, we establish some preliminary results starting with the following monotonicity formula.

Lemma 6.1

Let ${\mathfrak {C}}^h_{\ell ,\rho }$ be a smoothed cylinder with $2\rho< h < \ell -\rho$ and $Q_{\textrm{b}}$ its homeotropic boundary data given by (2.4). If Q is minimizing ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}_{Q_{\textrm{b}}}^\textrm{sym}{({\mathfrak {C}}^h_{\ell ,\rho })}$, then

$$\begin{aligned}{} & {} \frac{1}{r_2}{\mathcal {E}}_\lambda (Q,{\mathfrak {C}}^h_{\ell ,\rho } \cap B_{r_2}) = \frac{1}{r_1}{\mathcal {E}}_\lambda (Q, {\mathfrak {C}}^h_{\ell ,\rho } \cap B_{r_1}) + \int _{{\mathfrak {C}}^h_{\ell ,\rho } \cap (B_{r_2} \setminus B_{r_1}) } \frac{1}{\left| x \right| }\left| \frac{\partial Q}{\partial \left| x \right| } \right| ^2 \,dx \nonumber \\{} & {} \quad + \int _{r_1}^{r_2} \frac{1}{r^2} \left( \int _{{\mathfrak {C}}^h_{\ell ,\rho } \cap B_r} 2\lambda W(Q) \, dx \right) \,dr + \int _{r_1}^{r_2} \frac{h}{r^2} \left( \int _{\partial {\mathfrak {C}}^h_{\ell ,\rho } \cap B_r} \frac{1}{2}\left| \frac{\partial Q}{\partial \textbf{n}} \right| ^2 \,\textrm{d}{\mathcal {H}}^2 \right) \,dr \nonumber \\ \end{aligned}$$

(6.1)

for every $h< r_1 < r_2 \leqslant \ell -\rho$.

Proof

For $h < r \leqslant \ell -\rho$, the boundaries $\partial {\mathfrak {C}}^h_{\ell ,\rho }$ and $\partial B_r$ are transversal and $\partial B_r \cap \textrm{sing}(Q) = \emptyset$, hence Lemma 5.1 applies. Choosing the vector field $V(x) = x$ in Lemma 5.1, computations analogous to those leading to (5.12) yield

$$\begin{aligned}{} & {} \frac{d}{dr} \left\{ \frac{1}{r} \int _{{\mathfrak {C}}^h_{\ell ,\rho } \cap B_r} \left( \frac{1}{2} \left| \nabla Q \right| ^2 + \lambda W(Q) \right) \,dx \right\} \\{} & {} \quad =\frac{1}{r}\int _{{\mathfrak {C}}^h_{\ell ,\rho } \cap \partial B_r} \left| \frac{\partial Q}{\partial \textbf{n}} \right| ^2 \, d{\mathcal {H}}^2 + \frac{1}{r^2} \int _{{\mathfrak {C}}^h_{\ell ,\rho } \cap B_r} 2\lambda W(Q)\, dx + \frac{h}{r^2} \int _{\partial {\mathfrak {C}}^h_{\ell ,\rho } \cap B_r} \frac{1}{2} \left| {\frac{\partial Q}{\partial \textbf{n}}} \right| ^2 \,d{\mathcal {H}}^2, \end{aligned}$$

since $Q=\textbf{e}_0$ and $V\cdot \textbf{n}=h$ on $\partial {\mathfrak {C}}^h_{l,\rho } \cap B_r$. Integrating now over $r \in (r_1,r_2)$ yields (6.1). $\square$

The next result provides a first a priori estimate for the energy of minimizers in large cylinders.

Lemma 6.2

Let ${\mathfrak {C}}^h_{\ell ,\rho }$ be a smoothed cylinder and $Q_\textrm{b}$ its homeotropic boundary data given by (2.4). If Q is minimizing ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}_{Q_{\textrm{b}}}^\textrm{sym}({\mathfrak {C}}^h_{\ell ,\rho })$, then ${\mathcal {E}}_\lambda (Q, {\mathfrak {C}}^h_{\ell ,\rho }) \leqslant K \ell$ for a constant K independent of $\ell$.

Proof

We prove the announced energy estimate by constructing a suitable competitor ${\widetilde{Q}}$. To this purpose, we introduce the subdomains $\Omega '_\ell :={\mathfrak {C}}^h_{\ell ,\rho } \cap \{ \left| x' \right| < \ell -\rho \}$ and $\Omega ''_\ell := {\mathfrak {C}}^h_{\ell ,\rho } \cap \{\left| x' \right| > \ell -\rho \}$. Noticing that $Q_{\textrm{b}} = \textbf{e}_0$ on $\partial {\mathfrak {C}}^h_{\ell ,\rho } \cap \{|x_3| = h\}$, we set ${\widetilde{Q}}(x)=\textbf{e}_0$ for $x\in {{\overline{\Omega '_\ell }}}$. To define ${\widetilde{Q}}$ in ${{\overline{\Omega ''_\ell }}}$, we consider the vertical slice ${\mathcal {D}}^+_{\Omega ''_\ell }$ defined in (2.2). Notice that $\ell > 2\rho$, so that ${\mathcal {D}}^+_{\Omega ''_\ell }$ is a translate of ${\mathcal {D}}^+_{\Omega ''_{2\rho }}$. Moreover, the shape of ${\mathcal {D}}^+_{\Omega ''_\ell }$ is independent of $\ell$. We set ${\widetilde{Q}}(x)=Q_{\textrm{b}}(x)$ for $x\in {{\partial \Omega ''_\ell }}\cap \partial {\mathfrak {C}}^h_{\ell ,\rho }$ and, since ${\widetilde{Q}}(x)=\textbf{e}_0$ for $x\in {{\partial \Omega ''_\ell }}\cap \{|x^\prime |=\ell -\rho \}$, we have $\widetilde{Q}\in {{\,\mathrm{\textrm{Lip}}\,}}({{\partial \Omega ''_\ell }}; \mathbb {S}^4)$ and the translated map $\psi : (x_1,0,x_3)\in \partial {\mathcal {D}}^+_{\Omega ''_{2\rho }}\mapsto \widetilde{Q}(x_1-\ell +2\rho ,0,x_3)\in \mathbb {S}^4$ is independent of $\ell$. Since $\mathbb {S}^4$ is simply connected, $\psi$ admits an extension $\Psi \in \textrm{Lip} ({{\overline{ {\mathcal {D}}^+_{\Omega ''_\ell }}}}; \mathbb {S}^4)$. Then we set ${\widetilde{Q}}(x_1,0,x_3)=\Psi (x_1-\ell +2\rho ,0,x_3)$ for $(x_1,0,x_3)\in {\mathcal {D}}^+_{\Omega ''_\ell }$. Finally, we extend $\widetilde{Q}$ to $\Omega _\ell ''$ by $\mathbb {S}^1$-equivariance, that is setting ${\widetilde{Q}}(Rx)=R{\widetilde{Q}}(x)R^\textsf{t}$ for every $R \in \mathbb {S}^1$ and $x\in {\mathcal {D}}^+_{\Omega ''_\ell }$. By construction ${\widetilde{Q}}\in \textrm{Lip}({\mathfrak {C}}^h_{\ell ,\rho };\mathbb {S}^4)$ with a Lipschitz norm independent of $\ell$, ${\widetilde{Q}}$ is $\mathbb {S}^1$-equivariant, and ${\widetilde{Q}}=Q_{\textrm{b}}$ on $\partial {\mathfrak {C}}^h_{\ell ,\rho }$. Hence, as in (2.14), we have

$$\begin{aligned}{} & {} {\mathcal {E}}_\lambda (\widetilde{Q},{\mathfrak {C}}^h_{\ell ,\rho }) \\{} & {} \quad ={\mathcal {E}}_\lambda (\widetilde{Q},\Omega ''_\ell ) =\pi \int _{{\mathcal {D}}_{\Omega _\ell ''}} \bigg (|\nabla \Psi |^2 + \frac{|\Psi _1|^2 + 4|\Psi _2|^2}{x_1^2}+{{2}}\lambda W(\Psi ) \bigg )\,x_1\,dx_1dx_3 \leqslant K\ell , \end{aligned}$$

for some $K{{=K(h,\rho )}}>0$ independent of $\ell$. By minimality of Q, we have ${\mathcal {E}}_\lambda (Q, {\mathfrak {C}}^h_{\ell ,\rho }) \leqslant {\mathcal {E}}_\lambda (\widetilde{Q},{\mathfrak {C}}^h_{\ell ,\rho })$ and the conclusion follows. $\square$

Definition 6.3

Let ${\mathfrak {C}}^h_\ell$ be a cylinder with $h<\infty$. We call top/bottom boundary of the cylinder ${\mathfrak {C}}^h_\ell$, the set

$$\begin{aligned} \partial ^{=} {\mathfrak {C}}^h_\ell :=\partial {\mathfrak {C}}^h_\ell \cap \{|x_3|=h\}=\mathbb {D}_\ell \times \{-h,h\}. \end{aligned}$$

An equivariant map $Q\in W^{1,2}_{\textrm{loc}}({\mathfrak {C}}^h_\ell ;{\mathbb S}^4)$ is said to be an equivariant local minimizer of ${\mathcal {E}}_{\lambda }$ in ${\mathfrak {C}}^h_\ell$ up to the top/bottom boundary if for every $\eta \in (0,\ell )$, $Q\in W^{1,2}_{\textrm{sym}}({\mathfrak {C}}^h_\eta ;{\mathbb S}^4)$ and ${\mathcal {E}}_{\lambda }(Q,{\mathfrak {C}}^h_\eta )\leqslant {\mathcal {E}}_{\lambda }({\widetilde{Q}},{\mathfrak {C}}^h_\eta )$ for every $\widetilde{Q}\in W^{1,2}_{\textrm{sym}}({\mathfrak {C}}^h_\eta ;{\mathbb S}^4)$ satisfying $\widetilde{Q}=Q$ on $\partial {\mathfrak {C}}^h_\eta$.

Remark 6.4

According to Remark 3.8, the regularity theory from Sect. 3.1 applies to an equivariant local minimizer Q of ${\mathcal {E}}_{\lambda }$ in ${\mathfrak {C}}^h_\ell$ up to the top/bottom boundary satisfying $Q=\textbf{e}_0$ on $\partial ^{=} {\mathfrak {C}}^h_\ell$. It shows that Q is smooth in the interior of ${\mathfrak {C}}^h_\ell$ and up to $\partial ^{=} {\mathfrak {C}}^h_\ell$ away from finitely many points located on $\{x_3\text {-axis}\}\cap {\mathfrak {C}}^h_\ell$. As a consequence, the computations from the proof of Lemma 5.1 can be performed, and as in Lemma 6.1, we infer that identity (6.1) holds for $h<r_1<r_2<\ell$ and ${\mathfrak {C}}^h_\ell$ instead of ${\mathfrak {C}}^h_{\ell ,\rho }$.

The following compactness lemma will be repeatedly used in the sequel.

Lemma 6.5

Let ${\mathfrak {C}}^h_\ell$ be a bounded cylinder, and let $\{Q_j\} \subseteq W^{1,2}_{\textrm{sym}}({\mathfrak {C}}^h_\ell ;{\mathbb S}^4)$ be a sequence such that each $Q_j$ is an equivariant local minimizer of ${\mathcal {E}}_{\lambda }$ in ${\mathfrak {C}}^h_\ell$ up to the top/bottom boundary and $Q_j=\textbf{e}_0$ on $\partial ^{\mathrm{=}} {\mathfrak {C}}^h_\ell$. If $\sup _j {\mathcal {E}}_{\lambda }(Q_j,{\mathfrak {C}}^h_\ell )<\infty$, then there exists a (not relabeled) subsequence such that $Q_j \rightarrow Q_*$ strongly in $W^{1,2}( {\mathfrak {C}}^h_\eta )$ for every $\eta \in (0,\ell )$, where $Q_* \in W^{1,2}_\textrm{sym}({\mathfrak {C}}^h_\ell ;{\mathbb S}^4)$ is an equivariant local minimizer of ${\mathcal {E}}_\lambda$ up to the top/bottom boundary satisfying $Q_*=\textbf{e}_0$ on $\partial ^{\mathrm{=}} {\mathfrak {C}}^h_\ell$.

Proof

Since the sequence $\{Q_j\}$ has equibounded ${\mathcal {E}}_\lambda$-energy, $\{Q_j\}$ is bounded in $W^{1,2}_\textrm{sym}({\mathfrak {C}}^h_\ell )$, whence the existence of a (not relabeled) subsequence and $Q_* \in W^{1,2}_\textrm{sym}({\mathfrak {C}}^h_\ell ;\mathbb {S}^4)$ such that $Q_j \rightharpoonup Q_*$ weakly in $W^{1,2}({\mathfrak {C}}^h_\ell )$. In addition, $Q_*=\textbf{e}_0$ on $\partial ^{\mathrm{=}} {\mathfrak {C}}^h_\ell$ by locality and weak continuity of the trace operator.

We now argue as in Lemma 5.9. Fix an arbitrary $r \in (0,\ell )$ and $\delta \in (0,\ell -r)$. Extracting a further subsequence if necessary, by Fatou’s lemma and Fubini’s theorem there exists $\eta \in (r, r+\delta )$ such that

$$\begin{aligned} \lim _{j \rightarrow \infty }\int _{\Gamma _\eta } \left| Q_j - Q_* \right| ^2\, d{\mathcal {H}}^2 = 0\quad \text {and}\quad \int _{\Gamma _\eta } |\nabla Q_j|^2 + |\nabla Q_*|^2\, d{\mathcal {H}}^2 \leqslant C, \end{aligned}$$

where $\Gamma _\eta =\partial ^{\textrm{lat}} {\mathfrak {C}}^h_{\eta }$ (see (5.27)), and $C > 0$ does not depend on j. Setting $\gamma _\eta :=\{(\eta , 0,x_3): |x_3|<h\}$, we observe that $\Gamma _\eta =\bigcup _{R\in \mathbb {S}^1} R\cdot \gamma _\eta$. By $\mathbb {S}^1$-equivariance, we deduce that the restriction of $Q_j$ to $\gamma _\eta$ is weakly convergent to $Q_*$ in $W^{1,2}(\gamma _\eta )$. By the compact embedding $W^{1,2}(\gamma _\eta )\hookrightarrow C^0(\overline{\gamma _\eta })$, we infer that $Q_j \rightarrow Q_*$ uniformly on $\overline{\gamma _\eta }$. By equivariance again, $Q_j \rightarrow Q_*$ uniformly on $\overline{\Gamma }_\eta$.

We fix an arbitrary ${\bar{Q}}\in W^{1,2}_{\textrm{sym}}({\mathfrak {C}}^h_r; \mathbb {S}^4)$ satisfying ${\bar{Q}}=Q_*$ on $\partial {\mathfrak {C}}^h_r$. We extend ${\bar{Q}}$ to ${\mathfrak {C}}^h_\eta$ setting ${\bar{Q}}=Q_*$ in ${\mathfrak {C}}^h_\eta \setminus {\mathfrak {C}}^h_r$, and we set $\sigma _j:= \Vert {Q}_j - {Q}_* \Vert _{L^\infty (\Gamma _\eta )} + 2^{-j}\rightarrow 0$. For j large enough so that $\sigma _j < 1$ and $r< (1-\sigma _j)\eta$, we define

$$\begin{aligned}{} & {} v_j (x):=\\{} & {} {\left\{ \begin{array}{ll} \displaystyle \frac{\left| x' \right| -(1-\sigma _j)\eta }{\sigma _j\eta } \left( {Q}_j\left( \eta \frac{x^\prime }{|x^\prime |},x_3\right) - {Q}_*\left( \eta \frac{x^\prime }{|x^\prime |},x_3\right) \right) + {Q}_*\left( \eta \frac{x^\prime }{|x^\prime |},x_3\right) &{} \text{ if } x\in {\mathfrak {C}}^h_{\eta } \setminus {\mathfrak {C}}^h_{(1-\sigma _j)\eta } ,\\ \displaystyle \bar{Q} \left( \frac{x'}{1-\sigma _j},x_3 \right) &{} \text{ if } x\in {\mathfrak {C}}^h_{(1-\sigma _j)\eta } . \end{array}\right. } \end{aligned}$$

Then $v_j\in W^{1,2}_{\textrm{sym}}({\mathfrak {C}}^h_\eta ; {\mathcal {S}}_0)$, $|v_j|=1$ in ${\mathfrak {C}}^h_{(1-\sigma _j)\eta }$, and $v_j = Q_j$ on $\partial {\mathfrak {C}}^h_\eta$ (indeed, $v_j = Q_j = \textbf{e}_0$ on $\partial ^= {\mathfrak {C}}^h_\eta$). Since $\sigma _j\rightarrow 0$, we have $|v_j| \rightarrow 1$ uniformly in ${\mathfrak {C}}^h_{\eta } {\setminus } {\mathfrak {C}}^h_{(1-\sigma _j)\eta }$, and thus $\Vert |v_j|-1\Vert _{L^\infty ({\mathfrak {C}}^h_{\ell })}\rightarrow 0$. In addition, $v_j \rightarrow \bar{Q}$ a.e. in ${\mathfrak {C}}^h_\eta$ because $\bar{Q}(\cdot ,x_3) \in C^0(\overline{\mathbb {D}_\eta })$ for a.e. $x_3$ by Lemma 2.10. For j large enough we have $|v_j|\geqslant 1/2$ and we can define the competitor $\widetilde{Q}_j:= v_j/|v_j| \in W^{1,2}_{\textrm{sym}}({\mathfrak {C}}^h_{\eta };\mathbb {S}^4)$ which satisfies $\widetilde{Q}_j =Q_j$ on $\partial {\mathfrak {C}}^h_{\eta }$. As in the proof of Lemma 5.9, we have

$$\begin{aligned} \int _{{\mathfrak {C}}^h_\eta } |\nabla \widetilde{Q}_j|^2 \, dx \leqslant \int _{{\mathfrak {C}}^h_\eta } |\nabla \bar{Q}|^2 \,dx + C \sigma _j, \end{aligned}$$

which implies that ${\mathcal {E}}_\lambda (\widetilde{Q}_j,{\mathfrak {C}}^h_\eta )\rightarrow {\mathcal {E}}_\lambda (\bar{Q},{\mathfrak {C}}^h_\eta )$ as $j\rightarrow \infty$. In addition, by minimality of $Q_j$ we have ${{\limsup _j}}{\mathcal {E}}_\lambda ({Q}_j,{\mathfrak {C}}^h_\eta )\leqslant {{\limsup _j}} {\mathcal {E}}_\lambda (\widetilde{Q}_j,{\mathfrak {C}}^h_\eta )$. Letting $j\rightarrow \infty$ yields ${\mathcal {E}}_\lambda ({Q}_*,{\mathfrak {C}}^h_\eta )\leqslant \liminf _j {\mathcal {E}}_\lambda ({Q}_j,{\mathfrak {C}}^h_\eta )\leqslant {\mathcal {E}}_\lambda (\bar{Q},{\mathfrak {C}}^h_\eta )$ by weak lower semicontinuity of ${\mathcal {E}}_\lambda$. Since ${\bar{Q}}=Q_*$ in ${\mathfrak {C}}^h_\eta \setminus {\mathfrak {C}}^h_r$, it implies that ${\mathcal {E}}_\lambda ({Q}_*,{\mathfrak {C}}^h_r)\leqslant {\mathcal {E}}_\lambda (\bar{Q},{\mathfrak {C}}^h_r)$ proving the minimality of $Q_*$ in ${\mathfrak {C}}^h_r$. As in the proof of Lemma 5.9 again, choosing ${\bar{Q}}=Q_*$ implies the strong $W^{1,2}$-convergence of $Q_j$ in ${\mathfrak {C}}^h_r$. $\square$

6.2 Sublinear energy growth and proof of Theorem 1.4

The next result is a key step in proving Theorem 1.4, in particular to control the asymptotic location of the biaxiallity sets.

Lemma 6.6

Let $\ell _j\rightarrow +\infty$ be an increasing sequence. For each $j\in \mathbb {N}$, let $Q_j \in W^{1,2}_\textrm{sym}({\mathfrak {C}}^h_{\ell _j};\mathbb {S}^4)$ be an equivariant local minimizer of ${\mathcal {E}}_{\lambda }$ in ${\mathfrak {C}}^h_{\ell _j}$ up to the top/bottom boundary satisfying $Q_j =\textbf{e}_0$ on $\partial ^{\mathrm{=}} {\mathfrak {C}}^h_{\ell _j}$. If ${\mathcal {E}}_\lambda (Q_j, {\mathfrak {C}}^h_{\ell _j}) = O(\ell _j)$ as $j \rightarrow \infty$, then there exists a constant ${\bar{\varepsilon }} > 0$ independent of j such that the following holds: for every $\varepsilon \in (0,{\bar{\varepsilon }})$, there exist $d_\varepsilon > 0$ and $j_\varepsilon \in \mathbb {N}$ such that

$$\begin{aligned} {\mathcal {E}}_\lambda \big (Q_j,B_{\ell _j-d_\varepsilon } \cap {\mathfrak {C}}^h_{\ell _j}\big ) \leqslant C_* \,\varepsilon (\ell _j-d_\varepsilon )\qquad \forall j\geqslant j_\varepsilon , \end{aligned}$$

(6.2)

where $C_*$ denotes a constant independent of j and $\varepsilon$. In particular,

$$\begin{aligned} {\mathcal {E}}_\lambda \big (Q_j,B_{\sigma \ell _j} \cap {\mathfrak {C}}^h_{\ell _j}\big ) = o(\ell _j)\quad \hbox { as}\ j\rightarrow \infty \end{aligned}$$

(6.3)

for every $\sigma \in (0,1)$.

Proof

By assumption, ${\mathcal {E}}_\lambda (Q_j,{\mathfrak {C}}^h_{\ell _j}) \leqslant \bar{C} \ell _j$ for some $\bar{C}>0$ independent of j. We claim that for every $\varepsilon \in (0,1/2)$, there exists an integer $j_\varepsilon \geqslant 1$ and $d_\varepsilon >1$ independent of j such that

$$\begin{aligned} \inf _{r\in (\ell _j-d_\varepsilon ,\ell _j)}\frac{1}{r}{\mathcal {E}}_\lambda (Q_j,\Gamma _r)<\varepsilon \qquad \forall j\geqslant j_\varepsilon , \end{aligned}$$

where $\Gamma _r:=\partial ^{\textrm{lat}}{\mathfrak {C}}^h_{r}$ (see (5.27)). Indeed, given $\varepsilon \in (0,1/2)$ and $j_\varepsilon \geqslant 1$ to be chosen, we have for $0<d\leqslant \ell _{j_\varepsilon }$ and $j\geqslant j_\varepsilon$,

$$\begin{aligned}{} & {} \bar{C} \geqslant \frac{1}{\ell _j}{\mathcal {E}}_\lambda \big (Q_j,{\mathfrak {C}}^h_{\ell _j} \setminus {\mathfrak {C}}^h_{\ell _j-d}\big ) = \frac{1}{\ell _j}\int _{\ell _j-d}^{\ell _j} \bigg (\frac{{\mathcal {E}}_\lambda (Q_j,\Gamma _t)}{t} \bigg ) t \,dt \\{} & {} \quad \geqslant \left( \inf _{r \in (\ell _j-d,\ell _j)} \frac{{\mathcal {E}}_\lambda (Q_j, \Gamma _r)}{r} \right) \frac{1}{\ell _j} \int _{\ell _j-d}^{\ell _j} t\,dt \geqslant \left( \inf _{r \in (\ell _j-d,\ell _j)} \frac{{\mathcal {E}}_\lambda (Q_j, \Gamma _r)}{r} \right) \frac{d}{2} , \end{aligned}$$

and the claim follows whenever we choose $d_\varepsilon > \frac{2\bar{C}}{\varepsilon }$ and $j_\varepsilon$ such that $\ell _{j_\varepsilon }\geqslant d_\varepsilon$.

As a consequence, for an arbitrary $\varepsilon \in (0,1/2)$ and $j\geqslant j_\varepsilon$, there exists $r^\varepsilon _j\in (\ell _j-d_\varepsilon ,\ell _j)$ such that

$$\begin{aligned} \frac{1}{r_j^\varepsilon }{\mathcal {E}}_\lambda (Q_j, \Gamma _{r_j^\varepsilon }) < \varepsilon . \end{aligned}$$

(6.4)

Note that $r_j^\varepsilon \rightarrow {{+}} \infty$ since $\ell _j\rightarrow {{+}}\infty$. From (6.4) and $\mathbb {S}^1$-equivariance, we infer that for $j\geqslant j_\varepsilon$,

$$\begin{aligned} \pi \int _{\gamma _{r_j^\varepsilon }} \left| \frac{\partial Q_j}{\partial x_3} \right| ^2 \,dx_3 = \frac{1}{r_j^\varepsilon } \int _{\Gamma _{r_j^\varepsilon }} \frac{1}{2}\left| \frac{\partial Q_j}{\partial x_3} \right| ^2 \,d {\mathcal {H}}^2 \leqslant \frac{1}{r_j^\varepsilon }{\mathcal {E}}_\lambda (Q_j, \Gamma _{r_j^\varepsilon }) < \varepsilon , \end{aligned}$$

where $\gamma _{r_j^\varepsilon }:=\{(r_j^\varepsilon , 0,x_3): |x_3|<h\}$. Since $Q_j(r_j^\varepsilon ,0,\pm h) = \textbf{e}_0$, we deduce (again by $\mathbb {S}^1$-equivariance) that

$$\begin{aligned} \Vert {Q}_j - \textbf{e}_0\Vert _{L^\infty (\Gamma _{r_j^\varepsilon })} \leqslant C_*\sqrt{h\varepsilon } \qquad \forall j\geqslant j_\varepsilon , \end{aligned}$$

(6.5)

for some universal constant $C_*>0$.

Next we define for $j \geqslant j_\varepsilon$ and $x\in {\mathfrak {C}}^h_{r_j^\varepsilon }$,

$$\begin{aligned} v_j^\varepsilon (x):= {\left\{ \begin{array}{ll} \displaystyle \big (|{x'}| - r_j^\varepsilon + 1\big ) \bigg ({{Q_j}}\left( r_j^\varepsilon \frac{x^\prime }{|x^\prime |},x_3\right) -\textbf{e}_0\bigg ) + \textbf{e}_0&{} \text{ if } x\in {\mathfrak {C}}^h_{r_j^\varepsilon } \setminus {\mathfrak {C}}^h_{r_j^\varepsilon -1}, \\ \textbf{e}_0&{} \text{ if } x\in {\mathfrak {C}}^h_{r_j^\varepsilon -1}. \end{array}\right. } \end{aligned}$$

Then $v_j^\varepsilon \in W^{1,2}_\textrm{sym}({\mathfrak {C}}^h_{r_j^\varepsilon };{\mathcal {S}}_0)$ satisfies $v_j^\varepsilon =Q_j$ on $\partial {\mathfrak {C}}^h_{r_j^\varepsilon }$, and $|v_j^\varepsilon |=1$ in ${\mathfrak {C}}^h_{r_j^\varepsilon -1}$. Moreover, combining (6.4) and (6.5), we obtain

$$\begin{aligned} \int _{{\mathfrak {C}}^h_{r_j^\varepsilon } \setminus {\mathfrak {C}}^h_{r_j^\varepsilon -1}} |\nabla v_j^\varepsilon |^2 \,dx\leqslant C \varepsilon r_j^\varepsilon , \end{aligned}$$

for some constant C independent of $\varepsilon$ and j.

Now we choose ${{\bar{\varepsilon }}}\in (0,1/2)$ in such a way that $C_*\sqrt{h{{\bar{\varepsilon }}}}{{<}}1/2$. Then, for $\varepsilon \in (0,{{\bar{\varepsilon }}})$ arbitrary, we have $|1-|v_j^\varepsilon ||\leqslant |v_j^\varepsilon -\textbf{e}_0|<1/2$ in ${\mathfrak {C}}^h_{r_j^\varepsilon }$ by (6.5). Thus we can define for $j\geqslant j_\varepsilon$,

$$\begin{aligned} \widetilde{Q}_j^\varepsilon :=\frac{v_j^\varepsilon }{|v^\varepsilon _j|}\in W^{1,2}_{\textrm{sym}}({\mathfrak {C}}^h_{r_j^\varepsilon };\mathbb {S}^4){{,}} \end{aligned}$$

which satisfies $\widetilde{Q}_j^\varepsilon =Q_j$ on $\partial {\mathfrak {C}}^h_{r_j^\varepsilon }$, and

$$\begin{aligned} \int _{{\mathfrak {C}}^h_{r_j^\varepsilon } \setminus {\mathfrak {C}}^h_{r_j^\varepsilon -1}} |\nabla \widetilde{Q}_j^\varepsilon |^2 \,dx \leqslant C \varepsilon r_j^\varepsilon \end{aligned}$$

(6.6)

for a further constant C independent of $\varepsilon$ and j. In addition, $|\widetilde{Q}_j^\varepsilon -\textbf{e}_0|\leqslant 3 |v_j^\varepsilon -\textbf{e}_0|\leqslant 3C_*\sqrt{h\varepsilon }$ in ${\mathfrak {C}}^h_{r_j^\varepsilon }$ once again by (6.5). Consequently,

$$\begin{aligned} W(\widetilde{Q}_j^\varepsilon )\leqslant C^\prime \varepsilon \quad \text {in } {\mathfrak {C}}^h_{r_j^\varepsilon }, \end{aligned}$$

(6.7)

still for a constant $C^\prime$ independent of $\varepsilon$ and j, by Taylor expansion of W near $\textbf{e}_0$ and choosing ${{\bar{\varepsilon }}}$ smaller if necessary.

By minimality of $Q_j$, we conclude from (6.6) and (6.7) that

$$\begin{aligned} {\mathcal {E}}_\lambda (Q_j,{\mathfrak {C}}^h_{r_j^\varepsilon }) \leqslant {\mathcal {E}}_\lambda (\widetilde{Q}_j^\varepsilon ,{\mathfrak {C}}^h_{r_j^\varepsilon })= {\mathcal {E}}_\lambda \big (\widetilde{Q}_j^\varepsilon ,{\mathfrak {C}}^h_{r_j^\varepsilon } \setminus {\mathfrak {C}}^h_{r_j^\varepsilon -1}\big ) \leqslant C \varepsilon r_j^\varepsilon , \end{aligned}$$

where $C > 0$ is still independent of j and $\varepsilon$. Noticing that $B_{r^\varepsilon _j} \cap {\mathfrak {C}}^h_{\ell _j} \subseteq {\mathfrak {C}}^h_{r^\varepsilon _j}$, we deduce from Remark  6.4 that

$$\begin{aligned} \frac{1}{\ell _j-d_\varepsilon }{\mathcal {E}}_\lambda \big (Q_j,B_{\ell _j-d_\varepsilon }\cap {\mathfrak {C}}^h_{\ell _j}\big )\leqslant \frac{1}{r^\varepsilon _j} {\mathcal {E}}_\lambda \big (Q_j,B_{r^\varepsilon _j}\cap {\mathfrak {C}}^h_{\ell _j}\big )\leqslant C\varepsilon , \end{aligned}$$

proving (6.2).

To complete the proof, we fix an arbitrary $\sigma \in (0,1)$. Then $\ell _j - d_\varepsilon > \sigma \ell _j$ for j large enough, and by Remark  6.4 again,

$$\begin{aligned} \frac{1}{\sigma \ell _j} {\mathcal {E}}_\lambda \big (Q_j,B_{\sigma \ell _j} \cap {\mathfrak {C}}^h_{\ell _j}\big ) \leqslant \frac{1}{\ell _j-d_\varepsilon }{\mathcal {E}}_\lambda \big (Q_j, B_{\ell _j-d_\varepsilon } \cap {\mathfrak {C}}^h_{\ell _j}\big ) \leqslant C \varepsilon \,. \end{aligned}$$

Then (6.3) follows from the arbitrariness of $\varepsilon$ letting $j\rightarrow \infty$. $\square$

The following rigidity result is an immediate consequence of Lemma 6.6.

Corollary 6.7

Let $Q \in W^{1,2}_{\textrm{loc}}({\mathfrak {C}}^h_\infty ;\mathbb {S}^4)$ be an equivariant local minimizer of ${\mathcal {E}}_{\lambda }$ in ${\mathfrak {C}}^h_\infty$ up to the top/bottom boundary satisfying $Q=\textbf{e}_0$ on $\partial ^{\mathrm{=}} {\mathfrak {C}}^h_{\infty }$. If ${\mathcal {E}}_\lambda (Q, {\mathfrak {C}}^h_\ell ) = O(\ell )$ as $\ell \rightarrow \infty$, then $Q\equiv \textbf{e}_0$.

Proof

Let $\ell _j\rightarrow \infty$ be an increasing sequence, and set $Q_j:= Q_{|{{\mathfrak {C}}^h_{\ell _j}}}$. Then $Q_j$ is an equivariant local minimizer of ${\mathcal {E}}_{\lambda }$ in ${\mathfrak {C}}^h_{\ell _j}$ up to the top/bottom boundary satisfying $Q=\textbf{e}_0$ on $\partial ^{\mathrm{=}} {\mathfrak {C}}^h_{\ell _j}$ and ${\mathcal {E}}_\lambda (Q_j,{\mathfrak {C}}^h_{\ell _j}) = O(\ell _j)$. According to Lemma 6.6, we have ${\mathcal {E}}_\lambda (Q_j,B_{\ell _j/2} \cap {\mathfrak {C}}^h_{ \ell _j}) = o(\ell _j)$. Let us now fix an arbitrary $\ell \gg h$. From Remark 6.4, we deduce that for j large enough so that $\ell _j>2\ell$,

$$\begin{aligned} 0 \leqslant \frac{1}{\ell }{\mathcal {E}}_\lambda \big (Q,B_\ell \cap {\mathfrak {C}}^h_\infty \big )= \frac{1}{\ell }{\mathcal {E}}_\lambda \big (Q,B_\ell \cap {\mathfrak {C}}^h_{\ell _j}\big ) \leqslant \frac{2}{ \ell _j}{\mathcal {E}}_\lambda \big (Q_j,B_{\ell _j/2} \cap {\mathfrak {C}}^h_{\ell _j}\big ) \rightarrow 0 \quad \text{ as } j \rightarrow \infty . \end{aligned}$$

Hence ${\mathcal {E}}_\lambda (Q,B_\ell \cap {\mathfrak {C}}^h_\infty )=0$. From the arbitraniness of $\ell$, it follows that Q is constant, and thus $Q \equiv \textbf{e}_0$ in view of its values on $\partial {\mathfrak {C}}^h_\infty$. $\square$

We are now ready to prove Theorem 1.4.

Proof of Theorem 1.4

Step 1. We start proving that $Q^{(n)} \rightarrow \textbf{e}_0$ strongly in $W^{1,2}({\mathfrak {C}}^h_\ell )$ for every $\ell >0$. By Lemma 6.2, we have ${\mathcal {E}}_\lambda (Q^{(n)},\Omega _n) \leqslant K \ell _n$ for a constant K independent of n. Given an arbitrary $\ell > h$, we consider n large enough in such a way that $\ell _n >2 \ell +\rho$. Then ${\mathfrak {C}}^h_\ell \subseteq B_{2\ell }\cap \Omega _n\subseteq B_{\ell _n-\rho } \cap \Omega _n$. Applying the monotonicity formula (6.1) we obtain

$$\begin{aligned} {\mathcal {E}}_\lambda (Q^{(n)},{\mathfrak {C}}^h_\ell ) \leqslant {\mathcal {E}}_\lambda \big (Q^{(n)},B_{2\ell }\cap \Omega _n\big ) \leqslant \frac{2\ell }{\ell _n-\rho } {\mathcal {E}}_\lambda \big (Q^{(n)},B_{\ell _n-\rho }\cap \Omega _n\big ) \leqslant \frac{2K\ell \ell _n}{\ell _n-\rho }\leqslant 4K \ell \,. \nonumber \\ \end{aligned}$$

(6.8)

In view of Lemma 6.5, we conclude that, up to a (not relabeled) subsequence, $Q^{(n)} \rightarrow Q_*$ strongly in $W^{1,2}({\mathfrak {C}}^h_{\ell })$ for every $0<\ell <\infty$, where $Q_* \in W^{1,2}_{\textrm{loc}}({\mathfrak {C}}^h_\infty ;\mathbb {S}^4)$ is an equivariant local minimizer of ${\mathcal {E}}_\lambda$ up to the top/bottom boundary satisfying $Q_*=\textbf{e}_0$ on $\partial ^{\mathrm{=}} {\mathfrak {C}}^h_\infty$. By lower semicontinuity of ${\mathcal {E}}_\lambda$, letting $n\rightarrow \infty$ in (6.8) yields ${\mathcal {E}}_\lambda (Q_*,{\mathfrak {C}}^h_\ell ) \leqslant 4K\ell$. Hence Corollary 6.7 applies and $Q_*\equiv \textbf{e}_0$. By uniqueness of the limit, we now infer that the full sequence $\{Q^{(n)}\}$ strongly converges to $\textbf{e}_0$ in $W^{1,2}({\mathfrak {C}}^h_{\ell })$ for every $0<\ell <\infty$.

Step 2. We now accomplish the proof of (ii) proving that $\textrm{sing}(Q^{(n)})=\emptyset$ for n large enough and that $Q^{(n)}$ converges smoothly to $\textbf{e}_0$ locally in $\overline{{\mathfrak {C}}^h_\infty }$. To this purpose, we fix an arbitrary $\ell >h$ and we consider n large enough so that $\ell _n\gg \ell +h$.

Case 1: convergence near $\partial ^={\mathfrak {C}}^h_\ell$. We fix an arbitrary point $x_0\in \partial ^={\mathfrak {C}}^h_\ell$. Given a radius $0<r_*<h/2$, $B_{2r_*}(x_0)\cap \Omega _n\subseteq {\mathfrak {C}}^h_{\ell +h}$ is a half ball for n large enough and Remark 3.8 applies since $Q^{(n)}=\textbf{e}_0$ on $B_{2r_*}(x_0)\cap \partial \Omega _n=B_{2r_*}(x_0)\cap \partial ^={\mathfrak {C}}^h_{\ell +h}$. We fix a radius $r_0\in (0,r_*/4)$ such that the conclusion of Remark 3.8 holds (it only depends on $\lambda$). According to Step 1, we have ${\mathcal {E}}_\lambda (Q^{(n)},{\mathfrak {C}}^h_{\ell +h}\big )\rightarrow 0$ as $n\rightarrow \infty$. Therefore, $\frac{1}{r_0}{\mathcal {E}}_\lambda (Q^{(n)},B_{r_0}(x_0)\cap \Omega _n)\leqslant \varvec{\varepsilon }^\sharp _{\textrm{bd}}/2$ whenever n is large enough (independently of $x_0\in \partial ^={\mathfrak {C}}^h_\ell$), where $\varvec{\varepsilon }^\sharp _{\textrm{bd}}>0$ is the universal constant provided by Remark 3.8. Then Remark 3.8 tells us that $Q^{(n)}$ in smooth and bounded in $C^k(B_{\varvec{\kappa }^\sharp r_0/2}(x_0)\cap {{\overline{\Omega _n}}})$ for every $k\in \mathbb {N}$ (independently of $x_0$), where $\varvec{\kappa }^\sharp \in (0,1)$ is a universal constant. By arbitrariness of $x_0$, we deduce that $\textrm{sing}(Q^{(n)})\cap \{h-\delta _*{{<}}|x_3|\leqslant h\}=\emptyset$ for n large enough (recall that $\textrm{sing}(Q^{(n)})\subseteq \{x_3-\text {axis}\}$) and that $Q^{(n)}$ is bounded in $C^k({{\overline{{\mathfrak {C}}^h_\ell }}}\cap \{h-\delta _*{{<}}|x_3|\leqslant h\})$ for every $k\in \mathbb {N}$ with $\delta _*:=\varvec{\kappa }^\sharp r_0/2>0$. As a consequence, $Q^{(n)}\rightarrow \textbf{e}_0$ in $C^k({{\overline{{\mathfrak {C}}^h_\ell }}}\cap \{h-\delta _*{{<}}|x_3|\leqslant h\})$ for every $k\in \mathbb {N}$.

Case 2: convergence in the interior of ${\mathfrak {C}}^h_\ell$. We fix a radius $0<r_1<\delta _*$. In view of Step 1, we have ${\mathcal {E}}_\lambda (Q^{(n)},{\mathfrak {C}}^h_{\ell +\delta _*})\leqslant (\varvec{\varepsilon }_{\textrm{in}}r_1)/8$ for n large enough, where $\varvec{\varepsilon }_{\textrm{in}}>0$ is the universal constant provided by Proposition 3.5. Choosing $r_1$ small enough (depending only on $\lambda$) and an arbitrary point $x_0\in {\mathfrak {C}}^h_\ell \cap \{|x_3|\leqslant h-\delta _*\}$, we then have $\frac{1}{r_1}{\mathcal {E}}_\lambda \big (Q^{(n)},B_{r_1}(x_0)\big )\leqslant \varvec{\varepsilon }_{\textrm{in}}/8$ so that Proposition 3.5 applies. It shows that $Q^{(n)}$ is smooth and bounded in $C^k(B_{r_1/16}(x_0))$ for every $k\in \mathbb {N}$ (independently of $x_0$). Once again, it implies that $Q^{(n)}$ is smooth in ${\mathfrak {C}}^h_\ell \cap \{|x_3|\leqslant h-\delta _*\}$ for n large enough, so that $\textrm{sing}(Q^{(n)})=\emptyset$, and $Q^{(n)}\rightarrow \textbf{e}_0$ in $C^k({\mathfrak {C}}^h_\ell \cap \{|x_3|\leqslant h-\delta _*\})$ for every $k\in \mathbb {N}$.

Step 3: proof of (i). We observe that the assumptions ($HP_0$)–($HP_3$) from [11, 12] are satisfied by $Q^{(n)}$ for n large enough. Indeed, $\textrm{sing}(Q^{(n)})=\emptyset$ for n large enough so that ($HP_0$) holds (recall Theorem 3.2). Since the boundary condition $Q^{(n)}_{\textrm{b}}$ is positively uniaxial, ($HP_1$) holds. Then, $\Omega _n$ being a topological ball and $Q^{(n)}_\textrm{b}$ the homeotropic boundary data (2.4), ($HP_2$) and ($HP_3$) trivially hold. Hence $Q^{(n)}$ is a torus minimizer in the sense of [12, Definition 7.6] (for n large), and [12, Theorem 1.4] provides the announced properties of the function $\beta _n:=\widetilde{\beta }\circ Q^{(n)}$.

Step 4. Now it only remains to prove (iii). To this purpose, we fix an arbitrary $t\in [-1,1)$ and, since $\widetilde{\beta }(\textbf{e}_0)=1$, we infer from the previous step that there is an integer $\bar{n}_t$ such that $\{\beta _n \leqslant t \} \cap {\mathfrak {C}}^h_{2\,h} = \emptyset$ for all $n \geqslant \bar{n}_t$.

Since $Q^{(n)}$ is minimizing ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}_{Q_{\textrm{b}}}^{\textrm{sym}}(\Omega _n)$, Lemma 6.6 applies in ${\mathfrak {C}}^h_{\ell _n-\rho }$, and we consider the constant ${{\bar{\varepsilon }}}>0$ (independent of n) provided by this lemma. We fix a value $\varepsilon =\varepsilon (t)$ to be chosen later such that

$$\begin{aligned} 0<\varepsilon <\frac{1}{2}\min \big \{\varvec{\varepsilon }^\sharp _\textrm{bd}/(2C_*), \varvec{\varepsilon }_{\textrm{in}}/(8C_*),{{\bar{\varepsilon }}}\big \}. \end{aligned}$$

(6.9)

where $C_*$ denotes the constant in inequality 6.2. According to Lemma 6.6, we can find $d_\varepsilon >0$ and an integer $n_\varepsilon \geqslant {\bar{n}}_t$ such that

$$\begin{aligned} {\mathcal {E}}_\lambda \big (Q^{(n)}, B_{\ell _n-\rho -d_\varepsilon } \cap {\mathfrak {C}}^h_{\ell _n-\rho }\big ) \leqslant C_*\varepsilon (\ell _n-\rho -d_\varepsilon )\qquad \forall n\geqslant n_\varepsilon , \end{aligned}$$

(6.10)

Enlarging $n_\varepsilon$ and $d_\varepsilon$ if necessary (see the proof of Lemma 6.6), we can assume that $\ell _n>2d_\varepsilon +\rho +h$ for $n\geqslant n_\varepsilon$, and $d_\varepsilon >2\,h+\rho$ (so that $B_{2h}(x)\cap \partial B_{\ell _n-\rho -d_\varepsilon }=\emptyset$ for every $x\in B_{\ell _n-2d_{\varepsilon }}$).

Let us now fix a point $x_*\in B_{\ell _n-2d_\varepsilon } \cap (\overline{{\mathfrak {C}}^h_{\ell _n-\rho }}{\setminus } {\mathfrak {C}}^h_{2\,h})$ (possibly depending on n) that either belongs to $\partial ^={{\mathfrak {C}}^h_{\ell _n-\rho }}$ or to ${\mathfrak {C}}^h_{\ell _n-\rho }\cap \{|x_3|\leqslant h-\delta _*\}$. By $\mathbb {S}^1$-equivariance, we may assume without loss of generality that $x_*=(x_{*,1},x_{*,2},x_{*,3})$ satisfies $x_{*,2}=0$ and $x_{*,1}\geqslant 2\,h$. If $x_*\in \partial ^={{\mathfrak {C}}^h_{\ell _n-\rho }}$, we set $s:=r_0\in (0,h)$, and $s:=r_1\in (0,{{\delta _*}})$ if $x_*\in {\mathfrak {C}}^h_{\ell _n-\rho }\cap \{|x_3|\leqslant h-\delta _*\}$ (note that $B_{r_1}(x_*)\subseteq {\mathfrak {C}}^h_{\ell _n-\rho }$ in this case). Next we denote $\ell _*:=x_{*,1}\in [2h,\ell _n-2d_\varepsilon )$, $\Sigma ^*_s:=B_s(x_*)\cap {{\mathfrak {C}}^h_{\ell _n-\rho }}\cap \{x_2=0\}$, and we consider the sets

$$\begin{aligned} T^*_s:= \displaystyle \bigcup _{\phi \in \left( -\frac{2s}{\ell _*},\frac{2s}{\ell _*}\right) } R_\phi \cdot \Sigma ^{*}_s\;\,\,\text { and }\,\,\; {\mathfrak {T}}^{*}:= \displaystyle \bigcup _{\phi \in \left( 0,2\pi \right) } R_\phi \cdot \Sigma ^{*}_s. \end{aligned}$$

Notice that $B_s(x_*)\cap {{\mathfrak {C}}^h_{\ell _n-\rho }}\subseteq T^*_s$ and ${\mathfrak {T}}^{*}\subseteq B_{\ell _*+2\,h}\cap {{\mathfrak {C}}^h_{\ell _n-\rho }}$. Using the $\mathbb {S}^1$-equivariance and the monotonicity formula from Lemma 6.1, we derive that

$$\begin{aligned}{} & {} \frac{1}{s}{\mathcal {E}}_\lambda \big (Q^{(n)}, B_s(x_*) \cap {\mathfrak {C}}^h_{\ell _n-\rho }\big ) \leqslant \frac{1}{s} {\mathcal {E}}_\lambda \big (Q^{(n)},T^*_s) = \frac{2}{\pi \ell _*} {\mathcal {E}}_\lambda (Q^{(n)}, {\mathfrak {T}}^{*}) \nonumber \\{} & {} \quad \leqslant \frac{4}{\pi }\cdot \frac{1}{\ell _*+2h} {\mathcal {E}}_\lambda \big (Q^{(n)},B_{\ell _*+2h} \cap {\mathfrak {C}}^h_{\ell _n-\rho }\big ) \leqslant \frac{2}{\ell _n-\rho -d_\varepsilon }{\mathcal {E}}_\lambda \big (Q^{(n)}, B_{\ell _n-\rho -d_\varepsilon }\cap {\mathfrak {C}}^h_{\ell _n-\rho }\big ).\nonumber \\ \end{aligned}$$

(6.11)

In view of (6.10) and our choice of $\varepsilon$, we conclude that for $n\geqslant n_\varepsilon$,

$$\begin{aligned} \frac{1}{s}{\mathcal {E}}_\lambda \big (Q^{(n)}, B_s(x_*) \cap {\mathfrak {C}}^h_{\ell _n-\rho }\big ) \leqslant \min \big \{\varvec{\varepsilon }^\sharp _{\textrm{bd}}/2, \varvec{\varepsilon }_{\textrm{in}}/8\big \}. \end{aligned}$$

As in Step 2, by Proposition 3.5 and Remark 3.8, it implies that $|\nabla Q^{(n)}|\leqslant M$ in $B_{\delta _*}(x_*)$ if $x_*\in \partial ^={{\mathfrak {C}}^h_{\ell _n-\rho }}$, and $|\nabla Q^{(n)}|\leqslant M$ in $B_{r_1/16}(x_*)$ if $x_*\in {\mathfrak {C}}^h_{\ell _n-\rho }\cap \{|x_3|\leqslant h-\delta _*\}$, where M denotes a constant depending only on $\lambda$ and h. By arbitrariness of $x_*$ and in view of Step 2, we conclude that for $n\geqslant n_\varepsilon$,

$$\begin{aligned} |\nabla Q^{(n)}|\leqslant M\quad \text {in }B_{\ell _n-2d_\varepsilon } \cap {\mathfrak {C}}^h_{\ell _n-\rho } , \end{aligned}$$

(6.12)

for some constant M depending only on $\lambda$ and h.

We now claim that a suitable choice of $\varepsilon =\varepsilon (t)$ yields

$$\begin{aligned} \{\beta _n\leqslant t\}\cap (B_{\ell _n-2d_\varepsilon } \cap {\mathfrak {C}}^h_{\ell _n-\rho })=\emptyset \qquad \forall n\geqslant n_\varepsilon . \end{aligned}$$

(6.13)

To prove this claim, we assume by contradiction that for $n\geqslant n_\varepsilon$ (more precisely, for a not relabeled subsequence), there exists $x_t\in B_{\ell _n-2d_\varepsilon } \cap {\mathfrak {C}}^h_{\ell _n-\rho }$ such that $\beta _n(x_t)\leqslant t$. Since $n_\varepsilon \geqslant {\bar{n}}_t$, we must have $x_t\not \in {\mathfrak {C}}^h_{2\,h}$. In view of (6.12), we can find a radius $\tau \in (0,h)$ depending only on t, $\lambda$, and h such that $\beta _n\leqslant \frac{1+t}{2}$ in $B_\tau (x_t)\cap {\mathfrak {C}}^h_{\ell _n-\rho }$. By $\mathbb {S}^1$-equivariance, it implies that $\beta _n\leqslant \frac{1+t}{2}$ in the set

$$\begin{aligned} {\mathfrak {T}}^{t}:= \displaystyle \bigcup _{\phi \in \left( 0,2\pi \right) } R_\phi \cdot \big (B_\tau (x_t)\cap {\mathfrak {C}}^h_{\ell _n-\rho }\big ). \end{aligned}$$

Note that the volume of ${\mathfrak {T}}^{t}$ is at least half of the volume of the solid torus $\bigcup _{\phi \in \left( 0,2\pi \right) } R_\phi \cdot B_\tau (x_t)$. Setting $\ell _t:=|x^\prime _t|$ with $x_t=:(x_t^\prime ,x_{t,3})$, we thus have

$$\begin{aligned} \frac{1}{\ell _t}\int _{ {\mathfrak {T}}^{t}}W(Q^{(n)})\,dx \geqslant \pi ^2\tau ^2\frac{1-t}{6\sqrt{6}}=:c_t\qquad \forall n\geqslant n_\varepsilon . \end{aligned}$$

(6.14)

In addition to (6.9), we now choose $\varepsilon$ such that

$$\begin{aligned} \varepsilon < \frac{\lambda c_t}{2C_*}. \end{aligned}$$

As in (6.11), it follows from (6.10) and (6.14) that for $n\geqslant n_\varepsilon$,

$$\begin{aligned}{} & {} \lambda c_t\leqslant \frac{1}{\ell _t} {\mathcal {E}}_\lambda (Q^{(n)}, {\mathfrak {T}}^{t}) \leqslant \frac{2}{\ell _t+2h} {\mathcal {E}}_\lambda \big (Q^{(n)},B_{\ell _t+2h} \cap {\mathfrak {C}}^h_{\ell _n-\rho }\big ) \\{} & {} \quad \leqslant \frac{2}{\ell _n-\rho -d_\varepsilon }{\mathcal {E}}_\lambda \big (Q^{(n)}, B_{\ell _n-\rho -d_\varepsilon }\cap {\mathfrak {C}}^h_{\ell _n-\rho }\big )\leqslant C_*\varepsilon <\lambda c_t, \end{aligned}$$

a contradiction proving (6.13). Setting $d_t:=2d_\varepsilon +h$ and noticing that ${\mathfrak {C}}^h_{\ell _n-d_t}\subseteq B_{\ell _n-2d_\varepsilon } \cap {\mathfrak {C}}^h_{\ell _n-\rho }$, the conclusion follows with $n_t:=n_\varepsilon$. $\square$

6.3 Intermediate cylinders and coexistence results

The purpose of this subsection is to prove coexistence of smooth/torus and singular/split minimizers for intermediate cylinders. As a first step, we establish in Propositions 6.8 and 6.10 the persistence of regularity and persistence of singularities properties when changing the shape of a smoothed cylinder.

Proposition 6.8

(persistence of regularity) Let $h,\ell _\flat ,\rho >0$ be fixed with $0<4\rho<\ell _\flat < h$, and $\{\ell _n\}$ a sequence of positive numbers such that $\ell _n\geqslant 3 \ell _\flat$. Assume that $\ell _n\rightarrow \ell _*$ as $n\rightarrow \infty$. Setting $\Omega _\flat :={\mathfrak {C}}^h_{\ell _\flat ,\rho }$, $\Omega _n:={\mathfrak {C}}^h_{\ell _n,\rho }$, and $\Omega _*:={\mathfrak {C}}^h_{\ell _*,\rho }$ as well as $Q^{(n)}_\textrm{b}$ and $Q^*_{\textrm{b}}$ to be the corresponding homeotropic boundary conditions given by (2.4), let $Q_n$ and $Q_*$ be minimizers of ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}^\textrm{sym}_{Q_{\textrm{b}}^{(n)}}(\Omega _n)$ and ${\mathcal {A}}^{\textrm{sym}}_{Q_\textrm{b}^{*}}(\Omega _*)$ respectively. Assume that $Q_n\rightarrow Q_*$ strongly in $W^{1,2}(\Omega _{\flat })$ as $n\rightarrow \infty$.

• (i) If $\textrm{sing}(Q_*)=\emptyset$, then there exists an integer $n_*$ such that $\textrm{sing}(Q_n)=\emptyset$ for every $n\geqslant n_*$.

• (ii) If $\textrm{sing}(Q_n)=\emptyset$ for every integer n, then $\textrm{sing}(Q_*)=\emptyset$.

Proof

To simplify the notation, we write $\Omega _{\flat /2}:={\mathfrak {C}}^h_{\ell _\flat /2,\rho }$. Since $\partial \Omega _{\flat /2}\setminus \{|x_3|=h\}\subseteq \Omega _\flat$, the restrictions of $Q_n$ and $Q_*$ to $\partial \Omega _{\flat /2}$ belong at least to $C^2(\partial \Omega _{\flat /2})$ by Theorem 3.2 and Corollary 3.7 (applied at balls centered on $\partial \Omega _{\flat /2}\cap \{|x_3|=h\}$). To prove the proposition, we only have to show that $Q_n\rightarrow Q_*$ in $C^2(\partial \Omega _{\flat /2})$. Indeed, once this $C^2$-convergence is established, the conclusion follows from Corollary 3.10 in the domain $\Omega _{\flat /2}$.

First, we observe that for $\ell \leqslant 2\ell _\flat$, we have ${\mathfrak {C}}^h_{\ell }\subseteq \Omega _n$, so that $\partial {\mathfrak {C}}^h_{\ell }\cap \partial \Omega _n= \partial ^= {\mathfrak {C}}^h_{\ell }$. Setting $r_*:=\ell _\flat /2$, it implies that for every $x_*=(x_{*,1},x_{*,2},x_{*,3})\in \partial ^= {\mathfrak {C}}^h_{\ell _\flat }$, the set $\Omega _n\cap B_{2r_*}(x_*)$ is a half ball and $Q^{(n)}_{\textrm{b}}=\textbf{e}_0$ on $\partial \Omega _n\cap B_{2r_*}(x_*)$ so that Remark 3.8 applies.

By Theorem 3.2, $Q_*$ is smooth in a neighborhood of $\partial \Omega _*$. Therefore, we can find $r_1\in (0,r_*/4)$ (depending on $\lambda$) such that the conclusion of Remark 3.8 holds and

$$\begin{aligned} \frac{1}{r_1}\int _{B_{r_1}(x_0)\cap \Omega _{{*}}}|\nabla Q_*|^2\,dx\leqslant \frac{\varvec{\varepsilon }^\sharp _{\textrm{bd}}}{2} \quad \hbox { for every}\ x_0\in \partial ^= {\mathfrak {C}}^h_{3\ell _\flat /4}, \end{aligned}$$

where the universal constant $\varvec{\varepsilon }^\sharp _\textrm{bd}>0$ is given by Remark 3.8. Then we consider a finite covering of $\partial ^= {\mathfrak {C}}^h_{3\ell _\flat /4}$ by open balls $B_{\varvec{\kappa }^\sharp r_1/2}(x_j)$, $j=1,\ldots , J$, with $x_j \in \partial ^= {\mathfrak {C}}^h_{3\ell _\flat /4}$ and $\varvec{\kappa }^\sharp \in (0,1)$ the further universal constant given by Remark 3.8. Since $Q_n\rightarrow Q_*$ strongly in $W^{1,2}(\Omega _{\flat })$, we have for n large enough,

$$\begin{aligned} \frac{1}{r_1}\int _{B_{r_1}(x_j)\cap \Omega _n}|\nabla Q_n|^2\,dx\leqslant \varvec{\varepsilon }^\sharp _{\textrm{bd}} \quad \hbox { for every}\ j=1,\ldots ,J. \end{aligned}$$

Applying Remark 3.8, we deduce that $Q_n$ is bounded in $C^{2,\alpha }(B_{\varvec{\kappa }^\sharp r_1/2}(x_j)\cap \Omega _n)$ for every $\alpha \in (0,1)$ and each $j=1,\ldots ,J$. Hence $Q_n$ is bounded in the $C^{2,\alpha }$-topology in

$$\begin{aligned} L_\delta :=\overline{{\mathfrak {C}}^h_{3\ell _\flat /4}}\cap \big \{h-\delta \leqslant |x_3|\leqslant h\big \} \end{aligned}$$

for some $\delta \in (0,\varvec{\kappa }^\sharp r_1/2)$.

By Theorem 3.2 again, $Q_*$ is smooth away from $\{x_3\text {-axis}\}$. Hence we can find $r_2\in (0,\delta /4)$ such that

$$\begin{aligned} \frac{1}{r_2}\int _{B_{r_2}(x_0)}|\nabla Q_*|^2\,dx\leqslant \frac{\varvec{\varepsilon }_{\textrm{in}}}{8}\quad \hbox { for every}\ x_0\in \big (\overline{{\mathfrak {C}}^h_{3\ell _\flat /4}}\setminus {\mathfrak {C}}^h_{\ell _\flat /4}\big )\cap \big \{|x_3|\leqslant h-\delta /2\big \}, \end{aligned}$$

where $\varvec{\varepsilon }_{\textrm{in}}>0$ is the universal constant given by Proposition 3.5. Choosing $r_2$ small enough (depending on $\lambda$), and using the strong convergence in $W^{1,2}(\Omega _\flat )$ of $Q_n$ toward $Q_*$ combined with a covering argument (as above), we conclude from Proposition 3.5 that $Q_n$ is bounded in the $C^{2,\alpha }$-topology in $\big (\overline{{\mathfrak {C}}^h_{3\ell _\flat /4}}{\setminus } {\mathfrak {C}}^h_{\ell _\flat /4}\big )\cap \big \{|x_3|\leqslant h-\delta /2\big \}$ for every $\alpha \in (0,1)$.

To summarize, $Q_n$ is thus bounded in the $C^{2,\alpha }$-topology in the set

$$\begin{aligned} L_\delta \cup \bigg ((\overline{{\mathfrak {C}}^h_{3\ell _\flat /4}}\setminus {\mathfrak {C}}^h_{\ell _\flat /4}\big )\cap \big \{|x_3|\leqslant h-\delta /2\big \}\bigg )=L_\delta \cup \big (\overline{{\mathfrak {C}}^h_{3\ell _\flat /4}}\setminus {\mathfrak {C}}^h_{\ell _\flat /4}\big )=:N_\delta . \end{aligned}$$

From the strong $W^{1,2}(\Omega _\flat )$-convergence to $Q_*$, we conclude that $Q_n\rightarrow Q_*$ in $C^2(N_\delta )$. Observing that $\partial \Omega _{\flat /2}\subseteq N_\delta$, the conclusion follows. $\square$

Proposition 6.9

(persistence of singularities) Let $Q_n$ and $Q_*$ be as in Proposition 6.8. If $\textrm{sing}(Q_*)=\{a_1^*,\ldots ,a_K^*\}$, then there exists an integer $n_*$ such that for every $n\geqslant n_*$, $\textrm{sing}(Q_n)=\{a_1^n,\ldots ,a_K^n\}$ for some distinct points $a_1^n,\ldots ,a_K^n$ satisfying $|a^n_j-a^*_j|\rightarrow 0$ as $n\rightarrow \infty$.

Proof

As in the proof of Proposition 6.8, $Q_n\rightarrow Q_*$ in $C^2(\partial \Omega _{\flat /2})$, and the conclusion follows from Corollary 3.13 in the domain $\Omega _{\flat /2}$. $\square$

In combination with the previous propositions, we now provide the required compactness property of minimizers as $\Omega _n\rightarrow \Omega _*$.

Lemma 6.10

Under the assumptions (and notations) of Proposition 6.8, assume that $\ell _n \rightarrow \ell _*$ as $n \rightarrow \infty$. There exists a (not relabeled) subsequence and $Q_*$ minimizing ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}^\textrm{sym}_{Q_{\textrm{b}}^{*}}(\Omega _{*})$ such that $Q_n\rightarrow Q_*$ strongly in $W^{1,2}(\Omega _{\flat })$ as $n\rightarrow \infty$.

Proof

Notice that, by our choice of the parameters, we have $\{x\in \Omega _n: \ell _\flat \leqslant r< 2\ell _\flat \}={\mathfrak {C}}^h_{2\ell _\flat }{\setminus } {\mathfrak {C}}^h_{\ell _\flat }$ where $r^2:=x_1^2+x_2^2$, and the mapping $\Phi _n:{\overline{\Omega }}_n\rightarrow {\overline{\Omega }}_*$ given in cylindrical coordinates by

$$\begin{aligned} \Phi _n(r,x_3):={\left\{ \begin{array}{ll} (r,x_3) &{} \hbox { if}\ r<\ell _\flat ,\\ (\sigma _n r-\tau _n,x_3) &{} \hbox { if}\ \ell _\flat \leqslant r<2\ell _\flat ,\\ (r+\tau _n,x_3) &{} \hbox { if}\ 2\ell _\flat \leqslant r\leqslant \ell _n, \end{array}\right. } \quad \text {with }\sigma _n:=1+\frac{\ell _*-\ell _n}{\ell _\flat }\text { and }\tau _n:=\ell _*-\ell _n, \nonumber \\ \end{aligned}$$

(6.15)

is one-to-one and biLipschitz, $\mathbb {S}^1$-equivariant and such that $\Phi _n(\overline{{\mathfrak {C}}^h_{2 \ell _\flat }} {\setminus } {\mathfrak {C}}^h_{\ell _\flat }) = \overline{{\mathfrak {C}}^h_{2 \ell _\flat +\tau _n}} {\setminus } {\mathfrak {C}}^h_{\ell _\flat }$.

For an arbitrary map ${\widehat{Q}} \in {\mathcal {A}}_{Q_\textrm{b}^{(n)}}(\Omega _n)$, we define ${\widehat{Q}}_n:= {\widehat{Q}} \circ \Phi _n^{-1}$ and we observe that ${\widehat{Q}}_n \in {\mathcal {A}}_{Q_{\textrm{b}}^*}(\Omega _*)$. Combining the chain rule, a change of variables, and (6.15) we obtain

$$\begin{aligned} \frac{1}{C_n}{\mathcal {E}}_\lambda ({{{\widehat{Q}}}},\Omega _n)\leqslant {\mathcal {E}}_\lambda ({{{\widehat{Q}}_n}},\Omega _*)\leqslant C_n {\mathcal {E}}_\lambda ({{{\widehat{Q}}}},\Omega _n), \end{aligned}$$

(6.16)

for a constant $C_n\rightarrow 1$ as $n\rightarrow \infty$ depending only on $\Phi _n$. In addition, we notice that, if ${\widehat{Q}} \in {\mathcal {A}}^{\textrm{sym}}_{Q_n}(\Omega _n)$, then ${\widehat{Q}}_n \in {\mathcal {A}}^{\textrm{sym}}_{Q_{\textrm{b}}^*}(\Omega _*)$ because the $\Phi _n$’s are equivariant. Therefore, testing the minimality of $Q_n$ with the 0-homogenous extension of $Q^{(n)}_{\textrm{b}}$, we infer from direct computations that $\sup _n{\mathcal {E}}_\lambda (Q_n,\Omega _n)<\infty$, and thus, defining $\widetilde{Q}_n:= Q_n \circ \Phi _n^{-1}$ and using (6.16) with ${\widehat{Q}}_n = \widetilde{Q}_n$, it follows $\sup _n{\mathcal {E}}_\lambda (\widetilde{Q}_n,\Omega _*)<\infty$. As a consequence, we can find a (not relabeled) subsequence such that ${\widetilde{Q}}_n\rightharpoonup Q_*$ weakly in $W^{1,2}(\Omega _*)$. Since $\widetilde{Q}_n |_{\partial \Omega _*} = Q_{\textrm{b}}^*$ independently of n and since the symmetry and unit norm constraints are weakly closed, we have $Q_*\in {\mathcal {A}}^{\textrm{sym}}_{Q_{\textrm{b}}^{*}}(\Omega _*)$. In addition, by lower semi-continuity of the energy,

$$\begin{aligned} {\mathcal {E}}_\lambda (Q_*,\Omega _*)\leqslant \liminf _{n\rightarrow \infty } {\mathcal {E}}_\lambda ({\widetilde{Q}}_n,\Omega _*) . \end{aligned}$$

(6.17)

On the other hand, as above we have $Q_*\circ \Phi _n\in {\mathcal {A}}^{\textrm{sym}}_{Q_{\textrm{b}}^{(n)}}(\Omega _n)$, and the minimality of $Q_n$ together with (6.16) applied twice (once with ${\widehat{Q}}_n = \widetilde{Q}_n$ and once with $Q_* \circ \Phi _n$ in place of ${\widehat{Q}}$) yields

$$\begin{aligned} \frac{1}{C_n} {\mathcal {E}}_\lambda ({\widetilde{Q}}_n,\Omega _*) \leqslant {\mathcal {E}}_\lambda (Q_n,\Omega _n)\leqslant {\mathcal {E}}_\lambda (Q_*\circ \Phi _n,\Omega _n)\leqslant C_n {\mathcal {E}}_\lambda (Q_*,\Omega _*). \end{aligned}$$

Since $C_n\rightarrow 1$, taking the $\limsup _n$ above we deduce from (6.17) that $\lim _n {\mathcal {E}}_\lambda (\widetilde{Q}_n,\Omega _*)={\mathcal {E}}_\lambda (Q_*,\Omega _*)$. By the compact embedding $W^{1,2}(\Omega _*)\hookrightarrow L^4(\Omega _*)$, we have $W({\widetilde{Q}}_n)\rightarrow W(Q_*)$ strongly in $L^1(\Omega _*)$. Hence, $\int _{\Omega _*}|\nabla {\widetilde{Q}}_n|^2\,dx\rightarrow \int _{\Omega _*}|\nabla Q_*|^2\,dx$ so that ${\widetilde{Q}}_n\rightarrow Q_*$ strongly in $W^{1,2}(\Omega _*)$. Since ${\widetilde{Q}}_n=Q_n$ in $\Omega _\flat \subseteq \Omega _*$, we conclude that $Q_n\rightarrow Q_*$ strongly in $W^{1,2}(\Omega _\flat )$.

It now remains to show the minimality of $Q_*$. To this purpose, let us fix an arbitrary competitor $Q\in {\mathcal {A}}^{\textrm{sym}}_{Q_\textrm{b}^{*}}(\Omega _*)$. Once again, we observe that $Q\circ \Phi _n\in {\mathcal {A}}^{\textrm{sym}}_{Q_{\textrm{b}}^{(n)}}(\Omega _n)$, and by minimality of $Q_n$ along with (6.16),

$$\begin{aligned} \frac{1}{C_n} {\mathcal {E}}_\lambda ({\widetilde{Q}}_n,\Omega _*) \leqslant {\mathcal {E}}_\lambda (Q_n,\Omega _n)\leqslant {\mathcal {E}}_\lambda (Q\circ \Phi _n,\Omega _n)\leqslant C_n {\mathcal {E}}_\lambda (Q,\Omega _*). \end{aligned}$$

Letting $n\rightarrow \infty$, we thus obtain ${\mathcal {E}}_\lambda (Q_*,\Omega _*)\leqslant {\mathcal {E}}_\lambda (Q,\Omega _*)$, which completes the proof. $\square$

We are finally ready to prove our coexistence result for torus and split minimizers under homeotropic boundary data.

Proof of Theorem 1.5

Throughout the proof we set $\ell _\flat :=\ell _0/3<h$.

Step 1. Define

$$\begin{aligned} \ell _1:=\sup \bigg \{{{\bar{\ell }}} \geqslant \ell _0: \hbox { every minimizer of}\ {\mathcal {E}}_\lambda \hbox { over }{\mathcal {A}}^{\textrm{sym}}_{Q_{\textrm{b}}^{(\ell )}}(\Omega _{\ell })\hbox { is split for every} \ell _0\leqslant \ell \leqslant {{\bar{\ell }}} \bigg \}, \end{aligned}$$

and observe that $\ell _1<\infty$ by Theorem  1.4. We claim that $\ell _1>\ell _0$. Indeed, assume by contradiction that $\ell _1=\ell _0$. Then, there exists a strictly decreasing sequence $\{\ell _n\}$ such that $\ell _n\rightarrow \ell _0$, and for each integer n, ${\mathcal {E}}_\lambda$ admits a minimizer $Q_n$ over ${\mathcal {A}}^{\textrm{sym}}_{Q_{\textrm{b}}^{(\ell _n)}}(\Omega _{\ell _n})$ such that $\textrm{sing}(Q_n)=\emptyset$. By Lemma 6.10, there exists a (not relabeled) subsequence such that $Q_n\rightarrow Q_*$ strongly in $W^{1,2}(\Omega _{\ell _\flat })$ where $Q_*$ minimizes ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}^{\textrm{sym}}_{Q_\textrm{b}^{(\ell _0)}}(\Omega _{\ell _0})$. Applying Proposition 6.8, we infer that $\textrm{sing}(Q_*)=\emptyset$, i.e., $Q_*$ is torus, contradicting our assumption on $\ell _0$. Hence $\ell _1>\ell _0$.

We now claim that ${\mathcal {E}}_\lambda$ admits both a split and a torus minimizer over ${\mathcal {A}}^{\textrm{sym}}_{Q_\textrm{b}^{(\ell _1)}}(\Omega _{\ell _1})$. Indeed, assume first by contradiction that every minimizer is split. Arguing as above with $\ell _1$ in place of $\ell _0$, it would lead to the existence of $\delta >0$ such that for $\ell _1\leqslant \ell <\ell _1+\delta$, every minimizer is split, contradicting the definition of $\ell _1$. Whence the existence of a torus minimizer. To prove the existence of a split minimizer, let us consider a strictly increasing sequence $\ell _0<\ell _n<\ell _1$ such that $\ell _n\rightarrow \ell _1$. For each integer n, let $Q_n$ be a minimizer of ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}^{\textrm{sym}}_{Q_{\textrm{b}}^{(\ell _n)}}(\Omega _{\ell _n})$, which must be split by definition of $\ell _1$. Applying Lemma 6.10, we can find a (not relabeled) subsequence such that $Q_n\rightarrow Q_\sharp$ strongly in $W^{1,2}(\Omega _{\ell _\flat })$ where $Q_\sharp$ minimizes ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}^{\textrm{sym}}_{Q_\textrm{b}^{(\ell _1)}}(\Omega _{\ell _1})$. Since $\textrm{sing}(Q_n)\not =\emptyset$, we deduce from Proposition 6.9 that $\textrm{sing}(Q_\sharp )\not =\emptyset$, i.e., $Q_\sharp$ is a split solution.

Step 2. Define

$$\begin{aligned} \ell _2:=\inf \bigg \{{{\bar{\ell }}} \geqslant \ell _0: \hbox { every minimizer of}\ {\mathcal {E}}_\lambda \hbox { over }{\mathcal {A}}^{\textrm{sym}}_{Q_{\textrm{b}}^{(\ell )}}(\Omega _{\ell })\hbox { is torus for every } \ell \geqslant {{\bar{\ell }}} \bigg \}, \end{aligned}$$

and observe that it is indeed well defined and finite by Theorem 1.4 (as the set above is not empty). Clearly, $\ell _2\geqslant \ell _1$ by definition of $\ell _1$. Interchanging the roles of split and torus, we can argue exactly as in the previous step to infer that there exists a minimizer of ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}^{\textrm{sym}}_{Q_{\textrm{b}}^{(\ell _2)}}(\Omega _{\ell _2})$ which is split (assume by contradiction it does not exist, then use Proposition 6.8 and Lemma 6.10 along an increasing sequence $\ell _n\rightarrow \ell _2$ to deduce that for some $\delta >0$, every minimizer of ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}^{\textrm{sym}}_{Q_{\textrm{b}}^{(\ell )}}(\Omega _{\ell })$ is torus for $\ell _2\geqslant \ell >\ell _2-\delta$, hence contradicting the definition of $\ell _2$). The existence of a torus minimizer of ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}^{\textrm{sym}}_{Q_\textrm{b}^{(\ell _2)}}(\Omega _{\ell _2})$ also follows as in Step 1. We consider a strictly decreasing sequence $\ell _n\rightarrow \ell _2$ and corresponding torus minimizers of ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}^{\textrm{sym}}_{Q_{\textrm{b}}^{(\ell _n)}}(\Omega _{\ell _n})$. By Lemma 6.10 and Proposition  6.8, we can extract a subsequence strongly converging in $W^{1,2}(\Omega _{\ell _\flat })$ toward a minimizer over ${\mathcal {A}}^{\textrm{sym}}_{Q_{\textrm{b}}^{(\ell _2)}}(\Omega _{\ell _2})$ which must by be torus. $\square$

6.4 Symmetry breaking in intermediate cylinders

We complete this section exploiting Theorem 1.5 to show that a symmetry breaking occurs for intermediate cylinders of thickness $\ell$ close to the critical values $\ell _1$ and $\ell _2$. As in Corollary 5.13, it relies on the full regularity of global energy minimizers [11, Theorem 1.1] among nonsymmetric competitors, and on the continuity of the energy infimum with respect to the thickness of the cylinder stated in the following lemma.

Lemma 6.11

Let $h>0$ and $\rho >0$ be fixed with $h>2\rho$. For a smoothed cylinder ${\mathfrak {C}}^h_{\ell ,\rho }$, let $Q^{(\ell )}_{\textrm{b}}$ be its homeotropic boundary data given by (2.4). The functions

$$\begin{aligned} \ell \in (2\rho ,+\infty )\mapsto \textrm{Val}(\ell ):=\inf \Big \{{\mathcal {E}}_\lambda (Q,{\mathfrak {C}}^h_{\ell ,\rho }): Q\in {\mathcal {A}}_{Q^{(\ell )}_{\textrm{b}}}({\mathfrak {C}}^h_{\ell ,\rho })\Big \} \end{aligned}$$

and

$$\begin{aligned} \ell \in (2\rho ,+\infty )\mapsto \textrm{Val}^{\textrm{sym}}(\ell ):=\inf \Big \{{\mathcal {E}}_\lambda (Q,{\mathfrak {C}}^h_{\ell ,\rho }): Q\in {\mathcal {A}}^{\textrm{sym}}_{Q^{(\ell )}_{\textrm{b}}}({\mathfrak {C}}^h_{\ell ,\rho })\Big \} \end{aligned}$$

are continuous.

Proof

Let $\ell _n\rightarrow \ell _*$ be an arbitrary converging sequence satifying with $\ell _n>2\rho$ and $\ell _*>2\rho$. Applying the Direct Method of Calculus of Variations, we can find for each n a map $Q_n\in {\mathcal {A}}_{Q^{(\ell _n)}_{\textrm{b}}}({\mathfrak {C}}^h_{\ell _n,\rho })$ and $Q_*\in {\mathcal {A}}_{Q^{(\ell _*)}_\textrm{b}}({\mathfrak {C}}^h_{\ell _*,\rho })$ such that ${\mathcal {E}}_\lambda (Q_n,{\mathfrak {C}}^h_{\ell _n,\rho })=\textrm{Val}(\ell _n)$ and ${\mathcal {E}}_\lambda (Q_*,{\mathfrak {C}}^h_{\ell _*,\rho })=\textrm{Val}(\ell _*)$ (see [11]). Now, we consider the sequence of equivariant biLipschitz homeomorphisms $\Phi _n:\overline{{\mathfrak {C}}^h_{\ell _n,\rho }}\rightarrow \overline{{\mathfrak {C}}^h_{\ell _*,\rho }}$ from the proof of Lemma 6.10, recalling that their biLipschitz constants go to 1 as $n \rightarrow \infty$ and that $Q_\textrm{b}^{(\ell _n)}\circ \Phi ^{-1}_n= Q_{\textrm{b}}^{(\ell _*)}$ for all $n \in \mathbb {N}$.

We set ${\widetilde{Q}}_n:= Q_n\circ \Phi ^{-1}_n\in {\mathcal {A}}_{Q^{(\ell _*)}_{\textrm{b}}}({\mathfrak {C}}^h_{\ell _*,\rho })$ and ${{\widehat{Q}}}_n:= Q_*\circ \Phi _n\in {\mathcal {A}}_{Q^{(\ell _n)}_{\textrm{b}}}({\mathfrak {C}}^h_{\ell _n,\rho })$. Then, (6.16) and energy minimality yield

$$\begin{aligned}{} & {} \textrm{Val}(\ell _*)\leqslant {\mathcal {E}}_\lambda ({\widetilde{Q}}_n,{\mathfrak {C}}^h_{\ell _*,\rho }) \leqslant C_n {\mathcal {E}}_\lambda (Q_n,{\mathfrak {C}}^h_{\ell _n,\rho })= C_n \mathrm{{{Val}}}(\ell _n)\\{} & {} \quad \leqslant C_n {\mathcal {E}}_\lambda (\widehat{Q}_n,{\mathfrak {C}}^h_{\ell _n,\rho }) \leqslant C^2_n {\mathcal {E}}_\lambda (Q_*,{\mathfrak {C}}^h_{\ell _*,\rho })= C_n^2\textrm{Val}(\ell _*) , \end{aligned}$$

for a constant $C_n\rightarrow 1$ as $n\rightarrow \infty$. Hence, $\lim _n \textrm{Val}(\ell _n)=\textrm{Val}(\ell _*)$ showing that $\textrm{Val}$ is continuous at $\ell _*$. The same argument applies to $\textrm{Val}^{\textrm{sym}}$ since the $\Phi _n$’s are equivariant. $\square$

Corollary 6.12

Under the assumptions (and notations) of Theorem 1.5, there exists $\delta >0$ such that

$$\begin{aligned} \textrm{Val}(\ell )<\textrm{Val}^{\textrm{sym}}(\ell ) \qquad \forall \ell \in [\ell _0,\ell _1+\delta )\cup (\ell _2-\delta ,\ell _2+\delta ). \end{aligned}$$

In particular, for $\ell \in (\ell _0,\ell _1+\delta )\cup (\ell _2-\delta ,\ell _2+\delta )$, any minimizer of ${\mathcal {E}}_\lambda$ over ${\mathcal {A}}_{Q^{(\ell )}_{\textrm{b}}}({\mathfrak {C}}^h_{\ell ,\rho })$ is not $\mathbb {S}^1$-equivariant and there exists infinitely many minimizers.

Proof

By [11, Theorem 1.1], any map realizing $\textrm{Val}(\ell )$ is smooth. By definition of $\ell _0$, $\ell _1$, and $\ell _2$ (see Theorem  1.5), for each $\ell \in [\ell _0,\ell _1]\cup \{\ell _2\}$ there exists a singular map realizing $\textrm{Val}^{\textrm{sym}}(\ell )$. Hence $\textrm{Val}(\ell )<\textrm{Val}^{\textrm{sym}}(\ell )$ for every $\ell \in [\ell _0,\ell _1]\cup \{\ell _2\}$. By the continuity of $\textrm{Val}$ and $\textrm{Val}^{\textrm{sym}}$ provided by Lemma 6.11, it follows that $\textrm{Val}<\textrm{Val}^{\textrm{sym}}$ in a neighborhood of $[\ell _0,\ell _1]\cup \{\ell _2\}$. Then the orbit under the $\mathbb {S}^1$-action of a minimizer provides infinitely many other minimizers. $\square$

Appendix A: Uniqueness of 2D-minimizers for \(\lambda \) small

The aim of this appendix is to complete the proof of Theorem 4.21, showing that the minimizer of the 2D-LdG energy $E_\lambda$ in the class ${\mathcal {A}}^\textrm{sym}_{\overline{H}}(\mathbb {D})$ is unique whenever $\lambda >0$ small enough. According to Proposition 4.6, the claim holds for $\lambda =0$ where the harmonic map $u_{\textrm{S}}$ given by (4.19) is the unique minimizer even without the symmetry constraint. In Theorem A.3, we shall prove that the same unconstrained uniqueness holds for every $\lambda >0$ sufficiently small, and therefore in the restricted class ${\mathcal {A}}^{\textrm{sym}}_{\overline{H}}(\mathbb {D})$ as well. Our argument is inspired by the recent interesting paper [22] addressing a similar question for minimizers of the 2D-LdG energy in a more elaborated asymptotic analysis without the norm constraint.

We start with the following preliminary result (recall that the constant $\lambda _*>0$ is defined in Theorem 1.2).

Lemma A.1

Let $u_{\textrm{S}} \in \widetilde{{\mathcal {A}}}_{\textrm{S}}$ given by (4.19), $\lambda \in [0,\lambda _*)$, and $u_\lambda$ any minimizer of $\widetilde{E}_\lambda$ over the class $\widetilde{{\mathcal {A}}}_{g_{\overline{H}}}(\mathbb {D})$. The family $\{u_\lambda \}_{0<\lambda \leqslant \frac{\lambda _*}{2}} \subseteq C^2 (\overline{\mathbb {D}};{\mathbb S}^4)$ is bounded, and $u_\lambda \rightarrow u_{\textrm{S}}$ in $C^1(\overline{\mathbb {D}})$ as $\lambda \rightarrow 0$.

Proof

By Proposition 4.6 and the minimality of each $u_\lambda$, we have

$$\begin{aligned} \widetilde{E}_0(u_{\textrm{S}})\leqslant \widetilde{E}_0(u_\lambda )\leqslant \widetilde{E}_\lambda (u_\lambda )\leqslant \widetilde{E}_\lambda (u_{\textrm{S}}) \mathop {\longrightarrow }\limits _{\lambda \rightarrow 0} \widetilde{E}_0(u_{\textrm{S}}). \end{aligned}$$

The family $\{ u_\lambda \}_{0<\lambda \leqslant \frac{\lambda _*}{2}}$ is thus bounded in $W^{1,2}(\mathbb {D})$. Each $W^{1,2}$-weak limit $u_*$ along an arbitrary sequence $\lambda _n\rightarrow 0$ belongs to $\widetilde{{\mathcal {A}}}_{g_{\overline{H}}}(\mathbb {D})$ and satisfies $\widetilde{E}_0(u_{\textrm{S}})\leqslant \widetilde{E}_0(u_*)\leqslant \widetilde{E}_0(u_{\textrm{S}})$, again by Proposition 4.6 and the weak lower semicontinuity of $\widetilde{E}_0$. By uniqueness of $u_{\textrm{S}}$ in Proposition 4.6, we deduce that $u_*=u_{\textrm{S}}$. In addition, $\widetilde{E}_{\lambda _n}(u_{\lambda _n})\rightarrow \widetilde{E}_0(u_{\textrm{S}})$ also yields the strong $W^{1,2}$-convergence of $u_{\lambda _n}$ toward $u_{\textrm{S}}$ as $\lambda _n \rightarrow 0$.

To conclude the proof, it is enough to establish a $C^{2}({\overline{\mathbb {D}}})$-bound on $u_\lambda$ since the embedding $C^{2}({\overline{\mathbb {D}}}) \hookrightarrow C^1({\overline{\mathbb {D}}})$ is compact and $C^1(\overline{\mathbb {D}}) \subseteq W^{1,2}(\mathbb {D})$ is continuous. To obtain this $C^{2}$-bound, we rely on the regularity results from [11] in three dimensions.

We consider a fixed cylinder ${\mathcal {C}}={\mathbb D} \times (-1,1)$ and for each 2D-minimizer $u_\lambda$ we consider the boundary map $v_\lambda \in W^{1,2}(\partial {\mathcal {C}}; {\mathbb S}^4)$ as the trace of $u_\lambda$, the latter extended to the whole ${\mathcal {C}}$ independently of $x_3$. Clearly, $u_\lambda \in W^{1,2}_{v_\lambda }({\mathcal {C}};{\mathbb S}^4)$ and it is easy to see that it is indeed the unique minimizer because of its $\widetilde{E}_\lambda$-minimality for each $x_3 \in (-1,1)$. Thus, we may apply the results in [11] to infer full interior regularity, i.e., that $u_\lambda \in C^\omega ({\mathbb D};{\mathbb S}^4)$, and the full boundary regularity up to the lateral boundary $\partial {\mathbb D} \times (-1,1)$, so that $u_\lambda \in C^\omega (\overline{{\mathbb D}};{\mathbb S}^4)$. Finally, as $u_\lambda \rightarrow u_{\textrm{S}}$ in $W^{1,2}({\mathbb D})$ and in turn in $W^{1,2}({\mathcal {C}})$ we can apply interior and boundary $\varepsilon$-regularity results on the whole family $\{u_\lambda \}$, as the scaled energy on balls centered at $\bar{x} \in \overline{{\mathbb D}}\times \{0\}$ can be made uniformly small for $\lambda >0$ small enough, to derive uniform $C^2$-bounds for the minimizers $\{u_\lambda \}$ for $\lambda >0$ small enough. $\square$

In order to discuss the uniqueness property of $u_\lambda$, we first recall that its energy minimality and smoothness properties yield the criticality condition

$$\begin{aligned}{} & {} \widetilde{E}^{\prime }_\lambda (\Phi ;u_\lambda )\nonumber \\{} & {} :=\left[ \frac{d}{dt} \widetilde{E}_\lambda \left( \frac{u_\lambda +t\Phi }{|u_\lambda +t\Phi |} \right) \right] _{t=0} = \int _{{\mathbb D}} \left( -\Delta u_\lambda - \left| \nabla u_\lambda \right| ^2 u_\lambda + \lambda \nabla _{\textrm{tan}} \widetilde{W}(u_\lambda ) \right) \cdot \Phi \, dx =0 \,,\nonumber \\ \end{aligned}$$

(A.1)

together with the positivity of the second variation

$$\begin{aligned}{} & {} \widetilde{E}^{\prime \prime }_\lambda (\Phi ;u_\lambda ) \nonumber \\{} & {} :=\left[ \frac{d^2}{dt^2} \widetilde{E}_\lambda \left( \frac{u_\lambda +t\Phi }{|u_\lambda +t\Phi |} \right) \right] _{t=0} = \int _{{\mathbb D}} |\nabla \Phi _T|^2- |\nabla u_\lambda |^2 |\Phi _T|^2 +\lambda D^2 \widetilde{W} (u_\lambda ) \Phi _T.\Phi _T \, dx \,,\nonumber \\ \end{aligned}$$

(A.2)

defined for $\Phi \in C^\infty _c( {\mathbb D};\mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C})$ with $\Phi _T:=\Phi -u_\lambda (u_\lambda \cdot \Phi )$ denoting the tangential component of $\Phi$ along $u_\lambda$.

The following lemma guarantees injectivity of for the linearization of equations (A.1), i.e., strict positivity of the quadratic forms (A.2) for $\lambda \geqslant 0$ small enough.

Lemma A.2

Let $u_{\textrm{S}} \in {\mathcal {A}}_{\textrm{S}}$ be as in (4.19), $\lambda \in [0,\lambda _*)$ and $u_\lambda$ be any minimizer of $\widetilde{E}_\lambda$ over the class $\widetilde{{\mathcal {A}}}_{g_{\overline{H}}}(\mathbb {D})$.

Then there exists $m_0>0$ such that

$$\begin{aligned} \int _{{\mathbb D}} |\nabla \zeta |^2- |\nabla u_{\textrm{S}}|^2 |\zeta |^2 \, dx \geqslant m_0 \int _{{\mathbb D}} \left| \nabla \zeta \right| ^2 \, dx \,, \end{aligned}$$

(A.3)

for any $\zeta \in W^{1,2}_0( {\mathbb D};\mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C})$. As a consequence, for $\lambda \geqslant 0$ small enough we have

$$\begin{aligned} \widetilde{E}^{\prime \prime }_\lambda (\Phi ;u_\lambda ) \geqslant \frac{m_0}{2} \int _{{\mathbb D}} \left| \nabla \Phi \right| ^2 \, dx \,, \end{aligned}$$

(A.4)

for any $\Phi \in {\mathcal {H}}_\lambda :=\{ \Psi \in W^{1,2}_0({\mathbb D};\mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C}): \Psi \cdot u_\lambda \equiv 0 \, \}$.

Proof

In view of (4.19) we have $u_\textrm{S}(z)=(f_0(r),f_1(r)e^{i\theta },f_2(r)e^{i2\theta })$, where $z=re^{i\phi }\in {\mathbb D}$ and $f_0(r)=\frac{r^4-3}{r^4+3} \leqslant -\frac{1}{2}$ in $\overline{{\mathbb D}}$. Since $u_{\textrm{S}}$ is a harmonic map we have $-\Delta f_0= \left| \nabla u_{\textrm{S}} \right| ^2 f_0$, where $\left| \nabla u_{\textrm{S}} \right| ^2=\frac{96r^2}{(1+3r^4)^2}$ is bounded in $\overline{{\mathbb D}}$.

Since every $\zeta \in C^\infty _0({\mathbb D};\mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C})$ can be written as $\zeta =f_0 \xi$ for some $\xi \in C^\infty _0({\mathbb D};\mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C})$, a classical integration by parts argument using the equation for $f_0$ gives

$$\begin{aligned}{} & {} \int _{{\mathbb D}} \left| \nabla \zeta \right| ^2-\left| \nabla u_{\textrm{S}} \right| ^2 |\zeta |^2 \, dx= \int _{{\mathbb D}} \left| \nabla f_0 \right| ^2 |\xi |^2+ f_0^2 \left| \nabla \xi \right| ^2 -\left| \nabla u_{\textrm{S}} \right| ^2 f_0^2 |\xi |^2 \, dx \\{} & {} \quad +\frac{1}{2} \int _{{\mathbb D}} \nabla f_0^2 \cdot \nabla |\xi |^2 \, dx\\{} & {} \quad =\int _{{\mathbb D}} \left| \nabla f_0 \right| ^2 |\xi |^2+ f_0^2 \left| \nabla \xi \right| ^2 -\left| \nabla u_{\textrm{S}} \right| ^2 f_0^2 |\xi |^2 \, dx - \int _{{\mathbb D}} \Delta f_0 |\xi |^2 f_0+\left| \nabla f_0 \right| ^2|\xi |^2 \, dx\\{} & {} \quad =\int _{{\mathbb D}} f_0^2 \left| \nabla \xi \right| ^2 \, dx \,. \end{aligned}$$

The previous identity extends by density to any $\zeta \in W^{1,2}_0({\mathbb D};\mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C})$ (correspondingly, to any $\xi \in W^{1,2}_0({\mathbb D};\mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C})$), so that in particular $F(\zeta ):= \int _{{\mathbb D}} \left| \nabla \zeta \right| ^2-\left| \nabla u_\textrm{S} \right| ^2 |\zeta |^2 \, dx >0$ whenever $\zeta \ne 0$.

Now we set

$$\begin{aligned} \sigma _*:=\inf \{F(\zeta ) \,, \, \, \Vert \zeta \Vert _{L^2}=1 \, \,, \, \zeta \in W^{1,2}_0({\mathbb D};\mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C})\} \,. \end{aligned}$$

By the direct method in the Calculus of Variations it is easy to check that $\sigma _*$ is attained and it is nonnegative. Moreover, the previous observation shows that actually $\sigma _*>0$ because of the norm constraint. Thus, for any $\zeta \in W^{1,2}_0({\mathbb D};\mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C})$ we have

$$\begin{aligned} \int _{{\mathbb D}} \left| \nabla \zeta \right| ^2-\left| \nabla u_{\textrm{S}} \right| ^2 |\zeta |^2 \, dx\geqslant \sigma _* \int _{{\mathbb D}} |\zeta |^2 \, dx\geqslant \frac{\sigma _*}{\Vert |\nabla u_{\textrm{S}}|^2 \Vert _{L^\infty }} \int _{{\mathbb D}} \left| \nabla u_{\textrm{S}} \right| ^2 |\zeta |^2 \, dx \,,\end{aligned}$$

so that for $\eta := \frac{\sigma _*}{\Vert |\nabla u_{\textrm{S}}|^2 \Vert _{L^\infty }}>0$ and $m_0:= \frac{\eta }{1+\eta }$ inequality (A.3) follows.

Finally, inequality (A.4) follows easily from (A.3). Indeed, for $\lambda >0$ small enough to be chosen later and $\Phi \in {\mathcal {H}}_\lambda$, so that $\Phi =\Phi _T$, (A.2) can be rewritten and estimated as follows:

$$\begin{aligned} \widetilde{E}_\lambda ^{\prime \prime }(\Phi ;u_\lambda )= \int _{{\mathbb D}} |\nabla \Phi |^2- \left| \nabla u_{\textrm{S}} \right| ^2 |\Phi |^2 +(\left| \nabla u_{\textrm{S}} \right| ^2 -|\nabla u_\lambda |^2) |\Phi |^2 +\lambda D^2 \widetilde{W} (u_\lambda ) \Phi \cdot \Phi \, dx \\\geqslant m_0 \int _{{\mathbb D}} \left| \nabla \Phi \right| ^2 \, dx - \left( \Vert \left| \nabla u_{\textrm{S}} \right| ^2 -|\nabla u_\lambda |^2 \Vert _{L^\infty ({\mathbb D})}+\lambda \Vert D^2 \widetilde{W} ( \, \cdot \,)\Vert _{L^\infty (\mathbb {S}^4)} \right) \int _{{\mathbb D}} |\Phi |^2 \, dx \,.\end{aligned}$$

Then, applying 2D-Poincaré inequality the lower bound (A.4) follows from the $C^1$-convergence in Lemma A.1 for $\lambda >0$ small enough. $\square$

We are finally ready for the main result of the appendix.

Theorem A.3

Let $\lambda \in [0,\lambda _*)$ and $u_\lambda$ a minimizer for the energy $\widetilde{E}_\lambda$ over the class $\widetilde{{\mathcal {A}}}_{g_{\overline{H}}}(\mathbb {D})$. Then for $\lambda$ sufficiently small the minimizer is unique. As a consequence, $u_\lambda$ is $\mathbb {S}^1$-equivariant and it is the unique minimizer of $\widetilde{E}_\lambda$ over the class $\widetilde{{\mathcal {A}}}^{\textrm{sym}}_{g_{\overline{H}}}(\mathbb {D})$.

Proof

We aim to show that for all pairs of minimizers $u_\lambda , v_\lambda \rightarrow u_{\textrm{S}}$ we have $\Vert u_\lambda -v_\lambda \Vert _{L^2}\equiv 0$ for every $\lambda >0$ small enough. The main ingredient in the proof is equation (A.4) in Lemma A.2, i.e., the uniform strict positivity of the second variation $\widetilde{E}_\lambda ^{\prime \prime }(\cdot ; u_\lambda )$ along tangent vector fields in $W^{1,2}_0$ for $\lambda > 0$ small enough. Once uniqueness holds, then ${\mathbb S}^1$-equivariance of $u_\lambda$ obviously follows and in turn its minimality in the subclass $\widetilde{{\mathcal {A}}}^{\textrm{sym}}_{g_{\overline{H}}}(\mathbb {D})$, because of the invariance property of $\widetilde{{\mathcal {A}}}_{g_{\overline{H}}}(\mathbb {D})$ under the ${\mathbb S}^1$-action, namely, $(R * u) (z):=R u(R^\textsf{t}z)R^\textsf{t}$ for any $(u,R) \in \widetilde{{\mathcal {A}}}_{g_{\overline{H}}}(\mathbb {D})\times {\mathbb S}^1$, combined with constancy of the energy functional $\widetilde{E}_\lambda$ along its orbits.

We start by decomposing $v_\lambda$ along $u_\lambda$ as $v_\lambda =u_\lambda +w_\lambda$, where in turn the difference $w_\lambda$ is pointwise decomposed into its tangential and its orthogonal part along $u_\lambda$, i.e.,

$$\begin{aligned} v_\lambda =u_\lambda +w_\lambda ^T+w_\lambda ^\perp , \qquad w_\lambda ^\perp :=[ (v_\lambda -u_\lambda )\cdot u_\lambda ] u_\lambda \,, \quad w_\lambda ^T:=w_\lambda -w_\lambda ^\perp . \end{aligned}$$

(A.5)

From now on we assume that $|w_\lambda |<1/4$ uniformly on $\overline{{\mathbb D}}$, which is always the case for $\lambda$ small enough by Lemma A.1. Note that $|w_\lambda ^\perp |^2+|w_\lambda ^T|^2=|w_\lambda |^2=-2 u_\lambda \cdot w_\lambda ^\perp =2|w_\lambda ^\perp |$, whence $|w_\lambda ^\perp |=1-\sqrt{1-|w_\lambda ^T|^2}$ and in turn $w_\lambda ^\perp =u_\lambda \left( -1+\sqrt{1-|w_\lambda ^T|^2}\right)$.

Combining the uniform convergence and $C^1$-bounds from Lemma A.1 with (A.5),we see that the following pointwise inequalities hold uniformly on $\overline{{\mathbb D}}$ for every $\lambda > 0$ small enough (the symbol $\lesssim$ will mean inequality up to multiplicative constants independent of $\lambda$), namely,

$$\begin{aligned}{} & {} |w_\lambda ^\perp | \lesssim |w_\lambda ^T|^2<1/4 \,, \quad |\nabla w_\lambda ^\perp | \lesssim |w_\lambda ^T| \left( |w_\lambda ^T|+|\nabla w_\lambda ^T|\right) \,, \quad |w_\lambda ^T| \approx |w_\lambda | \,, \quad \nonumber \\{} & {} |\nabla w_\lambda ^T|\lesssim |\nabla w_\lambda |+|w_\lambda | \,. \end{aligned}$$

(A.6)

In view of (A.1) and (A.2), it is convenient to extend $\widetilde{W}$ to a degree-zero homogeneous function of $\mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C}\setminus \{0\}$ and to introduce the following operator,

$$\begin{aligned} E'_\lambda [\Psi ]= -\Delta \Psi - \left| \nabla \Psi \right| ^2 \Psi + \lambda D \widetilde{W}(\Psi ) \,, \qquad \Psi \in C^2(\overline{{\mathbb D}};\mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C}\setminus \{0\}) , \end{aligned}$$

(A.7)

together with its formal linearization at $u_\lambda$, namely,

$$\begin{aligned}{} & {} E^{''}_\lambda [u_\lambda ] \Phi := -\Delta \Phi - |\nabla u_\lambda |^2 \Phi -2 \Big ( \nabla u_\lambda \cdot \nabla \Phi \Big ) u_\lambda +\lambda D^2 \widetilde{W} (u_\lambda ) \Phi \,, \quad \nonumber \\{} & {} \Phi \in C^2(\overline{{\mathbb D}}; \mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C}) \cap {\mathcal {H}}_\lambda \,, \end{aligned}$$

(A.8)

so that by (A.1), (A.2) and pointwise orthogonality we have

$$\begin{aligned} \widetilde{E}^{\prime }_\lambda (\Phi ;u_\lambda )= \int _{{\mathbb D}} E'_\lambda [u_\lambda ] \cdot \Phi \, dx \,, \qquad \widetilde{E}_\lambda ^{\prime \prime }(\Phi ; u_\lambda )= \int _{{\mathbb D}} E''[u_\lambda ] \Phi \cdot \Phi \, dx \,. \end{aligned}$$

(A.9)

for any $\Phi \in C^2( \overline{{\mathbb D}}; \mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C}) \cap {\mathcal {H}}_\lambda$. Notice that $D\widetilde{W}(u_\lambda )\cdot \Phi = \nabla _\textrm{tan}\widetilde{W}(u_\lambda )\cdot \Phi$ and $D^2 \widetilde{W}(u_\lambda )\Phi \cdot \Phi = D^2_{\textrm{tan}} \widetilde{W}(u_\lambda )\Phi \cdot \Phi$ whenever $\Phi$ is tangent to ${\mathbb S}^4$ at $u_\lambda$ but, although these terms could be easily computed from (1.4) and (1.1), exact formulas are irrelevant, as for our purposes the corresponding contributions will be negligible as $\lambda \rightarrow 0$.

Since both $u_\lambda$ and $v_\lambda$ are solutions, we have $E'_\lambda [v_\lambda ]\equiv E'_\lambda [u_\lambda ] \equiv 0$, hence for $w_\lambda =w_\lambda ^\perp +w_\lambda ^T=v_\lambda -u_\lambda$ as above and $\Phi =w_\lambda ^T \in C^2( \overline{{\mathbb D}}; \mathbb {R}\oplus \mathbb {C}\oplus \mathbb {C}) \cap {\mathcal {H}}_\lambda$, from (A.7)–(A.8) we infer

$$\begin{aligned}{} & {} 0=\int _{\mathbb {D}} \left( E_\lambda '[v_\lambda ] -E_\lambda '[u_\lambda ]\right) \cdot w_\lambda ^T dx \\{} & {} = \int _{\mathbb {D}} \left( E_\lambda '[v_\lambda ]\mp E_\lambda '[u_\lambda +w_\lambda ^T]\mp E_\lambda ''[u_\lambda ]w^T_\lambda -E_\lambda '[u_\lambda ]\right) \cdot w_\lambda ^T dx \,, \end{aligned}$$

so that

$$\begin{aligned}{} & {} \int _{{\mathbb D}} E_\lambda ''[u_\lambda ]w^T_\lambda \cdot w_\lambda ^T dx=:I =II+III \\{} & {} \quad :=\int _{\mathbb {D}} \left( -E_\lambda '[u_\lambda +w_\lambda ] + E_\lambda '[u_\lambda +w_\lambda ^T] \right) \cdot w_\lambda ^T dx\\{} & {} \qquad +\int _{{\mathbb D}} \left( E_\lambda '[u_\lambda ] + E_\lambda ''[u_\lambda ]w^T_\lambda -E_\lambda '[u_\lambda +w_\lambda ^T] \right) \cdot w_\lambda ^T dx \,.\end{aligned}$$

Combining (A.9), (A.4) and Poincaré inequality we obtain $\Vert w_\lambda ^T\Vert ^2_{W^{1,2}} \lesssim I$, with uniform constant for $\lambda$ small enough. Thus, in order to conclude it is enough to show that $II+III \lesssim o(1) \Vert w_\lambda ^T\Vert ^2_{W^{1,2}}$ as $\lambda \rightarrow 0$, to obtain $w_\lambda ^T\equiv 0$ and in view of (A.6) also $w_\lambda ^\perp \equiv 0$, i.e., $v_\lambda =u_\lambda$ for $\lambda$ small enough.

Concerning III, an elementary calculation gives

$$\begin{aligned}{} & {} E_\lambda '[u_\lambda ] + E_\lambda ''[u_\lambda ]w^T_\lambda -E_\lambda '[u_\lambda +w_\lambda ^T]= \lambda \Big ( D \widetilde{W}(u_\lambda ) + D^2 \widetilde{W} (u_\lambda ) w_\lambda ^T - D \widetilde{W}(u_\lambda +w_\lambda ^T) \Big ) \\{} & {} \quad - \left| \nabla u_\lambda \right| ^2 u_\lambda - |\nabla u_\lambda |^2 w_\lambda ^T -2 \Big ( \nabla u_\lambda \cdot \nabla w_\lambda ^T\Big )u_\lambda + \left| \nabla (u_\lambda +w_\lambda ^T) \right| ^2 (u_\lambda +w_\lambda ^T) = \\{} & {} \lambda \Big ( D \widetilde{W}(u_\lambda ) + D^2 \widetilde{W} (u_\lambda ) w_\lambda ^T - D \widetilde{W}(u_\lambda +w_\lambda ^T) \Big ) + 2 \Big ( \nabla u_\lambda \cdot \nabla w_\lambda ^T \Big )w_\lambda ^T +\left| \nabla w_\lambda ^T \right| ^2 (u_\lambda +w_\lambda ^T) \,.\end{aligned}$$

Using the uniform $C^1$-bounds for $u_\lambda$, $v_\lambda$ and $w_\lambda$ together with Taylor’s theorem on $D \widetilde{W}$ we easily obtain the pointwise bound

$$\begin{aligned} \left| E_\lambda '[u_\lambda ] + E_\lambda ''[u_\lambda ]w^T_\lambda -E_\lambda '[u_\lambda +w_\lambda ^T] \right| \lesssim (1+\lambda )\left| w_\lambda ^T \right| ^2+\left| \nabla w_\lambda ^T \right| ^2 \,,\end{aligned}$$

so that for $\lambda <1$ small enough we obtain $III \lesssim \Vert w^T_\lambda \Vert _{L^\infty } \Vert w_\lambda ^T\Vert ^2_{W^{1,2}}=o(1) \Vert w_\lambda ^T\Vert ^2_{W^{1,2}}$ as $\lambda \rightarrow 0$ because of Lemma A.1 and (A.6).

Concerning II, another simple calculation leads to

$$\begin{aligned}{} & {} -E_\lambda '[u_\lambda +w_\lambda ] + E_\lambda '[u_\lambda +w_\lambda ^T]=\Delta w_\lambda ^\perp +\lambda \Big ( D W(u_\lambda +w_\lambda )-D W(u_\lambda +w_\lambda ^T) \Big ) \\{} & {} +\Big (2 \nabla (u_\lambda +w_\lambda ^T)\cdot \nabla w_\lambda ^\perp + \left| \nabla w_\lambda ^\perp \right| ^2 \Big )v_\lambda + \left| \nabla (u_\lambda +w_\lambda ^T) \right| ^2 w_\lambda ^\perp \,. \end{aligned}$$

In view of this last identity, the resulting terms in II can be pointwise estimated as follows. Since $w_\lambda ^\perp =u_\lambda \left( -1+ \sqrt{1-|w_\lambda ^T|^2} \right)$, by orthogonality we also have

$$\begin{aligned} \Delta w_\lambda ^\perp \cdot w_\lambda ^T= \left( -1+ \sqrt{1-|w_\lambda ^T|^2} \right) \Delta u_\lambda \cdot w_\lambda ^T+2 \left( \nabla \left( -1+ \sqrt{1-|w_\lambda ^T|^2} \right) \cdot \nabla u_\lambda \right) \cdot w_\lambda ^T \,, \end{aligned}$$

so that the $C^2$-bounds in Lemma A.1 together with (A.6) yield

$$\begin{aligned} \left| \Delta w_\lambda ^\perp \cdot w_\lambda ^T \right| \lesssim |w_\lambda ^T|^2 (|w_\lambda ^T|+|\nabla w_\lambda ^T|) \,, \end{aligned}$$

(A.10)

uniformly on $\overline{{\mathbb D}}$ for $\lambda$ small enough.

Next, using the Lipschitz property of $D \widetilde{W}$ on compact sets in combination with (A.6) we have the pointwise bounds

$$\begin{aligned} \lambda \Big ( D \widetilde{W}(u_\lambda +w_\lambda )-D \widetilde{W}(u_\lambda +w_\lambda ^T) \Big ) \cdot w_\lambda ^T \lesssim \lambda |w_\lambda ^\perp | |w_\lambda ^T| \lesssim |w_\lambda ^T|^3 \,, \end{aligned}$$

(A.11)

uniformly on $\overline{{\mathbb D}}$ for $\lambda <1$ small enough. Finally, the uniform $C^1$-bound from Lemma A.1 together with (A.6) also yield the pointwise bound

$$\begin{aligned}{} & {} \Big ( \Big (2 \nabla (u_\lambda +w_\lambda ^T)\cdot \nabla w_\lambda ^\perp + \left| \nabla w_\lambda ^\perp \right| ^2 \Big )v_\lambda + \left| \nabla (u_\lambda +w_\lambda ^T) \right| ^2 w_\lambda ^\perp \Big ) \cdot w_\lambda ^T \nonumber \\{} & {} \quad \lesssim |w_\lambda ^T| \left( |\nabla w_\lambda ^\perp | +|w_\lambda ^\perp |\right) \lesssim |w_\lambda ^T|^2 (|w_\lambda ^T|+|\nabla w_\lambda ^T|) \,, \end{aligned}$$

(A.12)

uniformly on $\overline{{\mathbb D}}$ for $\lambda$ small enough.

Collecting together (A.10)–(A.12) we finally obtain the pointwise estimate

$$\begin{aligned}{} & {} \left| \left( -E_\lambda '[u_\lambda +w_\lambda ] + E_\lambda '[u_\lambda +w_\lambda ^T] \right) \cdot w_\lambda ^T \right| \lesssim |w_\lambda ^T|^2 \left( |w_\lambda ^T|+|\nabla w_\lambda ^T|\right) \\{} & {} \lesssim |w_\lambda ^T| \left( |w^T_\lambda |^2+|\nabla w^T_\lambda |^2\right) , \end{aligned}$$

so that integrating and arguing as above we easily obtain $II \lesssim \Vert w^T_\lambda \Vert _{L^\infty } \Vert w_\lambda ^T\Vert ^2_{W^{1,2}} = o(1) \Vert w_\lambda ^T\Vert ^2_{W^{1,2}}$ as $\lambda \rightarrow 0$, which completes the proof. $\square$