The Saturn Ring Effect in Nematic Liquid Crystals with External Field: Effective Energy and Hysteresis

Abstract

In this work we consider the Landau–de Gennes model for liquid crystals with an external magnetic field to model the occurrence of the Saturn ring effect under the assumption of rotational equivariance. After a rescaling of the energy, a variational limit is derived. Our analysis relies on precise estimates around the singularities and the study of a radial auxiliary problem in regions, where a continuous director field exists. Studying the limit problem, we explain the transition between the dipole and Saturn ring configuration and the occurence of a hysteresis phenomenon, giving a rigorous explanation of what was derived and simulated previously by [H. Stark, Eur. Phys. J. B 10, 311–321 (1999)].

1 Introduction

Liquid crystals represent a state of matter with properties intermediate between liquids and crystalline solids. They are commonly referred to as rod like molecules (although there are others, for example disk shaped molecules) whose positional and orientational order may vary within space, time and parameters such as temperature. For a general and complete introduction, we refer to [5, 24]. Depending on the alignment of the molecules and its symmetries, liquid crystals are generally divided into nematic, smectic and cholesteric. Due to their unique properties, liquid crystals exhibit remarkable structures and applications; see for example [37, 41, 46].

From a mathematical point of view, several models have been introduced to study the phenomena arising from liquid crystals [9]. Roughly speaking, the Oseen–Frank model describes liquid crystals by a unit vector field ${\mathbf{n}}$, which represents the preferred direction of the molecules at a point, averaging the fluctuations of the molecules. A peculiarity is, that in practice, we do not distinguish between ${\mathbf{n}}$ and $-{\mathbf{n}}$, so that ${\mathbf{n}}$ should rather take values in a projective space ${\mathbb {R}}P^2$ to avoid problems with orientability.

In order to represent local averages of the directions of the molecules, one gets an additional degree of freedom. Models describing the liquid crystal with such a variable include for instance the Ericksen model [25, 52, Ch.6]. The Landau–de Gennes model goes one step further by using the idea to describe the arrangement of a liquid crystal by a probability distribution $\rho$ on the sphere of directions, taking into account that opposite points have the same probability. Then the first moment vanishes and the (shifted) second moment Q is a symmetric traceless tensor, which is used to model $\rho$. This allows to incorporate both the Oseen–Frank and Ericksen model into the Landau–de Gennes model. A more detailed introduction to the various models and even for more refined generalizations of the Landau–de Gennes model, for example the Onsager model or Maier–Saupe model, can be found in [8, 53]. For the challenges and a comparison of the mentioned descriptions, see [10,11,12, 17, 48]. In general, it is difficult to give precise descriptions of minimizers of the energy functionals associated with one of the models explicitly, except in some very special cases such as in [56] or for the radial hedgehog solution in [42].

Mathematically speaking, liquid crystal theory shares several techniques and results with other subjects, for example the Ginzburg–Landau model in micromagnetics, [15, 32, 35]. Also, parts of the description, such as function spaces [7] and liftings [34, 44], $Q-$tensors [16, 45], the formation of topological singularities [51] or similar energy functionals [22, 49], are of interest in a more abstract setting.

One interesting pattern one can observe in liquid crystals is the so called "Saturn ring" effect. Under certain circumstances the defect structure forming in order to balance a topological charge on the surface of an immersed object in liquid crystals, takes the form of a ring around the particle, see [1, 2, 33, 46]. Also more exotic structures such as knots are possible; we refer to [46] for an overview. In addition, an electromagnetic field can be used to manipulate the occurrence of a Saturn ring. While this is known in physics for several years [4, 27,28,29, 39, 40, 55], there are only few mathematical results [3]. Starting from the Landau–de Gennes model, an equilibrium configuration is found by minimization of the dimensionless free energy

$$\begin{aligned} {\mathcal {E}}_{\eta ,\xi }(Q) = \int _\Omega \frac{1}{2}|\nabla Q|^2 + \frac{1}{\xi ^2} f(Q) + \frac{1}{\eta ^2} g(Q) + C_0(\xi ,\eta ) \, {\mathrm{d}} x \end{aligned}$$

under suitable anchoring boundary conditions. Here $\Omega$ is the region filled with the liquid crystal, in our case the complement of the unit ball, that is $\Omega ={\mathbb {R}}^3{\setminus } B_1(0)$ and $C_0(\xi ,\eta )$ is a renormalization constant such that the energy is finite. The first term is the density for the elastic energy, while f is a potential inducing a force which tends to push the material into an ordered state. The parameter $\xi$ describes the ratio between elastic and bulk energy. We are going to consider the limit of $\xi$ converging to zero, which can be interpreted as the limit for a large particle. The effect of an external magnetic field is described by the function g, with the parameter $\eta$ coupling the field to the elastic and bulk energy densities. We will consider a regime where also $\eta \rightarrow 0$, not much slower than $\xi$. In our limit of $\xi ,\eta \rightarrow 0$, $C_0$ converges to zero. To complete our model, we impose a strong anchoring boundary condition on $\partial \Omega$ that corresponds to a radial director field ${\mathbf{n}}={\mathbf{e}}_r$. With $\xi$ and $\eta$ converging to zero, we can consider different regimes regarding the relative speed of convergence of both parameters.

• 1. The case of strong fields $\eta |\ln (\xi )|\ll 1$, where we expect to observe a Saturn ring was treated in [3].

• 2. The case $\eta |\ln (\xi )|\sim 1$, where the transition between dipole and Saturn ring takes place is precisely the purpose of this paper.

• 3. In the case $\eta |\ln (\xi )|\gg 1$ we expect only dipole configurations, see Remark 3.3.

Our work is organized as follows: in the first section we define the different parts of the free energy carefully, establish fundamental properties and discuss their effects in the minimizing process.

The second section contains the rescaling and states our main theorem, a sort of $\Gamma -$convergence result in a sense that will be precised later. We will prove, that in the limit $\eta ,\xi \rightarrow 0$ in our regime and under the assumption of rotational equivariance, the model reduces to a simple energy stated on the surface of the sphere ${\mathbb {S}}^2=\partial \Omega$, of the form

$$\begin{aligned} {\mathcal {E}}_0(F) = 2s_*c_*\int _F (1-\cos (\theta ))\, {\mathrm{d}} \omega +2s_*c_*\int _{F^c} (1+\cos (\theta ))\, {\mathrm{d}} \omega + \frac{\pi }{2}s_*^2\beta |D\chi _F|({\mathbb {S}}^2)\, , \end{aligned}$$

where $s_*,c_*>0$ are parameters depending on f and $F\subset {\mathbb {S}}^2$ is a set of finite perimeter that can be seen as the projection of the region in which a lifting of Q from ${\mathbb {R}}P^2$ to ${\mathbb {S}}^2$ exists and the orientation at infinity agrees with the outward normal of $\partial B_1$. In the same spirit, $F^c$ stands for the region where the lifting has the opposite orientation and $|D\chi _F|({\mathbb {S}}^2)$ denotes the perimeter of F in ${\mathbb {S}}^2$. In the above expression, $\theta$ stands for the angle between a point $\omega$ on the sphere and ${\mathbf{e}}_3$. We see the latter perimeter term as representation of a defect line. It tells us that switching from one orientation to the other comes with a cost, depending on the balance between the forces (modelled by $\beta$), $s_*$ which is related to the liquid crystal properties, $c_*$ which depends on the interaction between magnetic field and liquid crystal and the length of the defect line. This is the result we are going to prove in the next two sections.

Section 4 is divided into three parts. We first show that the energy bound implies the existence of only a finite number of singularities if we are at some distance from the ${\mathbf{e}}_3-$axis. The main idea will be to replace our functions $Q_{\eta ,\xi }$ by the minimizers of approximate problems and then use the higher regularity to derive a lower bound on the energy cost of a singularity. The energy bound then implies that in fact only finitely many singularities can occur. Next, we provide asymptotically exact lower bounds for the energy near those singularities. Then, the radial auxiliary problem is introduced. Given a ray from the surface $\partial \Omega$ to infinity such that $Q_{\eta ,\xi }$ is close to being uniaxial with prescribed scalar order parameter, we can explicitly calculate the energy necessary to turn along the ray from our boundary conditions to the preferred configuration parallel to the external field in ${\pm }{\mathbf{e}}_3-$direction. Combining the results, we are able to prove the lower bound part of the main theorem.

The construction of a recovery sequence is made in Section 5. We use our knowledge about the interplay of the three parts of the energy to define approximate regions close to the particle in which the energy of the first two terms of ${\mathcal {E}}_0$ is concentrated and Q is uniaxial. Here we profit from the exact formula of the optimal profile from the radial auxiliary problem. Apart from these regions, we construct the singularities that give rise to the perimeter term of ${\mathcal {E}}_0$.

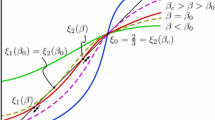
The remaining section deals with the limit energy. We calculate the minimizers (depending on $\beta$) and compare their energy with that of a dipole and a Saturn ring at the same $\beta -$value. We find that by varying $\beta$ a hysteresis phenomenon occurs. Our findings rigorously explain known numerical simulations and physical reasoning in [38, 50].

2 Scaling, Definitions and Preliminaries

Starting from the one constant approximation of the Landau–de Gennes free energy [47, Ch. 6, Secs. 3-4 and Ch. 10, Sec. 2.3] (see also [23, Ch. 3, Secs. 1-2]) in $\Omega _{r_0} = {\mathbb {R}}^3 {\setminus } \overline{B_{r_0}(0)}$ we find that

$$\begin{aligned} {\mathcal {E}}(Q) = \int _{\Omega _{r_0}} \frac{L}{2}|\nabla Q|^2 - \frac{a}{2}{\mathrm{tr}}(Q^2) - \frac{b}{3}{\mathrm{tr}}(Q^3) + \frac{c}{4}({\mathrm{tr}}(Q^2))^2 - \frac{1}{2}\chi _a {\mathbf{H}}\otimes {\mathbf{H}}:Q \, {\mathrm{d}} x \, , \end{aligned}$$

(1)

where the last term is added to the Landau–de Gennes model to incorporate the effect of the external magnetic field ${\mathbf{H}}$. The length $r_0$ is the particle radius, the parameter L is the elastic constant, a, b, c are the bulk constants depending on the liquid crystal material. They can be temperature dependent, although it is usually assumed that only a has a linear dependence, that is $a=a_0(T-T_{*})$ for a reference temperature $T_{*}$ [45]. However, this case will not be discussed here. As already noted, ${\mathbf{H}}$ is the magnetic field, which we choose to be parallel to ${\mathbf{e}}_3$, that is ${\mathbf{H}}=h {\mathbf{e}}_3$ and $\chi _a$ denotes the magnetic anisotropy. See [31] for more details on the modelling, in particular how magnetic fields differ from electric and gravitational fields.

In order to be able to work on a fixed domain, we apply the rescaling $\Omega :=\frac{1}{r_0}\Omega _{r_0}$ and ${\tilde{x}} = x/r_0$. We introduce the new function ${\widetilde{Q}}({\tilde{x}}) = Q(r_0 {\tilde{x}})=Q(x)$ and ${\widetilde{\nabla }}=\nabla _{{\tilde{x}}}= \frac{1}{r_0}\nabla _x$. Furthermore, we write ${\tilde{a}}=\frac{a}{c}$ and ${\tilde{b}}=\frac{b}{c}$. Then

$$\begin{aligned} {\mathcal {E}}(Q)&= \int _\Omega \frac{L r_0^3}{2 r_0^2} |\nabla {\widetilde{Q}}|^2 + r_0^3 c \left( - \frac{{\tilde{a}}}{2}{\mathrm{tr}}({\widetilde{Q}}^2) - \frac{{\tilde{b}}}{3}{\mathrm{tr}}({\widetilde{Q}}^3) + {\frac{1}{4}}({\mathrm{tr}}({\widetilde{Q}}^2))^2 \right) \\&- \frac{1}{2} \chi _a h^2 r_0^3 {\widetilde{Q}}_{33} \, {\mathrm{d}} \tilde{x} \, . \end{aligned}$$

Dividing by $L r_0$, we can define

$$\begin{aligned} \begin{aligned} {\widetilde{{\mathcal {E}}}}({\widetilde{Q}}) = \int _\Omega \frac{1}{2}|{\widetilde{\nabla }}{\widetilde{Q}}|^2 + \frac{1}{\xi ^2} \left( - \frac{{\tilde{a}}}{2}{\mathrm{tr}}({\widetilde{Q}}^2) - \frac{{\tilde{b}}}{3}{\mathrm{tr}}({\widetilde{Q}}^3) + {\frac{1}{4}}({\mathrm{tr}}({\widetilde{Q}}^2))^2 \right) - \frac{1}{\eta ^2} {\widetilde{Q}}_{33} \, {\mathrm{d}} \tilde{x}\, , \end{aligned} \end{aligned}$$

(2)

where we introduced the new dimensionless parameters $\xi = \sqrt{\frac{L}{c r_0^2}}$ and $\eta = \sqrt{\frac{L}{2\chi _a r_0^2 h^2}}$. We choose the coefficients ${\tilde{a}},{\tilde{b}}$ to be fixed from now on, which corresponds to choosing a material and keeping the physical system at a constant temperature. For a common liquid crystal material such as MBBA at a temperature of $25^\circ C$ we roughly find ${\tilde{a}}\approx 2.4$, ${\tilde{b}}\approx 1.8$ [47, p. 168]. The analysis and particularly the constants in the estimates that appear in the following will generally depend on f and thus on ${\tilde{a}}$ and ${\tilde{b}}$, even if we do not explicitly state this dependence.

We are interested in the limit $\eta ,\xi \rightarrow 0$. In the standard Landau–de Gennes model, $\xi \rightarrow 0$ can be interpreted as increasing the particle radius (see [30] for a detailed discussion). We impose the asymptotic relation $\eta |\ln (\xi )|\rightarrow \beta \in (0,\infty )$ which can be seen as a coupling of the parameters $r_0$ and h, that is slowly decreasing the field strength h, while increasing the particle radius in a way that keeps the system in a state where both Saturn ring and dipole configurations are likely to appear.

It is convenient to introduce a constant $C_0$ in the integral of (1) to obtain a non-negative energy density. In our case, this constant depends on $\xi$ and $\eta$, but tends towards a constant independent of those parameters as $\xi ,\eta \rightarrow 0$. We will discuss the issue later in this section.

From now on, we will only consider the rescaled model and thus drop all tildes in our notation. We continue this section by giving precise definitions for the function f modelling the bulk term and quantities mentioned in the introduction. We will, furthermore, introduce a more general function g for the magnetic term in (1).

Definition 2.1

We denote by ${\mathrm{Sym}}_{0}$ the space of symmetric matrices with vanishing trace

$$\begin{aligned} {\mathrm{Sym}}_{0}:=\{ Q\in {\mathbb {R}}^{3\times 3}\, : \,Q^\top = Q\, ,\, {\mathrm{tr}}(Q)=0 \}\, , \end{aligned}$$

equipped with the norm $|Q|=\sqrt{{\mathrm{tr}}(Q^2)}$. Furthermore, for $a,b,c\in {\mathbb {R}}$, $b,c>0$, we define

$$\begin{aligned} f(Q) = C - \frac{a}{2}{\mathrm{tr}}(Q^2) - \frac{b}{3} {\mathrm{tr}}(Q^3) + \frac{c}{4}\, ({\mathrm{tr}}(Q^2))^2\, . \end{aligned}$$

(3)

As we stated in the introduction, the definition of ${\mathrm{Sym}}_{0}$ is motivated by the second order moment of a probability distribution $\rho$ on a sphere. The symmetry between ${\pm }{\mathbf{n}}$ reads $\rho ({\mathbf{n}})=\rho (-{\mathbf{n}})$ for all ${\mathbf{n}}\in {\mathbb {S}}^2$, that is the expectation value of ${\mathbf{n}}$ vanishes, $\int _{{\mathbb {S}}^2} {\mathbf{n}}\, {\mathrm{d}} \rho = 0$. The second moment $\int _{{\mathbb {S}}^2} {\mathbf{n}}\otimes {\mathbf{n}}\, {\mathrm{d}} \rho$ is symmetric and has trace 1. From this we subtract the second moment of a uniform distribution on ${\mathbb {S}}^2$, that is ${\overline{\rho }} = \frac{1}{4\pi }$ to get the symmetric and traceless tensor Q.

The specific form of the function f comes from the requirement of being invariant under rotations. Indeed, assuming a polynomial function f and demanding frame indifference for the bulk energy (and of course for the elastic energy) we find that f has to satisfy $f(Q)=f(R^\top QR)$ for all $R\in O(3)$. This implies that f is the linear combination of ${\mathrm{tr}}(Q^2)$, ${\mathrm{tr}}(Q^3)$, $({\mathrm{tr}}(Q)^2)^2$, ${\mathrm{tr}}(Q^2){\mathrm{tr}}(Q^3)$, ${\mathrm{tr}}(Q^2)^2$, ${\mathrm{tr}}(Q^3)^2$, etc (see [8, Lemma 3]). It is convenient to consider only the first three terms although one could in principle add more. The constant C in (3) is chosen such that f is non-negative and vanishes on uniaxial $Q-$tensors of a prescribed scalar order parameter (the set ${\mathcal {N}}$ in Proposition 2.2 below). This is the main property of f one should keep in mind during our analysis.

Proposition 2.2

(Properties of f) There exists a constant C such that f given by (3) satisfies

• 1. $f(Q)\geqq 0$ for all $Q\in {\mathrm{Sym}}_{0}$ and $\min _{Q\in {\mathrm{Sym}}_{0}} f(Q)=0$. Let

  $$\begin{aligned} {\mathcal {N}}:=\left\{ s_*\left( {\mathbf{n}}\otimes {\mathbf{n}}- \frac{1}{3}{\mathrm{Id}}\right) \, : \,{\mathbf{n}}\in {\mathbb {S}}^2 \right\} \, , \end{aligned}$$

  where ${\mathbb {S}}^2\subset {\mathbb {R}}^3$ is the unit sphere and $s_* = {\frac{1}{4}\left( {\tilde{b}} + \sqrt{{\tilde{b}}^2+24{\tilde{a}}}\right) }$. Then ${\mathcal {N}}= f^{-1}(0)$ is a smooth, compact, connected manifold without boundary diffeomorphic to ${\mathbb {R}}P^2$. The constant C can be explicitly be calculated as $C = {\frac{{\tilde{a}}}{3}s_*^2 + \frac{2{\tilde{b}}}{27}s_*^3 - \frac{1}{9}s_*^4}$.

• 2. Furthermore, there exist constants $\delta _0,\gamma _1>0$ such that if $Q\in {\mathrm{Sym}}_{0}$ satisfies ${\mathrm{dist}}(Q,{\mathcal {N}})\leqq \delta _0$, then

  $$\begin{aligned} f(Q) \geqq \gamma _1\, {\mathrm{dist}}^2(Q,{\mathcal {N}})\, . \end{aligned}$$

• 3. There exist constants $C_1,C_2>0$ such that for all $Q\in {\mathrm{Sym}}_{0}$

  $$\begin{aligned} f(Q)\geqq C_1\bigg (|Q|^2 - \frac{2}{3}s_*^2\bigg )^2\, , \qquad Df(Q):Q \geqq C_1\, |Q|^4 - C_2 \, . \end{aligned}$$

Note that all constants appearing in the above proposition are depending on ${\tilde{a}}$ and ${\tilde{b}}$.

Proof

A proof of the first statement can be found in [44, Proposition 15]. For the second result, we refer to [20, Lemma 2.4 ($F_2$)]. The last assertions follows by elementary calculations as in [20, Lemma 2.4 ($F_0$)]. $\square$

The last two statements are of technical nature. The third property is used to establish $L^\infty -$bounds in Remark 3.2 and Proposition 4.4 and to establish Proposition 2.4 and Proposition 2.6. The estimate in 2. simply states that one can think of f as being quadratic close to its minimum which is attained on ${\mathcal {N}}$. The first statement gives an interesting connection between f and the space ${\mathrm{Sym}}_{0}$. In fact, ${\mathcal {N}}$ plays an important role in our analysis as it will allow us to identify Q and ${\pm } {\mathbf{n}}$ and thus give a intuitive meaning to Q. This is formalized in the next proposition.

Proposition 2.3

(Structure of ${\mathrm{Sym}}_{0}$)

• 1. For all $Q\in {\mathrm{Sym}}_{0}$ there exist $s\in [0,\infty )$ and $r\in [0,1]$ such that

  $$\begin{aligned} Q = s\left( \left( {\mathbf{n}}\otimes {\mathbf{n}}- \frac{1}{3}{\mathrm{Id}}\right) + r\left( {\mathbf{m}}\otimes {\mathbf{m}}- \frac{1}{3}{\mathrm{Id}}\right) \right) \, , \end{aligned}$$

  (4)

  where ${\mathbf{n}},{\mathbf{m}}$ are normalized, orthogonal eigenvectors of Q. The values s and r are continuous functions of Q.

• 2. Let ${\mathcal {C}}= \{ Q\in {\mathrm{Sym}}_{0}\, : \,\lambda _1(Q)=\lambda _2(Q) \}$, where we denoted by $\lambda _1,\lambda _2$ the two leading eigenvalues of Q. Then

  $$\begin{aligned} {\mathcal {C}}=\{ Q\in {\mathrm{Sym}}_{0}{\setminus }\{0\}\, : \,r(Q)=1 \}\cup \{0\} \quad \text {and}\quad {\mathcal {C}}{\setminus }\{0\} \cong {\mathbb {R}}P^2\times {\mathbb {R}}\, . \end{aligned}$$

• 3. There exists a continuous function ${\mathcal {R}}:{\mathrm{Sym}}_{0}{\setminus }{\mathcal {C}}\rightarrow {\mathcal {N}}$ such that ${\mathcal {R}}(Q)=Q$ for all $Q\in {\mathcal {N}}$. In particular, ${\mathrm{Sym}}_{0}{\setminus }{\mathcal {C}}$ and ${\mathcal {N}}$ are homotopic. The map ${\mathcal {R}}$ can be chosen to be the nearest point projection onto ${\mathcal {N}}$. In this case, for all $Q\in {\mathrm{Sym}}_{0}{\setminus }{\mathcal {C}}$ decomposed as in (4), ${\mathcal {R}}$ is given by ${\mathcal {R}}(Q)=s_*({\mathbf{n}}\otimes {\mathbf{n}}-\frac{1}{3}{\mathrm{Id}})$ .

Proof

The first part follows from [19, Lemma 1.3.1] for $s = 2\lambda _1+\lambda _2$ and $r=(\lambda _1+2\lambda _2)/s$, where $\lambda _1\geqq \lambda _2$ are the two leading eigenvalues of Q. The second part is a consequence of the definition of s, r in terms of the eigenvalues and [19, Lemma 1.3.5]. The last part is a reformulation of Lemma 1.3.6 and Lemma 1.3.7 in [19], together with Lemma 2.2.2. $\square$

The decomposition (4) provides us with a very useful tool to perform calculations, for example in Proposition 4.16, Proposition A.1 or Proposition A.2. In the second statement we introduce ${\mathcal {C}}$, a subset of the uniaxial $Q-$tensor, sometimes referred to as "oblate uniaxial" [26, 43]. One can think of ${\mathcal {C}}$ as a cone over ${\mathbb {R}}P^2$. If a $Q-$tensor is not oblate uniaxial, there exists a retraction onto ${\mathcal {N}}$ which coincides with the nearest point projection and is given by the element of ${\mathcal {N}}$ corresponding to the dominating eigenvector of Q.

In the remaining part of this chapter we are concerned with the magnetic energy term, which will be modelled by a function g. We require $g:{\mathrm{Sym}}_{0}\rightarrow {\mathbb {R}}$ to be of class $C^2$ away from 0 and to satisfy the following properties:

• 1. The function g does not grow faster than f, that is there exists a constant $C>0$ such that for all $Q\in {\mathrm{Sym}}_{0}$

  $$\begin{aligned} |g(Q)|&\leqq \ C\, (1+|Q|^4)\, , \end{aligned}$$

  (5)
  $$\begin{aligned} |Dg(Q)|&\leqq \ C\, (1+|Q|^3)\, . \end{aligned}$$

  (6)

• 2. The preferred eigenvector of Q for g is ${\mathbf{e}}_3$ in the following sense: g is invariant by rotations around the ${\mathbf{e}}_3-$axis and the function $O(3)\ni R\mapsto g(R^\top Q R)$ is minimal if ${\mathbf{e}}_3$ is eigenvector to the maximal eigenvalue of $R^\top Q R$.

  Decomposing Q as in (4) with ${\mathbf{n}}={\mathbf{e}}_3$ and keeping s and ${\mathbf{m}}$ fixed, then g(Q) is minimal for $r=0$. For a uniaxial $Q\in {\mathcal {N}}$, that is $Q=s_*({\mathbf{n}}\otimes {\mathbf{n}}-\frac{1}{3}{\mathrm{Id}})$ for $s_*\geqq 0$ and ${\mathbf{n}}\in {\mathbb {S}}^2$ we have

  $$\begin{aligned} g(Q) = c_*^2(1-{\mathbf{n}}_3^2)\, . \end{aligned}$$

  (7)

• 3. There exist constants $\delta _1,C>0$ such that if $Q\in {\mathrm{Sym}}_{0}$ with ${\mathrm{dist}}(Q,{\mathcal {N}})<\delta$ for $0<\delta <\delta _1$, then

  $$\begin{aligned} |g(Q) - g({\mathcal {R}}(Q))| \leqq C\, {\mathrm{dist}}(Q,{\mathcal {N}})\, . \end{aligned}$$

  (8)

The first and last conditions are technical assumptions. The former allows us to dominate g by f. This is necessary, since g may be negative. The latter states the Lipschitz continuity of g in a neighbourhood of ${\mathcal {N}}$ in normal direction. The second requirement contains the mathematical translation of the physical model. The homogeneous magnetic field parallel to ${\mathbf{e}}_3$ should favour the alignment of the dominating eigenvector of Q parallel to ${\mathbf{e}}_3$. Equation (7) expresses the compatibility of our $Q-$tensor analysis with the classical formulations for director fields. From a mathematical point of view, it is possible to replace (7) by 7’

and to obtain a similar limit energy, see Remark 4.18.

We note that the functions $g_1$ and $g_2$, defined as

$$\begin{aligned} g_1(Q)= \frac{2}{3}s_* - Q_{33} \quad \text {and} \quad g_2(Q) = \left\{ \begin{array}{ll} \sqrt{\frac{2}{3}} - \frac{Q_{33}}{|Q|} &{} Q\in {\mathrm{Sym}}_{0}{\setminus }\{0\} \\ 0 &{} Q=0 \end{array}\right. \, , \end{aligned}$$

(9)

satisfy the above assumptions on g (see “Appendix”). The function $g_1$ (with $c_*^2=s_*$) is the natural (physical) term to model a magnetic field [47, Ch. 10], we have used it to derive our scaling in (1), the constant $\frac{2}{3} s_*$ being part of $C_0$. Another possible choice is $g_2$, which is a useful approximation to $g_1$ introduced in [27] and used example in [3]. In this case $c_*^2=\sqrt{\frac{3}{2}}$.

We finish this section by two propositions. Note that if $g\geqq 0$ (for example in the case $g=g_2$), then both propositions are trivial. The first proposition shows that under the above assumptions on f and g there exists a unique minimizer $Q_{\infty ,\xi ,\eta }$ of $\frac{1}{\xi ^2}f(Q)+\frac{1}{\eta ^2}g(Q)$. This allows us to characterize a constant $C_0(\xi ,\eta )$ such that the bulk energy density becomes non-negative and vanishes only at $Q_{\infty ,\xi ,\eta }$. The second proposition expresses that if Q is close to ${\mathcal {N}}$ but the dominating eigenvector ${\mathbf{n}}$ far from ${\mathbf{e}}_3$, then g has to be strictly positive.

Proposition 2.4

For $\xi ,\eta >0$ with $\xi \ll \eta$, there exists a unique $Q_{\infty ,\xi ,\eta }\in {\mathrm{Sym}}_{0}$ such that

$$\begin{aligned} Q_{\infty ,\xi ,\eta } = \underset{Q\in {\mathrm{Sym}}_{0}}{\mathrm {argmin}} \, \frac{1}{\xi ^2}f(Q)+\frac{1}{\eta ^2}g(Q)\, , \end{aligned}$$

given by $s_{*,\xi ^{2}/\eta ^{2}}({\mathbf{e}}_3\otimes {\mathbf{e}}_3-\frac{1}{3}{\mathrm{Id}})$, where $|s_{*,t}-s_*| \leqq C t$ with $s_*$ as in Proposition 2.2. Hence, for $C_0(\xi ,\eta ) = -\frac{1}{\xi ^2}f(Q_{\infty ,\xi ,\eta })-\frac{1}{\eta ^2}g(Q_{\infty ,\xi ,\eta }) \geqq 0$ it also holds true that $C_0(\xi ,\eta )\leqq C \xi ^2/\eta ^4$.

Since $s_{*,\xi ^{2}/\eta ^{2}}\rightarrow s_{*,0} = s_*$ for $\xi ,\eta \rightarrow 0$ in our regime, we denote $Q_\infty :=s_*({\mathbf{e}}_3\otimes {\mathbf{e}}_3-\frac{1}{3}{\mathrm{Id}})$.

In the physically relevant case of $g=g_1$, we have the expansion ${s_{*,\xi ^{2}/\eta ^{2}}} = s_* + (-\frac{2}{3}a-\frac{4}{9}bs_*+\frac{4}{3}cs_*^2)^{-1}\frac{\xi ^2}{\eta ^2} + O(\frac{\xi ^4}{\eta ^4})$.

Proof

Let $Q\in {\mathrm{Sym}}_{0}$ be of norm $\sqrt{\frac{2}{3}}s_*$ and let $t\geqq 0$. Then we can estimate

$$\begin{aligned} \frac{1}{2\,\xi ^2}f(tQ) + \frac{1}{\eta ^2}g(tQ)&\geqq \frac{1}{2\xi ^2} C_f (t^2-1)^2 - \frac{C_g}{\eta ^2}(1+t^4) \, . \end{aligned}$$

So if we choose $|t-1|\geqq t_0>0$ and $\frac{\xi ^2}{\eta ^2}\leqq \frac{C_f}{2 C_g} \max _{|t-1|\geqq t_0}\frac{(t^2-1)^2}{t^4+1}$, the above expression is positive. Let $||Q|-\sqrt{\frac{2}{3}} s_*|\leqq \delta$ and ${\mathrm{dist}}(Q,{\mathcal {N}})>\delta$. Then $f(Q)\geqq f_{\mathrm{min}}:=\min \{f(Q)\, : \,Q\in {\mathrm{Sym}}_{0},\, {\mathrm{dist}}(Q,{\mathcal {N}})>\delta \}>0$ and

$$\begin{aligned} \frac{1}{2\, \xi ^2}f(Q) + \frac{1}{\eta ^2}g(Q)&\geqq \frac{f_{\mathrm{min}}}{2\xi ^2} - \frac{C}{\eta ^2}(1+\delta ^3) > 0\, , \end{aligned}$$

for $\xi ^2/\eta ^2\leqq \frac{f_{\mathrm{min}}}{2 C(1+\delta ^3)}$. By invariance of f under rotations and property 2. of g we know that a minimizer Q has the dominating eigenvector ${\mathbf{e}}_3$ or $-{\mathbf{e}}_3$ and has to verify $r=0$. This allows us to write $Q_s = s({\mathbf{e}}_3\otimes {\mathbf{e}}_3-\frac{1}{3}{\mathrm{Id}})$ for $s\in (-C\delta ,C\delta )$ for a constant $C>0$. Taking the derivative with respect to s in the energy of $Q_s$ we get

$$\begin{aligned} \frac{{\mathrm{d}}}{\mathrm{d} s}\left( \frac{1}{\xi ^{2}}f(Q_s) + \frac{1}{\eta ^{2}}g(Q_s)\right)&= \frac{1}{\xi ^{2}}\left( -\frac{2}{3}a s - \frac{2}{9}bs^{2} + \frac{4}{9}cs^{3}\right) \\&\quad - \frac{1}{\eta ^2}Dg(Q_{s}):\Big ({\mathbf{e}}_{3}\otimes {\mathbf{e}}_{3}-\frac{1}{3}{{\mathrm{Id}}}\Big ) = 0. \end{aligned}$$

We multiply by $\xi ^2$ and since $|Dg(Q_s)|$ is bounded and $\xi \ll \eta$ this equation admits a unique positive solution corresponding to a minimum in the energy density, which we call ${s_{*,\xi ^{2}/\eta ^{2}}}$. This gives the existence of a unique minimizer $Q_{\infty ,\xi ,\eta }$ and the claimed representation. By a standard perturbation theory argument we get the estimate $|s_{*,t} - s_*|\leqq C t$.

Since $|{s_{*,\xi ^{2}/\eta ^{2}}} - s_*|\leqq C \xi ^2/\eta ^2$, we have the estimates $f(Q_{\infty ,\xi ,\eta }) \leqq C (\xi ^2/\eta ^2)^2$ and $|g(Q_{\infty ,\xi ,\eta })|\leqq C \xi ^2/\eta ^2$ from which we get

$$\begin{aligned} C_0(\xi ,\eta ) \leqq C\frac{1}{\xi ^2}\frac{\xi ^4}{\eta ^4} + C \frac{2}{\eta ^2}\frac{\xi ^2}{\eta ^2} \leqq C \frac{\xi ^2}{\eta ^4}. \end{aligned}$$

Proposition 2.5

There exist ${\mathfrak {a}},\delta _0>0$ such that if $0<\delta <\delta _0$, then

$$\begin{aligned} \min \{ g(Q) \, : \,Q\in {\mathrm{Sym}}_{0}\text { with } {\mathrm{dist}}(Q,{\mathcal {N}})\leqq \delta \, , \, |Q-Q_\infty |\geqq {\mathfrak {a}}\sqrt{\delta } \} > 0\, . \end{aligned}$$

Proof

Let $0<\delta <\min \{\delta _1,1\}$, where $\delta _1$ is from (8). Let $Q\in {\mathrm{Sym}}_{0}$ such that ${\mathrm{dist}}(Q,{\mathcal {N}})\leqq \delta$. We can apply (8) to g(Q) to get

$$\begin{aligned} g(Q)&\geqq \ g({\mathcal {R}}(Q)) - C\, {\mathrm{dist}}(Q,{\mathcal {N}}) \ \geqq \ c_*^2(1-{\mathbf{n}}_3^2) - C\delta \, , \end{aligned}$$

where ${\mathbf{n}}_3$ is the third component of the dominating unit eigenvector of Q, see Proposition 2.3.

Since $|Q-{\mathcal {R}}(Q)|={\mathrm{dist}}(Q,{\mathcal {N}})\leqq \delta$ and $|{\mathbf{n}}|=|{\mathbf{e}}_3|=1$ we can estimate

$$\begin{aligned} |Q - Q_\infty |^2&\leqq 2|Q - {\mathcal {R}}(Q)|^2 + 2|{\mathcal {R}}(Q) - Q_\infty |^2 \leqq 2\delta ^2 + 2 s_*^2|{\mathbf{n}}\otimes {\mathbf{n}}-{\mathbf{e}}_3\otimes {\mathbf{e}}_3|^2 \\&\leqq 2\delta ^2 + 4s_*^2(1-{\mathbf{n}}_3^2)\, , \end{aligned}$$

and thus

$$\begin{aligned} g(Q)&\geqq \frac{c_*^2}{4s_*^2}|Q-Q_\infty |^2 - 4C\delta \geqq \Big (\frac{c_*^2}{4s_*^2}{\mathfrak {a}}- 4C\Big )\delta >0 \, , \end{aligned}$$

if $|Q-Q_\infty |\geqq {\mathfrak {a}}\sqrt{\delta }$ for ${\mathfrak {a}}>0$ large enough. In order to conclude, it remains to choose $0<\delta _0\leqq \min \{\delta _1,1\}$ in such a way that the set $\{Q\in {\mathrm{Sym}}_{0}\text { with } {\mathrm{dist}}(Q,{\mathcal {N}})\leqq \delta \,, \, |Q-Q_\infty |\geqq {\mathfrak {a}}\sqrt{\delta }\}$ is non empty for all $\delta \in (0,\delta _0)$. Setting $\delta _0=\min \{1,\delta _1,\frac{2}{3} s_*^2{\mathfrak {a}}^{-2}\}$, we have ${\mathfrak {a}}\sqrt{\delta }\leqq \sqrt{\frac{2}{3}}s_* + \delta$ for all $\delta \in (0,\delta _0)$, that is the set is non-empty. $\square$

As we have seen in Proposition 2.4, the minimizer $Q_{\infty ,\xi ,\eta }$ of the bulk term is not part of ${\mathcal {N}}$ (which has order parameter $s_*$). We will introduce a slightly modified manifold ${\mathcal {N}}_{\eta ,\xi }$ such that $Q_{\infty ,\xi ,\eta }\in {\mathcal {N}}_{\eta ,\xi }$ and such that $f(Q)+\frac{\xi ^2}{\eta ^2}g(Q)+\xi ^2 C_0(\xi ,\eta )$ controls the squared distance of Q to this new manifold, in analogy to $f(Q)\geqq \gamma _1{\mathrm{dist}}^2(Q,{\mathcal {N}})$ from Proposition 2.2.

Proposition 2.6

If $\xi ^2/\eta ^2\ll 1$, then there exists a smooth manifold ${\mathcal {N}}_{\eta ,\xi }\subset {\mathrm{Sym}}_{0}$, diffeomorphic to ${\mathcal {N}}$ such that

$$\begin{aligned} f(Q)+\frac{\xi ^2}{\eta ^2}g(Q)+\xi ^2 C_0(\xi ,\eta ) \geqq \gamma _2\, {\mathrm{dist}}^2(Q,{\mathcal {N}}_{\eta ,\xi }) \end{aligned}$$

(10)

for a constant $\gamma _2>0$. In particular $Q_{\infty ,\xi ,\eta }\in {\mathcal {N}}_{\eta ,\xi }$. Furthermore, there exists a constant $C>0$ such that

$$\begin{aligned} \sup _{Q\in {\mathcal {N}}_{\eta ,\xi }} {\mathrm{dist}}(Q,{\mathcal {N}}) \leqq C \frac{\xi ^2}{\eta ^2}\, . \end{aligned}$$

(11)

Proof

We introduce the notation $f_{\eta ,\xi }(Q)$ for the LHS of (10).

Step 1: Definition of ${\mathcal {N}}_{\eta ,\xi }$. Let $Q_0\in {\mathcal {N}}$ and $\{P_1,P_2,P_3\}$ a orthonormal basis of $(T_{Q_0}{\mathcal {N}})^\perp$. For $t\in {\mathbb {R}}^3$ we define $F(Q_0,t):=D_\nu f_{\eta ,\xi }(Q_0 + t_1 P_1 + t_2 P_2 + t_3 P_3)$, where $D_\nu$ denotes the derivative normal to ${\mathcal {N}}$. From perturbation theory it follows that there exists a $t_0\in {\mathbb {R}}^3$ with $|t_0|\leqq C\frac{\xi ^2}{\eta ^2}$ such that $F(Q_0,t_0)=0$. From Lemma 2.4 ($F_1$) in [20] we get that if $P\in {\mathrm{Sym}}_{0}$ orthogonal to $T_{Q_0}{\mathcal {N}}$, then $P\cdot (D^2 f(Q_0))P\geqq \gamma \Vert P\Vert ^2$. Hence, for $Q_t = Q_0 + t_1 P_1 + t_2 P_2 + t_3 P_3$ it holds that

$$\begin{aligned} D_t F(Q_0,t_0)&= \ D_\nu ^2 f(Q_t) + \frac{\xi ^2}{\eta ^2}D_\nu ^2 g(Q_t) \ \\&\geqq \ D_\nu ^2 f(Q_0) - C|t_0|{\mathrm{Id}}+ \frac{\xi ^2}{\eta ^2} D_\nu ^2 g(Q_t) \ \geqq \ \frac{\gamma }{2}{\mathrm{Id}}\, , \end{aligned}$$

since $D^2 g$ is bounded in a compact neighbourhood of ${\mathcal {N}}$, $|t_0|\leqq C \frac{\xi ^2}{\eta ^2}$ and $\frac{\xi ^2}{\eta ^2}\ll 1$. By the Implicit Function Theorem we conclude that there exists a smooth function $\psi :{\mathcal {N}}\rightarrow {\mathbb {R}}^3$ such that $F(Q_0,\psi (Q_0)) = 0$. Thus, ${\mathcal {N}}_{\eta ,\xi } := \{ Q_{t_0}\, : \,Q_0\in {\mathcal {N}}\text { and } t_0=\psi (Q_0) \}$ is a smooth manifold, diffeomorphic to ${\mathcal {N}}$. Furthermore, since $\psi$ is continuous and ${\mathcal {N}}$ is compact, we deduce that (11) holds.

Step 2: Control of the distance. Since $\xi ^2/\eta ^2$ is small and $f_{\eta ,\xi }$ grows faster than the RHS of (10), we can use (11) and argue similar to Proposition 2.4 to deduce that (10) holds if ${\mathrm{dist}}(Q,{\mathcal {N}}_{\eta ,\xi })\geqq \delta$ for some small but fixed $\delta >0$. Because of this, it is enough to show that (10) holds for all $Q\in {\mathrm{Sym}}_{0}$ with ${\mathrm{dist}}(Q,{\mathcal {N}}_{\eta ,\xi })<\delta$. For such Q, we first define $Q_0={\mathcal {R}}(Q)$. Let $Q_1\in {\mathcal {N}}_{\eta ,\xi }$ be the element corresponding to $Q_0$ according to step 1. Then $Q-Q_1\in (T_{Q_0}{\mathcal {N}})^\perp$ and by Taylor expansion it holds that

$$\begin{aligned} f_{\eta ,\xi }(Q)&\geqq \ f_{\eta ,\xi }(Q_1) + D_\nu f_{\eta ,\xi }(Q_1):(Q-Q_1)\\&\quad + \frac{1}{2}(Q-Q_1)\cdot D^2 f_{\eta ,\xi }(Q_1)(Q-Q_1) - C \delta |Q-Q_1|^2\, . \end{aligned}$$

Note that $f_{\eta ,\xi }(Q)\geqq 0$ and by construction $D_\nu f_{\eta ,\xi }(Q_1):(Q-Q_1)=0$. Evoking again Lemma 2.4 in [20], we get

$$\begin{aligned} f_{\eta ,\xi }(Q)&\geqq \ \Big (\frac{\gamma }{4} - C\delta \Big )|Q-Q_1|^2\, . \end{aligned}$$

Choosing $\delta >0$ small enough there exists a $\gamma _2>0$ such that $\frac{\gamma }{4} - C\delta \geqq \gamma _2>0$ and since ${\mathrm{dist}}(Q,{\mathcal {N}}_{\eta ,\xi })\leqq |Q - Q_1|$, (10) follows.

From Proposition 2.4 we know that $f_{\eta ,\xi }(Q_{\infty ,\xi ,\eta })=0$ and hence by (10) it follows that ${\mathrm{dist}}(Q_{\infty ,\xi ,\eta },{\mathcal {N}}_{\eta ,\xi })=0$, that is $Q_{\infty ,\xi ,\eta }\in {\mathcal {N}}_{\eta ,\xi }$. $\square$

3 Statement of Result

From equation (2) and using the notation introduced in the last section, we write our energy

$$\begin{aligned} {\mathcal {E}}_{\eta ,\xi }(Q) = \int _\Omega \frac{1}{2}|\nabla Q|^2 + \frac{1}{\xi ^2} f(Q) + \frac{1}{\eta ^2} g(Q) + C_0(\xi ,\eta ) \, {\mathrm{d}} x\, , \end{aligned}$$

(12)

which is the dimensionless free energy that was announced in the introduction. The natural space for this energy to be well defined is $H^1(\Omega ,{\mathrm{Sym}}_{0})+Q_{\infty ,\xi ,\eta }$ with $Q_{\infty ,\xi ,\eta }$ as in Proposition 2.4. Minimizing the first term would lead to a harmonic map; the second term prefers Q to be uniaxial with a certain scalar order parameter and hence norm, while the third term takes its minimum when the director is aligned parallel to ${\mathbf{e}}_3$. Thus the (spatially) constant uniaxial map $Q_{\infty ,\xi ,\eta } = {s_{*,\xi ^{2}/\eta ^{2}}}({\mathbf{e}}_3\otimes {\mathbf{e}}_3 - \frac{1}{3}{\mathrm{Id}})$ would be a minimizer of our free energy. However, this will violate the strong anchoring conditions we are going to impose on the boundary, namely we want $Q_{\eta ,\xi }\in H^1(\Omega ,{\mathrm{Sym}}_{0})+Q_{\infty ,\xi ,\eta }$ to satisfy

$$\begin{aligned} Q_{\eta ,\xi }= Q_b \quad \text {on }\,\,{\mathbb {S}}^2\, , \end{aligned}$$

(13)

where $Q_b(x) = s_*\left( {\mathbf{x}}\otimes {\mathbf{x}}- \frac{1}{3}{\mathrm{Id}}\right)$. The system is therefore frustrated and we expect the minimizer to be close to $s_*({\mathbf{e}}_3\otimes {\mathbf{e}}_3 - \frac{1}{3}{\mathrm{Id}})$ everywhere, except for a transition zone near the boundary. In this boundary layer, which will turn out to be of thickness $\eta$, we will find tubes of cross sectional area $\xi ^2$ containing the regions where $Q_{\eta ,\xi }$ is biaxial.

Since the problem is equivariant with respect to rotations around the ${\mathbf{e}}_3-$axis, it is natural to consider only rotationally equivariant maps. We say that a map Q is rotationally equivariant if Q is equivariant with respect to rotations around the ${\mathbf{e}}_3$-axis. In other words, using cylindrical coordinates, one has

$$\begin{aligned} Q(\rho ,\varphi ,z) = R_\varphi ^\top Q(\rho ,0,z) R_\varphi \, , \quad \text { where }\quad R_\varphi = \begin{pmatrix} \cos \varphi &{} -\sin \varphi &{} 0 \\ \sin \varphi &{} \cos \varphi &{} 0 \\ 0 &{} 0 &{} 1 \end{pmatrix}\, . \end{aligned}$$

For uniaxial maps $Q=s_*({\mathbf{n}}\otimes {\mathbf{n}}-\frac{1}{3}{\mathrm{Id}})$ this is equivalent to the usual notion of equivariance for vectors ${\mathbf{n}}(R_\varphi {\mathbf{x}}) = R_\varphi ^\top {\mathbf{n}}({\mathbf{x}})$. We define the set of admissible functions ${\mathcal {A}}$ to be the set of rotationally equivariant functions $Q_{\eta ,\xi }\in H^1(\Omega ,{\mathrm{Sym}}_{0})+Q_{\infty ,\xi ,\eta }$ satisfying the boundary condition (13). This motivates the definition for $Q\in H^1(\Omega ,{\mathbb {R}}^{3\times 3})+Q_{\infty ,\xi ,\eta }$

$$\begin{aligned} {\mathcal {E}}_{\eta ,\xi }^{\mathcal {A}}(Q) =\left\{ \begin{array}{ll} {\mathcal {E}}_{\eta ,\xi }(Q) &{}\quad \text {if }Q\in {\mathcal {A}}\, , \\ \infty &{}\quad \text {otherwise.} \end{array}\right. \end{aligned}$$

We believe that minimizers of ${\mathcal {E}}_{\eta ,\xi }$ are also rotationally equivariant, although this does not follow from our work and remains an open issue. We will remove the hypothesis of rotational equivariance in a work in preparation.

The following theorem is the main result of the paper:

Theorem 3.1

Suppose that

$$\begin{aligned} \eta |\ln (\xi )|\rightarrow \beta \in (0,\infty ) \quad \text { as } \eta \rightarrow 0\, . \end{aligned}$$

(14)

Then $\eta \,{\mathcal {E}}_{\eta ,\xi }^{\mathcal {A}}\rightarrow {\mathcal {E}}_0$ in a variational sense, where the limiting energy ${\mathcal {E}}_0$ for a set $F\subset {\mathbb {S}}^2$ is given by

$$\begin{aligned} {\mathcal {E}}_0(F)= & {} 2s_*c_*\int _F (1 - \cos (\theta )) \, {\mathrm{d}} \omega + 2s_*c_*\int _{F^c} (1 + \cos (\theta )) \, {\mathrm{d}} \omega \nonumber \\&+ \frac{\pi }{2}s_*^2\beta |D\chi _F|({\mathbb {S}}^2)\, . \end{aligned}$$

(15)

More precisely, we have the following statements:

• 1. Compactness: For any sequence $Q_{\eta ,\xi }\in {\mathcal {A}}$ such that $\eta \, {\mathcal {E}}_{\eta ,\xi }(Q_{\eta ,\xi })\leqq C$, there exists a measurable set of finite perimeter $F\subset {\mathbb {S}}^2$ that is invariant under rotations with respect to the ${\mathbf{e}}_3-$axis, measurable functions ${\mathbf{n}}^\eta :\Omega \rightarrow {\mathbb {S}}^2$ and a set $\omega _\eta \subset \Omega$ with $\lim _{\eta \rightarrow 0}|\omega _\eta |= 0$, $\Omega {\setminus }\omega _\eta$ simply connected, such that for all $\sigma >0$ it holds ${\mathbf{n}}^\eta \in C^0(\Omega {\setminus }(Z_\sigma \cup \omega _\eta ),{\mathbb {S}}^2)$ and for all $R>0$

  $$\begin{aligned} \lim _{\eta \rightarrow 0}\bigg \Vert s_*\bigg ({\mathbf{n}}^\eta \otimes {\mathbf{n}}^\eta -\frac{1}{3}{\mathrm{Id}}\bigg )-Q_{\eta ,\xi }\bigg \Vert _{L^2(B_R(0){\setminus } Z_\sigma )}=0\, , \quad \chi _{F_\eta }\rightarrow \chi _F \text { pointwise,} \end{aligned}$$

  (16)

  where $Z_\sigma =\{x\in {\mathbb {R}}^3\, : \,x_1^2+x_2^2\leqq \sigma ^2\}$ and $F_\eta =\{ x\in \partial \Omega \, : \,{\mathbf{n}}^\eta (x)\cdot \nu (x)=-1 \}$.

• 2. $\Gamma -$liminf: For any sequence $Q_{\eta ,\xi }\in {\mathcal {A}}$ and any measurable set of finite perimeter $F\subset {\mathbb {S}}^2$, measurable functions ${\mathbf{n}}^\eta :\Omega \rightarrow {\mathbb {S}}^2$ and a measurable set $\omega _\eta \subset \Omega$ that satisfy $\lim _{\eta \rightarrow 0}|\omega _\eta |= 0$, $\Omega {\setminus }\omega _\eta$ simply connected with ${\mathbf{n}}^\eta \in C^0(\Omega {\setminus }(Z_\sigma \cup \omega _\eta ),{\mathbb {S}}^2)$ and (16) hold for all $R,\sigma >0$, we have

  $$\begin{aligned} \liminf _{\eta \rightarrow 0} \eta \,{\mathcal {E}}_{\eta ,\xi }(Q_{\eta ,\xi }) \geqq {\mathcal {E}}_0(F)\, . \end{aligned}$$

  (17)

• 3. $\Gamma -$limsup: For any measurable set of finite perimeter $F\subset {\mathbb {S}}^2$ that is invariant under rotations with respect to the ${\mathbf{e}}_3-$axis there exists a sequence $Q_{\eta ,\xi }\in {\mathcal {A}}$ with $\Vert Q_{\eta ,\xi }\Vert _{L^\infty }\leqq \sqrt{\frac{2}{3}}s_*$ and measurable functions ${\mathbf{n}}^\eta :\Omega \rightarrow {\mathbb {S}}^2$ with ${\mathbf{n}}^\eta \in C^0(\Omega {\setminus }\omega _\eta ,{\mathbb {S}}^2)$, $\lim _{\eta \rightarrow 0}|\omega _\eta |= 0$, $\Omega {\setminus }\omega _\eta$ simply connected, such that (16) holds for all $R,\sigma >0$ and

  $$\begin{aligned} \limsup _{\eta \rightarrow 0} \eta \,{\mathcal {E}}_{\eta ,\xi }(Q_{\eta ,\xi }) \leqq {\mathcal {E}}_0(F)\, . \end{aligned}$$

  (18)

Remark 3.2

• 1. In view of (14) we can replace the bound $\eta \, {\mathcal {E}}_{\eta ,\xi }(Q_{\eta ,\xi })\leqq C$, by

  $$\begin{aligned} {\mathcal {E}}_{\eta ,\xi }(Q_{\eta ,\xi })\leqq C\, \left( 1+|\ln (\xi )|\right) \, . \end{aligned}$$

  (19)

• 2. The convergence we show is not a $\Gamma -$convergence in the classical sense since the limit functional is defined on a different functions space.

• 3. The compactness can also be formulated globally: It holds

  $$\begin{aligned} \lim _{\eta \rightarrow 0} \int _{\Omega {\setminus } Z_\sigma } {\mathrm{dist}}^2(Q_{\eta ,\xi },{\mathcal {N}}_{\eta ,\xi }) \, {\mathrm{d}} x \ = \ 0 \end{aligned}$$

  for the manifold ${\mathcal {N}}_{\eta ,\xi }$ as in Proposition 2.6 which is a small perturbation (at distance at most $C\frac{\xi ^2}{\eta ^2}$) from the manifold ${\mathcal {N}}$. In addition if g is non-negative (for example in the case $g=g_2$), ${\mathcal {N}}_{\eta ,\xi }={\mathcal {N}}$ and we have the convergence

  $$\begin{aligned} \lim _{\eta \rightarrow 0}\bigg \Vert s_*\bigg ({\mathbf{n}}^\eta \otimes {\mathbf{n}}^\eta -\frac{1}{3}{\mathrm{Id}}\bigg )-Q_{\eta ,\xi }\bigg \Vert _{L^2(\Omega {\setminus } Z_\sigma )} \ = \ 0\, . \end{aligned}$$

Remark 3.3

If $\beta =\infty$ in (14), then Theorem 3.1 holds for $F={\mathbb {S}}^2$ or $F=\emptyset$, that is no Saturn ring structure can occur in the limit. In the case of g being non-negative, this follows easily: For $Q_{\eta ,\xi }\in H^1(\Omega ,{\mathrm{Sym}}_{0})+Q_\infty$ with $\eta {\mathcal {E}}_{\eta ,\xi }(Q_{\eta ,\xi })\leqq C$ we can introduce ${\tilde{\xi }}$ such that $\eta |\ln ({\tilde{\xi }})|\rightarrow \beta \in (0,\infty )$, that is this new sequence ${\tilde{\xi }}$ decreases more slowly than $\xi$. Hence ${\mathcal {E}}_{\eta ,{\tilde{\xi }}}\leqq {\mathcal {E}}_{\eta ,\xi }$. Applying Theorem 3.1 to this new energy we get the existence of a set $F_\beta \subset {\mathbb {S}}^2$ such that

$$\begin{aligned} {\mathcal {E}}_0(F_\beta ) \leqq \liminf _{\eta \rightarrow 0} \eta \,{\mathcal {E}}_{\eta ,\xi }(Q_{\eta ,\xi }) \leqq C\, . \end{aligned}$$

Since the RHS is independent of $\beta \in (0,\infty )$, we find $|D\chi _{F_\beta }|({\mathbb {S}}^2)\rightarrow 0$ as $\beta \rightarrow \infty$. From this we conclude $F={\mathbb {S}}^2$ or $F=\emptyset$ which have the same energy ${\mathcal {E}}_0$. For the case of general g one cannot apply this trick, but using (42) it is possible to show that the perimeter of $F_{\eta }$ converges to zero and that ${\mathcal {E}}_0({\mathbb {S}}^2)$ is indeed a lower bound.

4 Lower Bound

In this section we prove the lower bound of Theorem 3.1. Our strategy to obtain the lower bound starts by approximating the sequence $Q_{\eta ,\xi }$ by a more regular one named $Q_\epsilon$. We use $\epsilon :=\xi$ to meet the notation in [3, 18, 19] and let out $\eta$ in our notation since $\eta$ and $\xi$ are related via (14), that is $\eta \sim \frac{\beta }{|\ln (\epsilon )|}$. We also write ${\mathcal {E}}_\epsilon$ instead of ${\mathcal {E}}_{\eta ,\xi }$. We find that away from the ${\mathbf{e}}_3$-axis the sequence $Q_\epsilon$ has only finitely many singularities in the neighbourhood of which $Q_\epsilon$ is far from ${\mathcal {N}}$. Then we can estimate the energy of $Q_\epsilon$ nearby these points from below by balancing $|\nabla Q_\epsilon |^2$ and $f(Q_\epsilon )$. In the region where $Q_\epsilon$ is close to ${\mathcal {N}}$, we will use the optimal radial profile found in [3] by balancing $|\nabla Q_\epsilon |^2$ and $g(Q_\epsilon )$.

4.1 Preliminaries

The construction of the approximation $Q_\epsilon$ of $Q_{\eta ,\xi }$ follows several steps. First, we are going to show that $Q_{\eta ,\xi }$ can be approximated by another function ${\widetilde{Q_{\eta ,\xi }}}$ which verifies an additional $L^\infty -$bound.

Proposition 4.1

Let $Q_{\eta ,\xi }\in H^1(\Omega ,{\mathrm{Sym}}_{0})+Q_{\infty ,\xi ,\eta }$ such that (19) holds. Then there exists a constant $C_1>0$ and ${\widetilde{Q_{\eta ,\xi }}}\in H^1(\Omega ,{\mathrm{Sym}}_{0})+Q_{\infty ,\xi ,\eta }$ which decreases the energy ${\mathcal {E}}_{\eta ,\xi }$, verifies

$$\begin{aligned} \Vert {\widetilde{Q_{\eta ,\xi }}} \Vert _{L^\infty (\Omega )} \leqq C_1 \end{aligned}$$

(20)

and ${\widetilde{Q_{\eta ,\xi }}}-Q_{\eta ,\xi }\rightarrow 0$ in $L^2$ as $\eta ,\xi \rightarrow 0$.

Proof

Let $N>\sqrt{\frac{2}{3}}s_*$ to be chosen later. We can define ${\widetilde{Q_{\eta ,\xi }}}$ as

$$\begin{aligned} {\widetilde{Q_{\eta ,\xi }}} :=\left\{ \begin{array}{ll} N\frac{Q_{\eta ,\xi }}{|Q_{\eta ,\xi }|} &{} \text {if }|Q_{\eta ,\xi }|>N\, , \\ Q_{\eta ,\xi }&{} \text {otherwise.} \end{array}\right. \end{aligned}$$

This function is clearly admissible and has lower Dirichlet energy. Since we cannot conclude that $g({\widetilde{Q_{\eta ,\xi }}})\leqq g(Q_{\eta ,\xi })$, we need to show that the (possible) increase of the energy in g is compensated by the decrease in f. So if $Q\in {\mathrm{Sym}}_{0}$ of norm 1 and $t>N$, we get, by (6) and Proposition 2.2,

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d} t} \left( \frac{1}{\xi ^2}f(tQ) + \frac{1}{\eta ^2}g(tQ) \right)&\geqq C\frac{t^3}{\xi ^2} - C \frac{1+t^3}{\eta ^2} \geqq 0 \end{aligned}$$

if $N\geqq N_1$ with a certain $N_1$ large enough, depending on f and g. Hence, the sum of bulk and magnetic energy of ${\widetilde{Q_{\eta ,\xi }}}$ is smaller than the one of $Q_{\eta ,\xi }$ and we conclude ${\mathcal {E}}_{\eta ,\xi }({\widetilde{Q_{\eta ,\xi }}})\leqq {\mathcal {E}}_{\eta ,\xi }(Q_{\eta ,\xi })$. The $L^\infty -$ bound is obvious, so it remains to show that $\Vert {\widetilde{Q_{\eta ,\xi }}}-Q_{\eta ,\xi }\Vert _{L^2(\Omega )}$ converges to zero as $\eta ,\xi \rightarrow 0$. We decompose $\Omega$ into two sets,

$$\begin{aligned} \Omega =\{x\, : \,|Q_{\eta ,\xi }(x)|\leqq N\}\cup \{x\, : \,|Q_{\eta ,\xi }(x)|> N\}, \end{aligned}$$

and note that $\int |{\widetilde{Q_{\eta ,\xi }}}-Q_{\eta ,\xi }|^2 =0$ if $|Q_{\eta ,\xi }|\leqq N$. Hence, we only need to estimate the difference $|{\widetilde{Q_{\eta ,\xi }}}-Q_{\eta ,\xi }|$ on the second set. By Proposition 2.2 and (5) we get that there exists $C,N_2>0$ (depending on f and g) such that if $N\geqq N_2$, then for $Q\in {\mathrm{Sym}}_{0}$ with $|Q|\geqq N$ it holds that

$$\begin{aligned} \Big | \frac{2}{3}s_*^2 - |Q|^2 \Big |^2&\leqq 2\left( \Big | \frac{2}{3}s_*^2 - |Q|^2 \Big |^{2} - \frac{\xi ^2}{\eta ^2}|Q|^4 + \xi ^2 C_0(\xi ,\eta )\right) \\&\leqq C \left( f(Q) + \frac{\xi ^2}{\eta ^2}g(Q)+\xi ^{2} C_0(\xi ,\eta )\right) \, . \end{aligned}$$

For $|Q|\geqq \max \{N_1,N_2\}$ we additionally have $|Q_{\eta ,\xi }-{\widetilde{Q_{\eta ,\xi }}}| = |N - |Q_{\eta ,\xi }||$. Taking N even bigger if necessary it holds that

$$\begin{aligned}&\int _{|Q_{\eta ,\xi }|>N} |Q_{\eta ,\xi }- {\widetilde{Q_{\eta ,\xi }}}|^2\, {\mathrm{d}} x \\&\quad = \int _{|Q_{\eta ,\xi }|>N} |N - |Q_{\eta ,\xi }||^2\, {\mathrm{d}} x \leqq C \int _{|Q_{\eta ,\xi }|>N} \Big |\frac{2}{3}s_*^2 - |Q_{\eta ,\xi }|^2\Big |^2\, {\mathrm{d}} x \\&\quad \leqq C \int _\Omega f(Q) + \frac{\xi ^2}{\eta ^2}g(Q)+\xi ^2 C_0(\xi ,\eta ) \, {\mathrm{d}} x \leqq C (1+|\ln \xi |)\xi ^2\, , \end{aligned}$$

which converges to zero as $\xi \rightarrow 0$. This proves our claim for $C_1\geqq N$. $\square$

Since g may not be regular in $Q=0$ (for example if $g=g_2$), we will replace g by $g\phi$, with a cut-off function $\phi$ such that $g\phi$ is smooth, but keeps the relevant information from g. In order to replace g in the energy, we just need to show that $\int (1-\phi )g(Q_{\eta ,\xi })\, {\mathrm{d}} x$ tends to zero in the limit $\xi ,\eta \rightarrow 0$. This is made precise in the next proposition.

Proposition 4.2

Let $\phi \in C^\infty ([0,\infty ),[0,1])$ be a cut-off function with $\phi =1$ on $[q_0,\infty )$ and $\phi =0$ on $[0,\frac{1}{2}q_0]$, where $q_0\in (0,\sqrt{\frac{2}{3}}s_*)$. Then the function $Q\mapsto g(Q)\phi (|Q|)$ is smooth and there exists a constant $C>0$ such that

$$\begin{aligned} \int _\Omega (1-\phi (|Q_{\eta ,\xi }|))g(Q_{\eta ,\xi })\, {\mathrm{d}} x&\leqq C \frac{\xi ^2}{\eta }\, . \end{aligned}$$

Proof

The smoothness of $g\phi$ is obvious, since $\phi$ is smooth and we supposed g smooth away from 0. So it remains the energy estimate. First note that if $Q\in {\mathrm{Sym}}_{0}$ with $|Q|\leqq q_0$, then for $\xi ,\eta$ small enough $f(Q) + \frac{\xi ^2}{\eta ^2}g(Q) + \xi ^2 C_0(\xi ,\eta )\geqq \frac{1}{2}f_{\mathrm{min}}>0$, where $f_{\mathrm{min}}=\min \{f(Q)\, : \,Q\in {\mathrm{Sym}}_{0},\, |Q|\leqq q_0\}$. Indeed, by Proposition 2.2$f_{\mathrm{min}}>0$ and by (5) we can choose $\frac{\xi ^2}{\eta ^2}$ small enough such that $\frac{\xi ^2}{\eta ^2}g(Q)\leqq \frac{1}{4}f_{\mathrm{min}}$. Since $\xi ^2 C_0(\xi ,\eta )$ converges to zero as $\xi ,\eta \rightarrow 0$, this can equally be bounded by $\frac{1}{4}f_{\mathrm{min}}$. Hence

$$\begin{aligned} C&\geqq \frac{\eta }{\xi ^2} \int _{\{x\in \Omega \, : \,|Q_{\eta ,\xi }(x)|\leqq q_0\}} f(Q_{\eta ,\xi }) + \frac{\xi ^2}{\eta ^2}g(Q_{\eta ,\xi }) + \xi ^2 C_0(\xi ,\eta ) \, {\mathrm{d}} x \\&\geqq \frac{1}{2}\frac{\eta }{\xi ^2} f_{\mathrm{min}} |\{ x\in \Omega \, : \,|Q_{\eta ,\xi }(x)|\leqq q_0 \}| \, . \end{aligned}$$

Now we use this estimate to bound

$$\begin{aligned} \int _\Omega (1-\phi (|Q_{\eta ,\xi }|))g(Q_{\eta ,\xi })\, {\mathrm{d}} x&\leqq C |\{ x\in \Omega \, : \,|Q_{\eta ,\xi }(x)|\leqq q_0 \}| \leqq C \frac{\xi ^2}{\eta }\, . \end{aligned}$$

$\square$

From now on, we simply write g(Q) instead of $g(Q)\phi (|Q|)$. We will also replace $\eta ,\xi$ in our notation by $\epsilon$, that is $\widetilde{Q_\epsilon }:={\widetilde{Q_{\eta ,\xi }}}$. For the sake of readability, we introduce the notation $f_\epsilon (Q):=f(Q) + \frac{\epsilon ^2}{\eta ^2}g(Q) + \epsilon ^2 C_0(\epsilon ,\eta )$. The next step will be defining the more regular sequence $Q_\epsilon$ replacing $\widetilde{Q_\epsilon }$. In view of the lower bound for the claimed $\Gamma -$limit we still want $Q_\epsilon$ to be rotationally equivariant and that it converges to the same limit as $\widetilde{Q_\epsilon }$, while decreasing the energy.

We thus define the three dimensional approximate energy for $0<\gamma <2$ and $\omega \subset \Omega$

$$\begin{aligned} E_\epsilon ^{3D}(Q,\omega ) = \int _\omega \frac{1}{2}|\nabla Q|^2 + \frac{1}{\epsilon ^2} f_{\epsilon }(Q) + \frac{1}{2\epsilon ^\gamma }|Q - \widetilde{Q_\epsilon }|^2 \, {\mathrm{d}} x\, . \end{aligned}$$

We seek $Q_\epsilon$ by minimizing $E_\epsilon ^{3D}(Q,\Omega )$ among rotationally equivariant fields Q. Because of the equivariance, the problem can be stated as a two dimensional problem. Indeed, calculating $|\partial _\varphi Q|^2$ for a rotationally equivariant map $Q\in H^1(\Omega ,{\mathrm{Sym}}_{0})+Q_{\infty ,\xi ,\eta }$, and using the equivariance, we can write $Q(\rho ,\varphi ,z) = R_\varphi ^\top Q(\rho ,0,z) R_\varphi$ and thus

$$\begin{aligned} |\partial _\varphi Q|^2&= \left| (\partial _\varphi R_\varphi )^\top Q R_\varphi + R_\varphi ^\top Q (\partial _\varphi R_\varphi ) \right| ^2 = |Q|^2 + 6 (Q_{12}^2 - Q_{11}Q_{22})\, . \end{aligned}$$

This expression does no longer depend on $\varphi$. In order to shorten notation, we introduce the matrix

$$\begin{aligned} Q_{2\times 2} :=\frac{1}{2}\left( \frac{\partial }{\partial Q_{ij}} |\partial _\varphi Q|^2 \right) _{ij} = \begin{pmatrix} 2(Q_{11} - Q_{22}) &{} 4 Q_{12} &{} Q_{13} \\ 4Q_{21} &{} 2(Q_{22}- Q_{11}) &{} Q_{23} \\ Q_{31} &{} Q_{32} &{} 0 \end{pmatrix}\, . \end{aligned}$$

Note that, $Q_{2\times 2}:Q = \frac{1}{2}|\partial _\varphi Q|^2$. So the whole energy does not depend on $\varphi$ any more and using cylindrical coordinates, it can be rewritten as

$$\begin{aligned} E_\epsilon ^{3D}(Q_\epsilon ,\Omega )&= \int _0^{2\pi } E_\epsilon ^{2D}(Q_\epsilon ,\Omega ') \, {\mathrm{d}} \varphi = 2\pi \, E_\epsilon ^{2D}(Q_\epsilon ,\Omega ') \, , \end{aligned}$$

where $E_\epsilon ^{2D}$ is the two dimensional energy given by

$$\begin{aligned} E_\epsilon ^{2D}(Q,\omega ') = \int _{\omega '} \frac{\rho }{2}|\nabla ' Q|^2 + \frac{1}{\rho } Q_{2\times 2}:Q + \frac{\rho }{\epsilon ^2} f_{\epsilon }(Q) + \frac{\rho }{2\epsilon ^\gamma }|Q - \widetilde{Q_\epsilon }|^2 \, {\mathrm{d}} \rho \, {\mathrm{d}} z\, , \end{aligned}$$

where $\nabla '=(\partial _\rho ,\partial _z)$ denotes the two dimensional gradient and $\omega '\subset \Omega '=\{ (\rho ,z)\in {\mathbb {R}}^2\, : \,\rho>0\, ,\, \rho ^2+z^2> 1 \}$. In order to shorten notation, we are going to write $\frac{1}{2}|\nabla Q|^2$ instead of $\frac{1}{2}|\nabla ' Q|^2+\frac{1}{\rho ^2}Q_{2\times 2}:Q$ whenever we make no use of this division of the gradient. Now we define $Q_\epsilon$ to be

$$\begin{aligned} Q_\epsilon :=\underset{Q\in {\mathcal {A}}'}{\mathrm {argmin}}\, E_\epsilon ^{2D}(Q,\Omega ')\, , \end{aligned}$$

(21)

where ${\mathcal {A}}'=\{Q\in H^1(\Omega ',{\mathrm{Sym}}_{0})+Q_{\infty ,\xi ,\eta }\, : \,(13) \text { holds for } \rho ^2+z^2=1 \}$. We eventually extend $Q_\epsilon$ to a map in $H^1(\Omega ,{\mathrm{Sym}}_{0}){+Q_{\infty ,\xi ,\eta }}$ which we will also call $Q_\epsilon$ by defining $Q_\epsilon (\rho ,\varphi ,z):=R_\varphi ^\top Q_\epsilon (\rho ,z) R_\varphi$.

Remark 4.3

• 1. Note that $\widetilde{Q_\epsilon }|_{\Omega '}$ is an admissible function in (21), so that $Q_\epsilon$ does exist.

• 2. The function $Q_\epsilon$ has lower energy than $\widetilde{Q_\epsilon }$.

• 3. Thanks to the energy bound in (19) we know that

  $$\begin{aligned} \Vert Q_\epsilon - \widetilde{Q_\epsilon }\Vert _{L^2(\Omega )}^2 \leqq C (|\ln \epsilon | + 1) \epsilon ^\gamma \rightarrow 0 \quad \text { as } \epsilon \rightarrow 0\, , \end{aligned}$$

  that is the two sequences have the same limit for vanishing $\epsilon$.

• 4. The minimizer $Q_\epsilon$ solves the two dimensional Euler-Lagrange equation

  $$\begin{aligned} -\rho \Delta Q_\epsilon + \frac{1}{\rho } Q_{\epsilon ,2\times 2} - \partial _\rho Q_\epsilon + \frac{\rho }{\epsilon ^2} Df_{{\epsilon }}(Q) + \frac{\rho }{\epsilon ^\gamma } (Q_\epsilon - \widetilde{Q_\epsilon }) = \Lambda \, {\mathrm{Id}}\, .\nonumber \\ \end{aligned}$$

  (22)

  Note that the equation contains an additional term (RHS) due to the fact that ${\mathrm{Sym}}_{0}$ is a subspace of the space of real matrices, that is a Lagrange multiplier $\Lambda$ is needed to ensure the tracelessness constraint.

• 5. The function $Q_\epsilon$ also solves the three dimensional Euler-Lagrange equation

  $$\begin{aligned} -\Delta Q_\epsilon + \frac{1}{\epsilon ^2} Df_{{\epsilon }}(Q_\epsilon ) + \frac{1}{\epsilon ^\gamma } (Q_\epsilon - \widetilde{Q_\epsilon }) = \Lambda _{3D}\, {\mathrm{Id}}\, , \end{aligned}$$

  (23)

  despite the fact that it does not need to be a minimizer of $E_\epsilon ^{3D}$. To see this, write

  $$\begin{aligned} \Lambda _{3D}\, {\mathrm{Id}}&= -\Delta Q_\epsilon + \frac{1}{\epsilon ^2} Df_{{\epsilon }}(Q_\epsilon ) + \frac{1}{\epsilon ^\gamma }(Q_\epsilon - \widetilde{Q_\epsilon }) \\&= -\partial _\rho ^2 Q_\epsilon - \frac{1}{\rho } \partial _\rho Q_\epsilon - \frac{1}{\rho ^2}\partial _\varphi ^2 Q_\epsilon - \partial _z^2 Q_\epsilon + \frac{1}{\epsilon ^2} Df_{{\epsilon }}(Q) + \frac{1}{\epsilon ^\gamma } (Q_\epsilon - \widetilde{Q_\epsilon }) \\&= R_\varphi ^\top \left( -\partial _\rho ^2 Q_\epsilon - \frac{1}{\rho } \partial _\rho Q_\epsilon - \partial _z^2 Q_\epsilon + \frac{1}{\epsilon ^\gamma } (Q_\epsilon - \widetilde{Q_\epsilon }) \right) R_\varphi \\&\quad - \frac{1}{\rho ^2}\partial _\varphi ^2 (R_\varphi ^\top Q_\epsilon R_\varphi ) + \frac{1}{\epsilon ^2} Df_{{\epsilon }}(R_\varphi ^\top Q_\epsilon R_\varphi )\, . \end{aligned}$$

  One can explicitly calculate that $\partial _\varphi ^2 (R_\varphi ^\top Q_\epsilon R_\varphi ) = R_\varphi ^\top Q_{2\times 2,\epsilon }R_\varphi$ and since $f_\epsilon$ is invariant under the change $Q\leftrightarrow R_\varphi ^\top Q R_\varphi$, for symmetric matrices Q, we also have $Df_\epsilon (R_\varphi ^\top Q_\epsilon R_\varphi ) = R_\varphi ^\top Df_\epsilon (Q_\epsilon ) R_\varphi$. This implies that a rotationally equivariant extended solution of (22) is also solution of (23).

The last part of this subsection will be the following proposition which quantifies the regularity we have gained by replacing $\widetilde{Q_\epsilon }$ with $Q_\epsilon$. This result relies on the three dimensional Euler-Lagrange equation. In fact, this is the only time we use (23) and cannot use (22) due to its singular behaviour near $\rho =0$.

Proposition 4.4

Let $\Vert \widetilde{Q_\epsilon }\Vert _{L^\infty }\leqq C_1$ for a constant $C_1\geqq \sqrt{\frac{2}{3}}s_*>0$ and let $Q_\epsilon$ be the rotationally equivariant extended minimizer of (21). Then $Q_\epsilon \in C^1(\Omega ,{\mathrm{Sym}}_{0})$,

$$\begin{aligned} \Vert Q_\epsilon \Vert _{L^\infty } \leqq C \quad \text {and}\quad \Vert \nabla Q_\epsilon \Vert _{L^\infty } \leqq \frac{C}{\epsilon }\, . \end{aligned}$$

Proof

From equation (23) and by elliptic regularity we deduce that for $\widetilde{Q_\epsilon }\in H^1$ we have $Q_\epsilon \in H^3$, that is $Q_\epsilon \in C^{1,\frac{1}{2}}$ since we are in dimension 3. Note that the boundary of $\Omega$ is smooth. To prove the $L^\infty$-bounds we take a constant $C_2>C_1$ such that $Df_{\epsilon }(Q):Q\geqq 0$ for all $Q\in {\mathrm{Sym}}_{0}$ with $|Q|\geqq C_2$. This is possible due to Proposition 2.2 and (6). We define a comparison map

$$\begin{aligned} \overline{Q_\epsilon } :=\left\{ \begin{array}{ll} C_2\frac{Q_\epsilon }{|Q_\epsilon |} &{} \text {if } |Q_\epsilon |>C_2\, , \\ Q_\epsilon &{} \text {otherwise.} \end{array}\right. \end{aligned}$$

Then $|\nabla \overline{Q_\epsilon }|\leqq |\nabla Q_\epsilon |$, $|\overline{Q_\epsilon }-\widetilde{Q_\epsilon }| \leqq |Q_\epsilon -\widetilde{Q_\epsilon }|$ and $f_{{\epsilon }}({\overline{Q}})\leqq f_{{\epsilon }}(Q_\epsilon )$ by Proposition 2.2 and our choice of $C_2$. Hence $E_\epsilon ^{3D}(\overline{Q_\epsilon },\Omega )\leqq E_\epsilon ^{3D}(Q_\epsilon ,\Omega )$ with strict inequality unless $\overline{Q_\epsilon }=Q_\epsilon$. The estimate $\Vert \nabla Q_\epsilon \Vert _{L^\infty } \leqq \frac{C}{\epsilon }$ follows from [14, Lemma A.2], using (23), (20) and $\gamma < 2$. $\square$

4.2 Finite Number of Singularities Away from $\rho =0$

We introduce the notation $\Omega _\sigma :=\{ x\in \Omega \, : \,x_1^2+x_2^2\geqq \sigma ^2 \} = \Omega {\setminus } Z_\sigma$ for $\sigma >0$, with $Z_\sigma$ defined as in Theorem 3.1. In the same spirit, we define the two dimensional analogue $\Omega _\sigma ' = \{(\rho ,z)\in \Omega '\, : \,\rho > \sigma \}$, that is $\Omega _\sigma$ can be obtained from $\Omega _\sigma '$ through rotation around the ${\mathbf{e}}_3-$axis.

The main theorem we want to prove in this subsection is the following:

Theorem 4.5

For all $\sigma ,\delta >0$ there exists $\lambda _0,\epsilon _0>0$ such that for $\epsilon \leqq \epsilon _0$ there is a set $X_\epsilon \subset \overline{\Omega '}$ which satisfies:

• 1. The set $X_\epsilon$ is finite and its cardinality is bounded independently of $\epsilon$.

• 2. If $x\in \Omega _\sigma '$ and ${\mathrm{dist}}(x,X_\epsilon )>\lambda _0 \epsilon$, then ${\mathrm{dist}}(Q_\epsilon (x),{\mathcal {N}})\leqq \delta$.

The general idea behind this subsection is the same as in [18, 19], where the analysis has been carried out for the case of minimizers of the energy $\int |\nabla Q_\epsilon |^2 + \frac{1}{\epsilon ^2} f(Q_\epsilon )$ and uses ideas from [13]. We will show that in our situation with the modified bulk potential $f_\epsilon$ and the additional term $\frac{1}{\epsilon ^\gamma }\Vert Q_\epsilon -\widetilde{Q_\epsilon }\Vert ^2_{L^2}$ the same results hold. There are two main ingredients for the proof of Theorem 4.5: Proposition 4.11 that tells us that a singularity has an energy cost of order $|\ln \epsilon |$ and Proposition 4.7 that allows us to deduce that $Q_\epsilon$ is close to ${\mathcal {N}}$ (and hence being uniaxial) provided $\frac{1}{\epsilon ^2}\int f_{{\epsilon }}(Q_\epsilon )$ is sufficiently small. While the second ingredient uses only the regularity of $Q_\epsilon$, the first one makes use of equation (22) in the form of the following proposition:

Proposition 4.6

(Pohozaev identity) Let $Q_\epsilon$ be the minimizer of (21) and $\omega '\subset \Omega '$ open with Lipschitz boundary, ${\overline{x}}\in \omega '$. Then

$$\begin{aligned}&\int _{\partial \omega '} \rho ((x-{\overline{x}})\cdot \nu ) \bigg ( \frac{1}{2}|\nabla ' Q_\epsilon |^2 + \frac{1}{2\rho ^2}|\partial _\varphi Q_\epsilon |^2 + \frac{1}{\epsilon ^2}f_{{\epsilon }}(Q_\epsilon ) + \frac{1}{2\epsilon ^\gamma } |Q_\epsilon - \widetilde{Q_\epsilon }|^2 \bigg ) \\&\quad = \frac{1}{2}\int _{\omega '} \rho |\nabla 'Q_\epsilon |^2 + \frac{1}{2}\int _{\omega '} \frac{1}{\rho } |\partial _\varphi Q_\epsilon |^2 + \frac{3}{\epsilon ^2} \int _{\omega '} \rho f_{{\epsilon }}(Q_\epsilon ) + \frac{3}{2\epsilon ^\gamma } \int _{\omega '}\rho |Q_\epsilon - \widetilde{Q_\epsilon }|^2 \\&\qquad + \frac{1}{\epsilon ^\gamma } \int _{\omega '}\rho (Q_\epsilon -\widetilde{Q_\epsilon }):((x-{\overline{x}})\cdot \nabla '{\widetilde{Q}}) + \int _{\partial \omega '} \rho \,((x-{\overline{x}})\cdot \nabla ' Q_\epsilon ):(\nu \cdot \nabla ' Q_\epsilon )\, , \end{aligned}$$

where $\nu$ denotes the outward unit normal vector on $\partial \omega '$.

Proof

To improve readability, we drop the subscripts $\epsilon$ in the proof. Our calculation only requires that Q is solution of equation (22).

Let $\omega '\subset \Omega '$ open with Lipschitz boundary and let ${\overline{x}}\in \omega '$ be an arbitrary point. By translation and without loss of generality we may assume that ${\overline{x}}=0$. Testing the ij-component of equation (22) with $x_k\partial _{k}Q_{ij}$ and summing over i, j, k we find

$$\begin{aligned} \begin{aligned} 0 =&\sum _{i,j,k} \int _{\omega '} -\rho \Delta Q_{ij} x_k\partial _k Q_{ij} + \frac{1}{\epsilon ^2}\int _{\omega '} \rho \frac{\partial f_{\epsilon }}{\partial Q_{ij}} x_k\partial _k Q_{ij} \\&+ \frac{1}{\epsilon ^\gamma }\int _{\omega '} \rho (Q_{ij}-{\widetilde{Q}}_{ij})x_k\partial _k Q_{ij} \\&- \int _{\omega '} \partial _\rho Q_{ij} x_k \partial _k Q_{ij} + \int _{\omega '} \frac{1}{\rho } Q_{2\times 2,ij} x_k \partial _k Q_{ij} \\ =:&I + II + III + IV + V. \end{aligned} \end{aligned}$$

(24)

Note, that the RHS of (22) vanishes since $Q_{ij}$ is traceless, that is

$$\begin{aligned} \sum _{i,j,k}\int _{\omega '}\Lambda \delta _{ij} x_k\partial _k Q_{ij} = \sum _k \int _{\omega '} \Lambda x_k\partial _k\left( \sum _{i,j}\delta _{ij}Q_{ij}\right) = \sum _k \int _{\omega '} \Lambda x_k\partial _k ({\mathrm{tr}}(Q)) = 0 \end{aligned}$$

For the first term (I) we calculate, using integration by parts

$$\begin{aligned} \begin{aligned} \sum _{i,j,k,l} \int _{\omega '} -\rho \,\partial _l^2 Q_{ij} x_k\partial _k Q_{ij} =&\sum _{i,j,k,l} \int _{\omega '} \rho \,\partial _l Q_{ij} \delta _{lk} \partial _k Q_{ij} + \int _{\omega '} \rho \,\partial _l Q_{ij} x_k \partial _l\partial _k Q_{ij} \\&- \int _{\partial \omega '} \rho \,\partial _l Q_{ij} x_k \partial _k Q_{ij} \nu _l + \int _{\omega '} \delta _{\rho l} \partial _l Q_{ij} \partial _k Q_{ij} x_k , \end{aligned} \end{aligned}$$

(25)

where $\nu$ is the outward-pointing normal vector on $\partial \omega '$. Note, that the last term reads $\int _{\omega '} (\partial _\rho Q):((x\cdot \nabla ')Q)$ and thus is cancelled by (IV). We apply another integration by parts to the second term on the RHS of (25). This yields

$$\begin{aligned} \sum _{i,j,k,l}\int _{\omega '} \rho \, \partial _l Q_{ij} x_k \partial _l\partial _k Q_{ij} =&\sum _{i,j,k,l}\frac{1}{2}\int _{\omega '} \rho \, x_k \partial _k(\partial _l Q_{ij} \partial _l Q_{ij}) \\ =&-\frac{2}{2}\sum _{i,j,l} \int _{\omega '} \rho \, \partial _l Q_{ij} \partial _l Q_{ij} \\&+ \sum _{i,j,k,l}\frac{1}{2}\int _{\partial \omega '} \rho \,\partial _l Q_{ij} \partial _l Q_{ij} x_k \nu _k \\&-\frac{1}{2} \int _{\omega '} \delta _{\rho k} x_k \partial _l Q_{ij} \partial _l Q_{ij}. \end{aligned}$$

Combined with (25), this gives

$$\begin{aligned} I+IV =&\left( 1-\frac{2}{2}-\frac{1}{2}\right) \int _{\omega '} \rho \,|\nabla ' Q|^2 + \frac{1}{2}\int _{\partial \omega '} \rho \,|\nabla ' Q|^2 (x\cdot \nu ) \nonumber \\&- \int _{\partial \omega '} \rho \,(x\cdot \nabla ' Q):(\nu \cdot \nabla ' Q). \end{aligned}$$

(26)

The second integral (II) simply gives

$$\begin{aligned} II = \sum _k \frac{1}{\epsilon ^2}\int _{\omega '} \rho \, \partial _k(f_{{\epsilon }}(Q)) x_k = -\frac{1}{\epsilon ^2} \int _{\omega '} 3\rho \,f_{{\epsilon }}(Q) + \frac{1}{\epsilon ^2} \int _{\partial \omega '} \rho \,f_{{\epsilon }}(Q) (x\cdot \nu ). \end{aligned}$$

(27)

For (III) we need to add (and subtract) the same integral with derivatives on $\widetilde{Q_{ij}}$. Then

$$\begin{aligned} \begin{aligned} III&= \frac{1}{\epsilon ^\gamma }\int _{\omega '} \rho \,(Q_{ij}-{\widetilde{Q}}_{ij})\partial _k Q_{ij} x_k \\&= \frac{1}{2\epsilon ^\gamma } \int _{\omega '} \rho \,\partial _k (Q_{ij}-{\widetilde{Q}}_{ij})^2 x_k + \frac{1}{\epsilon ^\gamma }\int _{\omega '} \rho \,(Q_{ij}-{\widetilde{Q}}_{ij})\partial _k{\widetilde{Q}}_{ij} x_k \\&= - \frac{3}{2\epsilon ^\gamma }\int _{\omega '} \rho \,(Q_{ij}-{\widetilde{Q}}_{ij})^2 + \frac{1}{2\epsilon ^\gamma }\int _{\partial \omega '} \rho \,(Q_{ij}-{\widetilde{Q}}_{ij})^2 x_k\nu _k \\&\quad + \frac{1}{\epsilon ^\gamma }\int _{\omega '} \rho \,(Q_{ij}-{\widetilde{Q}}_{ij})\partial _k{\widetilde{Q}}_{ij} x_k . \end{aligned} \end{aligned}$$

(28)

The fifth integral (V) simply gives

$$\begin{aligned} \begin{aligned} \int _{\omega '} \frac{1}{\rho } Q_{2\times 2}:((x\cdot \nabla ')Q)&= \int _{\omega '} \frac{1}{2\rho }(x\cdot \nabla ')(Q_{2\times 2}:Q) \\&= -\frac{1}{2}\int _{\omega '} \left( 0 + \frac{1}{\rho }\right) |\partial _\varphi Q|^2 + \frac{1}{2}\int _{\partial \omega '} (\nu \cdot x) \frac{1}{\rho } |\partial _\varphi Q|^2. \end{aligned} \end{aligned}$$

(29)

Combining (26), (27), (28) and (29), the equality (24) reads

$$\begin{aligned}&\int _{\partial \omega '} \rho (x\cdot \nu )\bigg (\frac{1}{2}|\nabla ' Q|^2 + \frac{1}{2\rho ^2} |\partial _\varphi Q|^2 + \frac{1}{\epsilon ^2}f_{{\epsilon }}(Q)+\frac{1}{2\epsilon ^\gamma }|Q-{\widetilde{Q}}|^2\bigg ) \\&\quad = \frac{1}{2}\int _{\omega '} \rho \,|\nabla ' Q|^2 + \frac{1}{\rho } |\partial _\varphi Q|^2 + \frac{3}{\epsilon ^2}\int _{\omega '} \rho \,f_{{\epsilon }}(Q) + \frac{3}{2\epsilon ^\gamma }\int _{\omega '} \rho \,|Q-{\widetilde{Q}}|^2 \\&\qquad + \frac{1}{\epsilon ^\gamma }\int _{\omega '} \rho \,(Q-{\widetilde{Q}}):(x\cdot \nabla '{\widetilde{Q}}) + \int _{\partial \omega '} \rho \,(x\cdot \nabla ' Q):(\nu \cdot \nabla ' Q), \end{aligned}$$

which gives the result. $\square$

Since almost all term in consideration contain a $\rho$ factor due to the passage from $\Omega$ to $\Omega _\sigma '$, it is natural to introduce

$$\begin{aligned} \rho _{\mathrm{min}}^{\sigma }(x_0,l) := \inf \big \{\rho \, : \,(\rho ,z)\in B_{l}(x_0)\cap \Omega _\sigma '\big \}\, , \end{aligned}$$

(30)

for a point $x_0\in \Omega _\sigma '$ and $l>0$. Note that if we write $x_0=(\rho _0,z_0)$, then $\rho _{\mathrm{min}}^{\sigma }(x_0,l)=\max \{\rho _0-l,\sigma \}$. In particular, $\rho _{\mathrm{min}}^{\sigma }(x_0,l)\geqq \sigma$.

The following proposition is a key ingredient in the proof of Theorem 4.5.

Proposition 4.7

For all $\delta >0$ there exist constants $\lambda _0,\mu _0>0$ such that for all $\sigma >0$, $x_0\in \Omega _\sigma '$, $\epsilon$ small enough and $l\in [\lambda _0\epsilon ,1]$ the following implication holds:

$$\begin{aligned} \frac{1}{\epsilon ^2} \int _{B_{2l}(x_0)\cap \Omega _\sigma '} \rho \, f_{{\epsilon }}(Q_\epsilon ) \leqq \mu _0\, \rho _{\mathrm{min}}^{\sigma }(x_0,2l) \quad \Rightarrow \quad {\mathrm{dist}}(Q_\epsilon ,{\mathcal {N}})\leqq \delta \text { on } B_l(x_0)\cap \Omega _\sigma '\, . \end{aligned}$$

Proof

We claim that $\lambda _0,\mu _0$ can be defined as

$$\begin{aligned} \lambda _0:=\frac{\delta }{2C}\, , \quad \mu _0:=\frac{\pi }{{8}}\lambda _0^2 f_{\mathrm{min}}\, , \end{aligned}$$

where C is a constant such that $\epsilon \Vert \nabla Q_\epsilon \Vert _{L^\infty } \leqq C$ (see Proposition 4.4) and $f_{\mathrm{min}}$ is the minimum of f on the set $\{ Q\in {\mathrm{Sym}}_{0}\, : \,|Q|\leqq \sqrt{\frac{2}{3}}s_*, {\mathrm{dist}}(Q,{\mathcal {N}})\geqq \delta /2 \}$. Note that $f_{\mathrm{min}}>0$ since on this compact set f is strictly positive. Furthermore, for $\epsilon$ small enough, we also have $f_\epsilon \geqq \frac{1}{2} f_{\mathrm{min}}$ on this set.

In order to show that the definition indeed gives the desired implication, we argue by contradiction. Therefore we assume that there exists $x_0\in \Omega$ and $l\in [\lambda _0\epsilon ,1]$ such that there is an $x\in B_l(x_0)\cap \Omega _\sigma '$ with $\frac{1}{\epsilon ^2}\int _{B_{2l}(x_0)\cap \Omega _\sigma '} \rho \, f_{{\epsilon }}(Q_\epsilon )\leqq \mu _0 \rho _{\mathrm{min}}^{\sigma }(x_0,2l)$ and ${\mathrm{dist}}(Q_\epsilon (x),{\mathcal {N}})>\delta$.

This implies that $B_{\lambda _0\epsilon }(x)\subset B_{2l}(x_0)\cap ({\mathbb {R}}^2{\setminus } B_1(0))$. Indeed one can show that ${\mathrm{dist}}(x,\partial \Omega )>\lambda _0\epsilon$. Otherwise one would have ${\mathrm{dist}}(Q_\epsilon (x),{\mathcal {N}})\leqq \Vert \nabla Q_\epsilon \Vert _{L^\infty }{\mathrm{dist}}(x,\partial \Omega )\leqq C\lambda _0=\frac{\delta }{2}$ by definition of $\lambda _0$. This clearly contradicts the assumption that ${\mathrm{dist}}(Q_\epsilon (x),{\mathcal {N}})>\delta$. Then, for all $y\in B_{\lambda _0\epsilon }(x)\cap \Omega _\sigma '$ by the triangle inequality

$$\begin{aligned} {\mathrm{dist}}(Q_\epsilon (y),{\mathcal {N}}) \geqq {\mathrm{dist}}(Q_\epsilon (x),{\mathcal {N}}) - |Q_\epsilon (x)-Q_\epsilon (y)| > \delta - \lambda _0\epsilon \Vert \nabla Q_\epsilon \Vert _{L^\infty } \geqq \frac{\delta }{2}\, . \end{aligned}$$

By definition of $f_{\mathrm{min}}$ this implies $f_{{\epsilon }}(Q_\epsilon (y))>{\frac{1}{2}}f_{\mathrm{min}}$. Since $B_{\lambda _0\epsilon }(x)\cap \Omega _\sigma '\subset B_{2l}(x_0)\cap \Omega _\sigma '$ and $|B_{\lambda _0\epsilon }(x)\cap \Omega _\sigma '|\geqq \frac{1}{2}\pi (\lambda _0\epsilon )^2$ we know that

$$\begin{aligned} \frac{1}{\epsilon ^2}\int _{B_{2l}(x_0)\cap \Omega _\sigma '} \rho \, f_{{\epsilon }}(Q_\epsilon )&\geqq \frac{1}{\epsilon ^2}\rho _{\mathrm{min}}^{\sigma }(x_0,2l)\int _{B_{\lambda _0\epsilon }(x)\cap \Omega _\sigma '} f_{{\epsilon }}(Q_\epsilon ) \\&\geqq \frac{1}{\epsilon ^2}\rho _{\mathrm{min}}^{\sigma }(x_0,2l) \frac{\pi }{2}(\lambda _0 \epsilon )^2 {\frac{1}{2}}f_{\mathrm{min}} = 2\mu _0 \rho _{\mathrm{min}}^{\sigma }(x_0,2l)\, , \end{aligned}$$

which contradicts our assumption. $\square$

The next lemma basically tells us that for $\alpha \in (0,1)$ there has to be some radius $r\leqq \epsilon ^{\alpha /2}$ so that we can control the energy on $\partial B_r$ in terms of the energy on $B_{\epsilon ^{\alpha /2}}$. It will become important later on when we will use it to bound the energy contributions of the boundary terms from Pohozaev identity (Proposition 4.6).

Lemma 4.8

For all $x_0\in \Omega '$ there exists $r\in (\epsilon ^\alpha ,\epsilon ^\frac{\alpha }{2})$ (depending on $x_0$ and $\epsilon$) such that

$$\begin{aligned}&\int _{\partial B_r(x_0)\cap \Omega '} \rho \left( \frac{1}{2}|\nabla Q_\epsilon |^2 + \frac{1}{\epsilon ^2} f_{{\epsilon }}(Q_\epsilon ) + \frac{1}{2\epsilon ^\gamma }|Q_\epsilon -\widetilde{Q_\epsilon }|^2 \right) \, {\mathrm{d}} x \\&\quad \leqq \frac{4 E_\epsilon ^{2D}(Q_\epsilon ,B_{\epsilon ^{\alpha /2}}(x_0)\cap \Omega ')}{\alpha r |\ln \epsilon |}\, . \end{aligned}$$

Proof

The proof consists of an averaging argument. Assume that no such r exists. With the notation $B'=B_{\epsilon ^{\alpha /2}}(x_0)\cap \Omega '$, this would imply

$$\begin{aligned} E_\epsilon ^{2D}(Q_\epsilon ,B')&= \int _0^{\epsilon ^{\alpha /2}} \int _{\partial B_r(x_0)\cap \Omega '} \rho \left( \frac{1}{2}|\nabla Q_\epsilon |^2 + \frac{1}{\epsilon ^2} f_{{\epsilon }}(Q_\epsilon ) + \frac{1}{2\epsilon ^\gamma }|Q_\epsilon -\widetilde{Q_\epsilon }|^2 \right) \, {\mathrm{d}} x \, {\mathrm{d}} r \\&\geqq \int _{\epsilon ^\alpha }^{\epsilon ^{\alpha /2}} \int _{\partial B_r(x_0)\cap \Omega '} \rho \left( \frac{1}{2}|\nabla Q_\epsilon |^2 + \frac{1}{\epsilon ^2} f_{{\epsilon }}(Q_\epsilon ) + \frac{1}{2\epsilon ^\gamma }|Q_\epsilon -\widetilde{Q_\epsilon }|^2 \right) \, {\mathrm{d}} x \, {\mathrm{d}} r \\&\geqq \frac{4 E_\epsilon ^{2D}(Q_\epsilon ,B')}{\alpha |\ln \epsilon |} \int _{\epsilon ^{\alpha }}^{\epsilon ^{\alpha /2}}\frac{1}{r} \, {\mathrm{d}} r \\&= \frac{4 E_\epsilon ^{2D}(Q_\epsilon ,B')}{\alpha |\ln \epsilon |} \frac{\alpha }{2} |\ln (\epsilon )| \\&= 2 E_\epsilon ^{2D}(Q_\epsilon ,B') \, . \end{aligned}$$

This gives that $E_\epsilon ^{2D}(Q_\epsilon ,B')=0$ and thus $Q_\epsilon$ is constant on $B'$ and $Q_\epsilon = \widetilde{Q_\epsilon }\equiv {Q_{\infty ,\epsilon }}$, but since the constant map $Q_{\infty ,\epsilon }$ satisfies the lemma, we get a contradiction. $\square$

The following two results (Lemma 4.10 and Proposition 4.11) are similar to [13], see also [19, Lemma 1.4.8, Proposition 1.4.9]. Lemma 4.10 states that we can derive a better bound (independent of $\epsilon$) than (19) on balls $B_{\epsilon ^\alpha }$ for the energy contribution of $f_{{\epsilon }}$. Then Proposition 4.11 tells us the cost in terms of energy for such a ball if $Q_\epsilon$ is not close to ${\mathcal {N}}$. Both results rely on the Pohozaev identity (Proposition 4.6) and Lemma 4.8. We start with a proposition that will help us in the proof of Lemma 4.10 to obtain estimates at the boundary of $\partial \Omega '$.

Proposition 4.9

There exist constants $C_\Omega ,\epsilon _1>0$ such that for all $0<\epsilon \leqq \epsilon _1$, $r\in (\epsilon ^\alpha ,\epsilon ^\frac{\alpha }{2})$ and $y\in \Omega '$ there exists $z\in B_r(y)\cap \Omega '$ such that

$$\begin{aligned} \nu (x)\cdot (x-z) \geqq C_\Omega r \quad \forall x\in \partial \Omega '\cap B_r(y)\, , \end{aligned}$$

where $\nu$ is the outward unit normal on $\partial \Omega '$.

Proof

Let us start by considering the domain $R=\{(x_1,x_2)\in {\mathbb {R}}^2\, : \,x_1,x_2>0\}$. Let $y\in R$ and $r>0$ such that $B_r(y)\cap \partial R\ne \emptyset$ (otherwise the result is trivial). Let $L_1=|\{x_2=0\}\cap B_r(y)|$ and $L_2=|\{x_1=0\}\cap B_r(y)|$. Then we define $z=y+\frac{r}{2}\left( R_1/L(0,1)^\top +L_1/L(1,0)^\top \right)$, where $L^2=L_1^2+L_2^2$. We will show that this definition of z indeed satisfies our claim. Without loss of generality we may assume that $y_1\geqq y_2$. We consider the following cases:

• 1. $(0,0)\in B_r(y)$. In this case, $L_1=y_1+\sqrt{r^2-y_2^2}$ and $L_2=y_2+\sqrt{r^2-y_1^2}$. Let $x=(x_1,0)$. Then $\nu (x)=(0,-1)^\top$ and

  $$\begin{aligned} \nu (x)\cdot (x-z) = (y_2-x_2) + \frac{r}{2}\frac{L_1}{L} \geqq \frac{r}{2} \frac{L_1}{L}\, . \end{aligned}$$

  Analogously, for $x=(0,x_2)$ we find $\nu \cdot (x-z)\geqq \frac{r}{2}\frac{L_2}{L}$. Since $y_1\geqq y_2$ we have also the inequality $L_1\geqq L_2$. Minimizing $L_2/L$ subject to the constraint $y_1\geqq y_2$ we get $y_1=y_2$ and thus $L_1=L_2$, that is $\nu (x)\cdot (x-z)\geqq \frac{r}{2\sqrt{2}}$.

• 2. $L_2\ne 0$ and $(0,0)\notin B_r(y)$. Then $L_1=2\sqrt{r^2-y_2^2}$ and $L_2=2\sqrt{r^2-y_1^2}$. A similar calculation as in the first case shows that $\nu (x)\cdot (x-z)\geqq \frac{r}{2\sqrt{2}}$.

• 3. $L_2=0$. The lengths $L_1,L_2$ are given as in the second case, but since $L_2=0$ we get directly $\nu (x)\cdot (x-z)\geqq \frac{r}{2} \frac{L_1}{L}=\frac{r}{2}$.

Now we consider the domain $\Omega '$. For a radius $0<r<\frac{1}{2}$ the angular difference between the normal vectors of $\Omega '$ and R is smaller than $\arccos (1-r)$. Thus, for $\epsilon _1$ small enough, $0<\epsilon \leqq \epsilon _1$, $r\in (\epsilon ^\alpha ,\epsilon ^\frac{\alpha }{2})$, we can find $C_\Omega >0$ such that

$$\begin{aligned} \nu (x)\cdot (x-z)\geqq & {} \frac{r}{2}\cos \left( \frac{\pi }{4} + \arccos (1-r)\right) \\\geqq & {} \frac{r}{2}\cos \left( \frac{\pi }{4} + \arccos (1-\epsilon _1^{\alpha /2})\right) \geqq C_\Omega \, r > 0\, . \end{aligned}$$

$\square$

Lemma 4.10

Let $x_0\in \Omega '$. Then there exists a constant $C_\alpha >0$ which depends only on $\alpha ,\gamma ,\Omega$, the energy bound in (19) and the boundary data in (13) such that if $\epsilon$ is small enough

$$\begin{aligned} \frac{1}{\epsilon ^2} \int _{B_{\epsilon ^\alpha }(x_0)\cap \Omega '} \rho \, f_{{\epsilon }}(Q_\epsilon ) \, {\mathrm{d}} x \leqq C_\alpha \, . \end{aligned}$$

Proof

By Lemma 4.8 there exists $r\in (\epsilon ^\alpha ,\epsilon ^\frac{\alpha }{2})$ and a constant ${\overline{C}}>0$ such that for $\epsilon$ small enough

$$\begin{aligned} \begin{aligned} \int _{\partial B_r(x_0)\cap \Omega '} \rho \bigg (\frac{1}{2}|\nabla Q_\epsilon |^2 +&\frac{1}{\epsilon ^2} f_{{\epsilon }}(Q_\epsilon ) + \frac{1}{2\epsilon ^\gamma }|Q_\epsilon -\widetilde{Q_\epsilon }|^2 \bigg ) \leqq \frac{{\overline{C}}}{\alpha r}\, , \end{aligned} \end{aligned}$$

(31)

where we also used the energy bound (19).

Now assume in a first step that $B_r(x_0)\subset \Omega '$. Using the Pohozaev identity from Proposition 4.6 with $\omega '=B_r(x_0)$ and ${\overline{x}}=x_0$, we find

$$\begin{aligned} \begin{aligned} \frac{3}{\epsilon ^2} \int _{B_r(x_0)}\rho \, f_{{\epsilon }}(Q_\epsilon ) \leqq&\int _{\partial B_r(x_0)} \rho \,((x-x_0)\cdot \nu )\left( \frac{1}{2}|\nabla Q_\epsilon |^2 + \frac{1}{\epsilon ^2} f_{{\epsilon }}(Q_\epsilon ) + \frac{1}{2\epsilon ^\gamma }|Q_\epsilon -\widetilde{Q_\epsilon }|^2 \right) \\&+ \frac{1}{\epsilon ^\gamma }\int _{B_r(x_0)} \rho \,|Q_\epsilon - \widetilde{Q_\epsilon }| |(x-x_0)\cdot \nabla ' \widetilde{Q_\epsilon }| \\&- \int _{\partial B_r(x_0)} \rho \,((x-x_0)\cdot \nabla ' Q_\epsilon ):(\nu \cdot \nabla ' Q_\epsilon )\, . \end{aligned} \end{aligned}$$

(32)

Notice that since $x\in \partial B_r(x_0)$ we have $(x-x_0)\cdot \nabla ' Q_\epsilon = r\nu \cdot \nabla 'Q_\epsilon$, that is

$$\begin{aligned} ((x-x_0)\cdot \nabla ' Q_\epsilon ):(\nu \cdot \nabla ' Q_\epsilon ) = r \left| \nu \cdot \nabla ' Q_\epsilon \right| ^2 \geqq 0\, , \end{aligned}$$

and $(x-x_0)\cdot \nu =r|\nu |^2 = r$. Substituting this into (32), one gets

$$\begin{aligned} \frac{3}{\epsilon ^2} \int _{B_r(x_0)} \rho \, f_{{\epsilon }}(Q_\epsilon ) \leqq&r \int _{\partial B_r(x_0)} \rho \,\left( \frac{1}{2}|\nabla Q_\epsilon |^2 + \frac{1}{\epsilon ^2} f_{{\epsilon }}(Q_\epsilon ) + \frac{1}{2\epsilon ^\gamma }|Q_\epsilon -\widetilde{Q_\epsilon }|^2 \right) \\&+ \frac{1}{\epsilon ^\gamma }\int _{B_r(x_0)} \rho \,|Q_\epsilon - \widetilde{Q_\epsilon }| |(x-x_0)\cdot \nabla ' \widetilde{Q_\epsilon }|\, . \end{aligned}$$

By (31) and Cauchy-Schwarz inequality this entails

$$\begin{aligned} \frac{3}{\epsilon ^2} \int _{B_r(x_0)} \rho \, f_{{\epsilon }}(Q_\epsilon ) \, {\mathrm{d}} x&\leqq r \frac{{\overline{C}}}{\alpha r} + \frac{r}{\epsilon ^\gamma }\left( \int _{B_r(x_0)} \rho \,|Q_\epsilon - \widetilde{Q_\epsilon }|^2\right) ^\frac{1}{2} \left( \int _{B_r(x_0)}\rho \,|\nabla ' \widetilde{Q_\epsilon }|^2\right) ^\frac{1}{2} \\&\leqq \frac{{\overline{C}}}{\alpha } + C\frac{\epsilon ^\frac{\alpha }{2}}{\epsilon ^\gamma }\left( (1+|\ln \epsilon |)^2\epsilon ^\gamma \right) ^\frac{1}{2} \leqq \frac{{\overline{C}}}{\alpha } + C\epsilon ^{(\alpha -\gamma )/4}\, , \end{aligned}$$

provided $\alpha >\gamma$ and $\epsilon$ small enough. This proves the claim in the case where $B_r(x_0)\subset \Omega '$.

In a second step we show that the result also holds if $B_r(x_0)\nsubseteq \Omega '$. We define $\Gamma = B_r(x_0)\cap \partial \Omega '$ which is now non-empty. This enables us to write $\partial (B_r(x_0)\cap \Omega ') = \Gamma \cup (\partial B_r(x_0)\cap \Omega ')$. Again we apply Proposition 4.6 with $\omega '=B_r(x_0)\cap \Omega '$ but this time we set ${\overline{x}}=z$, where $z\in \Omega '\cap B_r(x_0)$ is given by Proposition 4.9 for $y=x_0$. By Proposition 4.6 we get

$$\begin{aligned}&\frac{3}{\epsilon ^2} \int _{B_r(x_0)\cap \Omega '} \rho \,f_{{\epsilon }}(Q_\epsilon ) \, {\mathrm{d}} x\\&\quad \leqq \int _{\partial B_r(x_0)\cap \Omega '} \rho \,((x-{\overline{x}})\cdot \nu ) \left( \frac{1}{2}|\nabla Q_\epsilon |^2 + \frac{1}{\epsilon ^2} f_{{\epsilon }}(Q_\epsilon ) + \frac{1}{2\epsilon ^\gamma }|Q_\epsilon -\widetilde{Q_\epsilon }|^2\right) \\&\qquad + \int _{\Gamma } \rho \,((x-{\overline{x}})\cdot \nu ) \left( \frac{1}{2}|\nabla Q_\epsilon |^2 + \frac{1}{\epsilon ^2} f_{{\epsilon }}(Q_\epsilon ) + \frac{1}{2\epsilon ^\gamma }|Q_\epsilon -\widetilde{Q_\epsilon }|^2 \right) \\&\qquad - \frac{3}{2\epsilon ^\gamma }\int _{B_r(x_0)\cap \Omega '} \rho \,|Q_\epsilon -\widetilde{Q_\epsilon }|^2 - \frac{1}{\epsilon ^\gamma } \int _{B_r(x_0)\cap \Omega '} \rho \,(Q_\epsilon -\widetilde{Q_\epsilon }):((x-{\overline{x}})\cdot \nabla '{\widetilde{Q}}) \\&\qquad - \int _{\Gamma } \rho \,((x-{\overline{x}})\cdot \nabla ' Q_\epsilon ):(\nu \cdot \nabla ' Q_\epsilon ) - \int _{\partial B_r(x_0)\cap \Omega '} \rho \,((x-{\overline{x}})\cdot \nabla ' Q_\epsilon ):(\nu \cdot \nabla ' Q_\epsilon )\, , \end{aligned}$$

where we denoted $\nu$ the unit outward normal. For the integrals on $\partial B_r(x_0)\cap \Omega '$ and $B_r(x_0)\cap \Omega '$ we proceed as before using $|(x-{\overline{x}})\cdot \nu |\leqq 2r$. Note, that this time $(x-{\overline{x}})\cdot \tau$ does not necessarily vanish. Nevertheless, the integral involving this term can be estimated from above by $\int _{\partial B_r\cap \Omega '} 2r \rho \,|\nabla 'Q_\epsilon |^2$ and then be estimated using (31). Now we estimate the integrals involving $\Gamma$. First note that $Q_\epsilon =\widetilde{Q_\epsilon }=Q_b$ on $\Gamma \cap \partial \Omega$ with $f(Q_b)=0$, that is $\int _{\Gamma \cap \partial \Omega }\rho \, f(Q_\epsilon )=0$ ,$\int _{\Gamma \cap \partial \Omega }\rho \, f_{\epsilon }(Q_\epsilon )\leqq C_{Q_b} \epsilon ^{\alpha /2}/\eta ^2$ and $\int _{\Gamma \cap \partial \Omega } \rho \,|Q_\epsilon -\widetilde{Q_\epsilon }|^2=0$. On $\Gamma {\setminus } \partial \Omega \subset \{\rho =0\}$ we find that all integrals vanish because of the bounds in $Q_\epsilon$ established in Proposition 4.4. We are left with the two integrals on $\Gamma \cap \partial \Omega$ with gradients. The idea is now to split the gradient into a tangential and a normal part. The tangential part depends only on the boundary data $Q_b$, the normal part needs to be estimated. So let $\tau$ be the unit tangent vector on $\Gamma$. Decomposing $\nabla ' Q_\epsilon = (\nu \cdot \nabla ' Q_\epsilon )\nu + (\tau \cdot \nabla ' Q_\epsilon )\tau$ and substituting this into $\int _{\Gamma \cap \partial \Omega }\rho (x-{\overline{x}})\cdot \nu \frac{1}{2}|\nabla ' Q_\epsilon |^2$ yields

$$\begin{aligned}&\frac{3}{\epsilon ^2} \int _{B_r(x_0)\cap \Omega '} \rho \, f_{{\epsilon }}(Q_\epsilon ) \, {\mathrm{d}} x \\&\quad \leqq 4\frac{{\overline{C}}}{\alpha } + C\epsilon ^{(\alpha -\gamma )/4} + C_{Q_b}\epsilon ^{\alpha /4} - \int _{\Gamma \cap \partial \Omega } \rho \,((x-{\overline{x}})\cdot \nabla ' Q_\epsilon ):(\nu \cdot \nabla ' Q_\epsilon ) \\&\qquad + \frac{1}{2}\int _{\Gamma \cap \partial \Omega } \rho \,((x-{\overline{x}})\cdot \nu )|\nu \cdot \nabla ' Q_\epsilon |^2 + \frac{1}{2}\int _{\Gamma \cap \partial \Omega } \rho \,((x-{\overline{x}})\cdot \nu )|\tau \cdot \nabla ' Q_\epsilon |^2 \\&\quad \leqq 4\frac{{\overline{C}}}{\alpha } + C\epsilon ^{(\alpha -\gamma )/4} + C_{Q_b}\epsilon ^{\alpha /4} -\frac{1}{2}\int _{\Gamma \cap \partial \Omega } \rho \,((x-{\overline{x}})\cdot \nu )|\nu \cdot \nabla ' Q_\epsilon |^2 \\&\qquad -\int _{\Gamma \cap \partial \Omega } \rho \,((x-{\overline{x}})\cdot \tau )(\tau \cdot \nabla ' Q_b):(\nu \cdot \nabla ' Q_\epsilon )\, , \end{aligned}$$

where we used that $(x-{\overline{x}})=((x-{\overline{x}})\cdot \nu )\nu + ((x-{\overline{x}})\cdot \tau )\cdot \tau$ and that $\tau \cdot \nabla ' Q_\epsilon = \tau \cdot \nabla ' Q_b$ only depends on the given boundary values. We apply the inequality $ab\leqq a^2/(2C^2)+ C^2 b^2/2$ with $C=\sqrt{C_\Omega /2}$ from Proposition 4.9 to get

$$\begin{aligned}&\frac{3}{\epsilon ^2} \int _{B_r(Q_\epsilon )\cap \Omega '} \rho \, f_{{\epsilon }}(Q_\epsilon ) \, {\mathrm{d}} x \\&\quad \leqq 4\frac{{\overline{C}}}{\alpha } + C\epsilon ^{(\alpha -\gamma )/4} + C_{Q_b}\epsilon ^{\alpha /4} -\frac{1}{2}\int _{\Gamma \cap \partial \Omega } \rho \,((x-{\overline{x}})\cdot \nu )|\nu \cdot \nabla ' Q_\epsilon |^2 \\&\qquad + \frac{1}{C_\Omega }\int _{\Gamma \cap \partial \Omega } \rho \,|(x-{\overline{x}})\cdot \tau ||\tau \cdot \nabla ' Q_b|^2 + \frac{C_\Omega }{4}\int _{\Gamma \cap \partial \Omega } \rho \,|(x-{\overline{x}})\cdot \tau ||\nu \cdot \nabla ' Q_\epsilon |^2. \end{aligned}$$

Then we apply Proposition 4.9 to get

$$\begin{aligned} \frac{1}{\epsilon ^2} \int _{B_r(Q_\epsilon )\cap \Omega '} \rho \, f_{{\epsilon }}(Q_\epsilon ) \, {\mathrm{d}} x&\leqq 4\frac{{\overline{C}}}{\alpha } + C\epsilon ^{(\alpha -\gamma )/4} + C_{Q_b}\epsilon ^{\alpha /4} -\frac{1}{2}\int _{\Gamma \cap \partial \Omega } C_\Omega r \rho \,|\nu \cdot \nabla ' Q_\epsilon |^2 \\&\quad + \frac{C_\Omega }{4}\int _{\Gamma \cap \partial \Omega } 2 r \rho \,|\nu \cdot \nabla ' Q_\epsilon |^2 \\&= 4\frac{{\overline{C}}}{\alpha } + C\epsilon ^{(\alpha -\gamma )/4} + C_{Q_b}\epsilon ^{\alpha /4} \, . \end{aligned}$$

$\square$

We have now all the necessary tools to prove the second important ingredient for the proof of Theorem 4.5.

Proposition 4.11

For all $\delta ,\sigma >0$ there exist $\epsilon _2,\zeta _\alpha >0$ such that for $0<\epsilon \leqq \epsilon _2$ and $x_0\in \Omega _\sigma '$ the following implication holds:

$$\begin{aligned} {\mathrm{dist}}(Q_\epsilon (x_0),{\mathcal {N}})>\delta \quad \Rightarrow \quad E_\epsilon ^{2D}(Q_\epsilon ,B_{\epsilon ^\alpha }(x_0)\cap \Omega ') \geqq \zeta _\alpha (|\ln \epsilon | + 1)\rho _{\mathrm{min}}^{\sigma }(x_0,\epsilon ^\alpha )\, , \end{aligned}$$

with $\rho _{\mathrm{min}}^{\sigma }\geqq \sigma$ defined as in (30). The constant $\zeta _\alpha$ can be chosen to be dependent only on $\alpha$ and $\delta$, while $\epsilon _2$ depends on $\delta ,\sigma ,\alpha ,\gamma$.

Proof

Let’s assume that the conclusion does not hold at $x_0\in \Omega _\sigma '$, that is $E_\epsilon ^{2D}(Q_\epsilon ,B_{\epsilon ^\alpha }(x_0)\cap \Omega ') \leqq \zeta _\alpha (|\ln \epsilon | + 1)\rho _{\mathrm{min}}^{\sigma }(x_0,\epsilon ^\alpha )$. Then there exists a radius $r\in (\epsilon ^{2\alpha },\epsilon ^\alpha )$ such that

$$\begin{aligned} \int _{\partial B_r(x_0)\cap \Omega '} \rho \,\left( \frac{1}{2}|\nabla Q_\epsilon |^2 + \frac{1}{\epsilon ^2} f_{{\epsilon }}(Q_\epsilon ) + \frac{1}{2\epsilon ^\gamma }|Q_\epsilon -\widetilde{Q_\epsilon }|^2\right) \, {\mathrm{d}} x \leqq \frac{2\zeta _\alpha \rho _{\mathrm{min}}^{\sigma }(x_0,\epsilon ^\alpha )}{\alpha r}\, .\nonumber \\ \end{aligned}$$

(33)

Indeed, otherwise

$$\begin{aligned} E_\epsilon ^{2D}(Q_\epsilon ,B_{\epsilon ^\alpha }(x_0)\cap \Omega ') \geqq \int _{\epsilon ^{2\alpha }}^{\epsilon ^\alpha } \frac{2\zeta _\alpha \rho _{\mathrm{min}}^{\sigma }(x_0,\epsilon ^\alpha )}{\alpha r} \, {\mathrm{d}} r = 2\zeta _\alpha \rho _{\mathrm{min}}^{\sigma }(x_0,\epsilon ^\alpha )|\ln (\epsilon )|\, , \end{aligned}$$

which clearly contradicts our assumption for $\epsilon <\frac{1}{e}$.

Replacing (31) by (33) in the proof of Lemma 4.10, that is ${\overline{C}}=2\zeta _\alpha \rho _{\mathrm{min}}^{\sigma }(x_0,\epsilon ^\alpha )$, we find

$$\begin{aligned} \frac{1}{\epsilon ^2}\int _{B_r(x_0)\cap \Omega '} \rho \, f_{{\epsilon }}(Q_\epsilon ) \leqq \frac{8\zeta _\alpha \rho _{\mathrm{min}}^{\sigma }(x_0,\epsilon ^\alpha )}{\alpha } + C\epsilon _2^{(\alpha -\gamma )/4}\, , \end{aligned}$$

where the constant C can be chosen to be independent of $\alpha$ and $\epsilon$. We choose $\epsilon _2$ small enough such that it satisfies the estimate $\lambda _0 \epsilon _2 < \frac{1}{2}\epsilon _2^{\alpha }$. Now choose $\zeta _\alpha \leqq \frac{\alpha \,\mu _0}{16}$ and $\epsilon _2\leqq (\frac{\mu _0\sigma }{2C})^\frac{4}{\alpha -\gamma }$, where $\mu _0$ is the constant from Proposition 4.7. These bounds imply that $\mu _0\rho _{\mathrm{min}}^{\sigma }(x_0,\epsilon ^\alpha )\geqq \frac{8\zeta _\alpha \rho _{\mathrm{min}}^{\sigma }(x_0,\epsilon ^\alpha )}{\alpha } + C\epsilon _2^{(\alpha -\gamma )/4}$, that is we can apply Proposition 4.7 with $l=\frac{1}{2}\epsilon ^\alpha$. This implies ${\mathrm{dist}}(Q_\epsilon (x_0),{\mathcal {N}})\leqq \delta$, which proves the claim. $\square$

Now we can finally prove Theorem 4.5 and define the set of singularities $X_\epsilon$. To do this, one can proceed as follows: In a first step we cover $\Omega$ with balls of size $\epsilon ^\alpha$ and look for balls where the energy is large. The number of such balls has to be finite because of the energy bound. In view of Proposition 4.11, $Q_\epsilon$ will be almost uniaxial outside of these balls. In the second step we improve our estimates to the scale $\epsilon$. We cover the balls with high energy from step one with balls of size $\epsilon$ and determine balls where f is large. By Lemma 4.10 this number will be finite too and Proposition 4.7 implies that $Q_\epsilon$ is indeed close to ${\mathcal {N}}$ on all other balls. We can then take $X_\epsilon$ to be the set of all centers of balls with large energy.

Fig. 1

First covering argument: Find balls $B_{\epsilon ^\alpha }$, where the energy is large

Proof of Theorem 4.5 Let $\delta ,\sigma >0$ be given and choose $\alpha \in (0,1)$. Let $\{ B_{\epsilon ^{\alpha }}(y)\, : \,y\in \Omega ' \}$ be a covering of $\Omega '$. By Vitali Covering Lemma there exists a countable family of points $\{y_i\}_{i\in I_\epsilon }$ such that

$$\begin{aligned} \Omega '\subset \bigcup _{i\in I_\epsilon } B_{\epsilon ^{\alpha }}(y_i)\, , \quad B_{\frac{1}{5}\epsilon ^{\alpha }}(y_i)\cap B_{\frac{1}{5}\epsilon ^{\alpha }}(y_j) = \emptyset \text { if } i\ne j\, . \end{aligned}$$

Let $\zeta _\alpha >0$ be given as in Proposition 4.11. We define

$$\begin{aligned} J_\epsilon :=\left\{ i\in I_\epsilon \, : \,E_\epsilon ^{2D}(Q_\epsilon ,B_{2\epsilon ^{\alpha }}(y_i)\cap \Omega ') > \zeta _\alpha (1+|\ln \epsilon |)\sigma \right\} \, . \end{aligned}$$

Then by the energy bound (19),

$$\begin{aligned}&\zeta _\alpha (1+|\ln \epsilon |)\sigma \# J_\epsilon \nonumber \\&\leqq \sum _{i\in J_\epsilon } E_\epsilon ^{2D}(Q_\epsilon ,B_{2\epsilon ^{\alpha }}(y_i)\cap \Omega ') \leqq C E_\epsilon ^{2D}(Q_\epsilon ,\Omega ')\leqq C(1+|\ln \epsilon |)\, . \end{aligned}$$

(34)

Indeed, note that there is a constant C depending only on the space dimension such that each point in $\Omega '$ is covered by at most C balls. This implies the second inequality in (34). From (34) we directly infer that the cardinality of $J_\epsilon$ is bounded by a constant dependent on $\delta ,\sigma ,\alpha$ as well as the space dimension and the energy bound, but independent of $\epsilon$. Let $i\in I_\epsilon {\setminus } J_\epsilon$ and $x_0\in B_{\epsilon ^\alpha }(y_i)\cap \Omega _\sigma '$. If ${\mathrm{dist}}(Q_\epsilon (x_0),{\mathcal {N}})>\delta$ we deduce by Proposition 4.11 that $E_\epsilon ^{2D}(Q_\epsilon , B_{2\epsilon ^\alpha }(y_i)\cap \Omega ') \geqq E_\epsilon ^{2D}(Q_\epsilon , B_{\epsilon ^\alpha }(x_0)\cap \Omega ') > \zeta _\alpha (|\ln (\epsilon )|+1)\sigma$, a contradiction to $i\in I_\epsilon {\setminus } J_\epsilon$. Hence

$$\begin{aligned} {\mathrm{dist}}(Q_\epsilon (x),{\mathcal {N}})\leqq \delta \quad \forall x\in B_{\epsilon ^\alpha }(y_i)\cap \Omega _\sigma ', i\in I_\epsilon {\setminus } J_\epsilon ; \end{aligned}$$

see also Figure 1. Note, that this estimate is not good enough since we announced the radius around points in $X_\epsilon$ to be of order $\epsilon$ instead of $\epsilon ^\alpha$.

Fig. 2

Second covering argument: find balls, where $\frac{1}{\epsilon ^2}\int \rho f_{{\epsilon }}(Q_\epsilon )$ is large

Now fix $i\in J_\epsilon$. Again by Vitali Covering Lemma we can consider a covering of $B_{\epsilon ^{\alpha }}(y_i)\cap \Omega _\sigma '$ of the form

$$\begin{aligned} B_{\epsilon ^{\alpha }}(y_i)\cap \Omega _\sigma ' \subset \bigcup _{j\in I_{\epsilon ,i}} B_{\lambda _0\epsilon }(z_j)\, , \quad B_{\frac{1}{5}\lambda _0\epsilon }(z_j)\cap B_{\frac{1}{5}\lambda _0\epsilon }(z_k) = \emptyset \text { if } j\ne k\, , \end{aligned}$$

with all $z_j\in B_{\epsilon ^\alpha }(y_i)$ and where $\lambda _0$ is given by Proposition 4.7. Furthermore, we define

$$\begin{aligned} J_{\epsilon ,i} :=\left\{ j\in I_{\epsilon ,i} \, : \,\frac{1}{\epsilon ^2}\int _{B_{2\lambda _0\epsilon }(z_j)\cap \Omega _\sigma '} \rho \, f_{{\epsilon }}(Q_\epsilon ) \geqq \mu _0\,\sigma \right\} \, , \end{aligned}$$

with $\mu _0$ again from Proposition 4.7. By Lemma 4.10, recalling that $2\lambda _0\epsilon < \epsilon ^\alpha$,

$$\begin{aligned} \mu _0\,\sigma \, \# J_{\epsilon ,i} \leqq \sum _{j\in J_{\epsilon ,i}} \frac{1}{\epsilon ^2}\int _{B_{2\lambda _0\epsilon }(z_j)\cap \Omega _\sigma '} \rho \, f_{{\epsilon }}(Q_\epsilon ) \leqq \frac{C}{\epsilon ^2} \int _{B_{\epsilon ^\alpha }(y_i)\cap \Omega '} \rho \,f_{{\epsilon }}(Q_\epsilon ) \leqq C_\alpha \, \end{aligned}$$

(35)

so $\# J_{\epsilon ,i}$ is also bounded independently of $\epsilon$. Applying Proposition 4.7 to the sets $B_{2\lambda _0\epsilon }(z_j)$ for $j\in I_{\epsilon ,i}{\setminus } J_{\epsilon ,i}$ we get that ${\mathrm{dist}}(Q_\epsilon (x),{\mathcal {N}})\leqq \delta$ for all $x\in B_{\lambda _0\epsilon }(z_j)\cap \Omega _\sigma '$, see Figure 2. Thus, setting $X_\epsilon :=\bigcup \{ z_j \, : \,j\in \bigcup _{i\in J_\epsilon } J_{\epsilon ,i}\}$ yields the result. $\square$

4.3 Lower Bound Near Singularities

The goal of this subsection is to precisely determine the cost of a singularity. The plan is to use estimates as in [21, Chapter 6] which generalize the idea of [35, 49]. The general idea is to decompose the gradient of a function into a derivative of its norm and of its phase as for example

$$\begin{aligned} |\nabla u|^2 = |\nabla |u||^2 + |u|^2\Big |\nabla \frac{u}{|u|}\Big |^2 \end{aligned}$$

for any vectorial function u that does not vanish. Following [19], we replace the phase u/|u| by the projection of $Q_\epsilon$ onto ${\mathcal {N}}$. As a substitute for the norm, we introduce the auxiliary function $\phi$.

Definition 4.12

We define the function $\phi :{\mathrm{Sym}}_{0}\rightarrow {\mathbb {R}}$ by

$$\begin{aligned} \phi (Q) = \left\{ \begin{array}{ll} \frac{1}{s_*} s(Q)\left( 1-r(Q)\right) &{} Q\in {\mathrm{Sym}}_{0}{\setminus }\{0\}\, , \\ 0 &{} Q=0\, , \end{array}\right. \end{aligned}$$

where $s_*$ is given as in Proposition 2.2 and s, r are the parameters from the decomposition of Q in Proposition 2.3.

Proposition 4.13

The function $\phi$ is Lipschitz continuous on ${\mathrm{Sym}}_{0}$ and $C^1$ on ${\mathrm{Sym}}_{0}{\setminus }{\mathcal {C}}$ with $\phi (Q)=1$ for all $Q\in {\mathcal {N}}$. Furthermore, for a domain $\omega \subset \Omega$ and $Q\in C^1(\omega ,{\mathrm{Sym}}_{0})$, the function ${\mathcal {R}}\circ Q$ is $C^1$ on the open set $Q^{-1}({\mathrm{Sym}}_{0}{\setminus } {\mathcal {C}})$ and it holds that

$$\begin{aligned} |\nabla Q|^2 \geqq \frac{s_*^2}{3}|\nabla (\phi \circ Q)|^2 + (\phi \circ Q)^2 |\nabla ({\mathcal {R}}\circ Q)|^2 \quad \text { in } \omega \, , \end{aligned}$$

where we use the convention that $(\phi \circ Q)^2 |\nabla ({\mathcal {R}}\circ Q)|^2:=0$ if $Q(x)\in {\mathcal {C}}$.

Proof

The proposition follows directly from Lemma 2.2.3 and Lemma 2.2.7 in [19]. $\square$

The next theorem gives the desired lower bound close to a singularity on a two dimensional unit disk. A proof of this can be found in [20, Proposition 2.5]. Observe that we work here with the function f, not $f_\epsilon$.

Theorem 4.14

There exist constants $\kappa _*,C>0$ such that for $Q\in H^1(B_1,{\mathrm{Sym}}_{0})$ satisfying $Q(x)\notin {\mathcal {C}}$ for all $x\in B_1{\setminus } B_\frac{1}{2}$ and $({\mathcal {R}}\circ Q)|_{\partial B_1}$ being non-trivial, seen as element of $\pi _1({\mathcal {N}})$, it holds that

$$\begin{aligned} \int _{B_1} \frac{1}{2}|\nabla ' Q|^2 + \frac{1}{\epsilon ^2} f(Q) \, {\mathrm{d}} x \geqq \kappa _* \phi _0^2(Q,B_1{\setminus } B_\frac{1}{2})|\ln \epsilon | - C \end{aligned}$$

(36)

for a number $\phi _0(Q,B_1{\setminus } B_\frac{1}{2}) := \mathrm {essinf}_{B_1{\setminus } B_\frac{1}{2}}\phi (Q) > 0$. Furthermore, $\kappa _* = s_*^2\frac{\pi }{2}$.

The constant $\kappa _*$ can be calculated as in [20, Lemma 2.9] or [19, Lemma 1.3.4] and is specific for ${\mathcal {N}}\cong {\mathbb {R}}P^2$. For other manifolds, there are analogous results with different constants, see [21]. For our purposes, we will use the following version of Theorem 4.14:

Corollary 4.15

Let $x_0\in \Omega '$ such that $B_\eta (x_0)\subset \Omega '$. Let $Q\in H^1(B_\eta (x_0),{\mathrm{Sym}}_{0})$ satisfying $Q(x)\notin {\mathcal {C}}$ for all $x\in B_\eta {\setminus } B_{\frac{1}{2}\eta }$ and $({\mathcal {R}}\circ Q)|_{\partial B_\eta }$ is non-trivial, seen as element of $\pi _1({\mathcal {N}})$. Then, with the same constant $C>0$ as in Theorem 4.14

$$\begin{aligned} \int _{B_\eta (x_0)} \frac{1}{2}|\nabla ' Q|^2 + \frac{1}{\epsilon ^2} f(Q) \, {\mathrm{d}} x \geqq \kappa _* \phi _0^2(Q,B_\eta {\setminus } B_{\frac{1}{2}\eta })\big (|\ln \epsilon | - |\ln \eta |\big )-C\, , \end{aligned}$$

(37)

where $\kappa _*=s_*^2\frac{\pi }{2}$.

Proof

By translating $\Omega '$ we can assume that $x_0=0$. In order to apply Theorem 4.14, we define ${\overline{x}}=\frac{1}{\eta }x$ and ${\overline{Q}}({\overline{x}})=Q(\eta {\overline{x}})=Q(x)$. Therefore ${\overline{Q}}\in H^1(B_1(0),{\mathrm{Sym}}_{0})$ and verifies the hypothesis of Theorem 4.14 with ${\widetilde{\epsilon }}=\epsilon \eta$, that is

$$\begin{aligned} \int _{B_\eta (x_0)} \frac{1}{2}|\nabla ' Q|^2 + \frac{1}{\epsilon ^2} f(Q) \, {\mathrm{d}} x&= \int _{B_1(x_0)} \frac{1}{2}|\nabla ' {\overline{Q}}|^2 + \frac{1}{\eta ^2\epsilon ^2} f({\overline{Q}}) \, {\mathrm{d}} \overline{x} \\&\geqq \kappa _* \phi _0^2({\overline{Q}},B_1{\setminus } B_\frac{1}{2})|\ln {\widetilde{\epsilon }}| - C \\&\geqq \kappa _* \phi _0^2(Q,B_\eta {\setminus } B_{\frac{1}{2}\eta })\big (|\ln \epsilon | - |\ln \eta |\big ) - C \, . \end{aligned}$$

$\square$

4.4 Lower Bound Away from Singularities

The following proposition shows that we can uniformly bound the functions $\phi$ and $\phi _0$ from the previous section if Q is close to ${\mathcal {N}}$.

Proposition 4.16

Let ${\mathrm{dist}}(Q,{\mathcal {N}})\leqq \delta$ on $\omega \subset \Omega$. Then

$$\begin{aligned} 1-\frac{\sqrt{3}}{s_*}\delta \leqq (\phi \circ Q)(x) \leqq 1+\frac{\sqrt{3}}{s_*}\delta \, . \end{aligned}$$

Proof

Let $Q\in {\mathrm{Sym}}_{0}$ with ${\mathrm{dist}}(Q,{\mathcal {N}})\leqq \delta$. In other words, $|Q-{\mathcal {R}}(Q)|\leqq \delta$, since ${\mathcal {R}}$ is the nearest-point projection onto ${\mathcal {N}}$. We use Proposition 2.3 to write

$$\begin{aligned} Q = s\left( \left( {\mathbf{n}}\otimes {\mathbf{n}}- \frac{1}{3}{\mathrm{Id}}\right) + r\left( {\mathbf{m}}\otimes {\mathbf{m}}- \frac{1}{3}{\mathrm{Id}}\right) \right) \quad \text {and}\quad {\mathcal {R}}(Q) = s_*\left( {\mathbf{n}}\otimes {\mathbf{n}}- \frac{1}{3}{\mathrm{Id}}\right) \, , \end{aligned}$$

for ${\mathbf{n}},{\mathbf{m}}$ orthonormal eigenvectors of Q, $s>0$ and $r\in [0,1)$. We can estimate

$$\begin{aligned} \begin{aligned} |Q - {\mathcal {R}}(Q)|^2&= \left| (s-s_*)({\mathbf{n}}\otimes {\mathbf{n}}- \frac{1}{3}{\mathrm{Id}}) + sr ({\mathbf{m}}\otimes {\mathbf{m}}- \frac{1}{3}{\mathrm{Id}}) \right| ^2 \\&= \frac{2}{3}|s-s_*|^2 + \frac{2}{3}|sr|^2 - \frac{2}{3}sr(s-s_*) \\&\geqq \frac{1}{3}|s-s_*|^2 + \frac{1}{3}|sr|^2 + \frac{1}{3}|s-s_*-sr|^2\, , \end{aligned} \end{aligned}$$

(38)

that is $\delta ^2\geqq \frac{1}{3}|s(1-r)-s_*|^2= \frac{s_*^2}{3}|\phi (Q)-1|^2$. Hence $|\phi (Q)-1|\leqq \frac{\sqrt{3}}{s_*}\delta$. $\square$

Away from singularities the main contribution to the energy comes from the Dirichlet term and the external field since $Q_\epsilon$ is close to ${\mathcal {N}}$. More precisely, we only need the energy in radial direction, that is $|\nabla Q_\epsilon |^2$ can be replaced by $|\partial _r Q_\epsilon |^2$ and the problem becomes, essentially, one dimensional. We formalize this thought by introducing an auxiliary problem as in [3],

$$\begin{aligned} I(r_1,r_2,a,b) \ := \ \inf _{\underset{n_3(r_1)=a,\, n_3(r_2)=b}{n_3\in H^1([r_1,r_2],[0,1])}} \int _{r_1}^{r_2} \frac{s_*^2 |n_3'|^2}{1-n_3^2} + c_*^2(1-n_3^2) \, {\mathrm{d}} r, \end{aligned}$$

(39)

for $0\leqq r_1\leqq r_2\leqq \infty$, $a,b\in [-1,1]$. Note, that this is equivalent to minimizing $\int \left( \frac{1}{2}|\partial _r Q|^2 + g(Q)\right) \, {\mathrm{d}} r$ for a function Q taking values in ${\mathcal {N}}$ subject to suitable boundary conditions. For the infimum we have

Lemma 4.17

Let $0\leqq r_1\leqq r_2\leqq r_3\leqq \infty$ and $a,b,c\in [-1,1]$. Then

• 1. $I(r_1,r_2,a,b) + I(r_2,r_3,b,c)\geqq I(r_1,r_3,a,c)$.

• 2. $I(r_1,r_2,-1,1)\geqq 4s_*c_*$.

• 3. Let $\theta \in [0,\pi ]$. Then

  $$\begin{aligned} I(0,\infty ,\cos (\theta ),{\pm } 1) = 2s_*c_*(1{\mp } \cos (\theta ))\, . \end{aligned}$$

  Furthermore, the minimizer ${\mathbf{n}}(r,\theta )$ of $I(0,\infty ,\cos (\theta ),1)$ is $C^1$ and $|\partial _\theta {\mathbf{n}}|^2,|\partial _r {\mathbf{n}}|^2,|{\mathbf{n}}-{\mathbf{e}}_3|$ decay exponentially as $r\rightarrow \infty$. The minimizer can be explicitly expressed as

  $$\begin{aligned} {\mathbf{n}}(r,\theta ) = \begin{pmatrix} \sqrt{1-{\mathbf{n}}_3^2} \\ 0 \\ {\mathbf{n}}_3 \end{pmatrix}\, , \quad {\mathbf{n}}_3(r,\theta ) = \frac{A(\theta )-\exp (-2c_*/s_* r)}{A(\theta )+\exp (-2c_*/s_* r)}\, , \quad A(\theta )=\frac{1+\cos (\theta )}{1-\cos (\theta )}\, . \end{aligned}$$

Proof

The first part follows directly from definition, since any function that is admissible for $I(r_1,r_2,a,b)$ combined with one for $I(r_2,r_3,b,c)$ is admissible for $I(r_1,r_3,a,c)$. For the second claim, we use the inequality $X^2+Y^2\geqq 2XY$ with $X=s_*|{\mathbf{n}}_3'|/\sqrt{1-{\mathbf{n}}_3^2}$ and $Y=c_*\sqrt{1-{\mathbf{n}}_3^2}$ to get

$$\begin{aligned}&I(r_1,r_2,-1,1) \geqq 2s_*c_*\int _{r_1}^{r_2} |{\mathbf{n}}_3'| \, {\mathrm{d}} r \geqq 2s_*c_*\left| \int _{r_1}^{r_2} {\mathbf{n}}_3' \, {\mathrm{d}} r\right| \\&= 2s_*c_*|{\mathbf{n}}_3(r_2)-{\mathbf{n}}_3(r_1)| = 4s_*c_* \, . \end{aligned}$$

The third part follows from Lemma 3.4 and Remark 3.5 in [3]. $\square$

Remark 4.18

• 1. A close look at Lemma 4.17 reveals that it is enough to consider a rotationally symmetric function g which has a strict minimum on ${\mathcal {N}}$ at $Q=s_*({\mathbf{e}}_3\otimes {\mathbf{e}}_3-\frac{1}{3}{\mathrm{Id}})$. Indeed, then for $Q=s_*({\mathbf{n}}\otimes {\mathbf{n}}-\frac{1}{3}{\mathrm{Id}})$ we can write ${\tilde{g}}(n_3)=g(Q)$ and I becomes $I(r_1,r_2,a,b)=\inf \int _{r_1}^{r_2} \frac{s_*^2|n_3'|^2}{1-n_3^2} + {\tilde{g}}(n_3) \, {\mathrm{d}} r$. Taking a minimizer $n_3(r)$ for $n_3(0)=0$ and $\lim _{r\rightarrow \infty }n_3(r)=t$ we can define $G(t) = 2s_*\int \sqrt{\frac{{\tilde{g}}(n_3)}{1-n_3^2}}|n_3'| \, {\mathrm{d}} r$. One can then derive estimates analogous to Lemma 4.17, for example $I(r_1,r_2,-1,1)\geqq 2 G(1)$.

• 2. Lemma 4.17 and (39) only uses the form of g on ${\mathcal {N}}$. As we have seen in Proposition 4.2, we can neglect the behaviour of g far from ${\mathcal {N}}$ for smaller norms of Q due to the dominating character of f in our asymptotic regime. With the same argument one could also introduce a cut-off for higher norms as long as the growth assumption (5) is satisfied. Thus the essential information about how g contributes to the energy is $g|_{\mathcal {N}}$, that is (7).

Now we can combine all our previous results to prove the lower bound of Theorem 3.1. The idea consists in replacing $\widetilde{Q_\epsilon }$ by its approximation $Q_\epsilon$ and use the equivariance to write the energy as a two dimensional integral. By Theorem 4.5 we can exclude regions in $\Omega _\sigma '$ where $Q_\epsilon$ is far from ${\mathcal {N}}$. Extending the sets if necessary, we can assure that the union has vanishing measure in the limit $\eta ,\epsilon \rightarrow 0$ and that the complement $\Omega _0$ is simply connected. The scaling of $\eta$ and $\epsilon$ allows to apply Corollary 4.15 to each of these extended sets where the boundary datum is nontrivial. The expression we calculate here can later be identified as the perimeter term in ${\mathcal {E}}_0$. In the simply connected complement $\Omega _0$ there exists a lifting ${\mathbf{n}}^\epsilon$ of $Q_\epsilon$ which fulfils the compactness (16). We then want to apply Lemma 4.17 to the rays in $\Omega _0$ for the lower bound. We consider the rays with high energy (that we can estimate easily) and those with low energy where we need to be more precise about their behaviour far from the boundary $\partial \Omega$. Using a diagonal sequence, we can pass to the limit $\sigma \rightarrow 0$.

Proof of the lower bound (17) of Theorem 3.1 Let $\delta ,\sigma >0$ be arbitrary. We define $Q_\epsilon$ as in (21) and extend it rotationally equivariant. From Theorem 4.5 for $\epsilon \leqq \epsilon _0$ we know that there exists a finite set $X_\epsilon$ of singular points $x_1^\epsilon ,\ldots ,x_{N_\epsilon }^\epsilon$ in $\Omega _\sigma '$. In a first step, we suppose that all these points are included in the set $\Omega _{R}'=\Omega _\sigma '\cap B_{R}(0)$.

Since $\Omega _{R}'$ is bounded, there exists another finite set X, such that each sequence $x_j^\epsilon$ converges (up to a subsequence) to a point in X as $\epsilon ,\eta \rightarrow 0$. Note that there may be more than one sequence converging to the same point in X and we a priori only know that $X\subset \overline{\Omega '\cap B_R}$.

Fig. 3

Construction made in the proof of Theorem 3.1. The arrows represent a lifting ${\mathbf{n}}^\epsilon$. In the region $\Omega _1$ the director field ${\mathbf{n}}^\epsilon$ has non-trivial homotopy class, around the region $\Omega _2$, ${\mathbf{n}}^\epsilon$ has a trivial one

We first assume that the set X is contained in $\Omega _\sigma '{\setminus }\partial \Omega$. Since $\eta |\ln \epsilon |\rightarrow \beta \in (0,\infty )$ we know that $\epsilon \leqq C \exp (-\frac{1}{\eta })$. Assume that $\eta$ is small enough such that $2\lambda _0\epsilon \leqq \frac{1}{2}\eta$.

For $x_i\in X$ we define $\widetilde{\Omega _i^\epsilon }{'} = \mathrm {conv}\{ B_{\eta }(x_i)\cup \{0\} \}\cap \Omega '$. If $x_i$ is the only point of the set X that lies on the ray from 0 through $x_i$ we define $\Omega _i^\epsilon {'} :=\widetilde{\Omega _i^\epsilon }{'}$. If $x_j$ for $j\in J\subset I$ define the same ray, that is lie on a common line through 0, then we set $\Omega _j^\epsilon {'}:=\bigcup _{k\in J} \widetilde{\Omega _k^\epsilon }{'}$. After relabelling, we end up with a finite number N of sets $\Omega _k^\epsilon {'}$, $k=1,\ldots ,N$. We define $\Omega _0^\epsilon {'}:=\Omega _\sigma '{\setminus } \bigcup _{k=1}^N \Omega _k^\epsilon {'}$ (see Figure 3). Since all points in $X_\epsilon$ converge to some point in X, we may assume that $\epsilon$ is small enough such that

$$\begin{aligned} \bigcup _{x\in X_\epsilon }B_{\lambda _0\epsilon }(x)\subset \bigcup _{x\in X}B_{2\lambda _0\epsilon }(x) \subset \bigcup _{k=1}^N \Omega _k^\epsilon {'}\subset \Omega _\sigma '\, . \end{aligned}$$

(40)

We drop the $\epsilon$ in the notation of $\Omega _k^\epsilon {'}$ for simplicity and call $\Omega _k$ the three dimensional set defined by rotating $\Omega _k'$ around the ${\mathbf{e}}_3-$axis.

Using (21) and Remark 4.3 we can write

$$\begin{aligned} \begin{aligned} \eta \, {\mathcal {E}}_\epsilon (\widetilde{Q_\epsilon })&\geqq \eta \int _\Omega \frac{1}{2}|\nabla Q_\epsilon |^2 + \frac{1}{\epsilon ^2} f_{{\epsilon }}(Q_\epsilon ) + \frac{1}{2\epsilon ^\gamma }|Q_\epsilon -\widetilde{Q_\epsilon }|^2 \, {\mathrm{d}} x \\&\geqq \eta \int _{\Omega _0} \frac{1}{2}|\nabla Q_\epsilon |^2 + \frac{1}{\epsilon ^2} f_{{\epsilon }}(Q_\epsilon ) + \frac{1}{2\epsilon ^\gamma }|Q_\epsilon -\widetilde{Q_\epsilon }|^2 \, {\mathrm{d}} x \\&\quad + \eta \sum _{k=1}^N \int _0^{2\pi }\int _{\Omega _k'} \rho \,\left( \frac{1}{2}|\nabla Q_\epsilon |^2 + \frac{1}{\epsilon ^2} f_{{\epsilon }}(Q_\epsilon ) \right) \, {\mathrm{d}} \rho \, {\mathrm{d}} z \, {\mathrm{d}} \varphi \, . \end{aligned} \end{aligned}$$

(41)

For $x\in \Omega _0$ we know by Theorem 4.5 that ${\mathrm{dist}}(Q_\epsilon (x),{\mathcal {N}})\leqq \delta$. Since $\Omega _0'$ and thus $\Omega _0$ is simply connected there exist liftings ${\pm }{\mathbf{n}}^\epsilon :\Omega _0\rightarrow {\mathbb {S}}^2$ such that

$$\begin{aligned} s_*\left( {\mathbf{n}}^\epsilon \otimes {\mathbf{n}}^\epsilon -\frac{1}{3}{\mathrm{Id}}\right) = {\mathcal {R}}\circ Q_\epsilon \quad \text {and}\quad \left\| s_*\left( {\mathbf{n}}^\epsilon \otimes {\mathbf{n}}^\epsilon -\frac{1}{3}{\mathrm{Id}}\right) - Q_\epsilon \right\| _{\infty }\leqq \delta \quad \text { on }\Omega _0\, . \end{aligned}$$

In particular, $Q_\epsilon (x)\in {\mathrm{Sym}}_{0}{\setminus }{\mathcal {C}}$ for all $x\in \partial \Omega _k'$ for all $k=1,\ldots ,N$. Let ${\mathcal {M}}\subset \{1,\ldots ,N\}$ be the set of elements $k\in \{1,\ldots ,N\}$ such that $({\mathcal {R}}\circ Q_\epsilon )|_{\partial \Omega _k'}$ is non-trivial as an element of $\pi _1({\mathcal {N}})$. On $B_\eta (x_k)$ we apply Corollary 4.15 to $\int _{B_\eta (x_k)}\frac{1}{2}|\nabla Q_\epsilon |^2 + \frac{1}{\epsilon ^2} f(Q_\epsilon )$. The term $\eta \int _{B_\eta (x_k)} \frac{1}{\eta ^2} |g(Q_\epsilon )| + C_0(\epsilon ,\eta )$ is seen to be bounded by $C\eta$. On the remaining $\Omega _k'{\setminus } B_\eta (x_k)$ we use that the energy density $\frac{1}{2}|\nabla Q_\epsilon |^2 + \frac{1}{\epsilon ^2} f_\epsilon (Q_\epsilon )\geqq 0$ is non-negative. Hence we get

$$\begin{aligned} \begin{aligned}&\eta \sum _{k=1}^N \int _{\Omega _k'} \rho \left( \frac{1}{2}|\nabla Q_\epsilon |^2 + \frac{1}{\epsilon ^2} f_{\epsilon }(Q_\epsilon )\right) \, {\mathrm{d}} \rho \, {\mathrm{d}} z\\&\quad \geqq {} \eta \sum _{k=1}^N \inf _{\Omega _k'}\rho \int _{\Omega _k'} \left( \frac{1}{2}|\nabla Q_\epsilon |^2 + \frac{1}{\epsilon ^2} f(Q_\epsilon )\right) \, {\mathrm{d}} \rho \, {\mathrm{d}} z -C\eta \\&\quad \geqq {} \eta \sum _{k\in {\mathcal {M}}} \kappa _* \phi _0^2(Q_\epsilon ,B_{\eta }(x_k){\setminus } B_{\frac{1}{2}\eta }(x_k))\frac{\rho _k^\epsilon -\eta }{|x_k^\epsilon |} |\ln \epsilon |\eta \\&\qquad - C\phi _0^2(Q_\epsilon ,B_{\eta }(x_k){\setminus } B_{\frac{1}{2}\eta }(x_k))\,\eta |\ln \eta | - C \eta \\&\quad \geqq {} \left( 1-\frac{\sqrt{3}}{s_*}\delta \right) ^2 \sum _{k\in {\mathcal {M}}} \frac{\rho _k^\epsilon -\eta }{|x_k^\epsilon |} \frac{\pi }{2}s_*^2\eta |\ln (\epsilon )| \\&\qquad - C\left( 1+\frac{\sqrt{3}}{s_*}\delta \right) ^2 \eta |\ln \eta | - C \eta \, , \end{aligned} \end{aligned}$$

(42)

where we also applied Proposition 4.16 to estimate $\phi _0$ from below.

Before estimating the energy coming from $\Omega _0$, we need an additional information, namely we want to show that ${\mathbf{n}}^\epsilon (r\omega )$ approaches $+{\mathbf{e}}_3$ and $-{\mathbf{n}}^\epsilon (r\omega )$ approximates $-{\mathbf{e}}_3$ (or vice versa) as $r\rightarrow \infty$ for almost everywhere $\omega \in {\mathbb {S}}^2$. However, it will be enough for our analysis to just show that ${\mathbf{n}}^\epsilon$ is close to either $+{\mathbf{e}}_3$ or $-{\mathbf{e}}_3$ up to some factor times $\sqrt{\delta }$. To start with, we show that the vector ${\mathbf{n}}^\epsilon (r\omega )$ for $r\rightarrow \infty$ is close to $+{\mathbf{e}}_3$ or $-{\mathbf{e}}_3$ almost everywhere. By (21) and the energy bound we know, that for almost everywhere $\omega \in {\mathbb {S}}^2$ the integral

$$\begin{aligned} \int _R^\infty \frac{\eta }{\epsilon ^2}f(Q_\epsilon ) + \frac{1}{\eta } g(Q_\epsilon (r\omega )) + \eta C_0(\epsilon ,\eta ) \, {\mathrm{d}} r < \infty \, . \end{aligned}$$

(43)

We argue by contradiction, that is assume that there exists some $\omega \in {\mathbb {S}}^2$ satisfying (43) such that $\limsup _{r\rightarrow \infty }||{\mathbf{n}}_3^\epsilon (r\omega )|-1|>2 {\mathfrak {C}}{{\mathfrak {a}}}\sqrt{\delta }$ for a ${\mathfrak {C}}>0$ to be specified later and ${\mathfrak {a}}$ is the constant from Proposition 2.5. This implies that there exists a sequence $r_\ell$ such that $r_\ell \rightarrow \infty$ as $\ell \rightarrow \infty$ and $|{\mathbf{n}}_3^\epsilon (r_\ell \omega )|< 1-2{\mathfrak {C}}{\mathfrak {a}}\sqrt{\delta }$ for all $\ell \in {\mathbb {N}}$ or in other words $|Q_\epsilon -s_*({\mathbf{e}}_3\otimes {\mathbf{e}}_3-\frac{1}{3}{\mathrm{Id}})|> 2{\mathfrak {a}}\sqrt{\delta }$ for a suitably chosen ${\mathfrak {C}}$ (A calculation shows that ${\mathfrak {C}}\geqq \frac{5}{4\sqrt{2} s_*}$ is sufficient). By Lipschitz continuity of $Q_\epsilon$ this implies $|Q_\epsilon -s_*({\mathbf{e}}_3\otimes {\mathbf{e}}_3-\frac{1}{3}{\mathrm{Id}})|> {\mathfrak {a}}\sqrt{\delta }$ for all $r\in I_\ell :=(r_\ell -\frac{\epsilon {\mathfrak {C}}{\mathfrak {a}}\sqrt{\delta }}{C},r_\ell +\frac{\epsilon {\mathfrak {C}}{\mathfrak {a}}\sqrt{\delta }}{C})$. This implies that $g(Q_\epsilon )\geqq g_{\mathrm{min}}>0$ for such points in $I_\ell$, where we used $g_{\mathrm{min}}=\min \big \{ g(Q) \, : \,Q\in {\mathrm{Sym}}_{0}\, , {\mathrm{dist}}(Q,{\mathcal {N}})\leqq \delta \, ,|Q - s_*({\mathbf{e}}_3\otimes {\mathbf{e}}_3-\frac{1}{3}{\mathrm{Id}})|\geqq {\mathfrak {a}}\sqrt{\delta } \big \}>0$ by Proposition 2.5. With this estimate in mind it becomes clear that we have the lower bound

$$\begin{aligned} \frac{1}{\eta }\int _{I_\ell } \frac{\eta }{\epsilon ^2}f(Q_\epsilon ) + \frac{1}{\eta } g(Q_\epsilon (r\omega )) + \eta C_0(\epsilon ,\eta )\, {\mathrm{d}} r \geqq \frac{1}{\eta }g_{\mathrm{min}}|I_\ell | = \frac{1}{\eta }g_{\mathrm{min}} \frac{2\epsilon {\mathfrak {C}}{\mathfrak {a}}\sqrt{\delta }}{C} > 0 \, . \end{aligned}$$

Summing over disjoint intervals yields a contradiction to (43).

This implies that either $\limsup _{r\rightarrow \infty }{\mathbf{n}}_3^\epsilon (r\omega )\geqq 1-2{\mathfrak {C}}{\mathfrak {a}}\sqrt{\delta }$ or $\liminf _{r\rightarrow \infty }{\mathbf{n}}_3^\epsilon (r\omega )\leqq -1+2{\mathfrak {C}}{\mathfrak {a}}\sqrt{\delta }$. Indeed, ${\mathbf{n}}_3^\epsilon (r\omega )$ cannot alternate between ${\pm } 1$ since by continuity this yields a contradiction for $\delta$ small enough such that $2{\mathfrak {C}}{\mathfrak {a}}\sqrt{\delta } \ll \frac{1}{2}$. Next, consider the lifting ${\mathbf{n}}^\epsilon$ and suppose that there exist directions $\omega _+,\omega _-\in {\mathbb {S}}^2$ such that ${\mathbf{n}}^\epsilon (r\omega _+)$ is close to $+{\mathbf{e}}_3$ (resp. ${\mathbf{n}}^\epsilon (r\omega _-)$ close to $-{\mathbf{e}}_3$) as $r\rightarrow \infty$. Since our previous analysis holds almost everywhere, we can assume that the angle between $\omega _+$ and $\omega _-$ is smaller than $\pi$ and that $\omega _{\pm }$ are not parallel to ${\mathbf{e}}_3$. Let $v=\omega _+ - \omega _-$ and $w=\omega _+ + \omega _-$. We estimate the energy in new coordinates (r, s) in the segment between the rays defined through $\omega _+$ and $\omega _-$ to get that

$$\begin{aligned} C&\geqq \int _{R+1}^{{\tilde{R}}} \int _{-r|v|/2}^{r|v|/2} \rho \left( \frac{\eta }{2} \Big |\nabla 'Q_\epsilon \Big (r\frac{v}{|v|}+s\frac{w}{|w|}\Big )\Big |^2 + \frac{1}{\eta } g\Big (Q_\epsilon \Big (r\frac{v}{|v|}+s\frac{w}{|w|}\Big )\Big ) \right) \, {\mathrm{d}} s \, {\mathrm{d}} r \\&\geqq C(1-C\delta )^2 \int _{(R+1)}^{{\tilde{R}}} \int _{r|v|/2}^{r|v|/2} \rho \left( \eta s_*^2\Big |\frac{v}{|v|}\cdot \nabla ' {\mathbf{n}}^\epsilon \Big |^2 + \frac{1}{\eta } c_*^2(1-{\mathbf{n}}_3^\epsilon ) - C\delta \right) \, {\mathrm{d}} s \, {\mathrm{d}} r\, . \end{aligned}$$

Lemma 4.17 gives the lower bound $\int _{-r|v|/2}^{r|v|/2}\left( \eta s_*^2 |\frac{v}{|v|}\cdot \nabla ' {\mathbf{n}}^\epsilon |^2 + \frac{1}{\eta } c_*^2(1-{\mathbf{n}}_3^\epsilon ) \right) \, {\mathrm{d}} s \geqq 4c_* s_*-C\sqrt{\delta }$. Using $\rho \geqq r\min \{\sin (\theta _+),\sin (\theta _-)\}$ for $\theta _{\pm }$ being the angular coordinate of $\omega _{\pm }$, we end up with

$$\begin{aligned} C&\geqq C(1-C\delta )^2 \int _{R+1}^{{\tilde{R}}} r (4c_* s_* - C\sqrt{\delta }) \, {\mathrm{d}} r \geqq C_R(1-\sqrt{\delta }){\tilde{R}}^\frac{3}{2} > 0\, , \end{aligned}$$

provided $\delta >0$ small enough. Sending ${\tilde{R}}$ to infinity, we get a contradiction. Hence, ${\mathbf{n}}^\epsilon$ has to approach either $+{\mathbf{e}}_3$ or $-{\mathbf{e}}_3$ almost everywhere and thus we can distinguish the two liftings by their asymptotics far from $\partial \Omega$.

We now introduce sets $F_{\sigma ,\epsilon },\widetilde{F_{\sigma ,\epsilon }}$ which we use later to prove the compactness result. First choose one of the two possible liftings ${\mathbf{n}}^\epsilon \in C^0(\Omega _0,{\mathbb {S}}^2)$. Without loss of generality we choose the lifting such that ${\mathbf{n}}^\epsilon (r\omega )$ is close to $+{\mathbf{e}}_3$ as $r\rightarrow \infty$. The boundary conditions (13) imply that ${\mathbf{n}}^\epsilon (\omega )={\pm } \nu (\omega )$, where $\nu$ is the outward normal on ${\mathbb {S}}^2$ for all $\omega \in \partial \Omega _0\cap {\mathbb {S}}^2$. We define $F_{\sigma ,\epsilon }:=\{ \omega \in {\mathbb {S}}^2\cap \partial \Omega _0\, : \,{\mathbf{n}}^\epsilon (\omega )\cdot \nu (\omega ) = 1 \}$. Conversely, $\widetilde{F_{\sigma ,\epsilon }}$ is then given by $\widetilde{F_{\sigma ,\epsilon }} = \{ \omega \in {\mathbb {S}}^2\cap \partial \Omega _0\, : \,{\mathbf{n}}^\epsilon (\omega )\cdot \nu (\omega ) = -1 \}$. The remaining part of ${\mathbb {S}}^2\cap \Omega _\sigma$ is denoted $S_{\sigma ,\epsilon } = ({\mathbb {S}}^2\cap \Omega _\sigma ){\setminus }(F_{\sigma ,\epsilon }\cup \widetilde{F_{\sigma ,\epsilon }})=\bigcup _{k\geqq 1} ({\mathbb {S}}^2\cap \partial \Omega _k)$. Note that the sets $F_{\sigma ,\epsilon }$, $\widetilde{F_{\sigma ,\epsilon }}$ and $S_{\sigma ,\epsilon }$ are rotationally symmetric with respect to the $\varphi$ coordinate. Since the $\theta -$angular size of all $\Omega _k$ converges to zero (that is $|S_{\sigma ,\epsilon }|\rightarrow 0$ as $\epsilon \rightarrow 0$) and ${\mathbb {S}}^2\cap \Omega _\sigma$ is compact, we get that (up to extracting a subsequence) $\chi _{F_{\sigma ,\epsilon }}$ (resp. $\chi _{\widetilde{F_{\sigma ,\epsilon }}}$) converges pointwise to a characteristic function $\chi _{F_\sigma }$ (resp. $\chi _{\widetilde{F_\sigma }}$). By triangle inequality we get ${\mathrm{dist}}(\widetilde{Q_\epsilon },{\mathcal {N}}_\epsilon ) \leqq {\mathrm{dist}}(Q_\epsilon ,{\mathcal {N}}_\epsilon ) + |Q_\epsilon - \widetilde{Q_\epsilon }|$, where ${\mathcal {N}}_\epsilon$ is the manifold ${\mathcal {N}}_{\eta ,\xi }$ introduced in Proposition 2.6. By Remark 4.3, Proposition 2.6 and the energy bound (19) we get that $\int _{\Omega _0} {\mathrm{dist}}^2(\widetilde{Q_\epsilon },{\mathcal {N}}_\epsilon )\, {\mathrm{d}} x\rightarrow 0$ as $\epsilon ,\eta \rightarrow 0$. On bounded sets additionally use (11) to get the claimed $L^2-$convergence in (16).

As a last step, it remains the energy estimate on $\Omega _0$. We split the integral over $\Omega _0$ in (41) in several parts. For $\omega \in F_{\sigma ,\epsilon }$ such that the energy on the ray in direction $\omega$ is large, that is $\int _1^\infty \frac{\eta }{2}|\nabla Q_\epsilon |^2 + \frac{\eta }{\epsilon ^2} f(Q_\epsilon ) + \frac{1}{\eta } g(Q_\epsilon ) + \eta C_0(\epsilon ,\eta ) + \frac{\eta }{2\epsilon ^\gamma } |Q_\epsilon -\widetilde{Q_\epsilon }|^2 \, {\mathrm{d}} r \geqq 4 s_*c_*$, we can use Lemma 4.17, which implies

$$\begin{aligned}&\int _1^\infty \frac{\eta }{2}|\nabla Q_\epsilon |^2 +\frac{\eta }{\epsilon ^2} f(Q_\epsilon ) + \frac{1}{\eta } g(Q_\epsilon ) + \eta C_0(\epsilon ,\eta )\nonumber \\&\quad + \frac{\eta }{2\epsilon ^\gamma } |Q_\epsilon -\widetilde{Q_\epsilon }|^2 \, {\mathrm{d}} r \geqq 4 s_*c_* \geqq I(1,\infty ,\nu _3(\omega ),+1)\, . \end{aligned}$$

(44)

Analogously, for points $\omega \in \widetilde{F_{\sigma ,\epsilon }}$ with energy greater than $4 s_*c_*$ we use $I(1,\infty ,\nu _3(\omega ),-1)$ as a lower bound. Let’s consider the set of points $\omega \in {\mathbb {S}}^2\cap \partial \Omega _0$ such that the energy on the ray through $\omega$ is smaller than $4 s_*c_*$. We claim that there exists a constant ${\overline{C}}>0$ independent of $\omega$ and a radius $R_{\eta ,\omega }\in (R-{\overline{C}}\eta ,R]$ such that $||{\mathbf{n}}^\epsilon _3(R_{\eta ,\omega }\omega )|-1|\leqq 2{\mathfrak {C}}{\mathfrak {a}}\sqrt{\delta }\ll 1$. Indeed, if $||{\mathbf{n}}^\epsilon _3(R_{\eta ,\omega }\omega )|-1|> 2{\mathfrak {C}}{\mathfrak {a}}\sqrt{\delta }$ on $(R-{\overline{C}}\eta ,R]$ then on this set $|Q_\epsilon -s_*({\mathbf{e}}_3\otimes {\mathbf{e}}_3-\frac{1}{3}{\mathrm{Id}})|\geqq 2{\mathfrak {a}}\sqrt{\delta }$. Hence for ${\overline{C}}$ large enough this contradicts $4 s_*c_*\geqq \int \frac{\eta }{\epsilon ^2}f(Q_\epsilon )+ \frac{1}{\eta }g(Q_\epsilon ) + \eta C_0(\epsilon ,\eta ) \, {\mathrm{d}} r \geqq (R-(R-{\overline{C}}\eta ))\frac{C{\mathfrak {a}}\sqrt{\delta }}{\eta }$. In order to conclude that the energy from 1 to $R_{\eta ,\omega }$ is (up to some small contributions of size $\sqrt{\delta }$) close to $I(1,\infty ,\nu _3(\omega ),{\pm } 1)$ we need to show that for $\omega \in F_{\sigma ,\epsilon }$ the vector ${\mathbf{n}}^\epsilon (R_{\eta ,\omega })$ is close to $+{\mathbf{e}}_3$ and not $-{\mathbf{e}}_3$ (and vice versa for $\omega \in \tilde{F_{\sigma ,\epsilon }}$). Again we argue by contradiction, that is we assume that $|{\mathbf{n}}^\epsilon (R_{\eta ,\omega }) + {\mathbf{e}}_3|\leqq 2{\mathfrak {C}}{\mathfrak {a}}\sqrt{\delta }$. We subdivide the ray in direction $\omega$ from R to infinity into segments of length 1, identified with the intervals $J_\ell =[\ell ,\ell +1]$ for the radial variable, for integers $\ell \geqq R$. On every segment, the energy bound on the ray implies the existence of two points $a_\ell ,b_\ell \in J_\ell$ with $|a_\ell -\ell |\leqq {\overline{C}}\eta$, $|b_\ell -(\ell +1)|\leqq {\overline{C}}\eta$ such that $||{\mathbf{n}}^\epsilon _3(a_\ell )|-1|\leqq 2{\mathfrak {C}}{\mathfrak {a}}\sqrt{\delta }$, $||{\mathbf{n}}^\epsilon _3(b_\ell )|-1|\leqq 2{\mathfrak {C}}{\mathfrak {a}}\sqrt{\delta }$. Since we assumed ${\mathbf{n}}^\epsilon (R_{\omega ,\eta })$ close to $-{\mathbf{e}}_3$ and ${\mathbf{n}}^\epsilon$ approaches $+{\mathbf{e}}_3$ for $\ell \rightarrow \infty$, there exists some integer $\ell \geqq R$ such that $|{\mathbf{n}}^\epsilon _3(a_\ell )+1|\leqq 2{\mathfrak {C}}{\mathfrak {a}}\sqrt{\delta }$, $|{\mathbf{n}}^\epsilon _3(b_\ell )-1|\leqq 2{\mathfrak {C}}{\mathfrak {a}}\sqrt{\delta }$. Together with (8), this implies

$$\begin{aligned}&\int _{J_\ell } \frac{\eta }{2}|\nabla Q_\epsilon |^2 + \frac{1}{\eta } g(Q_\epsilon ) \, {\mathrm{d}} r \geqq I(\ell ,\ell +1,{\mathbf{n}}_3^\epsilon (a_\ell ),{\mathbf{n}}_3^\epsilon (b_\ell ))\\&- C({\mathfrak {C}}{\mathfrak {a}}+1)\sqrt{\delta } \geqq 4 s_*c_* - C\sqrt{\delta }\, . \end{aligned}$$

In order to show that for $\delta$ and $\epsilon$ small enough this contradicts the assumption of the ray having energy smaller than $4 s_*c_*$, we prove that the energy coming from the segment [0, R] has to be positive with a uniform lower bound. Since $\omega \in F_{\sigma ,\epsilon }\subset \partial \Omega _\sigma$ one can show as in 2. in Lemma 4.17 that on such a ray $\int _1^R \frac{\eta }{2}|\nabla Q_\epsilon |^2 + \frac{1}{\eta }g(Q_\epsilon )\, {\mathrm{d}} r \geqq 4 s_*c_*(\frac{1}{2}\sigma ^2 - 8{\mathfrak {C}}{\mathfrak {a}}\sqrt{\delta })$. So combining this result and the estimate for $J_k$, we get

$$\begin{aligned} 4 s_*c_* \geqq 4 s_*c_* - C\sqrt{\delta } + 2s_*c_*\Big (\frac{1}{2}\sigma ^2 - 8{\mathfrak {C}}{\mathfrak {a}}\sqrt{\delta }\Big )\, , \end{aligned}$$

which yields a contradiction for $\delta ,\epsilon$ small enough. For $\omega \in F_{\sigma ,\epsilon }$ we then use the change of variables $r = 1+\eta {\tilde{r}}$, (8), Proposition 4.13 and Proposition 4.16 to get

$$\begin{aligned} \begin{aligned} \int _1^R \frac{\eta }{2}|\nabla Q_\epsilon |^2 + \frac{1}{\eta } g(Q_\epsilon ) \, {\mathrm{d}} r&\geqq \int _0^{(R-1)/\eta } \frac{1}{2}|\nabla Q_\epsilon |^2 + g({\mathcal {R}}\circ {Q_\epsilon }) - C\,{\mathrm{dist}}(Q_\epsilon ,{\mathcal {N}}) \, {\mathrm{d}} \tilde{r} \\&\geqq (1-C\delta )^2 \int _0^{(R-1)/\eta } \frac{1}{2}|\nabla ({\mathcal {R}}\circ Q_\epsilon )|^2 + g(R\circ Q_\epsilon ) \, {\mathrm{d}} \tilde{r} - C\delta \\&\geqq I(0,(R_{\eta ,\omega }-1)/\eta ,\nu _3(\omega ),{\mathbf{n}}_3^\epsilon ((R_{\eta ,\omega }-1)/\eta ))- C\delta \\&\geqq I(0,(R_{\eta ,\omega }-1/\eta ,\nu _3(\omega ),+1) - C\delta \, , \end{aligned}\nonumber \\ \end{aligned}$$

(45)

where we also used Proposition 2.6 to get

$$\begin{aligned}&{\mathrm{dist}}(Q_\epsilon ,{\mathcal {N}})\leqq {\mathrm{dist}}\Big (Q_\epsilon ,{\mathcal {N}}_\epsilon \Big )\\&+ C\frac{\epsilon ^2}{\eta ^2} \leqq C\Big (f(Q_\epsilon ) + \frac{\epsilon ^2}{\eta ^2}g(Q_\epsilon ) + \epsilon ^2 C_0(\epsilon ,\eta )\Big )^\frac{1}{2} + C\frac{\epsilon ^2}{\eta ^2} \end{aligned}$$

and thus by Cauchy-Schwarz inequality and the energy bound on the ray $\int _0^{(R-1)/\eta } {\mathrm{dist}}(Q_\epsilon ,{\mathcal {N}})\, {\mathrm{d}} \tilde{r}\leqq C\sqrt{R} \frac{\epsilon }{\sqrt{\eta }} + CR\frac{\epsilon ^2}{\eta ^3}$. So by (44) and (45) we get that for $\omega \in F_{\sigma ,\epsilon }$ we have

$$\begin{aligned}&\int _{1}^\infty \frac{\eta }{2}|\nabla Q_\epsilon |^2 + \frac{1}{\eta } g(Q_\epsilon ) \, {\mathrm{d}} r \\&\quad \geqq \min \{ I(0,\infty ,\nu _3(\omega ),+1), \, I(0,(R_{\eta ,\omega }-1/\eta ,\nu _3(\omega ),+1) - C\delta \}\, . \end{aligned}$$

Furthermore, by compactness, $\chi _{F_{\sigma ,\epsilon }}$ converges point wise almost everywhere to $\chi _{F_\sigma }$. Since $(R_{\eta ,\omega }-1)/\eta \rightarrow \infty$ as $\eta \rightarrow \infty$ we can apply Fatou’s Lemma to get the energy contribution from $\Omega _0$ related to $F_{\sigma ,\epsilon }$ by

$$\begin{aligned} \begin{aligned} \liminf _{\epsilon ,\eta \rightarrow 0}&\int _{F_{\sigma ,\epsilon }} \int _1^\infty \frac{\eta }{2}|\nabla Q_\epsilon |^2 + \frac{\eta }{\epsilon ^2}f(Q_\epsilon ) + \frac{1}{\eta } g(Q_\epsilon ) + \eta C_0(\epsilon ,\eta ) \, {\mathrm{d}} r\, {\mathrm{d}} \omega \\&\geqq \int _{{\mathbb {S}}^2\cap \partial \Omega _0} \liminf _{\epsilon ,\eta \rightarrow 0} \\&\quad \min \{ I(0,\infty ,\nu _3(\omega ),+1), \, I(0,(R_{\eta ,\omega }-1/\eta ,\nu _3(\omega ),+1) - C\delta \} \chi _{F_{\sigma ,\epsilon }}(\omega ) \, {\mathrm{d}} \omega \\&\geqq \int _{F_\sigma } I\left( 0,\infty ,\nu _3(\omega ),+1\right) \, {\mathrm{d}} \omega - C\delta \, . \end{aligned} \end{aligned}$$

Now combine this estimate, the analogous result for $\widetilde{F_{\sigma ,\epsilon }}$, the formulae for $I(0,\infty ,\nu _3(\omega ),{\pm } 1)$ from Lemma 4.17 and (42) to get

$$\begin{aligned} \begin{aligned} \liminf _{\epsilon ,\eta \rightarrow 0} \eta {\mathcal {E}}_{\eta ,\xi }(Q_{\eta ,\xi }) {}\geqq&\int _{F_\sigma } 2 s_*c_*(1-\cos (\theta )) \, {\mathrm{d}} \omega + \int _{\widetilde{F_\sigma }} 2 s_*c_*(1+\cos (\theta )) \, {\mathrm{d}} \omega \\&+ \left( 1-C\delta \right) ^2 \sum _{k\in {\mathcal {M}}} \frac{\rho _k-\eta }{|x_k|}\pi ^2 s_*^2 \beta -C\delta \, , \end{aligned} \end{aligned}$$

for the points $x_k=(\rho _k,\theta _k)\in X$.

It remains to show that for all $k\in {\mathcal {M}}$, the point $x_k/|x_k|$ corresponds to a jump between $F_\sigma$ and $\widetilde{F_\sigma }$. For this it is enough to show that the orientation of ${\mathbf{n}}^\epsilon$ relative to the normal on $\partial \Omega$ changes when following $\partial \Omega _k'\cap \Omega '$ for all $k\in {\mathcal {M}}$. So let $k\in {\mathcal {M}}$ and consider the curve $\Gamma :\partial \Omega _k'\rightarrow {\mathbb {S}}^2$ defined by ${\mathbf{n}}^\epsilon |_{\partial \Omega _k'}$. By definition of ${\mathcal {M}}$, the curve is non-trivial in $\pi _1({\mathcal {N}})$, that is $\Gamma$ jumps an odd number of times from one vector to its antipodal vector on the sphere. Hence, the orientation has to change. In the limit $\epsilon ,\eta \rightarrow 0$, this implies that

$$\begin{aligned} 2\pi \sum _{k\in {\mathcal {M}}} \frac{\rho _k}{|x_k|} = |D\chi _{F_\sigma }|({\mathbb {S}}^2\cap \{\rho >\sigma \})\, . \end{aligned}$$

This implies our result in the case $X_\epsilon ,X\subset (\Omega '\cap B_R(0)){\setminus } \partial \Omega$.

We now explain the changes in our construction if there are some $x_i\in X\cap {\mathbb {S}}^2$. Basically, we use the same construction as before, but we need to take care that the lower bound involving Corollary 4.15 stays applicable. To see this, we extend the map $Q_\epsilon$ outside of $\Omega$ using the boundary values. We define

$$\begin{aligned} \overline{Q_\epsilon }(x) = \left\{ \begin{array}{ll} Q_\epsilon (x) &{} x\in B_\eta (x_i)\cap \Omega \, , \\ s_*\Big (\frac{x}{|x|}\otimes \frac{x}{|x|} - \frac{1}{3}{\mathrm{Id}}\Big ) &{} x\in B_\eta (x_i)\cap B_1(0)\, . \end{array}\right. \end{aligned}$$

Then $f(\overline{Q_\epsilon })=0$ and $|\nabla \overline{Q_\epsilon }|^2,|g(\overline{Q_\epsilon })|\leqq C$ on $B_\eta (x_i)\cap B_1(0)$, that is

$$\begin{aligned} \int _{B_\eta (x_i)\cap B_1(0)}\frac{1}{2}|\nabla \overline{Q_\epsilon }|^2 + \frac{1}{\epsilon ^2} f(\overline{Q_\epsilon }) + \frac{1}{\eta ^2} g(\overline{Q_\epsilon }) + C_0(\epsilon ,\eta ) \, {\mathrm{d}} x \leqq C_1\, . \end{aligned}$$

Thus, if $({\mathcal {R}}\circ Q_\epsilon )|_{\partial \Omega '_i}$ is non-trivial as element of $\pi _1({\mathcal {N}})$, we can apply Corollary 4.15 to the extension $\overline{Q_\epsilon }$, that is

$$\begin{aligned} \eta \int _{B_\eta (x_i)\cap \Omega '} \frac{1}{2}|\nabla {Q_\epsilon }|^2 + \frac{1}{\epsilon ^2} f({Q_\epsilon }) \, {\mathrm{d}} x&\geqq \eta \int _{B_\eta (x_i)\cap {\mathbb {R}}^2} |\nabla ' \overline{Q_\epsilon }|^2 + \frac{1}{\epsilon ^2} f(\overline{Q_\epsilon }) \, {\mathrm{d}} x - \eta \,C_1 \\&\geqq \left( 1-\frac{\sqrt{3}}{s_*}\delta \right) ^2 \frac{\pi }{2} s_*^2 \eta |\ln \epsilon | - C\,\eta |\ln \eta | - C\,\eta \, . \end{aligned}$$

If $({\mathcal {R}}\circ Q_\epsilon )|_{\partial \Omega '_i}$ is trivial, then we just estimate as before, using that the energy is non-negative.

It remains one last case. Assume that there is a point $x_k^\epsilon \in X_\epsilon$ such that $|x_k^\epsilon |\rightarrow \infty$ as $\epsilon \rightarrow 0$. This causes two modifications to our previous results: This time, we define $\widetilde{\Omega _k^\epsilon }{'}=\mathrm {conv}\{B_\eta (x_k^\epsilon )\cup \{0\}\}\cap \Omega '$. Doing so, we risk to exclude a region from $\Omega _0$ that is too large for proving the compactness, namely when we define the set $\omega _\eta$ afterwards. However, this is not really a difficulty, for two reasons. First, it is possible to extend ${\mathbf{n}}^\epsilon$ continuously in $\widetilde{\Omega _k^\epsilon }{'}{\setminus } \widehat{\Omega _k^\epsilon {'}}$, with $\widehat{\Omega _k^\epsilon {'}}=(B_\eta (x_k^\epsilon )\cup [0,x_k^\epsilon ])\cap \Omega '$, where $[0,x_k^\epsilon ]$ is the line segment between the points 0 and $x_k^\epsilon$. Second, in order to conclude that the measure of $\widehat{\Omega _k^\epsilon }$ is also bounded, we need to show that $\rho _k^\epsilon$ cannot grow to infinity. To see this, note that $x_k^\epsilon \in \Omega _\sigma$ and by applying Proposition 4.11 one gets from the energy bound that $\rho _{\mathrm{min}}^{\sigma }(x_k^\epsilon ,\epsilon ^\alpha )$ is indeed bounded. All estimates for the lower bound that we have done before stay valid in this setting.

So far, we have established the inequality

$$\begin{aligned} \begin{aligned}&\liminf _{\eta ,\xi \rightarrow 0} \eta {\mathcal {E}}_{\eta ,\xi }(Q_{\eta ,\xi }) \\&\quad \geqq (1-C\delta )^2 \frac{\pi }{2} s_*^2 \beta |D\chi _{F_\sigma }|({\mathbb {S}}^2\cap \{\rho \geqq \sigma \}) \\&\qquad + \int _{F_\sigma } 2 s_*c_*(1-\cos (\theta )) \, {\mathrm{d}} \omega + \int _{\widetilde{F_\sigma }} 2 s_*c_*(1+\cos (\theta )) \, {\mathrm{d}} \omega - C\sqrt{\delta } \, . \end{aligned} \end{aligned}$$

(46)

We now define the set $\omega _{\sigma ,\epsilon }$ as proxy for the set $\omega _\eta$ from Theorem 3.1. Let $\omega _{\sigma ,\epsilon }' := \bigcup _{k\geqq 1} \widehat{\Omega _k^\epsilon {'}}$, where the sets $\widehat{\Omega _k^\epsilon {'}}=\Omega _k^\epsilon {'}$ for bounded sequences $|x_k^\epsilon |$, and given as in the second construction if $|x_k^\epsilon |$ diverges. This is well defined for $\epsilon$ (and therefore $\eta$) small, depending on $\sigma$ and $\delta$. Recall that since $\eta |\ln \epsilon |\rightarrow \beta \in (0,\infty )$, we have the asymptotic $\eta \sim |\ln \epsilon |^{-1}$. Let $\omega _{\sigma ,\epsilon }$ be the corresponding rotational symmetric extended set. Then $|\omega _{\sigma ,\epsilon }'|\leqq C |\bigcup _{x\in X_\epsilon } B_\eta (x)|\leqq C \eta ^2 |X_\epsilon | \leqq C \frac{\eta ^2}{\delta ^4 \sigma ^2}$, that is choosing $\eta$ small we can force the measure of $\omega _{\sigma ,\epsilon }'$ to vanish in the limit. Note that this also implies that the measure of $\omega _{\sigma ,\epsilon }$ vanishes because we have an upper bound on the $\rho -$component of points in $X_\epsilon$.

We now want to send $\sigma \rightarrow 0$ and choose a diagonal sequence with the properties announced in the theorem. From our previous construction, for a sequence $\sigma _k\searrow 0$ there exist corresponding sequences $\delta _k\searrow 0$, $\eta _k\searrow 0$ and $\epsilon _k\searrow 0$ such that from (46)

$$\begin{aligned} \eta {\mathcal {E}}_{\eta ,\xi }(Q_{\eta ,\xi }) \geqq&\frac{\pi }{2} s_*^2 \beta |D\chi _{F_{\sigma _k,\epsilon }}|({\mathbb {S}}^2\cap \{\rho \geqq \sigma _k\}) \\&+ \int _{F_{\sigma _k,\epsilon }} 2 s_*c_*(1-\cos (\theta )) \, {\mathrm{d}} \omega + \int _{\widetilde{F_{\sigma _k,\epsilon }}} 2 s_*c_*(1+\cos (\theta )) \, {\mathrm{d}} \omega - \frac{1}{k} \, , \end{aligned}$$

and, furthermore, $|\omega _{\sigma _k,\epsilon }|\leqq \frac{1}{k}$, $|{\mathbb {S}}^2{\setminus }(F_{\sigma _k,\epsilon }\cup \widetilde{F_{\sigma _k,\epsilon }})|\leqq \frac{1}{k}$ and $\int _{\Omega _{\sigma _k}{\setminus }\omega _{\sigma ,\epsilon }} {\mathrm{dist}}^2(\widetilde{Q_\epsilon },{\mathcal {N}}_\epsilon ) \, {\mathrm{d}} x \leqq \frac{1}{k^2}$ for $\epsilon \leqq \epsilon _k$ and $\eta \leqq \eta _k$. The sequences $\epsilon _k$ and $\eta _k$ depend on $\sigma _k$ and $\delta _k$ and are related via $\eta _k|\ln \epsilon _k|\rightarrow \beta$ as $k\rightarrow \infty$.

Thus we can define the function ${\mathbf{n}}^\eta :\Omega \rightarrow {\mathbb {S}}^2$ announced in the theorem as ${\mathbf{n}}^\eta := {\mathbf{n}}^\epsilon$ on $\Omega _{\sigma _k}{\setminus }\omega _{\eta }$ for $\eta \in (\eta _{k+1},\eta _k)$, $\omega _\eta := \omega _{\sigma _k,\epsilon }$ and extend it measurably to a map $\Omega \rightarrow {\mathbb {S}}^2$. This definition assures that ${\mathbf{n}}^\eta \in C^0(\Omega _{\sigma _k}{\setminus }\omega _\eta ,{\mathbb {S}}^2)$ and the convergence in (16) holds. Furthermore, we define the set $F_\eta :=F_{\sigma _k,\epsilon }$ for $\eta \in (\eta _{k+1},\eta _k)$. Then our analysis shows that the sequence $\chi _{F_\eta }$ has the point wise almost everywhere limit $\chi _F$, for $F=\bigcup _{k>1} F_{\sigma _k}$ since $|\chi _F-\chi _{F_\eta }|\leqq |\chi _F - \chi _{F_{\sigma _k}}| + |\chi _{F_{\sigma _k}} - \chi _{F_{\sigma _k,\epsilon }}|$ and the measure of the set on which these two terms are nonzero is smaller than $C\sigma _k^2+\frac{1}{k}$.

This finishes the proof of the first part of Theorem 3.1 and (17). $\square$

5 Upper Bound

In this section we are going to prove the upper bound from Theorem 3.1, namely (18). Since all functions are rotationally equivariant, it is useful to introduce the two dimensional energy for sets $\omega '\subset \Omega '$

$$\begin{aligned} {\mathcal {E}}_\epsilon ^{2D}(Q,\omega ') = \int _{\omega '} \rho \left( \frac{1}{2}|\nabla ' Q|^2 + \frac{1}{\rho ^2}Q_{2\times 2}:Q + \frac{1}{\epsilon ^2}f(Q) + \frac{1}{\eta ^2} g(Q) + C_0(\xi ,\eta ) \right) \, {\mathrm{d}} \rho \, {\mathrm{d}} \theta \, . \end{aligned}$$

First, we prove the next lemma, which gives the upper bound in the case where there are no singularities near the axis $\rho =0$.

Remark 5.1

• 1. The energetically relevant part of the construction in Lemma 5.2 away from defects is carried out with uniaxial $Q-$tensors of scalar order parameter $s_*$. One could also carry this out by using the physically motivated order parameter ${s_{*,\xi ^{2}/\eta ^{2}}}$ to obtain a sharper upper bound for $\xi ,\eta >0$. In our regime of the limit $\xi ,\eta \rightarrow 0$, both constructions yield the same upper bound.

• 2. In the construction of the singularities in (55), we use an isotropic core $Q=0$. Other choices, such as a oblate uniaxial state surrounded by a biaxial region, are possible and would yield a sharper upper bound for $\xi ,\eta >0$ for certain parameters. However, our upper bound for $\xi ,\eta \rightarrow 0$ is independent of this choice.

Lemma 5.2

Let $\sigma >0$ and $F\subset {\mathbb {S}}^2$ be a rotationally symmetric set of finite perimeter such that ${\mathbb {S}}^2\cap \{\rho \leqq \sigma ,z>0\},{\mathbb {S}}^2\cap \{\rho \leqq \sigma ,z<0\}$ are contained in one of the sets $F,F^c$. Then there exists a rotationally equivariant sequence of functions $Q_\epsilon \in H^1(\Omega ,{\mathrm{Sym}}_{0})$ such that the compactness claim (16) holds, $\Vert Q_\epsilon \Vert _{L^\infty }\leqq \sqrt{\frac{2}{3}}s_*$ and

$$\begin{aligned} \limsup _{\epsilon \rightarrow 0} \eta \,{\mathcal {E}}_{\eta ,\xi }(Q_\epsilon ) \leqq {\mathcal {E}}_0(F)\, . \end{aligned}$$

Proof

The proof consists in providing an explicit definition for $Q_\epsilon$, generalizing the construction made in [3]. The idea is the following: let $F\subset {\mathbb {S}}^2\cap \{\rho \geqq \sigma \}$ be rotationally symmetric. Since we assume F to be of finite perimeter, $|D\chi _F|({\mathbb {S}}^2\cap \{\rho \geqq \sigma \})<\infty$. Let ${\overline{F}}\cap \overline{F^c}\cap \Omega _\sigma ' = \{\theta _0,\ldots ,\theta _M\}$ for some $M\in {\mathbb {N}}$ and $\theta _{i}<\theta _{i+1}$ for all $i=0,\ldots ,M-1$. We now define the map $Q_\epsilon$ on the two dimensional domain $\Omega '$. We divide $\Omega '$ into several regions and define $Q_\epsilon$ on each region separately (see Figure 4). After that, we derive the estimates that are needed to ensure that the rotated map $R_\varphi ^\top Q_\epsilon R_\varphi$ satisfies the energy estimate.

Let $\Omega '$ be parametrized by polar coordinates $(r,\theta )$. As usual, we denote by $F'=F\cap \Omega '$ and $F^c{'}=F^c\cap \Omega '$. Note that $\rho =r\sin \theta$. Let ${\mathfrak {R}}>2$ be fixed.

Fig. 4

Partition of $\Omega '$ into regions for the construction of $Q_\epsilon$ (arrows represent ${\mathbf{n}}^\epsilon$)

Step 1 (Construction on $F_\eta '$ and $(F^c)_\eta '$): We define $F_\eta ' = F'{\setminus } \bigcup _{i=0}^M B_{2\eta }(\theta _i)\subset {\mathbb {S}}^1\subset \Omega '$ and $(F^c)_\eta ' = F^c{'}{\setminus } \bigcup _{i=0}^M B_{2\eta }(\theta _i)\subset {\mathbb {S}}^1\subset \Omega '$. For $(r,\theta )\in [1,{\mathfrak {R}}]\times F_\eta '$ we define

$$\begin{aligned} Q_\epsilon (r,\theta ) :=s_*\left( {\mathbf{n}}\otimes {\mathbf{n}}- \frac{1}{3}{\mathrm{Id}}\right) \quad \text {with}\quad {\mathbf{n}}(r,\theta ) = \begin{pmatrix} \sqrt{1-{\mathbf{n}}_3^2((r-1)/\eta ,\theta )} \\ 0 \\ {\mathbf{n}}_3((r-1)/\eta ,\theta ) \end{pmatrix},\nonumber \\ \end{aligned}$$

(47)

where ${\mathbf{n}}_3$ is given by Lemma 4.17. Analogously, for $(r,\theta )\in [1,{{\mathfrak {R}}}]\times (F^c)_\eta$ we define

$$\begin{aligned} Q_\epsilon (r,\theta ) :=s_*\left( {\mathbf{n}}\otimes {\mathbf{n}}- \frac{1}{3}{\mathrm{Id}}\right) \quad \text {with}\quad {\mathbf{n}}(r,\theta ) = \begin{pmatrix} -\sqrt{1-{\mathbf{n}}_3^2((r-1)/\eta ,\pi -\theta )} \\ 0 \\ {\mathbf{n}}_3((r-1)/\eta ,\pi -\theta ) \end{pmatrix}\, . \end{aligned}$$

(48)

Since the defined $Q_\epsilon$ is uniaxial of scalar order parameter $s_*$, we have $f(Q_\epsilon )=0$ and by (7) we can estimate the energy on $\Omega _{F_\eta '}=\{(r,\theta )\, : \,\theta \in F_\eta ', r\in [1,{\mathfrak {R}}]\}$

$$\begin{aligned}&\eta {\mathcal {E}}^{2D}_\epsilon (Q_\epsilon ,\Omega _{F_\eta '}) \\&\quad = \eta \int _{F_\eta '} \int _1^{{\mathfrak {R}}} \rho \,\left( s_*^2|\partial _r {\mathbf{n}}|^2 + \frac{s_*^2}{r^2}|\partial _\theta {\mathbf{n}}|^2\right. \\&\qquad \left. + \frac{1}{\rho ^2}Q_{2\times 2,\epsilon }:Q_\epsilon + \frac{c_*^2}{\eta ^2} (1-{\mathbf{n}}_3^2) + C_0(\xi ,\eta ) \right) r \, {\mathrm{d}} r\, {\mathrm{d}} \theta \\&\quad = \int _{F_\eta '} \int _0^{({\mathfrak {R}}-1)/\eta } \left( s_*^2|\partial _{t} {\mathbf{n}}|^2 + c_*^2(1-{\mathbf{n}}_3^2) + C_0(\xi ,\eta ) \right) (1+\eta t)^2 \sin \theta \, {\mathrm{d}} t\, {\mathrm{d}} \theta \\&\qquad + \int _{F_\eta '} \int _0^{({\mathfrak {R}}-1)/\eta } \frac{\eta ^2s_*^2}{(1+\eta t)^2}\left[ |\partial _\theta {\mathbf{n}}|^2 + \frac{2}{\sin ^2\theta } (1-{\mathbf{n}}_3^2)\right] (1+\eta t)^2 \sin \theta \, {\mathrm{d}} t\, {\mathrm{d}} \theta \, , \end{aligned}$$

where we set $r = 1+\eta t$ and used that $Q_{2\times 2,\epsilon }:Q = |Q_\epsilon |^2-6s_*(1-{\mathbf{n}}_3^2)s_*{\mathbf{n}}_3^2=2s_*^2(1-{\mathbf{n}}_3^2)$. Estimating $C_0$ by Proposition 2.4 and using Lemma 4.17 we get

$$\begin{aligned}&\eta \,{\mathcal {E}}_\epsilon ^{2D}(Q_\epsilon ,\Omega _{F_\eta '}) \leqq \int _{F'} I(0,({\mathfrak {R}}-1)/\eta ,\cos \theta ,1)\sin \theta \, {\mathrm{d}} \theta + C \,\eta \nonumber \\&\quad \leqq 2s_*c_*\int _{F'} (1-\cos \theta )\sin \theta \, {\mathrm{d}} \theta + C \,\eta \, . \end{aligned}$$

(49)

Applying the same steps to $(F^c)_\eta '$, we get

$$\begin{aligned} \eta \,{\mathcal {E}}_\epsilon ^{2D}(Q_\epsilon ,\Omega _{(F^c)_\eta '}) \leqq 2s_*c_*\int _{F^c{'}} (1+\cos \theta )\sin \theta \, {\mathrm{d}} \theta + C \,\eta \, . \end{aligned}$$

(50)

Step 2 (Construction on $(\Omega _{\theta _i,\eta }^{+}){'}$ and $(\Omega _{\theta _i,\eta }^{-}){'}$): Next, we construct $Q_\epsilon$ for $(r,\theta )\in [1+4\eta ,{{\mathfrak {R}}}]\times \bigcup _{i=0}^M B_{2\eta }(\theta _i)$. Without loss of generality, we assume $\theta \in B_{2\eta }(\theta _0)$ and that smaller angles belong to $F'$, while larger values lie in $F^c{'}$. We define $(\Omega _{\theta _0,\eta }^{+}){'}=\{(r,\theta )\, : \,\theta _0-2\eta \leqq \theta \leqq \theta _0, {r\in [1+4\eta ,{\mathfrak {R}}}]\}$ and $(\Omega _{\theta _0,\eta }^{-}){'}=\{(r,\theta )\, : \,\theta _0\leqq \theta \leqq \theta _0+2\eta , r\in [1+4\eta ,{\mathfrak {R}}]\}$.

Since we want $Q_\epsilon$ to have $H^1$-regularity, we need to respect the values of $Q_\epsilon$ that we already constructed at $\theta =\theta _0-2\eta$ and $\theta =\theta _0+2\eta$. We do this by interpolating between these given values and $s_*({\mathbf{e}}_3\otimes {\mathbf{e}}_3-\frac{1}{3}{\mathrm{Id}})$ at $\theta =\theta _0$. More precisely, for $(r,\theta )\in (\Omega _{\theta _0,\eta }^{+}){'}$ we define

$$\begin{aligned} Q_\epsilon (r,\theta ) = s_*\left( {\mathbf{n}}\otimes {\mathbf{n}}- \frac{1}{3}{\mathrm{Id}}\right) \quad \text {with}\quad {\mathbf{n}}(r,\theta ) = \begin{pmatrix} \sin (\phi (r,\theta )) \\ 0 \\ \cos (\phi (r,\theta )) \end{pmatrix}\, , \end{aligned}$$

where the phase $\phi$ is given by

$$\begin{aligned} \phi (r,\theta ) = \frac{\theta _0-\theta }{2\eta } \arccos \left( {\mathbf{n}}_3\left( r,\theta _0-2\eta \right) \right) \, . \end{aligned}$$

(51)

Similarly, the phase for $(r,\theta )\in (\Omega _{\theta _0,\eta }^{-}){'}$ is given by

$$\begin{aligned} \phi (r,\theta ) = -\frac{\theta -\theta _0}{2\eta } \arccos \left( {\mathbf{n}}_3\left( r,\pi -(\theta _0+2\eta )\right) \right) \, . \end{aligned}$$

(52)

Note that $Q_\epsilon$ is indeed continuous for $\theta =\theta _0$ and that $Q_\epsilon$ coincides with our previous definition at $\theta =\theta _0-2\eta$ and $\theta =\theta _0+2\eta$.

Now we calculate the energy coming from the two regions. We assume that $(r,\theta )\in (\Omega _{\theta _0,\eta }^{+}){'}$, the estimates for $(\Omega _{\theta _0,\eta }^{-}){'}$ are similar. Since $Q_\epsilon$ is takes values in ${\mathcal {N}}$, $f(Q_\epsilon )=0$ and furthermore by (7)

$$\begin{aligned} g(Q_\epsilon )&= c_*^2 (1-\cos ^2(\phi (r,\theta ))) = c_*^2 \sin ^2(\phi (r,\theta )) \leqq c_*^2 \sin ^2(\phi (r,\theta _0-2\eta ))\, . \end{aligned}$$

For the gradient, we note that

$$\begin{aligned} \frac{1}{2}|\nabla ' Q_\epsilon (r,\theta )|^2&= s_*^2|\partial _r {\mathbf{n}}(r,\theta )|^2 + \frac{s_*^2}{r^2} |\partial _\theta {\mathbf{n}}(r,\theta )|^2 = s_*^2|\partial _r \phi (r,\theta )|^2 + \frac{s_*^2}{r^2} |\partial _\theta \phi (r,\theta )|^2 \\&= \left( \frac{\theta -\theta _0}{2\eta }\right) ^2 s_*^2|\partial _r \phi (r,\theta _0-2\eta )|^2 + \frac{s_*^2}{4r^2\eta ^2}|\phi (r,\theta _0-2\eta )|^2 \\&\leqq s_*^2|\partial _r {\mathbf{n}}(r,\theta _0-2\eta )|^2 + \frac{s_*^2}{4r^2\eta ^2}|\phi (r,\theta _0-2\eta )|^2\, . \end{aligned}$$

Note, that for $\eta \rightarrow 0$ the phase $\phi$ stays bounded. Furthermore, all terms decrease exponentially in r by Lemma 4.17 and are thus integrable. Since $\frac{1}{2}|\partial _\varphi Q_\epsilon |^2 = Q_{2\times 2}:Q = 2 s_*^2\sin ^2(\phi (r,\theta ))$, this term converges to zero exponentially and is bounded for $\eta \rightarrow 0$. So finally we use the estimates on $C_0(\xi ,\eta )$, the above calculations and the usual change of variables $t=1+\eta t$ to get

$$\begin{aligned} \eta \,{\mathcal {E}}_\epsilon ^{2D}(Q_\epsilon ,(\Omega _{\theta _i,\eta }^{+}){'}) \leqq C\,\eta \, . \end{aligned}$$

(53)

Analogously,

$$\begin{aligned} \eta \,{\mathcal {E}}_\epsilon ^{2D}(Q_\epsilon ,(\Omega _{\theta _i,\eta }^{-}){'}) \leqq C\,\eta \, . \end{aligned}$$

(54)

Step 3 (Construction on $B'$ and $D'$): Throughout this construction, we assume that we are in the same situation as in Step 2, namely that we are switching from $F'$ to $F^c{'}$ as the angle $\theta$ increases. In this situation, we are going to construct a defect of degree $-1/2$. Otherwise, one would need to define a defect of degree 1/2, that is one needs to switch the sign of the angle in the definition of $Q(\alpha )$.

• We first define a map $Q_B$ on the two dimensional ball $B_1(0)$ using polar coordinates as follows

  $$\begin{aligned} Q_B(r,\alpha ) = \left\{ \begin{array}{ll} 0 &{} r \in [0,\epsilon ) \\ \left( \frac{r}{\epsilon }-1\right) Q(\alpha ) &{} r \in [\epsilon , 2\epsilon ) \\ Q(\alpha ) &{} r \in [2\epsilon , 1)\, , \end{array}\right. \end{aligned}$$

  (55)

  where

  $$\begin{aligned} Q(\alpha ) = s_*\left( {\mathbf{n}}(\alpha )\otimes {\mathbf{n}}(\alpha ) - \frac{1}{3}{\mathrm{Id}}\right) \quad \text {with}\quad {\mathbf{n}}(\alpha ) = \begin{pmatrix} \sin (\alpha /2) \\ 0 \\ \cos (\alpha /2) \end{pmatrix}\, . \end{aligned}$$

• On $B_1{\setminus } B_{2\epsilon }$ we calculate

  $$\begin{aligned} \int _{B_1{\setminus } B_{2\epsilon }} \frac{1}{2}|\nabla ' Q_B|^2 \, {\mathrm{d}} x&= \frac{1}{2}\int _0^{2\pi } \int _{2\epsilon }^1 \left( |\partial _r Q_B|^2 + \frac{1}{r^2}|\partial _\alpha Q_B|^2\right) r \, {\mathrm{d}} \alpha \, {\mathrm{d}} r \\&= \frac{1}{2} \int _{2\epsilon }^1 \frac{1}{r} \, {\mathrm{d}} r \int _0^{2\pi }|\partial _\alpha Q_B|^2 \, {\mathrm{d}} \alpha \\&= - \ln (2\epsilon ) \int _0^{2\pi } s_*^2 \frac{1}{4}(\cos ^2(\alpha /2)+\sin ^2(\alpha /2)) \, {\mathrm{d}} \alpha \\&= \frac{\pi }{2} s_*^2 |\ln (\epsilon )| - \frac{\ln (2)\pi }{2}s_*^2\, . \end{aligned}$$

  Furthermore, $f(Q_B)=0$ on $B_1{\setminus } B_{2\epsilon }$ and $\int _{B_1{\setminus } B_{2\epsilon }} |g(Q_B)| \, {\mathrm{d}} x \leqq C |B_1{\setminus } B_{2\epsilon }|$. This implies

  $$\begin{aligned} \int _{B_1{\setminus } B_{2\epsilon }} \frac{1}{2}|\nabla ' Q_B|^2 + \frac{1}{\epsilon ^2}f(Q_B) + \frac{1}{\eta ^2}g(Q_B) \, {\mathrm{d}} x \leqq \frac{\pi }{2} s_*^2 |\ln (\epsilon )| + \frac{C_1}{\eta ^2} |B_1{\setminus } B_{2\epsilon }|\, . \end{aligned}$$

  (56)

• On $B_{2\epsilon }{\setminus } B_\epsilon$ we find

  $$\begin{aligned} \int _{B_{2\epsilon }{\setminus } B_{\epsilon }} \frac{1}{2}|\nabla ' Q_B|^2 \, {\mathrm{d}} x&= \frac{1}{2}\int _0^{2\pi } \int _{\epsilon }^{2\epsilon } \left( |\partial _r Q_B|^2 + \frac{1}{r^2}|\partial _\alpha Q_B|^2\right) r \, {\mathrm{d}} \alpha \, {\mathrm{d}} r \\&= \frac{1}{2}\int _0^{2\pi } \int _{\epsilon }^{2\epsilon } \left( \frac{1}{\epsilon }-1\right) ^2|Q(\alpha )|^2 r \\&\quad + \frac{1}{r}\left( \frac{r}{\epsilon }-1\right) ^2|\partial _\alpha Q(\alpha )|^2 \, {\mathrm{d}} r \, {\mathrm{d}} \alpha \\&= \frac{2}{3}\pi s_*^2 \left( \frac{1}{\epsilon }-1\right) ^2 \int _{\epsilon }^{2\epsilon } r \, {\mathrm{d}} r + \frac{1}{2}\pi s_*^2 \int _{\epsilon }^{2\epsilon } \frac{1}{r}\left( \frac{r}{\epsilon }-1\right) ^2 \, {\mathrm{d}} r \\&= \pi s_*^2 \left( \frac{1}{\epsilon }-1\right) ^2 \epsilon ^2 + \frac{\pi }{2}s_*^2\left( \ln (2) - \frac{1}{2}\right) \\&\leqq C\, . \end{aligned}$$

  In addition, $f(Q_B) =0$ and $\int _{B_{2\epsilon }{\setminus } B_{\epsilon }} |g(Q_B)| \, {\mathrm{d}} x \leqq C |B_{2\epsilon }{\setminus } B_{\epsilon }|$. Together, we get

  $$\begin{aligned} \int _{B_{2\epsilon }{\setminus } B_{\epsilon }} \frac{1}{2}|\nabla ' Q_B|^2 + \frac{1}{\epsilon ^2}f(Q_B) + \frac{1}{\eta ^2}g(Q_B) \, {\mathrm{d}} x \leqq C_2 \left( 1+\frac{1}{\eta ^2}\right) |B_{2\epsilon }{\setminus } B_{\epsilon }|\, .\nonumber \\ \end{aligned}$$

  (57)

  Finally, the gradient of $Q_B$ on $B_\epsilon (0)$ is zero. The contributions from f and g are easily seen to be bounded by $C |B_\epsilon |$, so that

  $$\begin{aligned} \int _{B_{\epsilon }} \frac{1}{2}|\nabla ' Q_B|^2 + \frac{1}{\epsilon ^2}f(Q_B) + \frac{1}{\eta ^2}g(Q_B) \, {\mathrm{d}} x \leqq C_3\left( \frac{1}{\epsilon ^2}+\frac{1}{\eta ^2}\right) |B_\epsilon |\, . \end{aligned}$$

  (58)

Combining (56), (57) and (58) we get

$$\begin{aligned}&\int _{B_1(0)} \frac{1}{2}|\nabla ' Q_B|^2 + \frac{1}{\epsilon ^2}f(Q_B) + \frac{1}{\eta ^2}g(Q_B) \, {\mathrm{d}} x\nonumber \\&\leqq \frac{\pi }{2} s_*^2 |\ln (\epsilon )| + C\left( 1+\frac{1}{\eta ^2}\right) |B_1(0)| + C\, . \end{aligned}$$

(59)

Note that we have the same bound for $Q_{B_{{\tilde{r}}}}(r,\alpha ) = Q_B(r/{{\tilde{r}}},\alpha )$ on $B_{{\tilde{r}}}(0)$, where ${\tilde{r}}\leqq 1$. In addition, this bound is invariant under rotations and translations of the domain. Again we assume that $\theta \in B_\eta (\theta _0)$. We use the construction of $Q_B$ to define $Q_\epsilon$ on the set $B:=B_\eta (1+2\eta ,\theta _0)\subset [1,1+4\eta ]\times [\theta _0-2\eta ,\theta _0+2\eta ]$ via

$$\begin{aligned} Q_\epsilon (r,\theta ) = R_{\theta _0} Q_B({\overline{r}}/\eta ,\alpha )\, , \end{aligned}$$

(60)

where $R_{\theta _0}$ is the rotation matrix around the $\rho -$axis with angle $\theta _0$, ${\overline{r}}^2 = (r-1-2\eta )^2+(\theta -\theta _0)^2$ and $\alpha$ being the angle between the vectors $(0,1)^\top$ and $(\theta _0-\theta ,r-1-2\eta )^\top$. Note, that the term $|B_1(0)|$ in (59) transforms to |B|, which can be estimated by $C\eta ^2$. For the remaining term of ${\mathcal {E}}_\epsilon ^{2D}$ we notice that $Q_{2\times 2,\epsilon }:Q_\epsilon$ is bounded on B and that $\rho \geqq \sigma -\eta$, thus $\int _B \rho ^{-1}Q_{2\times 2,\epsilon }:Q_\epsilon \leqq C (\sigma -\eta )^{-1}$. Then, using $\rho \leqq (1+2\eta )\sin (\theta _0)+\eta$, we get from (59) together with the estimate on $C_0(\xi ,\eta )$ from Proposition 2.4, that

$$\begin{aligned} \eta \,{\mathcal {E}}_\epsilon ^{2D}(Q_\epsilon ,B) \leqq ((1+2\eta )\sin (\theta _0)+\eta )\frac{\pi }{2} s_*^2 \eta |\ln (\epsilon )| + C\eta + \frac{C}{\sigma -\eta }\eta \, . \end{aligned}$$

(61)

We now want to construct the map $Q_\epsilon$ on the set $D=\{ (r,\theta )\in [1,1+4\eta ]\times [\theta _0-2\eta ,\theta _0+2\eta ] \}{\setminus } B$ by interpolating between the values given by Steps 1 and 2 on the one hand, and the values on $\partial B$ on the other hand. We use the same polar coordinates $({\overline{r}},\alpha )$ as for the definition of $Q_\epsilon$ on B to parametrize D. Let $\Phi _{\alpha /2}$ be the phase associated to the director of $Q_\epsilon (\eta ,\alpha )$ and $\Phi (\alpha )$ the phase of the boundary values on $\partial (D\cup B)$. We set

$$\begin{aligned} \phi ({\overline{r}},\alpha ) = \frac{R(\alpha )-{\overline{r}}}{R(\alpha )-\eta }\Phi _{\alpha /2} + \frac{{\overline{r}}-\eta }{R(\alpha )-\eta }\Phi (\alpha )\, , \end{aligned}$$

where

$$\begin{aligned} R(\alpha ) = \left\{ \begin{array}{ll} \frac{2\eta }{|\cos (\alpha )|} &{} \text {if }\alpha \in [-\pi /4,\pi /4]\cup [3\pi /4,5\pi /4]\, , \\ \frac{2\eta }{|\sin (\alpha )|} &{} \text {otherwise}\, . \end{array}\right. \end{aligned}$$

In particular, $|R(\alpha )|\leqq 2\sqrt{2}\eta$ and $|\partial _\alpha R(\alpha )|\leqq 2\sqrt{2}\eta$. Then we define

$$\begin{aligned} Q_{D}({\overline{r}},\alpha ) = s_*\left( {\mathbf{n}}({\overline{r}},\alpha )\otimes {\mathbf{n}}({\overline{r}},\alpha ) - \frac{1}{3}{\mathrm{Id}}\right) \quad \text {with}\quad {\mathbf{n}}({\overline{r}},\alpha ) = \begin{pmatrix} \sin (\phi ({\overline{r}},\alpha )) \\ 0 \\ \cos (\phi ({\overline{r}},\alpha )) \end{pmatrix}\, . \end{aligned}$$

Then $f(Q_\epsilon |_D)=0$ since $Q_\epsilon |_D$ is uniaxial and of scalar order parameter $s_*$ and $|g(Q_\epsilon |_D)|$ is bounded. We can estimate the gradient

$$\begin{aligned} \begin{aligned} \int _{D} \frac{1}{2}|\nabla ' Q_\epsilon |^2 \, {\mathrm{d}} x&= \int _{D} \frac{1}{2}\left( |\partial _r Q_\epsilon |^2 + \frac{1}{r^2}|\partial _\theta Q_\epsilon |^2\right) r \, {\mathrm{d}} r \, {\mathrm{d}} \theta \\&\leqq (1+4\eta ) \int _{0}^{2\pi } \int _\eta ^{R(\alpha )} \frac{1}{2}\left( |\partial _{{\overline{r}}} Q_\epsilon |^2 + \frac{1}{{\overline{r}}^2}|\partial _\alpha Q_\epsilon |^2\right) {\overline{r}} \, {\mathrm{d}} \overline{r} \, {\mathrm{d}} \alpha \\&\leqq (1+4\eta )s_*^2 \int _{0}^{2\pi } \int _\eta ^{R(\alpha )} \left( |\partial _{{\overline{r}}} \phi |^2 + \frac{1}{{\overline{r}}^2}|\partial _\alpha \phi |^2 \right) {\overline{r}} \, {\mathrm{d}} \overline{r} \, {\mathrm{d}} \alpha \, . \end{aligned} \end{aligned}$$

(62)

Since $\Phi _{\alpha /2}$ and $\Phi (\alpha )$ are bounded and $\partial _{{\overline{r}}}\phi = \frac{-1}{R(\alpha )-\eta }\Phi _{\alpha /2} + \frac{1}{R(\alpha )-\eta }\Phi (\alpha )$, we can easily infer that $|\partial _{{\overline{r}}}\phi |^2\leqq \frac{C}{\eta ^2}$. Furthermore it is clear by definition that $|\partial _\alpha \Phi _{\alpha /2}|^2\leqq C$. So it remains to derive bounds on $\partial _\alpha \Phi (\alpha )$. For $\alpha \in [0,\pi /4]$ we have $\Phi (\alpha ) = \arccos ({\mathbf{n}}_3(1+4\eta ,\theta _0-2\eta )) \frac{\sqrt{R(\alpha )^2-4\eta ^2}}{2\eta }$, that is $|\partial _\alpha \Phi (\alpha )|^2\leqq C$. Similarly, $\partial _\alpha \Phi$ is bounded for $\alpha \in [-\pi /4,0]$. For $\alpha \in [\pi /4,3\pi /4]$ and $r(\alpha ) = 1+\sqrt{R^2(\alpha ) + 8\eta ^2 -4\sqrt{2}R(\alpha )\eta \cos (3\pi /4-\alpha )}$ one can show that $\Phi (\alpha ) = \arccos ({\mathbf{n}}_3(r(\alpha ),\theta _0-2\eta ))$. An explicit calculation yields $|\partial _\alpha \Phi (\alpha )|^2\leqq C$. By the same argument, $\partial _\alpha \Phi$ is also bounded for $\alpha \in [-3\pi /4,-\pi /4]$ For $\alpha \in [3\pi /4,\pi ]$ we have $\Phi (\alpha ) = -2\eta \tan (\pi -\alpha )+\theta _0-\frac{\pi }{2}$, so that $|\partial _\alpha \Phi (\alpha )|^2$ is also bounded by a constant. We plug this result into (62) and use the fact that $Q_{2\times 2,\epsilon }:Q_\epsilon$ is also bounded, $\sigma \leqq 1+4\eta$ and $C_0\leqq C \xi ^2/\eta ^2$ to get

$$\begin{aligned}&{\mathcal {E}}_\epsilon ^{2D}(Q_\epsilon ,D) \leqq 2(1+4\eta )s_*^2 \int _{0}^{2\pi } \int _\eta ^{R(\alpha )} \left( C + \frac{C}{\sigma ^2} \right) \sigma \, {\mathrm{d}} \sigma \, {\mathrm{d}} \alpha \nonumber \\&+ \frac{C}{\sigma -c\eta } \leqq C + \frac{C}{\sigma -c\eta }\, . \end{aligned}$$

(63)

Hence by (61) and (63)

$$\begin{aligned} \eta \,{\mathcal {E}}_\epsilon ^{2D}(Q_\epsilon ,B\cup D) \leqq ((1+2\eta )\sin (\theta _0)+2\eta )\frac{\pi }{2}s_*^2\eta |\ln \epsilon | + C \eta + \frac{C}{\sigma -C\eta }\eta \, .\nonumber \\ \end{aligned}$$

(64)

This finishes our construction of $Q_\epsilon (\rho ,\theta )$.

Step 4 (Transition to $Q_\infty (\xi ,\eta )$): So far, we have constructed the sequence $Q_\epsilon$ inside a ball of radius ${\mathfrak {R}}$ around 0. Because of the exponential convergence of the optimal profile from Lemma 4.17 , the function $Q_\epsilon$ is close to $Q_\infty$ on $\partial B_{\mathfrak {R}}$. We will now construct a transition zone from $Q_\epsilon$ to $Q_\infty$ for $r\in ({\mathfrak {R}},{\mathfrak {R}}+\eta )$ and then from $Q_\infty$ to $Q_\infty (\xi ,\eta )$ for $r\in ({\mathfrak {R}}+\eta ,{\mathfrak {R}}+2\eta )$. Since $Q_\epsilon ({\mathfrak {R}},\theta )\in {\mathcal {N}}$ for all $\theta \in [0,\pi ]$ we can linearly interpolate the phase between $Q_\epsilon ({\mathfrak {R}},\theta )$ and $Q_\infty$ as in Step 2. We estimate as in Step 2 and thus the cost of this interpolation in terms of energy is given by

$$\begin{aligned} \eta \,{\mathcal {E}}_\epsilon ^{2D}(Q_\epsilon ,B_{{\mathfrak {R}}+\eta }{\setminus } B_{{\mathfrak {R}}}) \leqq C\,\eta \, . \end{aligned}$$

(65)

For $r\in ({\mathfrak {R}}+\eta , {\mathfrak {R}}+2\eta )$ we linearly interpolate between $Q_\infty$ and $Q_\infty (\xi ,\eta )$, that is we define

$$\begin{aligned} Q_\epsilon (r,\theta ) = \frac{1}{\eta }(({\mathfrak {R}}+2\eta -r)s_* + (r-{\mathfrak {R}}-\eta ){s_{*,\xi ^{2}/\eta ^{2}}})\left( {\mathbf{e}}_3\otimes {\mathbf{e}}_3 - \frac{1}{3}{\mathrm{Id}}\right) \, . \end{aligned}$$

Since $|{s_{*,\xi ^{2}/\eta ^{2}}}-s_*|\leqq C \xi ^2/\eta ^2$ and by Proposition 2.4 we get

$$\begin{aligned} \eta \,{\mathcal {E}}_\epsilon ^{2D}(Q_\epsilon ,B_{{\mathfrak {R}}+2\eta }{\setminus } B_{{\mathfrak {R}}+\eta })&\leqq C\,\eta ^2\left( \frac{\xi ^4}{\eta ^6} + \frac{\xi ^2}{\eta ^4} + \frac{\xi ^2}{\eta ^4} + \frac{\xi ^2}{\eta ^2}\right) \, . \end{aligned}$$

(66)

Finally, if $r\geqq {\mathfrak {R}}+2\eta$ we set $Q_\epsilon =Q_\infty (\xi ,\eta )$, which has energy 0.

If we now extend $Q_\epsilon$ to $\Omega$ by using the rotated function $Q_\epsilon (\rho ,\varphi ,\theta ) = R_\varphi ^\top Q_\epsilon (\rho ,\theta ) R_\varphi$ and integrate ${\mathcal {E}}_\epsilon ^{2D}$ in $\varphi$-direction, we get from (49), (50), (53), (54), (64), (65) and (66)

$$\begin{aligned} \begin{aligned} \eta {\mathcal {E}}_\epsilon (Q_\epsilon ,\Omega )&\leqq 2s_*c_*\int _0^{2\pi }\int _{F'} (1-\cos (\theta ))\sin (\theta ) \, {\mathrm{d}} \theta \, {\mathrm{d}} \varphi \\&\quad + 2s_*c_*\int _0^{2\pi }\int _{F^c{'}} (1+\cos (\theta ))\sin (\theta ) \, {\mathrm{d}} \theta \, {\mathrm{d}} \varphi \\&\quad + \frac{\pi }{2}s_*^2\eta |\ln \epsilon |\sum _{i=0}^{M-1}\int _0^{2\pi }((1+2\eta )\sin (\theta _i)+2\eta )\, {\mathrm{d}} \varphi + C\eta + \frac{C\eta }{\sigma -c\eta }\, . \end{aligned} \end{aligned}$$

(67)

Taking the limsup $\eta ,\epsilon \rightarrow 0$ in (67) yields the inequality

$$\begin{aligned}&\limsup _{\eta ,\epsilon \rightarrow 0} {\mathcal {E}}_{\eta ,\xi }(Q_\epsilon ) \leqq 2s_*c_*\int _{F} (1-\cos (\theta )) \, {\mathrm{d}} \omega \\&+ 2s_*c_*\int _{F^c} (1+\cos (\theta )) \, {\mathrm{d}} \omega + \frac{\pi }{2}s_*^2\beta |D\chi _F|({\mathbb {S}}^2) \\&= {\mathcal {E}}_0(F)\, . \end{aligned}$$

It remains to show the claimed convergence. It is clear by definition of $Q_\epsilon$ that $\bigcup _{\eta >0} F_\eta = F$ and $\bigcup _{\eta >0} (F^c)_\eta = F^c$ which implies the convergence for $\chi _F$. The continuity of ${\mathbf{n}}^\epsilon$ as a function with values in ${\mathbb {S}}^2$ outside a set $\omega _\eta$ is clear by construction if we choose $\omega _\eta$ to contain all balls B, we used in step 3. Taking $\omega _\eta$ as the union of all sets B and D from step 3. we can also achieve that $\Omega {\setminus }\omega _\eta$ is simply connected. Extending ${\mathbf{n}}^\epsilon$ inside B measurably, yields the compactness claim. $\square$

Proof of the upper bound (18) of Theorem 3.1 We choose a sequence $\sigma _k>0$ which converges to zero as $k\rightarrow \infty$. We approximate the set F by sets $F_k$ such that the domains ${\mathbb {S}}^2\cap \{\rho \leqq \sigma _k,z> 0\}$ and ${\mathbb {S}}^2\cap \{\rho \leqq \sigma _k,z< 0\}$ are fully contained in $F_k$ or $F_k^c$. By Lemma 5.2 there exist sequences $Q_{\epsilon ,k}$ such that $\limsup _{\eta ,\epsilon \rightarrow 0} {\mathcal {E}}_{\eta ,\xi }(Q_{\epsilon ,k})\leqq {\mathcal {E}}_0(F_k)$ and (16) holds. We observe that

$$\begin{aligned} |D\chi _{F_k}|({\mathbb {S}}^2) = |D\chi _{F_k}|({\mathbb {S}}^2\cap \{\rho \geqq \sigma _k\}) = |D\chi _{F}|({\mathbb {S}}^2\cap \{\rho \geqq \sigma _k\}) \end{aligned}$$

and

$$\begin{aligned}&\left| \int _{F} \big (1-\cos (\theta )\big ) \, {\mathrm{d}} \omega - \int _{F_k} \big (1-\cos (\theta )\big ) \, {\mathrm{d}} \omega \right| ,\\&\quad \left| \int _{F^c} \big (1+\cos (\theta )\big ) \, {\mathrm{d}} \omega - \int _{F_k^c} \big (1+\cos (\theta )\big ) \, {\mathrm{d}} \omega \right| \leqq C \sigma _k^2\, . \end{aligned}$$

Hence $\limsup _{\eta ,\epsilon \rightarrow 0} {\mathcal {E}}_{\eta ,\xi }(Q_{\epsilon ,k})\leqq {\mathcal {E}}_0(F_k) \leqq {\mathcal {E}}_0(F) + C \sigma _k^2$ and taking a diagonal sequence $Q_\epsilon =Q_{\epsilon ,k(\epsilon )}$ we get

$$\begin{aligned} \limsup _{\eta ,\epsilon \rightarrow 0} {\mathcal {E}}_{\eta ,\xi }(Q_\epsilon )\leqq {\mathcal {E}}_0(F)\, . \end{aligned}$$

The compactness (16) follows by triangle inequality. $\square$

6 Limit Problem, Transition and Hysteresis

Physicists have successfully manipulated the Saturn ring configuration by using electric fields [33] and observed a transition between dipole and Saturn ring by changing the strength of the field (see [6, p. 190ff] and [39, 40]) or the radius of the particle [54]. In [40, Fig. 1] a series of images shows the accelerated shrinking of a Saturn ring defect loop around a spherical particle towards a dipole defect, once the applied electric field is switched off. The configurations intermediate between dipole and Saturn ring are observed to be unstable. Similar transitions from Saturn ring to dipole have been observed by accelerating a droplet inside a liquid crystal [36, 57].

In [50] physical reasoning, scaling arguments and numerical simulations are conducted to explain this type of transition and the occurrence of a hysteresis phenomenon. To our knowledge the hysteresis has not yet been observed, but cannot be excluded [54]. Our limit model provides an analytical setting, in which we are able to reproduce the findings derived by H. Stark from physical arguments and numerical simulations. The reduced magnetic coherence length $\xi _H$ introduced in [50] corresponds to our parameter $\eta$ in the one constant approximation. As pointed out in the first section, our limit $\xi ,\eta \rightarrow 0$ corresponds to an increasing particle radius $r_0\rightarrow \infty$ and a simultaneously decreasing field strength $h\rightarrow 0$ since $\xi \sim r_0^{-1}$ and $\eta \sim h^{-1}\xi$. The slower the decrease of h, the stronger is the influence of the magnetic field in $\eta |\ln (\xi )|$ and thus in $\beta$. It is therefore reasonable to say that small values of $\beta$ correspond to strong magnetic field, relative to the size of $\xi |\ln (\xi )|$. This translates the assumption of high magnetic fields $\xi _H\ll 1$ (while keeping $r_0$ fixed) in [50] to smaller values of $\beta$ in our limit. Although the calculations in [50] are based on the Oseen–Frank model rather than the Landau–de Gennes that we are using, we are able to reproduce the behaviour of the energy ${\mathcal {E}}_0$ as a function of $\theta _d$, compare Figure 5 and [50, Fig. 11]. From our calculation, we also find the hysteresis for changing values of $\beta s_*$. For $\beta \gg 1$, that is small external fields, the dipole is the only stable configuration. Increasing the field, the system will maintain the dipole, until we reach $\beta =0$, where a transition to the Saturn ring takes place. Decreasing the field while starting from a Saturn ring, we will retain the structure until we reach $\frac{s_*}{c_*}\beta =\frac{8}{\pi } \approx 2.546$ and the Saturn ring closes to a dipole.

The rest of this section is devoted to the calculation of the minimal energy configurations of the limiting model which we have explained above.

In a first step, we claim that if F is a minimizer of ${\mathcal {E}}_0$, then F and $F^c$ are connected. Indeed, assume that one of the two sets, say F, is not connected. Then there are two possibilities: If $F^c$ is connected, then F also contains the point $\theta =\pi$ and we can decrease the energy ${\mathcal {E}}_0$ by handing over this set to $F^c$. If $F^c$ is also not connected, then we can similarly exchange points between F and $F^c$ while decreasing the energy until both sets are connected.

Now that we know that F and $F^c$ are connected, we deduce that there can only be one angle under which the defect line separating F and $F^c$ occurs. Let us name this angle $\theta _d\in [0,\pi ]$ and let $F\subset {\mathbb {S}}^2$ be the set corresponding to $0\leqq \theta \leqq \theta _d$. Then we can express the limit energy as

$$\begin{aligned} {\mathcal {E}}_0(F)&= 2s_*c_*\int _F (1 - \cos (\theta )) \, {\mathrm{d}} \omega + 2s_*c_*\int _{F^c} (1 + \cos (\theta )) \, {\mathrm{d}} \omega + \frac{\pi }{2}s_*^2\beta |D\chi _F|({\mathbb {S}}^2) \\&= 2s_*c_*\int _0^{2\pi } \int _0^{\theta _d} (1 - \cos (\theta ))\sin (\theta ) \, {\mathrm{d}} \theta \, {\mathrm{d}} \varphi \\&\quad + 2s_*c_*\int _0^{2\pi } \int _{\theta _d}^\pi (1 + \cos (\theta ))\sin (\theta ) \, {\mathrm{d}} \theta \, {\mathrm{d}} \varphi \\&\quad + \frac{\pi }{2}s_*^2\beta (2\pi \sin (\theta _d)) \\&= 8\pi s_* c_* \Big ( \sin ^4(\theta _d/2) + \cos ^4(\theta _d/2)\Big ) + \pi ^2 \beta s_*^2 \sin (\theta _d)\, . \end{aligned}$$

Setting the derivative of this expression to zero gives the equation

$$\begin{aligned} \pi s_* \cos (\theta _d)\Big ( \pi \beta s_* - 8c_* \sin (\theta _d)\Big ) = 0\, , \end{aligned}$$

which yields the two families of solutions $\theta _1 = \pi /2 + \pi {\mathbb {Z}}$ and $\theta _2 = \arcsin (\frac{\pi \beta s_*}{8c_*}) + 2\pi {\mathbb {Z}}$. We note that

• 1. For $\frac{s_*}{c_*}\beta = \frac{8}{\pi }\approx 2.546$, the two families are equal. We conclude that for $\frac{s_*}{c_*}\beta \geqq \frac{8}{\pi }$ the only stable configuration is a dipole at $\theta _d=0,\pi$ (see Figure 5).

• 2. The energy of the Saturn ring $\theta _d=\pi /2$ and the dipole $\theta _d=0$ are equal for $\frac{s_*}{c_*}\beta = \frac{4}{\pi } \approx 1.273$, which means for greater values of $\frac{s_*}{c_*}\beta$ the dipole is the globally energy minimizing configuration, while for smaller values the Saturn ring is optimal.

• 3. The case where $\theta _d=\pi /2$ is the only (local) minimizer corresponds to $\beta =0$, that is $\theta _2=0$.

In particular, we see that the only stable energy minimizing configurations are the dipole (which corresponds to $F=\emptyset$ or $F={\mathbb {S}}^2$) and the Saturn ring (where F is the upper half-sphere).

Fig. 5

Plot of the energy ${\mathcal {E}}_0$ for different values of $\beta \frac{s_*}{c_*}$ as a function of the angle $\theta _d$

Fig. 6

Left: Plot of the energy of the dipole and Saturn ring as a function of $\frac{s_*}{c_*} \beta$. Right: Hysteresis induced by changing $\frac{s_*}{c_*} \beta$

The available experimental and theoretical results are in agreement with these findings. Nevertheless, the conducted experiments mostly use an electric field to manipulate the orientation of the liquid crystals and were not yet able to observe the hysteresis phenomenon, described in [50] and in this work.

We hope that our analysis stimulates further research into this direction.

7 Conclusion

The goal of this article was to derive an effective energy of the Landau–de Gennes model for a spherical particle immersed into a nematic liquid crystals under the influence of a homogeneous external magnetic field, stated in the framework of variational convergence. We imposed strong anchoring conditions at the boundary of the particle and investigated the interplay of elastic, bulk and magnetic free energy in an intermediate regime parametrized by $\beta$ that exhibits singularities of both dipole and Saturn ring type. Studying the limit energy, we show that there are no stable minimizers other than the dipole or the Saturn ring and we determine ranges for $\beta$ in which either of the two is energy minimizing. We calculate values of $\beta$ where a transition between the two takes place, finding a hysteresis phenomenon.

Appendix

In this section we check that the two functions $g_1$ and $g_2$ as defined in (9) verify the assumptions on g, in particular (5), (6), (7) and (8). All calculations are straightforward.

Proposition A.1

(Properties of $g_1$) Let $g_1$ be given as in (9). Then

• 1. If $Q\in {\mathcal {N}}$ is given by $Q=s_*({\mathbf{n}}\otimes {\mathbf{n}}- \frac{1}{3}{\mathrm{Id}})$ with ${\mathbf{n}}\in {\mathbb {S}}^2$, then

  $$\begin{aligned} g_1(Q) = s_*\left( 1 - {\mathbf{n}}_3^2\right) \, , \end{aligned}$$

  that is $c_*^2=s_*$.

• 2. There exists a constant $C>0$ such that for all $Q\in {\mathrm{Sym}}_{0}$

  $$\begin{aligned} |g_1(Q) - g_1({\mathcal {R}}(Q))| \leqq C\, {\mathrm{dist}}(Q,{\mathcal {N}})\, . \end{aligned}$$

  (68)

• 3. The function $g_1$ satisfies the growth assumptions (5),(6) and is invariant by rotations around the $e_3-$axis. For fixed |Q|, $g_1(Q)$ is minimal if ${\mathbf{e}}_3$ is the eigenvector corresponding to the maximal eigenvalue of Q. For $Q=s(({\mathbf{e}}_3\otimes {\mathbf{e}}_3-\frac{1}{3}{\mathrm{Id}}) + r({\mathbf{m}}\otimes {\mathbf{m}}-\frac{1}{3}{\mathrm{Id}}))$ (using the notation of (4)), $g_1(Q)$ is minimized for $r=0$.

Proof

For $Q=s_*({\mathbf{n}}\otimes {\mathbf{n}}- \frac{1}{3}{\mathrm{Id}})$ with ${\mathbf{n}}\in {\mathbb {S}}^2$ and $s_*\geqq 0$ one easily checks that

$$\begin{aligned} g_1(Q)&= \frac{2}{3}s_* - s_*\Big ({\mathbf{n}}_3^2-\frac{1}{3}\Big ) = s_* - s_*{\mathbf{n}}_3^2\, . \end{aligned}$$

For the second assertion, we take a $Q\in {\mathrm{Sym}}_{0}$ and use Proposition 2.3 to write

$$\begin{aligned} Q = s\left( \left( {\mathbf{n}}\otimes {\mathbf{n}}- \frac{1}{3}{\mathrm{Id}}\right) + r \left( {\mathbf{m}}\otimes {\mathbf{m}}- \frac{1}{3}{\mathrm{Id}}\right) \right) \, , \end{aligned}$$

with $s>0$, $0 \leqq r <1$ and ${\mathbf{n}},{\mathbf{m}}$ orthonormal eigenvectors of Q and ${\mathcal {R}}(Q) = s_* \left( {\mathbf{n}}\otimes {\mathbf{n}}- \frac{1}{3}{\mathrm{Id}}\right)$. Then we can estimate

$$\begin{aligned} |g_1(Q) - g_1({\mathcal {R}}(Q))|&= \Big |s\Big ({\mathbf{n}}_3^2-\frac{1}{3}\Big ) + sr\Big ({\mathbf{m}}_3^2-\frac{1}{3}\Big ) - s_*\Big ({\mathbf{n}}_3^2-\frac{1}{3}\Big )\Big | \\&\leqq |s-s_*|\Big |{\mathbf{n}}_3^2-\frac{1}{3}\Big | + |sr|\Big |{\mathbf{m}}_3^2-\frac{1}{3}\Big |\, . \end{aligned}$$

On the other hand, as in (38),

$$\begin{aligned} {\mathrm{dist}}^2(Q,{\mathcal {N}})&= |Q - {\mathcal {R}}(Q)|^2 \geqq \frac{1}{3}|s-s_*|^2 + \frac{1}{3}|sr|^2\, . \end{aligned}$$

Combining these two expressions, we find that

$$\begin{aligned} |g_1(Q) - g_1({\mathcal {R}}(Q))|&\leqq \frac{4}{\sqrt{3}}\,{\mathrm{dist}}(Q,{\mathcal {N}})\, , \end{aligned}$$

which completes the proof of the second assertion for the choice $C=\frac{4}{\sqrt{3}}$.

The function $g_1$ is smooth and obviously satisfies (5) and (6). Furthermore, since $g_1$ only depends on $Q_{33}$, it is invariant under rotations around the ${\mathbf{e}}_3-$axis. Writing once again $Q\in {\mathrm{Sym}}_{0}$ in the form of Proposition 2.3, we get

$$\begin{aligned} g_1(Q) \ = \ \frac{2}{3}s_* - s \Big (\Big ({\mathbf{n}}_3^2 - \frac{1}{3}\Big ) + r\Big ({\mathbf{m}}_3^2-\frac{1}{3}\Big )\Big )\, . \end{aligned}$$

For fixed $s,r,{\mathbf{m}}$ this is minimized by ${\mathbf{n}}_3^2=1$, which corresponds to the principal eigenvector ${\mathbf{n}}$ equal to ${\mathbf{e}}_3$. We also see that for ${\mathbf{n}}={\mathbf{e}}_3$ and s fixed, g becomes minimal if $r=0$, since ${\mathbf{m}}\perp {\mathbf{n}}$. $\square$

Proposition A.2

(Properties of $g_2$) Let $g_2$ be given as in (9). Then

• 1. $g_2(Q)\geqq 0$ for all $Q\in {\mathrm{Sym}}_{0}$ with equality of and only if $Q=t({\mathbf{e}}_3\otimes {\mathbf{e}}_3 - \frac{1}{3}{\mathrm{Id}})$ for some $t\geqq 0$.

• 2. If $Q\in {\mathcal {N}}$ is given by $Q=s_*({\mathbf{n}}\otimes {\mathbf{n}}- \frac{1}{3}{\mathrm{Id}})$ with ${\mathbf{n}}\in {\mathbb {S}}^2$, then

  $$\begin{aligned} g_2(Q) = \sqrt{\frac{3}{2}}\left( 1 - {\mathbf{n}}_3^2\right) \, , \end{aligned}$$

  that is $c_*^2=\sqrt{\frac{3}{2}}$.

• 3. There exist constants $\delta _1,C>0$ such that if $Q\in {\mathrm{Sym}}_{0}$ with ${\mathrm{dist}}(Q,{\mathcal {N}})\leqq \delta$ for $0<\delta <\delta _1$, then

  $$\begin{aligned} |g_2(Q) - g_2({\mathcal {R}}(Q))| \leqq C\, {\mathrm{dist}}(Q,{\mathcal {N}})\, . \end{aligned}$$

  (69)

• 4. The function $g_2$ satisfies the growth assumptions (5),(6) and is invariant by rotations around the $e_3-$axis. For fixed |Q|, $g_2(Q)$ is minimal if ${\mathbf{e}}_3$ is the eigenvector corresponding to the maximal eigenvalue of Q. For $Q=s(({\mathbf{e}}_3\otimes {\mathbf{e}}_3-\frac{1}{3}{\mathrm{Id}}) + r({\mathbf{m}}\otimes {\mathbf{m}}-\frac{1}{3}{\mathrm{Id}}))$ (using again the notation of (4)), $g_2(Q)$ is minimized for $r=0$.

Proof

Minimizing $g_2$ under the tracelessness constraint, we get the necessary conditions

$$\begin{aligned} -\frac{1}{|Q|}+\frac{Q_{33}^2}{|Q|^3}-\lambda = 0\, , \quad \frac{Q_{33}Q_{jj}}{|Q|^3}-\lambda = 0 \text { for } j=1,2\, , \quad \frac{Q_{33}Q_{ij}}{|Q|^3} = 0 \text { for }i\ne j \end{aligned}$$

for a Lagrange multiplier $\lambda$. For $Q=0$ the claim is clear by definition. So let $Q\in {\mathrm{Sym}}_{0}{\setminus }\{0\}$. If $Q_{33}=0$ we get a contradiction. Hence we can assume $Q_{33}\ne 0$. Then the third equation from above implies $Q_{ij}=0$ for $i\ne j$ and the second $Q_{11}=Q_{22}$. By ${\mathrm{tr}}(Q)=0$, we have $Q_{33}=-2Q_{11}$. Then the first equation reads $0=\frac{3}{2}Q_{33}^2 - |Q|^2$, that is $Q_{33}=\sqrt{2/3}|Q|$. Inserting this into $g_2$ we get $\min _{{\mathrm{Sym}}_{0}} g_2 = 0$. Our conditions also imply the claimed representation $Q=t({\mathbf{e}}_3\otimes {\mathbf{e}}_3 - \frac{1}{3}{\mathrm{Id}})$. Reversely, it is obvious that $g_2=0$ for such Q.

For the second claim, it is straightforward to check that for $Q=s_*({\mathbf{n}}\otimes {\mathbf{n}}- \frac{1}{3}{\mathrm{Id}})\in {\mathcal {N}}$ we have $|Q|^2=\frac{2}{3}s_*^2$. Thus

$$\begin{aligned} g_2(Q)&= \sqrt{\frac{2}{3}} - \frac{s_*({\mathbf{n}}_3^2-\frac{1}{3})}{\sqrt{\frac{2}{3}}s_*} = \sqrt{\frac{2}{3}} + \frac{1}{3}\sqrt{\frac{3}{2}} - \sqrt{\frac{3}{2}}{\mathbf{n}}_3^2 = \sqrt{\frac{3}{2}}\left( 1 - {\mathbf{n}}_3^2\right) \, . \end{aligned}$$

For the next property we use the same notation as before (from Proposition 2.3) to write

$$\begin{aligned} Q = s\left( \left( {\mathbf{n}}\otimes {\mathbf{n}}- \frac{1}{3}{\mathrm{Id}}\right) + r \left( {\mathbf{m}}\otimes {\mathbf{m}}- \frac{1}{3}{\mathrm{Id}}\right) \right) \, , \end{aligned}$$

with $s>0$, $0 \leqq r <1$ and ${\mathbf{n}},{\mathbf{m}}$ orthonormal eigenvectors of Q. From the second part of this proposition, we infer that $g_2({\mathcal {R}}(Q)) = \sqrt{\frac{3}{2}}(1-{\mathbf{n}}_3^2)$. In order to calculate $g_2(Q)$, we note that

$$\begin{aligned} |Q|^2&= s^2 \left| {\mathbf{n}}\otimes {\mathbf{n}}- \frac{1}{3}{\mathrm{Id}}\right| ^2 + (sr)^2 \left| {\mathbf{m}}\otimes {\mathbf{m}}- \frac{1}{3}{\mathrm{Id}}\right| ^2 + 2 s^2r\\&\left( {\mathbf{n}}\otimes {\mathbf{n}}- \frac{1}{3}{\mathrm{Id}}\right) :\left( {\mathbf{m}}\otimes {\mathbf{m}}- \frac{1}{3}{\mathrm{Id}}\right) \\&= \frac{2}{3} s^2 \left( r^2 - r +1 \right) \, . \end{aligned}$$

This implies

$$\begin{aligned} |g_2(Q) - g_2({\mathcal {R}}(Q))|&= \left| \sqrt{\frac{2}{3}} - \frac{s(n_3^2 - \frac{1}{3}) + sr(m_3^2-\frac{1}{3})}{\sqrt{\frac{2}{3}} s \sqrt{1-r+r^2}}\right. \\&\left. - \sqrt{\frac{2}{3}} + \frac{s_*(n_3^2-\frac{1}{3})}{s_* \sqrt{\frac{2}{3}}} \right| \\&\leqq \frac{n_3^2-\frac{1}{3}}{\sqrt{\frac{2}{3}}} \left( \frac{1}{\sqrt{1-r+r^2}} - 1\right) + \frac{m_3^2-\frac{1}{3}}{\sqrt{\frac{2}{3}}} \frac{r}{\sqrt{1-r+r^2}}\, . \end{aligned}$$

Note, that the Taylor expansion at $r=0$ is given by $\displaystyle {\frac{1}{\sqrt{1-r+r^2}} - 1} = \frac{r}{2} + {\mathcal {O}}(r^2)$ and $\displaystyle {\frac{r}{\sqrt{1-r+r^2}} = r + {\mathcal {O}}(r^2)}$. Hence

$$\begin{aligned} |g_2(Q) - g_2({\mathcal {R}}(Q))| \leqq \frac{3}{2} r + {\mathcal {O}}(r^2)\, . \end{aligned}$$

(70)

As in Proposition A.1 we get that ${\mathrm{dist}}^2(Q,{\mathcal {N}})\geqq \frac{1}{3}|s-s_*|^2 + \frac{1}{3}|sr^2|$ and hence $|s-s_*|\leqq \sqrt{3}\,{\mathrm{dist}}(Q,{\mathcal {N}})$ and $\displaystyle {|r|\leqq \frac{\sqrt{3}\, {\mathrm{dist}}(Q,{\mathcal {N}})}{|s|}}$. We define $\displaystyle {\delta _1 = \frac{1}{2\sqrt{3}}s_*}$ and together with (70) we get

$$\begin{aligned} |g_2(Q) - g_2({\mathcal {R}}(Q))| \leqq C r \leqq \frac{\sqrt{3}{\mathrm{dist}}(Q,{\mathcal {N}})}{|s|} \leqq C\frac{2\sqrt{3}}{s_*} {\mathrm{dist}}(Q,{\mathcal {N}})\, . \end{aligned}$$

It remains to prove the last assertion. Again the growth assumptions (5) and (6) are trivially satisfied. With the same arguments as in Proposition A.1 (since |Q| is fixed), we get that $g_2(Q)$ is minimal for ${\mathbf{n}}={\mathbf{e}}_3$. Finally, we can compute

$$\begin{aligned} g_2\left( s\left( \left( {\mathbf{e}}_3\otimes {\mathbf{e}}_3-\frac{1}{3}{\mathrm{Id}}\right) + r\left( {\mathbf{m}}\otimes {\mathbf{m}}-\frac{1}{3}{\mathrm{Id}}\right) \right) \right) \ = \ \sqrt{\frac{2}{3}} - \frac{\frac{2}{3} s + sr\left( {\mathbf{m}}_3^2-\frac{1}{3}\right) }{\sqrt{\frac{2}{3}}s \sqrt{1-r+r^2}} \end{aligned}$$

and see that this is indeed minimal if $r=0$. $\square$