1 Introduction

The synchronization of fractional-order neural networks (FONNs) is used widely in many application fields, such as image encryption [1], cryptography [2], and secure communication [3]. Recently, the synchronization of delayed quaternion-valued neural network (QVNNs) gradually draws researchers’ attention, as the networks carry more information and have broad application prospects. Exploring the field in depth is of great significance.

Compared with integer-order neural networks (IONNs), FONNs describe the dynamic nature of neurons more accurately with their strong memory and more degrees of freedom. In the past few years, great progress has been made in the synchronization of FONNs [4,5,6,7,8,9,10]. Based on the developed fractional-order Gronwall inequality, a new criterion is derived to guarantee the finite-time synchronization of delayed fractional-order memristor-based neural networks in [4]. Under two different controllers, the synchronization of fractional-order competitive neural networks with reaction-diffusion terms and time delays is explored via a new method in [6]. Several sufficient conditions are deduced to ensure the global dissipativity and quasi-Mittag-Leffler synchronization of the considered FONNs in [8]. The non-decomposition method is employed to investigate the finite-time cluster synchronization of fractional-order complex-variable networks with nonlinear coupling in [10]. It is noted that the above researches are investigated in the real or complex domain. However, the real-valued neural networks (RVNNs) and the complex-valued neural networks (CVNNs) lose their advantages in dealing with multi-dimensional features.

In view of the powerful processing and generalization capabilities of quaternion neurons, QVNNs that can load more information are introduced to handle multi-dimensional feature problems. At present, the decomposition method (decomposing the system into two CVNNs or four RVNNs) and the Lyapunov direct method (considering the system as a whole) are proposed to explore the dynamic behaviors of QVNNs in [11,12,13]. For example, the exponential stability conditions for an impulsive disturbed delayed QVNNs are derived by utilizing the real-valued decomposition method and generalized norms in [11]. The global Mittag-Leffler stability of FOQVNNs with leakage and time-varying delays is studied directly in [13]. Nowadays, some researchers have concentrated on the synchronization of FOQVNNs in [14,15,16,17,18,19,20,21]. By using the Lyapunov direct method, some sufficient conditions are obtained to ensure the quasi-synchronization of fractional-order quaternion-valued discrete-time memristive neural networks in [14]. The projective synchronization of delayed FOQVNNs is studied based on the Lyapunov direct method and adaptive controllers in [16]. A vector ordering method is proposed to explore the stability and synchronization control of the fractional-order quaternion-valued fuzzy memristive neural networks in [18]. The FOQVNNs are separated into four real-valued systems to explore the adaptive impulsive synchronization in [20].

However, the synchronization of FOQVNNs is achieved in an infinite time in [14,15,16, 18,19,20,21], which brings a lot of time and economic consumption. Hence, finite-time synchronization which has the features of fast convergence and good robustness is proposed to shorten the synchronization time. Several great results on finite-time synchronization of FOQVNNs have been reported in [22,23,24,25,26,27]. Based on the quaternion-valued sign function, some lemmas are established to explore the finite-time projective synchronization of the established FOQVNNs in [22]. The non-separation method is used to investigate the robust finite-time synchronization of uncertain FOQVNNs in [23]. The problem of finite-time synchronization for delayed FOQVNNs is addressed by applying Lyapunov direct method in [24]. However, in [25,26,27], the decomposition method is employed to explore the finite-time synchronization of FOQVNNs, which inevitably leads to a large amount of calculations and complex analysis. It is quite tricky to separate multiple QVNNs in practical engineering. In [22, 23, 26], time delays are ignored in the established FOQVNNs, which is inconsistent with the actual situation, since the limited signal transmission speed between neurons inevitably leads to time delays. In addition, in [28,29,30,31], the problem of finite-time synchronization for the considered IONNs is analyzed via integral inequality method or maximum-value approach, instead of finite-time stability theorems. Although the integral inequality method and the maximum-value approach are valid for IONNs, these methods cannot be directly applied to FONNs.

Inspired by the above discussions, in this paper, we aim to directly explore the finite-time synchronization of delayed FOQVNNs through fractional finite-time stability theorems. The main difficulty is to directly explore the synchronization behavior of the system without decomposition. The main innovations are as follows:

  1. (1)

    Two inequalities about quaternion are developed to avoid using the decomposition method, which broaden the current achievements in the quaternion field.

  2. (2)

    A fractional differential inequality is established by using Laplace transform and applying the definition of Mittag-Leffler function. And the numerical results show that the setting time obtained by employing the established differential inequality is shorter than that obtained by the estimation method in [39, 40]. Obviously, a new way is provided to achieve stability and synchronization of FONNs in a shorter time.

  3. (3)

    Different from the decomposition method used in [19,20,21, 25,26,27], by applying the new inequalities, two different quaternion control strategies and fractional finite-time stability theorems, some conditions of finite-time synchronization for FOQVNNs are derived, which greatly simplifies the previous researches on synchronization for FOQVNNs.

The paper is organized as follows. In Sect. 2, some definitions and new inequalities are introduced, and a type of delayed FOQVNNs is established. In Sect. 3, some conditions are given to ensure the finite-time synchronization of the delayed FOQVNNs. In Sect. 4, the theoretical results are verified by two numerical simulations. Some useful conclusions are given in Sect. 5.

2 Preliminaries and model description

Notation: Let \({\mathbb {R}}\), \({\mathbb {R}}_{+}\), \({\mathbb {C}}\), \({\mathbb {Q}}\) and \({\mathbb {Q}}^n\) denote the set of real numbers, the set of nonnegative real numbers, the set of complex numbers, the set of quaternion numbers and n-dimensional quaternion space, respectively. For any \(z=z^R+iz^I+jz^J+kz^K\in {\mathbb {Q}}\), \({\overline{z}}=z^R-iz^I-jz^J-kz^K\) is the conjugate of z, where \(z^R\), \(z^I\), \(z^J\), \(z^K\in {\mathbb {R}}\), i, j, k are standard imaginary units and obey Hamilton rules: \(i^2=j^2=k^2=ijk=-1\), \(ij=-ji=k\), \(jk=-kj=i\), \(ki=-ik=j\). \(|z|_1=|z^R|+|z^I|+|z^J|+|z^K|\), \(|z|_2=\sqrt{{\overline{z}}z}\). For any \(Z=(z_1,z_2,\cdots ,z_n)^{T}\in {\mathbb {Q}}^{n}\), then \(||Z||_1=\sum \nolimits _{p=1}^n|z_p|_1\), \(||Z||_2=(\sum _{p=1}^n|z_p|_2^2)^{\frac{1}{2}}\).

2.1 Preliminaries

Some definitions, lemmas and new inequalities are introduced.

Definition 1

[32] The Caputo fractional derivative of order \(\alpha \in (0,1)\) for a function \(f(t)\in C^{1}([t_0,+\infty ), {\mathbb {R}})\) is defined by

$$\begin{aligned} _{t_0}^{C}D_{t}^\alpha f(t)=\frac{1}{\Gamma (1-\alpha )}\int _{t_0 }^t(t-s)^{-\alpha }f^{\prime }(s)ds, \end{aligned}$$

where \(\Gamma (\alpha )\) is Euler’s gamma function defined by \(\Gamma (\alpha )=\int _{0}^{+\infty }t^{\alpha -1}e^{-t}dt\).

Definition 2

[32] The Mittag-Leffler functions with two parameters and one parameter are defined as

$$\begin{aligned} E_{\alpha ,\beta }(\upsilon )=\sum \nolimits _{k=0}^{+\infty } \frac{\upsilon ^k}{\Gamma (k\alpha +\beta )},~~ E_\alpha (\upsilon )=\sum \nolimits _{k=0}^{+\infty }\frac{\upsilon ^k}{\Gamma (k\alpha +1)} \end{aligned}$$

where \(\alpha >0\), \(\beta >0\), \(\upsilon \in {\mathbb {C}}\).

Lemma 1

[33] The Laplace transform of function \((t-t_0)^{\beta -1}E_{\alpha ,\beta }(\lambda (t-t_0)^\alpha )\) can be described by

$$\begin{aligned} {\mathcal {L}}\{(t-t_0)^{\beta -1}E_{\alpha ,\beta }(\lambda (t-t_0 )^\alpha )\}=\frac{s^{\alpha -\beta }}{s^\alpha -\lambda }, \end{aligned}$$

where t, s are the variables in the time domain and Laplace domain, respectively. \(t\ge t_0\), \(\alpha >0\) , \(\lambda ,\beta \in {\mathbb {R}}\), and \(|\lambda s^{-\alpha }|<1\).

Lemma 2

[34] Let \(t\ge t_0\), \(0<\alpha <1\) , then \(E_\alpha (\varpi (t-t_0)^\alpha )\) is monotonically non-increasing, and \(0<E_\alpha (\varpi (t-t_0)^\alpha )\le 1\) and \(\lim \nolimits _{t\rightarrow +\infty }E_\alpha (\varpi (t-t_0)^\alpha )=0\) for \(\varpi \le 0\).

Lemma 3

[35] Assume that \(a_p\ge 0\) for all \(p=1,2,\ldots ,n\), then for any \(0<b\le 1\), one has

$$\begin{aligned} \sum _{p=1}^na^b_p\ge \left( \sum _{p=1}^na_p\right) ^b \end{aligned}$$

Lemma 4

[36] Let \(z(t)\in {\mathbb {Q}}\) is a continuously differentiable function, then for \(0<\alpha <1\), one has

$$\begin{aligned} \begin{aligned} _{t_0}^{C}D_{t}^\alpha \left( \overline{z(t)}z(t)\right) \le \left( _{t_0}^{C}D_{t}^\alpha \overline{z(t)}\right) z(t)+\overline{z(t)}~_{t_0}^{C}D_{t}^\alpha z(t). \end{aligned} \end{aligned}$$

Lemma 5

For any \(z\in {\mathbb {Q}}\) , the following inequality holds

$$\begin{aligned} z+{\overline{z}}=2z^{R}\le 2|z|_2\le 2|z|_1 \end{aligned}$$

Definition 3

[22] For any \(z\in {\mathbb {Q}}\), the sign function of z is defined by

$$\begin{aligned} {\widehat{z}}=sign(z^R)+isign(z^I)+jsign(z^J)+ksign(z^K). \end{aligned}$$

Lemma 6

[22] For any \(z(t)\in {\mathbb {Q}}\), the following statements hold:

  1. (i)
    $$\begin{aligned} \overline{{\widehat{z}}(t)}{\widehat{z}}(t)=|{\widehat{z}}(t)|_1. \end{aligned}$$
  2. (ii)

    For \(0<\alpha <1\),

    $$\begin{aligned} \begin{aligned}&_{t_0}^{C}D_{t}^\alpha \left( \overline{z(t)}{\widehat{z}}(t) +\overline{{\widehat{z}}(t)}z(t)\right) \\&\quad \le \left( _{t_0}^{C}D_{t}^\alpha \overline{z(t)}\right) {\widehat{z}}(t) +\overline{{\widehat{z}}(t)}~_{t_0}^{C}D_{t}^\alpha z(t). \end{aligned} \end{aligned}$$

Lemma 7

For any \(z(t), w(t), \delta \in {\mathbb {Q}}\), the following statements hold:

  1. (i)
    $$\begin{aligned} \overline{w(t)}{\widehat{z}}(t)+\overline{{\widehat{z}}(t)}w(t)\le 2|w(t)|_1. \end{aligned}$$

    Particularly, if \(w(t)=z(t)\), then

    $$\begin{aligned} \overline{z(t)}{\widehat{z}}(t)+\overline{{\widehat{z}}(t)}z(t)=2|z(t)|_1. \end{aligned}$$
  2. (ii)
    $$\begin{aligned} \begin{aligned}&-\overline{z(t)}~{\overline{\delta }}{\widehat{z}}(t) -\overline{{\widehat{z}}(t)}\delta z(t)\\&\quad \le 2(|\delta ^I|+|\delta ^J|+|\delta ^K|-\delta ^R)|z(t)|_1. \end{aligned} \end{aligned}$$

Proof

For any \(z(t)=z^R(t)+iz^I(t)+jz^J(t)+kz^K(t)\), \(w(t)=w^R(t)+iw^I(t)+jw^J(t)+kw^K(t)\) and \(\delta =\delta ^R+i\delta ^I+j\delta ^J+k\delta ^K \in {\mathbb {Q}}\), by Lemma 5, one has

$$\begin{aligned} \begin{aligned}&\overline{w(t)}{\widehat{z}}(t)+\overline{{\widehat{z}}(t)}w(t)\\&\quad =2\left( \overline{w(t)}{\widehat{z}}(t)\right) ^R\\&\quad =2[w^R(t)sign(z^R(t))+w^I(t)sign(z^I(t))\\&\qquad +w^J(t)sign(z^J(t))+w^K(t)sign(z^K(t))]\\&\quad \le 2|w(t)|_1. \end{aligned} \end{aligned}$$
(1)

Particularly, if \(w(t)=z(t)\), then

$$\begin{aligned} \overline{z(t)}{\widehat{z}}(t)+\overline{{\widehat{z}}(t)}z(t)=2|z(t)|_1. \end{aligned}$$

In addition,

$$\begin{aligned} \begin{aligned}&-\left( \overline{z(t)}~{\overline{\delta }}{\widehat{z}}(t) +\overline{{\widehat{z}}(t)}\delta z(t)\right) \\&\quad =-2(\overline{z(t)}~{\overline{\delta }}{\widehat{z}}(t))^{R}\\&\quad =-2\delta ^{R}(|z^R(t)|+|z^I(t)|+|z^J(t)|+|z^K(t)|)\\&\qquad -2\delta ^{I}[z^R(t)sign(z^I(t))-z^I(t)sign(z^R(t))\\&\qquad +z^J(t)sign(z^K(t))-z^K(t)sign(z^J(t))]\\&\qquad -2\delta ^J[z^R(t)sign(z^J(t))-z^I(t)sign(z^K(t))\\&\qquad -z^J(t)sign(z^R(t))+z^K(t)sign(z^I(t))]\\&\qquad -2\delta ^K[z^R(t)sign(z^K(t))+z^I(t)sign(z^J(t))\\&\qquad -z^J(t)sign(z^I(t))-z^K(t)sign(z^R(t))]\\&\quad \le -2\delta ^R|z(t)|_1+2(|\delta ^I|+|\delta ^J|+|\delta ^K|)|z(t)|_1\\&\quad = 2(|\delta ^I|+|\delta ^J|+|\delta ^K|-\delta ^R)|z(t)|_1 \end{aligned} \end{aligned}$$
(2)

The proof of Lemma 7 is completed.

Remark 1

In order to avoid using the decomposition method in [19,20,21, 25,26,27] to study FOQVNNs, some useful tools for quaternion-valued functions are given in this paper, which broaden the current research results in quaternion field. In particular, if \(w(t)=z(t)\in {\mathbb {Q}}\), Lemma 7(i) is reduced to Lemma 2 in [13] or Lemma 1 in [22]. If \(w(t)=z(t)\in {\mathbb {C}}\), Lemma 7(i) is reduced to Lemma 11 in [37]. Clearly, Lemma 7 is more general than the existing results [13, 22, 37] and supplements the non-decomposition method for FOQVNNs [14,15,16,17,18, 22,23,24].

Lemma 8

Let V(t) be a continuous and nonnegative function and satisfy

$$\begin{aligned} _{t_0}^{C}D_{t}^\alpha V(t)\le -\lambda V(t)-\rho ,~V(t)\in {\mathbb {R}}_{+}\backslash \{0\} \end{aligned}$$
(3)

where \(0<\alpha <1\), \(t\ge t_0\), \(\lambda \ge 0\), \(\rho >0\), then the following statements hold:

  1. (i)

    If \(\lambda =0\), then

    $$\begin{aligned} V(t)\le V(t_0)-\frac{\rho (t-t_0)^\alpha }{\Gamma (\alpha +1)} ,~V(t)\in {\mathbb {R}}_{+}\backslash \{0\}, \end{aligned}$$

    moreover, \(\lim \nolimits _{t\rightarrow t_1}V(t)=0\), and \(V(t)\equiv 0\) for \(\forall t\ge t_1\), the setting time \(t_1\) is estimated by

    $$\begin{aligned} t_1\le t_0+\left( \frac{V(t_0)\Gamma (\alpha +1)}{\rho }\right) ^{\frac{1}{\alpha }}. \end{aligned}$$
  2. (ii)

    If \(\lambda >0\), then

    $$\begin{aligned} V(t)\le & {} \left( V(t_0)+\frac{\rho }{\lambda }\right) E_\alpha (-\lambda (t-t_0)^\alpha )-\frac{\rho }{\lambda },\\&V(t)\in {\mathbb {R}}_{+}\backslash \{0\} \end{aligned}$$

    moreover, \(\lim \nolimits _{t\rightarrow t_2}V(t)=0\), and \(V(t)\equiv 0\) for \(\forall t\ge t_2\), the setting time \(t_2\) satisfies

    $$\begin{aligned} E_\alpha (-\lambda (t_2-t_0)^\alpha )=\frac{\rho }{\lambda V(t_0)+\rho } \end{aligned}$$

Proof

If \(\lambda =0\), inequality (3) is reduced to

$$\begin{aligned} _{t_0}^{C}D_{t}^\alpha V(t)\le -\rho ,~V(t)\in {\mathbb {R}}_{+}\backslash \{0\} \end{aligned}$$
(4)

the proof is similar to Lemma 10 in [37] and Proposition 1 in [38], which is omitted here.

If \(\lambda >0\), there exists a \(H(t)\ge 0\), such that

$$\begin{aligned} _{t_0}^{C}D_{t}^\alpha V(t)+H(t)=-\lambda V(t)-\rho ,~V(t)\in {\mathbb {R}}_{+}\backslash \{0\}. \end{aligned}$$
(5)

Taking Laplace transform on both sides of equation (5), we have

$$\begin{aligned} s^\alpha V(s)-s^{\alpha -1}V(t_0)+H(s)=-\lambda V(s)-s^{-1}\rho , \end{aligned}$$
(6)

where \(V(s)={\mathcal {L}}\{V(t)\}\), \(H(s)={\mathcal {L}}\{H(t)\}\), then

$$\begin{aligned} V(s)=\frac{s^{\alpha -1}V(t_0)}{s^\alpha +\lambda }-\frac{H(s)}{s^\alpha +\lambda }-\frac{s^{-1}\rho }{s^\alpha +\lambda } \end{aligned}$$
(7)

By Lemma 1, one has

$$\begin{aligned} \begin{aligned} V(t)&=V(t_0)E_\alpha (-\lambda (t-t_0)^\alpha )-H(t)\\&\quad *[(t-t_0)^{\alpha -1}E_{\alpha ,\alpha }(-\lambda (t-t_0)^\alpha )]\\&\quad -\rho (t-t_0)^\alpha E_{\alpha ,\alpha +1}(-\lambda (t-t_0)^\alpha ) \end{aligned} \end{aligned}$$
(8)

According to \(H(t)\ge 0\), \((t-t_0)^{\alpha -1}\ge 0\) and \(E_{\alpha ,\alpha }(-\lambda (t-t_0)^\alpha )\ge 0\), then \(H(t)*[(t-t_0)^{\alpha -1}E_{\alpha ,\alpha }(-\lambda (t-t_0)^\alpha )]\ge 0\). Furthermore,

$$\begin{aligned} V(t)\le & {} V(t_0)E_\alpha (-\lambda (t-t_0)^\alpha )\nonumber \\&-\rho (t-t_0)^\alpha E_{\alpha ,\alpha +1}(-\lambda (t-t_0)^\alpha ) \end{aligned}$$
(9)

By Definition 2, one has

$$\begin{aligned} \begin{aligned}&-\rho (t-t_0)^\alpha E_{\alpha ,\alpha +1}(-\lambda (t-t_0)^\alpha )\\&\quad = \frac{\rho }{\lambda }\sum ^\infty _{k=0}\frac{(-\lambda )^{k+1} (t-t_0)^{\alpha (k+1)}}{\Gamma (\alpha (k+1)+1)}\\&\quad = \frac{\rho }{\lambda }\sum ^\infty _{k=1}\frac{(-\lambda (t-t_0 )^\alpha )^k}{\Gamma (\alpha k+1)}\\&\quad = \frac{\rho }{\lambda }\left[ \sum ^\infty _{k=0}\frac{(-\lambda (t-t_0)^\alpha )^k}{\Gamma (\alpha k+1)}-1\right] \\&\quad = \frac{\rho }{\lambda }E_\alpha (-\lambda (t-t_0)^\alpha ) -\frac{\rho }{\lambda }\\ \end{aligned} \end{aligned}$$
(10)

Hence,

$$\begin{aligned} V(t)\le & {} \left( V(t_0)+\frac{\rho }{\lambda }\right) E_\alpha (-\lambda (t -t_0)^\alpha )-\frac{\rho }{\lambda },\nonumber \\&V(t)\in {\mathbb {R}}_{+}\backslash \{0\}. \end{aligned}$$
(11)

Let \(\Phi (t)=\left( V(t_0)+\frac{\rho }{\lambda }\right) E_\alpha (-\lambda (t-t_0)^\alpha )-\frac{\rho }{\lambda }\), by Lemma 2, \(\Phi (t)\) is monotonically non-increasing, and \(\Phi (t_0)=V(t_0)>0\), \(\lim \nolimits _{t\rightarrow \infty }\Phi (t)=-\frac{\rho }{\lambda }<0\). Therefore, there exists a constant \(t_2>t_0\), such that \(\Phi (t_2)=0\), which implies \(\lim \nolimits _{t\rightarrow t_2}V(t)=0\), and \(V(t)\equiv 0\) for \(\forall t\ge t_2\), and the setting time \(t_2\) satisfies

$$\begin{aligned} E_\alpha (-\lambda (t_2-t_0)^\alpha )=\frac{\rho }{\lambda V(t_0)+\rho }. \end{aligned}$$

If the above statements are wrong, then there exists a \(t^*_2>t_2\), such that \(V(t^*_2)>0\). From inequality (11), \(V(t^*_2)\le \Phi (t^*_2)\le \Phi (t_2)=0\), which contradicts \(V(t^*_2)>0\). Hence, \(V(t)\equiv 0\) for \(\forall t\ge t_2\). The proof of Lemma 8 is completed. \(\square \)

Remark 2

Under the condition of \(\lambda >0\) in inequality (3), in [39, 40], the researchers reduce inequality (3) to \(_{t_0}^{C}D_{t}^\alpha V(t)\le -\rho \) to estimate the setting time. Actually, the value of parameter \(\lambda \) is an important factor affecting the setting time. Hence, we introduce Lemma 8(ii) based on the Laplace transform and the definition of Mittag-Leffler function to explore the influence of \(\lambda \). And the numerical results show that the setting time obtained by using Lemma 8 is shorter than that given by the method used in [39, 40] (see Example 1). Obviously, a new way is provided to achieve stability and synchronization of FONNs in a shorter time. Besides, a novel proof idea is offered, which is different from Proposition 1 in [38].

Lemma 9

[37] Let V(t) be a continuous and nonnegative function and satisfy

$$\begin{aligned} _{t_0}^{C}D_{t}^\alpha V(t)\le -\lambda V^\gamma (t),~V(t)\in {\mathbb {R}}_{+}\backslash \{0\} \end{aligned}$$

where \(0<\alpha <1\), \(t\ge t_0\), \(\lambda >0\) and \(0<\gamma <\alpha \), then

$$\begin{aligned} V(t)\le \left( V^{\alpha -\gamma }(t_0)-\frac{\lambda (t-t_0 )^\alpha }{\alpha B(\alpha ,1-\gamma )}\right) ^{\frac{1}{\alpha }}, V(t)\in {\mathbb {R}}_{+}\backslash \{0\}, \end{aligned}$$

moreover, \(\lim \nolimits _{t\rightarrow t_3}V(t)=0\), and \(V(t)\equiv 0\) for \(\forall t\ge t_3\), the setting time \(t_3\) is estimated by

$$\begin{aligned} t_3\le t_0+\left( \frac{\alpha V^{\alpha -\gamma }(t_0)B(\alpha ,1 -\gamma )}{\lambda }\right) ^{\frac{1}{\alpha }} \end{aligned}$$

2.2 Model description

In comparison with RVNNs and CVNNs, QVNNs load more information, and they can be directly used to encode 3D affine transformations. For example, in image compression, the three imaginary parts of a quaternion-valued neuron encode the three color channels to achieve color image transmission. Moreover, FOQVNNs have the ability to describe complex dynamics more accurately based on the infinite memory of fractional-order derivatives. Therefore, the following delayed FOQVNNs are established:

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} _{t_0}^{C}D_{t}^\alpha x_p(t)&{}=-c_px_p(t)+\sum _{q=1}^na_{pq}f_q(x_q(t))\\ &{}\quad +\sum _{q=1}^nb_{pq}g_q(x_q(t-\tau ))\\ &{}\quad +I_p(t),~t\ge t_0,~p=1,2,\ldots ,n,\\ x_p(r)&{}=\phi _p(r)\in {\mathbb {Q}},~r\in [t_0-\tau ,t_0], \end{aligned} \end{array}\right. } \end{aligned}$$
(12)

where \(0<\alpha <1\), \(x_p(t)\in {\mathbb {Q}}\) is the state variable. \(c_p\in {\mathbb {Q}}\) is the neuron self-inhibition and satisfies \(c^R_q>0\). \(a_{pq}\in {\mathbb {Q}}\) and \(b_{pq}\in {\mathbb {Q}}\) are connection weights, \(\tau >0\) is time delay, \(I_p(t)\in {\mathbb {Q}}\) is the external input. \(f_q(x_q(t))\), \(g_q(x_q(t-\tau ))\in {\mathbb {Q}}\) are activation functions.

System (12) is regarded as the drive system, and the response system is as follows

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} _{t_0}^{C}D_{t}^\alpha y_p(t)&{}=-c_py_p(t)+\sum _{q=1}^na_{pq}f_q(y_q(t))\\ &{}\quad +\sum _{q=1}^nb_{pq}g_q(y_q(t-\tau ))\\ &{}\quad +I_p(t)+u_p(t),~t\ge t_0,~p=1,2,\ldots ,n,\\ y_p(r)&{}=\varphi _p(r)\in {\mathbb {Q}},~r\in [t_0-\tau ,t_0], \end{aligned} \end{array}\right. } \end{aligned}$$
(13)

where \(u_p(t)\in {\mathbb {Q}}\) is a controller.

Assumption 1

For u, \(v\in {\mathbb {Q}}\), there exist positive constants \(F_{lq}\), \(G_{lq}\), such that

$$\begin{aligned} \begin{aligned} |f_q(u)-f_q(v)|_l&\le F_{lq}|u-v|_l,\\ |g_q(u)-g_q(v)|_l&\le G_{lq}|u-v|_l, \end{aligned} \end{aligned}$$

where \(q\in \{1,2,\ldots ,n\}\), and the symbol \(|\cdot |_l\) denotes l norm, \(l=1,2\).

3 Main results

In this section, the conditions for FOQVNNs to complete finite-time synchronization are derived by using the new inequalities and two different controllers.

First, the controller \(u_p(t)\in {\mathbb {Q}}\) is designed as follows:

$$\begin{aligned} \begin{aligned} u_p(t)=-r_pe_p(t)-\eta _p{\widehat{e}}_p(t), \end{aligned} \end{aligned}$$
(14)

where \(e_p(t)=y_p(t)-x_p(t)\), \(r_p>0\), \(\eta _p>0\).

Combining (12)-(14), the error system is given by

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} _{t_0}^{C}D_{t}^\alpha e_p(t)&{}=-c_pe_p(t)+\sum ^n_{q=1}a_{pq} {\widetilde{f}}_q(e_q(t))\\ &{}\quad +\sum ^n_{q=1}b_{pq}{\widetilde{g}}_q(e_q(t-\tau ))\\ &{}\quad -r_pe_p(t)-\eta _p{\widehat{e}}_p(t),\\ &{}\quad t\ge t_0,~p=1,2,\ldots ,n, \end{aligned} \end{array}\right. } \end{aligned}$$
(15)

where \({\widetilde{f}}_q(e_q(t))=f_q(y_q(t))-f_q(x_q(t))\), \({\widetilde{g}}_q(e_q(t-\tau ))=g_q(y_q(t-\tau ))-g_q(x_q(t-\tau ))\).

Theorem 1

Under Assumption 1and controller (14), for some \(\mu >1\), if

$$\begin{aligned} M=M_1-\mu M_2\ge 0 \end{aligned}$$

where \(M_1=\min \nolimits _{p=1,2,\ldots ,n}\{c^R_p+r_p-(|c^I_p|+|c^J_p|+|c^K_p|+\sum _{q=1}^n|a_{qp}|_1F_{1p})\}\), \(M_2=\max \nolimits _{p=1,2,\ldots ,n}\{\sum _{q=1}^n|b_{qp}|_1G_{1p}\}\), then system (13) is synchronized with system (12) in a finite time.

Proof

Construct the following Lyapunov function

$$\begin{aligned} V_1(t)=\sum _{p=1}^n|e_{p}(t)|_1 \end{aligned}$$
(16)

By Lemmas 6 and 7, one has

$$\begin{aligned} \begin{aligned} _{t_0}^{C}D_{t}^\alpha V(t)&\le \frac{1}{2}\sum _{p=1}^n \left[ \left( _{t_0}^{C}D_{t}^\alpha \overline{e_p(t)}\right) {\widehat{e}}_p(t)+\overline{{\widehat{e}}_p(t)}~_{t_0}^{C}D_{t}^\alpha e_p(t)\right] \\&=-\frac{1}{2}\sum _{p=1}^n[\overline{e_p(t)}~\overline{c_p} ~{\widehat{e}}_p(t)+\overline{{\widehat{e}}_p(t)}c_pe_p(t)]\\&\quad +\frac{1}{2}\sum _{p=1}^n\sum _{q=1}^n[\overline{a_{pq} {\widetilde{f}}_q(e_q(t))}~{\widehat{e}}_p(t)\\&\quad +\overline{{\widehat{e}}_p(t)}~a_{pq}{\widetilde{f}}_q(e_q(t))]\\&\quad +\frac{1}{2}\sum _{p=1}^n\sum _{q=1}^n[\overline{b_{pq} {\widetilde{g}}_q(e_q(t-\tau ))}~{\widehat{e}}_p(t)\\&\quad +\overline{{\widehat{e}}_p(t)}~b_{pq}{\widetilde{g}}_q(e_q(t-\tau ))]\\&\quad -\frac{1}{2}\sum _{p=1}^nr_p[\overline{e_p(t)}{\widehat{e}}_p(t) +\overline{{\widehat{e}}_p(t)}e_p(t)]\\&\quad -\sum _{p=1}^n\eta _p \overline{{\widehat{e}}_p(t)}{\widehat{e}}_p(t). \end{aligned} \end{aligned}$$
(17)

And it follows from Lemma 7 that

$$\begin{aligned} \begin{aligned}&-\frac{1}{2}\sum _{p=1}^n[\overline{e_p(t)}~\overline{c_p} ~{\widehat{e}}_p(t)+\overline{{\widehat{e}}_p(t)}c_pe_p(t)]\\&\quad \le (|c^I_p|+|c^J_p|+|c^K_p|-c^R_p)|e_p(t)|_1. \end{aligned} \end{aligned}$$
(18)

According to Lemma 7 and Assumption 1, we have

$$\begin{aligned} \begin{aligned}&\frac{1}{2}\sum _{p=1}^n\sum _{q=1}^n[\overline{a_{pq}{\widetilde{f} }_q(e_q(t))}~{\widehat{e}}_p(t)+\overline{{\widehat{e}}_p(t)} ~a_{pq}{\widetilde{f}}_q(e_q(t))]\\&\quad \le \sum _{p=1}^n\sum _{q=1}^n|a_{pq}{\widetilde{f}}_q(e_q(t))|_1\\&\quad \le \sum _{p=1}^n\sum _{q=1}^n|a_{pq}|_1|{\widetilde{f}}_q(e_q(t))|_1\\&\quad \le \sum _{p=1}^n\sum _{q=1}^n|a_{qp}|_1F_{1p}|e_p(t)|_1. \end{aligned} \end{aligned}$$
(19)

Similarly,

$$\begin{aligned} \begin{aligned}&\frac{1}{2}\sum _{p=1}^n\sum _{q=1}^n[\overline{b_{pq}{\widetilde{g} }_q(e_q(t-\tau ))}~{\widehat{e}}_p(t)+\overline{{\widehat{e}}_p(t) }~b_{pq}{\widetilde{g}}_q(e_q(t-\tau ))]\\&\quad \le \sum _{p=1}^n\sum _{q=1}^n|b_{pq}{\widetilde{g}}_q(e_q(t-\tau ))|_1\\&\quad \le \sum _{p=1}^n\sum _{q=1}^n|b_{pq}|_1|{\widetilde{g}}_q(e_q(t-\tau ))|_1\\&\quad \le \sum _{p=1}^n\sum _{q=1}^n|b_{qp}|_1G_{1p}|e_p(t-\tau )|_1. \end{aligned} \end{aligned}$$
(20)

By Lemma 7, one has

$$\begin{aligned} \frac{1}{2}\sum _{p=1}^nr_p[\overline{e_p(t)}{\widehat{e}}_p(t) +\overline{{\widehat{e}}_p(t)}e_p(t)]=\sum _{p=1}^nr_p|e_p(t)|_1. \end{aligned}$$
(21)

Then, submitting (18)-(21) into (17) and combining the conditions of Theorem 1, for \(V_1(t)\in {\mathbb {R}}_{+}\backslash \{0\}\), we get

$$\begin{aligned} \begin{aligned}&_{t_0}^{C}D_{t}^\alpha V(t)\\&\quad \le -\sum _{p=1}^n\left[ c^R_p+r_p -\left( |c^I_p|+|c^J_p|+|c^K_p|+\sum _{q=1}^n|a_{qp}|_1F_{1p}\right) \right] |e_p(t)|_1\\&\qquad +\sum _{p=1}^n\sum _{q=1}^n|b_{qp}|_1G_{1p}|e_p(t-\tau )|_1-\sum _{p=1 }^n\eta _p\overline{{\widehat{e}}_p(t)}{\widehat{e}}_p(t)\\&\quad \le -M_1V_1(t)+M_2V_1(t-\tau )-\eta \sum _{p=1}^n\overline{{\widehat{e} }_p(t)}{\widehat{e}}_p(t), \end{aligned} \end{aligned}$$
(22)

where \(\eta =\min \nolimits _{p=1,2,\ldots ,n}\{\eta _p\}\).

By fractional-order Razumikhin theorem [41], for some \(\mu >1\), one has

$$\begin{aligned} _{t_0}^{C}D_{t}^\alpha V_1(t)\le -(M_1-\mu M_2)V_1(t) -\eta \sum _{p=1}^n\overline{{\widehat{e}}_p(t)}{\widehat{e}}_p(t). \end{aligned}$$
(23)

According to Lemma 6 and \(V_1(t)\in {\mathbb {R}}_{+}\backslash \{0\}\), then \(\overline{{\widehat{e}}_p(t)}{\widehat{e}}_p(t)\ge 1\), hence

$$\begin{aligned} _{t_0}^{C}D_{t}^\alpha V_1(t)\le -MV_1(t)-n\eta . \end{aligned}$$
(24)

When \(M=0\), inequality (24) is reduced to

$$\begin{aligned} _{t_0}^{C}D_{t}^\alpha V_1(t)\le -n\eta , ~V_1(t)\in {\mathbb {R}}_{+}\backslash \{0\}, \end{aligned}$$
(25)

and by Lemma 8, we have

$$\begin{aligned} V_1(t)\le & {} V_1(t_0)-\frac{n\eta (t-t_0)^\alpha }{\Gamma (\alpha +1)},\nonumber \\&V_1(t)\in {\mathbb {R}}_{+}\backslash \{0\}, \end{aligned}$$
(26)

moreover, \(\lim \nolimits _{t\rightarrow T_1}V_1(t)=0\), and \(V_1(t)\equiv 0\) for \(\forall t\ge T_1\). Therefore, under controller (14), system (13) is synchronized with system (12) in a finite time. And the setting time \(T_1\) is estimated by

$$\begin{aligned} T_1\le t_0+\left( \frac{V_1(t_0)\Gamma (\alpha +1)}{n\eta }\right) ^{\frac{1}{\alpha }}. \end{aligned}$$
(27)

When \(M>0\), according to Lemma 8,

$$\begin{aligned} V_1(t)\le & {} \left( V_1(t_0)+\frac{n\eta }{M}\right) E_\alpha (-M(t-t_0)^\alpha )-\frac{n\eta }{M},\nonumber \\&V_1(t)\in {\mathbb {R}}_{+}\backslash \{0\}, \end{aligned}$$
(28)

moreover, \(\lim \nolimits _{t\rightarrow T_2}V_1(t)=0\), and \(V_1(t)\equiv 0\) for \(\forall t\ge T_2\). Therefore, under controller (14), system (13) is synchronized with system (12) in a finite time. And the setting time \(T_2\) satisfies

$$\begin{aligned} E_\alpha (-M(T_2-t_0)^\alpha )=\frac{n\eta }{M V_1(t_0)+n\eta }. \end{aligned}$$
(29)

The proof of Theorem 1 is completed. \(\square \)

Remark 3

For controller (14), two control parameters are designed, and \(r_p\) is used to control the response system to synchronize with the drive system, see the conditions of Theorem 1. While \(\eta _p\) is used to estimate the setting time, see (27) and (29) in the proof of Theorem 1.

Then, the controller \(u_p(t)\in {\mathbb {Q}}\) is designed as follows:

$$\begin{aligned} u_p(t)=-r_pe_p(t)-\eta _p{\widehat{e}}_p(t)|e_p(t)|^\beta _2 \end{aligned}$$
(30)

where \(0<\beta <2\alpha -1\).

Meanwhile, the error system is given by

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} _{t_0}^{C}D_{t}^\alpha e_p(t)&{}=-c_pe_p(t)+\sum ^n_{q=1}a_{pq} {\widetilde{f}}_q(e_q(t))\\ &{}\quad +\sum ^n_{q=1}b_{pq}{\widetilde{g}}_q(e_q(t-\tau ))\\ &{}\quad -r_pe_p(t)-\eta _p{\widehat{e}}_p(t)|e_p(t)|^\beta _2,\\ &{}\quad t\ge t_0,~p=1,2,\ldots ,n, \end{aligned} \end{array}\right. } \end{aligned}$$
(31)

where \({\widetilde{f}}_q(e_q(t))=f_q(y_q(t))-f_q(x_q(t))\), \({\widetilde{g}}_q(e_q(t-\tau ))=g_q(y_q(t-\tau ))-g_q(x_q(t-\tau ))\).

Theorem 2

Under Assumption 1and controller (30), for some \(\nu >1\), if

$$\begin{aligned} M^*=M^*_1-\nu M^*_2\ge 0 \end{aligned}$$

where \(M^*_1=\min \nolimits _{p=1,2,\ldots ,n}\{2(c^R_p+r_p)-\sum _{q=1}^n(|a_{pq}|_2F_{2q}+|a_{qp}|_2F_{2p}+|b_{pq}|_2G_{2q})\}\) , \(M^*_2=\max \nolimits _{p=1,2,\ldots ,n}\{\sum _{q=1}^n|b_{qp}|_2G_{2p}\}\) , then system (13) is synchronized with system (12) in a finite time.

Proof

Construct the following Lyapunov function

$$\begin{aligned} V_2(t)=\sum _{p=1}^n\overline{e_p(t)}e_p(t) \end{aligned}$$
(32)

By Lemma 4, one has

$$\begin{aligned} \begin{aligned} _{t_0}^{C}D_{t}^\alpha V_2(t)&\le \sum _{p=1}^n\left[ \overline{e_p(t) }~_{t_0}^{C}D_{t}^\alpha e_p(t)+\left( _{t_0}^{C}D_{t}^\alpha \overline{e_p(t)}\right) e_p(t)\right] \\&=-\sum _{p=1}^n[\overline{e_p(t)}c_pe_p(t)+\overline{e_p(t)} ~\overline{c_p}e_p(t)]\\&\quad -2\sum _{p=1}^nr_p\overline{e_p(t)}e_p(t)\\&\quad +\sum _{p=1}^n\sum _{q=1}^n[\overline{e_p(t)}~a_{pq}{\widetilde{f} }_q(e_q(t))+\overline{a_{pq}{\widetilde{f}}_q(e_q(t))}~e_p(t)]\\&\quad +\sum _{p=1}^n\sum _{q=1}^n[\overline{e_p(t)}~b_{pq}{\widetilde{g} }_q(e_q(t-\tau ))\\&\quad +\overline{b_{pq}{\widetilde{g}}_q(e_q(t-\tau ))}~e_p(t)]\\&\quad -\sum _{p=1}^n[\overline{e_p(t)}{\widehat{e}}_p(t)+\overline{ {\widehat{e}}_p(t)}e_p(t)]\eta _p|e_p(t)|^\beta _2. \end{aligned} \end{aligned}$$
(33)

By Assumption 1 and Lemma 5,

$$\begin{aligned} \begin{aligned}&\sum _{p=1}^n\sum _{q=1}^n[\overline{e_p(t)}~a_{pq}{\widetilde{f}}_q (e_q(t))+\overline{a_{pq}{\widetilde{f}}_q(e_q(t))}~e_p(t)]\\&\quad =2\sum _{p=1}^n\sum _{q=1}^n\left( \overline{e_p(t)}a_{pq} {\widetilde{f}}_q(e_q(t))\right) ^{R}\\&\quad \le 2\sum _{p=1}^n\sum _{q=1}^n|e_p(t)|_2|a_{pq}|_2| {\widetilde{f}}_q(e_q(t))|_2\\&\quad \le 2\sum _{p=1}^n\sum _{q=1}^n|e_p(t)|_2|a_{pq}|_2|F_{2q}|e_q(t)|_2\\&\quad \le \sum _{p=1}^n\sum _{q=1}^n\left( |a_{pq}|_2F_{2q} +|a_{qp}|_2F_{2p}\right) \overline{e_p(t)}e_p(t). \end{aligned} \end{aligned}$$
(34)

Similarly,

$$\begin{aligned} \begin{aligned}&\sum _{p=1}^n\sum _{q=1}^n[\overline{e_p(t)}~b_{pq}{\widetilde{g}}_q(e_q(t -\tau ))+\overline{b_{pq}{\widetilde{g}}_q(e_q(t-\tau ))}~e_p(t)]\\&\quad \le \sum _{p=1}^n\sum _{q=1}^n|b_{pq}|_2G_{2q}\overline{e_p(t)}e_p(t)\\&\qquad +\sum _{p=1}^n\sum _{q=1}^n|b_{qp}|_2G_{2p}\overline{e_p(t-\tau )}e_p(t-\tau ). \end{aligned} \end{aligned}$$
(35)

According to Lemma 3, Lemma 5 and Lemma 7,

$$\begin{aligned} \begin{aligned}&-\sum _{p=1}^n\left( \overline{e_p(t)}{\widehat{e}}_p(t) +\overline{{\widehat{e}}_p(t)}e_p(t)\right) \eta _p|e_p(t)|^\beta _2\\&\quad \le -2\sum _{p=1}^n\eta _p|e_p(t)|^{1+\beta }_2\\&\quad =-2\sum _{p=1}^n\eta _p\left( \overline{e_p(t)}e_p(t)\right) ^\frac{1+\beta }{2}\\&\quad \le -2\eta \left( \sum _{p=1}^n\overline{e_p(t)}e_p(t)\right) ^\frac{1+\beta }{2}, \end{aligned} \end{aligned}$$
(36)

where \(\eta =\min \nolimits _{p=1,2,\ldots ,n}\{\eta _p\}\).

Then, submitting (34)-(36) into (33) and combining the conditions of Theorem 2, for \(V_2(t)\in {\mathbb {R}}_{+}\backslash \{0\}\), we have

$$\begin{aligned} \begin{aligned}&_{t_0}^{C}D_{t}^\alpha V_2(t)\\&\quad \le -\sum _{p=1}^n\{2(c^R_p+r_p)\\&\qquad -\sum _{q=1}^n(|a_{pq}|_2F_{2q} +|a_{qp}|_2F_{2p}+|b_{pq}|_2G_{2q})\}\overline{e_p(t)}e_p(t)\\&\qquad +\sum _{p=1}^n\sum _{q=1}^n|b_{qp}|_2G_{2p}\overline{e_p(t -\tau )}e_p(t-\tau )\\&\qquad -2\eta \left( \sum _{p=1}^n\overline{e_p(t)}e_p(t)\right) ^\frac{1+\beta }{2}\\&\quad \le -M^*_1V_2(t)+M^*_2V_2(t-\tau )-2\eta V^{\frac{1+\beta }{2}}_2(t) \end{aligned} \end{aligned}$$
(37)

By fractional-order Razumikhin theorem [41], for some \(\nu >1\) and \(V_2(t)\in {\mathbb {R}}_{+}\backslash \{0\}\), one has

$$\begin{aligned} \begin{aligned} _{t_0}^{C}D_{t}^\alpha V_2(t)&\le -(M^*_1-\nu M^*_2) V_2(t)-2\eta V^{\frac{1+\beta }{2}}_2(t)\\&\le -2\eta V^{\frac{1+\beta }{2}}_2(t). \end{aligned} \end{aligned}$$
(38)

Due to \(0<\beta <2\alpha -1\), it follows that \(0<\frac{1+\beta }{2}<\alpha \). According to Lemma 9,

$$\begin{aligned} V_2(t)\le \left( V_2^{\frac{2\alpha -1-\beta }{2}}(t_0) -\frac{2\eta (t-t_0)^\alpha }{\alpha B(\alpha ,\frac{1-\beta }{2 })}\right) ^{\frac{1}{\alpha }},~V_2(t)\in {\mathbb {R}}_{+}\backslash \{0\}, \end{aligned}$$
(39)

moreover, \(\lim \nolimits _{t\rightarrow T_3}V_2(t)=0\), and \(V_2(t)\equiv 0\) for \(\forall t\ge T_3\). Therefore, under controller (30), system (13) is synchronized with system (12) in a finite time. And the setting time \(T_3\) is estimated by

$$\begin{aligned} T_3\le t_0+\left( \frac{\alpha V_2^{\frac{2\alpha -1-\beta }{2}}(t_0)B(\alpha ,\frac{1-\beta }{2})}{2\eta }\right) ^{\frac{1}{\alpha }}. \end{aligned}$$
(40)

The proof of Theorem 2 is completed. \(\square \)

Remark 4

The decomposition method provided in [19,20,21, 25,26,27] is quite complicated since both the original system and the controller need to be decomposed. Therefore, in this paper, two inequalities about quaternion are established and two different quaternion-valued controllers are designed, which complements the direct exploration of synchronization of FOQVNNs and avoids the complex decomposition process. Especially for multiple multi-dimensional systems, our method has the advantages of simple operation, easy analysis and less calculation.

4 Numerical simulations

In this section, in order to verify the validity of the theoretical results, we simulate two examples based on the quaternion-valued recurrent neural networks model applied to image compression [42].

Example 1

Consider the following delayed FOQVNNs as the drive system:

$$\begin{aligned} _{0}^{C}D_{t}^\alpha x_p(t)= & {} -c_px_p(t)+\sum _{q=1}^2a_{pq}f_q (x_q(t))\nonumber \\&+\sum _{q=1}^2b_{pq}g_q(x_q(t-\tau ))+I_p(t), \end{aligned}$$
(41)

where \(t\ge 0\), \(p=1,2\), \(\alpha =0.96\), \(\tau =1.8\), \(I_p(t)=0\), \(f_q(x_q(t))=tanh(x^R_q(t))+itanh(x^I_q(t))+jtanh(x^J_q(t))+ktanh(x^K_q(t))\) and \(g_q(x_q(t))=sin(x^R_q(t))+isin(x^I_q(t))+jsin(x^J_q(t))+ksin(x^K_q(t))\), the initial values \(\phi _{1}=2+i-j-2k\) and \(\phi _{2}=1.2-2.5i-j+3.5k\) for \(t\in [-1.8,0]\), and

$$\begin{aligned} \begin{aligned} C&=diag(c_1,c_2)\\&=\left( \begin{array}{cc} 3.2+0.5i-0.7j+1.4k &{} 0 \\ 0 &{} 3+1.2i+0.1j-0.6k \end{array} \right) ,\\ A&=(a_{pq})_{2\times 2}\\&=\left( \begin{array}{cc} 0.4+0.3i+0.8j+1.5k &{} 0.9-i-0.1j-1.3k \\ -0.5+1.1i-0.1j+0.1k &{} 0.2+0.1i-j+k \end{array} \right) ,\\ B&=(b_{pq})_{2\times 2}\\&=\left( \begin{array}{cc} 0.7+i-0.5j-0.5k &{} 0.3-i+0.8j-0.1k \\ 0.1+1.5i-0.8j-0.4k &{} 1.4+0.5i-0.8j-0.2k \end{array} \right) . \end{aligned} \end{aligned}$$

The response system is described as follows

$$\begin{aligned} _{0}^{C}D_{t}^\alpha y_p(t)= & {} -c_py_p(t)+\sum _{q=1}^2a_{pq}f_q(y_q(t))\nonumber \\&+\sum _{q=1}^2b_{pq}g_q(y_q(t-\tau ))+I_p(t)+u_p(t), \end{aligned}$$
(42)

where the initial values \(\varphi _{1}=-0.5-1.4i+j-k\) and \(\varphi _{2}=-1+1.2j+2.3k\) for \(t\in [-1.8,0]\).

Fig. 1
figure 1

Synchronization error evolution for four parts without control

Full size image
Fig. 2
figure 2

Synchronization error evolution for four parts under controller (14)

Full size image

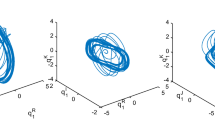
If \(u_p(t)=0\), the synchronization error evolution for four parts is depicted in Fig. 1, which indicates system (42) is not synchronized with system (41).

The parameters are set to satisfy the conditions of Theorem 1, as shown below. By calculation, for \(q=1,2\), we have \(F_{1q}=G_{1q}=1\). \(V_1(0)=16\), \(\sum _{q=1}^2|a_{q1}|_1F_{11}=4.8\), \(\sum _{q=1}^2|a_{q2}|_1F_{12}=5.6\), \(c^R_1-(|c^I_1|+|c^J_1|+|c^K_1|+\sum _{q=1}^2|a_{q1}|_1F_{11})=-4.2\), \(c^R_2-(|c^I_2|+|c^J_2|+|c^K_2|+\sum _{q=1}^2|a_{q2}|_1F_{12})=-4.5\), \(M_1=\min \{r_1-4.2,r_2-4.5\}\), \(\sum ^2_{q=1}|b_{q1}|_1G_{11}=5.5\), \(\sum _{q=1}^2|b_{q2}|_1G_{12}=5.1\), \(M_2=\max \{5.5,5.1\}=5.5\). Fixing \(\mu =1.1\), to ensure \(M=M_1-\mu M_2\ge 0\), we choose \(r_1=r_2=11\), then \(M_1=\min \{6.8,6.5\}=6.5\) and \(M=0.45\). According to the conditions of Theorem 1, at this time, we only need to ensure that the parameters \(\eta _1\) and \(\eta _2\) are greater than 0. Hence, we choose the special case of \(\eta _1=\eta _2=0.1\) and estimate the corresponding setting time \(T_2\approx 10.45\). Therefore, under controller (14), system (42) is synchronized with system (41) at \(T_2\approx 10.45\), which is shown in Fig. 2. However, when this set of parameters is fixed, the estimation method in [39, 40] is used, and the setting time is estimated as \(T^*_2\approx 94.4\). Obviously, our results are more accurate.

Example 2

Consider the following delayed FOQVNNs as the drive system:

$$\begin{aligned} _{0}^{C}D_{t}^\alpha x_p(t)= & {} -c_px_p(t)+\sum _{q=1}^2a_{pq} f_q(x_q(t))\nonumber \\&+\sum _{q=1}^2b_{pq}g_q(x_q(t-\tau ))+I_p(t), \end{aligned}$$
(43)

where \(t\ge 0\), \(p=1,2\), \(\alpha =0.98\), \(\tau =1\), \(I_p(t)=0\), the initial values \(\phi _{1}=1-i+j+k\) and \(\phi _{2}=-1-i-k\) for \(t\in [-1,0]\), and

$$\begin{aligned} \begin{aligned} f_q(x_q(t))&=g_q(x_q(t))\\&=\frac{1-e^{-x^R_q(t)}}{1+e^{-x^R_q(t)}} +i\frac{1-e^{-x^I_q(t)}}{1+e^{-x^I_q(t)}}\\&\quad +j\frac{1-e^{-x^J_q(t)}}{1+e^{-x^J_q(t)}}+k\frac{1-e^{-x^K_q(t)}}{1+e^{-x^K_q(t)}},\\ C&=diag(c_1,c_2)\\&=\left( \begin{array}{cc} 1-i+0.3j-k &{} 0 \\ 0 &{} 1.2-i+0.1k \end{array} \right) ,\\ A&=(a_{pq})_{2\times 2}\\&=\left( \begin{array}{cc} -1-i-j-k &{} -1+i+j+k \\ 0.5-i+2j-k &{} -2+j-k \end{array} \right) ,\\ B&=(b_{pq})_{2\times 2}\\&=\left( \begin{array}{cc} -2i+2j+2k &{} -2+2i-2.4j \\ -1-i+2k &{} -1.5i+j+k \end{array} \right) . \end{aligned} \end{aligned}$$

The response system is described as follows

$$\begin{aligned} _{0}^{C}D_{t}^\alpha y_p(t)= & {} -c_py_p(t)+\sum _{q=1}^2a_{pq} f_q(y_q(t))\nonumber \\&+\sum _{q=1}^2b_{pq}g_q(y_q(t-\tau ))+I_p(t)+u_p(t), \end{aligned}$$
(44)

where the initial values \(\varphi _{1}=-1+i-j\) and \(\varphi _{2}=1+i-j\) for \(t\in [-1,0]\).

Fig. 3
figure 3

Synchronization error evolution for four parts under controller (30)

Full size image
Fig. 4
figure 4

Evolution of setting time \(T_3\) versus \(\beta \) for \(\alpha =0.98\)

Full size image

The parameters are set to satisfy the conditions of Theorem 2, as shown below. By simple calculation, for \(q=1,2\), we have \(F_{2q}=G_{2q}=0.5\). \(V_2(0)=23\), \(2c^R_1-\sum _{q=1}^2(|a_{1q}|_2F_{2q}+|a_{q1}|_2F_{21}+|b_{1q}|_2G_{2q})\approx -5.84\), \(2c^R_2-\sum _{q=1}^2(|a_{2q}|_2F_{2q}+|a_{q2}|_2F_{22}+|b_{2q}|_2G_{2q})\approx -4.56\), \(M^*_1=\min \{2r_1-5.84,2r_2-4.56\}\), \(\sum _{q=1}^2|b_{q1}|_2G_{21}\approx 2.96\), \(\sum _{q=1}^2|b_{q2}|_2G_{22}\approx 2.89\), \(M^*_2=\max \{2.96,2.89\}=2.96\). Fixing \(\nu =2\), to ensure \(M^*=M^*_1-\nu M^*_2\ge 0\), we choose \(r_1=6\), \(r_2=5.5\), then \(M^*_1=\min \{6.16,6.44\}=6.16\) and \(M^*=0.24\). According to the conditions of Theorem 2, at this time, we only need to ensure that the parameters \(\eta _1>0\), \(\eta _2>0\) and \(0<\beta <0.96\). Hence, we choose the special case of \(\eta _1=\eta _2=0.5\) and \(\beta =0.4\), and estimate the corresponding setting time \(T_3\approx 8.27\). Therefore, under controller (30), system (44) is synchronized with system (43) at \(T_3\approx 8.27\), which is depicted in Fig. 3. Particularly, when fractional order \(\alpha \) and other parameters are fixed, the evolution of setting time \(T_3\) versus \(\beta \) is shown in Fig. 4. As shown in Fig. 4, the setting time \(T_3\) first decreases and then increases with the increase of \(\beta \). Hence, we can properly adjust parameter \(\beta \) to get a smaller setting time.

5 Conclusion

In this paper, the finite-time synchronization of delayed FOQVNNs is explored by using some new inequalities and control strategies. First, two inequalities about quaternion are developed and a fractional differential inequality is established by using Laplace transform and applying the definition of Mittag-Leffler function. Then, by applying new inequalities and two different controllers, some conditions are derived to guarantee the finite-time synchronization of the delayed FOQVNN. Finally, the theoretical results are verified by two numerical examples. The results of numerical example 1 show that the setting time is more accurate than that obtained by the estimation method in [39, 40]. The results of numerical example 2 suggest that if fractional order \(\alpha \) and other parameters are fixed, the setting time first decreases and then increases with the increase in fractional-order power law \(\beta \) in controller (30). Hence, the parameter \(\beta \) can be adjusted appropriately to obtain a smaller setting time. Regrettably, the estimation of the setting time is affected by the initial values of the system, and the initial values are difficult to know in advance. Therefore, discussing the fixed-time synchronization of delayed FOQVNNs that does not depend on the initial values will be our future research topic.