1 Introduction

Nonlinear systems are the most common in industrial processes where those are defined as their inputs are related to nonlinear to the outputs. These systems have an important area in the research field because the modeling and estimating system nonlinearities are more difficult and contain inherent uncertainties [1,2,3]. The development of a controller for the nonlinear systems should be skillful to track its output precisely. Noting that, the application of the traditional controllers for the nonlinear systems is inappropriate due to that such nonlinear systems normally suffer from many difficult problems, such as the nonlinear dynamic behavioral, the constraints on the manipulated variables, the uncertain and time-varying parameters, unmeasured and frequent disturbances [4, 5]. Thus, the development of the controller is necessary to control such challenges. Nowadays, many researchers are interested in artificial intelligent (AI) controllers because of their ability to make the nonlinear systems are stable [6,7,8,9,10].

In this concern, artificial neural networks (ANNs) are one of the AI, which are defined as biologically inspired programming paradigm. ANNs enable the controller to learn from observational data [11,12,13,14]. The ANNs are considered one of the most successful techniques in nonlinear control applications. In [15], ANN controllers were developed in order to control pressure. Also, it is described in [16] that the diagonal recurrent neural network controller (DRNNC) shows its ability to control the dynamic behavior of the nonlinear plant. The robust analysis of the neural network control was utilized for controlling the speed of a DC motor, which was described in [17]. The robustness was ensured using an internal model controller. In [18], feed-forward neural network controller (FFNNC) with a hybrid method (FFNNC-hybrid) was introduced. The learning of the FFNNC-hybrid was performed based on unsupervised (self-organized leaning) and supervised (gradient descent) method. In [19], the FFNNC and nonlinear autoregressive neural network were used to overcome the delay control for offshore platform system. A direct adaptive inverse control was introduced using FFNNC for controlling the nonlinear system [20]. An adaptive feed-forward neural controller and PID controller were used for controlling the joint-angle position of the SCARA parallel robot [21]. The FFNNC was used to control the angle with position of a nonlinear inverted pendulum system [22].

The controllers design was performed based on FFNNC, which are commonly related to the initialized weights. Noting that, if the process of initializing weights is not appropriate, the NN gets stumbling in local minima, leading the training procedure to unsatisfactory ending or the vanishing gradient issue is happened during the initial layers training and the NN training becomes infeasible [23]. This defect affects the performance of the controller, and it makes the controller unstable sometimes. On the other hand, machine learning (ML) is a part of AI, which is performed based on the techniques that make the computers to discover things from input data. In this concern, deep learning (DL) is a modern topic of ML. DL has learning numerous levels, which supports to deliver sense of data such as images [24,25,26], sound [27], and text [28]. The most common use of DL is the modeling process of the nonlinear systems.

1.1 Literature review

In [29], the DL framework was proposed for modeling the nonlinear systems. It learns deep reconstruction model, which is performed based on Elman neural network (ENN) and RBM (ENN-RBM) for initializing only the first layer. In [30], the regression and classification issues can be solved using the randomized algorithms and DL techniques. In this concern, these algorithms are used for constructing the statistical features and training the hidden weights. In [31], deep belief network (DBN) with partial least square regression (PLSR) was investigated for the nonlinear system modeling, where the problem of the weights improvement for DBN is performed based on PLSR. In [32], this work was tried for the prediction traffic speeds of multiple road links simultaneously by constructing a DL based on multitask learning model. In [33], the researcher proposed a new method for the optical identification of parts without specific codes, which is performed based on inherent geometrical features with DL. Finally, in [34,35,36,37], the researchers cover some DL techniques, which already are applied in radiology and identify radiogenomic associations in breast cancer for image processing.

1.2 Motivation

From the previous studies, it is clear that the application field of DL was limited only for modeling systems and image processing and it does not cover the control area. Besides, the nonlinear systems suffer from uncertainties and external disturbance. So, the main target of the present study is to shed further light on designing a stable feed-forward neural network deep learning controller (FFNNDLC), to be applied for controlling the nonlinear systems to overcome the problems of system uncertainties. The proposed FFNNDLC uses the RBM to initialize the weight values. Lyapunov stability method is used for updating the adaptation parameters laws. The FFNNDLC is learned swift to keep a track of trajectory and to overcome the outside disturbances and the changes in the system parameters. In this concern, FFNNDLC is utilized to the uncertain nonlinear systems in order to guarantee the optimum controlling and decreasing the influence of uncertainties and outside disturbances. Of course, these advantages of FFNNDLC make it sturdier than FFNNC under the same conditions. On the other hand, the proposed controller is implemented practically for controlling a real system.

1.3 Novelties and contributions

The major target of the present paper is summed up as:

  • A new controller is proposed in the control field based on DL technique.

  • Developing the adaptation law for the proposed controller parameters based on Lyapunov theorem to warranty a stable controller.

  • Implementing practically the proposed controller based on an ARDUINO DUE kit for controlling a real system.

  • The proposed controller has the ability to reduce the uncertainties influence and outside disturbances compared to other controllers under the same conditions.

The paper organization is as follows: Restricted Boltzmann machine is explained in part 2. The mathematical formulation for restricted Boltzmann machine is introduced in this section. Feed-forward neural network deep learning controller and the Lyapunov stability derivation of FFNNDLC are explained in part 3. The FFNNDL system and controller training steps are introduced in part 4. The simulation results for nonlinear systems are introduced in part 5. The practical results are introduced in part 6. Finally, part 7 presents the conclusion followed by the references.

2 Restricted Boltzmann machine

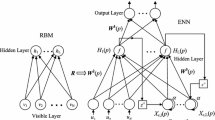
RBM is an energy-based model, which uses two layers: visible and hidden layers that consists of a group of the visible nodes; \( V \), and a group of the hidden nodes; \( H \). The conventional approach was introduced for training RBM where a linear nature of the neural units was considered the main drawback in this method [29, 38]. Another approach to derive RBM training rules and overcome the main shortcoming of traditional method was introduced in [39, 40]. It takes into computation nonlinear nature of neural nodes and minimizing the mean square error (MSE). The RBM uses three layers as illustrated in Fig. 1.

Fig. 1
figure 1

Structure of RBM

Full size image

Based on this approach, contrastive divergence (CD) was proposed by Hinton for learning RBM [41, 42]. Let \( V(q - 1) \) will be the input data, which shifts to the visible layer at time \( (q - 1) \). Then, the output of the hidden layer is determined as follows:

$$ H_{j} \left( {q - 1} \right) = F\left( {\sum\limits_{i}^{N} {W_{ij} } \,V_{i} \left( {q - 1} \right) + b_{j} } \right),\,\,\,i = 1, \ldots ,N\,\,\,\,j = 1, \ldots P\,\,{\text{and}}\,\,\,q = 1, \ldots ,K $$
(1)

where \( \varvec{b} = \left[ {\begin{array}{*{20}c} {b_{1} } & \cdots & {b_{P} } \\ \end{array} } \right]^{T} \) is the biases vector for the hidden nodes, \( V_{i} \) represents the binary state of the visible node, and \( W_{ij} \) represents the weight between the visible node \( i \) and the hidden node \( j \). \( N \) and \( M \) are the number of the visible nodes and the hidden nodes, respectively. \( F \) represents sigmoid activation function; \( F\left( Q \right) = {1 \mathord{\left/ {\vphantom {1 {\left( {1 + \exp \left( { - Q} \right)} \right)}}} \right. \kern-0pt} {\left( {1 + \exp \left( { - Q} \right)} \right)}} \).

The inverse layer reconstructs the data from the hidden layer. As a result, \( V\left( q \right) \) is obtained at time; \( q \) as follows:

$$ V_{i} \left( q \right) = F\left( {\sum\limits_{j}^{P} {W_{ji} H_{j} \left( {q - 1} \right) + a_{i} } } \right) $$
(2)

where \( \varvec{a} = \left[ {\begin{array}{*{20}c} {a_{1} } & \ldots & {a_{N} } \\ \end{array} } \right]^{T} \) is the biases vector for the visible nodes, \( H_{j} \) represents the binary status of a hidden node, \( W_{ji} \) represents the weight between the hidden node \( j \) and the visible node \( i \). Subsequently, \( V\left( q \right) \), which transfers to the visible layer and the hidden layer output, is obtained by the next procedure:

$$ H_{j} \left( q \right) = F\left( {\sum\limits_{i}^{N} {W_{ij} V_{i} \left( q \right) + b_{j} } } \right) $$
(3)

The parameters training rule for the weights and biases of nonlinear RBM in case of CD-K is illustrated as [40]:

$$ W_{ij} \left( {\hbar + 1} \right) = W_{ij} \left( \hbar \right) + \alpha \left( {\sum\limits_{q = 1}^{K} {\left( {H_{j} \left( q \right) - H_{j} \left( {q - 1} \right)} \right)\,V_{i} \left( q \right)\,F^{\prime}\left( {S_{j} \left( q \right)} \right) + \left( {V_{i} \left( q \right) - V_{i} \left( {q - 1} \right)} \right)\,H_{j} (q - 1)\,F^{\prime}\left( {S_{i} \left( q \right)} \right)} } \right) $$
(4)
$$ b_{j} \left( {\hbar + 1} \right) = b_{j} \left( \hbar \right) + \alpha \left( {\sum\limits_{q = 1}^{K} {\left( {H_{j} \left( q \right) - H_{j} \left( {q - 1} \right)} \right)\,F^{\prime}\,\left( {S_{j} \left( q \right)} \right)} } \right) $$
(5)
$$ a_{i} \left( {\hbar + 1} \right) = a_{i} \left( \hbar \right) + \alpha \left( {\sum\limits_{q = 1}^{K} {\left( {V_{i} \left( q \right) - V_{i} \left( {q - 1} \right)} \right)\,F^{\prime}\,\left( {S_{i} \left( q \right)} \right)} } \right) $$
(6)

where \( \alpha \) is the learning rate of RBM and \( \hbar \) is the iteration number.

RBM is the very important part for the deep controller, which is used for initializing the FFNN based on performing unsupervised pretraining, where all weights are equal to zero. The stack parameters of RBM also match to the parameters of the multilayer FFNN. Therefore, once the stack of RBM is trained, available parameters can be used to initialize the first layer of FFNN and so on the next layers.

3 Feed-forward neural network deep learning controller

Basically, any ANN with more than two layers is deep. DL is a relatively new advancement in ANN programming and represents a way to train deep neural networks [43]. The DL methods aim to learn feature hierarchies with features from the higher levels of the hierarchy formed by the composition of lower-level features. They include learning methods for a wide array of deep architectures, including ANN with hidden layers [44]. Merge with the features of RBM and multilayer FFNN, FFNNDLC is proposed.

3.1 Feed-forward neural network

The typical four-layer FFNN is shown in Fig. 2 [45]. It contains an input layer, two hidden layers and an output layer.

Fig. 2
figure 2

Feed-forward neural network

Full size image

Input layer: each node is an external input in this concern, and the inputs are denoted as \( x_{1} ,\,x_{2} ,\, \ldots ,\,x_{n} \).

Hidden layer (1): each node is determined as the following:

$$ net_{j}^{(1)} = \,\sum\limits_{i = 1}^{n} {\psi_{ji} x_{i} } + T_{j} \,,\,\,\,\,\,\,j = 1,\, \ldots ,\,J $$
(7)
$$ y_{j}^{(1)} = f\left( {net_{j}^{(1)} } \right),\,\,\,\,\,\,\,j = 1,\, \ldots ,\,J $$
(8)

where \( \psi_{ji} \) represents the weights between the input layer and the hidden layer (1), \( T_{j} \) represents the threshold value for each node, \( J \) is the number of the nodes, \( y_{j}^{(1)} \) is the output of each node, and \( f \) is a nonlinear activation function. In this paper, the hyperbolic tangent function is used and it ranges on the interval [− 1, 1], which is defined as:

$$ f\left( W \right) = \tanh \left( W \right) $$
(9)

and its derivative can be obtained by \( {{d\left[ {f\left( W \right)} \right]} \mathord{\left/ {\vphantom {{d\left[ {f\left( W \right)} \right]} {dy}}} \right. \kern-0pt} {dy}} = 1 - f^{2} \left( W \right) \).

Hidden layer (2): each node is determined as the following:

$$ net_{m}^{(2)} = \,\sum\limits_{j = 1}^{J} {\psi_{mj} \,y_{j}^{(1)} } + T_{m} \,,\,\,\,\,\,\,m = 1,\, \ldots ,\,M $$
(10)
$$ y_{m}^{(2)} = f\left( {net_{m}^{(2)} } \right),\,\,\,\,\,\,\,m = 1,\, \ldots ,\,M $$
(11)

where \( \psi_{mj} \) represents the weights between the hidden layer (1) and the hidden layer (2), \( T_{m} \) represents the threshold value for each node in this layer, \( M \) is the number of the nodes in this layer, and \( y_{m}^{(2)} \) represents the output of each node.

Output layer: its output is calculated as:

$$ u = \sum\limits_{m = 1}^{M} {\psi_{m} \,y_{m}^{(2)} + T} $$
(12)

where \( u \) represents the output of the network, \( \psi_{m} \) represents the weights between the hidden layer (2) and the output layer, and \( T \) represents the threshold value.

The NN is trained to minimize the error between the reference input and the measured output [46, 47]. The square of the error is defined as:

$$ E_{g} \left( \hbar \right) = \frac{1}{2}\left( {y_{d} \left( \hbar \right) - y_{a} \left( \hbar \right)} \right)^{2} = \frac{1}{2}e_{g}^{2} \left( \hbar \right) $$
(13)

where \( y_{d} (\hbar ) \) represents the reference input and \( y_{a} (\hbar ) \) represents the actual output.

3.2 Weights learning based on Lyapunov stability

A scalar function \( V_{x} \left( \hbar \right) \) is chosen as a positive definite function for all initial conditions of its arguments [48, 49]. Now, if the two conditions, which are described in Eqs. (14 and 15), are get together, the given system is considered asymptotic stable.

$$ V_{x} \left( \hbar \right) > 0l{\text{for all }}\hbar \,{\text{except }}\hbar = 0 $$
(14)
$$ \Delta V_{x} \left( \hbar \right) = V_{x} \left( {\hbar + 1} \right) - V_{x} (\hbar ) \le 0 $$
(15)

To put the basis of the weight learning algorithm, the weight update equation in a general form can be expressed as:

$$ \varPsi_{g} \left( {\hbar + 1} \right) = \varPsi_{g} (\hbar ) - \eta \Delta \varPsi_{g} (\hbar ) $$
(16)

where \( \varPsi_{g} \left( \hbar \right) \) is the generalized weight vector and \( \eta \) is the learning rate. \( \Delta \varPsi_{g} \left( B \right) \) indicates the desired weights modification.

Theorem 1

The parameters of the FFNNDLC, which warranty the stability, are obtained based on the following:

$$ \varPsi_{g} \left( {\hbar + 1} \right) = \varPsi_{g} \left( \hbar \right) + \eta \frac{{\beta \left( {\frac{\alpha }{\beta }e_{g} \left( \hbar \right)\frac{{\partial e_{g} \left( \hbar \right)}}{{\partial \varPsi_{g} \left( \hbar \right)}} + \varPsi_{g} \left( \hbar \right)} \right)}}{2\delta } $$
(17)

Proof

Assume the next Lyapunov function:

$$ V_{x} \left( \hbar \right) = V_{a} \left( \hbar \right) + V_{b} (\hbar ) + V_{c} \left( \hbar \right) $$
(18)

where \( V_{a} \left( \hbar \right) = \frac{\alpha }{2}\left( {e_{g} \left( \hbar \right)} \right)^{2} \),\( V_{b} \left( \hbar \right) = \frac{\beta }{2}\left( {\varPsi_{g} \left( \hbar \right)} \right)^{2} \),\( V_{c} \left( \hbar \right) = \frac{\delta }{2}\left( {\Delta \varPsi_{g} \left( \hbar \right)} \right)^{2} \),\( \alpha ,\beta \) and \( \delta \) are constants. \( \Delta V_{a} \left( \hbar \right) \), \( \Delta V_{b} \left( \hbar \right) \) and \( \Delta V_{c} \left( \hbar \right) \) are defined as:

$$ \begin{aligned} \Delta V_{a} \left( \hbar \right) & = V_{a} \left( {\hbar + 1} \right) - V_{a} (\hbar ) \\ & = \frac{\alpha }{2}\left( {e_{g} \left( {\hbar + 1} \right)} \right)^{2} - \frac{\alpha }{2}\left( {e_{g} \left( \hbar \right)} \right)^{2} \\ \end{aligned} $$
(19)
$$ \begin{aligned} \Delta V_{b} \left( \hbar \right) & = V_{b} \left( {\hbar + 1} \right) - V_{b} (\hbar ) \\ & = \frac{\beta }{2}\left( {\varPsi_{g} \left( {\hbar + 1} \right)} \right)^{2} - \frac{\beta }{2}\left( {\varPsi_{g} \left( \hbar \right)} \right)^{2} \\ \end{aligned} $$
(20)
$$ \begin{aligned} \Delta V_{c} \left( \hbar \right) & = V_{c} \left( {\hbar + 1} \right) - V_{c} (\hbar ) \\ & = \frac{\delta }{2}\left( {\Delta \varPsi_{g} \left( {\hbar + 1} \right)} \right)^{2} - \frac{\delta }{2}\left( {\Delta \varPsi_{g} \left( \hbar \right)} \right)^{2} \\ \end{aligned} $$
(21)

The term \( \frac{\alpha }{2}\left( {e_{g} \left( {\hbar + 1} \right)} \right)^{2} \) can be formulated based on the Taylor series as [2, 6]:

$$ \frac{\alpha }{2}\left( {e_{g} \left( {\hbar + 1} \right)} \right)^{2} = \frac{\alpha }{2}\left( {e_{g} \left( \hbar \right)} \right)^{2} + \frac{{\partial \left( {\frac{\alpha }{2}\left( {e_{g} \left( \hbar \right)} \right)^{2} } \right)}}{{\partial \varPsi_{g} \left( \hbar \right)}}\Delta \varPsi_{g} \left( \hbar \right) + {\text{higher}}\,{\text{order}}\,{\text{terms}}\,(HOT) $$
(22)

where HOT can be ignored. Therefore, Eq. (22) can be reformulated as:

$$ \frac{\alpha }{2}\left( {e_{g} \left( {\hbar + 1} \right)} \right)^{2} - \frac{\alpha }{2}\left( {e_{g} \left( \hbar \right)} \right)^{2} = \alpha e_{g} \left( \hbar \right)\frac{{\partial \left( {e_{g} \left( \hbar \right)} \right)}}{{\partial \varPsi_{g} \left( \hbar \right)}}\Delta \varPsi_{g} \left( \hbar \right) $$
(23)

Similarity,

$$ e_{g} \left( {\hbar + 1} \right) = e_{g} \left( \hbar \right) + \frac{{\partial e_{g} \left( \hbar \right)}}{{\partial \varPsi_{g} \left( \hbar \right)}}\Delta \varPsi_{g} \left( \hbar \right) $$
(24)

Equation (24) can be reformulated as:

$$ e_{g} \left( {\hbar + 1} \right) - e_{g} \left( \hbar \right) = \Delta e_{g} \left( \hbar \right) = \frac{{\partial e_{g} \left( \hbar \right)}}{{\partial \varPsi_{g} \left( \hbar \right)}}\Delta \varPsi_{g} \left( \hbar \right) $$
(25)

Then, by replacing \( \frac{{\partial e_{g} \left( \hbar \right)}}{{\partial \varPsi_{g} \left( \hbar \right)}}\Delta \varPsi_{g} \left( \hbar \right) \) in Eq. (23), we obtain

$$ \Delta V_{a} \left( \hbar \right) = \frac{\alpha }{2}\left( {e_{g} \left( {\hbar + 1} \right)} \right)^{2} - \frac{\alpha }{2}\left( {e_{g} \left( \hbar \right)} \right)^{2} = \alpha \,e_{g} \left( \hbar \right)\,\Delta e_{g} \left( \hbar \right) $$
(26)

Similarity, \( \Delta V_{b} \left( \hbar \right) = \beta \,\varPsi_{g} \left( \hbar \right)\Delta \varPsi_{g} \left( \hbar \right)\, \) and \( \Delta V_{c} = \delta \left( {\Delta \varPsi_{g} \left( \hbar \right)} \right)^{2} \)

The second stability condition is obtained as:

$$ \Delta V_{x} \left( \hbar \right) = \alpha \,e_{g} \left( \hbar \right)\,\Delta e_{g} \left( \hbar \right) + \beta \,\varPsi_{g} \left( \hbar \right)\,\Delta \varPsi_{g} \left( \hbar \right)\,\,\, + \delta \,\left( {\Delta \varPsi_{g} \left( \hbar \right)} \right)^{2} \le \,0 $$
(27)

Equation (27) can be reformulated as:

$$ \Delta V_{x} \left( \hbar \right) = \alpha \,e_{g} \left( \hbar \right)\Delta e_{g} \left( \hbar \right) + \beta \,\varPsi_{g} \left( \hbar \right)\,\Delta \varPsi_{g} \left( \hbar \right)\,\,\, + \delta \,\left( {\Delta \varPsi_{g} \left( \hbar \right)} \right)^{2} = - Z $$
(28)

where \( Z \ge 0 \) so as to achieve the condition, \( \Delta V_{x} \left( \hbar \right) \le \,0 \)

So

$$ \delta \,\left( {\Delta \varPsi_{g} \left( \hbar \right)} \right)^{2} + \beta \,\Delta \varPsi_{g} \left( \hbar \right)\,\left( {\frac{\alpha }{\beta }\,e_{g} \left( \hbar \right)\frac{{\Delta e_{g} \left( \hbar \right)}}{{\Delta \varPsi_{g} \left( \hbar \right)}} + \varPsi_{g} \left( \hbar \right)} \right) + Z = 0 $$
(29)

In this concern, suppose a general quadratic equation, which is defined as:

$$ a\,X^{2} + b\,X + c = 0 $$
(30)

The roots of Eq. (30) are calculated as:

$$ x_{1,2} = \frac{{ - b \pm \sqrt {b^{2} - 4ac} }}{2a} $$
(31)

From Eqs. (29) and (30), obviously, \( \Delta \varPsi_{g} \left( \hbar \right) \) acts as \( X \) in Eq. (30) and the values of \( a,\,b \) and \( c \) in Eq. (29) are obtained as:

$$ a = \delta ,\,\,\,\,\,\,b = \beta \,\left( {\frac{\alpha }{\beta }e_{g} \left( \hbar \right)\frac{{\Delta e_{g} \left( \hbar \right)}}{{\Delta \varPsi_{g} \left( \hbar \right)}} + \varPsi_{g} \left( \hbar \right)} \right)\,\,\,\,\,\hbox{and}\,\,\,\,\,c = Z $$
(32)

Equation (30) has a single unique solution, if \( \sqrt {b^{2} - 4ac} = 0 \). So,

$$ \beta^{2} \,\left( {\frac{\alpha }{\beta }e_{g} \left( \hbar \right)\frac{{\Delta e_{g} \left( \hbar \right)}}{{\Delta \varPsi_{g} \left( \hbar \right)}} + \varPsi_{g} \left( \hbar \right)} \right)^{2} - 4\delta \,Z\, = \,0 $$
(33)

and therefore, \( Z \) is determined as:

$$ Z = \frac{{\beta^{2} \,\left( {\frac{\alpha }{\beta }e_{g} \left( \hbar \right)\frac{{\Delta e_{g} \left( \hbar \right)}}{{\Delta \varPsi_{g} \left( \hbar \right)}} + \varPsi_{g} \left( \hbar \right)} \right)^{2} }}{4\delta } $$
(34)

Since \( Z \ge 0 \) which means

$$ \frac{{\beta^{2} \,\left( {\frac{\alpha }{\beta }e_{g} \left( \hbar \right)\frac{{\Delta e_{g} \left( \hbar \right)}}{{\Delta \varPsi_{g} \left( \hbar \right)}} + \varPsi_{g} \left( \hbar \right)} \right)^{2} }}{4\delta } \ge 0 $$
(35)

So, the unique root of Eq. (29) is \( x_{1,2} = \frac{ - b}{2a} \); similarly,

$$ \Delta \varPsi_{g} \left( \hbar \right) = - \frac{{\beta \,\left( {\frac{\alpha }{\beta }e_{g} \left( \hbar \right)\frac{{\Delta e_{g} \left( \hbar \right)}}{{\Delta \varPsi_{g} \left( \hbar \right)}} + \varPsi_{g} \left( \hbar \right)} \right)}}{2\delta } $$
(36)

Equation (36) can be reformulated as:

$$ \Delta \varPsi_{g} \left( \hbar \right) = - \frac{{\beta \,\left( {\frac{\alpha }{\beta }e_{g} \left( \hbar \right)\frac{{\partial e_{g} \left( \hbar \right)}}{{\partial \varPsi_{g} \left( \hbar \right)}} + \varPsi_{g} \left( \hbar \right)} \right)}}{2\delta } $$
(37)

So, by replacing \( \Delta \varPsi_{g} \left( \hbar \right) \) in Eq. (16), the updating equation is obtained as illustrated in Eq. (17).

4 FFNNDL controller training steps

In this section, the block diagram of the proposed FFNNDLC for nonlinear system is shown in Fig. 3. The output of the nonlinear system, \( y_{a} (\hbar ) \), is measured, and then the error signal, \( e_{g} \left( \hbar \right) \), between the reference input, \( y_{d} (\hbar ) \), and the measured output is calculated. The proposed FFNNDLC is received the error signal, and it calculates the control signal, \( u\left( \hbar \right) \), which feeds to the nonlinear system.

Fig. 3
figure 3

Block diagram of the FFNNDLC with nonlinear system

Full size image

Figure 4 shows the structure of the proposed FFNNDLC block in details. The first layer of the controller network consists of three nodes; the first node is the measured error signal, \( e_{1} \left( \hbar \right) = e_{g} \left( \hbar \right) \). The second node is the change of the error signal, \( e_{2} \left( \hbar \right) = e_{g} \left( \hbar \right) - e_{g} \left( {\hbar - 1} \right) \), and the third node is the change of the change of error signal, \( e_{3} \left( \hbar \right) = e_{g} \left( \hbar \right) - 2e_{g} \left( {\hbar - 1} \right) + e_{g} \left( {\hbar - 2} \right) \), and the output layer consists of one node, which is the control signal, \( u\left( \hbar \right) \). The proposed network consists of two parts: the first part is the feed-forward neural network and the second part is the RBM, which is used to perform the initial values for the weights of the feed-forward neural network as shown in Fig. 4. The overall procedures of the proposed FFNNDLC are illustrated as:

Fig. 4
figure 4

Structure of the FFNNDLC block

Full size image

  • Step 1 Enter the reference input for the nonlinear system and calculate the controller inputs, \( e_{1} \left( \hbar \right) \), \( e_{2} \left( \hbar \right) \) and \( \,e_{3} \left( \hbar \right) \). In this paper, we set, \( n = 3,\,J = 10 \) and \( M = 10 \).

  • Step 2 Choose the number of RBM weights, which are exactly like the weights between the input layer and the hidden layer (1). In this paper, we set \( N = 3,\,P = 10 \) and \( q = 1 \).

  • Step 3 Choose the appropriate value for the learning rate of RBM, \( \alpha \). Initialize the weights parameters of the RBM with zero. The number of the RBM inputs equals the number of the controller inputs.

  • Step 4 According to Eqs. (4), (5) and (6), update the RBMs weights parameters.

  • Step 5 Set the initial values of the FFNN weights matrix; \( \psi_{ji} \) (between input layer and hidden layer (1)) as the values of the RBM weights matrix.

  • Step 6 Calculate the outputs of the hidden layer (1); \( y_{j}^{(1)} \).

  • Step 7 Call RBM again where the number of the RBM weights is exactly like the weights between the hidden layer (1) and the hidden layer (2). In this paper, we set \( N = 10 \) and \( P = 10 \). The number of the RBM inputs equals the number of the outputs of the hidden layer (1); \( y_{j}^{(1)} \).

  • Step 8 Update the RBMs weights parameters based on Eqs. (4), (5) and (6).

  • Step 9 Set the initial values of the FFNN weights matrix; \( \psi_{mj} \) (between the hidden layer (1) and the hidden layer (2)) as the values of the RBM weights matrix.

  • Step 10 Calculate the outputs of the hidden layer (2); \( y_{m}^{(2)} \).

  • Step 11 Call the RBM again where the number of the RBM weights is exactly like the weights between the hidden layer (2) and the output layer. In this paper, we set \( N = 10 \) and \( P = 1 \). The number of the RBM inputs equals the number of the hidden layer (2); \( y_{m}^{(2)} \).

  • Step 12 Update the RBMs weights parameters based on Eqs. (4), (5) and (6).

  • Step 13 Set the initial values for the FFNN weights matrix; \( \psi_{m} \) (between the hidden layer (2) and the output layer) as the values of the RBM weights matrix.

  • Step 14 Calculate the control signal; \( u\,(\hbar ) \).

  • Step 15 Update the FFNN weights parameters according to the Lyapunov Stability formula, Eq. (17). After then, set the values for the RBM weights matrix as the values of the FFNN weights matrix.

  • Step 16 Calculate the plant output;\( y_{a} \left( \hbar \right) \).

  • Step 17 Go to step 1.

5 Simulation Results

The simulation results for the proposed FFNNDLC are compared with the results of the FFNNC with the same conditions and initial values to show the robustness of the proposed controller. Mean absolute error (MAE) and root-mean-square error (RMSE) are used to evaluate the performance of the proposed controller. RMSE and MAE are calculated as [50, 51]:

$$ MAE = \frac{1}{{k_{N} }}\sum\limits_{\hbar = 1}^{{k_{N} }} {\left| {e_{g} \left( \hbar \right)} \right|} $$
(38)
$$ RMSE = \sqrt {\left( {\frac{1}{{k_{N} }}\sum\limits_{\hbar = 1}^{{k_{N} }} {\left( {e_{g} \left( \hbar \right)} \right)^{2} } } \right)} $$
(39)

where \( k_{N} \) represents iterations number.

5.1 Example 1: Suppose the following mathematical system that is presented as [52]

$$ y_{a} \left( \hbar \right) = \frac{{y_{a} \left( {\hbar - 1} \right)y_{a} \left( {\hbar - 2} \right)\left( {y_{a} \left( {\hbar - 1} \right) + a_{4} } \right)}}{{a_{1} + a_{2} y_{a}^{2} \left( {\hbar - 1} \right) + a_{3} y_{a}^{2} \left( {\hbar - 2} \right)}} + u\left( \hbar \right) $$
(40)

where the parameters are set as \( a_{1} = a_{2} = a_{3} = 1 \) and \( a_{4} = 0.05 \).

5.2 Test 1: Tracking the reference signal trajectory

Figures (5 and 6) show the system response and its control signal for tracking the reference signal trajectory, respectively, for both FFNNC and the proposed FFNNDLC. In this concern, the reference trajectory signal is illustrated as:

Fig. 5
figure 5

System output for Test 1

Full size image
Fig. 6
figure 6

Control signal for both controllers (Test 1)

Full size image
$$ y_{d} \left( \hbar \right) = 0.5\sin \left( {0.1\hbar T} \right) $$
(41)

where \( T \) is sampling period.

The FFNNC and the proposed FFNNDLC weights are considered have zero values. It is clear at the beginning that there is a difference in tracking the signal in terms of the FFNNC. On the other hand, the proposed FFNNDLC can overcome the signal tracking as a result of learning from RBM, better than FFNNC.

5.3 Test 2: Uncertainty due to disturbance

During the present test, the robustness of the proposed FFNNDLC is tested after the system output has been reached the trajectory. This carried out by adding disturbance value equals 50% of its desired value to the system output at \( \hbar \) = 3000 instant. Figures 7 and 8 show the system output and the control signal, respectively, for both the FFNNC and the proposed FFNNDLC with 50% disturbances. Also, another test is carried out, at 80% disturbances, to ensure the robustness of FFNNDLC (Figs. 9 and 10). From which, it is shown that the response of the proposed FFNNDLC is recovered very quickly to the desired value. So, the proposed FFNNDLC is able to respond the external disturbance compared with the FFNNC.

Fig. 7
figure 7

System output under 50% disturbances

Full size image
Fig. 8
figure 8

Control signal for response of the system under 50% disturbances (Test 2)

Full size image
Fig. 9
figure 9

System output under 80% disturbances (Test 2)

Full size image
Fig. 10
figure 10

Control signal for the system response under 80% disturbances (Test 2)

Full size image

5.4 Test 3: Uncertainty in the system parameter

To show the robustness of the proposed FFNNDLC, the parameters (\( a_{1} ,\,a_{2} ,\,a_{3} \) and \( a_{4} \)) of the given plant are changed from their actual values (1, 1, 1 and 0.05) to (-3, 2.5, 1.5, 0.5) at \( \hbar \) = 3000th instant. The system output for the proposed FFNNDLC is recovered very quickly rather than the FFNNC as shown in Figs. (11 and 12). So, the proposed FFNNDLC is able to reduce the effect of parameters uncertainty compared with FFNNC.

Fig. 11
figure 11

System output under uncertainty of the system parameters (Test 3)

Full size image
Fig. 12
figure 12

Control signal for the system response (Test 3)

Full size image

5.5 Test 4: Uncertainty due to disturbance and parameter variation

Figures (13 and 14) show the effect of uncertainty due to disturbance and parameter variation to show the robustness of the proposed controller. At \( \hbar \) = 3000th instant, the disturbance with 50% from the reference input and the parameters variation are added to the system output. The parameters (\( a_{1} ,\,a_{2} ,\,a_{3} \) and \( a_{4} \)) are varied to values (-3, 2.5, 1.5, 0.5). The FFNNDLC response is able to respond the effect of the uncertainty due to the disturbance and system parameters variation.

Fig. 13
figure 13

System output under uncertainty of the system parameters and 50% disturbances (Test 4)

Full size image
Fig. 14
figure 14

Control signal for the system response under uncertainty of the system parameters and 50% disturbances (Test 4)

Full size image

The MAE and RMSE values for the proposed FFNNDLC, the FFNNC and other published schemes such as DRNNC [16], FFNNC with a hybrid method (FFNNC-hybrid) [18] and ENN-RBM [29] are shown in Tables 1 and 2. It is obvious that MAE and RMSE values for the proposed FFNNDLC are smaller than that are obtained for other controllers. Therefore, the proposed FFNNDLC, which uses the RBM network to initialize the values of the FFNN weights, is able to reduce the effect of external disturbance and system uncertainties compared with other schemes.

Table 1 MAE values (Example 1)
Full size table
Table 2 RMSE values (Example 1)
Full size table

5.6 Example 2: In this test, the following mathematical system, which is presented by the three sub-systems, is given as [53]

The first sub-system: for \( 0 < \hbar < 3000 \)

$$ y_{a} \left( \hbar \right) = 0.1y_{a} \left( {\hbar - 1} \right) + \frac{{u\left( \hbar \right)\left( {0.5 + u^{2} \left( \hbar \right)} \right)}}{{1 + 2u^{2} \left( \hbar \right)}} $$
(42)

The second sub-system: for \( 3000 \le \hbar < 6000 \)

$$ y_{a} \left( \hbar \right) = \frac{{\left[ {y_{a} \left( {\hbar - 1} \right)y_{a} \left( {\hbar - 2} \right)y_{a} \left( {\hbar - 3} \right)u\left( {\hbar - 1} \right)} \right]\left[ {y_{a} \left( {\hbar - 3} \right) - b\left( \hbar \right)} \right] + c\left( \hbar \right)u\left( \hbar \right)}}{{a\left( \hbar \right) + y_{a}^{2} \left( {\hbar - 2} \right) + y_{a}^{2} \left( {\hbar - 3} \right)}} $$
(43)

The time-varying parameters \( a\left( \hbar \right),\,b\left( \hbar \right)\, \) and \( c\left( \hbar \right) \) in the previous equation are defined as: \( a\left( \hbar \right) = 1.2 - 0.2\cos \left( {0.1\hbar T} \right), \) \( b\left( \hbar \right) = 1 - 0.4\sin \left( {0.1\hbar T} \right) \) and \( c\left( \hbar \right) = 1 + 0.4\sin \left( {0.1\hbar T} \right) \).

The third sub-system: for \( 6000 \le \hbar < 9000 \)

$$ \begin{aligned} y_{a} \left( \hbar \right) = 0.2\,y_{a}^{2} \left( {\hbar - 1} \right) + 0.2\,y_{a} \left( {\hbar - 2} \right) + 0.4\,\sin \,\,\left[ {0.5\,y_{a} \left( {\hbar - 1} \right) + 0.5\,y_{a} \left( {\hbar - 2} \right)} \right] \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,.\,\cos \,\,\,\left[ {0.5\,y_{a} \left( {\hbar - 1} \right) + 0.5\,y_{a} \left( {\hbar - 2} \right)} \right] + 1.2\,u\left( \hbar \right) \hfill \\ \end{aligned} $$
(44)

The system output and the control signal for the proposed FFNNDLC and the FFNNC for the three sub-systems are shown in Figs. (15, 16, 17, 18). It is obvious that the response of FFNNDLC is reached to the desired output faster than the FFNNC during the change from sub-system to another. The MAE and RMSE values for the proposed controller and other controllers are shown in Table 3.

Fig. 15
figure 15

First sub-system output

Full size image
Fig. 16
figure 16

Second sub-system output

Full size image
Fig. 17
figure 17

Third sub-system output

Full size image
Fig. 18
figure 18

Control signal for the three sub-systems

Full size image
Table 3 MAE and RMSE values for both controllers
Full size table

The main advantages of the proposed FFNNDLC are summarized as follows: 1) It is a fast-learning controller because it uses RBM network, which initializes the values of the FFNN. 2) It has the ability to handle system uncertainties and external disturbance due to the online learning for the proposed scheme based in the Lyapunov stability theorem. In the next section, the proposed scheme is applied practically to control a real plant.

6 Practical results

In this section, the proposed FFNNDLC is implemented practically to show the ability of the proposed controller to deal with a real system. Figure 19 shows the practical system. It is the DC machine, which consists of a DC motor that is coupled with a DC generator to test the load conditions. The feedback signal, which is the measuring speed, is done based on an optical encoder. The proposed FFNNDLC algorithm is implemented in ARDUINO DUE kit, which is a microcontroller board based on Atmel SAM3X8E ARM Cortex-M3 CPU. To show the ability of the proposed FFNNDLC in real system, different tests are performed.

Fig. 19
figure 19

Practical system

Full size image

6.1 Test 1: Tracking the different reference signal trajectory

In this test, different set points are considered. Figure 20 shows the system response and its control signal for tracking the different reference signal trajectory for the proposed FFNNDLC and the FFNNC when all the initial conditions for the weights equal zero for both controllers. It is clear that the response of the proposed FFNNDLC has fast tracking for the reference signal compared with FFNNC due to the advantage of the RBM, which is used to initialize the proposed network. To show the visual indications and robustness of the control performance, an objective measure of an error performance is done using MAE as shown in Fig. 21. It is clear that the MAE for proposed FFNNDLC is lower than that obtained for the FFNNC.

Fig. 20
figure 20

System response and its control signal for tracking the different reference signal

Full size image
Fig. 21
figure 21

MAE for tracking the different reference signal

Full size image

6.2 Test 2: Uncertainty due to load

In this test, a load value equals 35% of its desired value is applied to the system output at \( time = 18\,\sec . \) Figure 22 shows the system output and its control signal, for both the FFNNC and the proposed FFNNDLC due to the load. It is clear that the output response for the proposed FFNNDLC has smaller settling time than that is obtained for the FFNNC. Figure 23 shows the MAE for both controllers where the MAE for the proposed controller is lower than that is obtained for another controller. So the proposed FFNNDLC is better than the FFNNC, which has fast learned to overcome quickly the effect of uncertainty due to the external load.

Fig. 22
figure 22

System response and its control signal due to 35% load

Full size image
Fig. 23
figure 23

MAE for controlled system due to 35% load

Full size image

6.3 Test 3: Uncertainty due to the measurement error

During this test, the sensor reading error value is considered with 50% of its value to the system output at \( time = 18\,\sec . \) Figure 24 shows the system output and its control signal, for both the FFNNC and the proposed FFNNDLC due to uncertainty in the measurement error. Figure 25 shows that the MAE for the proposed FFNNDLC is less than that is obtained for another controller. So, the proposed FFNNDLC is better than the FFNNC, which has fast learned to overcome quickly the effect of uncertainty due to the measurement error.

Fig. 24
figure 24

System response and its control signal due to 50% uncertainty in measurement error

Full size image
Fig. 25
figure 25

MAE for controlled system due to 50% uncertainty in measurement error

Full size image

7 Conclusions

In this paper, the FFNNDLC is proposed, which consists of two parts. The first part is the FFNN which is the main network, and the other part is the RBM network, which is used to initialize the values of the FFNN weights. The weights of the proposed FFNNDLC are learned online based on the developed algorithm, which is proved based on the Lyapunov stability theorem to guarantee the controller stability. To show the robustness of the proposed network, it is applied to two nonlinear mathematical models. The performance of the proposed controller is tested when there is uncertainty in the controlled system due to the parameters variations and external disturbances. To show the advantages of the proposed controller, it is compared with other published schemes by measuring some performance indices such as MAE and RMSE. The simulation results show that the performance of the proposed FFNNDLC has fast-learning algorithm compared with other schemes.

In order to show the ability of the proposed controller to deal with a real system, it is implemented practically using an ARDUINO DUE kit for controlling a DC motor-generator system. The practical results show that the proposed controller is able to respond the effect of system uncertainty due to the measurement error and external disturbances. Thus, the methodology proposed in this study can be used to realize a robust, practically realizable, FFNNDLC capable of controlling a real system with system uncertainties and environmental disturbances.

Finally, the proposed FFNNDLC has fast-learning controller because it uses RBM network, which initializes the values of the FFNN. Furthermore, it has the ability to handle system uncertainties and external disturbance due to the online learning for the proposed scheme based on the Lyapunov stability theorem.