1 Introduction

The control of the industrial systems that have inherent uncertainties in terms of precision of the sensors, a noise produced by the sensors, nonlinear characteristic of the actuator and the system structure has been a serious challenge [1, 2]. The conventional control methodologies are found to be inadequate for meeting these requirements, especially when it is needed for controlling the nonlinear dynamical systems in real time [3]. Moreover, it is hard to apply the conventional control approaches when the system model is anonymous or slightly known. Accordingly, the development of more advanced techniques becomes more important, in particular such complex nonlinear dynamical systems [4]. Recently, the stable controllers for the nonlinear dynamical systems are presented based on the learning approaches such as genetic, sliding mode, backstepping and particle swarm optimization [5,6,7,8].

On the other hand, there is an active area of model-free approaches within the framework of machine learning and computational intelligence such as reinforcement learning (RL) [9,10,11]. The RL paradigm, which is called a goal-oriented system, is mainly depending on the concept of learning from the experience with the principle of the reward and the punishment. The RL algorithm obtains its experience and evolves strategies to take an optimal control policy for achieving a good control quality from unknown nonlinear dynamical system [12]. Q-learning, actor–critic learning, Sarsa learning and adaptive dynamic programming (ADP) are different algorithms normally used in the RL [13]. The Q-learning and Sarsa learning algorithms need a range of actions and the number of states to give the best response [14, 15]. Dynamic programming (DP) is a widely used method for generating the optimal control for nonlinear systems. This method employs Bellman’s principle of optimality, but it has a well-recognized problem, namely curse of dimensionality [16]. Because of the backward direction of research and the particular number of analytic conditions, the Hamilton–Jacobi–Bellman (HJB) equation makes the DP method prohibit the wide use in real-time control. The approximated solution for the Bellman equation was obtained by developing an element that is known as a critic [17]. The DP and the multilayer perceptron (MLP) neural network are incorporated together to obtain the ADP [18]. The adaptive critic designs (ACDs), which are considered the universal functional approaching structures, are formed from the artificial neural networks (ANNs) to adapt the controller parameters when the controlled plant is affected by disturbances, uncertainties and load changes [19, 20]. The asymptotic stability analysis issue for the ANNs is investigated in [21,22,23,24,25,26]. The reinforcement actor–critic learning methods have a separate memory structure to explicitly represent the policy independent of the value function, where the actor carries out the approximation of the control policy function by applying an action to the system and then the critic recognizes the approximation of the value function, i.e., assessing the current control policy.

In [27], the authors implemented the actor and the critic elements using the ANN, but their algorithm has not been tested under parameter variation uncertainty and disturbance effects. In [28,29,30], the critic and the actor elements were implemented using the feed-forward ANN (FFANN) where their structures utilize the states and the output of the actor as the inputs to the critic. In [31], the authors presented one network that represents the incorporation of the critic and the actor elements, the so-called consolidated actor–critic model (CACM), in which the prior values of the hidden layer nodes beside the states and the action are considered the inputs of the network. The researchers added a third network, which is used as a reference [32]. Accordingly, the ADP structure combines an actor, a critic and a reference network (ADPACRN). This structure facilities the learning by building an internal reinforcement signal. The third network may be considered a goal network as described in [33]. This structure is known as a goal representation heuristic dynamic programming (GRHDP). The inserted third network contributes to improving the performance of the controller; however, it increases the computational time as a result of incrementing the number of weights [34]. Moreover, the actor was represented by the Takagi–Sugeno (T–S) fuzzy system in which the Lyapunov theory was used for deriving the parameter adaptation law, namely adaptive T–S fuzzy using reinforcement learning based on Lyapunov stability (ATSFRL-LS) [35]. The structure of the ATSFRL-LS depends on the parallel distributed control (PDC), which is used for stabilizing the system. The PDC uses a fuzzy system for the system model and another fuzzy system.

The FNN merges the capability of the fuzzy inference technique and the capability of the ANNs for online learning from the plant [36]. There are two types of the FNN: the feed-forward FNN (FFNN) and the recurrent FNN (RFNN). The topologies of the RFNN involve feedback loops that can memorize the past data. In contrast to the FFNN architectures, which exhibit static input–output behavior, the RFNN is capable of storing the data from the past (e.g., previous plant states) and overcoming the network size problem. Therefore, it is more convenient for the nonlinear dynamic systems analysis [37, 38]. The FFNN and the RFNN cannot minimize the influence of system uncertainties in the real plant due to their dependence on the type-1 fuzzy sets (T1-FSs) [39]. On the other hand, the type-2 fuzzy logic systems (T2-FLSs), which use the type-2 fuzzy sets (T2-FSs), are capable of minimizing the effect of the system uncertainties compared with the type-1 fuzzy logic systems (T1-FLSs) counterpart. The T2-FLSs have been successfully applied in various applications [40,41,42,43,44,45]. In recent years, the interval type-2 FNNs (IT2-FNNs) have been used for handling the uncertainties and the interval type-2 TSK-FNNs (IT2-TSK-FNNs) are used for nonlinear systems identification and control. The learning accuracy and the network performance for the TSK-type IT2-FNNs are better than for the Mamdani-type IT2-FNNs [46,47,48].

All the previous works that were described in [27,28,29,30,31,32,33,34,35] have a less performance with the influence of the system uncertainties, external disturbances and measurement noise. For solving this problem, a novel structure of a recurrent interval type-2 TSK fuzzy neural network (RIT2-TSK-FNN) is proposed. The proposed RIT2-TSK-FNN is learned online using the RL scheme. The proposed RL scheme consists of two parts: The first part is the critic that is represented based on the ANN and the other is the actor that is implemented based on the proposed RIT2-TSK-FNN. The number of the IF-THEN rules for the proposed RIT2-TSK-FNN is obtained online based on the type-2 fuzzy clustering. The online learning method for the critic and the actor is developed based on the LM method, which gives a perfect exchange between the stability of the gradient steepest descent method and the speed of the Newton algorithm. To speed up the learning algorithm, the adaptive learning parameter is developed by utilizing a fuzzy logic system. The learning rates conditions are derived to guarantee the controlled system stability by using the Lyapunov stability theory. To show the robustness of the proposed structure to respond the system uncertainties, the proposed controller is applied to an uncertain mathematical nonlinear system and the heat exchanger process. The main advantages of the proposed controller over existing controllers are summarized as: (1) The proposed controller has a robustness performance with the influence of the system uncertainties and external disturbances compared to other learning techniques due to using the IT2-TSK-FNN. (2) The proposed controller has structure learning and has a good performance with small number of rules due to the recurrent in the input and rule layers. (3) The learning rates are changed online according to fuzzy logic system during the implementation of the algorithm to assure the stability and speed up the convergence.

The main contributions of this paper are summarized as: (1) Proposing a new structure of the RIT2-TSK-FNN. (2) Proposing a new online learning for the developed RIT2-TSK-FNN based on a reinforcement actor–critic scheme. (3) Developing the parameters of the actor–critic based on the LM algorithm. (4) Obtaining the optimal values for the learning rates using the fuzzy logic system and the Lyapunov function.

The rest of the paper is organized as follows: The structure of the RIT2-TSK-FNN is described in Sect. 2. Section 3 describes the proposed RL scheme. Section 4 presents the online learning of the proposed RL scheme. Section 5 describes the simulation results for nonlinear mathematical system and the steam-water heat exchanger process. This would be followed by the conclusion and the relevant references.

2 Proposed RIT2-TSK-FNN structure

This section presents the structure of the RIT2-TSK-FNN. Figure 1 shows the structure of the proposed network, which is composed of six layers. The antecedent parts of the RIT2-TSK-FNN are represented using the IT2-FSs. The consequent part for each fuzzy rule is characterized by the TSK type. Each type-2 fuzzy rule for the RIT2-TSK-FNN is defined as:

$${\text{Rule}}\,i:{\text{IF}}\,x_{1} \left( n \right)\,{\text{is}}\,\tilde{B}_{1}^{i} {\text{AND}} \ldots x_{k} \left( n \right)\,{\text{is}}\,\tilde{B}_{k}^{i} \,{\text{THEN}}\,h^{i} \left( n \right)\,\,{\text{is}}\,\,\tilde{b}_{0}^{i} + \sum\limits_{j = 1}^{k} {\tilde{b}_{j}^{i} } x_{j} \left( n \right),\quad i = 1,2, \ldots ,M,$$
(1)

where \(x_{1} \left( n \right), \ldots ,x_{k} \left( n \right)\) are the recurrent incoming inputs, \(\tilde{B}_{j}^{i}\) are the IT2-FSs, \(\tilde{b}_{0}^{i} ,\,\,\,\tilde{b}_{j}^{i} \,\) are interval sets where \(\tilde{b}_{0}^{i} = [c_{0}^{i} - s_{0}^{i} ,\,\,c_{0}^{i} + s_{0}^{i} ]\) and \(\tilde{b}_{j}^{i} = [c_{j}^{i} - s_{j}^{i} ,c_{j}^{i} + s_{j}^{i} ]\), and \(k\) and \(M\) are the network inputs and the number of the rules, respectively. For each layer, \(O_{j}^{\left( p \right)}\) is symbolizing the output of layer \(p\).

Fig. 1
figure 1

Structure of the proposed RIT2-TSK-FNN

Full size image

Layer 1: This layer is called an input layer, which is indicated in Fig. 1, in which the internal feedback connection can temporarily store the dynamic data and cope with temporal input noise efficiently. The mathematical expression for this layer is expressed as:

$$O_{j}^{(1)} \left( n \right) = x_{j} \left( n \right) + \alpha_{j} \left( n \right)\,O_{j}^{(1)} \left( {n - 1} \right),\quad j = 1, \ldots ,k,$$
(2)

where \(x_{j} \left( n \right)\) represents the input variable and \(\alpha_{j} \left( n \right)\) is the input recurrent weight.


Layer 2: This layer is called a membership layer, which is described in Fig. 1, in which each node is represented by a membership function (MF) where the fuzzification operation is performed. The output from the first layer \(O_{j}^{(1)} \left( n \right)\) is fuzzified using the Gaussian IT2-FS with a certain mean \(\left[ {m_{j1}^{i} ,m_{j2}^{i} } \right]\) and a fixed width \(\sigma\) as shown in Fig. 2, where \(i\) represents the fuzzy set. Each layer node can be symbolized as an upper MF, \(\bar{O}_{ij}^{\left( 2 \right)} \left( n \right)\), and a lower MF, \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{O}_{ij}^{\left( 2 \right)} \left( n \right)\), which are defined as:

Fig. 2
figure 2

Uncertain mean Gaussian IT2-FS

Full size image
$$\bar{O}_{ij}^{\left( 2 \right)} \left( n \right) = \left\{ {\begin{array}{*{20}l} {\exp \left( { - \frac{1}{2}\left( {\frac{{O_{j}^{(1)} \left( n \right) - m_{j1}^{i} \left( n \right)}}{{\sigma_{j}^{i} \left( n \right)}}} \right)^{2} } \right),} \hfill & {O_{j}^{(1)} \left( n \right) < m_{j1}^{i} \left( n \right)} \hfill \\ {1,} \hfill & {m_{j1}^{i} \left( n \right) \le O_{j}^{(1)} \left( n \right) \le m_{j2}^{i} \left( n \right)} \hfill \\ {\exp \left( { - \frac{1}{2}\left( {\frac{{O_{j}^{(1)} \left( n \right) - m_{j2}^{i} \left( n \right)}}{{\sigma_{j}^{i} \left( n \right)}}} \right)^{2} } \right),} \hfill & {O_{j}^{(1)} \left( n \right) > m_{j2}^{i} \left( n \right)} \hfill \\ \end{array} } \right.,$$
(3)
$$\underline{O}_{ij}^{\left( 2 \right)} \left( n \right) = \left\{ \begin{aligned} \exp \left( { - \frac{1}{2}\left( {\frac{{O_{j}^{(1)} \left( n \right) - m_{j2}^{i} \left( n \right)}}{{\sigma_{j}^{i} \left( n \right)}}} \right)^{2} } \right),\,\,\,\,\,\,\,\,\,O_{j}^{(1)} \left( n \right) \le \frac{{m_{j1}^{i} \left( n \right) + m_{j2}^{i} \left( n \right)}}{2} \hfill \\ \exp \left( { - \frac{1}{2}\left( {\frac{{O_{j}^{(1)} \left( n \right) - m_{j1}^{i} \left( n \right)}}{{\sigma_{j}^{i} \left( n \right)}}} \right)^{2} } \right),\,\,\,\,\,\,\,\,\,O_{j}^{(1)} \left( n \right) > \frac{{m_{j1}^{i} \left( n \right) + m_{j2}^{i} \left( n \right)}}{2}. \hfill \\ \end{aligned} \right.$$
(4)

Layer 3: This layer is called a recurrent layer, which is indicated in Fig. 1, where the number of the nodes equals the number of the recurrent rules, which corresponds to the number of the fuzzy sets in each input. Each recurrent rule node contains an internal feedback loop, which handles the uncertainties. The output of each node performs a temporal firing strength whose value does rely not only on the current spatial firing strength \(F^{i} \left( n \right)\) but also on the previous temporal firing strength \(F^{i} \left( {n - 1} \right)\). The output of each recurrent node is computed by a fuzzy AND operator. The firing strength can be described by a crisp interval as follows:

$$F^{i} \left( n \right) = \left[ {{\bar{\varOmega }}^{i} \left( n \right),\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varOmega }^{i} \left( n \right)} \right],\quad i = 1, \ldots ,M,$$
(5)
$$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varOmega }^{i} \left( n \right) = \prod\limits_{j = 1}^{k} {\underline{O}_{ij}^{\left( 2 \right)} } \left( n \right),{\bar{\varOmega }}^{i} \left( n \right) = \prod\limits_{j = 1}^{k} {\bar{O}_{ij}^{\left( 2 \right)} } \left( n \right).$$
(6)

The crisp interval of the temporal firing strength \(\left[ {\bar{O}_{i}^{\left( 3 \right)} \left( n \right),\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{O}_{i}^{\left( 3 \right)} \left( n \right)} \right]\) is a linear aggregation of the previous temporal firing strength \(O_{i}^{\left( 3 \right)} \left( {n - 1} \right)\) and the spatial firing strength \(F^{i} \left( n \right)\), which can be given as:

$$O_{i}^{\left( 3 \right)} \left( n \right) = l^{i} F^{i} \left( n \right) + \left( {1 - l^{i} } \right)O_{i}^{\left( 3 \right)} \left( {n - 1} \right),$$
(7)

where \(l^{i}\) is an internal feedback weight, \(\left( {0 \le l^{i} \le 1} \right)\). The value of \(l^{i}\) defines the achievement ratio between the immediate and previous inputs that effects on the network output. Thus, (7) can be written as:

$$\left[ {\bar{O}_{i}^{\left( 3 \right)} \left( n \right),\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{O}_{i}^{\left( 3 \right)} \left( n \right)} \right] = l^{i} \left[ {{\bar{\varOmega }}^{i} \left( n \right),\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varOmega }^{i} \left( n \right)} \right] + \left( {1 - l^{i} } \right)\left[ {\bar{O}_{i}^{\left( 3 \right)} \left( {n - 1} \right),\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{O}_{i}^{\left( 3 \right)} \left( {n - 1} \right)} \right],$$
(8)

where

$$\bar{O}_{i}^{(3)} \left( n \right) = l^{i} {\bar{\varOmega }}^{i} \left( n \right) + \left( {1 - l^{i} } \right)\bar{O}_{i}^{(3)} \left( {n - 1} \right)$$
(9)

and

$$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{O}_{i}^{(3)} \left( n \right) = l^{i} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varOmega }^{i} \left( n \right) + \left( {1 - l^{i} } \right)\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{O}_{i}^{(3)} \left( {n - 1} \right).$$
(10)

Layer 4: This layer is called a consequent layer, which is described in Fig. 1, in which each node output is implemented depending on the TSK type. The consequent parameters for each rule are T1-FS. The number of the layer nodes is corresponding to the number of the obtained rules. The output of this layer \(\left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{O}_{i}^{\left( 4 \right)} \left( n \right),\bar{O}_{i}^{\left( 4 \right)} \left( n \right)} \right]\,\) is expressed as:

$$\left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{O}_{i}^{\left( 4 \right)} \left( n \right),\bar{O}_{i}^{\left( 4 \right)} \left( n \right)} \right] = \left[ {c_{0}^{i} - s_{0}^{i} ,c_{0}^{i} + s_{0}^{i} } \right] + \left[ {\left( {\sum\limits_{j = 1}^{k} {c_{j}^{i} O_{j}^{\left( 1 \right)} (n) - \sum\limits_{j = 1}^{k} {s_{j}^{i} \left| {O_{j}^{\left( 1 \right)} (n)} \right|} } } \right),\left( {\sum\limits_{j = 1}^{k} {c_{j}^{i} O_{j}^{\left( 1 \right)} (n) + \sum\limits_{j = 1}^{k} {s_{j}^{i} \left| {O_{j}^{\left( 1 \right)} (n)} \right|} } } \right)} \right],$$
(11)

where

$$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{O}_{i}^{\left( 4 \right)} \left( n \right) = \sum\limits_{j = 0}^{k} {c_{j}^{i} O_{j}^{\left( 1 \right)} (n)} - \sum\limits_{j = 0}^{k} {s_{j}^{i} \left| {O_{j}^{\left( 1 \right)} (n)} \right|}$$
(12)

and

$$\bar{O}_{i}^{\left( 4 \right)} \left( n \right) = \sum\limits_{j = 0}^{k} {c_{j}^{i} O_{j}^{\left( 1 \right)} (n)} + \sum\limits_{j = 0}^{k} {s_{j}^{i} \left| {O_{j}^{\left( 1 \right)} (n)} \right|} ,$$
(13)

where \(O_{0}^{\left( 1 \right)} (n) = 1\).


Layer 5: This layer is called a type reduction layer, which is indicated in Fig. 1, in which the \(H\) factors are used to reduce the computation operations of the IT2-FLS [49]. The design factors \(\left[ {H_{l} ,H_{r} } \right]\) weight the sharing of lower and upper firing levels of each fired rule. The output of type reduction is represented by two nodes, which can be calculated as:

$$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{O}^{\left( 5 \right)} \left( n \right) = \frac{{\left( {1 - H_{l} } \right)\sum\nolimits_{i = 1}^{M} {\bar{O}_{i}^{\left( 3 \right)} \left( n \right)\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{O}_{i}^{\left( 4 \right)} } \left( n \right) + H_{l} \sum\nolimits_{i = 1}^{M} {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{O}_{i}^{\left( 3 \right)} \left( n \right)\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{O}_{i}^{\left( 4 \right)} \left( n \right)} }}{{\sum\nolimits_{i = 1}^{M} {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{O}_{i}^{\left( 3 \right)} \left( n \right) + \bar{O}_{i}^{\left( 3 \right)} \left( n \right)} }},$$
(14)
$$\bar{O}^{\left( 5 \right)} \left( n \right) = \frac{{\left( {1 - H_{r} } \right)\sum\nolimits_{i = 1}^{M} {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{O}_{i}^{\left( 3 \right)} \left( n \right)\bar{O}_{i}^{\left( 4 \right)} \left( n \right)} + H_{r} \sum\nolimits_{i = 1}^{M} {\bar{O}_{i}^{\left( 3 \right)} \left( n \right)\bar{O}_{i}^{\left( 4 \right)} \left( n \right)} }}{{\sum\nolimits_{i = 1}^{M} {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{O}_{i}^{\left( 3 \right)} \left( n \right) + \bar{O}_{i}^{\left( 3 \right)} \left( n \right)} }}.$$
(15)

Layer 6: This is the final layer, which represents the output layer. The defuzzified output is computed as:

$$O^{\left( 6 \right)} \left( n \right) = \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{O}^{\left( 5 \right)} \left( n \right) + \bar{O}^{\left( 5 \right)} \left( n \right).$$
(16)

3 Proposed RL scheme

The block diagram of the proposed RL structure is shown in Fig. 3, where it consists of two parts: the critic and the actor. The proposed RL structure has one input variable, \(e\left( n \right)\), which is the error signal between the reference trajectory and the system output, and one output variable, \(u\left( n \right)\), which is the control signal that is applied to the system. The actor part has two inputs: \(e\left( n \right)\) and change in error signal \(\Delta e\left( n \right)\). The critic part has three inputs: \(e\left( n \right)\), \(e\left( {n - 1} \right)\) and \(u\left( n \right)\). The reward signal \(r\left( n \right)\) is defined as:

$$r\left( n \right) = \varTheta_{{c_{1} }} \left( n \right) + \varTheta_{{c_{2} }} \left( n \right),$$
(17)

where

$$\begin{aligned} \varTheta_{{c_{1} }} \left( n \right) & = \left\{ {\begin{array}{*{20}l} 0 \hfill & {\left| {e\left( n \right)} \right| \le \delta } \hfill \\ { - 1} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. \\ \varTheta_{{c_{2} }} \left( n \right) & = \left\{ {\begin{array}{*{20}l} 0 \hfill & {\left| {e\left( n \right)} \right| \le \left| {e\left( {n - 1} \right)} \right|} \hfill \\ { - 1} \hfill & {\text{otherwise}} \hfill \\ \end{array} ,} \right. \\ \end{aligned}$$
(18)

where the symbol \(\delta\) symbolizes a small constant value, i.e., \(\delta = 0.001\). Simply the reinforcement reward signal gives the effect of applying the control signal from the actor to the system that can be represented by either a “zero” or “negative value” corresponding to “adequate” or “insufficiency,” respectively. The parameter \(e_{c} \left( n \right)\) represents the error of the critic network, \(e_{a} \left( n \right)\) represents the error of the actor network, \(V\left( n \right)\) represents the output of the critic and \(U_{a} (n)\) represents the required conclusive goal.

Fig. 3
figure 3

Block diagram of the proposed RL structure

Full size image

3.1 The critic network

The critic part shown in Fig. 3 is implemented using ANN, and the structure of this ANN is shown in Fig. 4. The inputs of the critic network are \(z_{1} \left( n \right) = e\left( {n - 1} \right),\)\(z_{2} \left( n \right) = e\left( n \right),\)\(z_{3} \left( n \right) = u\left( n \right)\), and the critic output is \(V\left( n \right)\). The critic output, \(V(n)\), is calculated as follows:

$${\text{net}}_{m} \left( n \right) = \sum\limits_{b = 1}^{3} {\mathop w\nolimits_{{c_{mb} }}^{(1)} \left( n \right)} z_{b} \left( n \right),\quad m = 1, \ldots ,N_{h} ,$$
(19)
$$q_{m} \left( n \right) = \frac{{1 - e^{{ - {\text{net}}_{m} \left( n \right)}} }}{{1 + e^{{ - {\text{net}}_{m} \left( n \right)}} }},\quad m = 1, \ldots ,N_{h} ,$$
(20)
$$V\left( n \right) = \sum\limits_{m = 1}^{{N_{h} }} {w_{{c_{m} }}^{\left( 2 \right)} \left( n \right)} q_{m} \left( n \right),$$
(21)

where \({\text{net}}_{m}\) is the \(m\)th hidden node input of the critic network, \(q_{m}\) is the hidden node output, \(\mathop w\nolimits_{{c_{mb} }}^{(1)} \left( n \right)\) is the weight between \(b\)th input node and \(m\)th hidden node, \(w_{{c_{m} }}^{\left( 2 \right)} \left( n \right)\) is the weight between \(m\)th hidden node and output node and \(N_{h}\) is the total number of hidden nodes.

Fig. 4
figure 4

Critic neural network

Full size image

The critic network parameters, \(\theta_{c} \left( n \right)\), are updated dependent on the prediction error of the critic network, which can be described as:

$$e_{c} \left( n \right) = V\left( {n - 1} \right) - r\left( n \right) - \gamma V\left( n \right).$$
(22)

3.2 The actor network

The actor part shown in Fig. 3 is implemented using the RIT2-TSK-FNN, which is explained in detail in Sect. 2. The inputs of the actor RIT2-TSK-FNN are \(x_{1} \left( n \right) = e\left( n \right),\,\)\(x_{2} \left( n \right) = \Delta e\left( n \right)\) and the output is \(O^{\left( 6 \right)} \left( n \right) = u\left( n \right)\). The actor network parameters, \(\theta_{a} \left( n \right)\), are updated based on the error between the required conclusive goal, which is denoted by \(U_{a} (n)\) and the approximate \(V\left( n \right)\) function from the critic network given in (23). In the design model, \(U_{a}\) is limited to “0,” which means the success of the reinforcement signal.

$$e_{a} \left( n \right) = V\left( n \right) - U_{a} \left( n \right).$$
(23)

4 Online learning for the proposed RL scheme

In this section, the online learning for the proposed RL scheme is composed of two parts which are described. The first part is the structure learning that aims to obtain the number of rules for the actor (RIT2-TSK-FNN). The other part is the parameter learning that updates the proposed RL scheme parameters based on the LM algorithm with an adaptive learning rate.

4.1 Structure learning

At each instant, the online structure learning creates the fuzzy rules based on the input data. Here, the type-2 fuzzy clustering is used to perform the structure learning with respect to the rule firing strength [50, 51]. The incoming data, \(x_{j} \left( n \right)\), are utilized for creating the first type-2 fuzzy rule. The first Gaussian IT2-FS parameters related to the first rule are designed as:

$$\left[ {m_{j1}^{1} ,m_{j2}^{1} } \right] = \left[ {O_{j}^{(1)} \left( n \right) - \Delta O,O_{j}^{(1)} \left( n \right) + \Delta O} \right],\quad \sigma = \sigma_{\text{const}} ,\quad j = 1, \ldots ,k,$$
(24)

where the parameter \(\Delta O\) is a constant value that represents the range of the initial IT2-FS. The parameter \(\sigma_{\text{const}}\) is a predefined value, which is set as \(\sigma_{\text{const}} = 0.3\). At each instant \(n\), the firing strengths are calculated as given in (7). The mean value of the firing strength \(O_{f}^{i}\) can be computed for each instant as follows:

$$O_{f}^{i} = \frac{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{O}_{i}^{(3)} \left( n \right) + \bar{O}_{i}^{(3)} \left( n \right)}}{2}.$$
(25)

For subsequent input data \(x_{j} \left( n \right)\), the calculation of the number of the rules is obtained using the following formula:

$$\Psi = \mathop {\arg \hbox{max} }\limits_{1 \le i \le M\left( n \right)} O_{f}^{i} ,$$
(26)

where \(M\left( n \right)\) denotes the number of the current rules at instant \(n\). A new rule is generated at \(M\left( {n + 1} \right) = M\left( n \right) + 1\) if \(O_{f}^{\Psi } \le O_{\text{th}}\) (\(O_{\text{th}}\) is a pre-specified threshold). The parameters of the Gaussian IT2-FSs for a new rule are defined as:

$$\left[ {m_{j1}^{M(n) + 1} ,m_{j2}^{M(n) + 1} } \right] = \left[ {O_{j}^{(1)} \left( n \right) - \Delta O,O_{j}^{(1)} \left( n \right) + \Delta O} \right],\quad j = 1, \ldots ,k,$$
(27)

and the spread is computed as:

$$\sigma^{M(n + 1)} = \vartheta \cdot \left| {O_{j} \left( n \right) - \left( {\frac{{m_{j1}^{\Psi } + m_{j2}^{\Psi } }}{2}} \right)} \right|.$$
(28)

When the overlapping parameter, \(\vartheta\), is defined as \(\vartheta = 0.5\), this indicates that the new Gaussian IT2-FS spread is chosen as the half of the Euclidean space from the best matching center. The initial consequent parameters for each new rule are as follows:

$$\begin{aligned} & c_{0}^{1} = c_{0}^{M(n + 1)} = r_{1} ,\quad c_{j}^{1} = c_{j}^{M(n + 1)} = r_{2} , \\ & s_{0}^{1} = s_{0}^{{M\left( {n + 1} \right)}} = r_{3} ,\quad s_{j}^{1} = s_{j}^{{M\left( {n + 1} \right)}} = r_{4} \quad j = 1, \ldots ,k, \\ \end{aligned}$$
(29)

where \(r_{1} ,\,r_{2} ,\,r_{3}\) and \(r_{4}\) are small random values. These parameters are learned online according to the proposed method.

4.2 Parameter learning

The Gauss–Newton (GN) strategy has good convergence characteristics. These characteristics, however, are based on the initial parameters’ values. If these values are not chosen properly, this method may easily diverge. On the other hand, the Gradient descent (GD) algorithm demonstrates an excellent behavior in the vicinity of a minimum point, but this algorithm is restricted by a slow speed of the convergence. The performance of the GD method is not adversely affected by the initial values selection [52]. Accordingly, the parameters of the critic and the actor are updated using the LM algorithm, which contributes a nice compromise between guaranteed convergence of the GD algorithm and the speed of the GN strategy. Therefore, the LM algorithm behaves as the GD algorithm when the immediate solution is quite from the correct one and behaves GN strategy when the immediate solution is close to the correct solution [53, 54].

The update rule for the critic weights and the actor parameters according to the GN strategy has the following formula:

$$\Delta \theta_{g} = - \left[ {\nabla^{2} E_{g} \left( {\theta_{g} } \right)} \right]^{ - 1} \nabla E_{g} \left( {\theta_{g} } \right),$$
(30)

which depends on the performance function, which is defined as:

$$E_{g} \left( {\theta_{g} } \right) = \frac{1}{2}e_{g}^{\rm T} \left( {\theta_{g} } \right)e_{g} \left( {\theta_{g} } \right),$$
(31)

where \(\theta_{g}\) is the weights/parameters vector, the suffix \(g\) denotes a general for the actor and the critic and \(\nabla^{2} E_{g} \left( {\theta_{g} } \right)\) represents the Hessian matrix. The Hessian term can be expressed as:

$$\nabla^{2} E_{g} \left( {\theta_{g} } \right) = B^{\rm T} \left( {\theta_{g} } \right)B\left( {\theta_{g} } \right) + S\left( {\theta_{g} } \right),$$
(32)

where the Jacobin matrix \(B\left( {\theta_{g} } \right)\) contains the first derivatives of the critic and actor errors with respect to their weights and parameters. The term \(S\left( {\theta_{g} } \right)\) contains the second derivatives of the critic and the actor errors with respect to their weights and parameters, and it is assumed that \(S\left( {\theta_{g} } \right)\) has a small value comparing with the product of the Jacobin. Therefore, (32) can be approximated as:

$$\nabla^{2} E_{g} \left( {\theta_{g} } \right) \approx B^{\rm T} \left( {\theta_{g} } \right)B\left( {\theta_{g} } \right).$$
(33)

Thus, the GN algorithm can be rewritten as

$$\Delta \theta_{g} = - \left[ {B^{\rm T} \left( {\theta_{g} } \right)B\left( {\theta_{g} } \right)} \right]^{ - 1} B^{\rm T} \left( {\theta_{g} } \right)e_{g} \left( {\theta_{g} } \right).$$
(34)

One limitation of this algorithm is that the simplified Hessian matrix might be invertible. To overcome this problem, a modified Hessian matrix can be used as:

$$\nabla^{2} E_{g} \left( {\theta_{g} } \right) \approx B^{\rm T} \left( {\theta_{g} } \right)B\left( {\theta_{g} } \right) + \lambda_{g} I,$$
(35)

where \(I\) denotes the identity matrix. The parameter \(\lambda_{g}\) should be chosen such that \(\nabla^{2} E_{g} \left( {\theta_{g} } \right)\) is positive definite and thus can be invertible. This modification in the Hessian matrix is corresponding to the LM algorithm. The LM modification to the GN strategy can be expressed as:

$$\Delta \theta_{g} = - \left[ {B^{\rm T} \left( {\theta_{g} } \right)B\left( {\theta_{g} } \right) + \lambda_{g} I} \right]^{ - 1} B^{\rm T} \left( {\theta_{g} } \right)e_{g} \left( {\theta_{g} } \right).$$
(36)

Here, the parameter \(\lambda_{g}\) guides the algorithm. If it is chosen as a large value, then (36) approximates the GD method, and if it is chosen as a small value, then (36) approximates the GN strategy. If the parameter \(\lambda_{g}\) is adaptively chosen, the LM algorithm can manage between its two extremes: the GD and GN algorithms. Consequently, the LM algorithm can merge the features of the GD and the GN algorithms, while bypassing their limitations.

The parameter \(\lambda_{g}\) is now written as \(\lambda_{g} \left( n \right)\), which is updated online during the implementation of the algorithm to guarantee the stability (confirming that the Hessian matrix is inverted) and makes the LM algorithm have a fast convergence.

The updating equation for the critic weights according to the LM method is given as:

$$\Delta \theta_{c} = - \left[ {B^{\rm T} \left( {\theta_{c} } \right)B\left( {\theta_{c} } \right) + \lambda_{c} \left( n \right)I} \right]^{ - 1} B^{\rm T} \left( {\theta_{c} } \right)e_{c} \left( {\theta_{c} } \right)$$
(37)

where \(\lambda_{c} \left( n \right)\) represents a generalized weights vector, i.e., (\(w_{{c_{mb} }}^{\left( 1 \right)} \left( n \right)\), \(w_{{c_{m} }}^{\left( 2 \right)} \left( n \right)\)), and the derivatives in the Jacobin matrix \(B\left( {\theta_{c} } \right)\) are derived as:

$$\frac{{\partial e_{c} \left( n \right)}}{{\partial w_{{c_{m} }}^{\left( 2 \right)} \left( n \right)}} = \frac{{\partial e_{c} \left( n \right)}}{\partial V\left( n \right)}\frac{\partial V\left( n \right)}{{\partial w_{{c_{m} }}^{\left( 2 \right)} \left( n \right)}} = - \gamma q_{m} \left( n \right),$$
(38)
$$\begin{aligned} \frac{{\partial e_{c} \left( n \right)}}{{\partial w_{{c_{mb} }}^{\left( 1 \right)} \left( n \right)}} & = \frac{{\partial e_{c} \left( n \right)}}{\partial V\left( n \right)}\frac{\partial V\left( n \right)}{{\partial q_{m} \left( n \right)}}\frac{{\partial q_{m} \left( n \right)}}{{\partial {\text{net}}_{m} \left( n \right)}}\frac{{\partial {\text{net}}_{m} \left( n \right)}}{{\partial w_{{c_{mb} }}^{\left( 1 \right)} \left( n \right)}}, \\ & = - \gamma w_{{c_{m} }}^{\left( 2 \right)} \left( n \right)\,\left[ {\frac{1}{2}\left( {1 - q_{m}^{2} \left( n \right)} \right)} \right]z_{b} \left( n \right). \\ \end{aligned}$$
(39)

The updating equation for the actor parameters according to the LM method is given as:

$$\Delta \theta_{a} = - \left[ {B^{\rm T} \left( {\theta_{a} } \right)B\left( {\theta_{a} } \right) + \lambda_{a} \left( n \right)I} \right]^{ - 1} B^{\rm T} \left( {\theta_{a} } \right)e_{a} \left( {\theta_{a} } \right),$$
(40)

where \(\theta_{a}\) represents a generalized actor parameters vector, i.e., (\(c_{j}^{i}\), \(s_{j}^{i}\), \(m_{j1}^{i}\), \(m_{j2}^{i}\), \(\sigma_{j}^{i}\), \(l^{i}\), \(\alpha_{j}\), \(H_{l}\) and \(H_{r}\)), and the derivatives in the Jacobin matrix \(J\left( {\theta_{a} } \right)\) are derived as:

$$\frac{{\partial e_{a} \left( n \right)}}{{\partial \theta_{a} \left( n \right)}} = \frac{{\partial e_{a} \left( n \right)}}{{\partial O^{\left( 6 \right)} \left( n \right)}}\frac{{\partial O^{\left( 6 \right)} \left( n \right)}}{{\partial \theta_{a} \left( n \right)}}.$$
(41)

The term \(\frac{{\partial e_{a} \left( n \right)}}{{\partial O^{\left( 6 \right)} \left( n \right)}}\) is calculated from the critic neural network as:

$$\frac{{\partial e_{a} \left( n \right)}}{{\partial O^{\left( 6 \right)} \left( n \right)}} = \frac{{\partial e_{a} \left( n \right)}}{\partial V\left( n \right)}\frac{\partial V\left( n \right)}{{\partial O^{\left( 6 \right)} \left( n \right)}} = \sum\limits_{m = 1}^{{N_{h} }} {w_{{c_{m} }}^{\left( 2 \right)} \left( n \right)} \left[ {\frac{1}{2}\left( {1 - q_{m}^{2} \left( n \right)} \right)} \right]\mathop w\nolimits_{{c_{m3} }}^{(1)} \left( n \right).$$
(42)

The term \(\frac{{\partial O^{(6)} \left( n \right)}}{{\partial \theta_{a} (n)}}\) is obtained as described in “Appendix A.”

4.3 Learning rate adaptation

The learning parameter \(\lambda_{g}\) in the LM method usually takes a constant value. This learning coefficient determines the dynamics of the analyzed RIT2-TSK-FNN controller and determines the system stability. Therefore, the learning rate \(\lambda_{g}\) (i.e., \(\lambda_{c}\) for the critic and \(\lambda_{a}\) for the actor) makes adaptively during the execution of the algorithm. The adaptation of the learning rate should be depending on the system output. When the error is a small value, the learning rate should take a relatively big value. When the error is a big value, the learning rate should take a smaller value.

The change in the learning rate \(\lambda_{g}\) is associated with the system operation conditions. Hence, the learning rate can be recognized using the fuzzy logic system in which the error value and the change in the error with the scaling factors, \(J_{e}\) and \(J_{\Delta e}\), respectively, are the input signals to the fuzzy logic system, while the \(\lambda_{c} \left( n \right)\) and \(\lambda_{a} \left( n \right)\) are the output with their scaling factors, \(J_{c}\) and \(J_{a}\), respectively, as shown in Fig. 5. The symmetrical triangular input MFs can be used, and for the simplicity of the defuzzification, the singleton method is performed as shown in Fig. 6. Fuzzy rules are described in Table 1, which is characterized the behavior of the learning rates.

Fig. 5
figure 5

Block diagram for updating the learning rates using fuzzy logic

Full size image
Fig. 6
figure 6

a Input MFs, b output MFs

Full size image
Table 1 Rule base
Full size table

For the online learning procedure of the RL scheme, the learning rate \(\lambda_{g} \left( n \right)\) should be chosen to assure the stability of the online updating of the weights/parameters for the critic and the actor, respectively. So, the technique for choosing properly \(\lambda_{g} \left( n \right)\) is developed.

Theorem

The learning rates\(\lambda_{c} \left( n \right)\)for the critic neural network and\(\lambda_{a} \left( n \right)\)for the actor RIT2-TSK-FNN, which are shown in (37) and (40), respectively, have the following constraints to guarantee the stability:

$$\lambda_{c} \left( n \right) \ge \frac{1}{2}\left\| {\frac{{\partial e_{c} \left( n \right)}}{{\partial \theta_{c} \left( n \right)}}} \right\|^{2} ,\quad \lambda_{a} \left( n \right) \ge \frac{1}{2}\left\| {\frac{{\partial e_{a} \left( n \right)}}{{\partial \theta_{a} \left( n \right)}}} \right\|^{2} .$$
(43)

Proof

The theorem proof is given in “Appendix B.”□

Remark 1

The derivatives in (43) are calculated previously, where the derivatives of the critic error with respect to its parameters are discussed in (38) and (39) and the derivatives of the actor error with respect to its parameters are discussed in (41) and (42).

Remark 2

The proposed RIT2-TSK-FNN controller using RL (RIT2-TSK-FNN-RL) is designed for controlling two nonlinear systems to handle the effect of system uncertainties due to the external disturbance and environmental noise.

5 Simulation results

In order to show the improvements in the proposed RIT2-TSK-FNN-RL controller, the simulation results for the RIT2-TSK-FNN controller in which the parameters are derived based on the fuzzy clustering and the LM learning without the RL are implemented for comparison purposes. Two performance indices are used to measure the performance of the proposed RIT2-TSK-FNN-RL controller, which are the integral absolute error (IAE) and the mean absolute error (MAE). These indices are defined as:

$${\text{IAE}} = T\sum\limits_{k = 1}^{{K_{N} }} {\left| {e\left( n \right)} \right|} ,$$
(44)
$${\text{MAE}} = \frac{1}{{k_{N} }}\sum\limits_{k = 1}^{{k_{N} }} {\left| {e\left( n \right)} \right|} ,$$
(45)

where \(k_{N}\) is the number of iterations and \(T\) is the sampling period.

Once the proposed RIT2-TSK-FNN-RL controller is initialized using one rule for the actor element, the initialized parameters of the rule consequence are described as (29) and the Gaussian membership function initialized as (24), it will be plugged into the system and works in the following procedure:

  • Step 1: The actor element receives the measured system states; \(x_{1} \left( n \right) = e\left( n \right),\,x_{2} \left( n \right) = \Delta e\left( n \right)\) and uses it to generate a new rule if the condition \(O_{f}^{\Psi } \le O_{\text{th}}\) is satisfied and initiate the parameters of the new rule as (27)–(29). The actor output is the control signal that is implemented according to (16).

  • Step 2: The critic element receives the measured system states: \(z_{1} \left( n \right) = e\left( {n - 1} \right),\,\)\(z_{2} \left( n \right) = \,e\left( n \right),\,\)\(z_{3} \left( n \right) = \,u\left( n \right)\), and uses it to calculate the output of the critic as \(V\left( n \right)\) as (21).

  • Step 3: The critic element will update its parameters according to (37)–(39) and the learning parameter \(\lambda_{c} \left( n \right)\) according to fuzzy logic given in Table 1.

  • Step 4: The actor element will update its parameters according to (40)–(42) and the learning parameter \(\lambda_{a} \left( n \right)\) according to fuzzy logic given in Table 1.

  • Step 5: Steps (1) to (4) are repeated in each sampling time step until the end of the simulation.

5.1 Case study 1

Consider a nonaffine nonlinear system defined as [56]:

$$x_{1} \left( {n + 1} \right) = m_{1} \left( n \right)\,x_{2} \left( n \right) + m_{2} \left( n \right)\,\,\sin \left( {x_{1} \left( n \right)} \right),$$
(46)
$$x_{2} \left( {n + 1} \right) = m_{3} \left( n \right)\cos \,\left( {x_{2} \left( n \right)} \right)\,\sin \left( {x_{1} \left( n \right)} \right) + m_{4} \left( n \right)\,u\left( n \right) + m_{5} \left( n \right)\,\tanh \left( {u\left( n \right)} \right) + d_{m} (n),$$
(47)
$$y\left( {n + 1} \right) = x_{1} \left( {n + 1} \right),$$
(48)

where the parameters are set as \(m_{1} \left( n \right) = 0.5,\,\)\(m_{2} \left( n \right) = - 0.3,\)\(m_{3} \left( n \right) = - 1,\)\(m_{4} \left( n \right) = 2,\)\(m_{5} \left( n \right) = - 2\) and \(d_{m} \left( n \right) = 0\).

5.1.1 Task 1—effect due to variation of desired output

Figure 7 shows the system response when the desired output changes, which is indicated by black line. The proposed RIT2-TSK-FNN-RL controller has a smaller time for tracking the reference trajectory than the RIT2-TSK-FNN controller due to the critic network and the adaptation based on the LM algorithm with adaptive learning rate that can enforce the actor parameters to converge quickly. The number of the generated rules for both controllers is \(M = 1\). This number of the rules is small due to the recurrent in the input and the rule layers.

Fig. 7
figure 7

Response of the tracking reference signal

Full size image

5.1.2 Task 2—variation of the system parameters

This task is carried out after the system output tracks the reference trajectory. The actual values of the system parameters are changed to \(m_{1} \left( n \right) = 0.7,\)\(m_{2} \left( n \right) = - 0.5,\)\(m_{3} \left( n \right) = 1,\,\)\(m_{4} \left( n \right) = 3\) and \(m_{5} \left( n \right) = - 2.5\) at \(n = 500{\text{th}}\) instant. Then, it changed again to \(m_{1} \left( n \right) = 0.2,\,\)\(m_{2} \left( n \right) = - 0.7,\)\(m_{3} \left( n \right) = - 1.5,\,\)\(m_{4} \left( n \right) = 2.2\) and \(m_{5} \left( n \right) = - 3\) at \(n = 1000{\text{th}}\) instant. These changes in system parameters are used to show the robustness of the controllers. Figure 8 shows that the response of the proposed RIT2-TSK-FNN-RL controller has a smaller settling time than that of the RIT2-TSK-FNN controller at the two changes. The number of the generated rules for both controllers is \(M = 1\).

Fig. 8
figure 8

Response of the system for uncertainty in the system parameters

Full size image

5.1.3 Task 3—disturbance uncertainty

The performance evaluation of the proposed RIT2-TSK-FNN-RL controller is tested by adding the disturbance value \(d_{m} \left( n \right)\) to (47) at \(n = 750{\text{th}}\) instant, which is given as:

$$d_{m} \left( n \right) = - \left( {0.3x_{1}^{3} \left( n \right) + 0.05x_{2}^{4} \left( n \right)} \right)\cos \left( {10nT} \right),$$
(49)

where \(T\) is the sampling period that equals 0.001.

Figure 9 shows that the proposed RIT2-TSK-FNN-RL controller tracks the trajectory after adding the disturbance but the RIT2-TSK-FNN has a large oscillation about the set point. The number of the generated rules for both controllers is \(M = 1\).

Fig. 9
figure 9

Response of the system due to disturbance

Full size image

5.1.4 Task 4—actuator noise

In this task, the performance of the proposed RIT2-TSK-FNN-RL controller is evaluated by adding the noise to the control signal at \(n = 750{\text{th}}\) instant. Figure 10 shows that the proposed RIT2-TSK-FNN-RL controller tracks the trajectory after adding the noise, but the RIT2-TSK-FNN has a large oscillation about the set point. The number of the obtained rules for both controllers is \(M = 1\).

Fig. 10
figure 10

Response of the system due to noise

Full size image

Tables 2 and 3 show the MAE and the IAE, respectively, for the proposed RIT2-TSK-FNN-RL controller, the RIT2-TSK-FNN controller and other controllers, which are published previously such as the FFANN [28,29,30], the ADPACRN [32], the GRHDP [33] and the ATSFRL-LS [35]. The results of the above simulation tasks are repeated using the average of 15 experiments. It is clear that the values of the MAE and IAE for the proposed RIT2-TSK-FNN-RL controller are smaller than those obtained for the RIT2-TSK-FNN, which are not used in the critic network. On the other hand, the values of the performance indices for the proposed controller, which depend on the RFNN and actor–critic learning scheme, are lower than those obtained for other controllers such as FFANN [28,29,30], ADPACRN [32] and GRHDP [33] which depend on the ANN and gradient descent method for the adaptation of the parameters. Also, the proposed controller is better than the ATSFRL-LS [35], which was implemented by fuzzy logic system and Lyapunov criteria for deriving the law of parameter adaptation.

Table 2 Average MAE values of 15 experiments
Full size table
Table 3 Average IAE values of 15 experiments
Full size table

5.2 Case study 2

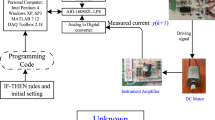
One of the universal elements in the process and chemical industry is the steam-water heat exchanger in which the temperature control is very important task, especially when the process is opened over a broad scale [57, 58]. The steam-water heat exchanger is described in Fig. 11. The two inputs are the input process water flow and the steam flow rate that can be controlled by two pneumatic control values. The steam condenses in the two-pass shell and tube heat exchanger, hence raising the process water temperature. The exchanger has a nonlinear behavior when using a fix steam flow rate [59]. Accordingly, the process input is the input flow rate while the output is the temperature of the process output fluid, which is measured by thermocouple sensor and the steam flow is considered constant. The complex behavior of the steam-water heat exchanger can be represented by

$$y\left( n \right) = a_{1} \left( n \right)y\left( {n - 1} \right) + a_{2} \left( n \right)y\left( {n - 2} \right) + a_{3} \left( n \right)\xi \left( {n - 1} \right) + a_{4} \left( n \right)\xi \left( {n - 2} \right) + 0.005r\,{\text{and}}\,(1),$$
(50)
$$\xi \left( n \right) = u\left( n \right) + a_{5} \left( n \right)u^{2} \left( n \right) + a_{6} \left( n \right)u^{3} \left( n \right) + a_{7} \left( n \right)u^{4} \left( n \right),$$
(51)

where the parameters are set as \(a_{1} \left( n \right) = 1.608,\)\(a_{2} \left( n \right) = - 0.6385,\)\(a_{3} \left( n \right) = - 6.5306\,,\,\)\(a_{4} \left( n \right) = 5.5652,\)\(a_{5} \left( n \right) = - 1.3228,\)\(a_{6} \left( n \right) = 0.7671\) and \(a_{7} \left( n \right) = - 2.1755\,.\)

Fig. 11
figure 11

Heat exchanger

Full size image

The models shown in (50) and (51) are derived using real data from the practical system as described in [57,58,59]. So, these equations are used in this paper, which simulate this system. Furthermore, the control simulation is based on measurement noise.

5.2.1 Task 1—effect due to variation of desired output

Figure 12 shows the heat exchanger process response when the desired trajectory signal is described as a black line. The proposed RIT2-TSK-FNN-RL controller has acceptable set-point tracking, which is realized with a rise time less than that obtained for the RIT2-TSK-FNN controller. The number of the obtained rules for both controllers is \(M = 2\). The recurrent in the rule layers has a major impact for decreasing the number of rules that contribute to the nonlinearities besides the recurrent in the input, which deals with the measurement noise.

Fig. 12
figure 12

Response of the tracking reference signal for heat exchanger process

Full size image

5.2.2 Task 2—process parameters uncertainty

Here, the robustness of the performance using the proposed RIT2-TSK-FNN-RL controller is evaluated under process parameters variations. The system response is shown in Fig. 13, in which the process parameters are changed at instant \(n = 500{\text{th}}\) to \(a_{1} \left( n \right) = 1.64,\,\)\(a_{2} \left( n \right) = - 0.8,\)\(a_{3} \left( k \right) = - 7.4\,,\)\(a_{4} \left( n \right) = 6.4,\)\(a_{5} \left( n \right) = - 1.8,\)\(a_{6} \left( n \right) = 0.47\) and \(a_{7} \left( n \right) = - 1.8\). It is clear that the proposed controller has a smaller settling time than RIT2-TSK-FNN controller. The RIT2-TSK-FNN controller has a large oscillation after applying this uncertainty. The number of the obtained rules for the proposed controller and the RIT2-TSK-FNN controller is \(M = 2\) and \(M = 5\), respectively.

Fig. 13
figure 13

Response of the process under parameters uncertainty

Full size image

5.2.3 Task 3—sensor measurement uncertainty

In this task, the performance evaluation of the proposed RIT2-TSK-FNN-RL controller is tested by adding the sensor measurement uncertainty value \(ds\left( n \right)\) to (50) at \(n = 500{\text{th}}\) instant, which is given as:

$$ds(n) = - 0.1\sin \left( {y\left( n \right) - 0.1y\left( {n - 1} \right)} \right).$$
(52)

Figure 14 shows that the proposed RIT2-TSK-FNN-RL controller tracks the trajectory after adding the sensor measurement uncertainty and it has a stronger anti-interference ability than the RIT2-TSK-FNN controller. The number of the generated rules for both controllers is \(M = 2\).

Fig. 14
figure 14

Response of the process under sensor measurement uncertainty

Full size image

5.2.4 Task 4—actuator failure due to noise

The performance of the proposed RIT2-TSK-FNN-RL controller is evaluated by adding the noise to the control signal at \(n = 500{\text{th}}\) instant. Figure 15 shows that the proposed RIT2-TSK-FNN-RL controller has an actuator noise rejection, which tracks the trajectory after adding the noise. However, the RIT2-TSK-FNN has a large error about the set point after adding the actuator noise. The number of the obtained rules for both controllers is \(M = 2\).

Fig. 15
figure 15

Response of the process under actuator noise uncertainty

Full size image

Tables 4 and 5 show the MAE and the IAE for the proposed RIT2-TSK-FNN-RL controller, the RIT2-TSK-FNN and other controllers that are published previously such as the FFANN [28,29,30], the ADPACRN [32], the GRHDP [33] and the ATSFRL-LS [35], respectively. The results of the above simulation tasks are repeated using the average of 15 experiments. It is clear that the values of the MAE and the IAE for the proposed RIT2-TSK-FNN-RL controller are smaller than those obtained for the RIT2-TSK-FNN, which are not used in the critic network. On the other hand, the values of the performance indices for the proposed controller are lower than those obtained for other controllers such as FFANN [28,29,30], ADPACRN [32], GRHDP [33] and ATSFRL-LS [35].

Table 4 Average MAE values of 15 experiments
Full size table
Table 5 Average IAE values of 15 experiments
Full size table

The proposed controller and other controllers are performed on a PC, which has a processor Intel(R), Core(TM) i5-250 M with CPU @ 2.5GHZ, RAM 4.0 GB, 64-bit operating system and Windows 10. The computation time for all controllers is indicated in Table 6.

Table 6 Computation time of all algorithms
Full size table

Remark 3

Although the proposed AC-IT2-TSK-FNN has a larger computation time than the other controllers, it has a better performance when the controlled system has uncertainties such as environmental noise, external disturbance and parameter uncertainties.

6 Conclusion

In this paper, the online learning for a novel structure of the RIT2-TSK-FNN based on RL scheme is proposed for controlling nonlinear systems. The LM algorithm with adaptive learning rate is developed for updating the parameters of the proposed controller. The stability conditions for the learning rates are achieved using the Lyapunov function. The output of the proposed RL controller forced the system to follow the reference input with one rule, which means that the proposed scheme has small parameters. The rule reduction was due to using the recurrent in the input layer and the firing layer. To evaluate the performance of the proposed controller, it is compared with the results of the RIT2-TSK-FNN controller and other published controllers. The proposed controller is tested using the mathematical nonlinear simulation system and the heat exchanger process with noisy measurement data. The results showed the superiority of the proposed controller to respond to the system uncertainties rather than the other controllers. The main advantages of proposed controller can be summarized as follows: (1) It has fast learning due to using reinforcement actor–critic method. (2) It has ability to handle the system uncertainties and noisy measurement data. (3) The number of the generated rules is small due to the recurrent in the input and the rule layers. (4) The learning rates are changed online according to fuzzy logic during the implementation of the algorithm to assure the stability (assuring that the Hessian matrix can be inverted) and the speed of the convergence. (5) The stability conditions are discussed using Lyapunov criteria. In future work, the authors will use a hierarchical deep RL framework.