Modeling of nonlinear system based on deep learning framework

Abstract

A novel modeling based on deep learning framework which can exactly manifest the characteristics of nonlinear system is proposed in this paper. Specifically, a Deep Reconstruction Model (DRM) is defined integrating with the advantages of the deep learning and Elman neural network (ENN). The parameters of the model are initialized by performing unsupervised pre-training in a layer-wise fashion using restricted Boltzmann machines (RBMs) to provide a faster convergence rate for modeling. ENN can be used to manifest the memory effect of system. To validate the proposed approach, two different nonlinear systems are used for experiments. The first one corresponds to the class-D power amplifier which operates in the ohmic and cutoff regions. According to error of time domain and spectrum, back propagation neural network model improved by RBMs (BP-RBMs) and ENN are compared with different input signals which are the simulated two-tone signal and actual square wave signal. The second system is a permanent magnet synchronous motor servo control system based on fuzzy PID control strategy. In terms of simulated and actual speed curves, BP-RBMs, DRM and ENN models are adopted on comparison, respectively. It is shown by experimental results that the proposed model with fewer parameters and iteration number can reconstruct the nonlinear system accurately and depict the memory effect, the nonlinear distortion and the dynamic performance of system precisely.

1 Introduction

The total nonlinear dynamic systems are defined as those where the model parameters and input (controller outputs) are subject to nonlinear to the output [1]. The modeling of nonlinear system [2] has become an essential part of system analysis because it provides a convenient and efficient method to predict system-level performance without the computational complexity of full system simulation or physical-level analysis, thereby speeding up the analysis process.

Power amplifiers (PAs) which can produce a high power output to drive the load under the condition of a certain distortion rate are increasingly used in a wide range of applications such as audio and communication applications [3]. Class-D power amplifier (CDPA) that works in switching mode is a typical nonlinear system. The fuzzy proportional integral derivative (PID) control strategy for a permanent magnet synchronous motor (PMSM) servo control system is another typical nonlinear system. The motor is controlled by electronic virtual shaft. Meantime, speed and torque of motor are decoupled, and the speed is sent back to the fuzzy PID controller through the encoder [4].

For the modeling of nonlinear system, there are a large amount of approximations and simplifications have to be performed. Unfortunately, they have a negative impact on the desired accuracy. In communication systems, the PAs of the transmitter distort the signal due to the nonlinear characteristic of circuit. In the PMSM control systems based on vector control strategy of the dynamic decoupling mathematical model, control algorithm can affect dynamic response and position accuracy of motor. Numerous studies have been conducted to model for these effects [5]. The known models of nonlinear system with memory effects are mainly based on Volterra series [6] and neural networks (NNs) [7], or their improved forms. However, the models based on Volterra series need a large number of coefficients to complicate their practical implementation. And the models based on NNs are always stuck with the initialized weights, if the initialized weights are not appropriate, the network gets stuck in local minima and leads the training process to a wrong ending, or the vanishing gradient problem is encountered during back propagation in the initial layers and the network becomes infeasible to train.

Deep learning has been successful in solving several engineering problems including speech and video signal processing [8, 9]. This work proposes the modeling based the deep learning framework. The proposed framework learns Deep Reconstruction Model (DRM) which integrated with the characteristics of restricted Boltzmann machines (RBMs) and Elman neural network (ENN). RBMs [10, 11] can be interpreted as neural network models which consist of two types of units called visible neurons and hidden neurons. Thus, RBMs always can be viewed as nonlinear feature detector [12]. Using trained RBMs for initializing the first layer of a multilayer neural network can provide a faster convergence rate for the modeling of nonlinear system. The Elman neural network is a partial recurrent network model first proposed by Elman in 1990. Its back-forward loop employs context layer which is sensitive to the history of input data, so the network can manifest the memory effect of the nonlinear system. In order to evaluate the performance of the proposed model, extensive experiments are done along with comparisons to existing models of nonlinear system. Simulation results have shown that the proposed model could well avoid the local minimum and has a faster convergence rate to reduce iteration number significantly, so further decrease the amount of calculation.

This paper is organized as follows. Section 2 is devoted to describing the theory of DRM. Numerical results and analysis based on simulated data and actual data are given in Sect. 3. The conclusion is shown in Sect. 4.

2 Deep reconstruction model

Deep learning methods aim at learning feature hierarchies with features from the higher levels of the hierarchy formed by the composition of lower level features. They include learning methods for a wide array of deep architectures, including neural networks with hidden layers and graphical models with levels of hidden variables [13]. Unsupervised pre-training works to render learning deep architectures more effective. Unsupervised pre-training acts as a kind of network pre-conditioner, putting the parameter values in the appropriate range for further supervised training and initializes the model to a point in parameter space that somehow renders the optimization process more effective, in the sense of achieving a lower minimum of the empirical cost function.

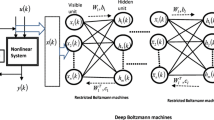
Restricted Boltzmann machines are the very important parts for the deep architecture models and used to initialize a multilayer neural network by performing unsupervised pre-training in a layer-wise fashion. The parameters of a stack of RBMs also correspond to the parameters of a deterministic feed-forward multilayer neural network. Hence, once the stack of RBMs is trained, one can use available parameters to initialize the first layer of a multilayer neural network.

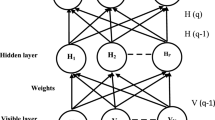
Integrating with the characteristics of RBMs and ENN, a Deep Reconstruction Modeling is proposed, as shown in Fig. 1.

Fig. 1

The architecture of DRM

2.1 Restricted Boltzmann machines

A restricted Boltzmann machine [14] is an energy-based model. It contains a set of visible units $\varvec{v}$ and a sequence of hidden units $\varvec{h}$ as shown in Fig. 2. Our work focus on binary RBMs where the random variables $(\varvec{v},\varvec{h})$ take values from $\{0,1\}$. The definition of the energy function about the state is:

$$\begin{aligned} B(\varvec{v},\varvec{h};\varvec{\theta })=-\sum _i^N \sum _j^L R_{ij} v_i h_j-\sum _i^N a_i v_i-\sum _j^L b_j h_j\nonumber \\ \end{aligned}$$

(1)

where $\varvec{\theta }=\{\varvec{R},\varvec{a},\varvec{b}\}$ are the parameters, $\varvec{a}$ is the vector of biases for visible units, $\varvec{b}$ is the vector of biases for the hidden units, $v_i$ and $h_j$ are the binary state of visible unit i and hidden unit j and $R_{ij}$ represent the weight between visible unit i and hidden unit j. N and L are the number of visible and hidden units. The probability of observable variables $\varvec{v}$ is denoted as

$$\begin{aligned}&p(\varvec{v};\varvec{\theta })=\frac{1}{Z(\varvec{\theta })} \sum _h exp(-B(\varvec{v},\varvec{h};\varvec{\theta })) \end{aligned}$$

(2)

$$\begin{aligned}&Z(\varvec{\theta })=\sum _v \sum _h exp(-B(\varvec{v},\varvec{h};\varvec{\theta })) \end{aligned}$$

(3)

where $Z(\varvec{\theta })$ indicates the partition function.

Fig. 2

A restricted Boltzmann machine with no inner connection in each layer

A restricted Boltzmann machine is an undirected graphical model in which visible variables are connected to stochastic hidden units, and there are no connections among hidden variables or visible variables. The conditional distributions over hidden and visible units are defined as

$$\begin{aligned} p(h_j=1|\varvec{v};\varvec{\theta })= & {} \hbox {sigm}\left( \sum _{i=1}^N R_{ij} v_i+b_j\right) \end{aligned}$$

(4)

$$\begin{aligned} p(v_i=1|\varvec{h};\varvec{\theta })= & {} \hbox {sigm}\left( \sum _{j=1}^L R_{ij} h_j+a_i\right) \end{aligned}$$

(5)

where $\hbox {sigm}(x)=1/(1+exp(-x))$ is the sigmoid activation function. RBMs learning algorithms are based on gradient ascent on the log-likelihood. The often stated gradients for the parameters $\varDelta R_{ij}, \varDelta a_i$ and $\varDelta b_j$ are

$$\begin{aligned}&\varDelta R_{ij}=\frac{\partial \log p(\varvec{v};\varvec{\theta })}{\partial R_{ij}}=[v_i h_j]_{\mathrm{data}}-[v_i h_j]_{\mathrm{model}} \end{aligned}$$

(6)

$$\begin{aligned}&\varDelta a_i=\frac{\partial \log p(\varvec{v};\varvec{\theta })}{\partial a_i}=v_i-\sum _v p(\varvec{v};\varvec{\theta })v_i \end{aligned}$$

(7)

$$\begin{aligned} \varDelta b_j= & {} \frac{\partial \log p(\varvec{v};\varvec{\theta })}{\partial b_j}\nonumber \\= & {} p(h_j=1|\varvec{v};\varvec{\theta })-\sum _v p(\varvec{v};\varvec{\theta })p(h_j=1|\varvec{v};\varvec{\theta })\nonumber \\ \end{aligned}$$

(8)

The reconstruct error is denoted as

$$\begin{aligned} E_{\mathrm{reconst}}=\{[v_i]_{\mathrm{data}}-[v_i]_{\mathrm{model}}\}^\mathrm{T}\{[v_i]_{\mathrm{data}}-[v_i]_{\mathrm{model}}\}\nonumber \\ \end{aligned}$$

(9)

and $R_{ij}, a_i$ and $b_j$ can be represented as

$$\begin{aligned}&R_{ij}(t)=R_{ij}(t-1)+\phi \varDelta R_{ij} \end{aligned}$$

(10)

$$\begin{aligned}&a_i(t)=a_i(t-1)+\phi \varDelta a_i \end{aligned}$$

(11)

$$\begin{aligned}&b_j(t)=b_j(t-1)+\phi \varDelta b_j \end{aligned}$$

(12)

where $\phi$ is the learning rate of RBMs and t is the iteration number.

2.2 Elman neural network

The architecture of ENN can be generally divided into four layers: input layer, hidden layer, context layer and output layer [15]. The input layer has N input nodes. It accepts the input variables and transmits to the hidden layer. The hidden layer has L nodes and contains the transfer function f. The context layer is the feedback loop of hidden layer with a self-loop coefficient $\alpha$ and it has L neural nodes, too. The output of the context layer at pth step is related to the output of the hidden layer at $(p-1)$th step. The output layer has M nodes, and the output $y_m (m=1,2,\ldots ,M)$ is the linear combination of the output of the hidden layer. There are three kinds of weights in the network: $\varvec{W^1}$ is the $L\times M$ dimensional weight matrix from the hidden layer to the output layer. $\varvec{W^2}$ is the $N\times L$ dimensional weight matrix from the input layer to the hidden layer. $\varvec{W^3}$ is the $L\times L$ dimensional weight matrix from the context layer to the hidden layer. The dynamical equations of the ENN model are as follows

$$\begin{aligned}&\varvec{y}(p)=\varvec{W^1}(p)\varvec{H}(p) \end{aligned}$$

(13)

$$\begin{aligned}&\varvec{H}(p)=f[\varvec{W^2}(p)\varvec{u}+\varvec{W^3}(p)\varvec{X_c}(p)] \end{aligned}$$

(14)

$$\begin{aligned}&\varvec{X_c}(p)=\alpha \varvec{H}(p-1) \end{aligned}$$

(15)

where p is the iteration number and f(x) usually represents the sigmoid function. $\alpha$ is the self-loop coefficient of the context layer. By using the gradient decent method, the weight values are adjusted so that the sum of squared error (SSE) is minimized after training cycles. Suppose that the pth iteration output of the network is $\varvec{y}(p)$, the objective performance error function is defined as

$$\begin{aligned} E(p)=\frac{1}{2}[(\varvec{y}_\mathrm{d}-\varvec{y}(p))^\mathrm{T}(\varvec{y}_\mathrm{d}-\varvec{y}(p))] \end{aligned}$$

(16)

where $\varvec{y}_\mathrm{d}$ is the desired output of the model. The partial derivative of error function with respect to the weight parameters is as follows

$$\begin{aligned}&\varDelta W^1_{lm}(p)=-\eta _1\frac{\partial E(p)}{\partial W^1_{lm}(p)}=\eta _1\delta _m^o (p)H_l(p) \end{aligned}$$

(17)

$$\begin{aligned}&\varDelta W^2_{nl}(p)=-\eta _2\frac{\partial E(p)}{\partial W^2_{nl}(p)}=\eta _2\delta _l^h (p)\frac{\partial H_l(p)}{\partial W_{nl}^2 (p)} \end{aligned}$$

(18)

$$\begin{aligned}&\varDelta W^3_{kl}(p)=-\eta _3\frac{\partial E(p)}{\partial W^3_{kl}(p)}=\eta _3\delta _l^h (p)\frac{\partial H_l(p)}{\partial W_{kl}^3 (p)} \end{aligned}$$

(19)

with

$$\begin{aligned}&\delta _m^o(p)=y_{d,m}-y_m(p) \end{aligned}$$

(20)

$$\begin{aligned}&\delta _l^h (p)=\sum _{m=1}^M \delta _m^o (p)W_{lm}^1(p) \end{aligned}$$

(21)

$$\begin{aligned}&\frac{\partial H_l(p)}{\partial W_{nl}^2(p)}=f_l^{'}(.)\left[ u_n+\alpha W_{ll}^3(p)\frac{\partial H_l(p-1)}{\partial W_{nl}^2(p-1)}\right] \end{aligned}$$

(22)

$$\begin{aligned}&\frac{\partial H_l(p)}{\partial W_{kl}^3(p)}=f_l^{'}(.)\left[ \alpha H_k(p-1)+\alpha W_{ll}^3(p)\frac{\partial H_l(p-1)}{\partial W_{kl}^3(p-1)}\right] \nonumber \\ \end{aligned}$$

(23)

where n represents the nth neuron of the input layer $(n=1,2,\ldots ,N)$, l represents the lth neuron of the hidden layer $(l=1,2,\ldots ,L)$, k represents the kth neuron of the context layer $(k=1,2,\ldots ,L)$, m represents the mth neuron of the output layer and $\eta _1, \eta _2 and \eta _3$ represent the learning rate of $\varvec{W^1}, \varvec{W^2}~\mathrm{and} \varvec{W^3}$, respectively. $f_l^{'}$ is the derived function of the transfer function f.

2.3 Training steps of DRM

The overall procedure of DRM algorithm is illustrated as follows

Algorithm: Deep Reconstruction Model

Step 1 Set appropriate SSE threshold value of ENN and reconstruct error threshold value of RBMs. Choose the number of hidden neurons L is the same as RBMs hidden units. Set the maximum iteration number of ENN $N_{\max }$.

Step 2 Prepare the training input and output data then normalize the data.

Step 3 Set the learning rate of RBMs $\phi$. Initialize the RBMs parameter matrix $\varvec{\theta }$ with zero matrix. Train RBMs using normalized input data.

Step 4 According to formulation (6), (7),(8), update the parameters $\varDelta R_{ij}, \varDelta a_i, \varDelta b_j$. Use formulation (10), (11),(12) to calculate $R_{ij}(t), a_i(t), b_j(t)$.

Step 5 According to formulation (9), if the reconstruct error is bigger than the threshold value, return to Step 4, else end the RBMs training process, get the updated weights matrix $\varvec{R}(t)$ and execute step 6.

Step 6 Initialize the ENN weights matrix $\varvec{W^2} (0)$ with $\varvec{R}(t)$ and $\varvec{W^1} (0), \varvec{W^3} (0)$ with zero matrix. Set $\partial H_l (0)/\partial W_{nl}^2 =0, \partial H_l (0)/\partial W_{kl}^3 =0$. The initial value of the context layer is $\varvec{X_c} (0)=\varvec{0}$. Set the self-loop coefficient of the context layer $\alpha$ and the learning rate $\eta _1, \eta _2, \eta _3$.

Step 7 According to formulation (13) (14) (15), calculate the output $\varvec{y}(p)$. Calculate the SSE with $\varvec{y}(p)$ and the training output. If the SSE is bigger than the threshold value, execute Step 8. If the SSE is smaller than the threshold value or the iteration number $p=N_{\max }$, end the training process and execute Step 9.

Step 8 According to formulation (16) (17) (18) (19), train ENN using normalized data to update the weights $\varDelta \varvec{W^1}(p), \varDelta \varvec{W^2}(p), \varDelta \varvec{W^3}(p)$. Then the parameters are updated as: $\varvec{W^1} (p+1) =\varvec{W^1} (p)+\varDelta \varvec{W^1} (p), \varvec{W^2} (p+1)=\varvec{W^2} (p)+\varDelta \varvec{W^2} (p), \varvec{W^3} (p+1)=\varvec{W^3} (p)+\varDelta \varvec{W^3} (p)$. Jump to Step 7.

Step 9 With the weight matrix obtained in Step 7, calculate the final output $\varvec{y}(p)$ of ENN.

Fig. 3

The circuit of half-bridge CDPA

Fig. 4

Error curves of BP with different kinds of initialization

Fig. 5

Error curves of DRM and ENN model versus iteration number

Table 1 The simulation results of the DRM and ENN model

Table 2 The iteration number and running time of the DRM and ENN model

3 Simulation results and analysis

In the sequel, in order to validate the preceding advantages, the proposed model is evaluated with simulated and actual data. The first system is CDPA circuit, according to the description of [16]. The model is also applied for data coming from automation engineering as PMSM servo control system.

Fig. 6

Comparison among three models in time domain. a BP-RBMs model. b ENN model. c DRM

There are some common parameters for all experiments. In RBMs model, the learning rate $\phi$ and the initial parameters $\varvec{\theta }$. Here, we choose $\phi =0.01$ and $\varvec{\theta }=\varvec{0}$. The weight $\varvec{R}(t)$ which is trained after $t=10$ iteration times is used for initialization. In ENN model, the learning rate $\eta _1=\eta _2=\eta _3=0.01$ and the self-loop coefficient of the context layer $\alpha =0.001$.

Table 3 The mean error $\bar{\sigma }$ and maximum transient error $\sigma _{\max }$ of three models in time domain

3.1 Performance of different initialization

In half-bridge CDPA, the simulation data are acquired from the circuit shown in Fig. 3. The pulse width modulation (PWM) signal z is produced by comparing the input signal x with triangular signal of which the frequency is 40 kHz. The logic level of the PWM signal z is $\pm$10 V. The output signal of power amplifier is termed as y. A group of the training data are extracted from 0 to 10 ms by the sampling frequency $f_\mathrm{s}=100$ kHz. The testing data have the same length and sampling frequency with the training data; the difference is the starting time.

To investigate the performance of the RBMs initialization, we study the SSE versus iteration number with different ways of initialization. Back propagation (BP) neural network is used for the experimental model. The number of hidden neurons of BP is 15 and set the maximum iteration number $N_{\max }=30$. Initialize the first layer of BP with different kinds of initialization and set the parameters of other layers with $\varvec{0}$. First, take the advantage of RBMs initialization to design a BP model. A stack of RBMs is trained then use those parameters to initialize. Second, random values are used to initial. Third, set the initial parameters with zero matrix. Normalized two-tone signal is used as the input signal x; 436 Hz and 3 kHz are the input frequencies.

As shown in Fig. 4, to achieve the same error threshold, RBMs initialization needs the fewest iteration number in three kinds of initialization. The SSE error curve of RBMs initialization drops fastest with the increasing iteration number. Random initialization is worse than zero initialization proves that improper initial parameters lead to get a lower convergence rate. After 30 iteration steps, the SSE of zero initialization is $-$6.1612 dB and random initialization is $-$5.8185 dB while the SSE of RBMs initialization is $-$8.3636 dB. Based on the advantage of RBMs initialization, a BP model improved by RBMs (BP-RBMs) is designed.

3.2 Reconstruction error of DRM and ENN model

For the DRM and ENN model, make the number of hidden neurons L increases from 15 to 25 with the interval of 5. The preceding two-tone signal is used as the input signal. All the tests were carried out using MATLAB R2010b on a desktop Intel Pentium(R) Dual-Core E5300 PC with Windows 7 system. After training the DRM and ENN model, the simulation results are shown in Fig. 5 and Table 1.

As shown in Fig. 5, with the increasing iteration number, the error curves of SSE drop rapidly. The larger the number of hidden neurons L is, the faster SSE decreases, and the less iteration number needed to reach the same SSE. With the same hidden neurons, the SSE error curves of DRM decrease faster than ENN model. As listed in Table 1, for example, fixing the number of hidden neurons $L=15$, the SSE of ENN model is $-$5.0046 dB, while DRM is $-$6.6331 dB after 25 iteration number.

To evaluate the convergence rate of DRM and ENN model, the threshold value of SSE is set as 20, 10 and 0 dB, respectively. The hidden neurons $L=15$ are chosen. If the SSE is smaller than the threshold value, end the training process and record the running time. The iteration number and running time are listed in Table 2.

As shown in Table 2, at the beginning of the iteration process, it takes less running time and iteration number for the DRM significantly. With the increasing iteration number, DRM still resumes less running time and iteration steps. It is evident that the convergence rate of DRM is much faster than the ENN model.

Fig. 7

Comparison among three models in frequency domain. a BP-RBMs model. b ENN model. c DRM

Table 4 Spectrum of the circuit and spectrum error of three models

Fig. 8

Square wave signal oscillogram, the upper waveform: input, the lower waveform: output

Fig. 9

Comparison among three models in time domain. a BP-RBMs model. b ENN model. c DRM

3.3 CDPA case

The construction of CDPA is the same as shown in Fig. 3.

3.3.1 Simulation experiment

To validate the effectiveness of the new model, preceding two-tone signal is used to test its modeling accuracy and convergence rate with comparison to the model of BP-RBMs and ENN. Set the number of hidden neurons $L=15$ and the iteration number $N=25$. For the BP-RBMs model, set the learning rate with 1.

The two-tone signal is often used to study the memory effect of the nonlinear system since the intermodulation distortion (IMD) of the signal is easy to measure [17]. Using the preceding two-tone signal as the testing input signal, the time domain simulation results are shown in Fig. 6. The mean error and maximum transient error of the models in time domain are listed in Table 3.

It can be seen in Fig. 6 and Table 3 that DRM is the most accurate model among three models. BP-RBMs, ENN and DRM have stable approximation capability. Under the same conditions, DRM is the most precise model. The final mean transient error of BP-RBMs is 0.0345 and ENN is 0.0150, while DRM is only 0.0087. The spectrum results are shown in Fig. 7.

In Fig. 7a, $f_1=436$ Hz and $f_2=3$ kHz are the input frequencies of the two-tone signal. $f_3=f_2-f_1$ and $f_4=f_1+f_2$ are the second-order IMD (IMD2). $f_5=f_2-2f_1$ and $f_6=f_2+2f_1$ are the third-order IMD (IMD3). The existent of IMD means the system is nonlinear, and the asymmetry of IMD demonstrates the memory effect of the system. The circuit output spectrum and the spectrum error are listed in Table 4.

Fig. 10

Comparison among three models in frequency domain. a BP-RBMs model. b ENN model. c DRM

Table 5 The mean error $\bar{\sigma }$, maximum transient error $\sigma _{\max }$ and SSE of three models in time domain

Table 6 The mean error $\bar{\delta }$ and maximum transient error $\delta _{\max }$ of three models in frequency domain

In Fig. 7 and Table 4, the spectrum error of BP-RBMs, ENN model and DRM are steady; under the same conditions, the spectrum error of BP-RBMs is 0.6711 dB and ENN is 0.2856 dB, while the spectrum error of DRM is only 0.1641 dB. The accuracy of DRM is much higher.

Fig. 11

Control strategy based on electronic virtual shaft

Fig. 12

Comparison among three models in time domain. a BP-RBMs model. b ENN model. c DRM

3.3.2 Actual measurement experiment

In order to test on the performance of the model further, the data which are collected by oscilloscope from actual power amplifier circuit are used. In the circuit, TPS28225 is a high-speed driver for N-channel complimentary driven power MOSFETs with adaptive dead-time control. CSD88537ND is a new type of power tube chip. This dual power MOSFET is designed to serve as a half bridge in low current motor control applications. Our test circuit is mainly composed of the two chips above. Square wave signal is used as the input signal and the amplitude of the signal is from 0 to 4 V. The logic level of the output signal can be amplified to $\pm$20 V, and the frequency of the signal is 1.2 MHz. The sampling frequency $f_\mathrm{s}=100$ MHz. The output oscillogram of the power amplifier from the oscilloscope is shown in Fig. 8.

Set the value of hidden neurons $L=15$ and the iteration number $N=25$ for BP-RBMs, ENN and DRM. Using the normalized data as the testing input, the time domain simulation results are shown in Fig. 9 and their spectrum results are illustrated in Fig. 10. The mean error, maximum transient error and SSE of the models in time domain are listed in Table 5. The spectrum errors are in Table 6.

Table 7 The mean error $\bar{\sigma }$, maximum transient error $\sigma _{\max }$ and SSE of three models in time domain

It can be seen that the models can reconstruct the output data from the input square wave signal with different accuracies. The error of BP-RBMs is much higher evidently. DRM is the more accurate model for analyzing the nonlinearity and memory effect of the nonlinear system in both time domain and frequency domain.

3.4 PMSM servo control system case

By integrating the virtual shaft control idea with the cross coupling control algorithm, an improved control strategy for PMSM servo system is proposed [4]. Controllers about speed and torque are decoupled and can be designed separately. The speed control strategy based on electronic virtual shaft is shown in Fig. 11. The compensation of $\omega _{\mathrm{A}} -\omega _{0}$ is sent back to the fuzzy PID controller, where $\omega _{0}$ is the speed of virtual shaft and $\omega _{\mathrm{A}}$ is the mechanical angular speed of PMSM. Use BP-RBMs, ENN and DRM for comparing, set the number of hidden neurons $L=25$ and iteration number $N=25$.

3.4.1 Simulation experiment

By using the MATLAB toolboxes of power system, a model of PMSM control system is built. The parameters and the initial values of speed compensator are listed in [4]. In the simulation experiment, some disturbances are added to the system; hence, the speed responses of shaft will change. We adopt the speed of virtual shaft on the testing input and the mechanical angular speed of MATLAB on the output. The time domain simulation results are shown in Fig. 12. The mean error, maximum transient error and SSE of the models in time domain are listed in Table 7.

Fig. 13

Comparison among three models in time domain. a BP-RBMs model. b ENN model. c DRM. d Speed deviation

In terms of the performance in time domain, the BP-RBMs, ENN and DRM can simulate the system with low error, but DRM is more accurate.

3.4.2 Actual measurement experiment

In practical engineering, the operating data of motor based on fuzzy PID control strategies are read out from PLC. The speed curves which can reflect system’s dynamics performance are drawn by MATLAB. Take the actual measurement data as the testing input, the time domain simulation results are shown in Fig. 13. The speed mean error, maximum transient error of speed and SSE of the models in time domain are listed in Table 8.

The reconstruction error of three models and the actual speed deviation which is read out from PLC are shown in Fig. 13. During the accelerated starts up process and the decelerated stops process, the speed deviation of model increased accordingly. The speed deviations of the three models are coincident with the actual data. When the crane is running at a constant speed, the mean error of speed deviation of BP-RBMs model is 4.1321E$-$05 r/s and ENN model is 8.4058E$-$06 r/s but that of DRM is 7.2793E$-$06 r/s. DRM can reconstruct the working process of the system, and the accuracy is more precise than that of other models.

Table 8 The mean error of speed $\bar{\sigma }$, maximum transient error of speed $\sigma _{\max }$ and SSE of three models in time domain

4 Conclusion

In this paper, Deep Reconstruction Model is proposed to analyze the characteristics of the nonlinear system. The model is based on ENN whose back-forward loop employs context layer and its parameters are initialized by performing unsupervised pre-training in a layer-wise fashion using RBMs. The DRM solves the problem of improper initial parameters which make the model tend to fall into local minimum and get a lower convergence rate. In CDPA case, according to the simulation results, with the same number of hidden neurons, DRM can more accurately characterize nonlinear system and get a higher convergence rate than BP-RBMs model and ENN model. Through the simulation of actual square wave signal, it can be seen that DRM has a higher reconstruction accuracy in both time and frequency domain. In the modeling of PMSM servo control system, DRM can reconstruct the working process excellently and the performance of using simulated data or actual data are all superior to BP-RBMs model and ENN model.

Based on the discussion above and the comparison of simulation results, it can be concluded that the proposed model is an efficient model and appropriate for nonlinear systems with memory effect, such as the distillation tower in the process of chemical industry, the pH titration, the modeling of retinal imaging process in biological control, the economic and financial field and the ecological control system.